Periodic catastrophes over human evolutionary history are necessary to explain the forager population paradox

Significance

Much of what is known about human life histories is based on studying modern hunter-gatherers experiencing rapid population growth. Yet, if populations are near-stationary over most of their evolutionary history, the positive growth of contemporary foragers is puzzling and potentially unrepresentative. Investigating multiple demographic scenarios in a large sample of human and chimpanzee populations, we find that periodic catastrophes combined with plausible fertility or mortality reductions can reasonably generate zero population growth. Our findings bolster arguments about the role of intergenerational cooperation and cumulative culture in supporting the colonizing potential of human populations once released from catastrophes.

Abstract

The rapid growth of contemporary human foragers and steady decline of chimpanzees represent puzzling population paradoxes, as any species must exhibit near-stationary growth over much of their evolutionary history. We evaluate the conditions favoring zero population growth (ZPG) among 10 small-scale subsistence human populations and five wild chimpanzee groups according to four demographic scenarios: altered mean vital rates (i.e., fertility and mortality), vital rate stochasticity, vital rate covariance, and periodic catastrophes. Among most human populations, changing mean fertility or survivorship alone requires unprecedented alterations. Stochastic variance and covariance would similarly require major adjustment to achieve ZPG in most populations. Crashes could maintain ZPG in slow-growing populations but must be frequent and severe in fast-growing populations—more extreme than observed in the ethnographic record. A combination of vital rate alteration with catastrophes is the most realistic solution to the forager population paradox. ZPG in declining chimpanzees is more readily obtainable through reducing mortality and altering covariance. While some human populations may have hovered near ZPG under harsher conditions (e.g., violence or food shortage), modern Homo sapiens were equipped with the potential to rapidly colonize new habitats and likely experienced population fluctuations and local extinctions over evolutionary history.

Humans exhibit long female postreproductive lifespans, slow juvenile growth with late sexual maturation, adult surplus production coupled with intergenerational resource transfers, and cumulative culture (1–3). Inferences about the selection pressures that helped shape these derived traits depend critically on reliable age profiles of survivorship and fertility among human hunter-gatherers, and among chimpanzees, who act as the closest surrogate for the last common chimpanzee–human ancestor ∼5 to 8 million y ago (4).

Contemporary foragers living under relatively ancestral conditions (i.e., natural fertility, subsisting on wild foods, minimal healthcare access or modern amenities) typically exhibit >1% annual population growth rates (5, 6), while wild chimpanzee populations have been in persistent decline (7). Neither fast population growth in humans nor decline in chimpanzees is sustainable over the long term and thus cannot accurately represent the long-term mean vital rates that would maintain species-typical zero population growth (ZPG) over evolutionary history. Nor are the positive growth rates observed among contemporary horticulturalists and agriculturalists low enough to reflect the slow, steady growth that occurred with the introduction of domestication during the Neolithic demographic transition 7,000 to 12,000 y ago (6, 8). A population of 100 humans under 1% annual growth would reach the current world population of 7.5 billion in under two millennia. Even the ∼0.5% growth rate originally reported for the Dobe !Kung (9) would result in a doubling time of just 139 y, leading a group of 100 to reach 48 billion in four millennia.

The potential for this paradox exists in all species and concerns about population regulation have been widespread in biology (e.g., Malthus, Darwin, Carr-Saunders, and Lack). We present a systematic attempt to resolve this “forager population paradox” (10–13) across populations and explore implications of different demographic scenarios. For example, higher adult mortality in the past would have increased dependency ratios and altered age profiles of food production, resource transfers, and the potential selective advantage of grandparental aid to descendant kin. An evolutionary history of periodic population crashes might shift psychological time preferences, personality, and life history traits even during periods of abundance. Rogers (14) derives the long-term interest rate (analogous to time preference) to be (ln 2)/T_g + r, where T_g is generation time and r is the intrinsic population annual growth rate, amounting to temporal discounting of roughly 2% per year under stationarity (r = 0). However, under regimes of variable population dynamics, time discounting could be steeper. Stochasticity in vital rates could also affect long-term growth rates and temporal preferences (15).

To resolve the paradox, we evaluate the plausibility of four demographic scenarios that reconcile the observed nonzero growth with the expectation that species-typical long-term growth rates must hover near zero. Long-term ZPG can be generated under the following conditions:

• i)Vital rate alteration: Populations are rendered stationary when births equal deaths over time. To attain stationarity, growing (or shrinking) populations must reduce (or increase) fertility or survival, or both. We estimate the changes in observed fertility and/or mortality required to attain stationarity.
• ii)Stochasticity: Environmental stochasticity driving vital rate variability reduces the stochastic population growth rate (15). If populations are near-stationary, then unstructured stochastic noise may be sufficient to ensure long-term persistence. However, if population growth is high enough, stochastic noise may be insufficient to reduce the long-term growth rate to zero. We calculate the degree of unstructured vital rate variability (i.e., “noise”) that would reduce the long-term stochastic population growth rate to zero.
• iii)Vital rate covariance: Vital rates may covary in response to the same environmental drivers, resulting in positive covariance when resource abundance or shortage affects both survival and fertility (16), or negative covariance if fertility and survival respond to environmental drivers differently (17). Negative covariance may also reflect life history trade-offs, as when survival is compromised during or after periods of high fertility (18). Positive covariance reduces population growth but negative covariance can buffer populations against the effects of stochasticity (19, 20). For example, a population of 1,000 alternating 1% growth and decline each year will first grow to 1,010, then decline to 999.9, and after 100 y will be at 995, demonstrating a net decline due to positive covariance. We estimate the covariance required between vital rates at different ages that would yield long-term ZPG.
• iv)Catastrophes: Stochastic environmental shocks could reduce population growth rates by increasing mortality, reducing fertility, or both (11, 21). Growing populations may be periodically “adjusted” by resource limitations, environmental catastrophes (e.g., floods, fires, or famines), or by competition and density-dependent interactions (e.g., overcrowding, violence, or warfare). We estimate the frequency and intensity of environmental shocks on mortality that could produce long-term persistence.

We assess these ZPG-generating scenarios among traditional small-scale societies and chimpanzee populations for which age-specific survivorship and fertility data exist concurrently: five precontact or isolated hunter-gatherers (Agta, Ache, Hadza, Hiwi, and Ju/’hoansi), three horticulturalist-foragers (Gainj, Tsimane, and Yanomamo), one acculturated hunter-gatherer (Northern Territory Aborigines), and one pastoralist (Herero) population. Wild chimpanzee populations are in East Africa (Gombe, Kanyawara, Mahale, and Ngogo) and West Africa (Taï) (SI Appendix, section 2 and Table S1). After generating the four sets of conditions favoring long-term ZPG, we evaluate their plausibility given the existing literature on population dynamics and environment among contemporary, prehistoric, and Paleolithic populations.

Results

Vital Rate Differences, Variability, and Population Growth.

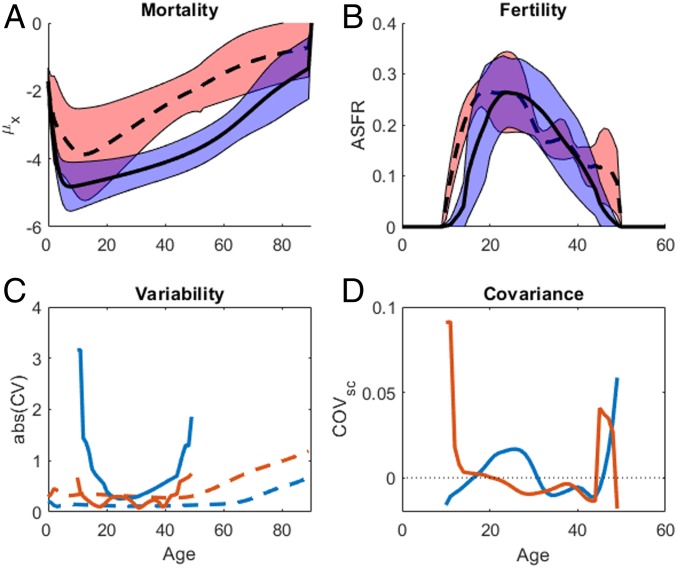
Mean mortality is lower among humans than wild chimpanzees except during infancy (<1 y), but variation among the two species overlaps at early ages (Fig. 1A). Fertility rates among humans and chimpanzees overlap at all ages except where chimpanzees exceed humans during early and late reproduction (Fig. 1B). Chimpanzee total fertility rate (TFR) clusters near the top of the human range, and contrary to prior reports (1) we find that on average TFR is higher among chimpanzees than humans (7.3 vs. 6.0; Table 1 and SI Appendix, Fig. S3B). The average resulting interbirth interval (IBI) among chimpanzees is only 6 mo longer than among hunter-gatherers (4.2 vs. 3.7 y; SI Appendix, Table S3). This average chimpanzee IBI is shorter than those typically reported for chimpanzees (∼5 to 6 y) because our average combines short IBIs where infants died early with long IBIs where infants survived (SI Appendix, section 2). Only Ngogo life expectancy (e₀) surpasses that of any human population (Table 1). Lower adult survivorship among chimpanzees means most females will have fewer births than the synthetic TFR measure which assumes survivorship across reproductive years. Survival varies more across chimpanzees, whereas fertility varies more across humans (Fig. 1C). Scaled covariance among vital rates is about an order of magnitude higher across chimpanzees than across humans (Fig. 1D).

Fig. 1.

Vital rate statistics. Mean ± SD for (A) mortality μ_x and (B) fertility m_x, across 10 small-scale societies (solid lines, blue fill) and five wild chimpanzee populations (dashed lines, red fill). (C) CVs for survival CV(p_x) (dashed lines) and fertility CV(m_x) (solid lines) are calculated across humans (bold lines) and chimpanzees (thin lines). (D) Scaled covariance COV_sc(p_x, m_x) for humans (solid line, left y axis) and chimpanzees (dashed line, right y axis). The horizontal dotted line shows where COV_sc crosses zero.

Table 1.

Baseline demographic characteristics and ZPG conditions

	Baseline				Stationarity				Variance		Covariance
Population		r, %	e0	TFR	Zq	e0q	Zm	TFRm	Zσ	Znσ	ZΣ	ZnΣ
Small-scale human societies
Ache	H	2.64	37.4	8.2	2.23	17.9	0.46	3.8	48	94	16	23
Agta	H	0.50	21.2	6.9	1.12	18.3	0.86	6.0	22	49	8.3	26
Hadza	H	1.38	34.7	6.2	1.51	22.9	0.67	4.2	35	NA	13	NA
Hiwi	H	0.39	27.1	5.5	1.12	24.3	0.90	5.0	18	23	6.5	115
Ju/’hoansi	H	0.17	33.9	4.3	1.06	32.2	0.95	4.1	12	15	4.9	2.3
HG mean LH	*	1.12	29.7	6.2	1.38	21.5	0.73	4.5	32	NA	12	NA
Aborigine	A	1.66	49.7	4.3	2.30	28.2	0.65	2.8	30	NA	11	NA
Gainj	F	0.26	31.1	4.3	1.12	28.7	0.92	3.9	17	32	6.7	6
Tsimane	F	3.81	42.8	9.2	3.23	14.9	0.34	3.1	52	84	18	34
Yanomamo	F	3.30	40.7	7.9	2.49	16.4	0.43	3.4	39	68	14	13
Herero	P	0.47	50.3	3.3	1.34	42.2	0.88	2.9	18	103	6.5	31
Human LH	*	1.65	34.8	6.0	1.70	21.4	0.63	3.8	37	NA	13	NA
Wild chimpanzees
Gombe	E	−1.36	15.5	6.4	0.75	19.8	1.38	8.9	−14	−5.0	−3.3	NA
Kanyawara	E	0.94	20.4	7.9	1.22	16.9	0.79	6.3	12	NA	2.7	NA
Mahale	E	−0.39	14.0	6.9	0.93	15.3	1.10	7.5	−7.5	NA	−1.8	NA
Ngogo	E	3.31	33.6	7.9	2.54	14.9	0.43	3.4	22	NA	5.1	NA
Taï	W	−9.64	8.2	7.5	0.34	20.4	>2	14.9	−35	−1,769	−10	−1.5
Mean LH (r < 0)	*	−3.67	10.6	6.9	0.57	18.5	2.00	13.8	−23	0.0	−5.6	0.0
Mean LH (r > 0)	*	2.15	25.8	7.9	1.69	16.2	0.58	4.6	18	0.0	4.1	0.0
Mean LH (all)	*	−1.29	14.2	7.3	0.80	17.6	1.35	9.9	−14	0	−3.3	0

Population labels: H: hunter-gatherer, A: acculturated hunter-gatherer, F: forager-horticulturalist, P: pastoralist; E: East African, W: West African chimpanzees. Baseline reflects observed rates: population growth (r, percent), life expectancy (e₀, years), total fertility rate (TFR, live births per surviving mother). Stationarity conditions show scaling factor Z^q, Z^m applied to mortality, fertility resulting in associated e₀^q, and TFR^m, respectively. Variance describes the force of stochasticity that would drive ZPG via stochastic noise (as a multiple of cross-population variance) applied to all rates (Z^σ), or relative to the variance estimated across the time-series available for each population n (Z_n^σ). Covariance shows the scalar multiple of cross-population covariance yielding ZPG when applied to all rates (Z^Σ), or based on within-population covariance (Z_n^Σ). Negative covariance scalars (Z^Σ < 0) indicate cases where positive correlations must be reversed to drive ZPG. Composite populations (*) use mean vital rates for H, all humans, chimpanzees (r < 0; r > 0; all). NA indicates no longitudinal data are available.

All human populations in our sample are growing, some very rapidly (e.g., Tsimane r = 3.8%, Yanomamo r = 3.3%). Only two hunter-gatherers hover near stationarity (Hiwi r = 0.4%, Ju/’hoansi r = 0.2%) (Table 1 and SI Appendix, Fig. S3A). On average, human population annual growth rate is 1.6 ± 1.4%. Only two of the five chimpanzee populations are growing (Kanyawara r = 0.94%, Ngogo r = 3.3%). Chimpanzees at Gombe are declining (r = −1.4%), Mahale is near-stationary (r = −0.4%), and the Taï group is crashing (r = −9.6%).

Scenario 1. Population Stationarity.

Large mortality or small fertility scalar multipliers are required to generate ZPG in growing human and chimpanzee populations; the opposite case is necessary to achieve ZPG among declining chimpanzees (Fig. 2). Holding survivorship constant, human fertility scalars Z^m range from 34% of baseline fertility among the Tsimane to 95% among the near-stationary Ju/’hoansi (Fig. 2B and Table 1). Holding fertility constant, human mortality scalars Z^q range from 106% of baseline mortality among the Ju/’hoansi to over three times baseline mortality among the Tsimane (Table 1). On average, the single rate multipliers yielding stationarity in humans (Z^q = 1.75 for mortality, Z^m = 0.71 for fertility) result in 38% reduction in e₀ (34.8 to 21.4 y), or a 37% reduction in TFR (6.0 to 3.8) (Table 1). Because there are larger fitness consequences to vital rate alterations in early life (SI Appendix, Fig. S4), especially before maturity, scalars for child mortality are 40% lower than for adult mortality (2.0 vs. 3.3; SI Appendix, Table S2).

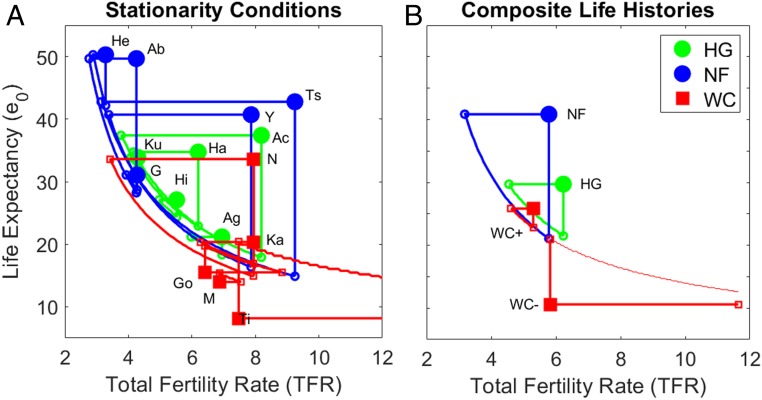
Fig. 2.

Stationarity conditions from vital rate alteration (scenario 1). (A) Conic sections delineate combinations of total fertility (TFR, x axis) and life expectancy (e₀, y axis) reflecting vital rate changes that yield stationarity. Green and blue colors refer to hunter-gatherers and nonforagers, respectively. Red color is for chimpanzees. Large filled symbols indicate baseline conditions, small unfilled symbols indicate single-rate changes yielding stationarity, and connecting curves indicate stationarity isoclines under different vital rate combinations. Note that predictions for Taï fall beyond the axis bounds and indicate unfeasibly high fertility. Ab: Northern Territory Aborigines, Ac: Ache, Ag: Agta, G: Gainj, Ha: Hadza, He: Herero, Hi: Hiwi, K: Ju/’hoansi !Kung, Ts: Tsimane, Y: Yanomamo; Go: Gombe, K: Kanyawara, M: Mahale, N: Ngogo, and Ta: Taï. (B) Same as A but shown for mean rates calculated across all human samples (Hs), hunter-gatherers (HG), declining chimpanzee populations (C−), increasing chimpanzees (C+), and the mean chimpanzee life history.

Among chimpanzees, fertility scalars range from 43% (Ngogo) to over 200% (Taï) and mortality scalars range from 34% (Taï) to 254% (Ngogo) (Fig. 2A and Table 1). The average growing chimpanzee population requires 37% lower e₀ (25.8 y to 16.29 y) or 13% lower TFR (5.3 to 4.6), while average declining chimpanzees require 75% higher e₀ (10.6 to 18.5 y), or almost double the baseline TFR to ∼14 live births.

Despite different stable age structures and minimally overlapping mortality schedules, human and chimpanzee ZPG isoclines fall along the same overall relationship between fertility and longevity (Fig. 2B). If the composite human population (e₀ = 34.8, TFR = 6.0) reduced TFR to 5, stationarity could be achieved at an e₀ of 26. Based on this common isocline, the life expectancy of a stationary population with replacement TFR (2.1) would be over 85 y.

Scenario 2. Stochastic Noise.

ZPG through stochastic noise may not be a reasonable proposition since only two human populations require less than 20 times cross-population variability: Hiwi (Z^σ = 18) and Ju/’hoansi (Z^σ = 12). The remaining human populations require 20 to 50 times the cross-population variability (Table 1). The average hunter-gatherer population requires 32 times the cross-population variability. If only survival or only fertility vary stochastically, the requirements for ZPG are more stringent; for example, Z_p^σ = 15 and Z_m^σ = 23 for the Ju/’hoansi (SI Appendix, Table S3). Restricting variability to vital rates at limited age ranges results in large Z multipliers for most populations (SI Appendix, Table S4). ZPG thresholds for stochastic noise among growing chimpanzee populations are in the human range (e.g., Z^σ = 12 for Kanyawara and 22 for Ngogo). The scalar for mean growing chimpanzee life history is less than half that of the mean human life history (Table 1). For declining chimpanzees to attain ZPG, variance in vital rates would have to be 7 to 35 times higher than that estimated across chimpanzees and reduce to zero (Table 1).

Among growing populations with longitudinal data, short-term variance is lower or comparable to cross-population variability (SI Appendix, Fig. S1 and Table S5). ZPG is attainable with 15 to 23 times the variability estimated over time among the near-stationary Ju/’hoansi and Hiwi and 32 to 103 times among six other human populations (Table 1). To attain ZPG at Gombe through variance elimination, variability would have to be five times published values (22) and over three orders of magnitude higher for Taï (23).

Scenario 3. Vital Rate Covariance.

For covariance to drive ZPG in humans, larger positive covariance than we observe across populations would be required (SI Appendix, section 6): Z^Σ = 4.9 to 6.5 times the cross-population CV for the near-stationary Hiwi and Ju/’hoansi but 8 to 16 for the other human populations and 12 for average hunter-gatherers (Table 1). If only fertility or only survival rates are correlated, covariance requirements are lower for fertility (for the mean human life history $Z_m^{\mathrm{\Sigma }}=15$) than for survival (mean $Z_p^{\mathrm{\Sigma }}=23$), and much less than for same-year fertility–survival covariance ($Z_x^{\mathrm{\Sigma }}=611$) (SI Appendix, Table S3).

Declining chimpanzees could be rescued by reversals in survival covariance (Z^Σ = −5.6) (Table 1). For declining chimpanzees, $Z_m^{\mathrm{\Sigma }}=-21$ and $Z_p^{\mathrm{\Sigma }}=-5.8$, while same-year fertility–survival covariance would have to increase greatly, $Z_x^{\Sigma }=-270$. Among growing chimpanzee populations, ZPG-inducing covariance needs to be roughly four times greater than observed cross-population covariance (Table 1 and SI Appendix, Table S3).

Vital rate covariance based on time-series data is similar in magnitude among Ju/’hoansi, Ache, and Gainj to covariance estimated in the cross-population sample, resulting in similar multipliers to attain ZPG. Among the remaining populations with time-series data, covariance is smaller, and so scaled temporal covariance multipliers would have to be considerably larger than cross-population estimates to attain ZPG (Table 1). For Taï chimpanzees, a sign reversal with 1.5 times the within-population covariance magnitude could halt decline, suggesting that positive covariance may be exacerbating population decline (Table 1).

Scenario 4: Stochastic Catastrophe Regimes.

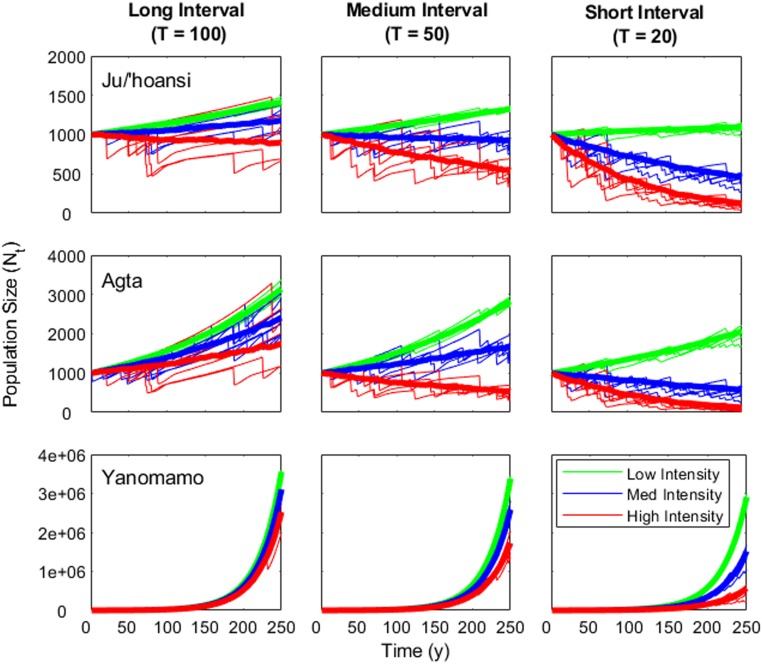
For many populations, the timing between catastrophes needed to generate ZPG under the full range of our modeled intensities is less than 15 y. Among the fastest-growing populations, catastrophes would have to be both intense and frequent (Fig. 3 and Table 2). Even at the maximum intensities where a catastrophe year resulted in a fivefold increase in child mortality and a 20-fold increase in adult mortality $\left(Z_c^q=5,Z_a^q=20\right),$catastrophes would have to occur <10 y apart to drive ZPG in rapid-growth populations. These high intensities would kill all infants and older adults and yet would still be insufficient to drive ZPG unless catastrophes occur frequently enough to be considered part of the background mortality profiles that would change the mean vital rates. For the Hadza, Herero, and other moderately growing populations, catastrophes would need to be under one generation apart (Table 2).

Fig. 3.

Population growth trajectories under stochastic catastrophes. Using three growing small-scale societies (Ju/’hoansi, top row; Agta, middle row; Yanomamo, bottom row) as examples, five random population growth trajectories are shown for each treatment, drawn from stochastic simulations with shock intervals (T) ranging from an average of 20 y to 100 y between shocks. Bold lines show means across 100 runs for each treatment. Line colors distinguish simulations with treatment applying catastrophe regimes of low (green: Z^q_c = 2, Z^q_a = 2), medium (blue: Z^q_c = 3, Z^q_a = 10), or high intensity (red: Z^q_c = 5, Z^q_a = 20).

Table 2.

Frequency and intensity of stochastic catastrophe regimes yielding ZPG

		Mortality scalar
Child (Zqc)		1				2				3				4				5
Adult (Zqa)		1	5	10	20	1	5	10	20	1	5	10	20	1	5	10	20	1	5	10	20
Population		Critical catastrophe interval T, y
Ache	H	*	*	3	5	*	2	3	6	*	2	4	6	2	3	4	7	2	3	5	7
Agta	H	*	7	16	33	7	14	23	40	11	18	27	45	13	20	29	47	15	22	31	49
Hadza	H	*	2	4	7	2	3	5	9	3	5	7	10	5	6	8	12	6	8	9	13
Hiwi	H	*	11	25	52	6	17	31	58	12	23	36	64	17	28	42	70	21	32	46	73
Ju/’hoansi	H	*	13	29	61	12	25	41	73	24	37	53	85	37	50	66	98	49	62	78	110
HG Mean	*	*	3	7	14	2	5	9	16	4	7	10	18	6	9	12	20	7	10	14	21
Aborigine	A	*	*	*	2	*	*	2	3	2	2	2	3	2	3	3	4	3	3	4	5
Gainj	F	*	9	20	43	6	15	27	49	12	21	33	55	18	28	39	62	25	34	45	68
Tsimane	F	*	*	*	2	*	*	2	3	*	*	2	3	*	2	2	3	2	2	2	4
Yanomamo	F	*	*	*	2	*	*	2	3	*	2	2	3	2	2	3	4	2	3	3	5
Herero	P	*	2	4	9	3	4	7	11	5	7	9	14	7	9	12	16	10	12	14	19
Human mean	*	*	2	4	8	1	3	5	9	2	4	6	10	3	5	7	11	4	6	8	12

Cell values are critical time intervals (T, years) between catastrophes for growing populations that would achieve long-term ZPG under shocks of different intensity on child mortality (Z^q_c, top row header) and on adult mortality (Z^q_a, second row header). Asterisks indicate cases where shocks would have to occur annually.

The slowest-growing populations are close enough to stationarity that infrequent mild catastrophes every few generations would be sufficient to drive long-term ZPG (Fig. 3 and Table 2). If catastrophes doubled child mortality but left adult mortality unaffected $\left(Z_c^q=2,Z_a^q=1\right),$ catastrophes would have to occur once every 12 y for the Ju/’hoansi and every 6 y for the Hiwi; if catastrophes increased adult mortality fivefold but left child mortality unaffected, they would have to occur once every 13 and 11 y, respectively. At the maximum intensity we modeled $\left(Z_c^q=5,Z_a^q=20\right),$ catastrophes need only occur every 70 to 110 y.

Discussion

All humans were hunter-gatherers since our species origin some 150 to 250 millennia ago up through the past 15,000 y (24) when Homo sapiens may have numbered between ∼4 and 10 million (13, 25). From 7,000 to 500 B.P., the human population is believed to have grown from ∼4 to 425 million (26), or ∼0.072% per year. However, we find that 20^th-century hunter-gatherers grew on average over an order of magnitude faster, at 1.1%, and other subsistence groups at 1.9%. A larger sample of 55 subsistence populations shows 40 of them growing above 1% per year (5), providing further evidence of this demographic paradox. We now assess plausibility of each of the four demographic scenarios.

Scenario 1.

Achieving ZPG through changes only in mean fertility or mortality is unlikely for humans. Fertility would have to be below four births for most populations, unusually low for natural fertility populations without prevalent sterility. Among 75 small-scale natural fertility subsistence societies, mean ± SD TFR was 5.98 ± 1.40, and only 7 (9%) had TFR < 4; among the 11 hunter-gatherers in that sample (5), two had TFR < 4 (Batak and Efe). However, Efe showed a low TFR of 2.6 due to secondary sterility from sexually transmitted infection (27).

Similarly, mortality alone would have to be increased substantially—by 68% yielding e₀ = 22, on average, and e₀ < 20 for fast-growing populations—similar to observed wild chimpanzees and well below that of any observed human population, past or present (5). Within the range 4 ≤ TFR ≤ 6, mortality adjustments would result in e₀ < 28 (Fig. 2). This combination comes close to bringing ZPG to the Hiwi, Gainj, and Ju/’hoansi but cannot realistically achieve ZPG in more rapidly expanding populations.

Although contemporary populations living traditional lifestyles provide our best estimates of ancestral fertility and mortality, it is possible that 20^th-century postcontact samples are unrepresentative of the past (SI Appendix, section 2). Indeed, the Ache were growing during a pioneering period in Paraguayan history after the Chaco War (11), while the Hadza benefited from colonial pacification of invading herding neighbors (10). Warfare is also likely reduced in most postcontact settings (28). On the other hand, conditions may have been more favorable in the distant past than in the present. First, measles, cholera, and other infectious diseases requiring large reservoir host populations were unlikely to have proliferated among small groups of nomadic hunter-gatherers, except after contact (29). Second, contemporary foragers may inhabit marginal environments unsuitable for cultivation and less favorable than those occupied when the planet was filled only with hunter-gatherers (30). However, the only empirical test of this claim shows no difference between forager and agriculturalist habitat productivity (31).

Despite different population structures, fertility, and survivorship, the vital rate combinations yielding stationarity drive life expectancy and lifetime fertility along a common ZPG isocline for chimpanzees and humans (Fig. 2). This highlights a fundamental similarity in the shape of human and chimpanzee life histories. Among chimpanzees, moderate alterations of mean mortality and fertility rates could result in ZPG, except among the fast-growing Ngogo and the rapidly declining Taï. These two populations may have experienced atypical circumstances: Ngogo experienced high mortality from respiratory infection shortly after the study period (32), and its current age distribution suggests their low mortality profile may reflect a transient phase. Likewise, Taï chimpanzees experienced anthropogenic impacts, including an Ebola epidemic and respiratory infection (23).

Scenario 2.

Stochasticity depresses long-term growth (19). Applying observed between- or within-population variability as a baseline for evaluating the effects of stochasticity revealed that most populations could not plausibly achieve ZPG. Except for the Hiwi and Ju/’hoansi, within-population scaled variability would need to be 6 to 49 times greater than the observed baseline. The longitudinal case studies spanning up to a half century suggest even greater difficulty in obtaining ZPG. We found that within-population variability in age-specific vital rates was roughly similar in magnitude to observed cross-population variability (SI Appendix, section 4), but if past environments were more volatile, or exhibited larger long-term fluctuations, then stochasticity may have been greater in the past. Although foragers show some density-dependent relationships with prey and plants resulting in population oscillations (33, 34), food sharing, trade, diet diversification, and limited storage help buffer vital rate variability among foragers. Major climate change could have surpassed cultural means of buffering (10), but on too long term a time scale to stave off the rapid growth observed in our sample. Other evidence suggests we may not be underestimating vital rate variability: Agrarian 18th-century Sweden showed less variability in mortality rates than across our small-scale societies (SI Appendix, Figs. S1 and S2 and Table S4). Vital rate variability among seven nonhuman wild primate species, including chimpanzees, is also substantially lower than our cross-population human estimates and had minimal effect on population growth; there was also no relationship between annual rainfall variability and variation in any vital rate (22).

Scenario 3.

Vital rate covariance would need to be positive and considerably stronger than our cross-population estimates to achieve ZPG in most human populations. Only among the Agta, Hiwi, Ju/’hoansi, and Herero does covariance within an order of magnitude of that observed across populations yield ZPG. Overall, vital rate covariance in humans and chimpanzees is relatively weak, so vital rates would need to hover close to the ZPG isocline of Fig. 3 for scenario 3 to be viable. Despite the difficulty of obtaining ZPG by altering covariance alone, covariance between survival rates has a greater potential for regulating population growth among chimpanzees, whereas humans respond more to covariance between fertility rates. Consistent with our findings, the abovementioned study of seven wild primate species also found weak covariance in vital rates with only trivial effects on population growth rates (22). Stronger covariance would require tighter tracking of environmental changes (i.e., positive covariance) or stronger trade-offs (i.e., negative covariance).

Scenario 4.

Recent simulations of stochastic hunter-gatherer population dynamics suggest mean time to extinction of a local band is 533 y, with roughly 20 extinction–expansion cycles occurring over a 10,000-y period (35). However, infrequent catastrophes are sufficient to drive long-term ZPG only in the slowest-growing populations at highest intensity (Table 2). Keckler (33) similarly found that a slow-growing population (r = 0.7%) experiencing periodic catastrophes every 50 to 100 y could attain ZPG if 25% of the population perished during each crash. For fast-growing populations, catastrophes would have to be of such high frequency and intensity that they would change underlying mean vital rates.

Potential catastrophes include warfare, food shortages, and infectious disease. Living memory and records covering roughly a century are inconsistent with catastrophes of high magnitude or frequency among the fast-growing Hadza, Ache, and Tsimane (10, 11, 36). Historical records of catastrophes are instead linked to virgin soil epidemics and targeted homicides associated with contact, followed often by recovery and recolonization (37). An analysis of 117 contact-related epidemics in Greater Amazonia revealed that on average roughly 30% of populations perished within a few years of an epidemic, with lower percentages during later epidemics (38). If these virgin soil epidemics represent an extreme, it is instructive that a similar fraction of the population perishes under our most severe catastrophic scenarios (SI Appendix, Table S6). It is also revealing that within a decade following a catastrophe many populations in Greater Amazonia show positive growth, and many are now growing at rapid rates (37).

Famines and epidemics are more commonly documented among agrarian populations over the past five centuries, with variable periodicity (39). Postcolonization recovery in depleted areas may represent a relatively unique period of human history that is overrepresented in anthropological data. Despite the lack of ethnographic evidence of severe catastrophes, it is possible that they were more common in the past, especially warfare (28, 40), which often diminishes upon contact. However, even if common, warfare or raids resulting mainly in the capture of women or children would not affect metapopulation demography and regional population sizes; only death would affect mean vital rates (see ref. 10 for effects of related scenarios on Hadza growth rates). Although infectious diseases typically requiring large reservoir populations (e.g., measles and smallpox) are believed to have been rare among hunter-gatherers, if sexually transmitted diseases were frequent in the past, then fertility rates could have suffered (41). Given upper-range sterility rates of 10 to 40% [for Chlamydia trachomatis and Neisseria gonorrhoeae infections (39)], primary or secondary infertility prevalences required to reduce fertility to ZPG levels would be extreme (10) and mostly unprecedented. We did not model the effect of catastrophes on fertility, but difficult years, such as droughts, can temporarily reduce fertility; Hadza TFR reduced to 3.99 in one excessively dry year (10). Infrequent fertility changes such as this have smaller effects than mortality fluctuations, which reduce fertility contributions at all subsequent ages. Similarly, bonanzas temporarily increasing fertility or survival do not usually have large persistent effects on population growth.

Combining Scenarios.

While we considered these four scenarios in isolation, combinations of vital rate change, stochastic noise, structured covariance, and catastrophes could jointly result in long-term ZPG. Only modest alterations would be needed for populations already near ZPG. However, the age patterning of mortality increase or fertility decline affects how scenario 1 combines with scenarios 2 and 3. Fertility declines or mortality increases at early ages reduce early-life fitness sensitivities, thereby requiring greater—rather than smaller—multipliers of vital rate variance and covariance to generate ZPG (SI Appendix, Fig. S7). When only adult mortality increases, lower variance and covariance could generate ZPG, although the combined effect is small (SI Appendix, Fig. S7B). The most effective and reasonable combination to generate ZPG is catastrophes plus altered mean vital rates (scenarios 1 and 4). For example, if the human mean TFR was reduced by just one birth to five children and mortality increased 20%, catastrophes could be more infrequent (holding intensity constant), or less intense (holding periodicity constant) (Table 3).

Table 3.

Combining vital rate change and catastrophes (scenarios 1 and 4)

	Mortality scalar
Child (Zqc)	1				2				3				4				5
Adult (Zqa)	1	5	10	20	1	5	10	20	1	5	10	20	1	5	10	20	1	5	10	20
Baseline	Critical catastrophe interval T, y
Zq (TFR = 5)
1.15	*	13	30	64	7	21	38	72	15	29	46	80	23	37	54	88	28	41	58	92
1.20	*	17	39	84	10	28	50	94	20	38	60	104	31	48	70	115	36	54	76	120
1.25	*	25	56	119	14	39	71	134	29	54	86	149	44	69	100	163	51	76	108	171
1.30	*	42	95	202	24	67	120	227	49	92	145	251	74	116	169	276	85	128	181	287
1.35	*	126	284	599	73	199	357	673	147	273	431	746	217	343	501	816	251	377	535	851

Critical time intervals (T, years) between catastrophes to attain long-term ZPG for the mean hunter-gatherer population, whereby crashes affect child mortality by a factor Z^q_c and adult mortality by Z^q_a (scenario 4), combined with mean vital rate alterations (scenario 1) where TFR is reduced by one (TFR = 5) and mortality increased by 15 to 35%. Asterisks indicate that ZPG could not be attained at these baseline rates without catastrophes.

Others have also proposed that periodic catastrophes combined with expansions may explain the forager population paradox (10–12, 33) and represent common features of human population dynamics (11, 35, 42). Our systematic approach builds on these earlier efforts, incorporates other ZPG scenarios, and employs the largest sample of foragers, subsistence populations, and chimpanzees to date. One limitation is that our demographic approach is not a bottoms-up population ecological model of density-dependent population growth and does not include environmental carrying capacity. Models invoking carrying capacity and density dependence with delayed feedbacks often show population crashes or oscillations (34, 35, 43), consistent with our findings. Our approach is silent about the mechanisms causing vital rate change but instead focuses on the demographic requirements for ZPG. Local groups could experience fission or fusion, or go extinct; the 10 population samples we model here could, in effect, reflect mean rates across regional metapopulations. Indeed, many of our samples are composed of multiple camps or villages that fluctuate in size. Another limitation is that we did not consider booms or catastrophes affecting fertility rates. Adding bonanzas would make it more difficult for catastrophes to yield ZPG but could help rescue declining chimpanzee populations.

Contemporary human subsistence populations are our best models of population dynamics and life history traits over our recent past. Similarly, wild chimpanzees offer the best glimpse of ancestral hominin life histories (4). If living populations today are postbottleneck survivors without major catastrophes in living memory, then most contemporary samples will be of growing populations, as previously noted (5, 6, 10, 11, 41). A saw-toothed population growth pattern, rather than a sinusoidal oscillation, is also consistent with more time spent in growth than in decline (11).

While slight to moderate perturbations of observed vital rates or their co/variance could result in ZPG in a few populations (e.g., Hiwi, !Kung, and Mahale), there is no reason to believe that these populations better represent past hunter-gatherers or chimpanzees than others in our sample (SI Appendix, section 2). Most human populations in the past likely experienced periodic catastrophes in combination with lower mean fertility and/or survivorship. These counter the human potential for rapid growth, although fast recovery from catastrophes (37) appears to be a key advantage for H. sapiens. Evidence for rapid population growth supports Homo species outcompeting Neandertals ∼35,000 to 55,000 y ago in western Europe (44), although the differential timing of species-typical life history traits, buffering strategies, and the capacity for postcatastrophe resilience remains uncertain. We speculate that a long evolutionary history of stochastic busts might have had other impacts on life history, contributing to the diversification of human preferences and behaviors. Evolved reaction norms potentially shaped by stochastic population dynamics include time and risk preferences, reproductive strategies along early and fast vs. delayed and slow schedules, and costly status investments that help buffer against environmental uncertainty (45).

That the relative absence of severe catastrophes now drives rapid population growth in postcontact subsistence-level humans is consistent with humans’ being a colonizing species (11). The dispersals of Homo throughout Africa and into Europe, Asia, and the Americas over the past 200 millennia (46) is testament to the success of a human life history favoring rapid recovery, and adult survivorship higher than among chimpanzees. A number of derived human adaptations that helped foster this fast growth stem from greater adult survivorship, including buffering via multigenerational food sharing and cooperation, divisions of labor, pedagogy, and cumulative culture.

Materials and Methods

Data Sources.

Age-specific fertility rates (ASFR) and survival probabilities (p_x) exist for 10 small-scale societies in Australia, Africa, and South America (see SI Appendix, Table S1 for population and sample information): Ache (11), Agta (47), Gainj (48), Hadza (10), Herero (49), Hiwi (28), Ju/’hoansi !Kung (9), Northern Territory Aborigines (50), Tsimane (36), and Yanomamo (51) (see SI Appendix, section 2 for ethnographic summaries). Additional methodological information is given in ref. 5. Chimpanzee mortality rates come from Hill et al. (7), with updates from Gombe (52) and Kanyawara (53), and the addition of the large Ngogo group (54). Mortality hazards were smoothed using a Siler competing hazards model, as in ref. 5, using the nonlinear regression procedure (NLIN) in SAS 9.3. Chimpanzee fertility data come from Emery Thompson et al. (55), with the addition of Taï (23). Fertility data were smoothed using a local polynomial regression (loess in R version 3.5.1; span = 0.5).

Vital Rate Statistics and Emergent Life History Traits.

After correcting for sex ratio at birth (assumed to be 1.05 live male births per live female birth), the number of daughters produced, m_x = ASFR/2.05, and survivorship, (p_x), appear in the first subdiagonal of the Leslie population projection matrix A [A = (a_ij); a_1x = m_x; a_x + _1,x = p_x] (see SI Appendix, Table S2 for variable definitions and equations). Single-year ages (x) range from 0 (newborns) to T (maximum lifespan), with fertility beginning at the age at first birth (α) and ending at age ω. The matrix A updates population size (N) across a single time step between times t and t + 1 (N_t+1 = A N_t). The single dominant eigenvalue (λ) of matrix A represents the asymptotic annual population growth rate if all rates remain constant (λ = N_t+1/N_t). From population vital rates we compute survivorship to age x, (l_x), life expectancy at birth, e₀, the intrinsic growth rate r [r = log(λ)], and the TFR of those that survive childbearing years. From the stable age distribution predicted from the right eigenvector w of the matrix A, we compute sensitivities (s_ij = ∂ λ/∂ a_ij) and elasticities [e_ij = s_ij (a_ij/λ)] (SI Appendix, Fig. S4). All calculations were made using MATLAB (version 2015a).

ZPG Scenarios.

We predict necessary conditions for population stationarity (r = 0, λ = 1) or fluctuations resulting in ZPG described by zero long-term stochastic population growth (i.e., $0=\log {\lambda }_S=\underset{t\to \infty }{\lim }\left(1/t\right)\log \left(N_t/N_0\right)$). We consider four scenarios: (i) changes in p_x and/or m_x yielding population stationarity, (ii) stochastic noise in vital rates yielding long-term ZPG, (iii) vital rate covariance yielding long-term ZPG without changes in mean vital rates, and (iv) ZPG conditions for growing populations under stochastic catastrophe regimes (uncorrelated negative shocks).

Scenario 1: Vital Rate Alteration.

Vital rate changes yielding stationarity (λ = 1) are calculated by solving for scaling factors Z that yield Δλ = −λ when applied in a life table response experiment (LTRE; see ref. 56 for details). LTREs estimate contributions to population-level differences in λ made by differences in vital rates using the formula $\Delta \lambda \approx {\displaystyle \sum s_{ij}\Delta a_{ij}}$, where s_ij are the sensitivities of the population growth rate to changes in vital rate a_ij (SI Appendix, Fig. S4). The difference $\Delta a_{ij}=a_{sj}-a_{ij}^{\mathrm{\ast }}$ is calculated between the vital rates of the target and reference population containing $a_{ij}^{\mathrm{\ast }}$ that would yield stationarity. We use LTREs to predict the asymptotic population growth rate λ as a function of mean vital rates (Δa_ij) in the target population. We identify combinations of fertility (m_x) and mortality (q_x = 1 − p_x) that would yield stationarity. For each population we compute the scaling factor Z^m, which is the ratio of fertility at stationarity to the baseline m_x assuming proportional change at every age (m_x* = Z^m m_x). We also vary annual mortality rates q_x, either scaling all mortality by Z^q (q_x* = Z^q q_x) or by scaling child (age < α) mortality by Z^c (q_x<α* = Z^c q_x) and adult mortality by Z^a (q_x≥α* = Z^a q_x).

We examine results for mortality scalars (Z^q, Z^c, Z^a) up to four times baseline rates, which result in the death of all newborns in some populations or all old individuals. We allow fertility to increase up to twice baseline rates (Z^m = 2), which would result in TFR over 6 in every population and over 15 in some. For each adjustment, we calculate the resultant lifetime fertility (TFR*) and life expectancy (e₀*) from vital rates (m_x*, p_x*) yielding stationarity.

Scenario 2: Stochastic Noise.

We use cross-population variability in vital rates as a proxy for potential within-group fluctuations experienced over time. We then estimate the multiplier Z^σ of cross-population variation [CV(a_ij)] that would drive ZPG if it occurred over time within each growing population. We compare our predictions to the variability observed using time-series data from four populations: Agta comparisons include “forager,” “transitional,” and “peasant” periods (47), Gainj includes five surveys during the 1970s (48), Tsimane includes five periods spanning 1950 to 1999 (36), and Yanomamo includes “Xilixana,” “Linkage,” and “Brazilian” periods (51). Although these time series are relatively short, they give some indication of short-term variability in vital rates. Four additional populations (Ache, Hiwi, Ju/’hoansi !Kung, and Herero) have two time point observations. For Gombe chimpanzees, variance is reported by ref. 22, and we calculate variance across three survey periods at Taï (23). Because uncorrelated stochastic noise can only decrease the population growth rate (19), scenario 2 results for declining populations must be interpreted differently: A negative Z^σ indicates the amount of variability that would be required over time within those populations to attain ZPG by subsequently reducing variance to zero.

To compute the scaling factor Z^σ, we use the small-noise approximation (19) of the stochastic growth rate set at ZPG (λ_S = 0) assuming no significant covariance (ρ_ij≠kl = 0 for all ij, kl). The small noise approximation thus depends only on the variance $\left({\sigma }_{ij}^2\right)$ and elasticities (e_ij) of vital rates (a_ij), $\log {\lambda }_S=0\approx r-\frac{1}{2}{\displaystyle \sum _{ij,kl}{e}_{ij}^{2}C{V}_{ij}^2}$. We insert the scaling factor Z^σ into the sum and solve for Z^σ (SI Appendix, section 3.1). We also calculate the scaling factors that would drive ZPG when applied only to rates of mortality $\left(Z_q^{\sigma }\right)$ or fertility $\left(Z_m^{\sigma }\right)$. For populations with longitudinal data, we estimate the required multiple $\left(Z_n^{\sigma }\right)$ of the variability estimated across time within each of those populations.

Scenario 3: Vital Rate Covariance.

Following the approach of scenario 2, we use cross-population covariance of vital rates as a proxy for potential covariance among vital rates over time within a population. We calculate covariance of m_x and p_x across the life cycle. We scale covariance by mean vital rates (a_ij), making it comparable to the CV.

Again we apply the covariance estimated across human or chimpanzee populations using the small noise approximation, $\left(\text{log}{\lambda }_s\approx r-\frac{1}{2}{\displaystyle \sum _{ij,kl}{e}_{ij}{e}_{kl}C{V}_{ij}C{V}_{kl}{\rho }_{ij,kl}}\right)$, where vital rate correlations are now assumed to be nonzero and equal to those estimated across populations. We solve for Z^Σ that yields zero long-term growth when applied to the CVs calculated across vital rates (SI Appendix, section 3.2). Because positive covariance decreases but negative covariance increases the stochastic population growth rate relative to deterministic estimates (20), we compute $Z^{\mathrm{\Sigma }}$ separately for increasing and declining chimpanzee populations. Here, a negative multiplier reverses the sign of correlation. We also compute scaling factors that would produce critical covariance sufficient to drive ZPG when applied to only covariance between: fertility rates $\left(Z_m^{\mathrm{\Sigma }}\right)$, mortality rates $\left(Z_q^{\mathrm{\Sigma }}\right)$, or fertility–mortality covariance at each age $x\left(Z_x^{\mathrm{\Sigma }}\right)$. For populations with time-series data, we calculate the required multiple $\left(Z_n^{\mathrm{\Sigma }}\right)$ of the covariance estimated across time within those populations.

Scenario 4: Catastrophic Shocks.

To estimate the potential for catastrophes to drive long-term ZPG in growing populations, we vary the frequency of catastrophes and the intensity of their impact on mortality. Following previous applications in stochastic disturbance-driven demography (57), we construct a block matrix array concatenating annual probabilities f of catastrophes acting with intensities Z^q_c on child mortality and Z^q_a on adult mortality. The expected time interval between shocks (mean period T_s) is the inverse of the frequency (T_s = 1/f) assuming an equal annual probability. Each element in the resulting stochastic disturbance matrix contains the product of two factors: (i) probability of being in either baseline or catastrophic state and (ii) age-specific vital rates during a baseline or catastrophe year. We consider population growth rates and ZPG isoclines under different combinations of frequency (f) and intensities (Z^q_c and Z^q_a).