Measuring the activation energy barrier for the nucleation of single nanosized vapor bubbles

Significance

While it is generally believed that bubble nucleation process is highly heterogeneous and stochastic, little is known on the nucleation rate and activation energy barrier of single nanosized bubble due to the lack of suitable techniques. We developed an optical apparatus consisting of optical tweezers (for bubble generation) and surface plasmon resonance microscopy (for measurement) to demonstrate the capability to quantify these important kinetic and thermodynamic properties of the nucleation of single nanobubbles. We mapped the distribution of local nucleation rate and local roughness on a flat substrate with a spatial resolution of 100 nm. The results show a previously unseen dependence of the nucleation activation barrier on the surface chemistry.

Abstract

Heterogeneous bubble nucleation is one of the most fundamental interfacial processes that has received broad interest from diverse fields of physics and chemistry. While most studies focused on large microbubbles, here we employed a surface plasmon resonance microscopy to measure the nucleation rate constant and activation energy barrier of single nanosized embryo vapor bubbles upon heating a flat gold film with a focused laser beam. Image analysis allowed for simultaneously determining the local temperature and local nucleation rate constant from the same batch of optical images. By analyzing the dependence of nucleation rate constant on temperature, we were able to calculate the local activation energy barrier within a submicrometer spot. Scanning the substrate further led to a nucleation rate map with a spatial resolution of 100 nm, which revealed no correlation with the local roughness. These results indicate that facet structure and surface chemistry, rather than geometrical roughness, regulated the activation energy barrier for heterogeneous nucleation of embryo nanobubbles.

Bubble nucleation plays critical roles in diverse fields covering boiling heat transfer (1–4), biomedical ultrasound imaging (5–7), micromotors (8, 9), and gas-generating chemical reactions (10–19). Although it was generally recognized that bubble nucleation was a highly stochastic and heterogeneous process (20, 21), such knowledge was often extracted from macroscopic observations and the microscopic understanding remained poor. For example, it was often vaguely suggested that microsized cracks and impurities were active sites for the generation of bubbles. However, it would be very difficult (if not impossible) to believe that so many molecules happened to simultaneously nucleate at the same time and in the same location to form such a large new phase. Studies have shown that the big bubbles were grown from much smaller embryo bubbles with a size at nanometer scale. Therefore, it is more suitable to consider such macroscopic-level features (cracks, impurities, etc.) as the sites for the coalescence and stabilization of large bubbles, rather than the sites for the nucleation of embryo nanobubbles.

To clarify the nanoscopic-level structural basis of nanobubble nucleation, it is highly desirable to develop a capability for monitoring the stochastic nucleation of nanosized bubbles with significantly improved spatial and temporal resolutions (22). Recently, the utilization of localized surface plasmon resonance effect for water evaporation has initiated a new wave on plasmonic heating with significant implications for solar energy harvesting and sterilization (23–26). Plasmonic heating has also become a powerful manner to induce the vapor bubbles because of the superior spatial and temporal controllability of light. Lohse and coworkers recently studied the generation of plasmonic bubbles by using an extremely fast camera that can record at a temporal resolution of ∼100 ns (27). Upon heating by applying a continuous-wave laser onto a surface deposited with gold nanoparticles, their results revealed counterintuitively rich bubble dynamics consisting of multiple successive periods. Explosive boiling of single-vapor nanobubble was investigated by coupled optical and acoustic methods, which also revealed complicated dynamics at a timescale between nanoseconds and microseconds (28, 29). Despite the superior temporal resolution, these studies lacked sufficient spatial resolution to monitor single nanobubbles. Among many important but unexplored microscopic and even nanoscopic aspects regarding the heterogeneous bubble generation, the local nucleation rate (not the bubble growth rate) as well as the activation energy barrier at a submicrometer position is one of the most interesting but elusive questions.

Optical microscopy is an appropriate choice for monitoring the nucleation of nanobubbles by providing balanced spatial and temporal resolutions. Several kinds of advanced optical microscopy with significantly improved spatial resolution and sensitivity have been recently introduced to achieve this goal. For instance, fluorescent dyes have been adopted to stain nanobubbles due to the accumulation of dyes in bubble–liquid interface, allowing for monitoring the generation and dissolution dynamics of single nanobubbles under fluorescence microscopes (11, 16, 30–32). To avoid the adoption of fluorescent dyes, the generation of H₂ nanobubble was found to enhance the plasmonic scattering of single Ag/Pd nanocatalysts (12). This method was recently utilized to map the chemical activity of nanocatalyst by analyzing the location of each individual nanobubble (13). A wide-field surface plasmon resonance microscopy (SPRM) that is capable of visualizing individual nanobubbles without labeling has been recently developed by others and us (10, 33–36). SPRM does not require the labeling of nanobubble because it measures the dielectric constant of nanobubble which is inherently much lower than that of the surrounding solution. The plasmonic enhancement ensured the superior sensitivity of SPRM to detect individual nanobubble as small as 40 nm (10), providing the opportunity to image the early stage of embryo nanobubbles. In addition, the temporal resolution of SPRM can go as fast as microsecond because it records the reflected light.

In the present work, we employed a submicrometer laser spot to locally heat a coverslip coated by a thin film of gold, resulting in the formation of individual vapor nanobubbles at the desired location and moment. It was found that the nucleation induction time between turning on the heating laser and the nanobubble formation is highly stochastic in hundreds of heating and cooling cycles, from which the local nucleation rate can be calculated according to the classical nucleation theory. The dependence of SPRM signals on the refractive index of water further allowed for quantitatively measuring the local temperature at the nucleation site. By doing so, both local temperature and local nucleation rate can be simultaneously determined from the same batch of optical images, enabling the determinations on the activation energy barrier for the nucleation of single nanobubbles.

Results and Discussion

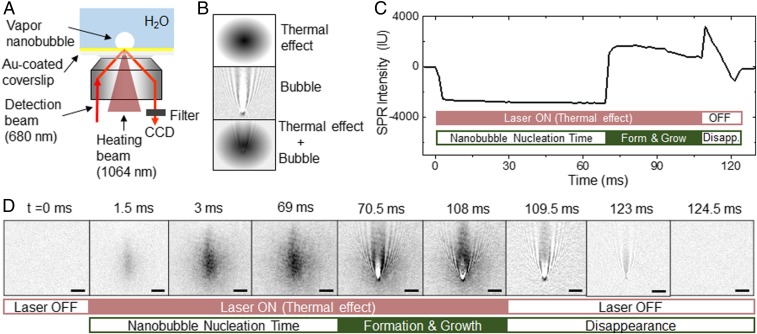
A home-built apparatus was developed to perform the present study by incorporating an optical tweezers system (for local heating) in an SPRM (for wide-field optical imaging). The schematic illustration is shown in Fig. 1A and the detailed optical configuration is provided in SI Appendix, Fig. S1. The detailed principle, apparatus, and features of SPRM can be found in previous publications (10, 33–36). Briefly, a coverslip coated by a 50-nm-thick gold film was placed on an inverted microscope equipped with an oil-immersed objective. A chamber containing pure water was placed on top of the gold film. A low-power 680-nm red beam (detection beam, operating power density = 2.5 mW·mm⁻²) was collimated to illuminate the gold-coated coverslip with a field of view around 200 μm. When the incident angle of detection beam matches the resonant angle at the gold–water interface, such Kretschmann configuration excites the collective oscillation of electrons in the gold film, which is also known as surface plasmon polaritons (SPPs) propagating at the interface. Existence of nanosized vapor bubble disturbed the SPPs and appeared as a wave-like pattern in SPRM images (37, 38).

Fig. 1.

(A) Schematic illustration of the apparatus for producing and monitoring single vapor nanobubbles. A near-infrared laser is focused onto a gold-film–coated glass coverslip to induce local boiling of water, resulting in nanosized vapor bubbles. (B) The increased local temperature reduces the refractive index of surrounding medium before the formation of vapor nanobubbles, accompanying with a dark shadow in SPRM image (thermal effect). Sudden nucleation of single nanobubble disturbed SPPs, resulting in a wave-like pattern (bubble). (C) SPRM intensity curve and (D) the corresponding time-lapsed SPRM images of a representative nanobubble event, consisting of the prenucleation, formation, growth, and disappearance stages (Scale bar: 5 μm).

An optical tweezers system is incorporated in the SPRM to focus a 25.92-mW near-infrared beam (λ = 1064 nm) onto the gold film (spot size 0.87 μm). The intensive power density of 4.4 × 10⁷ mW·mm⁻² immediately increased the local temperature of gold film. Rapid thermal diffusion also heated up the water and reduced the refractive index surrounding the heating spot. This effect can be visualized by SPRM because of the sensitive dependence of local reflectivity on the distribution of refractive index (it will be discussed later) (39). When the local temperature was higher than the boiling point of water, a nanosized vapor bubble was generated at the heating point. To minimize the lateral drift of the sample stage, a piezostage-based drift-correction system was built in the microscope according to a previous report (40), resulting in a lateral drift smaller than 5 nm in 2 h (see Materials and Methods and SI Appendix, Fig. S2 for details).

SPRM was capable of differentiating the thermal diffusion process below the boiling point and the generation of vapor nanobubble at the boiling point, because the thermal diffusion led to a Gaussian-like round pattern (Fig. 1B, Top) and the nanobubble resulted in a wave-like parabolic pattern in SPRM images (Fig. 1B, Middle). In a typical experiment, gentle detection beam was always illuminating on the gold film and SPRM images were continuously recorded at a temporal resolution of 1.5 ms (Fig. 1 C and D). At a certain moment (t = 0 ms), the heating beam was turned on and a decreased reflectivity was immediately observed in the next frame (t = 1.5 ms), which reached equilibrium rapidly (before t = 3 ms) and remained for tens of milliseconds (until t = 69 ms). The appearance of a dark shadow indicated the reduced refractive index of water surrounding the heating spot as a result of the thermal diffusion. At 70.5 ms, a wave-like pattern suddenly appeared in the SPRM image, indicating the formation of a nanosized bubble at the heating point. According to previous theoretical and experimental studies, this wave-like pattern represented the point-spread function of SPRM (37). In other words, any nanoobject, as long as its size is smaller than the diffraction limit (∼300 nm), will appear as the wave-like pattern in SPRM image. And in turn, the appearance of this pattern indicated the formation of a single nanobubble. After the generation of nanobubble, it gradually grew as indicated by the increased image contrast together with the broadening of wave-like pattern in SPRM images until the heating laser was turned off at 108 ms. The dark shadow disappeared within one frame after the withdrawal of heating laser (t = 109.5 ms). It was expected because it took almost the same time to reach the thermal equilibrium. However, the collapse of vapor nanobubble took a relatively longer time (15 ms in this particular case), depending on the size of nanobubble at the moment of heating beam withdrawal. Movie S1, containing all 150 snapshots in a recording time of 225 ms, is provided for comprehensive illustrations. According to these results, it is clear that the dark shadow before the appearance of nanobubble (0–69 ms) represents the pure contribution of thermal diffusion, and the wave-like pattern after the recovery of thermal equilibrium (109.5–124.5 ms) reveals the pure contribution of nanobubble. Combined effects lead to the superimposition of both dark shadow and wave-like pattern (70.5–108 ms). Note that the optical center of dark shadow is several micrometers above the heating point due to the propagation of SPPs (upward herein).

Several technical features of SPRM make it suitable for studying the local boiling of water. First, because SPRM detects the reflected light, the sufficient photon flux allows for reaching a temporal resolution determined by the frame rate of camera. When recording the early stage of bubble formation with a camera running at 100,000 frames per second, the appearance of a nanobubble took place within 1 frame (<10 μs, SI Appendix, Fig. S3). These results are consistent with a previous study that the nucleation occurred at nanosecond to microsecond timescales (27). Second, our previous study has concluded that the SPRM was capable for detecting nanobubbles as small as 40 nm (10), which was consistent with the reported sensitivity for inorganic nanoparticles (34–36). The superior sensitivity was experimentally validated by simultaneously recording the time-lapsed SPRM images and bright-field images for the same individual nanobubble with a dual-camera configuration (SI Appendix, Fig. S4 and Movie S3). SPRM not only exhibited much higher image contrast, it was also able to identify the appearance of nanobubbles several milliseconds earlier. Both the improved sensitivity and image contrast are critical for the accurate determinations of the nucleation time.

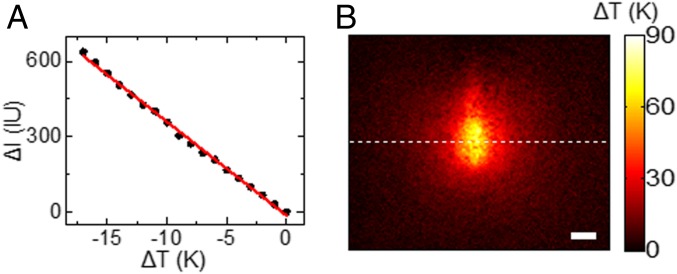
The local temperature at heating point can be calculated from SPRM images because of the quantitative dependence of local reflectivity on local temperature (39). When adding hot water in the sample chamber and letting it cool down to the room temperature, one can simultaneously record the SPR intensity and the bulk temperature by using SPRM and a thermocouple, respectively (SI Appendix, Fig. S5). It was found that a temperature increase of 10 K would reduce the SPR intensity by 374 intensity units (IU, Fig. 2A). This value is consistent with the theoretical value of −39.1 IU/K that is built on three conversions: (i) thermal expansion coefficient of water converting temperature increase to refractive index drop (ΔT→Δn), (ii) dependence of SPR angle on the refractive index of medium (Δn→Δθ_SPR), and (iii) sensitivity factor of the particular gold film (Δθ_SPR→ΔI). Detailed calibration and discussion are provided in SI Appendix, Figs. S6 and S7. With the help of this conversion factor, we were able to convert the SPRM image just before the generation of nanobubble (t = 69 ms) to the map of local temperature as shown in Fig. 2B. It was found that the central region of the heating spot reached a temperature increase by 82.5 K. The spatial distribution of local temperature and temporal dynamics of reaching thermal equilibrium were also consistent with the thermal diffusion theory (SI Appendix, Fig. S8) (41), indicating the validity of the optical-to-thermal conversion.

Fig. 2.

(A) SPR intensity linearly increases with the decreasing bulk temperature of water during cooling. (B) The map of local temperature is converted from SPRM image shown in Fig. 1D (t = 69 ms). (Scale bar: 5 μm).

As shown in Fig. 2B, the local temperature at the heating spot was determined to be 380.5 K, which just exceeded the boiling point of water. It was thus believed that the nanobubble was water vapor bubble rather than air bubble from dissolved air. The chemical identity was also supported by additional experimental results. First, the generation of such nanobubble was not affected when using degassed water to replace the normal air-saturated water (SI Appendix, Fig. S9). Second, a sigmoidal shape with a very narrow transition was observed in the dependence of successful rate of bubble generation on local temperature (SI Appendix, Fig. S10). If the nanobubble was an air bubble due to the decrease in gas solubility at high temperature, one should expect a more or less linear relationship.

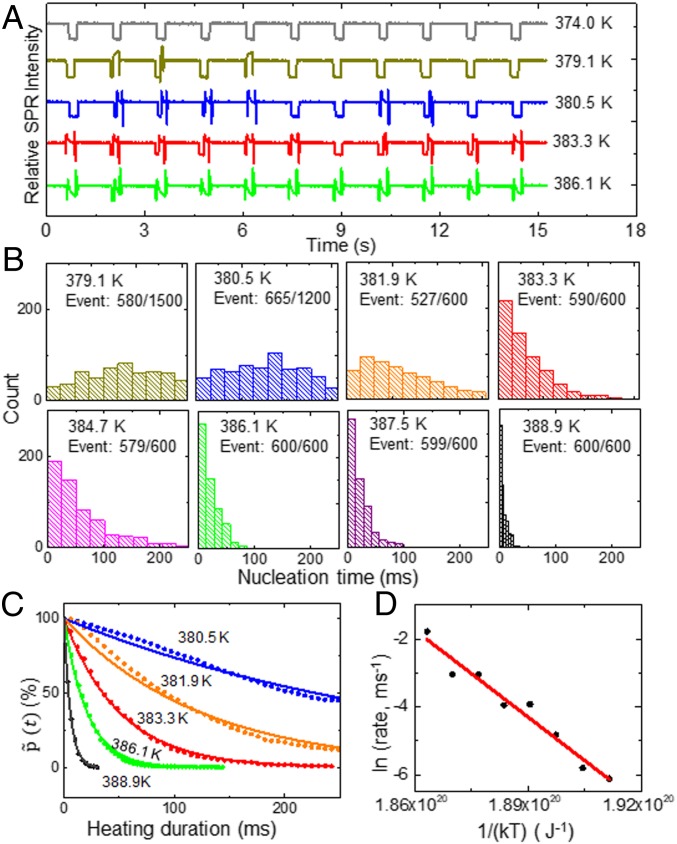
The nucleation time required to generate a single vapor nanobubble was found to be highly stochastic in hundreds of bubble generation and collapse cycles. The nucleation time here is defined as the time length between turning on the heating laser and the appearance of wave-like pattern, i.e., the nanobubble, in each cycle. The period of each cycle was 1,350 ms, consisting of 250-ms heating stage (laser on) and 1,100-ms recovery stage (laser off). A relatively longer recovery stage was required to ensure that all of the vapor nanobubbles completely collapsed before the next cycle. When plotting the representative SPR intensity curves in 10 consecutive cycles under different heating powers in Fig. 3A, a dependence of nucleation time on the local temperature is illustrated. Under lower heating power (374.0 K, gray curve), regular decrease and recovery of SPR intensity was observed in all cycles, indicating pure thermal effect and the absence of bubbles. However, when increasing the power of heating laser to reach an equilibrium temperature above the boiling point, we began to detect the stochastic generation of nanobubbles as indicated by the disturbed SPR intensity (for instance, the second cycle in dark-yellow curve). The appearance of a bright wave-like pattern in the center led to a rapid increase in the SPR intensity and followed by periodic fluctuations due to the growth of nanobubble (Fig. 1C). This feature is a sign of nanobubbles. Movie S2 illustrates the stochastic generation of nanobubbles. Computer codes were written to automatically identify the appearance of each nanobubble and to determine the nucleation time in each cycle (SI Appendix, Fig. S11).

Fig. 3.

(A) Representative SPR intensity curves under different laser powers (local temperatures). (B) Histograms of nucleation time distribution at 379.1, 380.5, 381.9, 383.3, 384.7, 386.1, 387.5, and 388.9 K, respectively. The fractions given in the histograms indicate the percentage of successful bubble events at each temperature. (C) Fitting the probability as a function of time reveals the temperature-dependent nucleation rate. (D) Logarithm of the nucleation rate linearly decreases with 1/(kT), allowing for determining the activation energy barrier E_a from the Arrhenius equation.

The histograms of nucleation time under eight different heating powers are displayed in Fig. 3B. At relatively lower temperature, nucleation times were evenly distributed from 10 to 250 ms. With the increase of heating power from 23.8 to 28.5 mW, not only the overall successful percentage increased from 0 to 100% (SI Appendix, Fig. S10), the distribution of nucleation time evolved from uniform distribution to a typical Poisson distribution, suggesting the increased possibility for heterogeneous nucleation at higher temperature.

According to the classical nucleation theory, one was able to calculate the nucleation rate constant by analyzing the probability distribution of events that do not generate bubbles, $\stackrel{\sim }{P}\left(t\right)$ (i.e., the fraction without bubbles), as a function of the corresponding heating duration time, t. This theory has been validated at macroscopic level by observing the nucleation of crystals in supercooled liquid droplets (42) and in nanoscale by recording the disturbed electron transfer at a nanoelectrode due to nanobubbles (17–19). In the present work, we examined its validity for understanding the generation of nanosized vapor bubbles under local heating conditions. The probability distribution $\stackrel{\sim }{P}\left(t\right)$ of cycles without bubbles as a function of heating duration time t is provided in Fig. 3C. Detailed conversion process can be found in SI Appendix, section 1.5. An exponential decay was observed as predicted by the classical nucleation theory, in which the exponential constant represents the first-order nucleation rate constant with a unit of ms⁻¹ (42). The linear dependence of logarithm of rate constant on 1/(kT) is further shown in Fig. 3D. The values in Fig. 3D are total results from three measurements (SI Appendix, Fig. S12). It was clear that the increase of temperature indeed enhanced the nucleation rate constant in an exponential dependence. Therefore, the local activation energy barrier for a single nanobubble can be obtained from the Arrhenius equation:

$$\ln \left(\text{rate}\right)=\ln \left(A\right)-\frac{E_a}{kT},$$ [1]

where k is Boltzmann’s constant. The activation energy (E_a) can thus be directly determined to be 8.5 × 10⁻¹⁹ J from the slope of ln(rate) as a function of 1/(kT) (Fig. 3D). This number is roughly one order of magnitude higher than the activation energy required for electrochemically generating a sub-10-nm H₂ bubble as demonstrated by White and coworkers (17). However, the mechanisms for bubble generation and the sizes of nanobubbles are different between the two cases.

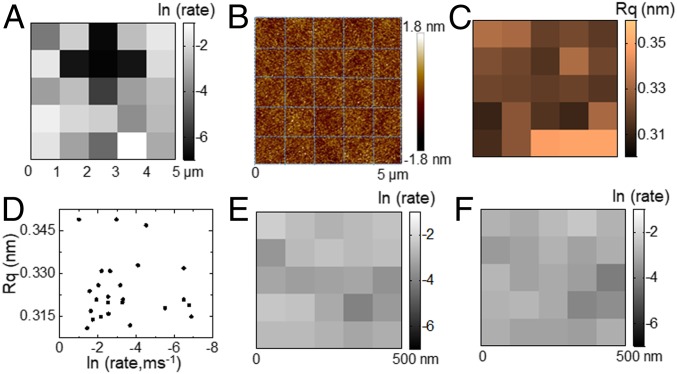
While it is generally accepted that the bubble nucleation is spatially heterogeneous, the spatial correlation between adjacent nucleation active sites, i.e., the effective size of a nucleation active site, is largely unexplored. By taking advantage of the superior spatial controllability of heating beam, a map of nucleation rate can be created by two-dimensionally scanning the sample stage with a step length of 1 μm. A representative map of nucleation rate constant in a 5 × 5-μm² region is displayed in Fig. 4A under logarithm scale to better present the features. Detailed probability distributions $\stackrel{\sim }{P}\left(t\right)$ of all 25 locations are provided in SI Appendix, Fig. S13. The nucleation rate is rather heterogeneous over a flat gold substrate. The maximal rate constant (0.36 ms⁻¹ at [5, 4]) is over 300 times higher than the minimal value (1.0 × 10⁻³ ms⁻¹ at [2, 3]) even though they are just several micrometers apart from each other. At the same time, the high-resolution atomic force microscope (AFM) image of the very same 5 × 5-μm² region is provided in Fig. 4B. The local root-mean-square roughness (Rq) of each 1-μm² segment was found to exhibit no correlation with the local nucleation rate (Fig. 4 C and D). Although macroscopic observations usually indicated that surface roughness was one of the most critical factors for producing and stabilizing large bubbles, other factors, such as facet orientations and surface chemistry, are more important barriers for the nucleation of embryo nanobubbles.

Fig. 4.

(A) Map of the logarithm of bubble nucleation rate constant, ln (rate, ms⁻¹), in a 5 × 5-μm² area with a step size of 1 μm. (B) AFM image of the very same 5 × 5-μm² area after SPRM experiments. The blue lines divide the area into 25 segments. (C) Map of the Rq of each segment. (D) No correlation is observed between the rate constant, ln (rate), and the Rq in 25 segments. (E and F) Map of ln (rate) in a 500 × 500-nm² region with a step length of 100 nm in two consecutive scans to demonstrate the repeatability of mapping.

Despite the illumination spot size of ∼1 μm, superlocalization of 400 nanobubbles revealed a much narrower distribution of the nucleation site in a range of 80 × 500 nm² (SI Appendix, Fig. S14). The superlocalization fitting of the wave-like SPRM patterns followed a previous method (38). The localization accuracy along the x direction was 6× better than that along the y direction because of the parabolic tails along the propagation direction (y) of SPPs. These results were consistent with the nonuniform spatial distribution of beam intensity. The center always exhibits higher power density and thus higher temperature to facilitate the nucleation. However, because the maximal temperature in the center of the beam was calculated from the temperature distribution in a large range of 20–30 μm according to the thermal diffusion theory (SI Appendix, Fig. S8), the quantification of the center temperature should be still valid. Because the effective nucleation region has a diameter of ∼80 nm, a step length of 100 nm was further adopted to scan over a region of 500 × 500 nm², revealing a significantly refined map of nucleation rate as shown in Fig. 4E. It was found that the pixel-to-pixel variation was smaller when the step length was shorter. It suggested that the nucleation activity tended to be more consistent at a spatial scale of ∼100 nm. To examine the reproducibility, the very same 500 × 500-nm² region was mapped again (Fig. 4F). The similarity between these two successive scans further indicated the validity of nucleation rate measurements.

To demonstrate how surface chemistry affected the nucleation rate, we measured the nucleation rates of the very same location by altering its oxidation states with in situ electrochemical oxidation and reduction. When applying an appropriate positive potential to the gold substrate, it was partially oxidized to change the surface chemistry, which significantly reduced the nucleation rate by 53% (SI Appendix, Fig. S15). The subsequent reduction led to the recovery of nucleation rate. These results provided direct evidence to indicate the roles of surface chemistry on regulating the nucleation rate.

Conclusion

In summary, we have proposed an SPRM approach to map the bubble nucleation rate at solid–liquid interface with ∼100 nm spatial resolution. This technique exhibits several strengths on studying the microscopic and even nanoscopic boiling when comparing with existing macroscopic techniques. First of all, in addition to reporting the local nucleation rate, it allowed for simultaneous measurement on the local temperature, which was one of the most critical parameters in bubble nucleation. In conventional studies on boiling processes, a video camera was employed to monitor the generation of bubbles at a microscopic location. A thermometer was placed at a different position in the bulk that could be far apart from the bubble location. The present work provided the capability for using the same microscope to correlate the temperature with boiling behavior at the very same submicrometer location. Second, the present work also achieved a good balance among spatial resolution, sensitivity, and temporal resolution by monitoring individual sub-100-nm nanobubble at a submicrometer location with a temporal resolution of 1.5 ms. The temporal resolution can be further improved to 10-μs level by employing ultrahigh-speed camera. The adoption of superlocalization strategy allowed for mapping the distribution of nucleation site in a region of 80 nm. Third, this work is also an attempt to map the heterogeneous distribution of nucleation rate. On the flat gold substrate, our results suggested that facet structure and surface chemistry, rather than geometrical roughness, might regulate the activation energy barrier for the heterogeneous nucleation of embryo nanobubbles. Relevant efforts are anticipated to move an essential step toward the eventual clarification of many open questions behind the heterogeneous bubble nucleation and boiling phenomenon.

Materials and Methods

Optical Microscope Setup.

SPRM was built on an inverted total internal reflection fluorescence microscope equipped with two decks (TIRFM, Nikon Ti-U). The light source used for SPRM imaging was a superluminescent diode (λ = 680 nm, Qphotonics Inc). The reflective light is collected by the same objective (60×, N.A. = 1.49) to produce SPRM images in a charge-coupled device camera (PIKE F-032B, Allied Vision Technology). The microscope was also equipped with a green LED (λ = 530 nm, M850L2, Thorlabs) for bright-field imaging from the top. The optical tweezers system (Aresis, Tweez 250si) was introduced to focus a continuous-wave near-infrared laser beam onto the gold film through the same objective. A fast camera (MEMRECAM GX-8F) was introduced to run at a speed of 100,000 frames per second. A polydimethylsiloxane chamber (Sarstedt) placed on top of the gold-film–coated coverslip served as the sample chamber. Deionized water filtered by 50-nm membrane filters twice was used throughout the work. This study was performed in a clean room with a controlled room temperature of 25 °C.

To minimize the lateral drift of the sample stage, a drift-correction system was built in the microscope according to a previous report (40). Briefly, a dichroic mirror was placed in front of the camera, so that the SPRM images (λ = 680 nm) and the bright-field images (λ = 530 nm) were simultaneously collected by two independent but synchronized cameras (TwinCam, Cairn Research). The red channel (SPRM) was used for measuring the temperature and for visualizing the nanobubbles. The green channel (bright field) was used to detect the lateral drift with an accuracy close to 2 nm by using image correlation analysis. The detected drift values were transferred to a piezostage (P-527.2CD, Physik Instrument PI) to compensate the drift in real time, resulting in a lateral drift smaller than 5 nm in 2 h (SI Appendix, Fig. S2).

Conversion from SPRM Intensity to Temperature (ΔI → ΔT).

The principle of using SPR intensity to calculate the local temperature relied on the dependence of SPR angle on the refractive index of water, which is a function of temperature. Hence we can calculate the temperature change of the water from the experimental measured SPR intensity change using the following equation:

$$\mathrm{\Delta }T=\frac{1}{\frac{\partial I}{\partial \theta }.\frac{\partial \theta }{\partial n}.\frac{\partial n}{\partial T}}.\mathrm{\Delta }I.$$ [2]

If we define the conversion factor β = (∂θ/∂n) · (∂n/∂T) · (∂I/∂θ), then Eq. 2 is simplified as

$$\mathrm{\Delta }\text{T}=\frac{1}{\beta }.\mathrm{\Delta }I.$$ [3]

Using the parameters calculated from SI Appendix, Figs. S6 and S7, we have β = −39.1 IU·K-1, which allows us to determine local temperature increase relative to room temperature from the captured SPRM images.

Determinations on the Nucleation Rate.

The periodic on and off time of the heating laser beam was controlled by the program of Tweez 250si. The linear change of the heating laser power was achieved by linear alteration of the trap strength of the preselected optical trap.

The histograms of nucleation time under eight different heating powers shown in Fig. 3B were converted into the probability distribution of events that do not produce bubbles, $\stackrel{\sim }{P}\left(t\right)$, as a function of corresponding heating duration time, t. We first assigned the nucleation time into equal time interval and then calculated the probability distribution:

$$\stackrel{\sim }{P}\left(t\right)=\frac{N\left(\text{total}\right)-N\left(t\right)}{N\left(\text{total}\right)}\times 100\%,$$ [4]

where t is the heating duration time, N (t) is the number of heating events that have nucleation time smaller than t, and N (total) is the number of total heating events. Therefore, N (total) − N (t) represents the number of heating events that do not produce bubbles even if the heating duration reaches t. After obtaining the probability distribution versus duration time, an exponential decay equation was introduced as follows:

$$\stackrel{\sim }{P}\left(t\right)=\text{exp}\left(-kt\right).$$ [5]