Flame-formed carbon nanoparticles exhibit quantum dot behaviors

Significance

Flame-formed carbon nanoparticles are observed to exhibit quantum confinement behaviors. We demonstrate that the size dependence of photoemission ionization energy in air and optical band gap of flame-generated carbon particles can be well explained by available quantum confinement theory. Carbon nanoparticles comprising mainly polycyclic aromatic hydrocarbons are widespread in nature. The results have important consequences in problems ranging from interpreting the infrared emission spectra of carbon dusts in the interstellar media, to evaluating the climate effects of atmospheric fine carbon particles, measuring soot nucleation and growth rates in flames, and developing applications of carbon nanoparticles in photovoltaic and electrochemical devices.

Abstract

We examine the quantum confinement in the photoemission ionization energy in air and optical band gap of carbon nanoparticles (CNPs). Premixed, stretched-stabilized ethylene flames are used to generate the CNPs reproducibly over the range of 4–23 nm in volume median diameter. The results reveal that flame-formed CNPs behave like an indirect band gap material, and that the existence of the optical band gap is attributed to the highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) gap in the polycyclic aromatic hydrocarbons comprising the CNPs. Both the ionization energy and optical band gap are found to follow closely the quantum confinement effect. The optical band gaps, measured both in situ and ex situ on the CNPs prepared in several additional flames, are consistent with the theory and the baseline data of CNPs from stretched-stabilized ethylene flames, thus indicating the observed effect to be general and that the particle size is the single most important factor governing the variation of the band gap of the CNPs studied. Cyclic voltammetry measurements and density functional theory calculations provide additional support for the quantum dot behavior observed.

Nanosized carbon grains composed of disordered polycyclic aromatic hydrocarbons (PAHs) are one of the most abundant forms of carbon material in nature (1). As a less-celebrated allotrope of carbon in comparison with fullerenes, nanotubes, and graphene, carbon nanoparticle (CNP) has its share of importance in a wide range of physical phenomena. Studies of interstellar emission spectra suggest that PAH dust grains or CNPs are ubiquitous in the interstellar media (2–5); and they are considered as the tracer of the star formation process (3, 6). CNPs are formed in flames during incomplete combustion. They are part of the soot-formation process. Mature soot or atmospheric black carbon particles often contain both elemental and organic carbon, the relative amounts of which vary by source (7). Soot impacts the global and region climate systems (8, 9) because of its light-absorbing properties (10, 11) and also as cloud condensation nuclei (12). CNPs 10–20 nm in size or fine carbon particles are themselves abundant in diesel exhausts (13). Their light-absorption properties and impact on climate forcing remain poorly characterized (14). As a material, however, CNPs have found their applications in photovoltaic and electrochemical devices, including perovskite solar cells in which flame CNPs act as a hole transfer medium (15).

In contrast to the notion that soot, young or mature with respect to its growth in flames, is a broadband light absorber, recent studies have shown that CNPs several nanometers in size have well-defined optical band gaps or band edges (16–18). The band gap arises from the energy gap between the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) of the constituent PAHs (18, 19). While previous studies (16–18) explored the variation of the optical band gap with respect to the compositional and/or structural changes, here we show that flame-formed CNPs exhibit size dependences in their photoemission ionization energy, optical band gap, and electrochemical ionization potential that are consistent with the behaviors of a quantum dot. We demonstrate that the observed behaviors can be treated by the existing quantum confinement theory. We carried out density functional theory (DFT) calculations for selected PAH clusters to shed light on the nature of the band gap and its quantum confinement effect.

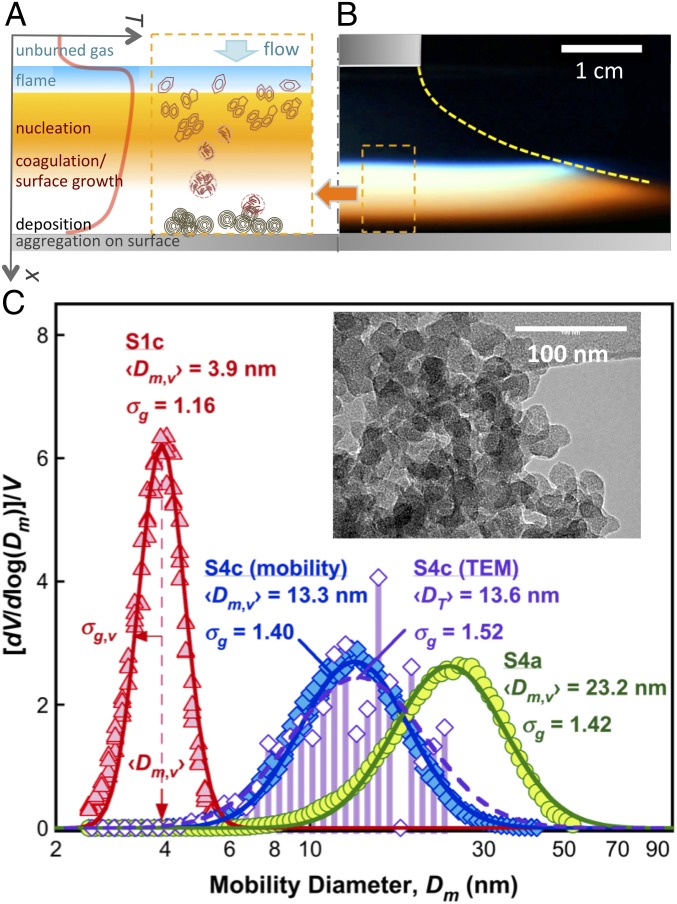
CNPs are prepared in five series of stretch-stabilized C₂H₄/O₂/N₂ flames (20) designated hereafter as the S1–S5 series. Each series comprises three flames (labeled as a–c), making a total of 15 baseline CNP samples covering the volume median diameter of the primary particles from 4 to 23 nm (SI Appendix, section S1). In a stretch-stabilized flame, a premixed unburned mixture is issued from an aerodynamic nozzle, forming a radially diverging flow that impinges against a water-cooled surface (20). As depicted in Fig. 1 A and B, the flame is quasi–one-dimensional; and the temperature gradient between the flat flame and cold surface is large (∼10⁴ K/cm). This produces a thermophoretic force on the growing particles, forcing them to be deposited on the chilled surface. The thus-prepared particles have narrow size distributions owing to the similarity of flow trajectories. The residence time of the particles from nucleation and growth to surface deposition and quenching is several milliseconds only, thus preventing them from reaching the size and maturity of soot particles found in typical combustion emissions. Varying the mixture composition and flow velocity enables the tuning of the particle growth time and rate, and hence the particle size. The compositions of similar flame CNPs have been well studied although not fully resolved due to their complexity (1). Studies using photoionization and thermal desorption aerosol mass spectrometry and Fourier-transform infrared spectroscopy show that the CNPs are composed of PAHs centered around 300 amu (e.g., coronene) (21, 22), some of which are functionalized by varying amounts of aliphatics and their oxygenates. Because of their relatively young ages in flame growth and processing, the CNPs resemble closer what is conventionally classified as organic carbon than black carbon.

Fig. 1.

CNP preparation method and typical volume size distributions. (A) Schematic showing CNP preparation processes. (B) Image of the premixed stagnation flame. (C) Normalized mobility volume distributions of three samples (filled symbols), covering the CNP sizes studied, from the smallest (S1c), medium (S4c), to the largest (S4a). Solid lines are lognormal representations of the data. (Inset) Typical TEM image for sample S4c. The corresponding TEM primary particle size distribution is presented as a histogram and the open symbols. The size parameters (median diameter $\langle D_{m,v}\rangle$ and geometric SD σ_g,v) are provided for comparison. The mobility and TEM volume distributions both assume sphericity, which is appropriate for the primary particles shown here (SI Appendix, section S2).

We measure the CNP size distribution function in gas extracted through a pinhole orifice on a circular probe imbedded in the stagnation surface plate by a mobility sizer (20, 23). Fig. 1C shows the normalized volume distributions of three representative CNP samples, covering the range of particle sizes studied. Similar size distributions are provided for all CNP samples studied in SI Appendix, section S2. The volume distributions are lognormal. Here we use the volume median particle diameter (〈D_m,v〉) and its geometric SD (σ_g,v) as the relevant size parameters, because the properties of interest, e.g., absorption, are all related to particle volume and not to particle number. In Fig. 1C (Inset) we show a transmission electron microscopy (TEM) image of sample S4c collected on the stagnation surface. The TEM primary particle size distribution is in close agreement with the mobility size distribution, indicating that the mobility size closely represents the primary particle size of the CNPs. To show the generality of the confinement effect, CNPs from several other flames are also prepared and analyzed (SI Appendix, section S1), as will be discussed later.

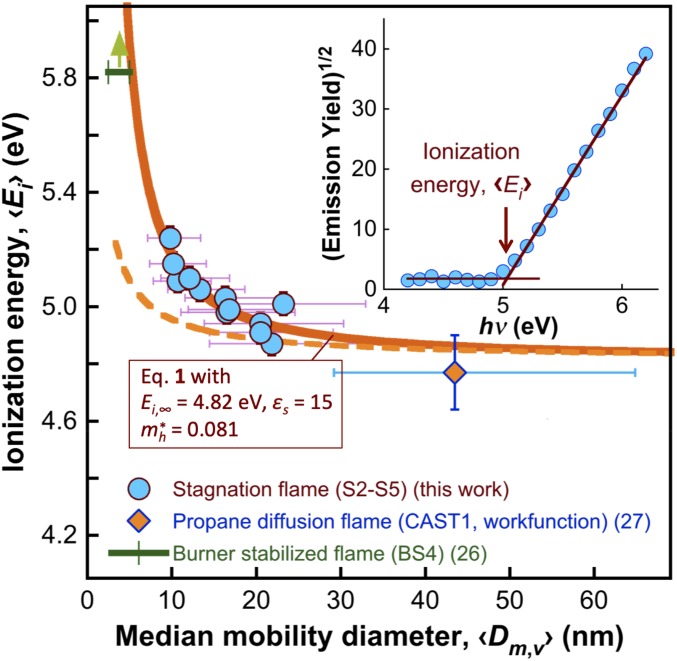
Ionization energy 〈E_i〉 of the S2–S5 CNPs exhibits a clear dependence on the particle size, as shown in Fig. 2. In photoelectron emission into air, the ionization energy is the sum of the energy of electron excitation over the band gap and the energy needed to overcome the Coulomb attraction leading to its emission into air. They are subject to the quantum confinement effect (24) and the image charge potential effect (25), respectively. Brus (24) treated the shifts of the conduction and valence bands by solving the first nonzero term of the Taylor expansion for the electron energy band in a spherical cluster. Induced image charge potential has been treated by Seidl and Perdew (25). Taking them together, the ionization energy may be expressed by (SI Appendix, section S3.2)

$$\langle E_i\rangle =E_{i,\infty }+\hspace{0.17em}\frac{h^2}{2m_0{m}_h^{\ast }}\langle \frac{1}{D_{m,v}^2}\rangle +\hspace{0.17em}\frac{e^2}{4\pi {\epsilon }_0}\left(\frac{1}{{\epsilon }_{\text{air}}}-\frac{1}{{\epsilon }_s}\right)\langle \frac{1}{D_{m,v}}\rangle ,$$ [1]

where 〈〉 represents an average quantity that is volume-weighted, E_i,∞ is the ionization energy of the bulk material, m₀ is the electron rest mass, $m_h^{\ast }$ is the effective hole mass, ε₀ is the vacuum permittivity, ε_air and ε_s are the relative permittivities of air and the particle material, respectively, h is the Planck constant, e is the elementary charge, and$\langle D_{m,v}^l\rangle$ is the lth moment of the particle volume distribution, which may be calculated from 〈D_m,v〉 and σ_g,v (SI Appendix, Eq. S6). The ionization energy data are treated using Eq. 1, yielding the solid line and the corresponding parameter (E_i,∞, $m_h^{\ast }$, and ε_s) values as shown in Fig. 2. We find that the quantum confinement term (i.e., the second term on the right-hand side of Eq. 1) has the dominant effect on 〈E_i〉. The image charge effect alone cannot explain the curvature of the measured ionization energy, as shown by the dashed line in Fig. 2.

Fig. 2.

Ionization energy of S2–S5 CNPs at room temperature (circles). The vertical error bars represent two SDs of the data; the horizontal error bars are the geometric SDs of the particle volume distribution. The dashed line is calculated without the second term in Eq. 1, i.e., neglecting the quantum confinement effect. Literature data: the lower limit of the photoionization energy of CNPs by in situ laser absorption in a burner-stabilized ethylene-air flame (BS4) (26) and the work function of CAST1 soot from a propane diffusion flame (27). For CAST soot, the median diameter of the volume distribution was obtained from modeling the size distribution as a lognormal distribution with the median mobility diameter of the number distribution reported in ref. 27 and the geometric SD estimated from SI Appendix, Eq. S2. (Inset) Square root of a typical emission yield curve as a function of the photon energy.

Ionization energy has been reported for 2–4-nm CNPs by in situ laser ionization (26). The work function values are also available for several soot samples produced in propane diffusion flames with primary particle diameters from 27 to 36 nm (27). Among them, only one of the samples, referred to by the authors as CAST1, resembles our CNPs in morphology and composition. The other two samples (CAST2 and CAST3) show evidence of postflame particle processing by organic vapors and thus liquid organic coatings. For this reason only the single datum from the CAST1 sample is included in Fig. 2 for comparison. Clearly, Eq. 1 reconciles all of the data well.

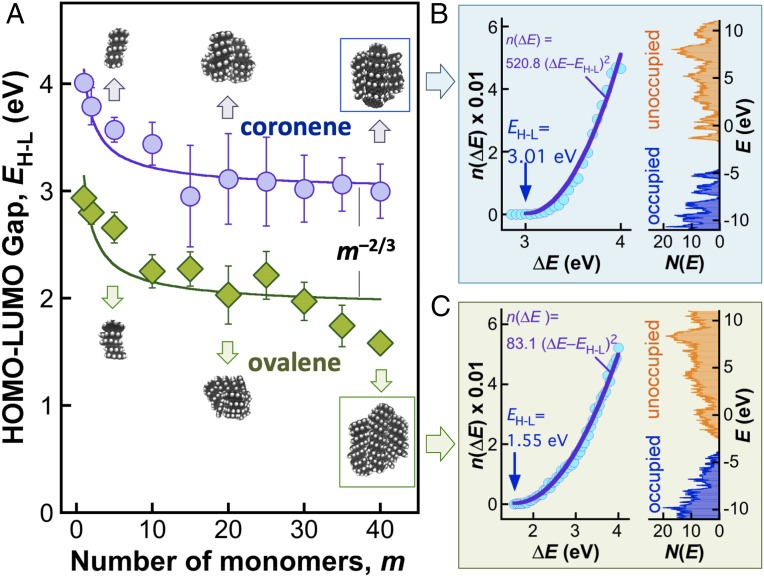
We discuss next the optical band gap. It is known that as the building block of CNPs, PAHs have well-defined HOMO–LUMO gaps (28, 29). The size of PAHs and their clustering and functionalization all impact the gap size (19, 30, 31). We illustrate some of these effects here by DFT calculations on homogeneous clusters of coronene and ovalene over the size range of 1–40 monomers. For each cluster size, configurations of at least five clusters were sampled by molecular dynamics (MD) at 300 K. The HOMO–LUMO gap (E_H–L) is then calculated for each configuration using Becke’s three-paramater exchange and Lee-Yang-Parr correlation functionals with the split-valence double-zeta basis set along with the d polarization functions on nonhydrogen atoms [what is commonly known as the B3LYP/6-31G(d) level of theory]. The resulting gap values are averaged and plotted in Fig. 3A. It shows that the size dependence of the band gap originates from both clustering (or stacking) and PAH sizes, and for each cluster type the HOMO–LUMO gap scales approximately with m^−2/3 or D⁻², where m is the number of monomer, and D is the cluster diameter. Such a dependence is consistent with the quantum confinement effect. The variation of the HOMO–LUMO gap is due to π–π* interactions, which are impacted by PAH size, composition, and degree of stacking. Obviously, the structure and composition of real CNPs are rather undefined and far more complex than the clusters calculated. As we indicated earlier, the DFT calculations are not intended for reproducing the measured optical band gap of CNPs. Rather, the calculations shed light on the nature of the observed band gap and more importantly, to unravel the underlying band structure, as will be discussed below.

Fig. 3.

Theoretical B3LYP/6–31G(d) results of the HOMO–LUMO energy gap E_H–L of selected PAH clusters. (A) E_H–L of coronene and ovalene clusters. The symbols and error bars are the mean and two SD of E_H–L over five relaxed MD clusters at 300 K. The lines illustrate the E_H–L∼m^−2/3 relationship by fitting the MD data using E_H–L = cm^−2/3, where c is a constant. (B and C) Densities of occupied and unoccupied energy states and n(ΔE) (symbols) calculated for coronene₄₀ and ovalene₄₀ where the lines are fits to the calculated n(ΔE) using k = 2.

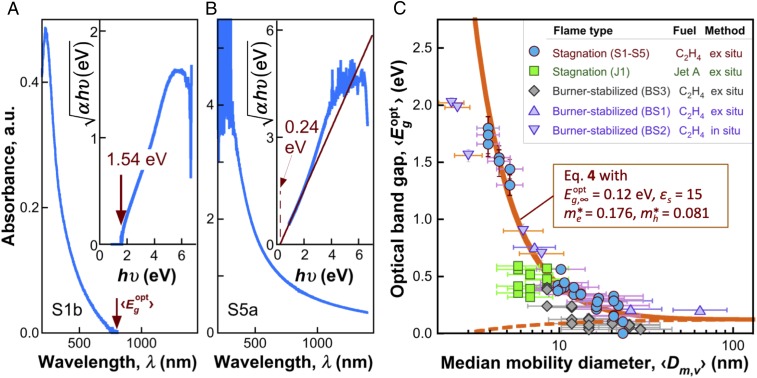
Following Davis and Mott (32), we determine the optical band gap $\langle E_g^{\text{opt}}\rangle$ from the absorption coefficient of the series S1–S5 CNPs using

$$\alpha h\upsilon \propto {\left(h\upsilon -\langle E_g^{\text{opt}}\rangle \right)}^k,$$ [2]

where α is the absorbance, and υ is the photon frequency. The exponent k varies with the band structure. The rule for crystalline semiconductor materials is that in the absence of excitonic transitions, k is equal to 1/2 for an allowed direct band-gap material and k = 2 for an allowed indirect band-gap material, and that the latter material excitonic transitions also have k = 1/2 (33). For the CNPs studied here, however, we find the k exponent is decidedly equal to 2 even though the transition is expected to be excitonic (34, 35). Following the Tauc analysis (36), we find that the experimental absorption spectra of the CNPs are best described by k = 2 (see Fig. 4 A and B, Insets and also SI Appendix, section S4). This conclusion is supported by the DFT calculations. Specifically, we again follow Tauc (36) by assuming that αhυ is proportional to the total possible transitions of energy states [n(ΔE)] from an unoccupied orbital at energy level E to an occupied orbital at E + ΔE, and find

$$\alpha h\upsilon \propto n\left(\mathrm{\Delta }E\right)={\displaystyle \int N_O\left(E\right)N_U\left(E+\mathrm{\Delta }E\right)dE},$$ [3]

where N_O and N_U are the densities of occupied and unoccupied energy states, respectively. Fig. 3 B and C show the energy band structures computed with DFT for coronene₄₀ and ovalene₄₀, respectively. For each case the resulting n(ΔE) is found to be proportional to (ΔE–E_H–L)², i.e., k = 2.

Fig. 4.

Measured optical absorption properties. (A and B) Absorbance spectra of S1b and S5a CNP samples. (Insets) The respective Tauc analyses. (C) Optical band gap of flame-formed CNPs at room temperature. The S1–S5 data (circles) are the baseline data used to obtain the parameter values of Eq. 4 (prediction plotted as the solid line). The dashed line is calculated without the second term in Eq. 4, i.e., neglecting the quantum confinement effect. Data from J1 and BS1–BS3 series of CNPs prepared in different flames are not used for obtaining the parameter values; they are shown for comparison. The vertical error bars represent the two SDs of the data. The horizontal error bars represent the geometric SDs of the volume distribution.

Tauc analyses (36) reveal two distinctive features in the spectral absorbance over the 15 CNP samples studied. Representative spectra are shown in Fig. 4 A and B. For small particles (e.g., S1b with 〈D_m,v〉 = 4.5 nm), a clear band edge exists; and the band gap is the band edge. For larger particles (e.g., S5a with 〈D_m,v〉 = 21.8 nm), the band gap is obtained from extrapolating (αhυ)^1/2 to zero. Collectively, the band-gap values are plotted for the S1–S5 series of CNPs in Fig. 4C as a function of 〈D_m,v〉. Clearly, the band gap exhibits the expected quantum confinement effect.

Following Brus (24), we write the optical band gap as,

$$\langle E_g^{\text{opt}}\rangle =E_{g,\infty }^{\text{opt}}+\frac{h^2}{2m_0}\left(\frac{1}{m_e^{\ast }}+\frac{1}{m_h^{\ast }}\right)\langle \frac{1}{D_{m,v}^2}\rangle -\frac{1.8e^2}{2\pi {\epsilon }_0{\epsilon }_s}\langle \frac{1}{D_{m,v}}\rangle ,$$ [4]

where $E_{g,\infty }^{\text{opt}}$ is the optical band gap of the bulk soot material, and $m_e^{\ast }$ is the effective electron mass. Applying Eq. 4 to the S1–S5 series data yields the theoretical line and the corresponding $m_e^{\ast }$ and $E_{g,\infty }^{\text{opt}}$ values as shown in Fig. 4C. Note that the $m_h^{\ast }$ and ε_s values have already been determined from the ionization energy and they are used here without modification. The $E_{g,\infty }^{\text{opt}}$ is 0.12 eV, close to zero. In fact, $E_{g,\infty }^{\text{opt}}$ = 0 eV describes the size dependence equally well when the level of data scatter is considered. The effective masses and the resulting exciton effective mass (μ* = 0.055) are close to those reported for graphene oxide (37). Again, we find the second term of Eq. 4 to be dominant in the size dependence of $E_{g,\infty }^{\text{opt}}$, and the Coulomb electron–hole interaction (i.e., the third term) to present a negligible effect, as shown by the dashed line of Fig. 4C.

To examine the generality of the quantum confinement behavior observed, we made optical band-gap measurement for four additional series of CNPs. These include in situ multiwavelength extinction and light scattering (16, 38, 39) of the burner-stabilized, BS2 samples in a burner-stabilized ethylene flame, and the ex situ measurements of samples from burner-stabilized ethylene flames in burner-stabilized (BS) flame facilities across two different laboratories (series BS1 and BS3) and for a series of samples collected in ethylene stagnation flame doped with a jet fuel (series J1). These additional data, also presented in Fig. 4C, collapse in the vicinity of, but somewhat below, the theoretical line determined from the S1–S5 CNPs. Hence, the quantum confinement effect observed is general, at least to the first order, and the single most important factor governing the band gap of CNP is its primary particle size. The deviations of the data from the S1–S5 line suggest that the CNP molecular structure and composition can impact the band gap to an extent. Additionally, an $E_{g,\infty }^{\text{opt}}$ value of 0 eV represents the BS3 series data better; and the CNP material does evolve into a complete broadband absorber as the size increases to above around 20 nm.

As discussed earlier, we use the volume median particle diameter as the relevant size parameter. The use of number median particle diameter yields the same conclusion with regard to the quantum confinement effect (SI Appendix, Fig. S13) except for the somewhat different $m_e^{\ast }$ and $m_h^{\ast }$ values that results. Another issue that can be raised concerns the nature of the size parameters used in Figs. 2 and 4C. Two sources of uncertainty in the size parameter can impact the data interpretation. The first source stems from the spheroidal geometry of primary particles. From the TEM aspect ratio distributions, we find that the spheroidal shape impacts the D_m,v value to no larger than 3% (SI Appendix). The second source is the effect of primary particle aggregation on the mobility size measurement. While particles with $\langle D_{m,v}\rangle$ < 20 nm are expected to be primary particles (40, 41), those with $\langle D_{m,v}\rangle$ > 20 nm could be aggregates of several primary particles (23). However, both the ionization energy and band gap have leveled off and become insensitive to the particle size above 20 nm. For this reason, we expect the size uncertainty to have a negligible effect on our data interpretation.

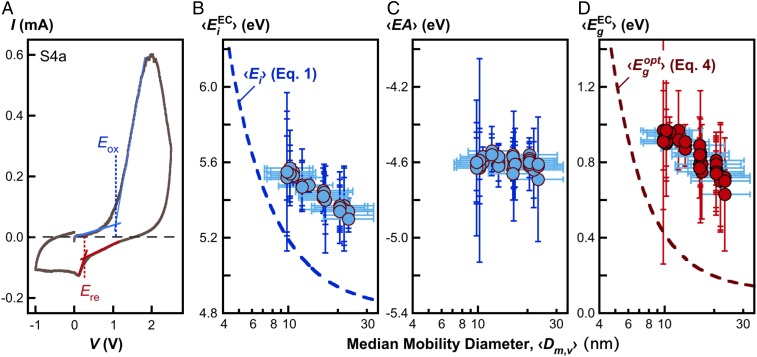
Lastly, we observe the confinement effect through cyclic voltammetry (CV), for which the details are provided in SI Appendix, section S5. Fig. 5A shows the oxidation potential 〈E_ox〉 and reduction potential 〈E_red〉 on a sample CV curve. The electrochemical ionization energy $\langle E_i^{\text{EC}}\rangle$ and electron affinity 〈EA〉 may be determined by $\langle E_i^{\text{EC}}\rangle =\langle E_{\text{ox}}\rangle +E_{\text{ref}}$ and $-\langle EA\rangle =\langle E_{red}\rangle +E_{\text{ref}}$ (42), where E_ref (= 4.32 eV) is the reference electrode potential relative to the vacuum. The electrochemical band gap$\langle E_i^{\text{EC}}\rangle$may be calculated as$\langle E_g^{\text{EC}}\rangle =\langle E_i^{\text{EC}}\rangle +\langle EA\rangle$. The ionization energy, electron affinity, and band gap are determined for S2–S5 series of CNPs and presented in Fig. 5 B–D, respectively. It is seen that while the electron affinity is independent of the particle size, the ionization energy and the band gap exhibit the clear confinement behavior. Their values are larger than the respective ionization energy in air and optical band gap, by about 0.5 eV (compare the symbols and dashed line of Fig. 5 B and D). This difference is expected because of electron–hole Coulomb interaction (43) and the electrolyte effect (44).

Fig. 5.

Measured electrochemical properties. (A) Typical cyclic voltammogram (the S4a CNP sample); (B) Electrochemical ionization energy $\langle E_i^{\text{EC}}\rangle$; (C) $\langle EA\rangle$; (D) Electrochemical band gap $\langle E_g^{\text{EC}}\rangle$, all measured at room temperature. In B–D the vertical error bars represent the two SDs of the data. The horizontal error bars represent the geometric SDs of the volume distribution. The dashed lines in the respective panels are ionization energy in air (Eq. 1) and optical band gap (Eq. 4) evaluated using the parameter values shown in Fig. 1C.

In summary, the quantum dot behavior of flame-formed CNPs is firmly demonstrated across their photoemission ionization energy, optical band gap, and electrochemical ionization energy. The results have several implications. In optically thick interstellar clouds, the observations of the emission bands at 3.3–3.4 μm (∼0.37 eV) (attributable to aromatic/aliphatic mixtures) (5) and longer than 6 μm (0.2 eV) (due to PAHs) (2, 3), are possible if the resulting carbon grains do not reabsorb at these wavelengths. This implies that the observable carbon grains should have optical band gaps corresponding to wavelengths longer than those of the emission bands. Using the observations of Fig. 4C as the guidance, we find these interstellar carbon grains to not exceed the size of ∼10 nm. The findings are also relevant to climate research. The absorption properties and their size and compositional effects of atmospheric fine carbon particles remain poorly characterized. For CNPs as a class of particulates that can be directly emitted into the atmosphere from combustion sources, the results depicted in Fig. 4C may present a relevant guidance for further study. More specifically, the ability of the CNPs to absorb light in the UV and visible regions but their inability to emit in some of the infrared region, depending on the CNP size, is a cause for concern with respect to their impact on the climate. Lastly, the quantum confinement effect has implications in laser-based soot diagnostics in flames. It indicates that the absorption coefficient is sensitive to particle size. It also establishes a key feature of flame CNPs for further investigation into their structure–property relationships. The composition and structure of flame CNPs can be highly sensitive to particle size, age, and local flame conditions in which they nucleate and grow (1). It remains unclear how key molecular properties of the CNPs, including PAH structure and size, surface functionalization, oxidation, and carbonization, impact the band gap, directly or indirectly, at a quantitative level.

Materials and Methods

Refer to SI Appendix for further details.

Materials.

Nascent soot samples were prepared using premixed stretch-stabilized flame and burner-stabilized flames. The size distributions are characterized using TEM and differential mobility analyzer.

Ionization Energy.

The ionization energy was determined from the photoelectron emission yield measured by a Photon-Electron Spectroscopy in Air (PESA) system (Riken AC-2) operating at room temperature. The ionization energy is determined as the inflection point of photoelectron emission by plotting square root of the photoelectron emission yield, _Υ1/2 against incident photon energy hυ (45, 46), as seen in Fig. 2, Inset.

Optical Band Gap.

Ex situ measurement of the optical band gap was carried out on particle samples deposited on quartz slides over the wavelength range of 185–1,400 nm at room temperature. In situ measurement was made by laser absorption using a hot plasma by optical breakdown of air. The plasma emits an unstructured spectrum of light from the visible to the far UV (21), which was guided through the flame. The transmitted light was detected between 200 and 600 nm by a spectrometer coupled to an intensified and gated charge coupled device (CCD) camera. For both measurements, the background-subtracted, transmitted light intensity is used to obtain absorbance, which was further analyzed on a Tauc plot (36), yielding the optical band gap for each particle sample, as seen in Fig. 4 A and B (Insets).

Electrochemical Potentials.

We used a 3.0-mm-diameter Pt disk as the working electrode, a Pt wire as the counter electrode, and the Accumet Ag/AgCl prefilled with 4 M KCl saturated with AgCl, as the reference electrode. We used 0.02 M ferrocene in acetonitile to calibrate the reference electrode potential relative to the vacuum. The electrolyte is made of 0.1 M tetrabutylammonium hexafluorophosphate (TBAPF6) in acetonitrile. The CNPs are coated onto the working electrode from a paste in dichloromethane. CV curves were recorded on an electrochemical workstation (Gamry Interface 1000) at room temperature. A sample CV curve is shown in Fig. 5A. The redox potentials were determined from the onsets of anodic and cathodic currents on the voltammogram.

Calculation.

Geometries of coronene and ovalene were optimized at the B3LYP/6–311+G(d,p) level of theory using Gaussian 09 (47). The atom-centered point charges were parameterized for the MD simulation by a transferable electrostatic model for PAH molecules (48). An isotropic potential (isoPAHAP) was used for intermolecular C–C, C–H, and H–H interactions (49). We adapted the intramolecular potential parameters from the optimized, all atom potentials for liquid simulations (OPLS-AA) force field (50) for all angles. Considering the Debye temperature of the C–H and C–C stretch modes is well over several thousand kelvins, they were frozen in MD simulations. Clusters were initialized using PACKMOL (51). Energy minimization produced relaxed geometries, which are then used as inputs to MD simulations to sample cluster configurations at 300 K. The resulting cluster configurations were selected for subsequent B3LYP/6–31G(d) calculations of the energy difference between the HOMO and LUMO Kohn–Sham orbitals.