Mesoscopic neural representations in spatial navigation

Abstract

Recent evidence suggests that mesoscopic neural oscillations measured via intracranial electroencephalography exhibit spatial representations, which were previously only observed at the micro- and macroscopic level of brain organization. Specifically, theta (and gamma) oscillations correlate with movement, speed, distance, specific locations, and goal proximity to boundaries. In entorhinal cortex, they exhibit hexadirectional modulation, which is putatively linked to grid cell activity. Understanding this mesoscopic neural code is crucial because information represented by oscillatory power and phase may complement the information content at other levels of brain organization. Mesoscopic neural oscillations help bridge the gap between single-neuron and macroscopic brain signals of spatial navigation and may provide a mechanistic basis for novel biomarkers and therapeutic targets to treat diseases causing spatial disorientation.

Towards a multi-level neural code of spatial navigation

Spatial navigation is a core ability of most animals and humans [1]. Successful navigation requires highly specialized neural representations (see Glossary) that encode information about the environment’s shape and content, neural codes that reflect the location, direction, and speed of the navigating organism, and neural mechanisms that underlie goal-directed behavior within the environment. These spatial representations have been identified at various levels of brain organization ranging from place, head direction, border, and grid cells [2–7] up to the macroscopic level of functional magnetic resonance imaging (fMRI), which revealed large-scale representations of locations [8], environments [9], directions [10–12], borders [13], and grid-like hexadirectional orientation [14–16].

Traditionally, there has been a gap between studies of spatial representations at the levels of single neurons and fMRI brain networks. This review focuses on the potential of intracranial electroencephalography (iEEG) recordings of local field potentials (LFPs) to bridge this gap, by providing spatial information at the mesoscopic level of relatively small neural assemblies (Box 1). These recordings have provided evidence for oscillatory signatures of multiple key components of spatial navigation, ranging from more general signals of movement, speed, and distance, to representations of specific spatial locations, goal proximity to boundaries, and very recently, to mesoscopic grid-like representations. First, we will review these results and discuss their relationship to the neural representations of space obtained at the microscopic, single-neuron level and the macroscopic level as observed with fMRI. Next, we will elaborate on the basic relationships between single-neuron spiking activity, LFPs, and the fMRI blood-oxygen-level dependent (BOLD) signal in order to address the question of how mesoscopic spatial representations relate to their microscopic and macroscopic counterparts. We will finally discuss the functional and clinical relevance of mesoscopic representations during spatial navigation.

Box 1. Detecting and analyzing mesoscopic brain oscillations.

Since the discovery of the scalp electroencephalography (EEG) by Hans Berger in the 1920s it has been known that cognition is accompanied by brain oscillations across a broad range of frequencies. EEG oscillations are classically divided into frequency bands: delta (1–4Hz), theta (4–8Hz), alpha (8–13Hz), beta (13–30Hz), low gamma (30–50Hz), and high gamma (>50Hz). Although it is more common to record these signals from the scalp, in rare circumstances researchers are able to measure these oscillations directly with high spatiotemporal resolution from the human brain when neurosurgical patients are implanted with intracranial depth, strip, or grid electrodes for clinical purposes (Fig. I). Contacts from these intracranial electroencephalographic (iEEG) electrodes record neuronal activity within a radius of several millimeters when electrode contacts are relatively large (macroelectrodes) [138]. Some patients are implanted with so-called microelectrodes which have smaller conductive surfaces and record neural signals from a region within a few hundred micrometers [98]. These microelectrode recordings also allow for the detection of multi- and single-unit spiking activity. During each patient’s implantation period, they can perform experimental tasks in order to identify neural activity related to cognitive functions [139]. Because iEEG patients are usually bedridden, these studies often probe spatial navigation via virtual navigation tasks performed on a bedside computer, although differences to real-world navigation have to be taken into account. During the analysis of iEEG data, both univariate and multivariate approaches (such as multivariate pattern analysis [140] and representational similarity analysis [141]) have been used effectively to identify general and feature-specific neural representations during spatial navigation.

Figure I. Basics on recording and quantifying mesoscopic oscillations.

(A) Coronal MR image showing an iEEG depth electrode in an epilepsy patient. Three electrode channels in hippocampal CA1 are highlighted in white. Regions are colored based on an automatic segmentation procedure (reprinted from [142]). (B) Main characteristics of brain oscillations include amplitude, period, and phase (as indicated by color). Phase-amplitude coupling (PAC) describes a systematic relationship between the phase of a slow-frequency oscillation (SFO) and the amplitude of a high-frequency oscillation (HFO). R, right; L, left; f, frequency.

Navigating the landscape of mesoscopic spatial representations

Movement, speed, time, and distance

Theta oscillations (Box 2) reliably appear during movement in the hippocampus of both rodents [17] and humans [18], although some characteristics of this signal differ between species. First, theta oscillations are more stable in rodents than in humans, in which theta oscillations occur in bursts of several cycles. Second, theta frequency may usually appear higher in rodents (4–10Hz) than in humans (1–4Hz) [19,20], possibly because larger anatomical assemblies tend to synchronize at lower frequencies [21]. However, this latter difference may also be attributed to real-world navigation versus virtual navigation [22,23] or to more frequent electrode placement in anterior parts of the human hippocampus (where theta oscillations may have a lower frequency) [24].

Box 2. Basics of theta oscillations.

Despite decades of research, the process of how hippocampal theta oscillations are generated is still under debate. Different models draw a complex picture of contributing brain regions, cell types, transmitters, and receptors, in which the medial septum and the diagonal band of Broca (MS-DBB) occupy major roles [17].

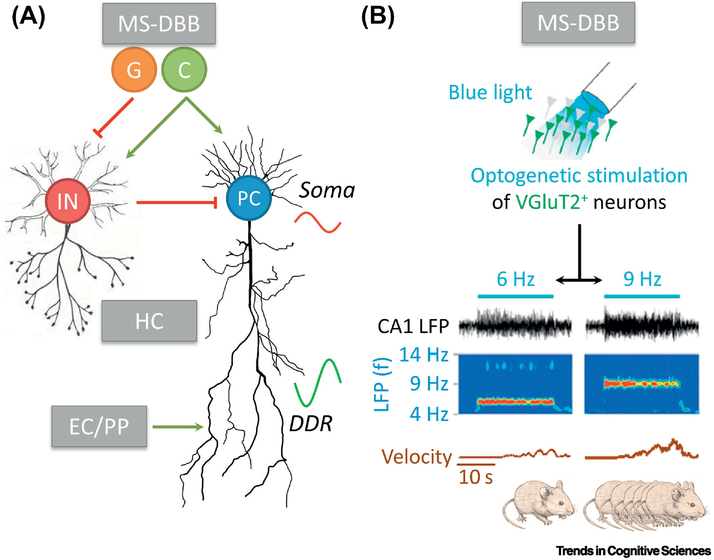
The classic model proposes that theta oscillations are generated by hippocampal pyramidal cells that receive inhibitory and excitatory input from the MS-DBB and the EC/perforant path, respectively (Fig. I). While the inhibitory input is induced by glutamatergic [143] and cholinergic [144] MS-DBB neurons and, via hippocampal interneurons, leads to inhibitory postsynaptic potentials (IPSPs) at the soma of the hippocampal pyramidal cells, the excitatory input results in excitatory postsynaptic potentials (EPSPs) at their distal dendritic region. The summed activity of somatic IPSPs and distal dendritic EPSPs then generates theta oscillations with specific amplitudes and phases [17].

Later work suggested multiple modifications of this model [17], of which we will describe three. First, different types of theta oscillations presumably emerge from different mechanisms. For example, atropine-sensitive theta oscillations, which appear during consummatory behaviors, may reflect the CA3 recurrent collateral system, whereas atropine-resistant theta oscillations, which correlate with movement, may be conveyed by entorhinal input. Second, interneuron activity driving the somatic IPSPs may not only depend on MS-DBB inputs, but also on CA1 recurrent collaterals, CA3 afferents, entorhinal afferents, and other interneurons with intrinsic oscillatory properties. These interneurons may consist of multiple classes [145] that target different parts of hippocampal pyramidal neurons. Third, the recurrent circuit of CA3 may form an intrinsic intrahippocampal theta generator and pyramidal neurons endowed with intrinsic properties to oscillate at theta frequency may produce single-cell theta oscillations.

Various potential functions have been proposed for hippocampal theta oscillations. Amongst others, these include information transfer between regions [17] and gating of information flow [146]. Furthermore, theta oscillations may enable the grouping and segregation of neuronal assemblies that were activated at different phases of the theta cycle, for example, during working memory [147]. Theta oscillations may also support mnemonic processes by inducing synaptic modifications of intrahippocampal associational pathways [148] and may allow the creation of temporally ordered memories [149]. Finally, theta oscillations may underlie phase coding by allowing single neurons to represent information by varying the timing of their spiking relative to theta oscillations during perception, navigation, and memory [29].

Figure I. Mechanistic basis of theta oscillations.

(A) Classic theta model (adapted from [17]). See Box 2 for explanations. Note that many extensions have been suggested to this model. C, cholinergic; DDR, distal dendritic region; EC/PP, entorhinal cortex and perforant path; G, glutamatergic; HC, hippocampus; IN, interneuron; MS-DBB, medial septum and diagonal band of Broca; PC, pyramidal cell. (B) MS-DBB VGluT2⁺ neurons as a key player in regulating locomotion. Increasing optogenetic stimulation (blue light) frequency of these neurons (from 6 to 9Hz) leads to higher theta oscillation frequency in CA1 and is followed by increased velocity of the rodent (adapted from [34]).

Another oscillatory signal that is involved in spatial navigation is the hippocampal gamma oscillation (30–100Hz), which increases in power during movement [25,26] and interacts with theta oscillations, such that gamma power varies across the theta cycle [25,27]. This phenomenon of cross-frequency coupling between gamma power and theta phase generalizes to other cognitive domains [28] and is thought to reflect phase coding [29], in order to, e.g., bind multiple stimuli into sequences.

In rodents, faster movement through an environment is associated with increases in both power [30] and frequency [31] of theta oscillations. Similar results have been obtained in human iEEG recordings, during virtual navigation [19] and during active walking [22,23]. This mesoscopic representation of speed is paralleled by single neurons in the hippocampus and medial EC that linearly increase their firing rate with speed [32,33]. A glutamatergic septal-hippocampal circuit that controls the initiation and velocity of locomotion [34] presumably occupies a key role in coordinating these single-neuron and mesoscopic representations of speed, which may nevertheless be dissociable from each other [35]. Functionally, increased theta frequencies during faster movements may serve to normalize the phase resolution within the theta cycle with respect to higher sampling rates of sensory information during faster movements [34].

In order to calculate travelled distance, speed must be integrated over time. Therefore, neural representations of time are likely important partners of spatial representations – particularly for accomplishing path integration [36]. In rodents, so-called “time cells”, which activate at particular time points in task intervals, are present in both the hippocampus [37] and in lateral EC [38]. At the macroscopic level, hippocampal BOLD patterns reflect the processing of temporal intervals within sequences [39] and precise temporal memories are associated with increased fMRI activity in lateral EC [40]. Interestingly, a neural signature of time may also be visible at the mesoscopic level, since rodent hippocampal theta oscillations exhibit increased power in a temporal discrimination task [41].

Since theta oscillations are related to the processing of movement, speed, and time, it is not surprising that they also contain information about distance travelled: theta power increases during long- versus short-distance “teleportation” during virtual navigation [42]. Similarly, theta oscillations are stronger before and during long versus short paths [43]. Increased theta power may serve to avoid cognitive overload due to increased sensory input during longer paths – for example by shortening the fraction of the theta cycle available for information processing and, thus, excluding less relevant information from being processed [44]. More broadly, these two studies indicate that theta oscillations are involved in the planning and initiation of movement, a finding that is paralleled by results in rodents [34]. Furthermore, an internal sense of movement seems to be sufficient for evoking hippocampal theta oscillations since they occur during virtual teleportation [42]. At the macroscopic level, hippocampal fMRI activity reflects distances between places [45] and path distance to goal-locations [46], but (to our knowledge) no fMRI study directly examined the BOLD correlates of previously travelled distance so far.

Locations, borders, and grids

Place cells fire whenever animals or humans are at a specific location within a spatial environment [2,3]. Place cells are mainly observed in the hippocampus [2,3], but they may also exist in extrahippocampal regions [47]. In addition, particularly during sharp-wave ripples, place cell activity often reflects future positions [48], and place-cell sequences “preplay” future paths to goal-locations [49]. Furthermore, place cells activate sequentially within theta cycles, allowing theta cycles to simulate time-compressed trajectories through space [50]. Interestingly, mesoscopic oscillations provide additional information about self-location when place cell firing phases are taken into account: Adding information about the theta phase at the moment of place-cell firing increases one’s ability to reconstruct the animal’s location [51,52]. As an extension of these findings, a rat’s position can be accurately decoded from the spatiotemporal structure of the theta rhythm obtained from multi-site, high-density hippocampal LFP recordings, without utilizing information from place-cell spiking activity [53]. These mesoscopic studies in rodents demonstrate that (multisite) oscillatory theta power and phase contain information regarding self-location. They are complemented by fMRI studies, which suggest that current and future locations can be decoded from human hippocampus and medial prefrontal cortex [8,54]. However, the possibility of finding reliable macroscopic representations of location in the hippocampus has been challenged [55] and their relationship to single place cells is unclear, because the hippocampus presumably employs sparse coding and hippocampal place cells lack a clear topographical organization [56–58].

Complementing place cells, border cells in the medial EC [5] and boundary-vector cells in the subiculum [59] activate adjacent to or at specific distances from a border, respectively. These cells may be instrumental in anchoring place [60] and grid fields [61] to an allocentric reference frame. At the macroscopic level, border representations were identified in the parahippocampal place area and retrosplenial cortex [13], and transcranial magnetic stimulation demonstrated a causal role of the occipital place area in representing environmental boundaries [62]. While a direct mesoscopic signal for borders has yet to be found, a closely related representation was recently identified in human subiculum using iEEG: when subjects encoded goal-locations near boundaries, power in the theta frequency range (4–10Hz) was stronger as compared to the encoding of goal-locations in the center of the virtual environment [63]. Of note, this study examined the distance between borders and the subject’s goal-locations (i.e., not the person’s own locations), and thus provide further evidence that the brain’s representations of space generalize from the self to others and also to inanimate objects for which an exact localization is important [64].

Grid cells fire at the vertices of an internally generated grid tiling the entire environment into equilateral triangles [6,7]. They were mainly observed in medial EC so far, where about 10–20% of all neurons are grid cells [33,65]. Grid cells may help to compute vector relationships and distances between spatial locations [66] – presumably constituting the neural basis for path integration [16,67]. In fMRI, there is evidence for macroscopic grid-like representations (i.e., hexadirectional modulation of the BOLD signal as a function of movement direction) in healthy participants who were scanned as they moved through a virtual environment [14–16]. FMRI grid-like representations were observed in EC, but also in extrahippocampal regions such as medial prefrontal cortex and parietal cortex ([14]; Supplemental Information, Text S1 and Table S1), warranting a brain-wide examination of grid cell density.

Crucially, two recent iEEG studies revealed grid-like representations at the mesoscopic level of brain organization, i.e., a hexadirectional modulation of entorhinal theta power by movement direction in epilepsy patients who performed a virtual navigation task [68,69]. Both studies found that this hexadirectional modulation was restricted to the EC and not present in neighboring similarly sized regions (hippocampus, amygdala) and other control regions, consistent with single-neuron [7] and fMRI recordings [14,15]. Furthermore, both studies showed that the effect was specific to six-fold rotational symmetry and specific to the theta frequency range. Importantly, both studies found a link between grid-like representations and spatial memory performance: Stronger hexadirectional modulation correlated positively with better spatial memory performance [69], conceptually in agreement with previous fMRI studies [14–16,70], and stronger grid-like representations were demonstrated in later as compared to earlier parts of the experiment after significant learning had occurred [68]. Furthermore, stronger hexadirectional modulation was revealed in parts of the environment closer to the environmental boundary of the virtual arena [68], potentially related to stabilized grid cell firing via error-correcting border cell input after encounters with environmental boundaries [61]. Moreover, mesoscopic grid-like representations were particularly observed during fast movements [68], in line with prior fMRI studies [14,15] and potentially related to speed modulation of grid cells and conjunctive grid by head-direction cells [14,71].

Mesoscopic grid-like representations were also observed in broad-band gamma activity: Building upon evidence for grid cell activity [72] and fMRI grid-like representations [73,74] during visual exploration in monkeys and humans, respectively, a recent study searched for modulations of oscillatory power as a function of gaze direction [75]. Indeed, hexadirectionally modulated signals were evident in broadband gamma activity (60–120Hz), both in MEG and in one epilepsy patient with iEEG electrodes in the EC.

Taken together, unique patterns of brain oscillations emerge when animals and humans navigate spatial environments, with theta [17–20,22–24,30,31,34,35,42,43,50,76] and gamma oscillations [25–27] being associated most often with characteristics of spatial navigation such as movement, speed, and distance. Crucially, recent evidence demonstrates that mesoscale neural networks oscillating in these frequency bands provide representations of locations, proximity of goals to boundaries, and grid-like hexadirectional orientation that were previously only observed at the microscopic or macroscopic level (Fig. 1, Key Figure). It is notable that, in particular, theta [51–53,63,68,69] and gamma oscillations [75] stand out as carriers of this feature-specific information. Although several of these findings are preliminary, and have not yet been demonstrated across species, their possible functional significance merits further investigation. Particularly, a thorough brain-wide examination of mesoscopic grid-like representations would be of interest, complementary to the brain-wide examination of grid cell density. Grid-like representations outside the EC may perform complementary computations for spatial navigation or they may support other cognitive functions that exploit similar computational principles as spatial navigation [66,77]. Furthermore, it remains elusive how the different scales of spatial representations are interconnected. This question is closely related to the fundamental issue of basic relationships between spiking activity, oscillatory power, and the BOLD signal.

Key Figure: Figure 1. Towards a multi-level neural code of spatial navigation.

Each third of the pie chart depicts exemplary neural representations of spatial locations (places, P), boundaries (B), and grids (G) at the microscopic, mesoscopic, and macroscopic level of brain organization, respectively. The microscopic (i.e., single-neuron) level shows activation maps of a place cell (P; adapted from [150]); a border cell (B; adapted from [5]); and a grid cell (G; adapted from [6]). Warmer colors correspond to higher firing rates (P and B) or higher autocorrelations (G), respectively. The mesoscopic level depicts hippocampal theta oscillations whose spatiotemporal structure allows the prediction (colored eclipses) of a rodent’s location (black line) (P; adapted from [53]); theta power in human subiculum encoding the proximity of goal-locations to a spatial boundary (B; adapted from [63]); and entorhinal theta power exhibiting hexadirectional modulation by movement direction (i.e., mesoscopic grid-like representations; G; adapted from [69]). Examples of spatial representations at the macroscopic level include multivariate hippocampal BOLD patterns that allow the decoding of goal-locations (3D bars indicate classifier accuracy; P; adapted from [8]); parahippocampal BOLD signals that encode the presence of boundaries in a spatial scene (B; adapted from [13]); and entorhinal BOLD signals exhibiting hexadirectional modulation by movement direction (i.e., macroscopic grid-like representations; G; adapted from [14]).

Common grounds for multi-level spatial representations?

Basic relationships between spiking activity, LFPs, and BOLD

Although it is widely agreed that links between spiking activity, LFP power, and the BOLD signal exist (Fig. 2), the details of these interrelations remain elusive. Here, we summarize what is currently known and propose that deepening this knowledge will boost our understanding of how spatial codes can coexist at multiple levels of brain organization.

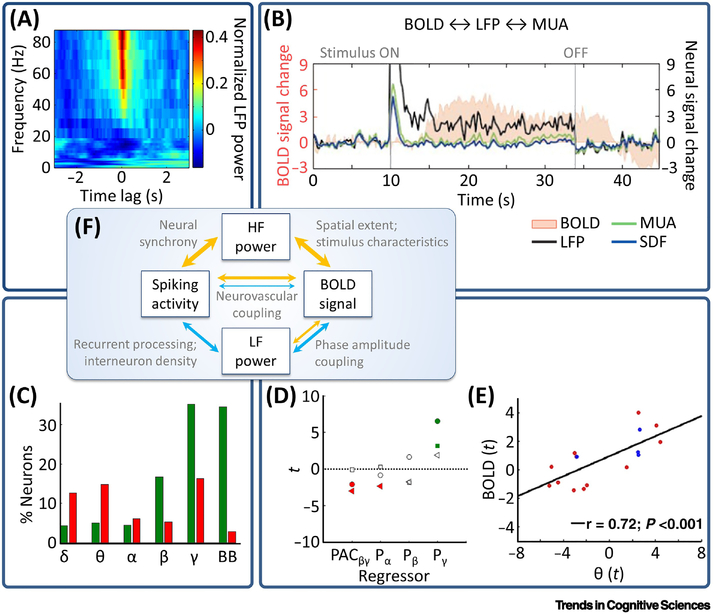
Figure 2. Relationships between spiking activity, LFPs, and BOLD.

(A) Spike-triggered average time-frequency power plot showing that spiking activity is accompanied by increases in high-frequency (“HF”) and decreases in low-frequency (“LF”) power (adapted from [79]). Power is normalized across time. (B) Close relationship between the (delayed) BOLD response and LFP high-frequency power, and weaker relationship between BOLD and multi-unit activity (MUA): Whereas MUA shows a transient response, BOLD and LFPs exhibit a sustained response throughout stimulus presentation. SDF, spike-density function (adapted from [98]). (C) Spiking activity (in widespread regions including frontal, parietal, and occipital cortices, amygdala, hippocampus, and the parahippocampal region) is positively related to broadband (“BB”) and high-frequency (gamma) power, but negatively related to low-frequency (delta, theta) power. Green/red bars, percentage of neurons showing a positive/negative relationship between spiking activity and LFP power (adapted from [78]). (D) While beta-gamma phase-amplitude coupling (PAC) and alpha power are negative BOLD predictors, gamma power relates positively to BOLD (adapted from [104]). Red, significantly negative; green, significantly positive. Each marker, one patient. (E) Positive relationship between theta power and parahippocampal BOLD signal (adapted from [83]). (F) Highly simplified model of the relationship between spiking activity, LFP power, and the BOLD signal. Orange arrows, positive relationships; light blue arrows, negative relationships. Thicker lines indicate stronger evidence. Deviations from this model can arise due to various modulating factors (see text annotations for non-exhaustive examples and the main text for details).

Various studies on the relationship between LFP power and spiking activity revealed that spiking activity correlates positively with broadband power and gamma power, in both human [78] and monkey neocortex [79,80], with high gamma (>80Hz) power being particularly tightly correlated with spiking activity in some studies [80,81]. Of note, neural synchrony may drive increases in gamma power to a greater extent than firing rate [80]. By contrast, low-frequency oscillations often have a negative relationship to spiking activity, as demonstrated for delta, theta, and alpha power in human and monkey neocortex [78,79]. In certain brain regions including the hippocampal area, the relationship between LFP power and spiking activity is even more complex. For example, in some studies spiking activity did not correlate with either broadband, theta-band, or gamma-band LFP power in human hippocampus and EC [82,83]. Such uncoupling between spiking activity and LFPs may be explained by multiple factors including reduced spike synchronization [82,84], pronounced recurrent processing, and high interneuron density [85,86]. Cell morphology and orientation, topological organization, and stimulus characteristics constitute additional determinants of the relationship between spiking activity and LFP power [87–89]. Notably, the spatial extent of gamma power is sometimes presumably too local [89] to establish indirect relationships between spiking activity and BOLD (given that gamma power is also associated with BOLD, see below).

Spiking activity is not only associated with oscillatory power, but is also modulated by the phase of neural oscillations, as demonstrated via the phenomena of phase locking [90] and phase precession [91]. Phase locking reflects the higher excitability of neurons during phase ranges that correspond to more depolarized membrane states. Since both theta [92] and alpha [44] oscillations putatively reflect rhythmically changing levels of inhibition, phase-locked neurons tend to fire during oscillatory troughs, which correspond to lower levels of inhibition. During rodent navigation, phase locking occurs in place cells [93], speed cells [33], grid cells [94], and less strongly in border cells [95]. In human virtual navigation, phase locking to oscillations in the delta, theta, and gamma frequency bands has been observed [96].

Phase precession describes the phenomenon in which a neuron fires at successively earlier phases of an ongoing oscillation, possibly resulting from an interaction of (theta) oscillatory inhibition and an (asymmetric) rate code, which can be induced, for example, when moving through the firing field of a place cell [92]. In rodents, both place [91] and grid cells [94] exhibit phase precession, while evidence for phase precession in humans is still missing. Various functions have been suggested for phase precession, including information processing via a phase code in which information is represented by the oscillatory phase at which a cell or cellular assembly activates [29,92].

Relating electrophysiology and BOLD via simultaneous iEEG/fMRI recordings is challenging for practical and safety issues [97]. Regarding the relationship between spiking activity and BOLD, simultaneous recordings in sensory neocortex showed that spiking activity and BOLD correlate less tightly than mean LFPs (in particular, gamma-band power) and BOLD [98]. Consecutive and parallel studies in both neocortex and hippocampus revealed variable results ranging from no correlation [83,99] and low degrees of concordance [100] to clear positive relationships between spiking activity and BOLD [101]. Again, divergent findings may be explained by region-specific recurrent processing and interneuron activity that cause dissociations between spiking activity and BOLD. In addition, region-specific neurovascular coupling [85,86] may account for inverse relationships between spiking activity and BOLD in situations when the ratio between blood flow and oxygen metabolism is atypically low [85].

Hence, given these caveats, the BOLD signal is generally thought to correlate more strongly with LFPs than with spiking activity [85,102]: Examining the relationship between high-frequency oscillations and BOLD, simultaneous recordings in monkey visual cortex showed pronounced positive correlations between BOLD and gamma power ([98]; for similar results in various regions and species, see e.g., [103,104]). These results were corroborated by consecutive recordings in human neocortex [105], as well as by parallel experiments in healthy participants and epilepsy patients in the medial temporal lobe [106]. Regarding low-frequency oscillations, simultaneous LFP/BOLD recordings showed negative relationships between BOLD and delta power in rat striatum [107], and between BOLD and alpha/beta power in human motor cortex [104]. Consecutive iEEG/fMRI studies showed similar negative associations between BOLD and beta power, however with pronounced differences between brain regions [108], again in line with the notion that the local circuitry and region-specific neurovascular coupling are modulating factors [85]. Particularly the investigation of theta power and BOLD in the hippocampal formation may lead to variable results, perhaps because this relationship is mediated by the presence or absence of theta/gamma-coupling [104], which depends on ongoing cognitive demands [109]. For example, theta (4–8Hz) power was found to correlate positively with BOLD in the parahippocampal region (including EC) but not in hippocampus [83].

Emergence of meso- and macroscopic spatial representations

Due to the complex associations between spiking activity, LFPs, and BOLD, it is under intense debate how meso- and macroscopic representations of space relate to the activity of spatially selective single neurons. Potential answers to this question have been suggested mainly for grid cells in the context of spatial representations. Apart from their main feature of firing fields being arranged with six-fold rotational symmetry, these cells exhibit unique functional and anatomical properties (Fig. 3A) that may facilitate the emergence of meso-/macroscopic grid-like representations. Specifically, grid cells are organized in a small number of modules [110] with grid cells of the same module exhibiting similar orientation, spacing, and theta modulation [6,110]. In the following paragraphs, we describe four potential explanations for how the features of grid cell spiking activity relate to hexadirectionally modulated meso-/macroscopic neural signals. All hypotheses assume that, across the grid cell population, the same number of firing fields (centers and peripheries) are traversed along paths of similar distance at any direction.

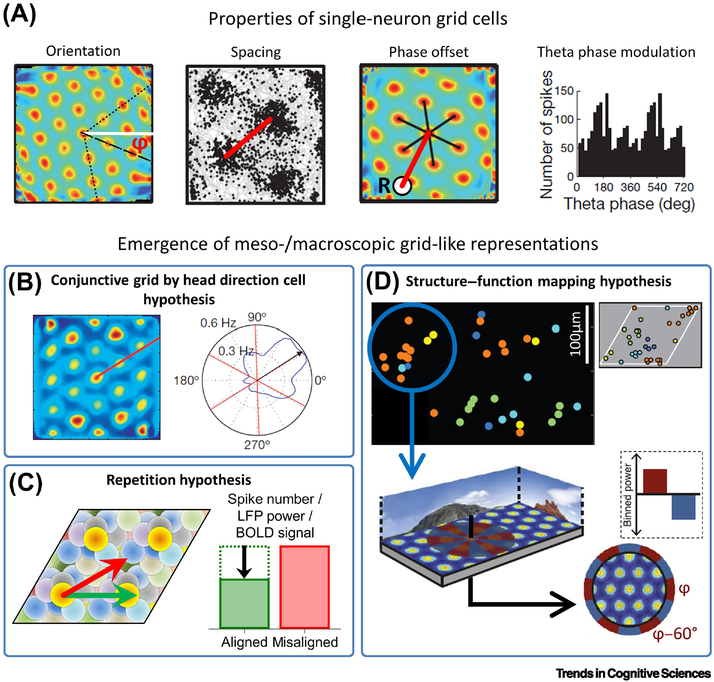
Figure 3. Grid cells and grid-like representations.

(A) Key characteristics of grid cells comprise orientation ϕ, spacing, and phase offset from a reference location (R; adapted from [110]) as well as theta phase modulation (adapted from [94]). (B) Grid-like representations may emerge from firing of conjunctive grid by head-direction cells that exhibit increased firing when moving aligned as compared to misaligned with the grid axes (reprinted from [14]). (C) In a grid cell population with similar orientation and spacing (but with random phases), aligned movements lead to more frequent activation (shorter distance between firing fields) of a smaller number of different grid cells, whereas misaligned movements lead to less frequent activation (larger distance between firing fields) of a higher number of different grid cells. Aligned movements may thus lead to more pronounced repetition suppression (black arrow) at the level of spiking activity and/or LFP power and/or BOLD signal (fMRI adaptation), resulting in meso- and/or macroscopic gridlike representations. Shaded circles represent firing fields of different grid cells with similar orientation and spacing, but different phase offsets. Each color, one grid cell. Green arrow, aligned movement; red arrow, misaligned movement. (D) Since anatomically adjacent grid cells exhibit similar phase offsets (upper panels adapted from [113]; similar color indicates similar phase offset) in addition to similar orientation and spacing, recording from a limited number of grid cells with a nonrandom distribution of phase offsets leads to grid-like representations (lower panels adapted from [69]).

The “conjunctive grid by head-direction cell hypothesis” (Fig. 3B) builds upon prior research which suggested that the firing of conjunctive grid by head-direction cells located in deeper layers of the EC and in pre- and parasubiculum [71] is aligned with the grid axes ([14]; but see [111]). Assuming that the directional tuning width of these conjunctive grid by head-direction cells is not too broad, movements aligned with the grid axes (as compared to misaligned movements) will result in increased spiking activity of the conjunctive grid by head-direction cell population – thus causing the appearance of meso-/macroscopic grid-like representations [14]. Of note, (i) the hexadirectional modulation of oscillatory power or BOLD reflects the activity of the population of conjunctive grid by head-direction cells (rather than the grid cells themselves) in this scenario, (ii) such hexadirectional modulation may also occur when the conjunctive grid by head-direction cells are aligned with the grid axes plus a consistent angular offset, and (iii) pure head direction cells whose preferred firing directions are 60° offset from each other may also result in hexadirectional modulation of oscillatory power or BOLD.

The “repetition hypothesis” (Fig. 3C) is based on the assumption that the phenomenon of repetition suppression, i.e., neural activity being reduced for repeated stimuli [112], holds true in the context of grid cells [14,72]. Relatively fewer different grid cells are activated more often during aligned movements and relatively more different grid cells are activated less often during misaligned movements. Thus, during aligned movements there would be a higher degree of repetition suppression at the level of spiking activity (which to the best of our knowledge has yet to be confirmed) and/or LFP power and/or BOLD signal (i.e., fMRI adaptation) as compared to misaligned movements – resulting in grid-like representations. Repetition suppression at the level of spiking activity may lead to hexadirectional modulation of LFP power in the theta band, since grid cells exhibit phase locking and phase precession with respect to theta oscillations (Supplemental Information, Text S2 and Fig. S1).

Regarding the “structure-function mapping hypothesis” (Fig. 3D), recent evidence demonstrates that the firing fields of anatomically adjacent grid cells not only have similar spacing and orientation [110], but also a similar phase offset to a reference location [113]. Therefore, recordings from a small area of the EC may sample grid cells with similar firing fields. Such a grid cell population shows higher average firing rates during aligned movements (since more firing fields are traversed) versus misaligned movements, possibly resulting in meso-/macroscopic grid-like representations. Of note, the anatomical area over which adjacent grid cells share a common phase offset may be markedly smaller than the area that is sampled by iEEG or standard fMRI – suggesting that it could be useful to examine fMRI grid-like representations at the high spatial resolution achievable with high-field (7 Tesla) fMRI [114]. Recording from a restricted area of the EC may nevertheless sample grid cells that are biased towards similar phase offsets, enabling the detection of grid-like representations at lower resolution.

The previous three hypotheses assume consistent (positive or negative) relationships between spiking activity, LFP theta power, and BOLD in EC – an assumption for which there is currently only limited evidence (Fig. 2E; [83]) and that should be further clarified in future studies (particularly via simultaneous iEEG/fMRI recordings). By contrast, the “independence hypothesis” states that six-fold rotational symmetry occurs independently at different levels of brain organization. This lack of a common neural basis does not exclude a biological and behavioral relevance of meso-/macroscopic grid-like representations, and removes the need for explaining how a limited number of grid cells in medial EC (about 10–20% [33,65], see also [115]) can result in a meso-/macroscopically visible neural signal. Of note, all hypotheses imply that meso- and macroscopic grid-like representations may also be observable in animal models. Furthermore, combinations of two or more of the hypotheses presented above may hold true – either amplifying or attenuating each other.

Redundant or complementary information systems?

Do mesoscopic representations simply mirror the spatial information of single-neuron representations or do they provide independent information? Findings in rodents and humans favor the latter option, but it currently remains elusive whether mesoscopic spatial representations are indeed part of the neural code for spatial navigation or whether they are epiphenomena.

For example, the accuracy of estimating a rat’s position can be improved when information about the LFP phases at which place cells fire is added to the information obtained from place cell firing alone [51]. Similarly, the LFP phases at which a place cell fires and its firing rate can independently represent the animal’s location within the place field and its movement speed through the field, respectively [52]. Additionally, spike sequences of place cells within theta cycles can be used to predict movement direction [116]. Regarding speed, single-neuron representations and mesoscopic representations may contribute independent information, as they are dissociable from each other analytically [32] and physiologically, via inactivation of the medial septum [35]. Furthermore, phase-specific neuronal firing encodes information about a patient’s prospective navigational goal in the absence of firing rate changes [117], and human single-neuron representations of specific passengers or landmarks in a virtual navigation task were shown to be uncorrelated with theta- and gamma-band LFP representations of these stimuli [82]. These studies suggest that micro- and mesoscopic brain signals may carry (partially) independent information and propose that different levels of brain organization make independent contributions to the neural code of spatial navigation. Specifically, as shaped out in this review, mesoscopic theta oscillations may constitute an important partner of microscopic spatial representations. Since several different features relevant to spatial navigation are all represented by theta power, they may jointly shape the functional role of theta for representing and integrating multiple pieces of information.

Behavioral and clinical relevance of multi-level spatial representations

Having described how features of navigation and space relate to micro-, meso-, and macroscopic brain signals, examining their relevance for behavioral performance is important. At the microscopic level, experimentally induced shifts of place fields were associated with impaired spatial behavior [118], increased place field stability correlated with better task performance [119], and disrupting grid cell activity reduced the accuracy of path integration [67]. At the mesoscopic level, abolition of the hippocampal theta rhythm impaired spatial memory [120] and stronger speed modulation of hippocampal theta frequency correlated with better performance [121]. The strength of mesoscopic grid-like representations correlated positively with spatial memory [69] and increased after learning [68]. Similarly, macroscopic grid-like representations in EC and medial prefrontal cortex showed positive associations with memory performance [14–16,70]. Moreover, stronger goal direction signals in human EC correlated with better task accuracy [11]. At the purely behavioral level, grid cell properties predicted biases in human path integration [122]. However, no study demonstrated six-fold rotational symmetry (in contrast to four-fold symmetry [123]) at the behavioral level to date. Future studies are needed to corroborate these findings on how multi-level spatial codes support specific aspects of spatial memory performance – e.g., via optogenetics or deep brain stimulation.

Behavioral relationships between neural representations of space and spatial memory performance suggest that our ability to understand and treat neurological and psychiatric diseases whose symptoms include spatial disorientation will benefit if we have a detailed fundamental understanding of the neural representations underlying spatial navigation and how they are disrupted from neuropathologies. Particularly, Alzheimer’s disease (AD) may lead to subtle changes in navigational strategies and altered neural representations of space already in very early disease stages [124]. Specific types of spatial representations may be impaired at consecutive AD stages, following either the spreading of neurofibrillary tangles or the development of amyloid β deposition – possibly enabling a “neurocognitive Braak staging” [125]. AD mouse models already revealed the adverse impact of tau pathology on grid cell functioning [126] and the degradation of place cell firing due to amyloid plaque burden [127], both pathological changes being accompanied by spatial memory deficits. Besides, AD mouse models identified disrupted phase locking of place cells to hippocampal theta and gamma oscillations [128] as well as reduced cross-frequency coupling of gamma to theta oscillations in medial EC [129]. The investigation of the associations between AD neuropathology and multi-level spatial codes will both enable mechanistic explanations of symptoms and allow the establishment of early biomarkers for AD [124,130,131] such as reduced grid-like representations [15]. In this respect, establishing meso- and macroscopic representations of space has also practical relevance, because single-neuron spatial representations can be measured from the human brain only under rare circumstances.

Concluding remarks

Mesoscopic representations of space based on electrophysiological recordings in humans point towards a multi-level neural code for spatial navigation. These mesoscopic representations exhibit complex connections to spatial representations based on single neurons or on macroscopic fMRI patterns, and may yet mediate the relationship between these two other levels of brain organization. Follow-up studies should thus further clarify the emergence of meso-/macroscopic spatial representations and show how their information content relates to single-neuron activity. Future research may go beyond the two-dimensional spatial domain and examine to which extent mesoscopic brain signals represent three-dimensional spatial information [132–134], support navigation through other n-dimensional “spaces” [66,70,77,135–137], and provide biomarkers for neurological and psychiatric diseases (see Outstanding Questions).

Highlights.

• Neural representations of spatial navigation have mainly been studied at the microscopic level of single neurons or at the macroscopic level of functional magnetic resonance imaging (fMRI).

• Recent intracranial EEG recordings in epilepsy patients revealed neural representations of spatial features including travelled distance, goal-proximity to boundaries, and grid-like hexadirectional orientation. These representations occur at the mesoscopic level of brain oscillations, particularly in the theta frequency band.

• Mesoscopic representations of space bridge the gap between their micro- and macroscopic counterparts. Experimentally testable scenarios may explain how the mesoscopic spatial representations relate to single-neuron firing, other neural oscillations, and fMRI signals.

• Neural spatial representations may offer novel tools for biomarkers of neurological and psychiatric diseases.

Glossary

Allocentric reference frame

representation of the spatial environment with regard to features of the external world independent of the moving subject; typically contrasted with an egocentric reference frame that is centered on the moving subject.

Blood-oxygen-level dependent (BOLD) signal

signal recorded using fMRI that – by measuring blood oxygenation in brain voxels – allows indirect conclusions about the neural activity underlying changes in blood oxygenation.

Frequency bands

canonical classes that summarize neural oscillations based on their frequency: delta (<4Hz), theta (4–8Hz), alpha (8–13Hz), beta (13–30Hz), and gamma (>30Hz).

Grid cell

neuron whose firing field pattern consists of a regular grid that tessellates the entire environment into equilateral triangles. Mainly observed in medial entorhinal cortex and presumably a key component of path integration. The firing pattern exhibits six-fold rotational symmetry and may thus be the source of hexadirectional modulation of meso- and macroscopic brain signals.

Hexadirectional modulation

characteristic of a neural signal (e.g., theta power or BOLD amplitude) to vary as a function of a circular variable (e.g., movement direction) after having transformed the circular variable from the classical 360° space into a 60° space.

Intracranial electroencephalography (iEEG)

technique to measure electrical activity via surgically implanted electrodes from inside the skull. Electrodes comprise grids and strips attached to the surface of the brain (electrocorticography, ECoG) as well as depth electrodes inserted into the brain (stereotactic electroencephalography, SEEG).

Local field potentials (LFPs)

electrophysiological signals that integrate neural activity within localized brain areas. Can be measured via iEEG that records the LFP from a few hundred micrometers up to a couple of millimeters depending on electrode size.

Neural representations

patterns of neural activity related to one specific stimulus of the external world or one specific mental content. Here we define “macroscopic neural representations” as those measured via fMRI, scalp-EEG, or MEG, “mesoscopic neural representations” as those obtained via iEEG, and “microscopic neural representation” as those occurring at the level of single neurons.

Oscillations

rhythmic fluctuations of neural activity, characterized by frequency (cycles per second), power (squared amplitude), and phase (momentary deflection angle). In general, neural oscillations bias input selection, temporally link neurons into assemblies, and facilitate synaptic plasticity, mechanisms that cooperatively support temporal representation and long-term consolidation of information.

Phase coding

neural mechanism by which information is represented via the phase of a (slow) oscillation at which activity of single neurons or cellular assemblies occurs.

Phase locking (here in the sense of spike-field coherence)

phenomenon that a neuron fires at identical phases of a concurrent oscillation across time.

Phase precession

phenomenon that a neuron fires at successively earlier LFP phases across time.

Virtual navigation task

in a weak sense, computerized task that lets the subject explore a virtual environment without the need of real-world movement. In a strong sense, task that allows subjects to navigate virtual environments by actual body movement.