Abstract
Matching methods are assumed to reduce the likelihood of a biased inference compared with ordinary least squares (OLS) regression. Using simulations, we compared inferences from propensity score matching, coarsened exact matching, and unmatched covariate-adjusted OLS regression to identify which methods, in which scenarios, produced unbiased inferences at the expected type I error rate of 5%. We simulated multiple data sets and systematically varied common support, discontinuities in the exposure and/or outcome, exposure prevalence, and analytical model misspecification. Matching inferences were often biased in comparison with OLS, particularly when common support was poor; when analysis models were correctly specified and common support was poor, the type I error rate was 1.6% for propensity score matching (statistically inefficient), 18.2% for coarsened exact matching (high), and 4.8% for OLS (expected). Our results suggest that when estimates from matching and OLS are similar (i.e., confidence intervals overlap), OLS inferences are unbiased more often than matching inferences; however, when estimates from matching and OLS are dissimilar (i.e., confidence intervals do not overlap), matching inferences are unbiased more often than OLS inferences. This empirical “rule of thumb” may help applied researchers identify situations in which OLS inferences may be unbiased as compared with matching inferences.
Keywords: causal inference, confounding, epidemiologic methods, matching, observational data
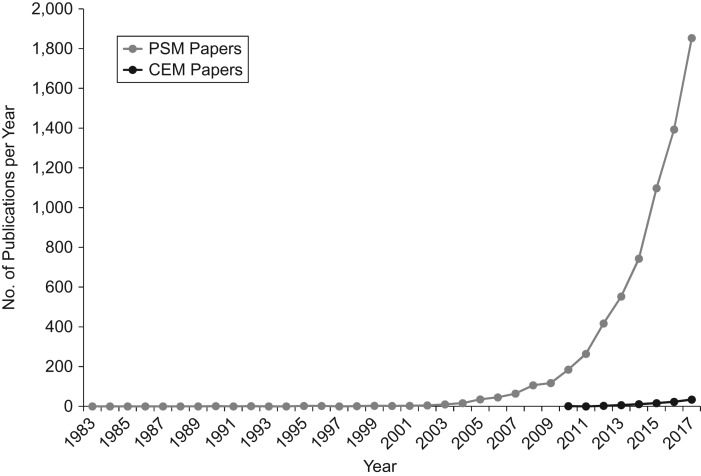
Matching methods are increasingly used to infer effects of an exposure from observational data (Figure 1). Matching methods align exposed and unexposed observations with similar measured covariates, while unmatched observations are typically excluded from analysis. For example, to assess the association between a housing program and health, one could match enrollees with nonenrollees such that the matched pairs have similar characteristics, so the remaining differences in health would be attributable to the effect of the housing program. In theory, matching produces less biased estimates of the causal effect of an exposure than does unmatched ordinary least squares (OLS) regression (1–3), particularly when “common support”—the overlap in characteristics between exposed and unexposed people before matching—is poor (2, 4). As applied to the housing program example, poor common support would arise if the distribution of income was lower for enrollees than for nonenrollees. Matching aims to restrict analysis to the area of support—that is, the region of the income distribution where nonenrollees could serve as a credible control population—to isolate the estimated effect of the housing program on health outcomes. Matching, therefore, presents a trade-off between common support and sample size: Matching produces an analytical sample with better “balance” (fewer differences between the exposed and unexposed groups on the measured covariates), by restricting the analysis to the range of support compared with conventional ordinary OLS.
Figure 1.
Annual numbers of published articles using propensity score matching (PSM) and coarsened exact matching (CEM) appearing in PubMed (National Library of Medicine, Bethesda, Maryland), by year, 1983–2017. Rosenbaum and Rubin’s paper introducing PSM (4) was published in 1983; since then, the body of literature based on matching has increased dramatically. Iacus et al.’s paper introducing CEM (3) was formally published in 2012, although a white paper was available earlier, and the first CEM publication in PubMed came out in 2010. The annual number of PSM publications indicates that each year, an increasing number of studies employ PSM; similarly, the annual number of studies using CEM is also starting to rise.
Use of propensity score matching (PSM) (4) has increased dramatically in recent years (Figure 1) (5, 6). In applying PSM, exposed and unexposed observations are matched on their predicted “propensity” (probability) of exposure, calculated by regressing exposure status against observed characteristics to create a matched analytical sample. PSM prioritizes similarities on variables that are strong predictors of the treatment. In common applications of PSM in the epidemiology and economics literatures, the PSM point estimates are the difference in mean outcomes between exposed and unexposed persons in the matched analytical sample.
A recently introduced alternative, coarsened exact matching (CEM) (3), matches observations not on a single variable (the propensity of exposure) but rather on the measured characteristics themselves, which can be “coarsened” (binned into categories) to facilitate matching. The uncoarsened variables are included as covariates in an outcome regression model in the matched analytical sample (3). The literature suggests that CEM typically outperforms PSM in achieving the best “balance” (the fewest differences in distribution of observed covariates between matched exposed and unexposed observations (1, 7, 8)). However, in previous work, investigators noted that methods which produce the best “balance” do not necessarily lead to inferences with the least bias (9, 10); whether bias in inferences is reduced by CEM as compared with PSM is unknown.
Prior analyses using experimental data found that matching did not lead to superior inferences compared with OLS (11–13). However, little work has used simulations to compare matching methods with covariate-adjusted OLS regression to identify which methods, under which circumstances, produce unbiased inferences at the expected type I error rate of 5% (6, 14).
We used simulated data sets for which the true relationship between the exposure and the outcome was null to compare inferences derived from PSM, CEM, and OLS. We systematically varied data-structure common support, the relationship between x1 and the exposure and/or outcome, exposure prevalence, and analytical model specification/misspecification to evaluate the methods’ comparative performance.
METHODS
Data generation
We simulated 9 data structures with 20,000 observations, a dichotomous exposure A, 2 continuous confounders x1 and x2, and a continuous outcome Y (data-generating equations and exceptions are noted in the Web Appendix and Web Figure 1, available at https://academic.oup.com/aje); we created 10,000 replications of each data structure. In all data structures, the true relationship between the exposure (A) and the outcome (Y) was null (Figure 2). The default data structure had a linear relationship between x1 and x2 (correlation approximately 0.25), x1 and the exposure, x1 and the outcome, x2 and the exposure, and x2 and the outcome, and an approximate 50:50 ratio of exposed observations to unexposed observations. From this default data structure, we systematically varied common support, the relationship between x1 and the exposure and/or outcome, and the prevalence of the exposure.
Figure 2.
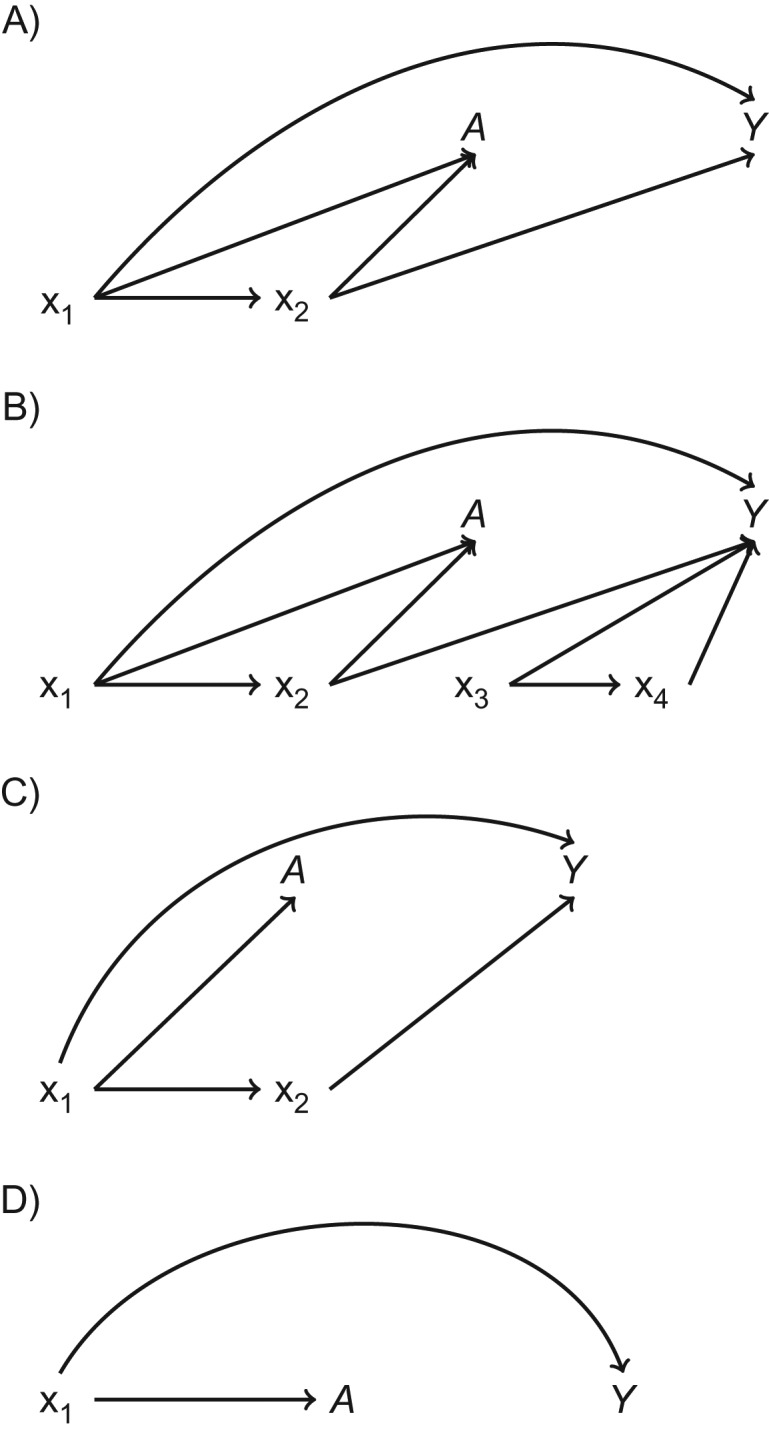
Directed acyclic graphs of data structures simulated to evaluate the performance of matching methods as compared with unmatched ordinary least squares regression. We simulated 9 distinct data structures that are represented by 4 directed acyclic graphs. A) “Confounder-outcome linear” data structures (data structures 1 and 2). B) “Confounder-outcome quadratic” data structures (data structures 3 and 4); we added the covariates x3 and x4 and dramatically increased the amount of random error (multiplied the error by 100; see Web Appendix and Web Figure 1B for data-generating equations) in order to evaluate the comparative performance of the methods when much of the variability in the outcome was not due to the confounders x1 and x2. C) Discontinuity data structures (data structures 5–7); the data-generating equations for the exposure do not include x2 (see Web Appendix and Web Figure 1C for data-generating equations). Although x2 is not included in the equation for the exposure in any of the discontinuity data structures, it is still a confounder for the exposure-outcome relationship because of its relationship with the exposure through x1. D) Exposure ratio 8:92 data structures (data structures 8 and 9); x2 is not included in the generation of the exposure or the outcome, so x2 is not a confounder.
We refer to the 9 data structures on the basis of the relationship we varied from the default state, as follows: confounder-outcome linear with 1) good and 2) poor common support, where the relationship between x1 and the outcome is linear (Figure 2A; Web Figure 1A); confounder-outcome quadratic with 3) good and 4) poor common support, where the relationship between x1 and the outcome is quadratic (Figure 2B; Web Figure 1B); 5) confounder-exposure discontinuity, where the relationship between x1 and the exposure included a discontinuity (Figure 2C; Web Figure 1C); 6) confounder-outcome discontinuity, where the relationship between x1 and the outcome included a discontinuity; 7) confounder-exposure and -outcome discontinuity, where the relationship between x1 and the exposure included a discontinuity and the relationship between x1 and the outcome included a discontinuity; 8) exposure ratio 8:92, confounder-outcome linear, where 8% of observations were exposed, 92% of the observations were unexposed, and the relationship between x1 and the outcome was linear (Figure 2D; Web Figure 1D); and 9) exposure ratio 8:92, confounder-outcome quadratic, where 8% of observations were exposed, 92% of the observations were unexposed, and the relationship between x1 and the outcome was quadratic. In the “exposure ratio 8:92” data structures, x1 is the only confounder (Figure 2D; Web Figure 1D). We varied the level of common support in some data structures, as matching methods are thought to have a comparative advantage over OLS when common support is poor (2, 4). We varied the prevalence of exposure in some data structures to more closely mimic applied analyses, where there are often many fewer exposed observations than unexposed observations (8, 15–17).
The data-generating equations are presented in Web Figure 1, and additional details on the data generation are presented in the Web Appendix and Web Table 1. In a subset of data structures (all presented online only), we systematically varied the correlation between the confounders x1 and x2 from 0.1 to 0.7.
Analytical approach
Within each simulated data set, PSM, CEM, and OLS were implemented using Stata 13 (StataCorp LLC, College Station, Texas). We used off-the-shelf Stata packages in these analyses to mimic approaches used by applied researchers. In all analytical models, the relationship between the confounder, x1, and the exposure, A, was assumed to be linear; by varying the data structures (as described above), we systematically varied analytical model specification/misspecification and confounding (in selected analytical models), to evaluate the methods’ comparative performance.
The analysis was implemented the same way across all data structures, with the exception of the unmeasured confounding analytical models, where the unmeasured confounder (i.e., either x1 or x2) was omitted from the analysis (all unmeasured-confounder results are presented online only). In all analytical models, the relationships between x1 and the exposure and x1 and the outcome were assumed to be linear across all data structures, which led to analytical model misspecification in some data structures as follows: the “confounder-outcome linear” 1) good and 2) poor common support data structure–analysis combinations were correctly specified; the “confounder-outcome quadratic” 3) good and 4) poor common support data structure–analysis combinations were misspecified because of the quadratic relationship between x1 and the outcome; the 5) “confounder-exposure discontinuity” data structure–analysis combination was misspecified because of a discontinuity in the relationship between x1 and the exposure; the 6) “confounder-outcome discontinuity” data structure–analysis combination was misspecified because of a discontinuity in the relationship between x1 and the outcome; the 7) “confounder-exposure and -outcome discontinuity” data structure–analysis combination was misspecified because of discontinuities in the relationship between x1 and the exposure and outcome; the 8) “exposure ratio 8:92, confounder-outcome linear” data structure–analysis combination was correctly specified; and the 9) “exposure ratio 8:92, confounder-outcome quadratic” data structure–analysis combination was misspecified because of a quadratic relationship between x1 and the outcome.
In supplemental analyses examining unmeasured confounding (evaluated in data structures 1–7), analytical model specification was the same, except that the unmeasured confounder was omitted from the analytical models (in data structures 8 and 9, x1 was the only confounder; see Figure 2 for directed acyclic graphs; data-generating equations are presented in the Web Appendix and Web Figure 1).
Propensity score matching
The propensity for exposure was estimated using a logit model that assumed a linear relationship between the confounders, x1 and x2, and the exposure, A. Exposed and unexposed observations were matched with replacement on their predicted probability of exposure (see Web Table 2 for distributions), using nearest-neighbor matching, and a caliper of 0.01 (sensitivity analyses examine other calipers). Frequency weights were applied to unexposed observations that were matched to multiple exposed observations, and nonmatches were excluded (see Web Table 3 for details on weights). The point estimate for the effect of the exposure, produced by the “psmatch2” package in Stata, was calculated as the difference between mean outcomes for the exposed and unexposed groups (the exposed group minus the unexposed group) in the weighted analytical sample. We did not use the alternative “teffects” command (18) because it can produce an error when implementing a caliper (19). We implemented PSM using the “psmatch2” package in Stata; software standard errors, discussed below, came from the “psmatch2” package.
The type I error rate was calculated as the proportion of t statistics (PSM point estimate/PSM standard error) greater than 1.96 or less than −1.96. As a robustness check, we additionally performed analyses using the propensity score as an inverse-probability-of-treatment weight (20).
Coarsened exact matching
CEM was implemented by coarsening the continuous confounders to the nearest integer. Exposed and unexposed observations were matched on the multivariate distribution of the coarsened confounders, and weights were applied so that the number of unexposed observations matched the number of exposed observations in each stratum (1); nonmatched exposed and unexposed observations were “pruned” from the analytical sample (given a weight of 0). The effect estimate was the coefficient for the exposure in a linear regression model that was adjusted for the uncoarsened version of the confounders (to adjust for any residual confounding from the coarsening) in the matched, weighted analytical sample (21); the software standard errors and P values were derived from the linear regression model, and the type I error rate was determined by the proportion of point estimates that were different from 0 (P < 0.05). We used the “cem” package in Stata to perform the matching (21).
OLS regression
Unmatched OLS regression was implemented by including the exposure A and the confounders x1 and x2 in a linear regression equation as independent variables and the outcome Y as the dependent variable. The software standard errors came from the linear regression model. The type I error rate was indicated by the proportion of point estimates that were different from 0 (P < 0.05).
Estimands
In OLS regression, the effect estimate is the average treatment effect, and point estimates are interpreted as the average effect of treatment that would be obtained if everyone were treated (or exposed) versus that which would be obtained if everyone were untreated (or unexposed); average treatment effect estimands are considered applicable to the population the underlying data represent. In our implementation of matching, the quantities estimated are the average treatment effect among the treated, because the untreated (or unexposed) observations are weighted to resemble the treated (or exposed) observations; average treatment effects among the treated estimands are considered applicable only to the treated/exposed population. However, if causal effects are constant over the unit of analysis, then the average treatment effect and the average treatment effect among the treated are the same (22). To fairly compare OLS and matching point estimates, we designed our data structures to have constant null effects (i.e., average treatment effect = average treatment effect among the treated = 0). Comparing estimates from OLS and matching methods is important, even though estimates reflect relationships in different populations (i.e., total sample vs. matched sample), because these are the comparisons made by applied researchers (6, 8, 15, 23).
Comparison metrics
We compared the balance of the analytical samples produced by the 3 approaches, point estimates, standard errors, and type I error proportions across analytical approaches. We compared the point estimate with the expected value of 0 (i.e., a null relationship between the exposure and the outcome). We evaluated both the software standard errors and the gold standard empirical standard errors across approaches. The software standard errors are discussed in the “Analytical approach” section above. The empirical standard errors were calculated as the standard deviation of the point estimates for each method across 10,000 simulations. By comparing the mean empirical standard error (i.e., the standard deviation of the point estimate) with the mean software standard error, we can determine whether the software standard errors are estimated accurately. The type I error proportion was compared with the expected value of 5%. In this paper, we consider inferences “biased” if the type I error rate does not approximate 5%.
RESULTS
Point estimates
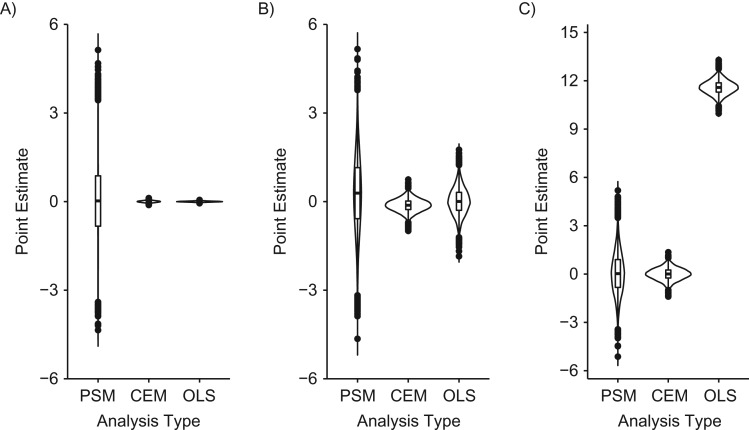
Point estimates from PSM, CEM, and OLS were unbiased on average in multiple scenarios when all confounders were measured (less than or equal to ±0.90 for all 3 methods, given a true effect of 0 (Table 1, Figures 3–6)). PSM estimates varied the most across simulations (Figures 3–6); for example, when analytical models were applied to the “confounder-outcome linear, good support” data structure (data structure 1), the distribution of PSM estimates was much wider (standard deviation (SD), 0.11) than that for CEM (SD, 0.01) or OLS (SD, 0.01) (Table 1). When common support was poor, both PSM and CEM had a wider distribution of estimates than OLS across simulations; for example, when analytical models were applied to the “confounder-outcome quadratic, poor support” data structure (data structure 4), PSM estimates had a standard deviation of 64.89, CEM estimates had a standard deviation of 36.18, and OLS estimates had a standard deviation of 21.90 across simulations (Table 1).
Table 1.
Distributions of Comparison Metrics Produced by Propensity Score Matching, Coarsened Exact Matching, and Ordinary Least Squares Regression When All Confounders Are Measured
| Data Structure and Analytical Model | Mean Point Estimate (SD, Empirical SE)a | Mean Software SE | Type I Error, % | Mean Analytical Sample Size (n) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data Structureb | Analysis Model as Applied to Data Structurec | PSM | CEM | OLS | PSM | CEM | OLS | PSM | CEM | OLS | PSMd | CEM | OLS |
| 1. Confounder-outcome linear, good support | Correctly specified | 0.00 (0.11) | 0.00 (0.01) | 0.00 (0.01) | 0.14 | 0.01 | 0.01 | 0.8 | 5.2 | 5.2 | 20,000 | 19,952 | 20,000 |
| 2. Confounder-outcome linear, poor support | Correctly specified | 0.02 (0.66) | 0.00 (0.02) | 0.00 (0.02) | 0.85 | 0.01 | 0.02 | 1.6 | 18.2 | 4.8 | 19,938 | 19,652 | 20,000 |
| 3. Confounder-outcome quadratic, good support | Misspecified | −0.56 (26.91) | −0.30 (21.15) | −0.25 (18.28) | 32.57 | 17.28 | 18.52 | 3.2 | 11.0 | 4.9 | 19,970 | 19,567 | 20,000 |
| 4. Confounder-outcome quadratic, poor support | Misspecified | 0.88 (64.89) | 0.08 (36.18) | 0.18 (21.90) | 92.26 | 17.94 | 21.69 | 7.9 | 32.9 | 5.4 | 19,864 | 18,176 | 20,000 |
| 5. Confounder-exposure discontinuity | Misspecified | 0.04 (1.27) | 0.00 (0.03) | 0.00 (0.02) | 1.39 | 0.01 | 0.02 | 3.6 | 33.0 | 5.2 | 25,534 | 19,764 | 20,000 |
| 6. Confounder-outcome discontinuitye | Misspecified | 0.27 (1.29) | −0.13 (0.21) | 0.01 (0.45) | 1.86 | 0.29 | 0.52 | 3.5 | 2.1 | 2.5 | 19,895 | 19,493 | 20,000 |
| 7. Confounder-exposure and -outcome discontinuity | Misspecified | 0.05 (1.28) | 0.00 (0.37) | 11.59 (0.43) | 1.39 | 0.42 | 0.46 | 3.5 | 2.3 | 100.0 | 25,534 | 19,763 | 20,000 |
| 8. Exposure ratio 8:92, confounder-outcome linear | Correctly specified | 0.56 (439.65) | 0.00 (0.13) | 0.00 (0.03) | 547.87 | 0.13 | 0.03 | 1.7 | 6.3 | 4.7 | 3,410 | 248 | 20,000 |
| 9. Exposure ratio 8:92, confounder-outcome quadratic | Misspecified | 36.92 (482.75) | −127.02 (53.76) | 130,394.90 (2,264.48) | 750.41 | 490.30 | 1,415.84 | 2.0 | 0.0 | 100.0 | 3,411 | 249 | 20,000 |
Abbreviations: CEM, coarsened exact matching; OLS, ordinary least squares; PSM, propensity score matching; SD, standard deviation; SE, standard error.
a The empirical SE equals the SD of the point estimates across 10,000 replications. This empirical SE is the gold standard (as opposed to the SE produced by the software). By comparing the mean empirical SE (i.e., the SD of the point estimate) with the mean software SE, we can determine whether the software SE is estimated accurately.
b In all data structures, the true relationship between the exposure and the outcome was null.
c The analysis was implemented in the same way across all 9 data structures, assuming a linear relationship between x1 and the exposure and x1 and the outcome. When applied to the various data structures, the same analysis model could either be correctly specified or misspecified. Additional details on the nature of the misspecification are provided in the “Analytical approach” subsection of the Methods section.
d Our implementation of PSM weighs the number of unexposed observations to equal the number of exposed observations, so the analytical sample size is double the number of exposed observations for which a match exists within the caliper we set of 0.01. Therefore, the size of the PSM analytical sample is always double the number of included exposed observations, and it sometimes exceeds the total number of observations in the original sample.
e See Web Table 4 for more details on the results from the “confounder-outcome discontinuity” data structure.
Figure 3.
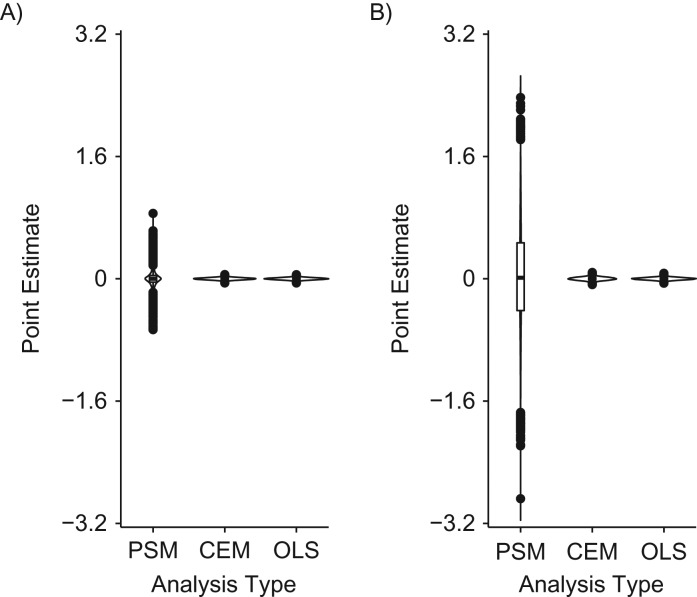
Distribution of propensity score matching (PSM), coarsened exact matching (CEM), and ordinary least squares (OLS) regression point estimates in data structures where the relationships between the confounders and the outcome are linear. A) “Confounder-outcome linear, good support” data structure (data structure 1); B) “confounder-outcome linear, poor support” data structure (data structure 2). PSM, CEM, and OLS estimates were unbiased, on average; however, the distribution of PSM point estimates was much larger than that of CEM or OLS estimates, particularly when common support was poor. Our proposed empirical “rule of thumb” indicates that OLS inferences are unbiased more often than matching inferences in these scenarios; that is, the OLS type I error rate approximates 5%, while the PSM and CEM type I error rates vary from the expected value of 5% (for CEM, this is only true in the “confounder-outcome linear, poor support” data structure (data structure 2)). See Table 1 for more information. The PSM point estimate is the difference in mean outcomes between the exposed and unexposed groups, while the CEM and OLS point estimates come from modeling the outcome; as a consequence, less information is used to calculate PSM point estimates than for CEM or OLS, resulting in a wider distribution of point estimates for PSM as compared with CEM or OLS.
Figure 6.
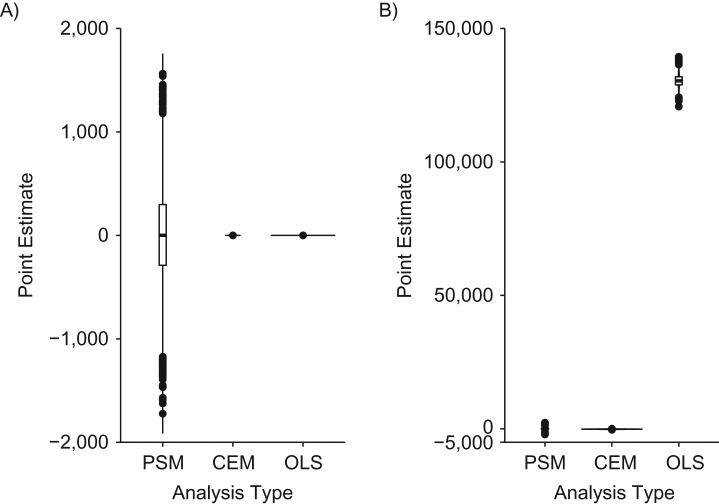
Distribution of propensity score matching (PSM), coarsened exact matching (CEM), and ordinary least squares (OLS) regression point estimates in data structures where the ratio of exposed observations to unexposed observations is 8:92. A) “Exposure ratio 8:92 confounder-outcome linear” data structure (data structure 8); B) “exposure ratio 8:92 confounder-outcome quadratic” data structure (data structure 9). PSM, CEM, and OLS point estimates were unbiased, on average, when applied to the “exposure ratio 8:92, confounder-outcome linear” data structure (data structure 8); however, the distribution of PSM estimates was larger than that of the CEM or OLS estimates. When analytical models were applied to the “exposure ratio 8:92, confounder-outcome quadratic” data structure (data structure 9), PSM and CEM point estimates were unbiased, on average, while OLS estimates were biased, on average. Our proposed empirical “rule of thumb” indicates that OLS inferences are unbiased more often than matching inferences in the first scenario (i.e., the type I error rate approximates 5%, while the PSM and CEM type I error rates vary from the expected 5%), while matching inferences are unbiased more often than OLS estimates in the second scenario (i.e., the OLS type I error rate is 100%, while the matching type I error rates are less than 5%; see Table 1 for more information).
Figure 4.
Distribution of propensity score matching (PSM), coarsened exact matching (CEM), and ordinary least squares (OLS) regression point estimates in data structures where the relationships between the confounders and the outcome are quadratic. A) “Confounder-outcome quadratic, good support” data structure (data structure 3); B) “confounder-outcome quadratic, poor support” data structure (data structure 4). PSM, CEM, and OLS point estimates were unbiased, on average; however, the distribution of PSM point estimates was larger than that of CEM or OLS estimates, particularly when common support was poor. Our proposed empirical “rule of thumb” indicates that OLS inferences are unbiased more often than matching inferences in these scenarios; that is, the OLS type I error rate approximates 5%, while the PSM and CEM type I error rates vary from the expected value of 5%. See Table 1 for more information.
In 2 of the 9 data structure–analysis combinations, OLS point estimates were biased. When analytical models were applied to the “confounder-exposure and -outcome discontinuity” data structure (data structure 7), PSM and CEM estimates were unbiased, on average (mean PSM estimate = 0.05 (SD, 1.28); mean CEM estimate = 0.00 (SD, 0.37) (Table 1, Figure 5C)), while OLS estimates were biased, on average (mean OLS point estimate = 11.59 (SD, 0.43) (Table 1, Figure 5C); see Web Table 4 for more details on the outcome discontinuity data structure). When analytical models were applied to the “exposure ratio 8:92, confounder-outcome quadratic” data structure (data structure 9), PSM and CEM estimates were unbiased, on average (mean PSM estimate = 36.92 (SD, 482.75); mean CEM estimate = −127.02 (SD, 53.76) (Table 1, Figure 6B)), while OLS estimates were biased, on average (mean OLS estimate = 130,394.90 (SD, 2,264.48) (Table 1, Figure 6B)).
Figure 5.
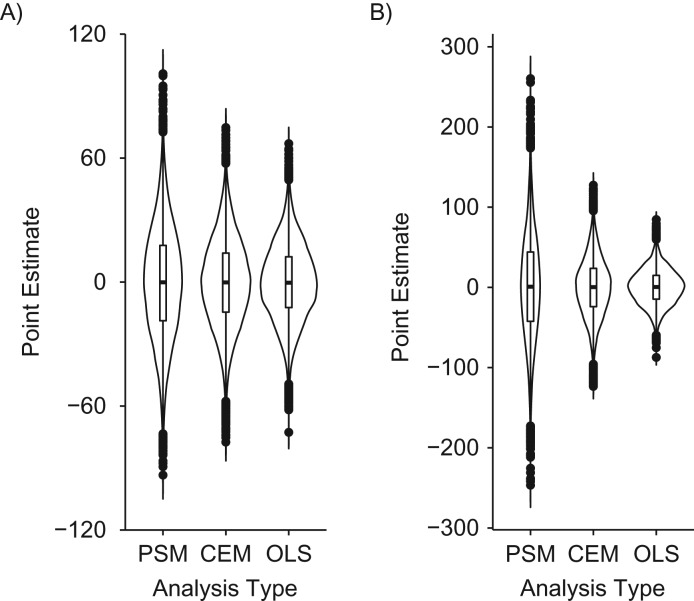
Distribution of propensity score matching (PSM), coarsened exact matching (CEM), and ordinary least squares (OLS) regression point estimates in data structures where the relationships between the confounders and the exposure and/or outcome variables include discontinuities. A) “Confounder-exposure discontinuity” data structure (data structure 5); B) “confounder-outcome discontinuity” data structure (data structure 6); C) “confounder-exposure and -outcome discontinuity” data structure (data structure 7). PSM, CEM, and OLS point estimates were unbiased, on average, when applied to the “confounder-exposure discontinuity” and “confounder-outcome discontinuity” data structures (data structures 5 and 6, respectively); however, the distribution of PSM estimates was larger than that of CEM or OLS estimates. When analytical models were applied to the “confounder-exposure and -outcome discontinuity” data structure (data structure 7), PSM and CEM estimates were unbiased, on average, while the OLS estimates were biased, on average. Our proposed empirical “rule of thumb” indicates that OLS inferences are unbiased more often than matching inferences in the first 2 scenarios (i.e., the OLS type I error rate approximates 5% in the “confounder-exposure discontinuity” data structure; see Web Table 4 for more details on the “confounder-outcome discontinuity” data structure), while matching inferences are unbiased more often than OLS estimates in the third scenario (i.e., the OLS type I error rate is 100%, while the matching type I error rates are less than 5%; see Table 1 for more information).
Standard errors
We recorded both the software standard error and the empirical standard error (the gold standard). For PSM, the mean software standard error was larger than the mean empirical standard error in all data structure–analysis combinations examined (Table 1). Additionally, the PSM standard errors, both software-derived and empirical, were consistently larger than the CEM and OLS standard errors; an exception was the “exposure ratio 8:92, confounder-outcome quadratic” data structure (data structure 9), where the OLS software and empirical standard errors were larger than those from PSM.
For CEM, the mean software standard errors were generally smaller than the empirical standard errors, particularly when common support was poor. For example, in the “confounder-outcome linear, poor support” data structure (data structure 2), the mean CEM empirical standard error was 0.02, while the mean CEM software standard error was 0.01 (Table 1; see Web Figure 2 for depictions).
For OLS, the software standard errors approximated the empirical standard errors (Table 1).
For all 3 methods, when analytical models were applied to the outcome discontinuity data structures (data structures 6 and 7) and the “exposure ratio 8:92, confounder outcome quadratic” data structure (data structure 9), software standard errors were larger than the empirical standard errors (Table 1).
Type I error
Type I error rates that did not approximate 5% indicated biased inferences. The type I error rate was generally the lowest for PSM (given large software standard errors), followed by OLS (usually around 5%; exceptions noted below), and largest for CEM (given the small software standard errors). When analytical models were applied to the “confounder-outcome linear, good support” data structure (data structure 1), the PSM type I error rate was 0.8% (vs. the expected 5%), while OLS and CEM both had type I error rates of 5.2% (Table 1). When common support was poor, the type I error rate for CEM was larger than that for OLS or PSM; when analytical models were applied to the “confounder-outcome linear, poor support” data structure (data structure 2), the type I error was 18.2% for CEM, 4.8% for OLS, and 1.6% for PSM. The CEM type I error rate was smaller than that of PSM or OLS only when there was a discontinuity in the outcome; for example, when analytical models were applied to the “confounder-outcome discontinuity” data structure (data structure 6), the CEM type I error rate was 2.1%, as compared with 2.5% for OLS and 3.5% for PSM (Table 1). Similarly, when analytical models were applied to the “exposure ratio 8:92, confounder-outcome quadratic” data structure (data structure 9), the CEM type I error rate was 0%, as compared with 1.96% for PSM and 100% for OLS (Table 1).
Unmeasured confounders
In the presence of unmeasured confounding, point estimates were equally biased across analytical approaches (Web Table 5). Metrics of performance improved for all methods as the correlation between covariates increased, and the measured confounder provided a better proxy for the unmeasured confounder (Web Table 6).
Robustness checks
We performed robustness checks by repeating these analyses using different calipers for implementing PSM (Web Table 7) and using inverse probably weighting as the analytical approach (Web Table 8). Results were not qualitatively changed. The OLS analytical sample had the worst balance, CEM had the best balance, and the balance of PSM was in-between (Web Table 9).
DISCUSSION
We compared 2 popular matching methods and OLS in scenarios that may be common in social science research and therefore have important implications for research. We found that matching inferences were often biased in comparison with OLS, particularly when common support was poor. When point estimates from OLS and matching methods were similar, PSM was statistically inefficient, while CEM type I error rates were higher than expected in comparison with OLS inferences; in other scenarios, OLS estimates and inferences were biased in comparison with matching methods. We suggest similarity in point estimates as an empirical “rule of thumb” for deciding when to use matching methods: If OLS and matching point estimates are similar (i.e., confidence intervals overlap), results suggest that OLS inferences are unbiased compared with matching inferences; however, if OLS and matching point estimates are dissimilar (i.e., confidence intervals do not overlap), results suggest that matching inferences are unbiased compared with OLS inferences. Our findings suggest that matching should only be implemented when a specific case can be made for its relevance, consistent with prior work finding that the benefits of matching are relatively narrow (14).
These results are consistent with the bias-variance trade-off: Matching purports to reduce bias by restricting the analysis to the range of support, but this reduction in bias comes at the expense of increased variance due to the reduction in sample size. When OLS estimates are unbiased, therefore, there are no comparative benefits to matching, while there are costs in the form of increased variance (assuming the matching standard errors are calculated correctly); only when OLS estimates are biased does matching present a comparative advantage.
OLS estimates may be unbiased despite poor common support when the relationships between the covariates and the outcome are substantively similar in terms of regions on and off support. However, in this study, when the relationships between the covariates and the outcome were not substantively similar with regard to regions on and off support, OLS estimates (and inferences) were biased in comparison with matching estimates (and inferences). Our proposed “rule of thumb” can help applied researchers identify both scenarios. Reviews of prior literature in the PubMed (National Library of Medicine, Bethesda, Maryland), Science Citation Index (Clarivate Analytics, Philadelphia, Pennsylvania), MEDLINE (National Library of Medicine), and Embase (Elsevier BV, Amsterdam, the Netherlands) databases indicated that estimates from the PSM and OLS approaches were similar more than 85% of the time when both methods were applied (6, 23); our results suggest that OLS produces unbiased inferences more often than matching methods in these settings. However, similarity in OLS and matching point estimates does not necessarily mean the point estimates are unbiased—unbiased effect estimates for both OLS and matching methods rely on the strong, untestable assumption of no unmeasured confounding. If there are unmeasured confounders, our results suggest that both OLS and matching methods may result in estimates that are similarly biased.
Notably, standard errors from both PSM and CEM were erroneously calculated by software packages that are often used in applied analyses (16, 17, 24, 25). Compared with the empirical standard errors, PSM software standard errors overestimated the variance of PSM point estimates, resulting in statistical inefficiency and low type I error in our simulated data structures, where the true relationship between the exposure and the outcome was null. Conversely, CEM software standard errors underestimated the variance of the CEM point estimates, resulting in higher-than-expected type I error rates. The CEM software standard errors may be underestimating the variance of CEM estimates because the CEM estimates come from a weighted OLS regression in the matched analytical sample, which assumes that all observations in the matched sample are independent. However, the CEM procedure often applies weights greater than 1 to unexposed observations, resulting in multiple copies of an observation in the matched sample; assuming that observations are independent when they are correlated (or the same observation) can result in misleading inferences (26).
Relatedly, Ho et al. (22) argued that matching can be used as a method of preprocessing data to create a matched analytical sample with better balance. Our results are consistent with those of Ho et al. in finding that matching can sometimes be a useful tool with which to preprocess data. However, we found that applied frequency weights are not always appropriately accounted for in the postmatching calculation of the standard errors. Accurate estimation of both the point estimate and the standard error are critical for unbiased inferences.
Our analyses have important limitations. We implemented a subset of possible PSM and CEM methods; alternative approaches (e.g., full matching (9, 27)) may lead to different conclusions. In sensitivity analyses, we found that varying the PSM caliper did not affect our results. Rigorously comparing all possible PSM implementations was beyond the scope of our analysis—we sought to compare common applications of PSM to mimic typical economic and epidemiologic analyses. Similarly, we did not combine matching with outcome regression techniques (i.e., doubly robust estimation (28)). Prior work has suggested that doubly robust approaches may improve performance (9). Additionally, our simulated data sets were simple by design, to assist in understanding the drivers of better or worse performance, and to enable rigorous evaluation across multiple factors potentially influencing inferences. We simulated data structures with constant effects and binary, time-invariant treatments. We did not perform analyses in which data on the exposure, outcome, or covariates were missing or the outcome variable was noncontinuous; these are important scenarios for future study. Important strengths of these analyses include a better understanding of when matching methods outperform OLS in making unbiased inferences and an empirical “rule of thumb” to help applied researchers determine when to implement matching.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Center for Population Health Sciences, Stanford University, Palo Alto, California (Anusha M. Vable, Emmanuel F. Drabo, Sanjay Basu); Center for Primary Care and Outcomes Research, Department of Medicine, School of Medicine, Stanford University, Palo Alto, California (Anusha M. Vable, Emmanuel F. Drabo, Sanjay Basu); Department of Social and Behavioral Sciences, T.H. Chan School of Public Health, Harvard University, Boston, Massachusetts (Mathew V. Kiang, M. Maria Glymour); Department of Epidemiology and Biostatistics, University of California, San Francisco, San Francisco, California (M. Maria Glymour); Quantitative Sciences Unit, Department of Medicine, School of Medicine, Stanford University, Palo Alto, California (Joseph Rigdon); Department of Health Research and Policy, School of Medicine, Stanford University, Palo Alto, California (Sanjay Basu); Center for Primary Care, Harvard Medical School, Boston, Massachusetts (Sanjay Basu); and School of Public Heath, Imperial College London, London, United Kingdom (Sanjay Basu). A.M.V. is currently at the Department of Family and Community Medicine, School of Medicine, University of California, San Francisco, San Francisco, California.
This research was supported by the National Institute on Minority Health and Health Disparities (award DP2MD010478 to S.B.) and the Stanford Center on the Demography and Economics of Health and Aging pilot grants program (A.M.V.), under a parent award from the National Institute on Aging (award AG017253).
We thank Dr. Ellicott Matthay, Dr. Michael Baiocchi, and Stanford’s Quantitative Sciences Unit for prior reviews of the methodology and manuscript.
Portions of this work were presented at the 51st Annual Meeting of the Society for Epidemiologic Research in Baltimore, Maryland, June 19–22, 2018. All data generation and analysis code is available on GitHub (https://github.com/anushavable).
Conflict of interest: none declared.
Abbreviations
- CEM
coarsened exact matching
- OLS
ordinary least squares
- PSM
propensity score matching
- SD
standard deviation
REFERENCES
- 1. King G, Nielsen R, Coberley C, et al. Comparative effectiveness of matching methods for causal inference. 2011. http://j.mp/2nydGlv. Updated December 9, 2011. Accessed May 5, 2014.
- 2. Stuart EA. Matching methods for causal inference: a review and a look forward. Stat Sci. 2010;25(1):1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Iacus SM, King G, Porro G. Causal inference without balance checking: coarsened exact matching. Polit Anal. 2012;20(1):1–24. [Google Scholar]
- 4. Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70(1):41–55. [Google Scholar]
- 5. Arceneaux K, Gerber AS, Green DP. A cautionary note on the use of matching to estimate causal effects: an empirical example comparing matching estimates to an experimental benchmark. Sociol Methods Res. 2010;39(2):256–282. [Google Scholar]
- 6. Stürmer T, Joshi M, Glynn RJ, et al. . A review of the application of propensity score methods yielded increasing use, advantages in specific settings, but not substantially different estimates compared with conventional multivariable methods. J Clin Epidemiol. 2006;59(5):437–447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. King G, Nielsen R Why propensity scores should not be used for matching. 2016. http://j.mp/2ovYGsW. Updated January 6, 2016. Accessed February 10, 2016.
- 8. Vable AM, Kiang MV, Basu S et al. . Military service, childhood socio-economic status, and late-life lung function: Korean War era military service associated with smaller disparities. Mil Med. 2018;183(9–10):e576–e582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Colson KE, Rudolph KE, Zimmerman SC, et al. . Optimizing matching and analysis combinations for estimating causal effects. Sci Rep. 2016;6:23222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Lee BK, Lessler J, Stuart EA. Improving propensity score weighting using machine learning. Stat Med. 2010;29(3):337–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Arceneaux K, Gerber AS, Green DP. Comparing experimental and matching methods using a large-scale voter mobilization experiment. Polit Anal. 2006;14(1):37–62. [Google Scholar]
- 12. Bloom HS, Michalopoulos C, Hill CJ, et al. . Can propensity-score methods match the findings from a random assignment evaluation of mandatory welfare-to-work programs? Rev Econ Stat. 2004;86(1):156–179. [Google Scholar]
- 13. Glazerman S, Levy DM, Myers D. Nonexperimental versus experimental estimates of earnings impacts. Ann Am Acad Pol Soc Sci. 2003;589(1):63–93. [Google Scholar]
- 14. Miller MK. The case against matching. 2013. https://pages.shanti.virginia.edu/PolMeth/files/2013/07/Miller.pdf. Updated July 9, 2013. Accessed September 5, 2018.
- 15. Vable AM, Canning D, Glymour MM, et al. . Can social policy influence socioeconomic disparities? Korean War GI Bill eligibility and markers of depression. Ann Epidemiol. 2016;26(2):129–135.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Vable AM, Kawachi I, Canning D, et al. . Are there spillover effects from the GI Bill? The mental health of wives of Korean War veterans. PLoS One. 2016;11(5):e0154203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Johnson PJ, Oakes JM, Anderton DL. Neighborhood poverty and American Indian infant death: are the effects identifiable? Ann Epidemiol. 2008;18(7):552–559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. StataCorp LP Stata Treatment-Effects Reference Manual: Potential Outcomes/Counterfactual Outcomes. College Station, TX: StataCorp LP; 2013. [Google Scholar]
- 19. Cunningham S. st: teffects, caliper, propensity score matching. 2014. https://www.stata.com/statalist/archive/2014-02/msg01225.html#. Accessed September 5, 2017.
- 20. Robins JM, Hernán MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11(5):550–560. [DOI] [PubMed] [Google Scholar]
- 21. Blackwell M, Iacus SM, King G, et al. . Cem: coarsened exact matching in Stata. Stata J. 2009;9(4):524–546. [Google Scholar]
- 22. Ho DE, Imai K, King G, et al. . Matching as nonparametric preprocessing for reducing model dependence in parametric causal inference. Polit Anal. 2007;15(3):199–236. [Google Scholar]
- 23. Shah BR, Laupacis A, Hux JE, et al. . Propensity score methods gave similar results to traditional regression modeling in observational studies: a systematic review. J Clin Epidemiol. 2005;58(6):550–559. [DOI] [PubMed] [Google Scholar]
- 24. Quesnel-Vallée A, DeHaney S, Ciampi A. Temporary work and depressive symptoms: a propensity score analysis. Soc Sci Med. 2010;70(12):1982–1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Prescott HC, Langa KM, Iwashyna TJ. Readmission diagnoses after hospitalization for severe sepsis and other acute medical conditions. JAMA. 2015;313(10):1055–1057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Fitzmaurice GM, Laird NM, Ware JH. Applied Longitudinal Aanalysis. 2nd ed Hoboken, NJ: John Wiley & Sons, Inc.; 2011. [Google Scholar]
- 27. Hansen BB. Full matching in an observational study of coaching for the SAT. J Am Stat Assoc. 2004;99(467):609–618. [Google Scholar]
- 28. Funk MJ, Westreich D, Wiesen C, et al. . Doubly robust estimation of causal effects. Am J Epidemiol. 2011;173(7):761–767. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.