Simultaneous Singlet–Singlet and Triplet–Singlet Förster Resonance Energy Transfer from a Single Donor Material

Abstract

For almost 70 years, Förster resonance energy transfer (FRET) has been investigated, implemented into nowadays experimental nanoscience techniques, and considered in a manifold of optics, photonics, and optoelectronics applications. Here, we demonstrate for the first time simultaneous and efficient energy transfer from both donating singlet and triplet states of a single photoluminescent molecular species. Using a biluminescent donor that can emit with high yield from both excited states at room temperature allows application of the FRET framework to such a bimodal system. It serves as an exclusive model system where the spatial origin of energy transfer is exactly the same for both donating spin states involved. Of paramount significance are the facts that both transfers can easily be observed by eye and that Förster theory is successfully applied to state lifetimes spanning over 8 orders of magnitude.

Förster resonance energy transfer (FRET) has found its way into various fields of natural sciences and is extensively used in biology and polymer research as a “spectroscopic ruler”.¹⁻³ Equally important, it is one of the few energy transfer mechanisms to be considered in various photonic^4,5 and optoelectronic⁶⁻⁹ systems when energy conversion steps are at play. Recently, FRET has been utilized in a novel emitter concept for organic light-emitting diodes (OLEDs) termed thermally activated delayed fluorescence (TADF)-assisted fluorescence (TAF; also called “hyperfluorescence”), which suggests 100% internal quantum efficiencies and enhanced color purity.¹⁰ The mechanism, whose theoretical description was first proposed by Förster in the 1940s, allows measurement of distances up to 10 nm and is based on nonradiative dipole–dipole coupling of energy-donating and -accepting molecules.¹¹ The restriction in distance is due to the energy transfer rate

1

being dependent on the inverse sixth power of the donor–acceptor separation r. The Förster radius is denoted by R_F and the pure donor decay rate as k_D.

Most studies of FRET focus on singlet–singlet (S–S) transfer because the dipole–dipole coupling is naturally associated with the allowed transitions between singlet states.^3,12,13 When spin–orbit coupling is strong, however, the triplet–singlet (T–S) transitions can obtain appreciable dipole strength too, enabling triplet states to be involved with a similar mechanism to S–S FRET.¹⁴⁻¹⁷ In this Letter, we use a biluminescent donor to show for the first time two FRET processes taking place simultaneously from both the excited singlet and triplet states of the same donating molecular species to the acceptor’s singlet. Furthermore, our analysis allows us to rule out the competing triplet–triplet (T–T) energy transfer^17,18 as an additional energy transfer route.

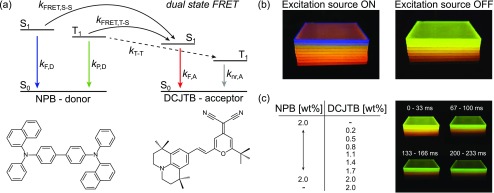
Biluminescence refers to the emission property of certain organic molecules being able to emit significant amounts of light from both their excited triplet and singlet states at room temperature. In our experiments, we use NPB [N,N′-di(naphtha-1-yl)-N,N′-diphenylbenzidine] embedded in a rigid polymer matrix of PMMA [poly(methyl methacrylate)] to suppress nonradiative triplet depopulation.^19,20 As the accepting molecule, the fluorescent dye DCJTB [4-(dicyanomethylene)- 2-tert-butyl-6-(1,1,7,7-tetramethyljulolidyl-9-enyl)-4H-pyran] is introduced into the host–guest system (Figure 1a).

Figure 1.

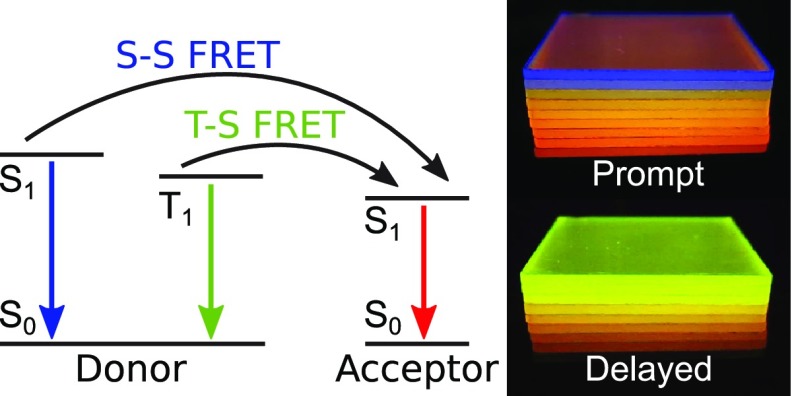
(a) Simplified energy state diagram of the donor–acceptor system, indicating dual-state FRET (k_FRET), spontaneous decay (k_F and k_P), and potential T–T transfer (k_T–T). Qualitatively, the arrows’ colors refer to the corresponding emission spectrum of radiative decays. (b) Verification of S–S and T–S FRET by eye, using different acceptor concentrations. (c) Afterglow characteristics depending on acceptor concentration (see the SI videos for the side-by-side and stacked samples).

Figure 1a shows the energy state system in our blend. Relaxed donor electrons get excited into higher singlet states by a 365 nm UV-LED and depopulate via several channels including radiative and nonradiative decay, intersystem crossing (ISC), and electron transfer (ET). The donor’s triplet, populated by ISC, decays also either radiatively, nonradiatively, or by again showing an ET rate toward the acceptor. Reverse ISC is not taken into account because the large S–T splitting of the donor NPB of ΔE_ST ≃ 0.55 eV²¹ renders this rate ineffective. As stated earlier, ET is incorporated by additional decay rates k_FRET,S–S, k_FRET,T–S, and k_T–T. As T–T transfer is a well-established phenomenon in organic host–guest systems,²²⁻²⁴ we considered it to be present in our blend (cf. Figure 1a). However, as we will see, apart from the indicated Förster transfers, no additional species of nonradiative ET appears to be of significant influence here. For the following analysis, the excited-state dynamics of donor and acceptor blends are considered to be governed by linear processes only, excluding excitonic annihilation.^22,25−27

The biluminescent nature of our material allows one to image simultaneous S–S and T–S transfers by eye. Figure 1b,c presents a series of material blends that are photoexcited under a nitrogen atmosphere, preventing oxygen quenching (see the SI for detailed information on sample preparation and data evaluation methods).²⁸ Under continuous-wave (CW) illumination (excitation source ON), the emission wavelength shifts with increasing amounts of acceptor concentration from blue (pure NPB luminescence, dominated by singlet emission) over orange to red (pure DCJTB fluorescence), indicating S–S transfer. Using a pulsed excitation, the afterglow intensity (excitation source OFF) decreases with increasing DCJTB content because more energy is transferred from the long-living donor triplet state onto the short-living acceptor singlet state (T–S transfer). Moreover, also the afterglow spectrum shifts from green (pure NPB phosphorescence) toward red (pure DCJTB fluorescence).

Now, the question arises what type of transfer is considerable because FRET is not a priori the only possibility. First, the energy of excited electrons can of course be mediated optically by photons. So-called radiative energy transfer is not spin-restrictive and of infinite range. Second, Förster and Dexter found spin-restricted transfer mechanisms based on Coulomb coupling and electron tunneling, respectively.^11,18 While Dexter’s occurs on the Angström scale and requires total spin conservation, FRET can overcome distances up to 10 nm and demands spin conservation of both the donor and acceptor separately. The latter statement might lead to the assumption that, while S–S FRET comes naturally, T–S FRET is not possible. This holds only true if the donor triplet deactivation is strictly forbidden, hence, does not possess an oscillator strength that is the basis for the diplole–dipole coupling of FRET. In the present donor material NPB, the triplet state shows efficient phosphorescence,^20,28 consequently sporting two potential FRET donor states. Furthermore, PMMA as a matrix prevents small-molecule aggregation and ensures donor–acceptor distances of more than 1 nm. Thus, we consider Dexter-type transfer to play a negligible role only, which will be proven further below.

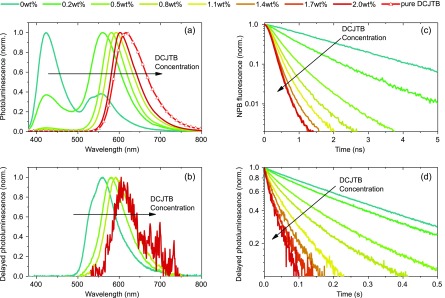
The differentiation from radiative transfer can be achieved by donor lifetime measurements. Figure 2 shows not only the discussed spectral shift for both states with increasing acceptor concentration, as shown earlier for fluorescence only,²⁹ but also the decrease of donor lifetimes on nanosecond and second time scales for singlet and triplet states, respectively. This temporal evolution is a clear signature for nonradiative ETs because radiative transfer would conserve the donor lifetimes. The following data analysis will even rule out radiative ET quantitatively. The respective donor-only decays of singlet and triplet states (cf. Figure 2c,d) do not show significant signs of nonlinearities, supporting the above assumption of a linear description of the system.

Figure 2.

Spectroscopic data taken at room temperature and in nitrogen for material blends consisting of 2 wt % donor and the indicated concentration of acceptor molecules. (a) CW illumination shows a red shift in emission wavelength with increasing acceptor concentration, indicating a transfer from the donor’s energy states toward the acceptor’s singlet. (b) The same holds true when examining only delayed spectra. Looking at the donor’s lifetime, one can see a decrease with increasing acceptor concentration for both the singlet (c) and triplet (d) state. Even though the delayed PL transients contain contributions from both molecular species, the figure still represents the donor’s triplet population because the acceptor’s singlet lifetime is in the nanosecond range. Note that all images are raw data, deconvoluted for further investigation in the case of (c).

From a change in lifetime, one can calculate the Förster transfer efficiency via

2

where ⟨τ_DA⟩ and ⟨τ_D⟩ are the donor’s amplitude-weighted lifetimes with and without acceptor, respectively.^30,31Equation 3 becomes important for extracting R_F from donor lifetimes. It features γ as a function of R_F

4

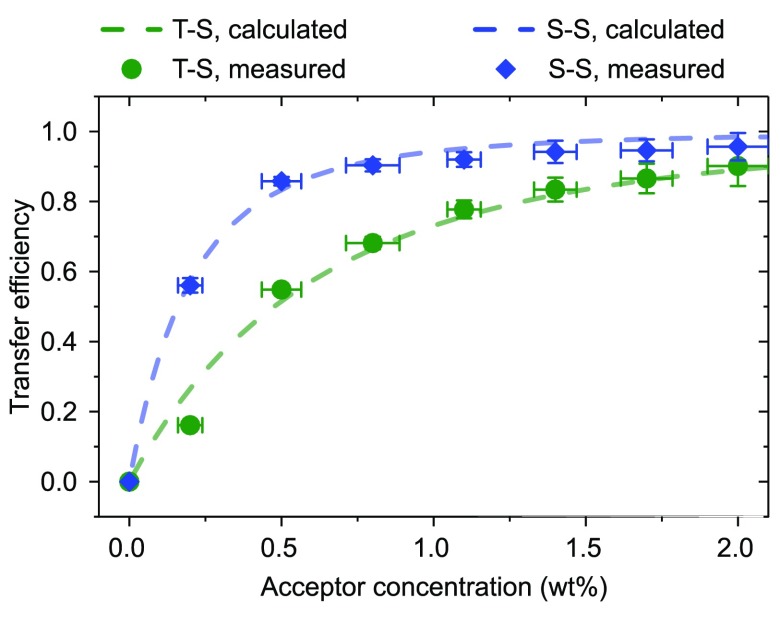
with C and Γ being the acceptor concentration and complete gamma function, respectively.³¹ The fluorescence transients with increasing acceptor concentration (cf. Figure 2c) were recorded using a time-correlated single-photon counting (TCSPC) setup. The triplet originating energy transfer was investigated by monitoring the transients of the integrated delayed photoluminescence using a silicon photodetector to reach high enough signals. The latter approach is valid as the rate-limiting persistent phosphorescence of the NPB donor is mapped onto the nanosecond-fast singlet states of DCJTB. Both sets of transients are fitted using biexponentials to extract their amplitude-weighted lifetimes³¹ (cf. SI Table 1). The concentration-dependent transfer efficiency can be calculated by eq 2. For extraction of R_F, one fits eq 3 to these transfer efficiency values with Φ_ET = Φ_ET(R_F), with R_F being the fit parameter³¹ (cf. Figure 3). The method yields R_F,S–S = 3.6 ± 0.1 nm and R_F,T–S = 2.5 ± 0.1 nm.

Figure 3.

Transfer efficiency determined for different acceptor concentrations. Dots are calculated from transient lifetimes and dashed lines with eq 3 using R_F as the fit parameter. Error bars for the concentration are mainly statistical pipetting uncertainties during sample preparation. Error bars for the efficiency indicate solely fitting deviations.

Figure 3 illustrates remaining problems despite the deconvolution operation of TCSPC data (see the SI for further information on data deconvolution). For acceptor concentrations above 1 wt %, the initial NPB singlet lifetime of ∼1.8 ns sinks toward the excitation laser decay time of about 100 ps. This induces a significant error, and the experimental transfer efficiency does not entirely approach unity. The error bars in efficiency do not consider that but only fitting uncertainties.

In order to check the liability of those values and to further exclude possible Dexter transfer influences, we determined singlet and triplet Förster radii by calculation and compared them to the values found above. As introduced by Förster, photophysical properties of the donor and acceptor are sufficient to determine their respective transfer characteristics.³²

The Förster radius, R_F, can be calculated using

5

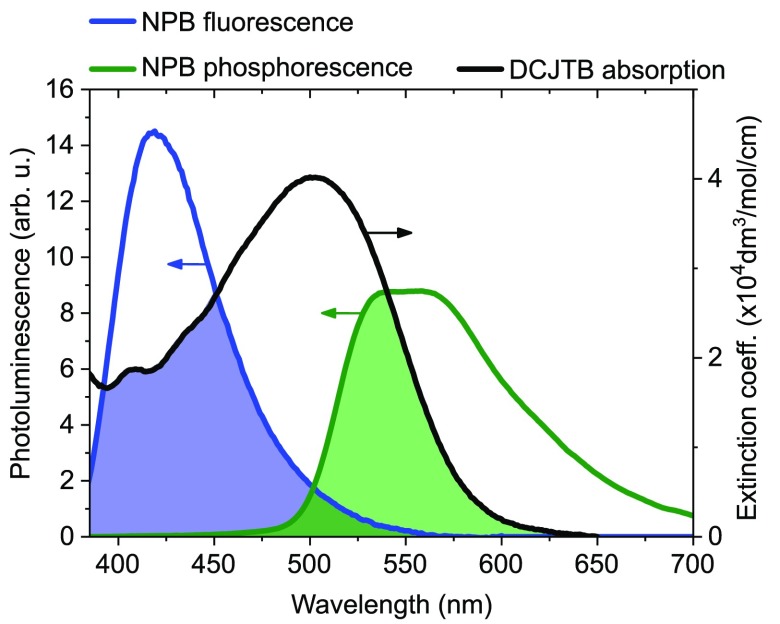
where κ represents the orientation factor of a molecular dipole, Φ_D the donor’s quantum yield, n the host’s refractive index, and J the overlap integral. J is a measure for how well donor emission and acceptor absorption overlap and implements the acceptor’s molar absorption ϵ_A(λ) and the donor’s area-normalized emission spectra.³³ The latter has to be normalized to unity and the former to the molar extinction coefficient, which is ϵ_max = 4.02 × 10⁴/(mol  cm) for DCJTB.³⁴

The overlap integrals were calculated to be J_S–S = 1.09 × 10¹⁵ and J_T–S = 1.23 × 10¹⁵ in units of (dm³ nm⁴)/(mol cm). Figure 4 depicts the emission–absorption overlap for fluorescence and phosphorescence. Note that even though the blue shaded area seems bigger J incorporates a factor λ⁴, and thus, J_T–S yields a higher value. As we assume our luminophores to be well-separated and randomly oriented during excitation, κ² = 0.476 has to be chosen.^31,35 The refractive index n of PMMA, which is by far the most prominent material in the blend, is about 1.5 ± 0.1 in the wavelength range of interaction.³⁶ Singlet and triplet quantum yields Φ_S = 0.28 ± 0.01 and Φ_T = 0.03 ± 0.01 of NPB were determined.³⁷ A minor deviation of those values to earlier values published from our lab²⁸ is due to different sample preparation recipes. Using eq 5, we determined R_F,S–S = 3.7 ± 0.2 nm and R_F,T–S = 2.6 ± 0.2 nm, which agree very well with the lifetime measurement results. This perfect agreement of the lifetime-extracted Förster radii with the calculated ones leads to the conclusion that potential Dexter-type transfer paths, e.g., T–T transfer, are negligible. In other words, the overall energy transfer scheme presented does not include a contribution to a “dark” terminal state (DCJTB triplet). This finding is also of key importance for the recently proposed emitter concept TAF for OLEDs,¹⁰ where such a k_D,T–T would result in an inherent exciton loss channel. However, for TAF OLED emission layers, the case might be different as the donor in such a system is typically not diluted but rather makes up the matrix material.

Figure 4.

Overlap of emission and absorption characteristics for both fluorescence (blue) and phosphorescence (green).

Finally, we want to provide a rudimentary model for theoretical understanding. The rate diagram presented in Figure 1a can be transferred into a system of differential equations. Annihilation processes are neglected so far, and only FRET and intrinsic decay, i.e., radiative and nonradiative depopulation in the absence of acceptors, are taken into account. For simulation, donor molecules and the appropriate amount of acceptors (depending on the concentration) were placed randomly in a virtual volume of respective size. Using R_F as calculated above, k_FRET was determined for every donor–acceptor combination via eq 1 for both S–S and T–S transfer. Now, for each donor molecule i, the singlet [S₁]_i and triplet [T₁]_i state populations were calculated, incorporating FRET to acceptors j.

6

7

The energy transferred from donor molecules i in turn populates acceptors j, which is represented by the following equation

8

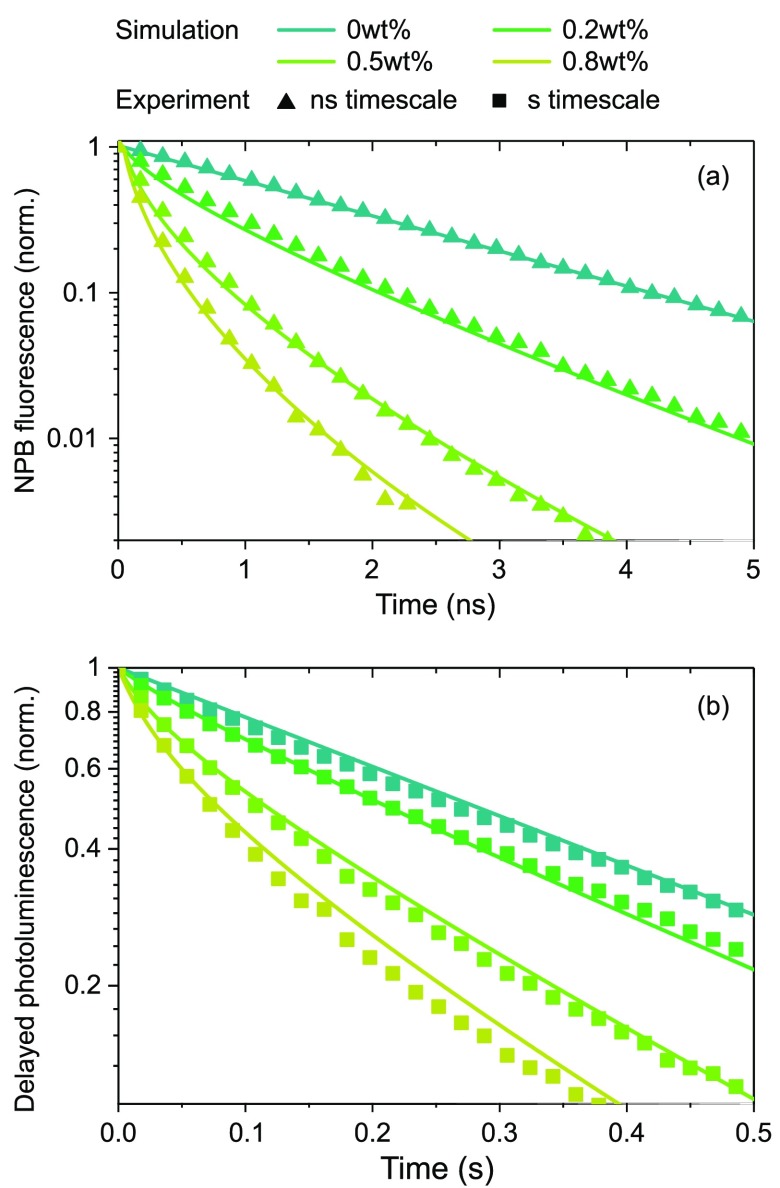
The lifetimes τ_i and τ_j are intrinsic, i.e., taken from pure NPB and DCJTB films, respectively (see the SI for extra information). Solving those equations numerically for all molecules yields total donor state populations over time, corresponding to the emitted photon count that can be related to the measured transient signal with good agreement (cf. Figure 5 and the SI for further details).

Figure 5.

Transients of donor state decay for the (a) singlet state and (b) triplet state. Lines were obtained solving the state population in eqs 6–8 numerically using R_F as calculated above, and symbols are from the experiment.

In conclusion, we have shown a dual-state FRET process taking place simultaneously from two spin states of the same donor species toward the singlet state of an acceptor molecule. Notably, the FRET framework yields a consistent description despite the fact that the NPB donor singlet and triplet lifetimes differ by about 8 orders of magnitude, demonstrating again the high generality of Förster’s theory. This large difference in lifetimes even allows differentiation of the two separate channels with the naked eye. Within the Förster framework, the lifetime measurements yielding the Förster radii dynamically show excellent agreement with the respective static values derived from spectroscopic overlap. In a simulation based on a simplified rate system using the experimentally determined Förster radii only, the excited-state dynamics of both spin manifolds could be modeled with the same random distribution of donor and acceptor sites. Apparently, annihilation and back-transfer processes can be rendered unimportant for the conditions used. It proves that neglecting ETs to the acceptor’s triplet is a valid approach, thus providing evidence that T–T transfer does not play a significant role. The concept of dual-state FRET can be provided by any biluminescent material and acceptor combination, featuring the required spectral overlap, opening up a versatile and general pathway to bring together energy transfer and exciton spin mixing.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.8b03668.

• Experimental and sample preparation details, deconvolution of the TCSPC signal, and rate model simulations (PDF)

• Video showing the thin film samples in a side-by-side comparison (MP4)

• Video showing all thin film samples with a variation of donor (NPB) and acceptor (DCJTB) concentrations in a vertical arrangement (MP4)

The authors declare no competing financial interest.