Generation Time, Net Reproductive Rate, and Growth in Stage-age Structured Populations

Abstract

Major insights into the relationship between life history features and fitness have come from Lotka’s proof that population growth rate is determined by the level (expected amount) of reproduction and the average timing of reproduction of an individual. But this classical result is limited to age-structured populations. Here we generalize this result to populations structured by stage and age by providing a new unique measure of reproductive timing (T_c) that, along with net reproductive rate (R₀), has a direct mathematical relationship to, and approximates, growth rate (r). We use simple examples to show how reproductive timing T_c and level R₀ are shaped by stage-dynamics (individual trait changes), selection on the trait, and parent-offspring phenotypic correlation. We also show how population structure can affect dispersion in reproduction among ages and stages. These macroscopic features of the life history determine population growth rate r, and reveal a complex interplay of trait dynamics, timing and level of reproduction. Our results contribute to a new framework of population and evolutionary dynamics in stage-and-age structured populations.

Introduction

How do individual life histories (vital rates) determine fitness? As Fisher (1930) famously discussed, when survivorship and fertility vary with age, fitness is the stable population growth rate r that solves Lotka’s equation. For age-structured populations, Lotka’s equation is now easily solved on a computer, but that does not provide an understanding of the relationship between fitness and the structure of a life history. In fact, much broad understanding of life history patterns relies on a simpler equation, $r\simeq (\log R_0/T_c)$, derived by Dublin & Lotka (1925). Here R₀, the expected lifetime reproduction of an individual, measures the level of reproduction in a life history, whereas T_c, the average age at which an individual reproduces, measures the timing of reproduction in the life history. These cohort parameters are computed directly from age-specific vital rates (see Table 1) and predict fitness r. Over many decades demographers and biologists have gained qualitative insight into the relationship between the age-pattern of survival and reproduction, on the one hand, and the macroscopic parameters R₀ and T_c, on the other. The level R₀ describes reproductive investment and the timing T_c describes the speed of a life history as well as its response to temporal variation. The relationship between these macroscopic parameters and fitness now underlies discussions of life history trade-offs, strategies, and environmental response (Southwood, 1988; May, 1976), comparative analyses of life histories and their evolution (Stearns, 1992; Tuljapurkar et al., 2009a; Jones et al., 2008), phylogenetic studies of life history change (Bielby et al., 2007; Cooper & Purvis, 2010; Evans et al., 2012), and human demography (Dublin & Lotka, 1925; Coale, 1972; Keyfitz, 1977; Keyfitz & Caswell, 2005).

Table 1:

Age-Only: Cohorts and Fitness

Quantity	Equation	Notes
Age	a = 1, 2,… Newborns are in age-class 1	Discrete age classes counted at a census
Survival probability	pa, Probability of surviving from a to a + 1
Survivorship	la, Probability of being alive at age a	Here, l1 = 1; l2 = p1 l1, l3 = p2 l2, etc.
Fertility	fa, Number of offspring of an individual of age a that recruit as newborns in next census
Stable Population	A population with unchanging age-structure and exponential growth rate r	Fitness equals r
Lotka’s equation	$1={\sum }_a{e}^{-ra}{l}_a{f}_a$	Largest real solution is r. Also known as Leslie equation.
Cohort	Group of individuals born together	Any cohort is a stable cohort; all its off-spring are age 1
Level of Reproduction by a Cohort	$R_0={\sum }_a{l}_a{f}_a$	Also called the Net Reproductive Rate
Age-distribution of Cohort Reproduction	${\varphi }_a=\frac{l_a{f}_a}{R_0}$	Fraction of cohort reproduction that occurs at age a. And ${\sum }_a{\varphi }_a=1$
Mean Age of Reproduction by a Cohort	$T_c={\sum }_{a}a{\varphi }_a$	Also called Cohort Generation Time
Mean Square Age of Reproduction	${\mu }_2={\sum }_a{a}^2{\varphi }_a$
Age-dispersion of Re- production	$V_a=({\mu }_2-T_c^2)$
Dublin-Lotka approximation	r1 = (log R0/Tc)
Dublin-Lotka: a better approximation	$r_2=r_1+V_a{(\log R_0)}^2/2T_c^3$

However life history analysis based on age ignores other traits that can influence survival and reproduction (Horvitz & Tuljapurkar, 2008; Caswell, 2001). Well-known examples are size in plants (Hoffmann, 1999), development stages in insects or birds (Hu & Tessier, 1995; Steiner et al., 2010), body mass in mammals (Coulson et al., 2010), and body-mass index in humans (Preston et al., 2012). We use “stage” to refer to all such traits (quantitative or qualitative, e.g., behavioural, physiological, developmental, morphological, (epi-)genetical, or geographical) as discussed by Caswell (2001). We assume, in general, that offspring can be produced in many stages, e.g., many different sizes, or different kinds as in seeds versus vegetative ramets, or in different locations. In recent decades stage-and-age structured models, in both matrix and integral population (IPM) forms (Cochran & Ellner, 1992; Caswell, 2001; Ellner & Rees, 2007; Steiner et al., 2010, 2012; Tuljapurkar et al., 2012) have provided a rich and useful description of population dynamics and life history evolution. For such models, matrix methods (Caswell, 2012) have been developed to compute r and its sensitivity to model parameters; and also for the sensitivity analysis of life span (Steiner et al., 2012).

We seek to generalize the Dublin-Lotka connection between level, timing and r. No such generalization has been obtained previously, to our knowledge. Indeed, it is not obvious that such a link must exist for stage- or stage-age-structured models. Why? The classical result relies on a central property of age-structured demography: that population growth rate solves the scalar Lotka equation (Table 1), so that r depends on the numbers f_a l_a (at age a, fertility is f_a and survivorship is l_a). Dublin-Lotka exploited this link to derive their expression for r, and the derivation identifies both R₀ and T_c. But for a stage-and-age structured model, survival and reproduction can vary with stage and age. In such cases, population growth is necessarily described by a matrix-vector equation that simultaneously determines growth rate (r) and the stable stage distribution (a vector u₁) of newborns. That equation cannot be analyzed in the same way as Lotka’s much simpler scalar equation, so there has been no progress in generalizing the Dublin-Lotka result.

For a general stage-and-age structured life history, can we find an equation for r that does not involve the stage distribution of newborns? If so, does that equation lead to an approximation that predicts r from the vital rates? Does that approximation identify canonical measures of the level (which we call R₀) and the timing (which we call T_c) of reproduction?

We show here that the answer to all three questions is yes. We prove that $r\simeq (\log R_0/T_c)$, where R₀ (old symbol but new definition) turns out to be the known average level of cohort reproduction (Cochran & Ellner, 1992; Caswell, 2001; Lebreton, 1996; Rogers, 1975) – this is satisfying but not a priori obvious. We also identify the quantity T_c (again, old symbol but new definition) that measures the speed of a life history, and turns out to be the average age of reproduction for a stationary cohort. These canonical macroscopic parameters are the only ones that approximate r as (log R₀/T_c). Our results go further. For age-structure, Dublin & Lotka (1925) found a better approximation to r that includes the age-dispersion of reproduction. Here we establish an analogous result that incorporates the stage and age dispersion of reproduction. Thus we identify for the first time, for stage-age structured populations, unique measures of timing that yield a direct mathematical relationship to, and approximation of, growth rate r. Note that our results immediately apply to stage-only populations.

Our results link life history components (stage-dependent growth and development, survival, reproduction, and parent-offspring transmission) and the speed of a life history, the level of reproduction, or both. This linkage will make possible a deeper understanding of the biological processes underlying the trade-offs and constraints that pervade the discussion of life histories. Developing a broad intuition about these processes in diverse life histories will require further work, but our analysis is a necessary first step.

Below we start by introducing stage-age structured models and an important concept, the stable cohort. We highlight why stage-structured stable cohorts differ from age-only cohorts. Next we present our main result that goes from vital rates to r, and discuss our measures of timing and level of reproduction. We show how our results illuminate the alternative possible measures of generation time discussed by Caswell (2001). We illustrate our results using three examples:

1. We show how our timing measures provide new information for stage-only models, using a stage-only model for Killer whales taken from Caswell (2001) based on Brault & Caswell (1993), see Fig. 1a.

2. We show how fitness varies with selection, growth and parent-offspring correlation, using a simple model with two age-classes and four size classes, see Fig. 1b.

3. We show how population structure can significantly affect dispersion, using a population model with migration between two spatial patches in which there are different age-dependent vital rates (Fig. 1c). This example also shows that our analysis can be used to understand growth rates in spatially distributed populations with dispersal.

Figure 1.

Life cycle for a) a stage-only structured population, the killer whale, with four stages (yearling, juvenile, mature female, postreproductive female), b) for a simple stage (size) and age structured population (Example II), with two ages and four stages (size 1 to 4), and c) a two patch (location=stage) structured population with limited dispersal among patches (Example III). In Example II (b), individuals are born (age 1) small (size 1), or large (size 2) and mainly reproduce small (size 1) offspring. If they survive they can grow to small (size 3) or large (size 4) two year olds. After the second year all individuals die. Reproduction at age 2 is higher compared to age 1. In Exapmle III, individuals in one patch (e.g. valley bottoms) reproduce more offspring early in life versus later in life, while in the other patch (e.g. mountain tops) reproduction increases throughout life. Adults are philopatric to their patch, but 10% of the offspring disperse to the other patch. Survival increases and decreases with age in both patches, but is higher in the mountain top patch.

Our description of vital rates and population growth follows mainly Coulson et al. (2010) but builds on earlier work (Le Bras, 1971; Rogers, 1975; Lebreton, 1996; Childs et al., 2004; Ellner & Rees, 2006). The text and tables present the results; mathematical details are in the Appendix.

Stage-Age Structure

Individual Vital Rates

We work with discrete time and age, and so with matrices. However our results apply to integral operators for continuous stages under the conditions given by Ellner & Rees (2006). At time t a census enumerates newborns (ages 0–1) in age class 1, and individuals in all higher age classes a = 2, 3, …, (see Appendix for terminal age). We use “age” and “age-class” interchangeably: a newborn arrives at age a = 1, moves to age 2 after one time interval, and so on. For convenience Table 1 summarizes known results for age-only models, where only age specific survival and fertility rates are known.

For stage-age structured populations we assume that an individual (we follow only females) of a given age a is in one of many discrete stages z (readers who use integral models should note that our discrete intervals can simply be considered bins on a continuous stage space). A population census at time t yields numbers n_a(z, t) for all ages a and stages z. For example, the number of newborns in stage z at time t is n₁(z, t). Stages are indicated by the symbols y, z.

Stage-age structured vital rates comprise information about one or multiple traits and their influence on survival, reproduction, trait change (dynamic across life), and the transmission of the trait from parent to offspring which can be due to processes including genetic inheritance, epigenetics, and maternal effects. All of these influences can change with age, and are captured by four relationships (summarized in Table 2) that can be estimated directly from data, as explained by Coulson et al. (2010). In what follows, the reader may find it helpful to think about an example in which stage is just size (see, e.g. Fig. 1b).

Table 2:

Stage and Age: Vital Rates

Quantity	Equation	Notes
Age	a = 1, 2,… Newborns are in age-class 1
Stage	y or z = 1, 2,… An individual has both stage and age. Stage-and-age composition counted at a census	Stages may include several dimensions (e.g., size & developmental state)
Total Recruitment	Ma(z), Number of offspring of age a, stage-z individual that recruit as newborns in next census
Inheritance	Da(y, z), Fraction of Ma(z) off-spring that is born into newborn stage y	Parent-offspring transmission function ${\sum }_y{D}_a(y,z)=1$
Fertility	Fa(y, z) = Da(y, z) Ma(z). Elements of matrix Fa	Number of stage-y recruits produced by a stage-z parent of age a
Survival probability	Sa(z), Probability that individual in stage z at age a survives to a + 1
Growth	Ga(y, z), Probability that individual in stage z at age a changes stage to y at a + 1.	Conditional on survival, so ${\sum }_y{G}_a(y,z)=1$
Stage Transition Matrix	Pa(y, z) = Ga(y, z) Sa(z), Probability that individual in stage z at age a is alive in stage y at a + 1. Elements of matrix Pa	Includes survival and stage change (e.g. growth).
Survivorship	La(y, z), Probability that newborn arriving in stage z is alive in stage y at age a. Elements of matrix La. Here L1(y, z) = 1 if y = z and zero else	L1 = I = the identity matrix. L2 = P1 L1, L3 = P2 L2, etc.

The preceding vital rates are used to assemble two matrices for each age (see Table 2).

1. Fertility F_a at age a is the number of stage-y offspring of age 1 produced by a stage-z parent of age a. This matrix (see Table 2) is determined by (i) the total number of offspring M_a(z) produced by a stage-z individual at age a, and (ii) the stage distribution of offspring: for a stage-z individual at age a, D_a(y, z) is the fraction of this individual’s offspring that is born into newborn stage y (clearly ${\sum }_y{D}_a(y,z)=1$).

2. Survivorship L_a is a matrix of cumulative survival probabilities from birth (at age 1) to age a. The matrix element L_a(y, z) is the probability that an individual born in stage z is alive in stage y at age a. An individual moves from stage-z at age a to stage-y at age (a+1) if (i) it survives with probability S_a(z), and (ii) changes stage from z to y with probability G_a(y, z) (so that ${\sum }_y{G}_a(y,z)=1$). The combined probabilities P_a(y, z) = G_a(y, z) S_a(z) of surviving and moving from stage-z at age a to stage-y at age (a + 1) are elements of a survival matrix P_a. In the convention used here, individuals are born into age class 1, which means that L₁ is just the identity matrix (see Table 2). Then L₂ = P₁ L₁ and so on, as shown in Table 2.

Note that in an age-only model stages do not matter. Instead of matrices, at each age a fertility is a number f_a and survivorship is also a number l_a.

Finding r: The First Step

Any initial population structure –be they age-only, stage-only or stage-age structured–converges to a stable population whose growth rate is r (for stage structured populations see also Table 3, Appendix, and (Lebreton, 1996; Rogers, 1975)). Stage structured populations have stable proportions of newborns in each stage, represented in a vector u₁. For any r define (Table 3) a renewal matrix,

$$\mathbf{A}(r)=\sum _a{e}^{-ra}{\mathbf{F}}_a{\mathbf{L}}_a.$$ (1)

Then the stable growth rate and population structure are together determined by solving

$$\mathbf{A}(r){\mathbf{u}}_1={\mathbf{u}}_1.$$ (2)

This equation, unfortunately, contains two unknowns: r and the vector u₁.

Table 3:

Stage and Age: Stable Population

Quantity	Equation	Notes
Stable Population	A population with unchanging stage-and-age structure and exponential growth rate r	Fitness equals r
Stable Stage-structure	In stable population, each age a has unchanging stage structure. New-borns have stable stage-structure u1. Then can deduce stable stage-structure for every age	If only age matters, There is effectively just one stage, and u1 collapses to a number
Renewal equation	${\sum }_a{e}^{-ra}{\mathbf{F}}_a{\mathbf{L}}_a{\mathbf{u}}_1={\mathbf{u}}_1$	Says that discounted reproduction by stable stage-structure must produce same structure
Renewal matrix	$\mathbf{A}(r)={\sum }_a{e}^{-ra}{\mathbf{F}}_a{\mathbf{L}}_a$	This matrix has dominant eigenvalue 1 and corresponding right eigenvector u1

We can find r numerically by tracking the population at every age (not just newborns) in terms of a large (higher dimensional) matrix whose dominant eigenvalue is e^r, as discussed and explored by Caswell (2012). But if we want an analytical connection between r and the matrices of fertility and stage-transition, we are led to a characteristic equation that is intractable.

Notice that (2) shows that the renewal matrix (for the stable growth rate) has dominant eigenvalue equal to 1. Equivalently, the logarithm of the dominant eigenvalue of A(r) is 0 and we use this fact to find an equation that determines r but does not contain u₁ (Appendix). When r is small, we can expand the latter equation (Appendix) to find the approximation we seek.

Stable Generations and Stable Cohorts

If age is all that matters, individuals born together are considered identical and make a birth cohort whose lifetime reproduction is readily described as in Table 1 just by age specific survival and reproduction. But when stage also matters, individuals in the same birth cohort can differ in their birth stage (e.g., by size, by kind as with plant seeds or vegetative ramets, or by location). Because birth stage affects subsequent survival, growth, and reproduction, two cohorts with different stage compositions but equal total number will produce different numbers of offspring. What happens to such differences as we look forward in time?

Newborns in the first offspring generation go on to produce offspring over their lives; the latter is the second offspring generation, grand-offspring of our original cohort. The number of individuals in successive offspring generations is determined by (see Appendix for more detail) the generation matrix

$${\mathbf{A}}_0=\sum _{a\ge 1}{\mathbf{F}}_a{\mathbf{L}}_a.$$ (3)

This matrix A₀ has three important properties (see Appendix for details) that are summarized in Table 4:

1. A dominant eigenvalue R₀. The total number of individuals in successive offspring generations will – eventually – change at the geometric growth rate R₀. Thus if R₀ > 1 any initial cohort will produce descendant generations that increase in the long-run, and vice-versa.

2. A corresponding right eigenvector c that describes the stage-structure of offspring generations in the long-run – this unique stage-structure defines a stable cohort. We set the sum of the components of c to 1, so the number c(z) is the fraction of the stable cohort born into stage z.

3. A corresponding left eigenvector d that describes the generational reproductive value. If we add one newborn of stage z to our initial cohort then in the long-run the size of each offspring generation will increase by an amount proportional to d(z). We set the total reproductive value of a stable cohort to 1.

Table 4:

Stage and Age: Cohorts to Fitness

Quantity	Equation	Notes
Generation matrix	${\mathbf{A}}_0={\sum }_a{\mathbf{F}}_a{\mathbf{L}}_a$	Given a cohort, determines stage-composition of offspring
Dominant eigenvalue of A0	R0	Net Reproductive Rate
Corresponding right eigenvector of A0	c, dimension equals number of stages, sum of components = 1	Stage-structure of stable cohort
Corresponding left eigenvector of A0	d, dimension equals number of stages, normalized so that (d, c) = 1	Generational reproductive value of stages in a cohort
Stable Cohort	Newborn cohort structure c with stage-structure c	A stable cohort’s offspring generations grow at rate R0
Level of Reproduction by Stable Cohort	R0	Net Reproductive Rate
Age-distribution of Stable Cohort Reproduction	${\varphi }_a=({\mathbf{d}}^T{\mathbf{F}}_a{\mathbf{L}}_a\mathbf{c})/R_0$, superscript indicates transposed vector	Fraction of stable cohort’s reproduction that occurs at age a.
Mean Age of Reproduction by a Cohort	$T_c={\sum }_{a}a{\varphi }_a$	Also called Cohort Generation Time
Mean Square Age of Reproduction	${\mu }_2={\sum }_a{a}^2{\varphi }_a$
Age-dispersion of Reproduction	$V_a=({\mu }_2-T_c^2)$
Stage-dispersion of Reproduction	$V_s={\xi }_1-T_c^2$
	${\mathbf{B}}_1=(1/R_0){\sum }_{a}a{\mathbf{F}}_a{\mathbf{L}}_a$
	$\mathbf{Z}=\mathbf{c}\hspace{0.17em}{\mathbf{d}}^T$
	$\mathbf{h}={\{\mathbf{I}-([{\mathbf{A}}_0/R_0]-\mathbf{Z})\}}^{-1}$
	${\xi }_1=({\mathbf{d}}^T{\mathbf{B}}_1\mathbf{h}{\mathbf{B}}_1\mathbf{c})$
Simple stage-age structured approximation	$r_1=(\log R_0)/T_c$	R0 and Tc differ compared to Dublin-Lotka approximation
Better stage-age structured approximation	$r_2=r_1+[V_a+2V_s]{(\log R_0)}^2/2T_c^3$	takes age and stage dispersion of reproduction into account

In a stage-age structured life history, a stable cohort of newborns has the unique stage-structure c. Such a cohort – and only such a cohort – produces offspring generations that grow at exactly the rate R₀.

For an age-only model, A₀ reduces to the number ${\sum }_a{f}_a{l}_a=R_0$, and the vectors c, d are each replaced by the single number unity.

Reproduction by a Stable Cohort

A stable cohort’s stage-structure is c, and at age a the stable cohort produces a fraction ϕ_a of its total reproduction if we weight it by the stage-specific reproductive value d:

$${\varphi }_a=\frac{({\mathbf{d}}^T{\mathbf{F}}_a{\mathbf{L}}_a\mathbf{c})}{R_0}.$$ (4)

Here the superscript T indicates a transpose. The net reproductive rate R₀ is the dominant eigenvalue of the generation matrix, and clearly (see above, or Appendix) the fractions ϕ_a sum to 1. This equation generalizes the simple product of survivorship and fertility for an age-only life history (given in Table 1).

Using the age-distribution of reproduction ϕ_a we can obtain an average age of reproduction

$$T_c=\sum _{a}a{\varphi }_a.$$

The quantity

$${\mu }_2=\sum _a{a}^2{\varphi }_a,$$

is the mean-square age of reproduction, and the age dispersion $V_a=({\mu }_2-T_c^2)$ describes how much reproduction occurs earlier or later than the mean age T_c. We now relate the stable cohort’s reproduction to the population’s long-run growth rate. These measures depend on the stable cohort’s stage-distribution c and stage-dependent reproductive value d as determined by the age-stage variation in fertility and survivorship.

For an age-only model, ϕ_a = (f_a l_a)/R₀, and T_c, µ₂, and V_a depend only on the pattern of age variation.

From Vital Rates to r: Final Result

For general stage-age models, we find that the stable population growth rate is given by the series,

$$r=\frac{\log R_0}{T_c}+\frac{[V_a+2V_s]{(\log R_0)}^2}{2T_c^3}+O\left(\frac{{(\log R_0)}^3}{T_c^3}\right).$$ (5)

This precise mathematical relationship identifies measures that can be computed directly from the stage-age structured life history and predict r. The two explicit terms in (5) predict r well so long as R₀ is close to 1. This equation is a direct generalization of the corresponding result in age-only structured demography, and can be extended to higher order in log R₀ if desired (e.g. third right hand term in (5)).

The above equation relates r to macroscopic parameters that we now discuss (see also Table 4). The first two parameters describe the amount and average timing of a stable cohort’s reproduction:

• ILevel of Reproduction. This is measured by the quantity R₀ which is computed as the dominant eigenvalue of the generational matrix A₀. We have shown that this parameter is the rate of increase of offspring generations produced by a stable cohort. It is satisfying but not a priori obvious that this measure is identical to the known net reproductive rate described by Caswell (2001).
• IITiming of Reproduction. This is measured by the new quantity T_c that we have identified as cohort generation time, i.e., the average age of reproduction by a stable cohort (see (4) above and Table 4). This summary parameter measures life history speed, but is calculated differently than the generation time for purely age-structured populations.

These two parameters yield the simple approximation r = (log R₀/T_c). As we show by example below, with our defintions of level and timing this approximation performs quite well.

The second term on the right of (5) describes how two kinds of reproductive dispersion influence r.

• IIIAge-Dispersion. Individuals of age a produce (a weighted) total of ϕ_a offspring, and this will often vary with age. The variance $V_a=({\mu }_2-T_c^2)$ measures the age-dispersion of this total reproduction around the mean age of reproduction T_c. Larger age-dispersion of reproduction increases r, because early (relative to T_c) reproduction increases growth rate more than later reproduction reduces it.
• IVStage-Dispersion. Suppose now that reproductive individuals produce the same stage-distribution of offspring at every age (note: the total number of offspring can still vary with parental age and stage). Then the stable cohort’s stage-distribution c will simply be the common offspring stage-distribution. In mathematical terms, every column of the generation matrix A₀ must be proportional to the vector c. In this case, there can only be age-dispersion of reproduction. But what if parents of different ages produce distinct distributions of offspring (e.g. young individual produce smaller off-spring than old individuals)? Then the stage-distribution of the total number of offspring changes with age, producing a new kind of reproductive dispersion that can only happen in stage-age-structured populations.

How important is this stage-dispersion? Clearly, the stable cohort stage-distribution c is an average over the different age-specific stage-distributions. So the magnitude of this new reproductive stage-dispersion depends on a suitable measure of distance between the offspring stage-distributions at different ages and the stable stage-distribution c. In mathematical terms, this distance depends on how rapidly the offspring of a cohort with a non-stable stage-distribution will approach the stable stage-distribution c. Equivalently, how rapidly do powers of the generation matrix converge? We find that this rate of convergence determines the magnitude V_s of reproductive stage-dispersion (see Appendix). The value of V_s can be positive, negative, or zero (see Cohen (1979) for a similar distance measures).

In many mammalian populations, life cycle reproduction is dominated by parents in a range of prime ages and the stage-distribution of offspring varies only modestly with age. So in such cases we expect (and find in examples) that V_s is close to zero and V_a is much larger. However, the age-pattern of reproduction can vary greatly between stages that are different environments or spatial locations. As an example, we consider later a population living in two spatial patches linked by weak dispersal, where the age-pattern of reproduction is different in the two patches. In such cases V_s can be large relative to V_a.

Examples

Example I: A Stage-only Model

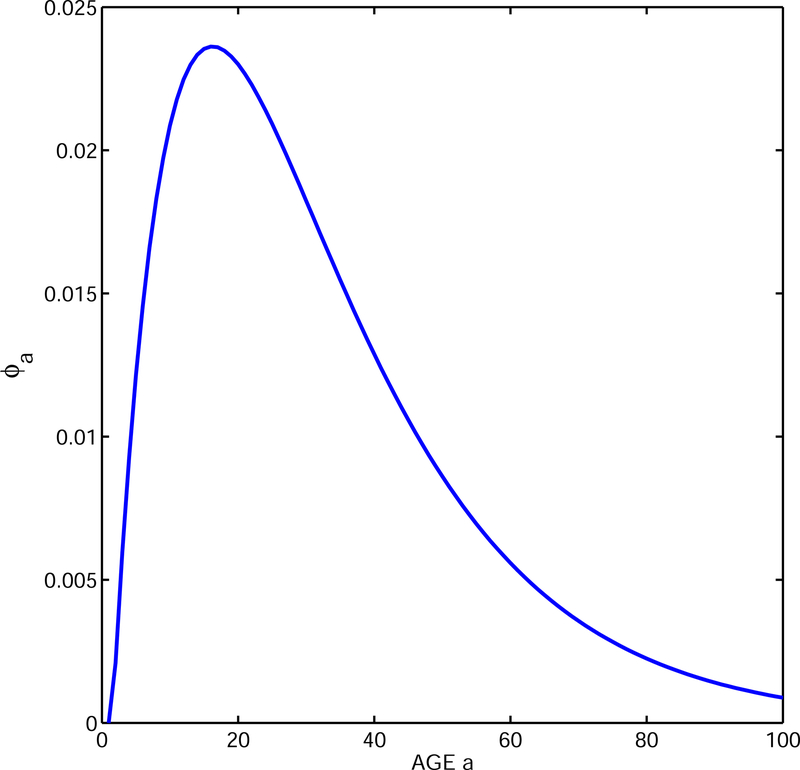
Consider the 4-stage model (no age variation) for Killer whales described in Caswell (2001) and based on Brault & Caswell (1993). The stages are yearlings, juveniles, mature females and post-reproductive females (Fig. 1a). There is only one stage of newborns so the single fertility matrix F has nonzero elements only in the first row, and there is a single survival (stage stransition) matrix P for every age. As Caswell explains, R₀ = 2.013 is the (1,1) element of the matrix FN where N = (I − P)⁻¹.

There is only one kind of newborn so c = d = (1, 0, 0, 0)^T where T indicates a transpose. Age is usually ignored in stage-only models but of course each individual has a chronological age, and L_a = P^(a−1) for ages a ≥ 1. Equation (4) then shows that at age a a stable cohort of these Killer whales will produce a fraction ϕ_a of its total reproduction, where

$${\varphi }_a=\frac{[(1,1)\hspace{0.17em}\text{element}\hspace{0.17em}\text{of}\hspace{0.17em}\text{matrix}\hspace{0.17em}\mathbf{F}{\mathbf{L}}_a]}{R_0},$$

and the result is plotted in Fig. 2. The Appendix, Table 3 and 4, present general formulas which yield new information: the stable cohort generation time is T_c = 32.2 and reproduction is highly dispersed by age (as obvious from Fig. 2) with dispersion $({\mu }_2-T_c^2)=22.86$. Given that there is only one stage of newborns, V_s = 0. The first term of equation (5) predicts a growth rate of 0.022 and the first two terms predict a growth rate of 0.026. A numerical calculation shows that r = 0.025 so the approximations perform well.

Figure 2.

Age-distribution of reproduction of a stable cohort of Killer whales. Note, this is a stage only structured model with only one kind of newborns (year-lings) produced.

Example II: Stages and Ages

The value of our formulas lies in showing how phenotypic variation affects the level and speed of life histories. How are these macroscopic properties affected by (i) selection on a phenotypic trait acting via survival or reproduction, (ii) the amount, timing, persistence and variability of ontogenetic change in the phenotype, (iii) age differences, e.g., as commonly found in mammals, young and senescent individuals produce smaller and/or fewer offspring than do prime-aged individuals (Coulson & Tuljapurkar, 2008), (iv) the phenotypic correlation between parents and offspring, e.g., when parents larger than average tend to produce offspring who are also larger than average (Coulson et al., 2010)? We illustrate with a simple example (Fig. 1b).

We consider a simple life cycle in which individuals are born as small young (stage 1, size z₁) or large young (stage 2, size z₂ > z₁), have low reproduction in their first year of life (a = 1), and if they survive grow to be small adults (stage 3, size z₃ > z₂) or large adults (stage 4, size z₄ > z₃) with higher reproduction (Fig. 1b, and Appendix). All individuals die at the end of the second year. An individual’s size and age affect survival, growth and reproduction:

1. Total reproduction at each age a increases with size, at a rate x (so, e.g., the fertility (m_a) of small young individuals is proportional to m₁ e^−x). We constrain the arithmetic average of the fertilities of small and large individuals to be m₁ = 0.5 at age 1 and m₂ = 1.1 at age 2. For weak selection we set x = 0.075 and for strong selection, x = 0.15. The difference between total offspring numbers produced by small versus larger individuals increases with x.

2. Survival from the first year to the second year depends on size and survival rate increases exponentially with size at rate w. For weak selection w = 0.075 and for strong selection w = 0.15. We constrain the arithmetic average of the survival rates of small and large young to be s₁ = 0.55 (first year survival).

3. Growth from age 1 to 2 depends on a probability g (see Appendix for more details) that relative size is maintained, i.e., that small (resp. large) young become small (resp. large) two year olds. We consider three cases. If there is no correlation between size and growth, g = 0.5 meaning that small or large young are equally likely to become small or large at age 2. If growth is positively correlated with size, we set g = 0.75, so that most small (resp. large) young become small (resp. large) adults. If there is over-compensatory growth, with small individuals growing much faster than large ones, there is a negative correlation between growth and size; here we set g = 0.25, so that most small (resp. large) young become large (resp. small) adults. In each case there is dispersion in growth.

4. Finally, the size-distribution of offspring (small or large) depends on the sizes and ages of their parents. We assume that individuals are not fully mature at age 1, so that m₁ < m₂, and furthermore small young parents make only small offspring, while large young parents make mostly (we use 80%) small offspring. At age 2, however, the fraction of offspring who inherit the relative size of their parent is allowed to vary, as described by a parameter d. When d = 0.5 there is no correlation between parent and offspring (half of the offspring are small and the other half are large, independent of the size of the two year old parent). If d = 1 there is perfect transmission of relative size. Note that small newborns may become large adults, so even if d = 1 we do not need to have perfect genetic heritability of birth size.

With this information we can formulate the matrices P₁, F₁ and F₂ that describe the model (see Appendix for details).

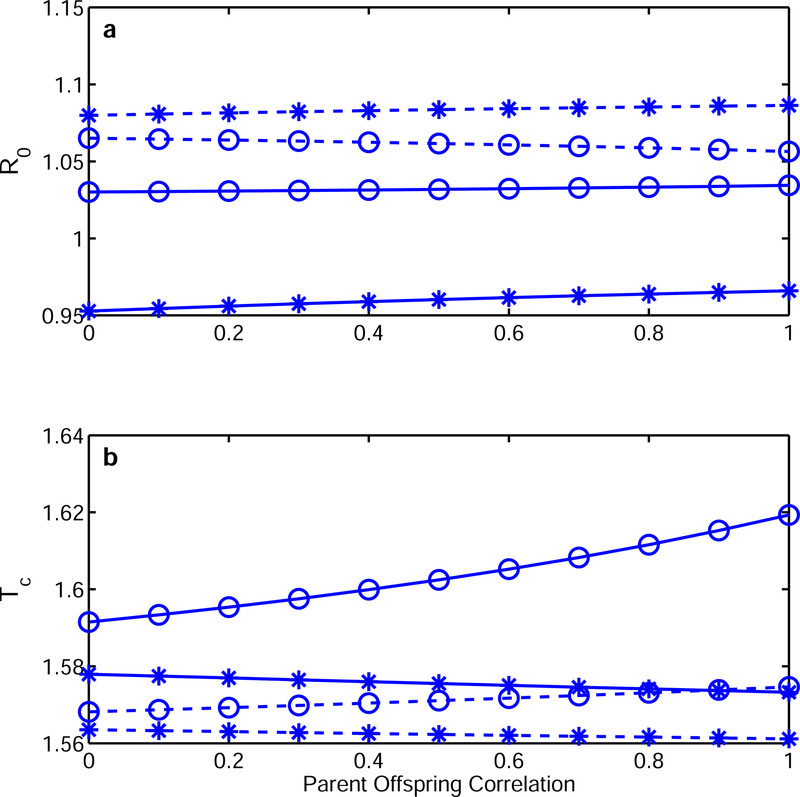
We focus on level R₀ and timing T_c because our approximation (5) accurately predicts r. For reference consider the neutral case: no selection, no growth correlation (g = 0.5 above) and no parent-offspring correlation at age 2 (so d = 0.5 above). In this case, R₀ = 1.105, T_c = 1.5475 and r = 0.0649. Fig. 3a shows how R₀ (on the vertical axis) changes with the parent-offspring correlation (on the horizontal), with dashed lines for weak selection, the solid lines for strong selection. Starred values obtain when there is negative correlation between growth and size; circles are values for the case of positive correlation between growth and size. Values for the case when there is no correlation between growth and size are intermediate between the preceding cases, and are not shown (for the neutral case there is also no correlation between growth and size). Fig. 3b shows corresponding values of T_c. The results were (to us) initially surprising, but led to a biological understanding.

Figure 3.

a) level of reproduction R₀ and b) generation time T_c along a gradient of parent-offspring correlation (0= no correlation, 1= perfect transission of relative size between the parent and the offspring). Dashed lines show estimates under weak selection, the solid lines resemble strong selection. Starred values obtain when there is negative correlation between growth and size (g = 0.25); circles are values for the case of positive correlation between growth and size (g = 0.75).

1. Selection, weak or strong, reduces R₀ but increases T_c relative to the neutral case (neutral case not shown in Fig. 3). This feature, and many other aspects of Fig. 3, is partly driven by our reasonable assumption that young individuals make fewer and mostly small offspring. When there is no selection, small young and large young survive at the same rate to contribute to reproduction at age 2. With survival selection, fewer small young survive to age 2. Selection on fertility means that larger individuals have higher fertility but the resulting increase is not enough to offset the loss of smaller young. In a stable cohort, the proportion of small young is thus lower than in the neutral case. When survival changes rapidly with size (survival selection), fewer small young survive to age 2, so the decline in reproductive output at age 2 is smaller than at age 1. The result is that R₀ declines, and the reduction in survival-weighted reproduction is greater at age 1 than age 2, so the balance between ages shifts towards the later age and increases T_c. Under selection we get slower life histories with lower reproduction.

2. For a given level of parent-offspring correlation (along the x-axis) and weak selection (dashed lines), the value of R₀ (Fig. 3a) is higher when there is negative correlation (stars) rather than positive correlation (circles) between growth and size. A negative correlation means over-compensatory growth that makes relatively small young likely to end up as relatively large two year old individuals. Since fertility increases with age and also with size, a negative growth correlation results in a higher R₀. For strong selection, the cost of early survival is too high to be overcome by a negative size correlation, that is, too many small young die before they would grow large and make substantial contributions to the overall R₀ (solid lines, Fig. 3a).

3. For a given parent-offspring correlation and growth correlation, R₀ is higher when there is weak (dashed lines) rather than strong (solid lines) selection on survival and reproduction. Reproduction is skewed to smaller individuals at age 1, and we lose more of them as survival selection becomes stronger. As noted above, overall fertility drops even though we have relatively more large individuals.

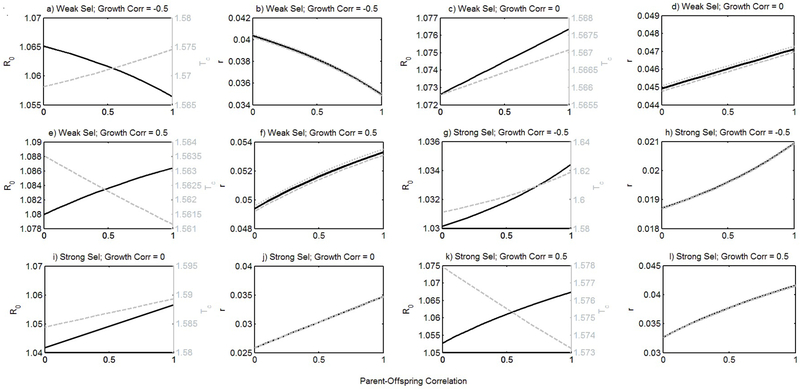
Our estimate of fitness based on the level and timing of reproduction (5) is an approximation. For Example II this approximation does fairly well as we show in comparison to the exact estimate, r₀, that is based on solving the complicated renewal equation (Table 3; see also Appendix Fig. B1).

This diversity of outcomes shows how biological intuition is shaped and educated by analyzing the speed T_c and the level of reproduction (R₀) across a range of life histories. Just computing r in these cases would not provide the same kind of understanding.

Example III: Dispersion and Stages

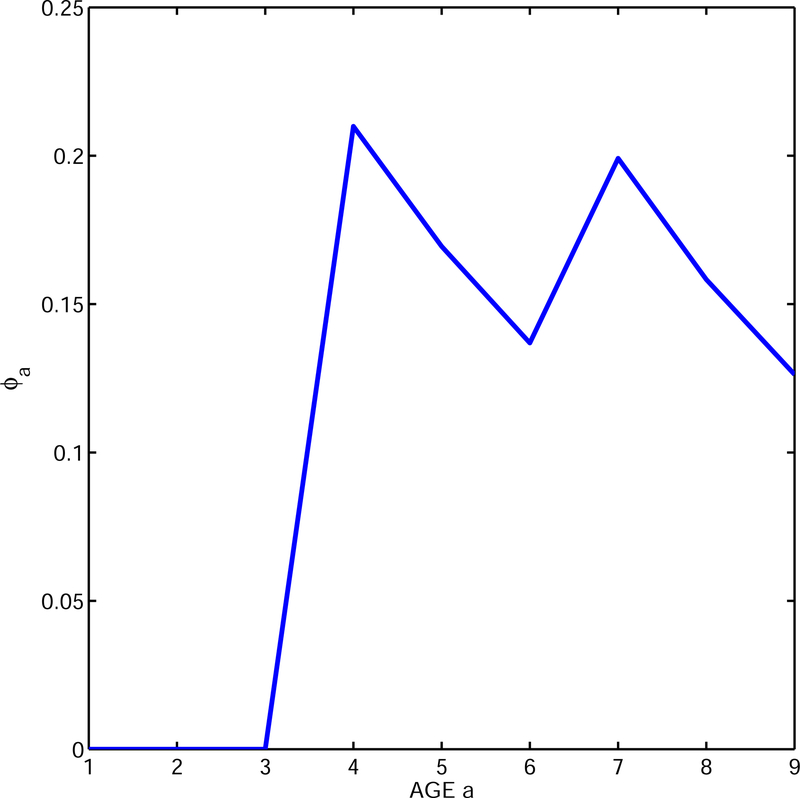
Stages can be phenotypic classes within a single location, or simply distinct locations. Consider a population that reproduces in two different spatial locations (think valley bottom and mountain top) with early maturation and reproduction in one patch and late maturation and reproduction in the other (Fig. 1c). The two locations are linked by a small amount (0.1) of natal dispersal. Now an individual’s stage is its location and the two stages will have different age-patterns of reproduction. This is the kind of setting in which the dispersion term V_s in (5) should be important.

We apply our results to a 2-patch population linked by weak dispersal with age-dependent reproduction as above (details in the Appendix). Stage equals location here. Fig. 4 shows the age-distribution of reproduction in the 2-patch system: the early age peak is for the conditions in patch 1 and the late age peak for the conditions in patch 2. The relative weights are determined using the generation matrix and (4).

Figure 4.

Age-distribution of reproduction in a stage-age structured population (Example III) with stages representing two patches differing in age-specific survival and reproduction patterns.

For just patch 1 in isolation, the net reproductive rate is 1.65, the cohort generation time is 4.87, and growth rate is 0.104; for patch 2 in isolation these numbers are 1.67, 7.62, and 0.068. For the 2-patch population with dispersal, we find that R₀ = 1.66, T_c = 6.35, and r = 0.089, which are all reasonable intermediate values. Turning to (5) we see that the first term in the approximation is (log R₀/T_c) = 0.080 so we consider the second term. Here we find that the age-dispersion is V_a = 2.89 while the stage-dispersion is V_s = 7.53. Putting these in, the two terms in (5) yield an approximation to growth rate of 0.091; without the dispersion V_s we get an approximate value of only 0.082.

So the new term V_s in the general approximation (5) matters when the offspring distribution among stages varies significantly by age. In our example, early reproduction is dominated by patch 1 (=stage 1) individuals whose offspring are likely to stay in patch 1. In contrast, late reproduction is dominated by patch 2 (=stage 2) individuals whose offspring are likely to stay in patch 2.

A reasonable question is: how can we understand level and timing in complex life histories when the matrices involve a large number of parameters. This is precisely where IPM methods are very useful, as pointed out by Ellner & Rees (2007) and illustrated in Coulson et al. (2010). For each age transition, we can work with parametric models in which, e.g., two parameters describe size specific survival and two describe size specific reproduction, four describe growth mean and variance, and four describe the parent-offspring phenotypic transmission. While that is certainly a lot of parameters, the total number is not huge. We have, in any case, little choice if we want useful and powerful biological theory, and our main result (5) applies equally to such more complex models as we show in the Appendix for an empirical model of Soay Sheep. The sheep example also illustrates that V_s can be negative, because similar (staged) offspring are produced at different ages.

Discussion

In this paper we extend to stage-and-age structure the classical result (Dublin & Lotka, 1925) that population growth rate r can be approximated by a canonical relationship between net reproductive rate R₀, and generation time T_c. In many situations, r is evolutionary fitness, and the classical result links life histories to population genetics and evolutionary change (Fisher, 1930, 1927; Charlesworth, 1994; Stearns, 1992; Caswell, 2001). Over almost a century, Lotka’s result has helped biologists understand – in a broad and general way – how life histories determine population growth and evolutionary change (Dublin & Lotka, 1925; Coale, 1972; Keyfitz, 1977; Southwood, 1988; May, 1976; Caswell, 2001). But these insights only describe how the age-pattern of survival and fertility, not the effect of variation in underlying phenotypic traits such as size, shapes fitness (Caswell, 2001; Tuljapurkar et al., 2012). The general results we give here shows how phenotypic traits determine key life history parameters including the generalizations of R₀ and T_c, and then links these parameters to growth rate r. These linkages can enrich the biological analysis of life histories in several ways, as we now discuss.

The results provide a route to understanding the consequences of variation in the rate of phenotypic change during ontogeny. E.g., when size is key (as in many plants, fishes, reptiles, or mammals), we can use our methods to examine how growth pattern (e.g. fast vs. slow, determinate vs. indeterminate) determines the timing and level of reproduction and hence fitness. Because stage-age structured models include variability in the rate of phenotypic change, we can also analyze how the plasticity (or predictability) of size change affects population dynamics. In addition, our results provide a route towards integrating work on the physiology and energetics of growth and development and their trade-offs into a life history perspective (Roff, 1992; Stearns, 1992).

Of course the effects of trait change depend on the nature of selection via survival and reproduction. In our model the latter are captured (see Table 2) by the functional relationship between survival and phenotype (stage), and the total recruitment and stage. For example, in size-dependent life histories, survival and recruitment may increase with size (directional selection), may be highest at intermediate sizes (stabilizing selection), or may vary with age (fluctuating selection favoring large size at some ages, small size at other ages). Phenotypic selection, as well as rates of phenotypic change and development, are often influenced by the abiotic environment, e.g., temperature is a major factor for many species in seasonal climates, and also by the biotic environment, e.g., presence of predators (Blanckenhorn, 2000; Blanckenhorn & Heyland, 2005; Endler, 1986). We can use our results to examine and compare the fitness consequences of such factors, and our examples show that the stage dynamics (be they phenotypic or spatial) can lead to surprising results.

The measures T_c and R₀ are essential in extending Dublin and Lotka’s classical result to stage(-age) structured populations. Earlier work has proposed several measures of timing, but has debated their merits and meanings. Caswell (2001) pointed out that we can define three different measures of generation time – he defines them for age-structure and points out that it is not clear how they generalize to situations when there are many types (stages) of newborns. Our measure T_c is the appropriate generalization of the mean age of parents produced by a stable cohort (what Caswell calls µ₁). If we suppose that we have computed both r and R₀: then we can compute a (tautologically defined) generation time T = log(R₀)/r and could use our main result (5) to show how r changes the difference between Caswell’s T and T_c. Caswell considers the average age of parents in the stable population: we cannot determine this without further analysis but it is clear that this average must depend explicitly on r. Other measures for stage-only models, are discussed by Cochran & Ellner (1992), and Hernandez-Suarez (2011). For stage-and-age models Lebreton (1996, 2005) discusses two measures of mean timing. None of these generation time measures relates R₀ to r as we have done. de Camino-Beck & Lewis (2008) propose measures of the timing and variance of reproduction using a graphical algorithm but do not show how their measures might predict r.

We show that fitness is affected by two kinds of reproductive dispersion. Age-dispersion describes how (weighted) total reproduction changes with age, and our contribution is to show how stage-dependence (e.g., the pattern of ontogenetic change or the mode of reproduction) affects age-dispersion. Age-dispersion in reproduction can vary substantially among taxa and populations because senescence and the pattern of stage change are highly variable (Stearns, 1992; Tuljapurkar et al., 2009b). For instance, consider a plant species in which large, old trees produce large amounts of seeds, reproductive dispersion will be particularly large when small, young trees also produce small vegatative ramets (Hoffmann, 1999). In such a system there exists a balance between fast turnover of a few recruits originating from small trees (fast life histories) and slow turnover of many recruits originating from old trees (slow life histories)– the results of this paper can be used to evaluate the contributions of both kinds of recruits to population growth.

We provide a new measure that describes stage-dispersion that matters (as illustrated above) when the stage-distribution of offspring varies significantly with age. This can easily occur in a spatially distributed population in which stage equals location, and there is environmental variation driving differences in reproduction among patches. A rather different example is a parasite that can infect different species of host (or different ages of one host species), and where parasite reproduction differs among the different possible hosts.

What about density-dependence? If vital rates are controlled by population density, our results are directly relevant to any equilibrium population that results. At a density-regulated equilibrium, the population’s growth rate is zero, which means that the net reproductive rate R₀ must be 1, but T_c can vary. Our definitions of R₀ and T_c still apply of course, which means that we can examine how specific kinds of density-dependence (e.g., predation, cannibalism, resource competition) constrain different components (growth, survival, recruitment, parent-offsping correlation, or dispersal among locations of a meta population) of a life history at equilibrium. We can examine variation in T_c which still measures the speed of a life history and its response to environmental signals.

We can usefully apply our results to models in epidemiology, conservation biology, and population management. In epidemiology a measure like R₀ is frequently used, based on multistage transmission matrixes, to predict if an infectious disease will spread (R₀ > 1) or not (R₀ < 1), and to analyze control measures (Diekmann & Heesterbeek, 2000). For such models, our T_c describes how fast a disease will spread, or how rapidly a control measure can be be effective. In conservation biology (e.g. tortoises) (Doak et al., 1994), T_c may inform us how fast invasive species will spread, or how rapidly conservation measures will show an effect.

The results we present show how the complex interplay of stage dynamics (trait, location), timing and level of reproduction determine fitness, and contribute to the powerful framework of stage-age structured models that are being applied in evolutionary and ecological population biology. In many populations, demographic dynamics, life histories and quantitative variation can only be accurately predicted by these more generally structured models. In particular, we hope that our results will aid the development of a broad understanding of the consequences of life history variation in development, morphology, physiology, migration, behavior, plasticity and many other stages along the life course.

Appendix A: Terminology, Matrices, Proofs, and Examples for article “Generation Time, Net Reproductive Rate, and Growth in Stage-age Structured Populations”

A. Appendix A

A.1. Form of Matrices

Stage-age-specific fertility matrices F_a have the form below – note that we enumerate all k stages, and newborns will usually be produced only in a subset of these, here labelled stages 1 through k₀,

$$\begin{array}{l}\stackrel{\text{newborn}\hspace{0.17em}\text{stages}\hspace{0.17em}\text{start}\hspace{0.17em}\text{here}}{\to }\hfill \\ ⋮\hfill \\ \stackrel{\text{newborn}\hspace{0.17em}\text{stages}\hspace{0.17em}\text{end}\hspace{0.17em}\text{here}}{\to }\hfill \end{array}\left(\begin{array}{cccc}{F}_a(1,1)& F_a(1,2)& \cdots & F_a(1,k)\\ ⋮& & & \\ F_a(k_0,1)& F_a(k_0,2)& \cdots & F_a(k_0,k)\\ 0& 0& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮\end{array}\right)$$

Stage-age-specific rates of transitioning between stages: the matrices P_a have the form

$$\begin{array}{l}\left(\begin{array}{cccc}{P}_a(1,1)& P_a(1,2)& \cdots & P_a(1,k)\\ ⋮& & & \\ P_a(k,1)& P_a(k,2)& \cdots & P_a(k,k)\end{array}\right)\\ =\left(\begin{array}{cccc}{G}_a(1,1)S_a(1)& G_a(1,2)S_a(2)& \cdots & G_a(1,k)S_a(k)\\ ⋮& & & \\ G_a(k,1)S_a(1)& G_a(k,2)S_a(2)& \cdots & G_a(k,k)S_a(k)\end{array}\right)\end{array}$$

Form of cohort size distribution,

$$\mathbf{h}(0)=\left(\begin{array}{c}h(1)\\ ⋮\\ h(k_0)\\ 0\\ ⋮\end{array}\right)\begin{array}{r}\hfill \stackrel{\text{newborn}\hspace{0.17em}\text{stages}\hspace{0.17em}\text{start}\hspace{0.17em}\text{here}}{\leftarrow }\\ \hfill ⋮\\ \hfill \stackrel{\text{newborn}\hspace{0.17em}\text{stages}\hspace{0.17em}\text{end}\hspace{0.17em}\text{here}}{\leftarrow }\end{array}.$$ (A-1)

A.2. Terminal Age

One common assumption is that individuals will die after reaching a maximum (terminal) age a_m, in which case we set ${\mathbf{L}}_{a_m+1}=\mathbf{0}$.

An alternate assumption is that after reaching some high age a_m, the stage-transition matrices remain fixed at a terminal value ${\mathbf{P}}_{a_m}$. In that case, we set

$${\mathbf{L}}_{a_m}={\mathbf{P}}_{a_m}{\mathbf{L}}_{a_m-1},\hspace{0.17em}{\mathbf{L}}_{a_m+m}={\mathbf{P}}_{a_m}^m{\mathbf{L}}_{a_m},\hspace{0.17em}m\ge 0.$$

A.3. Population Dynamics

The population vector at time t is

$$\mathbf{N}(t)=\left(\begin{array}{c}{\mathbf{n}}_1(t)\\ {\mathbf{n}}_2(t)\\ ⋮\\ n_{a_m}(t)\end{array}\right),\hspace{1em}\text{where}\hspace{0.17em}{\mathbf{n}}_a(t)=\{n_a(z,t)\}=\left(\begin{array}{c}{n}_a(1,t)\\ n_a(2,t)\\ ⋮\\ n_a(k,t)\end{array}\right).$$

Then

$$\mathbf{N}(t+1)=\left(\begin{array}{ccc}{\mathbf{F}}_1& {\mathbf{F}}_2& \cdots \\ {\mathbf{P}}_1& \mathbf{0}& \cdots \\ \mathbf{0}& {\mathbf{P}}_2& \cdots \\ ⋮& ⋮& ⋮\end{array}\right)\hspace{0.17em}\hspace{0.17em}\mathbf{N}(t).$$

The renewal equation in the text follows from the above for a stable population that has exponential growth rate r and a stable distribution u₁ of age 1 newborns (Lebreton, 1996).

A.4. The Renewal Matrix

Much as in the main text, let h⁽⁰⁾ be a stage-vector of newborns at time t – this is our initial cohort. Add together the size-distributions of this cohort’s offspring produced at each age a = 1, 2,… and so on, to see that the cohort will in total produce a first offspring generation whose stage-composition is

$${\mathbf{h}}^{(1)}={\mathbf{A}}_0{\mathbf{h}}^{(0)},\hspace{0.17em}\text{where}\hspace{0.17em}{\mathbf{A}}_0=\sum _a{\mathbf{F}}_a{\mathbf{L}}_a.$$ (A-2)

Matrix A₀ is assumed to be demographically strongly ergodic (Caswell, 2001), and so will have a dominant eigenvalue R₀ > 0 and corresponding right and left, respectively, eigenvectors c = {c(z)} and, respectively, d = {d(z)},

$${\mathbf{A}}_0\mathbf{c}=R_0\mathbf{c},\hspace{1em}{\mathbf{d}}^T{\mathbf{A}}_0=R_0{\mathbf{d}}^T;$$ (A-3)

here superscript T indicates a transposed (row) vector. We normalize the eigenvectors so that c is a vector of proportions with $1={\sum }_{z}c(z)$ and

$${\mathbf{d}}^T\mathbf{c}=\sum _{z}d(z)c(z)=1.$$ (A-4)

Consider the 2nd offspring generation, grand-children of the initial cohort (h⁰). This 2nd offspring generation will have stage-composition

$${\mathbf{h}}^{(2)}={\mathbf{A}}_0{\mathbf{h}}^{(1)}={\mathbf{A}}_0^2{\mathbf{h}}^{(2)}.$$

So the τ th offspring generation has stage-composition

$${\mathbf{h}}^{(\tau )}={\mathbf{A}}_0^{\tau }{\mathbf{h}}^{(0)}.$$ (A-5)

As we move farther into the future, τ gets larger. The properties of A₀ ensure that

$${\mathbf{A}}_0^{\tau }~R_0^{\tau }\mathbf{c}\hspace{0.17em}{\mathbf{d}}^T,\hspace{0.17em}\text{as}\hspace{0.17em}\tau \hspace{0.17em}\text{increases}.$$ (A-6)

This means that as τ increases the stage-composition of offspring generations changes as

$$\frac{{\mathbf{h}}^{(\tau )}}{R_0^{\tau }}\to ({\mathbf{d}}^T{\mathbf{h}}^{(0)})\hspace{0.17em}\mathbf{c}.$$ (A-7)

We conclude that the offspring generations in the far future: (a) increase in number at geometric rate R₀; (b) have stage-structure c; and (c) have ultimate size proportional to the total reproductive value of the initial cohort.

A.5. The Main Result Derived

For any matrix norm (indicated by $\Vert \hspace{0.17em}\cdot \hspace{0.17em}\Vert$) we have

$$\underset{\tau }{\lim }(1/\tau )\log \Vert {\mathbf{A}}^{\tau }(r)\Vert \hspace{1em}=\hspace{1em}0,$$ (A-8)

$$\underset{\tau }{\lim }(1/\tau )\log ({\mathbf{d}}^T{\mathbf{A}}^{\tau }(r)\mathbf{c})\hspace{1em}=\hspace{1em}0.$$ (A-9)

The limits here and later on are all as τ → ∞. The first equation above implies that the second must be true and either one determines r.

For small r expand

$$\mathbf{A}(r)=\sum _a{e}^{-ra}{\mathbf{F}}_a{\mathbf{L}}_a,$$

$$=\sum _a{\mathbf{F}}_a{\mathbf{L}}_a-r\sum _{a}a{\mathbf{F}}_a{\mathbf{L}}_a+\frac{1}{2}{r}^2\sum _a{a}^2{\mathbf{F}}_a{\mathbf{L}}_a+O(r^3),$$ (A-10)

$$={\mathbf{A}}_0-r{\mathbf{B}}_1+\frac{1}{2}{r}^2{\mathbf{B}}_2+O(r^3).$$ (A-11)

In that last line above, matrix A₀ is the same as in text (3), and matrices B₁, B₂ are defined by the corresponding terms in (A-10). Using (A-11),

$${\mathbf{A}}_0^{\tau }(r)={\mathbf{A}}_0^{\tau }-r{\mathbf{S}}_1+\frac{1}{2}{r}^2{\mathbf{S}}_2+r^2{\mathbf{S}}_3+O(r^3).$$ (A-12)

Here

$${\mathbf{S}}_1=\sum _{i=1}^{\tau }{\mathbf{A}}_0^{\tau -i}{\mathbf{B}}_1{\mathbf{A}}_0^{i-1},$$ (A-13)

$${\mathbf{S}}_2=\sum _{i=1}^{\tau }{\mathbf{A}}_0^{\tau -i}{\mathbf{B}}_2{\mathbf{A}}_0^{i-1},$$ (A-14)

$${\mathbf{S}}_3=\sum _{i=1}^{\tau -1}\sum _{j=1}^{\tau -1}{\mathbf{A}}_0^{\tau -i-j}{\mathbf{B}}_1{\mathbf{A}}_0^{j-1}{\mathbf{B}}_1{\mathbf{A}}_0^{i-1}.$$ (A-15)

Now observe that

$$\frac{{\mathbf{d}}^T{\mathbf{A}}_0^{\tau }\mathbf{c}}{R_0^{\tau }}\hspace{1em}=\hspace{1em}1,$$ (A-16)

$$\frac{{\mathbf{d}}^T{\mathbf{S}}_1\mathbf{c}}{R_0^{\tau }}\hspace{1em}=\hspace{1em}\sum _{i=1}^{\tau }{\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}=x_1,$$ (A-17)

$$\frac{{\mathbf{d}}^T{\mathbf{S}}_2\mathbf{c}}{R_0^{\tau }}\hspace{1em}=\hspace{1em}\sum _{i=1}^{\tau }{\mathbf{d}}^T\frac{{\mathbf{B}}_2}{R_0}\mathbf{c}=x_2,$$ (A-18)

$$\frac{{\mathbf{d}}^T{\mathbf{S}}_3\mathbf{c}}{R_0^{\tau }}\hspace{1em}=\hspace{1em}\sum _{i=1}^{\tau -1}\sum _{j=1}^{\tau -i}{\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}{\left(\frac{{\mathbf{A}}_0}{R_0}\right)}^{j-1}\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}=x_3.$$ (A-19)

Next, use these and expand to order r²

$$\begin{array}{l}(1/\tau )\log ({\mathbf{d}}^T{\mathbf{A}}_0^{\tau }(r)\mathbf{c})=\log R_0-r\frac{x_1}{\tau }+\frac{1}{2}{r}^2\frac{x^2}{\tau }+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+r^2\frac{x^3}{\tau }-\frac{1}{2}{r}^2\frac{x_1^2}{\tau }+O(r^3).\end{array}$$ (A-20)

Define

$${\varphi }_a=\frac{{\mathbf{d}}^T{\mathbf{F}}_a{\mathbf{L}}_a\mathbf{c}}{R_0},\hspace{0.17em}\text{noting}\hspace{0.17em}\text{that}\hspace{0.17em}\sum _a{\varphi }_a=1.$$ (A-21)

Using (A-10) and (A-17) and taking the limit of large τ,

$$\underset{\tau }{\lim }\frac{x_1}{\tau }={\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}=\sum _{a}a{\varphi }_a=T_c.$$ (A-22)

Also, from (A-10) and (A-18), in the limit of large τ,

$$\underset{\tau }{\lim }\frac{x_2}{\tau }={\mathbf{d}}^T\frac{{\mathbf{B}}_2}{R_0}\mathbf{c}=\sum _a{a}^2{\varphi }_a={\mu }_2.$$ (A-23)

We deal with the last 2 terms in (A-20) in three steps. Step 1: use (A-17) to rewrite the quantity $x_1^2$ thus:

$$\begin{array}{l}{x}_1^2=\sum _{i=1}^{\tau }{\left({\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}\right)}^2+2\sum _{i>j}\left({\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}\right)\left({\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}\right),\\ \hspace{1em}=\sum _{i=1}^{\tau }{\left({\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}\right)}^2+2\sum _{i>j}\left({\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{Z}\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}\right),\\ \hspace{1em}=\tau T_c^2+2\sum _{i>j}\left({\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{Z}\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}\right).\end{array}$$ (A-24)

Here

$$\mathbf{Z}=\mathbf{c}\hspace{0.17em}{\mathbf{d}}^T,$$ (A-25)

is a projection matrix, meaning that Z² = Z.

Step 2: recall from above (A-6) that, for large τ, ${\mathbf{A}}_0^{\tau }$ will approach the limiting matrix $R_0^{\tau }\mathbf{Z}$. Define the matrix

$$\mathbf{H}={\left(\mathbf{I}-\left[\frac{{\mathbf{A}}_0}{R_0}-\mathbf{Z}\right]\right)}^{-1},$$ (A-26)

which describes the cumulative sum of stage-structure transients, powers of the difference between (A₀/R₀) and the limit Z (see Cohen (1979) for a similar object in a very different context).

Step 3: compute the difference $[x_3-(1/2)x_1^2]$. Each term in x₃ (see (A-19)),

$${\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}{\left(\frac{{\mathbf{A}}_0}{R_0}\right)}^{j-1}\frac{{\mathbf{B}}_1}{R_0}\mathbf{c},$$

is matched by a term from $-(1/2)x_1^2$ that we can write (see last line of (A-24)) as

$$-{\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{Z}\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}.$$

Combining these we find (use (A-26) in the last two lines below) that

$$\begin{array}{l}\underset{\tau }{\lim }\frac{1}{\tau }[x_3-(1/2)x_1^2]={\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}{\left[\mathbf{I}-\left(\frac{{\mathbf{A}}_0}{R_0}-\mathbf{Z}\right)\right]}^{-1}\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\left({\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}\right)}^2-\frac{1}{2}{T}_c^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}={\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{H}\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}-{\left({\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}\right)}^2-\frac{1}{2}{T}_c^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}={\mathbf{d}}^T\frac{{\mathbf{B}}_1}{R_0}\mathbf{H}\frac{{\mathbf{B}}_1}{R_0}\mathbf{c}-T_c^2-\frac{1}{2}{T}_c^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}=V_s-\frac{1}{2}{T}_c^2.\end{array}$$ (A-27)

Assemble the above terms, recall that $V_a={\mu }_2-T_c^2$, and take the limit in equation (A-20) to arrive at

$$\frac{\log R_0}{T_c}=r-\frac{(V_a+2V_s)}{T_c}\frac{r^2}{2}+O(r^3).$$ (A-28)

Now use reversion of series (section 3.6.25 in Abramowitz & Stegun (1964)) to get

$$r=\frac{\log R_0}{T_c}+\frac{(V_a+2V_s)}{2T_c}{\left(\frac{\log R_0}{T_c}\right)}^2+O{\left(\frac{\log R_0}{T_c}\right)}^3,$$ (A-29)

Table 1 summarizes this result.

A.6. Example II: Ages and Stages

In our Example II there are four stages (n_s = 4) and 2 ages a = 1, 2. Individuals are born at age 1 into stage 1 (small young) or 2 (large young). If they survive to age 2, they move into stage 3 (small old) or 4 (large old). The sizes for stages 1 to 4 are z₁ < z₂, z₃ < z₄.

Fertility

Recall from the main text that fertility – total number of offspring – at age a for stage z is m_a(z).

At age 1, average fertility is m₁ but fertility depends on size; the size-dependence is given by the parameter x₁ and

$$m_1(1)=m_1{e}^{-x_1}/K_1,\hspace{0.17em}{m}_1(2)=m_1{e}^{+x_1}/K_1,\hspace{0.17em}{K}_1=(e^{-x_1}+e^{+x_1})/2,$$

x₁ is the strength of phenotypic selection on fertility at age 1. We arrange the fertilities at age 1 into a diagonal matrix according to the sizes (indexed with (1) small young, or (2) large young in the according columns for small (colum 1) or large (column 2))

$${\mathbf{M}}_1=\left(\begin{array}{cccc}{m}_1(1)& 0& 0& 0\\ 0& m_1(2)& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)$$

At age 2, average fertility is m₂ but the size-dependence of fertility is given by the parameter x₂ and

$$m_2(3)=m_2{e}^{-x_2}/K_2,\hspace{0.17em}{m}_2(4)=m_2{e}^{+x_2}/K_2,\hspace{0.17em}{K}_2=(e^{-x_2}+e^{+x_2})/2.$$

x₂ is the strength of phenotypic selection on fertility at age 2. We arrange the fertilities at age 2 into a diagonal matrix

$${\mathbf{M}}_2=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& m_2(3)& 0\\ 0& 0& 0& m_2(4)\end{array}\right)$$

Parent-Offspring Correlation of Phenotype

The size-distribution of offspring depends on the sizes and ages of their parents, and D_a(y, z) is the fraction of offspring of a parent of age a and size z that are born into stage y. At age 1, small parents make only small offspring, large parents make mostly small offspring,

$${\mathbf{D}}_1=\left(\begin{array}{cccc}1& 0.8& 0& 0\\ 0& 0.2& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)$$

At age 2, the distribution of offspring size is described by a parent-offspring correlation parameter b_h such that the fraction of offspring who inherit the relative size of their parent is d = 0.5 (1 + b_h). The parent-offspring correlation matrix summarize this as

$${\mathbf{D}}_2=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ d& (1-d)& 0& 0\\ (1-d)& d& 0& 0\end{array}\right)$$

Of course the fertility matrix F₁ = D₁ M₁.

Survival

The mean survival rate from age 1 to age 2 is s but survival may depend on size, with a strength of selection on survival given by parameter w so that

$$s(1)=s\hspace{0.17em}{e}^{-w_1}/H,\hspace{0.17em}s(2)=s\hspace{0.17em}{e}^{+w_1}/H,\hspace{0.17em}H=(e^{-w_1}+e^{+w_1})/2$$

so average survival for age 1 individuals is s₁. We summarize these in a survival matrix for age 1,

$${\mathbf{S}}_1=\left(\begin{array}{cccc}s(1)& 0& 0& 0\\ 0& s(2)& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)$$

Growth

We define a phenotypic correlation b_g between size at age 2 and size at birth (age 1). The probability that relative size is maintained (i.e., small young become small old) is g = 0.5 (1 + b_g). We summarize this in growth matrix for age 1

$${\mathbf{G}}_1=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ g& (1-g)& 0& 0\\ (1-g)& g& 0& 0\end{array}\right)$$

Putting it together

The overall transition matrix from age 1 to age 2, including survival and growth, is P₁ = G₁ S₁.

The fertility matrix at age a is F_a and includes fertility as well as parent-offspring transmission, so we have F₁ = D₁ M₁ and F₂ = D₂ M₂.

A.7. Example III: Dispersion and Stages

For this example we consider a population that reproduces in two different spatial locations (think valley bottom and mountain top). Individuals start reproducing at age 4 (Fig. 1c), and individuals at the valley bottom (patch 1) have high reproduction at ages 4–6 and low reproduction at ages 7–9, whereas individuals at mountain tops show the reverse pattern (low reproduction age 3–6, and high reproduction age 7–9). Most individuals recruit to their own patch (90%) and do not disperse at older ages; only a few newborn individuals (10 %) disperse to the other patch. Survival is higher at the mountain tops compared to the valley bottom, and onset of senescence in survival is earlier in the valley.

Age-specific total fertility for patch 1 are: 0, 0, 0, 1.5, 1.5, 1.5, 0.075, 0.075, 0.075;

Age-specific total fertility for patch 2 are: 0, 0, 0, 0.075, 0.075, 0.075, 1.5, 1.5, 1.5;

Age-specific survival for patch 1: 0.7, 0.8, 0.8, 0.8, 0.8, 0.4, 0.4, 0.4, 0.4;

Age-specific survival for patch 2: 0.8, 0.9, 0.9, 0.9, 0.9, 0.8, 0.8, 0.8, 0.4;

A.8. Example for a complex empirical population: IPM of Soay sheep

Here, we briefly show that our approximation is also accurate for a more complex empirical based stage-age model for the Soay sheep Ovis aries that uses body mass as a stage variable (Coulson et al., 2010). Newborns (lambs) differ in birth mass. Stage transitions (body mass change), survival, fertility, and reproductive allocation are age-dependent with four age categories: lambs (age class 1); yearlings (age class 2); prime aged adults (age classes 3–7); and senescent individuals (age classes ≥ 8). For simplicity we ignore twinning. The model was constructed as an IPM (Integral Projection Model, Ellner & Rees (2007)) with continuous values of body mass and a time unit of 1 year. The stage-age patterns of survival, body mass transitions, total offspring number, and reproductive allocation are shown in Coulson et al. (2010). For the illustation here we use a discrete version with k = 100 size classes; the vital rates are contained in 100 × 100 matrices P_a, a ≥ 1 and F_a, a ≥ 2. Features to note: survival and total offspring number are increasing functions of body mass at all ages; mass tends to increase through prime ages but to decrease in senescent individuals; reproductive allocation reflects heritability of parental birth mass with yearlings and senescent mothers producing, on average, smaller offspring than prime-aged mothers at a given size. For that, this empircial example is biological similar to the simple Example II of the main text and detailed above, exept that for this complex emprical example there are many more size classes, and age-classes (for more details see Coulson et al. (2010)).

The exact growth rate of a stable population of sheep found by solving the exact renewal equation (Table 3) is r = 0.0143. Using our main result (5)and estimating population growth rate based on the simplest approximation only using the amount R₀ and mean timing T_c reveals

$${\widehat{r}}_1=\frac{\log \left(R_0\right)}{T_c}=0.0141,\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\text{the}\hspace{0.17em}\text{sheep}.$$

This is, as in the simple Example II, close to the exact value.

The better approximation using the dispersion terms yields

$${\widehat{r}}_2={\widehat{r}}_1+\frac{[V_a+2V_s]{(\log R_0)}^2}{2T_c^3}=0.0143,\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\text{the}\hspace{0.17em}\text{sheep}.$$

The accurate approximation predicts the exact growth rate for a stable population very well.

Figure B1.

Generation time (a, c, e, g, i, k) T_c (hatched line) and level of reproduction R₀ (solid line), and (b, d, f, h, j, l) fitness r along a gradient of parent-offspring correlation (0= no correlation, 1= perfect transission of relative size between the parent and the offspring). Panels (a-f) resemble weak size specific phenotypic selection on survival (w₁ = 0.075) and fertility (x₁ = 0.075, x₂ = 0.075) while panel (g-l) illustrate strong phenotypic selection on the trait. Differences in phenotypic correlation in growth are shown for (a, b, g, h) negative correlation (g = 0.25), (c, d, i, j) no phenotpyic correlation in growth (g = 0.5), or (e, f, k, l) poistive phenotpyic correlation in growth (g = 0.75). For panels (b, d, f, h, j, l) three measures of fitness are shown, the exact growth rate r₀ (solid line) estimated from the complicated renewal equation (Table 3), the simplest approximation (hatched line) based on the main result (5) only using the amount R₀ and mean timing T_c, ${\widehat{r}}_1=\frac{\log (R_0)}{T_c}$, and the more accurate approximation (dotted line) using the dispersion terms ${\widehat{r}}_2={\widehat{r}}_1+\frac{[V_a+2V_s]{(\log R_0)}^2}{2T_c^3}$.