Computational Dissection of Dopamine Motor and Motivational Functions in Humans

Abstract

Motor dysfunction (e.g., bradykinesia) and motivational deficit (i.e., apathy) are hallmarks of Parkinson's disease (PD). Yet, it remains unclear whether these two symptoms arise from a same dopaminergic dysfunction. Here, we develop a computational model that articulates motor control to economic decision theory, to dissect the motor and motivational functions of dopamine in humans. This model can capture different aspects of the behavior: choice (which action is selected) and vigor (action speed and intensity). It was used to characterize the behavior of 24 PD patients, tested both when medicated and unmedicated, in two behavioral tasks: an incentive motivation task that involved producing a physical effort, knowing that it would be multiplied by reward level to calculate the payoff, and a binary choice task that involved choosing between high reward/high effort and low reward/low effort options. Model-free analyses in both tasks showed the same two effects when comparing unmedicated patients to medicated patients: dopamine depletion (1) decreased the amount of effort that patients were willing to produce for a given reward and (2) slowed down the production of this effort, regardless of reward level. Model-based analyses captured these effects with two independent parameters, namely reward sensitivity and motor activation rate. These two parameters were respectively predictive of medication effects on clinical measures of apathy and motor dysfunction. More generally, we suggest that such computational phenotyping might help characterizing deficits and refining treatments in neuropsychiatric disorders.

SIGNIFICANCE STATEMENT Many neurological conditions are characterized by motor and motivational deficits, which both result in reduced behavior. It remains extremely difficult to disentangle whether these patients are simply unable or do not want to produce a behavior. Here, we propose a model-based analysis of the behavior produced in tasks that involve trading physical efforts for monetary rewards, to quantify parameters that capture motor dynamics as well as sensitivity to reward, effort, and fatigue. Applied to Parkinson's disease, this computational analysis revealed two independent effects of dopamine enhancers, which predicted clinical improvement in motor and motivational deficits. Such computational profiling might provide a useful explanatory level, between neural dysfunction and clinical manifestations, for characterizing neuropsychiatric disorders and personalizing treatments.

Introduction

Why don't we make more effort? Is it because we don't want to, or just because we can't? This question is particularly hard to address in the case of patients with pathological conditions that combine motivational and motor deficits, such as Parkinson's disease (PD). Some of the motor symptoms that characterize PD, such as akinesia (paucity of movement) or bradykinesia (movement slowness), are difficult to disentangle from apathy (motivational deficit), usually defined as a reduction of goal-directed behavior.

Candidate neurobiological mechanisms underlying motor and motivational deficits both involve dopamine. Motor symptoms are primarily caused by the degeneration of dopaminergic neurons in the substantia nigra pars compacta that project on dorsal parts of the striatum (Ehringer and Hornykiewicz, 1960; Kish et al., 1988). Apathy, one of the most frequent nonmotor symptoms in PD (Starkstein et al., 1992; Brown and Pluck, 2000), might also relate to dopamine depletion (Czernecki et al., 2002; Thobois et al., 2010), but more specifically to the degeneration of dopaminergic projections to the ventral striatum arising from the ventral tegmental area (Remy et al., 2005; Brown et al., 2012). Thus, motor and motivational deficits in PD could arise from dopamine depletion in distinct territories. Capturing this dissociation requires a proper articulation of motivational and motor functions, an issue that has only recently received consideration in theoretical neuroscience (Shadmehr et al., 2010; Rigoux and Guigon, 2012).

Previous investigations of motor deficits have suggested that the kinematic characteristics of movements are preserved in PD, and that bradykinesia can be explained by a shift in a cost–benefit optimization process (Mazzoni et al., 2007; Baraduc et al., 2013). This optimization has been formalized in optimal control theory, which assumes that movement speed is adjusted so as to minimize a cost, related to the accuracy of the movement end point, or to the energy expended during movement execution (Harris and Wolpert, 1998; Todorov and Jordan, 2002). However, the impact of changing the expected benefits is typically not taken into account in these motor theories (Rigoux and Guigon, 2012).

On the other hand, investigations of motivational deficits following dopamine depletion have generally neglected motor processes, even if testing motivation involves reading a motor output. Incentive motivation can be construed as an implicit mechanism invigorating action execution in proportion to the expected reward, or as an explicit choice to exert more effort to get more reward (Berridge, 2004). It has been formalized in economic decision theory, as well as in optimal foraging theory, as an optimization process that maximizes reward value while minimizing effort cost (Stephens and Krebs, 1986). The role of dopamine in promoting high effort/high reward behavioral policy has been well established in animals (Walton et al., 2006; Salamone et al., 2007), and more recently evidenced in humans (Wardle et al., 2011; Treadway et al., 2012; Chong et al., 2015). However, the paradigms and analyses used in these seminal works did not allow specifying the promotivational effect of dopamine as either an enhancement of reward value or an alleviation of effort cost.

The aim of the present study is to provide a principled account of the motor and motivational functions of dopamine. For this, we developed a computational model that combines formalisms of motor control theory with decision-making principles. The model was fitted to the behavior produced by parkinsonian patients in a cost–benefit trade-off task to characterize the effects of dopaminergic medication. The task was adapted from a behavioral paradigm that has been used previously in fMRI and lesion studies to demonstrate the implication of the ventral striatopallidal complex in translating higher monetary incentives into greater physical effort (Pessiglione et al., 2007; Schmidt et al., 2008). Here, we implemented two versions of the paradigm (Fig. 1) to capture both the processes that have been described as implicit invigoration and as explicit decision making. The same model was applied to the two tasks and revealed two independent computational effects of dopamine enhancers.

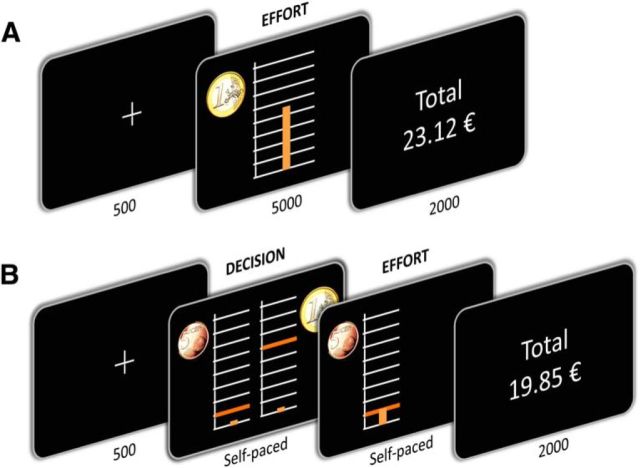
Figure 1.

Behavioral tasks. Successive screenshots displayed in one trial, with duration in milliseconds. A, The incentive force task. After a fixation cross, subjects were shown the monetary incentive as a coin image (€0.1, €0.2, €0.5, €1, €2, €5). This was the trigger to exert a force on a hand grip. Online feedback on the force produced was provided as a cursor moving up and down within a scale graduated from 0 to the maximal force of the subject. The height reached by the cursor determined the fraction of the monetary incentive earned in the current trial. B, The binary choice task. After a fixation cross, subjects were shown two options side by side, each corresponding to a potential monetary reward (coin image) associated with a required force level (orange bar). Subjects selected their preferred option on a keyboard and then had to produce the associated force (i.e., raise the cursor up to the orange bar). In both tasks, cumulative total of monetary earnings was indicated at the end of the trial.

Materials and Methods

Subjects

The study was approved by the Ethics Committee of the Pitié-Salpêtrière Hospital (Paris, France). A total of 49 subjects, with 24 PD patients (7 females, 17 males) and 25 healthy controls (13 females, 12 males), were included in the study. All subjects gave informed consent before taking part, and all data were recorded anonymously. Subjects were informed that they would not be paid for their voluntary participation and that the monetary earnings in the task were purely fictive. This was implemented to avoid discrimination, as it would be unethical to penalize patients financially for their deficits. Note that money was equally fictive for controls and patients, and that previous studies have obtained similar motivational effects with virtual and real money (Schmidt et al., 2008, 2012).

PD patients were consecutive candidates for deep brain stimulation, hospitalized for a clinical preoperative examination (for demographic and clinical details, see Table 1). Inclusion criteria were a diagnosis of idiopathic PD with a good response to levodopa [>50% improvement on the Unified Parkinson's disease rating scale (UPDRS-III)], in the absence of dementia (Mini Mental State score of >24) and depression (Montgomery and Asberg depression rating scale score of <20). PD patients were assessed twice, in the morning on 2 different days: once in their “Off” state, after overnight (>12 h) withdrawal of levodopa and a full day (24 h) withdrawal of dopamine agonists, and once in their “On” state, 1 h after intake of their habitual medication dose. The order of the On and Off assessments was counterbalanced across patients. For the sake of simplicity, we converted all medications as levodopa equivalents (Table 1), and we used the term “dopaminergic medication” to designate both levodopa and receptor agonists. Three of the 24 patients were tested in the On state, but were unable to perform the tasks in the Off state and were therefore not included in the analysis of medication effects. Because of organizational issues, the UPDRS score was missing in one patient, for both the On and the Off states. Apathy was assessed on both the On and Off days with Starkstein's scale, except for four patients, whose apathy was not assessed in the Off state. Although it was mainly developed for evaluating apathy over stable periods, the guidelines of the apathy evaluation scale suggest that it can also be used to assess treatment effects in hospitalized patients over short periods, as was done in previous studies (Czernecki et al., 2002).

Table 1.

Demographic and clinical data

	Controls (N = 25)	PD-On (N = 24)	PD-Off
Age (years)	57.0 ± 2.1	60.2 ± 1.6
Sex (female/male)	13/12	7/17
Education level (seven-point scale)	5.9 ± 0.3	5.2 ± 0.6
Disease duration (years)		11.4 ± 1.3
Dopaminergic daily dose (mg/d)		1148 ± 86
UPDRS-III motor score		11.7 ± 1.7	32.8 ± 3.2
Starkstein apathy score	5.2 ± 0.7	8.9 ± 0.8	14.3 ± 1.3
MADRS depression score	2.9 ± 0.7	5.9 ± 1.0
MMSE cognitive score		27.3 ± 1.3
Mattis dementia score		136.6 ± 14.3
Cued recall memory score		43.8 ± 5.0

MADRS, Montgomery and Asberg depression rating scale; MMSE, Mini Mental State Examination.

Healthy subjects were recruited from the community. They were screened for any history of neurological or psychiatric conditions, psychoactive substance abuse or dependence, or current medication that might have influenced cognitive skills. There was no significant difference between PD patients and healthy controls in terms of age, gender, or education level (Table 1).

Experimental settings

Before performing the tasks, participants were given written instructions, which were also repeated orally step by step. Before each task, they were asked to squeeze the handgrip as hard as they could. The maximum reached over three trials was taken as the calibration force, which served to adjust for each individual the force scale used in the tasks described below. All subjects used their dominant hand to produce forces. Force was recorded using a handgrip (MIE Medical Research), with a sample rate of 60 Hz. The recorded signal was digitalized and fed into the PC running the task program and read by an in-house MATLAB program (MathWorks). Stimuli presentation was programmed with MATLAB using the psychchophysics Toolbox Version 3 (www.psychtoolbox.org).

Force task.

The force task was designed to evaluate how subjects adjust their effort to incentive level. Subjects were instructed to try and win as much money as possible during the task and were encouraged to perform as if they were playing for real money. The task included 60 trials, corresponding to 10 repetitions of six monetary incentives (€0.1, €0.2, €0.5, €1, €2, and €5) presented in a random order. The incentives corresponded to the coins and notes that are most used in everyday life in France.

Each trial started by the display of a fixation cross for 500 ms. A monetary incentive then appeared on the top left of the screen, presented as a coin or a bill image, simultaneously with a graduated scale (Fig. 1A). The top line corresponded to producing the calibration force and winning the full incentive, and each graduation corresponded to a fraction (10%) of the monetary incentive. Subjects were told that the payoff was calculated as the fraction of the incentive proportional to the height they reached within the scale. They were provided with real-time visual feedback of the exerted force (with a cursor moving up and down within the scale). The appearance of the scale on screen was the trigger signal for subjects to start squeezing the handgrip to move the cursor up as high as possible, within a 5000 ms interval. After every trial, the cumulative total of the money earned up to that point was displayed for 2000 ms.

Choice task.

The choice task was designed to assess how subjects discount the value of reward prospects with the amount of effort that must be invested. Subjects were presented with a series of choices between low reward/low effort and high reward/high effort options. The low reward/low effort option was always presented on the left of the screen, and yielded a reward of €0.05 after exerting an effort corresponding to 10% of the subject's calibration force. The high reward/high effort option associates one of six possible rewards (€0.1, €0.2, €0.5, €1, €2, €5) with a force level varying between 10 and 90%. Each option was presented as a coin or a bill image on top of a graduated scale with a red bar indicating the required force level (Fig. 1B). Subjects decided whether or not it was worth exerting a higher effort to win a higher reward by pressing on the right or left arrow in a keyboard with the nondominant hand. The chosen option then remained on screen and the corresponding effort needed to be produced using the dominant hand, with the same visual display as in the force task. Note that the same hand was used whether the left or right option was selected, such that possible asymmetry in motor impairment would not influence choices. Also the trial did not end until subjects reached the selected force level, such that there was no possibility of failure, which discards the possibility of confounding effort with risk. After every trial, the cumulative total of the money earned up to that point was displayed for 2000 ms.

A staircase procedure was used to adjust the force level associated with every reward level in the high option, depending on subjects' choices, to gradually converge to indifference points, where subjects equally chose between the two options. At the beginning, the six possible rewards of the high option were respectively associated with efforts corresponding to 30, 40, 50, 60, 70, and 80% of the calibration force. This initial pairing was selected to approximate the indifference points observed in a pilot experiment. It also corresponds to the linear relationship observed between force produced and incentive level in the motivation task, where no initial pairing was imposed, discarding any possibility of anchorage effect. After each choice, the effort level was either increased by 5% for the next occurrence of the same incentive, if the high option was chosen, or decreased by 5% in the opposite case. The task was made up of 15 repetitions of the six monetary rewards presented in a random order, for a total of 90 trials. We checked this was sufficient to obtain a stable indifference point for each reward level in each group of participants.

Data analysis

For the force task, we considered three dependent variables: peak of force and positive and negative peak of yank (the temporal derivative of force) measured during the contraction and relaxation phases of force pulse (i.e., the period preceding and following the force peak). Force peak was extracted in every trial as the maximum reached within the 5 s effort period following the onset of the graduated scale. Force time series were low-pass filtered at 15 Hz (zero-phase second-order Butterworth filter), and yank was computed through numerical derivation. Contraction (positive) and relaxation (negative) yank peaks were obtained by extracting the maximal and the minimal (most negative) yank measure reached in the trial.

For the choice task, the dependent variable was the force level associated with each incentive level at the last trial of the session, hence, after convergence to indifference points. We also extracted yank peaks during the contraction but not the relaxation phase, as forces were only recorded until the required level was reached.

Forces were recorded in newtons, but were expressed, for both tasks, in proportion to the highest measure to eliminate interindividual differences in maximal grip force. For each participant, a single highest measure was taken across all sessions and calibration tests, to allow for comparison between tasks and sessions. For each task, dependent variables were compared across groups with the a priori hypothesis that dopamine depletion would have a deleterious effect; thus, main effects were assessed using one-tailed t tests. To assess motor effects of dopamine, we performed linear regressions of force peaks against yank peaks. One-tailed t tests were used to assess the significance of regression coefficients within groups as well as their difference across groups.

We report comparisons between healthy controls and Off-PD patients to assess disease effect, and between Off-PD and On-PD patients to assess medication effect. The two test sessions were pooled as the order of On and Off assessments was counterbalanced across patients. We nonetheless compared the two sessions in both controls and patients. There was no test–retest effect in any of our motor and motivational measures.

Computational model

The basic principle of the model (Figs. 2, 3) is a cost–benefit optimization, where subjects intend to choose and produce the optimal force peak F, i.e., the one that maximizes a discounted value V(F), calculated as the difference between expected benefits B(F) and expected effort cost C(F). We opted for linear discounting to allow for negative net values, which account for the fact that doing nothing is sometimes better:

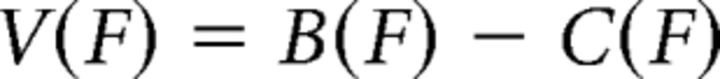The benefit term B(F) was decomposed into reward-dependent and reward-independent components:

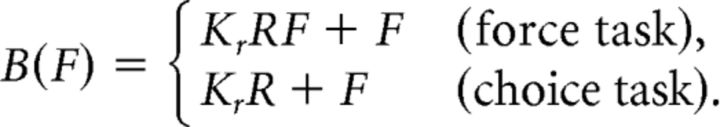The reward-dependent component corresponds to effort payoff, which was by design equal to the product of the reward at stake R and the exerted force F in the force task (Fig. 2E), and to the reward associated with the considered option in the choice task. It was weighted subjectwise by a free parameter K_r that measured sensitivity to reward.

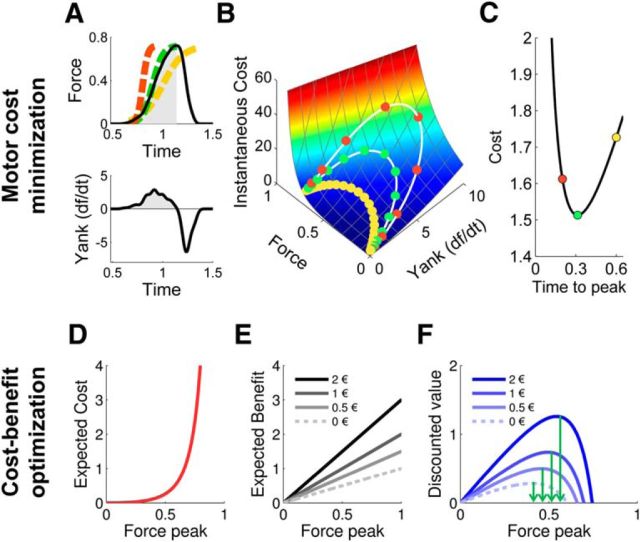
Figure 2.

Computational principles. A, Example of a force pulse (top), with force expressed in newtons. The x-axis indicates time after trial onset in seconds. Yank (bottom) was calculated as the temporal derivative of force. Active periods of force pulses (in gray) were modeled as sigmoid functions (dashed lines) that approximate the solutions of an optimal motor-control model (see Materials and Methods). The three colors correspond to three a priori possible trajectories in time. B, Instantaneous cost (arbitrary units) for each value of force and yank. Simulated force-yank trajectories in time for three force pulses of decreasing duration (0.6, 0.3, 0.2 s) and all reaching 70% of the maximal force are shown in the cost space (white lines). Circles indicate cost estimated at every 20 ms step. The total cost of each force pulse is the integral of instantaneous costs across the duration of the active period of force pulse. C, Total cost of force pulses (arbitrary units) as a function of effort duration (in seconds). This function defines the optimal duration (in green) that minimizes the cost of the force pulse. D, Expected cost (arbitrary units) associated with every force peak, simulated at the optimal duration of force pulse (peak latency). Force peaks are expressed as a proportion of the maximal force. E, Expected benefit (arbitrary units) is proportional to the incentive at stake and to the force peak in the incentive force task. Three possible monetary incentives are represented here (€0.5, €1, and €2). The model assumes that force production is valuable in itself, even if the expected financial reward is null. Because of this, the expected benefit can be superior to incentive level. F, Net value associated with every force peak for three incentives (€0.5, €1, and €2).

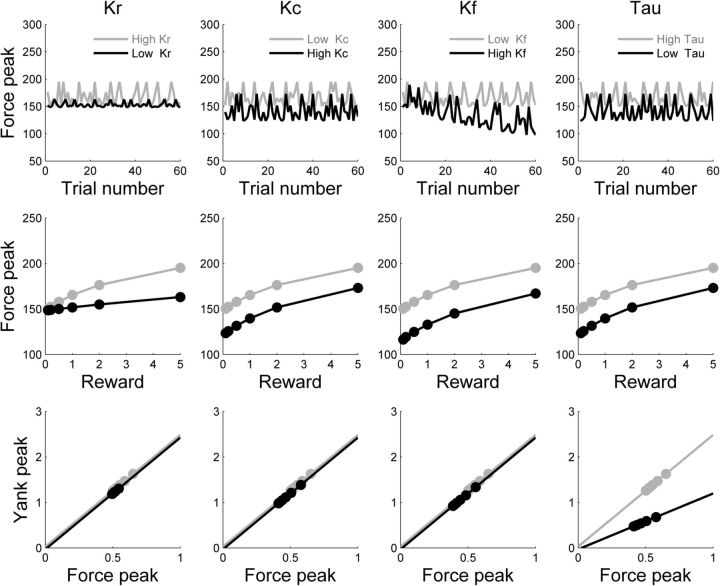
Figure 3.

Model predictions regarding force production. Top row, Simulation of force peaks (in newtons) in a session of 60 trials of the force task, with randomized incentives. Middle row, Effect of incentive level (in euros) on simulated force peaks. Bottom row, Scaling law relating force peak to yank peak (in newtons per second). Incentive categories are indicated by filled circles. Columns, Model free parameters: K_r (reward sensitivity), K_c (cost sensitivity), K_f (fatigability), and τ (motor activation rate). Graphs illustrate the effects of biasing each parameter toward weaker efforts (gray to black lines). Decreasing the reward weight K_r reduced the impact of incentives on force production. Increasing the cost weight (K_c) or fatigue weight (K_f) or decreasing the motor activation rate (τ) predicted an overall reduction of forces, independent of incentives. However, K_c predicted this shift to be isolated (main effect on force peak only), whereas K_f predicted an associated decay of force peak throughout the session (interaction with trial number), and τ an associated shift in the force-yank scaling law (lower yank peaks for given force peaks).

The reward-independent component reflects the benefits of producing an effort, outside of financial aspects, and was just proportional to the force level F. We acknowledge that this term is not well characterized at the psychological level. It could represent the satisfaction of pleasing the experimenter, or breaking previous record, or showing physical strength, etc. As it shifts the optimal force by a constant, its role was to account for the fact that most participants do produce some effort even when reward is negligible. There was no free parameter to weight this term, first, to preserve the identifiability of the other parameters, and second, because neither dopaminergic treatment nor disease status changed the force peaks observed for very low incentives. The reward-independent term might be preserved and susceptible to activate the behavior, based on sensory or social triggers, even when the reward-dependent term is deficient. This pattern has been observed in a severe apathy syndrome termed “auto-activation deficit” and caused by bilateral damage to the basal ganglia (Schmidt et al., 2008).

The expected cost C(F) was defined as the total motor cost M(F), multiplied by a subjective weight K_c and by a linear fatigue function (for the sake of simplicity), where N indicates the trial number and K_f the individual susceptibility to fatigue:

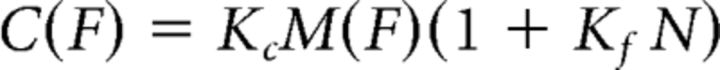The total motor cost M(F) was defined after motor control theory. It was calculated as the integral of the instantaneous motor cost over the active period [0, T], i.e., from effort onset to force peak of an optimal force pulse:

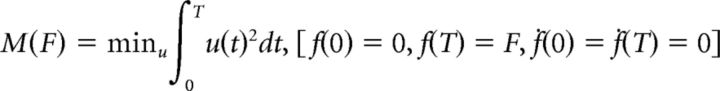Optimal force pulse (i.e., the rising dynamics that minimizes the total motor cost for a given target force F) was modeled as a sigmoid function (Fig. 2A) that approximates the solution of an optimal motor-control model (Rigoux and Guigon, 2012) and requires lower computational resources (see Resolution and approximation of the optimal control problem). We defined the instantaneous motor cost as the quadratic neural drive u(t)², since motor control theory has shown that optimizing this cost minimizes the signal-dependent motor variability and reproduces the cardinal features of movement production (Harris and Wolpert, 1998; Todorov and Jordan, 2002; Guigon et al., 2007). The neural drive was calculated at each time point of the force pulse through a simplified model of muscular contraction, in which the force dynamics ḟ (the dot denotes the temporal derivative) was determined by the neural drive u(t), by a free parameter τ that individually adjusts the rate of motor activation/deactivation, and by the current level of force, f, compared to the maximal theoretical muscular force of the subject, F_max:

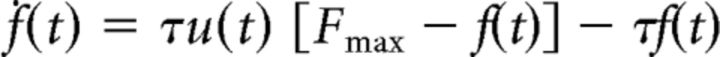Maximal force, F_max, was modeled as another free parameter, superior or equal to the highest force produced by the subject. It was meant to reflect the total muscular mass, and was thus a priori unaffected by pharmacological manipulations.

The three last equations result in a cost function C(F) that links force peak F with its expected cost. This means that for each force level there is a unique motor cost, corresponding to the optimal (sigmoid) dynamics of force trajectory (Fig. 2A–C, green trajectory). In other words, selecting a force peak automatically leads to selecting a trajectory in time with a given yank peak, as reflected in the scaling law. Note that the cost function is explosive (Fig. 2D): it goes to the infinite when subjects get closer to their maximal force. Thus, even if discounting is linear, the resulting net value function (Fig. 2F) is not linear but follows an inverted U shape, with a single maximum. The shape of the cost function C(F) is consistent with the demonstration that perceived effort increases as a power function with force (Stevens, 1957). It has been shown previously that concave (parabolic) cost functions provide a better fit of effort discounting than hyperbolic or linear functions (Hartmann et al., 2013). Divisive functions such as hyperbolic discounting are well adapted to delay discounting, since net values are kept positive, in accordance with the idea that an extremely delayed reward is still better than nothing. Yet this may not be true of effort discounting: climbing a mountain for a peanut may be worse than doing nothing. This is the reason why we opted for subtractive discounting, which allows for negative net values (worse than nothing).

Thus, the free parameters of the model (K_r, K_c, K_f, and τ) adjust the weights of objective quantities (reward, force, and trial number) to individual susceptibility, to compute a subjective net value. The modeled net value was then used to predict the behavioral response on each trial of both choice and force tasks, with specific policy rules. For the force task, the predicted force peak, F*, was simply the argument that maximized the net value function:

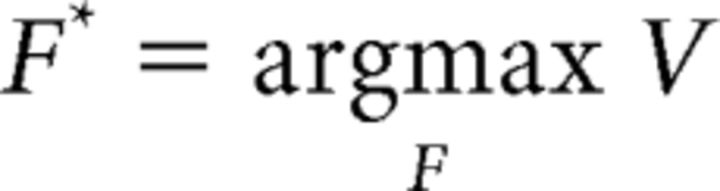In the choice task, there are only two possible reward and force levels. The decision was modeled with a softmax function

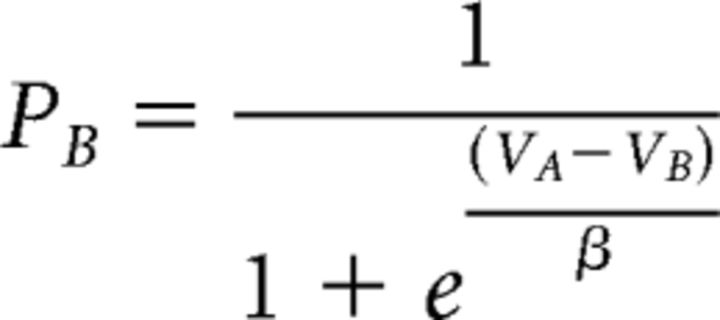that converted the difference in net value between the two options into choice probability, depending on a temperature parameter β. Finally, in both tasks, yank peak was predicted by the equation of muscular dynamics. Thus, the model was inverted by fitting three behavioral variables: choices, force peaks and yank peaks.

Resolution and approximation of the optimal control problem

We want to find the sequence of motor control u(t) that produces, at a given time T, a force peak F with a minimum of effort. The cost of movement is the sum of the (squared) motor drive exerted during movement execution:

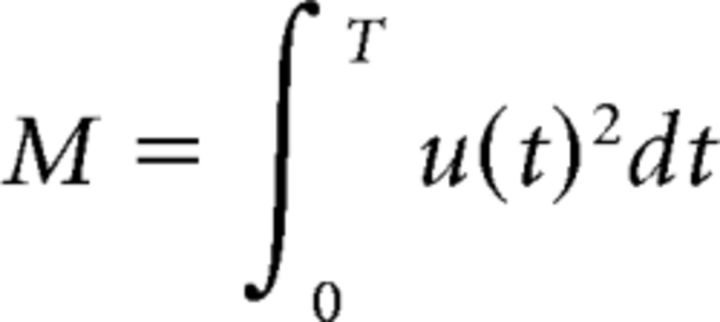The optimal control problem is thus to find the sequence of input u(t) that minimizes the cost M while satisfying the boundary conditions:

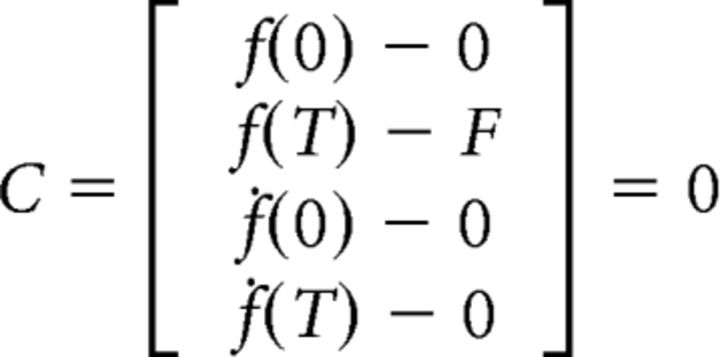Because the resolution of this boundary value problem is too greedy in computational resources to be used in the Bayesian model estimation, we approximated the optimal trajectories with a sigmoid function:

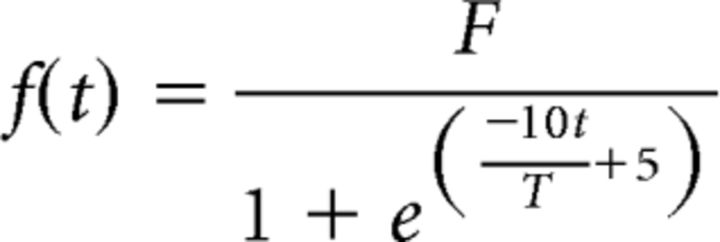This allowed us to derive analytically the motor cost and yank peak for any targeted force peak and pulse duration. While being computationally tractable, the sigmoid approximation produces trajectories very similar to those obtained with the optimal model (Rigoux and Guigon, 2012). More importantly, the sigmoid trajectories provided a very good quantitative approximation for the landmarks of interest (yank peak and motor cost) of the optimal force pulses (R² = 0.990 and R² = 0.986, respectively).

Bayesian model selection

We used Bayesian model selection (BMS) to test which free parameter of the computational model was affected by dopaminergic medication and whether the same parameters could account for the behavior observed in the two tasks. We did not include healthy controls in the model comparison because different individuals may have different parameters, independently of their dopamine level. The comparison within PD patients was therefore cleaner for isolating the impact of dopamine. The different models were inverted using a variational Bayes approach under the Laplace approximation (Friston et al., 2007; Daunizeau et al., 2009), implemented in a Matlab toolbox (available at http://mbb-team.github.io/VBA-toolbox/; Daunizeau et al., 2014). This algorithm not only inverts nonlinear models with an efficient and robust parameter estimation, but also estimates the model evidence, which represents a trade-off between accuracy (goodness of fit) and complexity (degrees of freedom; Robert, 2001). The BMS procedure included the same number of data points (one per trial) and put the same weight on prediction accuracy for the three measurements (yank, force, or choice). The log-evidences, estimated for each subject and model, were submitted to a group-level random-effect analysis, which assumes that models could differ between subjects and that they have a fixed (unknown) distribution in the population. The BMS procedure provided the exceedance probability (Stephan et al., 2009), which measures how likely it is that any given model is more frequent than all other models in the comparison set.

Results

Patients

Demographic data and clinical assessments are summarized in Table 1. Patients (n = 24) and controls (n = 25) did not differ in terms of gender (7 females, 17 males for PD vs 13 females, 12 males for control; χ₍₄₇₎² = 2.64, p = 0.10), age (60.2 for PD vs 57.0 for controls; t₍₄₇₎ = 1.63, p = 0.11), or education (5.2 for PD vs 5.9 for controls; t₍₄₀₎ = 1.15, p = 0.26). As one could expect, we found higher apathy scores in Off-PD patients than in controls (Starkstein score, Off, 14.3 vs controls, 5.2; t₍₄₂₎ = 6.63, p < 0.001). In PD patients, dopaminergic medication (either levodopa or dopamine receptor agonists) not only significantly decreased motor symptoms (UPDRS-III score, Off, 32.8 vs On, 11.7; t₍₂₂₎ = 9.75, p < 0.001), but also significantly reduced apathy scores (Starkstein score, Off, 14.3 vs On, 8.9; t₍₁₆₎ = 6.63, p < 0.001), yet without normalizing them to controls (Starkstein score, On, 8.9 vs controls, 5.2; t₍₄₄₎ = 3.52, p < 0.001). In the following, we report comparisons between controls and Off-PD patients to assess disease effect, and between Off-PD and On-PD patients to assess medication effect.

Dopamine effect on force pulse dynamics

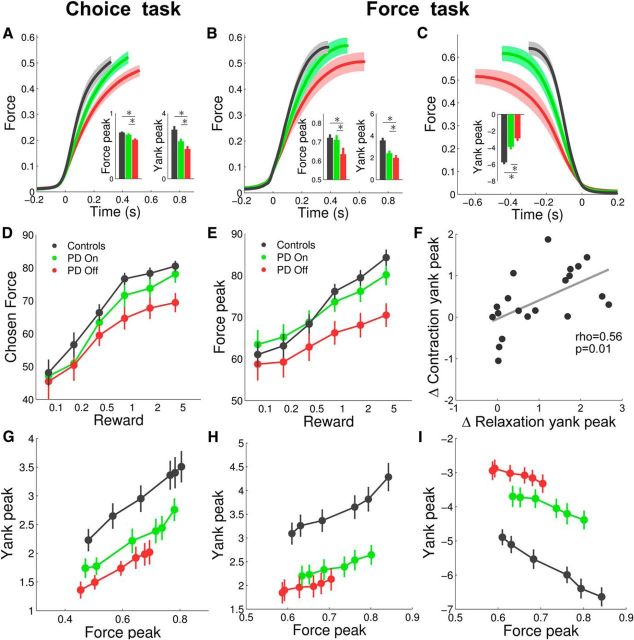
We first assessed how disease status and dopaminergic treatment affected motor contraction during force pulse, regardless of monetary incentives (Fig. 4A,B). Healthy controls (HC) and On-PD patients produced on average higher force peaks than Off-PD patients in both the force task (HC vs Off-PD, t₍₄₃₎ = 2.41, p = 0.010; On-PD vs Off-PD, t₍₁₉₎ = 2.29, p = 0.019) and the choice task (HC vs Off-PD, t₍₄₃₎ = 4.53, p < 0.001; On-PD vs Off-PD, t₍₁₉₎ = 3.27, p = 0.002). In addition, the force rise was faster, i.e., produced with higher peak of yank (the temporal derivative of force) in controls and On-PD compared to Off-PD patients in both the force task (HC vs Off-PD, t₍₄₃₎ = 4.51, p < 0.001; On-PD vs Off-PD, t₍₁₉₎ = 2.51, p = 0.011) and the choice task (HC vs Off-PD, t₍₄₃₎ = 4.07, p < 0.001; On-PD vs Off-PD, t₍₁₉₎ = 3.19, p = 0.002). A similar difference was observed during the relaxation phase (Fig. 4C): the decline in force also exhibited greater negative yank peak in controls and in On-PD compared to Off-PD patients (HC vs Off-PD, t₍₄₃₎ = 7.64, p < 0.001; On-PD vs Off-PD, t₍₁₉₎ = 4.84, p < 0.001). These slowing effects of dopamine depletion on contraction and relaxation yanks were correlated across patients (Pearson's ρ = 0.56, p = 0.01; Fig. 4F). Below, we intend to demonstrate that the effects on force and yank peaks stem from independent motivational and motor functions of dopamine.

Figure 4.

Model-free analysis of behavioral results. A–C, Average force dynamics for controls subjects (black), On-PD patients (green) and Off-PD patients (red). Histograms show the average force peaks and yank peaks. Yank is the derivative of force with respect to time. Force is expressed as a fraction of the subjectwise highest measure, and yank as this fraction per second. A, Contraction phase in the choice task. B, Contraction phase in the force task. C, Relaxation phase in the force task. D, E, Mean effects of incentives on selected forces (indifferent points) in the choice task (D) and on produced force peaks in the force task (E). Incentives are expressed in euros. F, Correlation between dopaminergic effects on contraction and relaxation yank peaks in the force task. Each dot is a patient. G–I, Scaling law relating yank peak to force peak. G, Contraction phase in the choice task. H, Contraction phase in the force task. I, Relaxation phase in the force task. In all graphs, error bars are ±intersubject SEM.

Dopamine effect on binary choice

We then tested whether PD and dopaminergic medication affect the amount of effort allocated to the different reward magnitudes in the choice task (Fig. 1B) by looking at the indifference points obtained after convergence of the staircase procedure. The three groups displayed a significant effect of incentives on choices (Fig. 4D), meaning that they were willing to produce higher force peaks for higher incentives (all p < 0.001). However, this effect (regression slope) was significantly reduced in Off-PD patients compared to both On-PD patients (t₍₁₉₎ = 2.19, p = 0.021) and controls (t₍₄₃₎ = 1.76, p = 0.039). Post hoc comparisons showed that controls and On-PD patients chose higher force peaks than Off-PD patients specifically for the highest (HC vs Off-PD, t₍₄₃₎ = 3.51, p < 0.001; On-PD vs Off-PD, t₍₁₉₎ = 2.76, p = 0.006) but not for the lowest incentive level (HC vs Off-PD, t₍₄₃₎ = 0.41, p = 0.341; On-PD vs Off-PD, t₍₁₉₎ = 0.50, p = 0.312).

Dopamine effect on incentive motivation

Next, we tested in the force task (Fig. 1A) whether disease status and dopaminergic medication affect incentive motivation, the process by which higher expected rewards are translated into greater efforts. The force peak significantly increased with incentive level in the three groups (Fig. 4E; all p < 0.001), but this effect (measured by the regression slope) was smaller in Off-PD compared to On-PD patients (t₍₁₉₎ = 2.11, p = 0.024) and to controls (t₍₄₃₎ = 2.35, p = 0.012). As in the choice task, post hoc comparisons showed that control subjects and On-PD patients produced more force than Off-PD patients for the highest (HC vs Off-PD, t₍₄₃₎ = 4.15, p < 0.001; On-PD vs Off-PD, t₍₁₉₎ = 2.92, p = 0.004) but not for the lowest incentive level (HC vs Off-PD, t₍₄₃₎ = 0.49, p = 0.315; On-PD vs Off-PD, t₍₁₉₎ = 1.36, p = 0.096).

Dopamine effect on motor scaling law

The preceding results indicate that dopamine has a similar role in the two tasks: it amplifies the weight of monetary incentives on effort production. Besides these motivational effects, motor effects were observed when examining the coupling of force kinematics parameters. Higher force peaks were linearly associated with greater yank peaks during both the contraction phase (Fig. 4G,H; all p < 0.001) and the relaxation phase (Fig. 4I; all p < 0.001). As shown in preceding analyses, the range of force peaks displayed by PD patients in response to incentive levels was narrower than in controls, and even more in Off compared to On patients. Yet the linear relationship between force and yank peaks was conserved in patients. Dopamine depletion manifested as a downward shift, meaning that equivalent force peaks were associated with lower yank peaks. This shift in the force-yank scaling law was significant in both the choice task (contraction phase, HC vs Off-PD, t₍₄₃₎ = 3.11, p = 0.002; On-PD vs Off-PD, t₍₁₉₎ = 2.34, p = 0.015) and the force task (contraction phase, HC vs Off-PD, t₍₄₃₎ = 4.79, p < 0.001; On-PD vs Off-PD, t₍₁₉₎ = 1.92, p = 0.035; relaxation phase, HC vs Off-PD, t₍₄₃₎ = 7.50, p < 0.001; On-PD vs Off-PD, t₍₁₉₎ = 3.44, p = 0.001). Thus, on top of the motivational effect of dopamine depletion that narrowed down the range of force peaks observed for the different incentive levels, a motor effect diminished the speed with which these force peaks were attained.

Computational analysis

We then studied how these dopamine-dependent modulations of effort production could be explained at the computational level. We developed a normative model that predicts how force dynamics should be selected in principle, depending on two contextual factors (incentive level and trial number) and four free parameters (reward sensitivity, cost sensitivity, fatigability, and motor activation rate: K_r, K_c, K_f, and τ). The predictions arise from a two-step optimization. The first step uses motor control equations to calculate the cost associated with each force peak (Fig. 2, top). This estimation determines the dynamics of force rise over time (and therefore the yank peak): the one that minimizes the motor cost. The second step uses decision theory to calculate the net value (benefits minus costs) of each force peak (Fig. 2, bottom). This valuation process determines which force peak will be produced in the force task or selected in the choice task: the one that maximizes the net value. Note that one additional parameter was included in the model to fit the choices: choice temperature (β), which captures the stochasticity of decisions.

We used simulations to verify that each parameter controlled a specific behavioral pattern (Fig. 3). We then examined which free parameters best explained the effects of dopaminergic medication on choices and force and yank peaks. These computational analyses were conducted using the same model with the same set of parameters for both tasks. Medication effects could a priori be accounted for by a modulation of any of the four parameters. We considered the 2⁴ possible combinations (modulation or no modulation for any of the four parameters). These 16 models were estimated in both tasks simultaneously and compared by families for each parameter using Bayesian model selection. The winning model was the one where dopaminergic medication affects both K_r and τ (with family exceedance probabilities xp > 0.95), increasing the weight of monetary incentives and decreasing the rate of motor contraction/relaxation (Fig. 5A). This model provided a good fit for the three behavioral measures, i.e., force peak (mean R² = 0.94), choice (mean accuracy, 0.70), and yank peak (mean R² = 0.92).

Figure 5.

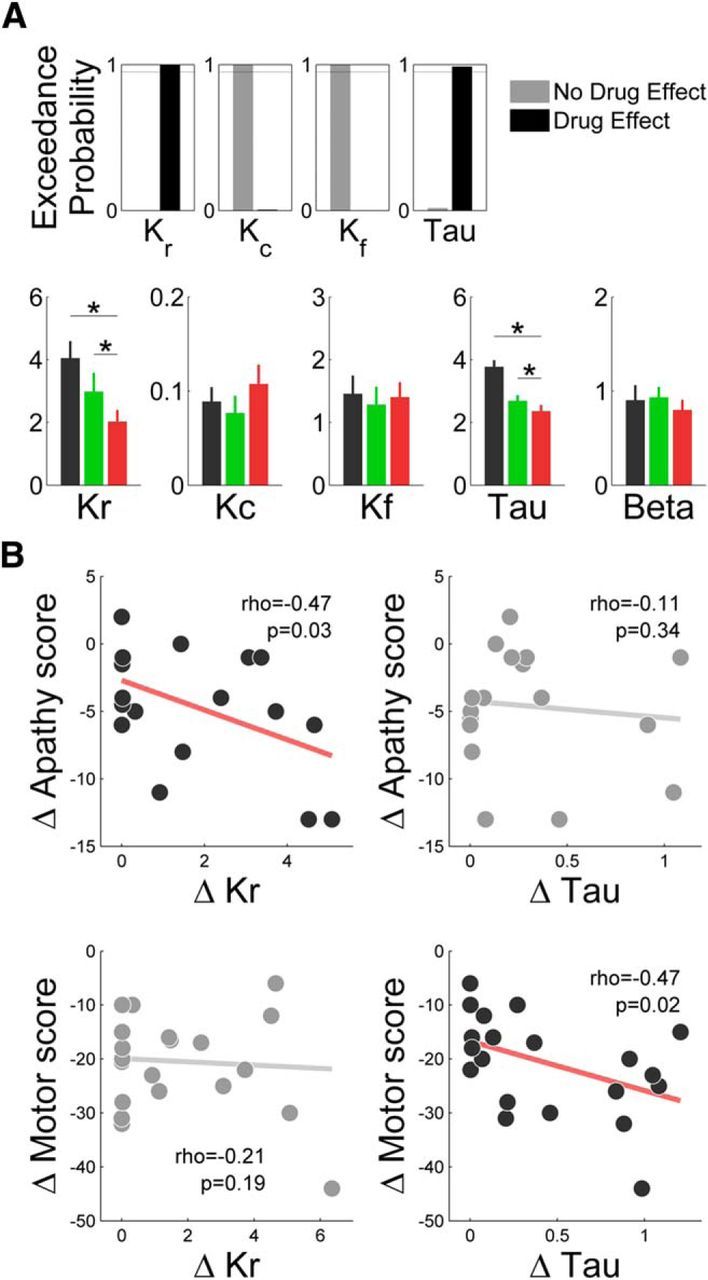
Computational characterization of dopaminergic medication effects. A, Top, Results of a Bayesian model selection comparing the plausibility of different possible modulations of behavioral response by dopaminergic medication in PD patients. For each parameter, the families of models with and without a modulation by dopaminergic medication were compared. Exceedance probability indicate how likely it is that one family is more frequent than the other in the population of PD patients. A, Bottom, Estimates of model parameters calculated at the session level in controls (black), On-PD patients (green), and Off-PD patients (red). *p < 0.05. B, Correlation of medication effects on computational parameters K_r and τ with clinical effects on apathy (Starkstein score) and motor dysfunction (UPDRS-III score). Each dot is a patient. For illustration only, a jitter of 0.5 points was added to y-axis scores to facilitate discrimination of overlapping dots.

We also tested whether the same parameters could account for the two tasks, by comparing this family of 16 models to an equivalent family with distinct sets of parameters for the two tasks. Although the latter better explained the data (xp > 0.95), none of the parameters showed a consistent effect of task across subjects (all p > 0.05). Moreover, we separately estimated medication effects in the two tasks and found correlated estimates across patients for both K_r (ρ = 0.78, p < 0.001) and τ (ρ = 0.43, p = 0.049). This result means that patients exhibiting large computational change (in K_r or τ) in one task also exhibit a large change in the same parameter in the other task. It strengthens the conclusion that using the same set of parameters for the two tasks is the best compromise between model complexity and data fitting.

Finally, we examined whether the model parameters could predict the clinical changes observed in patients after dopaminergic treatment. These clinical changes were improvement in both apathy and motor dysfunction assessed with the Starkstein apathy score and the UPDRS-III motor score, two effects that appeared unrelated across patients (ρ = −0.11, p = 0.66). Similarly, the effects of dopaminergic medication on K_r and τ seemed quite independent (ρ = −0.12, p = 0.69), meaning that patients who exhibited large medication effects on reward sensitivity were not the same as patients exhibiting large effects on motor activation rate. Thus, we tested the correlation between the changes in K_r and τ and the changes in apathy and motor dysfunction. We found that K_r modulation (ρ = −0.47, p = 0.03), but not that of τ (ρ = −0.11, p = 0.34), significantly predicted the alleviation of apathy, whereas τ modulation (ρ = −0.47, p = 0.02), but not that of K_r (ρ = −0.21, p = 0.19), significantly predicted the improvement of motor dysfunction (Fig. 5B). The same dissociation was obtained when, instead of testing separate correlations, the two computational effects (dopamine-induced changes in K_r and τ) were included as competing regressors in a same general linear model meant to explain the improvement in apathy (K_r, p = 0.030; τ, p = 0.305) or motor dysfunction (τ, 0.018; K_r, 0.160).

Discussion

In this study, we assessed the effects of dopamine depletion (comparing Off-PD patients to healthy controls) and dopamine repletion (comparing Off-PD to On-PD patients) on effort allocation, using both binary choice and incentive force tasks. Model-free analyses showed that dopamine is causally involved in (1) amplifying the boosting effect of potential rewards on force production and (2) speeding up force rise to the peak, regardless of expected rewards. We developed a computational model of effort production to further characterize the dissociation of motivational and motor effects, focusing on the effect of dopaminergic medication in PD patients. Model-based analyses showed that dopamine enhancers increase reward sensitivity and increase motor activation rate, while leaving unaffected other parameters such as cost sensitivity, fatigability, or choice temperature.

Our results are consistent with the idea that dopamine helps with producing greater effort to obtain greater reward, an idea that has received a good wealth of evidence in animals (Walton et al., 2009; Salamone et al., 2012). Previous studies in humans have shown that d-amphetamine, a dopamine enhancer, enhances the willingness to exert effort (Wardle et al., 2011; Treadway et al., 2012). However, effort cost was often confounded with delay of reward obtainment in previous studies. This confound was minimized in our paradigm since higher force pulses were not much longer to produce. In line with our study, a similar paradigm was used previously to demonstrate that dopamine promotes the choice of high reward/high effort options in PD patients, even in the absence of apathy (Chong et al., 2015).

Moreover, we provide the first demonstration in humans that dopamine similarly enhances the propensity to select high reward/high effort options (in the choice task) and the energy actually invested in instrumental behavior (in the force task). These two processes could be considered as two different components of the behavior: orientation (which goal is selected) and intensity (how much energy is expended in goal pursuit). Our model nonetheless treats them as two instances of a same decision problem that consists of choosing a pair of effort and reward levels. The difference is that only two options are available in one task, whereas the option set is continuous (between 0 and maximal force) in the other task, making binary choice a special case of the incentive motivation problem. Yet from a psychological perspective, a crucial difference might be that the selected reward–effort pair is explicitly expressed before effort production in the binary choice but not in the incentive force task. This could change the behavioral output (force peak), as whenever possible the decision might be dynamically refined on the basis of sensory feedback. Our model is essentially static: it determines the best option on the basis of anticipated estimation of costs and benefits. Although it provided a good fit of force data in both tasks, the absence of dynamic adjustment might be one of its limitations.

Although previous studies did show that dopamine enhances the willingness to exert higher effort for higher reward, they did not disentangle between the possibilities that dopamine could increase reward attractiveness or decrease effort painfulness. Our model-based analyses suggested that the motivational effect of dopamine can be accounted for by an increase in K_r, the subjective weight of expected reward in the cost–benefit computation. This is consistent with a previous study showing impaired incentive processing, as measured by neurophysiological markers, in apathetic PD patients (Martínez-Horta et al., 2014). This specific effect on K_r could also account for why dopamine helps overcoming various types of costs when seeking rewards, from effort (Salamone et al., 2012), to risk (St Onge and Floresco, 2009), or delay (Denk et al., 2005). The K_r effect is also consistent with the demonstration that midbrain dopaminergic neurons respond to stimuli that predict future rewards (Schultz et al., 1997), encode reward magnitude (Tobler et al., 2005; Roesch et al., 2007), and promote responses to reward-predicting cues (Tsai et al., 2009; Arsenault et al., 2014).

Conversely, dopamine did not change the fatigability parameter K_f, nor the subjective weight of effort cost K_c. These results are consistent with the absence of support for a role of dopamine depletion in fatigue (Willner et al., 1992), and with the observation that measures of nucleus accumbens dopamine or dopaminergic neuron activity are much more sensitive to expected reward than to expected effort (Gan et al., 2010; Pasquereau and Turner, 2013).

Crucially, we found another effect of dopaminergic medication that was independent from reward level: after dopamine depletion, equivalent force peaks were produced with lower yank peaks, and this was independent from the restriction of force peaks produced for the different incentive levels. A similar shift in the motor scaling law had already been observed in PD patients performing a nonisometric task (Baraduc et al., 2013; Hartmann et al., 2013). Our results accord well with the view that PD does not fundamentally change movement organization but restricts movement kinematics (Mazzoni et al., 2007; Baraduc et al., 2013). In our model, dopamine depletion decreased the motor activation rate τ, which adjusts how motor drive impacts movement kinematics. Lower τ translates into slower muscle contraction for a given motor drive, and also slower relaxation. The mechanisms by which dopamine depletion slows down motor dynamics might involve an impaired selectivity in basal ganglia processing, leading to a failure to activate appropriate agonist muscles, or to inhibit antagonist muscles (Mink, 1996; Pessiglione et al., 2005). The modulation of τ and its consequences on contraction and relaxation slowness could therefore account for both bradykinesia and rigidity.

Although the model clearly distinguishes motivational and motor processes, it nevertheless allows for motivation to help reducing motor impairment. Indeed, even if the coupling between motor command and movement kinematic is impaired, a high motivation can overcome effort cost and increase the motor command enough to attain standard movement speed (but still slower than that of healthy subjects with the same level of motivation). This may explain the benefits of increasing motivation on motor abilities in MPTP-induced parkinsonism (Pessiglione et al., 2004) and in PD (Kojovic et al., 2014), and perhaps the puzzling phenomenon termed “kinesia paradoxica,” i.e., the sudden ability of PD patients to exhibit normal movement speed in urgent situations such as fire or accident (Souques, 1921; Ballanger et al., 2006).

The motivational and motor functions of dopamine might be supported by topographically distinct functional networks, namely, the mesocorticolimbic and the nigrostriatal pathways. Apathy and motor symptoms might therefore reflect the heterogeneity in space and time of degeneration in PD. The dopaminergic loss occurs sooner and is stronger in the substantia nigra than in the ventral tegmental area (Hirsch et al., 1988; Damier et al., 1999). This translates into a gradient with stronger dopamine depletion in the dorsolateral putamen, compared to caudate and ventral striatum (Kish et al., 1988). The severity of motor symptoms in PD correlate with substantia nigra neurodegeneration (Gorell et al., 1995; Du et al., 2012) and with dopamine depletion in the dorsolateral striatum (Leenders et al., 1986), supporting involvement of the nigrostriatal pathway in motor dysfunction. In contrast, the ventral tegmental area has been hypothesized to play a key role in motivated behaviors (Tsai et al., 2009), through the mesolimbic projections to the ventral striatum (Berridge, 2007; Salamone et al., 2012), which has been conceived as a functional interface for translating motivational drives into motor or cognitive behaviors (Mogenson et al., 1980; Schmidt et al., 2012). In accordance with this view, apathy in PD has been proposed to depend on the mesolimbic rather than on the nigrostriatal pathway, and consequently to dopaminergic denervation in the ventral striatum (Javoy-Agid and Agid, 1980; Remy et al., 2005; Thobois et al., 2010; Brown et al., 2012; Martínez-Horta et al., 2014). In addition, the mesocortical pathway might contribute to incentive motivational effects, as, for instance, dopamine function in the ventromedial prefrontal cortex was found to predict the willingness to produce greater effort for larger reward (Treadway et al., 2012).

In conclusion, our computational analysis suggests that dopamine depletion downweights expected reward in the cost–benefit computation, and thus lowers the acceptable effort costs, resulting in a reduction of goal-directed behaviors, i.e., apathy. On top of this motivational deficit, dopamine depletion might also impair how acceptable costs are translated into movement kinematics, resulting in slower actions, i.e., bradykinesia. The motivational and motor effects of dopamine were captured by two distinct parameters of the model, which were correlated across patients to clinical assessments of motivational and motor deficits. We argue that computational phenotyping, i.e., the characterization of patients by model parameters adjusted on their behavior, might provide a useful intermediate explanation level between the clinical manifestations and the underlying neurophysiology. This computational approach could be applied to various pathological situations to help with personalizing treatments. In the present case, the two computational effects of dopamine are likely underpinned by distinct neural circuits, the mesolimbic and nigrostriatal pathways. Yet demonstrating such a link between computational parameters and underlying neural circuits requires further investigation.