Human Choice Strategy Varies with Anatomical Projections from Ventromedial Prefrontal Cortex to Medial Striatum

Abstract

Two distinct systems, goal-directed and habitual, support decision making. It has recently been hypothesized that this distinction may arise from two computational mechanisms, model-based and model-free reinforcement learning, neuronally implemented in frontostriatal circuits involved in learning and behavioral control. Here, we test whether the relative strength of anatomical connectivity within frontostriatal circuits accounts for variation in human individuals' reliance on model-based and model-free control. This hypothesis was tested by combining diffusion tensor imaging with a multistep decision task known to distinguish model-based and model-free control in humans. We found large interindividual differences in the degree of model-based control, and those differences are predicted by the structural integrity of white-matter tracts from the ventromedial prefrontal cortex to the medial striatum. Furthermore, an analysis based on masking out of bottom-up tracts suggests that this effect is driven by top-down influences from ventromedial prefrontal cortex to medial striatum. Our findings indicate that individuals with stronger afferences from the ventromedial prefrontal cortex to the medial striatum are more likely to rely on a model-based strategy to control their instrumental actions. These findings suggest a mechanism for instrumental action control through which medial striatum determines, at least partly, the relative contribution of model-based and model-free systems during decision-making according to top-down model-based information from the ventromedial prefrontal cortex. These findings have important implications for understanding the neural circuitry that might be susceptible to pathological computational processes in impulsive/compulsive psychiatric disorders.

SIGNIFICANCE STATEMENT Scholars from several disciplines have long been interested in the neural mechanisms of decision-making. An influential suggestion has structured decision-making into a flexible but expensive model-based system, and a more rapid but also more rigid model-free system. Here, we show that anatomical properties of the connections between frontal and striatal regions predict the use of a model-based system when individuals make decisions. Individuals with stronger top-down connectivity from the ventromedial prefrontal cortex to the medial striatum were more likely to rely on a model-based strategy during decision-making, suggesting that the ventromedial prefrontal cortex biases a striatal balance between model-based and model-free control. These findings qualify the neural implementation of decision-making computations and open the way for understanding decision-making pathologies.

Introduction

Instrumental actions are controlled by two distinct strategies: a flexible but computationally expensive goal-directed strategy and a rapid but rigid habitual strategy. This distinction has recently been formalized in a normative computational account in which two reinforcement learning strategies (a “model-based” and a “model-free” system) jointly control instrumental actions (Daw et al., 2005). The model-free system directly reinforces actions that lead to reward, ignoring the probabilistic structure of predictive cues in the environment. The model-based system uses an internal model of probabilistic regularities in the environment to evaluate candidate actions.

It is generally assumed that reliance on habitual actions is influenced by state factors. For instance, stress, dual-tasking, administration of dopaminergic drugs, transcranial magnetic stimulation, and striatal presynaptic dopamine affect the relative balance between model-based and model-free control (Wunderlich et al., 2012b; Otto et al., 2013a, b; Deserno et al., 2015). Those state-dependent effects have been indexed by population-level summary parameters, treating interindividual trait variability as noise. Indeed, structural differences in the neural circuits supporting model-free and model-based control might explain interindividual variability in the relative contribution of those two systems. Accordingly, this study considers whether human choice is systematically biased by stable neuroanatomical trait factors.

The available evidence suggests that model-based and model-free control systems rely on partly different frontostriatal circuits. Ventromedial prefrontal cortex (vmPFC) and the dorsomedial striatum are implicated in model-based control (Gläscher et al., 2010; Daw et al., 2011; Wunderlich et al., 2012a; Lee et al., 2014), whereas the dorsolateral striatum is implicated in model-free control (Wunderlich et al., 2012a). This neuroanatomical segregation of computational functions nicely overlaps with the long-standing distinction between goal-directed and habitual modes of behavioral control. Works with behaving rodents (Balleine and Dickinson, 1998; Corbit and Balleine, 2003; Yin et al., 2005) and healthy humans (Valentin et al., 2007; Tanaka et al., 2008; Gläscher et al., 2009) have shown that dorsomedial striatum as well as vmPFC are implicated in goal-directed actions. On the other hand, dorsolateral striatum has been shown to contribute to habitual responses (de Wit et al., 2012). Building on this evidence, in this study we tested whether interindividual variation in the strength of anatomical connectivity within those frontostriatal circuits predicts the relative contribution of model-free and model-based systems to human choice. We hypothesized that intersubject variability in the relative balance between model-based and model-free control depends on the integrity of anatomical frontostriatal connections, with the vmPFC and dorsomedial striatum implicated in model-based control and frontal motor areas and dorsolateral striatum implicated in model-free control.

Using probabilistic tractography of diffusion-tensor images (DTI), connectivity-based parcellation of the frontal lobe (Beckmann et al., 2009; Mars et al., 2011; Neubert et al., 2014), and a computationally explicit learning model of a multistep decision task (Daw et al., 2011), this study mechanistically grounds the balance between model-free and model-based control systems into the relative strength of different frontostriatal loops. To anticipate the results, we found evidence that the structural integrity of white-matter tracts between vmPFC and medial striatum predicts individuals' reliance on model-based control. By masking out bottom-up tracts, we found evidence that top-down afferences from the vmPFC to the medial striatum determine the relative contribution of model-based control during decision-making.

Materials and Methods

Participants.

We recruited 33 healthy volunteers. All participants gave informed consent, and the study was approved by the local ethics committee. All participants underwent two separate sessions: a diffusion-weighted MRI scan and a behavioral session during which subjects were tested on the multistep decision task used previously to quantify model-based and model-free components of instrumental actions in humans (Daw et al., 2011) (see Fig. 1A). Two participants quit the study after the first session. Thus, data from 31 participants (15 men, mean age 22.7 ± 2.5 years) were analyzed. Participants had no history of neurological and psychiatric disorders.

Figure 1.

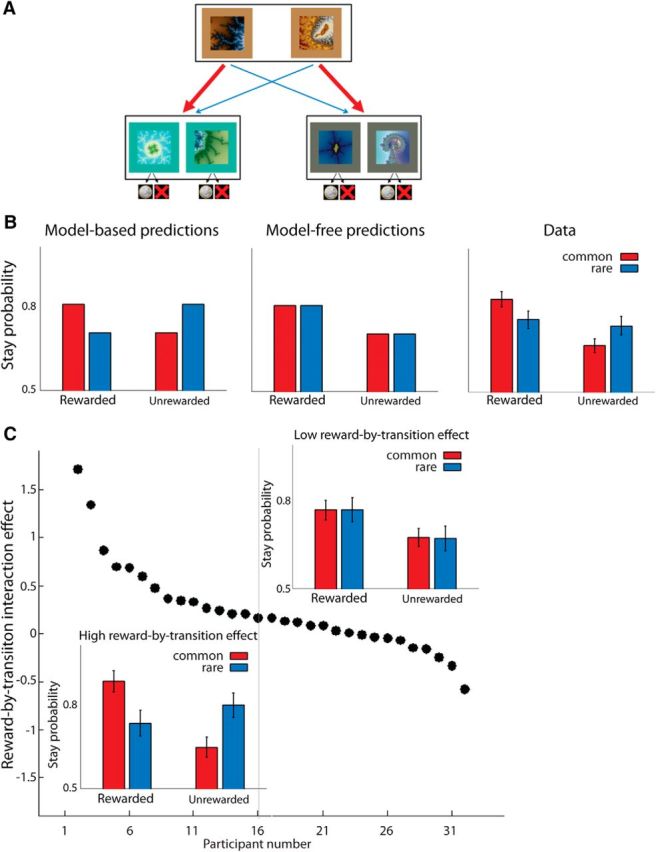
Task setup, model predictions, and behavioral data. A, Task setup: Participants chose between two fractal stimuli, which led probabilistically to one of the two different second-stage sets. B, Model predictions and observed behavior. Left, If choice were completely controlled by the model-based system, the first-stage choice predominantly associated with the rewarded second-stage choice would be reinforced. Middle, If choice were completely controlled by the model-free system, then repeating the first-stage choice in the subsequent trial (stay probability) is a function of reward delivery regardless of the transition occurred. Right, Data averaged over all subjects show signature of both systems. The analysis of stay probability data revealed a significant main effect of reward delivery (i.e., model-free signature) as well as an interaction between reward delivery and transition (i.e., model-based signature). C, Individual variability in the reliance on the model-based system. Subjects are sorted in descending order based on reward-by-transition interaction effect, which is an index of model-based control in the task. In half of participants, the hallmark of model-based control is clearly observable. However, the other half of participants show no evidence of reliance on the model-based strategy. Insets, Mean stay probabilities as a function of reward and transition. Bottom left inset, Data from the median-split half of individuals with a large reward-by-transition effect. Top right inset plot, Data from the median split half of individuals with a small reward-by-transition effect. Error bars indicate SEM.

Task.

On each trial of the task, subjects first made a choice between two fractal stimuli leading to one of the two different second-stage sets represented by different colors. Participants then made another choice between two stimuli presented in the second-stage set. Each stimulus at the second stage was associated with a specific probability of delivering a monetary reward. Similar to previous studies with this task (Daw et al., 2011; Smittenaar et al., 2013), the probabilities of delivering reward changed independently and slowly based on a Gaussian random walk to motivate participants to continue learning throughout the task. Critically, each choice at the first stage led predominantly (70%) to one of the two sets at the second stage (common transition) and, less frequently (30%), to the other set (rare transition). This feature of the task allowed us to distinguish contribution of model-based and model-free in choices. The task consisted of 201 trials.

Behavioral analysis.

Logistic regression was used to analyze responses at the first level of the task independently for each participant. The multistep task has a 2 × 2 factorial design, where the factors are transition (common or rare) and reward delivery on the previous trial (rewarded or unrewarded). Thus, first-stage choices, encoded as binary stay/switch responses, were regressed against four predictors: main effects of the two factors, interaction effect of the two factors, and an intercept representing the tendency to stay with the same choice regardless of transition and reinforcement factors (stickiness). Logistic regression was performed separately for each subject using the MATLAB Statistics toolbox (glmfit routine; The MathWorks). The degree of model-free and model-based deployment was quantified as the main effect of reward delivery and the interaction effect between reward delivery and transition, respectively.

Computational modeling.

We also fitted data to reinforcement learning models previously suggested to account for choices in this task (Daw et al., 2011). Thus, we fitted a reinforcement learning model-free algorithm, a reinforcement learning model-based algorithm, and a hybrid account, which assumes that choices at the first level are generated based on the weighted combination of values from these two reinforcement learning models.

The task has three distinct states corresponding to the three sets of fractal stimuli: the first-stage state, s_A, and two second-stage states, s_B and s_c. On each trial, t, subjects see a first-stage state, s_1,t (s_A), in which action a_1,t is taken. This is followed by a second-stage state, s_2,t (either s_B or s_C) in which action a_2,t is taken.

A model-free agent estimates a value function for each state-action pair. Thus, a prediction error, δ_i,t, is computed and used to update value of the corresponding state-action: Q_MF(s_i,t, a_i,t)←Q_MF(s_i,t, a_i,t) + α_i δ_i,t, where δ_i,t = r_i,t + Q_MF(s_i+1,t, a_i+1,t) − Q_MF(s_i,t, a_i,t) is the prediction error at each stage and α_i is the learning rate parameter at either stage. For first-stage choices, there is no direct reinforcement (r_1,t = 0) and for the second-stage choice, Q_MF(s_3,t, a_3,t) = 0 because there is no following state. The first-stage state-action value is also updated using an eligibility trace parameter, λ, to capture immediate effects of second-stage reinforcement on the first-stage state: Q_MF(s_1,t, a_1,t)←Q_MF(s_1,t, a_1,t) + α₁λδ_2,t.

A model-based agent takes into account transition probabilities to estimate the value of actions. Thus, this algorithm calculates the first-stage action based on the transition maps. Because the nature of the transition matrix (i.e., existence of rare and common transitions) is instructed, similar to Daw et al. (2011), it is assumed that subjects choose between two possibilities: whether s_B is the second-stage set commonly associated with action a_A at first stage or vice versa, that s_C is the one commonly associated with action a_A at first stage. Without loss of generality, similar to Daw et al. (2011), we assume that probability of common and rare transitions is 0.7 and 0.3, respectively; if these are changed, other parameters of the model will rescale to give the same likelihood (Daw et al., 2011). Therefore, the model-based values of first-stage actions are computed as follows:

where a_max is the action in the corresponding state that maximized Q_MF at the second stage. Because the second-stage states are terminal states, model-based value of actions at the second-stage is assumed to be equal to that of model-free.

Finally, the hybrid account computed a weighted average of action value of model-based with that of model-free: Q_hybrid = wQ_MB + (1 − w)Q_MF, where 0 < w < 1 is a weight parameter. Higher values of w are associated with higher degree of model-based (and lower degree of model-free) influences on choice. For w = 0 and w = 1, the hybrid account is equivalent to pure model-free and pure model-based, respectively. A softmax transformation was then used to generate probability of choice for all models based on distinct decision noise parameters for each stage, β_i, and a perseveration parameter, ϕ, which captures first-stage perseveration or switching tendency in choices regardless of action values (Lau and Glimcher, 2005).

Model fitting and model selection.

We estimated parameters of each model separately for each participant using nonlinear derivative-based optimization algorithm as implemented in fminunc tool in MATLAB (The MathWorks). All three models have second-stage learning rate, α₂, two decision noise parameters, β₁ and β₂, and the perseveration parameter, ϕ. The model-free and hybrid accounts have two additional parameters for updating actions values at the first stage, α₁ and λ. The hybrid model has one key weighting parameter, w, for combining action values of model-based and model-free at the first-stage. Four parameters (α₁, α₂, λ, and w) are bounded between 0 and 1. The decision noise parameters are bounded to positive values.

For bounded parameters of each model, we fitted parameters in the infinite real space of Gaussian distribution parameter values and transformed them before feeding them into the models using appropriate transformation functions (sigmoid for parameters bounded between 0 and 1; exponential for parameters >0). This method enabled us to use unconstrained optimization techniques that are usually more robust than constrained ones. Similar methods have been adopted for fitting reinforcement learning models to choice data in this task (e.g., Wunderlich et al., 2012b). A wide Gaussian prior, Normal(0,10), was assumed for all parameters (with zero mean and a broad variance of 10). Free parameters of each model were estimated to maximize log-likelihood of data plus log-prior (maximum a posteriori), where the likelihood is defined across both first-stage and second-stage choices, similar to previous works on this task (Daw et al., 2011). The prior distributions of parameters used in this study were broader than those of Daw et al. (2011).

We computed model evidence for every model and every subject using Laplace approximation (MacKay, 2003), which penalizes complexity of the model by integrating out the free parameters. We then used the approximated model evidence to perform a random-effect Bayesian model comparison across all participants, a procedure that takes the model identity as random, in contrast to fixed, effect (Rigoux et al., 2014). We also used the approximated model evidence to compare models for each subject separately. For this analysis, a log-Bayes-factor >3 was considered as significant because the corresponding Bayes factor is >20 (compare the classical p < 0.05 criterion). The log-Bayes-factor >2.3 was also considered as trend toward significance because it corresponds to p < 0.1.

Data acquisition and image processing.

Structural and diffusion images were collected using a 3 Tesla Siemens MRI scanner. T1-weighted high resolution MP-RAGE structural image was collected (voxel size = 1 mm isotropic, GRAPPA acceleration factor 2). DTI scanning was performed with the following parameters: 64 slices interleaved acquisition mode (TE/TR = 89/6700 ms, flip angle = 90, FOV = 220 mm, voxel size = 2.2 mm isotropic). DTI scans consisted of 7 scans without diffusion weighting (b = 0) and 61 scans with diffusion weighting (b = 1000 s/mm²) applied along the noncolinear directions.

All DTI preprocessing was conducted using FSL tools. Preprocessing of DTI data was performed based on the standard FSL protocol. BET was used to automatically extract brains from T1 (Smith, 2002), and images were manually checked for all samples and reextracted if not successful. FNIRT was used for nonlinear registration of structural images to standard template (Jenkinson et al., 2012). Registered images were manually checked, and FLIRT (Jenkinson and Smith, 2001; Jenkinson et al., 2002) was used for registration of structural images in four subjects where FNIRT was not successful. FDT was used to correct the DTI data for head movement and eddy current correction, brain extraction, and tensor model fitting. The diffusion parameters were then sampled for each voxel using BEDPOSTX (Behrens et al., 2007).

Imaging analysis pipeline.

The goal of this study was to investigate the relationship between behavioral indices of model-based/model-free control quantified by the multistep decision task and anatomical circuitry connecting the striatum to the frontal cortex using DTI and probabilistic tractography. To quantify frontostriatal structural connectivity, we used a fully automated procedure to compute connectivity maps between the striatum and the frontal cortex. To achieve this, we first performed a parcellation of frontal cortex based on its connectivity with the striatum. This analysis resulted in five clusters (see below). Next, connectivity between each striatal voxel and each of the five frontal clusters was computed. This resulted in five connectivity images per subject, quantifying connectivity between each striatal voxel and the five frontal clusters.

Striatum-based parcellation of frontal cortex.

First, we created a striatal mask in MNI space using the Harvard–Oxford subcortical atlas. The MNI frontal lobe mask was used for frontal cortex. For computational feasibility, the frontal mask was resampled to 4 mm isotropic voxel size. These masks were then transformed to each participant's native diffusion space using registration wrap images and matrices computed during preprocessing. Probabilistic tractography was then performed in native diffusion space using PROBTRACX (Behrens et al., 2007), where tracts seeded from every voxel within the frontal lobe and its connectivity with all striatal voxels was quantified in each participant (Behrens et al., 2007). This procedure computes a connectivity matrix, which characterizes every voxel within the frontal lobe based on its connectivity pattern with striatal voxels. The connectivity matrix was used to generate a symmetric cross-correlation matrix, which reflects the correlation in connectivity fingerprint of frontal voxels. This cross-correlation matrix was then subjected to K-means clustering, a well-known algorithm for clustering used previously for parcellation of brain regions (Beckmann et al., 2009; Mars et al., 2011; Neubert et al., 2014; Piray et al., 2015), to identify voxels sharing similar striatum-connectivity profiles. Because the correct number of frontal clusters is unknown, we performed a stability analysis to identify the most consistent and coherent number of clusters (see below for mathematical definition). Subjects were randomly divided into two groups, and a series of parcellation into 2–8 clusters was performed separately for each group. The clustering solutions based on data from two groups were then compared to examine their consistency as a function of number of clusters. This procedure was repeated for 100 randomly division of subjects to two groups and used to obtain a stability index. Tractography was performed separately for the right and left hemispheres.

Stability analysis of parcellation solution.

To ensure that the parcellation scheme is robust at the between-subject level, we performed a stability analysis, which identifies the largest number of clusters resulting in a significantly robust clustering solution. To achieve this, we assessed whether two clustering solutions calculated based on two independent datasets (e.g., by dividing subjects randomly to two groups) were matched. Here, we provide a mathematical explanation of our approach (Piray et al., 2015; their Appendix).

Two sets of clusters (A and B, each with K clusters) were defined as matched based on the following criteria: First, for every cluster in A and every cluster in B, an overlap index was defined, which corresponds to the number of voxels that overlap between the two clusters. Specifically, for every cluster a_i in A and every cluster b_j in B, the overlap index was defined as N_i,j/min(N_i, N_j), where N_i, N_j, and N_i,j are the number of voxels in a_i, b_j and their intersection, respectively. Next, for every cluster a_i in A, b_j in B was defined as matched if it had the largest overlap index with a_i. Finally, A and B were considered as matched if each cluster in A was matched with one and only one cluster in B; and vice versa if each cluster in B was matched with one and only one cluster in A. This procedure also gives a one-to-one mapping between “labels” of clusters in A and B, regardless of anatomical location of voxels.

Connectivity maps between the striatum and frontal clusters.

Having established the target frontal regions, probabilistic tractography (using PROBTRACKX tool in FSL) was seeded from each voxel in the striatum with the five identified clusters as targets (using the classification mask option in PROBTRACKX). This procedure created five images, one for each frontal target, of probability values where each voxel value corresponds to the number of pathways that begins at that voxel and ends in the target region. Tractography was performed separately for the right and left hemispheres. All maps were smoothed with a 6 mm Gaussian kernel.

We also performed an analysis to make inference on the anatomical directionality of tracts, which masks out those tracts passing through the thalamus. For this analysis, the Johns Hopkins University atlas was used to create a mask of the anterior limb of the internal capsule (Oishi et al., 2010). We used this mask as an exclusion mask and reperformed probabilistic tractography analysis to assess connectivity between the striatum and the frontal clusters. Therefore, this analysis simulates a lesion in anterior limb of the internal capsule, thereby discarding all fibers running from the striatum to frontal lobe along the striatal-thalamo-cortical pathway.

Statistical analysis.

We then investigated whether behavioral indices of model-based and model-free control could be predicted by frontostriatal connectivity maps computed in the previous steps. Because tract strength values are non-normally distributed, nonparametric analysis (rank correlation) was performed using tools from FSL software (FSL Randomize with 5000 permutation tests) (Winkler et al., 2014). Threshold-free cluster enhancement, as implemented in FSL (Smith and Nichols, 2009), was used to boost signal in areas that exhibit spatial clustering (with variance smoothing kernel of 6). All resulting statistical maps were corrected (p < 0.05) at the voxel level, separately for the left and right striatum, for family-wise error (FWE) due to multivoxel comparisons. All reported coordinates are the MNI coordinates.

Results

Behavioral data

The critical feature of the multistep decision task is the probabilistic nature of the transition from the first- to the second-stage set. Each first-stage choice led predominantly (70%) to one of the two second-stage sets (common transition) and, less frequently (30%), to the other set (rare transition) (Fig. 1A). Model-based and model-free accounts make different predictions about participants' choices in rare-transition trials. A model-based system reinforces the first-stage choice predominantly associated with the rewarded second-stage choice, which results in decreasing the probability of choosing the first-stage action that is ultimately rewarded after rare transitions (Fig. 1B, left). In contrast, a model-free system is blind to transition probabilities and therefore reinforces those first-stage choices ultimately rewarded regardless of the transition (Fig. 1B, middle). Therefore, one can model the probability of repeating the first-stage choice on the subsequent trial (stay probability) as a function of two key events on the current trial. The two key events are whether or not reward was delivered, and whether or not the transition was common or rare. Model-free and model-based components of behavior could then be quantified as the main effect of reward and the interaction effect of reward and transition, respectively.

Across participants, the presence of reward increased the probability of repeating the first-stage choice (main effect of reward, F_(1,30) = 28.53, p < 0.001), an indication that model-free control influenced participants' choices (Fig. 1B). Additionally, the type of transition also affected first-stage choices (reward-by-transition interaction, F_(1,30) = 8.29, p = 0.007), an indication that model-based control also influenced participants' choices (Fig. 1B). There was no main effect of transition on choice (F_(1,30) = 0.21, p = 0.65), as predicted by both model-based and model-free accounts. There was a significant positive intercept (F_(1,30) = 77.14, p < 0.001), indicating a tendency to implement the choice made on the previous trial regardless of reward delivery and transition (Lau and Glimcher, 2005). Table 1 summarizes the result of this analysis.

Table 1.

Logistic regression analysis of behavioral data^a

Effects	Estimate (SE)	p
Reward	0.32 (0.06)	<0.001
Transition	−0.03 (0.06)	0.65
Reward × transition	0.24 (0.08)	0.007
Intercept	1.31 (0.15)	<0.001

^aMean estimate of regression coefficients and their SE are shown (arbitrary unit). p values of effects across group are reported. This analysis indicates a significant effect of the reward of previous trial and an interaction between reward and transition of previous trial on stay probability on the current trial.

Next, we elaborated on this factorial group-level analysis by considering the whole history of rewards obtained before a given trial and by considering individual-level data. This was achieved with a Bayesian model selection procedure comparing the fit of the behavioral data with the predictions of three different models. The first model was a hybrid reinforcement learning model previously used to account for choices in this task (Daw et al., 2011). The hybrid model combines learned values of model-based and model-free strategies on a trial-by-trial basis and uses their combination for action selection. The other two models were pure model-free and pure model-based accounts. Across the group, random-effect Bayesian model selection (Rigoux et al., 2014) indicated that the hybrid account provides the most parsimonious model given the population-level data (exeedance probability of 1.0, expected posterior model probability of 0.94; Table 2). At the individual level, pairwise comparison between the hybrid and model-based accounts revealed that the hybrid account significantly outperformed the model-based account in 31 of 31 participants (log-Bayes-factor >3.0; Table 2), whereas a similar pairwise comparison between the hybrid and the model-free account revealed that hybrid outperformed model-free account only in 6 of 31 participants (log-Bayes-factor >3.0). The latter finding is not driven by a particular statistical threshold: relaxing the log-Bayes-factor to 2.3 (corresponding to p < 0.1 in frequentist statistics) leads to the hybrid account providing a better fit than the model-free account in 12 of 31 participants. The finding is also graphically confirmed by ranking participants according to their reward-by-transition interaction effect in the factorial analysis: whereas the signature of the model-based strategy was not evident in half of subjects, it was clearly seen in the other half (Fig. 1C). These findings suggest that the participants consistently used model-free control, whereas the use of model-based control varied across the sample.

Table 2.

Bayesian model comparison^a

Model	No. of free parameters	Exeedance probability	Expected posterior	No. favoring hybrid with LBF > 3.0	No. favoring hybrid with LBF > 2.3
Hybrid	7	1.0	0.94	0	0
Pure model-free	6	0.0	0.03	6	12
Pure model-based	4	0.0	0.03	31	31

^aThe hybrid model outperforms both pure model-based and pure model-free accounts based on random-effects Bayesian model comparison results as shown by both exceedance probability and expected posterior probability across models. However, large individual differences in deployment of model-based control are evident, as the hybrid account outperformed the pure model-free account only in 6 subjects with log-Bayes-factor of 3.0 (compare p < 0.05). Even for log-Bayes-factor of 2.3 (compare p < 0.1), the hybrid model outperformed the pure model-free account only in 12 subjects. LBF, log-Bayes-factor.

Further quantitative analyses confirmed the presence of large individual differences in the use of model-based control in this task. Namely, the reward-by-transition interaction values are not normally distributed across the sample (p = 0.017, Lilliefors test), despite its relatively large size (n = 31).

A similar set of analyses revealed that individuals exhibit less variability using model-free control. First, model fits showed that all subjects used model-free strategy, as the hybrid account outperformed pure model-based in all 31 participants significantly (Table 2). Furthermore, splitting the sample by the median value of reward effect shows that model-free deployment was significantly observable even in that half of subjects who used model-free strategy less than the other half (F_(1,15) = 6.75, p = 0.02). Finally, and in contrast to the reward-by-transition interaction effect, no evidence in favor of non-normal distribution of reward effect was found across the sample (Lilliefors test, p > 0.05).

Model-based correlation with striatal anatomical connectivity

DTI data were used to define a connectivity matrix between the striatum and frontal cortex in each participant, to test whether their structural connectivity predicts individual differences in using model-based control. The connectivity matrix was then used to parcellate frontal cortex by identifying voxels with a shared profile of connectivity with the striatum (Beckmann et al., 2009; Mars et al., 2011; Neubert et al., 2014). A stability analysis was performed to identify the most consistent and coherent number of clusters. This stability analysis revealed that five clusters could be identified reliably at the group level in both hemispheres (Monte Carlo randomization test, p < 0.001). In addition, although this parcellation scheme was blind to voxel location, voxels clustered into five anatomically coherent parcels, which were largely symmetric across both hemispheres (Fig. 2). There are additional mediolateral subdivisions within each of the five clusters when cytoarchitecture and corticocortical connections are considered (Beckmann et al., 2009; Sallet et al., 2013; Neubert et al., 2014). However, because the parcellation scheme only considered frontostriatal connectivity, the frontal clusters should be interpreted as cortical territories that are homogeneous from a striatal point of view, given DTI data.

Figure 2.

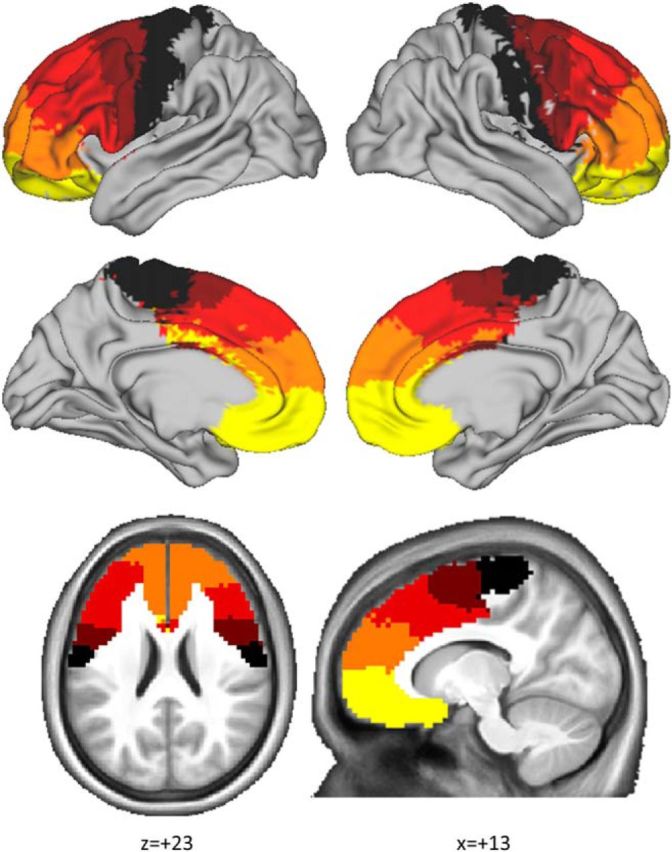
Connectivity-based parcellation of frontal cortex resulted in five distinct clusters consistently identified across participants. These clusters should be interpreted as frontal regions segregated according to their striatal connectivity profile. The data-driven parcellation (clustering procedure) was blind to the anatomical location of the frontal voxel, yet those voxels clustered into five anatomically coherent territories. This procedure resulted in a map with anteroventral to posterodorsal gradient organized in accordance with known profiles of frontostriatal connectivity (Draganski et al., 2008). The map consisted of five clusters: a precentral cluster (black), a posterior prefrontal cluster (brown), a dorsal prefrontal cluster (red), an anterior prefrontal cluster (orange), and a ventromedial prefrontal cluster (yellow).

The parcellation procedure resulted in a map with anteroventral to posterodorsal gradient organized in accordance with known bands of frontostriatal connectivity (Draganski et al., 2008; Cohen et al., 2009; Haber and Knutson, 2010). The five clusters included the following: (1) a precentral cluster overlapping with motor areas of the frontal lobe, such as frontal operculum cortex and precentral gyrus; (2) a posterior prefrontal cluster, including presupplementary motor area and posterior parts of superior and middle frontal gyrus; and (3) a dorsal prefrontal cluster, including a large portion of inferior frontal gyrus and anterior parts of middle and superior frontal gyrus. This dorsal prefrontal cluster also overlapped with posterior parts of anterior cingulate gyrus and paracingulate gyrus; (4) an anterior prefrontal cluster, including the most anterior part of the paracingulate and anterior cingulate gyrus as well as dorsal parts of frontal pole; and (5) a vmPFC cluster, including frontal orbital cortex and ventral parts of frontal pole.

The degree of model-based strategy deployment, quantified in each participant as the reward-by-transition interaction effect, was significantly associated with the strength of connectivity between the vmPFC cluster and the medial striatum (p < 0.05, FWE corrected; Fig. 3A; local maximum within the left striatum, x = −20, y = 6, z = −6; local maximum within the right striatum, x = 20, y = 2, z = −6). Individuals relying more on model-based control had stronger structural connectivity between the vmPFC cluster and the medial striatum. This effect was anatomically specific. No significant correlation was found between model-based control and striatal connectivity with the other frontal clusters. Furthermore, the effect was not driven by strong between-cluster inhomogeneities in connectivity variance. The maximum SDs across all striatal voxels for each map were comparable, with the anterior prefrontal cluster, the dorsal prefrontal cluster, and the posterior prefrontal cluster showing larger variability across participants than the vmPFC cluster.

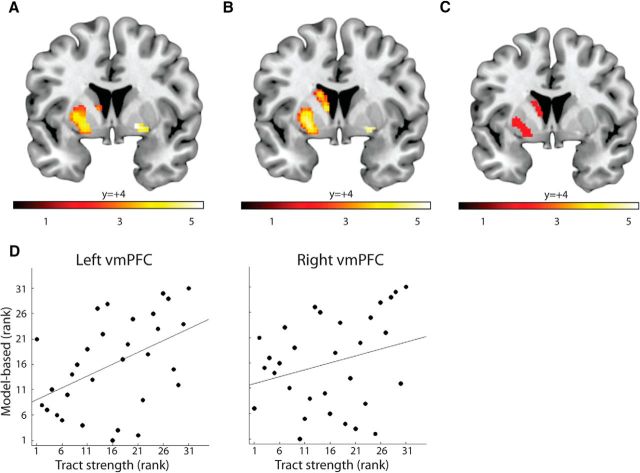
Figure 3.

Individual differences in model-based control were predicted by anatomical connectivity strength between the vmPFC cluster and the striatum. Maps represent pseudo t-statistics from nonparametric correlation analysis. All maps are thresholded at p < 0.05, FWE corrected. A, Connectivity between the vmPFC cluster and the bilateral striatum predicts individual differences in model-based control, as indexed by reward-by-transition effect shown in Figure 1C. The effects are present in the medial striatum, particularly the left medial caudate nucleus and bilateral dorsal anterior putamen. B, The same effects are present even when those tracts running from the striatum to the frontal cortex through thalamus were discarded, suggesting that effects are, at least partly, driven by top-down afferences from the vmPFC to the striatum. C, Similar correlation was found when we considered the weight parameter, w, of the hybrid model as the degree of model-based influences. D, Rank scatter-plot from A, separately for the left and right hemisphere tracts, averaged over all voxels showing significant correlation.

Similar results were obtained when the degree of model-based strategy deployment was indexed with the weighting parameter, w, of the hybrid model (Fig. 3C). Higher values of w, corresponding to higher degree of model-based control, are associated with stronger connectivity between vmPFC and medial striatum (significant in the left striatum, p < 0.05, FWE-corrected; local maximum, x = −26, y = −8, z = −4). This was expected, as the weighting parameter was strongly correlated with the degree of model-based quantified as reward-by-transition interaction effect in the factorial model (r = 0.64, p = 0.0001).

DTI does not provide directional information, but the anatomical organization of the frontostriatal circuits allows one to examine whether the effect described above is driven by direct projections from vmPFC to medial striatum, or by thalamus-mediated connections from medial striatum to vmPFC. Accordingly, we performed another tractography analysis, by masking out tracts passing through the thalamus, to make inference on the anatomical directionality of the effects. This analysis revealed effects similar to those reported above (Fig. 3B; p < 0.05, FWE corrected; local maximum within the left striatum, x = −20, y = 6, z = −6; local maximum within the right striatum, x = 24, y = 2, z = −8), suggesting that those effects are largely driven by top-down afferences from the vmPFC to the medial striatum. The complementary control analysis, seeding tractography from the anterior limb of internal capsule while excluding all striatal voxels, did not reveal significant effect even at a very lenient statistical threshold (p < 0.1 uncorrected for multiple comparisons). This control analysis provides a complementary, although negative, proof that the effects of corticostriatal connectivity on model-based control are driven by top-down connections from the vmPFC to the striatum.

We also performed a similar analysis to assess whether individual differences in model-free deployment, quantified as the main effect of reward in the task, could be predicted by the strength of connectivity between the striatum and the precentral/posterior prefrontal clusters. There was no significant correlation between the magnitude of model-free control and the strength of the connectivity between those frontal clusters with the striatum. A post hoc analysis extending this approach to the remaining frontal clusters revealed a significant negative correlation between right medial caudate nucleus and the dorsal prefrontal cluster (p < 0.05, FWE-corrected; local maximum, x = 10, y = 8, z = 2). Individuals with a higher degree of model-free strategy deployment had lower structural connectivity between the right dorsal prefrontal and the right medial caudate nucleus.

Based on animal and human literature on goal-directed and habitual behavioral control, we hypothesized that connectivity between the frontal cortex and the striatum predicts individual differences in model-based control. However, recent studies have suggested that there are other regions implicated in model-based control. Specifically, it has been hypothesized that model-based control might implicate the amygdala, hippocampus, lateral prefrontal cortex, and/or the default model network (Doll et al., 2012; Daw and Dayan, 2014; Dayan and Berridge, 2014). Therefore, we performed an exploratory analysis to test whether the connectivity between the vmPFC cluster and these regions is correlated with the degree of model-based control. These regions were defined according to the Harvard–Oxford atlas, except the lateral prefrontal cortex, which is defined according to diffusion-based connectivity-parcellation of human dorsal prefrontal cortex (cluster 6 in Sallet et al., 2013). These atlases are available in FSL.

We found marginal effects in a few voxels in the left posterior cingulate cortex, a hub of the default mode network. The connectivity between vmPFC and the left posterior cingulate was positively associated with the degree of model-based control (FEW < 0.05; peak at x = −4, y = −41, z = 38, corrected p value in peak, p = 0.048).

Model-based association with white matter bundles

Probabilistic tractography estimates the probability distribution of the parameters of a crossing fiber model of diffusion MRI data. The tensor model is a simpler model of diffusion MRI (Basser et al., 1994), which provides a scalar measure, referred to as fractional anisotropy, that has been related to white matter microstructure integrity (Song et al., 2003). Here, we use tract-based spatial statistics (Smith et al., 2006) to test whether the association between model-based behavior and vmPFC tract strength, as revealed by probabilistic tractography, is accompanied by an association between model-based behavior and tract integrity, as quantified using fractional anisotropy. To this end, we performed voxelwise correlation analyses of the skeletonized fractional anisotropy data, focusing on four major white matter bundles shown to carry tracts originating from the vmPFC (Lehman et al., 2011; Jbabdi et al., 2013): the uncinate fascicle, the corpus callosum, the superior longitudinal fascicle, and the cingulum bundle. All these masks were created based on Johns Hopkins University white-matter atlases (Wakana et al., 2007; Hua et al., 2008). This analysis revealed a significant correlation between tract integrity in the cingulum bundle and the degree of model-based control (p < 0.05, FWE corrected; local maximum, x = −19, y = −36, z = 34). No significant correlation was found in other masks.

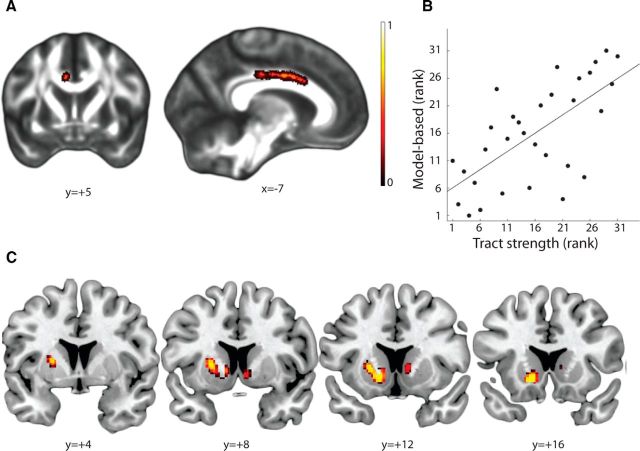
However, the interpretability of results obtained using the tensor model of diffusion data in regions with crossing-fibers has been questioned by many authors (Tournier et al., 2004; Parker and Alexander, 2005; Behrens et al., 2007; Jbabdi et al., 2010). One solution to this issue is to use tract-based spatial statistics with measurements from models dissociating different fibers in different directions (Jbabdi et al., 2010), such as bedpostX (Behrens et al., 2007). Therefore, we repeated the above analysis with partial volume fraction values estimated along with the first fiber orientation quantified by bedpostX. We found very similar results, with highly significant correlation between tract integrity voxels in the cingulum bundle and model-based scores (p < 0.05, FWE corrected; Fig. 4A; local maximum, x = −7, y = 5, z = 32), but not in other masks. These effects survived correction for comparison in multiple masks, too. Thus, participants with higher tract integrity in the cingulum bundle showed a higher degree of model-based behavior in the task (Fig. 4B).

Figure 4.

A, Individual differences in model-based control were predicted by anatomical connectivity strength, quantified using fractional anisotropy, in the white matter voxels of the cingulum bundle. Voxels in the cingulum bundle showing a significant positive correlation with the degree of model-based control in the task. B, Rank scatter-plot from A, averaged over all voxels showing significant correlation. C, Individual differences in model-based control were predicted by anatomical connectivity strength between the vmPFC cluster and the striatum, when only tracts passing through the cingulum bundle are included in the analysis. These results suggest that the association between the vmPFC and the striatum (Fig. 3) is mediated, at least partly, by individual differences in the integrity of the cingulum white matter bundle. For better visualization in A, voxels are dilated (thickened) into local tracts and overlaid on the white matter skeleton template.

One question raised by this analysis is whether the brain-behavior correlation with tracts connecting the vmPFC with the striatum (Fig. 3) is mediated by tracts passing through the cingulum bundle. To assess this, we repeated our original probabilistic tractography analysis of connectivity between the striatum and the vmPFC cluster and used the cingulum bundle as an inclusion mask. This analysis discards all the tracts do not pass through the cingulum bundle. We found that the strength of tracts between vmPFC and a dorsomedial striatal region, passing through the cingulum bundle, is significantly associated with the degree of model-based control (p < 0.05, FWE corrected; Fig. 4C; local maximum within the left striatum, x = −13, y = 14, z = −6; local maximum within the right striatum, x = 8, y = 8, z = −4).

Following a reviewer's comment, we have also performed voxel-based morphometry (Ashburner and Friston, 2000) analysis to assess whether individual variability in model-based control is also associated with individual variability in gray matter density in the vmPFC cluster and/or the striatum, using tools implemented in SPM8 software (Ashburner and Friston, 2000; Ashburner, 2007). Whole-brain analysis revealed no significant association, even at the lenient threshold of p < 0.001 uncorrected. Further region-of-interest analyses in the vmPFC and the striatum revealed no significant correlation either at the voxel level (FWE corrected, p < 0.05) or at the cluster level (not even when we used p < 0.01 as uncorrected p value for cluster-level inference). These analyses suggest that the correlation between model-based control and vmPFC-striatum tract strength is not accompanied by a similar correlation with gray matter density.

Discussion

In this study, we tested the hypothesis that the relative contribution of model-based and model-free control systems to decision making depends on the relative strength of anatomical connectivity within frontostriatal circuits involved in learning and behavioral control. We exploited the presence of large and systematic interindividual differences in the use of model-based control during instrumental actions (Fig. 1) (Daw et al., 2011). This study shows that the use of model-based control is predicted by neuroanatomical differences in the structural coherence of white-matter tracts from the vmPFC to the medial striatum. The finding indicates that individuals with more coherent afferences from vmPFC to medial striatum are more likely to rely on a model-based system to control their instrumental actions. Furthermore, an analysis based on making out of bottom-up tracts suggests that this effect is driven by top-down influences from vmPFC to medial striatum. These findings extend and qualify previous knowledge on how the control of goal-directed behavior is neuronally implemented through the vmPFC-striatal circuitry (Balleine and Dickinson, 1998; Corbit and Balleine, 2003; Yin et al., 2005; Valentin et al., 2007; Tanaka et al., 2008; Gläscher et al., 2009).

Ventromedial prefrontal and striatal contributions to goal-directed behavior

Previous work has suggested that, when goal-directed and habit-based control compete, model-based and model-free strategies are computed in the caudate nucleus and in the posterior putamen, respectively, while the vmPFC integrates those computations (Wunderlich et al., 2012a). The pattern of behavioral and cerebral interindividual differences observed in the present study suggests a different neurocognitive architecture. The present findings show that the vmPFC biases the balance between model-free and model-based control. The bias is implemented by modulating participants' reliance on model-based control through corticostriatal projections from the vmPFC to the caudate nucleus. This architecture fits well with a recent hierarchical model of action control, in which shifting from model-free to model-based control is itself a goal-directed decision controlled by a model-based system (Dezfouli and Balleine, 2013; Daw and Dayan, 2014). For instance, the pattern of vmPFC activity reported by Wunderlich et al. (2012a) could reflect the implementation of goal-directed choices between performing overtrained stimulus–response associations (presumably model-free) and navigating a complex decision-tree (presumably model-based). The present findings also fit with the notion that vmPFC contributes to decision making by encoding an abstract, cognitive map of task space (Wilson et al., 2014). The multistep decision task used here is designed to make participants choose between options followed by unobservable probabilistic transitions between states (Daw et al., 2011). By providing an explicit computational account on how those choices are biased toward model-free or model-based control systems, the present study extends previous reports linking vmPFC-caudate nucleus connectivity to flexible goal-directed control (de Wit et al., 2012). In that study, “slips of actions” were used to quantify habitual responses, but this behavioral outcome does not precisely capture the relative balance between model-based and model-free control (Dolan and Dayan, 2013). Here, we show that the vmPFC biases the relative contribution of model-based and model-free systems, as implemented in the caudate nucleus, on the basis of a cognitive map of task space.

Model-based control has previously been shown to vary with state factors, such as stress (Otto et al., 2013b), working memory capacity (Otto et al., 2013a), and dopamine synthesis capacity in the striatum (Deserno et al., 2015). In prior work, we have shown that frontostriatal tract strength can predict dopamine's effect on cognitive control and frontostriatal functioning (van Schouwenburg et al., 2013). Accordingly, it is possible that the correlation between model-based control and individual differences in the strength of the vmPFC-striatum tract, observed here, reflects differential sensitivity to dopamine-related states, such as stress and working memory. Another indirect evidence comes from studies showing that vmPFC response to reward is related to state stress levels (Treadway et al., 2013), and studies showing that prefrontal-dorsomedial striatal structural connectivity, measured using DTI, predict individual differences in reward dependence (Cohen et al., 2009). This hypothesis can be tested in future studies, combining DTI with an interventional (psychopharmacological or stress-induction) approach.

Implications for psychiatric disorders

Disruption of the balance between goal-directed and habitual modes of behavioral control might account for several impulsive/compulsive psychiatric disorders, such as impulse control disorders, obsessive-compulsive disorders, obesity, and drug addiction (Brewer and Potenza, 2008; Belin et al., 2013; Smith and Robbins, 2013; Gillan and Robbins, 2014). For instance, it has been recently shown that compulsive disorders are associated with a bias toward model-free control, at the expenses of reduced model-based control (Voon et al., 2015). The present findings raise the possibility that this pathological bias might be mechanistically implemented through altered anatomical connectivity between vmPFC and the caudate nucleus.

Interpretational issues

In this study, we exploited the presence of large individual differences in model-based control and investigated whether these differences could be predicted by neuroanatomical differences in frontostriatal circuitry. This approach builds on previous reports showing that subjects' behavior is stable across repetitions of this task (Wunderlich et al., 2012b; Smittenaar et al., 2013). For example, Wunderlich et al. (2012b) conducted a within-subject study in which subjects received levodopa and placebo in two sessions and were tested in the same paradigm used in this study. They found no evidence in favor of different performance, either in stay probability or parameter fits, across sessions. Similar observations have been reported in other within-subject studies that used the same multistep decision paradigm (Smittenaar et al., 2013).

The multistep decision task used in this study manipulated the value of actions, whereas the transition probabilities of the task were fixed. Therefore, it was not possible to dissociate two important aspects of model-based control, namely, learning the value of the task actions and learning a model of the task environment. In the present study, a post hoc analysis revealed that structural connectivity between the right dorsolateral prefrontal cortex and the right caudate nucleus is negatively correlated with reliance on model-free control. Accordingly, it has been shown that interference with the same portion of the right dorsolateral prefrontal cortex shifts the balance of the two systems toward model-based control (Smittenaar et al., 2013). Future studies challenging participants to learn multiple models of the task environment might be able to expand on the notion that the dorsolateral prefrontal cortex is associated with learning probabilities of state transitions (Gläscher et al., 2010), and show how this region interacts with the vmPFC-caudate circuit when goal-directed model-based actions are generated.

It might be argued that this study failed to isolate a structural counterpart to participants' reliance on habits, despite evidence linking structural connectivity between posterior putamen and premotor cortex to habitual responses (de Wit et al., 2012). Indeed, there are important differences between the habitual responses considered by de Wit et al. (2012), and the model-free actions elicited by the current multistep decision task. In contrast to habitual “slips of actions,” the current model-free actions remain sensitive to reinforcements but are blind to architecture of states in the environment. Furthermore, the responses performed in the multistep decision task had no consistent spatial mapping, as choices were randomized across trials. It remains to be seen whether other forms of model-free learning, such as action-sequence learning directly linking stimuli to sequences of actions (Dezfouli et al., 2014), might be suitable for capturing habitual responses.

There are important anatomical and functional differences between lateral and medial portions of each of the five frontal clusters considered in this study (Rushworth et al., 2011, 2012). Future studies might be able to test whether and how those differences, largely determined on the basis of cytoarchitectonic features and corticocortical connectivity, are also relevant for understanding the relation between frontostriatal connectivity and model-based control.

In conclusion, this study investigated neural sources of individual differences in the computational bases of human choice by linking parameters of a normative learning model to structural cerebral features. The evidence indicates that a circuit connecting vmPFC to the medial striatum predicts interindividual differences in participants' reliance on model-based control. Individuals with stronger afferences from vmPFC to medial striatum are more likely to rely on a model-based system when controlling their instrumental actions. Explaining interindividual variability in model-based decisions opens the way to provide a mechanistic understanding of pathological computational processes associated with deficits in the balance between the goal-directed and habitual action control (Belin et al., 2013; Voon et al., 2015).