Abstract
Topographic maps are common throughout the nervous system, yet their functional role is still unclear. In particular, whether they are necessary for decoding sensory stimuli is unknown. Here we examined this question by recording population activity at the cellular level from the larval zebrafish tectum in response to visual stimuli at three closely spaced locations in the visual field. Due to map imprecision, nearby stimulus locations produced intermingled tectal responses, and decoding based on map topography yielded an accuracy of only 64%. In contrast, maximum likelihood decoding of stimulus location based on the statistics of the evoked activity, while ignoring any information about the locations of neurons in the map, yielded an accuracy close to 100%. A simple computational model of the zebrafish visual system reproduced these results. Although topography is a useful initial decoding strategy, we suggest it may be replaced by better methods following visual experience.
SIGNIFICANCE STATEMENT A very common feature of brain wiring is that neighboring points on a sensory surface (eg, the retina) are connected to neighboring points in the brain. It is often assumed that this “topography” of wiring is essential for decoding sensory stimuli. However, here we show in the developing zebrafish that topographic decoding performs very poorly compared with methods that do not rely on topography. This suggests that, although wiring topography could provide a starting point for decoding at a very early stage in development, it may be replaced by more accurate methods as the animal gains experience of the world.
Keywords: computational model, sensory decoding, topographic map, zebrafish
Introduction
Topographic maps are a fundamental organizing principle of brain wiring, and their widespread presence across many species and sensory modalities suggests that such maps serve an important functional purpose (Kaas, 1997; Wandell and Winawer, 2011; Groh, 2014). One such possibility is minimal wiring (Cowey, 1979; Chklovskii and Koulakov, 2004): to perform local processing in stimulus space the neurons representing neighboring stimuli should be connected, and locating these neurons in close proximity in the brain reduces the length of wiring needed to connect them. However, minimal wiring does not imply that topography is actually required to decode sensory stimuli. The idea of a topography requirement for decoding is a much stronger claim; for example, that the topography of the map from the retina to the tectum is actually required for the spatial locations of objects in the visual field to be determined from tectal activity. Nonetheless, as pointed out many times before (Cowey, 1979), no in-principle requirement exists; for instance, a smartphone can perform face recognition without requiring that neighboring pixels in its camera be connected to neighboring positions on its circuit board. Organisms could still be using topographic relationships for decoding, but it remains unclear for most biological systems whether the accuracy of such decoding is at all close to that of statistically optimal methods that the animal could use, especially for distinguishing stimuli that are close together.
In many neural systems, such as the cortex or tectum, each sensory stimulus is represented by the combined activity of many neurons, ie, a population code (Georgopoulos et al., 1988; Niell and Smith, 2005). The activity of single neurons is often unreliable, and it is therefore the statistics of the population that provide decoding reliability (Averbeck et al., 2006). Simple population-based decoding methods, which treat the position of each neuron as indicating its feature preference can, under restricted circumstances, perform optimally. That is, they can find the stimulus that was statistically most likely to have generated that pattern of response (maximum likelihood estimation; Snippe, 1996). However, this equivalence only holds given many assumptions, not least of which is that the topography of the map must be perfectly ordered. How well topography-based population decoding performs in real systems is mostly unknown.
An attractive model system for studying these questions is the retinotectal map in zebrafish (Stuermer, 1988; Poulain and Chien, 2013). Hunting behavior in larval zebrafish is primarily guided by vision, and larval zebrafish start to hunt and capture live prey from 5 d postfertilization (dpf). At this age zebrafish visual acuity is ∼3° (Easter and Nicola, 1996; Haug et al., 2010). The optic tectum is essential for the accurate detection of prey, and the release of appropriately targeted behavioral responses (Ewert et al., 2001; Gahtan et al., 2005). However, tectal cells have very broad receptive fields (Niell and Smith, 2005), with an average width of ∼40° (Romano et al., 2015). Furthermore, despite the rough preservation of spatial relationships within the retinotectal map (Burrill and Easter, 1994; Muto et al., 2013; Kita et al., 2015), its topographic arrangement is quite imprecise, with substantial scatter in the mapping from spatial location in the visual field to position on the tectum (Niell and Smith, 2005; Northmore, 2011). This raises the obvious question of how effectively spatial location in the world can actually be determined using topography-based decoding from the activity of tectal neurons, which is the signal passed on to downstream targets. This question is particularly acute for distinguishing closely spaced stimuli, which produce largely overlapping patterns of tectal activity. Here we addressed this issue using a combination of calcium imaging of tectal activity and computational modeling.
Materials and Methods
Fish housing.
Nacre zebrafish embryos of either sex were collected and raised according to established procedures (Westerfield, 1993) and kept under a 14/10 h on/off light cycle. Larvae were fed rotifers (Brachionus plicatilis) from 5 d postfertilization (dpf).
Larval injections.
The calcium indicator dye Oregon Green 488 BAPTA-1-AM (OGB; Invitrogen) was dissolved in 4 μl of 20% pluronic/DMSO and diluted 1:15 with filtered NKH solution (125 mm NaCl, 2 mm KCl, 10 mm HEPES). Six to 8 dpf larvae were anesthetized in 0.02% tricaine, mounted in 1% low melting point agarose (Seaplaque, Lonza), and then bolus injected under a dissection microscope (20×), using a glass micropipette (tip opening 2–3 μm) and a digital-gated pressure injection system Femtojet (2–3 pulses of 500 ms at <1 psi). Adequate loading of the tectum was reached when the AlexaFluor 564 marker dye also present in the injection solution (42 μm, Invitrogen) was present throughout the stratum periventriculare (SPV) neurons. Immediately after the injections, larvae were excised from the agarose and left in the dark at 28.5°C in E3 medium for 1 h of recovery before experiments. Before time lapse imaging, fish were paralyzed using tubocurarine (Sigma-Aldrich) and mounted in 1.75% low melting point agarose in a custom made rectangular glass-bottomed chamber consisting of one vertical coverslip side through which the fish could see the visual cues presented.
Visual stimuli and image acquisition.
OGB-labeled tectal cells were imaged with a 63× water-immersion objective on an inverted 3i Yokogawa W1 spinning disk confocal microscope and a 488 nm diode laser. Images of 512 × 512 pixel resolution covering one plane of the labeled tectum were acquired at 5 Hz. Pixel size was set to 0.4 μm. Visual stimuli were generated using custom software based on MATLAB (MathWorks) and Psychophysics Toolbox, and consisted of 10-degree-wide black spots at three different positions (−10°, 0°, 10°), which were randomly presented for 1 s each, followed by 8 s of blank screen to allow calcium signals to return to baseline levels. Zero degrees was defined as being orthogonal to the body axis at the eye. Visual stimuli were projected on a screen 27 mm away from the fish covering ∼90° × 60° the visual field using an Optoma PK302 projector. A no. 47 Wratten Kodak filter was placed directly in front of the projector to block green light to prevent interference with the fluorescence emission of OGB. For synchronization of image acquisition and visual stimuli, we used a NA-USB-6501 I/O TTL device.
Image registration.
All fluorescence data stacks were corrected for x–y movements using custom-written MATLAB software. Trials that showed a drift in the z-plane were discarded. Single trial data stacks were first aligned with a reference frame within the movie using MATLAB custom-written code based on a rigid image registration algorithm. To align stacks between trials, the reference frames of all trials were aligned with the first trial's reference frame.
Cell detection.
Custom-written software in MATLAB was used to automatically detect the region-of-interest (ROI) of each active cell, ie, the group of pixels defining each cell. The software searched for active pixels, ie, pixels that showed changes in brightness across frames (Ahrens et al., 2012), resulting in an activity heat map of all the active regions across frames. The activity map was then segmented using a watershed algorithm. The threshold for the watershed algorithm was tuned to mark apparent cells on the activity map. Within each segmented region, we computed the correlation coefficients of all pixels in the region with the mean of the most active pixel and its eight closest neighboring pixels. Correlation coefficients showed a mainly bimodal distribution: one peak of highly correlated pixels representing pixels of the cell, and a second peak of relatively low correlation coefficients representing nearby pixels that were not part of the cell. Using a Gaussian mixture model, we looked for the correlation coefficient to threshold this bimodal distribution so that we could differentiate between pixels likely to form the active cell and neighboring pixels that were not part of the cell. Detected potential cells were also screened for the minimal number of pixels (60) to represent a cell. The software allowed visual inspection and modification of the parameters values where needed. All pixels within each cell's ROI were averaged to give a raw fluorescence trace over time. Raw calcium signals for each cell, F(t), were then converted to represent changes from baseline level, ΔF/F defined as (F(t) − F0(t))/F0(t). The time varying baseline fluorescence, F0(t), for each cell was a smoothed curve fitted to the lower 50% of the points. The value of F0 at each time point was the minimum of the smoothed fluorescence trace in a 4 s window before that time point.
Center of mass decoding.
For each population response vector, R = (r1, r2, …, rNc), the center of mass (CoM) was calculated as follows:
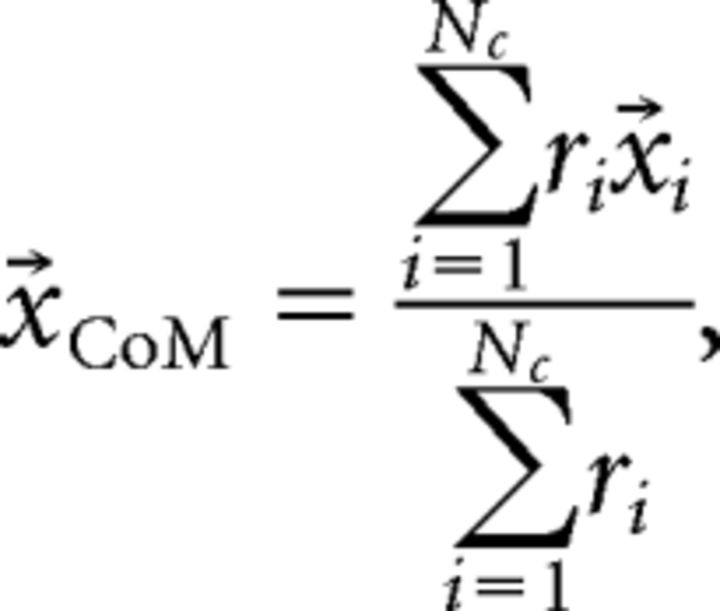 |
where ri is the response of cell i and x⃗i is the spatial coordinate vector of neuron i. To represent an averaged position on the map for each stimulus, we calculated the mean CoMs 〈x⃗CoM〉sj, where 〈 〉sj denotes the mean over all presentations j of the same stimulus s. Mean CoMs for the decoder were calculated from a training set separate from the test set to be decoded using a leave-one-out strategy, in which a single population response vector was decoded using the mean CoMs calculated from all other presentations but the test vector. The CoM of a given test population response vector x⃗CoM was computed, and the Euclidean distance of its CoM from each of the averaged CoMs representing the three stimuli d(x⃗CoM, 〈x⃗CoM〉sj) was calculated. The given test population response vector was then classified as the stimulus having its closest averaged CoM.
Maximum likelihood decoding.
Decoding the population response consisted of searching for the stimulus (sML), which had the highest probability of evoking a given population response R = (r1, r2, …, rNc):
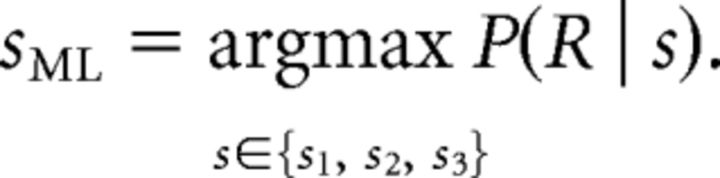 |
The probability distributions P(R | sj) were hard to estimate from the biological data because the dimensionality of R was high compared with the number of samples available. A simplifying assumption that is often made is to assume that the responses of all neurons are conditionally independent given the stimulus sj, in which case, P(R | sj) = ∏i=1Nc p(ri | sj). This model requires fewer observations to fit, because it requires estimation only of the one-dimensional distribution of ri for each stimulus. We therefore computed the conditional probability that each cell i had response ri given that stimulus sj was presented, P(ri | sj). Nc × Ns histograms were computed (Nc: number of cells, and Ns: number of stimuli) and probability density estimates based on a smoothed fit to the histogram using the MATLAB ksdensity function were computed for each histogram. Performance statistics for the decoder were calculated from a training set separate from the test set to be decoded, using a leave-one-out strategy, in which a single population response vector was decoded using the statistics calculated on the basis of all presentations other than the test vector. Decoding performance was defined as the proportion of the responses tested and classified correctly out of the total number of responses tested.
Linear decoding.
We also used linear discriminant analysis to decode the stimulus. The algorithm received as an input population response vectors and their respective stimulus labels (the stimulus evoking each response vector). The algorithm output the linear discriminant coefficients for the population for the three different stimuli. Given a test population response, linear scores were calculated for each stimulus and its respective stimulus probability. The test population response was classified as the most probable stimulus. The performance statistics for the decoder were calculated from a training set separate from the test set to be decoded, using a leave-one-out strategy, in which a single population response vector was decoded using the statistics calculated on the basis of all presentations other than the test vector. Decoding performance was defined as the proportion of the responses classified correctly out of the total number of responses tested.
Computational model.
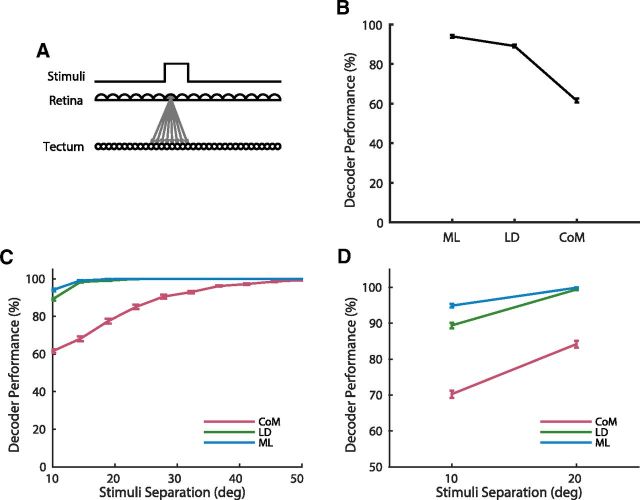
To more closely examine the performance of the decoders we developed a simple computational model of the zebrafish retinotectal system. The model consists of two one-dimensional layers of cells, representing the horizontal visual field of the retina and the anterior–posterior axis of the tectum, joined by directed weighted connections from the retinal layer to the tectal layer (see Fig. 5A).
Figure 5.
A simple computational model of the retinotectal system replicated the experimental results. A, Schematic of the model, showing the step function stimulus, and retinal and tectal layers. Arrows show connections with weights >0.1 from a single retinal cell, which were defined by a normalized Gaussian. B, The performance of the three decoders, CoM, LD, and ML, in the model matched well with their performance on the experimental data (Fig. 4A). C, The performance of the decoders increased with increasing separation (ie, gap) between stimuli, with CoM taking much longer to reach saturating performance. D, Comparison of decoder performance for 10° versus 20° separation. Mean and SEM from 10 simulations shown in B–D.
Stimuli were represented as step functions in a 160° field-of-view with coordinates in [−80°, 80°]. The Nr = 16 cells in the retinal layer had Fr = 10° wide receptive fields, based on experimentally found values in the range 7–13° (Sajovic and Levinthal, 1982b), which collectively covered the full field-of-view, with no gaps and no overlap. When a stimulus from s0 to s1 was presented to the model, each cell k's response rk was defined as a value in (0, 1) corresponding to the proportion of its receptive field the stimulus covered:
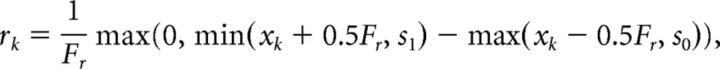 |
where xk is the position of the center of retinal cell k. The weight wk,i of the connection between retinal cell k and tectal cell i was defined by a Gaussian with SD σa = 0.15:
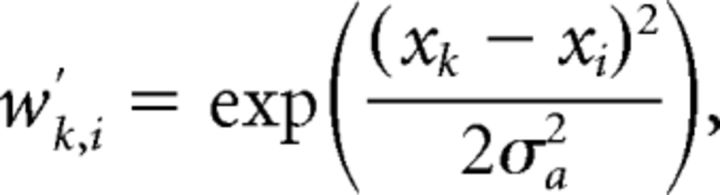 |
where xk and xi are the positions of the retinal and tectal cells, respectively, normalized so that their values were in the range [−1, 1] rather than [−80°, 80°]. These weights were then normalized such that the weights on the connections into each tectal cell summed to 1:
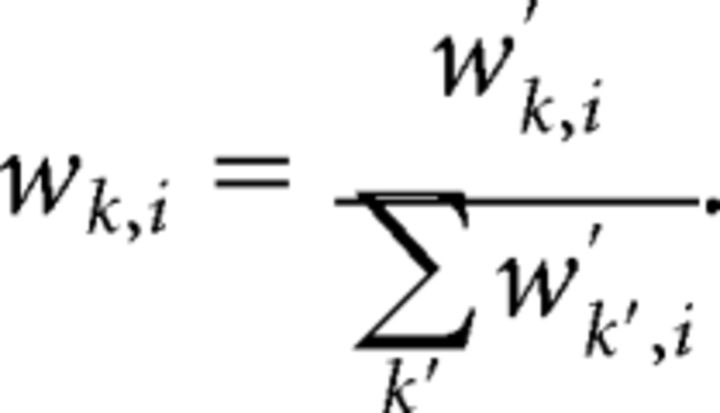 |
The tectal layer was comprised of Nt = 35 cells, based on a 250 μm tectum (anterior–posterior axis) with 7 μm wide cells approximately matching the fish we examined experimentally, spaced evenly along the tectum with no gaps or overlap. The response ri of each cell i was a sample from a Poisson process with firing rate λi determined by the weighted sum of the retinal cell responses,
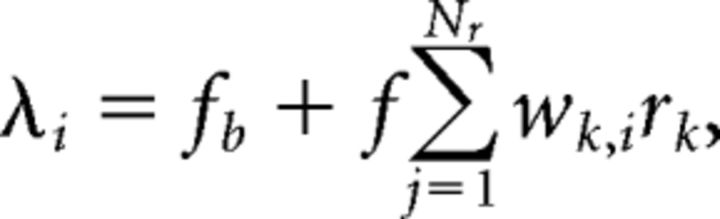 |
where fb = 5 Hz is the baseline firing rate and f = 30 Hz is the maximum firing rate. The baseline and maximum firing rates, ie, the signal-to-noise ratio of the tectal responses, were chosen such that the overall performance of the decoders matched their performance on the experimental data. We measured the tectal cell receptive fields in our model by fitting Gaussians to the responses of the tectal cells when each retinal cell was fully stimulated in turn, and the fits gave full-width at half-maximum values of ∼28°, which matches experimentally found receptive field widths in the range 25–39° (Sajovic and Levinthal, 1982b).
The stimuli used were as in the experiments, three spots of width 10° centered at −10°, 0°, and 10° around the center of the visual field, which are equivalent to step functions in our one-dimensional model. To generate responses for decoding, we presented each stimulus to the model 50 times, for a total of 150 presentations. The response ri of each tectal cell to each presentation of each stimulus was recorded. Decoding was performed as described above for the experimental data, using the center of mass, linear and maximum likelihood decoders, and a leave-one-out strategy for training and testing.
To investigate the effects of topography, we destroyed the topography of the retinotectal map by shuffling the positions of the tectal cells while leaving their connections intact. That is, we randomly shuffled the tectal cell position vector x = (x1, x2, …, xNt). We measured the level of disorder of a shuffled tectum as the Kendall tau distance (Kendall, 1938) between the shuffled vector of tectal indices and the sorted vector, divided by the maximum possible distance Nt(Nt − 1)/2 to obtain a value between 0 and 1. This measure is equivalent to the count of the number of swaps of unordered adjacent elements required by the bubble sort algorithm to sort the shuffled vector. To generate vectors with a specific level of disorder, we swapped ordered adjacent pairs of indices in a sorted vector until the desired Kendall tau distance was reached. To fairly test the performance of CoM with a shuffled tectum, we averaged its decoding performance over several runs, in each the stimuli being centered at a different point in the visual field, specifically −40, −30,…, 30, 40°, rather than just at 0°. To model the increase in retinal ganglion cell arbor size in the blumenkhol mutant zebrafish, we increased the parameter controlling the width of the Gaussian used to define the connection weights σa, and defined the arbor size as the full-width at half-maximum of the Gaussian.
Results
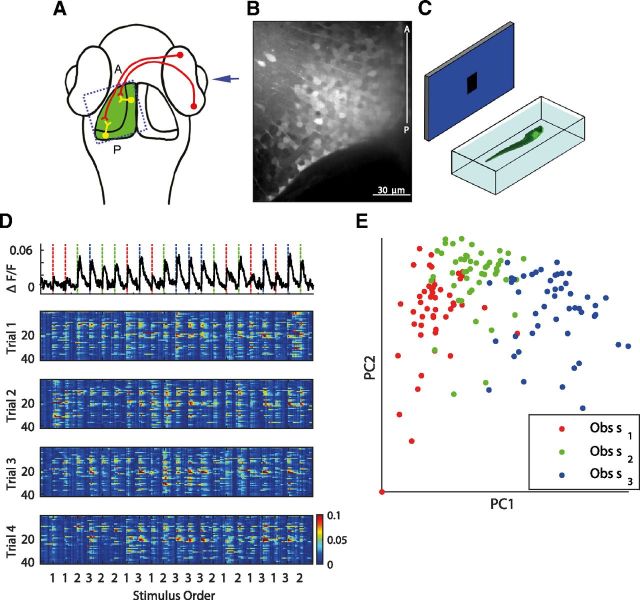
To study the functional role of the topographic map we performed calcium imaging on larval zebrafish (n = 5), for which the visual system has been well studied (Fig. 1A; Sajovic and Levinthal, 1982a; Stuermer, 1988; Easter and Nicola, 1996; Kinoshita and Ito, 2006). Injection of OGB into the tectum resulted in labeling of a substantial number of cell bodies in one hemisphere, in particular the cell bodies of the SPV, where a vast majority of the tectum's cell bodies are located (Fig. 1B). Paralyzed, unanesthetized OGB-labeled zebrafish larvae (6–8 dpf) were mounted in an imaging chamber, which allowed simultaneous calcium imaging of visually induced tectal responses, in conjunction with presentation of visual stimuli to the eye contralateral to the labeled tectum. Images were produced on a screen placed in front of the eye via a projector. We provided the fish with prey-like visual stimuli (Bianco and Engert, 2015), which consisted of 10° black spots presented at three different but adjacent positions of the visual field (−10°, 0°, 10°), where 0° was arbitrarily defined as orthogonal to the body axis at the eye (Fig. 1C). Spots were presented for 1 s each, followed by 8 s of blank screen to allow the calcium signals to return to baseline levels. In each trial, the three different stimuli were each presented in a random order a total of seven times. The number of trials varied between fish (3–7 trials), resulting in a total of 63–147 spot presentations per fish. Trial movies were registered to remove slow in-plane (XY) drifts and neurons were segmented using customized image processing algorithms (see Materials and Methods), resulting in calcium signals of each neuron in the population as a function of time.
Figure 1.
The population response is variable and largely overlapping. A, Dorsal view of the zebrafish head. Visual information enters the eye and is conveyed to the contralateral tectum via retinal ganglion cell axons, which synapse to the dendrites of the tectal SPV cells. Dotted, blue square indicates the region being imaged. The anterior (A) and posterior (P) ends of the tectum are indicated. B, A labeled tectum after injection of OGB. Middle-third of the tectum is cropped. C, Schematic of the visual stimulation assay. A zebrafish embedded in a chamber was imaged using confocal spinning disk microscopy. The eye contralateral to the labeled tectum was presented with a screen onto which the visual stimuli were projected. Visual stimuli consisting of 10° spots at three different positions (−10°, 0°, 10°) were randomly presented for 1 s each, followed by 8 s of blank screen. D, Top, Calcium signal from a randomly chosen cell. Dashed vertical lines represent the onset of spot presentations (red, −10°; green, 0°; blue, 10°). This particular cell responded to all three stimuli and showed variability in response amplitude to the same stimulus. Bottom, Multi-trial raster plot of evoked calcium transients induced in a population of 42 tectal cells (4 of 7 trials are shown) with many cells active due to the three stimuli presented. Stimuli were presented in a random order. E, Population response vectors projected onto the two-dimensional space defined by the first two principal components. The identity of the stimulus which evoked the response (dots) is color-coded.
Response to three adjacent stimuli is largely overlapping
Consistent with the broad receptive fields previously reported for tectal neurons (Sajovic and Levinthal, 1982a; Niell and Smith, 2005; Romano et al., 2015), we found that a single spot presented in the visual field elicited a response in a population of many cells. The three nearby spots produced largely spatially overlapping population responses. An example of the response of a single cell across time shows responsiveness to all three stimuli (Fig. 1D, top). High variability in the response amplitude to repeated presentations of the same stimulus is also apparent for this example. Thus, due to the noisy nature of neurons, the population pattern varied between repeated presentations of the same stimulus (Fig. 1D, bottom). As the response measure, we used the area under the calcium signal over one second from the stimulus onset. Other measures were also tested, such as the mean amplitude over different time windows from stimulus onset, or the peak amplitude during a 1 s time window from stimulus onset, but using these alternative measures did not qualitatively change our results.
A population response due to a stimulus can be described as an Nc dimensional vector, where Nc is the number of cells in the population. The dataset therefore contained a total of Ns × Np × NT such vectors (Ns: number of stimuli, Np: number of presentations of the same stimulus per trial, NT: number of trials). Every vector in this set of population response vectors can be described as a point in the Nc dimensional space, R = (r1, r2, …, rNc) where there is an axis for each cell, and the response of a single cell is the projection of this point onto the axis representing this cell. To help visualize the internal structure of this set of high-dimensional population response vectors, we projected each of these onto the first two principal components of the Nc dimensional space. The projected population responses reveal rough clustering representing the three stimuli (Fig. 1E), indicating shared features between vectors within the clusters. However, there was also substantial overlap between the clusters, suggesting that the features are also partially shared between clusters. This could potentially lead to ambiguity in differentiating response vectors evoked by different stimuli.
Linear and maximum likelihood decoding
Is it nonetheless possible to reliably decode the identity of the stimulus from these variable and strongly overlapping responses? We first applied a simple linear decoder (LD). This classifies the stimulus by taking a weighted sum of the activity of all the neurons, with the weights chosen so as to maximize the classification accuracy over all stimuli. The LD performed at an average accuracy rate of 90% (88%, 89%, 90%, 91%, and 92% for each fish; performance for other decoding strategies below is quoted in the same order of fish).
However, the LD is not a statistically optimal decoder. Assuming all stimuli are a priori equally likely, the unbiased decoder (ie, one for which the expected value of its decoding error is zero) which provides the smallest possible variance in the estimate is maximum likelihood (ML; Deutsch, 1965). This chooses the stimulus sj that is statistically most likely to have elicited a given population response R. That is, it calculates the likelihood function P(R | sj), the probability that the particular collection of neural responses R was generated by stimulus sj, for all possible sj, and chooses the sj that makes P(R | sj) the largest. Assuming that the responses of tectal neurons are statistically independent from each other, P(R | sj) is simply the product of the conditional probabilities P(ri | sj) that each cell i evoked response ri from neuron i given that stimulus sj was presented.
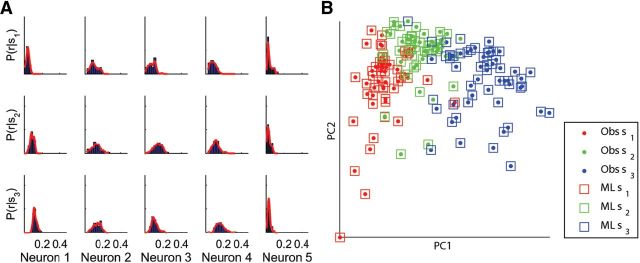
Histograms of P(ri | sj). were computed for all combinations of neurons i and stimuli j. To produce continuous probability estimates from these, each histogram was fitted by a smoothing function (see Materials and Methods; Fig. 2A). Smoothing parameters were optimized to achieve best performance, and were robust across datasets. To measure performance we used a leave-one-out cross-validation approach. That is, we used all but one of the set of population response vectors to learn the conditional probabilities, and then used these probabilities to determine the most likely stimulus for the one remaining response vector, leaving each response vector out in turn. The performance was defined as the proportion of population response vectors that were correctly classified. The ML decoder performed at an average accuracy rate of 95% (87%, 100%, 95%, 97%, and 97%; Fig. 2B). Thus, despite the apparent unreliability of the tectal response, it is still possible for the fish to decode with high reliability the identity of the stimuli presented.
Figure 2.
Maximum likelihood decoding. A, Normalized histograms of cell responses due to each of the stimuli (blue bars) and their estimated probability density (red curve; 5 different cells are shown). B, Population response vectors projected onto the two-dimensional space defined by the first two principal components for one fish. The identity of the stimulus which evoked the response (dots) is color-coded as in Figure 1E. Decoded stimuli (color-coded) are also shown for each untrained population response using the ML decoder (squares). Performance is given by the percentage of observations which were decoded correctly, for this fish 97%.
Topography-based decoding of visual targets
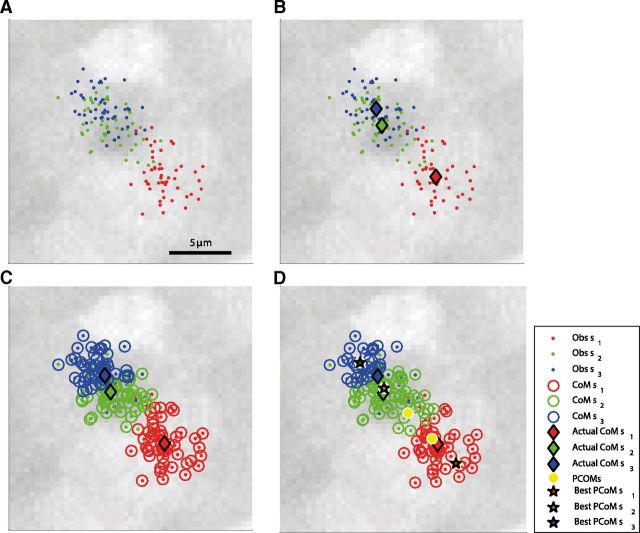
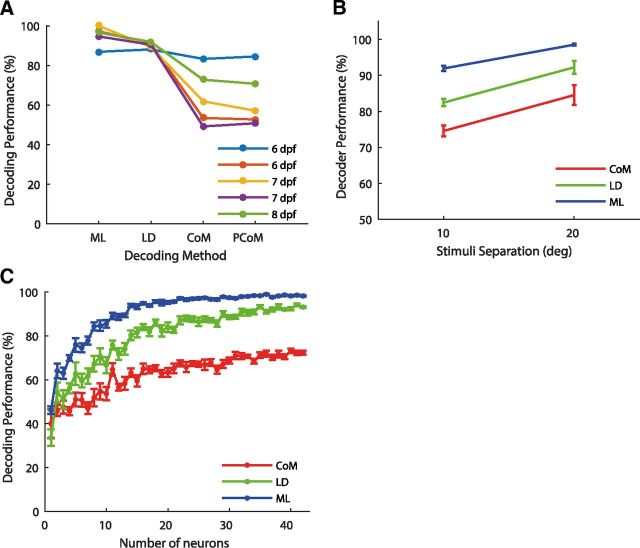
We then asked how well a simple topography-based decoder could identify the presented stimuli, based on the position of tectal cell activity. To characterize the position of the population response on the tectal topographic map, we used the CoM approach. The center of mass (CoM) for a given population response was calculated as the average of the cells' spatial coordinates weighted by their strength of response to the stimulus presented. We again used a leave-one-out cross-validation approach, dividing the set of population response vectors into training and test sets. We calculated the CoM of every population response vector in the training set. CoMs were widely spread and formed spatial clusters with some overlap, covering a region of ∼15 μm on the tectum. To characterize the typical spatial position of the population response due to each stimulus, we averaged all CoMs of all population responses in the training set elicited by a specific stimulus (ie, average CoM within each cluster). To test the decoder for a given population response, we calculated its CoM and classified it according to the stimulus having the closest average CoM. The performance was then defined as the proportion of population response vectors, which were correctly classified. An example of the spatial spread of the CoMs on the tectum due to each presentation is shown in Figure 3A. Also shown are the average CoMs, representing the response position on the map due to the three stimuli. These were only a few micrometers apart, whereas CoMs for individual presentations of the same stimulus were highly variable. The topography-based decoder performed at an average accuracy rate of only 64% (83%, 62%, 49%, 53%, and 73%). This is significantly better than chance (t test, p < 0.01), but also significantly inferior to the performance achieved by maximum likelihood (t test, p < 0.05). This indicates that, with respect to localizing nearby cues in the visual field, topographic decoding is somewhat informative but far from reliable.
Figure 3.
Topography-based decoding. A, Each population vector's center of mass (dot) plotted on the relevant area of the tectum, color-coded according to the stimulus. B, CoM of population vectors elicited by the same stimulus were averaged to find the mean position due to each of the stimuli (color-coded diamonds). Due to the high degree of overlap between responses, all averaged CoMs are located within 10 μm. C, Center of mass decoding. CoM decoded stimuli (color-coded circles) for each population vector (dot). Performance is given by the percentage of observations that were decoded correctly, for this fish 73%. D, Testing whether performance could be improved by choosing different mean positions for decoding. Potential centers were considered along the extended anterior–posterior axis defined by the original mean CoMs (diamonds); here we allowed up to 50% extension of this axis, so that each of the mean potential centers could be in any of five potential spots along this axis (5 yellow circles), ie, potential CoMs (PCoMs). The best decoding performance achieved due to a particular spread of the mean potential centers is shown by the color-coded stars. CoM decoded stimuli for each untrained population vector using these PCoMs are also shown (color-coded circles). In this case performance remained similar (71% of the population vectors were decoded correctly as opposed to 73% using the original mean CoMs).
The CoMs used above were defined by a very limited set of data. Could there be spatial reference positions in the tectum (for instance generated by averaging CoMs over a much larger set of data) against which each pattern of activity could be compared that would give better decoding performance? To test this we allowed the three potential reference points (which we still refer to as CoMs) to be placed on a linear grid of five different positions along the anterior–posterior axis of the tectum defined by the original CoMs axis. This axis was extended in length by 10–50%, allowing the CoMs to spread over a greater area than originally used. This yielded 5 × 4 × 3 = 60 potential CoM placement combinations in total (Fig. 3B). However this decoder showed only a slight improvement of 2–5% (Fig. 4A). Thus, the topography-based decoder remained inferior to the optimal decoder.
Figure 4.
Performance of the decoders. A, Performance comparison for all fish using the four different decoders: the optimal decoder (ML), the linear decoder (LD), or topography-based decoder (CoM), and the topography-based decoder using potential alternative centers (PCoM). Each color represents a different fish. B, Comparison of decoder performance for 10° versus 20° separation. C, Decoding performance of ML, LD, and CoM decoders as a function of number of neurons involved. Performance rapidly saturates as the number of neurons increases. Mean and SEM from 10 simulations with different random seeds are shown.
The role of stimulus spacing
Intuitively, one would expect the performance of all the decoders to improve as the stimuli move further apart, leading to more widely spaced patterns of activity on the tectum. To test this using our dataset we compared the decoding performance for the binary choices of spots 1 versus 2 and 2 versus 3 (10° separation between stimulus centers) compared with the binary choice of spots 1 versus 3 (20° separation). As expected there was an improvement for all decoders (Fig. 4B; though none of these improvements were statistically significant). ML showed the smallest improvement, because its performance is already close to perfect for 10° separation. These results reinforce the idea that CoM decoding can be an effective method for distinguishing widely separated spatial locations in this system, but is substantially inferior to more sophisticated methods for closely separated locations.
The role of population size
In several other systems it has been found that decoding accuracy is a sublinear function of the number of neurons used in the decoding (Wessberg et al., 2000), and that performance often effectively saturates within a few tens of neurons (Nicolelis and Lebedev, 2009). Is this true in zebrafish tectum, and is the rate of saturation affected by the decoding method used? To test this we averaged performance at each population size over 10 possible combinations of neurons. In agreement with results reported in primates (Nicolelis and Lebedev, 2009), performance rapidly increased with the number of neurons initially, but saturated at ∼20 neurons (Fig. 4C). These neuron-dropping curves demonstrate both the single neuron insufficiency principle (ie, individual neurons carry only a limited amount of information about a given variable) and the mass effect principle (ie, a certain number of neurons in a population is needed for their information capacity to stabilize at a high value; Nicolelis and Lebedev, 2009). Thus, independent of the decoding method used, only ∼20 tectal neurons were required to convey as much information about stimulus location as can be conveyed using that coding method on the full tectal population imaged.
Decoding in a computational model of the retinotectal system
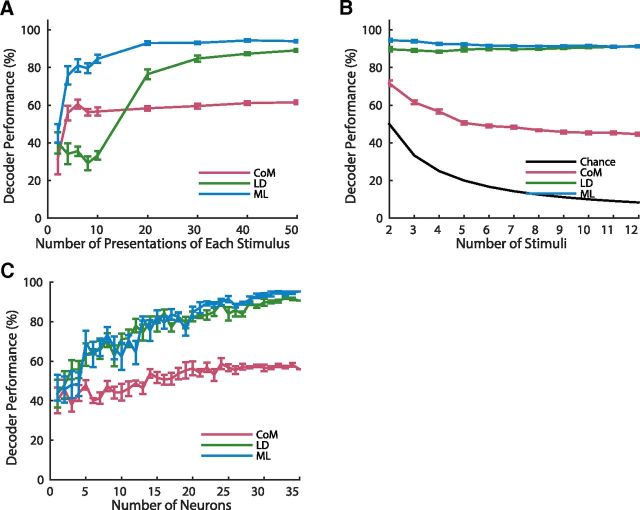
To more closely examine the performance of the decoders, and how they are affected by different aspects of the retinotectal system and visual stimuli, we developed a simple computational model of the zebrafish retinotectal system. The model consists of two one-dimensional layers of cells, representing the retina and the tectum, joined by weighted connections which send responses from the retina to the tectum (Fig. 5A; see Materials and Methods). The stimuli and decoding procedures were the same as those used for the experimental data (see Materials and Methods). The tectal cells in the model form a dense and regular array of approximately Gaussian tuning curves, (that is, the response of each cell drops off as a Gaussian function of distance from its preferred stimulus in the retina), in which case the center of mass decoder is equivalent to maximum likelihood (Snippe, 1996). However this equivalence is only true under the assumption that there is very little or no background noise of cells or other stimulus-independent activity (Seung and Sompolinsky, 1993; Snippe, 1996), which is not the case in the experimental data. To account for this in the model we adjusted the signal-to-noise ratio of the tectal cells to achieve overall decoding performance similar to the results obtained using the experimental data (see Materials and Methods). Although their overall performance was tuned to the data, the relative performance of the center of mass, linear, and maximum likelihood decoders in the model matched well with the experimental results (Fig. 5B), with the average performance of each decoder being 62% for CoM, 89% for LD, and 94% for ML (average of 10 simulations in each case).
We then varied the stimulus parameters in the model. When the separation between the stimuli was increased, all the decoders increased in performance (Fig. 5C). LD and ML performed perfectly for any separation larger than the spots themselves (10°), whereas CoM required almost 40° of separation between the stimuli to perform at 100%. The performance of the model also matched with the data comparing fine scale discrimination between two points 10° apart with two points 20° apart (Fig. 5D) with all decoders showing significant improvement (t test, p < 10−7 in each case).
We also measured the performance of the decoders as the number of presentations of each stimulus was varied from 2 to 50 (Fig. 6A). Whereas ML and LD performed poorly for very small numbers of presentations, the performance of CoM saturated very rapidly. This is because ML and LD require sufficient training data to form adequate representations of the responses, whereas CoM can perform well with only a single presentation per stimulus. Increasing the number of stimuli to be decoded caused further decreases in performance of CoM, but no substantial change in the performance of ML or LD (Fig. 6B). We generated the neuron-dropping curve for each decoder in the same way as above for the experimental data (Fig. 6C). As expected the performance of all decoders increased with the size of the neuron population used for decoding, and saturated at ∼25–30 cells.
Figure 6.
Performance of the decoders. A, Decoder performance as a function of the number of presentations of each stimulus, demonstrating that LD required more training to perform optimally. B, Decoder performance as a function of the number of stimuli discriminated, demonstrating that ML decoder is robust to the number of stimuli decoded, whereas CoM showed a decrease in performance. Mean and SEM from 10 simulations shown in A and B. C, The neuron dropping curve, showing performance as a function of the number of neurons used to perform the decoding. The performance rapidly saturated as the number of neurons increased as in the experimental data (Fig. 4C). Mean and SEM shown from five random subsets of neurons for each number of neurons.
Decoding in a model without topography
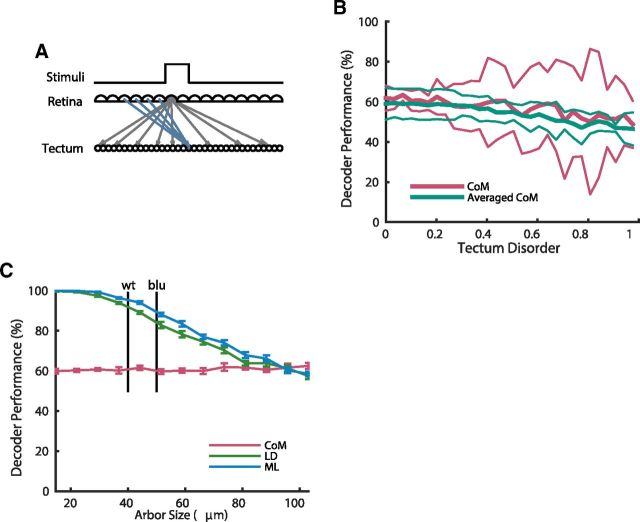
To probe the influence of topography on stimulus decoding, we first removed the topographic retinotectal map in the model by shuffling the positions of the tectal cells while leaving the connectivity between the retina and tectum intact (Fig. 7A). In this nontopographic model, the LD and ML decoders were unaffected as they do not make use of the positions of the tectal cells. In contrast, the average performance of the CoM decoder dropped from 62% in the topographic case to 48% when the tectum was shuffled. This is expected because it is reliant on a topographic representation of visual stimuli in the tectum. Surprisingly however, the variance in performance across simulations greatly increased for the CoM decoder, from a SD of 3% in the topographic case to 9% in the shuffled case, and for some shuffling instances, the performance of CoM actually increased compared with the topographic case.
Figure 7.
Modeling of perturbed topography. A, Schematic of the model where the positions of the tectal cells were randomly shuffled but the connections kept intact. Arrows show connections with weights >0.1 from a single retinal cell (gray) and to a single tectal cell (blue). B, CoM performance as a function of the disorder of the tectum, when only stimuli at the center of the visual field were used (red), and when performance was averaged over stimuli centered at several points across the visual field (blue-green). Mean (thick lines) and 2 SD (thin lines) shown for five simulations for each level of disorder. Although some random tectal orderings resulted in the CoMs being well separated for one particular set of stimuli, leading to higher variance, this effect was abolished when performance was averaged over a variety of stimuli. C, Decoder performance as a function of arbor size, defined as the full-width at half-maximum of the Gaussian defining the connection weights. Approximate values of the arbor size of wild-type and blumenkhol mutant zebrafish are shown with vertical lines (Smear et al., 2007). LD and ML decreased in performance with increased arbor sizes, whereas CoM was unaffected. Mean and SEM from 10 simulations shown.
To analyze this variance in performance, we gradually perturbed the initially topographic retinotectal map by only partially shuffling the tectal cell positions, to create varying levels of disorder. When CoM performance was analyzed as a function of this partial shuffling, the decoder showed an approximately linear decrease in performance with increasing map disorder, along with a large increase in variance (Fig. 7B). This increase in variance is expected however, because there will be some particular instances of a disordered tectum, which will by chance separate the responses to the three spot stimuli we used widely across the tectum, thereby separating the centers-of-mass and allowing the decoder to perform very well. To get a reliable performance measure, we averaged the performance of CoM over stimuli presented at points across the visual field rather than just at the center. This averaged performance now had approximately constant variance for all levels of tectal disorder, while showing the same decrease in decoding performance (Fig. 7B).
Although a completely nontopographic retinotectal map has not been produced experimentally in zebrafish, the blumenkhol mutant provides an interesting case. This mutant shows impaired visual acuity (Smear et al., 2007). This impairment was linked to reduced glutamate concentration at the retinotectal synapse cleft (Smear et al., 2007), which may lead to dispersed termination zones in small group of axons as a homeostatic response to lowered synaptic activity (Smear et al., 2007). Although it is unclear experimentally whether this acuity impairment represents a causal effect, we tested this computationally by increasing the width of the connections between the retina and the tectum in our model, effectively increasing the axonal arbor size. Surprisingly this resulted in decreased performance of the LD and ML decoders, while leaving the CoM decoder mostly unaffected (Fig. 7C). The increased arbor size results in a higher level of overlap between the responses to the three different stimuli, which is detrimental to the performance of the LD and ML decoders as they then have difficulty separating the responses. However the centers of these overlapping responses were largely unaffected by arbor size, and so the CoM decoder performed well regardless of the size of the arbors. As behaviorally the visual acuity of the blu mutant is decreased, these results are consistent with the hypothesis that a decoder like LD or ML, rather than a simple topography-based decoder like CoM, is used by zebrafish at the age of 6–8 dpf to localize visual stimuli.
Discussion
Maps serve as a ubiquitous organizing principle in the brain. In many sensory systems, such as audition, vision, and somatosensation, topographic maps are evident throughout multiple levels. Maps such as retinotopy and tonotopy persist from the receptor surface up to the cortex (Kaas et al., 1990; Kaas, 1997). However, despite the prevalence of topographic maps, the function they subserve is still unclear (for review, see Kaas, 1997). Here we have shown that fine scale localization of targets in the visual field of the larval zebrafish can be performed far more accurately by linear or maximum likelihood decoding than by topography-based decoding. Our computational model of the zebrafish visual system reproduced these results, and confirmed that topography-based decoding performs well only for widely separated stimuli. Thus, the retinotectal map in zebrafish is neither required in principle for stimulus decoding, nor does it provide a particularly accurate method for achieving this.
Topographic versus nontopographic decoding
For a dense and regular array of neurons forming a well organized map, and satisfying certain other conditions including low levels of background noise, a topography-based decoder is equivalent to maximum likelihood (Snippe, 1996). This concept of a perfect map helps support the idea that space within the brain is used to represent information about space in the world (Groh, 2014). However, although maps may be topographically smooth at the macroscale, they are often locally heterogeneous. In general, topographies have been reported as blurred, variable, distorted, incomplete, and biased due to the multidimensional nature of receptive fields, natural signal statistics, and behavioral relevance, particularly in awake animals (Evans and Whitfield, 1964; Recanzone et al., 1993; Schreiner and Winer, 2007; Schreiner and Polley, 2014). In the zebrafish in particular, although there is a approximately linear relation between the position of the cell and the center of its receptive field, this relationship is noisy (Niell and Smith, 2005; Romano et al., 2015), with a substantial proportion of “misplaced” cells (Northmore, 2011). As we have demonstrated, this leads to a substantial degradation in fine-scale stimulus discrimination for a topography-based decoder compared with a statistically optimal decoder that does not rely on topography. Moreover, the zebrafish blumenkhol mutant provides a case where the topographic map is altered via increased receptive field size. Intriguingly, simulating the blu mutant in our model has shown that the experimentally observed decrease in behavioral performance (which we equate with decoding accuracy) was reproduced by the LD and ML but not CoM decoders (Fig. 6C). Although in general the afferents of retinal ganglion cells terminating in the tectum could have more precise topography than the activity of tectal neurons, the only information passed on to downstream targets of the tectum is tectal cell activity. The notion that a degraded topography might aid decoding of stimuli in some way that we have not addressed is inconsistent with our finding that ML decodes almost perfectly.
Stimulus decoding during hunting behavior
Zebrafish hunting responses show mixed selectivity for combinations of visual features, specifically stimulus size, speed, and contrast polarity. Convergent saccades are specifically associated with prey capture and precede a strike at the prey. In tethered fish, dark 10° spots on a light background are the most effective stimuli to evoke a convergent saccade (Bianco and Engert, 2015). Conversely, in freely swimming fish, as well as in tethered fish, stimuli smaller than 5° produce orienting responses whereas stimuli >10° trigger aversive turns (Bianco et al., 2011; Trivedi and Bollmann, 2013). When a larval zebrafish engages in prey capture behavior, it performs several swim bouts within a few hundred milliseconds, during which the larva successively minimizes the angle and distance between its body axis and the prey, until it is close enough to capture the prey with high probability (McElligott and O'Malley, 2005; McClenahan et al., 2012). This series of swim bouts increases the angular size of the target from 4° to 12° (Trivedi and Bollmann, 2013). Hence, at the crucial moment in time before the larva strikes, when the target is ∼10° angular size, it needs its best accuracy in estimating the position of the target in its visual field. Thus, the 10° spots used in this study are highly relevant ecological stimuli, which require accurate decoding. The poor performance of the topography-based decoder for a spot size matching that at which the fish usually launches an attack (10°) suggests that this type of decoding may be insufficient for subserving effective predation.
Successful hunting behavior relies on two major components: accuracy in aiming at the prey during the strike, ie, snapping at the right resolved place (Beyer, 1980) and the speed of the strike, ie, preventing the prey from escaping (Drenner et al., 1978; Winfield et al., 1983). Catching performance in other fish species improves rapidly during development, mainly due to the strike speed (Drost, 1987). The hunting accuracy rate has not been thoroughly studied throughout zebrafish gestational development, but is 50% for 8 dpf larvae (Westphal and O'Malley, 2013). However, it is not clear whether it is strike speed or aiming accuracy that constrains this performance rate. Thus, although strike speed increases during development, it is also possible that the neural code itself adapts over time to improve stimulus decoding, thereby giving the larvae better aiming estimates.
To study the role of topography of the retinotectal map, we presented transiently appearing spots, rather than moving spots as commonly used for virtual prey. Although fast-moving spots are more likely to elicit hunting behavior (Bianco et al., 2011), our data and those of Niell and Smith (2005) show that transiently appearing spots in the visual field elicit visual responses in the tectum. It is possible that these visually evoked tectal responses did not evoke the motor program for hunting behavior (eg, convergent saccades that precede a strike at prey), but this does not alter our conclusions regarding the superiority of nontopographic decoding over topography-based decoding.
Implementation issues and a possible role for the retinotectal map
The tectal representation of a visual target must be transformed into an estimate of a position-related variable that can optimally guide behavior. Sensory likelihoods provide an optimal platform for generating these estimates. A biologically feasible transformation of sensory responses to sensory likelihoods requires a combination of each neuron's response and the logarithm of its own tuning curve (Jazayeri and Movshon, 2006). On the other hand, a linear decoder, which in our system performed almost as well as maximum likelihood, has a much simpler implementation and in general is more likely to be related to computations actually performed by the nervous system (Salinas and Abbott, 1994).
Although, like the topographic decoder, the performance of ML increases rapidly with the number of stimulus presentations, the more biologically plausible LD decoder requires substantially more training to reach high performance (Fig. 6A). This design feature of rough hard-wired decoding for the topographic decoder suggests the possibility that the brain might use the topographic map to localize targets during development when the network is still developing, but then switches to a more optimal method as a result of experience-dependent plasticity. In addition, there may be speed-accuracy trade-offs: perhaps, given biological constraints, topographic decoding can sometimes provide faster decoding than more statistically optimal methods. It is thus possible that decoding strategies are flexible, and can vary over both developmental and potentially even moment-by-moment timescales.
Footnotes
This work was supported by the Australian Research Council (Grant DP150101152). We thank Philip Dyer for his contributions to this work.
The authors declare no competing financial interests.
References
- Ahrens MB, Li JM, Orger MB, Robson DN, Schier AF, Engert F, Portugues R. Brain-wide neuronal dynamics during motor adaptation in zebrafish. Nature. 2012;485:471–477. doi: 10.1038/nature11057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Averbeck BB, Latham PE, Pouget A. Neural correlations, population coding and computation. Nat Rev Neurosci. 2006;7:358–366. doi: 10.1038/nrn1888. [DOI] [PubMed] [Google Scholar]
- Beyer JE. Feeding success of clupeoid fish larvae and stochastic thinking. Dana. 1980;1:65–91. [Google Scholar]
- Bianco IH, Engert F. Visuomotor transformations underlying hunting behavior in zebrafish. Curr Biol. 2015;25:831–846. doi: 10.1016/j.cub.2015.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bianco IH, Kampff AR, Engert F. Prey capture behavior evoked by simple visual stimuli in larval zebrafish. Front Syst Neurosci. 2011;5:101. doi: 10.3389/fnsys.2011.00101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burrill JD, Easter SS., Jr Development of the retinofugal projections in the embryonic and larval zebrafish (Brachydanio rerio) J Comp Neurol. 1994;346:583–600. doi: 10.1002/cne.903460410. [DOI] [PubMed] [Google Scholar]
- Chklovskii DB, Koulakov AA. Maps in the brain: what can we learn from them? Annu Rev Neurosci. 2004;27:369–392. doi: 10.1146/annurev.neuro.27.070203.144226. [DOI] [PubMed] [Google Scholar]
- Cowey A. Cortical maps and visual perception: the Grindley memorial lecture. Q J Exp Psychol. 1979;31:1–17. doi: 10.1080/14640747908400703. [DOI] [PubMed] [Google Scholar]
- Deutsch R. Estimation theory. Englewood Cliffs, NJ: Prentice-Hall; 1965. [Google Scholar]
- Drenner RW, Strickler JR, O'Brien WJ. Capture probability: the role of zooplankter escape in the selective feeding of planktivorous fish. J Fish Res Board Can. 1978;35:1370–1373. doi: 10.1139/f78-215. [DOI] [Google Scholar]
- Drost MR. Relation between aiming and catch success in larval fishes. Can J Fish Aquatic Sci. 1987;44:304–315. doi: 10.1139/f87-039. [DOI] [Google Scholar]
- Easter SS, Jr, Nicola GN. The development of vision in the zebrafish (Danio rerio) Dev Biol. 1996;180:646–663. doi: 10.1006/dbio.1996.0335. [DOI] [PubMed] [Google Scholar]
- Evans EF, Whitfield IC. Classification of unit responses in the auditory cortex of the unanesthetized and unrestrained cat. J Physiol. 1964;171:476–493. doi: 10.1113/jphysiol.1964.sp007391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewert JP, Buxbaum-Conradi H, Dreisvogt F, Glagow M, Merkel-Harff C, Röttgen A, Schürg-Pfeiffer E, Schwippert WW. Neural modulation of visuomotor functions underlying prey-catching behaviour in anurans: perception, attention, motor performance, learning. Comp Biochem Physiol A Mol Integr Physiol. 2001;128:417–461. doi: 10.1016/S1095-6433(00)00333-0. [DOI] [PubMed] [Google Scholar]
- Gahtan E, Tanger P, Baier H. Visual prey capture in larval zebrafish is controlled by identified reticulospinal neurons downstream of the tectum. J Neurosci. 2005;25:9294–9303. doi: 10.1523/JNEUROSCI.2678-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Kettner RE, Schwartz AB. Primate motor cortex and free arm movements to visual targets in three-dimensional space: II. Coding of the direction of movement by a neuronal population. J Neurosci. 1988;8:2928–2937. doi: 10.1523/JNEUROSCI.08-08-02928.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groh J. Making space: how the brain knows where things are. London: Belknap; 2014. [Google Scholar]
- Haug MF, Biehlmaier O, Mueller KP, Neuhauss SC. Visual acuity in larval zebrafish: behavior and histology. Front Zool. 2010;7:8–14. doi: 10.1186/1742-9994-7-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jazayeri M, Movshon JA. Optimal representation of sensory information by neural populations. Nat Neurosci. 2006;9:690–696. doi: 10.1038/nn1691. [DOI] [PubMed] [Google Scholar]
- Kaas JH. Topographic maps are fundamental to sensory processing. Brain Res Bull. 1997;44:107–112. doi: 10.1016/S0361-9230(97)00094-4. [DOI] [PubMed] [Google Scholar]
- Kaas JH, Krubitzer LA, Chino YM, Langston AL, Polley EH, Blair N. Reorganization of retinotopic cortical maps in adult mammals after lesions of the retina. Science. 1990;248:229–231. doi: 10.1126/science.2326637. [DOI] [PubMed] [Google Scholar]
- Kendall MG. A new measure of rank correlation. Biometrika. 1938;30:81–93. doi: 10.1093/biomet/30.1-2.81. [DOI] [Google Scholar]
- Kinoshita M, Ito E. Roles of periventricular neurons in retinotectal transmission in the optic tectum. Prog Neurobiol. 2006;79:112–121. doi: 10.1016/j.pneurobio.2006.06.002. [DOI] [PubMed] [Google Scholar]
- Kita EM, Scott EK, Goodhill GJ. Topographic wiring of the retinotectal connection in zebrafish. Dev Neurobiol. 2015;75:542–556. doi: 10.1002/dneu.22256. [DOI] [PubMed] [Google Scholar]
- McClenahan P, Troup M, Scott EK. Fin-tail coordination during escape and predatory behavior in larval zebrafish. PLoS One. 2012;7:e32295. doi: 10.1371/journal.pone.0032295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McElligott MB, O'Malley DM. Prey tracking by larval zebrafish: axial kinematics and visual control. Brain Behav Evol. 2005;66:177–196. doi: 10.1159/000087158. [DOI] [PubMed] [Google Scholar]
- Muto A, Ohkura M, Abe G, Nakai J, Kawakami K. Real-time visualization of neuronal activity during perception. Curr Biol. 2013;23:307–311. doi: 10.1016/j.cub.2012.12.040. [DOI] [PubMed] [Google Scholar]
- Nicolelis MA, Lebedev MA. Principles of neural ensemble physiology underlying the operation of brain-machine interfaces. Nat Rev Neurosci. 2009;10:530–540. doi: 10.1038/nrn2653. [DOI] [PubMed] [Google Scholar]
- Niell CM, Smith SJ. Functional imaging reveals rapid development of visual response properties in the zebrafish tectum. Neuron. 2005;45:941–951. doi: 10.1016/j.neuron.2005.01.047. [DOI] [PubMed] [Google Scholar]
- Northmore D. Encyclopedia of fish physiology: from genome to environment. Vol 1. San Diego: Elsevier; 2011. Optic tectum; pp. 131–142. [Google Scholar]
- Poulain FE, Chien CB. Proteoglycan-mediated axon degeneration corrects pretarget topographic sorting errors. Neuron. 2013;78:49–56. doi: 10.1016/j.neuron.2013.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Recanzone GH, Schreiner CE, Merzenich MM. Plasticity in the frequency representation of primary auditory cortex following discrimination training in adult owl monkeys. J Neurosci. 1993;13:87–103. doi: 10.1523/JNEUROSCI.13-01-00087.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romano SA, Pietri T, Pérez-Schuster V, Jouary A, Haudrechy M, Sumbre G. Spontaneous neuronal network dynamics reveal circuit's functional adaptations for behavior. Neuron. 2015;85:1070–1085. doi: 10.1016/j.neuron.2015.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sajovic P, Levinthal C. Visual cells of zebrafish optic tectum: mapping with small spots. Neuroscience. 1982a;7:2407–2426. doi: 10.1016/0306-4522(82)90204-4. [DOI] [PubMed] [Google Scholar]
- Sajovic P, Levinthal C. Visual response properties tectal cells of zebrafish. Neuroscience. 1982b;7:2427–2440. doi: 10.1016/0306-4522(82)90205-6. [DOI] [PubMed] [Google Scholar]
- Salinas E, Abbott LF. Vector reconstruction from firing rates. J Comput Neurosci. 1994;1:89–107. doi: 10.1007/BF00962720. [DOI] [PubMed] [Google Scholar]
- Schreiner CE, Polley DB. Auditory map plasticity: diversity in causes and consequences. Curr Opin Neurobiol. 2014;24:143–156. doi: 10.1016/j.conb.2013.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiner CE, Winer JA. Auditory cortex mapmaking: principles, projections, and plasticity. Neuron. 2007;56:356–365. doi: 10.1016/j.neuron.2007.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seung HS, Sompolinsky H. Simple models for reading neuronal population codes. Proc Natl Acad Sci U S A. 1993;90:10749–10753. doi: 10.1073/pnas.90.22.10749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smear MC, Tao HW, Staub W, Orger MB, Gosse NJ, Liu Y, Takahashi K, Poo MM, Baier H. Vesicular glutamate transport at a central synapse limits the acuity of visual perception in zebrafish. Neuron. 2007;53:65–77. doi: 10.1016/j.neuron.2006.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snippe HP. Parameter extraction from population codes: a critical assessment. Neural Comput. 1996;8:511–529. doi: 10.1162/neco.1996.8.3.511. [DOI] [PubMed] [Google Scholar]
- Stuermer CA. Retinotopic organization of the developing retinotectal projection in the zebrafish embryo. J Neurosci. 1988;8:4513–4530. doi: 10.1523/JNEUROSCI.08-12-04513.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trivedi CA, Bollmann JH. Visually driven chaining of elementary swim patterns into a goal-directed motor sequence: a virtual reality study of zebrafish prey capture. Front Neural Circuits. 2013;7:86. doi: 10.3389/fncir.2013.00086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wandell BA, Winawer J. Imaging retinotopic maps in the human brain. Vis Res. 2011;51:718–737. doi: 10.1016/j.visres.2010.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wessberg J, Stambaugh CR, Kralik JD, Beck PD, Laubach M, Chapin JK, Kim J, Biggs SJ, Srinivasan MA, Nicolelis MA. Real-time prediction of hand trajectory by ensembles of cortical neurons in primates. Nature. 2000;408:361–365. doi: 10.1038/35042582. [DOI] [PubMed] [Google Scholar]
- Westerfield M. The zebrafish book: a guide for the laboratory use of zebrafish (Brachydanio rerio) Ed 2. Eugene, OR: University of Oregon; 1993. [Google Scholar]
- Westphal RE, O'Malley DM. Fusion of locomotor maneuvers, and improving sensory capabilities, give rise to the flexible homing strikes of juvenile zebrafish. Front Neural Circuits. 2013;7:108. doi: 10.3389/fncir.2013.00108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winfield IJ, Peirson G, Cryer M, Townsend CR. The behavioural basis of prey selection by underyearling bream (Abramis brama (L.)) and roach (Rutilus rutilus (L.)) Freshw Biol. 1983;13:139–149. doi: 10.1111/j.1365-2427.1983.tb00666.x. [DOI] [Google Scholar]