Mice Can Use Second-Order, Contrast-Modulated Stimuli to Guide Visual Perception

Abstract

Visual processing along the primate ventral stream takes place in a hierarchy of areas, characterized by an increase in both complexity of neuronal preferences and invariance to changes of low-level stimulus attributes. A basic type of invariance is form-cue invariance, where neurons have similar preferences in response to first-order stimuli, defined by changes in luminance, and global features of second-order stimuli, defined by changes in texture or contrast. Whether in mice, a now popular model system for early visual processing, visual perception can be guided by second-order stimuli is currently unknown. Here, we probed mouse visual perception and neural responses in areas V1 and LM using various types of second-order, contrast-modulated gratings with static noise carriers. These gratings differ in their spatial frequency composition and thus in their ability to invoke first-order mechanisms exploiting local luminance features. We show that mice can transfer learning of a coarse orientation discrimination task involving first-order, luminance-modulated gratings to the contrast-modulated gratings, albeit with markedly reduced discrimination performance. Consistent with these behavioral results, we demonstrate that neurons in area V1 and LM are less responsive and less selective to contrast-modulated than to luminance-modulated gratings, but respond with broadly similar preferred orientations. We conclude that mice can, at least in a rudimentary form, use second-order stimuli to guide visual perception.

SIGNIFICANCE STATEMENT To extract object boundaries in natural scenes, the primate visual system does not only rely on differences in local luminance but can also take into account differences in texture or contrast. Whether the mouse, which has a much simpler visual system, can use such second-order information to guide visual perception is unknown. Here we tested mouse perception of second-order, contrast-defined stimuli and measured their neural representations in two areas of visual cortex. We find that mice can use contrast-defined stimuli to guide visual perception, although behavioral performance and neural representations were less robust than for luminance-defined stimuli. These findings shed light on basic steps of feature extraction along the mouse visual cortical hierarchy, which may ultimately lead to object recognition.

Introduction

In primates, visual processing along the ventral stream takes place in a hierarchy of areas characterized by an increase in both complexity of neuronal preferences and invariance to changes of low-level stimulus attributes. Evidence for gradually increasing complexity comes from studies examining neuronal preferences, which range from oriented edges in primary visual cortex (V1) (Hubel and Wiesel, 1959, 1962; De Valois et al., 1982), contours, textures, and combinations of orientations in V2 (Anzai et al., 2007; Willmore et al., 2010; Freeman et al., 2013), curvature in V4 (Pasupathy and Connor, 1999) to complex objects, such as faces, in inferior temporal (IT) cortex (Desimone et al., 1984; Logothetis and Sheinberg, 1996; Tanaka, 1996). Evidence for gradually increasing invariance comes from studies demonstrating conserved selectivity of IT neurons across changes in position and scale (Schwartz et al., 1983; Tovee et al., 1994; Hee et al., 1995; Logothetis and Pauls, 1995; Op De Beeck and Vogels, 2000) or context (Rust and Dicarlo, 2010).

One basic type of invariance is form-cue invariance (Baker and Mareschal, 2001), where neurons have similar preferences in response to first-order stimuli, defined by changes in luminance, and global features of second-order stimuli, defined by changes in contrast, texture, color, or other visual cues. Despite typically being less responsive to second-order than to first-order stimuli, cue-invariant neurons have been observed in primate V2 (Li et al., 2014; but see El-Shamayleh and Movshon, 2011; An et al., 2014), MT (Albright, 1992) and IT (Sáry et al., 1993), and cat area 18 (Zhou and Baker, 1994; Leventhal et al., 1998; Mareschal and Baker, 1998a, b; Zhan and Baker, 2006; Song and Baker, 2007).

In recent years, mice have become a popular model system for early visual processing, but it is currently unclear whether their vision can rely on more than luminance cues. Measurements of psychophysical performance (Andermann et al., 2010; Histed et al., 2012; Lee et al., 2012; Bennett et al., 2013) and neural activity across cortical visual areas (Van den Bergh et al., 2010; Andermann et al., 2011; Marshel et al., 2011; Glickfeld et al., 2013) have so far mostly used luminance-modulated, first-order gratings. It is therefore unknown whether mice can use second-order stimuli to guide visual behavior, and which cortical visual areas might have cue-invariant tuning.

Here we asked whether mice can use second-order stimuli to guide visual perception in a cue-invariant way and assessed potential cue-invariant representations of stimulus orientation in two areas of mouse visual cortex. We tested whether mice can generalize orientation discrimination learned with first-order, luminance-modulated gratings (LGs) to various untrained second-order, contrast-modulated gratings (CGs). We found that mice can partly generalize learning from familiar cue conditions to novel cue conditions. We then performed extracellular recordings in mouse areas V1 and LM, where we compared orientation tuning curves to LGs and CGs. In both areas, the responses to CGs were weaker and less selective than those to LGs, but orientation preference was broadly similar for the two types of stimuli. We conclude that mice can, at least in a rudimentary form, use second-order stimuli to guide visual perception.

Materials and Methods

All procedures complied with the European Communities Council Directive 2010/63/EC and the German Law for Protection of Animals, and were approved by local authorities, following appropriate ethics review.

Visual stimuli.

Visual stimuli were presented using custom software (EXPO; https://sites.google.com/a/nyu.edu/expo/home) on a calibrated liquid crystal display monitor (Samsung 2233RZ; mean luminance 50 cd/m²), placed 25 cm in front of the animal's eyes. To correct luminance nonlinearities of the display, we used an inverse gamma lookup table obtained regularly by calibration with a photometer.

For both behavioral and electrophysiological experiments, we used a common set of LGs and CGs, obtained by multiplying a contrast envelope with a noise carrier. We defined a two-dimensional moving sine wave grating as follows: S(x, y, t) = sin(2πf(sin(θ)x + cos(θ)y) + 2πvt), where f is the spatial frequency, θ is the orientation, and v is the temporal frequency. LGs were then generated as follows: LG(x, y, t) = l₀ + l₀cS(x, y, t), and CGs were generated as CG(x, y, t) = l₀ + l₀(S(x, y, t) + 1)/2 * N(x, y), where l₀ is the mean luminance, c is the contrast, and N(x, y) is the static noise carrier with a spatial frequency spectrum that dropped off as A(f_n) ∼ 1/(f_n + f_c). We created two types of CG stimuli that differed in the distribution of Fourier energy of the carrier. For CGs with low-frequency noise, we set f_c to 0.05 cycles/degree and imposed a high-frequency cutoff at 0.12 cycles/degree; for CGs with high-frequency noise, we used an f_c = 0 cycles/degree and a low-frequency cutoff at 0.12 cycles/degree. For recordings from area V1, the LGs and the envelope of the CGs had a spatial frequency f of 0.05 cycles/degree and a temporal frequency v of 1.5 Hz. To optimize stimulus parameters for the preferences of area LM, we conducted the LM recordings with f of 0.028 cycles/degree and v of 1.8 Hz (Marshel et al., 2011). Contrast c was set to 1, except for experiments where we matched the root-mean-square (RMS) contrast between first- and second-order gratings, in which case c was 0.335 for the LGs. The seed for generating the random Gaussian noise texture was varied across experimental sessions.

Analysis of visual stimuli.

Following An et al. (2014), we performed a spectral power analysis of the LGs and CGs. To reveal the difference in power between two orthogonal orientations, we first calculated D(ω_x, ω_y, τ) = P_o(ω_x, ω_y, τ) − P_{o_ortho}(ω_x, ω_y, τ), where the power P is the squared amplitude of the 3D Fourier transform of the drifting grating. To illustrate the difference in power as a function of space, D was further integrated to result in I(ω_x, ω_y) = ∫D(ω_x, ω_y, τ)dτ. To illustrate the difference in power as a function of orientation, I(ω_x, ω_y) was transformed into Ĩ(ρ, θ) and was further integrated to result in O(θ) = ∫Ĩ(ρ, θ)dρ. To assess the spatial frequency and temporal frequency content of the absolute differential power, we calculated S(ρ) = ∫|Ĩ(ρ, θ)|dρ and T(τ) = ∫∫|P_o(ω_x, ω_y, τ) − P_{o_ortho}(ω_x, ω_y, τ)|dω_xdω_y.

Surgical preparation for head-fixed visual behavior.

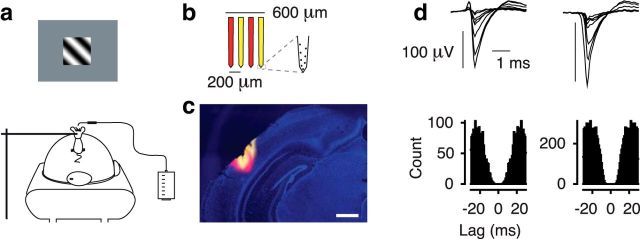
Behavioral experiments were performed in 2- to 5-month-old C57BL/6J mice of either sex (2 males, 4 females). General anesthesia was induced by 5% isoflurane and maintained during surgery at 1%–2%. Buprenorphine (0.1 mg/kg, s.c.) was used for analgesia and atropine (0.3 mg/g, s.c.) to reduce bronchial secretions. Animal temperature was kept at 37°C. A custom-designed head post was mounted to the skull using dental cement (Tetrik EvoFlow, Ivoclar Vivadent). Mice were implanted with two miniature screws over the cerebellum (#00-96X 1/16, Bilaney), serving as reference and ground for extracellular recordings. The skull over the target area was marked and sealed with KwikKast (WPI). For 3 d after surgery, mice were injected by antibiotics (Baytril, 5 mg/kg, s.c.) and longer-lasting analgesics (Carprofen, 5 mg/kg, s.c.). After recovery, mice were gradually habituated to being head-fixed and placed on an air-suspended Styrofoam ball (Hölscher et al., 2005; Dombeck et al., 2007) (Fig. 1a). A spout connected to a lick sensor was used to measure licks and deliver fluid rewards (Schwarz et al., 2010).

Figure 1.

Behavioral setup, recordings, and isolated single neurons. a, Setup for head-fixed behavior with air-cushioned spherical treadmill and lick-sensor. b, Schematic of the four-shank silicon probe. c, Coronal section. The four shanks of the electrode were stained in alternating fashion with DiI (yellow) and DiD (red). Blue represents DAPI. Scale bar, 400 μm. d, Average spike-waveforms and autocorrelograms of two example single units recorded from area V1. Units 144–5.x.31 and 144–4.x.5.

Orientation discrimination task and analysis of behavioral data.

After habituation to the setup, mice were placed on a water restriction regimen. Throughout all training phases, the animals' daily weight and fluid consumption were monitored and recorded, and the animals were checked for signs of potential dehydration (Guo et al., 2014). Following Guo et al. (2014), in a first phase, daily access to water was systematically reduced until the animal reached a target weight of ∼85% of its initial weight. After the weight had stabilized, training in the behavioral task started and mice received most of their water during performance in the behavioral apparatus.

Using classical conditioning, mice were trained to associate the orientation of the visual stimulus with a water reward. In each session, mice were presented with 120 trials of either 45 or 315 degree gratings, drifting for a duration of 3 s behind a square aperture of 32 degree. The presentation of the 315 degree grating was automatically followed by a fluid reward of 5–7 μl; the orthogonal grating was never rewarded. Stimulus presentations were separated by an interstimulus interval of 15 s added to a random delay drawn from an exponential distribution with a mean of 15 s. Drawing onset times from an exponential distribution yields a flat hazard rate, ensuring that animals cannot predict the time point of reward delivery.

To evaluate orientation discrimination performance, we focused on licks in anticipation of fluid reward. Following Gallistel et al. (2004), we computed, separately for each stimulus orientation, a lick index (LI): LI = (licks_stimulus − licks_baseline)/(licks_stimulus + licks_baseline), where licks_stimulus is the number of licks during the last 1 s of stimulus presentation and licks_baseline is the number of licks during the 1 s before stimulus presentation. To identify learning, we analyzed the cumulative records of LI, where changes in slope correspond to changes in the level of performance. For instance, a positive slope of the cumulative LI corresponds to increased licking during the stimulus compared with the baseline period and indicates that the animal anticipates reward after seeing any of the stimuli. A positive slope of the difference between cumulative LIs indicates that the animal licks more strongly during the rewarded than during the unrewarded grating, and shows that the animal has learned to discriminate grating orientations. To assign trials to different stages of orientation discrimination learning, we determined significant changes in the slope of the difference of the cumulative LI by using a change point analysis (Gallistel et al., 2001). To quantify discrimination performance across the different stages of learning, we performed an ideal observer analysis on the distributions of LIs for the two orientations.

We tested the mice in several conditions. We always started training using LGs until the animal reached stable and reliable orientation discrimination performance. Then, we replaced LGs with CGs with low-frequency noise carriers to test the generalization of orientation discrimination to second-order gratings. To test influences of stimulus contrast, we switched back to LGs, but with contrast reduced to 0.335, such that it matched the RMS contrast of CGs. After that, 2 animals were additionally tested with CGs with high-frequency noise carriers.

Surgical preparation for electrophysiological recordings.

Electrophysiological recordings were performed in 2- to 5-month-old C57BL/6J mice of either sex (4 males, 8 females). Surgical procedures were identical to those for behavioral experiments. After recovery and habituation to the setup, mice underwent a second surgical procedure under general anesthesia (1%–2% isoflurane, ∼15 min), in which a craniotomy was performed, which was sealed with KwikKast until the recording session. To avoid potential effects of anesthesia, recordings were never performed on the same day of the craniotomy.

Visual stimuli for electrophysiological recordings.

To estimate receptive field (RF) position, we mapped ON and OFF subfields of RFs using a sparse noise stimulus (Liu et al., 2009). This stimulus consisted of white or black squares (4° diameter) briefly flashed (150 or 200 ms) on a square grid (40° or 60° diameter). Subsequent stimuli were centered on the online estimates of the average RF maps for each shank of a 32-channel silicon probe (see Analysis of electrophysiological data; Fig. 1b). To measure orientation tuning curves, we interleaved in pseudo-random order LGs and CGs moving for a duration of 2 s in 8 different directions.

Analysis of electrophysiological data: unit extraction and spike sorting.

Recordings from V1 were obtained through a craniotomy (∼1.5 × 1.5 mm) located 3 mm lateral to the midline and 1.1 mm in front of the anterior margin of the transverse sinus. Recordings from LM were obtained from 4 mm lateral to the midline and 1.4 mm in front of the anterior margin of the transverse sinus (Wang et al., 2011). Recordings from V1 and LM were performed in separate sessions using 32-channel silicon probes in a 4-shank configuration (Buzsáki32-A32, Neuronexus; 200 μm intershank spacing; Fig. 1b). Extracellular signals were recorded at 30 kHz (Blackrock Microsystems). Online estimates of tuning properties relied on high-pass filtered signals crossing a fixed threshold (typically 4.5–6.5 SDs).

Wideband extracellular signals were analyzed using the NDManager software suite (Hazan et al., 2006). The 8 channels on each shank were treated as an “octrode.” Using a robust spike detection threshold (Quiroga et al., 2004) set to 6 SDs of the background noise, spike-waves were extracted for each “octrode” from the high-pass filtered continuous signal. The first three principal components of each channel were used for automatic clustering with KlustaKwik, followed by manual refinement of clusters (Hazan et al., 2006). This yielded high-quality single-unit activity as evident from distinct spike-wave shapes and a clear refractory period in the autocorrelogram (Fig. 1d). For analysis of retinotopy, we used the envelope of the multiunit activity (MUAe) (van der Togt et al., 2005), averaged across all channels in each shank.

Analysis of tuning.

To determine RF maps for single-unit spiking activity, we fitted ON and OFF subfields separately with a two-dimensional Gaussian (Liu et al., 2009) as follows: f(x, y) = B + $\frac{A}{2\pi ab}\exp \left(-\frac{x{\prime }^2}{2a^2}-\frac{y{\prime }^2}{2b^2}\right)$, where A is the maximum amplitude, B is the baseline response, a and b are half-axes of the ellipse, and x′ and y′ are transformations of the stimulus coordinates x and y, taking into account the angle θ and the coordinates of the center (xc, yc) of the ellipse. To quantify the progression of RF location in the recorded visual area, we constructed maps of z-scored MUAe activity, averaged between 0 and 0.35 s after stimulus onset. If these maps had a sufficient signal/noise ratio (SD > 0.035), we computed the average RF coordinates from the peak of the MUAe activity for each shank. Sessions with ambiguous maps were discarded from all further analyses.

Orientation tuning curves were fitted with a sum of two Gaussians with peaks 180 degrees apart, which could have different amplitudes but equal width and a constant baseline. To quantify orientation selectivity, we computed d′ (Berens et al., 2008) defined as follows: $d\prime =\frac{\left({\mu }_{\text{pref}}-{\mu }_{\text{ortho}}\right)}{\widehat{\sigma }}$, where $\widehat{\sigma }=\sqrt{\left({\sigma }_{\text{pref}}^2+{\sigma }_{\text{ortho}}^2\right)}/2$. In contrast to the more commonly used OSI (Niell and Stryker, 2008), this index has the advantage to not only consider modulation depth but also the variability of responses. We performed all our analyses also on OSI (both with and without spontaneous activity removed), and circular variance (Ringach et al., 2002); results obtained with these alternative measures were qualitatively similar. We only considered neurons that passed three selection criteria applied to the responses to LGs: (1) an average firing rate of at least 1 spike/s to at least one orientation; (2) average responses to at least two orientations differing from the response to the mean-luminance gray screen by at least 2.58× the SEM; and (3) explained variance of the Gaussian fit of at least 70%.

Comparison of responses to LGs and CGs.

On the population of selected neurons, we performed a log-linear analysis to statistically assess the proportion of neurons responsive to both LGs and CGs versus LGs only. To model the observed counts, we fitted a GLM with a Poisson link function considering the factors responsiveness (LGs and CGs vs LGs only) and area (V1 vs LM). We report all significant interactions with the factor responsiveness. In addition, we included the factor noise (low frequency vs high frequency) to assess differences in responsiveness across experiments with different noise textures.

To investigate differences in firing rates and orientation tuning in response to LGs and CGs, we performed an ANOVA with the within-subject factor stimulus (LGs vs CGs), and the between-subject factors area (V1 vs LM). To appropriately visualize the results, we show the mean and SE of the pairwise differences (Franz and Loftus, 2012). To compare the difference in responses to CGs versus LGs, for LGs with full contrast and matched RMS contrast, we performed an ANOVA with the within-subject factor stimulus (LGs vs CGs), and the between-subject factors contrast (full vs matched LG) and area (V1 vs LM). All post hoc pairwise contrasts were corrected for multiple comparisons (multcomp package in R, R Development Core Team (2015)).

To relate the preferred orientations in response to LGs and CGs, we used the circular version of the Pearson's product moment correlation as described by Jammalamadaka and Sengupta (2001) and implemented in MATLAB (The MathWorks) by Berens (2009).

Histology.

For postmortem histological reconstruction of recording sites (Fig. 1c), we coated each shank of the electrode alternating between a red-shifted fluorescent lipophilic tracer (DiD; D7757, Invitrogen) and an orange fluorescent lipophilic dye (DiI; D282, Invitrogen). After recordings, mice were transcardially perfused under pentobarbital sodium anesthesia (200 mg/kg) with 0.2 m sodium phosphate buffer (PBS), followed by 4% PFA in PBS. Brains were postfixed for 24 h at 4°C and then rinsed 3 times with 1× PBS. Brains were sliced (40 μm) using a vibratome (Microm HM 650 V, Thermo Scientific) and mounted on glass slides with Vectashield DAPI (Vector Laboratories), and coverslipped. Slides were inspected for the presence of the tracers using a Zeiss Imager.Z1m fluorescent microscope.

Results

Here we investigated whether mice can generalize orientation discrimination in a cue-invariant way, and assessed the selectivity and sensitivity of areas V1 and LM in visual cortex to second-order, CGs. As opposed to standard, first-order sine-wave LGs, second-order gratings were defined by modulations of contrast (Fig. 2).

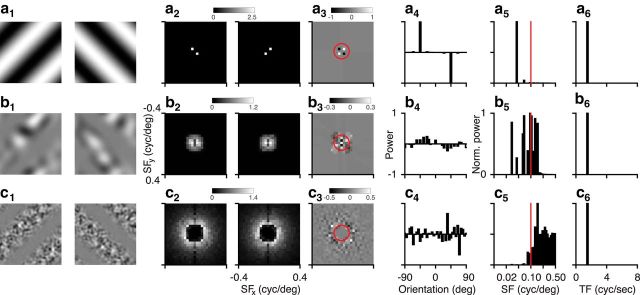
Figure 2.

Analysis of visual stimuli. a, LGs (32 degrees wide) of orthogonal orientations (a₁) and their power spectra (a₂). Differential power in the Fourier plane (a₃) and orientation domain (a₄). Spatial frequency (a₅) and temporal frequency content (a₆) of the absolute differential power distribution. b, Same as a, for the CGs with low-frequency noise. c, Same as a, for the CGs with high-frequency noise. Red circles and lines indicate a spatial frequency of 0.1 cycles/deg.

Because CGs can contain both global, second-order features and local, first-order features, we first performed a spectral analysis of the gratings used in these experiments. We illustrate this analysis on the grating orientations used for the behavioral experiments. LGs (Fig. 2a₁) are defined by their power at a single spatial frequency and orientation (Fig. 2a₂). The differential power in the orientation domain peaks at −45 and 45 degrees, corresponding to the grating orientations (Fig. 2a₃,a₄). The absolute differential power in the spatial frequency domain peaks at 0.05 cycles/degree (Fig. 2a₅), corresponding to the grating spatial frequency, and the absolute differential power in the temporal frequency domain peaks at 1.5 Hz (Fig. 2a₆), corresponding to the grating temporal frequency. CGs with low-frequency noise carriers (Fig. 2b₁,b₂) contain differential power parallel to the orientations of the envelope (Fig. 2b_3,b₄), which arises because the envelope induces inhomogeneity in the distribution of local luminance of the noise carrier. The peak of this differential power is ∼25% of that for the LGs and more broadly distributed across orientations. The absolute differential power in the spatial frequency domain has a broad distribution between 0.02 and 0.15 cycles/degree (Fig. 2b₅), and absolute differential power in the temporal frequency domain peaks at the drift rate of the envelope (Fig. 2b₆). In comparison, CGs with high-frequency noise carriers (Fig. 2c₁,c₂) contain little differential power across spatial frequencies (Fig. 2c₃), as there are no clear peaks and troughs of differential power around the orientations of the LGs (Fig. 2c₄). The absolute differential power in the spatial frequency domain is small for values <0.08 cycles/degree, peaks at 0.16 cycles/degree, and falls off toward higher spatial frequencies (Fig. 2c₅); the absolute differential power in the temporal frequency domain again peaks at the drift rate of the envelope (Fig. 2c₆).

Together, this analysis reveals that the two types of CGs will likely activate first-order luminance-sensitive mechanisms in the mouse visual system to a different degree: although first-order mechanisms could decode stimulus orientation using distortion signals in CGs with low-frequency noise carriers, such mechanisms might play a smaller role for CGs with high-frequency noise carriers. With high-frequency noise carriers, the differential orientation signal across spatial frequencies does not contain clear peaks and troughs around the orientation of the LGs and is concentrated at spatial frequencies, which are far from optimal for mouse V1 (0.045 cycles/degree) and LM (0.028 cycles/degree) neurons (Marshel et al., 2011).

Mice learn orientation discrimination for LGs

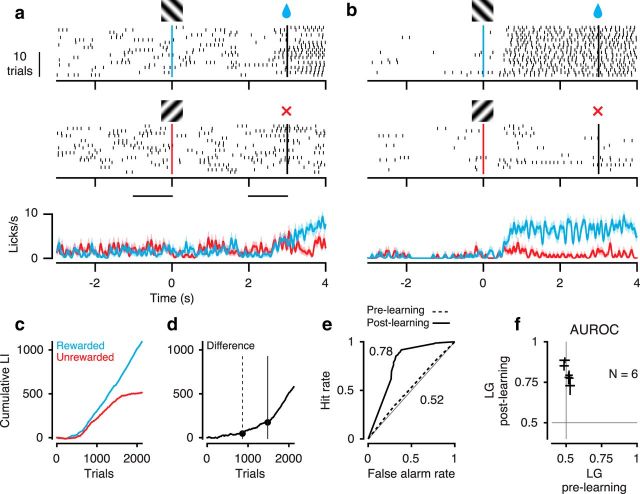
To assess whether mice can use second-order stimuli to guide visual perception in a cue-invariant way, we first trained head-fixed mice (Fig. 1a) in a classical conditioning paradigm to perform a coarse orientation discrimination on LGs (Fig. 3). We paired one of two orthogonal orientations with a fluid reward and assessed discrimination performance by the emergence of orientation-specific licking in anticipation of reward. At the beginning of training, animals licked spontaneously and only increased lick rates to consume the reward (Fig. 3a); after learning, animals licked vigorously during the presentation of the stimulus orientation that would be followed by reward (Fig. 3b). To quantify licking behavior, we computed, for each orientation separately, the cumulative sum of an LI, defined as the difference in the number of licks during the last 1 s of stimulus presentation and the 1 s before stimulus presentation, divided by their sum (Fig. 3c). We then focused on the difference between cumulative LIs to the rewarded and unrewarded orientations and extracted significant change points, which correspond to significant changes in orientation discrimination performance (Fig. 3d). An ideal observer analysis based on this animal's LI revealed that orientations could not be decoded before (area under the receiver operating characteristic [AUROC] = 0.52, 95% CI = 0.50–0.55), but after learning (AUROC = 0.78, 95% CI = 0.75–0.80). A similar pattern was observed across all animals tested, with average performance increasing from 0.51 ± 0.008 (SEM) to 0.80 ± 0.023.

Figure 3.

Orientation discrimination for LGs. a, Example behavioral session, before learning. Top, Licks to the rewarded orientation. Middle, Licks to the unrewarded orientation. Bottom, Trial-averaged lick density. Shaded regions represent mean ± SEM. Gratings indicate stimulus onset. Black vertical lines indicate stimulus offset. Black horizontal lines indicate baseline and stimulus period used for computing the LI. Session 5, b, Same as a, after learning. Session 21, c, Cumulative LI as a function of trial number for rewarded (blue) and unrewarded orientations (red). d, Difference of cumulative LIs between the two orientations. Dots indicate significant change points used for assigning sessions to training stages. Trials before the first change point were assigned to the prelearning stage (dashed vertical line). Trials after the last change point (solid vertical line) were assigned to the postlearning stage. e, ROC analysis based on distributions of LIs from the two conditions in the prelearning stage (dashed curve) and postlearning stage (solid curve). a–e, Example mouse 278. f, AUROC across mice (N = 6). Crosses represent 95% CIs.

Mice can generalize orientation discrimination in a cue-invariant way

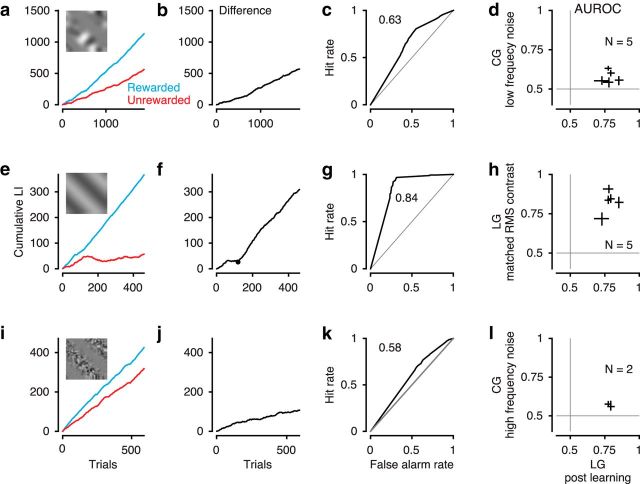
We next asked whether mice can generalize the learned orientation discrimination to gratings, in which orientation was defined by changes in contrast rather than luminance (Fig. 2b). After mice had successfully learned the orientation discrimination task, we replaced the LGs by CGs, keeping all other aspects of the task identical. To facilitate the transfer of learning, we first switched to CGs with low-frequency noise carriers. Despite the difference in global appearance between LGs and CGs with low-frequency noise carriers, mice could, in principle, judge the orientation of low-frequency CGs by relying on first-order mechanisms similar to those optimal for the learned task with LGs. We found that mice could tell apart the CGs from the mean-luminance gray background, as indicated by positive slopes of the cumulative LIs for rewarded and unrewarded stimuli. With the exception of one mouse, all tested animals could also discriminate between the orientations as indicated by a steeper increase of LI for the rewarded compared with the unrewarded condition (Fig. 4a). Mice did not need to acquire the orientation discrimination task de novo but instead could readily generalize from LGs to CGs as there were no significant changes in slope of the differential cumulative LI across trials (Fig. 4b). This lack of changes in slope also indicates that performance for CGs did not improve across extensive training of almost 2000 trials. Overall, performance for the CGs with low-frequency noise (AUROC = 0.63, 95% CI = 0.62–0.65; Fig. 4c) was considerably lower than for the LGs, and similar results were obtained for all animals tested (mean AUROC = 0.58 ± 0.017 SEM; Fig. 4d).

Figure 4.

Behavioral performance for CGs and control conditions. a–d, Performance for CGs with low-frequency noise carrier. a, Cumulative LI as a function of trial. Blue represents rewarded orientation. Red represents unrewarded orientation. b, Difference of cumulative LI between the two orientations. c, ROC analysis based on LIs. a–c, Example mouse 278. d, Comparison of AUROC values for LGs (after learning; Fig. 3f) and CGs (N = 5 mice). Crosses represent 95% CI. e–h, Same as a–d, for performance for LGs matched in RMS contrast. g, We only considered data with stable performance (i.e., trials after the first change point in f). i–l, Same as a–d, for performance for CGs with high-frequency noise carrier (N = 2 mice). Conventions as in Figure 3.

We wondered whether the overall lower performance for CGs was related to their lower RMS contrast compared with LGs. To test this hypothesis, we probed mice with LGs whose RMS contrast was lowered to match that of CGs. We found that mice could perform well during the orientation discrimination task for LGs matched in RMS contrast (mean AUROC = 0.83 ± 0.03 SEM; Fig. 4e–g). Indeed, across all animals tested, performance was similar for both levels of contrast (p = 0.23, paired t test; Fig. 4h).

Finally, we tested mice with CGs, for which we imposed a low-frequency cutoff on the noise carrier, such that it did not contain any energy at the spatial frequency of the learned LGs and little differential power across spatial frequencies at the learned orientations (Fig. 2c). Again, mice could see this type of CG, as indicated by the positive slope of cumulative LIs across trials (Fig. 4i). Importantly, they could also discriminate between the two grating orientations, as indicated by the increase in the difference of cumulative LIs (Fig. 4j); albeit performance was again considerably lower compared with that for LGs (AUROC = 0.58, 95% CI = 0.56–0.60; Fig. 4k). Similar results could be replicated in a second mouse (AUROC = 0.56, 95% CI = 0.53–0.60; Fig. 4l). Together, these results demonstrate that mice can use second-order stimuli to guide visual perception.

Identification of areas V1 and LM based on mirrored retinotopic representation of azimuth

To examine potential neural correlates of such cue-invariant generalization of orientation discrimination, we performed extracellular recordings from areas V1 and LM. Because of the shared vertical meridian with V1, area LM of the mouse is thought to be homologous to area V2 in higher-order mammals, where selectivity for second-order contours has been found (Zhou and Baker, 1994; Leventhal et al., 1998; Mareschal and Baker, 1998a, b; Zhan and Baker, 2006; Song and Baker, 2007; Li et al., 2014). In addition, area LM is one of the major targets of V1 projections (Wang et al., 2012), and its preferred spatial frequencies are significantly lower than those in area V1 (Marshel et al., 2011).

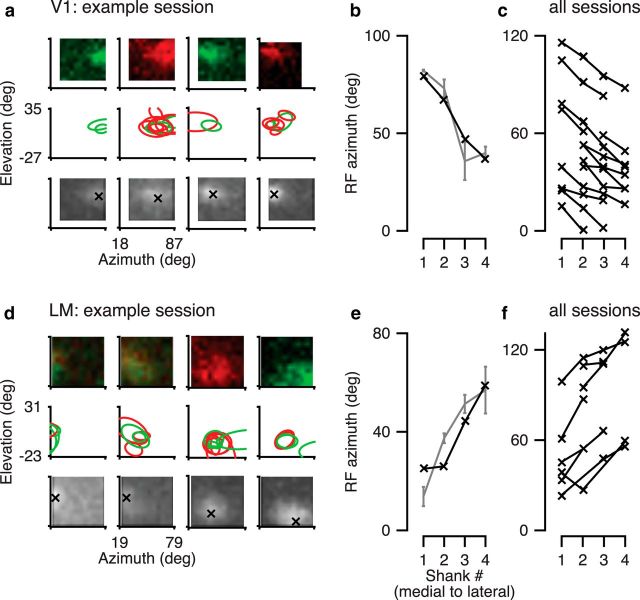
We first verified that our recording sites were indeed in areas V1 and LM by exploiting the mirrored progression of retinotopy along the azimuth in the two areas. We recorded with a 4-shank silicon probe (Fig. 1b,c) spanning a large range of azimuths in either area and used a sparse-noise stimulus to map RFs (Fig. 5). To obtain RF maps for individual neurons, we fitted to the maps of average firing rates (Fig. 5a,d, top) two-dimensional Gaussians, separately for ON and OFF stimuli (Fig. 5a,d, middle). Finally, for RFs with well-fit Gaussian profiles, we extracted the average azimuth and elevation per shank (Fig. 5b,e, gray). Because RF locations in mouse cortex exhibit considerable scatter (Smith and Häusser, 2010; Bonin et al., 2011), we also analyzed the MUAe (Supèr and Roelfsema, 2005), for which we determined the peak RF coordinates for each electrode shank (Fig. 5a,d, bottom, b,e, black). Consistent with the known retinotopy of mouse visual areas (Schuett et al., 2002; Wang and Burkhalter, 2007), we found that for recordings targeted at area V1, going from the most medial to the most lateral electrode shank, the azimuth of RF centers changed from more peripheral to more central (Fig. 5c); in contrast, for LM recordings, the azimuth of RF centers changed from more central to more peripheral (Fig. 5f).

Figure 5.

Identification of visual areas V1 and LM by mirrored retinotopic progression of azimuth. a, Top, Example single-unit RF maps in area V1 for each electrode shank in one example session. Red represents ON field. Green represents OFF field. Units 291-2-x.17, 46, 62, 76. Middle, Contours of all well-fitted RFs in this example session. Bottom, RF maps based on multiunit activity for this example session. b, RF azimuth in the example session based on average single-unit RF centers (gray) and multiunit activity (black). c, Summary of RF azimuth across all V1 recordings. N = 14 sessions. d–f, Same as a–c, for area LM. Units 241-4-x.47, 67, 70, 84. f, N = 8 sessions.

V1 and LM responses to CGs are weaker and less selective

We next centered visual stimuli on the mapped multiunit RFs and compared across areas V1 and LM orientation tuning curves in response to LGs and CGs with low-frequency noise. As expected from previous studies in higher-order mammals (Albright, 1992; Zhou and Baker, 1994; Mareschal and Baker, 1998a; Zhan and Baker, 2006; Li et al., 2014), we found a substantial number of neurons with no visually evoked activity to CGs despite significant responses to LGs (Fig. 6). Across the recorded population, only 72% of luminance-responsive neurons were also responsive to the CGs with low-frequency noise. This fraction was higher for V1 (77%, 178 of 230 recorded neurons) than for LM (61%, 69 of 114 recorded neurons, p < 0.001, two-way interaction, log-linear analysis). All following analyses will focus on those neurons with a significant response to both types of stimuli.

Figure 6.

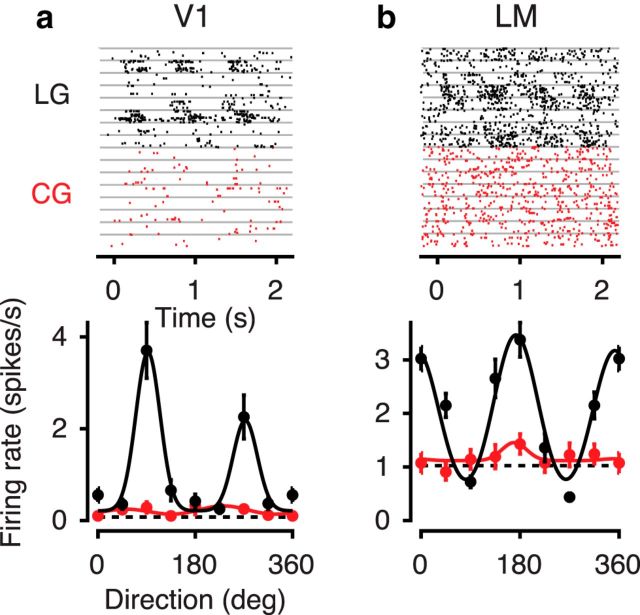
Example neurons unresponsive to CGs despite significant responses to LGs. a, Activity evoked by LGs (black) and CGs with low-frequency noise (red) of an example neuron from area V1. Top, Raster plots. Each gray horizontal line separates trials with different stimulus orientations. Bottom, Tuning curves of the same example neuron (Unit 280-2-4.61). Dashed horizontal line indicates response to gray screen; solid lines indicate fit of a sum-of-Gaussians model. b, Same, for an LM example neuron (Unit 245-5-10.35).

Among those neurons with significant responses to both LGs and CGs, example neurons in both areas V1 (Fig. 7a) and area LM (Fig. 7b) had lower peak firing rates for CGs with low-frequency noise compared with LGs. This reduction of peak firing rates to CGs was also evident in the population of recorded neurons. Peak responses across both recorded areas dropped by 27.8 ± 3.2%, from 11.2 spikes/s in response to LGs to 8.1 spikes/s in response to CGs (ANOVA, main effect, p < 10⁻¹⁶; Fig. 7c,d). This drop tended to be stronger in area LM (31.8 ± 7.3%) compared with area V1 (25.9 ± 3.1; interaction, p = 0.065). We also noted that the responses to the orthogonal orientation for CGs versus LGs were similar in area V1 (mean change 1.6 ± 0.5%), and more consistently decreased in area LM (mean change −18.6 ± 6.3%; interaction p = 0.0002; Fig. 7e,f).

Figure 7.

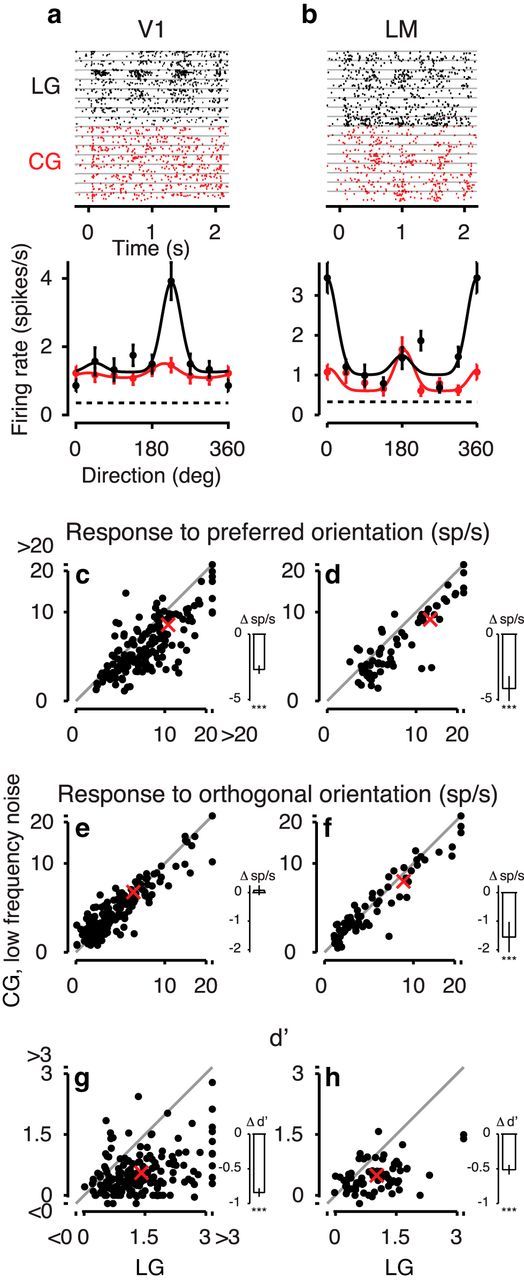
Responses to CGs with low-frequency noise carriers in mouse visual cortex. a, Responses to LGs (black) and CGs (red) of an example neuron from area V1. Top, Raster plots. Bottom, Tuning curves of the same example neuron (Unit 221-1-7.61). b, Same, for an LM example neuron (Unit 245-4-6.35). c, d, Response to the preferred orientation for CGs versus LGs in the population of responsive neurons recorded from V1, N = 178 (c) and LM, N = 69 (d). Insets, Mean pairwise differences and their SEM (Franz and Loftus, 2012). Stars represent significance of post hoc comparisons. e, f, Same as c, d, for response to orthogonal orientation. g, h, Same as c, d, for d′. Red crosses represent means. Conventions as in Figure 6.

This pattern of changes in responsiveness contributed to the drop in selectivity for stimulus orientation for CGs, both in the example cells (Fig. 7a,b) and in the population (Fig. 7g,h). We quantified orientation selectivity by computing d′, which does not only take into account the difference between responses to preferred and orthogonal orientations but also variability of responses (Berens, 2009). Overall, d′ was lower for LM than V1 (main effect, p = 0.003). More importantly, d′ was lower for CGs than LGs (main effect, p < 10⁻¹⁶), and this decrease was stronger for V1 (60.8 ± 4.5% from 1.39 for LGs to 0.54 for CGs) than LM (52.0 ± 6.9% from 0.99 for LGs to 0.47 for CGs; interaction, p = 0.003). Thus, responses to CGs with low-frequency noise carriers compared with LGs in mouse visual cortex are lower and less selective for orientation.

We wondered whether our finding of weaker responses and broader orientation tuning for CG than LG responses could be explained by the lower RMS contrast of CG gratings (Fig. 8). We performed control experiments, in which we measured responses to LGs that were matched in RMS contrast to the CGs. When comparing responses to preferred orientations between CGs and LGs matched in RMS contrast, we found that neurons in both visual areas still responded more weakly to CGs than LGs (7.3 spikes/s vs 8.8 spikes/s, main effect, p < 10⁻⁵; Fig. 8), but this reduction in responsiveness (17.1 ± 3.4%) was less pronounced compared with conditions with full contrast LGs (27.8 ± 3.2%; compare Fig. 7c,d and Fig. 8c,d; interaction, p = 0.009). We also observed that responses to the orthogonal orientations were enhanced for CGs versus LGs in V1 (4.41 sp/s vs 3.65 sp/s, 20.9 ± 4.2%) but did not differ significantly in area LM (8.5 sp/s vs 8.7 sp/s, −2.1 ± 4.7%; interaction, p < 0.01).

Figure 8.

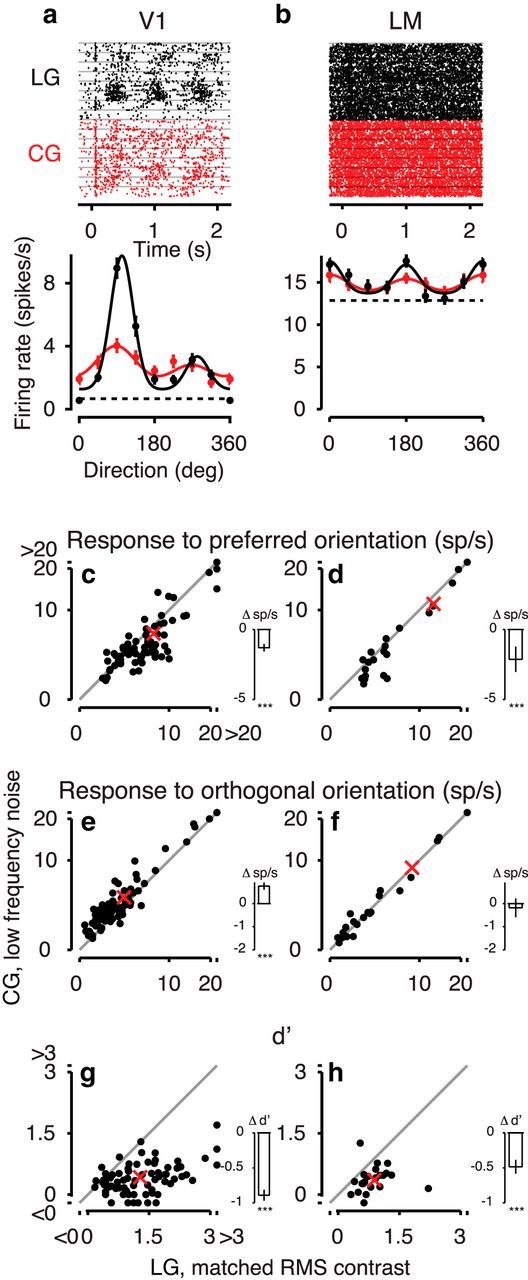
Comparison of responses to LGs matched in RMS contrast and CGs. a, Responses to LGs with matched RMS contrast (black) and CGs with low-frequency noise (red) of an example neuron from area V1. Top, Raster plot. Bottom, Tuning curves of the same example neuron (Unit 221-1-6.24). b, Same, for an LM example neuron (Unit 245-5-7.17). c, d, Responses to preferred orientations for CGs versus LGs with matched RMS contrast in the population of (c) V1 neurons, N = 73 and (d) LM neurons, N = 23. e, f, Same as c, d, for responses to orthogonal orientations. g, h, Same as c, d, for d′. Conventions as in Figure 7.

Even with matched RMS contrast, overall d′ was again lower for area LM (0.62 ± 0.05) than V1 (0.86 ± 0.06; main effect, p = 0.026). Similar to our results with full-contrast LGs, d′ also decreased considerably between LGs matched in RMS contrast and CGs (66.2 ± 5.5%, from 1.2 for LGs to 0.4 for CGs, main effect, p < 10⁻¹⁶). Indeed, d′ did not differ significantly between responses to full-contrast and reduced-contrast LGs (d′_full = 1.3, d′_matched = 1.2; compare Fig. 7g,h and Fig. 8g,h; two-sample t test, p = 0.4), which is probably related to the well-known phenomenon of contrast invariance of orientation tuning (Movshon et al., 1978; Albrecht and Hamilton, 1982; Sclar and Freeman, 1982). Interestingly, the drop in d′ between CGs and LGs with matched RMS contrast was again stronger in area V1 (68.3 ± 6.0%, from 1.3 to 0.41) than in area LM (56.3 ± 11.5%, from 0.86 to 0.38; interaction, p = 0.008).

Together, the reduced RMS contrast of CGs might contribute to the reduction in peak responsiveness to CGs but cannot account for the poorer orientation selectivity for CGs. Instead, the poorer orientation selectivity for CGs is probably more closely related to the broader distribution of orientation energy in CGs compared with LGs (Fig. 2a,b).

Activation of first-order, luminance-sensitive mechanisms in V1 and LM might contribute to the responses to CGs with low-frequency noise. Indeed, the pattern of decreased responses to preferred orientations of CGs of enhanced responses to orthogonal orientations and of broader orientation tuning compared with LGs, as observed in many V1 and some LM neurons, would be a pattern expected by the activation of luminance-sensitive mechanisms. To reduce local orientation-biased luminance fluctuations of the CGs in the spatial frequency range to which V1 and LM neurons are most sensitive, we performed additional experiments with CGs, in which the noise carrier's spatial frequency distribution was concentrated beyond the passband of many V1 and LM neurons (mean high-cutoffs of 0.07 and 0.055 cycles/degree) (Marshel et al., 2011) and for which there was little systematic differential energy at the orientations of the LGs across spatial frequencies (Fig. 2a,c).

We first observed that less than half of the recorded neurons with significant responses to LGs also had visually evoked activity to CGs with high-frequency noise (37%, 51 of 139 recorded neurons). This fraction of responsive neurons was considerably lower compared with that obtained for CGs with low-frequency noise (72%, p < 10⁻¹¹, log-linear analysis, interaction). Interestingly, the difference in responsiveness between the two types of CG stimuli was stronger for area V1 (77% vs 36%, 29 of 81 recorded neurons) than LM (61% vs 38%, 22 of 58 recorded neurons; p = 0.040, log-linear analysis, interaction).

Considering again only those neurons with significant responses to both LGs and CGs (Fig. 9), we found that the example neurons (Fig. 9a,b) as well as the population of recorded neurons had lower responses to CGs with high-frequency noise versus LGs. This was true for both the preferred orientation (decrease of 49.2 ± 9.8%, from 13 sp/s to 6.6 sp/s; ANOVA, main effect, p < 10⁻⁵; Fig. 9c,d) and orthogonal orientation (decrease of 29.0 ± 10.4%, from 7.6 sp/s to 5.4 sp/s; ANOVA, main effect, p = 0.008; Fig. 9e,f). Similarly, d′ decreased by 71.6 ± 6.7% for CGs with high-frequency noise compared with LGs (from 1.34 to 0.38; ANOVA, main effect, p < 10⁻¹³; Fig. 9g,h).

Figure 9.

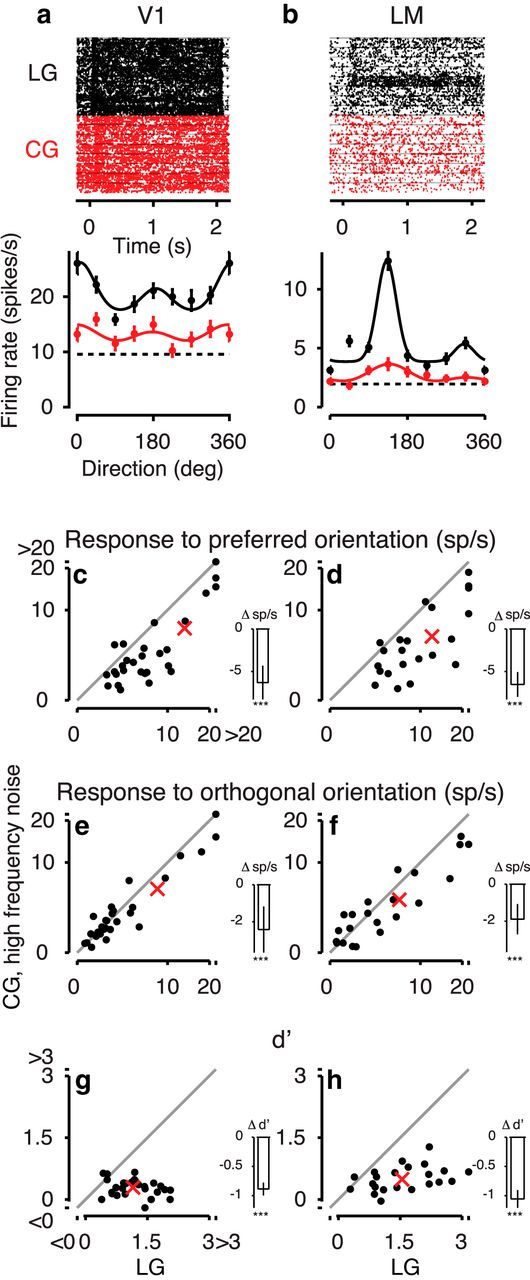
Responses to CGs with high-frequency noise carrier. a, Responses to LGs (black) and CGs with high-frequency noise (red) of a V1 example neuron. Top, Raster plots. Bottom, Tuning curves of the same example neurons (Unit 326-1-2.48). b, Same for an LM example neuron (Unit 299-3-13.42). c, d, Responses to preferred orientations for CGs with high-frequency noise versus LGs in the population of V1 neurons, N = 29 (c) and LM neurons, N = 22, (d). e, f, Same as c, d, for responses to orthogonal orientations. g, h, Same as c, d, for d′. For other conventions, see Figure 7.

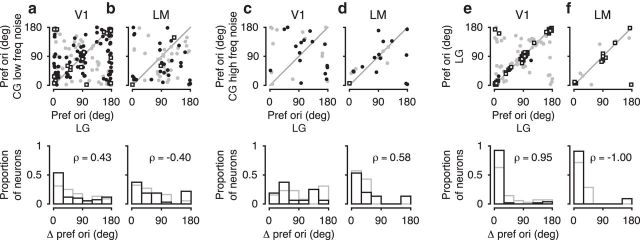
Finally, to examine whether the CG representation might contribute toward cue-invariant perception of stimulus orientation, we also compared the neurons' preferred orientation, separately for each grating type (Fig. 10). Because the reliability of estimating preferred orientation increases with increasing orientation selectivity, we focused on those units with d′ > 1 for LGs (Fig. 10, black) and first tested whether the distribution of differences in preferred orientations for LGs and CGs deviated from uniform. We found that, for CGs with low-frequency noise (Fig. 10a,b), differences in preferred orientation were nonuniformly distributed in both areas V1 (Rayleigh test, p < 10⁻¹⁰) and LM (Rayleigh test, p = 0.03). Indeed, preferred orientations for CGs with low-frequency noise and LGs were correlated for both areas V1 (ρ = 0.43, p < 10⁻⁴) and LM (ρ = −0.4, p < 0.02). This pattern of results would, of course, be consistent with the residual activation of luminance-sensitive mechanisms by the CGs with low-frequency noise. Interestingly, for CGs with high-frequency noise (Fig. 10c,d), the distribution of differences in preferred orientation was nonuniform only for area LM (Rayleigh test, p = 0.005) and preferred orientations were only correlated for area LM (ρ = 0.58, p = 0.02). This is remarkable, as area LM prefers lower spatial frequencies than V1 (Marshel et al., 2011), and should thus be less sensitive to any residual orientation signal potentially present at higher spatial frequencies. Finally, to assess how much of the observed scatter of preferred orientations arises from estimation errors due to limited data, we performed control experiments, in which we presented only LGs, keeping all other aspects of the experiments and analyses identical (Fig. 10e,f). This control condition reveals that variability due to limited data is minimal, at least for the strongly tuned neurons. Together, the broad similarity of preferred orientations between grating types provides some evidence for a coarse cue-invariance, which might in turn be part of the neural basis for perceptual generalization of orientation discrimination.

Figure 10.

Comparison of preferred orientation for contrast-modulated versus LGs. a, Top, Preferred orientations of V1 neurons in response to CGs with low-frequency noise carrier versus LGs. Bottom, Distribution of differences in preferred orientations. Black represents neurons with d′ > 1 for LGs (N = 110). Gray represents neurons with d′ < 1 (N = 68). Square markers represent neurons with d′ > 1 for both grating types. b, Same as a, for LM neurons (N = 32 with d′ > 1 and N = 37 with d′ < 1). c, Same as a, but for CGs with high-frequency noise carrier versus LGs (V1, N = 16 with d′ > 1 and N = 13 for d′ < 1). d, Same as c, for LM neurons (N = 15 with d′ > 1 and N = 7 for d′ < 1). e, Same as a, but repeating the LG condition (V1, N = 53 with d′ > 1 and N = 70 with d′ < 1). f, Same as e, for LM neurons (N = 11 with d′ > 1 and N = 7 with d′ < 1).

Discussion

Here we asked whether mice can use second-order stimuli in a cue-invariant way to guide visual perception during an orientation discrimination task, and screened for potential neural correlates in mouse visual cortex. We found that mice, after learning a coarse orientation discrimination involving only LGs, could readily generalize orientation discrimination to CGs, albeit with a substantial drop in performance. In accordance with these behavioral results, we observed that, in both areas V1 and LM, a lower fraction of neurons was responsive to CGs than LGs, and that those neurons responsive to CGs had generally weaker and less selective tuning for CGs than LGs. Despite these differences, preferred orientations in response to CGs and LGs were broadly similar, potentially underlying the rudimentary cue-invariant generalization in mouse orientation discrimination performance. Such simple form of cue-invariance might be a first step toward object recognition and categorization tolerant to substantial variation in object appearance, as recently demonstrated in rats (Zoccolan et al., 2009; Tafazoli et al., 2012; Vermaercke and Op de Beeck, 2012; Alemi-Neissi et al., 2013; Vinken et al., 2014; De Keyser et al., 2015).

From previous behavioral studies on the limits of rodent vision, it has become clear that the particularities of the paradigm can strongly influence the measured visual abilities. For example, estimates of mouse contrast sensitivity in a nose-poke 2AFC task do not only reflect perceptual limits but can also be limited by nonsensory factors (Busse et al., 2011), whereas rigorous psychophysical measurements using a lever-press paradigm under head fixation can reveal perceptual thresholds that are less contaminated (Histed et al., 2012). Because we wanted to make sure that the mice could, despite the low acuity of their visual system, perceive CGs, we chose a classical conditioning paradigm, which offers a distinct behavioral read-out for the visibility of the stimulus and discriminability of its orientation. This paradigm revealed that mice cannot only perceive the CGs, indicated by orientation-unspecific licking in anticipation of reward, but also, albeit with much lower performance, discriminate orientations of CGs, indicated by orientation-specific anticipatory licking. Despite offering powerful insights into several aspects of visual perception, it seems unlikely that the classical conditioning paradigm can reveal the limits of visual performance in this task: for example, because the classical conditioning paradigm does not require active participation of the animal to obtain reward, trial-to-trial fluctuations in motivation cannot be excluded. Therefore, we speculate that, in other paradigms, such as those using lever presses (Histed et al., 2012) or touch screen panels (Bussey et al., 2001), performance for discriminating orientations of CGs might be substantially better than observed during classical conditioning. Indeed, a recent study in rats trained in a touch-screen paradigm revealed considerable behavioral generalization across first- and second-order stimuli (De Keyser et al., 2015).

Although we demonstrate here that mice can readily generalize the learned orientation discrimination task from LGs to CGs, this generalization ability was rather limited. First, discrimination performance was dramatically lower for CGs than LGs, and performance for CGs did not improve qualitatively even with extensive training. Second, one mouse failed to perform reliable discriminations of CGs even after prolonged training. Third, we noticed that generalization to CGs only happened after initial training with sine-wave LGs, but never after initial training with square-wave LGs: 3 of 3 animals initially trained with square-wave LGs only showed a stimulus-related, unspecific conditioned response to CGs, and never an orientation-specific conditioned response (data not shown).

Neurons in mouse V1 and area LM retained some selectivity for stimulus orientation of CGs and a coarse correspondence between preferred orientations to CGs and LGs, which could potentially underlie the perceptual generalization of orientation discrimination from LGs to CGs. Human psychophysics (Landy and Graham, 2004) and electrophysiological studies in higher-order mammals guided by rich knowledge of spatiotemporal properties across visual areas (Movshon et al., 1978; Issa et al., 2000) suggested a two-stage model of second-order processing (Zhan and Baker, 2006). According to this filter-rectify-filter model, neurons with small RFs would respond to the carrier, and their rectified responses would in turn be summed by a coarser-scale RF, providing orientation selectivity to the envelope. Whether such second-order processing stages indeed exist in the primate or carnivore brain or whether responses to second-order stimuli arise from other mechanisms is an ongoing debate (e.g., Tanaka and Ohzawa, 2009; El-Shamayleh and Movshon, 2011; Hallum and Movshon, 2014; Li et al., 2014). Our current data cannot advance this debate, as the stimuli used in our study cannot rule out that cue-invariant responses to CGs arise either from residual activation of luminance-sensitive mechanisms or are mediated via suppressive mechanisms from the surround (Tanaka and Ohzawa, 2009; Hallum and Movshon, 2014). Our finding, however, that mouse area LM maintains some responsiveness and selectivity for CGs with high-frequency noise carriers, and shows a correspondence between preferred orientations for these CGs and LGs, hints at a potentially interesting role of area LM in the perception of texture boundaries. This possibility is particularly intriguing because properties of area LM are reminiscent of the filter-rectify-filter framework: it is a primary projection target of area V1 (Wang et al., 2011, 2012), has larger receptive fields (Van den Bergh et al., 2010), and prefers lower spatial frequencies than area V1 (Marshel et al., 2011). Direct tests of the existence of second-order mechanisms in the mouse model, however, will require future studies to focus on carriers with even higher spatial frequencies. In such experiments, demonstration of diverse tuning for carrier spatial frequency distinct from that for the envelope and different from that predicted by a surround mechanism (Tanaka and Ohzawa, 2009) would provide strong evidence against activation of luminance-sensitive mechanisms (Li et al., 2014).

It remains an open question whether any of the other mouse extrastriate areas are more strongly responsive to second-order stimuli. Although area LM can be considered a homolog of primate V2 based on its distinct connections and the shared representation of the vertical meridian (Coogan and Burkhalter, 1993; Wang and Burkhalter, 2007), it is currently debated whether it belongs to the mouse equivalent of the “ventral” or “dorsal” visual stream. Studies based on cytoarchitectonic and chemoarchitectonic markers and pathway tracing identified area LM as the gateway of the mouse ventral stream (Wang et al., 2011). Other studies based on functional response properties suggested that areas LI and PM with their preferences for higher spatial frequencies (Andermann et al., 2011; Marshel et al., 2011), and not so much area LM, might play a role in the analysis of detailed structure of visual scenes, and therefore resemble the primate ventral stream. Yet other studies (Juavinett and Callaway, 2015) propose that area LM, due to its responses to pattern motion, is more closely related to the dorsal stream. Besides the ongoing debate on the functional division of rodent extrastriate areas, it has been observed in rat visual cortex that responses in higher areas are more closely related to behavioral discriminability, whereas responses in the primary visual area reflect more closely physical differences between visual stimuli (Vermaercke et al., 2015). Responses to second-order stimuli might therefore be more prominent in higher areas of the mouse ventral stream, similar to what has been suggested for the processing of second-order contours in the nonhuman primate (An et al., 2012; Poort et al., 2012).

It is also currently unknown whether responses to second-order gratings are stronger during task performance. Ideally, neuronal responses to both grating types should be compared during orientation discrimination in both naive and trained animals. Recently, modulations of the V1 population response by learning of a visual discrimination task with LGs have been demonstrated (Poort et al., 2015), and it is likely that learning tasks for other grating types is accompanied by similar changes, acting to improve the representation of relevant orientations and potentially higher spatial frequencies.

In conclusion, we have here investigated the processing of different second-order visual stimuli in the mouse model. Having found a rudimentary form of behavioral generalization during orientation discrimination and the presence of orientation-tuned responses to second-order gratings provides a first starting point for testing in mice simple forms of invariance and their circuit-level neural mechanisms, where a whole arsenal of genetic tools is available for chronic imaging of all visual cortical areas (Andermann et al., 2011; Marshel et al., 2011), causal manipulation of specific cell types (Fenno et al., 2011), and circuit tracing (Wickersham et al., 2007).