Modulation of Neural Variability in Premotor, Motor, and Posterior Parietal Cortex during Change of Motor Intention

Abstract

The time course of neural variability was studied in three nodes of the parieto-frontal system: the dorsal premotor cortex (PMd, area 6), primary motor cortex (MI, area 4), and posterior parietal cortex (PPC, area 5) while monkeys made either direct reaches to visual targets or changed reach direction in response to an unexpected change of target location. These areas are crucial nodes in the distributed control of reaching and their lesion impairs trajectory formation and correction under different circumstances. During unperturbed reaches, neural variability declined before the onset of hand movement in both frontal and parietal cortex. When the original motor intention suddenly changed, neural variability displayed a complex and area-specific modulation because the perturbation of the motor state was signaled earlier in PMd than in MI and PPC. The comparison of perturbed versus unperturbed reaches revealed that, in the time between the onset of correction signal and trajectory change, identical hand movements were associated with different, therefore context-dependent, patterns of neural variability induced by the instruction to change hand movement direction. In PMd, neural variability was higher before the initiation of hand reach than before its correction, thus providing a neural underpinning to the phenomenon that it takes less time to correct than to initiate hand movement. Furthermore, neural variability was an excellent predictor of slow and fast reach corrections because it was lower during the latter than the former. We conclude that the analysis of neural variability can be an important tool for the study of complex forms of motor cognition.

SIGNIFICANCE STATEMENT No single study has been performed on neural variability during update of motor intention across monkey premotor, motor, and posterior parietal cortex. In perturbed reaches, target location changed unexpectedly during reaction time and the correction of hand trajectory required updating the original motor plan. Comparing unperturbed versus perturbed reaches revealed that neural variability displayed a complex context- and area-dependent pattern of modulation because, before trajectory correction, similar initial hand movements were associated with different patterns of variability depending on the instruction signal, and therefore on the future hand path and final destination. Furthermore, neural variability predicted both slow and fast hand movement corrections, also offering a neural underpinning to the phenomenon that it takes less time to correct than to initiate hand movement.

Introduction

In different brain centers, the firing activity of individual neurons displays a high degree of variability, a phenomenon first studied in the cerebral cortex by Werner and Mountcastle (1963) and then revitalized by Tolhurst et al. (1983) and Shadlen and Newsome (1998). When a sensory stimulus occurs repetitively (Churchland et al., 2010; Schölvinck et al., 2015) or a reach movement is performed several times (Lee et al., 1998; Churchland et al., 2006, 2010), neural activity shows a marked intertrial variability. Whether this reflects different sources of noise, from molecular to behavioral (Faisal et al., 2008), and/or is part of the neural code (Stein et al., 2005) has been debated for many years. Removing behavioral variability (Gur et al., 1997) or using sensory stimuli at the threshold level (DeWeese et al., 2003) reduces the mean-variance relationship of neural responses, which is traditionally considered a ubiquitous and crucial feature of the neural code.

A recent modeling study (Litwin-Kumar and Doiron, 2012) indicated that neural variability encodes information that is otherwise barely captured by rate coding. In fact, “doubly chaotic” cortical networks (see Churchland and Abbott, 2012, for a commentary) can generate both firing rate fluctuations and spontaneous spiking variability as emerging properties, the latter reflecting individual neuron activity and the former the collective behavior of cells acting as a synergic cluster that competes with others to maintain the active state. The presentation of a sensory stimulus or the birth of an action plan reduces the fluctuation in firing rate, but has a modest effect on spiking variability, probably because it drives clusters differently for resolving the competition. In alert, behaving monkeys, neural variability has been studied in motor, parietal, and supplementary motor cortex (Lee et al., 1998; Averbeck and Lee, 2003; Marcos et al., 2013) during different reaching tasks and when a decision is made about future eye movements (Churchland et al., 2011). During tasks contrasting proactive versus reactive arm movement (Maimon and Assad, 2009), it has been shown that the interspike interval distributions are more regular in parietal areas 5 and LIP than in areas MT and MST, suggesting that, across these areas, there might be important differences in the information processing that are not easily captured by a Poisson process (see Averbeck, 2009, for a commentary).

So far, no single study has explored the modulation of neural variability in alert, behaving monkeys during tasks requiring a real-time update of an original motor intention. In our study, an unexpected change of target location occurred during reach reaction time (RT), requiring the cancellation or update of the original reach plan to bring the hand to the novel destination.

The neurophysiological mechanisms of this process have been studied only through the analysis of the modulation of firing frequency of cells (Georgopoulos et al., 1983; Archambault et al., 2009, 2011; for reviews see Battaglia-Mayer et al., 2014; Archambault et al., 2015; Battaglia-Mayer et al., 2015). In the present study, we have analyzed the modulation of neural variability in posterior parietal cortex (PPC; PE/PEc, area 5), dorsal premotor cortex (PMd,F2, area 6), and primary motor cortex (MI,F1, area 4), different cortical areas of a same parieto-frontal processing stream responsible for coordinate transformation, composition, and update of motor intention, as well as for the state estimate of the motor periphery (for a recent review, see Caminiti et al., 2015).

Under these complex conditions, the modulation of neural variability often anticipates future motor states and relates in a complex and context-dependent fashion to real-time control and update of hand trajectory, also depending on the node of the parieto-frontal network considered. Furthermore, neural variability predicts whether the task demands will be satisfied through slow or fast corrections.

These results show that the modulation of neural variability depends on the behavioral motor set, which can be discussed within the frame of a recent study suggesting that neural variability reflects the cortical state associated with global fluctuation of activity in neuronal populations (Schölvinck et al., 2015).

Materials and Methods

Animals and behavioral tasks.

Two male macaque monkeys (Macaca mulatta, body weight: Monkey 1, 6 kg; Monkey 2, 7 kg) were surgically implanted with a head post and a scleral search coil under aseptic conditions. They were trained to perform a set of arm-reaching tasks (see below for details). When they achieved a success rate >85%, a recording chamber was positioned to allow neural recording through a seven-channel recording system (Thomas Recording). Electrodes were glass-coated tungsten-platinum fibers (1–2 MΩ impedance at 1 kHz). Neural recording was performed in the superior parietal lobule (area 5, PE/PEc), MI (area 4), and PMd (area 6) of a same hemisphere. The study was performed in accordance with the guidelines of the Italian national law (D.L. 116-92, D.L. 26-2014) and of the EU Directives (EU 116-92; EU 63-2010) on the use of animals in scientific research.

The tasks performed, as well as the modulation of the firing activity of single neurons, have been described in detail previously (Archambault et al., 2009, 2011). Briefly, the animals sat in a primate chair with their head and the unused arm gently restrained. They performed the task in total darkness by using the arm contralateral to the hemisphere of recording. Reaches were made to visual targets in 3D space under 2 different intermingled conditions.

Direct reach (DirR) trials.

Hand movements were made from a central push-button to 1 of 8 peripheral visual targets positioned by a robot arm at the vertices of a 8.5-cm-radius virtual cube (Fig. 1A). Therefore, these reaches were direct and unperturbed.

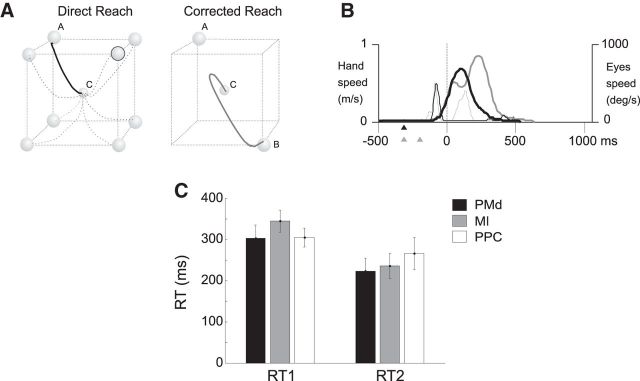
Figure 1.

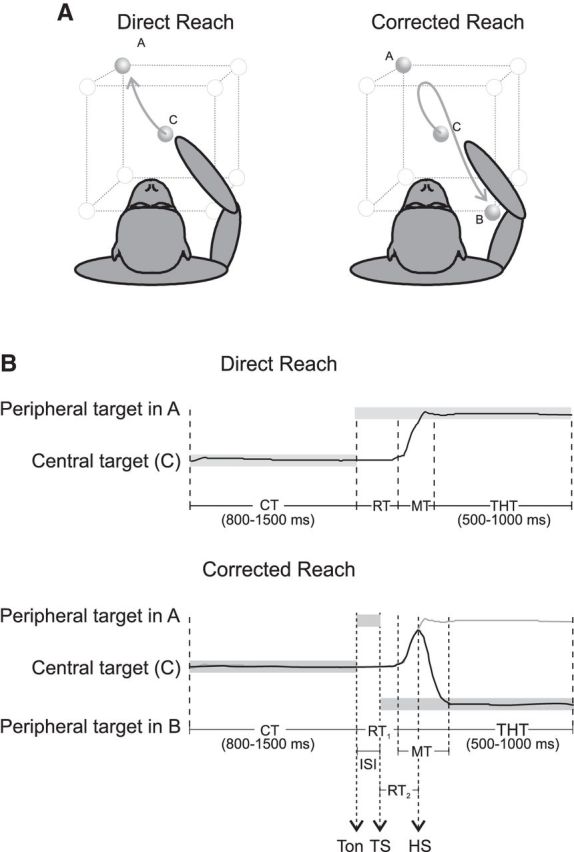
Experimental apparatus and tasks. A, Experimental apparatus. Monkeys, starting from a central position (C), performed direct reaches (toward A) or made hand movement corrections of 180° (from A to B) to peripheral targets arranged at the vertices of a virtual cube. In the CorR trials, the hand path originally directed to the first target location (A) reverses toward the new location (B) after the target “jump” occurring during the RT. B, Temporal structure of DirR and CorR trials. Gray horizontal bars indicate the duration of presentation of visual targets; black curves represent hand position in parametric form for a generic coordinate x_i(t). For the CorR trial, the hand position is also shown (gray line) in the absence of a target jump (DirR) for a direct comparison of the two movement conditions.

Corrected reach (CorR) trials.

In 50% of reaching trials, at approximately the midpoint of the hand RT, the peripheral target (placed in position A by one robot arm and referred as “first target”) was switched off and a different target (on a second robot arm) was lighted on the opposite vertex (at 180°, position B) of an imaginary cube, resulting in a virtual “target jump” from position A to B (Fig. 1A). The time of target switch (TS) was set at 165 ms (Monkey 1) and 225 ms (Monkey 2) after the first target presentation on the basis of the average values of the animal's RT measured in the final training sessions of the DirR task. To receive a liquid reward, monkeys had to redirect the hand toward the second target. Therefore, these reaches were perturbed and corrected. During a typical recording session, monkeys performed five to seven repetitions for the CorR trials and 20–28 repetitions for the DirR trials.

Eye position signals (vertical and horizontal angles) were recorded using a monocularly implanted scleral search coil (1° resolution) sampled at 200 Hz (Remmel Labs). Fixation accuracy was controlled through circular windows (5° diameter) around the targets. The angular velocity was first derived from the position signals. The onset and offset of the saccade was taken as the first of a sequence of three points exceeding or falling below a threshold of 50°/s, respectively.

Arm position was recorded in 3D using an opto-electronic system (Optotrak; Northern Digital) with a sampling frequency of 100 Hz. Six markers were attached to a tight-fitting sleeve, which was placed on the monkey's forearm. Hand trajectories were reconstructed for each recording day. The relationship between hand position and the markers placed on the monkey's forearm was calculated using a known reference point corresponding to a given hand rest position on a fixed peripheral target. This operation was then applied to all other data points. The location and orientation of a rigid body in space is determined by three sets of coordinates. To increase the accuracy in the calculation of the position of the hand, we adopted an algorithm based on singular value decomposition, which makes use of the redundant information in the least-squares sense (Soderkvist and Wedin, 1993; Archambault et al., 2009, 2011).

Using the instrumental behavioral control and kinematic information, we defined various behavioral epochs (Fig. 1B). The control time (CT) started when the animal pressed a lighted central button and ended with the presentation of the first peripheral target (Ton). In DirR trials, the RT was the time elapsing from (Ton) to the onset of hand movement. Only one period of hand movement (MT) was obviously detectable in this task condition, which was defined as the time elapsing from the release of the central target button and press of the peripheral target button. In the CorR trials, we defined two RTs: RT₁ was defined as the RT to the first stimulus presentation, that is, the time elapsing from the appearance of first target (A) to the MT onset toward it (Fig. 1B); RT₂ was instead defined as the time necessary to change hand movement direction. It was calculated from the time of switch of target location (t_TS) to the time of switch of arm movement direction (t_HS) (Archambault et al., 2009). The hand MT could also be divided in two distinct epochs (MT₁ and MT₂) separated by the t_HS. Therefore, MT₁ was the time during which the hand moved toward the first target location (A), whereas MT₂ was the MT from the change of hand trajectory (t_HS) to the final target position (B). In all cases, the trial ended with a target holding time (500–1000 ms) during which the hand was held immobile on the peripheral target (Fig. 1B).

Neural recording.

Extracellular activity recorded from each of the seven electrodes was preamplified, filtered, amplified, and sent to a set of dual-time-amplitude window discriminators (Bak Electronics) that allowed the discrimination of up 2 cells from each electrode and the isolation of spikes at 1 ms resolution. Therefore, we could have simultaneous recording up to 14 cells; however, in most instances, five to seven neurons were isolated at the same time.

Analysis of neural activity.

The analysis of neural activity was based on spike rates, the latter being computed as spike density function (SDF). Each spike was replaced by a Gaussian probability with an SD of 30 ms. The activities were aligned to different behavioral events, such as target presentation (Ton, TS), beginning of the hand movement (MTon), and time of switch of hand direction (HS), depending on the issue under analysis. We also computed the mean population activity (pop-SDF) by averaging the SDF of all cells in each task condition and movement direction and by adopting the above-mentioned temporal alignments.

Analysis of neural variability.

The analysis of the temporal evolution of neural variability across trials for repeated movements of the same type (same condition and direction) was performed on three datasets of units (see “Database” section) selected and analyzed through standard techniques, which makes our results comparable to previous studies (Churchland et al., 2006, 2010). The across-trial variability of firing rates was measured through the normalized variance (NV), in which firing rates were computed as SDF. We first computed NV_id(t) at a given time t, for each neuron i, in a given movement direction d as follows:

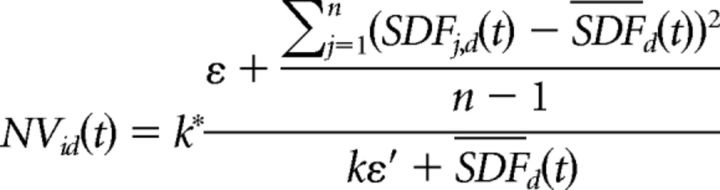where k is a unitless constant scaled to obtain an NV equal to unity for a neuron with Poisson spiking distribution and equal firing rate on every trial, SDF_j,d is the SDF of the j-th trial in direction d, and SDF_d is the mean SDF across all trials in the same direction; ε = ε′ = 0.01 are corrections introduced to avoid singularities. The computation of NV_id(t) was performed for the two types of reach trials (direct and corrected), with different alignments of cell activity based on the available behavioral markers. Finally, by averaging the NV_id values across movement directions and cells, the mean NV (as well as the SE) was computed as a function of time for each movement condition separately; that is, NV_DirR(t) and NV_CorR(t) for DirR and CorR, respectively. The NV(t) functions (±SE) reported in this study refer to the mean values computed (across cells and directions) independently for the populations of PMd, MI, and PPC cells. In one instance, when comparing NV_CorR(t) and NV_DirR(t) (see below), the mean NV (±SE) was computed across cells only (and not directions) because the NV(t) was computed in one movement class only (the anti-PD for DirR trials and anti-PD to PD in CorR trials, as described below).

To evaluate the difference of NV(t) under the two reaching conditions (DirR and CorR), we measured, at a given time t, the difference d(t) = NV_CorR(t) − NV_DirR(t) after alignment to behaviorally relevant events. To make the NV_DirR(t) and NV_CorR(t) comparable, avoiding a potential bias due to a different number of replications in these conditions, we first recalculated NV_DirR(t) by taking into account a reduced number (n = 5) trials, as was done for the computation of NV_CorR(t). For each cell, we selected randomly five replications from the 20–28 available. We were interested in comparing the temporal evolution of NV from the two datasets (DirR and CorR), the neural activities of which at the population level were initially similar in the two tasks (Archambault et al., 2011). In particular, we aimed at assessing when a significant difference emerged from the two conditions. The comparison was performed over time by aligning the NVs to the first target presentation (0 ms) and focusing on a time interval spanning from the 200 ms before to the 600 ms after it. We restricted our measurement of mean NV (across cells) to specific directions. In particular, NV_DirR was evaluated by considering only the activity at the anti-preferred direction (anti-PD) of each cell, whereas NV_CorR was computed on the neural activity of movements directed first to the anti-PD and then to the PD of each cell. In this way, the initial time span of our comparison, ranging from 200 ms before the first target presentation to TS, corresponded to an interval in which the two NVs were obtained from similar pattern of neural activity, in both instances related to movements toward the anti-PD. As statistical evaluation of the difference d(t), each data point d(t) was considered as significantly different from the mean if it was >2*SDs away from the mean value <d(t)>, computed within the ISI epoch; that is, between the first target presentation (Ton) and TS.

Database.

The database consisted of three datasets obtained by recording single-unit activity from PMd, MI, and PPC. The total number of cells isolated and analyzed was 119 in PMd, 155 in MI, and 250 in PPC. However, the analysis of NV was performed on a selection of cells based on their directional modulation in specific task conditions. For this, we estimated the “tuning range” value as described previously (Churchland et al., 2010). The datasets obtained after the selection procedure consisted of 42 cells in PMd, 63 in MI, and 50 in PPC for the DirR condition and 41 PMd cells, 54 MI cells, and 42 PPC cells for the CorR condition.

Determining the amount of decline and the onset time of NV change.

In some epochs of interest (e.g., RT), for each area, we have evaluated the amount of decline of NV and analyzed whether this variable was statistically different across cortical regions. Therefore, the percentage of decline was first measured for the NV calculated for each cell and direction (across replications) during a given epoch of interest. The mean of the values obtained at the single-cell level was calculated across N cells and eight directions separately for each area. For each unit, the percentage of decline was computed with respect to the maximum and minimum amount of NV calculated in subintervals with constant negative sign of the NV first derivative. Statistical differences of the three means (calculated for PMd, MI, and PPC) were assessed through a one-way ANOVA and post hoc analysis (t test with Bonferroni's correction; p < 0.05) applied to determine how the mean values differed from each other.

To determine the time at which the NV started changing after a given event, we first computed the mean value (μ_CT) and SD of the NV during the last 200 ms of CT, and then the sign of the first derivative of NV was computed in each 10 ms bin during RT. When NV was aligned to target presentation, the first time bin at which the two conditions NV < μ_CT − 2 SD and ṄV <0 were met for at least 10 consecutive bins was taken as the onset of a significant decrease of NV. To detect the onset of NV decline relative to movement onset, we computed backward in time from this event the sign of the first derivative of NV. The time of sign change was considered as the initial time of decline of NV during motor preparation. These times were calculated both at the population level on the mean NV computed across cell directions and at the single-cell level (across replications) to obtain information about the variance of onset times within each area and to allow a statistical comparison across them. The latter analysis consisted in a one-way ANOVA (factor: area) applied to the mean values of onset times averaged across cells and directions, followed by a post hoc comparison (t test with Bonferroni's correction; p < 0.05) to test how means were different from each other.

Analysis of NV associated with behavioral variables.

The modulation of NV was studied in relation to different behavioral variables. In particular, the animal capability to perform faster corrections was first investigated in relation of the mean NV observed in different epochs of two set of trials (“fast correction” vs “slow correction” trials). On a trial-by-trial basis, we classified each CorR trial as “fast” or “slow” depending on whether RT₂ was smaller or greater than the mean RT₂ computed across all trials in a given direction. For each cell, the NV was then calculated by selecting fast and slow correction trials separately and then the mean NV across cells was computed (see above), leading to NV_fast and NV_slow for each cell population. The two NV curves have then been compared statistically as a function of time in two ways. The first was aimed at detecting when a significant difference between NV_fast and NV_slow emerged in time along the entire duration of the trial. The mean values NV_fast(t) and NV_slow(t), obtained by averaging NV across cells and directions, were compared at each time t (1 ms resolution) through a t test (p < 0.05). The second method was used to compare across epochs the mean values of the differences NV_fast(t) − NV_slow(t). In particular, the nonparametric Kruskal–Wallis test (p < 0.05) was used to compare statistically, for a given area, the three means of the differences NV_fast(t) − NV_slow(t) obtained by averaging the values across the following three epochs: (1) the interstimulus interval (ISI); i.e., between the first and second target TS presentation; (2) TS-MTon, the time between the TS and movement onset; and (3) MTon-HS, the time between the movement onset and the switch of hand direction.

A further investigation on the relationships between behavior and NV concerned the observed differences between RT₁ and RT₂; that is, between the time needed to initiate the first movement (RT₁) after target presentation and the time necessary to switch the direction of hand trajectory from the change of location of the final target (RT₂). In both monkeys, we first compared the length of RT₁ and RT₂ across trials (1630 from Monkey 1, 2014 from Monkey 2). Because, in both animals, RT₁ was significantly longer (paired t test, p < 0.001) than RT₂, we postulated that these differences could be dependent on significant differences in the NV in particular nodes of the parieto-frontal network. Therefore, for every premotor, motor, and parietal cell, we calculated the minimum values attained by NV across replications in a given direction during RT₁ and RT₂ separately. We then related the minimum values to the mean values of RT₁ and RT₂ obtained from the same set of trials. Therefore, for each cortical area, we obtained two datasets of N values (N = number of cells × eight directions) each for the two RT epochs (RT₁ and RT₂) that were compared statistically with a t test (p < 0.05). All the analyses and the statistical tests were performed with MATLAB 2011b (The MathWorks).

Results

Hand trajectories and speed profiles

The hand trajectories observed for movements performed in different conditions were stereotyped and similar across animals. During direct reaches, the hand described a slightly curved trajectory in all movement directions (Fig. 2A). During corrected reaches, the hand initially moved toward the first target and then changed direction toward the second one (Fig. 2A) at a time here referred to as the t_HS, which varied across trials (Fig. 1B). Therefore, in the corrected reaches, the first part of the hand trajectory was identical to that of the direct reaches and then diverged. Direct reaches displayed the typical bell-shaped velocity profile with a single peak, whereas a double-peak profile was characteristic of corrected reaches (Fig. 2B), with the minimum speed between the two peaks corresponding to the change of hand movement trajectory toward the new target location. Similarly to the hand trajectory, the velocity profile of corrected reaches in the first portion of the movement toward the first target tended to be identical to the speed profiles measured during direct reaches (Fig. 2B). Therefore, all corrected trials in a given direction were basically characterized by trajectories and velocity profiles that in their initial part were virtually identical to those observed during direct reaches performed in absence of target jump.

Figure 2.

Behavioral performance during direct and corrected reaches. A, Examples of hand trajectories (single trials) for the DirR condition, from their common origin (C) to the eight different targets and for one CorR trial when a change of intention occurred, from target A to target B. B, Typical speed profile for hand (thick curve) and eye (thin curves) movements performed directly (black) or after a target jump (gray) occurring during the RT obtained from the same trials (solid black and gray curves) shown in A. Triangles refer to the times of target presentation under the two reaching conditions: DirR (black) with a single target and CorR (gray) with presentation of two consecutive targets in different positions. C, Mean RTs observed across sessions during recording in each area. Mean values of RT₁ were 302 ± 32 ms, 344 ± 26 ms, and 304 ± 22 ms for recording sessions in PMd, MI, and PPC, respectively. Mean values of RT₂ were 223 ± 30 ms, 235 ± 30 ms, and 265 ± 38 ms in the same areas, respectively.

Hand RT, MT, and correction time

Concerning RTs, the two monkeys behaved similarly, although the hand RT of the first animal was shorter than that of the second one across all target directions. In the direct reaches, the mean hand RT to the presentation of the visual target was 305 ms (±26 SD) in Monkey 1 and 349 ms (±31 SD) in Monkey 2. Interestingly, in the corrected reaches, the presentation of the second target during the RT did not affect the length of the RT to the first one (RT₁), which, on average, remained identical to that observed for direct reaches. Conversely, the RT to the second target (RT₂) was 267 (±36 SD) for Monkey 1 and 283 ms (±38 SD) for Monkey 2, in both cases significantly shorter (t test, p < 0.001) by ∼40 and ∼65 ms than the RT₁ of both direct and corrected reaches. For the purposes of this study, we report the animals' mean RTs observed across sessions during recording in each area (Fig. 2C).

The hand movement in direct reaches lasted 259 ± 43 ms (Monkey 1) and 313 ± 48 ms (Monkey 2). During perturbed reaches the entire duration of MTs (MT₁+ MT₂) was on average 421 ± 53 ms (Monkey 1) and 471 ± 53 ms (Monkey 2), with mean MT₁ (movement toward the first target) equal to 129 ms (Monkey 1) and 115 ms (Monkey 2).

NV modulation during direct unperturbed reaching

The NV in PMd, MI, and PPC was studied separately for direct and corrected reaches obtained from the DirR and the CorR trials, respectively. It was first studied at the single-cell level. However, as shown previously (Churchland et al., 2006), this approach did not provide statistically robust results, so the analysis of NV was performed at the population level across cells, trials, and directions. Figure 3, A and B, shows the temporal evolution NV in PMd, MI, and PPC aligned to target presentation (Fig. 3A) or to movement onset (Fig. 3B) for direct reach trials. First, when the modulation of NV was aligned to the target presentation, a time-locked decline was observed in all the frontal and parietal areas studied, which differed statistically in amount across areas (one-way ANOVA, p < 0.0001). This decline, averaged across cells, was significantly stronger in magnitude in PMd (78%) and MI (89%), and therefore in the frontal lobe, than in PPC (50%), as assessed through post hoc analysis (t test with Bonferroni's corrections). No statistical difference was found between PMd and MI declines. As for the temporal order, we compared the mean values of the first significant decline of NV (see Materials and Methods) across areas. After target presentation, the onset of decline was significantly different across areas (one-way ANOVA, p = 0.013) and occurred first in PMd (78 ± 75 ms, mean ± SD) and then in MI (87 ± 69 ms) and PPC (93 ± 77 ms). The onset times of decline observed for PMd cells were significantly earlier than those observed in PPC, whereas the mean time of decline onset obtained from MI cells was not statistically different from those computed in PMd and PPC, as assessed by post hoc statistics (t test with Bonferroni's correction). It is worth noting that, across areas, this decrease was not time locked to the overall increase of the neural activity as detected at the population level. When the modulation of NV was aligned to the hand movement onset, moving backward in time across all areas studied, we found a decline spanning the time of motor preparation. At the population level, mean NV declined first in PMd (−180 ms), then in MI (−160 ms), and finally in PPC (−140 ms). After MT onset, the NV continued its decline in PMd, whereas in both MI and PPC, it was enhanced during the entire duration of hand movement.

Figure 3.

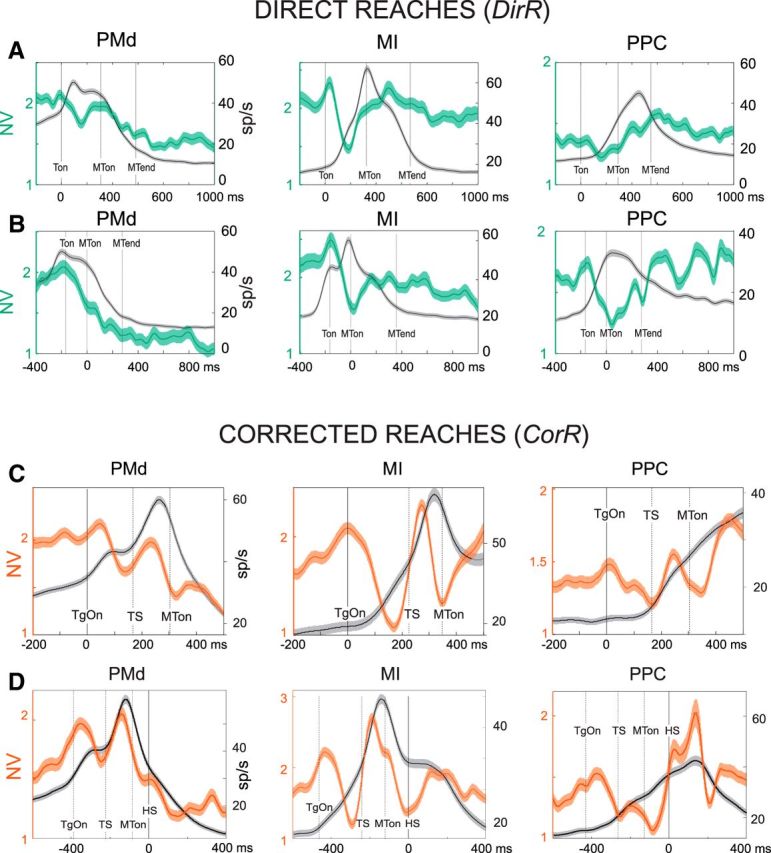
Time course of neural variability during DirR and CorR conditions across areas. Shown are NV (green/red curve) ± SE and superimposed population spike density function ± SE (SDF, gray) from neural activity recorded during DirR trials (A, B) and CorR trials (C, D) aligned to target presentation (A, C), to movement onset (B), and to time of switch of hand movement direction (D). In all graphs, the primary y-axis (left) refers to the measure of NV and the secondary y-axis (right) refers to SDF (sp/s). Solid vertical lines indicate time of alignment (0 ms); dotted lines refer to mean values of temporal events. NV and SE are computed across number of cells and directions (see Materials and Methods).

NV modulation during corrected reaching

When the hand movement was corrected, the temporal evolution of NV displayed a more complex pattern (Fig. 3C,D) that accounted both for the perturbation, consisting of the switch of target location (TS), and for the update of hand movement trajectory. In all the three areas, a first decline was time locked to the presentation of the first target (Fig. 3C), similar to what was seen for the direct reach trials. This was followed by an increase and then a further decline in correspondence of the TS. Although, in PMd and PPC, the enhancement was observed after the TS perturbation, in MI, it seemed to overlap to the previous increase independently of the target jump because it also occurred in the direct reach trials. After TS, the temporal evolution of NV followed that observed during unperturbed reaches. When the NV was aligned to the movement onset, a similar pattern emerged. Therefore, all three areas under study presented a similar pattern of the temporal evolution of NV as if subtending a common process across parieto-frontal areas. However, a difference emerged on the timing and the amount of change of NV.

Neural variability at the time of change of hand trajectory

A crucial event of correction trials is the moment when the hand switches its movement direction to update its trajectory and move toward the new target location. The time of hand switch generally occurs with a variable latency after the presentation of the second target. From the continuous monitoring of the hand path in 3D, the exact time of hand switch was determined (Archambault et al., 2009, 2011) and the evolving NV was aligned to it (Fig. 3D) to study how this behavioral event was reflected in the pattern of NV across areas. In PMd, a continuous decrease of NV was observed, starting after the presentation of the second target and lasting until the hand changed movement direction (HS). This motor update resulted in a brief interruption of a further decline that persisted until the end of the movement, as observed in the direct reaches. The NV decrease was not interrupted by the onset of hand movement to the first target, suggesting that corrective signals about the update of hand movement direction, but not the movement initiation itself (Fig. 3D), slightly perturbs the natural evolution of NV in PMd, the activity of which reaches its optimal state (i.e., the minimum in neural variability) at the end of MT. In motor cortex, the alignment of the neural activity to HS showed that, around this time, NV achieved the minimum value, followed by an increase during the remaining part of movement execution (Fig. 3D). This minimum of ∼1.4 is similar in magnitude to that observed at the MT onset (1.7) when aligning MI activity to this event.

Therefore, two different pictures emerged, depending on the alignment, but they are not contradictory. They might simply suggest that movement initiation and its sudden correction are both events that are signaled in MI by optimal patterns of firing rates, with the consequence of a minimization of the neural variability. In PPC, the hand switch briefly interrupted the continuous increase of NV that characterized the entire duration of movement execution. Therefore, in parietal cortex, the presence of a short NV decrease when planning the movement toward a new direction suggests a late signaling of change of hand trajectory.

Pattern of NV associated with slow and fast movement corrections

An interesting question was whether NV reflected the duration of the time required to switch hand movement trajectory. The results (Fig. 4A) show that, in PMd, MI, and PPC, slow corrections were associated with an overall higher level of NV compared with fast ones. Significant changes of NV associated with either fast or slow corrections were observed at different times depending on the population of cells considered. The NV in slow trials was significantly higher during the time elapsing from the presentation of the first and the second target (ISI) in premotor cortex and just before movement onset in MI and PPC (Fig. 4A). We evaluated the mean differences during the three behavioral epochs: the ISI, TS-MTon, and MTon-HS. In PMd, the strongest difference, with higher values of NV associated with slow movement corrections, was observed earlier in time with respect to MI and PPC (Fig. 4B) during the first part of the RT (ISI) corresponding to the time elapsing from the first target presentation (Ton) to the change of target location (TS). In MI and PPC, the highest differences (Fig. 4B) were in both cases observed in proximity to the movement initiation (late RT), with a clear enhancement of NV time locked to the target jump for slow correction trials. The difference of NV between slow and fast corrections, the mean of which was calculated during each of the three epochs reported above, changed significantly (Kruskal–Wallis test, p < 0.001) across time in all the three areas.

Figure 4.

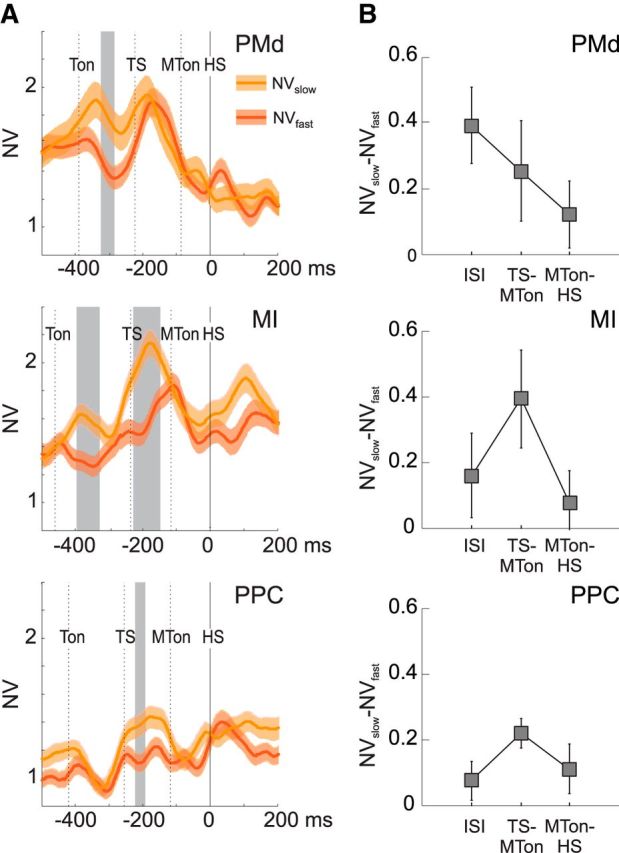
Neural variability associated with slow and fast corrections. A, Comparison of NV (mean ± SE) computed for fast (NV_fast; red) and slow (NV_slow; orange) corrective movements. Fast/slow corrective trials are defined as those with a short/long time of hand switch (see Materials and Methods). Time intervals with significant differences between NV_slow(t) and NV_fast(t) (t test; p < 0.05) are reported in gray shading. The analysis is performed on sets of cells (41 in PMd, 54 in MI, 42 in PPC) selected on the basis of their directional modulation in the CorR task (see Materials and Methods); mean and SE are computed across cells. The temporal axis is aligned to the time of switch of hand trajectory (HS; 0 ms). The dashed vertical lines indicate the mean times (across all recording sessions) relative to Ton, TS, and MTon. B, Mean values (± SD) of the differences NV_slow(t) − NV_fast(t), averaged across time bins, in the three consecutive behavioral epochs ISI, TS-MTon, and MTon-HS.

Influence of perturbation on NV: differences between DirR and CorR trials across areas

To assess significant differences of NV during corrected reaches compared with direct reaches, we computed their difference in time d(t) (Fig. 5, gray line), aiming at detecting the times in which d(t) was statistically significant with respect to measurement-related fluctuations of d(t) observed in epochs that were behaviorally identical (see Materials and Methods). This analysis was performed separately for PMd, MI, and PPC by aligning the neural activity at the moment of the first target presentation. In all the three areas, we observed that the presentation of the second target elicited a significant increase of NV with respect to that associated with the direct reaches, followed by a drop-off. In PMd and MI, this enhancement occurred ∼50 ms earlier than in PPC. In all three areas, the enhancement accounted for the ∼30% variability measured during the direct reaches.

Figure 5.

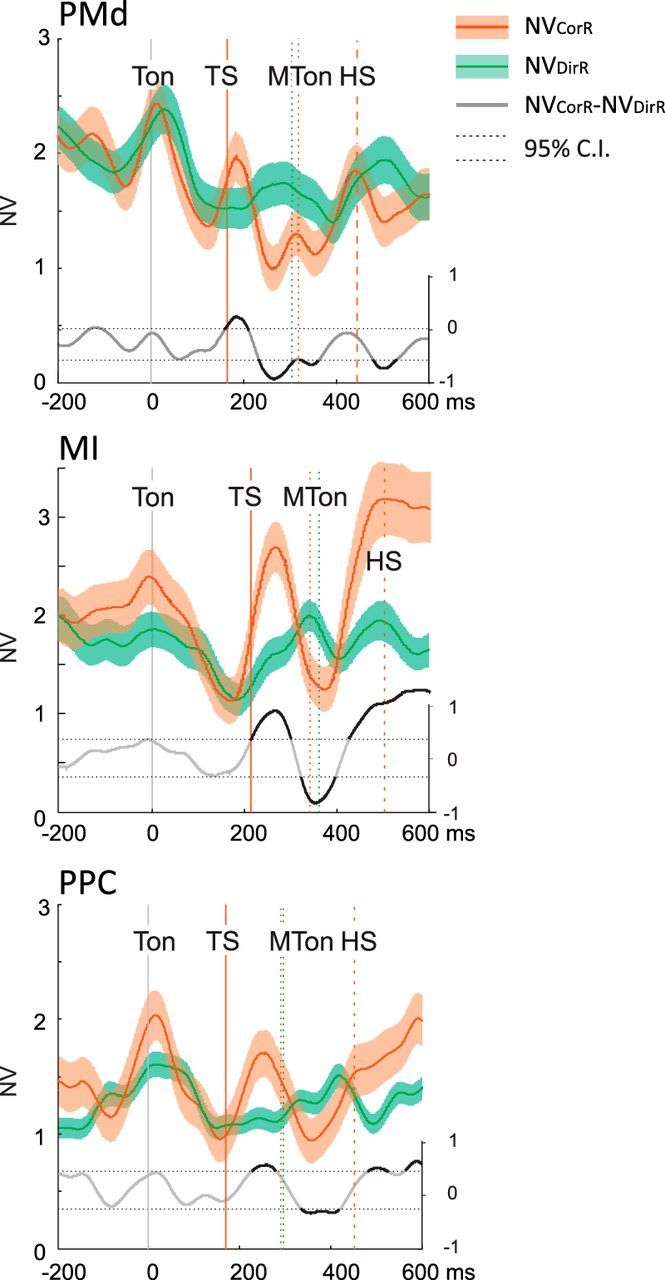
Direct comparison of NV (mean ± SE) computed during DirR (green) and CorR trials (red) and relative difference d(t) = NV_CorR(t) − NV_DirR(t) (gray curve). Time intervals corresponding to significant difference (see Materials and Methods) between NV_CorR and NV_DirR are highlighted in black on the d(t) curve. To compare curves aligned to a common event (Ton; 0 ms) and obtained from neural activities that were identical before the TS, NV_DirR was evaluated from neural activity at the anti-preferred direction (anti-PD) of each cell; NV_CorR was evaluated from neural activity of movements directed first to the anti-PD and then to PD of each cell. The vertical lines indicate the mean times of main behavioral events relative to CorR (red) and DirR (green) task. SE is computed across the number of cells (see Materials and Methods). Labels are as in Figure 4.

Modulation of NV associated with different phases of movement planning

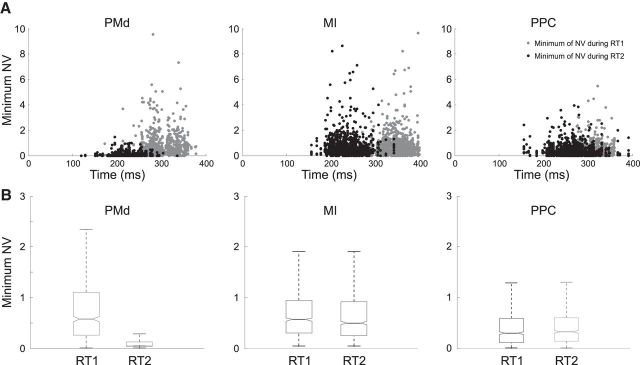
In both monkeys, the RT to the first target was significantly (paired t test, p < 0.001) longer than that to the second target presentation. This difference between mean RT values was 79 ms for behavioral sessions during recording in PMd, 109 ms during recording in MI, and 39 ms during recording in PPC. The question then arises as to whether this was related to a different modulation in amplitude of NV in the two behavioral epochs and, if so, if this difference could be detected in all the cortical areas studied. Figure 6A shows, for each cortical area, the minimum values attained by neural variability for each neuron and a given movement in one direction as function of the mean RT₁ (gray dots) and RT₂ (black dots). The means of these NV values are plotted in Figure 6B for the two phases of movement planning (RT₁ and RT₂). In PMd, minimum NV values were significantly lower (t test, p < 0.001) when computed during RT₂ with respect to those calculated during RT₁. This association of values attained by NV with different phase of movement planning was not found in MI and PPC, as revealed by the statistical comparison of the means of the minimum NV associated with the two types of RTs measured for the activity recorded in the two areas (p = 0.52 for MI ; p = 0.33 for PPC).

Figure 6.

Values of neural variability for different phases of movement planning. A, Minimum values attained by NV when recording the activity during CorR trials in the three areas versus different values of RT₁ (gray dots) and RT₂ (black dots) measured for each cell in a given movement direction (N × 8, total number of data points, where N is the total number of cells). B, Boxplots of NV values plotted in A for the two phases of movement planning (RT₁ and RT₂).

Discussion

This study was devoted to the modulation of neural variability in premotor, motor, and superior parietal cortex during change of motor intention. These areas are considered as crucial nodes in the streamline for the composition and correction of reaches to visual targets (Archambault et al., 2009, 2011). In monkeys, reversible inactivation of superior parietal cortex impairs reach correction (Battaglia-Mayer et al., 2013), as parietal lesions do in humans (Gréa et al., 2002; see Battaglia-Mayer et al., 2014; Caminiti et al., 2015).

Neural variability associated with unperturbed reaching movement across parieto-frontal areas

In all three areas studied, after the first target presentation, a significant decline of NV was observed, which was stronger in magnitude in PMd and MI than in PPC. It first occurred in PMd (78 ms), then in MI (87 ms), and finally in PPC (93 ms) and lasted during motor preparation in both frontal and parietal areas. This decay was more profound in MI and in PMd than in PPC.

These results extend to MI and PPC what was shown previously for PMd (Churchland et al., 2006); that is, a decline of NV predicts the process of target localization and movement onset. The prolonged decline during movement execution in PMd seems in conflict with the hypothesis that movement planning is complete when NV attains a minimum, as in the Churchland et al. (2006) studies. This conflict is only apparent if one considers that we used a reaction time task, while they used an instructed delay paradigm.

The development of NV in different task events suggests that, in general, the increase of the NV is related to the decrease of firing rate only within specific time windows that depend on the area considered. In PMd, this relation was observed within a 150 ms window after target presentation; in MI and PPC, within 170 ms before the hand movement onset.

Neural variability associated with change of motor plan

During corrected reaches, the original motor plan was updated as a consequence of the presentation of the second target during the hand RT to the first one. This evoked first an increase and then a decrease of NV in PMd, PPC, and MI. In the latter, the increase occurred just before the presentation of the second target. This earlier increment of variability in MI was also observed in the late phase of the RT of direct reaches and was therefore independent of the second target presentation. This suggests that visual signals about target location modulate NV for a shorter time in MI compared with PMd and PPC, probably because of the paucity and modest influence of visual signals on motor cortex.

In PMd, the decrease of NV started shortly before movement onset and lasted throughout MT, as was also observed in MI. In MI, however, the decline occurred entirely during RT. In PPC, NV declined for only a short time before movement onset. This suggests that, in the time window before the change of movement direction, the decline of NV was earlier and more profound in MI than in PMd and PPC.

The decrease of NV occurring before the onset of movement could be due either to the second target presentation or to the onset of reach correction. In PMd, it could reflect the process of updating hand trajectory, both in terms of suppressing the old motor plan (Archambault et al., 2009, 2011; Mirabella et al., 2011; Marcos et al., 2013; Mattia et al., 2013) and composing a new one. This interpretation is strengthened by the evolution in time of the population firing activity that was highest after second target presentation and decreased after MT onset. The decline of NV observed before the switch of hand trajectory points to the same conclusion. In MI, the decline of NV after the presentation of second target might primarily reflect the composition of the new motor command, with MI being more removed than PPC and PMd from the process of coordinate transformation and, at the same time, directly related to the motor output. It can be concluded that the temporal evolution of NV explains the events spanning the time between the change of target location and the composition of a new motor plan.

After the presentation of the second target, the hand switched movement direction, thus updating its trajectory. Interestingly, the decline of NV classically associated with motor preparation was not interrupted by the onset of hand movement to the first target, suggesting that the same hand movement influenced the temporal evolution of NV in a different fashion, depending on when it occurred: after the first or after the second target presentation. Therefore, neural variability is modulated in a task-dependent fashion because it decreases when a target calls for a direct reach, whereas it increases and then decreases when it calls for the suppression of an ongoing plan and the formation of a new one. In MI, a long-lasting decline of NV occurred before the onset of hand movement and continued until the change of movement trajectory, after which it started to increase. In PPC, instead, a continuous increase of NV starting after MT was interrupted by the change of hand trajectory. The modulation of neural variability relative to the time of switch of hand trajectory shows that this event is clearly signaled in the parieto-frontal system, although in a different fashion depending on the area considered.

NV associated with slow and fast corrections

An interesting question is whether NV reflects the time required to switch hand movement trajectory. Slow corrections were associated with an overall higher level of modulation of NV compared with fast corrections. In PMd, NV associated with slow corrections attained the highest values after the first target presentation, although a second increase was time locked to the second target onset. In MI and PPC, the highest difference of NV between fast and slow corrections occurred later in time, always before movement onset but after the second target presentation.

We also studied the relationship between NV and the length of RTs taken to initiate the first reach (RT₁) or to correct it (RT₂). We hypothesized that the longer RT to the first than that to the second target was dependent on a different modulation of NV during different phases of movement planning. Therefore, we postulated a higher level of neural noise before movement initiation, as opposed to a reduction of NV during movement execution, when the motor system attains its optimal subspace to achieve its goal successfully (Churchland et al., 2006). We found that the minimum of NV was indeed observed during the RT to the second target; that is, during movement execution. This was only true for PMd, confirming its critical role in prompting update of movement plans (Battaglia-Mayer et al., 2014).

This relation between neural variability and RT is similar to that reported by Churchland et al. (2006), who showed that, in PMd, fast hand RTs are associated with lower levels of neural variability (see also Marcos et al., 2013). This observation offers a neural underpinning to the phenomenon that movement planning is faster when the selected effector is already in motion.

The dependence of NV from the motor set can be discussed within the frame proposed by Schölvinck et al. (2015) that, in sensory systems, global fluctuation of activity, intended as cortical states (Harris and Thiele, 2011), subtend the modulation of NV. During the different phases of the task used in our study, the difference in NV modulation across areas could reflect different cortical desynchronized states, which not only are typical of alert, behaving animals (Poulet and Petersen, 2008), but also favor the representation of events that extend (Pachitariu et al., 2015; Marguet and Harris, 2011; Duarte and Morrison, 2014) and mostly change over time, such as those of our task.

In conclusion, the analysis of neural variability associated with the composition and update of motor intention remains a good descriptor of motor behavior, not only during simple unperturbed reaches, but also when a perturbation of the action space requires the change of an original motor intention. Therefore, the study of NV represents a useful tool for the analysis of the neural code underlying cognitive-motor behavior under different states of the motor system.

A final interesting question is whether there exists an interaction between NV and movement kinematics, such as direction of reach, especially in areas with anisotropic distribution of preferred directions, such as MI (Naselaris et al., 2006a, 2006b) and inferior parietal cortex (Battaglia-Mayer et al., 2005). The NV decline is a phenomenon observed independently from cell firing frequency because it also emerges at low rates, such as those observed at the cell anti-preferred direction (Churchland et al., 2010 and the present study). However, the profound influence of reach direction on cell firing throughout the parieto-frontal networks suggests that movement direction might modulate neural variability as well. This will be the subject of a future study.