Congruence of Inherent and Acquired Values Facilitates Reward-Based Decision-Making

Abstract

Most real-life cues exhibit certain inherent values that may interfere with or facilitate the acquisition of new expected values during associative learning. In particular, when inherent and acquired values are congruent, learning may progress more rapidly. Here we investigated such an influence through a 2 × 2 factorial design, using attractiveness (high/low) of the facial picture as a proxy for the inherent value of the cue and its reward probability (high/low) as a surrogate for the acquired value. Each picture was paired with a monetary win or loss either congruently or incongruently. Behavioral results from 32 human participants indicated both faster response time and faster learning rate for value-congruent cue–outcome pairings. Model-based fMRI analysis revealed a fractionation of reinforcement learning (RL) signals in the ventral striatum, including a strong and novel correlation between the cue-specific decaying learning rate and BOLD activity in the ventral caudate. Additionally, we detected a functional link between neural signals of both learning rate and reward prediction error in the ventral striatum, and the signal of expected value in the ventromedial prefrontal cortex, showing a novel confirmation of the mathematical RL model via functional connectivity.

SIGNIFICANCE STATEMENT Most real-world decisions require the integration of inherent value and sensitivity to outcomes to facilitate adaptive learning. Inherent value is drawing increasing interest from decision scientists because it influences decisions in contexts ranging from advertising to investing. This study provides novel insight into how inherent value influences the acquisition of new expected value during associative learning. Specifically, we find that the congruence between the inherent value and the acquired reward influences the neural coding of learning rate. We also show for the first time that neuroimaging signals coding the learning rate, prediction error, and acquired value follow the multiplicative Rescorla–Wagner learning rule, a finding predicted by reinforcement learning theory.

Introduction

Value-based decision-making requires accurately representing and updating the adaptive value of a given choice among a range of options (Montague et al., 2006; Rangel et al., 2008). Yet most decisions take place in contexts already saturated with value well before an organism has any experiences associating a given object with an explicit reward. Naturally occurring stimuli generally are not valuationally neutral, but carry inherent values that are important for understanding subsequent learning (Friston et al., 1994). This is seen, for example, when marketing campaigns pair new products with attractive or respected spokespersons. Inherent values also influence adaptive decision-making in socially significant areas such as financial markets. Western business students perceive Western assets from their own home countries to be less risky investments, compared with assets from other Western countries (Weber et al., 2005). Studies of classic conditioning also reveal influences of inherent valuation, as when monkeys and phobic humans more readily associate images of snakes and spiders with negative feedback, compared with other images (Ohman and Mineka, 2001). Understanding how the brain processes the interaction of inherent and acquired value is critical for understanding the evolutionary biology, the development, and the societally significant manifestations and limitations of adaptive behavior.

In reinforcement learning (RL; Sutton and Barto, 1998), the neural encoding of acquired value and valuational updating are known to involve the ventromedial prefrontal cortex (vmPFC) and the ventral striatum (vStr), respectively (Seymour et al., 2005; Hampton et al., 2006; Gläscher et al., 2009). Updating the acquired expected value (EV) depends in part on the learning rate (LR), which modulates the influence of the reward prediction error (RPE; see Eq. 1 in Materials and Methods). Whether any of these signals are directly affected by inherent value, as suggested by previous models (Friston et al., 1994), is as yet unknown, since investigations of RL signals in the brain have relied on cues lacking inherent values (Bray et al., 2007, 2008; Gläscher et al., 2009).

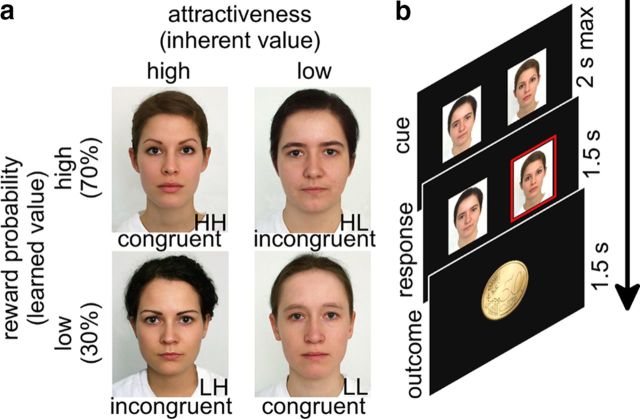
Here, we investigated the effect of the inherent value of facial attractiveness on the neural encoding of acquired value for facial images. Attractive faces consistently elicit higher preference ratings (Langlois et al., 2000) and greater motivation (Aharon et al., 2001). Furthermore, in heterosexual participants, attractive faces of the opposite gender activate parts of the reward network, including the vStr (Bray and O'Doherty, 2007; Cloutier et al., 2008). These findings suggest that attractive faces have inherent values and are therefore well suited to investigate the effects of inherent value on learning. We manipulated the congruence of inherent and acquired value during RL (Fig. 1a). Value congruence means that the inherent value of a given option/stimulus has the same valence as the reward that is likely to result from selecting that option. Incongruence means opposing valences. A modulatory effect of value congruence on decision-making predicts that associative learning with a reward will be facilitated by a positive inherent value of a stimulus cue (e.g., an attractive face), and associative learning with a punishment will benefit from a negative inherent value. In these cases, LRs should be larger. On the other hand, value incongruence between the inherent value of a cue and the outcome would impede acquiring new values, resulting in smaller LRs.

Figure 1.

Experimental task and design. a, Experimental design matrix: HH and LL have congruent values, while HL and LH have incongruent values. b, Trial sequence: (1) two pictures are shown; (2) the subject selects a picture; and (3) depending on the reward probability of the picture, the result is either a win or a loss.

We tested whether inherent value modified neural representations in a probabilistic decision-making task with stable reward contingencies (Fig. 1). We modeled participant choices using the Rescorla–Wagner (RW) learning rule (Eq. 1) and found that inherent value promoted faster initial learning when it was congruent with acquired value. Furthermore, we identified activities in the ventral caudate that tracked this dynamic LR. Using a connectivity analysis seeded with the neural signals from these regions in vStr, we demonstrated for the first time that a multiplicative interaction of the BOLD signals for RPE and LR correlated with activation in the vmPFC partially overlapping with the EV signal, just as the RW model equation prescribed.

Materials and Methods

Participants.

Thirty-two participants (mean age, 25.1 ± 4 years; age range, 19–34 years; 16 females) were recruited from the student population at the University of Hamburg. They were compensated with a base payment of €20 plus the net amount of coins (each coin paid 5 cents) they had won during the experiment. This study was approved by the Ethics Committee of the Medical Association of Hamburg (PV 3661).

Experimental design and task.

Two sets of cues (four male and four female faces, all neutral) drawing from a large study investigating facial features contributing to attractiveness (Braun et al., 2001) were used in the experiment. Within each set, two cues were attractive and two were unattractive (mean normative ratings in Table 1). Attractive and unattractive faces were systematically associated with high (70%) or low (30%) reward probability, thus forming a 2 × 2 factorial design, with attractiveness and reward probability as the two main factors (Fig. 1a). Participants viewed only faces of the opposite gender. We considered the facial attractiveness to be a valid measure for the inherent value since in the pre-experimental rating task of the pictures, all participants showed similar preferences for the attractive pictures over the unattractive ones (Table 1). A third, orthogonal factor (value congruence) is embedded in the 2 × 2 design, and its levels are marked in the pictures (Fig. 1a).

Table 1.

Facial cue ratings from the Braun study of 116 participants and the current study of 32 participants, normalized scale (0–1)

	Cue	Braun et al.		Participants′ ratings
		Mean	SD	Mean	SD
Female	HH	0.67	0.22	0.63	0.22
	HL	0.21	0.14	0.18	0.12
	LH	0.78	0.18	0.49	0.25
	LL	0.25	0.16	0.31	0.20
Male	HH	0.76	0.17	0.62	0.23
	HL	0.27	0.15	0.13	0.12
	LH	0.76	0.19	0.55	0.20
	LL	0.31	0.18	0.18	0.14

Participants were instructed to learn the probabilistic cue–reward associations (face pictures). Each trial started with two cues presented side by side on the screen (Fig. 1b). Participants had a maximum of 2 s to select one of the cues by pressing a left or right button on the keypad with the right index or middle finger. When participants failed to select a response, the computer randomly picked a cue, and that particular trial was marked as “no-response.” The chosen cue (either by the participant or the computer) was then enclosed in a red box and displayed for 1.5 s, after which the screen went blank for a variable delay of 3–7 s. Following the delay, participants saw the display of the outcome for 1.5 s, which consisted of either a coin (indicating a win) or a coin with a red “X” on top (indicating a loss). The trial then ended with another variable blank delay for 2–5 s. Each of the six pairs of cues was presented 24 times, for a total of 144 trials per participant, in bins of 12 trials, with each bin showing each pair twice. This procedure ensured balanced and individual event trains for all participants.

Statistical contrast for modulatory effect of value congruence.

Our experimental design involved the following two factors: facial attractiveness (high vs low, proxy for inherent value) and reward probability (70% vs 30%, proxy for acquired value). The factorial table (Table 2) visualizes the design.

Table 2.

Factorial design

	Attractiveness
	High	Low
Reward probability
70%	HH congruent	HL incongruent
30%	LH incongruent	LL congruent

The two main effects (MEs) and the interaction of this classic 2 × 2 factorial design are computed as follows:

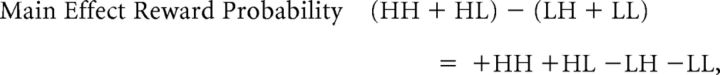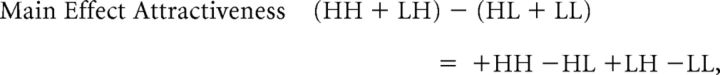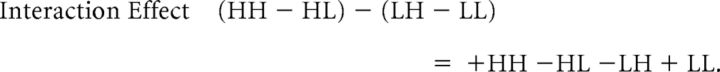Valence-specific modulatory effects of value congruence exaggerate the choice probabilities implied by the reward probability, as follows: HH (high reward probability, high attractiveness) is chosen most frequently, and LL (low reward, low attractiveness) is chosen least frequently. Statistically, this is expressed by a larger difference between HH and LL compared with the difference between HL (high reward, low attractiveness) and LH (low reward, high attractiveness): (HH − LL) − (HL − LH) = +HH −HL +LH −LL. As can be seen in Table 2 above, this corresponds to a main effect of attractiveness. Therefore, to statistically assess our main research question (does value congruence affect the learning of new reward-based EVs?), we examined the main effect of attractiveness in combination with the main effect of reward probability, which assesses whether the participants have learned the task at all.

Computational modeling.

We used classic RL (Rescorla and Wagner, 1972; Sutton and Barto, 1998) as the base model for the subject's choice behavior. At every trial t, each cue was represented by an EV (V_t). The EV of the subject's chosen cue was then updated in proportion to the RPE (the difference between the actual reward R_t and V_t) according to Equation 1, while the values of all the other cues (i.e., nonchosen, computer selected, or not shown) remained the same (i.e., V_t+1 = V_t).

Cue selection was then modeled as a softmax action probability (Eq. 2), where the probability of choosing cue j is dependent on the values of all the cues shown (x) and the softmax temperature parameter (τ), as follows:

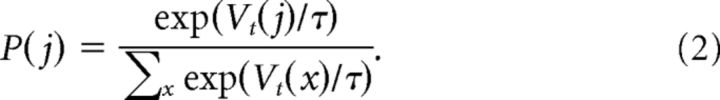Based on this core RL model, we implemented several variants using different combinations of the initial cue values (V₀) and the LRs (α) from Equation 1 as free parameters.

In our models, we tested three basic factors (attractiveness, reward probability, and value congruence) for their influences on learning, and we also fitted initial cue value as a free parameter so that we could capture an attractiveness bias at the beginning of the task. Model comparisons (Table 3) indicated that models having initial values (V₀) for attractiveness as two free parameters were better fits to the data than their counterparts without those initial value parameters. Moreover, models with a single LR for all of the cues (i.e., attractive and unattractive pictures), even with the initial values incorporating attractiveness, performed worse than models with 2 LRs in each of the respective categories. Among the 2-LR models, the congruence model performed best, confirming our hypothesis that value congruence influences the speed of learning. All of this demonstrated that participants appeared to group stimuli according to value congruency and then learn the cue values in each factor level (congruent and incongruent) at the same speed.

Table 3.

DIC for all model variants

	Model variant	Number of free parameters	DIC
2 LR models, cue based	2 constant LR (a/ua cues)	3	4162.4
	2 constant LR (c/ic cues)	3	4171.8
	2 constant LR (high/low rp cues)	3	4293.4
	2 constant LR (a/ua cues) + 2 iv(a/ua cues)	5	3854.1
	2 constant LR (c/ic cues) + 2 iv(a/ua cues)	5	3886.0
	2 constant LR (high/low rp cues) + 2 iv(a/ua cues)	5	4036.3
	2 decaying (2 α0, 2b) LR (a/ua cues)	5	4053.2
	2 decaying (2 α0, 1b) LR (a/ua cues)	4	4071.5
	2 decaying (2 α0, 2b) LR (c/ic cues)	5	3956.5
	2 decaying (2 α0, 1b) LR (c/ic cues)	4	4018.1
	2 decaying (2 α0, 2b) LR (high/low rp cues)	5	4069.1
	2 decaying (2 α0, 1b) LR (high/low rp cues)	4	4118.1
	2 decaying (2 α0, 2b) LR (a/ua cues) + 2 iv(a/ua cues)	7	3824.1
	2 decaying (2 α0, 1b) LR (a/ua cues) + 2 iv(a/ua cues)	6	3834.1
	2 decaying (2 α0, 2b) LR (c/ic cues) + 2 iv(a/ua cues)	7	3810.8
	2 decaying (2 α0, 1b) LR (c/ic cues) + 2 iv(a/ua cues)	6	3825.2
	2 decaying (2 α0, 2b) LR (high/low rp cues) + 2 iv(a/ua cues)	7	3977.9
	2 decaying (2 α0, 1b) LR (high/low rp cues) + 2 iv(a/ua cues)	6	3958.3
2 LR models, outcome based	2 constant LR (c/ic cues)	3	4191.8
	2 constant LR (high/low rp cues)	3	4119.4
	2 constant LR (c/ic cues) + 2 iv (a/ua cues)	5	3874.6
	2 constant LR (high/low rp cues) + 2 iv (a/ua cues)	5	4034.4
	2 decaying LR (c/ic cues)	5	3902.5
	2 decaying LR (high/low rp cues)	5	4063.5
	2 decaying LR (c/ic cues) + 2 iv (a/ua cues)	7	3838.3
	2 decaying LR (high/low rp cues) + 2 iv (a/ua cues)	7	3929.1
1 LR models	1 constant LR	2	4450.7
	1 constant LR + 2 iv (a/ua cues)	4	4059.6
	1 decaying LR	3	4283.2
	1 decaying LR + 2 iv (a/ua cues)	5	4030.9
Bias models	ϵ -attractiveness-bias	1	5750.0
	Attractiveness-bonus, 1 constant LR	3	4302.3
	Attractiveness-bonus, 1 decaying LR	4	4069.2
	Attractiveness-bonus, 2 decaying LR (a/ua cues)	6	3913.4
	Attractiveness-bonus, 2 decaying LR (c/ic cues)	6	3882.0
	Attractiveness-bonus, 2 decaying LR (high/low rp cues)	6	4008.1
	Association-bias, observed outcome, 2 decaying LR (a/ua cues) + 2 iv(a/ua cues)	7	4154.0
	Association-bias, observed outcome, 2 decaying LR (c/ic cues) + 2 iv(a/ua cues)	7	4048.4
	Association-bias, observed outcome, 2 decaying LR (high/low rp cues) + 2 iv(a/ua cues)	7	4132.2
	Association-bias, observed outcome, 1 decaying LR + 2 iv(a/ua cues)	5	4388.8
	Association-bias, opposite outcome, 2 decaying LR (a/ua cues) + 2 iv(a/ua cues)	7	3824.3
	Association-bias, opposite outcome, 2 decaying LR (c/ic cues) + 2 iv(a/ua cues)	7	3820.1
	Association-bias, opposite outcome, 2 decaying LR (high/low rp cues) + 2 iv(a/ua cues)	7	3886.4
	Association-bias, opposite outcome, 1 decaying LR + 2 iv(a/ua cues)	5	4075.1

a, Attractive; ua, unattractive; c, congruent; ic, incongruent; rp, reward probability; iv, initial value.

We investigated another dimension in our models by parameterizing the LR as an exponentially decaying function of the number of times (k) the cues associated with that particular LR was chosen (Eq. 3; Sutton and Barto, 1998), where α₀ (range, 0–1) is the initial LR and b (range, 0–∞) is the decay constant.

A decaying LR effectively tunes down the influence of the RPE on the value update as the experiment progresses and the subject learns about the reward contingencies. In experiments with stable contingencies such as the present one, this makes sense because after the EVs have been learned, the remaining RPEs represent noise induced by the probabilistic nature of the task, but they should not play an influential role in the value update anymore. Indeed, model comparisons showed that all models with the decaying LRs fit the data better than their counterparts with constant LRs.

We also examined the alternative scenario where congruency and probability models were based on the actual outcomes rather than the predesigned associations with the cues. The reason for this is that the participants did not know the reward probability associated with the cue beforehand and could only infer the probability and thus congruency from the outcome of the trial. While this idea had certain merit, we believed that as the observed outcome frequencies approached the preassigned reward probabilities over the course of the experiment, outcome-based models would quickly converge to cue-based models. Furthermore, outcome-based models would introduce unrealistic volatilities in the LR, where the same cue could jump from one LR to another within adjacent trials. In fact, results from model fitting did not indicate any significant advantages of the outcome-based models over the cue-based models; therefore, we discarded that series of models from further analyses.

We also tested a variety of alternative accounts. To rule out that a simple and general choice bias toward attractive faces was responsible for the choice data, we implemented an ε-attractiveness-bias model, which chooses the attractive over the unattractive faces with a certain probability, ε, and randomly selects a cue when both are attractive or unattractive, regardless of the current EV. Additionally, in the attractiveness bonus model, attractive faces add a bonus to the current EV in the softmax choice function. This model examines the possibility that the inherent value of the face exerts a direct bias on choice probabilities. Finally, attractive faces may simply be more associable with a reward than unattractive faces. This could result in reward associations with attractive faces, even though the unattractive face was chosen on a particular trial. We have implemented this association bias model by updating both the chosen and the unchosen values with our basic RW update rule.

Altogether, these combinations of LRs and initial cue values produced a total of 44 model variations (Table 3). The congruency model with two decaying LRs and two initial cue values was the best model according to the deviance information criteria (DIC; Spiegelhalter et al., 2002), suggesting that congruency of the cue–outcome associations as well as the attractiveness of the cue influenced the participants' learning. This model is depicted graphically in Figure 2. The best fitting parameters are shown in Table 4.

Figure 2.

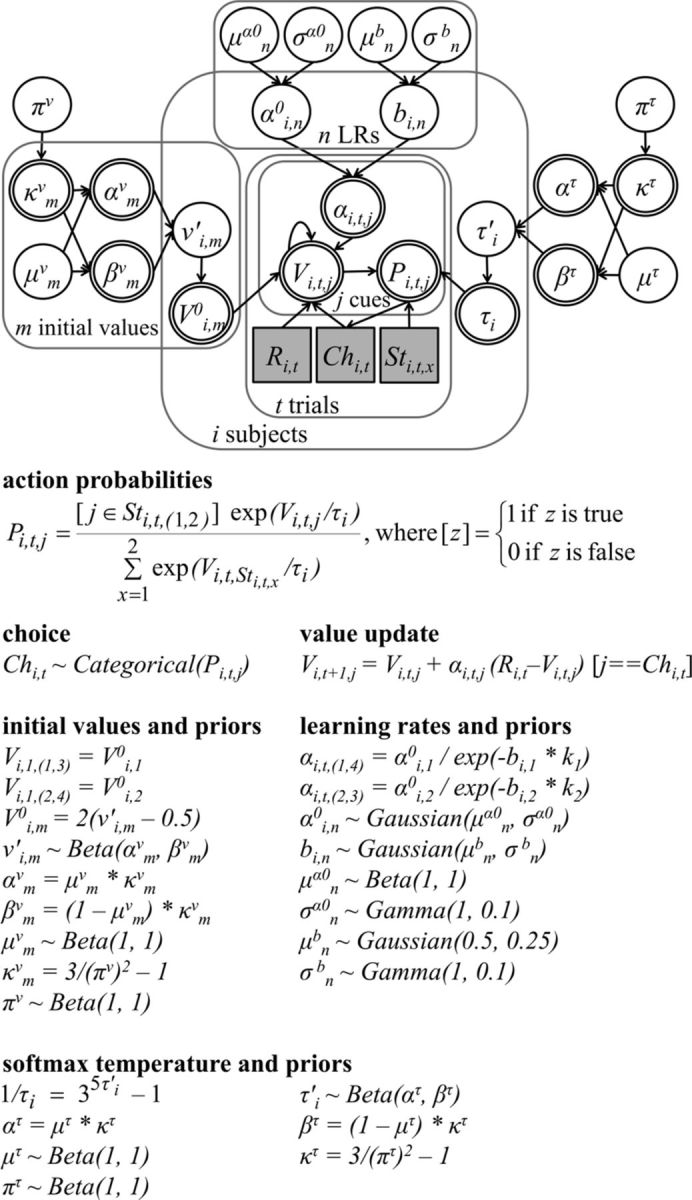
Graphical depiction of the best-fitting model with the priors. Plates represent iterations. Arrows indicate dependencies among the nodes. Square and circular nodes are discrete and continuous variables, respectively. Double-bordered nodes are deterministic, while single ones are stochastic. Observed variables (i.e., data) are gray, and unobserved variables are white. Key variables are abbreviated as follows (subscripts represent iterations): St_i,t,x, shown cues; R_i,t, reward; Ch_i,t, choice; P_i,t,j, action probability; V_i,t,j, EV; α_i,t,j, LR; V_i,m⁰, initial value; τ_i, softmax temperature; α_i,n⁰, initial LR; b_i,n, LR decay constant. The rest are reparameterizations and hyper-priors.

Table 4.

Optimal model parameters for best-fitting model, group posterior mean, and 95% highest posterior density (bottom, top)

Model parameters	Female	Male	All
Initial LR (α0)
Congruent cues	0.484 (0.001, 0.946)	0.341 (0.001, 0.910)	0.125 (0.001, 0.621)
Incongruent cues	0.211 (0.001, 0.815)	0.071 (0.001, 0.150)	0.053 (0.001, 0.120)
LR exponential decay constant (b)
Congruent cues	0.067 (0.001, 0.152)	0.063 (0.001, 0.155)	0.040 (0.001, 0.093)
Incongruent cues	0.075 (0.001, 0.213)	0.056 (0.001, 0.147)	0.028 (0.001, 0.067)
Softmax inverse temperature (1/τ)	3.178 (1.900, 4.613)	4.712 (2.762, 7.046)	4.560 (2.931, 6.343)
Initial value (V0)
Attractive cues	−0.226 (−0.533, 0.081)	−0.627 (−0.876, −0.371)	−0.431 (−0.623, −0.254)
Unattractive cues	−0.066 (−0.486, 0.332)	−0.794 (−0.998, −0.546)	−0.478 (−0.706, −0.266)

Model fitting and model selection.

Model fitting and parameter estimation were conducted using hierarchical Bayesian analysis (HBA; Gelman, 2004) by estimating the actual posterior distribution through Bayes rule. We used HBA rather than the more common maximum likelihood estimation (MLE) approach because HBA resulted in better parameter estimation compared with MLE. In fact, for some of the models, MLE failed to produce an estimate while HBA succeeded. The model parameters that were estimated included the LRs, the softmax temperatures, and the initial cue values. In HBA, the parameters of individual participants were drawn from the group-wise distributions. An initial unspecific assumption of the group distributions was supplied in the form of uniform β distributions (priors), and HBA proceeded to estimate the actual posterior distribution through Bayes rule by incorporating the data. Computation of the posterior was performed through the Markov chain Monte Carlo (MCMC) method using the JAGS software (Plummer, 2003) and its runjags R interface. Five MCMC chains were run for 50,000 iterations after 50,000 burn-ins, which resulted in 10,000 posterior samples after a 5-fold thinning. Each estimated parameter was checked for convergence both visually (from the trace plot) and through the Gelman–Rubin test. Models were compared using their DIC, and the one with the lowest DIC was selected as the best model for subsequent analysis.

fMRI data acquisition and analysis.

fMRI data collections were conducted on a Siemens Trio 3 T scanner with a 32-channel head coil. Each brain volume consisted of 42 axial slices (voxel size, 2 × 2 × 2 mm with 1 mm spacing between slices) acquired using a T2*-weighted echoplanar imaging (EPI) protocol (TR, 2510 ms; TE, 25 ms; flip angle, 80°; FOV, 216°) in descending order. Orientation of the slice was tilted at 30° to the anterior commissure-posterior commissure (AC-PC) axis to improve signal quality in the orbitofrontal cortex (Deichmann et al., 2003). Data for each participant were collected in a single session with volumes ranging from 730 to 750, and the first 4 volumes were discarded to obtain a steady-state magnetization. In addition, a gradient echo field map was acquired before EPI scanning to measure the magnetic field inhomogeneity, and a high-resolution anatomical image (voxel size, 1 × 1 × 1 mm) was acquired after the experiment using a T1-weighted MPRAGE protocol.

fMRI data analysis was performed using SPM8 (Wellcome Trust Center for Neuroimaging, University College London, London, UK). After converting the raw DICOM images to NIfTI format, image preprocessing continued with slice timing correction using the middle slice of the volume as the reference. Next a voxel displacement map (VDM) was calculated from the field map to account for the spatial distortion resulting from the magnetic field inhomogeneity (Jezzard and Balaban, 1995; Andersson et al., 2001; Hutton et al., 2002). Incorporating this VDM, the EPI images were then corrected for motion and spatial distortions through realignment and unwarping (Andersson et al., 2001). The participant's anatomical image was manually checked and corrected for the origin by resetting it to the AC-PC. The EPI images were then coregistered to this origin-corrected anatomical image. The anatomical image was then skull stripped and segmented into gray matter, white matter, and CSF, using the “New Segment” tool in SPM8. These gray and white matter images were used with the SPM8 DARTEL toolbox to create individual flow fields as well as a group anatomical template (Ashburner, 2007). The EPI images were then normalized to the MNI space using the respective flow fields through the DARTEL toolbox normalization tool. A Gaussian kernel of 8 mm full-width at half-maximum was used to smooth the EPI images.

We conducted model-based statistical analysis of fMRI data (Gläscher and O'Doherty, 2010), using the parameters from our RL models of behavior to generate the EVs, RPEs, and dynamic LRs on each trial. Our first-level design matrix in SPM8 consisted of a constant term plus the following 16 regressors: 3 experimentally measured regressors represented the onset timing for cue, button press, and outcome; 2 parametric modulators of the cue (LR and EV); 2 parametric modulators of the outcome (reward value and RPE); 3 nuisance regressors accounted for the cue, button press, and outcome onset timing for all of the “no-response” trials; and 6 motion parameters. We avoided the automated orthogonalization in SPM to capture signal variances that were unique to the individual modulators. This proved to be particularly important for RPE and reward outcome signals, as they are known to be correlated in model-based fMRI studies using RL. The resulting β images served in group analyses at the second level, using one-sample, two-tailed t tests for significant effects across the participants, with a threshold of p < 0.05, FWE corrected.

Our a priori predictions, based on previous work on the RPE signal in the lateral putamen (Seymour et al., 2004), on the EV signal in the vmPFC (Wunderlich et al., 2010; McNamee et al., 2013), and on the reward outcome in the ventromedial striatum (Reuter et al., 2005) allowed us to perform small volume corrections using 8 mm search volumes around the peak coordinates in those studies. Activations for which we had no a priori expectations (e.g., for LR) resulted from whole-brain analyses using an FWE-corrected threshold of p < 0.05. The display threshold in the figures was set to 0.001, uncorrected except as noted.

A physiophysiological interaction (PPI) analysis operates on entire time series representing different computational signals. We seeded with the entire BOLD time series from two 6-mm-radius spherical regions of interests (ROIs) in the vStr, centering at the peak coordinates for LR, which was detected at the time of the cue, and RPE, which was detected at the time of the outcome. Although these events are spaced 3 s apart, an LR signal could still be present at the time of the outcome, albeit at a lower threshold, which could then be processed with the RPE to render and update the neural signal. The first-level design matrix included three regressors (two entire BOLD time series from the seed ROIs and their interaction) and a constant term. The first-level interaction regressors were then raised to a second-level t test to establish the group connectivity results. As a control, we also conducted a separate PPI analysis on a set of (task-free) resting-state fMRI data from different subjects using the same vStr ROIs to control for inherent connectivity originating in the vStr.

Results

Inherent value signal

Before the experimental task, participants rated the attractive pictures higher than the unattractive pictures on a normalized Likert scale (Table 1; female faces rated by male participants effect size, 1.446; male faces rated by female participants effect size, 2.368).

Assessment of learning

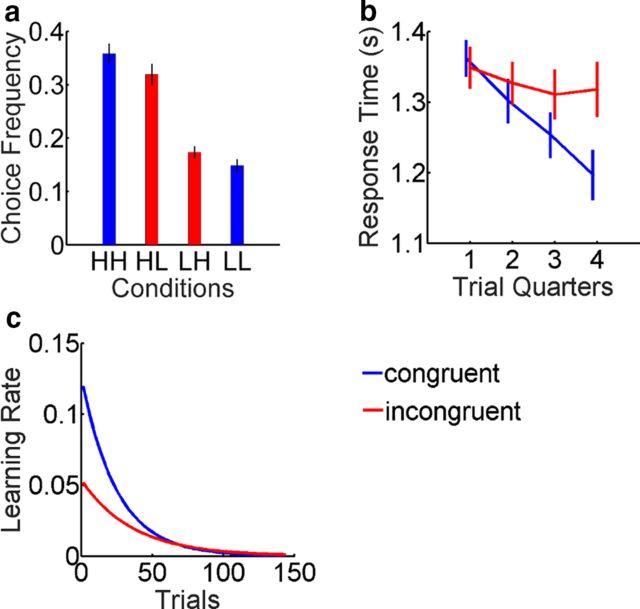
The sole goal of the participant was to maximize the payoff. We therefore tested for the success of learning with the ME of reward probability (high > low), which was highly significant (F_(1,31) = 108.9, p = 1.15 × 10⁻¹¹; Fig. 3a), indicating that participants were able to learn the acquired values.

Figure 3.

Analysis of choice behavior. All error bars indicate the SEM. Blue and red colors indicate value congruence and incongruence, respectively. a, Choice probability (average normalized frequency of cue selections) for all cues. b, Mean response time for all subjects split by value congruence across four trial quarters (36 trials each). c, Dynamic LRs for value-congruent and incongruent cues, based on the posterior mean of the group distribution from which individual offset and slope parameters are sampled (for details, see Materials and Methods).

Modulation of decision-making by inherent values

A modulatory effect of value congruence on decision-making critically depends on the valence of the outcome: positive inherent values will increase the choice probabilities for reward associations, whereas negative inherent values will decrease the choice probabilities for punishment associations. Stated differently, value congruence will exaggerate the choice probabilities implied by the outcome. Statistically, this is tested with an ME of attractiveness (for a derivation, see Materials and Methods). Our participants indeed exhibited such a bias toward the attractive cues (ME attractiveness, F_(1,31) = 4.323, p = 0.046; Fig. 3a).

We also conducted this analysis separately for women and men, finding that both groups showed highly significant MEs of reward probability (men: F_(1,15) = 70.88, p = 4.57 × 10⁻⁰⁷; women: F_(1,15) = 40.9, p = 1.2 × 10⁻⁰⁵), while only men showed a significant ME of attractiveness (men: F_(1,15) = 5.683, p = 0.031; women: F_(1,15) = 0.706, p = 0.414). However, a mixed-effects model testing for the interaction of probability, attractiveness, and gender showed no effect (F_(1,30) = 1.619, p = 0.213). In summary, participants consistently chose the stimulus of high reward probability, indicating that they learned the task. More interestingly, however, men (more so than women) also appeared to take advantage of value congruence by choosing the HH image most frequently and the LL image the least frequently, suggesting that value congruence modulates reward-based learning in a valence-specific way.

To further investigate the role of value congruence on learning over time, we divided the behavioral data according to the congruence of the chosen cue. We first analyzed the reaction times of the participants over the course of the experiment (Fig. 3b), finding that congruent cues resulted in faster responses over the course of the task (congruence × time: F_(3,93) = 4.963, p = 0.003; ME congruence: F_(1,31) = 2.77, p = 0.106; ME time: F_(3,93) = 6.11, p = 0.0008). We again analyzed the response times separately for each gender, finding that men exhibited significant MEs of congruence and time along with a highly significant interaction (congruence × time: F_(3,45) = 6.829, p = 0.0007; congruence: F_(1,15) = 6.189, p = 0.025; time: F_(1,15) = 3.374, p = 0.026), whereas women showed a significant ME of time (F_(1,15) = 3.291, p = 0.029). This finding suggests that the inherent cue value may facilitate the learning of new EVs (particularly in male subjects) if the two are congruent.

RL modeling of learning and choice

To examine the computational processes underlying the subject's decision, we fitted the behavioral data with a series of RL models. Given the probabilistic nature of the task, we decided to use the RW model (Eq. 1) as a template for the different model variants. The RW model provides two mechanisms by which value congruence can influence EV. Either the LRs could differ or the initial EVs of the model (V₀), before any learning, could differ. To test which mechanism is operative, we derived several model variants that differed in the number of LRs and whether the initial values V₀ were estimated as free parameters. All models were fitted using hierarchical Bayesian analysis with Markov chain Monte Carlo sampling techniques (Gelman, 2004), and model selection was performed using DIC.

Our family of models included (1) models that assigned either LRs to the different factor levels, one factor at a time (i.e., two LRs for high and low attractiveness, high and low reward probability, or value-congruent and incongruent stimuli); (2) models with constant versus exponentially decaying LRs across time; (3) models with or without initial cue values, V₀, as free parameters; and (4) models with attractiveness represented as various bias factors. For a detailed account of model design, estimation, and selection, see Materials and Methods.

Among the models we tested (Table 3), we obtained the best fit using two decaying LRs, one for congruent and one for incongruent stimuli, and two free initial values, V₀, one for attractive and one for unattractive images; optimized model parameters are shown in Table 4. Decaying LRs differed between congruent and incongruent stimuli (Fig. 3c).

LR for congruent stimuli was higher at the beginning of the experiment (Fig. 3c; Wilcoxon signed rank test: signed rank = 381, p = 0.028), suggesting that value congruence facilitated more rapid learning early on in the experiment. Although there was no significant difference in the decay constant (signed rank = 331, p = 0.217), the larger initial LR of congruent stimuli implied a faster decay rate (Fig. 3c), since the decay rate at any particular time is the product of the current LR and the decay constant. Initial values, V₀, were also significantly higher for attractive than for unattractive faces (signed rank = 377, p = 0.0341).

Neuroimaging: value congruence and reward probability

A main effect of attractiveness constitutes a test for a valence-specific modulation of value congruence on reward-based learning (see Materials and Methods). This contrast elicited differential activation in the vmPFC (Fig. 4a), which is consistent with other studies on encoding facial attractiveness and the EV of a chosen option (Hampton et al., 2006; Bray and O'Doherty, 2007; Cloutier et al., 2008; Gläscher et al., 2009). This suggests that value congruence modulates reward-based learning of EVs in the vmPFC, which is consistent with our analysis of choice outcomes.

Figure 4.

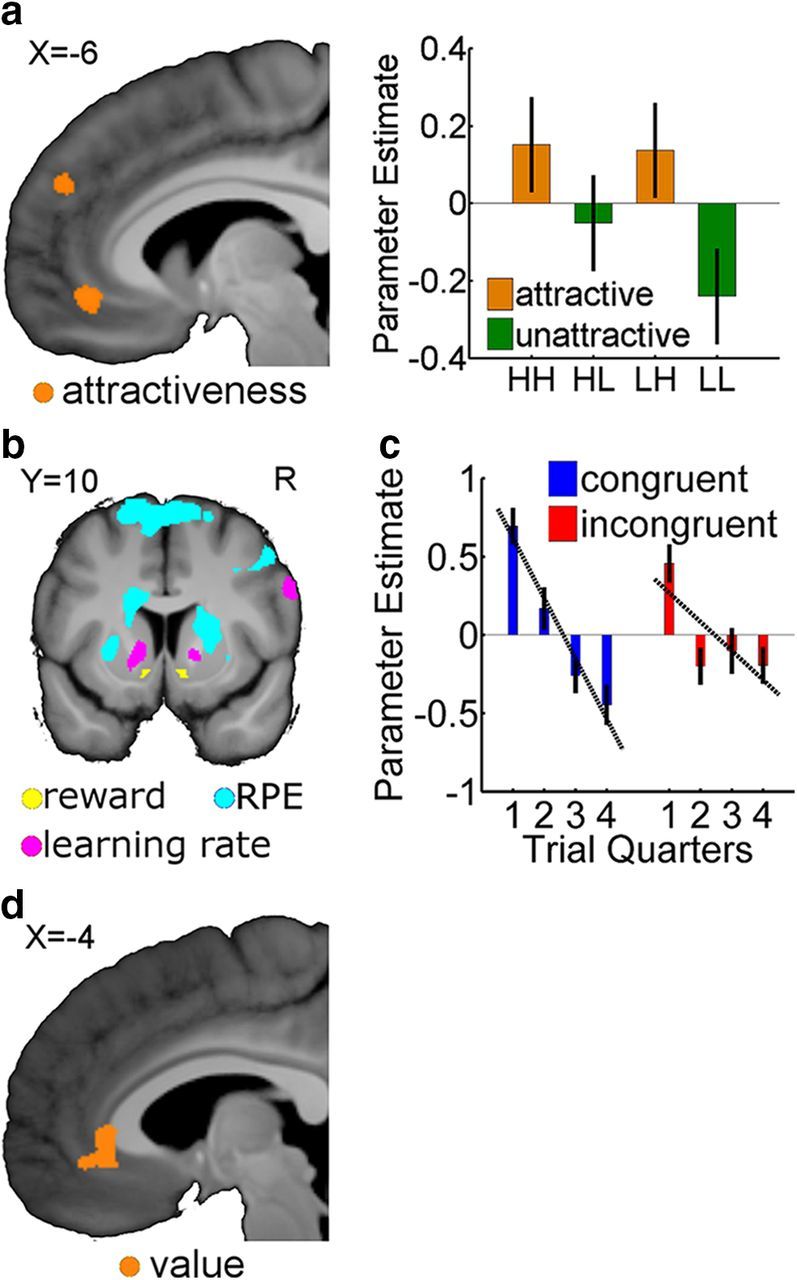
fMRI analysis (display threshold is 0.001 uncorrected except as noted). a, Left, Attractive faces elicited higher differential activation compared with unattractive faces in left vmPFC [peak MNI coordinates (x, y, z) −6, 42, −9; 146 voxels] and in the left rostral cingulate zone (peak MNI coordinates −6, 50, 30; 56 voxels). Right, Parameter estimates in the peak vmPFC voxel from the four constituents showing attractive cues having higher activations than unattractive cues. b, Activations elicited by three parametric modulators. Win trials elicit greater activation (yellow) than Lose trials in bilateral vStr [peak MNI coordinates −12, 6, −12 (20 voxels); 8, 12, −9 (81 voxels), respectively], primarily in the NAc. Larger RPEs (cyan) elicited greater activation in dorsolateral striatum, primarily involving the bilateral putamen and right dorsolateral caudate. A decreasing LR (magenta, p < 0.05 FWE) correlates with activation in left caudate head and inferior frontal gyrus. Note that the LR regressor does not separate between congruent and incongruent trials—it samples the LR of the chosen stimuli from the respective decaying exponential. c, Parameter estimates in the peak LR voxel from the ventral caudate separated between congruent and incongruent trials decline with LR. d, EV from the computational model activates a perigenual region in the vmPFC.

Neural encoding of the RL model

Using the optimized group parameters (Table 4) from our best-fitting model, we generated a parametric modulator of LR for the chosen stimulus and included that in our design matrix. In addition, we also constructed subject-specific parametric modulators for outcome (reward vs no reward), RPE, and EV of the chosen stimulus. Parametric modulators were not orthogonalized, thus ensuring that only their unique contributions were correlated with the fMRI data. We found several activations in distinct subregions of the vStr (Fig. 4b; Table 5). LRs correlated significantly with activation in the ventral part of the caudate head [left (MNI coordinates x, y, z): −14, 14, −3; right: 16, 8, −3; whole-brain correction], exhibiting a steeper decline of BOLD activation for congruent (slope = −0.3855) versus incongruent (slope = −0.1857) cues (p = 0.0229; Fig. 4c), and so mirroring the differentially decaying LRs obtained in the behavioral modeling (Fig. 3c).

Table 5.

Peak coordinates of fMRI analyses

Contrast	Region	MNI coordinates			Cluster size	Maximum t value
		x	y	z
Attractiveness	vmPFC	−6	42	−9	146	4.43*
(high-low)	Rostral cingulate	−6	50	30	56	3.78*
LR	Left vStr	−14	14	−3	61	8.68**
	Right vStr	16	8	−3	28	7.50**
Value	vmPFC	4	28	0	120	4.85***
Reward	Left vStr	−12	6	−12	20	3.80***
	Right vStr	8	12	−9	81	3.57***
RPE	Left vStr	−26	6	0	77	4.64***
	Right vStr	30	2	−6	491	4.56***
PPI analysis	vmPFC	−4	42	9	21	6.26**
		0	32	−6	6	6.23**

*p < 0.001 uncorrected,

**p < 0.05 (whole-brain FWE correction),

***p < 0.05 (small volume correction).

Reward outcome and RPEs correlated with activity in the nucleus accumbens (NAc) and ventral putamen (vPut), respectively (small volume correction, 8 mm sphere), consistent with previous results (Knutson et al., 2005; Reuter et al., 2005; Seymour et al., 2005; Burke and Tobler, 2011). EVs correlated significantly (small volume correction, 8 mm sphere) with perigenual region of the vmPFC (Fig. 4d), also consistent with prior findings (Hampton et al., 2006). These findings support the idea that anatomically distinct areas in the vStr and vmPFC encode anatomically separable processes of an RL algorithm (O'Doherty, 2004; Daw and Doya, 2006), whose outputs are computationally combined to update EVs.

Encoding EV: physiophysiological interaction

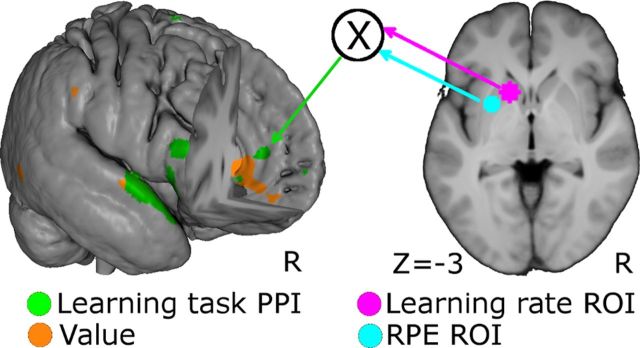
To confirm our previous result of EV encoding in the vmPFC (Fig. 4d) and the validity of our RL model of EV updating, we sought to elicit activation from areas covarying with the product of the LR * RPE BOLD signals on a trial-by-trial basis. In our RL model (see Materials and Methods), EV is updated by multiplying LR and RPE, so neural regions whose BOLD signals covary with the product of the BOLD LR and RPE can be taken to encode the EV given by the model. In PPI analysis (Friston et al., 1997), values from peak regions around the LR and RPE activations were extracted and multiplicatively combined to yield a seed regressor in the design matrix (Fig. 5, right). Activations elicited in the vmPFC by this LR * RPE regressor (Fig. 5, left) partially overlapped with that previously identified by the parametric modulator of EV (Fig. 4d). To control for nonspecific functional connectivity unrelated to our task, we conducted the same PPI in the resting-state fMRI dataset using the same seed voxels as in the previous PPI. Target regions were identified as bilateral insula and overarching opercula, pre-central gyrus, post-central gyrus, putamen, and superior temporal sulcus using the automated anatomical labeling templates (Tzourio-Mazoyer et al., 2002). We then constructed an exclusive mask from these anatomical templates and used it to filter out anatomical regions of nonspecific functional connectivities resulting from our seed regions.

Figure 5.

PPI analyses. Right, Seeds for subsequent analyses, based on spheres around peak voxels of LR (magenta) and RPE (cyan). Left, Activations (green, p < 0.05 FWE) elicited by the seed regressors. The activations in vmPFC region (green arrow) partially overlapped with the model-derived EV signal (orange; p < 0.001 uncorrected) that is also shown in Figure 4d.

Discussion

In this study, we introduced the concepts of value congruence and incongruence to systematically explore the influence of inherent values on the RL of acquired values. We paired faces that were rated high and low in attractiveness with both reward and punishment while measuring decision outcomes. As previously reported (Bray and O'Doherty, 2007; Cloutier et al., 2008), faces high in attractiveness elicited a greater signal in dorsomedial and ventromedial prefrontal cortex (Fig. 4a), indicating an inherent valuation signal. Participants learned acquired values in all conditions, but most often they selected attractive faces associated with a reward, while most often avoiding unattractive faces associated with punishment (Fig. 3a). RL modeling of behavior revealed faster LRs at the beginning of the experiment that also decayed more quickly under conditions of value congruence (Fig. 3c). Neuroimaging analyses showed previously known activations for EV in vmPFC (Fig. 4d), for reward in vStr, and for RPE in vPut, along with a novel region in the ventral caudate encoding LR (Fig. 4b). A regressor using a multiplicative combination of signals derived from the LR and RPE regions, the same calculation specified in the RW learning rule (Eq. 1), activated an area in vmPFC that was partially overlapping with activation elicited by EV alone (Fig. 5). To our knowledge, this activation reveals for the first time that the valuational updating of the brain is well approximated by the multiplicative combination of its LR and RPE signals.

Our analyses strongly suggest that the effect of inherent value on learning new values, at least in the social domain of facial processing, is to modify LRs rather than directly modifying reward signals or RPE. That is, inherent value representations do not directly modulate reward processing, but rather affect the LR that modulates the effect of reward processing. Further, decaying LRs suggest that participants reduce their sensitivity to the RPE as they learn to make the correct choices in this task, which is common to many RL implementations (Sutton and Barto, 1998): as long as reward probabilities do not change rapidly and EVs are learned, the RPE reduces to an uninformative noisy signal, so it makes intuitive sense to decrease the sensitivity to it.

The notion that LR and not RPE would receive modulation by inherent valuation is consistent with previous work showing the importance of adaptive LRs. Adaptive LRs have been proposed both on theoretical grounds to ensure convergence of the RL algorithms (Sutton and Barto, 1998) and have been identified via neuroimaging (Behrens et al., 2007; Krugel et al., 2009; Nassar et al., 2010; Mathys et al., 2011; Iglesias et al., 2013; McGuire et al., 2014). It has been argued that dynamic LRs should be adjusted based on the uncertainty in the estimate of the EV (Behrens et al., 2007), which makes intuitive sense because, during a time when reward contingencies are unstable, a large LR ensures that maximal information is used to update EVs. When the environment (i.e., reward contingencies) becomes stable again and EVs have been learned, a large LR would be sensitive to the inherent noise imposed by a probabilistic reward. This reasoning would predict dynamically decreasing LRs for our stable decision-making task, just as we observed. Furthermore, under conditions of strong inherent valuation, similar external reward contingencies may be processed differently as signals of either high or low valuational salience, depending on the valence of the inherent value and the pairing with the reward, thus resulting in the distinct observed LRs for high and low congruence.

The concept of value congruence pays tribute to the fact that human decision-making normally does not take place in a sterile, value-neutral laboratory, but rather in a world in which the decision cues themselves exhibit inherent values that affect learning and the acquisition of new outcome-based EVs. These inherent values represent an initial bias for new learning trajectories. The modulatory influence of inherent values on choice behavior has been also investigated using pavlovian-to-instrumental transfer paradigms, where positive and negative reward associations are (passively) learned, which subsequently bias instrumental responding (Huys et al., 2011; Prévost et al., 2012). The typical finding is that participants select the instrumental option associated with the positive stimulus more frequently (Bray et al., 2008) or with more response vigor (Talmi et al., 2008), an effect that might be modulated by the availability of (striatal) dopamine (Hebart and Glascher, 2015). In addition, (inherent) Pavlovian values might even override or impair the acquisition of reward-based EV, if the pavlovian and instrumental learning systems are pitted against each other (Chumbley et al., 2014). These previous findings and our data also suggest that a residual modulatory influence of the inherent value persists even at the end of the experiment (Fig. 3b), underlining the advantage that value-congruent cues exhibit in terms of response times. On a more fundamental level, the concept of value congruence addresses the observation that human decision-making is not only driven by expected rewards, but also by how the decision options are presented. For instance, our data clearly show that options associated with attractive cues are selected more frequently. This fact is widely exploited in advertisement, where attractive models are presented together with the product to facilitate a transfer of the inherent value of the model to the product. Our data show that this influence of inherent values on decision-making is systematic and long lasting, but that this influence is limited by merely biasing human choice, not overcoming reward-based learning.

Congruent and incongruent stimuli and task conditions have been widely explored in other domains of cognitive neuroscience, such as perceptual decision-making (Shadlen and Newsome, 2001; Roitman and Shadlen, 2002), spatial attention (Fan et al., 2002), visual search (Eckstein, 2011), and cognitive control (Stroop, 1935), leading either to performance improvements or to deteriorations for congruent or incongruent stimuli, depending on task condition and context. For example, increasing the motion coherence (or motion congruence) during perceptual decision-making leads to better performance (Shadlen and Newsome, 2001; Roitman and Shadlen, 2002), whereas incongruent distractor stimuli in a visual search will improve performance (Eckstein, 2011). The concept of value congruence as presented here is a subtle but effective dimension of human decision-making, because our findings suggest that value-congruent stimuli lead to better and faster decisions that are initially learned more quickly. This resonates with the findings of a recent study (Watanabe et al., 2013) reporting that an unrelated emotional facial expression is capable of accelerating associative learning when it is presented before the cue by raising the LR.

Our fMRI findings revealed that neural correlates of several essential model-based signals populated distinct subregions of the vStr. A hitherto unknown signal for decaying LRs correlated with the ventral part of the caudate head, whereas the NAc exhibited a differential encoding of win and losses, while the vPut correlated with the RPE. The NAc is often reported to represent both outcome encoding (wins vs. losses) and RPE (O'Doherty et al., 2003; Knutson et al., 2005; D'Ardenne et al., 2008; Burke and Tobler, 2011), an effect most likely attributed to the commonly very high correlation between these two signals (>0.9). This multicollinearity can pose an interpretational challenge when outcome and RPEs are included as orthogonalized predictors, because the shared variance will be assigned to one of them, which in turn dominates the interpretation (Mumford et al., 2015). In contrast to this common practice, we included outcome and RPE signals without orthogonalization, ensuring that the neural correlates we report reflect only the unique contribution of either signal. Interestingly, under these circumstances outcomes and RPEs dissociate to the NAc (Knutson et al., 2005; Reuter et al., 2005) and the vPut (Seymour et al., 2005), respectively. The likely interpretation of this finding is that the underlying neuronal populations interact in a way that directly correlates with the computations specified in our RL model. This is strengthened by our functional connectivity analysis (Fig. 5), which extends the local interaction in the vStr between neural signals encoding RPEs and the dynamic LR to vmPFC, where we found neural correlates of model-derived EVs. The close correspondence between model computations and the interaction of brain regions encoding the internal variables of the model underlines the applicability of RL models for investigating the neural basis of decision-making.

In this study, we have demonstrated that congruence between inherent values of cues and the EVs acquired through probabilistic associative learning is a subtle yet relevant dimension affecting human decision-making both at the behavioral and neural level. The concept has an immediate applicability in real-life situations, such as advertisement or political campaigns. We also observed some gender differences in the behavioral analysis that are most likely caused by the asymmetric response of male and female participants to attractive and unattractive faces of the opposite gender (Sprecher et al., 1994; Li et al., 2002). Future research is needed to explore the effect of value congruence with other cues that are not so prone to elicit a gender-specific response. In addition, further research should widen the scope of value congruence beyond stable reward contingencies and explore the effects of changes in cue–outcome associations on dynamic LRs.