Dynamic Multisensory Integration: Somatosensory Speed Trumps Visual Accuracy during Feedback Control

Abstract

Recent advances in movement neuroscience have consistently highlighted that the nervous system performs sophisticated feedback control over very short time scales (<100 ms for upper limb). These observations raise the important question of how the nervous system processes multiple sources of sensory feedback in such short time intervals, given that temporal delays across sensory systems such as vision and proprioception differ by tens of milliseconds. Here we show that during feedback control, healthy humans use dynamic estimates of hand motion that rely almost exclusively on limb afferent feedback even when visual information about limb motion is available. We demonstrate that such reliance on the fastest sensory signal during movement is compatible with dynamic Bayesian estimation. These results suggest that the nervous system considers not only sensory variances but also temporal delays to perform optimal multisensory integration and feedback control in real-time.

SIGNIFICANCE STATEMENT Numerous studies have demonstrated that the nervous system combines redundant sensory signals according to their reliability. Although very powerful, this model does not consider how temporal delays may impact sensory reliability, which is an important issue for feedback control because different sensory systems are affected by different temporal delays. Here we show that the brain considers not only sensory variability but also temporal delays when integrating vision and proprioception following mechanical perturbations applied to the upper limb. Compatible with dynamic Bayesian estimation, our results unravel the importance of proprioception for feedback control as a consequence of the shorter temporal delays associated with this sensory modality.

Introduction

Our ability to make decisions about the present state of the world depends on prior knowledge about the world as well as new information provided by various sensory modalities. In situations where time has minimal impact, research has shown that humans and animals combine or integrate sensory signals in a near-optimal (Bayesian) manner (Gold and Shadlen, 2007; Körding, 2007; Angelaki et al., 2009; Fetsch et al., 2013). In other words, the internal estimate of a variable (such as hand location) approaches the best representation possible given the available sensory data and priors acquired through development and learning (van Beers et al., 1999; Ernst and Banks, 2002; Körding and Wolpert, 2004; Vaziri et al., 2006). Although the high resolution of the fovea often provides vision with a dominant role (Welch and Warren, 1980), this role can be flexibly adjusted in situations where somatosensory feedback becomes more reliable (van Beers et al., 2002; McGuire and Sabes, 2009; Tagliabue and McIntyre, 2014). Hence, minimizing estimation variance is a key aspect of multisensory integration.

However, information on the state of the world can be delayed, impacting our ability to make decisions for the present. This is particularly true for motor function as sensory transduction and conduction velocity from sensory organs to the CNS leads to non-negligible delays. In this context, time becomes a critical hindrance to multisensory integration, because different sensory modalities are affected by distinct temporal delays. For example, a transcortical pathway influences muscle responses to mechanical perturbations in as little as 50 ms (Scott, 2012), whereas vision can take ∼100 ms to influence upper-limb motor control (Georgopoulos et al., 1983; Lamarre et al., 1983). Such a difference between sensory delays is not negligible (Cameron et al., 2014; Cluff et al., 2015), in particular when one considers the ability of motor systems to generate task-specific feedback in ∼50 ms of a mechanical perturbation (Scott, 2012). In fact, the diversity of sensory organs and their distribution over the whole body suggests that combining asynchronous sensory signals is likely a ubiquitous challenge for the brain.

To date, the question of how the nervous system performs multisensory integration in real-time remains open. More specifically, it remains unknown whether rapid multisensory integration is determined by the variance of each sensory signal or inferred variables, as commonly reported for perception or decision-making (Angelaki et al., 2009; Drugowitsch et al., 2014), or whether the nervous system also considers differences in temporal delays across sensory modalities when combining sensory signals over short time intervals.

In theory, dynamic Bayesian estimation can be derived from a Kalman filter, which optimally combines feedback and priors computed from integrating the system dynamics with the known control input (Kalman, 1960). To address the influence of feedback delays on multisensory integration, we first highlight that this model makes predictions that significantly depart from the usual static model, in which the weighting factors are entirely determined by the variance of each sensory signal. We then present a series of experiments combining visual tracking of the fingertip motion with upper-limb responses to perturbations to probe the mechanism underlying multisensory integration during feedback control. A clear difficulty is that there is no instantaneous readout of internal estimates of hand motion during movement, which motivated us to use the visual system as a way to probe internal estimation of perturbation-related motion.

This approach confirms differences in time delays across sensory modalities, and shows that multisensory integration following perturbations is well captured in a Kalman filter (implementing Bayesian estimation for linear systems) considering the different sensory delays associated with vision and limb afferent feedback. Altogether, this study suggests that the nervous system considers not only sensory variance but also temporal delays to perform optimal multisensory integration during feedback control.

Materials and Methods

Participants

A total of 25 participants were tested in one or several experiments (12 females, between 19 and 33 years of age). Fifteen of them participated in the main experiments presented below. Three of them participated in Experiments 1 and 2. Four participants from Experiment 1 were also involved in the first control experiment. The remaining 10 participants were involved in the second control experiment. The experimental procedures were approved by the ethics committee at Queen's University.

Main experiments

Participants were seated and an adjustable linkage was attached to their arm (KINARM, BKIN Technologies; Scott, 1999; Singh and Scott, 2003). The linkage supported the participants' arm against gravity and allowed motion in the horizontal plane. The visual targets were projected on a virtual reality display and direct vision of the participants' arm was blocked. The initial joint configuration was 45° and 90° of shoulder and elbow angles, respectively. In all cases, mechanical perturbations consisted in equal amounts of shoulder and elbow torque, which generates pure elbow motion for ∼150 ms following the perturbation (Crevecoeur and Scott, 2013).

Experiment 1.

Mechanical perturbations of varying amplitude (step torques, 20 ms buildup, ±1, ±1.5, and ±2 Nm) were randomly interleaved with visual perturbations. During visual perturbations, the cursor followed a trajectory fitted to participants' individual hand paths following 1.5 Nm perturbations recorded during a practice set of 20 trials. The fit was composed of two Gaussian functions fitted to x- and y-coordinates of hand motion using least square procedure to approximate the bell-shaped profile of perturbation-related motion.

The time course of a trial was as follows. A visual target was presented with a center dot and a circle around the dot (radii 0.6 and 2 cm, respectively) at the fingertip location corresponding to the initial joint configuration. Participants (N = 8) were instructed to place their fingertip (white cursor, radius 0.5 cm) in the center dot. After a random delay uniformly distributed between 2 and 4 s following stabilization in the center dot, either a mechanical perturbation was applied to the arm, or the cursor was moved following the fitted hand trajectory. In the case of mechanical perturbations, participants were instructed to counter the load and return to the circular target within 800 ms. In addition, they were asked to track their fingertip visually as accurately as possible. In the case of visual perturbations, they were instructed to track the cursor. We mentioned explicitly that upper limb motor corrections were needed only when their hand was displaced away from the target. Hand motion did not influence the cursor trajectory during the visual perturbations.

Possible cognitive factors related to the multiple aspects of the tasks were assessed by comparing participants' responses from the random and blocked conditions, in which the perturbation type and associated instruction were always the same. In the random condition, the probability of visual perturbations was 1/3 (80 visual perturbations for 160 mechanical perturbations). Perturbations of ±1.5 Nm were twice as frequent as the other perturbation magnitudes. Trials were separated in four blocks of 60 trials. The blocked condition consisted of 60 mechanical perturbations with visual feedback (±1.5 Nm), or 60 visual perturbations. The ordering of conditions (randomized, visual blocked or mechanical blocked) was counterbalanced across participants. We chose a rather slow perturbation buildup, because we were interested to generate smooth hand motion and improve the resemblance between hand motion and the fitted hand trajectories displayed as visual perturbations.

Experiment 2.

This experiment interleaved mechanical perturbations with visual feedback (M and V, ±1.5 Nm), mechanical perturbations of the same amplitude but without visual feedback (M), and visual perturbations fitted to the grand average of hand trajectories from Experiment 1 (V). The time course of a trial was identical as in the previous experiments. In addition to countering the perturbation loads, participants (N = 10) were instructed to track their fingertip as accurately as possible (with or without visual feedback), or the cursor in the case of visual perturbations. Equivalently, a non-ambiguous instruction (also given to participants) was to track any motion of the fingertip or cursor. Participants performed three blocks of 60 trials. Each block consisted of 20 perturbations of each type randomly interleaved (M, M and V, or V; 10 per flexion/extension).

Control experiments

Control Experiment 1.

The first control experiment was performed to verify that the difference in SRT across visual and mechanical perturbations was not due to artificial delay in the virtual reality display. There are known delays between the real-time computer-generated cursor motion and the actual display on the virtual reality monitor (40 ms). This delay was removed from all SRTs following purely visual perturbations only. In addition, we instructed participants (N = 4, also involved in Experiment 1) to track a green LED attached to the robot linkage approximately at the location of the fingertip, while allowing direct vision of the limb and of the LED. Thus, participants had direct vision of a physical target and there was no virtual reality display. Participants removed their arm from the linkage and the robot applied a viscoelastic torque approaching critical damping following the perturbation to reproduce smooth corrective movements.

As shown below, the difference between SRTs across mechanical and visual perturbations was reproduced in this control experiment. However, it was not possible to perform the main experiments with this approach mainly for two reasons. First, it is difficult to match the visual stimulus precisely across mechanical and visual perturbations, as the perturbation-related motion slightly differs across participants due to individual differences in biomechanical properties. In contrast, it is easy to fit the cursor trajectory to the actual movement for each participant without any constraint. The second and more important reason why we used the computer display was that the visual perturbations in the control experiment had to be performed with the arm outside of the exoskeleton. Thus, it was not possible in this case to interleave visual and mechanical perturbations. For these reasons, we use the computer display throughout the study, after correcting all SRT following visual perturbations for the monitor delay.

Control Experiment 2.

The second control experiment was performed to address whether switching off the hand-aligned cursor for the mechanical perturbations in Experiment 2 provided a cue to generate a saccade toward the fingertip. To address this concern, we tested a different group of 10 participants in a protocol similar to that of Experiment 2, with the difference that the hand-aligned cursor remained attached to the visual target in 50% of the mechanical perturbations trials. Participants were instructed to track their fingertip as accurately as possible in all cases. Participants first performed a practice set of 10–20 trials, followed by five blocks of 60 trials. Four of these blocks interleaved mechanical perturbations with or without congruent motion of the hand-aligned cursor (15 × flexion or extension × M or M and V), and the fifth block consisted of 60 visual perturbation trials (30 × flexion or extension direction). Visual perturbations were performed in a separate block to avoid ambiguous instructions regarding the tracking of the cursor. The ordering of blocks was counterbalanced across participants.

Apparatus and data collection

We sampled the shoulder and elbow angles at 1 kHz. The activity of the major muscles spanning the elbow joint was collected during Experiment 1 to investigate whether the visual perturbation engaged a limb motor response (brachioradialis, biceps, triceps lateralis, and triceps long). Muscle activities were collected with standard surface electrodes attached on the muscle belly after light abrasion of the skin (DE-2.1, Delsys). Muscle recordings were digitally bandpass filtered (10–500 Hz), rectified, averaged across trials, and normalized to the activity evoked by a constant load of 2 Nm applied to the elbow joint. Muscles activity was averaged across trials and epochs following standard definitions: −50 to 0 ms for the pre-perturbation activity (Pre), 20–50 ms for short-latency (SL), 50–100 ms for long-latency (LL), and 90–180 ms for visuomotor feedback (VM). We used these partially overlapping epochs to follow previously defined LL or visuomotor time windows (Franklin and Wolpert, 2008; Pruszynski et al., 2011).

The intersection between gaze and the horizontal workspace was sampled at 500 Hz with a head free tracking system (Eyelink 1000, SR Research). Thus, eye movements were represented in Cartesian coordinates. We extracted the onset [Saccadic Reaction Time (SRT)], the endpoint and the amplitude of the first saccade following the perturbation using a threshold equal to 5% of peak saccade velocity. The first and last samples above this threshold determine the saccade onset and end. The two-dimensional variance of the saccade endpoint was computed as the area of the variability ellipse in Cartesian coordinates. The variances along the main and secondary axes of endpoint error as a function of the saccade latency, and the slope of the relationship between these variables were calculated based on singular value decomposition of their covariance matrix (ie, orthogonal regression). The end of upper limb corrective movements was estimated based on a threshold equal to 10% of the peak return-hand velocity. The variability of fingertip location following perturbations was computed with singular value decomposition of the covariance matrix as for saccade endpoint errors. Comparisons of fingertip endpoint variance throughout the movement was calculated for each perturbation direction independently, and then averaged across directions.

Based on visual inspection, we selected only the trials in which there was a response saccade following the perturbation. Trials without a saccade, or with an eye blink around the perturbation onset, were removed (∼20% of trials on average across participants and experiments). After removal of these trials, the average number of trials per condition was 72 ± 16 in Experiment 1 (minimum across participants: 35) and 45 ± 11 in Experiment 2 (minimum: 15). All trials were included in the analyses of muscle response and upper-limb motor corrections.

Changes in saccade latencies from individual trials across conditions were analyzed for each participant based on nonparametric K–S tests, which allowed assessing the presence of significant differences without making assumption about the underlying distribution. Single comparisons were performed with paired t tests. When more than one comparison is involved, we assessed the main effects across conditions based on ANOVA using participants' mean value for the variable of interest in each condition. In all cases, we subtracted the participants' overall mean across conditions to account for idiosyncratic differences. Post hoc tests were then performed with Bonferroni corrections to correct for multiple comparisons. Finally, we performed a sliding t test to determine the moment when visually guided movements of the upper limb exhibited reduced variance in comparison with the condition where the fingertip cursor was extinguished. Observe that the sliding t test is not protected against multiple comparisons, and therefore likely provide early estimates of the moment when significant differences arise.

Model

We consider a biomechanical model to formulate the problems of optimal estimation and control in the presence of multiple sensory delays. Such model is important because state estimation uses priors, or predictions, that are dynamically updated based on internal knowledge of the system dynamics and on the known control input. Thus, it is a natural choice to use a biomechanical model that approximates limb mechanics. In addition, the control model is also necessary to derive quantitative predictions about motor corrections to external disturbances.

The model describes the angular motion of the forearm (inertia, I = 0.1 Kgm²) rotating around the elbow joint. The physical model includes a viscous torque opposing and proportional to the joint velocity with damping factor G equal to 0.15 Nms/rad, corresponding to the linear approximation of viscosity at the elbow joint in humans (Crevecoeur and Scott, 2014). The equation of motion was coupled with a first order, low-pass filter linking motor commands captured in the control input u, with the controlled torque as a linear model of muscles dynamics. The rise time of the muscle force in response to changes in control input was τ = 66 ms (Brown et al., 1999). Thus the state variables include the joint angle (θ), velocity (θ̇) and muscle torque (T). These variables were augmented with the external torque (T_E, not controllable) used to simulate the external perturbation. Finally, the state vector was augmented with the target coordinate that will be necessary for the control problem.

With these definitions, the continuous differential equation of the system is as follows:

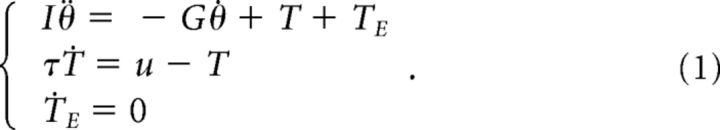Defining the target coordinate by θ*, the vector representing the state of the system is x = [θ, θ̇, T, T_E, θ*]^T. This choice of state vector is motivated by the fact that neural controls are closely related to joint torques; however, considering other state variables, such as joint acceleration would be equivalent to the present formulation. The dynamics of the external torque from the point of view of the controller corresponds to the assumption that it follows step functions (Ṫ_E = 0). The continuous differential equation above was transformed into a discrete time system by using Euler integration with a time step of δt = 10 ms. The discrete time system allows us adding additive and signal-dependent noise. The state-space representation of the discrete-time control system is as follows:

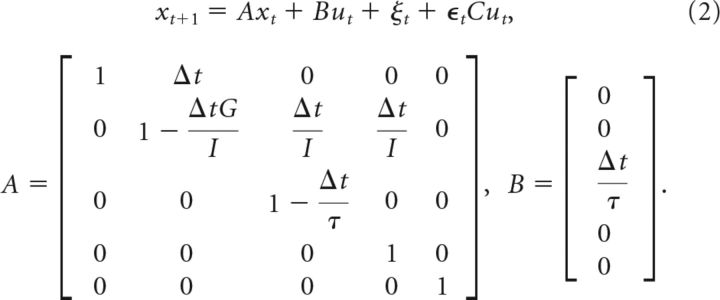ξ_t is an additive multivariate Gaussian noise with zero-mean and known covariance matrix, C is a scaling matrix and ϵ_t is a zero mean and unit variance Gaussian noise (observe the last two rows of A and B correspond to the non-controllable external torque and goal target).

To handle feedback delays explicitly, we must augment the system with past states and let the controller observe the most delayed state. Using δt_p and δt_v to designate the proprioceptive and visual delays in number of sample times, the augmented state vector is as follows (superscript T represents the transpose operator):

With O_n and I_n representing zero and identity square matrices of size n, respectively, n being the dimension of the initial state vector x_t, the observation matrix H is defined as follows:

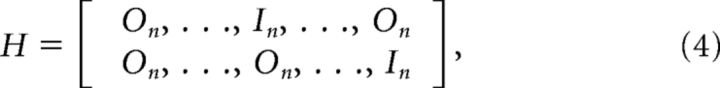where the identity matrix in the first block-row corresponds to time step t − δt_p, and the identity matrix of the second block-row is at the last block-index corresponding to time step t − δt_v. Simulations with proprioceptive or visual feedback only were performed by using only the first or second block-row of the Matrix H, respectively. Let ω_t represent the additive noise composed of the proprioceptive and visual noise (ω_t^T = [ω_p,t^T, ω_v,t^T]), the feedback equation can be written as follows:

The covariance matrix of ω_t, called Σ_ω, is a block-diagonal matrix defined with the covariance matrices of proprioceptive (Σ_p) and visual (Σ_v) feedbacks: Σ_ω = daig[Σ_p,Σ_v]. Observe that Equation 5 is equivalent to the following form:

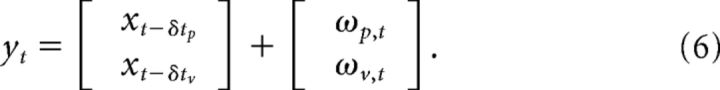This feedback equation assumes that all components of the state vectors are observable in each sensory modality, which must be justified. First, the encoding of joint angle, velocity, and muscle torque is compatible with muscle afferent feedback known to contain information about these variables (Shadmehr and Wise, 2005). Regarding the visual system, position, and velocity may be directly measured from retinal images and retinal slip. The assumption that visual system has access to torque signals is not directly compatible with the physiology. However, considering partially observable states in the visual system yielded qualitatively similar results, because the Kalman filter reconstructs all signals of the state vector. Thus, the effects reported below are indeed due to differences in temporal delays and not to differences in encoded state variables. As a consequence, we kept the feedback signal as in Equation 6 for simplicity.

Dynamic Bayesian estimation is computed based on Kalman filtering, which optimally weighs sensory feedback and priors while taking the system dynamics and control input into account. The computation of the prior corresponds to the motor prediction, which is the expected value of the next state given the present estimate (x̂_t) and control input (u_t), and is obtained by simulating the system dynamics over one time step:

where variability in the prediction is captured in ζ_t, which represents a zero-mean Gaussian noise with covariance Σ_INTERNAL that must be defined (see below). Then, the estimated state can be expanded as follows by taking the definition of y_t into account (Eqs. 5, 6):

where y_t,1 and y_t,2 are the block components of y_t corresponding to visual and proprioceptive signals, and the corresponding block components of the Kalman gain matrix applied (K_P and K_v) must be computed. Equation 8 makes clearly apparent that the current feedback, y_t is compared with the prior at the corresponding time step for each sensory input, which is a critical feature of dynamic state estimation. Recall that the computation made by the Kalman filter are based on the assumption that the system follows the dynamics described in Equations 1 and 2, including the relationship between torque, velocity and position while assuming a constant external torque (Ṫ_E = 0). The consequence of assuming a constant external torque is that the inferred temporal profile of a change in this variable follows a step function.

The main limitation of system augmentation is that it requires knowing the temporal delays. As such, it is not designed to handle uncertainty in these delays. However, assuming that temporal delays are known is a common approach in theoretical neuroscience (Miall and Wolpert, 1996; Bhushan and Shadmehr, 1999; Izawa and Shadmehr, 2008), and the interesting question of handling uncertain temporal delays is beyond the scope of the present study. Despite this limitation, system augmentation achieves optimal estimation of the delayed-feedback system in the sense that, similar to standard Kalman filtering of non-delayed systems, the posterior estimate is the projection on the true state onto the linear space generated by the feedback observations (Anderson and Moore, 1979; Zhang and Xie, 2007). Thus, the optimal estimator obtained with this technique is the solution of a well defined estimator design, and the online compensation for temporal delays falls out of the block structure of the augmented system.

The model definitions also allows us to compute the solution of the control problem by using a standard extension of the linear quadratic Gaussian control design that is iteratively optimized in parallel with the sequence of Kalman gains. The cost-function to minimize is a quadratic penalty on position error and control:

with R = 10⁻⁴. This cost parameter was chosen to generate stereotyped trajectories and has no influence on the estimation dynamics. The optimal control policy is given by a linear control law of the form:

In agreement with the modeling of a postural control task, we used a time horizon sufficiently long to ensure that the feedback gains (C) had reached stationary values. Details about the derivation of the optimal feedback gains and Kalman gains can be found elsewhere (Todorov, 2005; Crevecoeur et al., 2011; Crevecoeur and Scott, 2013).

We now define the different noise parameters. Following standard approaches, the covariance matrix of the additive noise was defined as ∑_ξ = σ² BB^T, with σ = 0.006, and the scaling of signal-dependent noise was set to C = 0.4 × B (Todorov, 2005). For the sensory noise, we fixed the covariance matrix of the proprioceptive noise to ∑_p = 10⁻⁵ × I_n, where n is the dimension of the state vector and I_n is the identity matrix of size n. The variance of the visual noise was defined to satisfy ∑_p = α × ∑_v, and we varied α (Fig. 1 shows the results). The remaining noise to be defined is the internal noise affecting the computation of the prior estimate. We chose ∑_INTERNAL = 0.8 × 10⁻⁶ at each time step, which (following accumulation over time) generated internal priors with covariance matrix similar to that of visual feedback. We verified that the covariance matrices and the Kalman gains had reached steady state before extracting the numerical values reported in the analyses below. The model predictions are therefore independent of the amount of time elapsed since the beginning of the simulation.

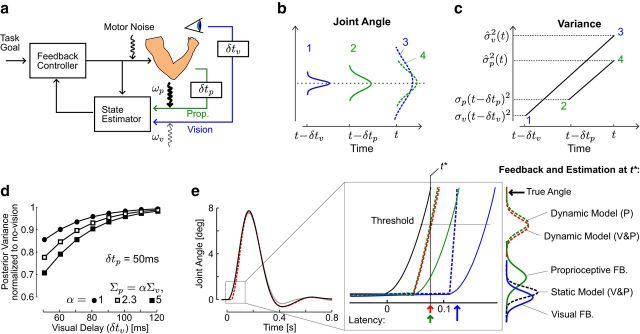
Figure 1.

Dynamic Bayesian model. a, Illustration of the real-time feedback controller based on state estimation. The model considers two sources of sensory information (vision, blue; limb afferent feedback, green) affected by distinct temporal delays (δt_p.v) and sensory noise (ω_p,v). b, Schematic representation of how uncertainty in sensory feedback increase over time. Green and blue distributions correspond to the feedback about limb motion at two distinct points in time, and the dashed distributions show how related estimates in the present state are impacted by the accumulation of uncertainty over the delay period. c, Schematic illustration of how the increase in variance over the delay period can lead to higher uncertainty associated with vision. The variances of proprioceptive and visual signals are σ_p(t − δt_p)² and σ_v(t − δt_v)² and the variance of the estimated states at the present time are σ̂_p,v². d, Theoretical posterior variance of the joint angle estimate for distinct values of visual delays and distinct variance ratios. The posterior variance was normalized to the value obtained without visual feedback, so that a value of 1 indicates equal posterior variances with or without vision. The value of 2.3 corresponds to weighting vision by 70% and proprioception by 30%. e, Changes in actual (solid) or estimated (dashed) angle following a step torque applied on the joint. Solid traces represent simulated perturbations with (black) or without (gray) vision. The two traces are superimposed for almost the entire course of the corrective response. The inset magnifies the actual angle (solid black), delayed feedback (proprioception in solid green and vision in solid blue), and estimated angles following the perturbation computed by the Kalman filter. Vertical arrows represent hypothetical estimation latency with vision only (blue), proprioception only (green), or combined visual and proprioceptive feedback (red) based on exemplar threshold crossed at t*. Distributions represent the sensory feedback or estimated joint angle at t* (vertical thin line).

Because the Kalman filter uses a model of expected sensory consequences (using the matrix H; Wolpert et al., 1995), the vector y_t is compared with previous priors. Although the values of the noise parameters impact the Kalman gains, the main features of dynamic estimation being the dependency of the sensory delays on the weighting factors and the comparisons of current feedback with priors at the corresponding time step, do not depend on these noise parameters. Thus, the different noise parameters do not impact the model predictions qualitatively. The prediction of the static model relative to how the combination of vision and proprioception should affect the SRT directly follow from considering a linear combination of instantaneous feedback signals. Thus, when signals depend on time as under dynamic conditions, static multisensory integration clearly become sensitive to differences in temporal delays across sensory systems.

Results

Model predictions: impact of temporal delays on optimal state estimation

Dynamic multisensory integration is illustrated in Figure 1a, which represents a feedback controller using the output of a state estimator to generate motor commands (Todorov and Jordan, 2002). The impact of sensory delays on optimal state estimation is illustrated schematically in Figure 1, b and c, showing that the accumulation of noise over the delay period potentially makes visual input less accurate for estimating the present state. Observe that the increase in variance over the delay period is due to motor noise, thus the variance of the present estimate given delayed feedback increases at similar rate for the two sensory modalities.

The first main prediction of the model is the dependency of sensory weight upon sensory delays. We illustrate this effect by computing the variance of the estimated joint angle (or the posterior) obtained with visual feedback, normalized to the variance obtained without visual feedback. We then varied theoretically the visual delay in a range including visual delays in humans (up to 120 ms), as well as the ratio between the sensory noise covariance matrices (Fig. 1d; Σ_p and δt_p were fixed, δt_p = 50 ms). Strikingly, for visual delays approaching ∼100 ms, the reduction in posterior variance obtained in the combined condition when both vision and proprioception are available was <10% of the variance obtained with proprioception only, which is much smaller than the reduction expected if the signals were combined based on their variance only. Such modest variance reduction occurred even when vision was five times more reliable than proprioception (Fig. 1d, filled squares; Σ_p = 5 × Σ_v).

The second main prediction of the model is that feedback responses to mechanical perturbations are similar with or without vision (Fig. 1e, black and gray traces, respectively). The two traces are superimposed for almost the entire corrective movement, as a result of the similar estimation dynamics in these two conditions (for these simulations, Σ_p = 2.3 × Σ_v). The main reason why estimation dynamics is similar across these two conditions is that the delayed sensory signals are compared with previous priors, as a result of the estimator design (Eq. 8). Static and dynamic models of multisensory integration shortly after the perturbation (t*) are illustrated in Figure 1e. When sensory signals are directly combined based on their variance, the posterior estimate is between visual and limb afferent feedbacks (Fig. 1e, black dashed distribution). Thus, this model predicts that the estimation from multiple sensory systems must be sensitive to the temporal delays that affect them, due to the fact that this integration does not account for temporal differences across sensory systems. In contrast, according to the dynamic model, the detection of a perturbation from limb afferent feedback generates a similar correction of the estimated state (Fig. 1e, dashed red and green distributions). Observe also that the dynamic estimates are not aligned with the current (delayed) proprioceptive feedback, but they are pushed toward the true state. This operation is a property of the Kalman filter, which computes the present state given the delayed sensory feedback under the assumption made about the system dynamics and external torque (T_E; Eq. 1). Because the delay is taken into account (Eq. 3), the calculation made by the Kalman filter effectively corresponds to integrating feedback about the perturbation over the delay period (Crevecoeur and Scott, 2013; recall that the external torque and velocity change ahead of the position as a result of the discrete dynamics). As well, the theory captures the fact that these computations are driven by sensory feedback because the control input just after the perturbation is close to zero. Behavioral correlates of such sensory extrapolation were reported previously (Bhushan and Shadmehr, 1999; Crevecoeur and Scott, 2013).

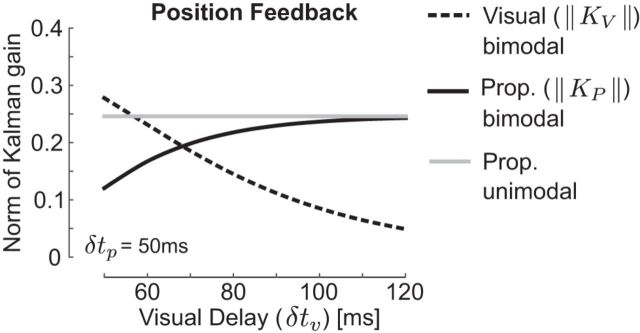
Figure 2 further illustrate the dependency of the components of the Kalman gain matrix on the difference in temporal delays across sensory modalities for a fixed value of sensory variances (Σ_p = 2.3 × Σ_v). Because the feedback signal is composed of two state vectors, one can decompose the Kalman gain matrix into the components applied to proprioceptive and visual feedbacks (K_P and K_v, see Materials and Methods; Eq. 8). The figure focuses on the gain of feedback about the joint angle for illustrative purposes. The norm of the Kalman gain in Figure 2 shows the general effect of temporal delays on the sensory weights across all components of the state vector influencing the estimate of position, and the gains corresponding to the other state variable follows generally the same profile. When visual delays increase, K_P becomes almost equal across conditions in which vision is available or not (solid traces), leading to almost identical weighting of limb afferent feedback with or without vision. In parallel, the weight of visual feedback decreases when visual delays increase (bimodal, dashed black).

Figure 2.

Norm of Kalman gains. Effect of sensory delays on the norm of the block components of the Kalman gain matrix (Eq. 8). Black traces correspond to situations in which vision (dashed) and proprioception (solid) are available (bimodal). The gray correspond to situations in which proprioception is the only source of sensory feedback available (unimodal). Displays are the norm of the block components of the Kalman gain matrix influencing the estimation of the joint angle. All values were calculated with Σ_p = 2.3 × Σ_v as reported in previous work.

The foregoing simulations emphasized experimentally testable differences between static and dynamic models of multisensory integration. The difficulty was to extract participant's internal estimate of limb motion. To do so, it was necessary to combine visual tracking with upper-limb feedback control to assess how participants corrected their estimate of the hand location just after the perturbation. The use of visual tracking was motivated by previous work using visual tracking as a probe of the online state estimator in the brain (Ariff et al., 2002). Because the state estimation follows similar dynamics with or without vision, the dynamic integration model predicts that SRTs and estimation errors should be similar with or without vision, while estimation variance should only display moderate reduction in the case when both vision and proprioception are available (Fig. 1d). Further, similar estimation dynamics also imply similar upper-limb corrective movements across conditions including or not visual feedback. In contrast, if sensory weights are entirely determined by their variance, the state estimation must be sensitive to the different temporal delays, as a straightforward consequence of the linear combination of these sensory signals.

Tracking hand motion: experimental results

Experiment 1

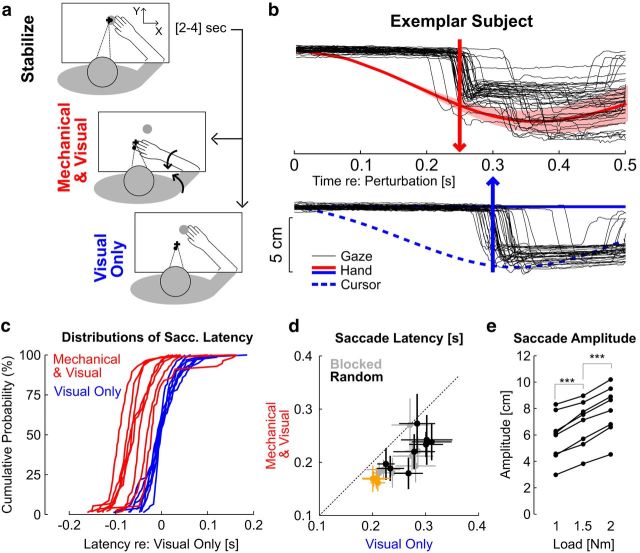
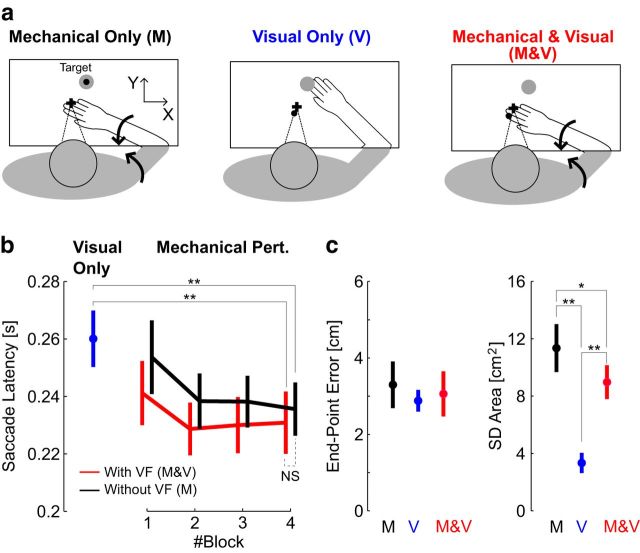
The purpose of the first experiment was to investigate whether SRTs reflected temporal differences between visual and somatosensory feedback. Participants (N = 8) were instructed to track the motion of the hand-aligned cursor while countering mechanical loads applied to their arm (Fig. 3a, Mechanical and Visual). We interleaved visual perturbations (Fig. 3a, Visual Only), during which the cursor followed a trajectory similar to participants' hand motion (see Materials and Methods). Matching the visual information across perturbations allowed us identify the contribution of limb afferent feedback to SRTs.

Figure 3.

Results of Experiment 1. a, Experimental paradigm. Participants were instructed to stabilize in the start target (top), then to visually track the cursor (small black dot) following Mechanical and Visual perturbation (red) or Visual Only (blue). The big gray dot illustrates the target used during the postural control task. The curved arrows (middle) illustrate the multi-joint perturbation torque applied on the limb. b, Individual eye movements from one representative subject (thin black), and average hand movement (solid) or cursor movement (dashed). The shaded area represents 1 SD across trials (hand and cursor traces are superimposed for the Mechanical and Visual perturbations). The vertical arrows illustrate the average saccade latency following combined mechanical and visual perturbations (red, top), or visual only (blue, bottom). c, Individuals' cumulative distributions of saccade latencies aligned on the 50th percentile of the distribution of responses to visual perturbations for each subject. d, Saccade latencies following each perturbation type. Crosses represent the mean ± SD across trials for each individual subject. Black and gray crosses correspond to random and blocked conditions, respectively. The orange crosses represent data from participants tracking a physical LED without any virtual reality display (see Materials and Methods, Control experiments). e, Modulation of saccade amplitude across perturbation magnitudes. Connected dots are the average saccade amplitude as a function of the perturbation load for each participant. Stars indicate significant differences based on paired comparisons with post hoc Bonferroni corrections (see Materials and Methods).

We found an important difference in SRT across visual and mechanical perturbations. Saccades triggered by the combined visual and mechanical perturbations occurred on average 54 ± 24 ms earlier than following visual-only perturbations (Fig. 3b,c; t₍₇₎ = 6.12, p < 0.001; Mechanical and Visual: 221 ± 31 ms; Visual Only: 275 ± 31 ms; mean ± SD across participants). The distributions of SRT across perturbations were significantly different for all participants (Fig. 3c; K–S test, D_i,j > 0.3, i and j > 56, p < 0.05). The same difference was observed when the perturbations were presented in a blocked fashion (difference in latency: 50 ± 26 ms; t₍₇₎ = 5.31, p < 0.01), although we measured an overall reduction in saccade latency of ∼16 ms in this condition (Fig. 3d). On average, all participants exhibited a modulation of the first saccade amplitude with the load magnitude (Fig. 3e; one-way ANOVA on participants' individual means: F_(2,21) = 183, p < 10⁻¹⁰). Post hoc analyses performed with Bonferroni correction confirmed that the paired differences across perturbation loads were strongly significant. Hence, much like upper-limb motor responses (Pruszynski et al., 2011), the oculomotor system considered the magnitude of limb motion in saccade generation.

The first control experiment was performed to address the possibility that the virtual reality display affected SRTs following visual perturbations. In this experiment, direct vision of the limb and of an LED attached to the robot linkage was provided, thereby removing any potential impact of the virtual reality display (see Materials and Methods). SRTs decreased following both mechanical and visual perturbations, but the difference across conditions was reproduced (K–S test on SRT distributions: D_i,j > 0.7; i and j > 30, p < 10⁻⁸; difference: 38 ± 7 ms, mean ± SD). The data from this control experiment are reported in Figure 3d (orange crosses). This control experiment revealed that the absolute SRTs were impacted by the monitor display. However, our main findings depend on the difference in SRTs across conditions.

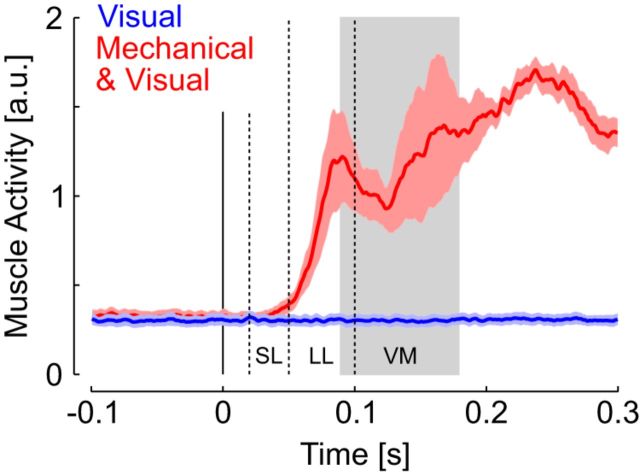
Notably, we did not observe any consistent upper-limb response to visual perturbations. Trials for which the fingertip exited the initial target following the visual perturbations represented <5% across participants involved in Experiment 1, and were paradoxically directed toward the cursor. We analyzed the activity of the major muscles spanning the elbow joint and found virtually no change in muscle activity following the visual perturbations (Fig. 4; see Materials and Methods for definitions of the different response epochs). Muscle responses to mechanical perturbations started in the SL epoch, although did not reach significance (SL ≈ Pre.: t₍₇₎ = 1.34, p = 0.22). This is expected as a consequence of low initial activity and of the rather slow perturbation buildup of 20 ms. Robust responses were observed in the long-latency and visuomotor epochs following mechanical perturbations (paired t tests: LL > Pre.: t₍₇₎ = 3.63, p = 0.008, VM > Pre.: t₍₈₎ = 4.04, p = 0.005). In contrast, the visual perturbation did not evoke any significant response (for all comparisons: t₍₇₎ < 0.87, p > 0.1). Recall that the visual and mechanical perturbations were randomly interleaved, thus participants could not prepare distinct response strategies for each perturbation. The lack of EMG response following visual perturbation is thus further indicative that proprioception plays a central role in the generation of a motor response.

Figure 4.

Muscle responses to mechanical perturbations. Grand average of muscle activity across muscle samples and participants. Traces were smoothed with a 10 ms moving average for illustration purposes. Colored areas represent 1 SE across participants. The vertical dashed lines delineate the epochs of motor responses (SL: 20–50 ms; LL: 50–100 ms), and the gray rectangle corresponds to the time window associated with rapid visuomotor feedback (90–180 ms).

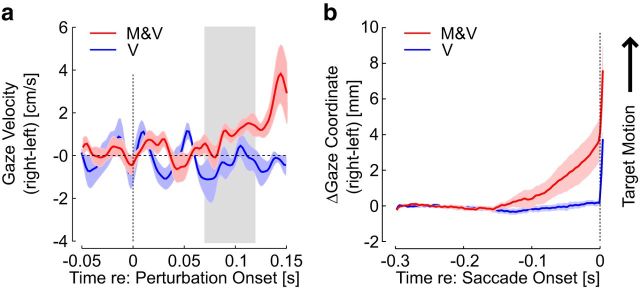
Turning back to visual tracking, we found that the perturbation-related motion evoked very quick buildup of smooth eye displacement before triggering the saccades. Figure 5a shows the buildup of eye velocity before the saccade, averaged across trials and participants (mean ± SEM; positive indicate target direction/velocity). The average velocity from 70 to 120 ms was significantly greater following mechanical perturbations than the velocity in the same time window following the visual perturbations (Fig. 1a, gray rectangle; t₍₇₎ = 2.71, p = 0.025). This early buildup in eye motion toward the target was clearly apparent when the gaze was aligned on the saccade onset (Fig. 5b). The gaze coordinate and velocity just before the saccade onset was clearly directed toward the fingertip motion, and the velocity before the saccade onset was significantly greater following mechanical perturbations than following visual perturbations (t₍₇₎ = 4.3, p < 0.005). Recall that saccades occurred on average later following the visual perturbations, thus the stronger buildup of eye displacement toward the fingertip evoked by the mechanical perturbations occurred with smaller cursor eccentricity and retinal slip than following the visual perturbations.

Figure 5.

Smooth eye displacement. a, Gaze velocity following the onset of the mechanical (red) or visual (blue) perturbations. The gray rectangle illustrates the time window of 70–120 ms, during which the gaze velocity following mechanical perturbations displayed significant modulation toward the fingertip. b, Gaze displacement toward the target. Traces were aligned on saccade onset. a, b, Shaded areas represent SE across participants.

Because there was no clear buildup in eye velocity following the visual perturbations, it was necessary to concentrate on the saccadic responses to compare oculomotor tracking across the different perturbation types. The difference between SRTs across perturbations can be explained by the afferent delays from the periphery to the CNS, and provides an estimate of internal sensorimotor processing times of ∼150 ms for saccadic responses computed as follows. We extracted the 10th percentile of the distribution of SRTs for each participant to approach the minimum reaction time, reflecting conduction delays and rapid internal processing. We reasoned that the 10th percentile would provide reliable estimates in comparison with other metrics (eg, distribution average or median), which includes trials affected by factors such as reduced attention or fatigue. In the blocked condition, the 10th percentile of SRT across participants was 180 ± 25 ms, including afferent and efferent delays. Considering ∼20 ms of afferent delay from muscle spindles to primary somatosensory area (S1), and another ∼20 ms of efferent delay between superior colliculus and saccade onset (Sparks, 1978; Munoz and Wurtz, 1995), our data suggest that it takes ∼140 ms for limb afferent feedback to start generating saccadic responses (range across subjects 115–202 ms). For visual-only perturbations, the 10th percentile of SRT was 226 ± 28 ms, which after removing afferent and efferent delays (∼90–100 ms; Stanford et al., 2010) provides a similar estimate of 126–136 ms for internal sensorimotor processing (range, 93–170 ms). Observe that these estimates were likely conservative due to the virtual reality display (see Materials and Methods, Control experiments; and Fig. 3d). These considerations validate the use of SRTs to probe participants' estimates of hand motion following the perturbation, as it is compatible with differences in sensorimotor delays across sensory systems.

Experiment 2

Building on the results of Experiment 1, the second experiment was designed to test the predictions from static and dynamic Bayesian models more directly. We used visual perturbations as in Experiment 1 (Fig. 6a, V), and mechanical perturbations during which the fingertip-aligned cursor was extinguished, so that saccadic responses could only use limb afferent feedback to estimate the location of their fingertip (Fig. 6a, M). These two perturbations were interleaved with perturbations providing combined mechanical and visual information (Fig. 6a, M and V). We instructed participants to follow the motion of their fingertip (for M and M and V perturbations) or of the cursor (V). Equivalently, a non-ambiguous instruction given to the participants was to track any moving stimulus, fingertip, or cursor. We extracted saccade endpoints to characterize participants' estimate of fingertip location.

Figure 6.

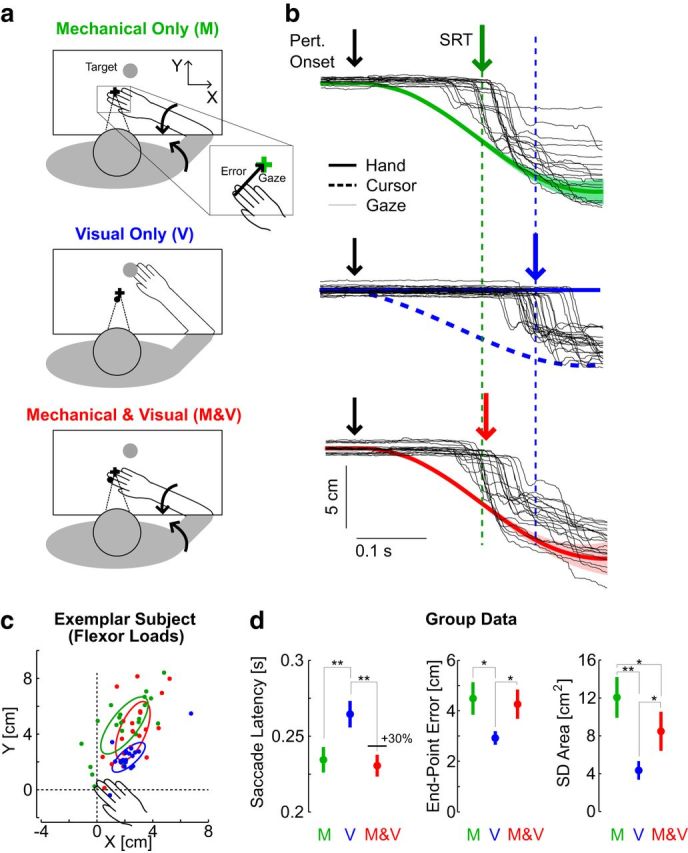
Results of Experiment 2. a, Illustration of the three perturbation types: Mechanical Only (green, M) during which the hand aligned cursor was extinguished, Mechanical and Visual (M and V, red), and Visual Only (V). The initial stabilization was identical to the first experiment and was omitted here for clarity. Inset, The endpoint error vector computed as the difference between the hand or cursor and gaze coordinates at the end of the first saccade. b, Average (solid) and SD (shaded area) of fingertip or cursor motion from one exemplar subject with similar color codes as in a. The gaze coordinate from individual trials is represented with thin black traces. Colored arrows and vertical dashed lines are aligned on the average SRT for this representative participant with the same color code as in a. Observed that the red arrow is aligned on the average SRT from the purely mechanical condition c, Saccade endpoints from one representative subject relative to the fingertip and/or cursor location. Errors are mainly located in the first quadrant following elbow flexor loads. Two-dimesional ellipses obtained from singular value decomposition of the saccade endpoint distribution are presented for each perturbation following the same color code as in a and b. d, Saccade latency (left), norm of endpoint error (center) and two-dimensional endpoint dispersion computed as the area of the endpoint dispersion ellipses as represented in c. Error bars represent 1 SEM across participants. Significant differences revealed by paired comparisons with post hoc Bonferroni corrections are illustrated with *p < 0.05 or **p < 0.01.

The changes in latencies across perturbation types relative to each participant's overall mean were strongly significant (F_(2,27) = 22, p < 0.001). Post hoc tests with Bonferroni corrections indicated that there was no increase in SRT when vision was provided during a mechanical perturbation (Fig. 6b,d, M compared with M and V; p > 0.1), and the latencies in these two cases were significantly shorter than following visual-only perturbations (p < 0.001). The similar SRTs following mechanical perturbations with or without vision is illustrated in Figure 6b (data from one representative subject). Second, we found that the norm of endpoint errors were statistically similar across the two conditions involving a mechanical perturbation (Fig. 6c,d; post hoc analysis with Bonferroni correction on the error across perturbation types, p > 0.1), whereas the error following visual perturbations was significantly smaller (M > V, p = 0.003; M and V > V, p = 0.011). Finally, we observed a significant reduction of estimation variance when vision was available, as measured from the area of saccade endpoint dispersion for the combined estimates (Fig. 6d, right; M > M and V, p = 0.034). Notably, the endpoint variance in this case remained clearly greater than following visual-only perturbations (M and V>V: p = 0.013). The variance of the saccade endpoint following combined perturbation was also significantly greater than following visual perturbations (p < 0.001). Qualitatively, the endpoint error and variance displayed similar differences across perturbation types when the analysis was performed on the trials with overlapping SRTs. To observe this, we extracted for each participant the trials with SRT between the interquartile range of all SRTs across the three perturbation types (25–75%), thereby discarding on average the slowest responses to visual perturbation and the fastest responses for the mechanical perturbations with or without vision. Thus, the results in Figure 5d are not simply due to the comparison of saccades having distinct latencies.

It was necessary to verify that this result was not confounded by the fact that the stimulus was more variable in the case of mechanical perturbations due to biological variability. On average, the variability of the fingertip location at 250 ms was 0.4 cm², or ∼3% of saccade endpoint variance following purely mechanical perturbations. Thus, correcting for the stimulus variability does not impact the conclusions. The moderate variance reduction (Fig. 6d) confirms that multisensory integration occurred within the time window corresponding to internal processing, which we estimated above to be ∼150 ms.

The dynamic model of multisensory integration captures the similar SRTs, endpoint error and the moderate variance reduction observed across the two conditions involving a mechanical perturbation (Fig. 1). Simulations in Figure 1d generated less variance reduction than observed experimentally (∼30%), but a quantitative match without altering the estimation dynamics is possible by changing the noise parameters. In fact, capturing the observed reduction in the variance of saccade endpoints without altering the estimation latency cannot be reproduced by combining signals directly according to their variance. Indeed, considering static multisensory integration and assuming a flat prior, it is possible to compute that a reduction of ∼30% of estimation variance as observed experimentally corresponds to a visual weighting of 0.3. Thus, if vision and limb afferent feedback are combined linearly, the observed reduction in saccade endpoint variance implies that the latency in the combined case be delayed by 30% of the difference in SRT across purely visual and purely mechanical trials. We computed that 30% of the measured differences between SRTs following mechanical and visual perturbations corresponded to delaying SRTs by 9 ± 8 ms in the combined cases (Fig. 6d, black horizontal line in saccade latency). Actual changes in SRTs in this condition were significantly smaller than ∼9 ms (t₍₉₎ = 4.5, p < 0.01), and in fact the measured change in SRTs tended to be slightly negative (M and V and M = −4 ± 7 ms). Likewise, matching a near-zero difference in SRT across mechanical perturbations with a static combination of vision and proprioception suggests that the visual weight was almost zero, which is incompatible with the observed reduction in variance. The dependency of the variance reduction and saccade latency should also be observed when considering a Gaussian prior over the state of the joint. Thus, regardless of the prior, a direct combination of instantaneous sensory signals cannot explain why estimation variance decreased with vision without affecting the SRT. In contrast, this aspect is captured in the dynamic model.

We verified in the second control experiment that these results were not confounded by the fact that switching off the cursor provided a visual cue to trigger a saccade. The control experiment was similar to Experiment 2, with the difference that the hand-aligned cursor remained attached to the target for half of the mechanical perturbation trials (Fig. 7a; see Materials and Methods). We observed in this control experiment that SRTs across blocks decreased, which was indicative of the fact that participants needed some time to familiarize with the task (Fig. 7b). Such habituation across blocks was not observed in the main experiments. After habituation, we observed a similar behavior to that of Experiment 2 (Fig. 7b). There were clear main effects of the block number (two-way ANOVA: F_(3,89) = 7.45, p < 0.0005) and of the perturbation types (F_(2,89) = 10.16, p < 0.0005). Post hoc tests revealed that there was no statistical difference between SRTs following M or M and V perturbations across the last three blocks for both perturbation types following mechanical perturbations (Fig. 7b; paired comparisons with Bonferroni corrections: p > 0.1), and the SRT following mechanical perturbations (with or without vision) in these last three blocks were significantly shorter than those observed following visual perturbations (Fig. 7b; p < 0.005). There was no significant difference in endpoint error across perturbations (one-way ANOVA: F_(2,27) = 0.46, p > 0.1). The variance of saccade endpoint reproduced the results of Experiment 2: we observed a significant reduction when both proprioceptive and visual feedbacks were available (M and V), and the endpoint variance in this case was clearly greater than following visual perturbations (Fig. 7c; post hoc tests with Bonferroni correction, *p < 0.05, **p < 0.01). In conclusion, this experiment reveals that switching off the cursor in Experiment 2 did not impact our results qualitatively.

Figure 7.

Results of the second control experiment. a, Illustration of the three perturbation types used in this control experiment. For Mechanical Perturbations only (M), the hand-aligned cursor (black dot) remained attached to the target. These mechanical perturbation trials are illustrated in black to emphasize that they are distinct from the purely mechanical perturbations used in Experiment 2. Visual (V, blue) and combined Mechanical and Visual perturbations (M and V, red) were identical to those of Experiment 2. The initial stabilization was identical to the first experiment and was omitted here for clarity. b, Saccadic reaction times across blocks with similar color code as in Figure 6a. Significant differences from paired comparisons at the level are represented with *p < 0.05 and **p < 0.01. c, Norm of the saccade endpoint error (left) and endpoint variance measured as the area of the two-dimensional dispersion ellipses as in Figure 6. Vertical bars represent the SEM across participants.

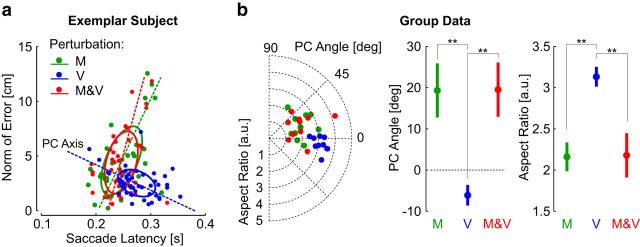
The pattern of saccade endpoint error also revealed a modest influence of vision on the saccades triggered following mechanical perturbations (data from Experiment 2). A known signature of the saccadic system is that saccades associated with longer latencies are more accurate (Edelman and Keller, 1998; Blohm et al., 2005). We observed a similar effect following visual perturbations, as the relationship between the dispersion of endpoint errors and SRTs exhibited a negative principal component on average and relatively large aspect ratio indicative of small trial-to-trial dispersion (Fig. 8a). There was a categorical difference between this pattern and the latency-error relationship of saccades triggered following mechanical perturbations (M, M and V). These saccades presented a positively oriented principal component on average, and a reduced aspect ratio that reflected greater intertrial dispersion (Fig. 8b). This pattern was identical regardless of whether visual feedback was available. Thus, although visual information following mechanical perturbations reduced the estimation variance (Fig. 8d), the mechanism responsible for triggering saccadic responses following mechanical perturbations appeared to rely predominantly on limb afferent feedback.

Figure 8.

Relationship between SRT and accuracy. a, Relationship between saccade latency and endpoint error from one representative subject (data from Experiment 2). Ellipses represent the 1 SD along each axis. Dots represent individual trials. b, Left, Polar plot representing the ellipses computed from each participant. The radii are the ellipses aspect ratio (ie, the ratio between principal and secondary components), and the angles represent the orientation of the principal component (PC) mapped between −90° and 90°. The norm of error and latency were expressed in meters and seconds before computing the ellipses orientation and aspect ratios, such that an angle of 45° corresponds to a slope of 1 (observe that the axes in a have different scales for illustration). Right, Comparison of principal component angle and of the aspect ratio across the three perturbation types. Significant differences are illustrated (paired comparisons, p < 0.01).

Limited impact of vision during feedback control

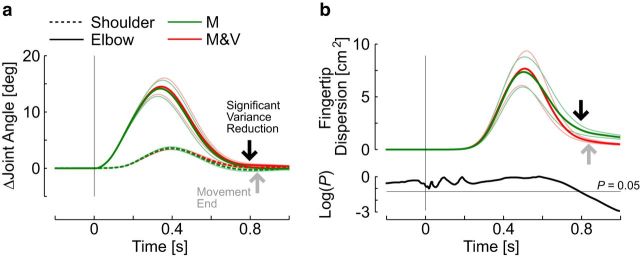
As a corollary of the fact that state estimation is almost identical with or without vision, the dynamic model makes the seemingly puzzling prediction that upper-limb feedback responses should be minimally influenced by vision (Fig. 1e). We used data from Experiment 2 to address this prediction (Fig. 9). On average, the maximum shoulder and elbow displacements, as well as the joint reversal times, were statistically similar across perturbations with or without visual feedback (Fig. 9a; for all comparisons: t₍₉₎ < 1.23, p > 0.25). The influence of vision became apparent near the end of the corrective movement (∼800 ms), where we observed a reduction in variability across trials (Fig. 9a,b, black arrow; paired comparisons of endpoint variances: t₍₉₎ > 3.25, p < 0.01). We used a threshold of 10% of the peak return velocity to estimate the movement end, and found that it occurred shortly after the reduction in fingertip variance (gray arrow; 840 ± 37 ms, mean ± SD). Movement duration was statistically similar across the two conditions (t₍₉₎ = 0.2, p = 0.8). This result shows that vision mostly influenced fine control near the end of movement, whereas motor corrections before this time appear primarily driven by limb afferent feedback.

Figure 9.

Upper-limb motor corrections. a, Ensemble average of perturbation-related changes in shoulder (dashed) and elbow (solid) joints following positive (flexion) perturbations. Perturbation trials with or without visual feedback are represented in red or green, respectively (data from Experiment 3). Thin lines represent 1 SEM. The vertical arrows illustrate the estimated time when vision contributes to reducing the endpoint variability (black arrow), as well as the movement end estimated from hand velocity (gray arrow; see Materials and Methods). b, Top, Two-dimensional fingertip dispersion area following perturbations (mean ± SEM). The SD area was computed from the covariance matrix of x- and y-coordinates at each time step. The area of fingertip dispersion across trials was computed for each perturbation direction independently, and averaged across directions (see Materials and Methods). Bottom, Time series of p values from paired t test comparison of fingertip standard dispersion across conditions with or without visual feedback. The black arrows corresponds to the time when the p value becomes <0.05.

Again, this observation is compatible with dynamic state estimation, which predicts similar estimation (Fig. 1c) and therefore similar feedback response with or without vision. In the framework of static multisensory integration, one expects to find initially slower corrections, as the estimate of the perturbation-related motion would be delayed by the visual information. In addition, the variance reduction obtained by combining visual and limb afferent feedback linearly should have impacted the variability of hand trajectories across trials, because humans typically strive to limit variance in dimensions constrained by the task (Todorov and Jordan, 2002). However, it was not until the end of the reaching movement, and well beyond visual delays, that the influence of vision on variability across trials became apparent.

Alternative control hypotheses that do not assume the continuous use of feedback to generate motor commands, such as pre-planned triggered reactions or through adjustments of limb mechanical impedance, are not compatible with the time-varying profile of positional variance shown in Figure 9b. To summarize, the similarity in saccadic responses and upper-limb feedback corrections to mechanical perturbations support the dynamic Bayesian model, in which estimation dynamics is essentially similar with or without vision due to the difference in temporal delays across sensory modalities.

Discussion

An important challenge for real-time multisensory integration is to handle distinct temporal delays across sensory modalities. We combined standard upper-limb perturbations with visual tracking, and used participants' feedback responses to address how vision and proprioception contribute to dynamic estimation of hand motion. Our approach is based on the fact that oculomotor tracking can capture participants' online estimate of hand motion (Ariff et al., 2002), and that state estimation underlies rapid motor responses to mechanical perturbations (Crevecoeur and Scott, 2013). Thus, the lower SRTs following mechanical perturbations were expected, and the goal of Experiment 1 was to verify that the paradigm was adequate for extracting the corresponding differences in estimation latencies. These differences do not appear to be related to the instructions associated with each perturbation type, as they were reproduced when participants responded to the same perturbations presented in a blocked fashion. Furthermore, Experiment 1 highlighted a rapid buildup of smooth eye displacement associated with limb motion that likely contributed to the saccade generation (Fig. 5), and also after the detection of the perturbation (Fig. 6).

Our main finding is the similar estimation dynamics following mechanical perturbations with or without vision, characterized by similar saccadic reaction times and estimation error (Fig. 6), similar integration of sensory inflow (Fig. 8), and similar upper-limb motor corrections for almost the entire course of the corrective movement (Fig. 9). We analyzed this behavior in light of two candidate models: the variance-dependent weighting of vision and proprioception (Angelaki et al., 2009), and a dynamic model considering limb dynamics and sensorimotor delays. Our data clearly showed that the nervous system does not combine sensory information about the perturbation as predicted by static multisensory integration. In contrast, participants' behavior was well explained by the dynamic model in which multisensory integration depends not only on sensory noise, but also on feedback delays. Due to the functional similarity between feedback responses to external perturbations and voluntary control in a broad range of tasks (Scott et al., 2015), we expect that our conclusions may apply to real-time state estimation in general.

Of course, the importance of vision is not in question, as the visual system is known to provide exquisite information to guide movements. Previous work shows that visually guided movements are rapidly updated following changes in the visual target (Goodale et al., 1986; Prablanc and Martin, 1992; Day and Lyon, 2000), and online corrections for cursor or target jumps are modulated by the reliability of visual feedback (Körding and Wolpert, 2004; Izawa and Shadmehr, 2008). Studies have also documented that visual perturbations evoke rapid and task-dependent motor corrections during reaching (Franklin and Wolpert, 2008; Knill et al., 2011; Oostwoud Wijdenes et al., 2011). Without questioning the importance of vision, our observation that the visual perturbations did not engage any motor response suggests that the relationship between state estimation and visuomotor feedback during reaching deserves further investigation.

Our model does not adequately address how the nervous system should resolve conflicting cues as arise following a cursor jump, because it assumes that the feedback signals are sampled from the same process. Playing-back perturbation-related motion without any perturbation, we found that the inferred joint displacement was ∼25% of the actual displacement, while the evoked control response was reduced by 85% compared with mechanical perturbations (simulations not shown). Thus, in principle, comparing motor responses to visual or mechanical perturbations during reaching may provide additional insight into dynamic multisensory integration. In addition to the importance of vision for online control of reaching, vision also enables anticipation of predictable events, such as when catching a ball for which predicting the time of impact improves stabilization of the limb (Lacquaniti and Maioli, 1989). Here our data suggest that when dealing with unpredictable events, such as external disturbances, vision plays a secondary role to proprioceptive feedback.

Our model explains well participants' behavior following mechanical perturbations, but leaves unexplained the fact that estimation variance following purely visual perturbations was smaller than in the combined case (Figs. 6d, 7d). In theory, the property that a combined estimate is better than any unimodal estimate remains true for dynamic models. Thus, the fact that the estimation variance was lower following purely visual perturbations suggests that the visual process was not fully contributing following the mechanical perturbations. Indeed, it is possible that computations performed in pathways specific to the visual system (Munoz and Everling, 2004) are not fully engaged when tracking limb motion. Interestingly, separate neural mechanisms underlying visual processing of body or target motion were also suggested to account for specific modulation of visuomotor feedback during reaching (Reichenbach et al., 2014). In all, a key general finding is that proprioception plays a major role during control, and we suggest that it is due to the shorter temporal delay associated with this sensory modality.

Intuitively, proprioception always provides newer information about limb motion, and therefore this sensory modality contributes the most during movement. Dynamic estimation converges to the well documented variance-dependent weighting of distinct sensory signals when sensory delays are ignored. However, it is important to realize that such integration may become problematic during movement, as temporal delays as short as tens of milliseconds can no longer be ignored (Crevecoeur and Scott, 2013, 2014). The dynamic model that we propose does not directly capture how the most reliable signal dominates again under static conditions without re-weighting sensory signals while assuming no difference in temporal delays, because the dynamics estimator optimally handles sensorimotor noise in addition to external disturbances. Although developing a general theory capturing context-dependent weighting is beyond the scope of this study, it is conceivable that the neural mechanisms underlying multisensory integration differ across posture and movement tasks in a way that parallels the known differences in control (Brown et al., 2003).

Dynamic Bayesian models may have important implications for understanding decisional strategies when sensory evidence changes over time. In general, drift-diffusion models are often used to describe how sensory evidence accumulates toward a decision bound (Gold and Shadlen, 2007). Although very powerful, the drift-diffusion model fails to capture some aspects of decisions made in the presence of time-varying evidence for the rewarded choice (Cisek et al., 2009; Drugowitsch et al., 2014; Thura and Cisek, 2014). For instance, in a body-heading discrimination task combining vestibular and visual cues, Drugowitsch et al. (2014) emphasized the dominance of vestibular signals observed when reaction times were under the participants' control. More precisely, behavioral discrimination thresholds of heading direction appeared dominated by the vestibular signals (Drugowitsch et al., 2014, their Fig. 2), which, similar to our study, contrasted with the hypothesis of static weighting of visual and vestibular sensory feedback. These results were explained by considering a model that computes an optimal posterior estimate of the heading direction based on velocity and acceleration signals conveyed in the visual and vestibular systems, respectively. Although this study demonstrated that time-varying properties of the stimulus are a determinant factor of cue combination, it did not address the possible impact of a difference in temporal delays across the two sensory systems. Here we suggest a direct parallel between the observations made by Drugowitsch et al. (2014) and the present study, because both studies emphasize a dominance of faster sensory cues (proprioception or vestibular) over the more accurate, but slower visual feedback. The dominance of the faster sensory signal can be explained by the presence of a dynamic state estimator, without assuming differences in state variables encoded in each sensory system.

In our view, the (time-varying) drift-diffusion model suffers from the fact that the decision variable is not directly linked to the online control of behavior. This limitation questions drift-diffusion models for multisensory integration during movement, given the known interaction between decision-making and motor control, and the fast time scales at which these neural processes are engaged (Cisek, 2012; Wolpert and Landy, 2012; Scott et al., 2015). In contrast, dynamic Bayesian estimation provides parsimonious account for the dominance of faster sensory signals, and directly bridges decision-making with motor control. Indeed, the estimated state can be used as a decision variable, relative to which decision bounds can be defined. Because the estimated state converges gradually toward the variable of interest at a rate determined by the different noise parameters, this model also captures the speed-accuracy tradeoff resulting from the accumulation of sensory evidence.

This interpretation is qualitatively consistent with recent theories of decision-making based on a multiplicative interaction between the available sensory evidence and the urgency to acquire the reward (Cisek et al., 2009). In our study, oculomotor responses likely reflected a rapid estimation based on the information about body motion available shortly after the perturbation. From a control perspective, the urgency to correctly estimate body motion following a perturbation is obvious, given the extremely detrimental impact of temporal delays on control performance (Miall and Wolpert, 1996; Crevecoeur and Scott, 2014). Altogether, we suggest that dynamic Bayesian estimation may provide a common framework to interpret decision-making, rapid motor decisions (Nashed et al., 2014), and multisensory integration in an unsteady world.