Phase-Dependent Interactions in Visual Cortex to Combinations of First- and Second-Order Stimuli

Abstract

A fundamental task of the visual system is to extract figure–ground boundaries between objects, which are often defined, not only by differences in luminance, but also by “second-order” contrast or texture differences. Responses of cortical neurons to both first- and second-order patterns have been studied extensively, but only for responses to either type of stimulus in isolation. Here, we examined responses of visual cortex neurons to the spatial relationship between superimposed periodic luminance modulation (LM) and contrast modulation (CM) stimuli, the contrasts of which were adjusted to give equated responses when presented alone. Extracellular single-unit recordings were made in area 18 of the cat, the neurons of which show responses to CM and LM stimuli very similar to those in primate area V2 (Li et al., 2014). Most neurons showed a significant dependence on the relative phase of the combined LM and CM patterns, with a clear overall optimal response when they were approximately phase aligned. The degree of this phase preference, and the contributions of suppressive and/or facilitatory interactions, varied considerably from one neuron to another. Such phase-dependent and phase-invariant responses were evident in both simple- and complex-type cells. These results place important constraints on any future model of the underlying neural circuitry for second-order responses. The diversity in the degree of phase dependence between LM and CM stimuli that we observed could help to disambiguate different kinds of boundaries in natural scenes.

SIGNIFICANCE STATEMENT Many visual cortex neurons exhibit orientation-selective responses to boundaries defined by differences either in luminance or in texture contrast. Previous studies have examined responses to either type of boundary in isolation, but here we measured systematically responses of cortical neurons to the spatial relationship between superimposed periodic luminance-modulated (LM) and contrast-modulated (CM) stimuli with contrasts adjusted to give equated responses. We demonstrate that neuronal responses to these compound stimuli are highly dependent on the relative phase between the LM and CM components. Diversity in the degree of such phase dependence could help to disambiguate different kinds of boundaries in natural scenes, for example, those arising from surface reflectance changes or from illumination gradients such as shading or shadows.

Introduction

Natural scenes contain a multiplicity of complex features that provide important information concerning object position, surface structure, boundaries and contours, spatial scale, motion, and relative distance. The visual system uses these cues to detect and identify objects in a scene by segregating them from their background. An object may be delineated from its background by intensive “first-order” properties—for example, variations in luminance or color within different regions of the image—or by more complex “second-order” attributes, in which areas are differentiated by cues such as contrast, texture, relative motion, and binocular disparity. In natural images, there is a highly structured spatial relationship between occurrences of first- and second-order information (Schofield, 2000; Johnson and Baker, 2004). Human psychophysical studies show that combined first- and second-order cues improve texture segmentation (Smith and Scott-Samuel, 1998; Johnson et al., 2007) and could potentially be used to help resolve ambiguities in first-order information, for example, to distinguish surface reflectance versus illumination effects (Schofield et al., 2006, 2010; Sun and Schofield, 2011).

Neurons responsive to both first- and second-order stimuli are evident in many visual cortical areas (V1, V2, and V5/MT) of the monkey (Albright, 1992; Chaudhuri and Albright, 1997; but see El-Shamayleh and Movshon, 2011; Li et al., 2014) and areas 17 and 18 of the cat (Zhou and Baker, 1994; Tanaka and Ohzawa, 2006; Rosenberg and Issa, 2011). Many of these demonstrate form–cue invariance to first- and second-order motion patterns in that they respond to either kind of stimulus with consistent direction selectivity and preferred orientation (Albright, 1992; Geesaman and Anderson, 1996; Mareschal and Baker, 1999; Li et al., 2014). Human fMRI also reveals orientation- or direction-selective responses to first- and second-order stimuli in many extrastriate cortical areas and in primary visual cortex (Nishida et al., 2003; Seiffert et al., 2003; Larsson et al., 2006; Hallum et al., 2011).

In natural images, first- and second-order information often occurs at coincident locations (Johnson and Baker, 2004) such as at occlusion boundaries. Therefore, it is important to understand how these two types of information are combined in visual cortex. However, previous neurophysiological studies have only examined neuronal responses to first- or second-order stimuli in isolation. Here, we measured systematically responses of cortical neurons to the spatial relationship between superimposed periodic luminance-modulated (LM) and second-order contrast-modulated (CM) stimuli with contrasts adjusted to give equated responses. These recordings were done in area 18 of the cat, in which neurons show CM and LM responses largely similar to those in macaque area V2 (Li et al., 2014). We found that many of the neurons exhibited responses to compound stimuli that were highly dependent on the relative phase between the LM and CM components, with differing degrees of suppressive and/or facilitatory interactions in different neurons. Such phase-dependent and phase-invariant responses are evident in both simple- and complex-type cells.

Materials and Methods

Animal preparation and maintenance.

Initial anesthesia of adult cats of either sex was induced by isoflourane/oxygen (3–5%) inhalation, followed by intravenous cannulation and bolus intravenous delivery of thiopentone sodium (8 mg/kg) or propofol (5 mg/kg), atropine sulfate (0.05 mg/kg), and dexamethasone (0.2 mg/kg). The corneas were protected during surgery with topical carboxymethylcellulose (1%). Surgical anesthesia was maintained with supplemental doses of thiopentone as required or with propofol (6 mg/kg/h) and all surgical wounds were infused with bupivacaine (0.25%). A secure airway was established by tracheal cannulation or intubation. A craniotomy (H-C A3/L4) provided access to cortical area 18 (Tusa et al., 1979) using glass-coated platinum-iridium or parylene-coated tungsten microelectrodes (Frederick Haer). The cortical surface was protected with 2% agarose (Sigma-Aldrich, Type 1-A) and petroleum jelly.

After completion of surgery, animals were paralyzed with an intravenous bolus injection of gallamine triethodide (10 mg/kg), followed by infusion (10 mg/kg/h). Anesthesia was maintained with sodium pentobarbital (1.0 mg/kg/h) in earlier experiments or with fentenyl (9 μg/kg bolus, then 26 μg/kg/h) and propofol (5 mg/kg/h) in later experiments, supplemented with oxygen/nitrous oxide (70:30) and dextrose–saline (2 ml/h). Expired CO₂, blood O₂, heart rate, electroencephalogram, and temperature were monitored throughout the experiment and maintained at appropriate levels. Corneal protection was provided by neutral contact lenses and emmetropia at a distance of 57 cm was provided by spectacle lenses selected with slit retinoscopy and artificial pupils (2.5 mm). All animal procedures were approved by the McGill University Animal Care Committee and are in accordance with the guidelines set out by the Canadian Council on Animal Care.

Visual stimuli.

Visual stimuli were produced on a Macintosh computer (MacPro 4.1, MacOS 10.6.8, 2.66 Ghz/4 core, 6 Gb, NVIDIA GeForce GT120) using custom software written in Matlab (The Mathworks) with the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997; Kleiner et al., 2007). Stimulus patterns were displayed on a CRT monitor (NEC FP1350, 20”, 640 × 480 pixels, 75 Hz, 36 cd/m², bit depth 8) placed at a viewing distance of 57 cm. The monitor's gamma nonlinearity was measured with a photometer (United Detector Technology) and corrected with an inverse lookup table.

Three types of stimulus patterns were used: first-order luminance-modulated (LM) gratings, second-order contrast-modulated (CM) envelopes, and a compound of the two (LM + CM). In each case, these were zero-balanced patterns of contrast against a mean luminance background, L₀.

Luminance gratings were spatially 1D sinusoidal modulations (Fig. 1A,E) as follows:

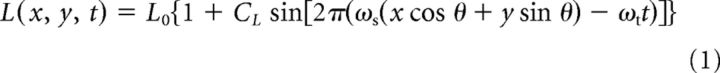where C_L is the Michelson contrast of luminance modulation, ω_s is spatial frequency, θ is orientation, and ω_t is temporal frequency. The second-order stimuli (“contrast envelopes”; Fig. 1B,F) were spatially 1D sinusoidal modulations of the contrast of a high-spatial frequency carrier grating:

The carrier grating was a high spatial frequency, stationary sine wave grating:

where C_c is the carrier contrast, ω_c is carrier spatial frequency, and θ_c is carrier orientation. The carrier was multiplied by an envelope pattern consisting of a low spatial frequency, drifting sine wave grating:

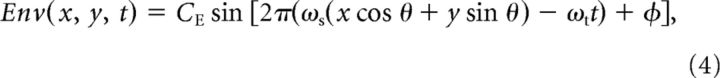where C_E is the envelope contrast, ω_s and ω_t are the envelope spatial and temporal frequency, respectively, and θ is the envelope orientation. The compound stimuli were superpositions of the LM and CM patterns:

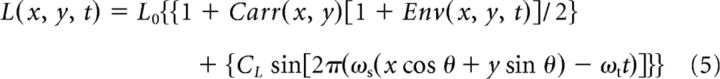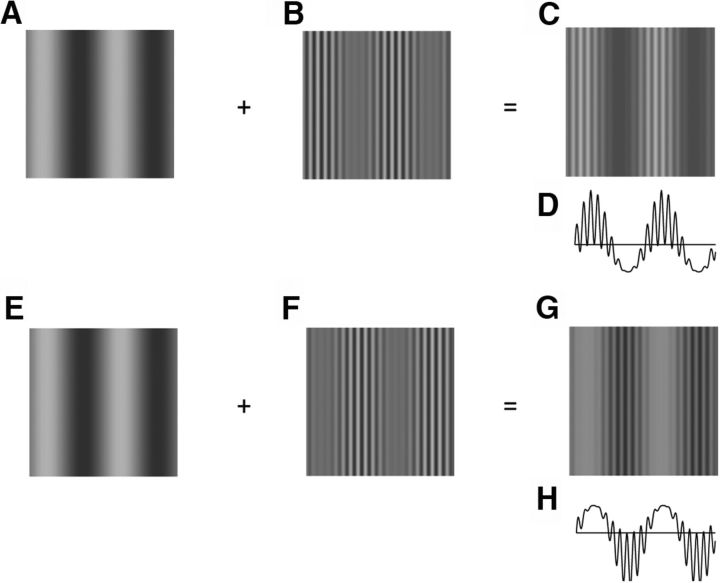
Note that these three stimuli have identical envelope orientation (θ) and spatial and temporal frequencies (ω_s, ω_t), but can have varying values of relative spatial phase (φ). Examples of single frames and 1D profiles are shown in Figure 1, C and D, and Figure 1, G and H (φ = 0° and φ = 180°, respectively). LM and CM stimuli were considered to be “in-phase” (0°) when the high and low luminance bars of the grating were centered on the high- and low-contrast bars of the envelope and “antiphase” (180°) in the opposite case; this definition was determined a priori.

Figure 1.

Examples of stimulus composition for main experiment, in which one LM phase is combined with two different CM phases. A–C, LM (A) added to CM of the same spatial phase (B) produced an in-phase (0° offset) composite stimulus (C). Note that only the contrast variations about the mean background were added, as detailed in Equation 5. Luminance and contrast modulations (LM and CM) were taken to be in-phase when high- and low-luminance and high- and low-contrast bars of the grating and envelope, respectively, were phase aligned. D, 1D luminance profile corresponding to stimulus image in C. E–H, Same as A–D but the component patterns were summed in antiphase (180° relative phase offset), producing a composite stimulus G in which the high- and low-luminance bars of the grating were centered on the low- and high-contrast bars of the envelope, respectively. See text for further details.

Stimulus patterns were presented within a cosine-tapered circular aperture, against a uniform background at the mean luminance of the pattern. The same mean luminance was also maintained during intervals between stimuli, and was presented as blank conditions for measurement of spontaneous activity.

Electrophysiology.

The microelectrode was advanced with a stepping-motor microdrive (M. Walsh Electronics). Single units were isolated with a window discriminator (Frederick Haer) and isolation was monitored on a delay-triggered oscilloscope. Manually controlled bar-shaped stimuli were used to map the receptive field approximately and determine ocular dominance. The display screen was centered on the receptive field and subsequent stimuli were delivered only to the neuron's dominant eye. Spike times were recorded with 0.1 ms resolution (ITC-18; Instrutech) and their temporal registration with the stimulus was established with reference to an optical sensor (T2L12S; TAOS) placed over a corner of the display containing stimulus timing information. Within an experimental run, different stimulus conditions were presented for 0.5–1.0 s in randomly interleaved order (0.5 s for LM gratings, 1.0 s for CM or LM + CM stimuli), with 5–20 repetitions of each stimulus. Poststimulus time histograms and plots of average spike frequency as functions of varied stimulus parameters were displayed online. Spike times and stimulus information were recorded to hard disk files for subsequent detailed analysis.

Each neuron was characterized quantitatively with conventional tuning-curve measurements using first-order grating patterns to establish its optimal orientation, spatial/temporal frequency, simple/complex classification, and location and size of its receptive field. Each neuron was assessed for responsiveness to second-order stimuli using procedures similar to those used previously (Mareschal and Baker, 1999; Tanaka and Ohzawa, 2006). Contrast envelope stimuli were presented using envelope parameters (orientation, spatial/temporal frequency) that were optimal for first-order stimuli and a series of relatively high carrier spatial frequencies were tested (typically ∼0.5–3.0 cpd). A neuron was considered envelope responsive if the data exhibited a band-pass-tuned response to the spatial frequency of the carrier, which was clearly distinct from its response to luminance gratings, such that the contrast envelope response clearly could not be mediated by the same mechanism underlying the response to first-order gratings. Then, using this optimal carrier spatial frequency, the response to a series of carrier orientations was tested systematically to further optimize the response. All subsequent tests used these individually optimized parameters for contrast envelopes, and first-order luminance gratings were used with parameters matched to those of the second-order envelopes.

After these preliminary measurements, subsequent experiments were performed on envelope-responsive neurons. Contrast response functions (Ledgeway et al., 2005) were measured for both first-order (luminance grating) and second-order (contrast envelope) stimuli using identical values of envelope orientation and spatial/temporal frequency. From these data, contrast values for the two stimuli were selected that would produce approximately equated responses. Because neurons are typically more responsive to LM than to CM patterns, a high CM envelope contrast (typically 100%) was chosen and the spike frequency was matched with an equivalent LM contrast. Unless otherwise noted, these values were used for the compound (LM + CM) stimuli that were presented at a series of values of relative spatial phase.

Quantitative measurements for this study were obtained from 76 neurons in nine animals. Note that this work was performed in conjunction with other studies on the same animals being conducted concurrently. Of these neurons, 28 were significantly envelope responsive and their isolation was maintained sufficiently long (∼2 h) to obtain all of the preliminary measurements and the contrast response and phase interaction datasets to qualify for inclusion in the study.

Data analysis.

Spike times were collected into poststimulus time histograms (bin width 10 ms) and plots of time-averaged spike frequency as functions of varied parameters were constructed. Neurons were classified as simple or complex type based on the ratio of response at the first harmonic of stimulus temporal frequency to the average firing rate (Skottun et al., 1991). Optimal parameters for descriptive mathematical functions (see below) were estimated using curve-fitting functionality of Kaleidagraph (Synergy Software) or Matlab (The Mathworks).

Results

Contrast response functions

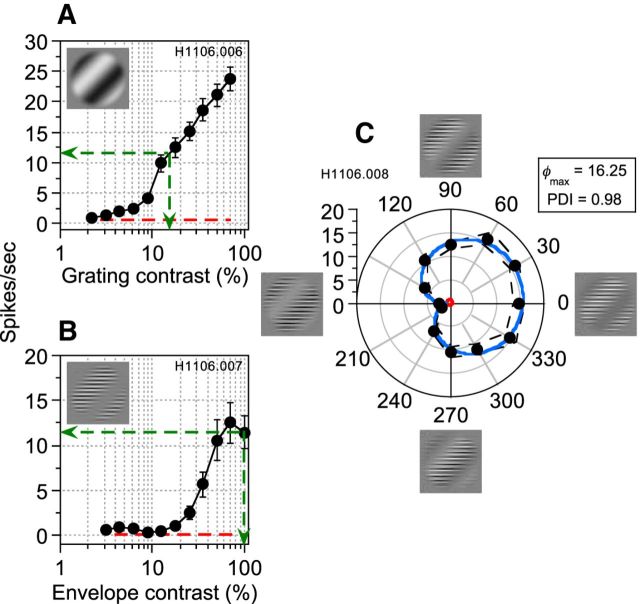
Neurons were markedly less responsive to CM than to LM stimuli, consistent with previous studies (Ledgeway et al., 2005). To maximize the opportunity to detect interactions between the two stimuli and to ensure that the response would not be dominated by the LM stimulus, we amplitude-equated (‘matched’) the two stimulus types in terms of each neuron's responsiveness. This was achieved by measuring contrast response functions (CRFs) for each stimulus type using optimized stimulus parameters as outlined above. Note that, for each neuron, the orientation, spatial frequency, temporal frequency, and direction of motion of the modulation waveforms were identical for LM and CM and, in the case of CM, the optimal carrier was also used. Based on these measurements, we selected values of grating and envelope contrast that elicited an approximately equivalent response (Fig. 2A,B, green dashed lines). A CM carrier contrast of 70% was used throughout to ensure that the sum of carrier contrast for CM and luminance contrast for LM would be physically realizable; that is, not exceeding 100%.

Figure 2.

CRFs and phase-dependent interaction for LM and CM stimuli in which parameters are optimized for an example complex-type cell. A, B, CRFs for a luminance grating and an envelope, respectively. Error bars indicate ±1 SEM. Dashed red lines represent spontaneous activity (responses to a blank field). Dashed green lines show the LM and CM contrast that elicited an equivalent average spike frequency from the neuron. These response-matched contrasts were used to superimpose the grating and envelope at a series of relative phase offsets (0–330°). Both components of the composite stimuli moved together in the neuron's preferred direction. C, Average spike frequencies as a function of relative phase offset of the composite stimuli. Dashed black lines represent ±1 SEM. The red line indicates spontaneous activity. This neuron exhibited responses that depended upon the relative phase relationship between LM and CM stimuli, with maximal response when they were superimposed approximately in-phase and minimal response when close to antiphase. These data were well fit (solid blue line) by a descriptive function (Equation 6) used to derive a PDI (Equation 7) and an estimate of the phase offset (φ_max) that produced maximal responses.

Phase-dependent responses

LM and CM stimuli were superimposed at their response-matched amplitudes and responses (average spikes/s) were recorded as a function of their relative spatial phase offset. In the example of a complex-type cell shown in Figure 2C, the response was markedly dependent on the relative spatial phase difference between LM and CM stimuli, with a peak response at a relative spatial phase somewhat greater than zero (close to phase alignment; Fig. 1C). As the spatial phase offset between the two stimuli increased, responses became less vigorous, producing the weakest responses when LM and CM stimuli were close to antiphase (180°; Fig. 1G).

To quantify the magnitude of spatial phase dependence of a neuron's responses, the measured spontaneous activity was subtracted and the response R as a function of relative spatial phase φ was fit with a descriptive function as follows:

where φ is relative spatial phase between the stimuli, R_min is the minimum response (spikes/s), a is a scaling factor, and φ_max is the spatial phase producing maximum response (R_max = R_min + a). This function corresponds to linear vector summation between two sinusoids of equivalent amplitude. R_max would only equal R_min if there were no vector summation (i.e., if the summation process was phase invariant). An example of such a curve fit is shown by the blue contour in Figure 2C; for illustration purposes, the spontaneous rate has been added back onto the fitted function values to compare to the data points on the plots that also include the spontaneous rate.

To assess the degree of anisotropy in a neuron's response vs the relative spatial phase, a phase-dependency index (PDI) was calculated as follows:

where R_max and R_min are the maximal and minimal spontaneous-subtracted responses, respectively. This PDI value lies between zero, indicating no phase-dependent interaction (i.e., spike frequency remained relatively constant regardless of the relative spatial phase between LM and CM), and unity, indicating a pronounced interaction (highest degree of anisotropy with a well defined “null” phase having zero response).

Six additional examples of such relative phase responses are shown in Figure 3. In the majority of cases exhibiting a marked phase interaction, maximal responses corresponded to a spatial phase offset close to 0° (in-phase). However, some neurons responded maximally at other relative spatial phase offsets (for an example, see Fig. 3E). Minimal responses typically occurred at ∼180° relative to the phase offset that produced the maximal response and corresponded to either a distinct null or to a general “flattening” of responses at a number of phase offsets around antiphase. However, the responses of some neurons showed little or no phase dependency (e.g., the complex cell in Fig. 3D) and were largely invariant regardless of the phase relationship between the two superimposed visual stimuli.

Figure 3.

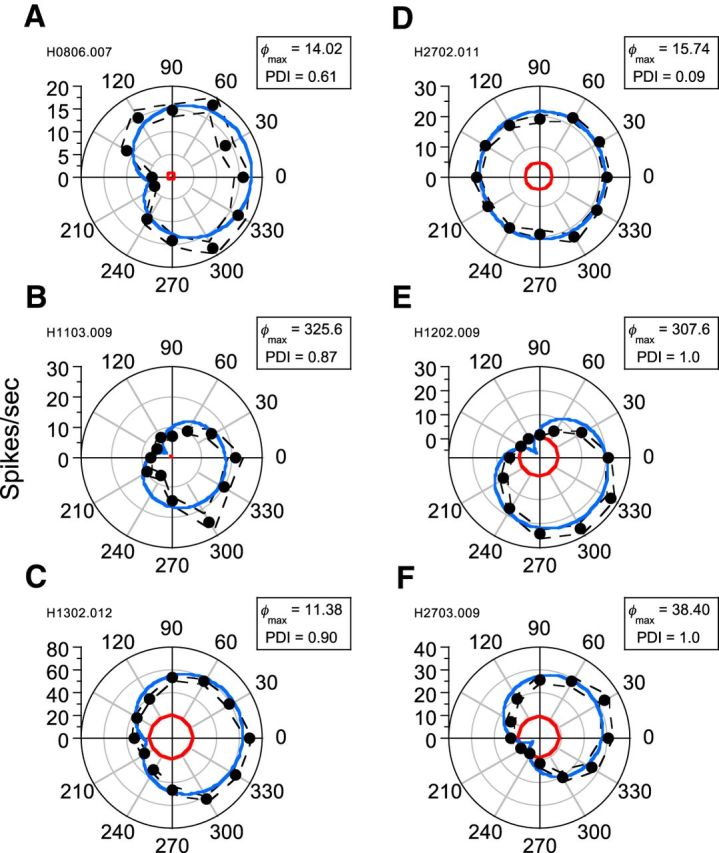
Phase-dependent interactions for six representative neurons. Average spike frequency is plotted as a function of the spatial phase offset between response-equated LM and CM stimuli. Dashed black lines indicate ±1 SEM. Red lines show spontaneous activity. Data from each neuron have been fit (solid blue lines) with a descriptive function (Equation 6). Data from simple-type (B, E) and complex-type (A, C, D, F) cells are shown. Neurons displayed varying amounts of phase-dependent interaction. Phase offsets (φ_max) corresponding to maximal responses and PDI are shown at the top right of each polar plot.

For cells with low PDI, it is possible that the estimated φ_max could depend heavily on the initial value chosen for the curve fitting procedure. To address this concern, we reran the curve fitting for every neuron using a series of initial φ_max values. For this, we used a least-squares simplex (Nelder–Mead) method to fit Equation 6 repeatedly to each neuron's spontaneous-subtracted data and varied the initial φ_max estimate systematically from 0 to 360° in steps of 1°. The initial estimates for the other curve fit parameters were jittered by ±50% on each pass. We then found the set of best-fitting parameters that gave the highest goodness-of-fit (R²) overall for each cell. Therefore, we are confident that the tendency for a φ_max close to 0° is not an artifact of initial conditions in the curve-fitting procedure.

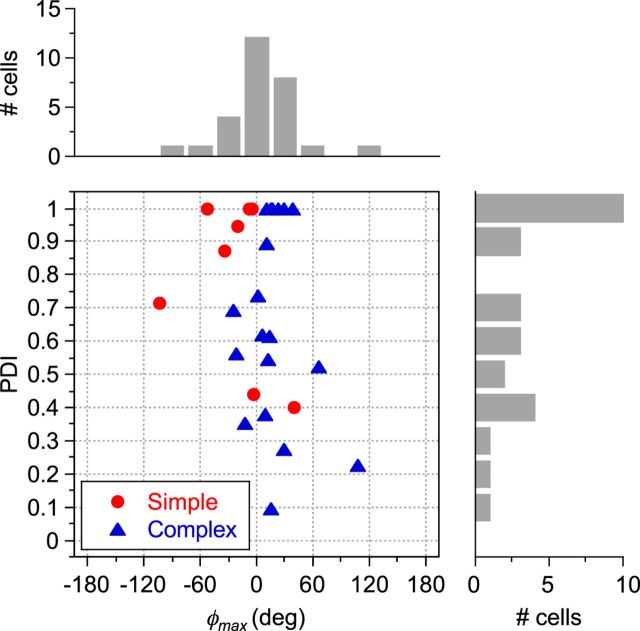
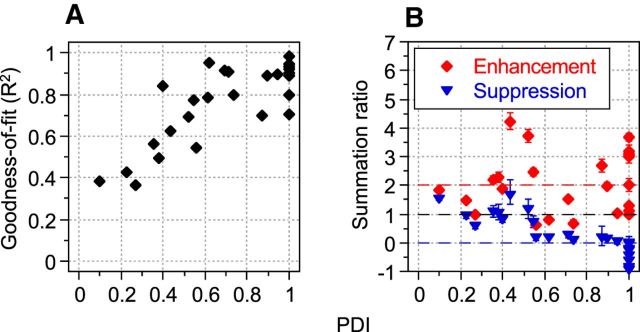
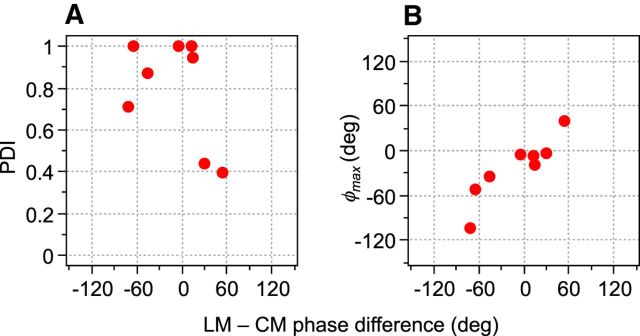
A scatterplot of PDI values and φ_max (degrees) for each neuron in our sample (N = 28) is shown in Figure 4. Different neurons displayed a wide range of responses to the combined LM and CM patterns, with many examples exhibiting a “peak” with maximal response at one particular spatial phase and therefore having a PDI substantially greater than zero. A paired-samples t test confirmed that maximal and minimal responses were significantly different (t = 5.829; df = 27; p < 0.0001) across the sample population, demonstrating the existence of phase-dependent interactions between LM and CM responses. Regardless of their PDI value, neurons typically produced their maximal responses at spatial phase offsets (φ_max) close to 0°. This was true of both simple (circles) and complex cells (triangles) (Fig. 4). Indeed, 86% of neurons exhibited their peak response at spatial phases within ±45° of zero. A complete null (PDI = 1.0) was exhibited by 36% of the neurons. The relationship between PDI and goodness-of-fit (R²) values derived from fitting Equation 6 is shown in Figure 5A. Although, in principle, a relatively low R² could equally reflect either a weak phase dependency or a jagged (noisy) but strong phase dependence, there is a clear systematic trend for low R² values to be associated with the low PDI values, suggesting that it is predominantly a characteristic of cells exhibiting little or no phase selectivity.

Figure 4.

PDIs plotted against optimal phase alignments (φ_max) for all neurons in the sample (N = 28). Simple-type neurons are denoted by red circles and complex-type by blue triangles. Marginal histograms show the distribution of φ_max (top) and PDI (right) values within the sample population. φ_max ranged from −103.42 to 107.35, with a mean of 6.57°. PDI values ranged from 0.09 to 1.0, with a mean of 0.71, indicating a wide range of relative phase dependencies in different neurons.

Figure 5.

Goodness-of-fit and summation ratios for phase-dependent interactions. A, R² values derived from fitting Equation 6 to each neuron's responses to the combined LM and CM patterns plotted against the corresponding PDI values. Equation 6 best fit responses of neurons that exhibited a high degree of interaction with a well defined null phase (PDI values ∼ unity). B, Enhancement and suppression ratios (Equations 8 and 9, respectively) indicating neurons' responses to LM and CM stimuli in isolation compared with responses to their composite at φ_max (enhancement ratio, red diamonds) and φ_max − 180° (suppression ratio, blue triangles). An enhancement ratio of two (red dashed line) indicates that the R_max of the cell is exactly twice as much as both stimuli together as to each in isolation (linear summation). A suppression ratio of zero (blue dashed line) indicates complete nulling of the neuron's response at R_min. Different neurons exhibited a range of enhancement and suppression ratios not always consistent with simple linear summation. Error bars around each of these ratios indicate 68% confidence intervals (∼equivalent to ±1 SE) generated by a nonparametric, bias corrected and accelerated (BCa) bootstrapping technique that created 10,000 bootstrapped replications of each fitted function without assuming a Gaussian distribution for the raw data or the residuals (Efron and Tibshirani, 1993).

Because the anesthesia changed between earlier and later experiments, we investigated whether the anesthesia type was predictive of the degree of phase sensitivity. For each anesthesia type, the PDIs were distributed across the possible range. An independent-samples t test showed that the PDIs did not differ significantly with the type of anesthesia (t = 1.76; df = 26; p = 0.0902). Therefore, we do not believe the change in anesthesia had an effect on the degree of phase sensitivity.

The preference of most neurons for a near-zero phase might suggest that this is a consequence of visual neurons responding better to “dark” than to “light” stimuli (e.g., Jin et al., 2008; Yeh et al., 2009) because there is a perceptual appearance that the dark bars of LM appear more prominent for the in-phase condition (Fig. 1C,G). However, in our stimuli, the LM was simply linearly added to the CM so that both the light and dark bars/bands of the LM were always physically present (i.e., at all relative spatial phases). From the 1D profiles in Figure 1, D and H, it is clear that the net excursions above and below the mean are equivalent for both the in-phase and antiphase stimuli.

Our electrode penetrations were slightly oblique to the surface, traversing all of the laminae down to white matter. However, there was no systematic significant relationship between the PDI value and depth of the recording (Pearson product–moment correlation r = −0.0248; df = 26; p = 0.9023). The neurons with the highest PDI values (1.0) spanned the full range of recorded depths. Therefore, it is highly unlikely that the high PDI cells were concentrated preferentially within a particular range of depths.

To quantify how a given neuron's summation of the two kinds of stimuli differs from simple linear additivity and how this nonlinearity differs from one neuron to another, we also calculated the following ratios:

where R_eq is the firing rate of the neuron that was chosen to equate the grating and envelope contrasts of the stimuli used to investigate phase interactions and R_spon is the neuron's spontaneous firing rate. Note that R_spon is not removed in the numerators of these ratios because R_max and R_min are obtained from curve fits to spontaneous-subtracted responses. R_eq, however, is a measured response value that includes the spontaneous rate. The R_spon values were measured from the average responses to the blank conditions that were interleaved with the phase conditions in the LM + CM experiment. These spontaneous rate values were not significantly different from those similarly obtained from the LM and CM contrast response measurements, as confirmed with a 1-way, repeated-measures ANOVA (F_(2,50) = 1.335; p = 0.2724).

One neuron was excluded from this analysis because its R_spon value marginally exceeded its R_eq values. An enhancement ratio of two (red dashed line in Fig. 5B) indicates that the maximal response (R_max) of the cell is exactly twice as much to both stimuli together as to each in isolation (linear summation). Similarly, a suppression ratio of zero (blue dashed line in Fig. 5B) indicates complete nulling of the neuron's response when the stimuli are in antiphase (R_min) relative to φ_max. Enhancement ratios spanned 0.627 to 4.209 (mean = 2.082) and suppression ratios spanned 1.647 to −0.933 (mean = 0.342), indicating considerable heterogeneity among our neuron population (Fig. 5B). There was a moderate tendency for the magnitude of the suppression ratio to decrease as PDI increased, indicating a greater suppressive influence for neurons that exhibited the largest phase dependencies. Whether neurons were of the simple or complex type did not affect either ratio systematically.

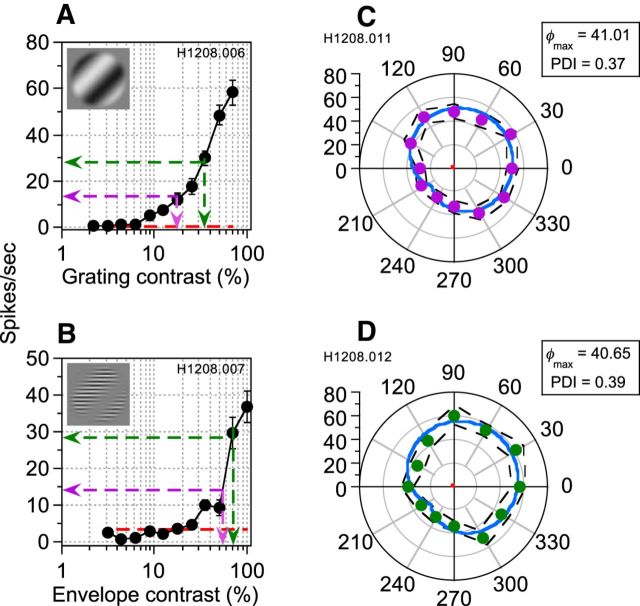
To confirm the appropriateness of our LM and CM response-matching procedure, for a number of neurons, we measured phase-dependent interactions between LM and CM at two different response-matched contrasts. An example from a simple-type neuron is shown in Figure 6. LM (Fig. 6A) and CM (Fig. 6B) contrasts were matched at either 14 (purple dotted lines) or 28 (green dotted lines) spikes/s. Comparable phase dependence was evident at both response-matched amplitudes (14 spikes/s; Fig. 6C; 28 spikes/s; Fig. 6D), with similar φ_max and PDI values for each, thereby verifying the robustness of our matching paradigm and confirming that the absolute firing rate chosen to equate the two types of stimuli was not critical to the pattern of results found.

Figure 6.

CRFs and phase-dependent interactions at two different response-matched contrasts for a simple-type neuron. A, B, CRFs for a LM and a CM, respectively. Error bars indicate ±1 SEM. Dashed red lines represent spontaneous activity. Dashed purple and green lines show the stimulus contrasts evoking equivalent responses from the neuron at two different spike frequencies (14 and 28 spikes/s, respectively). C, Phase-dependent interaction plot for component stimuli matched at 14 spikes/s. D, Same as C, but for response-matching at 28 spikes/s. In C and D, dashed black lines above and below the data points represent ±1 SEM. The red line shows spontaneous activity. Data were well fit by a descriptive function (Equation 6, solid blue line), which produced qualitatively and quantitatively similar results regardless of the absolute firing rate chosen to equate the two types of stimuli. Note that the derived φ_max and PDI values are almost identical (φ_max values were 41.01° and 40.65° and PDIs were 0.37 and 0.39) in each case.

Some of the sampled neurons were simple-type cells and thus had modulated responses to the drifting LM or CM stimuli. We wondered whether analysis of the temporal phases of these responses might be related to the dependence on relative spatial phase of LM and CM stimuli. To investigate this, we examined the temporal phase of the first harmonic at the equated contrast value in the contrast response measurements (interpolating where necessary) for LM and CM gratings. Figure 7A shows that the amount of phase interaction, PDI, did not show a significant relationship with the difference in temporal phases for LM and CM responses (Pearson product moment correlation coefficient r = −0.4750; df = 6; p = 0.2342), although this may not be surprising in view of the small sample size. However, in Figure 7B, φ_max shows a clear and statistically significant positive association (r = 0.9088; df = 6; p = 0.0018) with the temporal phase difference. As the temporal phase difference increases, the φ_max also increases systematically. Therefore, it looks like a lawful and expected relationship, for the simple cells at least, that the variation in φ_max away from a relative spatial phase of zero is driven by the difference in the temporal phases of the response to the two types of stimulus.

Figure 7.

Relationship of LM + CM phase interactions to temporal phase lags of responses in simple-type cells. A, Amount of PDI as a function of difference in temporal phase lag measured for LM and for CM stimuli presented alone in simple-type cells having modulated discharges. B, Same as A, but optimal phase (φ_max) for response to LM + CM compound stimuli showing an approximately linear relationship.

Amplitude-dependent responses

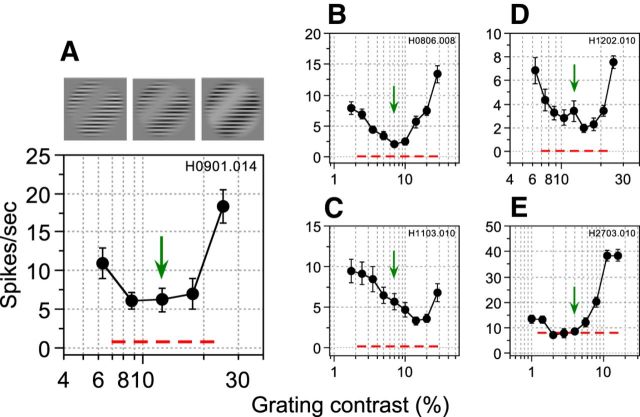
Neurons typically exhibited an enhanced response when LM and CM stimuli were phase aligned and a diminished response at or around antiphase (Figs. 2C, 3, 6C,D). However, the magnitude of the neuronal response might be determined, not only by the spatial phase offset between LM and CM, but possibly also by other factors such as the relative amplitudes of the two spatially superimposed stimuli. When LM and CM stimuli were equated in terms of response, neurons produced a null or minimum response at antiphase compared with their in-phase response. This is presumably because, in the former condition, LM and CM effectively cancelled each other out (Fig. 1G) and no net driving signal was available to the neuron. At antiphase, effective visual information can be reintroduced by increasing the amplitude of one stimulus relative to the other so that they are no longer effectively balanced. If one stimulus drives the neuron more strongly than the other, then the nulling would be abolished and the neuron should become more responsive. To test this notion, we fixed the amplitude of the CM stimulus at the value used to measure phase-dependent interactions and varied the contrast of the LM stimulus at the neuron's null phase so that it was less than, greater than, or equal to that derived from the response-matching procedure (green arrows in Fig. 8). When stimuli were superimposed in antiphase with their amplitudes carefully equated, the neuron produced a minimal response. However, when the LM contrast was either reduced or increased beyond this match point, the neuron's response increased as the two superimposed stimuli became progressively mismatched. Figure 8, B–E, shows results from a further four representative neurons. The precise nature of the interaction varied according to the contrast range used in each neuron, which was determined by the CRFs for each stimulus type and constrained by the requirement that the sum of the LM grating contrast and CM carrier contrast cannot exceed 100%. Among the examples of these measurements shown in Figure 8, some cells exhibited responses that were reasonably symmetrical around the central match point (Fig. 8A,B,D), indicating that LM and CM were well equated at this contrast level. In some cases, the responses were appreciably less symmetrical, which may be due in part to imperfect equating of the stimulus components (Fig. 8C) or the limited contrast range available (Fig. 8E).

Figure 8.

Contrast dependent interactions for five representative neurons. Data from simple-type (C,D) and complex-type (A,B, E) neurons are shown. LM and CM were superimposed at the phase offset that produced the minimal response (A: 210°, B: 180°, C: 150°, D: 120°, and E: 180°) and their relative amplitudes (contrasts) varied. An example stimulus set is shown in A. CM contrast was fixed at 100% and LM contrast varied above and below the response-matched value. Red dashed lines show spontaneous activity. Green arrows show response-matched grating contrasts. Error bars indicate ±1 SEM. In most cases examined, firing rates increased as the two superimposed stimuli became progressively mismatched.

Discussion

We have shown that neurons in early visual cortex, which respond form–cue invariantly to first-order LM and second-order CM, responded in a systematic manner to the relative spatial phase offset between the two kinds of patterns when they were superimposed. In both simple- and complex-type cells, maximal responses typically occurred when response-equated LM and CM were superimposed at or close to phase alignment, with a minimal response when in antiphase. In many cases, maximal and minimal responses were markedly different to varying degrees in different neurons. Neurons varied substantially in the relative roles of suppressive or facilitative interaction effects. The degree of this interaction between LM and CM at antiphase could be modified by increasing the amplitude of one stimulus relative to the other. When the LM amplitude was either reduced or increased around a fixed CM amplitude, responses increased as the two superimposed stimuli became progressively mismatched.

An important concern in experiments using CM stimuli is that the observed neuronal responses might be due to “distortion products” from nonlinearities of the display device or the photoreceptors (MacLeod et al., 1992; Zhou and Baker, 1994). Such artifactual responses would occur regardless of carrier pattern characteristics. CM responses here were tuned selectively to relatively high values of carrier spatial frequency well outside of the luminance passband and thus were highly unlikely to be artifactual. The phase dependence of the response to combined LM and CM could arise in a similarly artifactual manner. However, in that case, the optimal phase value would always be the same; for example, an early expansive nonlinearity would always give φ_max = 0°. This is because an expansive nonlinearity introduces a distortion product into the neural representation of a contrast-modulated image with the same frequency and phase as the modulating waveform (see Fig. 1 of Smith and Ledgeway, 1997) that will combine with a superimposed luminance grating of the same spatial phase to produce a maximal response. We observed a considerable scatter in values of optimal phase in different neurons, again making such a possibility highly unlikely.

It is entirely possible that we may have missed some relevant neurons due to our protocol. Our neuron search stimulus was a bar of light and, as such, would not reveal neurons that were responsive to only CM stimulus attributes or even possibly a CM-driven neuron in which the response to CM can be modulated by LM. We only examined neurons that responded both to LM and to CM in isolation, so we might have missed, for example, neurons that are unresponsive to CM in isolation, but with an LM response that is affected differentially by superposition of CM stimuli in different relative phases. Moreover, there might exist neurons that respond only to specific stimulus combinations, but not to LM or CM stimuli alone. Currently, there is no evidence for the existence of neurons having such highly nonlinear summation, but if they were present, we would have missed them.

Psychophysical studies of LM and CM mixtures

Psychophysical studies have examined the degree to which first- and second-order cues interact perceptually when they are spatially superimposed. For example, Smith and Scott-Samuel (1998) showed that spatial frequency discrimination and speed discrimination could be enhanced when first- and second-order gratings were superimposed compared with when each was presented alone. Similarly, Johnson et al. (2007) found that texture discrimination was enhanced or impaired depending on whether the local elements comprising the textures contained spatially correlated or uncorrelated LM and CM information, respectively.

Masking studies have also investigated whether LM and CM gratings interact in a phase-specific manner, the underlying assumption being that, if the two types of stimuli are encoded by a common mechanism, then detection should be highly dependent on the two patterns' relative spatial phase. For example, Badcock and Derrington (1989) explored the possibility that second-order motion, defined by variations in contrast, is detected on the basis of a distortion product, by adding a moving sine grating (LM) to a drifting beat (CM) pattern of the same spatial frequency. The LM was 180° out of phase with the CM and its amplitude was varied in an attempt to null the hypothetical distortion product. They found that direction identification performance was unimpaired by the presence of the moving LM. Lu and Sperling (1995) also found no appreciable phase dependency when performance was measured for combinations of drifting LM and CM noise matched for spatial frequency and effective amplitude, although others (Scott-Samuel and Georgeson, 1999; Allard and Faubert, 2013) have reported phase dependence, but only at high temporal frequencies (15 Hz). Studies using stationary patterns are also equivocal with regard to the influence of relative spatial phase. Some have found moderate to strong phase selectivity (Henning et al., 1975; Nachmias, 1989), whereas others have reported that masking magnitude is independent of phase (Cropper, 1998; Willis et al., 2000). A complication is that other factors such as extended practice, individual differences, local luminance cues in the image, and the predictability of the phase relationships on each trial are also known to influence performance on this task (Nachmias and Rogowitz, 1983; Badcock, 1984). One possibility that could reconcile these discrepant results is that the human visual system contains neurons responsive to both LM and CM, but with a range of phase selectivity (cf. Fig. 3). Performance in a given situation could depend on which neurons are most sensitive, giving rise to either phase-independent or phase-specific masking.

Neural mechanisms

In early visual cortex of the cat and the macaque, a substantial fraction of the neurons respond both to first- and second-order patterns (Zhou and Baker, 1994; Li et al., 2014). Most proposed models of such responses involve two parallel signal processing pathways, each specialized for one or the other type of stimulus, the signals of which are then combined (Mareschal and Baker, 1999). Alternatively, cortical second-order responses could originate from LGN (and ultimately retinal) Y-cells, the responses of which carry both luminance information at low spatial frequencies and specificity for carrier attributes at high frequencies (Rosenberg and Issa, 2011). The present findings of phase-dependent combination are not incompatible with either of these schemes. Models based on human psychophysics have involved separate early detection of the two kinds of stimuli, with subsequent interactions at a later stage (Georgeson and Schofield, 2002). A model with crosswise gain control interactions between pathways carrying a mixture of first-and second-order information (Schofield et al., 2010; Sun and Schofield, 2011) predicts our observations of stronger responses to in-phase than antiphase conditions.

As a baseline reference, it is worth considering that a cortical neuron might just linearly add the separately computed responses to LM and CM stimuli. In the case of a simple-type cell, the modulated responses to the LM and CM stimuli would sum maximally at one phase and cancel out at the opposite phase, giving a PDI approaching unity. In fact, the optimal relative phase values were linearly predictable from the phase lags of the LM and CM alone (Fig. 7B). The lack of relationship to the PDI value (Fig. 7A) may be because the effect of the temporal phase lag is to effectively shift the φ_max value in a neuron that already is or is not phase selective. Complex-type cells might be thought of as linearly adding energy-like responses to LM and CM stimuli, which would not be modulated and thus their summation should be phase invariant (PDI = ∼0). Alternatively, a complex cell might result from an energy-type operation on pooled responses of simple cell (modulated) responses to LM and CM stimuli, early summation of which would give a high PDI. In our sample, the complex-type cells showed a wide range of PDI values (Fig. 4), suggesting a continuum between such types of models.

Functional implications/significance

These neurons show complex interactions between both amplitude and phase of LM and CM components, which are in some cases consistent with vector summation. This finding suggests a modification of the form–cue invariance principle (Albright, 1992). Although these neurons are form–cue invariant to orientation, spatial frequency, and motion direction, they are in most cases not invariant to the relative phase of superimposed first- and second-order components.

These properties might have implications for how the visual system processes natural images. Neurons with little or no LM + CM phase dependence would respond to boundaries regardless of the configuration of their components, whereas those having a strong phase dependency would respond selectively to particular co-occurrences of first- and second-order information in natural images (Johnson and Baker, 2004). These neurons' responses carry information that may help to disambiguate whether luminance changes in the retinal image arise from surface reflectance changes or from illumination gradients such as shading or shadows (Schofield et al., 2006, 2010; Sun and Schofield, 2011). More generally, the heterogeneity in degree of phase-dependent interactions and suppression versus enhancement might provide a basis for disambiguating or decoding a variety of different kinds of boundaries. A promising future direction would be to examine the relative phases of LM and CM components at boundaries in natural images that arise from different causes.