Memory Transformation Enhances Reinforcement Learning in Dynamic Environments

Abstract

Over the course of systems consolidation, there is a switch from a reliance on detailed episodic memories to generalized schematic memories. This switch is sometimes referred to as “memory transformation.” Here we demonstrate a previously unappreciated benefit of memory transformation, namely, its ability to enhance reinforcement learning in a dynamic environment. We developed a neural network that is trained to find rewards in a foraging task where reward locations are continuously changing. The network can use memories for specific locations (episodic memories) and statistical patterns of locations (schematic memories) to guide its search. We find that switching from an episodic to a schematic strategy over time leads to enhanced performance due to the tendency for the reward location to be highly correlated with itself in the short-term, but regress to a stable distribution in the long-term. We also show that the statistics of the environment determine the optimal utilization of both types of memory. Our work recasts the theoretical question of why memory transformation occurs, shifting the focus from the avoidance of memory interference toward the enhancement of reinforcement learning across multiple timescales.

SIGNIFICANCE STATEMENT As time passes, memories transform from a highly detailed state to a more gist-like state, in a process called “memory transformation.” Theories of memory transformation speak to its advantages in terms of reducing memory interference, increasing memory robustness, and building models of the environment. However, the role of memory transformation from the perspective of an agent that continuously acts and receives reward in its environment is not well explored. In this work, we demonstrate a view of memory transformation that defines it as a way of optimizing behavior across multiple timescales.

Introduction

Over short time periods, the natural world is highly correlated with itself, whereas over longer time periods, short-term correlations give way to larger statistical patterns. For example, if a bird discovers fruit on a tree, then returns to the same tree an hour later, it is likely to find more. In contrast, if the bird returns to the same tree a month later all of the fruit may be gone, making the memory for that individual tree less useful. Nonetheless, combining many such memories provides the bird with general knowledge of where food may typically be found. Hence, two types of memory (specific vs general) may be more or less useful depending on the amount of time that has passed.

Given these considerations, it makes sense that the brain relies on multiple systems to guide behavior (Klein et al., 2002; Doll et al., 2012, 2015), including those that capture general patterns (schematic memories) and those that capture specific experiences (episodic memories) (Tulving, 1972; Lengyel and Dayan, 2007). Moreover, humans and animals often rely on recent episodic memories to make decisions, but episodic memories give way to schematic memories over time as part of a memory reorganization process (Moscovitch et al., 2006; Tse et al., 2007; Winocur et al., 2010; Tse et al., 2011; Winocur and Moscovitch, 2011; Richards et al., 2014), sometimes referred to as “schematization” or “memory transformation” (Winocur et al., 2010; Winocur and Moscovitch, 2011). The benefits of this episodic to schematic transformation are usually assumed to be reduced memory interference (McClelland et al., 1995; O'Reilly and Rudy, 2001), and the formation of a more stable memory (Squire and Alvarez, 1995). However, these perspectives do not consider the potential advantages of memory transformation for making decisions that exploit the temporal statistics of the environment.

Some computational work has explored the idea that episodic to schematic transitions could be beneficial for guiding behavior (Lengyel and Dayan, 2007). These results suggest that there is a performance improvement in using episodic memories soon after a novel experience and schematic memories after more experience. However, this considers only the accumulation of data, and not the passage of time. In the real world, there are periods of data accumulation (e.g., foraging) and periods without data (e.g., rest, migration), and memory transformation occurs regardless of whether data are being accumulated or not (Winocur et al., 2007; Richards et al., 2014).

To test whether the benefits of memory transformation are a consequence of the accumulation of time itself, we developed a computational model of an agent with both episodic and schematic memories. The agent uses only its position in a 2D environment and rewards found at specific spatial locations to learn a navigational model, store episodic memories, and build schematic memories via replay. We trained the agent in an environment where the reward locations constantly changed, such that new reward locations were correlated in the short-term but were independent and sampled from a stable distribution in the long-term. As well, we varied the amount of time between foraging trials. We show that the best strategy in this environment is to rely on episodic memories after short delays but to shift to schematic memories after long delays, independent of data accumulation. We also find that the timing of this shift depends on the temporal statistics of the environment. When in environments that tend to be consistent for long periods of time, the optimal strategy is to shift to schematic memories slowly. Finally, we explored whether memory transformation was also beneficial when the long-term distribution of rewards was nonstationary. We found that the benefits of schematic memories are limited to cases where the long-term pattern of rewards is relatively stable. These results suggest that the temporal statistics of the world are one of the principal reasons that both episodic and schematic memories are used by the brain to guide behavior. Furthermore, the extent to which an animal relies on detailed or gist-like memories at different times may be tuned to optimize reinforcement learning in different contexts (Moscovitch et al., 2006; Winocur et al., 2010; Winocur and Moscovitch, 2011).

Materials and Methods

Simulated foraging task.

In this study, we use a simulated foraging task wherein a model agent must navigate a space to find a moving reward. Here, the reward moves within a bounded space of arbitrary units, with the boundaries set to [0, 1]. The reward location, l(t), moves with incremental shifts within a “bout” or sudden shifts between “bouts” (see Fig. 1). Incremental shifts correspond to the addition of a white noise variable to l(t), whereas sudden shifts correspond to a resampling of the reward location according to a predefined multivariate normal distribution in space. Specifically:

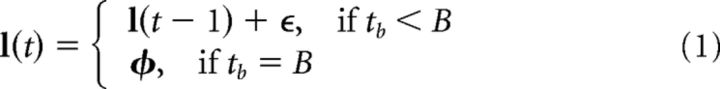Here, ϵ = [ϵ₁, ϵ₂], where ϵ₁, ϵ₂ ∼ 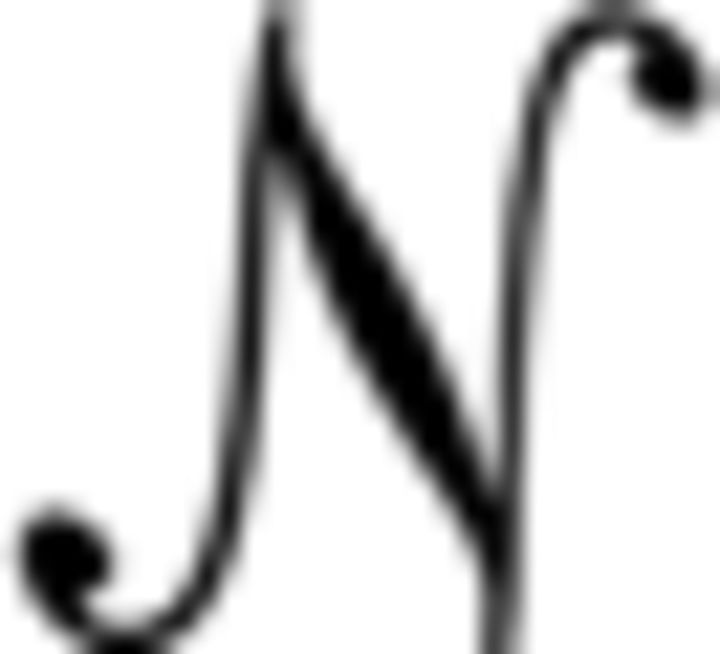(0, σ_ϵ). Similarly, φ = [φ₁, φ₂], where φ₁, φ₂ ∼ 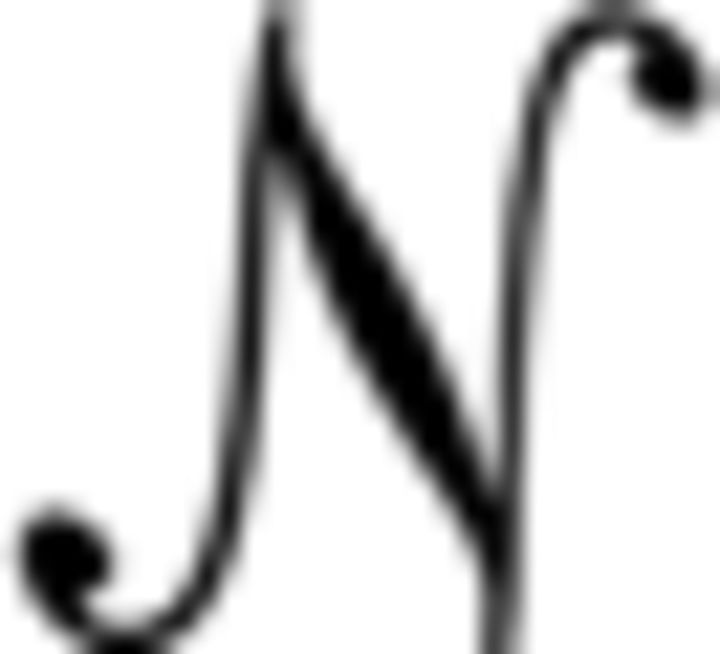(μ, σ_φ), and thus represents a randomly selected new location for the reward at the start of a new bout with mean value μ. t_b refers to the time within a bout of length B. In some simulations, B was held at a constant value (see Figs. 4, 6, 7), whereas in other simulations, it was sampled from an exponential distribution with rate parameter β_bout (see Fig. 5).

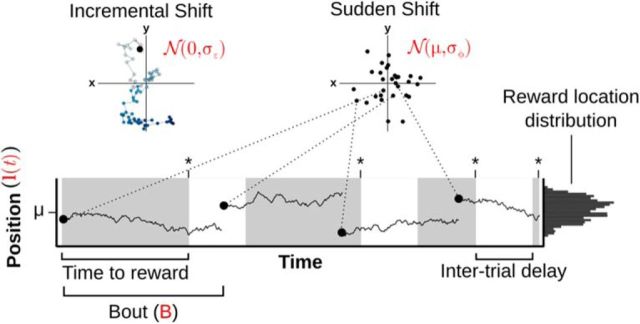
Figure 1.

Illustration of a simulated foraging task and the passage of time. The agent was tasked to find reward locations that moved through a bound environment. After finding a reward (considered one trial, shown as gray regions, asterisks indicate found rewards), the agent was given a “rest” period termed the “intertrial delay.” The position of the reward, l(t), moved incrementally within a bout of length B. At the end of a bout, the location was resampled from a Gaussian distribution with mean μ. Importantly, the movement of the reward proceeded regardless of whether the agent was foraging (gray regions) or resting (white regions). This implies that reward locations would tend to stay in approximately the same location at short intertrial delays but would tend to be sampled from the long-term distribution after long intertrial delays.

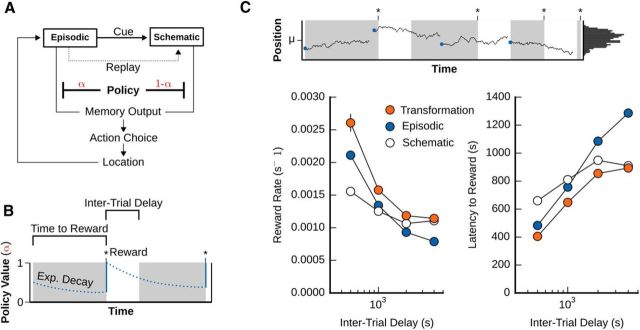
Figure 4.

Shifting from episodic to schematic memory over time improves agent performance. A, Diagram of the memory transformation process. The memory transformation agent combined episodic and schematic models using a policy unit α to switch between episodic (α = 1) and schematic (α = 0) output for guiding navigation. B, Dynamics of the policy unit. The policy unit exhibited an exponential decay as time passed, reverting back to episodic navigation immediately after reward had been found. So, the intertrial delay directly impacted the agent's initial search strategy when starting a new trial. C, Performance of the episodic-only, versus schematic-only versus transformation models. The memory transformation agent outperformed the best performance (both mean latency to reward, and reward rate) of either the episodic or schematic systems alone across all intertrial delays (delay ∈ {500, 1000, 2000, 4000}).

Figure 6.

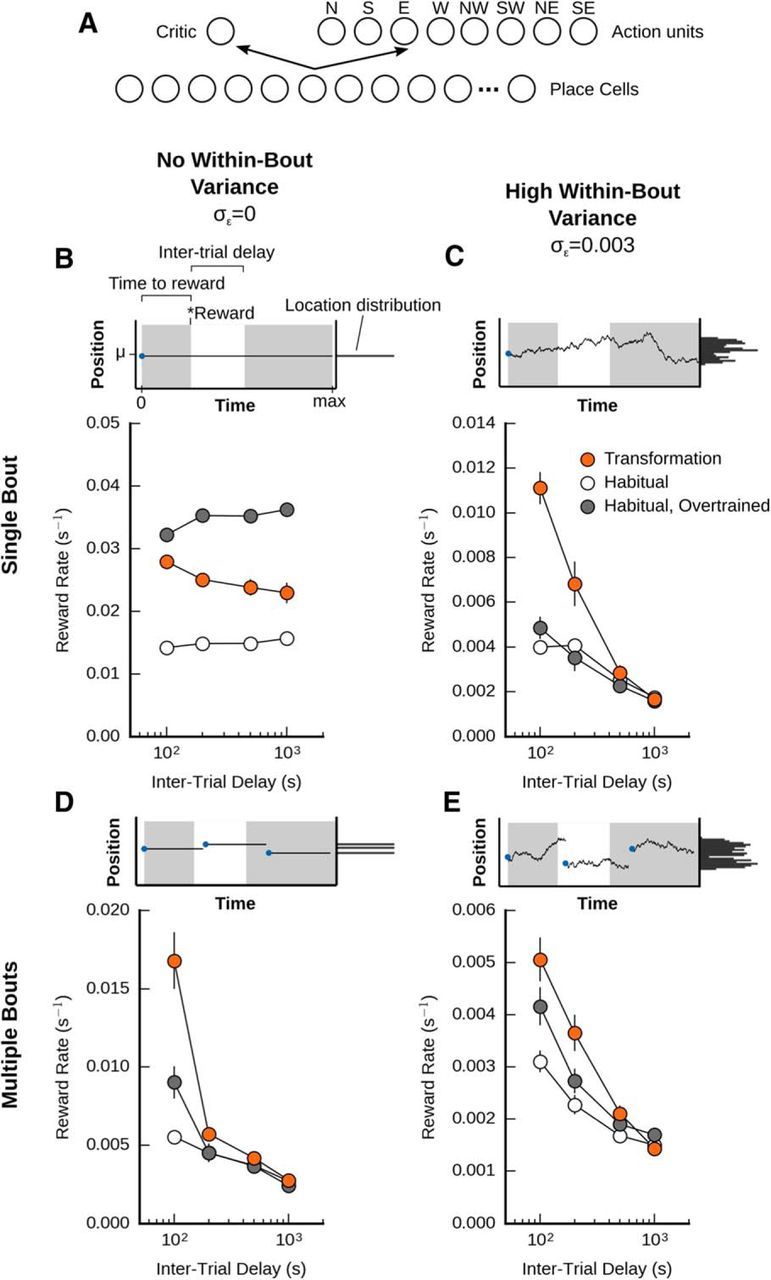
A habitual agent is not as effective at foraging as the memory transformation agent in a variable environment. A, Illustration of the habitual agent architecture. The agent with memory transformation was pitted against a habitual (model-free) system, composed of place cells that interacted with a critic, which learned a value function, and an actor that learned a place-to-action function. B, Performance of the agents when the reward location was constant. When tasked to find a stationary reward within a single bout, the habitual system with 400 trials of extra training outperforms an episodic model-based system, which in turn outperforms a model-free system that received an equivalent amount of training. C, Performance of the agents with some within-bout variance (incremental changes), but no new bouts (i.e., no between-bout variance). D, Performance of the agents with no within-bout variance, but some between-bout variance (i..e. multiple bouts). E, Performance of the agents with both between-bout and within-bout variance.

Figure 7.

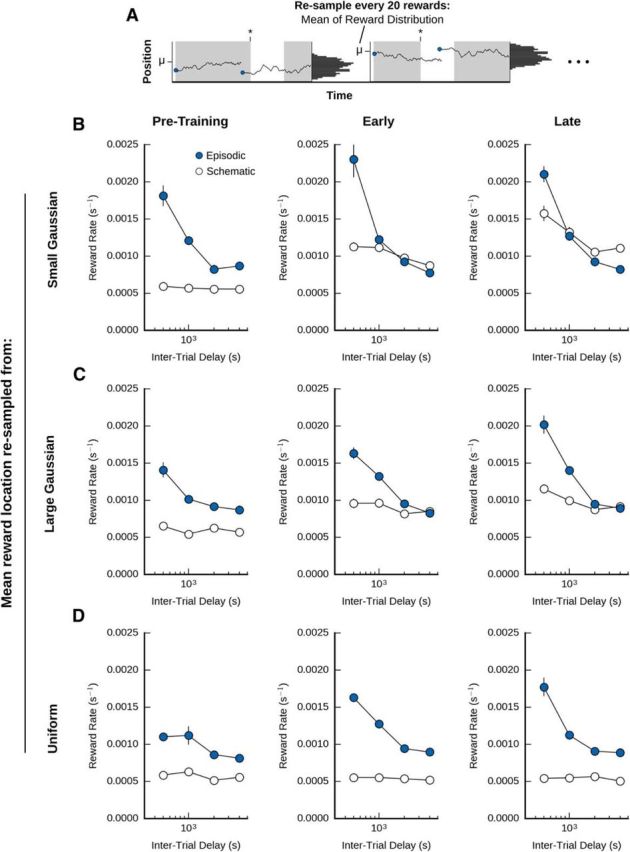
The benefits of schematic memory depend on a stable long-term distribution of reward locations. A, Illustration of a nonstationary long-term distribution. We trained agents in a set of tasks where the mean of between-bout reward locations (μ, see Fig. 1) was itself sampled from another distribution after every 20 trials. B, Performance of episodic-only and schematic-only agents in the case where new μ values were resampled from a small Gaussian distribution, μ ∼ 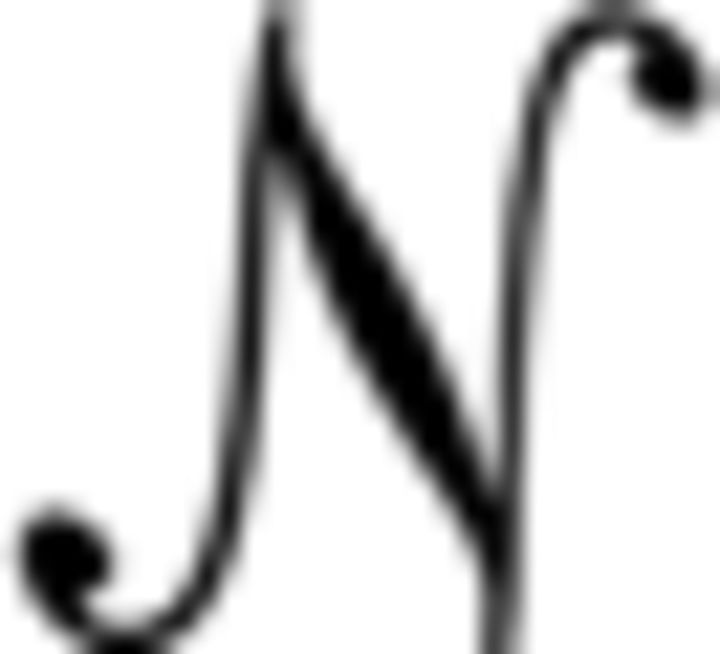(0.7, 0.05). C, Performance of the agents in the case where new μ values were resampled from a large Gaussian distribution, μ ∼ 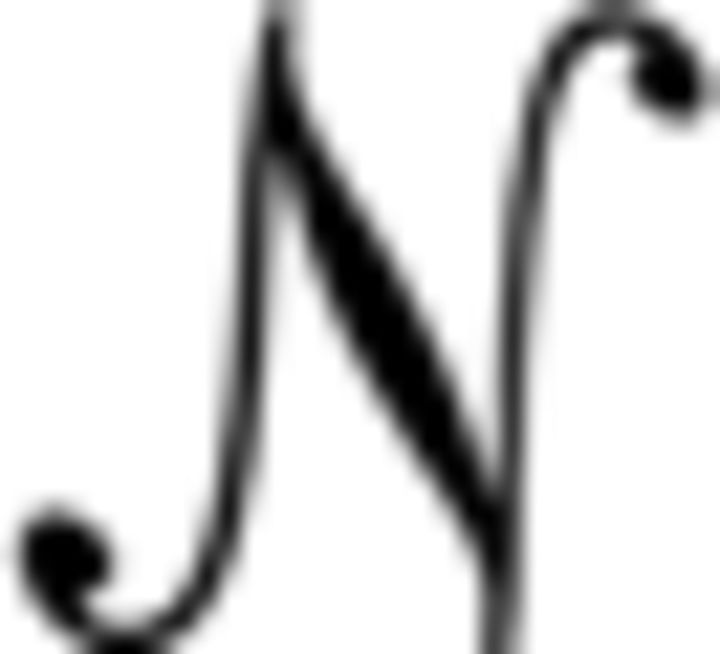(0.7, 0.11). D, Performance of the agents in the case where new μ values were resampled from a uniform distribution (μ ∼ U (0, 1)). We examined the performance of the agent during the first 20 trials (pretraining, left columns), the second set of 20 trials (early training, middle columns), and the last set of 20 trials (late training, right columns). In the first trials of pretraining the episodic system outperformed the schematic system. However, the schematic memory system came to outperform the episodic system at high intertrial delays when μ was resampled from a low variance Gaussian distribution (B, middle and right columns). When μ resampling was done with a uniform distribution, the episodic system always outperformed the schematic system (C, D).

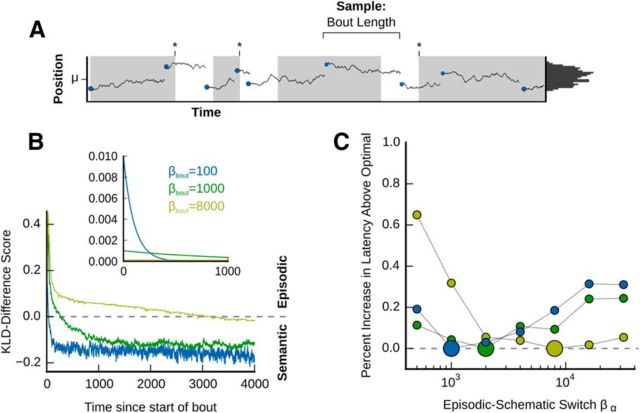
Figure 5.

Memory transformation can be optimized to the temporal dynamics of the environment. A, Illustration of the foraging task with randomly sampled bout lengths (the end of a bout is indicated by a jump in the reward location). B, Comparison of the accuracy of episodic versus schematic memories over time. If bouts are sampled from an exponential distribution, then the time it takes for the memory output from the schematic system to more accurately match an analytically computed expected reward distribution is dependent on the rate parameter for bout sampling (β_bout, inset). A negative value in the Kullback–Leibler divergence (KLD) difference score indicated better schematic match, whereas positive values indicated better episodic match. C, Test of the ability of a combined network to optimize its performance under conditions where bouts were sampled using different β_bout values. Larger circles represent the best performing episodic-schematic switch value (β_α), with other values being compared with this best performing value. As the bout lengths increased (blue vs green vs yellow circles), the optimal episodic-schematic switch time similarly increased.

Importantly, this formulation ensures that over short time spans the expected value of the reward location is correlated with its last location, whereas over longer time spans the reward location tends to be a random variable that is independent of any previous, specific locations, given knowledge of the underlying distribution (see Expected reward probability distribution). Although this is a very abstract environment, we would argue that this principle tends to hold true in the real world (i.e., the world tends to be correlated with itself over short periods of time and regress to a general distribution over longer periods of time). Additionally, by changing σ_ϵ or β_bout, the degree of the correlation in reward locations over different time spans can be modulated.

At the start of each trial, the agent is initiated in a random location in the space. Whenever a reward is found, a trial ends and the agent “rests” for an intertrial delay. Importantly, although the agent is not interacting with the environment during the intertrial delay, the reward location continues to move, meaning that the reward will be at a new location when the agent begins a new trial. Hence, the length of the intertrial delay influences the probability that the reward location is correlated with the location where the agent last found it.

We tasked the agent to find 120 rewards in total and measured its performance on the final 100 rewards (the first 20 rewards were considered the “pretraining period” for the agent). We calculated the agent's performance as the reward rate (s⁻¹), or mean latency to reward (s). Reward rate is computed as the inverse mean latency to reward. Each simulation (i.e., the finding of 100 rewards) counts as one sample in the data presented, within which the mean or inverse mean is computed. In all the data presented in this paper, we use n = 20 samples per condition.

Basic agent architecture.

The agent we use in this simulated foraging task has three major components: an episodic memory system, a schematic memory system, and a forward model for navigation (see Fig. 2A). In addition, the agent has a critic module that estimates the value of any given location in space based on the agent's reward history, which then enables the calculation of a prediction error for rewards (for details, see Temporal difference learning). In most of the simulations in this paper, the agent makes decisions about where to move in the environment by using the outputs from its episodic and schematic memory systems as goal locations, and using the forward model to determine how to navigate to those goals. The one exception is the “habitual” agent (see Habitual agent; see Fig. 6), which uses an actor module coupled to the critic module to implement a typical actor-critic reinforcement learning strategy (Sutton and Barto, 1998; Foster et al., 2000).

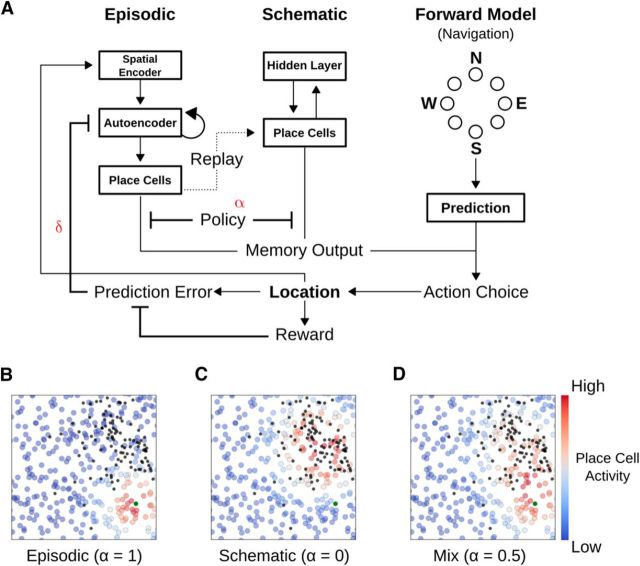
Figure 2.

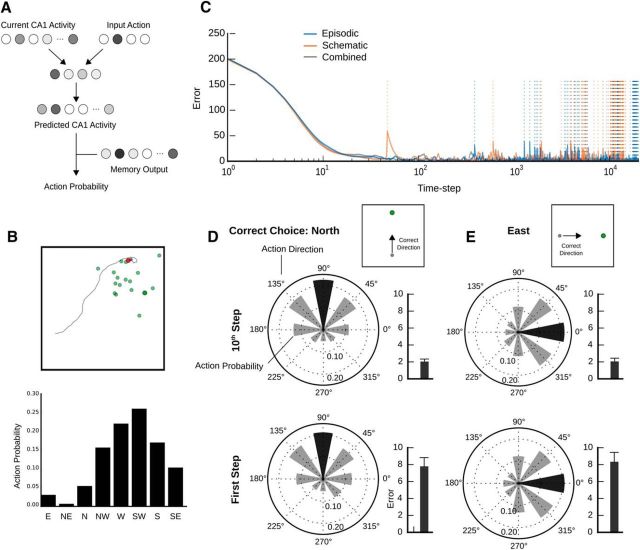
A neural network model of a foraging agent with two memory systems. A, Illustration of the neural network model. To perform the task, the agent was equipped with both episodic and schematic memory stores, as well as a navigation network. The episodic network consisted of a spatial encoder, autoencoder, and place cells, whereas the schematic network was a two-layer network (specifically, an RBM). Recall outputs from these memory systems were fed into the navigation network, which chose actions such that the agent's subsequent position was most probably congruent with the memory systems' encoded reward location. Computed prediction errors influenced the strength of encoding of the agent's current position, with encoding occurring in an online, continuous fashion. B–D, Examples of recalled place cell activities for the different types of memory. A policy unit, α, determined the relative influence of the episodic and schematic systems to the overall memory output on the place cells. Each colored circle represents a place cell, with the color showing the activity level. B, Episodic memory output. High levels of α promoted episodic output, which produced place cell activities congruent with the most recently found reward (large green circle). C, Schematic memory output. Schematic outputs (small α) produced place cell representations congruent with the statistics of all previously learned reward locations. Black dots represent previously found rewards. D, Mixed memory output. A mix (α = 0.5) produced a blend of the two memory systems in place cell activity.

Episodic system architecture and information flow.

The episodic memory system in our agent is a neural network designed to have the following properties: (1) store specific reward locations, (2) emphasize more recent memories, and (3) store new memories continuously, with the strength of storage modulated by the relevance of the memory to finding rewards. We chose these properties because they are in line with the characteristics of episodic memory in mammals (Clayton et al., 2007; Conway, 2009; Kumaran et al., 2016), although we note that these characteristics are by no means a complete representation of true episodic memory, which has many more components to it (Hassabis and Maguire, 2007; Conway, 2009). We designed the episodic memory network as an abstraction of the medial temporal lobes (see Fig. 2A), which are central to episodic memory storage in mammals (Kumaran et al., 2016). Within this framework, our episodic network consists of a spatial encoder, a recurrent network (in analogy to the CA3 region of the hippocampus) and a network of place field units (in analogy to the CA1 region of the hippocampus). Although we make obvious reference to these subregions, we note that we are capturing the believed computations of these regions, and are not necessarily making statements or predictions of the neurophysiology, or algorithms implemented within them. To borrow from Marr's level of analysis (Marr, 1982), we are assuming certain computational properties while being general, and/or agnostic about the algorithmic and implementation details. The number of units per region is as follows: N_s = 2 (spatial encoder), N_e = 490 (autoencoder), and N_m = 980 (place cells). The initial synaptic weights between the spatial encoder and autoencoder, autoencoder and itself (recurrent connections), and autoencoder and place cells are sampled from a Gaussian distribution, 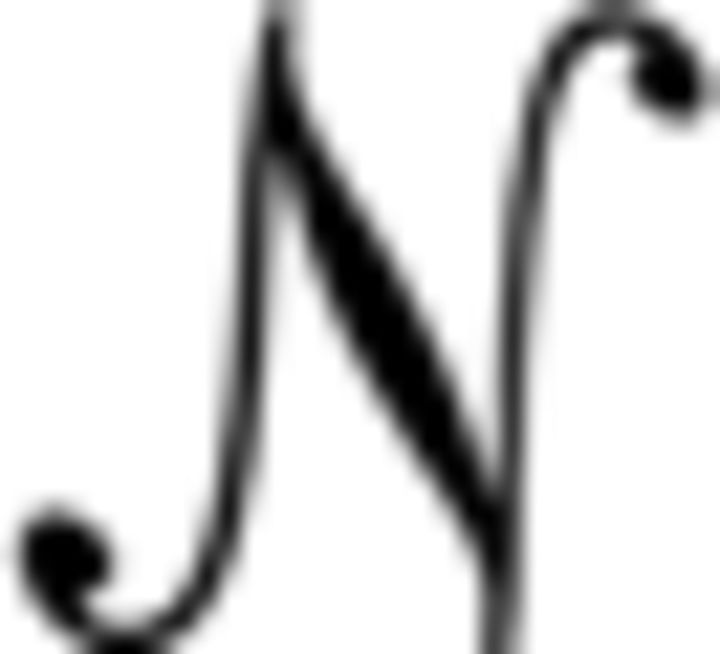(0, 0.1).

The spatial encoder acts as the input for the episodic network, responding to location-based information. Spatial inputs (i.e., Cartesian coordinates) elicit activation states equal to the coordinate values (one unit represents the x position, one unit represents the y position). Population activity for the autoencoder, e, is calculated as a function of the weighted sum of the spatial encoder activity, s, as follows:

The autoencoder is a three-layer feedforward network through time, with the synaptic weight matrices W_AE-AE being equal between each “layer” of time. Autoencoder activities in subsequent time layers are calculated as functions of the previous layer's activity and the recurrent weight matrix. The superscript in autoencoder activity (e.g., e⁽⁰⁾) refers to the feedforward time layer, indexed as an element of the set (0, 1, 2). As such, activity is calculated as follows: e^(t+1) = sig(W_AE-AEe^(t)), where e⁽⁰⁾ = sig(W_SE-AEs). The final time layer, e⁽²⁾, then projects to the place cells.

The activity of the place cells is the ultimate memory readout for the episodic system and is denoted by m. These activities are calculated differently depending on whether the agent is encoding its location or retrieving a memory. When retrieving a memory, activity is calculated similar to the autoencoder as follows:

However, when encoding a location, place cell activity is calculated using each unit's place cell receptive field and the current location as follows:

where x_t is the vector of the agent's current position, s_i is the vector of the center of cell i's place field, and σ_m controls the breadth of the place fields. Here, s_i = [s₁, s₂]_i, where s₁ and s₂ are each uniformly sampled from the interval [0, 1], and σ_m = 0.16.

Episodic memory storage.

In line with the third property of episodic memories listed above, as the agent moves throughout space, it constantly encodes its location, but in a manner that is modulated by the relevance to its goal of finding rewards. To do this, it passes activity through the spatial encoder and into the autoencoder. The autoencoder activity state is then stored in its recurrent synapses using a back-propagation through time algorithm (Rojas, 1996) computed to three time steps. And so, the autoencoder, which is a three-layer feedforward network through time, learns to recapitulate this spatial encoder-driven activity state in its final temporal layer as it passes activity through its recurrent synapses. Thus, the supervised training vector for the final autoencoder layer is identical to the initial activity vector in the autoencoder given the spatial encoder input (see below). However, to ensure that the storage is goal-relevant, we modulate the learning rate by a prediction error term (see Temporal difference learning).

Mathematically, the autoencoder's initial activity is dependent on spatial encoder input, e, and the synaptic weight matrix between the spatial encoder and the autoencoder, W_SE-AE as follows:

where the superscript in e⁽⁰⁾ refers to the feedforward time layer, indexed as an element of the set (0, 1, 2). The activity states in subsequent layers are calculated similarly as follows:

The weight matrix is updated in accordance with the derivation in Rojas (1996), but with the additional modulation of the prediction error term, δ_t as follows:

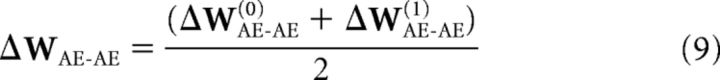where ζ is the error vector computed for a particular layer, Q is the derivative matrix for all the units in that layer, d is the difference between the final layer activity state and the training data (i.e., d = e⁽²⁾ − e⁽⁰⁾), W_AE-AE is the autoencoder weight matrix, and λ is the learning rate. At each time step, one training epoch occurs. However, when a reward is found, 50 training epochs occur.

The weights between the autoencoder and place cells are learned using the perceptron learning rule, treating the system as a two-layer feedforward network. Here, the input is e⁽²⁾ and the training data are place cell activity m_t = [m₁(x_t), m₂(x_t), …, m_Nm(x_t)], where m_i(x_t) is place cell i's activity given the agent's current position. With this training, the network learns to map the activity patterns stored in the autoencoder to place field activity patterns. This is what then allows the system to recall place field patterns it has previously encountered. Indeed, with these learning rules, the episodic network exhibits the desired properties, showing an ability to recall specific place field patterns, but with a clear bias toward the most recent reward location (see Fig. 2B).

Schematic system architecture and information flow.

The schematic system is a neural network designed to store a general statistical model of reward locations, in line with the current understanding of schematized memories in the mammalian brain (Ghosh and Gilboa, 2014; Richards et al., 2014). To achieve this, we built the schematic system as a Restricted Boltzmann Machine (RBM), which is a two-layer neural network architecture that can store a generative model of the probability distribution of a dataset (Hinton, 2010), and which has been used to model schematic memory in previous papers (Káli and Dayan, 2004). The lower layer of the network is a direct projection of the place cells from the episodic network. This layer functions as the visible layer, v, in the RBM and contains 980 units. The second layer functions as the hidden layer in the RBM, h, which models the probability distribution of its inputs and consists of 300 units. Thus, the second layer receives information from the place cell projection and determines the statistical regularities contained within (see Fig. 2D). These two layers are connected bidirectionally, and symmetrically, with a weight matrix W_CTX. Again, despite the obvious analogy to the neocortex, we emphasize that we are agnostic as to the brain's actual implementation of the schematic store. Indeed, there is some evidence to suggest that the traditional “episodic” regions of the medial temporal lobes may be capable of learning probabilities or statistics across memories (Turk-Browne et al., 2010; Kumaran and McClelland, 2012).

Schematic memory storage and recall.

Learning in the schematic network is conducted offline, via episodic replay events that occur during “rest” at the end of a trial. This design was motivated by the current understanding of the neurobiology of memory transformation, wherein schematic memories are built via replay in the hippocampus during rest (Frankland and Bontempi, 2005; Winocur et al., 2010). Details of the replay events are provided in the next section.

Training of the schematic network is accomplished with the contrastive divergence algorithm. According to the contrastive divergence, algorithm computed to one step (Hinton, 2010) as follows:

where w_i,j is the weight in W_CTX between unit i in the visible layer and unit j in the hidden layer. The first term, 〈v_ih_j〉_data, is computed in a single step by clamping the visible layer to some training data, and sampling the hidden layer. Place cell activity states, as they are replayed during offline states after a reward is found, constitute the input at the visible layer, and hence the training data (for details on how these training data are generated, see Episodic replay). The probability of activation of a hidden unit is stochastic and is given by the following:

where b_i is the bias to unit i. That is, the value of hidden unit h_j is set to 1 given an input in the visible layer with a probability defined by the sigmoid of the sum of all its inputs. So, as the weights of the inputs to a particular hidden unit increase, the probability of its activation increases.

During the reconstruction step, the activity of a visible unit is given by the following:

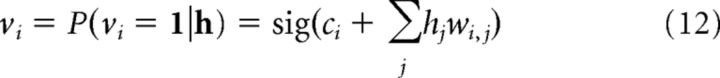where c_j is the bias to unit j the difference here being that the activity state of the reconstructed visible unit is set to its probability value, rather than being set to 1 with some probability. This update allows us to reconstruct a visible layer with values contained within the interval (0, 1), which better map onto actual place cell values. The result is a more accurate determination of the hidden layer's prediction of a particular place cell activity state. Recall in the schematic system involves a single reconstruction step as described above, taking a cue activity vector over v, passing it to the hidden layer, then passing it back to determine the probabilities in the visible layer, which then constitute the recalled memory.

The products v_ih_j for both the data and the reconstruction are determined by computing the outer products of the vectors of activation. The overall weight update to the weigh matrix is given by the following:

with λ being the learning rate. We use 200 epochs of training for the schematic network in each “rest” period for the agent.

Replay.

Replay is initiated by the episodic network using random activity in the spatial encoder. This is then propagated through to the autoencoder-place cell system. Here, the activity elicits a recall event by first triggering pattern completion in the autoencoder recurrent network by running it forward for three time steps. The completed pattern is then used to activate the place cells. The resultant place cell activity pattern, m_R, is then passed to the schematic system visible layer, v, and schematic training occurs using m_R as the training data. Because episodic storage is modulated by a prediction error term, the result is that the schematic system tends to receive any recently discovered reward location for training, in line with the in vivo recording literature (Kudrimoti et al., 1999; Euston et al., 2007). This is potentially more biologically plausible than the assumption of iid sampling from the episodic memory store and thus is an important difference from previous models of consolidation (McClelland et al., 1995; Mnih et al., 2015). The ultimate result of replay is that the schematic system learns a generative model of relevant reward locations. We note that this is consistent with a recent proposal regarding the potential utility of memory replay for learning goal-relevant statistics (Kumaran et al., 2016).

Moving through space.

As mentioned above, to navigate through space the agent uses a forward model and an action selector. The forward model is a three-layer neural network: the first layer contains 988 units, consisting of the 980 place cells, and 8 action units. The last layer contains 980 place cell units. The action units a_t ∈ {N, NE, E, SE, S, SW, W, NW} correspond to each of the eight principal cardinal directions. The network functions to predict place cell activity should a movement in a direction be taken; that is, given current place cell activity, m(x_t), and a potential action choice a_t (e.g., N, the network outputs a vector in its final layer that is a prediction of place cell activity should a movement be taken at the current position in the north direction; see Fig. 3A). So, at each time step, the network cycles through all eight potential actions, setting the appropriate action unit, a_i, to 1, and initiates a prediction for the outcome of that action using current place cell activity, m(x_t).

Figure 3.

Navigation by the foraging agent. A, Illustration of the forward model. The agent's forward model takes in current place cell activity, as well as a potential action choice, and outputs the predicted place cell state if the action were to be taken. B, An example path showing the agent navigating to a goal (red circle). The predicted state from the forward model is compared with the memory output to determine the probability of that action being taken, leading the agent to navigate a path (black line) directly to its goal. This goal may or may not be in the same position as the actual current reward location (large green dot) but will always depend on previous reward locations (small green dots). Bottom, Probability of the next action to be taken by the agent. C, Plot of forward model error during learning. As the agent wanders through space searching for rewards, the learning error for the forward model prediction decreases rapidly, but experiences sharp spikes whenever the agent is reinitiated in a new location (dotted lines). D, E, Tests of the navigation system. Despite the increase in learning error observed when the agent is initialized in new positions, it is still able to appropriately weight the probability of actions. This holds even in the first step after a learning error spike (bottom).

The probability that an action is chosen by the action selector is as follows:

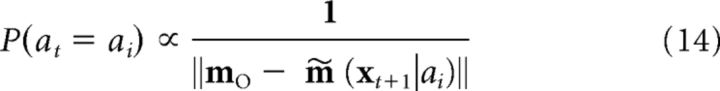where m∼(x_t+1|a_i) is the predicted place cell activity pattern and where m_O is the combined memory output from the episodic and schematic memory systems (see below). To introduce some randomness in choices as the task progresses, the probability that some action choice a_i is taken is calculated as follows:

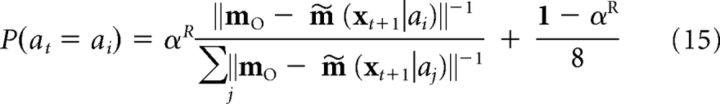where α^R is a random policy unit that decreases as time within a trial increases as follows:

where t_L is the time since the start of the current trial. α^R is bound to the interval (0, 1) and resets to 1 at the start of every trial. Therefore, the agent shifts toward random actions as the trial proceeds without finding a reward. This design helps to ensure that the agent explores the space sufficiently if it is having trouble finding a reward.

Ultimately, when the agent is not behaving randomly, it chooses the action that it predicts will bring it closer to the location recalled from memory, m_O (see Fig. 3B). To compute m_O, a recall event is initiated at each time step. This is accomplished by allowing the current location, x_t to act as a cue for the episodic and schematic networks. Activity passes through the episodic and/or schematic system, as described previously, to produce an output (m_E or m_S for the episodic and schematic outputs, respectively, or m_O; for more information on combining outputs using a policy unit, see below).

The forward model is trained in an online manner to predict place cell activity (i.e., m∼(x_t+1|a_t)) given current place cell activity (i.e., m(x_t)) and an action. After a movement is chosen by the agent, the true value of m(x_t+1|a_t) is computed as the agent moves in the space and its place cells are activated, and this activity is used as a training vector for the forward model given its previous place cell activity m(x_t) and action choice a_t as inputs. Thus, the forward model is only trained using place cell activity from positions it actually traverses and movements it actually makes. Training proceeds using a back-propagation algorithm (Rumelhart et al., 1988) with a learning rate of 0.05.

Episodic and schematic policy unit.

As described above, memory recall events produce goals for the forward model, m_O. These goals are convex combinations of the outputs from the episodic and schematic memory systems, m_E and m_S, respectively. Specifically:

with α being a policy unit that sets the balance between episodic and schematic control. α is computed using an exponential function as follows:

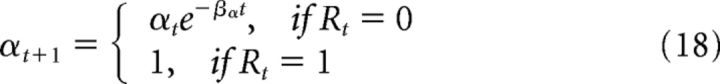where β_α is the exponential decay constant. Importantly, this means that, in the absence of a reward, over time the memories being used to guide navigation gradually switch from what the episodic system is recalling to what the schematic system is recalling. This is ultimately how we implement the process of memory transformation in this network. We emphasize again that we remain agnostic as to the actual mechanisms in the brain. Indeed, we think it extremely unlikely that memory transformation is implemented by the exponential decay of a single policy unit. But we note that this captures the general computational principle of memory transformation, and it leads to a switch in the agent's foraging behavior from focusing on specific locations to focusing on statistical patterns of locations, as we previously observed in water-maze search behavior in mice (Richards et al., 2014).

Temporal difference learning.

As described above, the agent modulates the strength of memory storage using an internal prediction error, δ_t. The agent calculates δ_t by estimating the value of each position in space with its critic function, C(m(x_t)), and setting as follows:

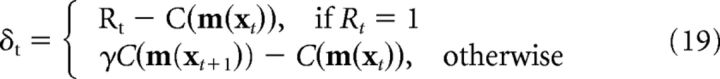Where γ is a temporal discounting factor and C(m(x_t+1)) is the new critic value after a move has been made at time t. C(m(x_t)) is calculated as a weighted linear sum of the place cell units: C(m(x_t)) = W_PC-Critic m(x_t). The weights, W_PC-Critic, are updated at each time step via a temporal difference learning algorithm, as in previous models of navigation (Foster et al., 2000) as follows:

Habitual network.

The habitual, or model-free, network (see Fig. 6) is an actor-critic network (Sutton and Barto, 1998) that consists of three components, two of which were described above: place cell units that receive location coordinates as their input and output f(x_t), and a critic that outputs C(m(x_t)). The third, novel component is the “actor.” The actor consists of 8 units corresponding to the principle cardinal directions and receives connections from the place cell units (see Fig. 6A). As the agent moves through space, place cell-to-actor weights, W_PC-Actor, are modulated according to the critic's computed temporal difference error (for this computation, see the previous section) and the action selected as follows:

where λ is the learning rate, a_t is the selected action, and δ_t is the temporal difference error computed by the critic. Hence, the model-free network learns a value function across space via the critic and uses this predicted value to influence actor choices given place cell activity. Ultimately, the model-free network learns to select appropriate actions given m(x_t) and is driven to reward locations based on this mapping. For a comprehensive explanation of an actor-critic network using place cells, see Foster et al. (2000).

Expected reward probability distribution and Kullback–Leibler divergence difference score.

To estimate whether the episodic or schematic systems provided better predictions for the reward location, we compared the distribution of recalled locations with the expected probability distribution for the reward. Specifically, if a new bout starts at time t_s with the reward at location x_s, and t_b is the length of the new bout (with t_b ∼ Exp(β_bout)), then according to Equation 1, the expectation with respect to t_b of the reward probability distribution function at time t > t_s is given by the following:

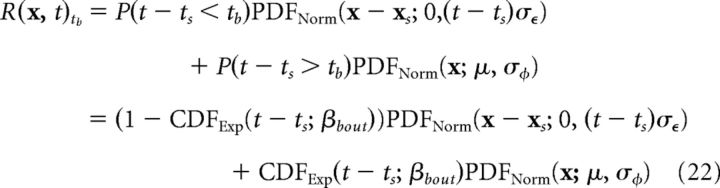where CDF_Exp is the cumulative distribution function for the exponential distribution and PDF_Norm is the probability density function for the normal distribution. Essentially, this equation shows that the expectation of R(x, t) is comprised of a Brownian motion term multiplied by the probability that a new bout has not occurred, plus a Normal distribution with mean μ multiplied by the probability that a new bout has occurred.

Comparison between the expected reward probability distribution and the output of the memory systems was accomplished with a Kullback–Leibler divergence difference score. Formally, this difference score, S, was defined as follows:

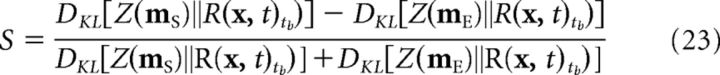where D_KL(·‖·) is the Kullback–Leibler divergence and Z(.) is a distribution defined as the normalized inverse Euclidean distance in place cell activity between each point in space and the memory trace. According to this formula, S is closer to 1 when the episodic memory is a better match to the expected distribution reward, and S is closer to −1 when the schematic memory is a better fit to the expected reward distribution.

Symbols and parameter values.

Table 1 provides a list of all of the symbols used in the equations above and provides the values that were used for the parameters in the simulations.

Table 1.

Symbols used in the equations and values that were used for the parameters in the simulations

Variable	Description	Value (if applicable)
Ns	No. of spatial units	2
Ne	No. of units in recurrent network (autoencoder)	490
Nm	No. of place cells	980
Nv	No. of cortical units (layer 1)	980
Nh	No. of cortical units (layer 2)	300
β	Bout length	Variable (see text)
tb	Time elapsed within bout	[0, β]
Rt	Reward administered at time t	{0, 1}
σϵ	Within-bout variance	0 (none) or 0.003
σφ	Interbout variance	0 (none) or 0.11
σf	Place cell breadth	0.16
ϕ	Sampled reward location (sudden shift)	∼N(μ, σφ) bound to [0, 1]
ϵ	Incremental shift	∼N(μ, σϵ)
lt	Reward location at time t	[0, 1]
xt	Agent location at time t	[0, 1]
si	Place cell centerfield	[0, 1]
s	Spatial cell activation vector	—
e(k)	Recurrent network (autoencoder) layer k activation vector	—
m	Place cell activation vector (memory)	—
mE	Episodic output	—
mS	Schematic output	—
mO	Combined episodic/schematic output	—
mR	Output from replay event	—
m∼(xt+1|ai)	Predicted output given action ai	—
V	Cortex layer 1 activation vector	—
H	Cortex layer 2 activation vector	—
WSE-AE	Spatial encoder to autoencoder weights	—
WAE-AE	Autoencoder recurrent weights	—
WAE-PC	Autoencoder to place cell weights	—
WCTX	Cortical weights	—
	Agent speed	0.04
at	Action taken at time t	ϵ{N, NW, W, SW, S, SE, E, NE}
ai	Possible action at time t	ϵ{N, NW, W, SW, S, SE, E, NE}
αt	Policy unit (episodic, schematic) at time t	[0, 1]
αRt	Policy unit (random) at time t	[0, 1]
δt	Temporal difference error	—
γ	Temporal difference discounting factor	0.95
λ	Learning rate (autoencoder)	δt 0.1
	Learning rate (cortex)	0.00001
	Learning rate (place cells, actor)	0.0075
	Learning rate (place cells, critic)	0.04

Software.

All simulations were performed using custom code written in the Python programming language (RRID: SCR_008394) with the NumPy (RRID: SCR_008633) and SciPy (RRID: SCR_008058) libraries. The software is freely available as a github repository (https://github.com/adamsantoro/episodic-semantic-network.git).

Results

Simulating foraging and the passage of time

In natural environments, resources such as food have predictable, but often changing, locations. Importantly, one can distinguish two categories of change. First, there are small incremental changes where the resource, or reward, stays in approximately the same location, but drifts over time. In such situations, memories for recently found reward locations hold high predictive value for future reward locations because reward location deviations are small. Second, there are sudden changes, where reward location deviations may be quite large. In such cases, memories for recently found rewards may not hold high predictive value, but a statistical model of where rewards occur in general could be advantageous.

To simulate both types of change in an environment, we devised a foraging task wherein a reward is located in a bounded 2D space, with the reward location changing in an incremental or sudden fashion (Fig. 1). Time is divided into distinct epochs (or bouts), of length B, with each bout corresponding to a period of relative stability in the environment where the reward location shifts in an incremental manner. The time in a given bout, t_b, is set to zero at the start of the bout and increments upwards until t_b = B, at which point a new bout begins. When a new bout begins, the reward location is randomly sampled from a 2D normal distribution with mean μ, and so, potentially large and sudden shifts in the reward location can occur. (Formally, the location of the reward at any time, l(t), is given by Eq. 1). When a reward is found, a “rest” period is enforced before the start of a subsequent foraging trial, which is called the intertrial delay. During this delay, the reward location continues to move. So, large intertrial delays most probably entail large deviations from the last found reward location, whereas small intertrial delays probably entail only small deviations from the last found reward location. Therefore, we hypothesize that, when the delay is small, specific memories will be more predictive, but when the delay is large, a generalized model will be more predictive.

A neural network model of a foraging agent with two memory systems

To perform this task, we developed an agent that moves through the 2D space searching for rewards. Ultimately, the agent's search behavior is governed by a model-based system that consists of three interacting components: an episodic memory store, a schematic memory store, and a navigation system (Fig. 2A). The episodic memory store performs computations thought to occur in the medial temporal lobes. The first stage is a spatial encoder, which receives the current agent position as Cartesian coordinates. The encoder acts as an interface to the mnemonic system, consisting of an autoencoder (analogous to CA3) and a place cell cognitive map (analogous to CA1). The autoencoder functions to encode activity states induced by the spatial encoder. Place cell activities are calculated differently depending on whether or not the agent is engaged in memory storage or memory recall. When the agent is engaged in memory storage, we assume that the place cells receive direct spatial information from the spatial encoder. In this case, place cell activity is a direct reflection of the agent's current position (calculated using Eq. 4). When the agent is engaged in memory recall, the place cell activities are functions of the autoencoder's input and thus reflect whatever location the autoencoder has stored (as in Eq. 3). Importantly, episodic encoding occurs constantly as the agent moves through the space, with the strength of encoding being modulated by a prediction error signal δ_t (as in Eqs. 7–9, 19). The consequence of this is an episodic memory system that, when primed with any location in the space, settles on attractor points located at specific locations in space where new, unexpected rewards were recently found. This is similar to the recall of recent spatial memories we have observed in rodents in navigation tasks (Richards et al., 2014).

The schematic memory in the agent is a two-layer generative model (i.e., it stores information about probability distributions and can sample from them). This is in line with the current understanding of schematic memory (Winocur et al., 2010; Ghosh and Gilboa, 2014) and a previous computational model of schematic memory in the neocortex (Káli and Dayan, 2000, 2004). The input layer to the schematic memory system is a direct copy of the place cells in the episodic system, and it is trained with place cell activity generated via offline replay in the episodic system during the intertrial delay (the learning algorithm is detailed in Eqs 10–13). Recall in the schematic system involves cuing it with a given place cell activity pattern at its input layer, then activating the upper layer, before reactivating the input layer via the upper layer, providing a new set of place cell activities modified to the expectations of the schematic memory system.

Because the episodic system stores recently discovered unexpected reward locations, replay provides the schematic system with data that reflect the underlying distribution from which reward locations are sampled between bouts. Thus, recall in the episodic and schematic systems provides very different patterns of place cell activity: episodic recall leads to place cell activity patterns that reflect the most recently discovered reward location, whereas schematic recall leads to place cell activity patterns that match the overall pattern of where new platform locations appear (Fig. 2B–D). Put another way, the episodic system recalls specific, recent reward locations, and the schematic system recalls the probability distribution that governs the location of rewards in the environment.

Navigation by the foraging agent

The final major component of the agent is the navigation system, which is composed of a forward model and an action selector. The navigation system uses place cell activity to predict which action would bring the agent closer to goals recalled by the memory systems (Fig. 3A). The goals, m_O, are a combination of the place cell activities generated by recall in the episodic and schematic memory systems. The extent to which the goal reflects episodic or schematic recall is determined by a policy unit, α, such that α = 1 ensures purely episodic goals, α = 0 ensures purely schematic goals, and 0 < α < 1 ensures goals that are some mixture of episodic and schematic recall (Fig. 2B–D; see Eq. 17).

Actions at any point in time, a_t, correspond to movements in any one of the eight principle cardinal directions (i.e., a_t ∈ {N, NE, E, SE, S, SW, W, NW}). At every time step, the forward model receives both the current location as encoded by the place cell activities, m(x_t), and a potential action, a_i. It then predicts subsequent place cell activities should this action be taken, m∼(x_t+1|a_i). The action selector compares this prediction to the goal location m_O and chooses a_t = a_i to bring it closer to m_O (Fig. 3B). (However, the action selector becomes increasingly random as trials proceed to encourage exploration, see Eqs. 14–16.)

To make the situation faced by the agent more ecologically realistic, the forward model is trained online during the search for a reward. In other words, although the forward model provides the agent with an understanding of the consequences of movement in the environment, it does not possess this understanding a priori. Therefore, performance in this task depends critically on the ability of the forward navigation model to accurately and rapidly learn to predict future place cell activity given the agent's current state and a potential action. So, as an initial test of the system, we examined the forward model's ability to guide search behavior. The forward model quickly learned to predict future place cell activity, exhibiting a vastly reduced error in its predictions in as quickly as 10 time steps, regardless of whether it was using only episodic recall, schematic recall, or a combination for its goals. As the agent completed the task and found rewards, it was reinitiated in random locations in space where the forward model had no experience. This resulted in spikes in the error rate for the forward model's predictions (Fig. 3C, dashed lines). To show that this increase in learning error did not compromise the agent's ability to navigate, we performed a control experiment (Fig. 3D,E). First, the agent explored the space until it found a reward in the due north, or due east location in the space. Next, it was transported to a location directly south (for the north condition) or west (for the east condition), and the navigation system calculated what its next action would be. If the navigation system were to function properly, an accurately encoded memory should direct the agent to choose the action “north” for the north condition (Fig. 3D) and “east” for the east condition (Fig. 3E). Indeed, the most probable actions selected by the action selector were the correct choices (Fig. 3D,E). Most importantly, the distribution of action probabilities did not change appreciably even in instances where the agent was in a new location with higher levels of error in the forward model's predictions (Fig. 3D,E, bottom). Together, these results indicate that the navigation system functions adequately within just a few time steps in the environment and continues to perform well even as the forward model's error momentarily increases throughout the task. Moreover, it exhibits consistent performance whether it uses just its episodic system, schematic system, or a combination for its goals.

Shifting from episodic to schematic memory over time improves agent performance

To explore how memory transformation (i.e., a shift from episodic to schematic memory over time) might improve reinforcement learning in our foraging task, we implemented a time-dependent decay in the α variable (Fig. 4A). Specifically, α decayed exponentially over time with decay constant β_α, but increased back to 1 whenever a reward was found (Fig. 4B; see Eq. 18). We note that this decay occurred with the passage of time, independently of data accumulation. Hence, α decayed during the intertrial delays as well as during foraging. This design ensured that after short intertrial delays the goals used by the navigation system were primarily episodic (as a reward was found recently in this case), and after long intertrial delays the goals used by the navigation system were primarily schematic.

We predicted that this system of decaying α would lead to improved performance in foraging, given that recent, specific locations would be highly predictive of the reward locations with small intertrial delays, but the overall probability distribution governing the interbout sampling would be more predictive with large intertrial delays. As expected, we observed that, when we clamped α = 1 (purely episodic goals), the agent performed better at short intertrial delays than long intertrial delays (Fig. 4C, blue circles). In contrast, when we clamped α = 0 (purely schematic goals), we found that the performance of the agent was largely flat across intertrial delays, such that it was worse than the purely episodic system at short intertrial delays but better than the purely episodic system at longer intertrial delays (Fig. 4C, white circles).

Given these results, we predicted that a system with exponential decay of α would combine the best performance of both systems. Indeed, we found that the “transformation” model exhibited better overall performance than either the purely episodic of purely schematic systems. Indeed, the transformation from episodic to schematic memory did not merely achieve the best of the reward rates from either individual memory system. Instead, it had a higher rate of reward discovery than either system in isolation at every intertrial delay (Fig. 4C, orange circles). This result was somewhat unexpected, although we believe that it can be explained by the fact that a combined goal (0 < a < 1) is a better predictor when some amount of time has passed because the expected location of the reward itself would be determined by some combination of the most recent specific location and the probability distribution governing interbout samples. Our data suggest that, if an agent is presented with an environment where short-term, temporal correlations give way to long-term stochastic patterns, then reinforcement learning can be enhanced by memory transformation.

Memory transformation can be optimized to the temporal dynamics of the environment

In our simulated foraging task, there is regularity to the rate at which new bouts occur. As such, we reasoned that a combined system could optimize its performance by tuning the speed at which it switches between its episodic and schematic systems. In other words, if new bouts occur frequently, meaning that the environment regresses to the long-term distribution rapidly, then it may be best to switch to the schematic system more quickly. In contrast, if new bouts occur infrequently, meaning that the reward locations remain correlated with the previous location for extended periods of time, then it may be best to have the episodic system drive behavior for longer.

To explore this idea, we measured the degree of matching between the memory output for the episodic and schematic systems to an analytically computed expected probability distribution of reward locations under conditions where the bout length was sampled from an exponential distribution (Fig. 5A, B, inset). Because this introduced a new random variable (i.e., bout length, whose sampling was controlled by different values of the rate parameter β_bout), we reasoned that different values of β_bout would result in different degrees of matching to the episodic and schematic systems as a function of time. The reward distribution (i.e., Gaussian Brownian motion with variable length bouts sampled from an exponential distribution, see Eq. 22) was compared with the distribution of recalled place cell activities output by both the episodic and schematic systems using a Kullback–Leibler Divergence difference score (Fig. 5B; see Eqs. 22,23). The manner in which we designed this difference score ensured that a score >0 corresponds to a better match between the episodic memory output and the reward distribution, whereas a score <0 corresponds to a better match between the schematic memory output and the reward distribution. As expected, as the β_bout values increased (i.e., as the mean bout lengths increased), the time it took for the schematic system to be more predictive increased. Conversely, as β_bout decreased, the episodic system ceased to be more predictive more quickly (Fig. 5B).

To test whether we could tune the rate at which memory transformation occurred to the environmental statistics, we ran the agent in the reward-finding task under different β_bout values while modulating the rate at which the agent decayed toward schematic recall (β_α; see Eq. 18). To visualize the effects of modulating β_α, we computed the percentage increase in reward-finding latency above the best-performing β_α (Fig. 5C, larger circles) for each value of β_bout. In line with our predictions, as the value of β_bout increased, the optimal β_α increased (Fig. 5C). However, one unexpected result was that the disadvantage of switching to the schematic system too quickly in conditions with a high β_bout was drastic (Fig. 5C, yellow circles, low β_α values). We believe that this may be because the rapid transformation to the schematic system prevents the agent from exploiting the precision of the episodic system under conditions where the reward tends to remain in a similar location. Alternatively, the effects of switching to the episodic system too slowly under the lower β_bout conditions (Fig. 5C, blue circles, high β_α values) were not as pronounced, which may be due to the fact that the episodic system will still direct the agent to the general area in which rewards occur, unless it is recalling a recent outlier.

These results suggest that the speed at which memory transformation occurs can be optimized to the environment: environments with rapid regression to a pattern demand rapid transformation, whereas environments that regress to a pattern slowly demand extended use of episodic memory. However, we also found that switching to the schematic system too quickly is particularly disadvantageous. This implies that a potentially good “default” for an agent in a new environment with unknown conditions is to engage in very slow memory transformation, which may provide a normative reason for the long transformation times in experimental conditions where subjects are unfamiliar with the environment (Kim and Fanselow, 1992), and the rapid transformation times seen when subjects are familiar with the task already (Tse et al., 2007, 2011; McClelland, 2013). The mechanistic reason is likely to involve the nature of memory storage in distributed networks with preexisting schemata (McClelland, 2013).

A habitual agent is not as effective at foraging as the memory transformation agent in a variable environment

In addition to an episodic to schematic transformation, researchers have demonstrated that, with enough training, there is a shift from goal-directed (or model-based) behavior to habitual (or model-free) behavior (Daw et al., 2005; Dolan and Dayan, 2013). This suggests that habitual systems may be superior to goal-directed systems when sufficient data have been accumulated. However, habitual systems do not adapt quickly to altered contingencies, such as changes to the action-reward associations in the environment (Dolan and Dayan, 2013). As such, it may be that a goal-directed system, such as our memory transformation agent, would be superior to a habitual agent in a variable environment, though inferior in a constant environment.

To explore this, we built a habitual agent for our foraging task. The agent was based on a previous model of reinforcement learning for navigation (Foster et al., 2000). Like our memory-transformation agent, the habitual agent possessed a set of place cells and a critic system to estimate the value of different locations in the environment. However, the habitual system did not navigate using an explicit goal recalled from memory. Instead, it used an “actor” module that decided which action to select based purely on the current place cell activity (Fig. 6A). In other words, the habitual agent made decisions using location-to-action associations that it formed during learning (see Eqs. 19–21). We then compared the performance of our memory transformation agent to the habitual agent, both at a variety of intertrial delays and at different levels of variance in the incremental (σ_ϵ) and interbout (σ_φ) movement of the reward (Fig. 6B–E, top rows).

When there was no variance in the environment (i.e., when the reward stayed in one place), we found that the memory transformation agent (Fig. 6B, blue circles) was actually better at foraging than the habitual agent (Fig. 6B, white circles), when both agents were given equivalent amounts of training (20 pretraining trials followed by 100 regular trials). This held regardless of the intertrial interval. However, we found that, with overtraining (400 additional trials), the habitual agent came to outperform our memory transformation agent (Fig. 6B, gray circles). We believe that this is because the memory transformation agent is using its forward model, which is accurate but not perfect, whereas in a constant environment the habitual agent learns a very accurate map of the value of each action at different points in space. Hence, our data suggest that, in a nonchanging environment, a habitual system is better than a goal-directed system as long as sufficient data can be accumulated.

However, the situation was very different when the reward location was variable. In these cases, the memory transformation agent generally outperformed the habitual agent. In particular, if we introduced some within-bout variance, we found that the memory transformation agent was markedly better than the habitual agent at lower intertrial delays, even if the habitual agent received five times the training (Fig. 6C). We saw similar results at low intertrial delays if we introduced between-bout variance (Fig. 6D) or both within- and between-bout variance (Fig. 6E). However, interestingly, we found that the memory transformation agent did not outperform the habitual agent at higher intertrial delays (Fig. 6C–E). Indeed, with both within- and between-bout variance present, we observed a slight advantage for the overtrained habitual agent at the longest intertrial delay we tested (Fig. 6E). Nonetheless, given the general performance of the two systems, it would appear that in a variable environment it is generally better to rely on a goal-directed agent with memory transformation capabilities, except after very long periods of time.

The benefits of schematic memory depend on a stable long-term distribution of reward locations

When considering the benefits of memory transformation in our foraging task, we wondered how much it depended on the presence of a stable long-term distribution of reward locations. In other words, if the distribution of between-bout reward locations was nonstationary, would schematic memories actually provide any benefit, or would they become “out-of-date” too quickly to be useful? Further, we wanted to explore whether the schematic system's performance in a nonstationary environment would depend on the amount of training.

To explore these issues, we trained the agent with either episodic only (α = 1) or schematic only (α = 0) memories in a set of tasks where the mean of between-bout reward locations (μ, see Fig. 1) was itself sampled from another distribution after every 20 trials (Fig. 7A). Specifically, we tested the agent in conditions where μ was resampled every 20 trials from either a normal distribution with low variance ((0.7, 0.05); Fig. 7B), a normal distribution with high variance ((0.7, 0.11); Fig. 7C), or a uniform distribution (U(0, 1); Fig. 7D). As well, we examined the performance of the agent during the first 20 trials (pretraining; Fig. 7, left column), the second set of 20 trials (early training, Fig. 7, middle column), and the last set of 20 trials (late training, Fig. 7, right column). In agreement with other studies of episodic versus schematic control (Lengyel and Dayan, 2007), we found that, during the first trials of pretraining, the episodic system outperformed the schematic system, regardless of the type of μ resampling or the intertrial delay (Fig. 7, left column). However, differences emerged when we examined later training. In particular, we found that, if the resampling of μ was done with low variance, then as training proceeded, the schematic memory system came to outperform the episodic system at high intertrial delays (Fig. 7A, middle, left), as we observed with a stationary distribution (Fig. 4B). In contrast, when μ resampling was done with high variance, the schematic system only ever tied with the episodic system in its performance at higher intertrial delays (Fig. 7B). Furthermore, when μ resampling was done with a uniform distribution, the episodic system always outperformed the schematic system (Fig. 7C). In total, our results demonstrated that the benefits of the schematic memory system (and with it, memory transformation) depended on the presence of a stable long-term distribution, or at the very least, a relatively low degree of nonstationarity coupled with sufficient training. Alternatively, a schematic memory system that actually attempts to develop a model of higher-order changes in the long-term pattern of reward locations may be able to further enhance reinforcement learning in more thoroughly nonstationary environments like these.

Discussion

Evidence of a transformation from specific memories to general or statistical memories during consolidation has become stronger in recent years (Wiltgen and Silva, 2007; Winocur et al., 2007; Durrant et al., 2011; Richards et al., 2014; Sekeres et al., 2016). However, the question of why this transformation may be beneficial has typically been framed in terms of reducing mnemonic interference or increasing mnemonic stability (McClelland et al., 1995; Squire and Alvarez, 1995; O'Reilly and Rudy, 2001). Here, we explored whether shifting from episodic to schematic systems over time is an advantageous strategy in environments where short-term consistency gives way to long-term patterns. We simulated a foraging task in which a reward shifted its location both gradually and suddenly throughout the environment, and built an agent that could use episodic or schematic memories to guide its searches. We observed a performance distinction between episodic and schematic memory-based control. With short delays between foraging trials, the episodic system more accurately predicted subsequent reward locations. With long delays between foraging trials, the schematic system more accurately predicted subsequent reward locations, even in the absence of further data accumulation. As such, when the agent was given the ability to switch between episodic and schematic control (transformation), it could take advantage of each system's strengths and could efficiently find rewards regardless of the delay between foraging trials. We also found that the optimal timing of the shift was sensitive to the temporal dynamics of the environment: if the reward location regressed to a general statistical distribution very slowly, it was better to prolong the use of episodic memories. Further, we showed that our agent using episodic and schematic memories could generally outperform a habitual agent in variable environments, although our transformation agent performed worse in a constant environment if the habitual agent was given sufficient training. Finally, we showed that the benefits of the schematic memory system depended on the presence of either a stable long-term distribution for reward locations, or a nonstationary distribution with relatively low variance paired with sufficient training. Together, these results demonstrate that episodic and schematic memories have unique and complementary advantages for guiding behavior, and combining them in a manner that matches the statistics of the environment can produce sophisticated reinforcement learning. This may help to explain the evolution of memory transformation in the mammalian brain.

Influenced by the ideas of Marr (1970, 1971), McClelland et al. (1995) considered the potentially complementary nature of episodic and schematic memory systems. They demonstrated that episodic systems may be good for rapidly encoding data for later replay, to allow schematic systems to slowly identify statistical patterns across events. Indeed, there is neuropsychological evidence supporting the idea that there are distinct learning systems in the brain with these complementary capabilities (Tulving, 1972; McClelland et al., 1995; Tse et al., 2007, 2011; Richards et al., 2014). In our model, we made the same fundamental distinction between these two forms of memory, but we embedded it within the larger context of reinforcement learning. As a natural extension of McClelland et al. (1995), our episodic system was designed for storing specific reward locations on-line, whereas our schematic system was designed for learning the general pattern of reward locations across time via episodic replay. Although our model shares these essential features with McClelland et al. (1995), it builds on their framework in three important ways. First, our model operates in a fully online, autonomous fashion with learning and consolidation occurring continuously in the environment as experiences occur, consistent with the situations faced by animals. This allowed us to explore how complementary episodic and schematic systems perform in tasks with realistic temporal dynamics (i.e., the passage of time in the absence of further data accumulation). Second, memory encoding in our model is controlled by a prediction error signal rather than being externally determined. This adds an additional layer of autonomy and ensures that only data relevant to unexpected rewards (i.e., changes) get stored in memory. It is also in line with neurophysiological evidence showing that learning is modulated by dopaminergic signaling that encodes a temporal difference prediction error (Schultz et al., 1997; O'Carroll et al., 2006; Bethus et al., 2010). Third, our model did not require interleaved learning for the schematic system, eliminating the need for independent and identically distributed memory replay events. Instead, recent events were replayed with higher probability in our model. This resembles the organization of memory replay observed in vivo (Kudrimoti et al., 1999; Euston et al., 2007). In considering these differences, our model implements episodic and schematic systems in a more realistic scenario. Moreover, it reframes complementary learning systems as a solution to reinforcement learning in changing environments. We believe that this new perspective fits well with the most recent articulation of the complementary learning systems theory from McClelland and colleagues, which emphasizes the relevance of the theory to the design of intelligent agents (Kumaran et al., 2016).

Neuropsychological studies in humans and experimental animals have also explored the idea of complementary learning systems, especially from the perspective of systems consolidation (Zola-Morgan and Squire, 1990; Frankland and Bontempi, 2005; Moscovitch et al., 2006; Wang and Morris, 2010; Winocur et al., 2010; Winocur and Moscovitch, 2011). These studies have uncovered two major components of systems consolidation. First, as memories age, the cortex plays an increasingly important role in their expression. Second, aged memories tend to be less specific and less contextually dense, and instead are more gist-like (or schematic) in nature. Such findings are typically interpreted as reflecting a consolidation process that renders memories less vulnerable to disruption over time (Frankland and Bontempi, 2005). Our model expands on this proposed function of systems consolidation. It suggests that, in addition to protecting memories from interference, the consolidation process functions to optimize reward seeking behavior. By this account, systems consolidation need not be a unidirectional process. Instead, it suggests that the brain shifts back and forth between episodic and schematic control depending on which provides the best predictions. In our model, if a new reward is encountered, the network switches back to reliance on its episodic memory system. Consistent with this, there is evidence in the neuropsychology literature that remote memories recontextualize (i.e., become more episodic) following reminders (Hupbach et al., 2007). However, in the absence of reminders, there is a tendency to shift from episodic to schematic retrieval over time (Winocur et al., 2010). We would suggest that, as in our simulated foraging task, the real world tends to be relatively consistent over short time periods but regresses to general distributions over long time periods. Thus, schematic systems will usually be best for control after long periods of time have passed since an experience, which could provide a normative account for instances of temporally graded retrograde amnesia following damage to the episodic system (Scoville and Milner, 1957). However, we note that one component of our model that is likely different from the reality in the brain is that our episodic memory system only ever forgot as a result of overwriting. In contrast, in the regular brain, there is evidence that episodic memories are typically highly transient (Conway, 2009). Thus, switching between episodic and schematic memories in the real brain will also depend on the dynamics of forgetting. Future research should explore how forgetting would affect the importance of memory transformation for optimizing decisions.

Our results can also be understood as being part of a broader examination of how the brain uses different memory systems to make decisions (Klein et al., 2002; Daw et al., 2005; Doll et al., 2012; Wunderlich et al., 2012). Researchers have observed a switch between goal-directed (or model-based) behavior, guided by memories of past events and action outcomes, to habitual (or model-free) behavior, guided by stimulus–response associations (Daw et al., 2005). This switch may be desirable because, in stable environments, habitual systems are both competent and computationally efficient (Watkins and Dayan, 1992; Sutton and Barto, 1998). However, in changing environments, habitual systems deal poorly with altered contingencies (Foster et al., 2000; Dolan and Dayan, 2013). In these cases, goal-directed systems typically offer a better solution because memories of recent events can be used to update action-outcome predictions (Dayan and Niv, 2008; Dolan and Dayan, 2013). In the simulated environment we used here, a habitual system did indeed struggle with the moving reward location (Fig. 6), although it performed better than our model with sufficient training when the reward location was stationary. It should be noted, however, that with enough time, and the right parameter settings, a habitual system can learn a stable, long-term distribution of reward locations. Nonetheless, what our work demonstrates is that a goal-directed system that uses a combination of both specific, recent memories and a generative model based on multiple memories can easily take advantage of both short-term correlations and long-term statistical patterns without the large amounts of training that a habitual system requires. Given our results, and previous research into switching between memory systems (Daw et al., 2005), we hypothesize that the optimal strategy for guiding behavior may be to rely on episodic, goal-directed control when experience is limited, switch to schematic, goal-directed control when enough time has passed to render episodic memories nonpredictive, and then switch to habitual control when accumulated experience and/or environmental stability are relatively high.

This proposal is broadly in agreement with the work of Lengyel and Dayan (2007), which suggested that episodic systems should guide behavior early in training, and schematic systems should guide behavior late in training. However, our model examines the benefits of an episodic to schematic switch even in the absence of the accumulation of new data. By emphasizing the passage of time in addition to data accumulation, our model makes some explicit, novel predictions about the relationship between the structure of the environment and the optimal balance between episodic and schematic control. In highly stochastic environments (i.e., situations with a rapid regression to the underlying distribution), we predict that the brain will rapidly shift to schematic control. In contrast, in environments where changes always occur gradually, such that the most recent experiences accurately predict new events, we predict that the brain will rely on episodic control for longer periods of time. This seems to contrast with Lengyel and Dayan's (2007) prediction that the episodic system should generally be engaged in rapidly changing environments. Perhaps these different predictions result from our focus on the general passage of time as opposed to more training data. However, it is important to note that there are other significant differences between our work and theirs. First, we used a one-step forward model for both episodic and schematic control, whereas Lengyel and Dayan (2007) did not use a forward model for episodic control (episodic control for them was explicit recapitulation of previous actions). This meant that for us, unlike for Lengyel and Dayan (2007), the difference between episodic and schematic systems boiled down to whether a specific or general model of reward locations was used, not whether a forward model was used. Second, we did not alter the action-state transitions that our agent faced, meaning that the agent's one-step forward model was always fairly accurate following the initial pretraining phase (Fig. 3). In other words, whereas uncertainty about the accuracy of the forward model was a key feature of Lengyel and Dayan (2007), it did not factor into our study. Although there are many situations animals face in which the accuracy of their forward models may be uncertain, we would argue that for foraging tasks such as the one we studied here that is not the case: barring totally new environments, or major motor changes, animals are likely to have good internal models of how their movements alter their position in space. Thus, whereas for Lengyel and Dayan (2007) one of the central advantages of episodic control was that it did not depend on a forward model, in our work, this issue was not central to the episodic versus schematic division, nor clearly a major issue for the specific task we were studying. More research that explores how the passage of time would impact a system where uncertainty is embedded within model-based control would help clarify these discrepancies. Once these issues have been explored, a more comprehensive theory of the utility of memory transformation for animal survival can be fleshed out.