Blood pressure-induced physiological strain variability modulates wall structure and function in aorta rings

Abstract

Vascular smooth muscle cells respond to mechanical stretch by reorganizing their cytoskeletal and contractile elements. Recently, we showed that contractile forces in rat aorta rings were maintained when the rings were exposed to 4 h of physiological variability in cycle-by-cycle strain, called variable stretch (VS), mimicking beat-to-beat blood pressure variability. Contractility, however, was reduced when the aorta was exposed to monotonous stretch (MS) with an amplitude equal to the mean peak strain of VS.

Objective

Here we reanalyzed the data to obtain wall stiffness as well as added new histologic and inhibitor studies to test the effects of VS on the extracellular matrix.

Main results

The results demonstrate that while the stiffness of the aorta did not change during 4 h MS or VS, nonlinearity in mechanical behavior was slightly stronger following MS. The inhibitor studies also showed that mitochondrial energy production and cytoskeletal organization were involved in this fluctuation-driven mechanotransduction. Reorganization of β-actin in the smooth muscle layer quantified from immunohistochemically labeled images correlated with contractile forces during contraction. Histologic analysis of wall structure provided evidence of reorganization of elastin and collagen fibers following MS but less so following VS. The results suggested that the loss of muscle contraction in MS was compensated by reorganization of fiber structure leading to similar wall stiffness as in VS.

Significance

We conclude that muscle tone modulated by variability in stretch plays a role in maintaining aortic wall structural and mechanical homeostasis with implications for vascular conditions characterized by a loss or an increase in blood pressure variability.

Introduction

Cells and tissues in the cardiovascular system are subject to repeated mechanical strains resulting from cyclic blood pressure (BP) variations generated by the heart. With each heartbeat, blood vessels experience circumferential strain, shear strain on the inner surface of the wall, and compressive radial strain [7]. The blood pressure generated by the heart depends on multiple factors including blood volume, cardiac output and systemic vascular resistance and compliance [11]. Furthermore, blood pressure is regulated by various feedbacks such as nervous inputs from the baroreceptor reflex, as well as hormonal control via the renin-angiotensin system [33]. As these systems interact nonlinearly in a noisy environment, they produce fluctuations in blood pressure over a range of time scales, which in turn cause fluctuations in cell and tissue strain [9]. Thus, the mechanical environment of cells in blood vessels is dynamic and can be better characterized by cycle-by-cycle variations in strains, rather than laboratory standard monotonous repetition of identical cycles.

The amount of blood pressure variability (BPV) has been characterized in both healthy human subjects and patients, and found to increase in cardiovascular diseases [10, 16, 38]. Recently, variability in systolic BP has been shown to be a strong predictor of stroke independent of mean systolic BP [26]. Likewise, short-term variability in systolic BP has an independent but moderate relation to aortic stiffness, which is a known risk factor for heart disease, stroke, renal disease and cognitive impairment [19, 28]. Furthermore, increases in BPV can induce aortic and left ventricular hypertrophy without an accompanying increase in mean blood pressure, as demonstrated by the results of sinoaortic denervation experiments [18]. Levels of target organ damage were reported to be positively correlated with BPV in both human patients [24] and a rat model of hypertension [34]. While baroreceptor reflex function has been shown to negatively correlate with BPV [34], further studies are needed to elucidate the sources and effects of abnormal BPV in diseases. Nevertheless, variations in cyclic wall deformation induced by BPV has recently been shown to contribute to smooth muscle, cardiac, and endothelial cell function [3, 16, 36]. Potential mechanisms for such fluctuation-driven mechanotransduction were summarized in a recent review [35].

Aortic stiffening associated with hypertension has historically been attributed to the composition and amount of proteins in the extracellular matrix (ECM), rather than the smooth muscle cells located in the media layer of the vessel [25, 27, 38]. Conversely, new studies suggest that vascular smooth muscle cells (VSMCs) contribute significantly to aortic stiffness, particularly in cases of aging and hypertension [10, 29–31]. Both cell and tissue level stiffness measurements revealed an increase in stiffness during hypertension due to contractility of VSMCs and their adhesion to the ECM [29, 31]. These findings raise the possibility that the contractile behavior of VSMCs can be a potential target in treating abnormal aortic stiffness in hypertensive patients.

In a previous study, we demonstrated that in cell culture and excised aorta, a physiological level of variable stretch (VS) in which the amplitude of sinusoidal strain varies from cycle to cycle mimicking normal BPV, can maintain VSMC metabolic and contractile function that requires ATP, compared to monotonous stretch (MS) with a constant amplitude, which decreases contractile force [3]. Since mitochondrial ATP production is influenced by the cytoskeleton [2] which determines cellular stiffness [37], in the present study, we hypothesized that changes in contractility due to MS versus VS will also result in different mechanical properties of the aorta wall. To test this hypothesis, we first determined the amount of strain variability in aortas corresponding to normal BPV of Wistar-Kyoto (WKY) rats. Next, we exposed thoracic aorta rings from rats to MS or VS. At each cycle in both the baseline and contracted states, the dynamic mechanical properties and the contractile force of the tissue were quantified to determine how variability in strain modulates smooth muscle contraction and the stiffness of the aorta. To assess the microscopic origins of any changes, we also imaged β-actin, elastin and collagen in the aorta wall.

Methods

All studies were approved by the Institutional Animal Care and Use Committee of Boston University and were performed in accordance with the relevant guidelines and regulations. Part of the data were collected in our previous study [3], including rat aorta rings stretched with monotonous stretch (MS; n = 10), variable stretch (VS; n = 9) and during the inhibitor oligomycin (n = 9). However, only the contractile force recordings were evaluated and reported. In the current study, we used the same data set to calculate the mechanical properties as well as collected new physiological data on both contractility and mechanical properties during exposure of aorta rings to the non-muscle myosin II inhibitor blebbistatin (n = 8). Finally, we carried out new histological and image analyses to structurally characterize VSMCs and the ECM.

Blood pressure measurements

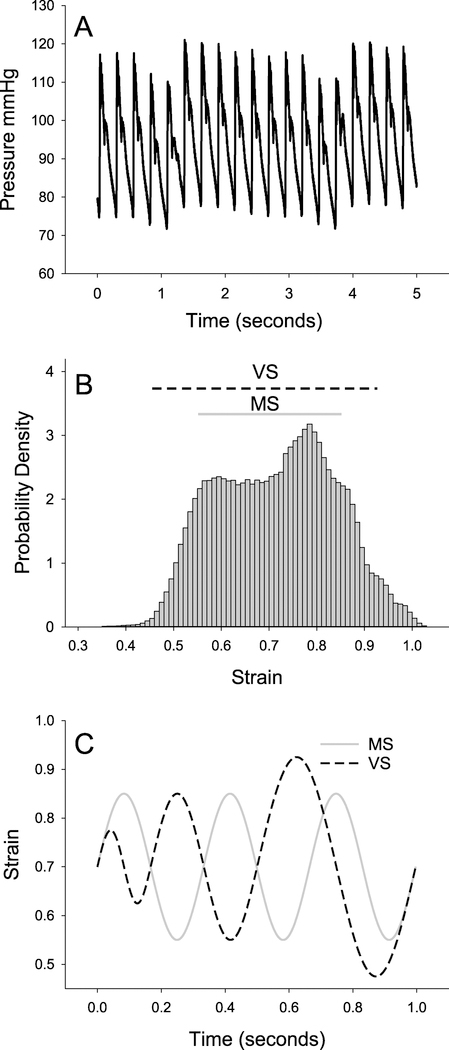
Blood pressure measurements were made in WKY rats (280–320 g; n = 4). Rats were anesthetized using 70 mg kg⁻¹ ketamine and 10 mg kg⁻¹ xylazine. A small incision was made above the carotid artery in order to cannulate it with a DTX-1 BP pressure transducer connected to a TA-100 amplifier (CWE Inc.). Data were recorded at 1000 Hz for up to 20 min using a National Instruments DAQ 6221 and a custom Labview program. The blood pressure time series (figure 1(A)) was then used to convert pressure tracing at each sampled time point to radius tracing utilizing an absolute pressure-radius relationship from the literature [4]. From the measured zero pressure radius and the radius tracing, we computed a strain time series which was subsequently used to establish the strain distribution (figure 1(B)). Finally, we determined the static and cyclic components of the strains for both MS and VS as shown in figures 1(B) and (C).

Figure 1.

Cycle-by-cycle variability in blood pressure and strain. (A) Example tracing of blood pressure in a rat showing cycle-by-cycle variations for up to 5 s. (B) Aortic strain was calculated from the blood pressure tracings at each time point according to a known aortic pressure-radius relationship (see main text). The probability density distribution of strains shows an average value of 0.71. (C) To test the effect of cycle-by-cycle variability, a static strain of 0.7 was applied to excised aorta rings while cyclic strains were superimposed in two different conditions: (1) monotonous stretch (MS, solid grey line) that consisted of a repeated sinusoid with a peak-to-peak strain amplitude of 0.3 and a frequency of 3 Hz and (2) variable stretch (VS, dashed black line) that had peak strains drawn from a uniform distribution between 0.15 and 0.45 and explored frequencies between 2 and 6 Hz. The range of strains explored by MS and VS is represented in (B) by the solid grey and dashed black lines, respectively.

Stretching protocol

Thoracic aortae were harvested from WKY rats and immediately placed in physiological salt solution (PSS) containing 120 mM NaCl, 5.9 mM KCl, 11.5 mM dextrose, 25 mM NaHCO₃, 1.2 mM NaH₂PO₄, 1.2 mM MgCl₂, 2.5 mM CaCl₂ at a pH of 7.4 and equilibrated with a mixture of 95% O₂–5% CO₂ as previously described [3]. The surrounding tissue was dissected away and the samples with approximate dimensions of inner diameter of 1 mm, thickness of 0.2 mm and axial width of 10 mm, were placed into a bath of PSS in a uniaxial stretching system consisting of a lever arm force transducer (Model 300B, Aurora Scientific). The lever arm applied strains in the circumferential direction while simultaneously measuring the force generated by the tissue. First, a static strain (ε) of 0.7 corresponding to the mean blood pressure was applied to all samples for a period of 45 min. Next, a zero mean sinusoidal cyclic strain was superimposed on the static strain with a pre-programmed pattern of either MS (n = 10) or VS (n = 9). MS consisted of a repeated sine wave with peak-to-peak amplitude of ε = 0.3 and frequency of 3 Hz. VS, however, consisted of sine waves varying from cycle to cycle in peak-to-peak amplitude according to a uniform distribution of peak-to-peak ε between 0.15 and 0.45 (figure 1(C)). Thus, MS explored a range of absolute ε from 0.55 to 0.85, while the range for VS was from 0.475 to 0.925 with both having a mean of 0.7. The product of peak strain amplitude and frequency (between 2 and 6 Hz) was held constant in VS so as to maintain a constant strain rate equal to that in MS. After 15 min of pre-conditioning with MS or VS, VSMC contraction was induced via PSS containing 51 mM KCl to establish the first or baseline (BL) contraction as previously [8]. After 30 min of contraction, the high KCl/PSS was washed out and the rings were continued to be exposed to MS or VS for 4 h in regular PSS, and a second contraction was induced. Additionally, two sets of inhibitor experiments were also executed. In a subset of samples (n = 9 for both MS and VS), a third contraction was induced after incubation for an hour in PSS that contained 5 μM oligomycin A, an ATP synthase inhibitor. In a second set of experiments (n = 8 for both MS and VS), blebbistatin was added to PSS at a concentration of 10 μM immediately after the first washout, and was maintained in the solution for the subsequent 4 h of stretch as well as the second contraction. At this low concentration, blebbistatin preferentially inhibits the activity of non-muscle myosin II [15].

Complex modulus and harmonic distortion index calculations

The force and displacement signals were transformed to stress (σ) and ε by accounting for the dimensions of the tissue. The complex modulus (G*) was calculated for each cycle by taking the discrete Fourier transform of the time-domain σ(t) and ε(t) signals (t is time) and was defined in the frequency domain as

$$G^{*}=G^{\prime }(\omega )+i{G}^{\prime \prime }(\omega )=\frac{\sigma (\omega )}{\epsilon (\omega )}$$ 1

where $i=\sqrt{-1}$ and w is the angular frequency. The storage (G′) modulus is the real part of G*, representing the component of stress in phase with strain. Note that G′ and stiffness will be interchangeably used. The loss (G″) modulus is the imaginary part of G* and represents the component of stress out of phase with strain and hence related to viscous dissipation in each cycle. The value for G* is defined only at the input frequency of strain, thus for MS it was always 3 Hz and for VS, it varied from 2 to 6 Hz. Since G* was frequency and strain dependent, G* in VS was only compared to MS at those cycles which had an input frequency of ~3 Hz and equal strain amplitude.

In order to quantify the nonlinearity of the system, a nonlinearity index, called the harmonic distortion (K_D), was also computed [40]. The K_D is defined according to equation (2), where P_tot is the total energy in the output signal at all frequencies, while P_ni is the energy at non-input frequencies:

$$K_D=\sqrt{\frac{P_{NI}}{P_{TOT}}}\ast 100\%.$$ 2

Specifically, if the input is a sine wave, P_tot is the squared Fourier amplitudes summed over all frequencies in the output, whereas P_ni excludes from this sum the term corresponding to the input frequency. By definition, a linear system’s response to an arbitrary input wave contains only the frequencies that are also present in the input and hence K_D = 0. Due to measurement noise, however, K_D > 0, albeit small. Alternatively, a nonlinear system produces power at non-input frequencies, called the harmonics or cross-talks of the input frequencies and hence K_d > 0 even in a noise-free system. Since the input is strain and the output is stress, K_D provides a simple index characterizing the mechanical nonlinearity of the aorta. The advantage of using KD is that it can be obtained without having to stop the periodic stretching to assess the quasi-static stress–strain curve.

Immunohistochemistry and histology

A set of aorta rings (n = 8) was used for histology within 30 min after isolation to preserve the in situ conditions as much as possible; these are called unstretched (US) samples. Aorta rings following stretching with MS or VS as well as US samples were formalin (10%, neutral buffered) fixed, paraffin-embedded and sectioned. A total of eight random sections per rat were deparaffinized and rehydrated in decreasing alcohol series. Endogenous peroxidase activity was quenched by 1% H₂O₂ and sections were washed in PBS (pH 7.5). The ImmPRESS™ HRP Anti-Rabbit IgG (Peroxidase) Polymer Detection Kit, made in Horse (Vector Lab, Burlingame CA), was used for immunodetection. A protein blocking step was performed with horse serum and sections were incubated for 1 h with rabbit anti-β-actin antibody at a concentration of 2.5 μg ml⁻¹ (Abcam Inc., Cambridge, MA). Rabbit IgG (20 ng ml⁻¹) as well as omitting the primary or secondary antibodies were used as technical controls (supplemental figure 1 (stacks.iop.org/PM/39/105014/mmedia)). After PBS washes, the ImmPRESS reagent was applied for 30 min. Enzyme substrate Vector SG (blue) for 10 min and counter staining (Nuclear Fast Red, Vector Lab) were applied followed by dehydration, clearing and mounting. To visualize collagen and elastin, the well-established methods of Masson’s trichrome¹ and Verhoeff’s elastic staining² were used, respectively. All conditions were processed simultaneously. Images were captured randomly selected locations by a Nikon Eclipse 50i microscope.

Image analysis

Before any processing, the mean background intensity was subtracted from all images and the media layer of the aorta without the adventitia was segmented as follows. First, the proper actin, elastin or collagen pixels were determined using the color thresholder in Matlab (The Mathworks, MA). Next, morphological operations were used to identify the media layer on the thresholded images and the color thresholded pixels within this layer served as a mask. The pixel values on the mask in the original image were then inverted so that darker colors corresponded to stronger β-actin expression or elastin/collagen staining. All further analyses were carried out in a predefined rectangular box within the media layer. The fractal dimension D_f was determined on color thresholded structures using the box counting algorithm. Briefly, a square box of size n was defined and the number of boxes (N) required to cover the structure was counted. The procedure was repeated for different n and D_f was obtained as the slope of the N versus n relation on a double logarithmic graph. After computing the gray-level co-occurrence matrix, the following image texture-related parameters were obtained [12]: contrast (a measure of average intensity contrast between neighbor pixels), correlation (a measure of intensity correlations between neighboring pixels in the circumferential direction), homogeneity (a measure of width of the distribution of grayscales) and entropy [21] (a statistical measure grayscale randomness). Additionally, the Euler number, defined as the number of objects minus the number of holes, was computed on thresholded images. Since elastin showed distinct darker fibrous lamellar structures, we separately segmented the inter-lamellar space from the fibrous lamellae using a second color thresholding. This allowed us to separately analyze density and D_f of the inter-lamellar space. Density was calculated as the intensity weighed sum of pixels normalized by the area of the rectangle. Finally, to analyze fiber waviness, we used a skeletonization algorithm to reduce the thresholded lamellar fibers to single curves. Small side branches were removed and the remaining structures were visually inspected to make sure a single fiber was obtained. To characterize waviness (w), we computed the ratio of the contour length and the end-to-end distance of each lamellar fiber.

Statistical analysis

For normally distributed data, results were reported as mean ± standard deviation (SD) for mechanical properties and mean ± standard error (SE) for image-derived results. When the data were not normally distributed (mostly from image analysis), data were presented as medians and their 95% confidence intervals obtained via the bootstrap method. Not normally distributed data were log transformed before further analysis. All comparisons were made using one-way or two-way ANOVA with factors being the type of stretch and the first BL contraction versus the contraction following stretch (control: Cnt) or one of the inhibitors (blebbistatin: Bls or oligomycin: Oli). Results were taken as significant for p < 0.05.

Results

Strain variability

Blood pressure in WKY rats varied from 80 to 121 mmHg (figure 1(A)) with a mean of 101 mmHg, producing a wide distribution of strains (figure 1(B)) with a mean and SD of 0.71 ± 0.12. Blood pressure waveforms were approximated using sinusoids (figure 1(C)) with MS exploring strains in the range of 0.55 to 0.85 and VS exploring a larger range of 0.475–0.925. The range for the single sinusoidal MS was chosen as representative of physiological strains, while the range for VS included the less likely yet still physiologically relevant tails of the strain distribution.

Force measurements

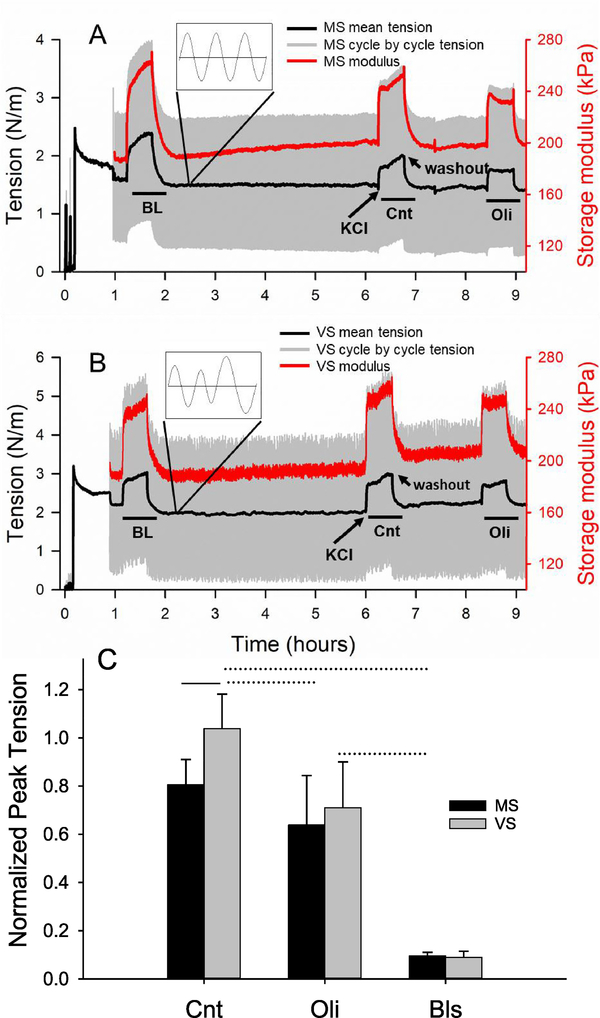
Representative force traces presented as tension (force per unit axial width of aorta ring) for two contractions are shown for MS and VS in figures 2(A) and (B), respectively. Figure 2(C) presents the statistics of the normalized peak force in which the second and, if present, the third contraction was normalized by the peak value of the first. The first contraction will be referred to as the baseline (BL) contraction. The second contraction in the absence of inhibitors represents the effect of 4 h stretch and is designated as the control (Cnt). For Cnt, VS maintained the contractile force (1.03 ± 0.14) while MS decreased it by 20% (0.80 ± 0.10) (p < 0.001). The difference between MS and VS disappeared following the ATP-synthase inhibitor oligomycin A (Oli), reducing the force generated in both conditions. These results are the same that we reported recently [3]. The non-muscle myosin II inhibitor blebbistatin (Bls) drastically decreased the contractility eliminating the difference between MS and VS. The effects of both Bls and Oli on peak force during contraction were statistically significant (p < 0.005).

Figure 2.

Force and stiffness as a function of stretch type and contraction. Cycle by cycle (gray) and mean (black) tension, defined as force per unit width, and storage modulus (red) for each cycle are plotted for the length of an experiment featuring (A) monotonous stretch (MS) and (B) variable stretch (VS), which was imposed at time 1 h after a 45 min stress-relaxation period at a static strain of 0.7. Fifteen minutes later, the first or baseline (BL) contraction was induced for 30 min using 51 mM KCl. After washout, stretching with MS or VS continued for 4 h followed by a second contraction (Cnt). In a subset of experiments, a third contraction was also induced following an additional hour-long incubation with oligomycin A (Oli), an ATP synthase inhibitor. In another set of experiments, blebbistatin (Bls), a non-muscle myosin II inhibitor, was introduced immediately after the first contraction (not shown). Example timing of KCl challenge and washout are indicated with arrows. The insets show a zoom into the cycle by cycle tension. (C) The peak tension generated by the various contractions were normalized by the peak tension of the BL contraction. The control (Cnt) represents the effects of 4 h stretch (MS or VS) on force generation without inhibitors. There is a significant difference between MS (n = 10) and VS (n = 9) (p < 0.001) in Cnt, but not in the presence of Oli or Bls. The effects of Oli (n = 9) and Bls (n = 8) are significant (p < 0.005). Solid and dotted lines above the bars denote intra-group and inter-group differences, respectively. The tension curves in A and B were modified from the force data published in [3]. 2015 Copyright © Springer Nature. With permission of Springer.

Wall mechanical properties

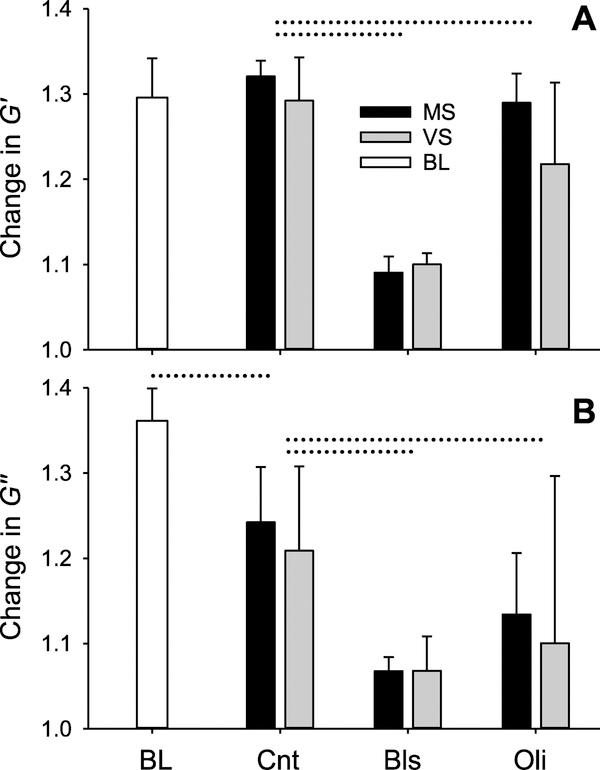
Storage (G′) and loss (G″) moduli as well as the harmonic distortion coefficient (K_D) were computed for every cycle with example traces for G′ shown in figures 2(A) and (B). Absolute values of G′, G″ and K_D obtained in regions just before contraction, at the peak of contraction and after relaxation are summarized in table 1. The BL values correspond to the first contraction in figure 2 just before the start of the 4 h stretch period. The BL G′ values showed no significant difference between MS and VS and hence were averaged in table 1. Figure 3(A) presents G′ normalized by its pre-contraction BL value. During BL contraction G′ increased by about 30%. After 4 h of stretch, G′ still increased by about 30% during the second contraction. Surprisingly, however, the G′ values for MS and VS were within 3% and did not show any differences at the peak of the contraction or after relaxation (table 1). Raw BL G″ values for MS and VS also did not show any significant differences and were averaged as for G′. The G″ normalized by the pre-contraction BL values increased by ~35% during contraction but there were no differences between MS and VS during the second contraction (figure 3(B)). Interestingly, the 4 h stretch resulted in a small, but statistically significant decrease (~13%) in G″ from BL to Cnt for both MS and VS (p < 0.001). The inhibitors Oli and Bls significantly decreased both G′ and G″ (p < 0.001) (figures 3(A) and (B)).

Table 1.

Absolute values of the mean and standard errors (SE) of the storage modulus (G′), loss modulus (G″) and the harmonic distortion coefficient (K_D) at baseline (BL) and following 4 h of monotonous stretch (MS) or variable stretch (VS).

	Stretch	Pre	SE	Peak	SE	Post	SE
G′ (kPa)	BL	130.3	12.9	168.7	15.1	132.0	13.6
	MS	140.7	11.0	175.9	12.3	145.4	14.3
	VS	131.5	16.1	164.1	16.8	142.0	18.8
G″ (kPa)	US	12.5	1.4	17.0	1.9	12.4	1.5
	MS	12.1	2.1	15.6	2.4	12.3	3.0
	VS	11.6	1.6	15.1	2.2	11.8	2.7
KD	US	2.65	0.63	3.06	0.61	2.72	0.69
	MS	2.63	0.83	3.48	0.76	3.24	0.72
	VS	2.78	0.56	3.33	0.60	2.91	1.04

Note: Pre, peak and post represent the values just before contraction, at the peak contraction and following washout.

Figure 3.

Changes in storage and loss moduli during MS and VS with and without inhibitors. Peak values of the storage moduli G′ (A) and loss moduli G″ (B) moduli normalized by their value measured at pre-contraction in baseline (BL, defined in figure 2). In control, G′ did not differ between MS and VS whereas G″ showed a significant difference between BL and following 4 h stretch with no inhibitors (Cnt) (p < 0.001). The inhibitors (defined in figure 2 caption) significantly decreased both G′ and G″ (p < 0.001). Dotted lines above the bars denote differences between two groups.

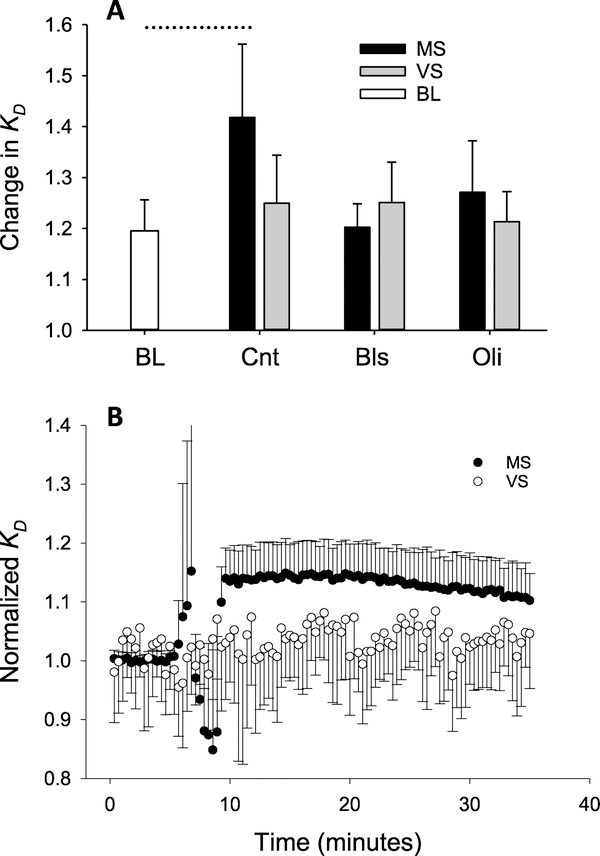
The nonlinear nature of tissue mechanics was assessed using K_D, defined in equation (2), which is sensitive to changes in the nonlinearity of the dynamic stress–strain relation [12]. Absolute values of K_D for MS and VS did not show significant differences at BL when the muscle was relaxed and these were averaged (table 1). Changes in K_d due to contraction in figure 4(A) were obtained by normalizing with their pre-contraction BL value. Comparing the normalized values at the peak of contractions with one-way ANOVA, there is a noticeable increase of 15% from BL to Cnt, the second contraction, during MS, while the increase during VS is only 5%. Although the difference between MS and VS did not reach significance, two-way ANOVA performed on K_d showed a significant dependence on 4 h stretch implying that K_d was higher during the second contraction when MS and VS were considered together (p < 0.001). Furthermore, there was a significant interaction between the type of stretch (i.e. MS versus VS) and contraction number indicating that the effect of 4 h stretch depended on stretch type (p = 0.02). As with G′ and G″ both Oli and Bls significantly reduced K_d and removed the effects of stretch (p < 0.001). To eliminate some of the inter-sample variability, the second contraction was further normalized by the first on a sample-by-sample basis (figure 4(B)) which resulted in a clear separation of K_d between MS and VS with smaller values during the latter throughout the time course of the contraction (p < 0.001).

Figure 4.

Harmonic distortion during MS and VS with and without inhibitors. (A) Peak values of the harmonic distortion coefficient K_D normalized by their value measured at pre-contraction in baseline (BL, defined in figure 2). Two-way ANOVA showed a significant dependence on contraction type showing thus the effects of 4 h stretch (BL versus Cnt) (p < 0.001) and the presence of interaction between the type of stretch (MS versus VS) and the type of contraction (BL versus Cnt) (p = 0.02). Oli and Bls removed the effects of stretch type on K_D (B) K_D during second contraction normalized by the peak of the first contraction displays a clear separation between MS and VS (p < 0.001). Dotted line above the bars denotes differences between two groups.

Wall organization

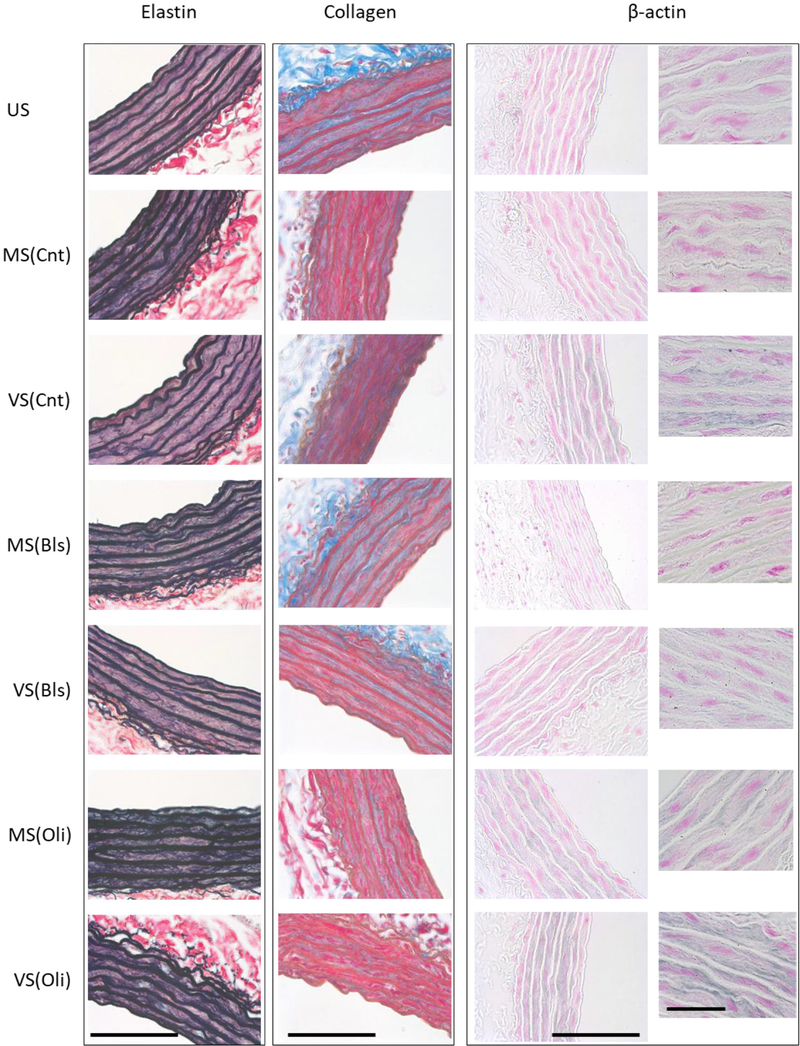
Example images of elastin, collagen and β-actin corresponding to all conditions are shown in figure 5. For elastin, there are strong wavy elastic lamellae within the media layer of the vessel which appear dark blue and are interspersed with bundles of dark red/pink smooth muscle cells. The thick lamellar fibers and the thin interlamellar fibrils appear wider and looser and hence darker during MS as well as in the presence of both inhibitors. The thin network of collagen fibrils appears as bright blue in the media and adventitia. Immunohistochemistry revealed a significant stretch dependence of the thin network of β-actin in the smooth muscle layer (labeled blue).

Figure 5.

Representative images of elastin, collagen and β-actin. Example images are shown for elastin, collagen and β-actin for each experimental condition including unstreched (US) samples following isolation, samples following 4 h of monotonous stretch (MS) or variable stretch (VS) without inhibitors (Cnt) and samples following MS or VS with blebbistatin (Bls) or oligomycin A (Oli). Elastin is stained dark blue using the Verhoeff’s elastic staining whereas collagen is light blue stained by Masson’s trichrome method. The delicate network of cytoskeletal β-actin within the smooth muscle layer is shown in blue by immunohistochemistry with pink counterstained nuclei. The smaller images in the right most column show β-actin at 100× magnification with a scale bar of 50 μm. The scale bars on all other images correspond to 100 μm.

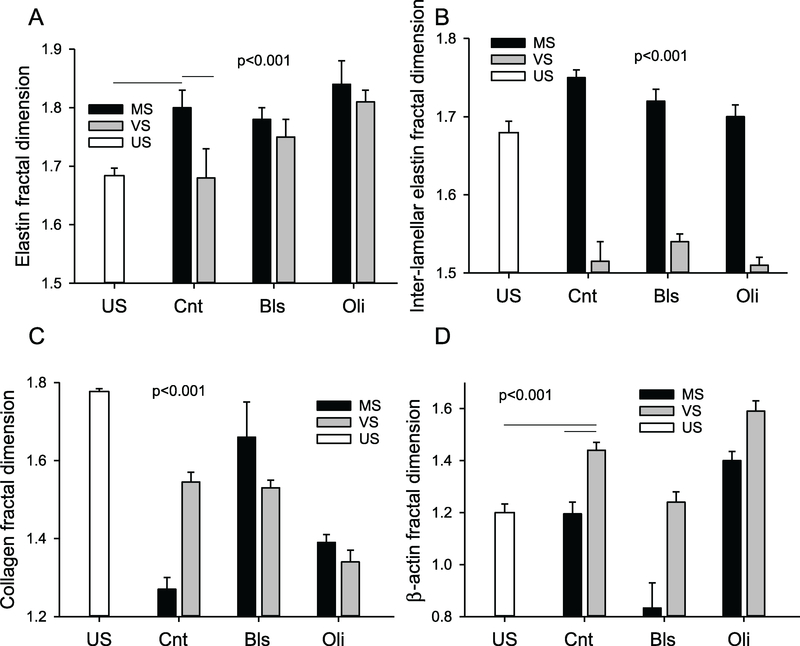
To characterize the global space-filling capacity and organization of these structure, the fractal dimension D_f was calculated with ~50 images per condition (figure 6). Generally, D_f varied significantly with both stretch pattern and inhibitors. Elastin D_f after MS was higher than in US samples or after VS while the latter two did not differ (figure 6(A)). The D_f was also higher after MS than VS independent of inhibitors (p < 0.001). Most of these differences were due to the inter-lamellar structure since D_f was higher after MS under all conditions (figure 6(B)). Collagen D_f also depended on stretch type and inhibitors (figure 6(C)). Following VS, D_f was much closer to its value in US than following MS and Bls did not affect D_f. Compared to control, Oli increased D_f during MS, but decreased it during VS. Compared to US, D_f of β-actin increased following VS (figure 6(D)). Bls decreased D_f for both MS and VS, with D_f < 1 after MS, whereas Oli increased D_f Finally, independent of inhibitors, D_f was significantly higher after VS than MS (p < 0.001).

Figure 6.

Statistics of elastin, collagen and β-actin fractal dimension. Fractal dimension D_f of total elastin (A), inter-lamellar elastin (B), collagen (C) and β-actin (D) are shown in US, MS- or VS-stretched control (Cnt) samples and MS and VS samples in the presence of Bls or Oli. One-way ANOVA among the US and Cnt conditions showed that except for US and VS for elastin and US versus MS for β-actin, all conditions were significantly different from each other (p < 0.001). Two-way ANOVA on the effects of stretch type and inhibitors showed that all conditions were different from each other (p < 0.001).

To characterize the local neighborhood features of the images, texture analysis was carried out for elastin and collagen summarized in tables 2 and 3, respectively. Generally, there was a strong statistical difference between conditions for a given texture parameter even if the values were very close. For example, pairwise comparison of local correlations without inhibitors resulted in significant differences for elastin among the US (0.94), MS (0.88) and VS (0.93) groups (table 2) which demonstrates that VS maintains local structure better than MS compared to US samples which likely better reflect the in vivo ECM configuration. A similar picture is obtained for collagen (table 3). In fact, this trend held for all parameters because the root mean square relative error between US and MS was 122% whereas that between US and VS was only 15%. These numbers were 82% and 68% for collagen. With regard to the inhibitors, most texture parameters changed significantly, but except for elastin after Oli due to the Euler number, all parameters were more sensitive to inhibitors after MS than VS.

Table 2.

Texture and density properties derived from elastin-stained images.

Condition Parameter	Control			Blebbistatin		Oligomycin
	US	MS	VS	MS	VS	MS	VS
Euler #	42q,s	−69x,y,z	53x,y,z	−8.2x	32x	−117x	−50.6
Contrast	0.15q,r,s	0.23x,z	0.18	0.2x	0.17	0.19	0.19
Correlation	0.94q,r,s	0.88x,z	0.93y,z	0.91x	0.92	0.87x	0.9
Homogeneity	0.98q,r,s	0.96x,y,z	0.98y,z	0.97x	0.98	0.96x	0.97
Entropy	3.06q,s	4.26x,z	2.81y,z	3.64	3.17	4.7x	3.97

Note: Significances are indicated by letters in superscript as follows. For the control condition, one-way ANOVA was run and superscripts q, r, and s represent differences respectively between US and MS, US and VS, and MS and VS and the symbol is always above the US value. For the inhibitors, two-way ANOVA was used. Superscripts x, y and z above MS in control represent differences between control and blebbistatin, control and oligomycin, and blebbistatin and oligomycin. Superscripts above VS in control denote the corresponding differences for VS. A superscript x above MS in blebbistatin denote difference between MS and VS in blebbistatin. An x above VS in blebbistatin denotes difference between VS in blebbistatin and oligomycin. Finally, a superscript x above MS in oligomycin denotes a difference between MS and VS in oligomycin.

Table 3.

Texture and density properties derived from collagen-stained images.

Condition Parameter	Control			Blebbistatin		Oligomycin
	US	MS	VS	MS	VS	MS	VS
Euler #	−688q,s	317x,z	204y,z	−282x	139	288x	362
Contrast	1.28q,r,s	0.35x,y,z	0.51x,z	1.13x	0.94	0.59x	0.51
Correlation	0.85q,r,s	0.79x,y,z	0.83y,z	0.84	0.84	0.82x	0.79
Homogeneity	0.93q,r,s	0.98x,y,z	0.96y,z	0.94x	0.96	0.97x	0.98
Entropy	3.53q,r,s	0.63x,y,z	1.69y,z	2.45x	1.65	0.95x	0.77

Note: The description of statistical significances is detailed in table 1.

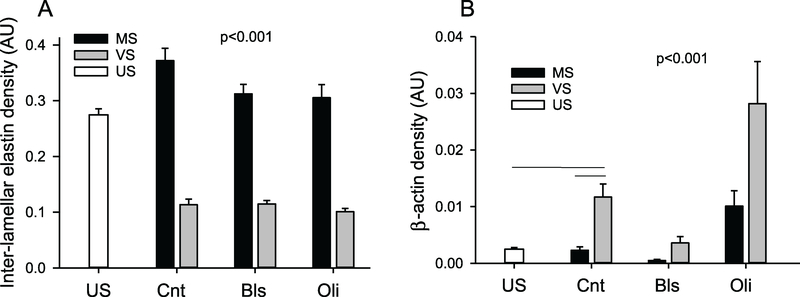
There were strong and significant changes in inter-lamellar elastin densities with stretch pattern suggesting that smaller fibrils became scattered between the thick lamellar fibers resulting in a more than 3 times higher density during MS than VS (figure 7(A)). The density of the β-actin network did not change from US after MS (figure 7(B)), but significantly increased 4-fold after VS (p < 0.001). Bls significantly decreased and Oli significantly increased β-actin density in a stretch type dependent manner with VS always resulting in higher levels.

Figure 7.

Statistics of inter-lamellar and β-actin density. Inter-lamellar elastin density (A) and β-actin density (B) in US samples, MS- or VS-stretched control (Cnt) samples and MS and VS samples in the presence of Bls or Oli. Density is defined as the sum of intensity weighted elastin or β-actin pixels within a pre-defined rectangular area of the media layer. One-way ANOVA among the US and Cnt conditions showed that all conditions were significantly different (p < 0.001) except for US and MS in β-actin. Two-way ANOVA on the effects of stretch type and inhibitors showed that all conditions were different from each other (p < 0.001).

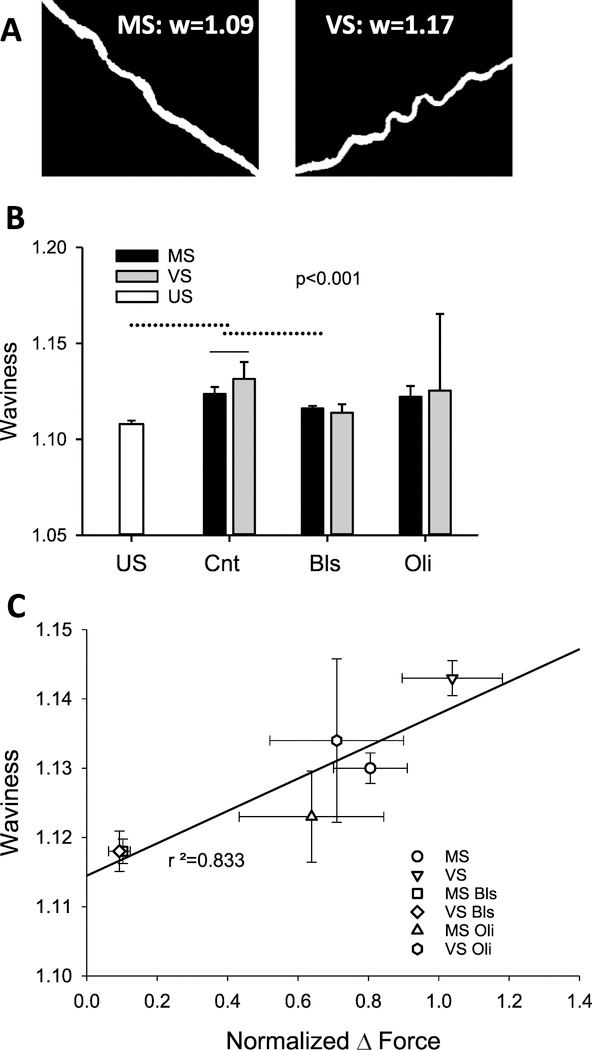
Examples of isolated lamellar fibers and their waviness (w) are shown in figure 8(A) and the full statistics (n > 120 fibers per condition, except for Oli with n ~ 20) are summarized in figure 8(B). Compared to US, both MS and VS resulted in a higher w. Also, w was higher after VS than MS (p < 0.001). Among the inhibitors, only Bls decreased significantly w and the dependence on stretch type also disappeared. Unexpectedly, there was a strong correlation between the normalized force and w with an r² = 0.833 (figure 8(C)).

Figure 8.

Waviness of elastin and its relation to force. (A) Example binary images of lamellar elastin fibers after MS (left) and VS (right). The corresponding values of waviness, defined as the ratio of contour length and end-to-end distance of a fiber, are given in each image. (B) Statistics of waviness in US, MS- or VS-stretched control (Cnt) and MS and VS samples in the presence of Bls or Oli. One-way ANOVA among the US and Cnt conditions showed that all conditions were significantly different (p < 0.001). Two-way ANOVA on the effects of stretch type and inhibitors showed that Bls but not Oli reduced waviness and removed the difference between MS and VS (p < 0.001). Solid and dotted lines above the bars denote intra-group and inter-group differences. (C) Regression between the median waviness from (B) and normalized force from figure 2(C).

Discussion

Fluctuation-driven mechanotransduction (FDM), in which the ever present variations in stress and strain in an organ influence cell function, may be a general phenomenon in mechanobiology [35]. The primary aim of this study was to evaluate whether FDM affects the main functional and structural properties of the vascular wall. We hypothesized that wall stiffness will respond to the presence of cycle-by-cycle variability in strain. To test this, we quantified the level of variability in aortic strain in rats at normotensive blood pressure conditions and applied both variable and monotonous stretch patterns to excised thoracic aorta rings. The force generated by the aorta was measured and stiffness and the harmonic distortion index were calculated on a cycle-by-cycle basis during a 4 h stretching period both preceded and followed by a KCl-induced contraction. At the conclusion of the experiments, we also imaged several structural components of the aorta wall. Our main findings include: (1) in contrast to our original hypothesis, the storage and loss moduli did not depend on the type of stretch, namely MS versus VS; (2) VS maintained normal contractility compared to MS as before [3] but this difference disappeared after reducing ATP supply or inhibition of myosin motors; (3) nonlinearity of the mechanical properties assessed by the harmonic distortion index was the same for MS and VS at baseline, but the increase during contraction was higher during MS; and (4) despite the lack of a response in stiffness to FDM, stretch pattern (MS versus VS) caused significant differences in the structural organization of main components of the aorta wall including elastin, collagen and β-actin.

Myogenic tone potentiation

To interpret the above findings, we first note that in vitro experiments suggest that smooth muscle force generation is influenced by both muscle length and length oscillations [10, 32]. Recently, we reported that the decline in force in MS relative to VS in rat aorta was due to a decrease in ATP content and production in the former [3]. However, other mechanisms such as myogenic potentiation through Ca channels [20] may contribute to our stretch-induced difference in force generation. For example, Seow showed in rabbit carotid arteries that mild to moderate length oscillations potentiate force generation in future contractions with a maximum force around ε = 0.13 strain amplitude of the oscillation, while amplitudes larger than 0.3 attenuate contractile force [32]. Thus, the difference in force generation between VS and MS could in part be due to increases in myogenic tone potentiation caused by the different strain regimes explored during VS over the 4 h of stretch. We superimposed a sinusoidal strain amplitude of ε = 0.15 (half of peak-to-peak value of 0.3) on a static strain of 0.7 for MS and a range of amplitudes from ε = 0.125 to ε = 0.225 for VS. Since the range of length oscillations explored by VS occured on both sides of the myogenic potentiation maximum at ε = 0.13, myogenic tone potentiation is likely not the main reason for the different forces generated during MS and VS. Instead, it is likely that the downregulation of both ATP production and phosphorylation of myosin light chain by MS [3] is responsible for the observed data. Our inhibitor studies further support this conclusion since both limiting ATP availability with Oli and reducing active contractile force due to weakening of cortical actin cross-linking by Bls eliminated the difference between MS and VS (figure 2(C)).

Vascular wall structure

Our imaging results suggest unexpectedly large changes in the ECM due to stretch type as well as inhibitors (figures 5–8, and tables 2 and 3). The parameters studied are related to structural organization with the possible exception of density, which is more related to amount. Although the length of the experiments is not sufficient to increase ECM protein amounts by active production and deposition, the density of elastin in the inter-lamellar space can increase (figure 7(A)) simply as product of straying finer fibers from lamellar structure. However, since actin can rapidly polymerize in response to stretch [1, 39] and because detection is based on a selective antibody, we interpret our β-actin data in figure 7(B) as real density reflecting the amount of the actin molecules.

The density of inter-lamellar elastin was higher following MS than US or VS independent of inhibitors (figure 7(A)). Since the Euler number (# of objects minus # of holes) was always lowest during MS, the stretch pattern in MS creates more holes in elastin structure with reduced neighborhood correlation and increased randomness as expressed by the correlation and entropy parameters in table 2, respectively. In contrast, collagen appears to behave in the opposite way for many of the parameters (table 3). These changes in ECM structure imply a looser elastic lamella and more compact collagen fibers following MS. However, in the muscle layer it is likely that following isolation of the aorta, actin is quickly depolymerized in the unstretched US samples because of the lack of ~30 min stretch before fixation. Thus, the β-actin density results provide evidence that stretch pattern in fact has a larger effect on the β-actin network than stretch itself since the density is unaltered by MS compared to US while it is much larger following VS (figure 7(B)). These differences should in turn influence cortical actin organization, ECM stiffness sensing and the response of the actin network organization to cyclic stretch [22]. For elastin, the fractal dimension D_f as a measure of space-filling capacity (figure 6), was higher following MS than VS that originates from the inter-lamellar space, whereas for collagen and actin, D_f is lower after MS. Taken together, since in most cases, the ECM structural parameters following VS are closer to US than following MS, these results are consistent with the notion that by allowing a stronger muscle tone, VS better maintains the natural organization of the ECM than MS.

Contractility, mechanics and wall structure

An interesting observation was that FDM maintained a higher residual waviness of elastin seen on histologic images that were taken in the unstretched state (figure 8(B)). The reduced waviness following MS may have resulted in stronger recruitment of elastin during contraction which in turn could explain the increased nonlinearity in figure 4(B). Furthermore, there is some similarity between waviness in figure 8(B) and contractile forces in figure 2(C) that manifested in a strong correlation between them (figure 8(C)). Since the waviness is significantly reduced by Bls treatment independent of stretch type (figure 8(B)), VSMC contractility must be responsible for the differences in waviness between MS and VS after 4 h of stretch. We interpret these data as a consequence of a more contractile muscle under VS which in turn may have caused a stronger compression of elastin resulting in a higher degree of residual waviness. These differences in the organization of elastin and collagen induced by MS and VS must also have contributed to wall stiffness. Thus, we conclude that through reduced contractility, MS disorganizes the ECM (looser elastin and tighter collagen) which becomes slightly stiffer compared to VS and hence even if the amount of β-actin and hence the contractile force is less during MS, the macroscopic stiffness remains similar to that during VS. Furthermore, the reduction in both the density and organization of β-actin following MS (figures 6(D) and 7(B)) may produce a few highly stressed actin fibers during the second contraction which can also increases the nonlinearity of wall mechanics [14] observed in figure 4(B).

Limitations

Limitations of this study result from the experimental setup for measuring aorta mechanics, which are known to vary in rats from in vitro to in situ and in vivo conditions [6]. Blood pressure variability is also significantly reduced during anesthesia in children [ 5]. Thus, we may have underestimated the tails of the strain distribution in figure 1(B) due to anesthesia. A possible implication of this is that the reduced strain variability during long-term anesthesia may disturb homeostatic maintenance of the wall. While in vivo the aorta experiences longitudinal and circumferential strains, we only explored the effects of variability in circumferential strain and left the longitudinal boundary unconstrained. Likewise, any contribution of shear-stress to mechanotransduction in the endothelial layer due to blood flow [36] was neglected as we did not simulate flow in our experiments. Since the release of nitric oxide by the endothelium strongly influences contractility and wall stiffness [8], the lack of blood flow and potentially the variability in blood flow [36], may also have contributed to the lack of difference in stiffness during VS and MS in our in vitro experiments. Hormonal or neuronal effects were also not present in our experiments. These limitations are the result of sacrifices made in order to measure force and stiffness during controlled circumferential strain. An additional limitation is that we did not recreate the specific time domain shape of the blood pressure-induced strain of the arterial wall, instead we used sinusoids. The actual blood pressure waveform does include higher harmonics which would excite the increased MS-related nonlinearities as well as the viscous losses during contraction and could render the apparent wall stiffness higher during MS than VS. It is also possible that the 0.7 static strain estimated based on literature data was higher than the in situ static component of the strain. A consequence of that would be that the fibers may have been almost fully aligned and straight and hence the dynamic stretch could not induce proper recruitment. The latter could in turn act to reduce any difference in stiffness between MS and VS. Additionally, we controlled strain whereas in vivo strain is a result of blood pressure fluctuations and wall properties. In preliminary experiments, we determined that the rate of force increase slowed by 30 min following KCl challenge. However, it is possible that the steady state was not always reached. We also noticed that the shape of the second contraction was sometimes different from that of the first (figure 2). While we did not find a systematic dependence of the time constant of force increase on stretch type, it is possible that the 30 min interval allowed for contraction influenced the peak force recording. Since application of Oli required a third contraction, in two aorta rings we verified that the third contraction was similar in magnitude to the second without the inhibitor. While we argued that the US samples approximate best the in situ ECM, at least for actin, the 30 min period before the samples were fixed certainly affected the actin amount and structure.

Implications for stiffness and ECM regulation

Despite the above limitations, our study shows that even with simple sinusoids and equal mean and peak strains, cycle-by-cycle variability in stretch alters force-generation, intracellular actin structure as well as the ECM structure of the aorta. These in turn can have implications for the control of aortic stiffness and adaptability. First, our results point to an important yet experimentally often overlooked feature of the mechanical environment of the aorta whose dynamic nature due to normal blood pressure variability affects VSMC contractility and ECM structure. Second, changes in strain variability, due to increased blood pressure variability in patients with hypertension and aging [23], may alter the contractile properties of the aorta as well as its healthy homeostatic beat-to-beat mechanotransduction. Third, during medical interventions involving long-term anesthesia in human subjects [5], strain variability decreases which may reduce contractility and disorganize the ECM of the vessel wall. Finally, the classical view that aortic stiffness can mostly be attributed to the ECM has recently been challenged demonstrating that VSMCs contribute substantially to the stiffness of the aorta in aging and hypertension [8, 29, 31]. For example, Gao et al showed that in mice, VSMCs’ contribution to wall stress and stiffness is under persistent control of endothelial nitric oxide levels and has the ability to increase aortic stiffness by 100% in its absence [8]. Similarly, Sehgel et al showed that VSMCs become stiffer in hypertensive rats [29, 31]. In the context of force generation, VSMCs are important in keeping the homeostatic mechanical environment of the vessel wall by contraction or relaxation to keep an appropriate wall shear stress on the endothelial layer, as well as maintaining proper wall tension [13, 25]. Our results also suggest that muscle tone regulated by variability in strain is necessary for proper homeostatic ECM organization, a notion that is in good agreement with a recent report that mechanical homeostasis appears to restore collagen fibril waviness in tendon via active fibroblast contraction [17]. In summary, we propose that cycle-by-cycle variability in strain due to the corresponding fluctuations in blood pressure plays an important role in vascular homeostasis including both mechanical function as well as ECM structural organization.