Interactions of Water and Alkanes: Modifying Additive Force Fields to Account for Polarization Effects

Abstract

Atomistic biomolecular simulations predominantly utilize additive force fields (FF), where the electrostatic potential is modeled by fixed point charges. Among other consequences, the lack of polarizability in these models undermines the balance of hydrophilic/hydrophobic non-bonded interactions. Simulations of water/alkane systems using the TIP3P water model and CHARMM36 parameters reveal a 1 kcal/mol overestimate of the experimental transfer free energy of water to hexadecane; more recent optimized water models (SPC/E, TIP4P/2005, TIP4P-Ew, TIP3P-FB, TIP4P-FB, OPC, TIP4P-D) overestimate this transfer free energy by approximately 2 kcal/mol. In contrast, the polarizable SWM4-NDP and SWM6 water models reproduce experimental values to within statistical error. As an alternative to explicitly modeling polarizability, this paper develops an efficient automated workflow to optimize pair-specific Lennard-Jones parameters within an additive FF. Water/hexadecane is used as a prototype and the free energy of water transfer to hexadecane as a target. The optimized model yields quantitative agreement with the experimental transfer free energy and improves the water/hexadecane interfacial tension by 6%. Simulations of five different lipid bilayers show a strong increase of water permeabilities compared to the unmodified CHARMM36 lipid FF which consistently improves match with experiment: the order-of-magnitude underestimate for monounsaturated bilayers is rectified and the factor of 2.8 – 4 underestimate for saturated bilayers is turned into a factor of1.5 – 3 overestimate. While agreement with experiment is decreased for the diffusion constant of water in hexadecane, alkane transfer free energies, and the bilayers’ area per lipid, the method provides a permeant-specific route to achieve a wide range of heterogeneous observables via rapidly optimized pairwise parameters.

Graphical Abstract

1. Introduction

The accuracy of molecular dynamics (MD) simulations critically depends on the force field (FF), which defines all atomistic interactions in the simulation. While current additive lipid FFs reproduce many macroscopic observables (e.g. area per lipid, compressibility moduli of bilayers), important subtler effects (e.g. dipole potential inside the membrane,¹ diffusion of lipids,² membrane permeability^3–5) are still not well modeled.

One reason for these shortcomings is the use of decades old water models that are intertwined with biological FFs due to historical reasons and a well-validated cancellation of errors. Rather than being an interchangeable component, the water model often constitutes the foundation of the atomistic model, preserving the necessary hydrophobic/hydrophilic balance in biological simulations. For instance, the CHARMM36 (C36) FF¹ has been fine-tuned to be compatible with TIP3P,⁶ a model from the 1980s that yields the temperature of maximum density, self-diffusion constant and viscosity of water in dramatic mismatch with experiment.^7,8

Recent years have brought forward a variety of highly-optimized water models, parameterized to reproduce a wide range of physical properties of pure water.^11,14,15,17 Such a bias towards homogeneous observables can negatively affect properties of heterogeneous systems, especially when the models are used in concert with biological FFs. For example, deviations of the simulated membrane dipole potential and water permeability from experiment increased when C36 was used with TIP3P-FB instead of TIP3P.⁴ The limited transferability of the FF parameters arises primarily from a lack of electrostatic polarization. By definition, rigid additive water models are restricted to a fixed dipole moment, usually pre-polarized for the bulk aqueous environment. While a water molecule in the gas phase has a dipole moment of approximately 1.85 D,¹⁸ models used in condensed-phase simulations have significantly larger dipole moments to account for the self-polarization of water (cf. Table 1). This increased polarity may be problematic in more hydrophobic environments. For example, a water permeating through a cell membrane is unable to modulate its dipole moment in response to the bilayer’s apolar core.

Table 1:

Dipole moments μ / D of selected fixed-point charge water models with three, four, and five sites.

Water Model	μ / D	Reference
SPC	2.274	9
SPC/E	2.350	10
TIP3P	2.347	6
TIP3P-FB	2.419	11
TIP4P	2.177	6
TIP4P/2005	2.305	12
TIP4P-Ew	2.321	13
TIP4P-FB	2.428	11
OPC	2.480	14
TIP4P-D	2.403	15
TIP5P	2.292	16

One way to account for some of these effects is to employ a flexible water model, where the dipole moment can change depending on its local environment.^19,20 This is the motivation behind the highly flexible F3C water model.²¹ The authors explain that F3C implicitly accounts for some polarization effects without explicit inclusion of polarizability. Such approaches have not gained widespread adoption for several reasons relating to unwanted heat capacity and more stringent timestep requirements,²² but some modern force fields still include water flexibility. For example, the AMOEBA water model²³ includes flexibility to account for part of its polarization response.

A long-term remedy is offered by explicitly polarizable models that employ Drude particles or induced multipoles, such as the polarizable CHARMM,^24,25 AMOEBA,^23,26 and iAMOEBA²⁷ FFs. Those models are capable of adjusting their charge distributions to the intermolecular environment, which better mimics the actual physics than fixed-charge models.²⁸ However, this flexibility comes at an increased computational cost and massive reparameterization efforts, which discourages their use in the study of biomolecular systems on larger length- and timescales. Therefore, additive FFs remain attractive for many studies.

The present work explores the strengths and limitations of using fixed-point charges and the Drude approach to model hydrophobic interactions. In the first part (Section 3), the behavior of water in water/alkane systems is scrutinized. The second part (Sections 4 and 5) optimizes the pairwise water-alkane interactions in the C36 lipid FF, pushing the limits of the additive framework.

The water/alkane systems studied in the first part represent simplistic membrane models. This relationship is famously stated by Overton’s rule that the transfer free energy from water to oil indicates a substance’s ability to permeate cell membranes.^29,30 This analogy makes these systems an important target for both experimental and simulation studies.^29,31–33

For this study, hexadecane is chosen since it has been identified as a reasonable model for the interior of a bilayer.³⁴ The transfer free energy of water to hexadecane can be extracted from conventional molecular dynamics simulations using systems that are divided into a water and a hexadecane slab. However, the sampling of water in the hexadecane phase is naturally poor, requiring long simulations (> 100 ns) to obtain reliable results. Therefore, the slab systems are only analyzed for TIP3P and TIP4P-Ew. To enhance sampling and to allow the water models in Table 1 to be studied in a reasonable time, transfer free energies for all of these models are calculated from alchemical free energy simulations. This efficient methodology also allows for the inclusion of shorter alkanes (i.e. ethane, octane) that are allowed to transfer between the two phases present in the simulation, and enables two different alkane models (C36 and OPLS-AA³⁵) to also be included in this study.

The restriction to only water and alkanes facilitates isolating the hydrophobic effect. It also opens a more unbiased view than simulations of full bilayers, as the alkane models under consideration were developed independently from any water models.^1,35 In contrast, other C36 atom types were fine-tuned in concert with TIP3P to reproduce experimental lipid observables.

The second part of this work is an optimization of the water-alkane interactions, a last resort to defer more extensive reparameterization of the polarizable FF and recover the experimental water partitioning within the current C36 lipid FF. Such a preliminary refitting of an additive FF is still challenging due to the high sensitivity of the bilayer observables to small changes in the potential energy function. Fortunately, the optimization can be restricted to the pair-specific Lennard-Jones (LJ) parameters, which represent the dominant interaction between water and alkanes. This approach does not explicitly model an electrostatic response of the water dipole and will therefore not capture polarization effects comprehensively. However, it mimics desirable behavior of polarizable water models, when passing through an interface via migration from bulk into a hydrophobic environment. Therefore, tuning individual interaction pairs provides a means to account for local environmental changes within an additive force field.

Similar strategies have been followed previously. Best et al. found that strengthening water-protein dispersion interactions by 10% improves the properties of disordered proteins and biases solvated proteins away from compact states.³⁶ Ashbaugh et al. optimized pairwise water-alkane interactions to reproduce alkane hydration free energies using a united-atom FF.³⁷ Notably, the current C36 force field employs atom-pair specific LJ parameters for specific interactions (e.g. ions) to improve hydration free energies,³⁸ a strategy that is termed NBFIX. In contrast, rather than targeting hydration free energies, the present work optimizes the transfer free energy from water to hexadecane. For membrane permeability modeling, this change places the focus onto the (relative) partitioning of substances within a bilayer model rather than their (absolute) solvation free energies within the individual phases.

Tuning only the LJ interactions between individual atom types has some clear advantages. First, it does not alter the properties of the individual water and alkane phases. In the case of C36, the alkane parameters have been validated carefully,³⁹ so a change to the current parameters would have to pass a similarly thorough probe. Second, an adjustment of the water-alkane interactions will presumably have a narrower impact on the complete bilayer, as opposed to exchanging the water model. Third, the usual choice to determine the pairwise LJ interactions (in C36 and OPLS-AA) is through the Lorentz-Berthelot combining rules. These rules present a heuristic approach that is based on ease of implementation rather than physical laws. Even the LJ potential itself presents an approximation that encapsulates repulsion and dispersion from multiple orders into two empirically tuned parameters.^40,41 Thus, inserting customized LJ parameters for water-alkane interactions does not violate the underlying principles of the model. Fourth, a replacement of individual LJ terms does not present technical difficulties and can be done without introducing any performance penalties. Finally, an automated optimization of these terms can be carried out very efficiently since free energy predictions are accessible via multistate reweighting (MR),^42,43 without performing further simulations.

By way of outline, Section 2 describes the simulation methodology, followed by a test of several additive and polarizable water models in Section 3. In Section 4, MR is utilized to rapidly reparameterize the LJ parameters between water and alkanes in an automated manner. A thorough validation of the optimized parameters in Section 5 highlights the advantages and disadvantages of this approach compared to explicit polarization. This proof-of-concept includes heterogeneous properties of water/alkane systems and simulations of five different lipid bilayers. Section 6 provides discussion and conclusions.

2. Methodology

2.1. Slab Simulations

Simulations of water/n-hexadecane slabs were simulated using Gromacs version 5.1.4 with a leap-frog integrator and a 1 fs time step in the NPAT ensemble.⁴⁴ The reference temperature (298.15 K) and normal pressure (p_z = 1 atm) were controlled via the Nosé-Hoover thermostat and Parrinello-Rahman barostat, respectively.^45–47 The area tangential to the interface was fixed to A_xy = 50 × 50 Ų, to prevent the interface from collapsing under the influence of the interfacial tension. Three different system sizes were simulated that vary in the number of water, hexadecane and ethane molecules present, which are given in Table 2.

Table 2:

Designation and model parameters for simulations of water/hexadecane slabs.

System	Number of Molecules
	Water Model	Water	Hexadecane	Ethane	Dispersion Method
${\text{Wat}}_{1\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{1\times }-[\text{Cut}]$a	TIP3P	2159	126	0	Force-switch Cutoff
${\text{Wat}}_{1\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{1\times }-[\text{LR}]$a	TIP3P	2159	126	0	LJ-PME
${\text{Wat}}_{1\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{2\times }-[\text{Cut}]$a	TIP3P	2159	252	0	Force-switch Cutoff
${\text{Wat}}_{1\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{2\times }-[\text{LR}]$a	TIP3P	2159	252	0	LJ-PME
${\text{Wat}}_{2\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{1\times }-[\text{Cut}]$a	TIP3P	4318	126	0	Force-switch Cutoff
${\text{Wat}}_{2\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{1\times }-[\text{LR}]$a	TIP3P	4318	126	0	LJ-PME
${\text{Wat}}_{1\times }^{\text{TIP}4\text{P}-\text{Ew}}{\text{Hexd}}_{1\times }-[\text{Cut}]$a	TIP4P-Ew	2159	126	0	Force-switch Cutoff
${\text{Wat}}_{1\times }^{\text{TIP}4\text{P}-\text{Ew}}{\text{Hexd}}_{1\times }-[\text{LR}]$a	TIP4P-Ew	2159	126	0	LJ-PME
${\text{Wat}}_{1\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{1\times }\text{Eth}-\text{[Cut]}$a	TIP3P	2159	126	10	Force-switch Cutoff
${\text{Wat}}_{1\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{1\times }\text{Eth}-\text{[LR]}$a	TIP3P	2159	126	10	LJ-PME

^a[Cut] denotes simulations using a force-switch cutoff, while [LR] denotes simulations using long-range LJ interactions via LJ-PME. The subscript “2×” represents doubled sizes of the water (Wat) and hexadecane (Hexd) phases, while “1×” refers to the original size, i.e. 2159 water and 126 hex adecane molecules.

All slab simulations used C36. First, LJ interactions were cut off using a switching function between 10 Å and r_VDW = 12 Å.⁴⁸ These runs were then repeated using LJ Particle Mesh Ewald (LJ-PME) to account for the sensitivity of interfacial tensions, γ to long-range dispersion.^49–51

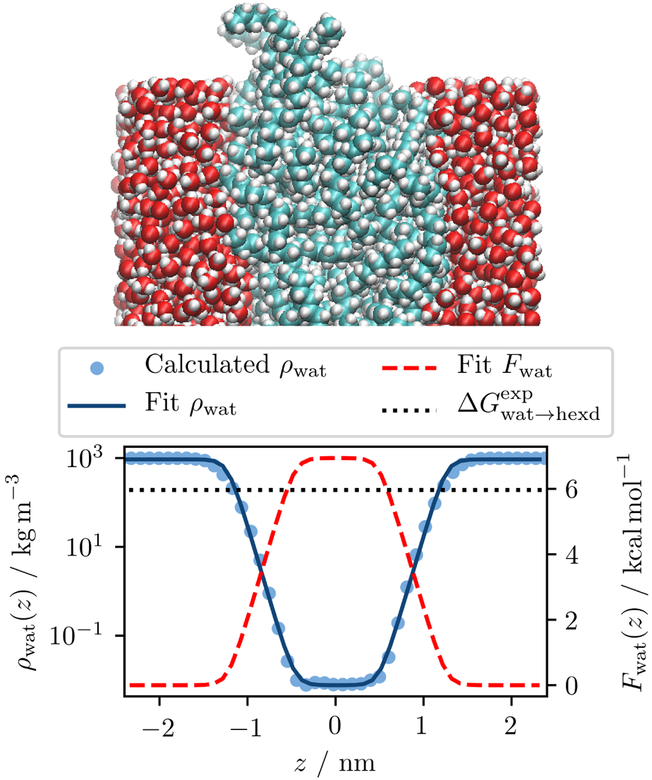
These simulations were run for 200 ns to provide sufficient sampling of water (ethane) molecules in the hexadecane (water) phase. The distribution of the permeating molecules along the normal axis ρ(z) was fit with an analytic function of the form

$$\rho \left(z;C_1,\dots ,C_5\right)=C_1+C_2\text{tanh}\left(\frac{\left|z-C_3\right|-C_4}{C_5}\right)$$

via the parameters C₁, …, C₅, see Figure 1. (In practice, the logarithm of the function was fit to the logarithm of the simulated water distribution to ensure a proper weighting of the plateau in the hexadecane phase.) The partition functions ρ(z) and the corresponding potentials of mean force

$$F(z)=-k_{B}T\text{ln}\left(\rho (z)/\rho \left(z_w\right)\right)$$

were extracted from the fits, where k_B, T, and z_w denote the Boltzmann constant, temperature, and center of the water slab, respectively. The free energies of transfer were obtained from the fit functions as ΔG_wat→hexd = F (z_h) − F (z_w), where z_h denotes the center of the hexadecane slab.

Figure 1:

Water density (ρ_wat) distribution in a TIP3P/hexadecane slab. The potential of mean force (F_wat) overestimates the experimental free energy of transfer $\left(\text{Δ}{G}_{\text{wat}\to \text{hexd}}^{\text{exp}}\right)$ by 1 kcal/mol.

2.2. Free Energy Simulations (Additive Models)

For the free energy simulations, all runs employed Langevin Dynamics in Gromacs with a friction constant of 1/ps and a reference temperature of 298.15 K. The initial models were subjected to an energy minimization, followed by individual NVT and NPT equilibration simulations of 100 and 300 ps, respectively. Production NPT simulations lasted for 1 ns for the comparison of the water models in Section 3. For all simulations involved in the optimization procedure in Section 4, simulations were extended to 5 ns. We observed that all torsion angles between octane carbons flipped 5 to 10 times per nanosecond, confirming sufficient sampling of the conformational space.

For the C36 and OPLS-AA force fields, the van der Waals cutoff was set to 12 Å and 11 Å, and the switching distance to 10 Å and 10.5 Å, respectively. OPLS-AA simulations were run with an analytic tail correction for energy and pressure that isotropically models long-range LJ interactions.⁵² C36 simulations were run without correction. SHAKE was used to constrain the intramolecular hydrogen valence bonds for water and alkanes in both force fields.⁵³

For each set of alchemical free energy simulations, one solute was solvated in two solvent boxes (one box containing 2000 water molecules and the other containing 126 hexadecane molecules). Electrostatic and steric interactions between a solute and a solvent molecule were simultaneously switched o using 18 λ-states. Free energy calculations were performed using the Bennett Acceptance Ratio Method (BAR),⁵⁴ as implemented in Gromacs. The resulting free energies of solvation in pure water and pure hexadecane, ΔG_hydr and ΔG_solv(hexd), were combined to get the free energy of transfer using

$$\text{Δ}{G}_{\text{wat}\to \text{hexd}}=-\text{Δ}{G}_{\text{hydr}}+\text{Δ}{G}_{\text{solv}(\text{hexd})}.$$

2.3. Free Energy Simulations (Polarizable Models)

The free energies for the polarizable models were calculated using the polarizable Drude FF^55–57 in alchemical growth simulations. Simulations were carried out using the “pert” module in CHARMM, with 12 different λ-states engaged in Hamiltonian replica exchange for enhanced sampling. Perturbations were performed with 12 states (4 for turning o electrostatics and 8 for soft-core van der Waals interactions). BAR was used to extract the free energy differences between the λ-states. Five independent runs of 1 ns were carried out for each system. For octane, all trajectories were extended to 3 ns for better sampling. The SWM4-NDP⁵⁸ and SWM6⁵⁷ Drude water models were used in the simulations. SWM4-NDP is the “default” Drude water model, while SWM6 is a more recent six-site model that includes the addition of two more explicit lone pairs.

Note that computing free energies with BAR for Drude simulations can prove problematic due to discrepancies in the polarization response (i.e., the Drude particle placement) based on the change in Hamiltonian. While others have used thermodynamic integration instead of BAR to circumvent this issue,^59,60 recent work by König et al.⁶¹ suggests that BAR may be used to evaluate solvation free energies for the Drude force field. To validate the results from alchemical simulations, the water and ethane transfer free energies for the Drude model were also computed by slab simulations, reported in Ref. 3, and yielded results consistent with the BAR calculations.

2.4. Validation Simulations

Calculations of the diffusion constant of water in hexadecane were performed using Gromacs. Temperature and pressure were kept constant via a Nosé-Hoover thermostat and a Parrinello-Rahman barostat.^45–47 To calculate the infinite dilution diffusion constants and avoid water aggregation, a single water molecule was placed into a box of 126 hexadecane molecules. Since sampling is naturally poor for only one molecule, 100 replicas of 10 ns were run at 298.15 K for the modified models and for C36. The mean-square-displacement in each replica was fit by linear functions, allowing the extraction of $D_{\text{ hexd }}^{\text{ wat }}$ from the average slope.

A 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) bilayer with 36 lipids per leafletwas run at atmospheric pressure and 323.5 K. Similarly, a 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) bilayer was run at 303.5 K. DPPC was chosen because its saturated palmitoyl chainsare similar to hexadecane; DOPC was simuated because its permeability with C36 showedthe largest difference with experiment.³ In both simulations, a Lennard-Jones force switching scheme was used between 8 and 12 Å. After 15 ns of equilibration, four replicas of 60 ns were simulated using Domdec in CHARMM version 41b1.⁶² An extended system barostat and Nosé-Hoover thermostat were used for pressure and temperature control, respectively. For a broader validation and more efficient sampling, simulations for five different lipid bilayers were run in OpenMM.⁶³ In addition to DOPC and DPPC (for a check of consistency), this set included homogeneous bilayers of 1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC), 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC), and 1-palmitoyl-2-oleoyl-snglycero-3-phosphocholine (POPC). See supplementary information, Section S.2, for more details.

3. Study of Existing Models

3.1. Slab Systems

C36 Alkanes with TIP3P Water

Two observables were extracted from the simulations of water/hexadecane slabs: interfacial tensions and free energies of transfer. As shown in Table 3, both properties were consistent between the three system sizes.

Table 3:

Results for water/hexadecane slabs simulated using C36 and TIP3P water.

System	γ / 10−3N·m−1	$\text{Δ}{G}_{\text{wat}\to \text{hexd}}^{\text{wat}}/\text{kcal}\cdot {\text{mol}}^{-1}$	$\text{Δ}{G}_{\text{wat}\to \text{hexd}}^{\text{ethane}}/\text{kcal}\cdot {\text{mol}}^{-1}$
${\text{Wat}}_{1\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{1\times }-[\text{Cut}]$	46.61 ± 0.05	6.94	-
${\text{Wat}}_{1\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{1\times }-[\text{LR}]$	47.96 ± 0.04	7.07	-
${\text{Wat}}_{1\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{2\times }-[\text{Cut}]$	46.85 ± 0.17	6.71	-
${\text{Wat}}_{1\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{2\times }-[\text{LR}]$	47.90 ± 0.20	7.42	-
${\text{Wat}}_{2\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{1\times }-[\text{Cut}]$	46.58 ± 0.08	6.92	-
${\text{Wat}}_{2\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{1\times }-[\text{LR}]$	48.10 ± 0.15	7.03	-
${\text{Wat}}_{1\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{1\times }\text{Eth}-\text{[Cut]}$	46.35 ± 0.28	-	−3.04
${\text{Wat}}_{1\times }^{\text{TIP}3\text{P}}\text{Hexd}{}_{1\times }\text{Eth}-\text{[LR]}$	47.62 ± 0.08	-	−2.83
Experiment	53.5 ± 0.2a	5.98b	−2.50b

^aThe experimental interfacial tensions were averaged over three values: 53.59, 53.5, and 53.3, as reported by Aveyard and Briscoe,⁶⁴ Wu and Hornof,⁶⁵ and Drelich and Miller,⁶⁶ respectively.

^bThe experimental free energies of transfer were calculated from the partition coefficients reported by Abraham et al.⁶⁷

The average interfacial tension without long-range dispersion was 46.48±0.12 · 10⁻³ N/m, underestimating the experimental result by more than 10%. This result was not noticeably altered by the presence of ethane molecules in the system. Using LJ-PME increased the interfacial tension slightly, to an average value of 47.99 ± 0.08 · 10⁻³ N/m. This 2–3% increase fits with the observation that long-range dispersion particularly affects interfacial properties.^39,51 Compared with liquid-vapor interfaces, the effect on the present liquid-liquid interface is understandably smaller, and not nearly sufficient to match the experimental value.

The experimental free energy of transfer was overestimated by approximately 1 kcal/mol for water and underestimated by 0.5 kcal/mol for ethane. Especially the mismatch for water is undesirable; a 1 kcal/mol error is propagated and exponentiated in formulas for the permeability, leading to errors as large as a factor of five.

Considering the well-known deficiencies of TIP3P water, a natural approach to correct these errors is to use a better water model. Therefore, one of the water/hexadecane slabs was also simulated using TIP4P-Ew, a model that yields more realistic condensed-phase properties over a wide range of temperatures and pressures.^14,68

C36 Alkanes with TIP4P-Ew Water

As shown in Table 4, the interfacial tensions were considerably closer to experiment when using TIP4P-Ew. The reference value was only overestimated by 3% (cutoff and 5% (PME), in line with the generally better bulk properties. A similar trend was previously observed for the water-vapor interface,⁶⁹ where TIP4P-Ew and TIP3P underestimated the experimental surface tensions by 9% and 27%, respectively.

Table 4:

(Continuation of Table 3) Results for the TIP4P-Ew water model.

System	γ / 10−3Nm−1	$\text{Δ}{G}_{\text{wat}\to \text{hexd}}^{\text{wat}}/\text{kcal}\cdot {\text{mol}}^{-1}$
${\text{Wat}}_{1\times }^{\text{TIP}4\text{P}-\text{Ew}}{\text{Hexd}}_{1\times }-[\text{Cut}]$	55.05 ± 0.04	7.71
${\text{Wat}}_{1\times }^{\text{TIP}4\text{P}-\text{Ew}}{\text{Hexd}}_{1\times }-[\text{LR}]$	56.21 ± 0.13	8.03
Experiment	53.5 ± 0.2	5.98

In contrast, the free energy of transfer was even worse, indicating a possible disadvantage of optimized fixed-point charge models. However, even a simulation time of 200 ns was insufficient to provide accurate free energies, due to the limited sampling of water in the hydrophobic phase. This shortcoming of conventional MD simulations motivates the use of alchemical free energy simulations in the following section.

3.2. Free Energy Simulations

3.2.1. Additive Models

Free energy simulations were used to evaluate the transfer free energies ΔG_wat→hexd for all water models listed in Table 1. This list of water models comprises classical models like TIP3P (the CHARMM variant with LJ interactions for hydrogens), standard TIP3P [denoted TIP3P(s)], TIP4P, and TIP5P, as well as more recent, highly optimized models, such as TIP3P-FB, TIP4P-FB, OPC and TIP4P-D.

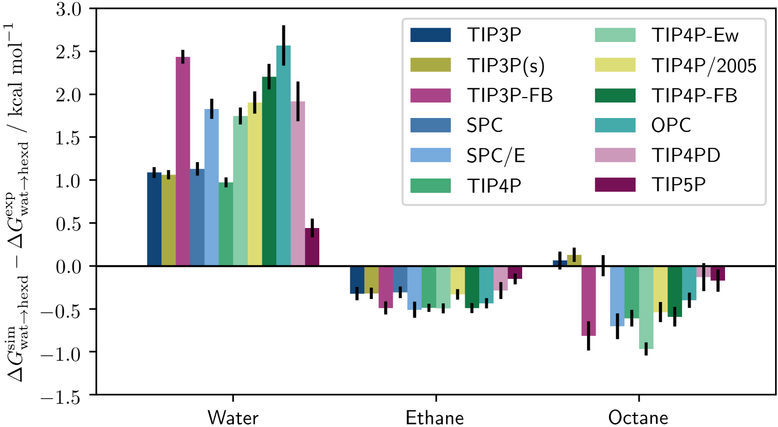
Figure 2 shows the deviations of $\text{Δ}{G}_{\text{ wat }\to \text{ hexd }}^{\text{ solute }}$ from experiment for three different solutes: water, ethane, and octane. A first, basic observation is that the errors for TIP3P and TIP4P-Ew agreed well with the slab systems from the previous sections: The water transfer free energies were overestimated by 1.0 and 1.7 kcal/mol respectively; the ethane transfer free energy (for TIP3P) was underestimated by approximately 0.3 kcal/mol.

Figure 2:

Deviations between simulated $\left(\text{Δ}{G}_{\text{ wat }\to \text{ hexd }}^{\text{ sim }}\right)$ experimental $\left(\text{Δ}{G}_{\text{wat}\to \text{hexd}}^{\text{exp}}\right)$ free energies of transfer from the water to the hexadecane phase for the three different solutes (i.e. water, ethane, octane).

This general trend of overestimation of water and underestimation of alkane transfer free energies was found in all water models. Moreover, the absolute errors were comparably larger for water as a solute than for alkanes. Especially so, the most recent and highly optimized models failed to reproduce the experimental $\text{Δ}{G}_{\text{ wat }\to \text{ hexd }}^{\text{ water }}$; for example, between TIP3P and TIP3P-FB the error worsened from 1.0 to 2.4 kcal/mol. This result is not surprising since water models are usually parameterized as solvents; the fine-tuned parameters have not been validated to reproduce the partitioning of water into an apolar phase.

This bias of optimized parameters towards the liquid phase is particularly evident in their fitting to experimental enthalpies of vaporization. Since a depolarization from the condensed-phase dipole moment to the 1.85 D gas-phase dipole moment¹⁸ cannot be reflected in additive models, the experimental reference values are typically modified by a gas-phase correction during parameterization.^10,13 The correction term accounts for the self-energy due to polarization which, in effect, increases the optimal dipole moment (μ), cf. Table 1. This parameterization strategy thereby sacrifices the correct liquid/vapor partitioning to improve the description of bulk-phase properties such as densities, diffusion and dielectric constants.¹⁷

This bias towards liquid water not only affects water partitioning into vacuum (vaporization) but also into other low dielectric media (for here: alkanes). As shown in Figure 3, the errors in the water transfer free energies correlate strongly with μ for water models. In sum, the inclusion of a gas-phase correction in the optimization of water models also undermines a correct water/alkane partitioning.

Figure 3:

Deviations from experiment for the free energy of transferring a water molecule from the water phase into the hexadecane phase versus the dipole moment.

The only tested five-point model, TIP5P, presents an outlier in Figure 3. Here, the presence of explicit hydrogen bond acceptors allows for additional flexibility in the choice of the dipole moment. As a consequence, TIP5P was the only tested fixed point charge model that yielded all transfer free energies within 0.5 kcal/mol of experimental values.

To assure ourselves that the erroneous transfer free energies of water are not an artifact of C36, the simulations were repeated using the OPLS-AA alkane parameters. As depicted in Figure 4, the free energies for OPLS-AA were shifted to slightly higher values, but strongly correlated with C36 otherwise. While the shift led to a slightly more accurate representation of alkane transfer, the errors for water as a solute increased even further.

Figure 4:

Correlation of errors in free energies between simulations using C36 and OPLS-AA.

Taken together, these results highlight the limited transferability of the functional form of most additive force fields: Models that were parameterized for a certain charge environment, may behave poorly in other environments. This issue is particularly acute for simulations of membrane permeability. While traversing the different regions of a lipid bilayer, permeants will inevitably be exposed to different electrostatic environments.⁷⁰ To account for these changes, one can either include explicit polarization or assign pair-specific parameters. Other possible FF extensions that would improve the representation of the underlying physics include higher-order dispersion terms^40,71 or smeared charges.^72–74 Those approaches are not investigated further in the present work.

To test the effect of polarizability, the free energies of transfer were evaluated for the CHARMM polarizable FF based on the classical Drude oscillator model (“Drude”).

3.2.2. Polarizable Models

The Drude water models, SWM4-NDP and SWM6, were parameterized to reproduce the excess chemical potential and enthalpy of vaporization, respectively. In contrast to additive models, an explicit response to the electrostatic environment is governed by a displacement of the charged Drude particles so that the experimental reference values do not need correction for the self-polarization energy.

The transfer free energies obtained with the CHARMM polarizable FF are listed in Table 5. In comparison, slab simulations of water and ethane transfer using the SWM4-NDP model yielded 5.8±0.1 and −2.8±0.1 kcal/mol, respectively.³ The match between the two methods, again, indicates that using BAR within the Drude force field does not significantly affect the free energies. For SWM4-NDP, the experimental transfer free energies of water and ethane were reproduced to within 0.2 kcal/mol, while octane was too favorable for the hexadecane phase, by approximately 0.7 kcal/mol. For the six-site SWM6 model, all transfer free energies were reproduced to within 0.2 kcal/mol.

Table 5:

Free energies (kcal/mol) of transfer from water to hexadecane for the CHARMM polarizable force field.

Model	Solute
	Water	Ethane	Octane
SWM4-NDP	5.87 ± 0.11	−2.61 ± 0.13	−7.14 ± 0.17
SWM6	6.09 ± 0.14	−2.66 ± 0.11	−7.72 ± 0.17
Experimenta	5.98	−2.50	−7.84

^aThe experimental free energies of transfer were calculated from the partition coefficients reported by Abraham et al.⁶⁷

Compared to all tested additive models, the results for the polarizable model mark a substantial improvement. Figure 5 shows that the Drude water models adjusted their charge distribution appropriately to polar and apolar solvents. The average dipole moment of a water molecule in bulk water was 2.46 D (SWM4-NDP) and 2.43 D (SWM6); in hexadecane, it was 1.89 D (SWM4-NDP) and 1.88 D (SWM6). The standard deviations of the mean were smaller than 0.01 in all simulations. The distribution of water dipole moments was also much wider in the polar phase: standard deviations were 0.17 D (SWM4-NDP) and 0.15 D (SWM6) for water in water and one order of magnitude lower (0.02 D) for water in hexadecane.

Figure 5:

Probability distribution of water dipole moment when solvated in the polar water phase (black solid line) and in the apolar hexadecane phase (red dash line) obtained from the polarizable Drude simulations.

While polarizability improves the representation of the physics, the current Drude FF for lipids⁷⁵ is not as well optimized as the additive models for many bilayer properties (e.g. surface areas, compressiblities). Using the Drude approach also increases computational cost, where the performance penalty depends on the system and simulation program. CHARMM is currently lacking an efficient domain decomposition implementation so that simulations are roughly one order of magnitude slower than with additive force fields. A recent OpenMM implementation⁷⁶ alleviates the performance penalty to a factor of four (a factor of two due to an increased number of particles and a more sophisticated integration step, and another factor two for the more stringent 1 fs time step requirement). Despite this progress, additive models are still the most used for a majority of biomolecular simulations. Therefore, the remainder of this paper follows the second alternative of optimizing pair-specific Lennard-Jones terms to push the limits of the additive methodology.

4. Optimization of Additive Models

4.1. Optimization Procedure

The LJ parameters σ_ij and ε_ij between TIP3P water and alkane were optimized to reproduce the experimental free energy of transferring a water molecule from the water to the hexadecane phase. To achieve the correct transfer free energy, water-alkane repulsion can be weakened by either increasing ε_ij or decreasing σ_ij. Therefore, the Lorentz-Berthelot combining rules between water and alkane atoms were modified by two scaling factors, λσ and λε:

$$\begin{gathered} {\sigma }_{ij}={\lambda }_{\sigma }\cdot \frac{{\sigma }_i+{\sigma }_j}{2}, \\ {\epsilon }_{ij}={\lambda }_{\epsilon }\cdot \sqrt{{\epsilon }_i{\epsilon }_j}. \end{gathered}$$

Modifications of these scaling factors will affect the transfer free energies, which can be decomposed into three terms as follows:

$$\text{Δ}{G}_{\text{wat}\to \text{hexd}}^{\text{wat}}\left({\lambda }_{\sigma },{\lambda }_{\epsilon }\right)=-\text{Δ}{G}_{\text{hydr}}^{\text{wat}}+\text{Δ}{G}_{\text{solv}(\text{hexd})}^{\text{wat}}+\text{Δ}{G}_{\text{nbfix}}\left({\lambda }_{\sigma },{\lambda }_{\epsilon }\right).$$ (1)

The first two terms denote the solvation free energy of TIP3P water in boxes of water and hexadecane, as obtained from the simulations above. These terms are not affected by a change in the scaling factors. The third term denotes the “free energy of the NBFIX”, which is the free energy difference between the original system of water in hexadecane and the perturbed state with scaled LJ parameters. These two states have suitable conformational overlap, as long as the scaling is kept moderate.

To predict ΔG_nbfix(λσ,λε) without computing additonal trajectories, a one-sided free energy reweighting was applied,⁷⁷ similarly as in Refs. 38 and 37. In contrast to these previous works, the reweighting was based on multiple states via the Python package pymbar.^42,43 Given small changes in the parameters, pymbar is able to predict free energies and thermodynamical properties of a perturbed state by using snapshots that were generated in other reference states;^42,78 it also provides error estimates for these predictions.⁴³

The final three λ-states from the alchemical growth were taken as reference states, which avoids evaluations of state-trajectory pairs with little conformational overlap. The one-sided multistate reweighting (MR) described was used to predict $\text{Δ}{G}_{\text{nbfix}}^{\text{MR}}\left({\lambda }_{\sigma },{\lambda }_{\epsilon }\right)\approx \text{Δ}{G}_{\text{nbfix}}\left({\lambda }_{\sigma },{\lambda }_{\epsilon }\right)$. Each evaluation of $\text{Δ}{G}_{\text{nbfix}}^{\text{MR}}$ requires the potential energy of the perturbed state U(λσ,λε) in all snapshots from the reference states; such energy calculations are orders of magnitude faster than explicitly computing trajectories.

In this context, MR acts as a physics-based metamodel; the term metamodel, or “response surface model”,⁷⁸ designates a function that can be used to estimate the outcome of a simulation without running one. Such metamodels are capable of effectively reducing the number of simulations in automated FF optimization.^78,79 In contrast to typical models used in machine learning, such as the neural networks in Ref. 79, the MR metamodel incorporates the physics from each snapshot into its predictions.

To choose feasible values for λσ and λε the loss function

$$f\left({\lambda }_{\sigma },{\lambda }_{\epsilon }\right)\stackrel{\text{Eq}.(1)}{=}\left(-\underset{\text{ experimental reference }}{\underbrace{\text{Δ}{G}_{\text{ wat }\to \text{ hexd }}^{\text{ wat },\text{ exp }}}}-\underset{\text{ from alchemical growth }}{\underbrace{\text{Δ}{G}_{\text{ hydr }}^{\text{ wat }}+\text{Δ}{G}_{\text{solv}\left(\text{hexd}\right)}^{\text{ wat }}}}+\text{Δ}{G}_{\text{ nbfix }}^{\text{MR}}\left({\lambda }_{\sigma },{\lambda }_{\epsilon }\right)\right){}^2$$ (2)

was minimized using a steepest descent optimizer with Armijo step length control.⁸⁰ Gradients were evaluated via finite differences with an increment of δ_λ = 10⁻⁴. To prevent the optimization process from diverging into poorly sampled regions, Armijo steps were rejected whenever MR estimated an error larger than 0.05 kcal/mol. The optimization was considered converged if one of the following stop conditions was fulfilled:

1. The target free energy was matched to within 0.1 kcal/mol.

2. The error estimate from MR exceeded 0.025 kcal/mol.

3. The norm of the loss function’s gradient, cf. Eq. (2), was lower than 10⁻³.

4. No reduction of the loss function occurred within 7 Armijo steps.

This optimization procedure results in a pair of scaling factors that minimizes the error between experiment and simulation, as predicted by MR.

After the optimization was converged, a control simulation was performed using the optimized pairwise LJ values. The samples from the control simulation were incorporated into the reference set of the MR metamodel, by reevaluating the potential energies from all previous reference states for the new trajectory coming from the control simulation. First, this update of the metamodel allows a more accurate two-sided calculation of $\text{Δ}{G}_{\text{nbfix}}^{\text{MR}}\left({\lambda }_{\sigma },{\lambda }_{\epsilon }\right)$ using the Multistate Bennett Acceptance Ratio Method (MBAR).⁴² Second, it improves the accuracy of one-sided free energy predictions. Therefore, the optimization can be iteratively repeated with the updated metamodel if $\text{Δ}{G}_{\text{ wat }\to \text{ hexd }}^{\text{ wat }}\left({\lambda }_{\sigma },{\lambda }_{\epsilon }\right)$ does not match the experimental reference value to within 0.1 kcal/mol.

This iterative algorithm is depicted in Figure 6 and can be summarized as follows:

Figure 6:

Illustration of the optimization procedure. Grey circles represent simulations from the alchemical free energy simulation, i.e. Step 1 of the optimization procedure. Green circles represent control simulations from Step 6 of the optimization procedure. One- and two-headed arrows represent one- and two-sided free energy calculations, respectively.

1. Perform an alchemical growth of solute in hexadecane and solute in water using the original model.

2. Calculate $\text{Δ}{G}_{\text{ hydr }}^{\text{ wat }}$ and $\text{Δ}{G}_{\text{ solv}(\text{hexd })}^{\text{ wat }}$ for the original model using the two-sided BAR.

3. Save the trajectories from the final three lambda states and their respective energy functions in a set of reference states

   $$R^{\text{ref}}:=\left\{{\left(r_i^{3N},U\right)}_{{\lambda }_1},{\left(r_i^{3N},U\right)}_{{\lambda }_2},{\left(r_i^{3N},U\right)}_{{\lambda }_3}\right\}.$$

4. Cross-evaluate all potential energy functions $U_{{\lambda }_i}$ in the reference set for all snapshots ${\left(r_j^{3N}\right)}_{{\lambda }_k}$ in the reference set, and then setup an MR model using these energies.

5. If the free energy $\text{Δ}{G}_{\text{wat}\to \text{hexd}}^{\text{wat}}\left({\lambda }_{\sigma },{\lambda }_{\epsilon }\right)$ obtained for one potential energy function in the reference set matches the experimental free energy to within 0.1 kcal/mol, then stop the optimization and return the optimal parameters. If this criteria is not fulfilled, then minimize the loss function, Eq. (2), using a numerical optimization algorithm.

6. Perform a simulation using the optimal parameters from Step 5.

7. Add the newly generated trajectory and its potential energy function to R^ref and continue from Step 4.

4.2. Optimization Runs

Two different independent optimization cycles were performed with the above algorithm. First, λ_σ:= 1 was kept constant, increasing the conformational overlap between the thermodynamic reference states and the perturbed states. Second, both scaling factors were optimized simultaneously.

The resulting optimized pairs of scaling factors will be referred to as NBFIX-1 and NBFIX-2. For NBFIX-1, ε increased by 45%, deepening the well of the LJ potential. Interestingly, this strengthening of dispersion interaction between water and alkanes is in line with the recent TIP4P-D model by Piana et al.¹⁵ They suggested an increase of the water dispersion coefficient by 50% to bias intrinsically disordered proteins away from too compact, globular states. Despite this similarity, TIP4P-D overestimated the experimental water transfer free energy by 2 kcal/mol, cf. Figure 2. This mismatch can be attributed to TIP4PD’s large dipole moment, which counteracts the stronger dispersion in simulations of the transfer free energy. For NBFIX-2, ε was increased by 7%, accompanied by a roughly 15% decrease in σ. A consequence of this decrease is that water molecules can be more easily accommodated into the voids that form within the liquid hexadecane phase.

Both optimizations were converged after one iteration (i.e. only one control simulation was required per optimization). The calculations finished in less than one day, each running on a single GPU node equipped with two NVIDIA K20 cards.

5. Assessment of the Optimized Models

Several test simulations were conducted to assess the quality of the two optimized models.^a Since pure water and hexadecane systems are unaffected by the NBFIX, the final check incorporated heterogeneous properties. Specifically, these properties were alkane transfer free energies; interfacial tension between water and hexadecane; the diffusion constant of water in alkane; the area per lipid; free energy profile and permeability of water in a lipid bilayer.

5.1. Transfer Free Energies

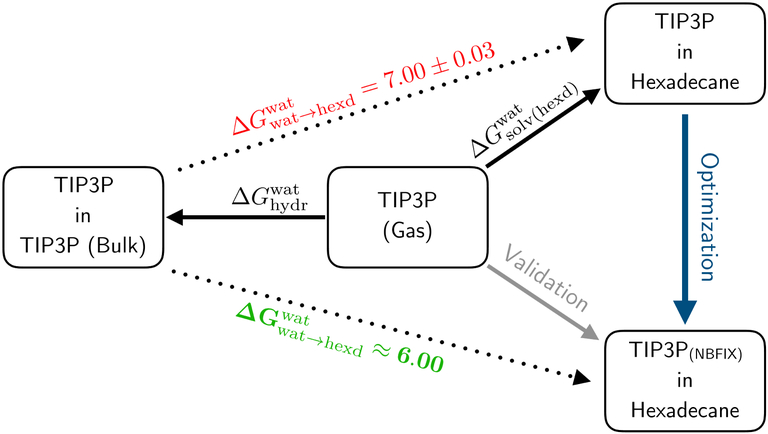
For the purpose of validation, the full alchemical growth of water in hexadecane was repeated for NBFIX-1 and NBFIX-2, closing the thermodynamic cycle in Figure 7. Additional al-chemical growth simulations were performed to calculate the transfer free energies for ethane, butane, and octane using the optimized models, see Table 6.

Figure 7:

Thermodynamic cycle used in the optimization process.

Table 6:

Transfer free energies $\text{Δ}{G}_{\text{ wat }\to \text{ hexd }}^{\text{ solute }}$ (kcal/mol) of optimized models for different solutes, including the original model and experimental values.

Model	λε	λσ	Solute
			Water	Ethane	Butane	Octane
C36 (no NBFIX)	1	1	7.00 ± 0.03	−2.81 ± 0.02	−4.51 ± 0.05	−7.74 ± 0.03
NBFIX-1	1.45	1	5.89 ± 0.03	−0.28 ± 0.01	−0.36 ± 0.03	−0.60 ± 0.06
NBFIX-2	1.07	0.84456	6.08 ± 0.04	−1.84 ± 0.03	−3.79 ± 0.03	−7.62 ± 0.04
Experimenta	-	-	5.98	−2.50	−4.27	−7.84

^aThe experimental free energies of transfer were calculated from the partition coefficients reported by Abraham et al.⁶⁷

As predicted by the MR metamodel, the experimental transfer free energies of water were matched to within 0.1 kcal/mol for both models. Most importantly, the 1–2 kcal/mol mismatch by all tested additive three- and four-site water models was corrected by the NBFIX. However, the two models varied in the transfer free energies that they predicted for alkanes. NBFIX-1 nearly eliminated the preference of the alkanes for the apolar hexadecane phase. In contrast, NBFIX-2 maintained this important preference, reproducing the experimental transfer free energies of ethane, butane, and octane to an accuracy of approximately 0.7,0.5 and 0.2 kcal/mol. Compared to the original TIP3P model, the alkane transfer free energies were consistently increased, while the original model still performed better for all three alkanes (i.e. slightly better for octane and butane, and considerably better for ethane).

These results indicate that improvements in the water transfer require concessions in the alkane transfer free energies, in line with the results for the various water and alkane models in the previous section. This demonstrates the limited transferability of additive force fields.

5.2. Other Heterogeneous Properties

Due to the fundamental nature of the Lennard-Jones parameters, additional MD observables were also investigated. This included the radial distribution functions for the carbon-oxygen distance, see Figure 8. For NBFIX-1, the radial distribution function of the original C36 model was retained, except for a slightly more pronounced peak in the first solvation shell. In contrast, NBFIX-2 shifted the distributions towards smaller radii. Unsurprisingly, the 15% shift of the peaks closely reflects the 15% decrease in σ_ij.

Figure 8:

Radial distribution functions between carbon and oxygen atoms g_CO(r) for one ethane molecule in water and one water molecule in hexadecane. The optimized models NBFIX-1 and NBFIX-2 are compared to the original C36 model.

These distributions elucidate the behavior of the two optimized models, but are hard to assess due to lacking experimental data. Therefore, the diffusion constant of water in hexadecane and the interfacial tension of a water/hexadecane slab were evaluated instead.

Table 7 shows that the diffusion constant was significantly affected by the NBFIX. Understandably, NBFIX-1 slowed down diffusion by approximately 20%; the enhancement of attractive forces through the deeper Lennard-Jones well discourages displacements. In contrast, NBFIX-2 increased diffusion by almost 80%. This can be understood from the radial distribution functions. From the point of view of the hexadecane phase, water molecules became smaller and could more easily hop between the cavities found within the liquid long-chain alkanes.

Table 7:

The interfacial tension γ and diffusion constant of water in hexadecane $D_{\text{ hexd }}^{\text{ wat }}$ for the optimized models, including the original model and experimental values.^{64–6,6,81,82}

Model	λε	λσ	γ / 10−3N m−1		$D_{\text{ hexd }}^{\text{ wat }}/{10}^{-5}{\text{cm}}^2{\text{s}}^{-1}$
			Cutoff	LJ-PME
C36	1	1	46.6 ± 0.1	48.0 ± 0.1	4.31 ± 0.14
NBFIX-1	1.45	1	19.0 ± 0.4	16.3 ± 0.6	3.57 ± 0.18
NBFIX-2	1.07	0.84456	55.6 ± 0.3	61.6 ± 0.4	7.68 ± 0.36
Experiment	-	-	53.5 ± 0.2a		1.1 (300 K)b, 4.16 (303 K)c, 4.59 (308 K)c

^aThe experimental interfacial tensions were averaged over three values: 53.59,53.5, and 53.3, as reported by Aveyard and Briscoe,⁶⁴ Wu and Hornof,⁶⁵ and Drelich and Miller,⁶⁶ respectively.

^bfrom Su et al.⁸¹

^cfrom Schatzberg⁸²

Comparing the diffusion constants with experiment is challenging due to large discrepancy in the reported values. While $D_{\text{ hexd }}^{\text{ wat }}$ was long believed to be in the range of 4–5×10⁻⁵ cm²/s,⁸² a more recent study suggested 1.1×10⁻⁵ cm²/s.⁸¹ In comparison to these values, the diffusion constant in the NBFIX-2 simulation was too large, while the ones from NBFIX-1 and C36 were in better agreement.

The disparity between the three models was even more pronounced for the interfacial tension of water/hexadecane. As has been discussed above, C36 underpredicted the experimental interfacial tension by 10%, even when long-range LJ interactions were taken into account. For NBFIX-1, γ dropped to an unrealistic value of 19 × 10⁻³ N/m. The incorpo ration of LJ-PME even weakened the interface further. In contrast, NBFIX-2 improved the match with experiment, with the reference value being reproduced to within 4% error when using dispersion interactions without LJ-PME. This close match resembles the accuracy of the TIP4P-Ew water model discussed above.

In concert, these validation simulations demonstrate that a large range of physical properties becomes accessible when both σ_ij and ε_ij are incorporated into the parameterization of pair-specific LJ interactions. For all tested heterogeneous properties, from free energies and radial distribution functions to diffusion constants and surface tensions, NBFIX-1 and NBFIX-2 performed very differently. While NBFIX-2 yielded reasonable values for all properties, NBFIX-1 failed to reproduce the surface tension and transfer free energies of alkanes.

The significant change of these water-alkane properties indicates that biological systems could be strongly affected by the modified water-alkane interactions. As a proof of concept, a final set of simulations was run to assess the two models for lipid bilayer systems.

5.3. Lipid Bilayers

The C36 force field underestimates the permeability of water through selected lipid bilayers by a factor 3–10.³ Before discussing such simulations of lipid bilayers, the effect of the optimized models on the water permeability can be estimated based on the homogeneous solubility-diffusion model

$$P=\frac{KD}{h},$$

where K, D, and h denote the oil/water partition coefficient, the diffusion constant of the solute in the membrane and the thickness of the bilayer, respectively.

The partition coefficient K is related to the transfer free energy through

$$K=\text{exp}\left(\frac{-\text{Δ}{G}_{\text{ wat }\to \text{ hexd }}^{\text{ solute }}}{k_{B}T}\right).$$

The optimized models modify the free energy by 1 kcal/mol, which is exponentiated and increases K by a factor of exp(1 kcal · mol⁻¹/(k_BT)) ≈ exp(1.688) ≈ 5.4. In concert with the change in the diffusion constants, the water permeabilities for NBFIX-1 and NBFIX-2 are expected to change by factors of 4.8 and 9.6, respectively. Note that unsaturation will likely not alter these factors greatly as long as chains consist of mostly saturated groups (which includes most relevant lipids). A simulation study by Carl and Feller⁸³ using C27, a predecessor of C36, revealed that unsaturation changes the water transfer free energy by0.2–0.3 kcal/mol per double bond. Contributions of unsaturated groups to the total error in transfer free energy will arguably be only a fraction of this number.

A biphasic water/hexadecane system is clearly a very simplistic model of a bilayer. To make more definitive statements about the feasibility of the optimized models, DOPC and DPPC lipid bilayers were simulated in CHARMM and the study was extended to DLPC, DMPC, and POPC in OpenMM (see Section S.2 in the supplementary information). The previously optimized scaling factors λσ and λε were applied to all interactions between water and saturated acyl groups.

For NBFIX-1, the strongly enhanced attraction between water and acyl atoms led to instabilities. The optimized model was unable to maintain the interface and broke up the bilayer structure, see Figure S2 in the supplementary information. This catastrophic weakening of the interface is consistent with the more than two-fold reduced interfacial tension between water and hexadecane.

For NBFIX-2, the bilayers remained intact. However, the surface area per lipid of DOPC shrank from 69.0 ± 0.3 Ų for C36¹ to 63.9 ± 0.1 Ų. For comparison, experimental measurements⁸⁴ at a at a slightly higher temperature of 308.15K yielded 67.4 ± 1.0 Ų. A similar decrease from 62.9 ± 0.3 to 58.3 ± 0.1 Ų occured for DPPC, where the experimental reference value is 63.0 ± 1.0± Ų,⁸⁴ and also for the bilayers simulated in OpenMM, see Table S2 in the supplementary information. This contraction of the bilayer area is also consistent with the alleviated interfacial tension of the water/hexadecane slab. Moreover, the water that solvates the headgroup region plays a vital role in maintaining the surface area. By decreasing the repulsion between water and lipid atoms in the upper tail region, the atoms can move closer together.

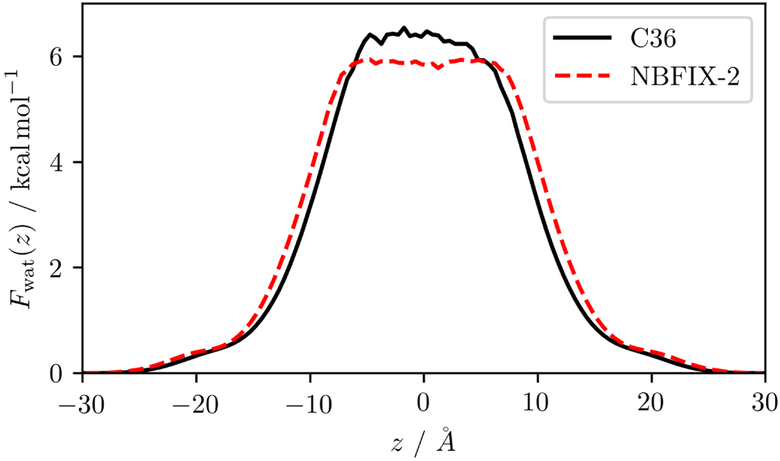
In combination with the contraction of the membrane area, the thickness increased as reflected in the potential of mean force in Figure 9. For C36, the barrier height of approximately 6.5 kcal/mol matched previous simulation studies of water permeation through DOPC bilayers that employed the Berger FF and SPC water;^85,86 however, as shown before, the SPC water model also overpredicts the water transfer free energy by 1 kcal/mol. When the optimized model was used, the plateau in the hydrophobic core of the bilayer widened and flattened (see PMFs of all five bilayers in the supplementary information, Figure S1). This flattening lowered the barrier in the center, indicating that water penetration into the membrane was enhanced while retaining the overall structure and water distribution in the outer part of the membrane.

Figure 9:

Potential of mean force F_wat(z) of water along the bilayer normal of DOPC for the optimized model NBFIX-2 and the original C36 force field.

Finally, the water permeability was explicitly calculated by counting water transits through the membrane (see supplementary information, Table S3, for numbers of transits). The transit rate per unit area r is related to the permeability through

$$P=\frac{r}{2c_w},$$

where c_w denotes the average concentration of permeant in the water phase (see Ref. 3 for a detailed derivation and explanation). Statistical uncertainties were evaluated over four replicas.

Figure 10 and Table 8 compare the permeabilities for C36 and the optimized NBFIX-2 to experiment. Permeabilities obtained using the optimized model are consistently increased by an order of magnitude. Notably, the correction factor that was derived from the homogeneous solubility-diffusion model (= 9.6) results in good agreement, thereby providing a straightforward explanation for the observed difference between C36 and NBFIX-2. While C36 strongly underpredicts the permeabilities, the optimized model improved match with experiment. For the saturated lipids DLPC, DMPC, and DPPC, experimental permeabilities were overestimated by factors 2.7, 2.9, and 1.5 using NBFIX-2, while they are underestimated by factors 2.8, 4.2, and 4.0 using C36. For the monounsaturated lipids DOPC and POPC, the factor-of-10 underestimate in C36 was rectified by the optimized model.

Figure 10:

Water permeabilities through different homogeneous bilayers for the optimized model NBFIX-2 and the original C36 force field compared to experiment.

Table 8:

Permeability P of water through lipid bilayers in 10⁻³ cm/s.

Lipid	C36 (CHARMM)a	NBFIX-2 (CHARMM)	NBFIX-2 (OpenMM)b	Experiment
DLPC	3.7 ± 0.7	-	27.6 ± 4.2	10.4 ± 0.5c
DMPC	2.0 ± 0.7	-	24.4 ± 7.0	8.3± 0.8c
POPC	1.3 ± 0.4	-	12.6 ± 2.3	13.0 ± 0.4c
DOPC	1.5 ± 0.4	15.9 ± 5.3	10.7 ± 2.0	15.8 ± 0.6c
DPPC	6.7 ± 0.8	44.6 ± 10.4	41.5 ± 3.5	27.0 ± 4.0d

^afrom Venable et al.³

^bsee supplementary information, Section S.2

^crom Mathai et al.⁸⁷

^dfrom Guler et al.⁸⁸

6. Discussion and Conclusions

The performance of 13 different additive and polarizable water models was tested in water/alkane systems. As illustrated by the performance of TIP5P and SWM6, the match with experimental free energies of transfer is improved by including explicit hydrogen bond acceptors. All tested additive three- and four-site models failed to accurately reproduce the free energy of transferring water molecules from a bulk phase into an apolar hexade-cane phase. Errors ranged from 1.0 to 2.5 kcal/mol and were strongly correlated with the water dipole moment, so that the most recently published, optimized models yielded the worst agreement. In contrast, the polarizable SWM4-NDP and SWM6 models yielded water transfer free energies in close agreement with experiment.

An alternative to explicit polarizability within the additive framework, optimization of the pairwise Lennard-Jones interactions between water and alkanes also attained very good agreement with experiment for the transfer free energy in water/hexadecane and improved the description of water permeability through bilayers. Though less transferable, this approach is inexpensive, both in terms of simulation time and parameterization effort. Importantly, water-alkane transfer free energies, the only experimental data required for reparameterization, is commonly found in the literature. Rapid optimization of the pair-specific Lennard-Jones parameters was fully automated and accomplished within one day on a single GPU node.

The key component of this efficient optimization procedure is the prediction of simulated values using one-sided multistate reweighting, based on the Multistate Bennett Acceptance Ratio Method. These predictions facilitated finding optimal parameters by evaluating potential energy functions from modified parameters in snapshots of an alchemical free energy simulation, and performing one short additional control simulation. Since multistate reweighting is capable of predicting general thermodynamic properties,⁸⁹ the proposed algorithm is directly transferable to parameterization problems involving other observables.

Two sets of parameters were optimized to fit the experimental transfer free energy of water, one with a fixed Lennard-Jones width σ_ij (NBFIX-1), and one where both the Lennard-Jones well depth and width were modified simultaneously (NBFIX-2). As a validation, transfer free energies of alkanes, the diffusion constant of water in hexadecane and the permeability of a lipid bilayer were calculated for the optimized models. In these simulations, the two optimized models produced widely different results, highlighting the flexibility that is gained by incorporating σ and ε into the optimization of pairwise Lennard-Jones interactions.

A scaling of the Lennard-Jones well depth, as in NBFIX-1, would arguably be a more satisfactory solution than a change in radius as in NBFIX-2 since it changes the energetics, while retaining the radial distribution function between water and alkanes. However, NBFIX-1 failed to reproduce alkane transfer free energies between water and hexadecane, and caused a dramatic weakening of the water-hexadecane interface. In contrast, NBFIX-2 retained the strong preference of alkanes for the hexadecane phase and reproduced the experimental interfacial tension between water and hexadecane within 4%.

The NBFIX-2 model also rendered the permeability of water through lipid bilayers much more accurately. While the original C36 model underpredicts permeabilities by up to an order of magnitude, the optimized model reproduced experimental values for five different bilayers within a factor of 3 for saturated lipids, and within statistical error for monounsaturated lipids. However, the optimization almost doubled the diffusion constant of water in hexadecane (i.e., a considerable overestimate of experimental values) and also compromised the area per lipid and partitioning of alkanes in water. Consequently, in this framework each class of permeant molecules requires its own set of pair-specific Lennard-Jones parameters to ensure a proper membrane/water partitioning. The present optimization should thus be viewed as a proof-of-concept rather than an amendment to the C36 field. Optimized parameters should be validated carefully before used in production simulations.

Water was chosen as an important yet intricate example. When transfering the approach to other solutes, an optimization of the Lennard-Jones well depth could be more workable, due to a lesser effect of the membrane-permeant interactions on the stability of the water-bilayer interface. Furthermore, the solute-hexadecane and solute-water interactions could be tuned separately to reproduce the individual solvation free energies in the two phases (and thus the partition coefficient).

The implications of this work for future force-field development efforts are twofold: First, a more physically appropriate and transferable description of membrane permeability will likely require explicit polarizability. Second, experimental partition coefficients can be recovered rapidly in existing additive models through automated optimization of pairwise Lennard-Jones interactions until more physically appropriate lipid force fields become available.