Spectroscopy and DFT Calculations of Flavo-Diiron Nitric Oxide Reductase Identify Bridging Structures of NO-Coordinated Diiron Intermediates

Abstract

Flavo-diiron proteins (FDPs) are widespread in anaerobic bacteria, archaea, and protozoa, where they serve as the terminal components of dioxygen and nitric oxide reductive scavenging pathways. FDPs contain an N,O-ligated diiron site adjacent to a flavin mononucleotide (FMN) cofactor. The diiron site is structurally similar to those in hemerythrin, ribonucleotide reductase, and methane monooxygenase. However, only FDPs turn over NO to N₂O at significant rates and yields. Previous studies revealed sequential binding of two NO molecules to the diferrous site, forming mono- and dinitrosyl intermediates leading to N₂O formation. In the present work, these mono- and dinitrosyl intermediates have been characterized by EPR and Mössbauer spectroscopies and DFT calculations. Our results show that the iron proximal to the cofactor binds the first NO to form the diiron mononitrosyl complex, implying the iron distal to the FMN binds the second NO to form the diiron dinitrosyl intermediate. The exchange-coupling constants, J (H = JS₁·S₂), were found to differ substantially, +17 cm⁻¹ for the diiron mononitrosyl and +60 cm⁻¹ for the diiron dinitrosyl. Notwithstanding this large difference, our findings indicate retention of at least one hydroxo bridge throughout the NOR catalytic cycle. The Mossbauer hyperfine parameters and DFT calculations confirmed a semibridging NO⁻ ligand in the mononitrosyl intermediate that lowers the exchange parameter. The DFT calculations on the dinitrosyl intermediate suggest a contribution to J from direct exchange between the S = 1 spins on the NO⁻ ligands, which could initiate N-N bond formation. Our results provide insight into why FDPs are the only known nonheme diiron enzymes that competently turn over NO to N₂O.

Graphical Abstract

INTRODUCTION

Flavo-diiron proteins (FDPs) contain a nonheme diiron site proximal to a flavin mononucleotide cofactor (FMN). FDPs are widespread in anaerobic bacteria, archaea, and protozoa, serving as the terminal components for reductive scavenging of dioxygen and/or nitric oxide.^1,2 Nanomolar intracellular levels of nitric oxide are capable of inhibiting aerobic respiration and energy metabolism.³ Additionally, nitric oxide in aerobic environments can react with O₂ to produce more reactive species, such as NO₂, peroxynitrite (ONOO⁻), and NO⁻, all of which have been shown to induce cellular damage.⁴ Consequently, NO levels in organisms are tightly regulated. Eukaryotic cells respond to microbial infection by producing NO and O₂⁻ to induce nitrosative and oxidative stress in the pathogenic organisms.⁵ In response, pathogens can utilize FDPs to reductively scavenge and eventually detoxify free nitric oxide to the less potent nitrous oxide (N₂O). Most FDPs show both dioxygen reductase (water as product) and nitric oxide reductase (NOR, N₂O as product) activities, but the relative turnover rates vary significantly among FDPs.^1,2 The nonheme diiron site in FDPs is distinct from those in bacterial respiratory NORs, which contain a dinuclear heme/nonheme iron site, or fungal NORs, which contain mononuclear P450-type heme NORs.^6,7 The catalytic mechanisms for NORs are still a topic of debate.^6,8,9

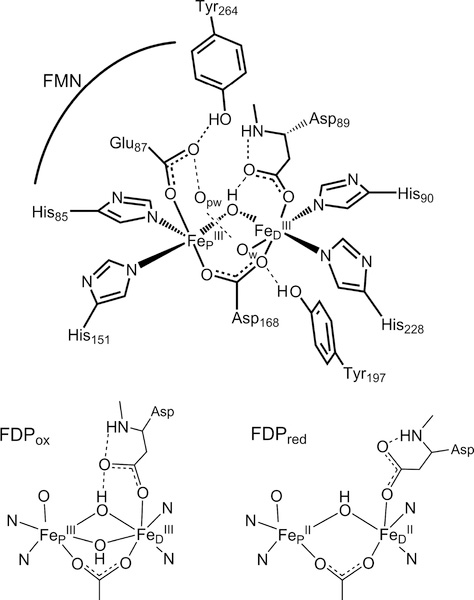
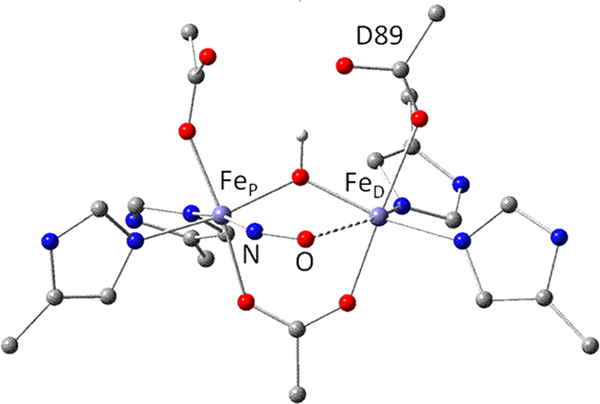
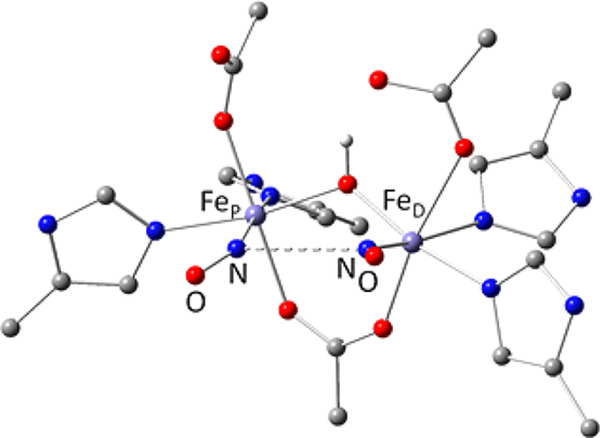
FDPs show a characteristic head-to-tail homodimer structure, in which FMN is located approximately 4 Å from the diiron site across the subunit interface (Figure 1).¹⁰ The homodimer thus contains two symmetrically disposed active sites ~40 Å apart. Within the active site, the Fe_P-Fe_D distance is ~3.4 Å, where Fe_P and Fe_D refer to the irons located proximal and distal to the FMN, respectively. Nearly all structurally characterized FDPs show each iron with two histidine ligands and a terminal monodentate carboxylate ligand from either aspartate (to Fe_D) or glutamate (to Fe_P) (Figure 1). A bridging bidentate carboxylate from an aspartate residue and a bridging solvent ligand complete the diiron coordination sphere.^1,11 Second coordination sphere residues which could conceivably have functional relevance are also shown. The open or solvent-occupied coordination sites trans to H85 and H90 form a pocket facing the diiron site and constitute reasonable candidates for binding NO or O₂.

Figure 1.

Schematic structure of the diferric site from the crystal structure of Thermotoga maritima deflavo FDP based on PDB entry 1VME (top), and first coordination spheres in oxidized and reduced sites (bottom) derived from previous spectroscopic results. O_pw indicates a pocket water, which is hydrogen bonded to the Fe_D ligand water O_w in the crystal structures.

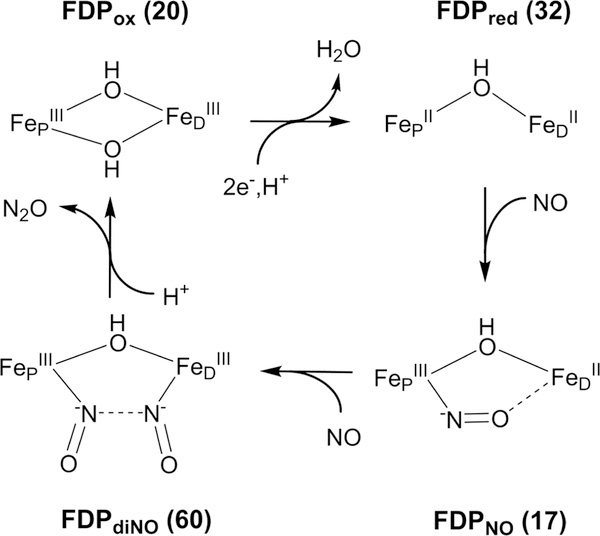
As shown in Figure 1, our previous spectroscopic characterization of FMN-diferric FDP (FDP_ox) from T. maritima (Tm) identified a bis-μ-hydroxo diferric structure that was inconsistent with the crystal structure.¹² This inconsistency may be specific to Tm FDP or due to differences between frozen solution and the crystalline state. The spectroscopic studies also showed that the FMNH₂-diferrous state of Tm FDP (FDP_red) contains a mono-μ-hydroxo diiron structure shown in Figure 1 but without Fe_D-coordinated water (O_w). Our previous results are consistent with this diferrous structure being catalytically functional for NO or O₂ reduction. Rapid kinetics monitoring of reactions of Tm FDP_red with NO showed successive formation of a S = ½ diiron mononitrosyl species [Fe²⁺{FeNO}⁷] followed by a S = 0 diiron dinitrosyl [{FeNO}⁷]₂ species (where {FeNO}⁷ is the Enemark–Feltham notation).^13,14 These species will hereafter be referred to as FDP_NO and FDP_diNO, respectively, both of which contain predominantly the two-electron-reduced FMN cofactor (FMNH₂). A catalytic mechanism consistent with these results involves rate-determining ON-NO bond formation in FDP_diNO, leading to N₂O generation and reformation of the diferric state. The proximal FMNH₂ then rapidly two-electron reduces the diferric site for another round of N₂O formation by the same FDP_NO and FDP_diNO pathway.¹⁴

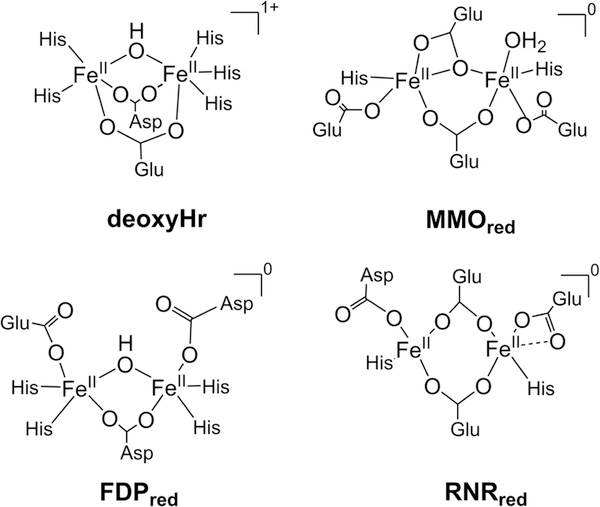
The diiron site of FDP shows similarities to those of the O₂ binding protein hemerythrin (Hr) and the prototypical O₂-activating enzymes, class Ia ribonucleotide reductase (RNR) and methane monooxygenase (MMO) (Figure 2).^15–17

Figure 2.

Diferrous active site structures and charges for nonheme O,N-ligated diiron sites in proteins that bind NO.

Despite the structural similarities, these proteins perform diverse functions. Hr reversibly binds oxygen at its diiron center for oxygen transport, RNR generates and stabilizes a tyrosine radical, and MMO catalyzes the hydroxylation of methane. The diiron active sites in these enzymes contain one or two bridging carboxylates and, depending on oxidation state, solvent-derived bridging ligands. The higher histidine/carboxylate ligation ratio in FDP and Hr lowers the electronic charge donation to the irons. In the diferrous sites, this lower charge donation is compensated by retention of a hydroxo bridge. Despite these O/N donor differences, the diferrous sites of all these proteins readily bind O₂ and NO;^18–20 however, only FDPs among these proteins have been shown to be competent NORs.

Here we use spectroscopic and computational methods to characterize the electronic properties of the FDP_NO and FDP_diNO intermediates. EPR and Mossbauer spectroscopies combined with rapid freeze quench (RFQ) experiments have allowed determination of the electronic exchange interaction between the Fe_P and the Fe_D centers of the diiron sites and the contributions to these interactions from the NO ligands. These interactions may help explain why only FDP among proteins with similar O,N-ligated diiron sites turns over NO into N₂O. Results in this and the previous paper¹² provide spectroscopic methodologies for determining the exchange interaction of all observed diiron states of FDP during its reaction with NO. Using engineered variants in which the Fe_D ligand residue His90 (Figure 1) was replaced by Ala, Asn, or Asp;²¹ we also determined which iron center binds the NO in FDP_NO.

EXPERIMENTAL SECTION

Tm FDP Preparation and Manipulation

Rapid freeze–quenched samples of Tm FDP_red were prepared and reacted with NO as reported previously.^13,14 All reactions were carried out under anaerobic conditions under an N₂ atmosphere. All spectra were obtained in frozen solutions at the indicated temperatures. All FDP concentrations are listed on a diiron site basis. The Tm FDP H90 ligand residue variants, H90A, H90D, and H90N, were prepared as previously described,²¹ and their RFQ samples were prepared identically to those of the wildtype Tm FDP. Wild-type (WT) is used in the text where necessary to distinguish the native Tm FDP amino acid sequence from those of the H90 variants. All samples of WT and variant Tm FDPs contained a FMN/Fe mol ratio of ~1:2 when analyzed as previously described.^{21 57}Fe enrichment of Tm FDP was carried out as described previously.¹¹

Desulfovibrio vulgaris (Dv) FDP Expression, Isolation, and Sample Preparation

The nucleotide sequence encoding the gene for Dv FDP²² codon-optimized for expression in E. coli was inserted into the NcoI/BamHI sites of plasmid pKB6H by Genscript, which also verified the correct nucleotide sequence.²³ This plasmid encodes a 6xHis tag at the N-terminal end of the encoded protein. E. coli strain BL21(DE3) (Invitrogen) was transformed with this plasmid. The Dv FDP was expressed from this transformed strain grown as 1 L cultures in Luria-Bertani broth supplemented with ampicillin (100 mg/L) using a previously described protocol.²⁴ The thawed cell pellets were resuspended in 100 mM MOPS, 500 mM NaCl, and 20 mM imidazole, pH 7.4 (4 mL/g pellet) and sonicated at 4 °C to lyse the cells, and the filtered supernatant from the lysed cells was applied to a Ni Sepharose High Performance resin (GE Healthcare) pre-equilibrated with the resuspension buffer. The column was washed with the same buffer, and the His-tagged Dv FDP was eluted with 5 column volumes of 100 mM MOPS, 500 mM NaCl, and 500 mM imidazole, pH 7.4. The eluted protein was transferred to 50 mM MOPS pH 7.3 by extensive dialysis. The as-isolated Dv FDP had <5% of that expected for full occupancy of the diiron sites and similarly minor occupancy of the FMN sites based on flavin and iron analyses.

For ⁵⁷Fe enrichment of the protein, an Fe²⁺ stock solution was prepared as follows. A 0.2 mmol amount of solid ⁵⁷Fe was dissolved in 2.5 mol equiv of H₂SO₄. The solution was allowed to react at room temperature overnight and then adjusted to pH 4 by titration with ammonium hydroxide. The solution was suspended in 50 mM MES, pH 6.5, placed in septum-capped vials, and deoxygenated by vacuum/N₂ gas purge cycles on a Schlenk line before transfer to an anaerobic N₂ gas-filled glovebox (Omnilab system, Vacuum Atmosphere Inc.). The ⁵⁷Fe(II) concentration was determined using a standard ferrozine assay. The as-isolated Dv FDP in 50 mM MOPS pH 7.3 was anaerobically incubated with ~2 mol equiv per protein monomer of the ⁵⁷Fe(II) solution for 1 h at room temperature under an N₂ atmosphere. The iron/protein solution was then exposed to air by gentle pipetting in order to oxidize the iron. The air-exposed protein was washed by concentration/redilution with 50 mM MOPS and 5 mM EDTA at pH 7.3 to remove the excess iron followed by concentration/redilution cycles with 50 mM MOPS pH 7.3 in order to remove the EDTA. ⁵⁷Fe-enriched Dv FDP in 50 mM MOPS pH 7.3 was incubated with ~2 mol equiv of FMN per FDP monomer at room temperature overnight. Excess FMN was removed by repetitive concentration/redilution cycles in the same buffer until the filtrate was colorless. The FMN:iron mole ratio using this method was ~1:2 when analyzed as described previously.²²

Preparation of Reduced Dv FDP (Dv FDP_red)

All manipulations were carried out at room temperature. All Dv FDP concentrations are listed on a diiron site basis. Oxidized Dv FDP (60–2200 μM, Dv FDP_ox) solutions in buffer were placed in septum-capped vials and deoxygenated by vacuum/N₂ gas purge cycles on a Schlenk line before transfer to an anaerobic N₂ gas-filled glovebox (Omnilab system, Vacuum Atmosphere Inc.). All further manipulations were performed in this glovebox at room temperature. Dv FDP_ox was reduced by addition of 2.2 mol equiv of NADH per FDP active site in the presence of 2 μM Tm NADH oxidoreductase and 30 μM Dv rubredoxin.²² Overnight incubation under these conditions resulted in the four-electron-reduced yellow-colored Dv FDP_red. After reduction, the samples were exchanged into 50 mM TAPS, pH 9.0, via centrifugal concentrators and successive rounds of concentration and redilution. Dv FDP_red solutions were then loaded onto the RFQ apparatus. NO preparation and RFQ setup was identical to that described for Tm FDP.¹⁴

EPR and Mössbauer Spectroscopies

X-band EPR spectra were recorded on a Bruker ELEXSYS spectrometer equipped with an Oxford ESR-910 liquid helium cryostat and a Bruker bimodal cavity for generation of microwave fields parallel and transverse to the applied magnetic field. The quantification of all signals was measured relative to a CuEDTA spin standard prepared from a copper atomic absorption standard (Sigma-Aldrich). The microwave frequency was calibrated with a frequency counter and the magnetic field with a NMR gaussmeter. The sample temperature was calibrated against a calibrated cernox sensor (Lakeshore CX-1050) mounted inside an EPR tube. A modulation frequency of 100 kHz was used for all EPR spectra. Mössbauer spectra were recorded on either a strong-field or a weak-field spectrometer operating in a constant acceleration mode in a transmission geometry using Janis Research Inc. cryostats that allow for a variation in temperature from 1.5 to 300 K. One of the dewars housed a superconducting magnet that allowed for the application of magnetic fields up to 8 T parallel to the γ-radiation. Isomer shifts are reported relative to Fe metal at 298 K.

The simulation software SpinCount was written by one of the authors.²⁵ The software diagonalizes the electronic terms of the spin Hamiltonian

$$H=J{\mathbf{S}}_1\cdot {\mathbf{S}}_2+H_1+H_2$$ 1

$$\begin{gathered} H_i=\beta {\mathbf{S}}_i\cdot {\mathbf{g}}_i\cdot \mathbf{B}+{\mathbf{S}}_i\cdot {\mathbf{D}}_i\cdot {\mathbf{S}}_i+{\mathbf{S}}_i\cdot {\mathbf{A}}_i\cdot {\mathbf{I}}_i-g_n{\beta }_n\mathbf{B}\cdot {\mathbf{I}}_i+{\mathbf{I}}_i\cdot {\mathbf{P}}_i\cdot {\mathbf{I}}_i \\ (i=1,2) \end{gathered}$$

$${\mathbf{S}}_i\cdot {\mathbf{D}}_i\cdot {\mathbf{S}}_i=D_i\left[{S_{zi}}^2-S_i\left(S_i+1\right)/3+{(E/D)}_i\left({S_{xi}}^2-{S_{yi}}^2\right)\right]$$

$${\mathbf{I}}_i\cdot {\mathbf{P}}_i\cdot {\mathbf{I}}_i=\left(eQ{V}_{zi}/12\right)\left[3{I_{zi}}^2-I_i\left(I_i+1\right)+{\eta }_i\left({I_{xi}}^2-{I_{yi}}^2\right)\right]$$

where the parameters have the usual definitions²⁶ and performs least-squares fitting of simulations to the spectra. The spin S_i refers to individual Fe²⁺ (2) or {FeNO}⁷ (3/2) sites depending on the state of FDP. Euler angles (α, β, γ) rotate D₂ (coaxial with g₂) relative to D₁ (coaxial with g₁).²⁷ The tensors P_i (coaxial with A_i) can each be independently rotated relative to D₁. The quantitative simulations are generated with consideration of all intensity factors, which allows computation of simulated spectra for a specified sample concentration. For calculations of the g-tensor for Fe²⁺ sites, we used the relations²⁶

$$\begin{gathered} g_x=g_z-(2k/\lambda )(D-E) \\ {g}_y=g_z-(2k/\lambda )(D+E) \end{gathered}$$ 2

The value of the orbital reduction factor was assumed to be k = 0.8 and the spin-orbit constant λ = −100 cm⁻¹.²⁶

The EPR signal intensity data were analyzed with a Boltzmann population of states according to the energies determined from eq 1. The EPR signal intensity is proportional to the difference in the population of the spin states of the doublet in resonance. For temperatures well above hν/k, this difference is dominated by Curie law behavior: Signal intensity is proportional to (multiplet population)/(temperature). The data and fit are plotted as (signal intensity) × (temperature) to remove the overwhelming Curie law dependence from the data to better show the curvature due to the change in multiplet population which determines J.

DFT

The DFT calculations were performed on various states of the FDP diiron site with G′09 (see Supporting Information for reference) using the hybrid functional B3LYP and basis set 6–311G.^28,29 First and second coordination sphere atoms were included and optimized as described previously (see Supporting Information).¹² The FDP crystal structures show that the FMN cofactor has no direct contact with any of the iron ligands, and because there is no change in the FMNH₂ oxidation state among FDP_red, FDP_NO, and FDP_diNO,¹² the FMN was excluded from the DFT models. The exchange-coupling constants between paramagnetic subunits A and B were calculated with the expression J_AB = 2(E_f − E_BS)/n_An_B, where n_A and n_B are the numbers of unpaired electrons associated with A and B, respectively, and E_F and E_BS are the energies for the ferromagnetic state (F) and broken-symmetry configuration (BS).^30–32 The reliability of the calculated J values using our DFT methodology was previously verified for a number of synthetic diferric and diferrous complexes.¹² Details of the DFT treatment of the exchange interactions involving the paramagnetic nitrosyl ligands in FDP_NO and FDP_diNO are given in the Supporting Information. The calculations for the ⁵⁷Fe isomer shifts (δ) and quadrupole splitting (ΔE_q) were calibrated as described previously.¹²

RESULTS

EPR and Mössbauer Spectroscopies of FDP_NO

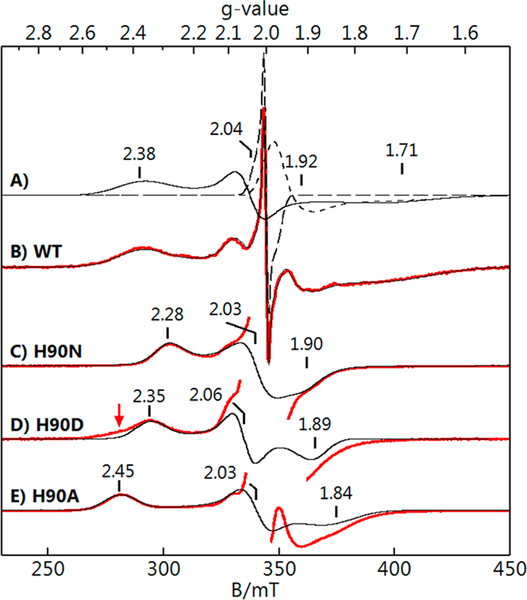
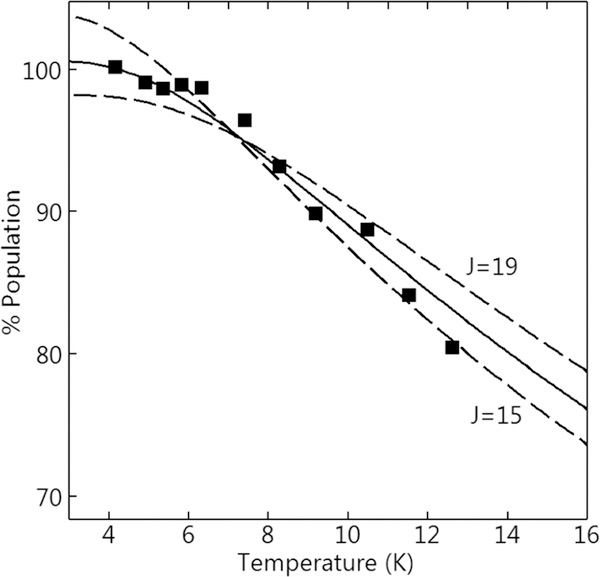
The titration of up to 1 equiv of NO per diferrous site of Tm FDP_red resulted in a stable mononitrosyl complex (FDP_NO) with nearly 100% yield.^14,20,33 This species has EPR and Mössbauer spectra of a S = ½ system spin, originating from the ground spin state of a diiron site consisting of S_FeNO = 3/2 {FeNO}⁷ coupled antiferromagnetically to a S_Fe2+ = 2 Fe²⁺ site. The EPR signal of FDP_NO, shown in Figure 3B, was composed of three overlapping signals. The spectra of the individual species were obtained by least-squares deconvolution from the simulations shown in Figure 3A The sum of the simulations of the three species is the black trace on Figure 3B. The sharp signal at g = 2 is a minor radical species (<5% of the protein concentration) which was presumably from FMN. The signal at g = 1.93 was due to a minor variable amount of free NO. The g values from the simulation of the FDP_NO complex are listed in Table 1. The EPR signal was recorded at various temperatures below 15 K. Figure 4 shows a plot of the signal intensity × temperature versus temperature, which is proportional to the fractional population of the S = ½ state. The observed decrease in the population is due to the population of excited spin S > ½ states at higher temperatures. Above 15 K, broadening of the EPR signal prevented measurement of the fractional S = ½ population.

Figure 3.

EPR data (red) and simulations (black) of ~1 mM Tm FDP_NO. (B) WT FDP_No and (C-E) FDP_NO of H90 residue variants as listed. Principal components of the S = ½ g tensors are indicated. (A) Simulations of the individual species giving B: WT (solid line), radical impurity (long dash), free NO (short dash). Red arrow for H90D indicates a shoulder matching the H90A species. Conditions: temperature, 6 K; microwaves, 0.2 mW at 9.646 GHz. Simulations (black traces) use the parameters listed in Table 1.

Table 1.

Electronic Parameters of Tm FDP_NO and Variants

FDPNO	observed g	J (cm−1)	DFe2+ (cm−1)	(E/D)Fe2+	gFe2+a	DFeNO (cm−1)b
WT	1.71, 2.38, 2.04	17(2)	−7.3	0.274	2.21, 2.15, 2.30	14
H90N	1.90, 2.28, 2.03	17	−5.9	0.210	2.10, 2.06, 2.17	14
H90D	1.89, 2.35, 2.06	17	−6.2	0.230	2.14, 2.09, 2.22	14
H90A	1.84, 2.45, 2.03	17	−7.1	0.215	2.18, 2.13, 2.27	14

^ag_x and g_y values from eq 2.

^bg_FeNO = 2.0, (E/D)_FeNO = 0. D_FeNO rotated relative to D_Fe2+ by (α, β, γ) = (56, 11, 81)° for all species.

Figure 4.

Signal intensity × temperature versus temperature of the WT FDP_no EPR signal from Figure 3B. Ordinate axis scale is the % population of the S = ½ doublet in the exchange-coupled relationship given by eq 1, which is proportional to signal intensity. Solid line is calculated from eq 1 for J = 17 cm⁻¹ and other parameters given in Table 1. Dashed lines show the uncertainty in J of ±2 cm⁻¹.

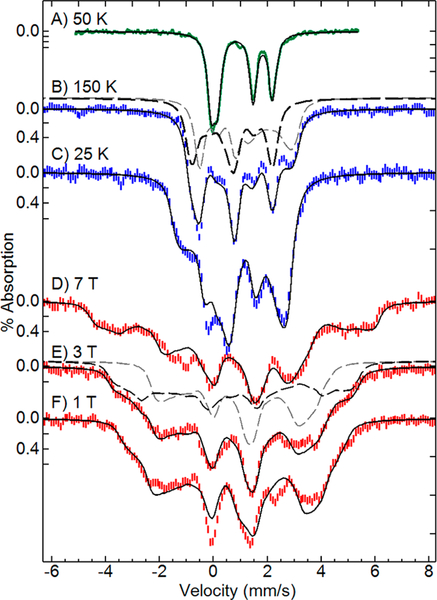
Mössbauer spectra of FDP_NO in zero applied field at a temperature of 50 K showed two doublets of equal areas with parameters indicative of S_FeNO = 3/2 {FeNO}⁷ and S_Fe2+ = 2 Fe²⁺ sites (Figure 5A, Table 2). This zero-field spectrum reproduces our previous work.¹⁴ For T ≥ 25 K, the electronic relaxation was fast relative to the ⁵⁷Fe nuclear Larmor frequency. The value of ΔE_q for the {FeNO}⁷ site showed no change over the range 4–150 K, whereas ΔE_Q for the Fe²⁺ site changed from 2.10 to 1.98 mm/s over the same temperature range (values in Table S1). These temperature dependences of ΔE_q are typical of nonheme {FeNO}⁷ and Fe²+ centers, respectively. The Mössbauer spectra of FDP_NO of Figure 5 were recorded for various magnetic fields and temperatures. Due to population of higher spin states, the Mössbauer spectra could not be fit with a simple S = ½ spin Hamiltonian and were instead analyzed using eq 1 for exchange-coupled S_FeNO = 3/2 and S_Fe2+ = 2 sites.

Figure 5.

Mössbauer spectra and simulations (black lines) of FDP_NO: (A) 50 K, 0 T; (B) 150 K, 7 T; (C) 25 K, 7 T; (D-F) 4 K at fields listed. Dashed lines in B and E show the simulated contributions from the Fe²⁺ (gray) and {FeNO}⁷ (black) sites. Simulation parameters: J = 17 cm⁻¹; Fe²⁺: S = 2, D = −7 cm⁻¹, E/D = 0.27, g = (2.21, 2.15, 2.30), A/g_nβ_n = (−13, −16, −8) T, δ = 1.15 mm/s, ΔE_q = +2.05 mm/s, η = 0, P rotation (0, 75, 90)°; {FeNO}⁷: S = 3/2, D = +14 cm⁻¹, E/D = 0, g = 2, A/g_nβ_n = (−23, −24, −33) T, δ = 0.69 mm/s, ΔE_Q = −1.54 mm/s, η = 0.6, P rotation (35, 50, 65)°. D_FeNO rotated relative to D_Fe2+ by (55, 10, 80)°.

Table 2.

Selected Properties of NO Adducts of Nonheme O,N-Ligated Diiron Sites in Proteins

protein	J ( cm−1)a	solvent bridgeb	δ (mm/s)	ΔEq (mm/s)d	ref
Fe2+{FeNO}7
FDPNO	17(2)	OH−	1.15, 0.68	+2.05, −1.56	e
deoxyHrNO	28	OH−	1.25, 0.72c	+2.66, + 0.61	34
[{FeNO}7]2
FDPdiNO	60(10)	OH−	0.71	1.85	e
RNRdiNO	5	H2O or none	0.75	−2.13, −1.73	18
MMOdiNO	>0	?	0.72	1.55	19

^aH_ex= J S₁∙S₂.

^bFe_p—Fe_D bridging ligand. Additional carboxylate bridging ligands are not listed.

^cδ4_K = δ_100K + 0.04 mm/s.

^dδ and ΔEQ values reported at 4.2 K. Signs of ΔE_q are omitted if not determined.

^eThis work.

The data of Figures 3B, 4, and 5 provided a strong set of constraints that allowed determination of the exchange coupling and electronic parameters for both iron centers in FDP_NO, analogous to a study of the NO adduct of deoxyHr.³⁴ The problem is complicated owing to the possible parameters and orientation of the Fe²⁺ site and the relatively small value of J. The software SpinCount allowed simultaneous least-squares fitting of EPR and Mössbauer spectra and their temperature and field dependencies using eq 1. A large parameter space was searched by starting the least-squares fitting at thousands of different initial points spanning the acceptable ranges of all variables. The fits that converged to agree with the data all gave approximately the same parameters. The simulations shown in Figures 3B, 4, and 5 are the best fits using the parameters listed in Tables 1 and 2 and the Figure 5 legend. The fitted exchange-coupling constant J = 17(2) cm⁻¹ is consistent with a hydroxo bridge between Fe_P and Fe_D.¹² The fitting of the data used minimal assumptions, specifically, g_FeNO = 2.0, (E/D)_FeNO ≈ 0, values which are typical of all known nonheme {FeNO}⁷ protein sites, and the values for g_x and g_y of the Fe²⁺ site determined from eq 2. For comparable magnitudes of J and D, as in the case of FDP_NO, the observed S = ½ g-tensor depends on J and the D- and g-tensors of the individual iron centers. Although the g values of the ferrous site are all greater than 2.0, spin coupling with the {FeNO}⁷ site results in one component of the observed S = ½ g-tensor which is significantly less than 2.0. The line width of the EPR spectrum was dominated by a Gaussian distribution of the (E/D)_Fe2+ values with a width of 0.03. The Mössbauer spectra are composed of equal contributions from the {FeNO}⁷ and Fe²⁺ sites. The contributions for two of the spectra are displayed in Figure 5B and5E (dashed lines). The parameters may not constitute a unique solution for parameters involving rotation tensors, but the value of J has been determined, and the values of δ, ΔE_q, D, E/D, and the A-tensors of the {FeNO}⁷ and Fe²⁺ sites determined here for FDP_no are typical of those observed for {FeNO}⁷ and Fe²⁺ sites of nonheme O,N-ligated iron sites in proteins.^18,34–38 For example, an equally good fit to all data was obtained with coaxial D-tensors for the iron sites if the constraints of eq 2 were removed (Figure S2), but the value of J was unchanged, and except for the g-values of the Fe²⁺ site (all ~2.2), the other parameters did not change significantly. All fits to the data with J outside the range 15–19 cm⁻¹ were significantly poorer.

EPR Spectroscopy of H90 Variants Plus 1 Equiv of NO

Three engineered variants of Tm FDP, in which the Fe_D-coordinating His90 residue (Figure 1) was substituted with Asn, Asp, or Ala (H90N, H90D, and H90A, respectively), were examined. These variants showed similar diiron site structures and activities to those of WT FDP.²¹ The major structural differences were substitutions N90, D90, or water in place of the H90 ligand in H90N, H90D, and H90A, respectively. The addition of ~1 equiv of NO to FDP_red samples of each variant produced the S = ½ EPR signals shown in Figure 3C-E. As was the case for WT FDP_no, the spectra showed minor variable amounts of a free NO signal at g = 1.93 and a radical species at g = 2.0. As described above for the WT FDP_no, simulations were used to deconvolute these components to obtain the H90 variant FDP_no signals and their respective S = ½ g-tensors. For the H90 variants, only the simulations of the FDP_no signals, extracted from the deconvolution, are overlaid on the experimental spectra in Figure 3. The EPR spectrum of H90D had a low-field shoulder (red arrow in Figure 3) on the g = 2.35 feature due to a second species with g = 2.45, the fraction of which is preparation dependent (~40% of the protein in the sample shown). This second species closely resembles that of the H90A signal in which the non-coordinating alanine side chain has left a vacancy for a water ligand on Fe_D.²¹ This suggests that a fraction of the Fe_D sites in the H90D sample has the D90 ligand replaced by water. This interpretation is consistent with the H90D FDP crystal structure (PDB 5V8S).

The temperature dependences of the EPR signals of the H90 variants (Figure S1) were all within error the same as that of WT, indicating they all have the same value of the exchange-coupling constant, J = 17 cm⁻¹. The H90 variant FDP_no EPR spectra were simultaneously least-squares fit using eqs 1 and 2 while allowing only D_Fe2+, (E/D)_Fe2+, and g_z of the Fe²⁺ site to vary independently among the variants; all other parameters were set equal to those for WT. The spectra of the variants were well fit using the parameters listed in Table 1. The variations in the observed g-tensors for the H90 variants and WT FDP_NO could be accurately simulated exclusively by adjustments in the D-tensor of the Fe²⁺ center. Attempts to fit the spectra by varying the electronic parameters of only the {FeNO}⁷ center were unsuccessful. The significant variation in the ligand-field energies (~200 cm⁻¹, using λ²/D) required to fit the observed differences in the D-tensor of the Fe²⁺ site can arise only from changes in the first coordination sphere. Similar changes in D values and implied ligand-field energies have been observed for changes in the first coordination spheres of synthetic Fe²⁺ complexes and other N,O-coordinated nonheme Fe²⁺ sites in proteins.^39,40 Since the first coordination sphere at Fe_D indeed differs among the WT and the three H90 variants,²¹ we conclude that Fe_D is the Fe²⁺ site and Fe_P is the {FeNO}⁷ site.

DFT Calculations for FDP_NO

From our previous work, the structure of the diiron active site of FDP_red is composed of two 5-coordinate high-spin Fe²⁺ sites with a monohydroxo bridge (Figure 1).¹² The NO binding to Fe_P creates an active site having three spins (S_P = 5/2, S_NO = 1, and S_D = 2), and their exchange interactions have been described by the spin Hamiltonian j_pnoŜ_p⋅Ŝ_nO + J_FeFeŜ_p⋅Ŝ_D, where J_FeFe refers to the superexchange path though the bridging hydroxo of the diiron site and the P or D subscripts refer to the Fe_P or Fe_D centers, respectively. The exchange contribution from the bridging carboxylate is insignificant compared to that of the hydroxo bridge.^41,42 The electronic structure of the S = 3/2 {FeNO}⁷ is formulated as an S = 5/2 Fe³⁺ strongly antiferromagnetically coupled to S =1 NO⁻.³² This formulation is supported by the ⁵⁷Fe hyperfine parameters, which resemble those typical for a high-spin Fe³⁺ site rather than those for an Fe²⁺ site. Our DFT calculations give an exchange-coupling constant for this Fe³⁺NO⁻ formulation of J_PNO ≈ 2000 cm⁻¹, which is much larger than J_FeFe. The difference in magnitude is expected given the direct (J_PNO) and indirect (J_FeFe) character of these interactions. Consequently, the coupled spin S_PNO = 3/2 is a good quantum number, and the spin Hamiltonian can be simplified with the help of a spin-projection factor to that of a two-spin system, JŜ_pNO⋅Ŝ_D, where J = (7/5) J_FeFe can be identified with the experimentally observed exchange-coupling constant. Thus, if the structure of the diiron core upon binding of NO were unchanged from that of FDP_red except for coordination of NO to Fe_P, we would expect the value of J to increase by ~7/5 for FDP_NO relative to that of FDP_red. However, since the experimental value for FDP_NO (J = 17(2) cm⁻¹) is significantly smaller than that of the diferrous site in FDP_red (32(5) cm⁻¹), we must consider other possibilities. Oxo- and aqua-bridged diiron sites are precluded as their exchange couplings are, respectively, an order of magnitude larger and smaller than the experimental value.¹²

In the DFT models of FDP_NO, a molecule of NO was added as a ligand to Fe_P in the diferrous structures considered in our previous work,¹² including all atoms shown in Figure S4, and then optimized using the same constraints as in reference 12. The results for the structures are listed in Tables S2 and S3 with a representative diiron first coordination sphere structure shown in Figure 6. The results in the top half of Table S2 are for a model with a water molecule coordinated to Fe_D (corresponding to O_w in Figure 1). Although this water ligand is absent in the diferrous structure determined from our previous spectroscopic results (Figure 1),¹² we tested O_w models for the sake of comparison. The values of J_FeFe in the O_w FDP_NO models are similar to those of the diferrous and diferric models with the same bridging arrangements (hydroxo and carboxylato). After spin projection, J for one of the models (3_no, Figure S4) is close to the experimental value. We have considered structures with and without D89 protonated (labeled D89 in Figure 6). D89 protonation (unlikely at neutral pH) weakens the hydrogen bond to the hydroxo bridge and mimics the effect of the loss of the hydrogen bond without having to constrain the geometry of D89. However, as discussed below, a semibridging NO interaction has a significantly larger effect on J than does the presence or absence of the μ-OH—D89 hydrogen bond.

Figure 6.

First coordination sphere structure of a DFT diiron site model for FDP_no with a 5-coordinate Fe_D (5_no^NW of Table S2). Except for the H of the hydroxo bridge, hydrogen atoms have been omitted for clarity. Dashed line indicates the close NO⁻⋅⋅⋅Fe_D contact. Color code: C, gray; Fe, gray-blue; H, white; N, blue; O, red.

The lower half of Table S2 presents FDP_NO diiron structures without a water ligand. As in the model structures containing the O_w ligand to Fe_D, the optimized structures obtained without O_w have bent Fe_P-N-O geometries. However, in the absence of O_w the Fe_P ligand nitrosyl oxygen interacts with Fe_D leading to short NO⁻•••Fe_D distances ranging from 2.4 to 3.2 Å (see Figure 6). This distinctive interaction was found for models both in the presence and in the absence of the μ-OH—D89 hydrogen bond. The NO⁻•••Fe_D interaction provides an additional exchange path that modifies the exchange-coupling constant in the spin Hamiltonian JŜ_PNO⋅Ŝ_D to J = (7/5)J_FeFe – (2/5)J_NO−D, where J_NO−D accounts for the NO⁻•••Fe_D exchange. The multipliers 7/5 and −2/5 are factors for spin projection onto S_PNO = 3/2. The {FeNO}⁷ iron oxidation state is essentially ferric, and we have shown previously that the value of J_FeFe is not strongly dependent on iron oxidation state.¹² Both J_FeFe and J_NO–D are positive quantities, and their contributions to J therefore partially cancel, explaining why the experimental J value for FDP_NO is significantly smaller than that of FDP_red.

The optimized structures were computed for both the BS and the F configurations of the complex, in which the spins on the individual units (S_P, S_NO,S_D) are aligned as ↓↑↑ and ↑↓↑, respectively. We noticed that the NO⁻•••Fe_D distance of the optimized structures showed an unusually strong dependence on spin state. In the BS state the iron spins are antiparallel, which forces the spins in NO⁻•••Fe_D to be parallel, causing spin frustration and a weakening of the interaction between NO⁻ and Fe_D. As a result, the NO⁻•••Fe_D distance in the BS state is longer by as much as 0.6 Å relative to the F state, where the NO⁻ spin is antiparallel to the Fe center spins. Consequently, the spin-state energies depend on both exchange and distortional contributions and cannot be described by the conventional Heisenberg Hamiltonian, which applies only to fixed geometries. For the optimized structures in which the NO⁻•••Fe_D interaction was blocked by O_w coordination to Fe_D, the structural differences between the BS- and the F-optimized structures were minor, corroborating the above interpretation of the spin dependence of the NO⁻•••Fe_D distance.

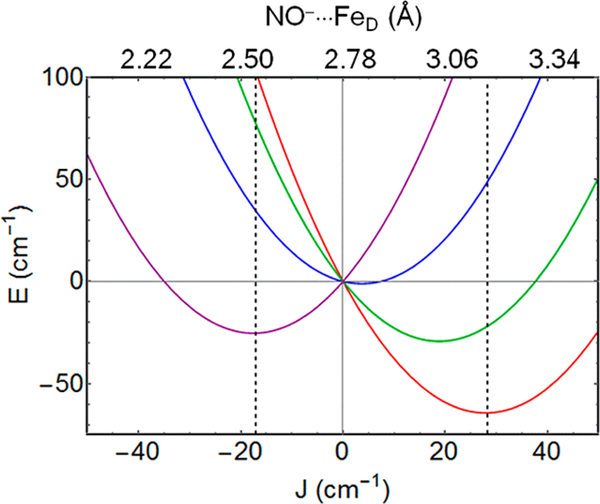
The above significant structural dependence on spin state, without an oxidation state change, is uncommon if not unprecedented. The following analysis is a first attempt to model the dependence of the spin-state energies on structure. The dependence of the spin-state energy on the NO⁻•••Fe_D distance implies that the relative spin-state energies are not simply described by an exchange parameter but also contain contributions from elastic distortion energies. The values of J_FeFe and J_NO-D were estimated for the optimized structures of both F and BS states as described in the Supporting Information. Owing to the shorter NO⁻•••Fe_D distance in the F configuration, the value for J_NO-D is higher than its value for the BS configuration, while J_FeFe is essentially unchanged for the two geometries (Table S2). The change in J_NO-D as a function of NO⁻•••Fe_D distance (3.17 Å for BS, 2.54 Å for F) at fixed J_FeFe was found to be approximately linear in the distance range of interest. This linear dependence justifies an analysis of the potential energy surfaces for the FDP_NO models as a function of the effective exchange parameter J = (7/5)J_FeFe - (2/5)J_NO-D. For this analysis we chose a model structure, 5_no^nw (Figure 6), that has essentially no hydrogen bond between the D89 carboxylate and the bridging hydroxo and gave results compatible with experiment. The values for J_BS and J_F obtained from the optimized structures were used to construct the potential energy surfaces shown in Figure 7. Since the structure is near a potential energy minimum, the distortion energy was assumed to be a quadratic function of the NO⁻•••Fe_D distance, i.e., elastic (see Supporting Information). The significant dependence of J on J_NO-D causes J to flip sign between the geometries for the BS and F configurations (J_BS >0, J_F < 0, Table S2). The potential wells in Figure 7 intersect at J = 0, which represents an intermediate NO•••Fe_D distance where (7/5)J_FeFe = (2/5)J_no-d.

Figure 7.

Potential energy curves for FDP_no for model 5_no^NW as a function of J (= (7/5)J_FeFe - (2/5)J_no-d), which is assumed to be a linear function of NO⋅⋅⋅Fe_D distance (see text and Supporting Information). Relative spin-state energies at any fixed NO⋅⋅⋅Fe_D distance are described by the conventional exchange Hamiltonian: S = ½ (red), 3/2 (green), 5/2 (blue), 7/2 (purple). Dashed lines passing through the energy minima for the S = ½ and S = 7/2 curves intersect the horizontal axis at the values for the exchange-coupling constants, J = +28 cm⁻¹ (from BS state) and J = −18 cm⁻¹ (from F state, S = 7/2) listed in Table S2. Axis at the top is determined from the NO⁻•••Fe_D distances of 2.54 and 3.17 Å at the minima for the F and BS states, respectively (dashed lines).

Analysis of Figure 7 shows a set of energetically close-lying energy minima that among the cases considered best approach the temperature dependence of the EPR data and the Mössbauer parameters (Table S3). The experimental value of J =17 cm⁻¹, which was determined with the standard exchange Hamiltonian JŜ_PNO•Ŝ_D, is controlled by the energy of the S = 3/2 state, which is the excited spin state with the highest population for the temperature range of the measurements. While the standard Hamiltonian does not accurately describe the energy differences between the four spin states owing to the structural changes between them, it is able to represent the energy gap separating the S = 3/2 state from the S =½ ground state. The thermal population of the S > ½ multiplets reduces the relative occupancy of the S = ½ ground state to 0.75 at 20 K. At the same temperature the population of the S = ½ state calculated with the theoretical model of Figure 7 is 0.70, which is close to the ground state population inferred from the EPR data. While these calculations are compatible with experiment, the assumptions of the elastic model are simplistic and should not be interpreted as giving preference to a particular structure. Nevertheless, this modeling supports a spin-state-dependent semibridging NO⁻•••Fe_D interaction in FDP_NO.

Mössbauer Spectroscopy of FDP_diNO

In our previous work, Tm FDP_diNO was observed as a metastable intermediate, which was trapped by RFQ methods upon mixing the FDP_red with 3 equiv of NO per active site.¹⁴ Due to the relatively low affinity of Tm FDP_NO for the second NO, our best RFQ samples produced ~40% yield of the FDP_diNO intermediate, which allowed us to determine that the exchange coupling between {Fe_DNO}⁷ and {Fe_PNO}⁷ centers is antiferromagnetic and to set a lower limit on J. We have since been able to obtain higher yields of FDP_diNO using Dv FDP_red, which has a higher affinity for the second NO than does Tm FDP_red²² and which rapidly forms the FDP_diNO intermediate. The Dv FDP_diNORFQ sample was prepared analogously to that of Tm FDP but at pH 9 rather than 7, which slowed the decay of the FDP_diNO species. A quantitative relation between the decay rate and the pH is beyond the scope of the present paper, but this observation suggests that the rate-limiting step for the diNO decay is proton dependent, at least in Dv FDP.

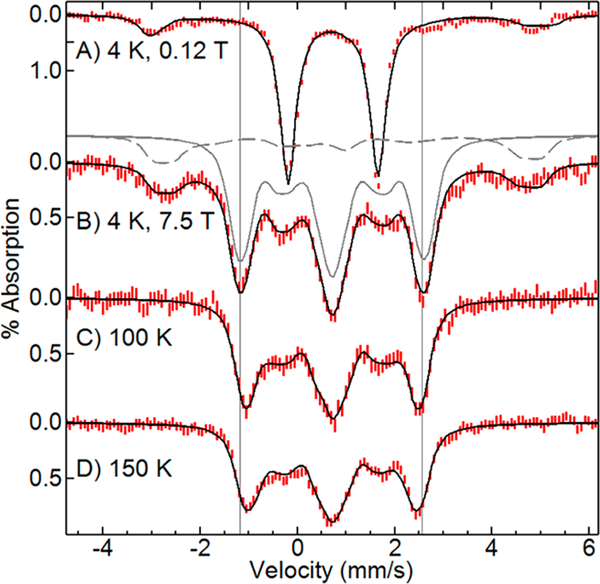
Figure 8 shows Mössbauer spectra as a function of magnetic field and temperature for Dv FDP_red quenched at 100 ms following reaction with 2 equiv of NO. In low magnetic field at 4.2 K, the spectrum showed two species. The doublet (δ = 0.71 mm/s, ΔE_q = 1.85 mm/s), representing ~85% of the total iron, had parameters equal to that of the Tm FDP_diNO intermediate.¹⁴ In zero applied field, the value of ΔE_q was unchanged from 4 to 150 K. A minor impurity species accounting for ~15% of the iron was consistent with mononuclear S = 3/2 {FeNO}⁷.

Figure 8.

Mössbauer spectra (red lines) and simulations (black lines) of ~0.8 mM Dv FDP_red mixed with 2 equiv of NO quenched at 100 ms. Temperature and magnetic field: (A) 4 K, 0.12 T, plotted at half area, (B) 4 K, 7.5 T, (C) 100 K, 7.5 T, (D) 150 K, 7.5 T. For one of the simulations (B), gray lines show the species contributing to the sum. Simulation parameters for equivalent {FeNO}⁷ sites (solid line): J = 66 cm⁻¹, S = 3/2, D = +14 cm⁻¹, E/D = 0, g = 2, A_iso/g_nβ_n = −27 T, δ = 0.71 mm/s, ΔE_q = 1.85 mm/s, η = 1. Impurity species (dashed line): S = 3/2, D = +13 cm⁻¹, E/D = 0, g = 2, A_iso/g_nβ_n = −27 T, δ = 0.70 mm/s, ΔE_q = 1.65 mm/s, η = 1.

In a magnetic field of 7.5 T at 4.2 K, the spectra of the majority species showed a diamagnetic pattern, indicating that the S = 3/2 {FeNO}⁷ sites of the Dv FDP_diNO intermediate couple antiferromagnetically to give a system spin S = 0 state lowest in energy, consistent with the behavior of the corresponding Tm FDP_diNO spectra.¹⁴ At elevated temperatures, the overall line splitting of the spectra in Figure 8 decreased due to the population of excited spin states, whose magnetic moments oppose the direction of the applied field. Fitting the spectra to eq 1 allowed determination of the exchange-coupling constant. The simulations were sensitive to the values of J and the isotropic ⁵⁷Fe hyperfine tensor, A_iso. The A_iso values for characterized S = 3/2 {FeNO}⁷ sites range from −27 to −23 T.¹⁸ The S = 3/2 {FeNO}⁷ site of the FDP_NO complex had A_iso = −27 T (Figure 5), which is at the upper limit of this range. Fits to the spectra of Figure 8 within this range of A_iso values gave J = 60(10) cm⁻¹. The fits included the 15% mononuclear S = 3/2 {FeNO}⁷ impurity species which is best observed in Figure 8B. The Mössbauer spectra of FDP_diNO from Tm FDP were complicated by the presence of other species¹⁴ but nevertheless displayed (Figure S3) the same overall width and temperature dependences, indicating that the J values of FDP_diNO from Tm and Dv are approximately equal.

DFT Calculations of FDP_diNO

Compared to that for FDP_no (17 cm⁻¹), the J value of 60 cm⁻¹ for FDP_diNO is remarkably large. The S = 3/2 {Fe_PNO}⁷ and {Fe_DNO}⁷ centers are thus strongly antiferromagnetically coupled. If the spin-state energies of the FDP_diNO were dependent only on a Fe(μ-OH)Fe superexchange interaction, they would be described by the spin Hamiltonian JŜ_PNO•Ŝ_DNO, where S_PNO = S_DNO = 3/2, and the observed exchange-coupling constant would be expressed as J = (7/5)² J_FeFe = 1.96 J_FeFe. Making the reasonable assumption that the Fe(μ-OH)Fe core in the structure of FDP_diNO resembles that of FDP_red, which is the species that reacts with NO, we used the exchange-coupling constant of FDP_red (J_FeFe = 32 cm⁻¹)¹² to obtain J = 63 cm⁻¹, which is in good agreement with the experimental value for FDP_diNO. Although the iron valences in the diiron dinitrosyl species are formally closer to +3 than +2, our previous spectroscopic and DFT results showed that the value of J_FeFe is similar for 5-coordinate diferrous and diferric oxidation states of FDP with the same hydroxo-bridged active site structure.¹²

Figure 9 shows a representative DFT model structure for the diiron site in FDP_diNO (Table S4). The optimized structure shows bent Fe-N-O geometries for both sites, with the nitrosyl nitrogens oriented to give a weak ⁻ON•••NO⁻ interaction. Three optimized structures are listed in Table S4, which differ in the hydrogen bonding between D89 and the bridging hydroxo (as shown in Figure S4). These models show ⁻ON•••NO⁻ distances ranging from 2.6 to 2.9 Å. This close approach introduces an additional exchange term, J_on-no, between the two S = 1 NO⁻ ligands. For this case the spin projection leads to J = (7/5)² J_FeFe + (−2/5)² J_on-no The contributions to J from Fe(μ-OH)Fe exchange and ⁻ON•••NO⁻ exchange have the same sign. Thus, unlike the opposing exchange interactions in FDP_NO, which lowers the value of J, those in FDP_diNO reinforce each other, thereby increasing the value of J. The distance between the interacting NO⁻ moieties depends on spin state, albeit to a lesser degree than in the case of the Fe_P-NO⁻•••Fe_D interaction in FDP_NO. Calculations were performed for both the ferromagnetic (F) ↓↑↑↓ (S_NO(P), S_P, S_D, S_NO(D)) and the antiferromagnetic (BS) ↓↑↑↓ iron spin configurations, where S_NO(P) = 1 and S_NO(D) = 1 represent the two NO⁻ spins, which are antiparallel to the iron spins, S_P = 5/2 and S_D = 5/2 within the{FeNO}⁷ centers. The shorter ⁻ON•••NO⁻ distance was found to occur for the BS configuration in all models because antiparallel orientation of the S_NO(P) and S_NO(D) spins is favorable for the ⁻ON•••NO⁻ interaction. Since the exchange-coupling constant J is a function of both J_FeFe and J_ON-NO, the energies of the BS and F states depend on both of these quantities. The Supporting Information presents two procedures for estimating J from DFT calculations, both of which show that the BS state is lower in energy. Table S4 shows values that are compatible with experiment, but owing to the uncertainty in the strength of the ⁻ON•••NO⁻ exchange coupling, our estimates of the relative contributions of J_FeFe and J_ON-NO to the exchange coupling are approximate.

Figure 9.

DFT structure of the diiron site in FDP_diNO (5_diNO of Table S4). Except for the H of the hydroxo bridge, hydrogen atoms have been omitted for clarity. Dashed line indicates the close ON•••NO contact. Color code: C, gray; Fe, gray-blue; H, white; N, blue; O, red.

The Supporting Information also presents results of DFT calculations for the synthetic diferrous alkoxo,carboxylato-bridged complex Fe₂(Et-HPTB)(O₂CPh) and its di-NO adduct [(FeNO)₂(Et-HPTB)(O₂CPh)]²⁺ ([{FeNO}⁷]₂). Both the diferrous and the [{FeNO}⁷]₂ complexes have been crystallographically and magnetically characterized,^43,44 and their DFT structures are shown in Figure S7. The [{FeNO}⁷]₂ complex has an Fe-Fe distance of 3.4 A, and the nitrogen atoms of the two {FeNO}⁷ centers are separated by a distance of 2.8 Å. The DFT-optimized structures find that the N•••N distance between the nitrosyls increases from 2.78 (BS) to 2.95 Å (F), indicating a spin dependence of the structure comparable to that of the FDP_diNO models (Table S4). The experimental values of J for the synthetic diferrous and [{FeNO}⁷]₂ complexes are 23 and 46 cm⁻¹, respectively, in good agreement with the increase by the factor (7/5)² expected for retention of the alkoxo bridge and little or no change in J_FeFe. Although the ratio of the experimental J values is close to the predicted value of (7/5)², analysis of the DFT results for the dinitrosyl species suggests that the explanation for the ratio exclusively in terms of spin projection factors may be too simplistic. DFT calculations suggest that the exchange term from the ⁻ON•••NO⁻ interaction could contribute up to one-half of the experimental value of J.

DISCUSSION

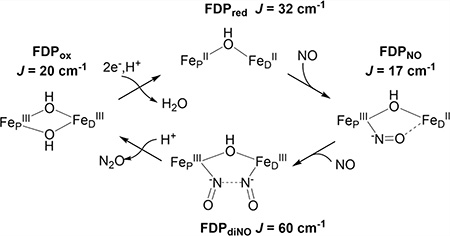
The previous and present work have together characterized four states of the FDP diiron site relevant to the NOR catalytic cycle: FDP_ox, FDP_red, FDP_NO, and FDP_diNO. On the basis of spectroscopy and DFT modeling, the proposed structures for these species are shown in Figure 10. The exchange-coupling constants have been experimentally measured for all four species and show a large variation (J = 17–60 cm⁻¹). Nevertheless, the J values are consistent with the presence of at least one hydroxo bridge between the iron ions in all four states. The significant variation in J among these four species can be explained in the context of the bridging ligand(s) and the exchange interactions involving the NO ligands. As described in our previous work, the value of J for FDP_red is within error equal to that of μ-hydroxo diferrous sites of deoxyHr and synthetic complexes, and both its Mössbauer spectroscopic parameters and J value were well modeled by DFT calculation.¹² The spectroscopic methodologies for determining the exchange interactions have been employed previously for relatively few complexes and proteins, but here we demonstrate the feasibility and importance of these methods in application to all observed states of the FDP enzymatic cycle.

Figure 10.

Core structures for the observed diiron species in the FDP catalytic cycle based on the results presented here (FDP_no and FDP_diNO) and in ref 12 (FDP_ox and FDP_red). Experimental values of J (cm⁻¹) are listed in parentheses. Additional iron ligands shown in Figure 1 are omitted for clarity.

Tm FDP_NO was formed in nearly quantitative yield by adding ≤1 equiv of NO per diiron site to Tm FDP_red.^14,20 If the first coordination sphere of FDP_red remains essentially unchanged upon NO binding, we expect the experimental value of J to increase from ~30 cm⁻¹ in FDP_red to ~45 cm⁻¹ in FDP_NO, based on the spin projection factor applied to J_FeFe in FDP_NO. However, the experimental value of J for FDP_NO (17 cm⁻¹) is significantly lower than that of the diferrous site in FDP_red, albeit still indicative of a hydroxo bridge. The unexpectedly low experimental value of J for FDP_NO is attributed to an additional Fe³⁺NO⁻•••Fe²⁺ exchange interaction through the semibridging NO. This semibridging interaction was first proposed based on an unusually low N–O stretching frequency in FDP_NO compared to other S = 3/2 {FeNO}⁷ complexes.²⁰ This low frequency was attributed to polarization of the {FeNO}⁷ center toward Fe³⁺−NO⁻, thereby increasing electron density in π-antibonding orbitals on NO. This polarization is also supported by the ⁵⁷Fe isomer shift of the {FeNO}⁷ center in FDP_NO, which is lower than that of the {FeNO}⁷ sites in FDP_diNO (Table 2). The lower isomer shift is consistent with a more pure Fe³⁺ character.

The exchange-coupling constant reported here for FDP_diNO, 60(10) cm⁻¹, is the largest value of J observed for any diiron species so far detected in the NOR catalytic cycle of FDP. Assuming that binding of NO does not induce significant structural changes in the bridging groups from that of diferrous, the diNO adduct should show a significant increase in J (approximately double) relative to that of diferrous owing to the spin coupling between iron and NO within the {FeNO}⁷ centers. Indeed, the experimental increase in the value of J for FDP_diNO relative to FDP_red was predicted by the spin projection factor, J = (7/5)² J_FeFe, using the experimental J_FeFe value for the diferrous site in FDP_red. This prediction suggests the diiron bridging structure of FDP_diNO is similar to that of FDP_red. The published J values for two synthetic alkoxo-bridged diferrous complex, Fe₂(Et-HPTB)(O₂CPh) and Fe₂(BPMP)(OPr), and their respective diNO adducts also support a doubling of J.^44,45

The DFT-optimized structures for the F and BS states of FDP_diNO show that the ⁻ON•••NO⁻ distance decreases from 3.07 to 2.94 Å, respectively, for the structure shown in Figure 9. This decrease can be attributed to an antiparallel orientation of the two S = 1 NO⁻ ligand spins in the BS state. A similar ⁻ON•••NO⁻ distance decrease (from 2.95 to 2.78 Å) was found from our DFT calculations on the di-NO adduct of Fe₂(Et-HPTB)(O₂CPh). These ⁻ON•••NO⁻ distances indicate a relatively weak interaction compared to other dinitrosyl species, such as the cis-NO dimer (N-N, 2.18 Å) and a di-Ru-NO complex (N-N, 1.86 Å).^33,46 The additional ⁻ON•••NO⁻ interaction in the FDP_diNO DFT model increases the observed exchange interaction in accordance with J = (7/5)² J_FeFe + (−2/5)² J_on-no. DFT calculations give J_on-no ≈ 150 cm⁻¹ for a ON•••NO separation of ~2.9 Å. The large J_on-no coupling arises from the direct overlap of the magnetic NO⁻ orbitals. However, the spin projection factor of (−2/5)² = 0.16 for the two {FeNO}⁷ centers significantly attenuates the ⁻ON•••NO⁻ contribution, such that the overall value of J for the FDP_diNO model is dominated by the J_FeFe term. Our DFT results on the synthetic [{FeNO}⁷]₂ complex, [(FeNO)₂(Et-HPTB)(O₂CPh)]²⁺, suggest that the exchange term from the ⁻ON•••NO⁻ interaction contributes approximately one-half of the experimental value of J.⁴⁴ Thus, while both Fe-Fe and a ⁻ON•••NO⁻ spin exchange may contribute to the observed value of J in the FDP_diNO, their relative contributions cannot at present be accurately determined.

NOR Mechanism of FDP

The results described here together with those from previous reports are consistent with the Tm FDP NOR mechanism depicted in Figure 10.^{12–14,20,21} The active site of FDP_ox contains a bis-μ-hydroxo diferric core. Reduction of FDP_ox to FDP_red results in loss of one hydroxo bridge and loss of the hydrogen bond between the remaining hydroxo bridge and Asp89. We suggest that the hydrogen bond in FDP_ox may aid in retention of one hydroxo bridge, thus allowing loss of the other hydroxo bridge. This loss opens syn-oriented coordination sites on Fe_D and Fe_P for NO binding. The importance of the syn orientation has been discussed.⁴⁷ The first NO binds in submilliseconds to give FDP_NO (Fe²⁺{FeNO}⁷}), and the bound NO weakly interacts with Fe_D, thus stabilizing the mononitrosyl adduct. The second NO binds over the course of 100 ms to form the FDP_diNO [{FeNO}⁷}]₂ intermediate. The spectroscopy and DFT-optimized structures for FDP_diNO are consistent with a hydroxo bridge and ⁻ON•••NO⁻ spin pairing in a (Fe³⁺NO⁻)₂ formulation, which could facilitate N-N bond formation.

Our previous rapid kinetics results are consistent with rate-determining conversion of FDP_diNO to the diferric site and release of N₂O without transfer of additional reducing equivalents into the [{FeNO}⁷}]₂ site.^13,14,48 The diferric active site after turnover has the same EPR and Mössbauer spectra and the same exchange interaction as that of resting FDP_ox, indicating that the bis-μ-hydroxo diferric structure of FDP_ox reforms after turnover. The oxygen of the second μ-hydroxo entering the diiron site could be derived from NO during the final step of N₂O formation. The absence of a water-derived bridge in synthetic alkoxo, carboxylato-bridged diiron-dinitrosyl complexes may partially account for their lack of NO to N₂O turnover without input of additional reducing equivalents.⁶ As discussed elsewhere,¹⁴ our results do not support a NOR mechanism involving {FeNO}⁸, although this possibility is still debated.^6,9,12

Two protons are required in the overall reaction of NO to N₂O. One of these protons enters the mechanism during the reduction of FDP_ox. The first proton participates in the loss a bridging OH⁻ upon reduction to open sites for NO binding. The second proton is suggested to enter after formation FDP_diNO to evolve N₂O (Figure 10). Reformation of the second hydroxo bridge could come from the OH⁻ released upon protonation and cleavage of one of the N–O⁻ bonds. Analogous to FDP turnover of NO to N₂O without involvement of an {FeNO}⁸ species, a synthetic dinuclear ruthenium complex of hydrotris(pyrazolyl)borate (Tp) has been shown to evolve N₂O from NO.^33,49 The observed [{RuNO}⁷]₂ intermediate generates N₂O and a μ-(hydr)oxo-(RuTp)₂ complex under acidic conditions, thus supporting participation of protons at a similar oxidation level as that of FDP_diNO prior to N₂O formation.

Why Are Hr, RNR, and MMO Not Competent NO Reductases?

The higher ratio of His/carboxylate coordination in the diiron center of FDP relative to that of MMO and RNR results in less negative charge donation to the irons from the protein ligands, which we suggest serves to stabilize a hydroxo bridge in FDP_red. Figure 2 shows that the retention of a single hydroxo bridge in FDP_red results in the same overall charge for the active site as those of MMO_red and RNR_red which have no solvent bridge. Similarly to FDP, the diferric site of MMO has a bis-μ-hydroxo, μ−1,3-carboxylato structure, whereas the RNR diiron site has a μ-oxo, μ−1,3-carboxylato structure.¹⁷ Unlike FDP, both RNR and MMO diiron sites lose their μ-oxo/μ-hydroxo bridges upon reduction.

Among nonheme O,N-ligated diiron sites in proteins a stable diiron mononitrosyl adduct has been observed only for FDP_red and diferrous Hr.³⁴ A diiron dinitrosyl species is not observed in Hr because one of the irons is coordinatively saturated and cannot bind a second NO (Figure 2). Our results on FDP show the reaction toward N₂O proceeds only after binding of a second NO to iron, rather than a pathway where a second free NO attacks the initially formed {FeNO}⁷.^14,50 Such a process could conceivably occur in Hr but has not been observed.

Like FDP, both diferrous MMO and RNR bind two NO molecules to form the diiron dinitrosyl adduct. While only FDP contains an FMN cofactor, the FDP diiron site turns over NO to N₂O also in the deflavinated protein.^13,48 Therefore, the absence of a flavin cofactor in MMO and RNR cannot by itself explain their low efficiency in reducing NO to N₂O. The J value for the [{FeNO}⁷]₂ site in RNR (Table 2) is much smaller than would be expected for a hydroxo bridge but is consistent with a dicarboxylato-bridged structure and possibly an aqua bridge. The absent or weak solvent bridge may render the diferrous and [{FeNO}⁷]₂ sites of RNR incapable of enforcing an appropriate distance and orientation between the NO ligands for efficient turnover to N₂O. Studies of NOR efficiency of diiron dinitrosyl model complexes have highlighted the need for a syn configuration of the two {FeNO}⁷ centers to promote N—N bond formation.^19,51 For FDP, we propose that the persistence of the hydroxo bridge throughout the NOR catalytic cycle serves to enforce a scaffold in which the two NO molecules are forced to bind syn to each other, thereby facilitating N—N bond formation. However, the interaction distance and orientation cannot be the only reaction determinants. For example, the diNO complex of Fe₂(Et-HPTB)(O₂CPh) has a close interaction distance and a syn NO orientation but does not generate N₂O. The diNO complex does produce N₂O under illumination⁵² but in a process differing from the mechanism of FDP which does not utilize additional photonic energy. The N/O donor ratio of the primary coordination sphere for the irons of FDP is lower than that of the synthetic BPMP complex and higher in comparison to RNR and MMO, all of which form a diNO complex. This suggests to us that the donor N/O ratio is not critical for the further reaction of the diNO complex toward N₂O release and that residues in the second sphere of the active site in FDP may bequeath this system with its unique reactivity.

CONCLUSIONS

The exchange-coupling constants between the iron centers of Tm FDP have now been determined for four states (diferric, diferrous, diiron mononitrosyl, and diiron dinitrosyl), all of which appear to participate in the NOR reaction cycle (Figure 10). The J values indicate that all four states retain at least one hydroxo bridge between the irons. The retention of a hydroxo bridge throughout the catalytic cycle may be important for maintaining proper orientation and close interaction distance of the {FeNO}⁷ centers leading to N—N bond formation. DFT calculations indicate that the experimental J value for the diiron mononitrosyl includes an exchange interaction between a semibridging NO^- from the {FeNO}⁷ center and the Fe²⁺ center. The J value for the diiron dinitrosyl could include an ⁻ON•••NO⁻ exchange interaction imminent to N—N bond formation. We have demonstrated the feasibility of a combined spectroscopic/DFT approach to characterization of the bridging structures of all observed states of the FDP NOR catalytic cycle. The application of these methodologies to the rich array of FDPs from other organisms may reveal important electronic and structural variations, which could provide insights into their differing NOR activities.