Strong Light-Field Driven Nanolasers

Abstract

Einstein established the quantum theory of radiation and paved the way for modern laser physics including single-photon absorption by charge carriers and finally pumping an active gain medium into population inversion. This can be easily understood in the particle picture of light. Using intense, ultrashort pulse lasers, multiphoton pumping of an active medium has been realized. In this nonlinear interaction regime, excitation and population inversion depend not only on the photon energy but also on the intensity of the incident pumping light, which can be still described solely by the particle picture of light. We demonstrate here that lowering significantly the pump photon energy further still enables population inversion and lasing in semiconductor nanowires. The extremely high electric field of the pump bends the bands and enables tunneling of electrons from the valence to the conduction band. In this regime, the light acts by the classical Coulomb force and population inversion is entirely due to the wave nature of electrons, thus the excitation becomes independent of the frequency but solely depends on the incident intensity of the pumping light.

Nanoscale lasers are considered as a next frontier in laser research revolutionizing development of optoelectronics, on-chip photonic devices and ultrasensitive sensors. Enormous progress was achieved over the past decade in design and application of a huge variety of nanolasers emitting coherent radiation covering the spectral range from ultraviolet to near-infrared.^1,2 Although electrical pumping of nanolasers is of primary interest for many applications, optical excitation is still very a important mechanism of pumping especially for biological applications.² The majority of semiconductor nanowire lasers, realized up to date, require UV, vis, or NIR excitation for single-photon resonance pumping.¹ This spectral domain as the pumping source might set hard limitations when nanolasers are integrated in a complex photonic circuit or dissolved in a biological solution. Therefore, possibilities for nonresonant pumping with longer wavelength sources are of great interest for applications and fundamental physics of nanoscale semiconductor lasers.

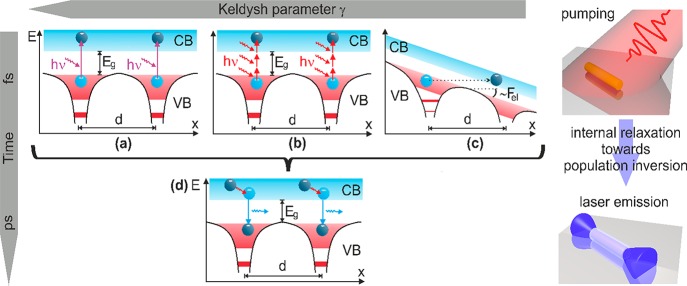
The concept of optical pumping and lasing in semiconductors is depicted in Figure 1 for three different excitation regimes, determined by the frequency and the intensity of the pumping light. In the case of an above bandgap single-photon absorption (Figure 1a), the excitation rate is proportional to the pumping intensity I and the net population in the conduction band (CB) is naturally determined by the pumping fluence. This is the usual case of optical pumping in laser physics, and due to the (near) resonance nature of the excitation process it can be realized with low intensities, long pump pulses, or even under continuous-wave conditions.³⁻⁵ Thus, the physics of this excitation mechanism can be understood in the particle picture of light and was explained in the fundamental work by Einstein⁶ establishing the quantum theory of radiation and paving the way for laser physics. In the case of pumping with photon energies below the bandgap, photoexcitation can occur only at a substantially higher level of intensities and can be still described solely by the particle picture of light, extending the quantum concept of light to multiphoton absorption (Figure 1b). In this nonlinear interaction regime, excitation and population inversion depend not only on the photon energy but also on the intensity of the incident pumping light.

Figure 1.

Upper panel represents the photoexcitation step, taking place on the femtosecond time scale (for details see text) by (a) single-photon and (b) multiphoton absorption of quanta with the energy hν, or (c) tunneling of carriers from the valence band (VB) to the conduction band (CB) through a barrier formed by an intense light-field F_el. Here, the potentials from two neighboring atoms/ions in a lattice, separated by a lattice period d, are schematically depicted as a function of the spatial coordinate x. The lower panel depicts the intraband carrier relaxation (red arrow) and photoemission (magenta arrow) proceeding on picosecond time scale, which is independent of the pumping process.

Here, we demonstrate that significantly lowering the pump photon energy still enables population inversion in semiconductors. In this case, the strong electric field of the pump light bends the electronic bands and enables tunneling of electrons from the valence to the conduction band (Figure 1c). The light acts as classic Coulomb force and population inversion is built up entirely due to the wave nature of electrons, thus excitation becomes independent of the photon energy but solely depends on the intensity of the pumping light.

A respective theory on high intensity excitations in semiconductors and atoms was developed by Keldysh in 1964.⁷ Whether multiphoton absorption or tunneling is the dominant mechanism under strong field excitation is determined by the so-called Keldysh parameter 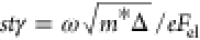, where ω and F_el are the pumping frequency and the electric field amplitude, respectively, m* is the effective mass of the electrons, e is the elementary charge of an electron, and Δ is the band gap energy of the material/semiconductor. For γ ≫ 1, valence band electrons are excited by multiphoton absorption and the excitation rate depends on the pumping intensity scaling with I^N, where N = ⟨Δ/ℏω⟩ is the number of absorbed photons with ⟨ ⟩ denoting the integer part of a number. For intense, low frequency light fields, the Keldysh parameter becomes γ ≪ 1 and the transition proceeds via tunneling. The excitation rate is then ,² that is, proportional to the exponential function of the laser electric field strength F_el. High-pumping intensities required for both regimes efficiently heat the electrons in the conduction band resulting in a breakdown of the material, unless the duration of the pump pulse is less than the time scale of an avalanche. That is why both multiphoton absorption and tunneling excitation of semiconductor lasers might be realized only under the condition of a sufficiently short pumping pulses (femtosecond time scale, as it is depicted in Figure 1).

Together with the population inversion, a cavity is essential prerequisite to realize laser emission. Semiconductor nanowires provide in principle all necessary prerequisites for design of nanoscale lasers.⁸ Waveguiding cylindrical geometry together with reflecting end facets naturally form a cavity supporting Fabry-Pérot modes, whereas the semiconductor material acts as an optical gain medium.⁸⁻¹⁰ Moreover, a large confinement factor provided by the nanowire geometry enables lasing that in practice would not be possible for a different cavity geometry under conditions of ultrashort cavity length,¹ and in the case of below bandgap intense pumping, ultrashort duration of a pump pulse. Laser emission from individual ZnO nanowires or arrays of nanowires pumped via two- or three-photon absorption was demonstrated before.^11,12

Our experiments were conducted with single ZnO nanowires having diameters of 200–250 nm and lengths of 5–15 μm and nanowire-arrays, consisting of randomly oriented nanowires with similar length and diameter (see Supporting Information for details). Magnified CCD images of the single-wire nanolaser, pumped by 105 fs pulses at 3.6 μm wavelength and operating in the spontaneous emission regime with a homogeneous, isotropic emission along the whole nanowire and with the emission concentrated at the end facet in the case of lasing¹³ are presented in Figure 2a,b, respectively. Typical intensity-dependent emission spectra of an individual ZnO nanowire pumped by 30 fs laser pulses at 0.8 μm wavelength as well as by 105 fs pulses at 3.6 μm wavelength are shown in Figure 2c,d, respectively (the experimental setup is presented in Supporting Information Figure S2). The spectra show very similar features for both wavelengths. At pumping intensities slightly above the laser threshold I_th = 0.7 TW/cm² (measured for 0.8 μm, the value for 3.6 μm pumping is slightly lower), the broad spectrum of spontaneous luminescence transforms into a much narrower spectrum of stimulated emission, which resembles Fabry-Pérot (FP) modes of the nanowire.⁸ The spectral narrowing and the observed longitudinal mode structure of the emission are clear indications of the transition from spontaneous to stimulated emission.¹⁴ For pumping well above the threshold, the emission spectrum becomes significantly broader and experiences a redshift, whereas the distinct FP modes structure vanishes. The redshift and the spectral broadening might be caused by a band gap renormalization in the highly excited semiconductor and by heating up the gain medium,¹⁵⁻¹⁹ whereas the vanishing of the FP modes is attributed to the dynamical change in the refractive index caused by a fast change in the carrier density due to stimulated emission in the strong excitation regime.^15,16

Figure 2.

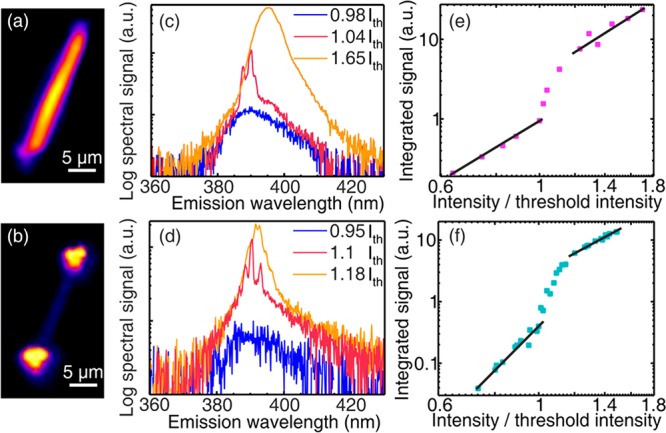
Magnified CCD images of an emitting single ZnO nanowire pumped by a 3.6 μm laser when the pumping intensity is (a) below the lasing threshold and (b) above the lasing threshold. The emission spectrum of a single nanowire for pumping (c) by three-photon absorption from a 0.8 μm femtosecond laser source and (d) by the tunnel excitation using a 3.6 μm femtosecond laser source. Three spectra are shown for each case: below the lasing threshold (blue), slightly above threshold (red), and well above threshold (orange). Log–log scale dependence of the UV emission yield from a single nanowire pumped (e) by three-photon absorption from a 0.8 μm femtosecond laser source and (f) by the tunnel excitation using a 3.6 μm femtosecond laser source.

Figure 2e,f depicts the dependence of the UV emission yield of the individual nanowire laser on the pumping intensity in a log–log scale for the case of the three-photon absorption pumping at the 0.8 μm wavelength and tunneling excitation at the 3.6 μm wavelength, respectively. It exhibits the expected characteristic S-shape course and shows a clear transition from spontaneous emission to ASE and, finally, to laser emission.⁸Figure 2a–d clearly demonstrates that lasing of a single semiconductor nanowire can be achieved in both the three-photon absorption and the tunneling excitation regime (Keldysh parameter γ ≪ 1). Remarkably, the threshold pumping intensity is very similar in both regimes of excitation (Figure 2e,f) despite the large difference in the excitation wavelengths (nearly a factor of 5) and a qualitative and significant difference in the physical mechanism.

Similar results were obtained also with single cadmium sulfide (CdS) nanowires, another direct-gap semiconductor with the bandgap 2.35 eV, proving that pumping by optical tunneling is a general mechanism not specific to a particular semiconductor material (see Figure S3 in Supporting Information). The CdS nanowires were 5–10 μm long and had diameters in the range of 200–300 nm, similar to that of the ZnO nanowires.

To rule out the dependence of spectral characteristics of the nanolaser emission on orientation and statistical variations in geometric parameters of individual wires, we studied the emission as a function of the intensity and wavelength of the pumping pulses for randomly oriented arrays of nanowires (Figure S1, details of the experimental setup are given in Figure S4 of Supporting Information). A detailed comparison of emission characteristics of a single wire and the disordered array of wires with the morphology used in our experiments is provided in ref (20). Briefly, emission from the disordered array can be considered as an incoherent superposition of the emission from individual nanowire lasers. Figure 3a depicts the dependence of the UV emission yield on the pumping intensity in a log–log scale for a ZnO nanowire array, which was synthesized using the same conditions as for the array used to select individual nanowire (see Supporting Information).

Figure 3.

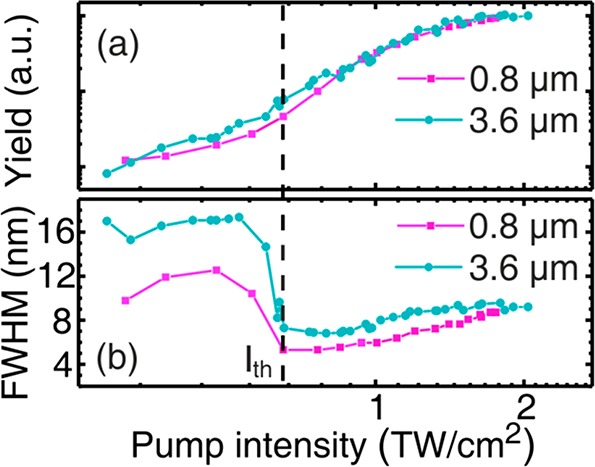
Spectrally integrated intensity (a) and the spectral width at the full width at half-maximum level of the UV emission of nanowire arrays as a function of pump intensity. The dashed vertical line with the arrow indicates the threshold pumping intensity.

In comparison to the single wire measurements, the S-shape is not that pronounced due to the superposition of many individual nanolasers with different length, orientations and quality in the array, leading to a smearing of the threshold. The transition to lasing appears in a much clearer manner in the dependence of the emission’s spectral bandwidth (Figure 3b), which demonstrates a significant spectral narrowing during the transition from spontaneous to stimulated emission, an effect well-known in laser physics. The pumping intensity corresponding to the inflection point in the S-curve and to the onset of the spectral narrowing is defined as the threshold pumping intensity I_th at which lasing is enabled. The lasing threshold is essentially the same for pumping the nanowire array at 0.8 and 3.6 μm wavelengths and amounts to about 0.7 TW/cm² (Figure 3b). The corresponding Keldysh parameters for 0.8 and 3.6 μm pumping are 2.5 and ∼0.4, respectively. Thus, the increase in the pumping wavelength by a factor of 5 does not essentially require an increase in the pumping intensity to achieve laser emission from the NWs. It is also worth noticing that the threshold intensity value determined at 0.8 μm pumping wavelength for the disordered array of nanowires is very close to the threshold measured for an individual nanowire. Also, the spectral width of the UV lasing emission and its dependence on the pumping intensity for the nanowire array is almost identical to the dependence measured for the single wire (see Figure 2c,d and Figure 3). Although we cannot completely rule out the occurrence of random lasing, the independence of the laser threshold on the pump spot size (see Supporting Information Figure S5 and refs (21 and 22) as well as the comparable laser thresholds of the individual NW in Figure 2 and the NW ensemble in Figure 3 show no indication of a random laser (network).

Figure 4a (black dots) shows the dependence of the threshold pumping intensity as a function of pumping wavelength in the entire spectral range from 0.8 to 4 μm. Note that these measurements at different wavelengths were carried out with the same nanowire array sample but at different lateral positions at the sample, thus the results in Figure 4a include possible statistical variations along the nanowire array. The error bars show the variation of the threshold intensity value with the diameter of the pumping beam, which varied for different wavelengths and for the measurements at a fixed wavelength within a factor of 2. It is obvious that intensities well below 1 TW/cm² are sufficient for lasing initiation in the entire near-IR–mid-IR spectral range and that the threshold is almost independent of the wavelength.

Figure 4.

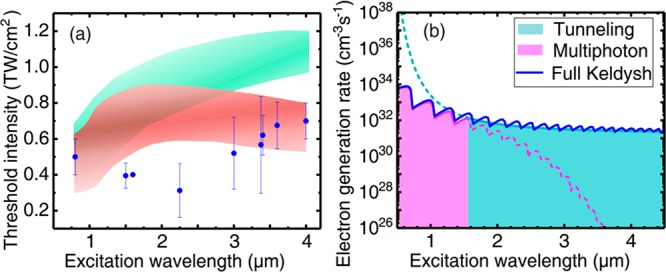
(a) Threshold pumping intensity as a function of the pumping wavelength measured experimentally (blue dots) and simulated numerically for the same experimental parameters using the model without FCA (greenish band) and including FCA and impact excitation (red band). The bands mark the range of threshold intensities calculated for the range of pump pulse duration used in the experiments. (b) Strong field excitation rate as a function of the laser wavelength calculated by applying Keldysh’s theory for the fixed intensity 0.6 TW/cm². The magenta curve shows the asymptotic solution for multiphoton excitation rate, the aquamarine curve is the asymptotic solution corresponding to tunnel excitation rate, the blue solid line is the excitation rate calculated using the exact Keldysh formula (see Supporting Information). The color filling under the curves marks the spectral ranges where the multiphoton (γ > 1, magenta filling) and the tunneling (γ < 1, aquamarine filling) asymptotic solutions are applicable. Solid and dashed line patterns mark the regions where the corresponding asymptotic solution follows the exact calculations and where it deviates from the exact result.

Gaining insight into the physics of this dependence demands the development of a model, which includes the strong field excitation rate calculated using Keldysh’s theory⁷ and electron impact excitation, free carrier photoabsorption (FCA), thermalization, and relaxation of carriers in the conduction band (the detailed description of the model is given in the Supporting Information).

The calculated dependence of the excitation rate of carriers as a function of the laser wavelength for a fixed laser intensity of 0.6 TW/cm² is shown as a blue line in Figure 4b. In the limit γ > 1, the rate follows the multiphoton excitation solution, which exhibits a sharp intensity dependence with pronounced oscillations, corresponding to transition from n to (n + 1) photon absorption, and a strong decrease for longer wavelengths (>1.5 μm) (lower photon energies). In the opposite limit of γ < 1, the rate shows an asymptotic saturation and follows the tunnel excitation solution. The saturation as a function of the wavelength can be easily understood from the physical mechanism of tunnel ionization based on classical work of the laser electric field over the electron. In this case, the photon energy does not matter anymore and only the electric field strength governs the tunneling process. Detail discussion on strong field off-resonant excitation in solids can be found in a recent review.²³ Note that the tunnel asymptotic solution strongly overestimates the excitation rate for wavelengths below 1 μm in comparison to the exact and multiphoton asymptotic solutions. The transition from multiphoton to tunnel excitation occurs for laser wavelengths at around 1.5 μm and the excitation rate is almost wavelength independent for higher wavelengths. Thus, pumping with 0.8 μm wavelength proceeds clearly in the multiphoton regime, whereas for the 3.6 μm pumping wavelength it is clearly in the tunneling regime.

A threshold carrier density n_th of electrons in the conduction band, enabling negative absorption, that is, gain, is a value, which is independent of the geometry or structure and represents a universal quantitative characteristic of the semiconductor active medium. Therefore, we define the threshold pumping intensity in our simulations by the condition that the carrier density in the conduction band reaches n_th by the end of the pumping pulse. This is in fact one necessary condition to achieve lasing, but obviously not sufficient because the threshold is also determined by the interplay between losses and gain of the cavity. In simulations, we use the value n_th = 2 × 10¹⁹ cm^–3 suggested for bulk ZnO in ref (16). This density is 1 order of magnitude above the Mott density (∼1.5 × 10¹⁸ cm^–3 in ZnO at room temperature¹⁵), thus gain and emission occur via an electron–hole plasma (EHP).^11,15,24,25

The simulated wavelength dependence for the threshold pumping intensity is shown in Figure 4a for two situations, with and without free carrier absorption (depicted by red and green bands respectively), together with the experimental data. The colored bands in Figure 4a represent the variations when changing the pump pulse width from minimum to maximum values used in the experiments. Although results of simulations in both cases agree with the experimental values within a factor ≤2.5, the model including the absorption of the laser energy by free carriers in the conduction band agrees better with the observed saturation of the threshold intensity as a function of the pumping wavelength in the mid-IR range. Also, as follows from Figure 4b, the strong field excitation rate in the three-photon absorption regime at 0.8 μm pumping wavelength is almost 2 orders of magnitude higher than the excitation rate in the tunnel regime at the 3.6 μm pumping wavelength. As a result, simulations without free-carrier absorption predict an increase in the threshold pumping intensities by a factor of 2 by changing the wavelength from 0.8 to 3.6 μm (Figure 4a) which is in contradiction with the experiment. However, including free-carrier absorption enables saturation and even a slight decrease in the pumping intensity within the considered wavelength range. This can be explained by more efficient heating of free carriers with increasing pumping wavelength that enables additional excitation based on electron–electron scattering. The acceleration of the electrons in the conduction band by the electric field scales with the laser intensity and wavelength as I*λ². Thus, the absorption at mid-IR wavelengths also triggers electron impact ionization/excitation, which makes a significant contribution to the population of the conduction band for pumping wavelengths above 1.5 μm. Free carrier absorption also explains the strict limitations in the pumping pulse duration, which should be shorter than the characteristic time of the avalanche process to avoid significant heating of the material (finally via electron–phonon coupling).

Despite the simplicity of our model and the limitations of the Keldysh theory, which are discussed in detail in ref (26), and other uncertainties mentioned above, the numerical simulations provide reasonable agreement between the absolute values of the threshold pumping intensity and the experimentally measured ones. Astonishingly, the differences are in the range of a factor of 2 rather than in orders of magnitude. This is especially surprising, because the experimentally observed threshold pumping intensities are determined by the balance between gain and loss and therefore depend on the nanowire geometry (length, diameter), the structural quality, and so forth. The difference in the trend of the curves derived numerically and measured experimentally can also be related to variations in the focal beam size for different pumping wavelengths investigated in the experiments (see Supporting Information) and spatial inhomogeneity of the disordered nanowire array.

In conclusion, we report on the experimental realization of light-field driven semiconductor nanolasers excited by the tunneling of the carriers from the valence to the conduction band. Pumping of lasers in the tunneling regime was demonstrated so far only in semiconductor heterostructures biased by a dc electric field in quantum cascade lasers.²⁷ Our results provide evidence that the electric field of an optical excitation beam enables pumping of a semiconductor laser. This pumping mechanism was demonstrated not only for semiconductor nanowire lasers based on ZnO but also for CdS, strongly indicating that this is a general phenomenon rather than characteristic for a particular material. We tuned the pumping wavelength from near- to mid-IR spectral ranges demonstrating the possibility of “arbitrary” wavelength pumping of semiconductor lasers without lowering the lasing threshold. Therefore, these results pave a way for realizing several visionary applications, such as nanophotonic integrated circuits in lab-on-chip applications.^28,29 In particular, biological imaging or therapy applications³⁰⁻³⁴ might benefit, as UV–visible lasers might be pumped in the transparency window of biological tissue without tremendous loss in the pumping efficiency and damage to the surrounding host medium.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.9b00510.

• Sample preparation and images, CdS data, optical setup, spot size dependence, numerical model (PDF)

Author Present Address

^# (S.A.) DESY - FS-LA, Notkestrasse 85, 22607 Hamburg, Germany.

Author Contributions

R.H. carried out experiments, data processing and numerical simulations; P.M., V.S., S.A., and A.P. contributed in experimental measurements and OPA operation; M.Z. helped with the growth of the nanowires and contributed to the discussion and interpretation of the results; R.R., C.R., A.B., and C.S. contributed to the discussions and interpretation of the results; D.K. suggested the idea of the experiment and contributed in experimental measurements and interpretation of the results; D.K., R.H., and C.S. wrote the manuscript with contribution from all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.