Topological Correction of Infant White Matter Surfaces Using Anatomically Constrained Convolutional Neural Network

Abstract

Reconstruction of accurate cortical surfaces without topological errors (i.e., handles and holes) from infant brain MR images is very important in early brain development studies. However, infant brain MR images typically suffer extremely low tissue contrast and dynamic imaging appearance patterns. Thus, it is inevitable to have large amounts of topological errors in the segmented infant brain tissue images, which lead to inaccurately reconstructed cortical surfaces with topological errors. To address this issue, inspired by recent advances in deep learning, we propose an anatomically constrained network for topological correction on infant cortical surfaces. Specifically, in our method, we first locate regions of potential topological defects by leveraging a topology-preserving level set method. Then, we propose an anatomically constrained network to correct those candidate voxels in the located regions. Since infant cortical surfaces often contain large and complex handles or holes, it is difficult to completely correct all errors using one-shot correction. Therefore, we further enroll these two steps into an iterative framework to gradually correct large topological errors. To the best of our knowledge, this is the first work to introduce deep learning approach for topological correction of infant cortical surfaces. We compare our method with the state-of-the-art methods on both simulated topological errors and real topological errors in human infant brain MR images. Moreover, we also validate our method on the infant brain MR images of macaques. All experimental results show the superior performance of the proposed method.

Graphical Abstract

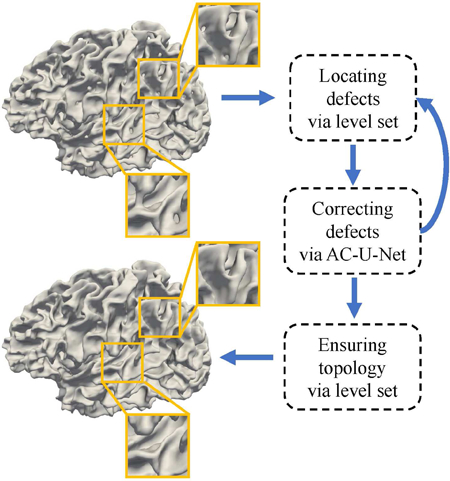
The proposed pipeline for topological correction on infant cortical surfaces. We first locate topological defect regions and extract candidate voxels, and then infer the new labels of these candidate voxels. The above two steps are incorporated into an iterative framework using fixed-sized patches to correct large and complicated topological errors. Finally, a topology-preserving level set method is further applied to guarantee a spherical topology.

1. Introduction

Accurate reconstruction of cortical surfaces for representation of the thin and convoluted cerebral cortex is critical for computational analysis of brain MR images Mangin et al. (1995); Fischl et al. (1999); MacDonald et al. (2000); Van Essen et al. (2001); Shattuck and Leahy (2002); Han et al. (2004); Kim et al. (2005); Shi et al. (2013). However, this is a very challenging task for the infant brain Li et al. (2012); Lyall et al. (2014); Li et al. (2019); Geng et al. (2017). The main reason is that, due to the ongoing myelination Paus et al. (2001), the infant brain MR images typically exhibit very low tissue contrast and regionally-heterogeneous, dynamical imaging appearances. Although several infant-dedicated segmentation methods have been proposed for automated brain tissue segmentation Wang et al. (2014, 2015); Zhang et al. (2015) and achieved reasonable results, the above-mentioned challenges still inevitably cause many tissue segmentation errors, which lead to abounding topological defects on the reconstructed cortical gray matter (GM) and white matter (WM) surfaces. Notably, even very small segmentation errors, as illustrated in Fig. 1, where blue and red contours enclose misclassified voxels, could result in significant topological defects on the cortical surface, thus bringing larger errors in subsequent surface-based analysis.

Figure 1.

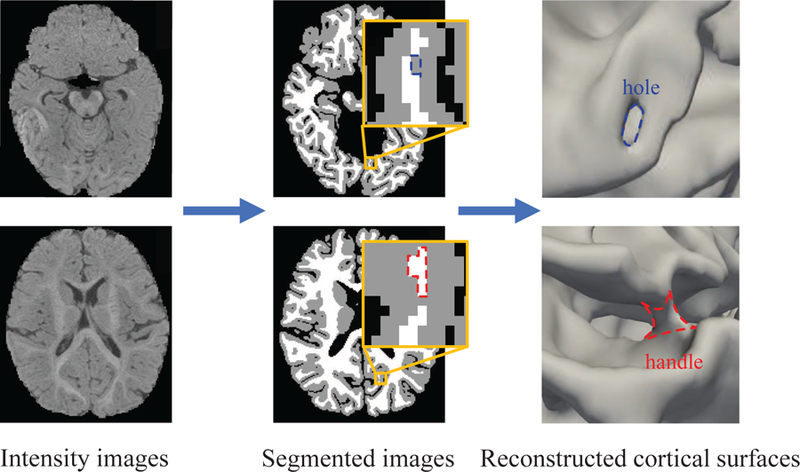
Illustration of topological errors in the tissue segmentation result of a 6-month-old T1-weighted MRI. Although the image was segmented automatically by an infant-dedicated tissue segmentation method Wang et al. (2018), it still inevitably contains many segmentation errors, which lead to abounding topological errors on the reconstructed cortical surfaces. The blue and red contours in the segmented image and cortical surface indicate topological defects (with the blue contour indicating a hole and the red contour indicating a handle).

Typically, topological correction of the cortical surface is performed on the WM surface, since the GM surface is typically obtained by deforming the WM matter surface to the boundary of GM and cerebrospinal fluid (CSF) (e.g., in FreeSurfer Ségonne et al. (2007), BrainSuite Shattuck and Leahy (2001), etc.), while preserving the initial topology of the WM surface. This is because the GM surface cannot be directly reconstructed due to strong partial volume effects, especially in deep tight opposing sulcal banks. Therefore, as long as the WM surface has the correct topology, the reconstructed GM surface obtained by topology-preserving deformation will also have the correct topology. Meanwhile, topological correction is typically performed on the left/right hemisphere independently, considering the prior knowledge that the cortex of each brain hemisphere is topologically equivalent to a sphere. More specifically, topological correction typically involves two main steps, i.e., (1) locating topological defect regions, and (2) correcting these topological defect regions. For the first step, based on the prior knowledge that each brain hemisphere is topologically equivalent to a sphere, several methods have been proposed to locate topological errors on two hemispheres independently, e.g., by identifying cyclic graph loops of the white matter volume Shattuck and Leahy (2001); Han et al. (2002); Shi et al. (2013) or overlapping surface meshes after spherical mapping of the white matter surface Fischl et al. (2001); Ségonne et al. (2007); Yotter et al. (2011). In comparison, the second step is more challenging, because holes and handles are typically hard to distinguish when solely relying on geometric information. As shown in Fig. 1, both holes and handles lead to hole-like shapes in morphology, but a real hole (indicated by the blue contour) is a perforation on the cortical surface, while a handle (indicated by the red contour) is an erroneous bridge on the cortical surface. Several heuristic methods based on the minimal correction criterion or ad hoc rules relying on the appearance patterns of MR images have been proposed for correction of the topological defect regions. For instance, two popular software packages, i.e., BrainSuite Shattuck and Leahy (2001, 2002) and FreeSurfer Fischl et al. (1999); Ségonne et al. (2007), integrate the topological correction step into the pipeline of cortical surface reconstruction. In BrainSuite Shattuck and Leahy (2001), the topological correction algorithm analyzes the connectivity information in each slice of the 3D MR image and produces graph-based representations of the foreground (white matter, WM) and background, respectively. After that, it checks the topology of the constructed graphs according to a tree criterion Kruskal (1956). Specifically, if the graphs are not tree-like, the corresponding topology is then corrected using the minimal correction criterion. One disadvantage of this method is that, since the non-tree-like graph is cut, all topological errors (i.e., holes and handles) will be broken. FreeSurfer Ségonne et al. (2007) first maps the original WM surface onto a sphere, which is as close as possible to the homeomorphism. The overlapping triangles on the sphere can be regarded as topological defects. Then, this method randomly generates a set of non-separating loops for each topological defect and corrects it by opening and sealing the surface. Finally, the Bayesian framework based on the prior of MR image intensities and cortical surfaces is used to refine the corrected result. Although FreeSurfer achieves good performance on the adult cortical surfaces, it cannot properly handle typically large and complicated topological errors on the infant cortical surfaces, which make these rule-based methods less appropriate. Meanwhile, since infant structural brain MR images typically have regionally-variable low tissue contrast and changing appearances along time, the intensity and appearance patterns are not reliable and informative for correction of infant topological. Also, FreeSurfer tends to break big holes on the cortical surface. To address these issues, Hao et al. (2016) proposed a sparse dictionary learning method, called SDLM, for correction of the topological errors on the infant cortical surfaces. Capitalizing on a set of infant brain atlases (free of topological errors), this method learns a sparse dictionary representation without reliance on any predefined rules and achieved competitive performance. Specifically, each atlas is warped into a to-be-corrected image space, and then each to-be-corrected image patch from topological defect regions is first sparsely reconstructed by a set of corresponding anatomically-correct patches extracted from warped atlases. Next, tissue labels for voxels in the atlas patches are propagated to the corresponding voxel in the to-be-corrected image patch by weighted voting, where the voting weights are the sparse reconstruction coefficients. However, since this method relies on accurate registration between the to-be-corrected image and atlas images, and also needs to construct the region-specific dictionary, it is sensitive to registration errors and time-consuming.

Recent advances in deep learning methods, e.g., convolutional neural networks (CNNs) Ronneberger et al. (2015); Çiçek et al. (2016); Huang et al. (2017), have shown competitive performance in the field of medical image analysis Kamnitsas et al. (2017); Li et al. (2018); Chen et al. (2018); Lian et al. (2018); Hoochang et al. (2016); Zhang et al. (2017); Iakovidis et al. (2018); Anthimopoulos et al. (2016); Liu et al. (2018). By automatically learning task-oriented features, CNNs may also capture high-level patterns from tissue-segmented images for discrimination between different topological defects and then for prediction of the corresponding accurate corrections. As one of the state-of-the-art deep learning methods, U-Net Ronneberger et al. (2015); Çiçek et al. (2016), can effectively combine high-resolution spatial information with high-level contextual information for segmentation. Specifically, the U-Net architecture usually consists of a contracting path and an expanding path, where the contracting path processes the input image to capture high-level contextual knowledge, while the subsequent expanding path progressively up-samples the low-resolution feature maps to generate high-resolution segmentation map for the input image. Due to skip connections between the contracting and expanding paths, global contextual information and complementary local details can be automatically fused in U-Net to improve the reliability of the output segmentation map. Hence, the U-Net architecture and its variants have been widely applied in diverse medical image computing tasks Salehi et al. (2017); Chen et al. (2018); Lian et al. (2018); Zhang et al. (2017); Payer et al. (2016). However, the direct application of existing CNN architectures in our specific task may yield sub-optimal results, considering the challenges caused by complicated anatomical structures of the infant cerebral cortex. Therefore, in this paper, we proposed a specific CNN-based method, called anatomically-constrained U-Net (AC-U-Net), for topological correction of infant cortical surfaces. Fig. 2 shows the pipeline of our proposed method. Specifically, in both the training and testing stages, we first adopted a topology-preserving level set method to locate topological defect regions in the segmented image, and then selected candidate voxels (i.e., central points) to extract 3D image patches from these located regions for topological correction. In the training stage, for each extracted 3D image patch with topological defects, we not only used the corresponding manual correction as the ground truth, but also incorporated the corresponding patches extracted from a set of atlas images as additional anatomical constraints. Accordingly, a hybrid loss function was proposed, in which the anatomical prior from multi-atlas images was combined with manually-corrected tissue label map for construction of a reliable AC-U-Net model. In the testing stage, after locating candidate voxels through a shrinking-wrapping topology-preserving level set method, we applied the trained AC-U-Net model to inferring the accurate tissue label of each candidate voxel. Importantly, considering that infant cortical surfaces generally contain large and complicated handles and holes, which are hard to be completely corrected using one-shot correction, the above two steps were iteratively executed in the testing stage to gradually correct these challenging topological defects. Finally, a topology-preserving level set method was further used to guarantee a spherical topology for each cortical surface.

Figure 2.

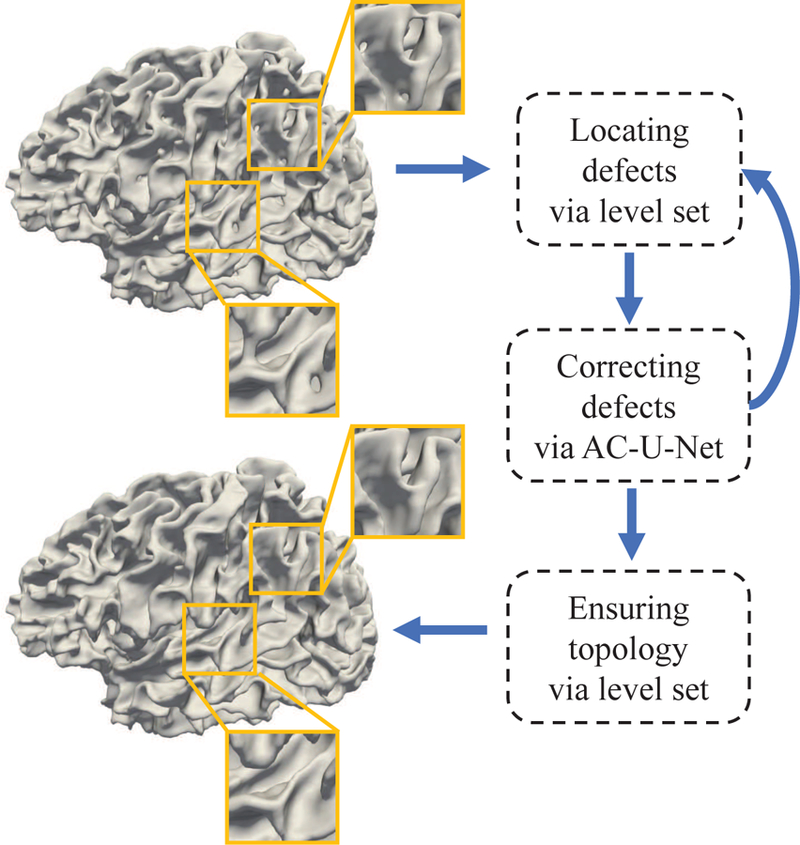
The proposed pipeline for topological correction on infant cortical surfaces. We first locate topological defect regions and extract candidate voxels, and then infer the new labels of these candidate voxels. The above two steps are incorporated into an iterative framework using fixed-sized patches to correct large and complicated topological errors. Finally, a topology-preserving level set method is further applied to guarantee a spherical topology.

Our main contributions are two-fold. First, to the best of our knowledge, we are the first to leverage a convolutional neural network (CNN) based method for infant cortical topological correction, without needing any predefined rules. We propose a novel hybrid loss function for imposing anatomical constraints, thus introducing anatomical priors from multiple atlases. Second, we incorporate CNN and topology-preserving level set method into an iterative framework to gradually correct large and complicated topological defects. We validate our proposed method on simulated topological errors on 6-month-old infant brain MR images, real topological errors on infant brain MR images of 4-month-olds to 15-month-olds, as well as real topological errors on macaque brain MR images from 3 months to 18 months of age. Experimental results show the excellent performance of our method. The code is now publicly available¹.

The remainder of the paper is organized as follows. In Section 2, we first introduce datasets used in our study, and then present our proposed AC-U-Net method. In Section 3, we evaluate the performance of our method by comparing with several state-of-the-art methods. In Section 4, we further investigate the impact of different experimental settings and discuss the limitations of our current work. Finally, a brief conclusion is drawn in Section 5.

2. Material and Methods

In this section, we first introduce datasets and MR image processing pipeline used in this study, and then present the details on the localization of topological defect regions and the proposed anatomically constrained U-Net (AC-U-Net) and the corresponding hybrid loss function for network training. Finally, we present an iterative scheme based on the trained AC-U-Net for correction of topological defects on unseen infant cortical surfaces.

2.1. Datasets and Image Processing

Three datasets were used in our study to evaluate the effectiveness of our proposed method, including 1) a human infant MRI dataset with simulated topological errors, 2) a human infant MRI dataset with real topological errors, and 3) a macaque infant MRI dataset with real topological errors. Figures S1–S3 in the Supplementary Materials show some representative tissue segmented images and their corresponding WM surfaces from each dataset. Informed written consent was obtained from the parents of all human participants and human study protocols were approved by the University of North Carolina at Chapel Hill Institutional Review Board.

1. Human Infant MRI Dataset with Simulated Topological Errors: There are totally 65 manually-corrected cortical surfaces (i.e., free of topological errors) reconstructed based on the infant brain MR images acquired at the age of 6 months using a Siemens 3T scanner. T1-weighted MR images were acquired with 160 sagittal slices using parameters: TR=2400 ms, TE=3.16 ms and resolution=1×1×1 mm³. T2-weighted MR images were obtained with 160 sagittal slices using parameters: TR=3200 ms, T2=499 ms and resolution=1 × 1 × 1 mm³. We randomly generated topological errors (including handles and holes) on each cortical surface using the ITK-SNAP Yushkevich et al. (2006) with the help of surface-based rendering. Hence, 65 pairs of tissue-segmented images with simulated topological errors and the corresponding ground truth were obtained, where 15 subjects were randomly selected as the training images, 30 subjects were used as the testing images, and the remaining 20 subjects were selected as the atlas images.

2. Human Infant MRI Dataset with Real Topological Errors: Totally 50 infant brain MR scans from 4 to 15 months of age in the UNC/UMN Baby Connectome Project (BCP) dataset Howell et al. (2019) were collected. T1- and T2-weighted MR images were acquired on 3T Siemens Prisma MRI scanners using Siemens 32 channel head coils. T1-weighted images were acquired with a MPRAGE sequence: TE=2.24 ms, TR=2400/1060 ms, resolution=0.8 × 0.8 × 0.8 mm³. T2-weighted images were acquired with a Space sequence: TE=564 ms, TR=3200 ms, and resolution=0.8 × 0.8 × 0.8 mm³. These images were automatically segmented by the anatomy-guided densely-connected U-Net Wang et al. (2018). After automated segmentation, topological errors on the resulting cortical surfaces were manually corrected by experts to obtain the ground truth by using ITK-SNAP with the help of surface rendering. Finally, 10 subjects were randomly selected as the atlas images, and the remaining 40 subjects were randomly divided as two sets with similar age distribution (each with 20 subjects) for 2-fold cross-validation.

3. Macaque Infant MRI Dataset with Real Topological Errors: To more comprehensively validate the effectiveness of our method, we also included a dataset consisting of 44 macaque infant brain MR scans, which have a similar topology as human brains and are widely used for neuroscience studies. T1-weighted MR images were acquired using a 3T Philips scanner, TE=7.01 ms, TR=14.23 ms, with resolution of 0.375 × 0.375 × 0.5 mm³ Chen et al. (2017). These images were acquired at the ages from 3 months to 18 months. After resampling these images to the resolution of 0.375 ×0.375 ×0.375 mm³, all images were automatically segmented by a conventional machine learning method based on random forests Wang et al. (2015). After segmentation, topological errors on the resulting cortical surfaces were manually corrected by experts by using ITK-SNAP with the help of surface rendering. Finally, 10 images were randomly selected as the atlas images, and the remaining 34 images were randomly divided as two sets with similar age distribution (each with 17 images) for 2-fold cross-validation.

2.2. Topological Defect Localization

Localization of potential topological defect regions is an important step in both the training and testing stages of our proposed method. Specifically, to train an effective AC-U-Net model for topological correction, we should aggressively sample training patches from topological defect regions, instead of randomly sampling them from the whole tissue-segmented images, considering that the regions without topological errors are less relevant to our task. Also, in the testing stage, localizing topological defect regions is beneficial for the efficiency of our proposed method.

Therefore, a shrinking-wrapping topology-preserving level set method Han et al. (2003) is leveraged in our study for topological defect localization, considering it can easily fill all topological errors, and further use the morphological dilation to locate the potential topological defect regions. Specifically, first, the initial zero level set is set as the cerebral hull surface with a spherical topology, which covers all white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) voxels in a hemisphere of the tissue-segmented image. Then, the level set function is gradually evolved and converged to the WM surface, and meanwhile its initial spherical topology is preserved based on the simple point criterion Bertrand (1994); Kong and Rosenfeld (1989); Saha and Chaudhuri (1994). Herein, a voxel is identified as a simple point, when removing it from or adding it to the level set will not change the topology of the object. The volume obtained by the converged level set evolution (denoted as V_LS) can be regarded as the result of a pure hole-filling process performed on the WM volume (denoted as V_WM). As shown in Fig. 3, all hole-like regions (i.e., both holes and handles) on the cortical surface are filled by the topology-preserving level set method, but all handles are also considered as holes and thus incorrectly filled. In terms of V_LS and V_WM, the potential topological defect regions (denoted as V_CAN) are then defined by a XOR operation, i.e., V_CAN = V_LS ⊕ V_WM. Since some located regions are caused by erroneous perforation of WM (i.e., holes in anatomy), while other are spin-off products of the erroneous connections of WM (i.e., handles in anatomy), we finally use a morphological dilation operation to further enroll the neighboring voxels of the located region into V_CAN. In this way, V_CAN is actually a set of to-be-corrected voxels that contains both holes and handles.

Figure 3.

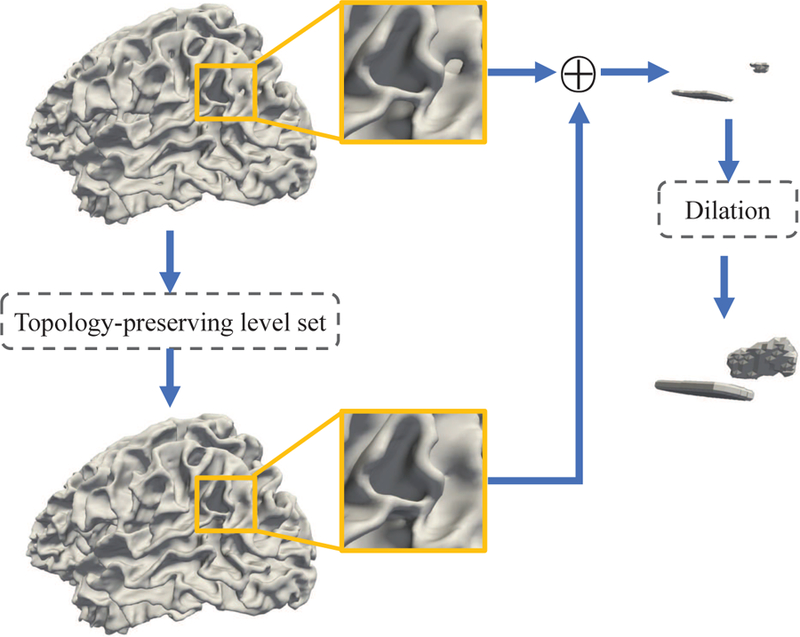
Illustration of locating potential topological defect regions. All hole-like regions are filled by the shrinking-wrapping topology-preserving level set method. Among them, some fixed hole-like regions are erroneous perforation of white matter (holes), and others are spin-off products of the erroneous connection of white matter (handles). We then use a morphological dilation method to further enroll their neighboring candidate voxels into the candidate set. Therefore, both holes and handles are located.

2.3. Anatomically Constrained U-Net

2.3.1. Generation of Training Samples

Let ${\mathbf{I}}_{train}=\{{\mathbf{I}}_1,{\mathbf{I}}_2,\cdots ,{\mathbf{I}}_P\}$ be a set of tissue-segmented images (labeled as WM, GM, and CSF) gathered for network training, and ${\mathbf{L}}_{train}=\{{\mathbf{L}}_1,{\mathbf{L}}_2,\cdots ,{\mathbf{L}}_P\}$ is a corresponding set of manually-corrected tissue-segmented images without topological errors. Notably, we use the hard segmentation map in our experiments, similar to existing methods Shattuck and Leahy (2001); Ségonne et al. (2007). Typically, topological correction is only performed on the WM surface, which has much less partial volume effects, compared to the gray matter surface. Note that, the corrected WM surface, which is not the final WM surface, is then typically used as the initial surface and further deformed to reconstruct the final WM and GM surfaces in existing cortical surface reconstruction methods. The partial volume effects are thus usually considered in the deformation step of surface reconstruction, rather than in the topological correction step. Fig. 4 shows the generation of training samples from a tissue-segmented image. As discussed in Section 2.2, we first apply the shrinking-wrapping topology-preserving level set method to localize potential topological defect regions V_CAN (the red regions in Fig. 4) in each tissue-segmented image I_p. Subsequently, regarding each candidate voxel v in V_CAN as the center, we extract a d × d × d patch x(v) (the orange squares in Fig. 4) from I_p as a training instance, and also extract the corresponding label map y(v) (the yellow squares in Fig. 4) from L_p as the ground truth. Note that, the local patch centered at each candidate voxel encodes local structural information for more reliable correction of this voxel. Finally, we use $\mathbf{X}=\{{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_N|{\mathbf{x}}_i\in R^{d\times d\times d}\}$ and $\mathbf{Y}=\{{\mathbf{y}}_1,{\mathbf{y}}_2,\cdots ,{\mathbf{y}}_N|{\mathbf{y}}_i\in R^{d\times d\times d}\}$ to denote all training image patches and their corresponding label maps extracted from I_train and L_train, respectively.

Figure 4.

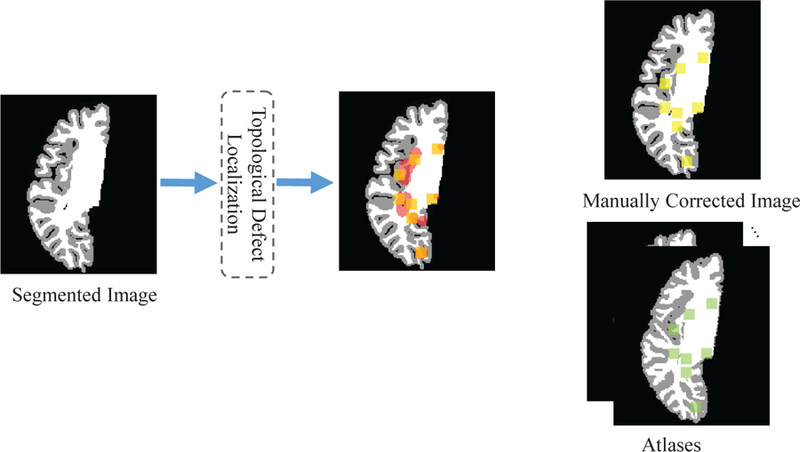
Illustration of the generation of training samples. We first locate topological defect regions (shown in red). Then, we extract the training patches (orange squares), corresponding label maps (yellow squares) and atlas reference patches (green squares) from the located regions.

On the other hand, considering the infant brain MR images exhibit large inter-subject variability in brain structure, we also propose to incorporate anatomical prior from atlas images $\mathbf{A}=\{{\mathbf{A}}_1,{\mathbf{A}}_2,\cdots ,{\mathbf{A}}_K\}$ (without topological error) to facilitate the training of our AC-U-Net model. To this end, each atlas A_k is first affinely registered onto each tissue-segmented image by FLIRT in the FSL toolbox Smith et al. (2004). Then, the affinely-aligned A_k for each tissue-segmented image is further nonlinearly aligned onto the same image using the Diffeomorphic Demons method Vercauteren et al. (2009). Specifically, in the segmented label map, we set intensity values of CSF, GM and WM as 10, 150 and 250, respectively. We then combine the affine transformation matrix and the deformation field as a single nonlinear deformation field. Based on this combined deformation field, we warp and interpolate the label map and further perform thresholding to obtain the deformed label map (i.e., the CSF is in the range of [4, 49], GM is in the range of [50, 180] and the WM is greater than 180). Based on the resulting deformation field, for each to-be-corrected voxel v in each tissue-segmented image, we extract the corresponding reference patch p^k(v) (the green squares in Fig. 4) from the nonlinearly-deformed label map ${\mathbf{L}}_k^A$ of each atlas A_k. As the result, corresponding to X and Y, we get the reference set $\mathbf{R}=\{{\mathbf{r}}_1,{\mathbf{r}}_2,\cdots ,{\mathbf{r}}_N|{\mathbf{r}}_i\in R^{d\times d\times d\times K}\}$, where r_i consists of the atlas reference patches for the i-th training sample, and N and K denote the numbers of training images and atlases, respectively.

2.3.2. Network Architecture

Based on the training dataset consisting of X, Y and R, we learn an AC-U-Net model for topological correction. The architecture of our proposed AC-U-Net is illustrated in Fig. 5. Specifically, each block of the contracting path consists of two convolutional layers and a max-pooling layer to learn the high-level contextual features. Each convolutional operation is performed using 3 × 3 × 3 kernel, followed by batch normalization (BN) and rectified linear units (ReLU). Then, a 2 × 2 × 2 max-pooling operation with stride 2 is used for the down-sampling of convolutional feature maps. Each block of the expanding path consists of one deconvolutional layer and two convolutional layers. The deconvolutional layer is used for up-sampling the low-resolution feature maps to high-resolution feature maps. Also, the output of the deconvolutional layer is first combined with the corresponding high-resolution feature map from the contracting path, which is then used as the input of the subsequent convolutional layer. Due to the skip connection operation, the high-level contextual features and complementary local details can be fused in the network for subsequent operation. In the expanding path, we perform deconvolutional operation with 2 × 2 × 2 kernels, and also convolutional operation with 3 × 3 × 3 kernels. Each convolutional layer is further followed by BN and ReLU. In the final layer, a 1 × 1 × 1 convolution followed by softmax non-linear unit is used to output the probability map $\mathbf{H}=\{{\mathbf{h}}_1,{\mathbf{h}}_2,\cdots ,{\mathbf{h}}_N|{\mathbf{h}}_i\in R^{d\times d\times d\times C}\}$ for $\mathbf{X}=\{{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_N|{\mathbf{x}}_i\in R^{d\times d\times d}\}$, where C is the number of tissue categories. Typically, each tissue-segmented image has four labels, i.e., WM, GM, CSF and background (BG). Therefore, the output probability map has four channels in our work, where each channel corresponds to the probability of the respective tissue type. More implementation details of the network architecture can be found in the Supplementary Materials.

Figure 5.

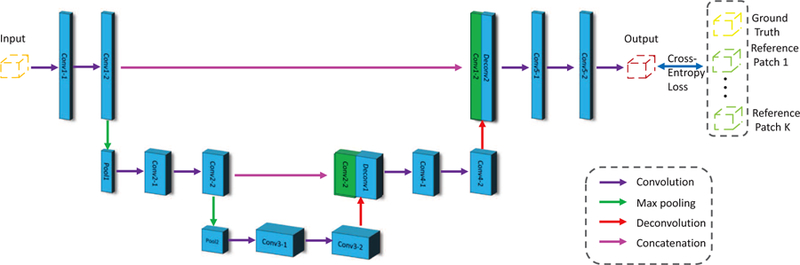
The architecture of our proposed Anatomically Constrained U-Net (AC-U-Net) method. The purple, green, red and peach arrows represent the convolution, max pooling, deconvolution, and concatenation operations, respectively. The orange, red, yellow and green patches represent the input, output, ground truth and atlas reference, respectively.

2.4. Hybrid Loss Function

We propose a hybrid loss function to train our AC-U-Net model illustrated in Fig. 5, which consists of the penalties in terms of both the ground truth and the atlas-based anatomical prior information. Specifically, based on the manually-corrected label map (i.e., the ground truth), a cross-entropy loss to learn automated topological correction is defined as

$$L_{GT}=-\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^{d^3}\sum _{c=1}^C\delta (y_{i,j}=c)\log h_{i,j,c}$$ (1)

where δ(y_i,j = c) is a Dirac function, which equals to 1 when y_i,j = c and 0 otherwise. Scalar h_i,j,c represents the probability of the j-th voxel in the i-th patch belonging to the c-th category.

However, training the network using solely the manually-corrected label maps may be not adequate. This is mainly because 1) infant brain MR images exhibit extremely low tissue contrast and dynamically changing image appearances and brain size and shape along time; 2) infant MR images suffer large inter-subject variability. Inspired by the fact that multi-atlas methods have been successfully applied in medical image segmentation, especially for the images with low tissue contrast and large inter-subject variability, we also include atlas-based prior knowledge as an anatomical guidance to reinforce the learning process in our task. Therefore, the loss in terms of the atlas prior knowledge for the training of our AC-U-Net is defined as

$$L_{MA}=-\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^{d^3}\sum _{c=1}^C\sum _{k=1}^K\delta (p_{i,j,k}=c)\log h_{i,j,c}$$ (2)

Hence, based on Eq. 1 and Eq. 2, the hybrid loss function used in this paper is defined as

$$L=L_{GT}+\frac{\lambda }{K}{L}_{MA}$$ (3)

where the tuning-parameter λ balances the losses from the ground truth and anatomical references. By minimizing Eq. 3, we can effectively infer conceivable structures of topological defect regions under anatomical constraint.

It is worth noting that, the second term of Eq. 3 actually reflects the degree of ambiguity concerning the tissue labels of local patches. Specifically, we assume a voxel has an explicit label, if the ground-truth label of this voxel is consistent with reference labels on the atlases (i.e., reference voxels in atlases have the same label); otherwise, we assume this voxel has an ambiguous label. Hence, the first term in Eq. 3 can be regarded as a hard term, while the second term can be regarded as a flexible term to make the loss function fuzzy for providing a flexible solution on the prediction. In detail, Eq. 3 can be reformulated as

$$L=-\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^{d^3}\sum _{c=1}^C[\delta (y_{i,j}=c)+\frac{\lambda }{K}\sum _{k=1}^K\delta (p_{i,j,k}=c)]\log h_{i,j,c}$$ (4)

Using F_i to represent $\delta (y_{i,j}=c)+\frac{\lambda }{K}{\sum }_{k=1}^K\delta (p_{i,j,k}=c)$ in Eq. 4, we can further normalize F_i to the range of [0, 1] by using a constant, i.e.,

$$F_i^{\text{'}}=\frac{1}{1+\lambda }{F}_i$$ (5)

where the constant term $\frac{1}{1+\lambda }$ is determined by the balance parameters λ. As a result, F_i can be regarded as a soft label for the i-th patch, which is calculated based on the manually-corrected label and the anatomical prior (i.e., the labels of the atlases). Specifically, if λ = 0, the proposed model turns to be a conventional U-Net trained using only hard labels. More details of the above analysis can be found in the Supplementary Materials.

2.5. Iterative Scheme for Topological Correction

In the testing stage, as shown in Fig. 2, given a tissue-segmented image I_test, we first locate the potential topological defect regions via the procedure described in Section 2.2. Then, we extract a d × d × d patch centered at each candidate voxel and infer the probability maps for the extracted patches using the trained AC-U-Net introduced in Section 2.3. Notably, since we have integrated the anatomical constraints into the hybrid loss function during the training stage, there is no more need of any registration step in the topological correction stage (i.e., the testing stage). Due to this property, our method is much more efficient than the SDLM method Hao et al. (2016), and avoids the negative influence of registration errors on the correction of unseen subjects. As each candidate voxel in the localized topological defect regions may be contained in multiple to-be-corrected patches, we calculate the label probability of each voxel by weighted voting across all extracted patches that contain this voxel. Thus, the probability of l_v = c is calculated as

$$p(l_v=c)=\frac{1}{V}\sum _i^{V}p(l_v=c|r_i)$$ (6)

where p(l_v = c|r_i) is the probability of l_v = c that is provided by the to-be-corrected patch centered at voxel r_i. The scalar V is the number of to-be-corrected patches containing the voxel v. Finally, we use the MAP criterion to obtain the new label for each candidate voxel, i.e., arg max_c p(l_v = c).

Nevertheless, the infant cortical surfaces often contain many large and complex handles and holes, which are usually very difficult to be completely corrected using only one operation. As shown in Fig. 2, we further incorporate 1) locating topological defect regions and 2) correcting topological defect regions using the trained AC-U-Net model with a fixed patch size into an iterative framework. By iteratively repeating these steps, large topological defect regions will be gradually corrected. After the iterative correction by our AC-U-Net model, we further used the topology-preserving level-set method Han et al. (2003) to ensure that the corrected cortical surface has a spherical topology. This is achieved by gradually deforming the convex hull surface with a spherical topology to the WM surface, and during this final step all the remaining topological errors will be considered as holes and are thus filled.

3. Experiments

3.1. Experimental Settings

In our experiments, the proposed AC-U-Net model was implemented by TensorFlow Abadi et al. (2016). To train our network, we randomly selected 10, 000 patches from the located topological defect regions in each training image. The patch size was kept constant as 19×19×19 across all experiments in this work. The atlas number was set as 10, the tuning-parameter λ in the proposed hybrid loss function set as 0.5 and the number of epochs was set as 10, which consists of 15, 000, 20, 000 and 17, 000 iterations per epoch for human infant data with simulated topological errors, human infant data with real topological errors and macaque infant data with real topological errors, respectively. We empirically set the mini-batch size as 10 and the learning rate as 0.001, respectively.

Using the manual correction as the ground truth, three complementary metrics, i.e., 1) successful rate (SR), 2) Dice ratio (DR), and 3) average surface distance (ASD), were used in our experiments to quantitatively assess the performance of automated topological correction methods. Specifically, SR quantifies the proportion of topological defects that are successfully identified and corrected, i.e., the correct distinction between holes and handles, and the correct filling of holes and breaking of handles. The DR and ASD are defined as

$$DR=\frac{2\times \left|W_1\cap W_2\right|}{\left|W_1\right|+\left|W_2\right|}$$ (7)

$$\begin{gathered} ASD=\frac{1}{2}(\frac{1}{n_1}\sum _{w_1\in S(W_1)}d(w_1,S(W_2)) \\ \hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{1}{n_2}\sum _{w_2\in S(W_2)}d(w_2,S(W_1))) \end{gathered}$$ (8)

where W₁ and W₂ denote a WM volume corrected by an automatic method and the corresponding WM volume manually corrected by an expert (i.e., the ground truth), respectively. It is worth mentioning that, when computing DR and ASD, we only used the localized topological defect regions to better reflect the performance of different methods. In Eq. 7, the operator $|\cdot |$ calculates the number of voxels. In Eq. 8, the function $d(\cdot ,\cdot )$ measures the Euclidean distance, and n₁ and n₂ are the numbers of vertices on the surfaces S(W₁) and S(W₂), respectively.

3.2. Competing Methods

On the human infant dataset with simulated topological errors, we compared our proposed AC-U-Net method with the U-Net based method (without anatomical constraint) and the sparse dictionary learning method Hao et al. (2016), i.e., SDLM, which is designed for topological correction on the infant cortical surfaces. Among them, the U-Net based method also uses our topology-preserving level set method for locating topological defect regions, and further infers new labels by the U-Net. For a fair comparison, the U-Net based method was implemented to have the same network structure and optimization parameters as our proposed AC-U-Net.

On the human and macaque infant datasets with real topological errors, we still compared our AC-U-Net with the original U-Net (without anatomical constraint) and SDLM. Meanwhile, we also compared our AC-U-Net with two popular topological correction algorithms integrated in two widely-used software packages, i.e., BrainSuite Shattuck and Leahy (2001) and FreeSurfer Ségonne et al. (2007). Besides, we further compared our proposed method with the topology-preserving level set method (TPLS) Han et al. (2003), considering that it was used to locate the topological defect regions in our proposed method.

3.3. Results on the Human Infant MRI Dataset with Simulated Topological Errors

On the human infant data with simulated topological errors, our proposed AC-U-Net method was compared with the original U-Net and the SDLM method. The quantitative comparison results are summarized in Table 1, from which we can have at least two observations. First, the deep learning-based methods (i.e., U-Net and our AC-U-Net) consistently outperform the traditional learning-based method (i.e., SDLM), which indicates the effectiveness of deep learning methods in this specific task of topological correction on infant cortical surfaces. For example, the DR values for the original U-Net and our AC-U-Net are 98.65 ± 0.79% and 98.83 ± 0.33%, respectively, which are significantly better than the SDLM method with 92.91 ± 1.60% (p < 1.0e − 10 based on the paired t-test with AC-U-Net and U-Net, respectively). Second, our proposed AC-U-Net method is superior to the original U-Net in terms of all evaluation metrics. This implies that incorporating additional anatomical guidance provided by the multiple atlas images can effectively improve topological correction results.

Table 1:

Quantitative comparison with other topological correction methods on human infant MRI dataset with simulated topological errors.

Method	SR	DR (mean ± std)	ASD (mean ± std)
SDLM	96.70%	92.91 ± 1.60%	0.105 ± 0.025 mm
U-Net(ours)	97.80%	98.65 ± 0.79%	0.022 ± 0.014 mm
AC-U-Net(ours)	98.35%	98.83 ± 0.33%	0.018 ± 0.006 mm

3.4. Results on the Human Infant MRI Dataset with Real Topological Errors

On the infant cortical surfaces with real topological defects, we compared our proposed AC-U-Net with BrainSuite, Freesurfer, TPLS, SDLM, and the original U-Net. The quantitative and qualitative results are shown in Table 2 and Fig. 6, respectively.

Table 2:

Quantitative comparison with other topological correction methods on human infant MRI dataset with real topological errors. The symbol * indicates our proposed AC-U-Net method is significantly better than the competing methods (p < 0.05) based on the paired t-test in terms of DR.

Method	SR	DR (mean ± std)	ASD (mean ± std)
*Brainsuite	15.63%	97.30 ± 1.71%	0.031 ± 0.021 mm
*FreeSurfer	83.04%	85.59 ± 3.16%	0.203 ± 0.079 mm
*TPLS	84.38%	97.42 ± 1.67%	0.031 ± 0.024 mm
*SDLM	90.63%	93.67 ± 1.60%	0.063 ± 0.029 mm
*U-Net(ours)	91.52%	97.63 ± 1.37%	0.024 ± 0.015 mm
AC-U-Net(ours)	92.41%	98.78 ± 0.78%	0.013 ± 0.010 mm

Figure 6.

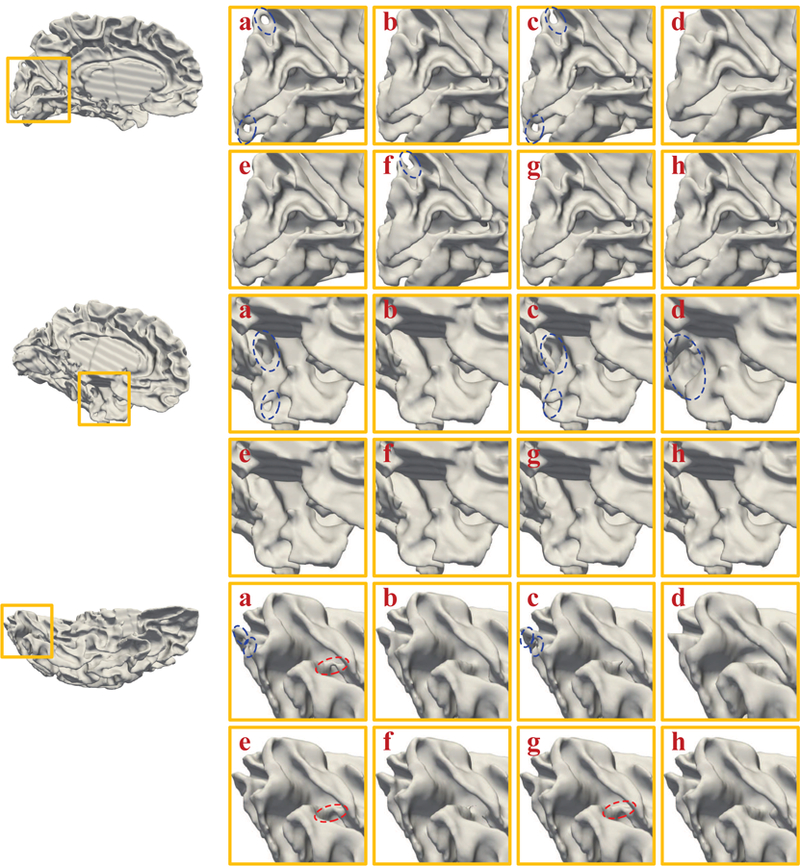
Visual inspection of the original white matter surfaces (a), manually corrected surfaces (b), BrainSuite corrected surfaces (c), FreeSurfer corrected surfaces (d), TPLS corrected surfaces (e), SDLM corrected surfaces (f), U-Net (ours) corrected surfaces (g), and AC-U-Net (ours) corrected surfaces (h) on human infant MRI dataset with real topological errors. The red and blue circles represent handles and holes, respectively.

In terms of the SR presented in Table 2, we can find that, compared with other methods, our AC-U-Net method achieves the best result. The SR obtained by our AC-U-Net is 92.41%, which is higher than 15.63% obtained by BrainSuite, 83.04% by FreeSurfer, 84.38% by TPLS, 90.63% by SDLM and 91.52% by U-Net. BrainSuite and FreeSurfer have relatively poor performance, since they were primarily designed for adult brain analysis, and thus could not properly handle specific challenges for the infant cortical surfaces.

On the other hand, in terms of the DR and ASD summarized in Table 2, we can also observe that the automated correction obtained by our proposed method is anatomically more consistent with the ground truth than other competing methods. We also performed the paired t-test in terms of DR, and the symbol * in Table 2 indicates that our proposed AC-U-Net method performs significantly better than the competing methods (p < 0.05). All quantitative results suggest that our proposed method can effectively correct topological defects and achieve high anatomical accuracy on the infant cortical surfaces.

Also, we show the illustrative topological correction results obtained by six competing methods in Fig. 6. The red circles and blue circles in Fig. 6 indicate handles and holes, respectively. These illustrative results further indicate the superior performance of our proposed method. The training and testing loss curves of the proposed AC-U-Net are shown in Fig. 7. We calculated the average training loss per epoch and the average testing loss on 10, 000 testing patches per epoch. We can observe from Fig. 7 that the training and testing loss can be converged, which contains 20, 000 iterations per epoch.

Figure 7.

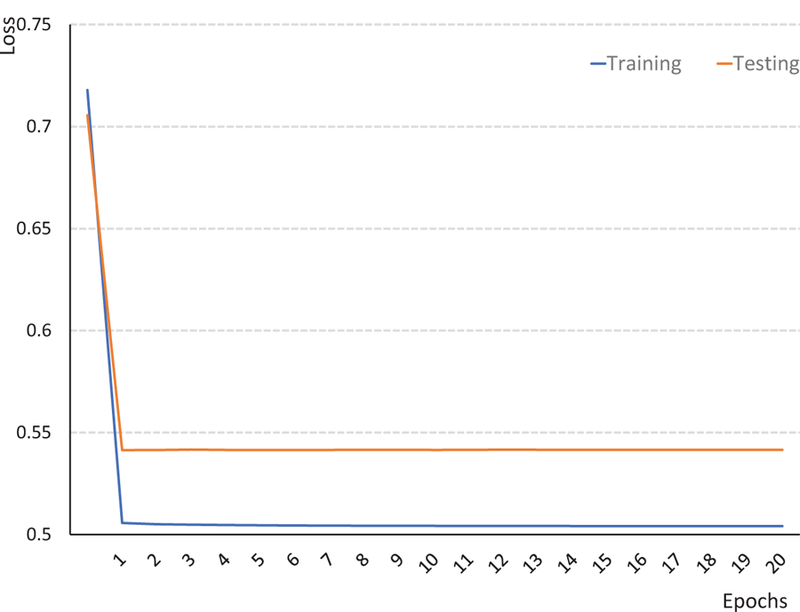
The curves of training and testing loss of our AC-U-Net model on human infant data with real topological errors.

BainSuite tends to simply break topological defects, which ignores the fact that many topological defects on infant cortical surfaces are holes. However, due to the minimal correction criterion, BrainSuite only modifies a small number of voxels in the tissue-segmented image and meanwhile the majority of voxels in tissue-segmented image is not related to topological errors. Hence, the corrected image by BrainSuite is close to the ground truth in terms of DR and ASD. In contrast, FreeSurfer often breaks big holes and removes their adjacent voxels on the infant cortical surfaces, which leads to large errors in terms of DR and ASD on the cortical surface (as shown is Fig. 6). Therefore, FreeSurfer achieves poor results in terms of DR and ASD. The TPLS method performs worse than the SDLM, the original U-Net, and our proposed AC-U-Net, since it improperly fills all topological defects on the cortical surfaces, thus failing to correct handles. Consistent with the conclusion drawn on the simulated data, our proposed AC-U-Net also outperforms the SDLM method and the original U-Net in this experiment.

3.5. Results on the Macaque Infant MRI Dataset with Real Topological Errors

To further validate the effectiveness of our AC-U-Net method, we also compared it with BrainSuite, FreeSurfer, TPLS, SDLM, and U-Net for correction of real topological errors on the macaque infant cortical surfaces. Table 3 shows the topological correction results obtained by six competing methods. As can be seen, our proposed AC-U-Net achieves the best topological correction results on the monkey cortical surfaces, as the SR, DR, and ASD are 96.30%, 98.84 ± 1.08%, and 0.0030 ± 0.0042 mm, respectively. We further performed the paired t-test in terms of DR. It can be observed that our proposed AC-U-Net shows significant improvement (p < 0.05) over BrainSuite, FreeSurfer, TPLS, SDLM and U-Net, as indicated by ‘*’ in Table 3. These results imply the good generalization ability of our proposed methods.

Table 3:

Quantitative comparison with other topological correction methods on macaque infant MRI dataset with real topological errors. The symbol * indicates our proposed AC-U-Net method is significantly better than the competing method (p < 0.05) based on the paired t-test in terms of DR.

Method	SR	DR (mean ± std)	ASD (mean ± std)
*Brainsuite	31.48%	97.82 ± 1.88%	0.0065 ± 0.0067 mm
*Freesurfer	79.63%	90.63 ± 3.79%	0.0239 ± 0.0106 mm
*TPLS	68.52%	98.02 ± 1.96%	0.0061 ± 0.0069 mm
*SDLM	92.59%	93.48 ± 1.45%	0.0156 ± 0.0039 mm
*U-Net(ours)	94.44%	97.79 ± 2.30%	0.0066 ± 0.0083 mm
AC-U-Net(ours)	96.30%	98.84 ± 1.08%	0.0030 ± 0.0042 mm

4. Discussion

In this section, we first investigate the sensitivity of the proposed method with respect to the number of atlases, the number of iterations for topological correction, and the tuning-parameter λ in Eq. 3. Then, we present the robust analysis and time analysis of our proposed method. Finally, we present the limitations of the current work and possible future research directions.

4.1. Impact of the Number of Atlases

The number of atlases is an important parameter for our proposed method. Using the infant dataset with simulated topological errors as an example, we evaluated the performance of our AC-U-Net method with respect to different number of atlases, i.e., [0, 5, 10, 15, 20]. Notably, our AC-U-Net degenerates to the original U-Net, when the number of atlases is 0. It is worth noting that, independent of the varying numbers of atlases, the numbers of training and testing images were kept the same in Section 3.3. Table 4 shows the quantitative results in terms of different numbers of atlases. We can observe that the best performance is obtained when the atlas number is around 10. The results also indicate that incorporating an appropriate number of atlases will increase the performance of our proposed method, while too many atlases will increase the ambiguity of the trained model, which may potentially hamper the performance of our proposed method. Hence, for the remaining evaluations on the human infant MRI dataset with real topological errors and the macaque infant MRI dataset with real topological errors, we set the atlas number as 10 for our AC-U-Net method.

Table 4:

Impact of the number of atlases on human infant MRI dataset with simulated topological errors.

Atlas Number	SR	DR(mean ± std)	ASD(mean ± std)
0	97.80%	98.65 ± 0.79%	0.022 ± 0.014mm
5	97.91%	98.75 ± 0.38%	0.020 ± 0.008mm
10	98.35%	98.83 ± 0.33%	0.018 ± 0.006mm
15	97.91%	98.44 ± 0.32%	0.025 ± 0.006mm
20	97.91%	98.34 ± 1.53%	0.028 ± 0.009mm

4.2. Impact of the Number of Iterations

As infant cortical surfaces often contain large holes and handles, it is very difficult to correct these topological errors by one-shot correction. Hence, in Section 2.5, we propose an iterative scheme, where the steps of localization of topological defect regions and topological correction by the trained AC-U-Net are alternatively performed to gradually correct large topological errors on the infant cortical surfaces. To evaluate the impact of the number of iterations on the performance of our proposed method, we orderly set it as 1, 2, 3 and 4, and applied the resulting model to all three datasets, respectively. The corresponding results are summarized in Fig. 8. From Fig. 8, we can observe that the performance of our proposed method typically converged at the third iteration, which is largely consistent across different datasets. We also visualize topological correction results on simulated dataset in Fig. 9, based on which we can observe that the big handles are gradually broken since the second iteration.

Figure 8.

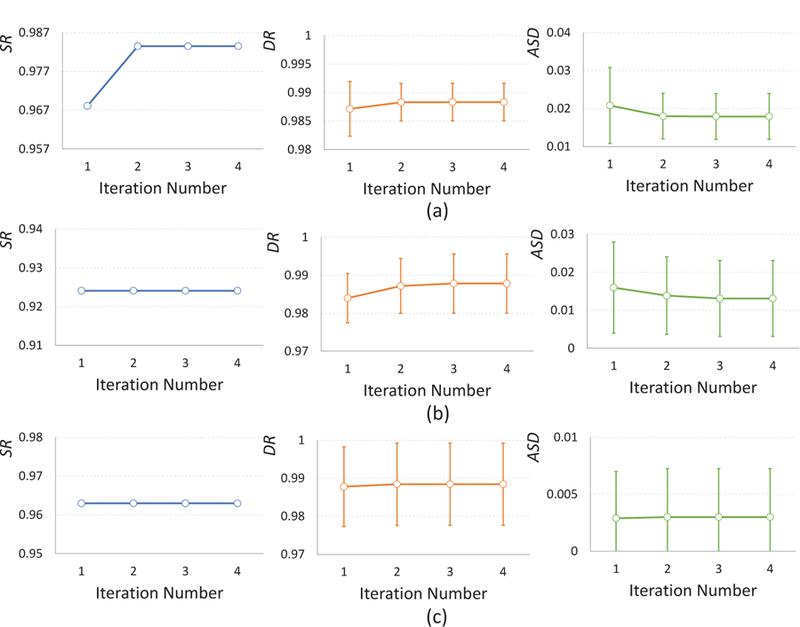
Impact of the number of iterations on the infant MRI dataset with simulated topological errors (a), human infant MRI dataset with real topological errors (b) and the macaque infant MRI dataset with real topological errors (c), respectively.

Figure 9.

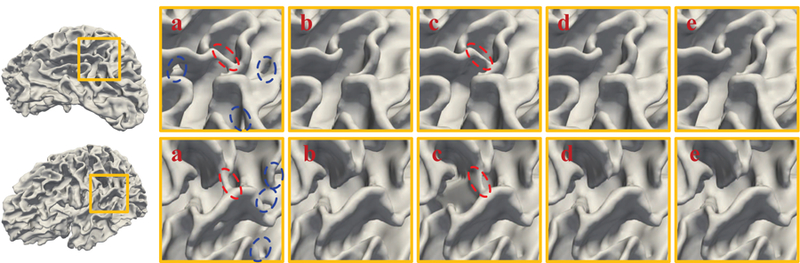
Visual inspection of the original white matter surfaces (a), manually corrected surfaces (b), and AC-U-Net corrected surfaces at the 1^st iteration (c), 2^nd iteration (d), and 3^rd iteration (e) on human infant MRI dataset with simulated topological errors, respectively. The red and blue circles represent handles and holes, respectively.

4.3. Impact of Parameter λ

The parameter λ in Eq. 3 is used to balance the contributions of the loss from the ground truth and from the atlas images. Therefore, we also investigated the effect of the parameter λ, by orderly choosing its value from the set [0.1, 0.25, 0.5, 0.75, 1.0]. Fig. 10 (a) shows the quantitative results (in terms of SR, DR and ASD) achieved by our proposed method with different values of λ on the infant dataset with simulated topological errors. We can observe from Fig. 10 (a) that our proposed AC-U-Net achieves promising results with λ ∈ [0.5, 1]. For simplicity, we empirically set λ = 0.5 in the experiments.

Figure 10.

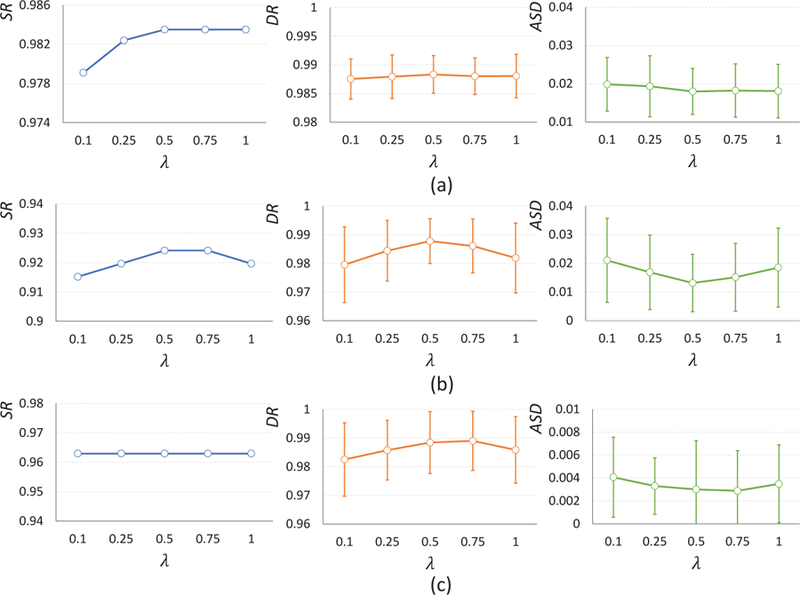
Impact of the parameter λ on the infant MRI dataset with simulated topological errors (a), human infant MRI dataset with real topological errors (b) and the macaque infant MRI dataset with real topological errors (c), respectively.

We also validated the impact of λ for topological correction on the human infant and macaque infant datasets with real topological errors. Figures 10 (b) and 10 (c) show the results yielded by AC-U-Net with different values of λ on these two datasets, respectively. We can see that the proposed AC-U-Net also achieved competitive results with λ = 0.5 on these two datasets, which is consistent with the conclusion drawn on the infant dataset with simulated topological errors.

4.4. Robustness Analysis

We calculated the 20% trimmed mean of DR and ASD (excluding the 10% highest and 10% lowest results) to assess the robustness of our proposed method on the three different datasets, respectively. According to the results presented in Table 5, we can observe that our AC-U-Net is consistently less prone to outliers than the original U-Net across all datasets. These results suggest that incorporating the anatomical prior knowledge did improve the robustness of our proposed method.

Table 5:

The trimmed mean results of Dice ratio and average surface distance on the infant MRI dataset with simulated topological errors (simulated), human infant MRI dataset with real topological errors (human infant) and the macaque infant MRI dataset with real topological errors (macaque infant), respectively.

	Simulated		Human infant		Macaque infant
	Trimmed DR	Trimmed ASD	Trimmed DR	Trimmed ASD	Trimmed DR	Trimmed ASD
U-Net	98.79%	0.019 mm	97.79%	0.022 mm	98.16%	0.0049 mm
AC-U-Net	98.85%	0.017 mm	98.82%	0.012 mm	98.96%	0.0024 mm

4.5. Time Analysis

In Table 6, we summarize the times used by our proposed method and other competing methods for topological correction. BrainSuite and TPLS only need 14.9 seconds and 4.9 minutes for a subject, respectively. Since our proposed method is an iterative method, the consumed time is 28.6 minutes with 3 iterations for each subject. The consumed times for FreeSurfer and SDLM are 36.2 minutes and 202.5 minutes, respectively. Although our proposed method is slower than BrainSuite and TPLS, our successful rate is much higher. Compared with FreeSurfer and SDLM, our proposed method is not only faster, but also achieves better topological correction performance.

Table 6:

Time consuming analysis of different topological correction methods on simulated data.

	Brainsuite	FreeSurfer	TPLS	SDLM	AC-U-Net
Times	14.9 sec	36.2 min	4.9 min	202.5 min	28.6 min

4.6. Limitations and Future Work

Although the proposed AC-U-Net method works well for topological correction on the infant MR images in all presented experiments, there are still several limitations in current work. First, in our current implementation, we extract reference patches for each to-be-corrected voxel from the same location at the atlas images. It would be interesting to use the non-local mean strategy Coupé et al. (2011); Zhang et al. (2012) for extraction of reference patches, considering possible registration errors. Second, we use the topology-preserving level-set method to locate topological defect regions, which is time-consuming. As another future work, we plan to develop a faster method for localization of topological defect regions. Third, we use the U-Net architecture for topological correction, and other deep learning architectures could also be employed by integrating the proposed anatomical constraint. Besides, due to the huge differences in terms of brain size, shape and cortical folding between the human and macaque infant images (as shown in Figs. S1–S3 of Supplementary Materials), it is very difficult to directly apply the model trained on human brain images to correct topological errors on macaque images. Also, as two human datasets have large differences in imaging resolutions, anatomical details, segmentation methods, topological errors, and developmental stages with rapid brain growth, it is not very appropriate to simply apply the model trained in one dataset to another one. However, we would like to mention that, compared with the conventional U-Net, our proposed AC-U-Net showed superior performance of topological correction on both datasets with large time span.

5. Conclusion

In this paper, we have proposed an anatomically-constrained U-Net (AC-U-Net) for topological correction of the infant cortical surfaces. Specifically, in the training stage, we located topological defect regions by leveraging a topology-preserving level set method and sampled informative training sample patches from the located regions. We also used anatomical prior knowledge from a set of atlases without topological errors to improve the effectiveness of the trained network. In the testing stage, we designed an iterative scheme based on the topology-preserving level set method and the trained AC-U-Net model to correct large complicated topological errors on unseen infant cortical surfaces. To the best of our knowledge, we are the first to leverage a deep learning method for infant cortical topological correction. We have comprehensively validated our proposed method on three different datasets. Experimental results have shown superior performance of our proposed method, compared with the state-of-the-art methods. Notably, our proposed method has good generalization capacity, as it has also been successfully applied to the macaque infant brain MR images.