Neuronal Modulation in the Prefrontal Cortex in a Transitive Inference Task: Evidence of Neuronal Correlates of Mental Schema Management

Abstract

When informed that A > B and B > C, humans and other animals can easily conclude that A > C. This remarkable trait of advanced animals, which allows them to manipulate knowledge flexibly to infer logical relations, has only recently garnered interest in mainstream neuroscience. How the brain controls these logical processes remains an unanswered question that has been merely superficially addressed in neuroimaging and lesion studies, which are unable to identify the underlying neuronal computations. We observed that the activation pattern of neurons in the prefrontal cortex (PFC) during pair comparisons in a highly demanding transitive inference task fully supports the behavioral performance of the two monkeys that we tested. Our results indicate that the PFC contributes to the construction and use of a mental schema to represent premises. This evidence provides a novel framework for understanding the function of various areas of brain in logic processes and impairments to them in degenerative, traumatic, and psychiatric pathologies.

SIGNIFICANCE STATEMENT In cognitive neuroscience, it is unknown how information that leads to inferential deductions are encoded and manipulated at the neuronal level. We addressed this question by recording single-unit activity from the dorsolateral prefrontal cortex of monkeys that were performing a transitive inference (TI) task. The TI required one to choose the higher ranked of two items, based on previous, indirect experience. Our results demonstrated that single-neuron activity supports the construction of an abstract, mental schema of ordered items in solving the task and that this representation is independent of the reward value that is experienced for the single items. These findings identify the neural substrates of abstract mental representations that support inferential thinking.

Introduction

An inferential process allows individuals to anticipate the result of a grand slam tennis match, based on the known international ranks of the players. When premises that are related to the previous performance of the opponents are available, a conclusion can be drawn without direct experience.

Transitive inference (TI) has been used in various forms to study inferential problem-solving and knowledge manipulation in humans and other animals (Bryant and Trabasso, 1971; Paz-y-Miño et al., 2004; Libben and Titone, 2008; Brunamonti et al., 2011; Merritt and Terrace, 2011; Mou et al., 2014). In a typical TI task, participants are first required to learn, by trial and error, the relationship between multiple premises that share overlapping elements (e.g., A > B, B > C, C > D, D > E, and E > F in the series A-B-C-D-E-F). Then, when never-experienced pairs (e.g., B vs D) are presented, subjects are asked to select the higher-ranked item using transitive processes (Merritt and Terrace, 2011; Brunamonti et al., 2014).

Two effects characterize typical performance in the test phase of TI: the symbolic distance effect (SDE) and the serial position effect (SPE). SDE corresponds to the linear increase in performance as a function of the distance between the ranks of the items that form each pair (e.g., comparing B with E is easier than comparing B with C). SPE refers to the significant decline in inferential performance for comparisons that include the middle items of the series and is also observed for learned pairs (e.g., CD in the test phase elicits poorer performance compared with AB or EF). Together, these behavioral effects are often proposed as signatures of how knowledge is mentally organized and manipulated to make logical inferences between related facts (Merritt and Terrace, 2011; Gazes et al., 2012; Zeithamova et al., 2012b). During learning, the acquired knowledge is hypothesized to be integrated in a spatially oriented mental schema (Merritt and Terrace, 2011; Zeithamova et al., 2012a; Preston and Eichenbaum, 2013; Gazes et al., 2014).

At the neural level, it remains unknown how the brain supports the mental schema formation that underlies transitive comparisons. The little data that exist have been derived primarily from lesion and functional brain imaging studies in humans and animal models (Dusek and Eichenbaum, 1997; Waltz et al., 1999; Acuna et al., 2002; Van der Jeugd et al., 2009; De Vito et al., 2010; Koscik and Tranel, 2012). These reports have provided information on the gross neuroanatomy that is involved in logical reasoning and the timing of activation of various areas of the brain during TI (Goel, 2007; Van Opstal et al., 2008; Wendelken and Bunge, 2010). However, no study has described the neural computations that underlie this function. Current findings suggest that several brain areas support TI, including the hippocampus and prefrontal cortex (PFC; Goel, 2007; Zeithamova et al., 2012b). Specifically, the PFC appears to manage the mental schema that is used to extract the conclusion of the inferential process that is tested (Zeithamova et al., 2012a; Preston and Eichenbaum, 2013). This evidence has led to the hypothesis that if the PFC supports the formation and manipulation of a mental schema, the modulation of neural activity in this area should parallel the principal behavioral effects that are observed in the TI task.

To test this hypothesis, we studied the activity of single neurons of the PFC in two macaque monkeys that were performing a TI task (Brunamonti et al., 2014). We found that their response patterns correlated with the SPE and SDE, suggesting that they contribute to the neural underpinning of the formation of the mental schema. Similarly, observing the neuronal modulation during all pair comparisons, we estimated the shape of the tuning of the mental representation of the ranked items. The shape of the tuning curves, which rarely coded for items at the extremes of the series, suggests a mental schema that is based on the relative value of items rather than on reward-driven activation and reinforcement.

Materials and Methods

Subjects.

Two male rhesus monkeys (Macaca mulatta), weighing 5.50 kg (Monkey 1) and 6.50 kg (Monkey 2), were tested on a TI task (Fig. 1A), based on a ranked series of nonsense stimuli while neural (single unit) activity was recorded, extracellularly targeting the dorsal portion of the PFC (dPFC) and using a five-channel multielectrode system (Thomas Recording). The recording chambers were surgically implanted over the left frontal lobe at known stereotaxic coordinates (anterior: 32, lateral: 19 in Monkey 1; anterior: 30, lateral: 18 in Monkey 2), with head restraint devices. The locations of the electrodes in the PFC were confirmed at the end of the neurophysiological experiments by structural MRI (Monkey 2) or visual inspection after surgical opening of the dura during the implantation of a chronic array (Monkey 1). All surgical procedures were performed using aseptic techniques under general anesthesia (1–3% isoflurane-oxygen, to effect).

Figure 1.

TI task and behavioral performance. A, Time sequence of the task during the learning and test blocks. The gray bars indicate the analysis epochs. Top, Sample of rank-ordered stimuli at the beginning of a daily experimental session. B, Schematic of all 15 possible combinations of item pairs, labeled as learned (white boxes) or novel (filled boxes). C, Average performance on all pairs during the test phase for both animals in all sessions. The gray region highlights data referring to novel pairs. Error bars are SE.

Animal care, housing, and experimental procedures conformed to European (Directive 210/63/EU) and Italian (DD.LL. 116/92 and 26/14) laws on the use of nonhuman primates for scientific research. The research protocol was approved by the Italian Health Ministry (Central Direction for the Veterinary Service). The housing conditions and experimental procedures were established per the Weatherall report (use of nonhuman primates in research).

Test stimuli and task design.

We constructed a set of 80 stimuli (black and white bitmaps, 16° × 16° visual angle), consisting of abstract images. Each stimulus had the same proportion of white area over a black background. During each session, the monkeys were required to learn the relationships between 6 new items, which were selected from the original set of 80 and randomly rank-ordered by one of the authors (Fig. 1A, top). The same item was never assigned an identical rank between sessions and was never repeated until sufficient time had passed. The stimuli that constituted the series were changed daily to avoid providing a simple solution that was based on symbol familiarity and absolute knowledge (Guez and Audley, 2013).

Each session comprised two learning phases and a test phase. During the learning phases, the monkeys had to learn the relationships between the 6 ranked items; during the test phase, they had to use that knowledge to solve inference problems. In the initial learning phase, pairs of items with adjacent ranks (Fig. 1B, learned) were presented sequentially to the monkey. For each pair, the animal had to identify the rewarded item by trial and error in blocks of 15 (Monkey 1) or 20 (Monkey 2) trials. We repeated the block until the percentage of correct responses was at least 90% for the pair. Then, the next pair was presented per the same rules.

Once the animal reached the learning criterion of a 90% correct choice rate for all pairs, it advanced to the second step of the learning phase, which involved larger blocks of trials. In this phase, all five previously experienced pairs were presented in random order. A different learning criterion (>60% correct trials) was used, and additional blocks of trials were presented until this threshold was reached. A key piece of information that was provided to the animals during learning was that an item (with the exclusion of those at the extremes of the series) had a disparate value, depending on the item with which it was simultaneously presented (e.g., C was always reinforced when presented with D but never when presented with B).

During the test phase, the monkeys were tested in a block of at least 14 trials for each problem. Both learned pairs and novel pairs were presented (Fig. 1B), and monkeys were required to generalize the basic rules. For novel pairs, the monkeys had to infer the correct response by referring to the rank order representation of the items that were acquired during the learning phase (e.g., in the pair BE, concluding that the reinforced target is B due to the relationship of B and E with the adjacent C and D, respectively).

The behavioral task was administered using the Cortex software package (dally.nimh.nih.gov) to control the visual display on which the stimuli were presented and a touchscreen (MicroTouch, sampling rate of 200 Hz) that was connected to a PC by a serial port to detect the choice. An RX6 TDT system (Tucker-Davis Technologies), synchronized to the behavioral events, detected the neural activity during each behavioral trial and recorded eye position signals. We used the learning time to isolate single neurons; neural activity was recorded only during the test phase. Eye movements were monitored and recorded using an infrared tracking system (Arrington Research) at sampling rate of 220 Hz.

The structure of each behavioral trial was identical for the learning and test phases (Fig. 1A, bottom). The beginning of each trial was signaled by the appearance of a red spot (13.5° × 13.5° visual angle) at the center of the screen. The monkeys had 5 s to push a button in front of them to start the task; otherwise, the trial was aborted. Two hundred milliseconds after the button was pushed, a pair of items was presented for a variable epoch (referred to here as delay; Fig. 1A), after which the central red spot vanished (Go signal), and the monkeys indicated which item of the pair was higher in rank (target item; i.e., the one that was associated with the reward) by touching it on the monitor. Each target item of a pair was randomly presented to the left or right of the central spot. The duration of the delay in the learning phases was always 0, whereas in the test phases, it varied randomly between 600 and 1200 ms.

Behavioral and neuronal correlates of SPE and SDE.

The SDE and SPE characterize one's performance on a TI task. The SDE predicts that performance improves as the difference in the rank of the items that are compared widens, for example, comparing B and E should be easier than comparing B and D. The SPE predicts that at a given symbolic distance, the performance when comparing items with extreme ranks should be better than comparing items with intermediate ranks.

By one-way Kruskal–Wallis and Fisher least significance difference (LSD) post hoc comparisons, we examined whether the behavior of the monkeys reflected the SPE and SDE. To determine whether their behavioral performance increased with rank distance, as predicted by the SDE, we analyzed the behavioral data by linear regression. Then, we evaluated whether these behavioral effects were mirrored by neural activity. These steps enabled us to determine whether performance and neural activity that was related to the choice of a given target item changed, depending on the rank of the paired items. The neuronal response properties were studied during a baseline epoch (200 ms preceding the onset of the pair of items) and two periods in the decision-making epoch: (1) early delay, beginning 100 ms from the pair onset and ending 300 ms later, and (2) late delay, 300 ms preceding the Go signal (Fig. 1A, bottom, gray lines).

We considered a neuron to have been modulated by the task if its activity during the early or late delay differed significantly from the baseline epoch. To determine whether neural activity encoded the SPE, we performed three-way ANOVA (epoch × serial position × location of target item on the screen) to compare each neuron's response to the presentation of items. Then, we defined a neuron as having been modulated by the serial position factor if a significant main effect of serial position or a significant interaction between the location of the rewarded item and serial position was observed (p < 0.05). Similarly, three-way ANOVA (epoch × symbolic distance × location of target item) was applied to the response of each neuron to examine the relationship with symbolic distance. Any task-related neuron that showed a significant main effect of symbolic distance or a significant interaction between symbolic distance and the location of the rewarded item was classified as SDE-related (p < 0.05). Following this preliminary analysis, the pattern of responses of both groups, SPE- and SDE-related neurons, was studied in their preferred spatial location only; i.e., the site that elicited a higher response to the presentation of the target items (see the following analysis).

The response of each SPE-related neuron was fit using a second-degree polynomial function (y = ax² + bx + c) to determine the cell's tuning preference. Here, we used the sign of the parameter a to estimate whether the response to middle items was higher than for extreme items and vice versa. Thus, if the coefficient a was positive, then the SPE tuning curve was U-shaped; if a was negative, the SPE tuning curve had an inverted U-shape. A similar analysis was performed for SDE. We used a linear fit to separate neurons with positive and negative trends.

To evaluate the response patterns of SPE- and SDE-related neurons across the population, we normalized their activity by calculating the difference (percentage) between the activity for each pair comparison and the comparison with maximum activity. To obtain comparable tuning curves across the neural population, the tuning curves of neurons with negative trends were inverted along the x-axis and aligned to those of neurons with a positive trend as follows: g(x) = − f(x) + k, where f(x) is the response of neurons with negative tuning and k is the sum of the maximum and minimum values of f(x). Positively tuned neurons and inverted neurons were then grouped. We used one-way Kruskal–Wallis and Fisher LSD post hoc comparisons to determine whether serial position modulated the neural activity. One-way Kruskal–Wallis and linear regression analysis were used to examine whether the symbolic distance was significantly reflected in the neural population responses.

By receiver operating characteristic (ROC) analysis, we determined whether the neurons could discriminate between comparisons at various serial positions and symbolic distances. We reasoned that if a neuron encoded the SPE, its response tuning for the five serial positions would follow a U or inverted U-shape, expressing the minimal/maximal response for the comparisons for the third serial position (SP3), an intermediate-intensity response for the second and fourth serial positions, and the maximum/minimum rates of response for the first and fifth serial positions. Thus, the difference in response between the third serial position and the extreme positions should be higher than that between the third position and the intermediate ones.

For each neuron and preferred spatial location, by ROC analysis, we computed a measure of accuracy of discrimination between the third position and the middle and extreme positions in moving windows of 150 ms (step 20 ms), starting 100 ms after the appearance of the pair for 1000 ms. The time at which the neuron crossed the value of 0.65 was the estimate of time at which it began to discriminate between serial positions. To compare the accuracy in discriminating between the two conditions across the population of neurons, we aligned the ROC to the beginning of the discrimination time and performed consecutive rank sum tests.

A similar approach was used to determine whether the neurons discriminated between symbolic distances. For each neuron, we computed a measure of discrimination between distances >1 with the symbolic distance of 1 at the corresponding preferred spatial location by ROC analysis. To determine whether the neural activity encoded the symbolic distance, we assessed if the ROC value increased with the difference between symbolic distances. Kruskal–Wallis tests were performed over time after the alignment of the ROC to the beginning of the discrimination time.

To exclude the influence of eye behavior in the task, we analyzed the eye position and direction of the saccades during the task. For each spatial location of the target items, during the early and late delay epochs, we quantified the relative times in which the horizontal eye position was on the target and nontarget stimuli. Then, we calculated the eye position index (IDX) as follows:

Similarly, we counted the number of saccades toward the target or nontarget during the delay periods and calculated an index of their distribution as follows:

For both indices, a positive, negative, or 0 value indicated that the monkeys directed their eye (oriented the saccades) primarily at the location of the target item or in the opposite direction or that they distributed their eye position (oriented the saccades) with comparable frequencies to both locations, respectively. We organized the data in agreement with the main behavioral effects and performed one-way ANOVA to determine whether their eye behavior differed significantly during the comparisons of pairs with disparate ranks or symbolic distances.

Finally, for each neuron, we computed the choice probability (Britten et al., 1996) as the area under the ROC (auROC) of the mean firing rate between the correct and error trials in the early and late delays, independent of the serial position or the symbolic distance. One-sample t test was used to determine whether the average choice probability differed from 0.5 across neurons. To test whether the choice probability of each neuron differed from the chance level, we recalculated the choice probability values by randomly shuffling the correct and error trials. We repeated this procedure 500 times; then, we considered the choice probabilities above or below the higher or lower 2.5 percentile of the distribution of choice probabilities that was calculated by shuffling procedure (α = 0.05).

Estimate of value of each item in the learned series from the neural response during all pair comparisons.

We assumed that the neural activity that was recorded during each pair comparison would reflect the difference between the neural representations of the rank of each item of the pair in the series. Thus, the neural representation of each item was estimated as the solution of a system of simultaneous linear equations (one for each pair; Fig. 1B). For example, the neural value of B was obtained, starting from the observation of the neural activity when B was compared with A, C–F. To estimate the unknown coefficients for each of the possible combinations (for 6 items, 6! = 720), we first normalized activities and then used the least-squares algorithm in MATLAB (backslash “/” matrix operator; www.mathworks.com). Finally, of the 720 curves, for each neuron, we selected the curve for which the modeled data (possible differences) maximized the goodness of fit with the observed data (see Results for a specific example).

Results

At the end of the learning phases (see Materials and Methods), the average performance of the monkeys was 66 ± 2% (Monkey 1) and 70 ± 2% (Monkey 2) in selecting the target object in learned pairs.

Behavioral performance suggests use of a mental schema to solve the TI task and the absence of a relationship of the schema with reward history

During the test phase, the performance on novel pairs (including the so-called critical pairs: BD, BE, CE; i.e., those that do not include extreme items; Fig. 1C, highlighted region) was well above chance [Monkey 1: average p(correct) = 0.97 (SD: 0.06), t test: p < 0.001; Monkey 2: average p(correct) = 0.97 (SD = 0.07), t test: p < 0.001]. Overall, the performance on novel pairs was better than that for learned pairs (one-way Kruskal–Wallis and post hoc comparisons between symbolic distances >1 and symbolic distance = 1; Monkey 1: p < 0.05; Monkey 2: p < 0.05). Both monkeys demonstrated an SDE, i.e., their performance improved linearly, following the difference in rank of the compared items (symbolic distance; Fig. 1C; one-way Kruskal–Wallis and linear regression analysis; Monkey 1: p < 0.001; Monkey 2: p < 0.001). Finally, the performance on comparisons that included stimuli with intermediate ranks was worse than that for pairs that were formed by stimuli with extreme ranks (one-way Kruskal–Wallis and post hoc comparisons: Monkey 1: p < 0.05; Monkey 2: p < 0.05), indicating an SPE. These effects demonstrate that the monkeys could solve the TI task efficiently by learning and manipulating a new series every day, and that they were potentially using a mental schema to solve the inferential problems.

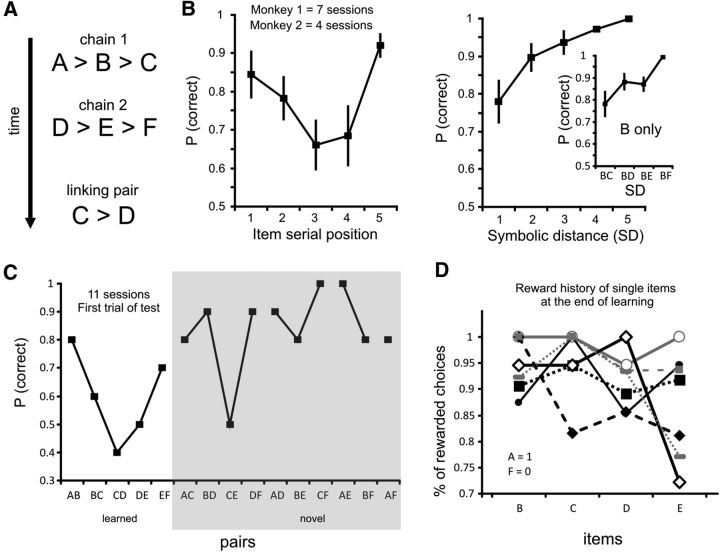
We noted that this mental schema was independent of the reward history of the various items in the learning phase. The monkeys continued to express the SPE (one-way Kruskal–Wallis and post hoc comparisons: p < 0.05) and SDE (one-way Kruskal–Wallis and linear regression analysis: p < 0.01) and solve novel problems at a high level when they had to learn sequentially two separate three-item lists (A > B > C, and then D > E > F) that were later joined by training on a pair of stimuli that linked the 2 lists (C > D; Fig. 2A,B). For instance, the monkeys correctly chose target B of the critical BE pair (Fig. 2B, inset), despite B and E being associated with a similar history during learning (Fig. 2A). High performance was evident, starting from the first trial of the test [Figure 2C; p(correct) for first trials of each session] for most novel pairs, including those with equal values, as expected from the associated reward during learning.

Figure 2.

Monkeys' performance on linked chains of items. A, Schematic of the behavioral sessions with two-chain learning. The learning of each chain included blocks of 20 trials, during which each pair of items of a chain was presented (e.g., AB, BC for Chain 1; A–C). Once the monkeys performed well above chance levels [threshold: p(correct) >80%] on each pair, they performed blocks of 20 trials with the two pairs randomly presented, until their performance in the block reached at least 60% of correct choices. The same procedure was used to learn Chain 2 (D–F). Subsequently, the monkeys performed 20 trials with the CD pair to link the two chains of items. B, Average performance of both monkeys during the test phase, expressed as a function of SPE (left) and overall symbolic distance (right). Inset, The average performance for pairs that included the second item (i.e., B) in the series. C, Performance for the first presentation of all pairs in the test phase after learning the two chains in 11 sessions. D, Percentage of reinforced choices for each item presentation during learning. The extreme items A and F are always and never reinforced when touched, respectively. Each line indicates the percentage of rewarded choices for the seven learning sessions analyzed. Error bars in B are SE.

In this dataset, we investigated the relationship of the mental schema with reward history by estimating the value of each item at the beginning of the test phase from the proportion of positive feedback responses (rewarded choices) that were received during learning. In one animal (Monkey 1, 7 sessions), for which we stored learning behavioral data, we counted the times in which a given item was selected when it was the winner of a pair and divided this value for the total times it was selected, independently of the fact that it was the winner or not. For example, the item B was rewarded if selected when paired with C but not if paired with A. Therefore, the proportion of reward obtained by the item B in the pair BC was divided by the times it was selected in the pair BC plus the times it was selected in the pair AB.

The difference between the estimated values for each item of the pair was used as a predictor of behavior in each session (e.g., performance for BE in test, as B_value minus E_value), assuming that the overall performance followed an exponential function: p(correct) = 1/(1 + exp [β * (rewarded choice 1 − rewarded choice 2)]). The β value for the fitting and the corresponding residuals were estimated using the “nlinfit” and “nlparci” functions in MATLAB.

Based on this analysis, the estimated values of the rewarded choice were similar for all items at the end of the learning sessions (Fig. 2D; each line corresponding to data from one session), and consequently, in none of the sessions did the value of β differ significantly from 0 (95% confidence interval residuals; p < 0.05), arguing against the possibility of using the model and explaining the observed behavior on the basis of the reward history during learning. The performance during the learning phase, with percentage of rewarded choices often >80% (Fig. 2D), also suggested that the monkeys adopted a consolidated strategy, wherein they were able to rapidly individuate the target item in each presented pair, likely by implementing a “switching rule.”

Analysis of the influence of eye position and saccade direction on behavior and neural modulation

Figure 3 shows the distribution of eye positions, with the trials sorted according to the symbolic distance for the target items when located to the right, of a sample session for Monkey 1 during the test phase. As seen in Figure 3A, the monkey started the trials by looking to the left or right or at the center of the working space, corresponding to the central spot or one of the two peripheral items. Then, once the pair of stimuli appeared, the monkey began moving its eye to explore the stimuli and identify the target item. However, the statistical tests revealed that the eye movements were distributed equally between the left and right positions and that the eye position IDX and saccade direction IDX did not differ between symbolic distances (Fig. 3A,B highlights the performance during the early delay). In our analysis of eye behavior in both epochs for all behavioral sessions (Monkey 1, n = 30; Monkey 2, n = 32), the saccade direction IDX and eye position IDX were not significantly affected by the serial position or symbolic distance of the target item (Tables 1, 2; one-way ANOVA: p > 0.05), suggesting a lack of influence of eye behavior on the observed neural modulation.

Figure 3.

Eye movement behavior in a sample session of Monkey 1, with the target item always on the right. A, Distribution of horizontal eye positions. Each trial is organized according to the symbolic distance and aligned to the pair onset. Early delay epoch is highlighted (orange). The value of the saccade direction IDX for each symbolic distance is reported. B, Distribution of eye positions throughout the working space during the early delay epoch. The value of the eye position IDX for each symbolic distance is reported.

Table 1.

Eye position index for the two monkeys

	Target left				Target right
	Target ON		GO signal		Target ON		GO signal
	Monkey 1	Monkey 2	Monkey 1	Monkey 2	Monkey 1	Monkey 2	Monkey 1	Monkey 2
Serial position
1	−0.23 (0.05)	0.12 (0.09)	0.27 (0.06)	0.02 (0.11)	−0.06 (0.04)	−0.06 (0.07)	0.18 (0.06)	−0.01 (0.09)
2	−0.29 (0.06)	0.11 (0.08)	0.14 (0.09)	−0.07 (0.10)	0.05 (0.06)	−0.12 (0.06)	0.29 (0.06)	0.06 (0.10)
3	−0.16 (0.05)	0.13 (0.08)	0.20 (0.07)	−0.04 (0.10)	0.11 (0.05)	−0.13 (0.07)	0.28 (0.06)	0.07 (0.09)
4	−0.17 (0.07)	0.04 (0.08)	0.16 (0.08)	−0.06 (0.10)	0.14 (0.06)	−0.19 (0.06)	0.23 (0.07)	−0.06 (0.09)
5	−0.12 (0.07)	−0.08 (0.10)	0.11 (0.10)	−0.10 (0.10)	0.00 (0.07)	−0.04 (0.08)	0.07 (0.09)	−0.14 (0.09)
	F(4,139) = 1.19;	F(4,140) = 2.1;	F(4,139) = 1.05;	F(4,135) = 0.79;	F(4,138) = 2.44;	F(4,135) = 2.44;	F(4,138) = 2.44;	F(4,131) = 2.44;
	p = 0.32	p = 0.39	p = 0.08	p = 0.53	p = 0.53	p = 0.20	p = 1.55	p = 0.87
Symbolic distance
1	−0.27 (0.05)	−0.10 (0.08)	0.14 (0.06)	−0.08 (0.09)	0.16 (0.05)	−0.04 (0.06)	0.19 (0.06)	0.01 (0.08)
2	−0.28 (0.06)	0.02 (0.11)	0.20 (0.07)	−0.06 (0.10)	0.13 (0.05)	−0.06 (0.07)	0.24 (0.06)	0.05 (0.07)
3	−0.27 (0.05)	−0.08 (0.11)	0.19 (0.05)	−0.03 (0.10)	0.18 (0.06)	−0.15 (0.08)	0.25 (0.05)	−0.03 (0.08)
4	−0.31 (0.05)	−0.06 (0.10)	0.29 (0.08)	−0.06 (0.12)	0.11 (0.07)	−0.03 (0.06)	0.37 (0.06)	−0.02 (0.08)
5	−0.19 (0.07)	−0.21 (0.12)	0.24 (0.07)	−0.20 (0.11)	0.01 (0.06)	−0.10 (0.07)	0.25 (0.08)	−0.08 (0.10)
	F(4,138) = 0.67;	F(4,149) = 0.71;	F(4,139) = 1.44;	F(4,144) = 0.47;	F(4,139) = 0.62;	F(4,140) = 0.34;	F(4,139) = 1.29;	F(4,145) = 0.31;
	p = 0.61	p = 0.58	p = 0.22	p = 2.43	p = 0.65	p = 2.44;	p = 0.35	p = 0.87

Table 2.

Saccade direction index for the two monkeys

	Target left		Target right
	Monkey 1	Monkey 2	Monkey 1	Monkey 2
Serial position
1	0.18 (0.06)	0.16 (0.05)	−0.19 (0.04)	−0.26 (0.07)
2	0.17 (0.06)	0.21 (0.07)	−0.28 (0.05)	−0.24 (0.08)
3	0.23 (0.08)	0.20 (0.07)	−0.17 (0.08)	−0.33 (0.08)
4	0.19 (0.07)	0.20 (0.07)	−0.25 (0.07)	−0.39 (0.08)
5	0.17 (0.10)	0.30 (0.12)	−0.25 (0.11)	−0.27 (0.11)
	F(4,140) = 0.10; p = 0.98	F(4,140) = 0.43; p = 0.78	F(4,140) = 0.37; p = 0.83	F(4,130) = 0.51; p = 0.72
Symbolic distance
1	0.17 (0.06)	0.20 (0.06)	−0.25 (0.07)	−0.31 (0.07)
2	0.29 (0.05)	0.17 (0.07)	−0.26 (0.05)	−0.33 (0.06)
3	0.18 (0.08)	0.19 (0.06)	−0.23 (0.06)	−0.33 (0.07)
4	0.09 (0.08)	0.23 (0.07)	−0.22 (0.08)	−0.29 (0.08)
5	0.17 (0.08)	0.21 (0.09)	−0.09 (0.07)	−0.19 (0.11)
	F(4,140) = 0.87; p = 0.48	F(4,140) = 0.09; p = 0.98	F(4,135) = 1.09; p = 0.36	F(4,120) = 0.61; p = 0.65

Neurons in the dPFC are modulated by the task and follow the behavioral effects

We analyzed the neural activity during each trial of the test phase for all sessions with standard learning procedures (Monkey 1, n = 30; Monkey 2, n = 32), focusing on two periods of the decision-making epoch (early and late delay; see Materials and Methods). We found that the discharge rate of single neurons in the dPFC (Fig. 4A) was modulated by the identity and relationship of the pairs that were presented.

Figure 4.

Recording area and neural modulation in the test phase. A, Electrode tracks for both animals. AS, Arcuate sulcus; PS, principal sulcus. The relative proportion of SPE- and SDE-related activity is indicated for each entry point. Entry points located posteriorly to the arcuate sulcus are indicated by black dots only. B, Activity histograms (aligned to the pair onset; vertical bar) for all comparisons during the test phase with the target item presented in the preferred location for a task-related neuron. The average neural activity and the activity during the first trial of the test phase in the early delay epoch are indicated by black dots and red triangles, respectively. Filled gray squares denote the average neural activity for groups of pairs organized by symbolic distance.

Figure 4B shows the mean activity (black dots) and activity during the first trial (red triangles) for the preferred spatial location of a task-related neuron for all possible pair comparisons—learned (symbolic distance = 1) and novel (symbolic distance > 1)—during the test phase. The motor output of the monkey was always directed toward the same location, but movements were made toward different target stimuli, with disparate (relative) values as a consequence of the learning phases. A complex interaction between the neural representation of the rank position of each item in the series and the relative value that was derived from the relational comparisons is evident in the figure: (1) the neural activity is tuned to the learned pairs (Fig. 4B, symbolic distance 1), and (2) for each target item (e.g., B), neural activity also depends on the symbolic distance between (the difference in the ranks of) items in the pair.

For all neurons, to extract an overall profile of the two main behavioral effects (SPE and SDE) and thus establish a neuronal correlate of the mental representation of learned items, we grouped the comparisons by symbolic distance or serial position (see Materials and Methods). In the sampled neurons (n = 257), 115 cells (45%) were modulated by the behavioral task effects. This population of task-related neurons was obtained by selecting those with a confirmed anatomical location. Neurons that were located posteriorly to the arcuate sulcus (n = 3 from Monkey 1, and n = 10 from Monkey 2; Fig. 4A) were excluded from further analyses due to their limited total number.

For the selected neurons, the activity during the early and the late delay epochs differed significantly from baseline and were modulated by the SDE and SPE. Specifically, 64/115 (56%) neurons displayed significant modulation by the SDE, 74/115 (64%) neurons were modulated by the SPE across all symbolic distances, and 23 (20%) cells were modulated by both the SDE and SPE (Table 3). Eighty-seven (76%) of the task-related neurons also showed a significant spatial preference for the presentation of the target item (significant main effect by three-way ANOVA (p < 0.05) and SPE/SDE × location of target item interaction: p < 0.05; Table 3). Seventy-eight percent (58/74) of SPE-modulated neurons were modulated in the early and late delays (main effect of serial position p < 0.05), whereas 12% (9/74) neurons were significantly modulated in the early delay versus 12% (9/74) in the late delay (significant interaction serial position × epoch or serial position × epoch × target location and post hoc comparisons: p < 0.05).

Table 3.

Proportion of neurons modulated by the task conditions

No. of neurons (%)	Epoch 147 (57)	SPE 57 (20)	Spatial position 41 (16)	Epoch × SPE 15 (6)	Epoch × spatial position 35 (14)	SPE × spatial position 47 (18)	Interaction 22 (9)
No. of neurons (%)	Epoch 163 (63)	SDE 49 (20)	Spatial position 74 (29)	Epoch × SDE 12 (5)	Epoch × spatial position 49 (19)	SDE × spatial position 33 (13)	Interaction 12 (5)

Similar results were obtained for SDE-modulated neurons: 71% (46/64) neurons were modulated by the SDE independently of the epoch of the trial (main effect of symbolic distance position p < 0.05), whereas 8% (5/64) expressed the SDE in the early delay, compared with 16% (10/64) in the late delay (significant interaction symbolic distance × epoch or symbolic distance × epoch × target location and post hoc comparisons: p < 0.05). To remove the effect of the side of presentation of the target item in the observed neural modulation, we used only the preferred response in the following analyses.

Figure 5 shows the average performance and the corresponding neural modulation for the entire population of task-related neurons (n = 115). As a population, the pattern of activity reflected the SPE (one-way Kruskal–Wallis and post hoc comparisons: p < 0.01) and SDE (one-way Kruskal–Wallis and linear regression analysis: p < 0.01), mirroring the behavioral performance of both monkeys (Kruskal–Wallis and post hoc comparisons: p < 0.01).

Figure 5.

Neural and behavioral modulation for SPE and SDE. Mean and SEM for the performance of Monkey 1 (top, black lines) and Monkey 2 (top, red lines) and normalized population neural activity in the early (bottom, black) and late (bottom, gray) delays for each serial position (left) and symbolic distance (right). A, data related to SPE. B, data related to SDE.

Neural activity discriminates serial positions and symbolic distances and predicts performance

For all task-related neurons, we performed ROC analysis to compute a measure of accuracy of the discriminability between serial positions (Fig. 6A) and symbolic distances (Fig. 6B) for target items in the preferred location (see Materials and Methods). Each plot in Figure 6, A and B, shows data sorted by time of calculation of the threshold (ROC = 0.65) from the presentation of the pair. Time of discrimination (Fig. 6A,B; average and distribution in the top portion of each panel) between serial positions (rank-sum test: p > 0.05) and symbolic distances (Kruskal–Wallis: p > 0.05) from pair onset did not differ significantly.

Figure 6.

Discriminability analysis for task-modulated neurons. A, Time evolution of accuracy (auROC) in discriminating between middle and extreme items from SP3 aligned to the pair onset (color plots) and time at which the accuracy value reached 0.65 (starting time of discrimination; top histograms; vertical arrows indicate median values). B, Time evolution of accuracy in discriminating between symbolic distances (color plots) and the start time of the discrimination (top histograms; vertical arrows indicate median values). C, Average (shaded areas indicate SEM) value across population aligned at the start of discrimination for serial position (left) and symbolic distance (right). The differences between conditions over time are indicated (horizontal black segment). Insets, Values obtained using only neurons with significant values. Horizontal bars in C, time of significant difference. *p < 0.05.

To better quantify the effect, the ROC values of each neuron that reached the threshold were realigned to the time at which they occurred and averaged across the population (Fig. 6C). Based on the statistical tests, the discrimination of extreme serial positions from the third serial position was significantly more accurate in the 150–350 ms range from reaching of threshold (Fig. 6C, left; rank-sum tests p < 0.05), and the accuracy of discriminating differences in symbolic distances from distance 1 in the 150 ms epoch starting from the time of the threshold was significantly greater (Fig. 6C, right; Kruskal–Wallis: p < 0.05). From the presentation of the pair, the discriminability for the serial position emerged ∼400 ms later. Conversely, the discriminability for the symbolic distance was evident at ∼300 ms after presentation of the pair (Fig. 6).

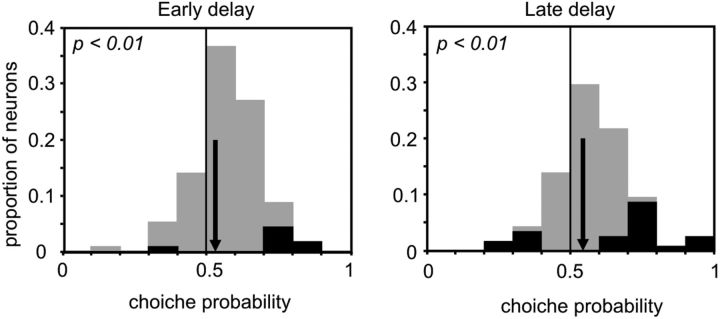
Finally, by choice probability analysis, we evaluated whether the neural activity during the early and late delay epochs could predict the performance on the task (error vs correct trials). Choice probabilities of 0.5 indicate that neural activity is not a reliable predictor of performance, whereas values that differ significantly from 0.5 can predict it.

The distribution of choice probabilities for each dPFC task-related neuron in both epochs is reported in Figure 7. By statistical analysis, 7% of neurons had a choice probability that differed from chance levels in the early delay versus 20% in the late delay. Across the population, the choice probability in both epochs was significantly >0.5 (t tests: p < 0.05).

Figure 7.

Distribution of choice probability. Distribution of choice probability across the task-related neurons in the early (left) and late (right) delays. Dark points indicate values that are significantly different from chance after permutation. Average values of the distributions (vertical arrows) were significantly >0.5 (t test: p < 0.01).

Support of TI by neural modulation is evident from the first trial of the test phase

We were aware that after several trials of the test phase, memory and associative learning effects could prevail and influence behavior, even using a novel rank of stimuli each day. Thus, we included additional controls in our data to ensure that our animals were able to perform transitively. To this end, we focused on the first trial of each session. Figure 8A,B shows the normalized activity of all modulated neurons (bottom plots) and the behavioral performance in the experimental sessions (n = 24 for Monkey 1, n = 18 for Monkey 2; top plots) during the first test trial for each stimulus pair that was presented at the preferred spatial location.

Figure 8.

Behavioral performance and neural modulation for SPE and SDE in the first test trial. A, Top, Behavioral performance for the first trials of pairs organized according to the serial position of the target (rewarded) item. Middle, Corresponding neural modulation for task-related neurons. B, Top, Behavioral performance for the first trials of pairs organized according to the symbolic distance of items forming the pair. Middle, Corresponding neural modulation for task-related neurons. C, Top, Behavioral performance for comparisons of adjacent pairs (learned) in the first test trial and the corresponding neuronal modulation (middle). D, Behavioral (top) and neural modulation (middle) for the symbolic distance for item B. The lower part of the figure shows the pairs used for data in A and B (lower left) and for data in C and D (lower right).

The mental schema was immediately available, in terms of behavioral performance and neural modulation. The monkeys' performance was above chance levels for never-experienced transitive pairs (symbolic distances >1; average proportion of correct responses: Monkey 1 = 0.82, SD = 0.19; t test, p < 0.01; Monkey 2 = 0.88, SD = 0.15; t test, p < 0.01) during the first trial of the test phase, suggesting that they were making reasoning-driven decisions at that time. Further, from the first trial onward, the behavioral performance was better for novel transitive pairs than for learned pairs, perhaps reflecting a conflict between existing memories (learned pairs) and new events (transitive pairs) during the test (Preston and Eichenbaum, 2013). Also, the behavioral performance followed the SPE and SDE from the beginning of the test phase (Fig. 8A,B, top plots; χ² tests: p < 0.05), and notably, the neuronal activity was modulated accordingly (Fig. 8A,B, middle plots; one-way Kruskal–Wallis tests p < 0.01). Thus, our evidence demonstrates that a unified schema is created during the learning phase and that neurons are rapidly and directly involved in supporting the formation of an integrated representation of stimuli that are used for transitively solving new problems.

Next, we tested the hypothesis that monkeys manipulated the schema from the beginning of the test by examining the serial position of learned items (at symbolic distance 1) and the symbolic distance for item B (at SP2). Even for these pair comparisons, the SPE and SDE significantly modulated the behavior (χ² tests: p < 0.05) and the related neural activity in the early delay (Kruskal–Wallis: p < 0.05). In the late delay, the neural activity was significantly modulated by the SPE (Kruskal–Wallis: p < 0.05) but not the SDE (Kruskal–Wallis: p = 0.16), despite the activity following a symbolic distance trend. Notably, the performance for the BD and BE comparisons, not including extreme items, was above the chance (binomial test p < 0.05) level immediately after learning (Fig. 8C,D), suggesting that the animals were able to transitively conclude about novel problems rapidly, also using never-experienced items.

The shape of the estimated neural representation of the rank of the items suggests the use of an internal model

To understand the form of the representation of the ranked items in the brain, we examined the activity of task-modulated neurons for all pair comparisons during the test phase. The form of this representation, which can be defined as a “mental schema” (Preston and Eichenbaum, 2013), is useful for describing the possible strategy that is adopted by animals when adding information to behavioral evidence. Because the stimuli were presented only as pairs, the value/position of each item in the schema could be derived only mathematically.

Two primary hypotheses have been developed to account for behavioral outcomes in TI (for review, see Vasconcelos, 2008). The value transfer hypothesis (von Fersen et al., 1991) emphasizes the reward association mechanisms that take place during the learning phase of the task. At the end of the learning phase, the always-rewarded item A acquires the maximum value, and the never-rewarded item F receives the lower value. The intermediate items, rewarded 50% of the time, acquire moderate values that are proportional to their proximity to the two extreme items. According to this hypothesis, the SPE and SDE emerge from the comparison between the value (measured as the probability of obtaining a reward) of each item in a pair, not necessarily due to the engagement of a reasoning-based process. Our behavioral control with linked chains (Fig. 2) indicates that this possibility is unlikely, because we have observed that the SDE and SPE continue to emerge when two anchor items become intermediate.

The exploration of a mental representation hypothesis (Merritt and Terrace, 2011; Gazes et al., 2014) opines that during learning, subjects build a mental schema of the ranked items, in which items with adjacent ranks are represented as adjacent instances of the schema. Reasoning processes during TI thus follow this second view, based on the evaluation of the internal representation (within the schema) of pairs of items, in which the difficulty in discriminating depends on how the mental representation is scanned or on the reciprocal proximity of the representation, which is behaviorally expressed in the SPE and SDE (Merritt and Terrace, 2011).

These alternative hypotheses generate disparate predictions about the form of the internal representation that emerges from the modulation of neural activity during pair comparisons. In the value transfer hypothesis, the neural activity that is associated with the representation of the ranked items should be maximal (or minimal) for item A and minimal (or maximal) for item F. In contrast, if the brain activity encodes a mental schema of the ranked items, it is reasonable to expect that the list of ranked items is represented as a tuned response of brain activity, with a maximum response for 1 of the ranked items and a gradual decrease in response as the items that are presented diverge from the preferred item (U-shaped tuning).

Figure 9A shows all 720 estimated representations of the set of ranked items for the example neuron in Figure 4B, obtained using the least-squares algorithm that has been described in the Materials and Methods section, starting from the average responses that were observed during each pair comparison in the early delay epoch (Figs. 5B, black dots, 4B) and assuming that each value was derived from the difference in values of the single items (e.g., observed average activity in BC = average activity in target item B − average activity in nontarget item C). For this neuron, Figure 9A, thick red line, is the best model of the neural representation of the six items. This estimate is the result of the measure of the goodness of fit between the modeled activity during the pair comparisons, taken as the absolute difference between the estimated representation of the items of a given pair (e.g., BC = |B − C|) and the observed neural response.

Figure 9.

Estimated neural representation of rank order supporting the observed SPE and SDE. A, Estimated neural representations (n = 720) of a rank-ordered set of items that could model the observed neural responses during all pair comparisons in B (observed; black dots). Colored lines are for curves with R-square > 0.1 when tested as in B. The thick red curve is for the highest R-square value in the group. B, Comparison between the observed (black) and modeled (empty dots; obtained from best fit in A) responses of a neuron during pair comparisons. A measure of the goodness of fit (R-square) is reported. C, Distribution of R-square values obtained for all task-related neurons. The gray bar indicates the proportion of neurons with R-square <0.1. The average R-square is indicated (black arrow). D, Distribution of the estimated families of curves sorted by frequency of observation. The thickness of the lines and the size of the dots increase with the proportion of the curve belonging to the same group.

Figure 9B represents the best modeled neural activity for all pair comparisons (empty dots), obtained from the (best) representation of the items in Figure 8A. For this neuron, the modeled response accounted for the observed data, with a goodness of fit of 0.57. Using this method, we estimated a similar representation for each of the 115 task-related neurons, always using the tuning curve that corresponded to the best model. In 99 neurons (86%), we observed an R-square value that differed from 0 in at least 1 curve, with an average value of 0.4 (Fig. 9C; black bars). In our analysis of the distribution of tuning curve shapes, they followed the prediction of the reward association hypothesis (curves peaking at 1 of the extremes) in eight cases. In contrast, most neurons represented the item's rank with a U-shaped modulation, with a maximum for 1 of the intermediate items in the series (Fig. 9D), suggesting the presence of a neural mental schema. Across the population, the average estimated neural representation of the middle items differed significantly from that of the extreme items (one-way Kruskal–Wallis and post hoc comparisons p < 0.01).

Similar results were obtained in the same analysis of the late delay epoch: 98/115 (85%) had a non-zero R-square value with an average of 0.4 (SD = 0.15). Seven tuning curves had a maximum at 1 of the extreme items, and across the population, the average estimated neural representation of the middle items showed a significant difference between the middle and extreme items (one-way Kruskal–Wallis and post hoc comparisons p < 0.01). This analysis accounts for ∼40% of the variability in the neuronal data, explaining in part the neural representation of the item ranks. However, because our main objective was to identify a neuronal correlate of schema manipulation, we could only provide an indirect estimate of it. Other experimental approaches that use a match-to-sample paradigm would be more appropriate in generating a measure of the neuronal representation of single items.

Overall, these results argue against a reward-based mechanism and instead support TI processes and a unified representation of the related knowledge. It is likely that the mechanisms of TI in the dPFC are based on principles that are comparable to those that have been hypothesized for representing and comparing quantities (Nieder, 2005; Nieder and Dehaene, 2009).

Discussion

Based on our experimental evidence, inferential reasoning is reflected in the activity of single neurons in the dPFC, emerging from the first test trials, and more importantly, the observed pattern of activation is consistent with the manipulation of a mental schema that represents rank-ordered items, as suggested by several studies in humans (for review, see Preston and Eichenbaum, 2013). The two widely reported behavioral effects that are observed during TI, the SPE and SDE, are signatures of how related facts are mentally organized and used during inferential processes (Zeithamova et al., 2012a). Several pieces of data have suggested that after related facts are learned, they are organized in a unified mental representation that is hierarchically organized. Also, TI problems have been proposed to be solved by comparing the hierarchy of the represented information (Treichler and Van Tilburg, 1996; Merrit and Terrace, 2011; Gazes et al., 2012; Zeithamova et al., 2012a). In our study, these comparison processes are well represented by the pattern of activity of dPFC neurons.

To exclude the effect of associative learning after repeated presentation of the same problem in the test, we examined the behavioral correlates and neural modulation, selecting only the first presentation of each problem for each session. We observed that on average, neurons maintained their modulation, and moreover, the modulation was evident for the presentation of pure transitive pairs (those that did not include items at the extreme positions in the series). We believe that this observation represents a key new finding of our study. With few exceptions (Jensen et al., 2013), behavioral studies have rarely tested the emergence of SDE/SPE during the first trials of transitive problem solving.

The involvement of the PFC in TI has been documented primarily in brain-damaged patients (Koscik and Tranel, 2012), in lesion studies on monkeys and rodents (Dusek and Eichenbaum, 1997; Buckmaster et al., 2004; Van der Jeugd et al., 2009; Devito et al., 2010), and in neuroimaging studies (Zeithamova et al., 2012a; Preston and Eichenbaum, 2013). Damage to the PFC impairs the ability to solve inferential problems, whereas normal problem-solving performance is maintained for tasks that are supported by other cognitive functions (Devito et al., 2010; Koscik and Tranel, 2012). Further, neuroimaging studies have reported that the PFC is significantly activated during inferential processes but not during the acquisition or retrieval of information (Acuna et al., 2002; Wendelken and Bunge, 2010; Zeithamova et al., 2012b). This evidence supports the hypothesis that an integrated representation of ranked items is activated in the PFC during the inferential process, allowing them to be compared and a decision to be made (Nieder, 2005; Van der Jeugd et al., 2009; Zeithamova et al., 2012a; Preston and Eichenbaum, 2013). Our findings also support this hypothesis, showing that inferential reasoning is characterized by the activation patterns of single neurons in the PFC, which is consistent using a mental schema of ranked items from the very first trial of the test phase.

As an alternative to schema manipulation, the process of value transfer from extreme to middle items has been hypothesized to explain performance during TI (von Fersen et al., 1991; Frank et al., 2003). Per this model, the value of item A, which is always rewarded during learning, and the value of item F, which is never rewarded, are transferred to intermediate items, which are equally reinforced during learning. To rule out this explanation, we tested the monkeys after a learning phase with two lists of items, thereby controlling for the influence of extreme items (Treichler and Van Tilburg, 1996; Merritt and Terrace, 2011). Under this learning condition, the SPE and SDE continued to characterize the monkeys' behavior, supporting that their inferential process was based on the construction and manipulation of a mental schema in which items were rank-ordered. In addition, on a neuronal level, we determined that a representation of the ranked items, based on the expectation of the reward, could not account for the pattern of activity in the neurons during the pair comparisons.

Evidence of a neural correlate of symbolic distance in the PFC has recently been reported (Lennert and Martinez-Trujillo, 2011). Two monkeys were trained for several days in learning the relationship between a set of motion-dot stimuli that were rank-ordered by color. Their performance and underlying PFC neural activity in detecting changes in the motion of random dots were influenced by the difference in values between the target and distractor. This symbolic distance effect, again, suggests that the monkeys were using a mental schema manipulation rather than a memory retrieval process to solve the task. However, these results failed to address whether the schema emerged after intensive training on the ranked objects and whether it could drive the extraction of information that is not provided directly by the available hints.

In our study, we demonstrated that mental schemas drive the acquisition of new information from the beginning of the test phase; subtend the extraction of new information that is not directly provided, because the SDE modulates the performance with novel, never-experienced pairs; and are reflected in the response of PFC neurons; finally, we show that tuning of the symbolic distance also emerges for the target that is presented in the preferred spatial position—not only through the interaction between target and distractor (Lennert and Martinez-Trujillo, 2011).

In a recent study, inferential processes were reported to modulate the response of PFC neurons that were associated with the expectation of the amount of a reward (Pan et al., 2014). Reward-related PFC neurons modulated their activity for learned and inferred amounts of a reward that was associated with various categories of stimuli. In our study, we extended these findings by determining which neural mechanisms were responsible for reasoning-driven decision-making, independent of the reward-modulating properties of PFC neurons, and studying the neuronal correlates of the symbolic representations that underlie logical reasoning.

These results highlight that the neural mechanisms of transitive reasoning are comparable to those of the encoding of physical quantities or numbers (Nieder, 2005; Nieder and Dehaene, 2009). It is likely that disparate populations of neurons represent the different ranks of the items, which are used as neural filters to evaluate the differences and compare the items (Nieder et al., 2002). Notably, the presence of neural correlates of TI reasoning in the dPFC expands the function of this region to an even higher-level representation of relational information, beyond the physical attributes of the stimuli. Previous studies have shown that the dPFC encodes the relative metrics of dimensions, such as quantities, numbers, and time (Nieder et al., 2002; Walsh, 2003; Genovesio et al., 2014). For example, neurons in the PFC (Genovesio et al., 2009, 2011) encode relative duration and distance, based on order and stimulus features. The processing of ordinal distance in the PFC has also been demonstrated to support the attentional processes of object selection by filtering out distracter stimuli (Lennert and Martinez-Trujillo, 2011).

The capacity to reason is a central hallmark of human cognition. Understanding this highly complex ability is a daunting but compelling challenge. In this study, we used a novel form of the TI task in which animals were required to experience a never-practiced series every day. Our results show that the activity patterns of single neurons in the PFC of monkeys that were performing a TI task support schema manipulation, leading to inferential deductions. The specific function of other brain regions, including the hippocampus (Van Opstal et al., 2008; De Vito et al., 2010; Wendelken and Bunge, 2010; Preston and Eichenbaum, 2013), and the relative timing of their participation in the learning of novel information might depend on the context and demands of the task (Zeithamova et al., 2012a; Preston and Eichenbaum, 2013).

These findings increase our understanding of how the brain works to create abstract thinking and the impairments to reasoning in degenerative, traumatic, and psychiatric pathologies. Compared with matched controls, patients who suffer from schizophrenia or degenerative processes that affect the PFC, perhaps due to insufficient contribution of the PFC to the functioning of the hippocampal complex and striatum (Friston, 1998; Fornito et al., 2011), are unable to solve a TI task (Titone et al., 2004). Similarly, the administration of subanesthetic doses of ketamine, an NMDA receptor antagonist that is occasionally used as a pharmacological model of schizophrenia (Fletcher and Honey, 2006), causes monkeys to perform poorly on a TI task (Brunamonti et al., 2014). The combination of pharmacological and neuronal recording techniques has the potential to guide the development of new therapies for many types of mental diseases.