A Biophysical Model for Cytotoxic Cell Swelling

Abstract

We present a dynamic biophysical model to explain neuronal swelling underlying cytotoxic edema in conditions of low energy supply, as observed in cerebral ischemia. Our model contains Hodgkin—Huxley-type ion currents, a recently discovered voltage-gated chloride flux through the ion exchanger SLC26A11, active KCC2-mediated chloride extrusion, and ATP-dependent pumps. The model predicts changes in ion gradients and cell swelling during ischemia of various severity or channel blockage with realistic timescales. We theoretically substantiate experimental observations of chloride influx generating cytotoxic edema, while sodium entry alone does not. We show a tipping point of Na⁺/K⁺-ATPase functioning, where below cell volume rapidly increases as a function of the remaining pump activity, and a Gibbs–Donnan-like equilibrium state is reached. This precludes a return to physiological conditions even when pump strength returns to baseline. However, when voltage-gated sodium channels are temporarily blocked, cell volume and membrane potential normalize, yielding a potential therapeutic strategy.

SIGNIFICANCE STATEMENT Cytotoxic edema most commonly results from energy shortage, such as in cerebral ischemia, and refers to the swelling of brain cells due to the entry of water from the extracellular space. We show that the principle of electroneutrality explains why chloride influx is essential for the development of cytotoxic edema. With the help of a biophysical model of a single neuron, we show that a tipping point of the energy supply exists, below which the cell volume rapidly increases. We simulate realistic time courses to and reveal critical components of neuronal swelling in conditions of low energy supply. Furthermore, we show that, after transient blockade of the energy supply, cytotoxic edema may be reversed by temporary blockade of Na⁺ channels.

Introduction

Cerebral edema is classically subdivided into cytotoxic and vasogenic edema (Klatzo, 1987; Kempski, 2001; Simard et al., 2007). Vasogenic edema originates from a compromised blood–brain barrier and the accumulation of water in the extracellular space due to the entry of osmotically active particles from the vasculature. This is observed in a variety of conditions, such as traumatic brain injury, tumors, or ischemia (Donkin and Vink, 2010). Otherwise, cytotoxic edema most commonly results from energy shortage, such as in cerebral ischemia, and arises from the swelling of neurons or astrocytes due to a redistribution of extracellular fluid to the intracellular compartment. While this does not lead to tissue swelling, it generates the driving force for the movement of constituents from the intravascular space into the brain, which does cause tissue swelling (Simard et al., 2007).

The formation of cerebral cytotoxic edema is often recognized as an important pathophysiological mechanism leading to initial neuronal damage or secondary deterioration in patients with cerebral ischemia (Stokum et al., 2016). In this population, interindividual differences with regard to the speed and degree of cytotoxic edema formation are large and not well understood (Hofmeijer et al., 2009). A better understanding of the key processes involved in cytotoxic edema formation, and the potential explanations for the large variability in extent and time course observed in the clinic, may help to identify patients who are at risk and to assist in defining potential targets for intervention.

Since the vast majority of osmotically active particles in the brain are ions (Somjen, 2004), the study of cytotoxic edema is essentially the study of maladaptive ion transport (Stokum et al., 2016). We here introduce a dynamic biophysical model to identify the fundamental determinants of cytotoxic cell swelling and to simulate its development. Following the approach originally introduced for cardiac cells (DiFrancesco and Noble, 1985) and ion concentration dynamics during seizures and spreading depression in neurons (Kager et al., 2000), we extend the Hodgkin–Huxley formalism (Hodgkin and Huxley, 1952) to include dynamic intracellular ion concentrations and resulting volume dynamics. Our model allows quantitative predictions of cytotoxic cell swelling with regard to its timescale, severity, and relation to the availability of energy. In the original Hodgkin–Huxley equations, ion concentrations and corresponding Nernst potentials are assumed to be constant. This assumption holds in physiological conditions where the ATP supply is sufficient to maintain ion homeostasis and firing rates are modest. However, it loses its validity if the ATP supply does not meet its need (Zandt et al., 2011, 2013b), as observed in ischemia (Stokum et al., 2016), or pathological brain states that are intrinsically characterized by a massive redistribution of ions, such as seizures (Fröhlich et al., 2008; Raimondo et al., 2015) and spreading depolarization (Somjen, 2001; Zandt et al., 2013a). Recently, a similar approach was used in a three-compartment model to study cell swelling in astrocytes and neurons during spreading depolarization (Hübel and Ullah, 2016). We focus on neuronal swelling only and assume that extracellular ion concentrations are constant, yielding a single-compartment model. While this is clearly not in agreement with biological reality, it closely resembles conditions in brain slice experiments. Furthermore, all ion fluxes in the model are purely biophysical, and corresponding parameters can therefore be measured directly in experiments.

The model explains why the intracellular chloride levels and remaining activity of ATP-dependent pumps are major determinants of cytotoxic edema. Our simulations demonstrate that, at a critical value of pump activity, the cell volume strongly increases and a pathological Gibbs–Donnan-like equilibrium state is reached. Neurons in this state do not recover if the Na/K pump activity returns to baseline or even beyond. However, subsequent temporary blockade of sodium channels provokes the reversal of cytotoxic edema and functional recovery. This may explain why blockers of voltage-gated sodium channels have been shown to prevent neuronal death in various experimental models of cerebral ischemia (Lynch et al., 1995; Carter, 1998) and may assist in better patient selection for therapeutic strategies.

Materials and Methods

Neuron model.

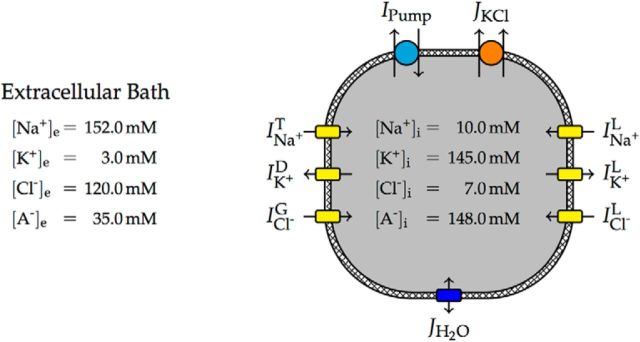
Our model neuron consisted of a single intracellular compartment with a variable volume separated from the extracellular solution by a semipermeable cell membrane (Fig. 1). The extracellular bath was assumed to be infinite, such that all properties of the extracellular space were constant model parameters (Table 1). The model contained a transient sodium current (INa+T), a delayed rectifier potassium current (IK+D), and specific leak currents for sodium (INa+L), potassium (IK+L), and chloride (ICl−L). It was recently shown that the ion exchanger SLC26A11 is highly expressed in cortical and hippocampal neurons (Rahmati et al., 2013), acts as a chloride channel that is opened by depolarization of the membrane, and plays an important role in cell swelling (Rungta et al., 2015). An additional voltage-gated current, (ICl−G), modeled this chloride flux (Fig. 2). Physiological intracellular resting concentrations were maintained by Na+/K+-ATPase, which generated a net transmembrane current (IPump), and an electroneutral KCl cotransporter, which generated a molar transmembrane ion flux (JKCl). The cell volume changed due to osmotically induced water flux (JH2O).

Figure 1.

Schematic model overview with typical ion concentrations. Negatively charged, impermeant macromolecules are denoted by A⁻. Leak and voltage-gated ion channels (yellow) yield ion currents that are balanced by the electrogenic ATP-dependent Na⁺/K⁺ pump (cyan) and the electroneutral KCl cotransporter (orange). While the pump moves both Na⁺ and K⁺ against their electrochemical gradients and therefore needs ATP to run, the KCl cotransporter uses the energy stored in the standing transmembrane gradient of K⁺ to move Cl⁻ out of the cell. Any difference in osmolarity between the intracellular and extracellular space will yield a water flux across the membrane (blue), changing the cell volume.

Table 1.

Model constants, parameters, and variables with default (resting) values

	Value	Description
Constant
F	96485.333 C/mol	Faraday's constant
R	8.3144598 (C/V)/(mol K)	Universal gas constant
T	310 K	Absolute temperature
Parameter
C	20 pF	Membrane capacitance
PNa+T	800 μm3/s	Maximal transient Na+ permeability
PNa+L	2 μm3/s	Leak Na+ permeability
PK+D	400 μm3/s	Maximal delayed rectifier K+ permeability
PK+L	20 μm3/s	Leak K+ permeability
PCl−G	19.5 μm3/s	Maximal voltage-gated Cl− permeability
PCl−L	2.5 μm3/s	Leak Cl− permeability
QPump	54.5 pA	Maximal Na+/K+ pump current
UKCl	1.3 fmol/(s/V)	KCl cotransporter strength
[Na+]e	152 mmw	Extracellular bath Na+ concentration
[K+]e	3 mm	Extracellular bath K+ concentration
[Cl−]e	135 mm	Extracellular bath Cl− concentration
LH2O	2 μm3 (s bar)	Effective membrane water permeability
[S]e	310 mm	Total extracellular solute concentration
NiA−	296 fmol	Intracellular amount of impermeant anions
Variable
V	−65.5 mV	Membrane potential
M	0.013	Transient Na+ activation gate
H	0.987	Transient Na+ inactivation gate
N	0.003	Delayed rectifier K+ activation gate
[Na+]i	10 mm	Intracellular Na+ concentration
[K+]i	145 mm	Intracellular K+ concentration
[Cl−]i	7 mm	Intracellular Cl− concentration
W	2000 μm3	Intracellular volume

Figure 2.

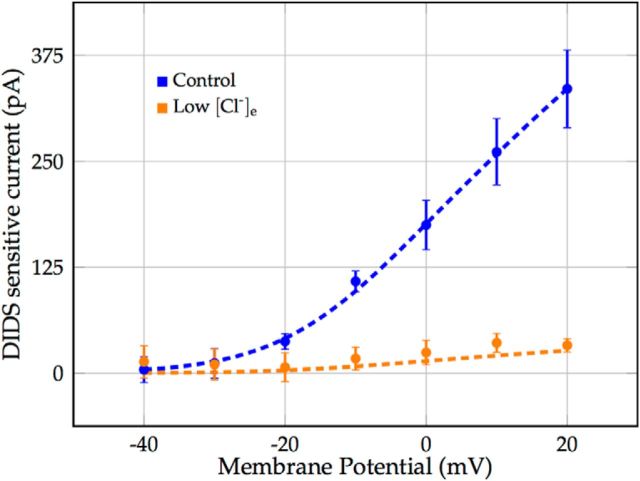
Voltage-gated chloride current through the ion exchanger SLC26A11. Marks denote voltage-clamp recordings of the transmembrane current blocked by application of DIDS in coronal brain slices of rats, reported in the study by Rungta et al. (2015; Fig. 7D). Error bars represent the SEM. Raw data were provided by the Brian MacVicar laboratory. Dashed lines depict the modeled voltage-gated chloride current ICl−G for normal ([Cl−]e = 135 mm and low [Cl−]e = 10.5 mm extracellular and corresponding resting intracellular chloride concentrations.

Fast transient Na⁺ and delayed rectifier K⁺ current.

The kinetics of the transient sodium and delayed rectifier potassium current were based on a model by Kager et al. (2000), as follows:

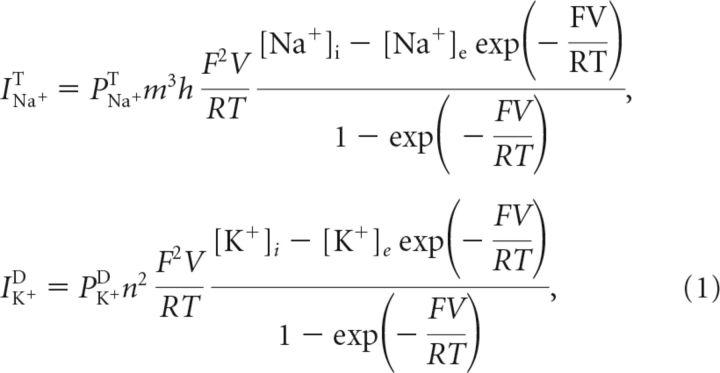where V was the membrane potential, PNa+T and PK+D were maximal membrane permeabilities, and F, R and T were Faraday's constant, the universal gas constant and the absolute temperature, respectively (Table 1). The variables q ∈ {m, h, n} were the usual Hodgkin–Huxley gates as follows: sodium activation, sodium inactivation, and potassium activation, respectively. They evolved according to the following:

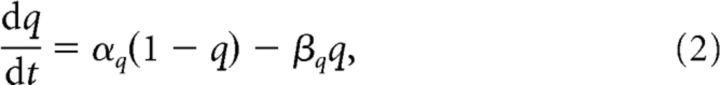with voltage-dependent opening rates, α_q, and closing rates, β_q (Table 2).

Table 2.

Opening and closing rates of gating variables (Kager et al., 2000)

Term	Expression	Description
αm	$\frac{0.32\left(V+52\mathrm{mV}\right)\mathrm{kHz}/\text{mV}}{1-\exp \left(-\frac{V+52\mathrm{mV}}{4\mathrm{mV}}\right)}$	Opening rate transient Na+ activation gate
βm	$\frac{0.28\left(V+25\mathrm{mV}\right)\mathrm{kHz}/\text{mV}}{\exp \left(\frac{V+25\mathrm{mV}}{5\mathrm{mV}}\right)-1}$	Closing rate transient Na+ activation gate
αh	$0.128\exp \left(-\frac{V+53\mathrm{mV}}{18\mathrm{mV}}\right)\mathrm{kHz}$	Opening rate transient Na+ inactivation gate
βh	$\frac{4\mathrm{kHz}}{1-\exp \left(-\frac{V+30\mathrm{mV}}{5\mathrm{mV}}\right)}$	Closing rate transient Na+ inactivation gate
αn	$\frac{0.016\left(V+35\mathrm{mV}\right)\mathrm{kHz}/\text{mV}}{1-\exp \left(-\frac{V+35\mathrm{mV}}{5\mathrm{mV}}\right)}$	Opening rate delayed rectifier K+ activation gate
βn	$0.25\exp \left(-\frac{V+50\mathrm{mV}}{40\mathrm{mV}}\right)\mathrm{kHz}$	Closing rate delayed rectifier K+ activation gate

Voltage-gated Cl⁻ current through the ion exchanger SLC26A11.

Gating of the chloride current through SLC26A11 was assumed to be instantaneous and given by a sigmoidal function of the membrane potential, fitted to experimental data of Rungta et al. (2015) (Fig. 2), as follows:

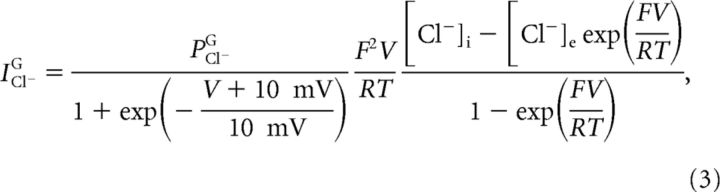where PCl−G was the maximal gated chloride permeability.

Specific leak currents.

The sodium, potassium, and chloride leak currents were modeled as regular Goldman–Hodgkin–Katz currents (Hille, 2001) with fixed leak permeabilities P_X^L for X ∈ {Na⁺, K⁺, Cl⁻}, as follows:

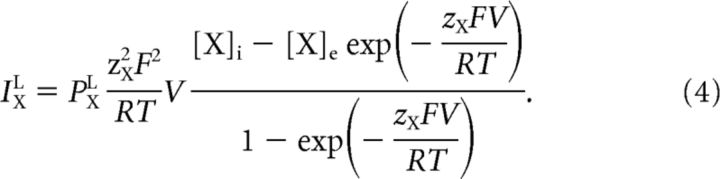Both the sodium and chloride permeability were low compared with the potassium permeability (Table 1). The total leak current was fitted to experimental data from coronal brain slices of rats (Rungta et al., 2015; see Fig. 7C).

Figure 7.

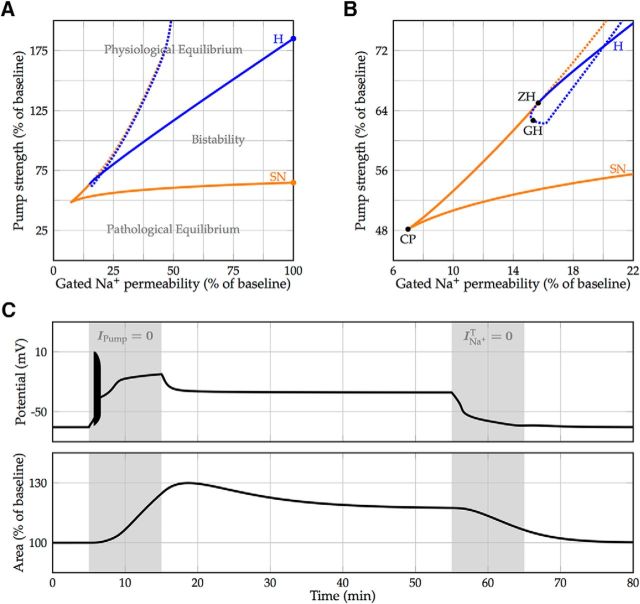
Bistability for physiological pump strengths. A, Continuation of the saddle-node (orange) and Hopf (blue) bifurcation (denoted by the two marks) with the maximal transient sodium permeability as an additional free parameter. Bifurcation of stable equilibria are denoted by a solid line, and bifurcations of unstable equilibria are denoted by a dotted line and are shown for completeness. The region of bistability between the solid lines shrinks with decreasing sodium permeability. B, Magnification with codimension-two bifurcations. The two branches of saddle-node bifurcations meet in a cusp singularity (CP). To the left of this point, the model transitions smoothly between the physiological and pathological state. The Hopf bifurcation curve intersects a saddle-node branch at a zero-Hopf point (ZH) and undergoes a generalized Hopf bifurcation (GH), becoming supercritical. C, Model simulation illustrating bistability and a possible way to return to the physiological resting state. Transition to the pathological equilibrium is induced by a 10 min blockade of the Na⁺/K⁺-ATPase (simulating ouabain perfusion or oxygen-glucose deprivation). After temporary blocking of the voltage-gated sodium channels (simulating the effect of, e.g., TTX), the neuron returns to its physiological equilibrium.

Na⁺/K⁺-ATPase.

In each cycle, the Na⁺/K⁺-ATPase exchanges three intracellular sodium ions for two extracellular potassium ions, and therefore generates a net transmembrane current I_Pump. The net pump current was modeled after the experimental data of Hamada et al. (2003) as a function of the intracellular sodium concentration, as follows:

where Q_Pump was the maximal pump current. While the experimental data in Hamada et al. (2003) corresponds to dorsal root ganglia neurons, the Na⁺/K⁺ pump of cortical neurons of approximately the same size should behave similarly. Indeed, this choice of pump current let to a plausible resting membrane potential and intracellular sodium concentration (Table 1).

KCl cotransport.

Under physiological conditions, the chloride Nernst potential is hyperpolarized with respect to the resting membrane potential due to cotransporter-mediated active transport of KCl of the cell (Blaesse et al., 2009). It is natural to assume that the molar cotransporter flux is proportional to the difference of the chloride and potassium Nernst potential (Østby et al., 2009), such that:

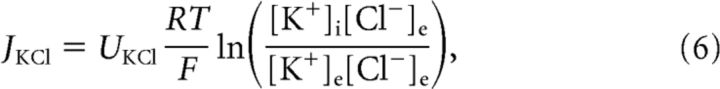where U_KCl was the cotransporter strength, which was chosen to get a resting chloride Nernst potential of approximately E_Cl⁻ = − 80 mV for an extracellular chloride bath concentration of [Cl⁻]_e = 135 mM.

Intracellular concentrations and tshe membrane potential.

The transmembrane currents and cotransporter flux determined the evolution of the intracellular molar amounts, N_X, of the different permeant ions, X ∈ {Na⁺, K⁺, Cl⁻}, as follows:

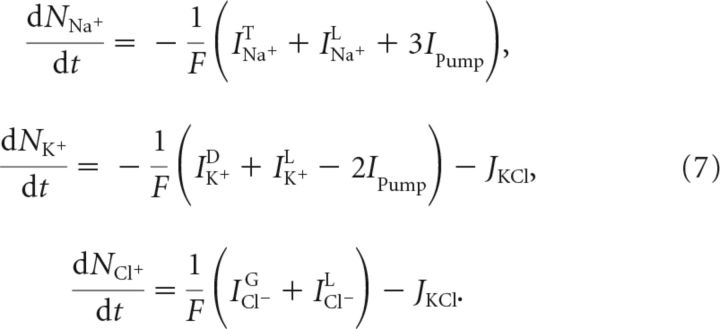Intracellular concentrations were computed by dividing N_X by the intracellular volume W, as follows:

Since we kept track of all the intracellular ion amounts, it was not necessary to introduce an additional differential equation for the membrane potential V. It directly followed from the excess of intracellular charge and the membrane capacitance C, and was given by the following:

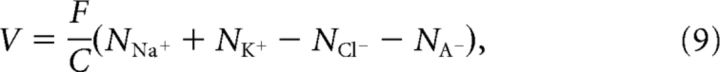where N_A⁻ was the constant amount of intracellular impermeant anions A⁻.

Cell volume and water flux.

The time course of the cell volume W was determined by the transmembrane water flux J_H2O, as follows:

Although the exact pathways for the entry of water molecules into neurons are still debated (Andrew et al., 2007), neuronal swelling is driven by an osmotic gradient (Lang et al., 1998). We therefore modeled the transmembrane water flux as follows:

where L_H2O is the effective membrane water permeability, and Δπ = RT([S]_i − [S]_e) is the osmotic pressure gradient for ideal solutions (Van't Hoff, 1887), with [S] denoting the total solute concentration. Finally, we assumed that the total intracellular solute concentration was given by the total intracellular ion concentration, as follows:

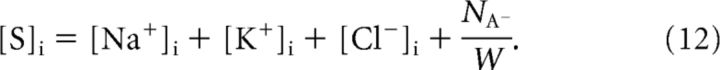Model parameter estimation and validation against experimental data.

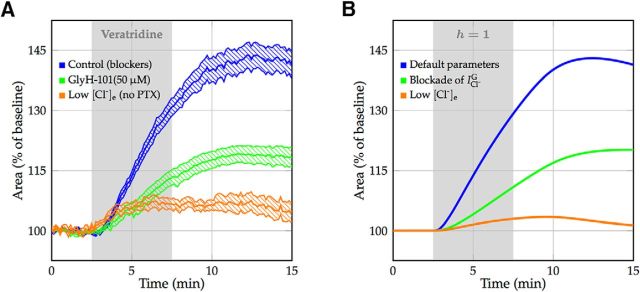
Recently, neuronal swelling in hippocampal and cortical brain slices of rats was studied by selective modulation of sodium channel kinetics by, for example, veratridine (Rungta et al., 2015). Veratridine blocks the inactivation of the transient sodium current, thereby greatly increasing the membrane sodium permeability (Strichartz et al., 1987). Under these circumstances, the Na⁺/K⁺ pump is no longer able to compensate for the increased sodium influx, and the cell converges to a Gibbs–Donnan-like equilibrium with corresponding changes in cell volume (Fig. 3A, top trace). Since our model contained a sodium inactivation gate, it was straightforward to perform such veratridine experiments in silico (Fig. 3B, top trace). This enabled us to estimate the effective cell membrane water permeability, and to validate the model in its prediction of the development of cytotoxic cell swelling by comparing it to experimental data under different conditions (Fig. 3A, middle and bottom trace). There was excellent agreement with regard to the onset of edema formation, the time course of swelling, and the achieved cell volumes (Fig. 3B, middle and bottom trace).

Figure 3.

Neuronal swelling after the application of veratridine. A, Experimental data of neuronal swelling in hippocampal and cortical brain slices of rats with mean and SEM, reported in the study by Rungta et al. (2015; Figs. 3F, 6E). Bath application of veratridine is indicated by a shaded area. Control resembles a blocker cocktail of APV, CNQX, Cd2⁺, and picrotoxin (PTX). Swelling is inhibited by the SLC26A11 blocker GlyH-101 and is largely prevented by reducing extracellular chloride concentration to 10.5 mm. Raw data were provided by the Brian MacVicar laboratory. In the low [Cl]_e experiments, the lack of the GABA_A receptor blocker PTX leads to an additional chloride influx, which is not taken into account in the model. B, Model simulations closely mimic experimental results. The application of veratridine is modeled by blocking the sodium inactivation gate. Shown are default parameter values, blockade of the voltage-gated chloride current modeling the effect of GlyH-101, and low extracellular chloride [Cl⁻]_e of 10.5 mm. Swelling is triggered by a very small and brief excitatory sodium current at t = 2.5 min. For calculation of the cross-section area, we assume that neurons are spherical. The water permeability of the cell membrane is identical in all three conditions.

Numerical implementation.

All simulations of the model were performed in MATLAB [version 8.2., MathWorks (RRID:SCR_001622)], using the stiff differential equation solver ode15s.

When the effect of pharmacological blockers was simulated by turning certain currents off or on, they converged exponentially to their new values with a time constant of 30 s. For calculations of the cross-section area A, we assumed neurons to be spherical, such that:

Bifurcation diagrams were created with Matcont (Dhooge et al., 2003; RRID:SCR_012822).

Results

Intracellular osmolarity is essentially defined by [Cl⁻]_i

Anions, being negatively charged, express strong forces on cations, and in biological systems the total charge of freely moving cations and anions in a solution is always zero, a condition known as electroneutrality (Nelson, 2003; Plonsey and Barr, 2007).

The concentrations, as defined in Equation 8, include the excess of charge at the cell membrane boundary that generates the membrane potential and are, therefore, strictly speaking not equal to the electroneutral bulk concentrations. However, the difference between the two is negligible. For a neuron with a membrane capacitance of C = 20 pF and volume of W = 2000 μm³, the charge generating a membrane potential of V = ±100 mV corresponds to an intracellular (monovalent) ion concentration of ∼0.01 mm.

This implies that a significant influx of cations (e.g., Na⁺) needs to be accompanied either by efflux of a different cation (e.g., K⁺), netting no change in osmolarity, or by an influx of anions (e.g., Cl⁻), increasing the total ion content of the cell. Since the cell membrane is impermeable to the large, negatively charged proteins, chloride is the main permeant anion. Therefore, for a fixed cell volume, the total intracellular ion concentration increases if and only if the intracellular chloride concentration increases.

Osmotic pressure in Gibbs–Donnan equilibrium

When all energy-dependent, active transmembrane transport is shut down, a neuron will eventually reach the Gibbs–Donnan equilibrium (Donnan, 1911), a thermodynamic equilibrium that is independent of specific ion permeabilities and in which the Nernst potentials (Nernst, 1888) of all permeant ions are equal to the membrane potential. In our neuron model with three different permeant ion species, this implies the following:

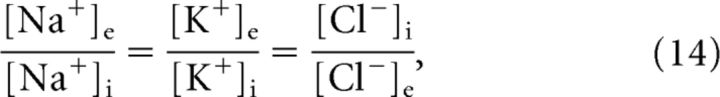where the inverse for chloride results from its valency, z_Cl⁻ = −1. Additionally, the principle electroneutrality dictates the following:

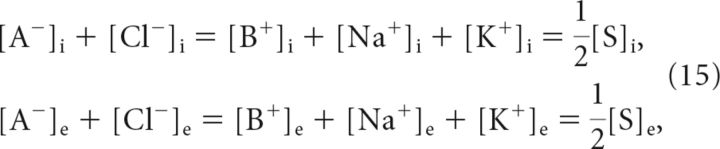where we have added impermeant cations B⁺ for generality. Combining Equations 14 and 15, and using the fact that concentrations cannot become negative, yield the membrane voltage V_GD and solute concentration gradient Δ[S] = [S]_i − [S]_e at the Gibbs–Donnan equilibrium. They are given by the following:

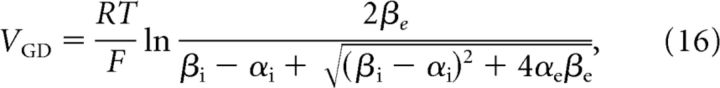and

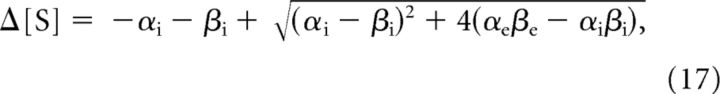respectively, where

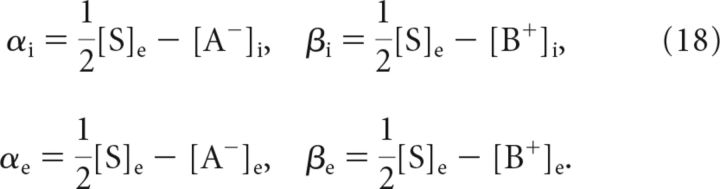If we for the moment assume that the cell volume is constant, the osmotic pressure in Gibbs–Donnan equilibrium can be computed with the help of Equation 17. For a neuron with a water-permeable membrane, convergence to the Gibbs–Donnan equilibrium is accompanied by an increase in cell volume if and only if Δ[S] > 0, which is equivalent to the following:

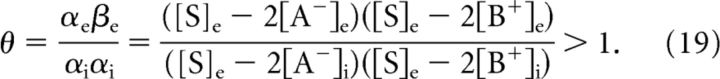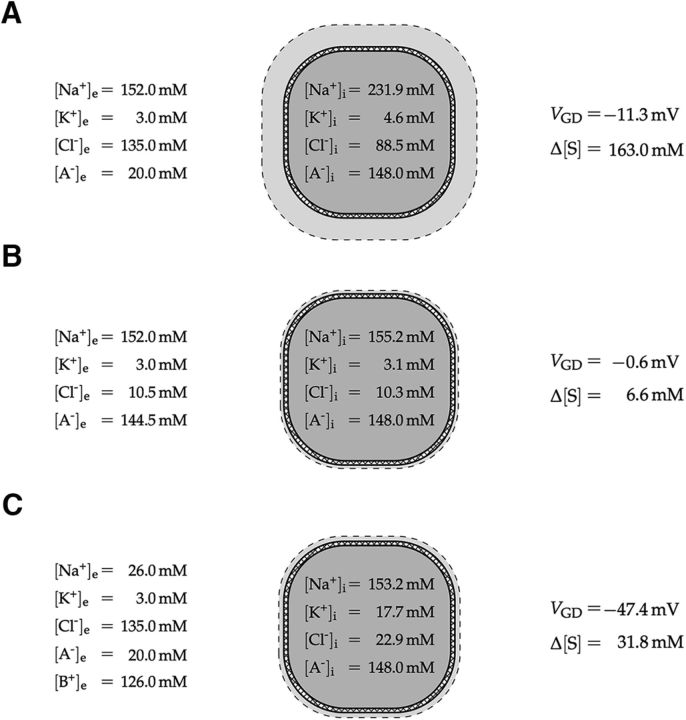
Hence, if the concentration of impermeant cations is equal on both sides of the membrane, cell swelling will occur only if [A⁻]_i > [A⁻]_e. It is also apparent that the numerator in Equation 19, and therefore the value of θ and the amount of swelling decrease if we increase the concentration of extracellular impermeant ions, [A⁻]_e and or [B⁺]_e. Quantitative examples are shown for three different extracellular bath solutions (Fig. 4), with corresponding θ values of ∼18.5, 1.6, and 3.5. An extracellular solution with physiological concentration of sodium, potassium, chloride, and impermeable anions results in a total ion concentration gradient of ∼160 mm, and a Gibbs–Donnan potential of approximately −10 mV (Fig. 4A). Partial iso-osmotic replacement of extracellular chloride and sodium with impermeant anions and cations, respectively, leads to a significant reduction of the osmotic pressure in Gibbs–Donnan equilibrium (Fig. 4B,C).

Figure 4.

Illustration of the Gibbs–Donnan equilibrium for different extracellular bath solutions. A, For a bath solution resembling brain interstitial fluid under physiological conditions, the Gibbs–Donnan equilibrium is associated with a Gibbs–Donnan potential of V_GD = −11.3 mV and a large total solute concentration gradient of Δ[S] = [S]_i − [S]_e = 163.0 mm. B, C, Iso-osmotic replacement of extracellular chloride and sodium by cell membrane-impermeant anions A⁻ and cations B⁺, respectively, leads to a significant reduction of the total ion concentration gradient Δ[S], and therefore osmotic pressure, in Gibbs–Donnan equilibrium. Qualitative estimates of associated changes in cell volume are indicated with a dashed line. Note that in all situations electroneutrality is preserved and that [Cl⁻]_i defines the osmotic pressure.

Ion permeabilities determine speed of neuronal swelling

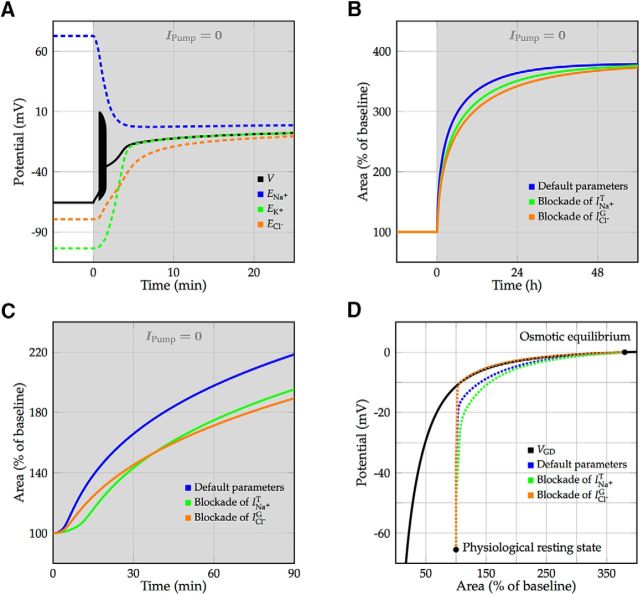
Although the Gibbs–Donnan equilibrium and associated Gibbs–Donnan potential do not depend on the (relative) permeabilities of the permeant ion species, ion permeabilities do affect transient behavior, and thus determine the time course of reaching Gibbs–Donnan equilibrium and subsequent cell swelling. If water can enter the cell, the Gibbs–Donnan equilibrium itself becomes dynamic, since the influx of water will dilute the intracellular concentration of impermeant ions, therefore changing the corresponding equilibrium.

Convergence of a neuron from physiological resting state to Gibbs–Donnan equilibrium was simulated by shutting down the Na⁺/K⁺ pump current. Soon after the Na⁺/K⁺-ATPase was blocked, the membrane potential rose and reached the spiking threshold, which led to a burst of action potentials that terminated in depolarization block (Fig. 5A). The cell volume increased to 95% of its final size after ∼24 h of Na⁺/K⁺-ATPase blockade (Fig. 5B). To investigate the role of ion permeabilities in neuronal swelling, we simulated the effect of two different channel blockers, which, as expected, did not change the equilibrium volume (Fig. 5B). However, the blockade of the transient sodium current, simulating the effect of TTX, and the blockade of the voltage-gated chloride current, simulating the effect of GlyH-101 or DIDS, both slowed down neuronal swelling (Fig. 5B,C). In all conditions, the vast majority of swelling resolved after the cell membrane had depolarized, along the branch of Gibbs–Donnan equilibria (Fig. 5D). Note that the cell volume in the model can increase without bound. In reality, neurons will lyse before their cross-section area increases to >350% of its physiological value.

Figure 5.

Convergence toward Gibbs–Donnan equilibrium and subsequent cell swelling after blocking the Na⁺/K⁺-ATPase, simulating ouabain perfusion or OGD. A, Membrane depolarization and evolution of Nernst potentials for default parameters. After blocking the Na⁺/K⁺-ATPase, the neuron starts spiking for ∼1 min (illustrated by a filled black region), terminating in depolarization block. B, Time course of the increase in cell volume using blockers for the transient sodium current (simulating the effect of TTX) or voltage-gated chloride current (simulating the effect of GlyH-101 or DIDS). In both conditions, neuronal swelling is slowed down, but the final cell volume is not affected. C, Closeup of the volume dynamics during the first 90 min after shutdown of the Na⁺/K⁺-ATPase. Blockade of the transient sodium current prevents spiking and slows down the depolarization of the cell, which yields a delay in the opening of the voltage-gated chloride channel. Blockade of the voltage-gated chloride current limits the chloride flux and therefore the water flux into the cell. D, Convergence from the physiological resting state toward the osmotically balanced Gibbs–Donnan equilibrium (both denoted by marks). Fast voltage fluctuations due to spiking are averaged out. While converging toward the branch of Gibbs–Donnan equilibria (solid black line), swelling speeds up once the voltage-gated chloride current gets activated (Fig. 2).

The equilibrium volume critically depends on the remaining pump activity

Thus far, we only discussed and simulated conditions with no activity of the Na⁺/K⁺-ATPase, corresponding to complete anoxia. Our model enabled us to also study compromised pump function (e.g., that seen in the penumbral region of patients with ischemic stroke; Liang et al., 2007). Systematic, mathematical study of the dependence of a model on a certain parameter, in our case the strength of the Na⁺/K⁺-ATPase, is known as bifurcation theory. It permits us to follow the equilibria of the model and to detect tipping points, bifurcations, at which the qualitative behavior of the dynamic system changes (Kuznetsov, 2004).

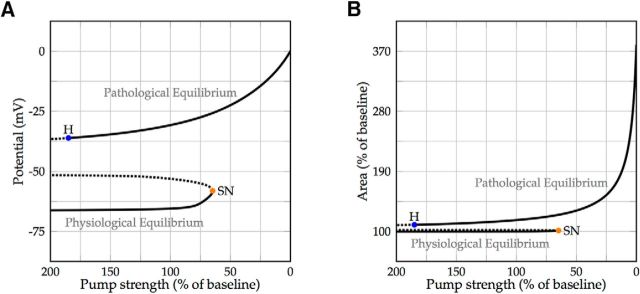
Following the physiological resting state while slowly decreasing the Na⁺/K⁺ pump strength revealed that a tipping point exists at ∼65% of the default pump strength, after which the physiological state disappeared. For pump rates below this critical level, the cell evolved toward a depolarized pathological equilibrium state (Fig. 6A). At this point, the cell size critically depended on the remaining pump activity. Minor differences in remaining pump strength resulted in major differences in the observed swelling (Fig. 6B).

Figure 6.

Bifurcation diagram with the Na⁺/K⁺-ATPase strength as a free parameter. A, Stable equilibria are denoted by a solid line, and unstable equilibria are denoted by a dotted line. At ∼65% of the baseline pump strength, the physiological resting state disappears via a saddle-node bifurcation (SN; orange). For lower values of the pump strength, the cell will converge to a depolarized Gibbs–Donnan-like equilibrium. This pathological state is stable for pump strengths of up to ∼185% of the baseline pump rate, where it loses stability due to a subcritical Hopf bifurcation (H; blue). B, The cell volume is almost constant in the physiological equilibrium branch, but is highly dependent on the pump strength in the pathological equilibrium branch, where minor differences in the remaining pump rate cause major differences in equilibrium cell size.

Vanishing of a stable equilibrium due to collision with an unstable equilibrium is called a saddle-node bifurcation. Close to a saddle-node bifurcation, small changes in circumstances can lead to sudden and dramatic shifts in observed behavior.

The depolarized state is not restored at physiological pump strengths

The depolarized, pathological equilibrium corresponds to a Gibbs–Donnan-like state in which the potential energy that is normally stored in the electrochemical ion gradients has largely dissipated (Dreier et al., 2013) and is therefore also known as a state of free energy-starvation (Hübel et al., 2014). This equilibrium state appeared to be stable up to a pump strength of ∼185% of the default value, such that the model is bistable for a wide range of Na⁺/K⁺ pump rates (Fig. 6). The model also predicted that the cell volume may be returned to values near baseline, while the cell membrane is still depolarized if the pump has returned to its baseline value: at a pump strength of 100%, cell volume in the pathological state is ∼115%, while the membrane voltage is approximately −35 mV (Fig. 6). This potential lies within the range where the transient sodium current is partially activated but inactivation is yet incomplete, generating a “window” current (Attwell et al., 1979) that the Na⁺/K⁺-ATPase cannot overcome. This implies that, once the cell has converged to this pathological state due to a failure of the Na⁺/K⁺ pump to maintain physiological homeostasis, a return to the physiological resting state is possible only if the pump strength is increased far beyond its nominal value.

The loss of stability of the pathological equilibrium is due to a subcritical Hopf bifurcation, at which an unstable limit cycle branches from the equilibrium state. After a dynamic system passes a subcritical Hopf bifurcation point, it will jump to a distant attractor, which, similar to the saddle-node case, can cause dramatic shifts in observed behavior.

Na⁺ channel blockers may reverse cytotoxic edema

If the cell has entered the pathological equilibrium with the associated increase in volume (Fig. 6), and pump strength returns to baseline or beyond, this state remains. Due to the aforementioned window current, the membrane is more permeable to sodium if the cell is partially depolarized. In this state, the sodium current may be too large to be compensated for by the Na⁺/K⁺-pump. Blockade of the voltage-gated sodium current should therefore facilitate a return to the physiological resting state, as it reduces the sodium influx in depolarized conditions. To test this hypothesis, we followed the earlier detected tipping points while slowly reducing the voltage-gated sodium permeability (Fig. 7A). Indeed, the range of pump strengths that permitted a state of free-energy starvation shrank with decreasing permeability. When the sodium permeability was reduced to less than ∼40% of its baseline and the pump strength was set to its nominal value, the physiological resting state was the only stable equilibrium. These findings predict that, as long as the Na⁺/K⁺-ATPase strength is sufficient, temporary (partial) blockade of sodium channels allows cells to return to their physiological resting equilibrium (Fig. 7B).

Discussion

In a dynamic biophysical model, we showed that electrodiffusion and the principle of electroneutrality essentially dictate the occurrence of neuronal swelling in conditions of low or absent ATP supply. With energy depletion decreasing pump strengths up to 65% of baseline, the membrane potential was largely preserved and cytotoxic cell swelling was prevented. However, further lowering of the energy supply was associated with a rapid reduction of ion gradients and corresponding changes in Nernst potentials. In turn, this led to an influx of sodium and chloride, resulting in an osmotic imbalance and subsequent cell swelling.

Our single-neuron model based on the Hodgkin–Huxley framework contained the following three timescales: ion-gating kinetics on the order of milliseconds; concentration dynamics on the order of minutes; and cell volume dynamics on the order of hours. It reliably reproduced experimental data of ouabain-induced anoxic depolarization (Zandt et al., 2013b; Figs. 5A, 7B) and veratridine-induced neuronal swelling (Rungta et al., 2015; Fig. 3). Furthermore, timescales resembled those observed in patients with ischemic stroke (Thrane et al., 2014). The blocking of a brain artery in the absence of compensatory collateral circulation leads to the loss of neuronal functioning and consequent neurological impairment within seconds. Subsequent secondary deterioration from brain edema occurs on the first or second day after symptom onset. In a sufficiently large infarct, malignant transformation classically occurs within 48 h (Hofmeijer et al., 2004, 2009).

Recently, Rungta et al. (2015) established experimentally that chloride influx is essential for neuronal swelling and that permeability to chloride is a major determinant of cytotoxic edema (Fig. 3). We showed that this directly results from the principle of electroneutrality. Anions, being negatively charged, express strong forces on cations, and in biological systems the total charge of freely moving cations and anions in a solution is always zero (Nelson, 2003; Plonsey and Barr, 2007). A chloride influx will always be accompanied by an influx of positive charge (primarily sodium), as intracellular negative charge carriers merely consist of impermeable proteins. Therefore, chloride influx generates cytotoxic edema by adding to the total number of intracellular particles, while the entry of sodium alone does not (Fig. 4). A similar argument was recently used to point out a fundamental connection between cell volume and anion fluxes in cells with osmosis-driven volume dynamics (Hübel and Ullah, 2016). We derived a theoretical measure (Eq. 19) for the osmotic pressure and the subsequent volume increase in Gibbs–Donnan equilibrium, which is independent of membrane ion permeabilities. Indeed, model simulations showed that channel blockers could slow down the development of cytotoxic edema, but do not affect the equilibrium volume (Fig. 5).

Using bifurcation analysis, we showed that a tipping point exists, at which the Na⁺/K⁺ pump can no longer maintain physiological ion homeostasis (Fig. 6). Below this point of ∼65% of the nominal value, small differences in pump strength resulted in large changes in equilibrium cell volume. This may be associated with observations in patients with ischemic stroke. In 2–5% of these patients, space-occupying, life-threatening edema formation occurs, with a relatively sudden onset. Various clinical and radiological variables have been associated with such “malignant transformation,” of which infarct size was the most important determinant (Hofmeijer et al., 2008; Thomalla et al., 2010). Apparently, if perfusion levels are low in a sufficiently large part of the brain, small fluctuations in the remaining perfusion levels may suddenly cause the transition between hardly any and severe progressive cytotoxic edema formation. This is supported by the notion that malignant transformation almost exclusively occurs in the absence of proper collateral circulation, excluding the main compensatory potential (Horsch et al., 2016).

We showed that a stable physiological equilibrium and a stable depolarized Gibbs–Donnan-like state (a state of “free energy starvation”) coexist for a wide range of physiological Na⁺/K⁺ pump strengths (Fig. 6). This bistability has been shown before in single-cell models without volume dynamics (Hübel et al., 2014). It is in agreement with experimental data (Brisson and Andrew, 2012; Brisson et al., 2013) that revealed that pyramidal cells in cortical and thalamic brain slices remain in a depolarized state after 10 min of oxygen–glucose deprivation (OGD) or ouabain perfusion, despite restoration of normoxia and normoglycemia or ouabain washout. In contrast, magnocellular neuroendocrine cells in the hypothalamus, exposed to the same experimental conditions, do repolarize after the restoration of physiological conditions, possibly resulting from a larger efficiency of the Na-K-ATPase (Brisson and Andrew, 2012).

Based on our model simulations, the restoration of membrane potentials to physiological values and the reversal of cytotoxic edema need pump strengths values much larger than baseline (Fig. 6). We emphasize that the neuron may still be depolarized when the pump returns to the baseline value, even when cell swelling has diminished. This is also in agreement with experimental results: after exposure to 10 min of OGD, the maximal depolarization of −5 mV slowly returns to approximately −20 mV in pyramidal neurons, while their volume, as evaluated with light transmittance, returns to baseline values (Brisson and Andrew, 2012; Fig. 1).

At last, we demonstrated that this abnormal equilibrium (i.e., the depolarized state) is caused by the sodium window current (Attwell et al., 1979), and it therefore resolved when voltage-gated sodium channels were (partially) blocked (Fig. 7). Prolonged membrane depolarization is accompanied by calcium influx, which leads to cell death, even if swelling is prevented (Rungta et al., 2015). Our findings may therefore explain why blockers of voltage-dependent sodium channels prevent neuronal death in various experimental models of cerebral ischemia (Lynch et al., 1995; Carter, 1998). We hypothesize that if applied before calcium-induced cell death sets in, sodium channel blockers can prevent neuronal death and restore neuronal functioning after periods of ischemic cytotoxic edema.

Limitations of the model include an infinite extracellular space with constant concentrations, which is convenient for simulating brain slice experiments, but clearly is not in agreement with biological reality. Since the total extracellular volume is much smaller than the total intracellular volume, extracellular concentrations can fluctuate strongly, which could influence transient behavior. Furthermore, we did not explicitly model the influence of volume-regulatory mechanisms (Basavappa and Ellory, 1996) and active cotransport of water (Zeuthen, 2010), but instead assumed that all volume changes are driven by an osmotic gradient. The effective total water flux was fitted to match experimental results (Fig. 3). Because we focused on neuronal swelling, we also ignored calcium due to its relatively very low concentration. Experiments with brain slices in calcium-free and calcium-containing bath solutions showed that neuronal swelling is indeed independent of calcium influx (Rungta et al., 2015). On the other hand, the blockade of the calcium- and ATP-sensitive nonspecific cation channel SUR1-TRPM4 has been shown to be effective at reducing cytotoxic and ionic edema (Simard et al., 2012). Finally, we have not explicitly modeled various other sodium cation channels that may be activated during ischemia. For instance, the activation of glutamate receptors during ischemia may enhance the persistent sodium current (Dong and Ennis, 2014), resulting in a faster depolarization of the cell. It is straightforward to add additional ion channels, pumps, cotransporters, ion species, or dynamic extracellular concentrations to the model. However, in its current implementation, it contains the minimum amount of biophysics that appears necessary and sufficient to faithfully reproduce and explain the key processes involved in the development of cytotoxic edema, and may assist in the identification of new treatment targets.