Low Somatic Sodium Conductance Enhances Action Potential Precision in Time-Coding Auditory Neurons

Abstract

Auditory nerve fibers encode sounds in the precise timing of action potentials (APs), which is used for such computations as sound localization. Timing information is relayed through several cell types in the auditory brainstem that share an unusual property: their APs are not overshooting, suggesting that the cells have very low somatic sodium conductance (g_Na). However, it is not clear how g_Na influences temporal precision. We addressed this by comparing bushy cells (BCs) in the mouse cochlear nucleus with T-stellate cells (SCs), which do have normal overshooting APs. BCs play a central role in both relaying and refining precise timing information from the auditory nerve, whereas SCs discard precise timing information and encode the envelope of sound amplitude. Nucleated-patch recording at near-physiological temperature indicated that the Na current density was 62% lower in BCs, and the voltage dependence of g_Na inactivation was 13 mV hyperpolarized compared with SCs. We endowed BCs with SC-like g_Na using two-electrode dynamic clamp and found that synaptic activity at physiologically relevant rates elicited APs with significantly lower probability, through increased activation of delayed rectifier channels. In addition, for two near-simultaneous synaptic inputs, the window of coincidence detection widened significantly with increasing g_Na, indicating that refinement of temporal information by BCs is degraded by g_Na. Thus, reduced somatic g_Na appears to be an adaption for enhancing fidelity and precision in time-coding neurons.

SIGNIFICANCE STATEMENT Proper hearing depends on analyzing temporal aspects of sounds with high precision. Auditory neurons that specialize in precise temporal information have a suite of unusual intrinsic properties, including nonovershooting action potentials and few sodium channels in the soma. However, it was not clear how low sodium channel availability in the soma influenced the temporal precision of action potentials initiated in the axon initial segment. We studied this using dynamic clamp to mimic sodium channels in the soma, which yielded normal, overshooting action potentials. Increasing somatic sodium conductance had major negative consequences: synaptic activity evoked action potentials with lower fidelity, and the precision of coincidence detection was degraded. Thus, low somatic sodium channel availability appears to enhance fidelity and temporal precision.

Introduction

The timing of action potentials (APs) is used in the auditory system to encode sound features. Extremely precise timing of APs, on the scale of 10 μs, carries information for behaviorally important functions, such as sound localization (Grothe, 2003). Relaying accurate timing through early stages of the auditory pathway depends critically on the precision of AP initiation. In most neurons, AP initiation results from synaptically driven activation of Na channels first at the axon initial segment (AIS) followed immediately by the soma (Edwards and Ottoson, 1958; Bean, 2007), leading to the familiar overshooting AP.

However, there are exceptions to this general rule. Interestingly, several auditory neurons concerned with precise timing have very low-amplitude APs, including bushy cells (BCs) in the anteroventral cochlear nucleus (AVCN) (Oertel, 1983), octopus cells in the posteroventral cochlear nucleus (Golding et al., 1995), and principal cells of the medial superior olive (MSO) (Scott et al., 2005). Mature principal cells of the medial nucleus of the trapezoid body (MNTB) show APs that reach slightly higher peaks, close to 0 mV (Roberts et al., 2014). These neuron types demonstrate additional common characteristics, including low input resistance and high rectification to current injection, which are thought to contribute to their remarkable temporal precision for AP initiation, on the order of 20 μs (Golding et al., 1995; Xu-Friedman and Regehr, 2005a; Gittelman and Tempel, 2006). Small APs are also found in time-coding neurons in the avian auditory pathway in nucleus magnocellularis and nucleus laminaris (Kuba et al., 2006; Kuba and Ohmori, 2009). The reason for this unusual intrinsic property is unclear.

One possibility has been investigated in MSO neurons. An interesting study found that the somatic Na channels of MSO neurons had a negatively shifted inactivation voltage sensitivity (Scott et al., 2010). Despite this, the Na channels appeared to be activated by synaptic potentials, significantly amplifying them. However, this does not explain why somatic Na channels have such unusual inactivation sensitivity. Computer models indicate that MSO APs initiate normally in the AIS or even at more distant nodes of Ranvier (Lehnert et al., 2014), and models of their analogous neurons in nucleus laminaris suggest that initiating APs far down the axon and excluding Na channels from the soma enhance sensitivity to interaural time differences (Kuba et al., 2006; Ashida et al., 2007). Thus, somatic Na channels could modulate responsiveness of the AIS Na channels that initiate the AP.

To test directly whether somatic g_Na interferes with AP reliability and precision in this class of time-coding neurons, we focused on BCs in the AVCN. We used nucleated patches to measure the biophysical properties of Na channels in BCs as well as T-stellate cells (SCs) in the AVCN, which have overshooting APs. Our results revealed that g_Na density in BCs was lower, and the voltage for half-maximal inactivation was more hyperpolarized compared with SCs. Both factors reduced availability of somatic g_Na in BCs during AP initiation. Then we used dynamic clamp to add g_Na to BCs, which decreased AP probability and precision in response to synaptic activation by enhancing K channel activation. The precision of coincidence detection was also significantly degraded with g_Na. Thus, low levels of somatic g_Na seem to enhance fidelity and temporal precision in this class of specialized neurons.

Materials and Methods

Slice preparation.

Experimental procedures were approved by the Institutional Animal Care and Use Committee at the University at Buffalo. Slices were prepared from P14-P25 CBA/CaJ mice (RRID:IMSR_JAX:000654) of either sex as described previously (Ngodup et al., 2015; Yang and Xu-Friedman, 2015). Briefly, slices (150 μm) were cut in an ice-cold solution containing the following (in mm): 76 NaCl, 75 sucrose, 25 NaHCO₃, 25 glucose, 2.5 KCl, 1.25 NaH₂PO₄, 7 MgCl₂, and 0.5 CaCl₂. Slices were transferred to normal ACSF until recording as follows (in mm): 125 NaCl, 26 NaHCO₃, 2.5 KCl, 1.25 NaH₂PO₄, 20 glucose, 1.5 CaCl₂, 1 MgCl₂, 4 Na-l-lactate, 2 Na-pyruvate, and 0.4 Na-l-ascorbate, bubbled with 95% O₂-5% CO₂. The recording chamber was perfused at 3–4 ml/min using a pump (403U/VM2; Watson-Marlow), with saline running through an in-line heater to maintain the temperature at 34°C (SH-27B with TC-324B controller; Warner Instruments).

Cells were patched under an Olympus BX51 microscope with a Multiclamp 700B (Molecular Devices) controlled by the National Instruments PCI-6221, driven by custom-written software running in Igor (WaveMetrics). Recordings were performed in the presence of 10 μm strychnine to block glycine receptors.

Nucleated patch recordings.

Pipettes were pulled from borosilicate glass (OD: 1.5 mm, ID: 0.86 mm; Sutter Instruments) to a resistance of 3–4 MΩ and filled with internal solution containing the following (in mm): 135 CsCl, 5 EGTA, 10 HEPES, 4 ATP-Na₂, 20 TEA, 2 NaOH, pH 7.3, 305 mOsm. BCs were identified in AVCN slices by spontaneous mEPSCs with half-width ≤0.5 ms (width at 50% of the peak amplitude). SCs had mEPSCs with half-width >0.5 ms (Chanda and Xu-Friedman, 2010b). Once cell identity was established, nucleated patches (Schmidt-Hieber and Bischofberger, 2010) were generated by applying constant negative pressure to the pipette, which was then pulled out of the brain slice. Na currents were isolated by adding to the ACSF as follows (in mm): 10 TEA, 2 CoCl₂, 0.5 NiCl₂, and 0.05 CdCl₂. Data were low-pass filtered at 10 kHz (four-pole Bessel) and acquired at 100 kHz. The junction potential was measured as 9 mV, which is close to the theoretical value of 10 mV according to Clampex. Data were not corrected for liquid junction potential.

Current- and dynamic-clamp recordings.

The internal solution in current- and dynamic-clamp patch pipettes contained the following (in mm): 130 KMeSO₃, 10 NaCl, 2 MgCl₂, 0.16 CaCl₂, 0.5 EGTA, 10 HEPES, 4 Na₂ATP, 0.4 NaGTP, and 14 Tris-CrPhos, pH 7.2, 302 mOsm. The junction potential for this solution in normal ACSF was calculated as 8.6 mV in Clampex, and no further correction was done. For current clamp, cells were patched with 1–2 MΩ pipettes. For dynamic clamp, BCs were patched simultaneously with two 3–5 MΩ pipettes. One electrode measured cell voltage, and the other passed current. Resting potential was maintained at −60 mV between trials by passing small currents. For experiments with evoked synaptic responses, auditory nerve fibers (ANFs) were isolated and stimulated using 6–20 μA pulses passed through a small glass micropipette placed in the neuropil. Train stimuli were applied every 30 s.

BCs, SCs, octopus cells, and DCN fusiform cells were recorded in sagittal sections of the cochlear nucleus. BCs can be reliably distinguished from SCs by their response to strong depolarizing current pulses with single, undershooting APs (Wu and Oertel, 1984). Octopus cells are located near the border between AVCN and DCN and show undershooting APs. DCN fusiform cells are recognized by their elongated shape and distinguished from cartwheel cells by the absence of complex APs. MNTB and lateral olivocochlear (LOC) neurons were recorded in transverse sections of the brainstem. LOC neurons are located in the lateral superior olive, and are identified by their large soma and delayed response to depolarizing current pulses (Adam et al., 1999; Sterenborg et al., 2010).

The Markov feature of mafDC was used to apply g_Na (Yang et al., 2015). The Na channel model was based on the Na currents recorded in Figure 2. We assessed the speed of the dynamic clamp using the test feature of mafDC, which depended on the specific experimental conditions. When the dynamic clamp was used for g_Na alone (see Fig. 5), the speed was 20 μs/cycle (50 kHz), the latency was 30 μs, and the jitter was 6 μs. For both g_Na and current pulse (see Fig. 4), the speed was 29 μs/cycle (35 kHz), the latency was 48 μs, and the jitter was 9 μs. For g_Na and g_AMPA (see Figs. 6; 7), the speed was 28 μs/cycle (36 kHz), the latency was 47 μs, and the jitter was 9 μs.

Figure 2.

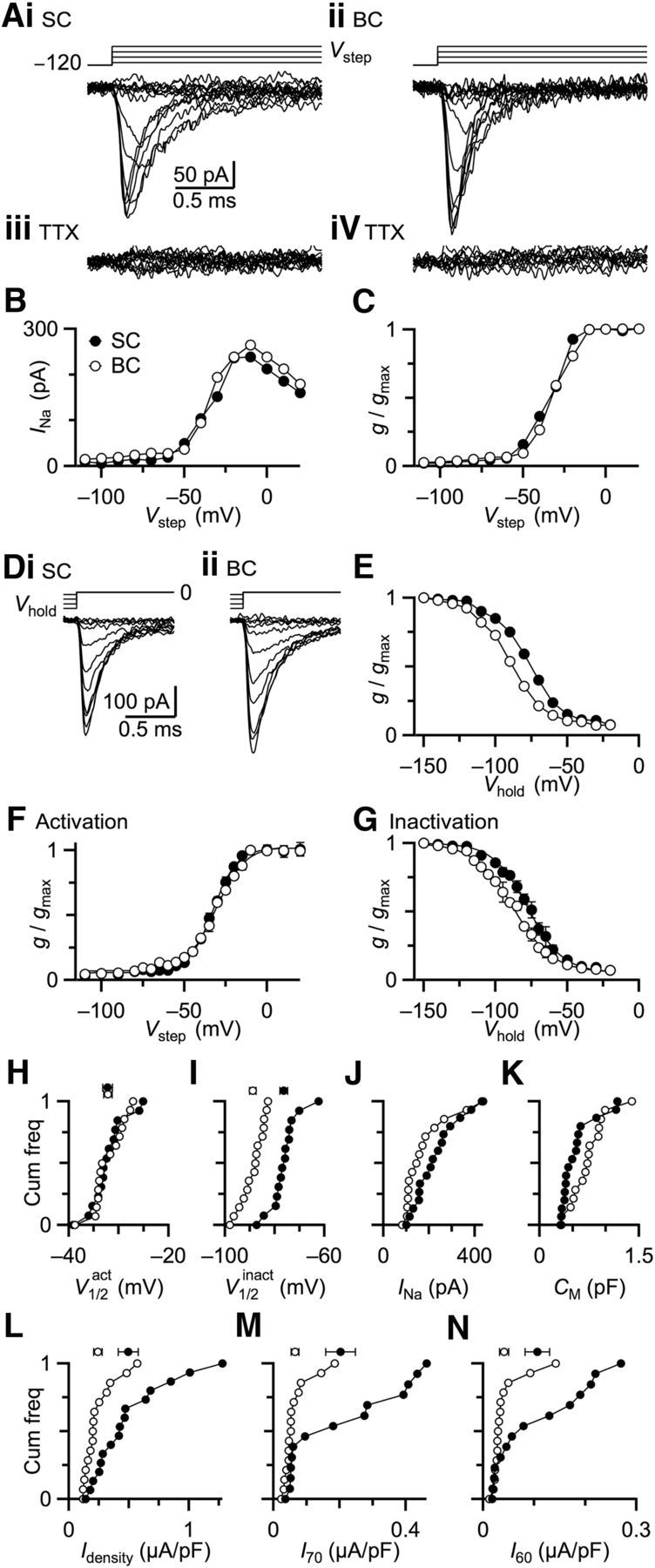
Na currents in BCs show negative shift of inactivation sensitivity and low current density. A, Measuring Na channel activation in nucleated patches from a representative SC (i) and BC (ii). Top traces represent the voltage command, which was stepped from −120 mV to V_step between −110 and −20 mV. Bottom traces represent recorded Na currents. iii, iv, TTX abolished remaining current, confirming it is Na current. B, Peak Na current for the SC in Ai and BC in Aii for different V_step. C, Normalized conductances calculated from curves in B. D, Measuring Na channel inactivation from a representative SC (i) and BC (ii). Top traces represent the voltage command, which was held at V_hold from −150 to −20 mV and stepped to 0 mV. E, Normalized conductance as a function of V_hold for the cells in D. F, Average activation curves from 14 SCs (closed circles) and 15 BCs (open circles). Data were fit with a Boltzmann function: g/g_max = 1/{1 + exp[(V_1/2^act − V)/k_act]}, with V_1/2 = −33.0 mV, k = 7.1 mV for SCs and V_1/2 = −31.5 mV, k = 8.1 mV for BCs. G, Average inactivation curves from 14 SCs (closed circles) and 15 BCs (open circles). Data were fitted with a Boltzmann function, with V_1/2 = −75.4 mV, k = −12.1 mV for SCs and V_1/2 = −87.7 mV, k = −13.9 mV for BCs. H–N, Comparisons of BCs and SCs. Plots are cumulative histograms of data from individual patches, and markers at the top are mean ± SEM. H, Half-activation voltages. I, Half-inactivation voltages. J, Maximal Na current amplitudes. K, Membrane capacitance of nucleated patches. L, Maximal Na current densities from data in J and K. M, N, The Na current densities available at −70 mV (M) and −60 mV (N).

Figure 5.

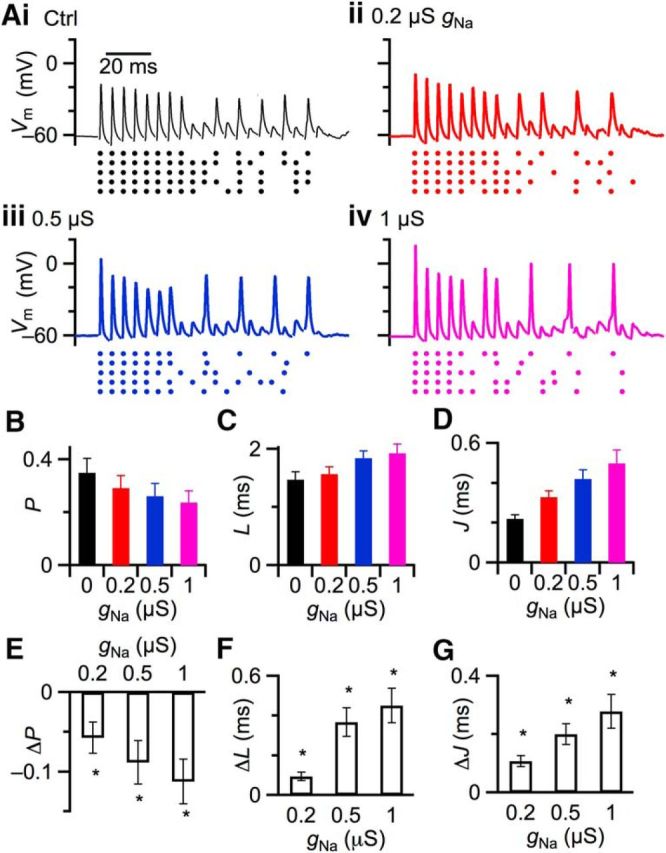
Effects of g_Na on AP probability and timing in response to evoked synaptic activity. A, Representative experiment. Top traces represent responses of BC to trains of fiber stimulation at 200 Hz. Stimulus artifacts are removed for clarity. Bottom raster plots represent timing of APs from 5 similar trials. B–D. Average measurements from 6 BCs showing effect of g_Na on (B) AP probability, (C) AP latency, and (D) SD of AP latency (jitter). E–G, Changes in AP probability (E), latency (F), and jitter (G) with respect to control (0 μS g_Na). *p < 0.05.

Figure 4.

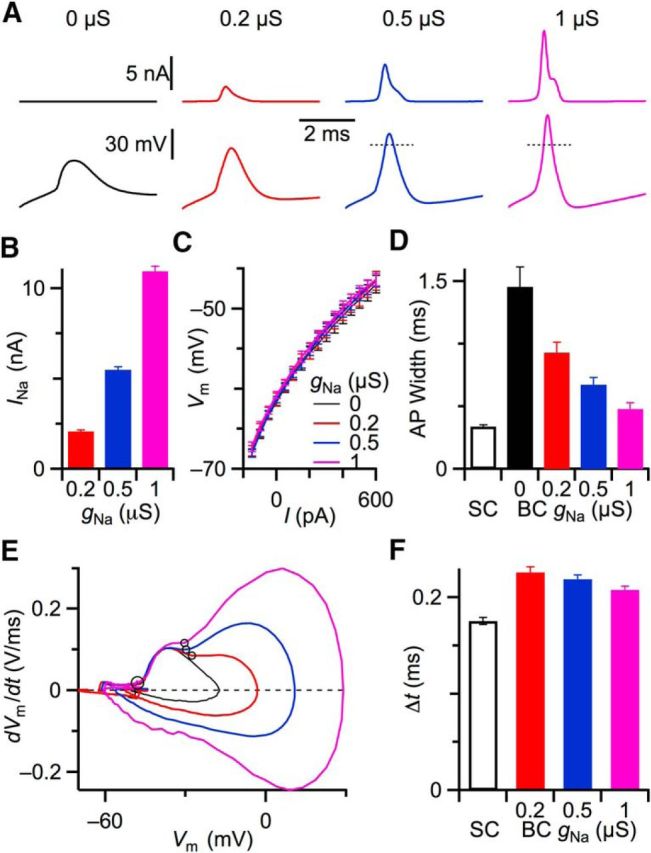
Adding a somatic Na conductance (g_Na). using dynamic clamp. A, Effect of g_Na on APs in a representative BC. APs were evoked by 600 pA current injection. Top traces represent Na current injected by dynamic clamp. Bottom traces represent APs. Short dashed lines indicate 0 mV. With increasing g_Na, the BC fired faster, overshooting APs. B, Average peak amplitude of Na currents injected for different g_Na (N = 10). C, Plots of average membrane potential as a function of current injection for BCs with different amounts of g_Na. Adding g_Na with dynamic clamp had no effect on BC input resistance (R_in for 0 μS = 40.8 ± 4.6 MΩ; R_in for 1 μS = 44.3 ± 3.8 MΩ; p = 0.4, N = 10). D, Average half-width of evoked AP in BC for different g_Na (N = 31 cells). Half-width of SC AP is shown for comparison (N = 29 cells). E, Phase-plane plots of the example BC in A with different amounts of g_Na. Circles represent the start of first and second phases. F, Time intervals between two phases of AP for SCs (N = 29) and BCs (N = 24) with different levels of g_Na.

Figure 6.

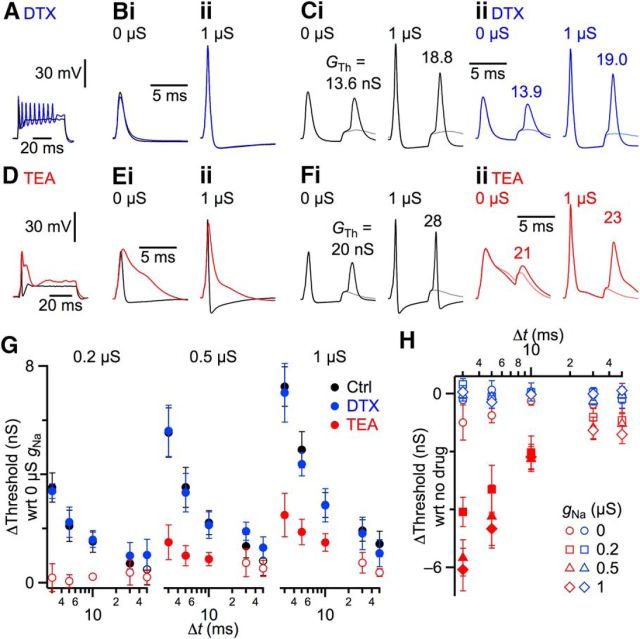
Recruitment of K channels by somatic g_Na. A, D, Representative responses to current injection (600 pA) before (black) and after application of 50 nm DTX (A, blue) or 1 mm TEA (D, red). B, E, Representative APs in control (i) and with 1 μS g_Na (ii) before and after DTX (B) or TEA (E) application. AP shape is unchanged in DTX but greatly prolonged in TEA. C, F, Measuring the effects of g_Na on conductance threshold. A conditioning suprathreshold synaptic conductance was applied in dynamic clamp, followed by a test conductance of varying amplitude. Each panel shows two traces overlaid, for test conductances just below (light traces) or above threshold (dark traces). Threshold conductances (G_Th) are indicated above each trace. i, Traces represent responses without (left) and with 1 μS g_Na added in dynamic clamp (right). The same assessment was done in the presence of DTX (Cii, blue) or TEA (Fii, red). G, Summary of multiple experiments showing changes in threshold with different amounts of g_Na compared with control (0 μS g_Na) before (black, 9 experiments) and after DTX (blue, 4 experiments), or TEA (red, 5 experiments). Threshold increases most at short intervals and with high levels of g_Na. Solid symbols represent significant increases in the different conditions at the p < 0.05 level comparing against 0 μS g_Na. H, Relative change in threshold after DTX (blue) or TEA (red) application compared with control (no blocker). DTX had no effect on threshold, but adding TEA eliminated increases in threshold. Solid symbols represent significant differences compared with control (no antagonist) in the different conditions at the p < 0.05 level.

Figure 7.

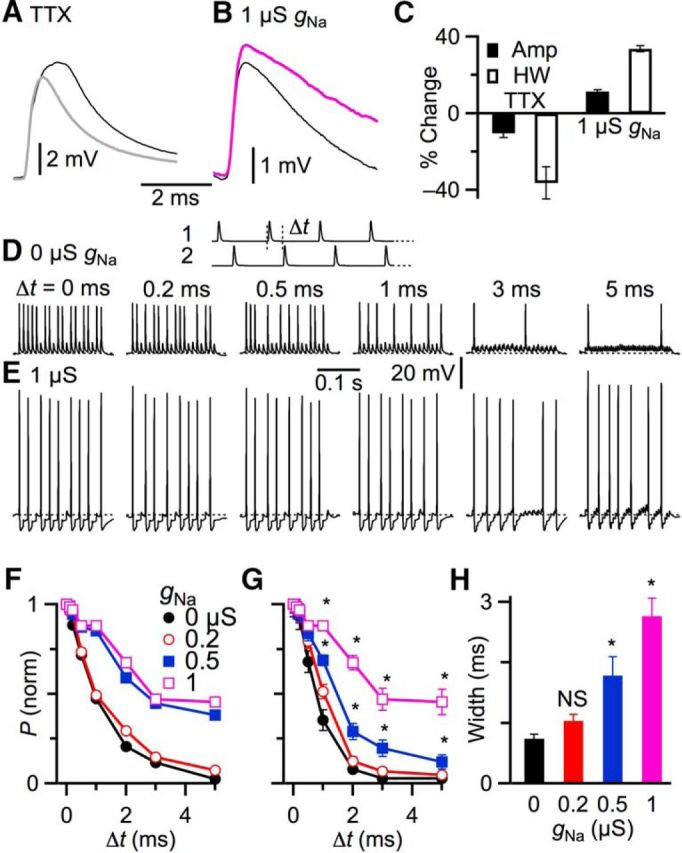
The precision of coincidence detection in BCs is degraded by somatic g_Na. A, Effects of blocking endogenous g_Na on subthreshold EPSPs. Traces are averaged EPSPs resulting from a synaptic conductance applied in dynamic clamp, before (black) and after (gray) application of TTX. B, Effects of added somatic g_Na on subthreshold EPSPs. Traces are averaged EPSPs resulting from a synaptic conductance without (black) and with (purple) 1 μS g_Na applied in dynamic clamp. C, Average percentage change in EPSP amplitude and half-width resulting from TTX application or addition of 1 μS g_Na. All results are significantly different from 0 (p < 0.01). D, E, Assessing the window of coincidence detection. Schematic at top represents the stimulation paradigm, which was two 100 Hz trains of subthreshold synaptic conductances with a time offset (Δt). Traces show representative responses to this stimulation paradigm for several Δt, (D) without and (E) with 1 μS g_Na applied by dynamic clamp. F, AP probability for the representative experiment in D and E. AP probability is normalized to 1 at zero offset between the trains. G, Summary of 7 similar experiments showing average AP probability as a function of offset with different amounts of g_Na. H, Average width of the coincidence window across 7 experiments for different amounts of g_Na. *p < 0.018, significant differences with respect to control (0 μS g_Na).

Data are presented as mean ± SEM. Significance was determined using paired or unpaired, two-tailed, Student's t test, except where otherwise stated.

Results

Auditory neurons that process precise timing lack somatic APs

We first examined representative neurons in the auditory pathway that do not encode precise timing: SCs in the AVCN, LOC neurons in the lateral superior olive, and fusiform cells in the DCN. SCs encode sound amplitude and in vivo fire a burst of APs not locked to the stimulus (Frisina et al., 1985; Kim et al., 1990). LOC neurons form an efferent pathway regulating cochlear responses (Vetter and Mugnaini, 1992). DCN fusiform cells integrate auditory and nonauditory inputs to control movement and balance (Oertel and Wu, 1989; Shore, 2005). All these cells fired normal overshooting APs (Fig. 1A–C, top). We also examined the properties of APs using phase-plane plots, which show the derivative of membrane potential (dV_m/dt) as a function of instantaneous membrane potential. Phase-plane plots of APs in these cells showed two distinct phases (Fig. 1A–C, bottom traces), and this was consistent in each cell examined (Fig. 1G, solid bars). The first, low-threshold phase is thought to reflect Na channel activation in the AIS, followed by a second, larger amplitude phase, which is the somatic AP (Bean, 2007).

Figure 1.

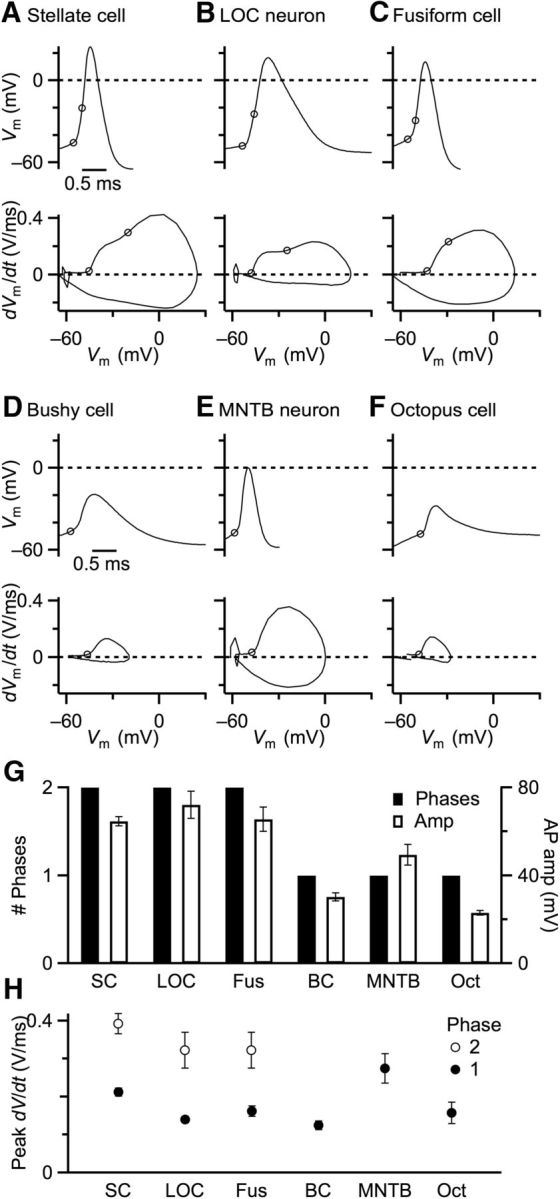
APs of auditory neurons. A–F, Representative single traces from neurons with overshooting APs (A–C) and nonovershooting APs (D–F). Top traces represent responses to current injection (600 pA). Bottom traces represent phase-plane plots. The start of each phase is indicated by open circles on the phase-plane plots with the corresponding time on the top traces. G, H, Quantification of auditory APs, showing number of phases in phase-plane plots (G, solid bars), overall AP amplitude (G, open bars), amplitude of first (H, closed circles), and second phases (H, open circles). Values are mean ± SEM.

We compared these against auditory neurons that have a number of cellular specializations associated with precise AP timing: BCs in the AVCN, principal neurons in MNTB, and octopus cells in posteroventral cochlear nucleus. BCs relay temporal information from ANFs to MNTB neurons (Spirou et al., 1990; Kuwabara et al., 1991; Smith et al., 1991; von Gersdorff and Borst, 2002), which in turn relay precise timing information to various auditory brainstem targets (Joris et al., 1998; Brand et al., 2002). Octopus cells integrate temporal information across groups of ANFs (Golding et al., 1995; Oertel et al., 2000). All these cells had nonovershooting APs (Fig. 1D–F, top traces). The phase-plane plots of these cells showed a single phase, most likely from the AIS (Fig. 1D–F, bottom traces), and this was consistent in multiple cells of each type (Fig. 1G, solid bars).

We quantified AP characteristics from several cells of each type (5 SCs, 4 LOC neurons, 6 DCN fusiform cells, 5 BCs, 6 MNTB neurons, 3 octopus cells). The three cell types with 2 phases had high-amplitude APs, whereas the three cell types with 1 phase had low-amplitude APs (Fig. 1G, open bars). We also quantified the peak derivative for each AP phase in both groups. In cells with two phases, if a clear maximum was not reached for the first phase, then the amplitude was taken from the inflection point between the two phases. The first phases had very similar amplitudes across all cell types, except for MNTB neurons, which were larger (Fig. 1H, closed symbols). This suggests that the AIS functions similarly across all the neurons we considered. For the cells with second phases, the peak rate of depolarization was similar (Fig. 1H, open symbols), suggesting that Na channel activation in the soma was similar for that group of neurons. These data indicate that there is a significant dichotomy in AP characteristics, with a specialized subset that possesses cellular characteristics associated with precise timing appearing to lack somatic APs.

Properties of somatic Na currents in BCs and SCs

We investigated why BCs lack a somatic AP by comparing with neighboring SCs, which do have somatic APs. We compared the properties of somatic Na currents using nucleated patches. This approach allowed excellent voltage control, isolation of strictly somatic Na channels, and reduced patch capacitance, all of which were important for rapid recordings near physiological temperature.

We measured the voltage dependence of g_Na activation by holding patches at −120 mV and stepping to V_step from −110 to 20 mV. Na currents during the depolarizing capacitance transient were revealed by adding the inverse capacitance transient occurring at the end of the voltage pulse. Na currents were pharmacologically isolated by using TEA, Co²⁺, Ni²⁺, and Cd²⁺ to block K and Ca channels. Representative individual traces are shown for a SC and BC in Figure 2A, showing current that activated and inactivated extremely rapidly. In the currents of Figure 2A, the fastest activation reached a peak within ∼100 μs, and inactivation had a decay τ of <0.2 ms. We confirmed that these were Na currents by applying TTX (1 μm), which completely abolished the remaining current (Fig. 2Aiii,iv). This gives us high confidence in the quality of the voltage clamp in dealing with such fast currents. We derived I–V curves for the data in Figure 2A, which showed that the amplitude of Na current was maximal at ∼−10 mV in both BCs and SCs (Fig. 2B). We converted these currents to conductances using the relationship g_Na = I/(V_step − E_Na). We estimated E_Na to be 72 mV based on the Nernst equation for our experimental conditions, and 70 mV by linear extrapolation of the I–V curve, which are in very close agreement, again giving us confidence in the quality of our voltage clamp. After converting to conductance, we normalized to the maximal conductance g_max and plotted against V_step to obtain activation curves (Fig. 2C). BCs and SCs showed similar voltage dependence of activation.

To compare inactivation characteristics, the nucleated patches were held at voltages (V_hold) from −150 to −20 mV and stepped to 0 mV (Fig. 2D). Normalized conductance g/g_max was plotted against V_hold to obtain steady-state inactivation curves (Fig. 2E). The steady-state inactivation curve of the BC was shifted to more hyperpolarized values, similar to what was found in MSO neurons (Scott et al., 2010).

We found similar results in 14 SCs and 15 BCs. Averages of activation and inactivation curves are shown in Figure 2F, G. The activation data of individual cells was fitted with a Boltzmann function as follows:

The two cell types did not differ significantly in slope factor, k_act (SCs: 7.7 ± 0.7 mV; BCs: 8.3 ± 0.9 mV; p = 0.11) or in half-activation voltage, V_1/2^act (SCs: −35.1 ± 1.2 mV; BCs: −34.2 ± 1.0 mV; p = 0.58; Fig. 2H). The inactivation data were also fitted with an equivalent Boltzmann function. The slope factor k_inact of the inactivation curve was significantly different between SCs and BCs (SCs: −12.1 ± 0.3 mV; BCs: −13.9 ± 0.2 mV; p < 0.001), indicating that the voltage dependence of inactivation is significantly steeper for BCs. In addition, the half-inactivation voltage V_1/2^inact was strongly hyperpolarized in BCs compared with SCs (SCs: −73.1 ± 1.9 mV; BCs: −86.2 ± 1.4 mV; p < 0.001; Fig. 2I). The hyperpolarization of V_1/2^inact likely decreases the proportion of available (i.e., deinactivated) Na channels in BC somata, contributing to the lack of somatic AP.

We also compared the amplitude of the Na currents. The peak magnitude of the Na current was highly variable across patches (Fig. 2J). One source of this variability was rapid rundown of Na currents. We tried to minimize this effect by completing recordings as quickly as possible, and keeping the delays similar across BC and SC recordings. A second source of variability was the size of patches, which can be estimated by quantifying capacitance (Fig. 2K) (Gentet et al., 2000). Peak current was normalized to patch capacitance to yield the current density (I_density), which was significantly lower in BCs compared with SCs (U = 51.5, p = 0.0054, two-tailed Mann-Whitney-Wilcoxon test; Fig. 2L). Functionally, what is important to spiking is the availability of Na channels, which is affected by both their density and the degree of inactivation around resting membrane potential. Resting membrane potential is near −60 mV for both BCs and SCs (Oertel, 1983). We compared I_density at −70 mV (Fig. 2M) and −60 mV (Fig. 2N), and both were lower in BCs compared with SCs. The difference was significant at −70 mV (U = 47, p = 0.0091, two-tailed Mann-Whitney-Wilcoxon test), but not at −60 mV (U = 67, p = 0.093). Thus, the low availability of Na channels at rest probably causes BCs to lack somatic APs.

Na channel model and dynamic clamp

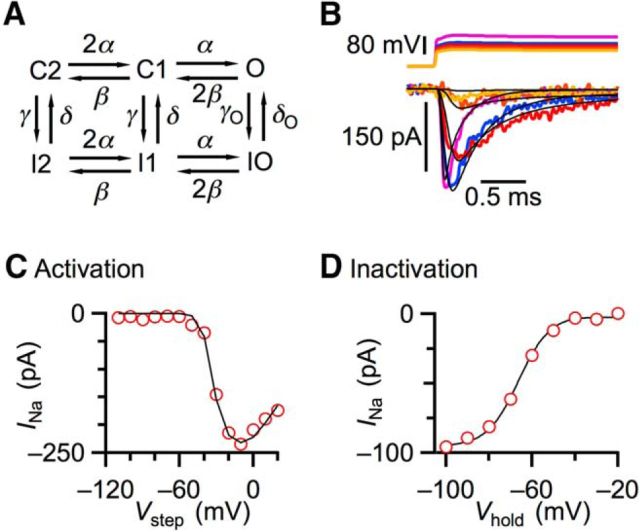
We wanted to understand how the precision of AP initiation in BCs would change if they expressed Na channels like those that SCs have. To address this, we aimed to use dynamic clamp to mimic current based on a model of g_Na. We used a simple 6-state Markov model with 2 closed states (C₁, C₂), 3 inactivated states (I₁, I₂, I_O), and a single open state (O) (Fig. 3A). The transitions between states were given by voltage-dependent rates α, β, γ, δ, γ_O, and δ_O, each of which took the same general form with two free parameters (Table 1). The parameters were adjusted to fit the activation and inactivation data of Figure 2. Example activation data and the model fits are shown in Figure 3B. The model yielded activation and inactivation curves very similar to actual data (Fig. 3C,D). Thus, this simple model was successful at capturing Na channel behavior.

Figure 3.

Na channel model. A, Gating scheme of the six-state kinetic Markov model used for reproducing Na channel-gating properties. B, Top traces represent voltage pulse protocol. Bottom traces represent simulated Na currents using the model (black traces) matched with the actual current traces (color traces). C, D, Predictions of Markov model of Na current (black lines) compared with data recorded (red circles), for peak activation (C) and inactivation (D).

Table 1.

Transition rates for Markov model of g_Na in Figure 3^a

Rate	A (s)	B (mV)
α	97719.6	30.8128
β	1088.88	−8.99497
γ	1714.73	15.0341
δ	0.164334	−13.7795
γO	3320.14	110.382
δO	0.104053	−11.7251

^a Each transition rate is voltage-dependent according to the equation, X (V) = A exp (V/B), with A and B given according to the table.

The fast kinetics of Na channels require a dynamic clamp that performs very rapidly. To confirm that the dynamic clamp was fast enough in real cells near physiological temperature, we recorded from BCs with two-electrode dynamic clamp and injected current pulses to elicit APs. We also needed to determine how much g_Na was needed to generate an overshooting AP in BCs. This amplitude could differ from SCs because of differences in cellular architecture and input resistance, so this had to be determined empirically by bracketing the likely g_Na between 0.2 and 1 μS. With g_Na of up to 1 μS, the “Na current” passed by the dynamic clamp increased the depolarization following a stimulus (Fig. 4A, top traces), leading to large, overshooting APs with fast kinetics (Fig. 4A, bottom). The peak conductance and current reached very high levels, which necessitated the use of two-electrode dynamic clamp to avoid large pipette capacitance artifacts. We verified that g_Na had no effect on input resistance around resting membrane potential (R_in at −60 mV for 0 μS = 40.8 ± 4.6 mΩ; R_in for 1 μS = 44.3 ± 3.8 mΩ; p = 0.4; N = 10; Fig. 4C).

The overshooting APs generated using the dynamic clamp looked quite normal in their kinetics. The half-width of APs decreased as g_Na increased, and for 1 μS g_Na, APs in BCs were nearly as fast as in SCs (0.47 ± 0.05 ms in 31 BCs vs 0.34 ± 0.01 ms in 29 SCs; Fig. 4D). Furthermore the shapes of phase-plane plots in BCs with g_Na implemented in dynamic clamp were qualitatively similar to SCs, notably during the upstroke of the AP (compare Fig. 4E and Fig. 1A). We quantified the time interval between the first and second phases of the BC AP (Fig. 4E, circles) when using the dynamic clamp. These were similar between SCs and BCs with g_Na added (at 1 μS, 0.21 ± 0.00 ms in 24 BCs vs 0.18 ± 0.00 ms in 29 SCs; Fig. 4F). These results indicated our g_Na model in dynamic clamp ran fast enough to qualitatively and quantitatively reproduce overshooting APs in BCs.

Somatic g_Na reduces AP probability and precision

We tested how g_Na influenced synaptically evoked APs by recording from BCs using two-electrode dynamic clamp, and stimulating a single ANF at physiologically relevant rates (200 Hz). Different levels of g_Na were applied by the dynamic clamp on interleaved trials. AP probability, latency, and SD of latency (“jitter”) were quantified during the second half of the stimulus train (pulses 11–20) when EPSP amplitudes are relatively uniform. Raster plots show a clear decrease in AP probability for g_Na ≥0.2 μS (Fig. 5Ai vs Fig. 5Aii–iv). We found similar results in 6 experiments. The absolute AP probability, latency, and jitter are shown in Figure 5B–D, and the changes relative to control (0 μS g_Na) are shown in Figure 5E–G. AP probability decreased significantly (p < 0.02; Fig. 5E), latency increased (p < 0.02; Fig. 5F), and jitter increased (p < 0.01; Fig. 5G). Thus, AP reliability and precision were degraded as a result of somatic g_Na.

g_Na suppresses APs by recruiting K_V3 channels

The reduction in spiking in the experiments of Figure 5 was surprising because the Na conductance is fundamentally excitatory, so one might expect an increase in spiking, particularly for EPSPs near threshold. In addition, the AP was accelerated with increased g_Na, so one might expect BCs to be able to respond more quickly to subsequent synaptic input. However, we observed the opposite, suggesting that when an AP was triggered, the increased depolarization in the soma recruited processes that interfered with initiation of subsequent APs in the AIS. Two possibilities for a higher-amplitude AP to suppress subsequent APs could be either by increased activation of K channels, or by increased inactivation of Na channels in the AIS. Both possibilities were explored by measuring how AP threshold changed with different levels of g_Na. We applied pairs of synaptic conductances in dynamic clamp. The first, conditioning pulse was always suprathreshold, followed by a second, test pulse at different time intervals. We quantified the minimum conductance amplitude required to fire an AP during the test pulse (“threshold conductance”).

We examined how potassium channel activation influenced the threshold conductance, focusing on K_V1 and K_V3 channels, which are likely to be activated in BCs by larger APs (Manis and Marx, 1991; Wang et al., 1994; Grigg et al., 2000). α-Dendrotoxin (DTX, 50 nm), which blocks K_V1 channels, significantly affected firing of BCs in response to current injection (Fig. 6A) but had only a minor effect on AP shape and afterhyperpolarization (Fig. 6B). We wanted to investigate how transient activation of DTX-sensitive channels during the AP might influence subsequent threshold, independent of their role in setting resting membrane potential (Cao et al., 2007), so we corrected resting membrane potential to −60 mV throughout the experiment. DTX had little effect on threshold. In the example of Figure 6Ci, the threshold conductance of the test pulse was 13.6 nS in control, and increased to 18.8 nS when 1 μS g_Na was applied using dynamic clamp, consistent with the reduced spiking of Figure 5. This situation was unchanged by the addition of DTX. In DTX, threshold for the test pulse was 13.9 nS with no added g_Na, and increased to 19.0 nS with 1 μS g_Na (Fig. 6Cii). Thus, K_V1 channels appeared not to contribute to the increase in threshold with added g_Na.

We obtained quite different results with tetraethyl ammonium (TEA), which primarily blocks K_V3 channels at 1 mm concentration. TEA had a large effect on AP shape, greatly lengthening the duration, and eliminating the afterhyperpolarization (Fig. 6D,E). Most importantly, adding g_Na had less effect on conductance threshold in the presence of TEA. In the representative example of Figure 6Fi, in control conditions the conductance threshold of the test pulse increased from 20.0 nS to 28.0 nS when 1 μS g_Na was applied, similar to Figures 5 and 6Ci. However, after adding TEA, the threshold increased less when 1 μS g_Na was applied, from 21.0 to 23.0 nS.

Similar results were found in multiple experiments. In control conditions (i.e., no antagonist), addition of g_Na increased the conductance threshold, especially at the shortest intervals and with highest g_Na (Fig. 6G, black symbols; filled symbols mark significant differences compared with 0 μS g_Na with p < 0.02; 9 experiments). This increase in threshold had a duration (>10 ms) that greatly outlasted both the underlying synaptic conductance (∼0.5 ms) and the AP it triggered (∼2 ms), which indicates that the increase in threshold is a long-lasting aftereffect of the AP. These effects were nearly identical in DTX (Fig. 6G, blue symbols; 4 experiments). When we computed the difference between control and DTX conditions within experiments, DTX had no significant effect on threshold for any level of g_Na at any time intervals (p > 0.18 for all comparisons between DTX and no drug; Fig. 6H, blue symbols), suggesting that K_V1 channels did not contribute to the increased AP threshold. By contrast, in TEA, changes in threshold after the conditioning pulse were particularly reduced at short intervals and with high g_Na (Fig. 6G, red symbols; 5 experiments). The effects of TEA compared with control were significant for g_Na ≥0.2 μS and at intervals ≤10 ms (Fig. 6H, red, filled symbols mark comparisons between TEA and no drug with p < 0.04). These results are consistent with increased AP amplitudes enhancing the activation of K_V3 channels and raising AP threshold, which reduces the likelihood of subsequent APs.

An alternative explanation might be that TEA influences the conductance threshold simply by prolonging the conditioning AP, such as by depolarizing the BC closer to threshold. If that were the case, then TEA should reduce threshold for all levels of g_Na. However, this was not what we observed. We saw a large decrease in conductance threshold only when g_Na was added, but not in the absence of added g_Na (Fig. 6Fi,ii, left; Fig. 6H, red circles). This indicates that the prolonged AP alone did not reduce conductance threshold.

These results also provide insight into whether increased AP amplitudes significantly inactivate Na channels in the AIS. If larger APs did cause significant inactivation of Na channels in the AIS, then broadening of APs by TEA application should increase conductance threshold yet further. However, we observed the opposite: adding TEA reduced the conductance threshold during the test pulse (Fig. 6H), which suggests that taller APs in the soma negligibly inactivate Na channels in the AIS. Thus, in normal BCs, low levels of somatic g_Na appear to prevent overactivation of K_V3 channels, supporting the ability of BCs to follow high rates of synaptic activation.

g_Na degrades the precision of coincidence detection

BCs receive synapses from multiple ANFs and can refine temporal information through coincident activity of these ANFs within a short time window (Burkitt and Clark, 1999; Xu-Friedman and Regehr, 2005a, b; Wang and Manis, 2008; Cao and Oertel, 2010; Chanda and Xu-Friedman, 2010a). In MSO neurons, Na channels can influence EPSPs (Scott et al., 2010), and thereby might affect coincidence detection. We tested this in BCs by examining the effects of 0.5 μm TTX on subthreshold EPSPs applied in dynamic clamp. TTX caused EPSPs to get smaller and faster (Fig. 7A), with average amplitudes decreasing by 10.4 ± 2.4% (N = 5, p < 0.01) and half-widths decreasing by 36.2 ± 8.5% (p < 0.01) (Fig. 7C). This indicates that endogenous Na channels play a role in amplifying and slowing EPSPs. However, we were unable to distinguish whether these effects resulted from endogenous somatic or AIS Na channel activation.

To address whether somatic g_Na could amplify EPSPs, we examined the amplitude and time course of subthreshold EPSPs applied in dynamic clamp in the added presence of 1 μS g_Na. We found that this caused EPSPs to get bigger and slower (Fig. 7B), with average amplitudes increasing by 11.5 ± 0.5% (N = 7, p < 0.001) and half-width increasing by 33.8 ± 1.5% (p < 0.001) (Fig. 7C). This raises the possibility that somatic g_Na could cause EPSPs to summate over longer intervals, reducing the precision of coincidence detection.

To test this possibility, we applied two subthreshold synaptic inputs using dynamic clamp in trains at varying time offsets and quantified AP probability. An example experiment is shown in Figure 7D. The BC fired many APs over the course of the train when the two inputs were simultaneous, but the AP probability decreased as the offset increased >0.5 ms, reflecting a precise window of coincidence detection.

However, when g_Na was added, we observed two effects. First, the AP probability for simultaneous inputs decreased (Fig. 7E), likely for the reasons explored in Figures 5 and 6. To focus on other effects, we normalized AP probability at 0 ms offset to 1 for all g_Na levels. More strikingly, the AP probability was elevated for offset inputs, even when the offset was as large as 5 ms (Fig. 7E). In control (0 μS g_Na), AP probability dropped >50% for 1 ms offset. With g_Na ≥0.5 μS, AP probability decreased by only 20% for 1 ms offset (Fig. 7F).

We found similar results in 7 experiments. AP probability increased significantly with g_Na ≥0.5 μS, particularly for offsets ≥1 ms (N = 7, p < 0.05; Fig. 7G). The greatest increases in AP probability were seen at long time intervals (Fig. 7G). We quantified the width of the coincidence window by fitting the AP probability data with the function P = 1/[1 + (t_1/2/Δt)^1/k], where t_1/2 is the offset at which P drops to 50%. The window was significantly wider for g_Na ≥0.5 μS (0.74 ± 0.07 ms for 0 μS, 1.78 ± 0.31 ms for 0.5 μS, and 2.77 ± 0.29 ms for 1 μS, N = 5, p < 0.018; Fig. 7H), indicating that coincidence detection is less precise with somatic g_Na. Thus, EPSPs appeared to activate a small, but significant, endogenous Na current, which increased and prolonged depolarization. With additional amplification by somatic g_Na, EPSPs were more likely to summate and cross threshold, which can decrease precision of coincidence detection.

Discussion

Here we show that a number of time-coding auditory neurons have APs dominated by activity in the AIS, with a minimal somatic AP. In BCs, this lack of somatic AP appears to result from low Na channel density and hyperpolarized inactivation voltage sensitivity, similar to what has been described in MSO neurons (Scott et al., 2010). Using dynamic clamp, we showed that minimal g_Na in the soma enhances response to repetitive synaptic activation, most likely by limiting activation of K_V3 channels. In addition, low somatic g_Na enhances the precision of coincidence detection, probably by minimizing amplification and prolongation of EPSPs by Na channel activation. Thus, low somatic g_Na appears to be an adaptation for enhancing spiking fidelity and precision. This is likely a common principle for additional time-coding neurons in the auditory pathway.

Inactivation

Our nucleated-patch measurements of somatic Na channels in BCs show activation characteristics highly similar to SCs, but with inactivation sensitivity shifted to more negative potentials. Therefore, at resting membrane potential, there is very little Na current available. This likely explains the lack of somatic AP in BCs.

This raises the question, mechanistically, why BC Na channels have negatively shifted inactivation sensitivity. One possible explanation is that SCs and BCs express different Na channel α subunits. The most common α subunits in the CNS are Na_V1.1, 1.2, 1.3, and 1.6 (Smith and Goldin, 1998; Yu and Catterall, 2003). In expression systems, Na_V1.6 appears to have the most hyperpolarized inactivation sensitivity, ranging from V_1/2 = −48 to −69 mV in different studies (Isom et al., 1992; Xie et al., 2001; Burbidge et al., 2002; Chen et al., 2008; He and Soderlund, 2014). β subunits could also contribute to inactivation voltage sensitivity, depending on the specific α and β subunit (Smith and Goldin, 1998; Meadows et al., 2002; Zhao et al., 2011; Calhoun and Isom, 2014). Little is known about which α or β subunits are expressed by BCs or SCs.

A second important question is, functionally, why BCs retain Na channels if they are largely inactivated at rest. In MSO neurons, which also have Na channels with relatively hyperpolarized inactivation sensitivity, g_Na amplified EPSPs arriving at the dendrites and preserved a linear response (Scott et al., 2010). In our dynamic clamp experiments in BCs, such amplification also had the consequence of driving a cell over threshold even when synaptic inputs were poorly coincident. If that also happened in MSO neurons, it would seem to interfere with their function in sound localization, which likely depends on precise coincidence detection (Goldberg and Brown, 1969; Yin and Chan, 1990; Joris et al., 1998). It is possible that g_Na has less effect on EPSP kinetics in MSO neurons, perhaps because of the anatomical arrangement of synaptic inputs onto distal dendritic branches, whereas in BCs synapses are axosomatic.

Dynamic clamp of g_Na

Dynamic clamp was very useful in studying the effects of somatic g_Na in BCs. The effects of somatic g_Na on coincidence detection have primarily been studied using pure computer models (Kuba et al., 2006; Ashida et al., 2007). By using dynamic clamp, we could study the effects of g_Na without making assumptions about the characteristics of BCs synapses, AIS Na channels, or K conductances. This could be an issue because the specific properties of AIS Na channels are not well understood and are critical for AP initiation (Colbert and Pan, 2002). Dynamic clamp experiments leave the endogenous AIS intact, which preserves the characteristics of AP initiation as much as possible.

Furthermore, dynamic clamp has advantages over transgenic approaches for increasing Na channel density because dynamic clamp allows the conductance amplitude to be adjusted over a wide range within a single experiment, so that more conditions can be tested. In addition, acute expression of the Na conductance by dynamic clamp makes it less likely for other conductances to be upregulated or downregulated, such as in response to changes in activity.

Potassium channels and g_Na

Our study may help illuminate why somatic g_Na levels are low in time-coding neurons. A large somatic g_Na appears to recruit K channels following APs. Considerable evidence indicates that K channels contribute to precise spiking in BCs (Manis and Marx, 1991; Brew and Forsythe, 1995; Rothman and Manis, 2003b). K_V1 channels suppress repetitive APs and accelerate the membrane time constant so that BCs respond rapidly and with only a single AP to synaptic activity (Manis and Marx, 1991; Rothman and Manis, 2003a; Cao et al., 2007; Cao and Oertel, 2010). They also help suppress APs driven by asynchronous neurotransmitter release (Yang and Xu-Friedman, 2010).

The K_V3 channels contribute to rapid AP repolarization and the AHP, which speeds recovery of Na channels from inactivation (Manis and Marx, 1991; Wang et al., 1998), so a BC can be ready as rapidly as possible for the next EPSP. Indeed, for time-coding auditory neurons in the MNTB, K_V3 channels appear to be upregulated in response to high levels of activity, which supports rapid spiking (Song et al., 2005). However, our results suggest that, if K_V3 activation is too strong, it may suppress synaptically evoked APs (Fig. 6). Neurons with low somatic g_Na may thereby moderate activation of K_V3, which could optimize responses to rapid synaptic input. Our experiments reveal that the balance of potassium channel activation must be carefully regulated.

Time-coding neurons show unusually high expression of K conductances, which has led to intense experimental and modeling investigation for many years: in BCs (Manis and Marx, 1991; Rothman and Manis, 2003a); in MSO (Svirskis et al., 2003; Scott et al., 2010; Khurana et al., 2011); in MNTB (Brew and Forsythe, 1995; Wang et al., 1998; Klug and Trussell, 2006); in octopus cells (Golding et al., 1999; Bal and Oertel, 2001). Such results as well as ours underscore that the interactions can be complex and unexpected, particularly in the context of AP initiation.

Somatic AP and precise timing

The group of time-coding neurons in the auditory pathway we examined are unusual in that they display exceptional fidelity and precision while also experiencing extremely high levels of activity, of up to 500 Hz (Johnson, 1980; Joris et al., 1994; Taberner and Liberman, 2005; Lorteije et al., 2009). These neurons also had reduced AP amplitudes, and phase-plane plots indicated that this likely results from activity only in the AIS and not the soma. MSO neurons in gerbils also have reduced APs, and their somatic Na channels also have hyperpolarized voltage sensitivity (Scott et al., 2010). These adaptations are likely shared by octopus cells, which have very reduced AP amplitudes.

MNTB neurons differ somewhat from the other time-coding neurons we have focused on. The MNTB AP reaches a higher peak than BCs, MSO neurons, and octopus cells. On the other hand, the AP size is lower than conventional neurons and only a single phase is discernible, indicating that the soma has unusually low Na channel activation. Na currents have been examined in MNTB neurons in a few studies (e.g., Leão et al., 2006; Johnston et al., 2008), and they have not shown unusual characteristics, although the experimental conditions differ significantly from the ones used here, in terms of temperature, maturation, and whether the recordings include both soma and AIS. It may be that the AIS is electrotonically close to the soma, which would yield midsized AP amplitude with a single phase. It will be interesting to investigate the mechanism for these reduced APs in MNTB further and how they may influence spiking.

Indeed, in neurons of the avian nucleus magnocellularis, which have similar function to BCs in the mammalian AVCN, AP amplitude varies tonotopically, with high- and middle-frequency neurons showing the smallest AP amplitude, and low-frequency neurons having relatively tall APs (Kuba and Ohmori, 2009). This seems to correlate with the length and intensity of AIS immunostaining for Na channels. Computer simulations suggested that a high density in the AIS could enhance responsiveness, particularly to small synaptic inputs (Kuba and Ohmori, 2009). This effect seems similar to the widening we observed for the window of coincidence detection upon adding somatic g_Na to real neurons using dynamic clamp (Fig. 7). Thus, amplification of EPSPs can have both positive and negative consequences.

In non–time-coding neurons, the adaptive pressures may be quite different. First, activity levels may be lower and precision less stringent, so the negative consequences of somatic Na channels may be low. Furthermore, somatic Na channels may support additional functions. Synapses on distal dendrites may use information about spiking activity to dictate long-term plasticity. Passive back-propagation from the AIS alone may be inadequate without amplification by Na channels in the soma. This seems most important in neurons that express long-term plasticity in extremely large dendrites, such as in cortex or hippocampus (Magee and Johnston, 1997; Markram et al., 1997).

Remarkably, few forms of long-term plasticity have been described in the time-coding auditory neurons, so it is possible that retrograde signaling is less important (Taschenberger and von Gersdorff, 2000; Futai et al., 2001; Joshi et al., 2007). In MSO neurons, a role has been proposed for Na channels in anterograde dendritic signaling (Scott et al., 2010). The dendrites of BCs appear to largely receive inhibitory inputs (Ostapoff and Morest, 1991), so it may be that somatic Na channels have little benefit. Thus, it appears that there are primarily significant costs to expressing Na channels in the somata of BCs, so lacking them seems more adaptively advantageous.