Survey and Classification of Operational Control Problems in Discrete Event Logistics Systems (DELS)

Abstract

This paper reviews and classifies literature on operational control of discrete event logistics systems (DELS). Operational control manipulates the flow of items through a DELS. Each control problem addressed in the surveyed literature is classified based on the control decision that the analysis model is formulated to support. These control decisions are defined by abstract functional definitions focusing on analysis model inputs, outputs, and variables. This classification of control problems shows that five kinds of atomic control decisions are needed to cover the literature, either by themselves or in combination. Standard functional definitions of operational control decisions enable discovery and interoperability of decision-support analysis models.

1. INTRODUCTION

Discrete Event Logistics Systems (DELS) transform items flowing through a network of interconnected resources (Mönch et al. 2011). DELS include systems such as supply chains, manufacturing systems, transportation networks, warehouses, and health care systems. Traditionally, each kind of DELS is addressed with its own dedicated research and development field. However, these systems share a common abstraction — products transformed by processes executed by resources configured in a facility — and are integrated into complex enterprises. For example, production systems integrate storage and fulfillment capabilities as well as material handling and transportation systems. Supply chains integrate flows between warehouses, transportation systems, and manufacturing or health care facilities.

Designing, operating, and analyzing these complex, integrated systems require that models of them include operational control behaviors for managing flows of items through the system, such as admitting/rejecting jobs or customers to the system (admission control problem) or assigning resources to serve admitted jobs (resource assignment problem). Analysis models supporting operational control decisions (decision-support methods) are well-studied in industrial engineering and operations research. Decision-support methods recommend control actions when given potential alternatives and associated outcomes. However, identifying requirements for control decisions, including their desired effects, and defining possible actions for achieving that effect are less well-studied.

It is challenging to identify suitable decision support methods for each kind of control decision and integrate them with system models. The operational control literature, including analysis models and solution methods, is often classified by the name of the control activity. However, many domain-specific names are used for each control activity, leading to overloaded, ambiguous, or vague terminology. Some control problems, such as scheduling, involve multiple decisions and result in multiple actions. Inconsistent or incomplete definitions of operational control lead to implementation and interoperability problems. This makes it difficult to extend and reuse research. A unifying abstraction of operational control decisions across heterogeneous DELS would be beneficial to classifying and organizing research, as well as identifying applicable analysis models and suitable tools for implementation.

The survey of operational control literature in this paper focuses on how control problems are modeled, as described in Section 2. Control problems are classified according to the expected effect of decisions and the resulting actions (“control functions”). For the admission example given above, a decision to serve a particular task requires a corresponding action, such as triggering a conveyor actuator, to bring the task and its associated workpiece into the system. This definition of control ties “what kind of decision has to be made?” to “what actions can be taken?”. We distinguish between the kind of decision to be made (what function is required) and how the decision is made (the method, logic, or algorithm used). Functional definitions are an abstraction of the behaviors that implement them, both for decision support and decision execution. Using standard functional definitions (kinds of decisions) to classify operational control decision-support enables discovery of analysis models and methods applicable to a particular kind of decision. Each paper in the literature addresses one control problem, which may involve one or more atomic control decisions; analysis models are formulated to make their control problems mathematically precise and accessible; analysis methods start with a mathematical formulation of a problem and provide a solution to it.

The classification shows that five kinds of decisions (atomic control functions, outlined in Section 2) are needed to cover the operational control literature, either by themselves or in combination. The survey identifies commonalities across heterogeneous DELS domains by emphasizing well-cited examples of each control problem in each domain, drawing connections to applications in adjacent domains. This approach places less emphasis on novel solutions to classic problems and less coverage of contemporary research. The survey includes selected papers that provide a clear description of the control problem formulated with decision variables linking the decision to be made to execution of the selected action. The classification scheme and surveyed literature are summarized in Section 9.

Standard definitions of these control functions provide a suitable theoretical foundation for specifying and designing operational control in DELS. This model of control decisions extends others found in queuing systems (Tadj and Choudhury 2005) and discrete event systems (Cassandras and Lafortune 2008). We first present the model used to classify operational control problems, including one for the plant under control (Section 2). Sections 3 through 7 are each dedicated to one atomic control function that has one effect on the system and defines a class of control problems that conform to a standard definition of that function.

2. Modeling Operational Control

An operational control model articulates the atomic control decisions involved in managing system behavior. It also provides a framework for classifying analysis models that support making these control decisions. To provide context for operational control, consider the simplified plant-controller model in figure 1. A controller interacts via sensors and actuators with the base system, or plant. The controller consists of a decision-maker and decision support. The decision-maker observes the system and reacts by querying decision-support about potential actions it can take on the base system. Decision-support formulates an analysis model to answer the question (solve the control problem). The decision-maker uses the answer as input to selecting an action to be executed by an actuator in the base system. This architecture links decision making and support in the controller to executing control actions in the plant.

Figure 1.

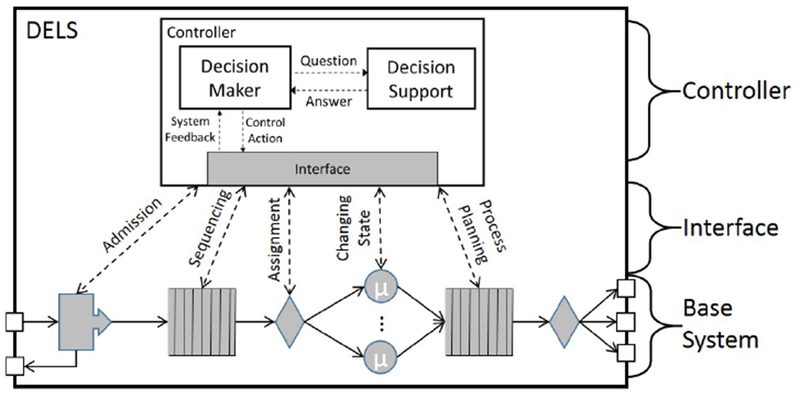
A standard set of control questions defines a comprehensive functional specification of all decision-making mechanisms that controllers need to manage system behavior.

The classification of control problems in the following sections proposes that five kinds of atomic control functions cover the literature for each kind of DELS. The informal control questions (enumerated below) make it easier to understand the kinds of DELS control decisions and actions required to manipulate the flow of items through the system (figure 1). The label associated with each control question below provides a succinct identifier, to stand in for the variety of equivalent terms used in the literature. The models in Sections 3 through 7 contain standard functional definitions for the control questions. The questions are:

• (1)‘should a task be served?’ (admission);
• (2)if so, ‘when should the task be served?’ (sequencing);
• (3)and, ‘by which resource?’ (assignment);
• (4)then, ‘what process step does the task require next?’ (dynamic process planning);
• (5)as well as, ‘in which state does a resource need to be?’ (changing-state).

This survey provides evidence that these questions, and the corresponding control functions, support a complete classification of DELS operational control behaviors. These atomic control functions can be combined into joint decision problems that select control actions for two or more control functions at the same time. For example, scheduling combines sequencing and resource assignment decisions and requires variable(s) that represent actions implementing both sequencing and assignment choices. Joint control decisions are discussed in Section 8. The next two sections describe a framework for modeling each control function, including an abstraction for describing the plant under control (section 2.1), and components of the functional definition used to define (model) control behaviors of the plant and controller (section 2.2).

2.1. System Under Control

One defining characteristic of DELS models is they share a common abstraction of their plants (systems under control). Each DELS plant/system model is specialized from a common abstraction of system behavior (figure 2): products transformed by processes executed by resources configured in a facility (PPRF). Additionally, tasks are the unit of work in DELS modeling, they authorize a process to be executed. Several other ontologies and information models for DELS share this abstraction; see, for example, Smith and Becker (1997), Madni et al. (2001), and Cutting-Decelle et al. (2007).

Figure 2.

A common abstraction of DELS (systems under control).

Abstract system models like this enable integration and interoperability of analysis models that support operational control decision making. Analysis methods designed for one kind of DELS can be applied (reused) on related DELS by mapping the descriptions of the systems to a common abstraction. For example, analysis methods for solving the traveling salesman problem (TSP) can be used to construct manufacturing schedules (Lenstra and Kan 1975), and methods for scheduling manufacturing job shops can be applied to scheduling nurses or operating rooms in a hospital (Pham and Klinkert 2008).

This paper uses the abstraction in figure 2 to refer to the plant under control in formulating operational control problems in Sections 3 through 7.

2.2. Operational Control Functions

The survey in this paper classifies control problems by a functional definition of the control behavior that is central to the problem. The definitions have two related components: a decision function and an actuator function, specifying the control behaviors of the controller and plant (system), respectively. This section defines these two functions and illustrates them with the resource assignment problem, which will be discussed more thoroughly in section 5.

Decision functions map system objects (input state) to control action alternatives (action space). This transformation formalizes the control question/answer interface between a controller’s decision-making and decision-support components. For example, the resource assignment decision function maps a task and set of capable resources (inputs) to the subset of resources assigned to serve the task (output action). Analysis models supporting resource assignment decisions should conform to this function.

Decision functions formalize patterns of selecting or specifying decision variables used to formulate optimization analysis models. In well-defined classes of control problems, decision variables have a specific structure that define (restrict) the input/output (state/action) spaces. For example, decision variables used in resource assignment problems prescribe an assignment of resources (control action) to serve a task. Rules that map input states to output actions are derived from analysis models formulated with explicit decision variables, where rules and variables both conform to the decision function; for example, see policies constructed by Markov decision process models (Puterman 2014). In optimization models, it is common to aggregate individual decisions or use implicit formulations to reduce computational complexity. Aggregated and implicit formulations conforming to a decision function can be evaluated and translated into explicit control decisions. Decision functions are abstract definitions of variables, rules, and policies that can be used to formulate analysis models addressing the associated control function (decision).

Actuator functions define the expected effects of actuators in the plant (desired outcome of executing control behaviors). While the decision function for resource assignment outputs a matching (assignment) of resources to tasks, the actuator function specifies that executing an assignment decision is a control action that acquires the assigned resources. Actuator functions do not prescribe how they are implemented or carried out. Actuators in the plant implement specialized behaviors to execute an actuator function. For example, assignment behaviors may depend on the type and location of resources to be acquired, quantity of resources, distance to be traveled, etc. However, the behaviors conform to an actuator function that requires bringing a task and its assigned resources together.

A complete model of an operational control function has a decision function linked to an actuator function: decision-support methods conform to the decision function and prescribe a control behavior (action) that conforms to the actuator function. This relationship between controller and plant functions enforces selection of control behaviors that the actuator is able to execute. Pragmatically, it links the value of optimization variables to actions that an actuator takes in the plant.

The following sections reference examples of control problem formulations (analysis models) and associated applications in the literature, classifying them by the control function they address. Each ‘control problem formulation’ section gives a pattern for formulating analysis models using optimization variables that conform to the decision function and whose solutions can be directly input into control behaviors executed by system actuators. The pattern is captured as a decision expression consisting of an optimization variable and semantics for interpreting the variable. For brevity, only the positive (true) result for each decision expression is given. In most cases, negative results for a decision expression indicate inaction (“do nothing”). For example, a “yes” result to a resource assignment indicates a particular task will be served by a particular machine; whereas a “no” result likely indicates that some other machine will serve that task, but does not require (or trigger) any action to execute. Each section describes representative operational control problems from a variety of DELS that can be mapped to the standard control function definitions. This illustrates that membership in each class of control problem is defined by conformance to the decision and actuator functions.

3. ‘Which tasks to serve?’ (Admission)

When a task requests a service (process), the controller must decide whether to serve it. This decision controls the flow rate of tasks (work) into the system by accepting or rejecting arriving tasks (Kitaev and Rykov 1995). However, rejecting a task typically incurs a cost to the system, such as monetary penalties or lost sales and goodwill. The development of good acceptance rules, coupled with capacity-planning tools, leads to greater control over resource capacity. The admission decision function maps (↦) a task to a Boolean value (1). If the result is true, the corresponding actuator in the plant admits the task, which functionally means adding it to the system’s taskSet (2).

$$\mathit{Admission}:\text{Task}\mapsto \mathit{Bool}$$ (1)

$$\mathit{Admit}(\mathit{Task})≔\mathrm{System}.\mathrm{taskSet}\leftarrow \mathrm{System}.\mathrm{taskSet}\cup \mathit{Task}$$ (2)

System.taskSet in (2) denotes that the taskSet belongs to (is a component of) the System. The actuator function (2) is defined by (:=) updating/setting (←) the system component on the left side to the expression on the right side (component ← expression).

3.1. Control Problem Formulation

Define $\widehat{\mathcal{L}}$ as the set of tasks requested to be served, but not yet admitted, and $\mathcal{L}$ as the set of tasks already admitted. The control problem is formulated to select which additional tasks are admitted, ${\mathcal{L}}^{*}\subseteq \widehat{\mathcal{L}}$ (Godfrey and Powell 2002). The admitted tasks ${\mathcal{L}}^{*}$ are added to the system. Then the set of tasks available for the system to serve is $\mathcal{L}=\mathcal{L}\cup {\mathcal{L}}^{*}$ and the tasks rejected are $\widehat{\mathcal{L}}\backslash {\mathcal{L}}^{*}$ This control problem can be formulated with the decision variable in (3).

$$x_l=1,\text{if arriving task}l\in \widehat{\mathcal{L}}\text{is admitted}$$ (3)

3.2. Applications

When demand exceeds the capacity of available resources, order acceptance (admission) decisions select orders to maximize expected net present value (Slotnick 2011; De et al. 1993; Melchiors et al. 2018). Capacity allocation methods reject some orders (tasks) for less valuable products or from lower priority customers in anticipation of future demand from more valuable products or higher-priority customers (Topkis 1968; Balakrishnan et al. 1996; Ha 1997a). Capacity-driven order acceptance methods determine whether the system has capacity to serve an arriving order, and rejects it if it does not (Roundy et al. 2005). In assemble-to-order systems with limited inventory of common components, these components must be rationed to multiple end products with different profit margins by rejecting orders for products with lower margins (Balakrishnan et al. 1996). Partial back-ordering control policies reject customers when the back-order queue is greater than a preset threshold (Rabinowitz et al. 1995). Some vehicle routing problems (VRP) require only a predetermined subset of customers to be served and the remaining customers might be served if profitable to do so (Desrochers et al. 1990; Psaraftis et al. 2016; Ritzinger et al. 2016). In self-storage warehouses, storage orders (requests for a storage space) may be rejected to preserve future availability (Zhang et al. 2016). Formulation of order acceptance decisions is consistent with modeling of multi-choice, multidimensional knapsack problems, which are the foundation of many heuristic approaches (Hifi et al. 2004).

The task arrival and admission process may include a negotiation step. The negotiation includes a request for proposal, which the service provider responds to by offering a price, lead time, and any other contract parameters for the task; see, for example, project management applications (Herbots et al. 2007; Hartmann and Briskorn 2010; Melchiors et al. 2018; Öner-Közen and Minner 2018). Service providers may offer predefined menus of price and lead time combinations (posted-price model) for customers to select from (Duenyas 1995; Gallego and Van Ryzin 1997; Pekgün et al. 2008). Customer orders can be rejected explicitly, or implicitly by offering unacceptable contract parameters (Xie et al. 2016).

In health care systems, admission control in the form of advanced access or walk-in policies helps manage waiting times (Hulshof et al. 2012; Ahmadi-Javid et al. 2017). Admission planning methods for general hospitals select elective patients from waiting lists or determine the optimal mix of patients to be admitted to optimize utilization of available resources while reserving capacity for emergency admissions (Kusters and Groot 1996; Vissers et al. 2007; Range et al. 2018).

In each application, decision-support analysis models are formulated to provide yes or no (Boolean) answers to admission requests. For yes answers, the actuator adds the customer’s task to the system’s task set. Implicit approaches, such as using price/lead time menus, formulate policies offline and use them to guide online admission control decisions. Like explicit yes/no decision variables, each policy conforms to the decision function: if the price and lead time are agreeable to the customer, then admit the task.

4. ‘When, or in what order, an admitted task is served?’ (Sequencing)

Once the controller decides to admit a task, it must decide when, or in what order, to serve it. Sequencing methods range from constructing complete sequences of all admitted tasks to partial sequences of a subset of tasks. For example, predictive schedulers sequence all tasks in advance, whereas reactive schedulers choose which task (or sub-sequence of tasks) to serve in real time (Valavanis 1990). Dynamic or adaptive methods, such as those using dispatch rules, are a kind of partial sequencing that determine only the next task to be served, eventually sequencing all tasks awaiting service (Blackstone et al. 1982; Wein 1991). The sequencing decision function (Index) maps a task to its position relative to other admitted tasks in a priority list (4). The plant’s actuator function sorts the taskSet according to the position (Index) of each task (5):

$$\mathit{Index}:\text{Task}\mapsto \mathbb{N}$$ (4)

$$\mathit{Sequence}(\mathit{Index})≔\text{System.taskSet}\leftarrow \mathit{sort}(\text{System.taskSet},\mathit{Index})$$ (5)

4.1. Control Problem Formulation

Given admitted tasks, $\mathcal{L}$, a complete sequence of tasks is expressed as $\mathbf{\sigma }=\{l_1,l_2,\mathrm{\dots },l_n\},\forall l\in \mathcal{L}$. The corresponding control problem uses the variable $x_{l,j}$ to denote whether task l is sequenced in the $j^{th}$ position:

$$x_{l,j}=1,\text{if task}l\text{is served}{j}^{th}$$ (6)

Partial task sequences can be constructed by partitioning tasks into K subsets: $\mathbf{\sigma }=\{{\mathbf{\sigma }}_1,{\mathbf{\sigma }}_2,\mathrm{\dots },{\mathbf{\sigma }}_K\},\text{where}{\mathbf{\sigma }}_k=\{l_{k(1)},l_{k(2)},\mathrm{\dots },l_{k(n_k)}\}$ is the sequence of tasks in the $k^{th}$ partition (De et al. 1993). This approach can produce a complete ordering of tasks in a single partition, such as the partition to be served next, while leaving the other partitions partially ordered. The corresponding control problem may use the variable $x_{\mathit{l}}^k$ to denote that task l ∈ $\mathcal{L}$ is assigned to partition k ∈ K (7). The variable can be refined into $x_{l,j}^k$, which denotes that task l is sequenced in the j^th position within partition k (8):

$$x_l^k=1,\text{if task}l\text{is assigned to partition}k$$ (7)

$$x_{l,j}^k=1,\text{if task}l\text{is sequenced in the}{j}^{th}\text{position in partition}k$$ (8)

4.2. Applications

Sequencing jobs (tasks) is well-studied in the manufacturing domain; see, Adolphson (1977) for an early overview of single-machine, job sequencing models; Graham et al. (1979) for an overview of job sequencing problems in more general manufacturing systems; and Boysen et al. (2009) for an overview of sequencing problems and models in mixed-model assembly lines, where different products can be jointly manufactured in intermixed product sequences (lot size of one) on the same line.

In vehicle routing problems (VRP), sequencing determines the order in which tasks are served, or customers visited, by vehicle resources (Federgruen and Zipkin 1984; Golden et al. 2008; Toth and Vigo 2014; Grippa et al. 2016). Similar to sequencing pick-ups and drop-offs in CVRP (CVRPPD) (Desaulniers et al. 2000), dual-command cycles for automated storage and retrieval systems (ASRS) enable storage and retrieval requests to be sequenced on the same resource (Roodbergen and Vis 2009; Meneghetti et al. 2015; Thomasson et al. 2018). VRP models are used to sequence the dispersion of supply resources in disaster relief problems (Haghani and Oh 1996; Golden et al. 2014). In the health care literature, job shop models and solution heuristics are used to sequence surgical cases (Pham and Klinkert 2008; Dexter et al. 1999; Ahmadi-Javid et al. 2017). The control decision sequences patients, including priority emergency cases, in the waiting room while accommodating existing appointments (Magerlein and Martin 1978; Pham and Klinkert 2008; Hulshof et al. 2012). In maintenance systems, priority rules, such as passive opportunity windows, sequence maintenance tasks (jobs) to minimize impact on production (downtime/idle time of bottleneck resource) (Hoffman et al. 2018).

The following sections discuss common decision-making problems related to deciding “when, or in what order, to serve tasks,” using the sequencing formulation described above. These problems include partitioning task sets (section 4.3), coordinating multiple tasks (section 4.4), delaying service of tasks (section 4.5), batching tasks (section 4.6), and splitting tasks (section 4.7).

4.3. Partitioning the Task Set

Two common partitions used in sequencing formulations are based on time or on existing resource assignment decisions (see section 5). In the case of temporal partitioning, the variable $x_l^t$ may express whether task $l\in {\mathcal{L}}_t$ is served in period $t,t\in \{1,2,\mathrm{\dots },T\}$ (Godfrey and Powell 2002). The time-based formulation can be further reduced to two time buckets: this period and all other time periods. Then the decision simplifies to whether a task will be served in this period or not. Dynamic dispatching policies focus on selecting the next task to serve, where the size of the first partition is one. Hierarchical production planning and scheduling methods roughly partition tasks into time- and resource-based partitions, which are further refined into detailed schedules, often using heuristic approaches such as dynamic dispatch rules (Hax and Meal 1975).

4.4. Coordinating Tasks

Tasks can be sequenced to coordinate and optimize the usage of resources and subsystems, such as coordinating production and distribution tasks (Chandra and Fisher 1994; Chen 2010; Kim et al. 2015). In multi-item inventory systems, economies of scale can be realized by coordinating replenishment orders (tasks) for groups of items (Federgruen et al. 1984). The joint replenishment problem coordinates replenishing multiple products for multiple customers (Federgruen and Zipkin 1984; Campbell et al. 1998; Khouja and Goyal 2008). Vendor managed inventory (VMI) arrangements enable vendors to coordinate replenishment of multiple inventory items and consolidate shipping (Federgruen and Zipkin 1984; Çetinkaya and Lee 2000; Lee et al. 2003).

4.5. Delaying Service of a Task

The sequencing decision may delay service of a task until a later period. Backordering and inventory rationing are flexible strategies that complement pure admission or rejection decisions (Rabinowitz et al. 1995; Xie et al. 2016; Alfieri et al. 2017). Lower-margin (or priority) orders might be backlogged to reserve capacity for possible orders from high-margin, higher-priority customers (Çetinkaya and Lee 2000; Cattani and Souza 2002; Deshpande et al. 2003). This strategy may be used even when resource capacity, either machine time or inventory units, is available. For example, direct channel firms can postpone shipments to customers until later and then use more expensive, expedited shipment modes (such as drop-shipping) (Cattani and Souza 2002; Caggiano et al. 2006; Ayanso et al. 2006). Health care systems can respond to unplanned events, such as emergencies, by dynamically re-sequencing patients into future appointment slots (Magerlein and Martin 1978; Hulshof et al. 2012; Geng et al. 2017).

4.6. Batching Tasks

Sequencing methods can consecutively sequence any number of similar jobs, and batching is a type of sequencing method that waits for a pre-determined number of similar jobs before serving them. Also known as lotsizing, batching methods sequence items for transportation or manufacturing processing at the same time (Kuik et al. 1994; van der Zee 2017). Batching delays service of some jobs to use resources more efficiently by reducing setups. In the warehouse order partitioning problem, orders must be partitioned in time for ‘batch picking’ (Gu et al. 2007; Roodbergen and Vis 2009; Van Gils et al. 2018). In semiconductor wafer fabrication, tasks are sequenced to optimize batch process tools (Fowler et al. 1992; Kim et al. 2015). In freight consolidation, the transportation system decides whether to ship each arriving order immediately by itself, ship it immediately as part of a consolidated load (the order triggers the load release), or delay shipping to consolidate the order into a future load (Higginson and Bookbinder 1994). In same-day delivery systems, the decision maker chooses whether to dispatch a vehicle to make deliveries, and which tasks (orders) will be served at that time (Klapp et al. 2016). Batching may be considered a combination of ‘coordination’ and ‘delay service’-type decisions, where batching chooses to delay service of some tasks to improve the system efficiency by coordinating tasks that require similar processing.

4.7. Splitting a Task

Task splitting decisions, also referred to as activity, demand, or lot splitting, determine how a task’s work should be divided to accommodate constraints on capacity, due-date, priority, etc. Task completion is delayed until a later period. Often activity-splitting and preemption are considered to be interchangeable (Lawler et al. 1993; Cheng et al. 2015). In manufacturing production scheduling, just-in-time shipments (tasks) can be split into multiple production orders (tasks) to accommodate capacity constraints (Roundy et al. 2005). Split delivery VRP (SDVRP) enables customer demands to be satisfied by more than one delivery (Dror and Trudeau 1990). Activity splitting is also permitted as an extension of the resource-constrained project scheduling model (Buddhakulsomsiri and Kim 2006). Partial-service models are used for distributing disaster relief supplies (Barbarosoğlu et al. 2002; Özdamar and Ertem 2015).

The applications discussed in this section feature sequencing behaviors that produce complete or partial orderings of tasks waiting for sequence. Many applications use implicit variables or priority rules for sequencing tasks, but every application can be modeled with variables that provide a unique index for each task. Actuators, such as queues, use the index to sort available tasks and decide which task to serve next.

5. ‘Which resource is assigned to serve a task?’ (Assignment)

Each task authorizes the execution of a process, which requires resources to be executed. The type of process authorized by the task determines the required resource capabilities. Resource assignment control problems match tasks to a resource, or group of resources, that have the required capabilities, thereby allocating the resource’s capacity or availability to serving the task. The decision function maps a given task and capable resources to specific resource(s) to assign (match) to the task (9). The actuator function acquires resource(s) assigned to the next process step when needed (10). The acquired resource(s) fulfill the requiredlnputResource requirement (or slot).

$$\mathit{Assign}:\mathit{Task}\times \mathit{Resource}(s)\mapsto \mathit{Resource}(s)$$ (9)

$$\mathit{Acquire}(\mathit{Task},\mathit{Resource}(s))≔\mathrm{Task}.\mathrm{nextProcessStep}.\mathrm{requiredInputResource}\leftarrow \text{Resource}(s)$$ (10)

5.1. Control Problem Formulation

Each task in the system requires the completion of p_l process steps (O_l,1,…,O_l,pl). Each step can be processed by any resource $m\in M_{l,j}\subseteq \mathcal{M},\text{where}{M}_{l,j}$ is the subset of all resources $\mathcal{M}$ that can execute process step $O_{l,j}$. Multi-resource process steps require a resource group $R_{l,j}\subseteq \mathcal{R},\text{where}\mathcal{R}$ is defined as the set of all atomic resources. For multi-mode process steps, there are multiple capability-feasible resource groups,$\{R_{l,j}\}$. Resource groups are defined by composing atomic resources into aggregate resources, or “federations,” that collectively have the capability to serve a particular task (Mati and Xie 2011). Note, the process step notation O_i,j originates from job shop models, which define operations as the atomic unit of work (leaf) and ‘jobs are composed of operations’.

Many assignment formulations abstract, or simplify, the control problem by only assigning the bottleneck resource and/or only the next process step required by a task (dynamic assignment). In simplified assignment problems, $\mathcal{M}\subseteq \mathcal{R}$ is a subset of resources, such as critical machines, bottleneck resources, etc. Explicit assignment formulations define decision variables for each possible match between resources and tasks (11). This enables the solution to the optimization problem (“which specific, identifiable resource should be acquired?”) to be mapped directly to an executable action.

$$x_l^m=1,\text{if resource}m\in \mathcal{M}\text{is assigned to execute the next process step of task}l$$ (11)

The decision expression above can be extended to assign resources to multiple process steps at once (12). Another extension can assign resource groups (multiple resources) to one or more process steps (13).

$$x_{l,j}^m=1,\text{if resource}m\in \mathcal{M}\text{is assigned to execute the}{j}^{th}\text{process step of task}l(O_{l,j})$$ (12)

$$x_{l,j}^R=1,\text{if resource group}R\subseteq \mathcal{R}\text{is assigned to execute the}{j}^{th}\text{process step of task}l(O_{l,j})$$ (13)

5.2. Applications

Resource assignment decisions are featured prominently in job-shop scheduling problems (JSP), coupled with job sequencing decisions (scheduling is a non-atomic control problem, see Section 8.1). Flexible JSP (FJSP) considers multiple possible resources, usually machines, for each process step or operation (Brandimarte 1993; Kim et al. 2015). Capacitated processing networks model multi-resource allocation decisions, where resource capacity, such as machines or inventory, is allocated to fulfill demands (Van Mieghem and Rudi 2002). In assemble-to-order systems, inventory of common components are allocated to satisfy demands for several finished goods (Elhafsi et al. 2015). The complexity of resource assignment problems can be characterized by the degree of coordination required between types of resources (Powell et al. 2001). Resource-constrained project scheduling generalizes resource assignment decisions found in the classic JSP to apply beyond a manufacturing context (Herroelen et al. 1998; Hartmann and Briskorn 2010).

While CVRP is discussed extensively in the context of sequencing visits to customers, little of it focuses on which transportation resource should be assigned to a particular move task (Golden et al. 2008; Sassi and Oulamara 2017). Fleet sizing and composition decisions are integrated into the VRP formulation by considering heterogeneous collections of vehicle options of varying capacities and capabilities (Golden et al. 1984; Salhi and Rand 1993). Networks of autonomous UAVs delivering goods from depots to customers require assigning a particular transportation resource to each customer request (Grippa et al. 2016).

In health care systems, assigning patients to available resources requires knowledge about capabilities of clinical staff, support staff or medical equipment, and medical characteristics of patients (Magerlein and Martin 1978; Pham and Klinkert 2008; Hulshof et al. 2012; Ahmadi-Javid et al. 2017). In certain situations, patients may need to be assigned to specific nurses (resources) having special skills (capabilities) (Punnakitikashem et al. 2008; Ahmadi-Javid et al. 2017).

Warehouses have many interrelated resource allocation problems where labor and material handling equipment are assigned to load and unload the carrier trucks and pick and put-away products into storage (Rouwenhorst et al. 2000; Gu et al. 2007; Roodbergen and Vis 2009). However, auxiliary resources such as docks, sorter lanes, and storage locations also need to be assigned to trucks, orders, and SKUs, respectively. Warehouses might store a particular SKU in multiple locations, then must assign an inventory stocking location to fill an order from (Daniels et al. 1998; Alonso-Ayuso et al. 2013; Wutthisirisart et al. 2015). Storage systems must choose a location to store each item, such as selecting a slot in a storage rack or selecting from multiple onsite and offsite (3PL) storage warehouses (Wutthisirisart et al. 2015; Meneghetti et al. 2015; Yuan et al. 2018). In container terminal operations, berth allocation methods assign ships to available berths for loading and unloading (similar to warehouse truck-to-dock-door assignment problems), and quay crane scheduling methods often include assignment of vehicles and storage spaces to unload container ships (Bierwirth and Meisel 2010).

Disaster relief operations assign resources, including vehicles and labor, to transport casualties to medical care (Fiedrich et al. 2000; Rettke et al. 2016), distribute relief supplies (Haghani and Oh 1996; Özdamar et al. 2004; Balcik et al. 2008; Rawls and Turnquist 2010), and perform other tasks such as structure stabilization, lifeline restoration, and repairing major damage to public works (Brown and Vassiliou 1993; Fiedrich et al. 2000; Hu et al. 2016; Song et al. 2018).

Maintenance tasks (generated by a changing state control action, see section 7) must be assigned to maintenance resources with the required specialized capabilities (Nikolopoulos et al. 2003; Sriram and Haghani 2003). In maintenance, repair, and overhaul (MRO) logistics, operational decision-making requires trading off allocation of consumable resource capacity and renewable resource capacity through the joint allocation of available repair capacity among different items and available inventories to field stocking locations (Caggiano et al. 2006).

Domain-specific applications incorporate many kinds of resources with unique behaviors and constraints. Formulating assignment problems requires modeling constraints on valid assignments, including provided and required capabilities, and behaviors of resources such as “how capacity or availability is allocated to serve a task”. For each application, the resource assignment control function matches tasks to available, capable resources, and acquires those resources to execute authorized process steps.

6. Which process does the task require next?’ (Dynamic Process Planning)

After completing each step in a task’s process plan, the controller chooses the next step to do. Process planning is often defined as a tactical planning decision (or design activity) that constructs a complete sequence of steps (process plan) to produce a product (Wein 1991; Lee and DiCesare 1994; Wysk and Smith 1995). This is reflected in classical job shop models that use linear process plans defined as a single, complete sequence of process steps. Process plans define the steps required to complete the task and constraints on the execution of those steps. The process plan contains information regarding what has been done (completed steps), won’t be done (pruned steps), should be done (next steps), could be done (options for future steps).

Dynamic process planning selects the next step from options in the process plan. Flexible process plans include alternative sequences of steps (execution options) in a single process plan (Hutchinson and Pflughoeft 1994). Process plans with execution options (flexibility) enable controllers to cope with uncertainty, respond to unplanned events, and improve resource utilization. Dynamic process planning can also augment process plans that only contain ‘primary’ make-type operations with auxiliary steps such as move, testing, or storage. Dynamic process planning manipulates the process plan by pruning unnecessary paths or augmenting it with additional auxiliary steps, updating that information by marking the process plan, and the resulting ‘marked’ process plan indicates the next step to be executed. The decision function maps a process plan to a new or updated process plan (14). The actuator function updates the task’s process plan (incorporating new decisions such as next Process Step) and passes it back (returns) to the Task (15):

$$\mathit{DynamicProcessPlanning}:\text{ProcessPlan}\mapsto {\text{ProcessPlan}}^{\prime }$$ (14)

$$\mathit{UpdateProcessPlan}(\mathit{Task},{\mathit{ProcessPlan}}^{\prime })≔\mathrm{Task}.\mathrm{processPlan}\leftarrow {\mathit{ProcessPlan}}^{\prime }$$ (15)

6.1. Control Problem Formulation

The base flexible job-shop scheduling problems (FJSP) model consists of a set of tasks $\mathcal{L}$, each having a process plan ρ_l = (O_l,1,…,O_l,pl) defined as an sequence of p_l process steps required to complete the task. Linear process plans specify a single, complete sequence of process steps. They can be extended to include process plans that specify precedence constraints between process steps and allow the analysis method to define execution sequences (Lenstra and Rinnooy Kan 1978). FJSP with process plan flexibility (FJSP-PPF) allows multiple process plans for each type of task (Özgüven et al. 2010). In this model, each task has a set of ${\tau }_l$ process plans ${\mathcal{P}}_l=\{{\rho }_{l,1},\dots ,{\rho }_{l,{\tau }_l}\}$. Each process plan ${\rho }_{l,k}$ for task l is a sequence of p_l,k process steps, ρ_l,k = (O_l,k,1,…,O_l,k,pl,k). It is assumed that the process plans are known in advance and are all linear.

Network-based representations of flexible process plans capture execution options (flexibility) using AND/OR digraphs (Wysk and Smith 1995). These are acyclic directed graph ${\mathcal{P}}_l=\langle O,A,B\rangle ,$ ¹ where O is a finite set of nodes representing individual process steps, A is a finite set of arcs representing precedence constraints between process steps, and B is the set of AND/OR junctions connecting nodes to arcs. AND junctions indicate that all arcs within the junction, and the target process steps (nodes), need to be completed, without specifying in which order they will be completed. OR junctions indicate that exactly one arc (process step) must be selected.

Multiple linear process plans can be merged into a single complex plan specification, such as an AND/OR digraph. Process steps from multiple linear process plans are consolidated into one AND/OR digraph, simplifying the representation and eliminating redundant process steps (nodes). Dynamic process planning methods manipulate AND/OR digraphs by resolving flexibility (execution options) captured by AND/OR junctions.

Linear alternative process plans (LAPP) can be generated from complex process plans represented as AND/OR digraphs (Saygin and Kilic 1999). Each LAPP is a sequence of process steps representing a single path through the graph found by resolving AND and OR junctions. This linearization method reduces the process plan selection problem to the same one described above (Özgüven et al. 2010).

Control problems that select from multiple linear process plans $({\mathcal{P}}_l=\{{\rho }_{l,1},\mathrm{\dots },{\rho }_{l,{\tau }_l}\})$ formulate a variable for each process plan candidate and imply the next process step (16).

$$x_{l,k}=1,\text{if process plan}{\rho }_{l,k}\in {\mathcal{P}}_l\text{is selected for task}l$$ (16)

If the set of linear process plans is represented as a single flexible process plan $({\mathcal{P}}_l=\langle O_{l,j,}{A}_i\rangle )$, the decision variable selects the next process step $(O_{l,j})$ from process plan ${\mathcal{P}}_l$ (17).

$$x_{l,j}=1,\text{if process step}{O}_{l,j}\in {\mathcal{P}}_l\text{is the next process step of task}l$$ (17)

6.2. Applications

Dynamic process planning selects a process plan, or determines the sequence of process steps (operations), for each part passing through the system (Bastos 1988; Gamila and Motavalli 2003; Bilge et al. 2015). Flexible manufacturing controllers dynamically select from a predetermined set of process plans (Sarin and Chen 1987; Wysk and Smith 1995; Shen and Norrie 1999; Brandimarte 1999; Eguia et al. 2017). Flexible job-shop scheduling problems (FJSP) can be extended to include process plan selection explicitly as a sub-problem (FJSP-PPF) (Özgüven et al. 2010; Doh et al. 2013; Sobeyko and Mönch 2017).

Process plan selection methods can be applied to selecting optimal paths for material flow through DELS by modeling flows as sequences of move process steps (Christofides et al. 1981). Agent-based automated material handling systems (AMHS) can be modeled as networks of autonomous ‘node agents’ (Lau and Woo 2008). These networks are distributed decision-makers for the problem of selecting the best sequence of move process steps (process plan). Distribution of goods and services for disaster relief, humanitarian, and emergency logistics applies agent-based, dynamic route finding methods due uncertainty in travel paths (Barbarosoğlu et al. 2002; Özdamar et al. 2004; Vitoriano et al. 2011; Özdamar and Ertem 2015; Wang and Zlatanova 2016). When not confined to rigid transportation networks, autonomous UAVs require path (process) planning similar to AMHSs Grippa et al. (2016).

In warehouse order picking problems, process planning methods incorporate batching, routing, and sorting strategies to formulate complex process plans for assembling outbound shipments (Petersen and Aase 2004; Gu et al. 2007; Van Gils et al. 2018). Picking routes can be coordinated across multiple pickers and dynamically adjusted to reduce congestion (Chen et al. 2016). For health care patients, treatment typically consists of multiple stages and process plans constructed by distinguishing patient types and designing customized patient routes (process plans) (Hulshof et al. 2012).

Dynamic process planning uses pre-specified plans as an input, then makes operational decisions to execute the plan, such as choosing among predetermined alternatives (execution options) and augmenting the plans with auxiliary steps. When process steps can be performed by alternative machines (resource flexibility), dynamic process planning can be combined with resource assignment to become a routing problem (see section 8.2).

7. ‘Which state should a resource be in?’ (Changing State)

The four control decisions discussed so far focus on flows of tasks through DELS. Another decision is needed to manage the “state” of resources when resource capacity or capability are controllable. Resource capability and capacity can be represented as resource State. Capability states of mobile resources might include location; for example, an AGV at one location must move (change location state) to pick up a load currently at a different location. The states of discrete-state resources might include availability states, such as being off/down, idle, or busy; or functional capability states, such as being set up to perform a particular process or not (Kitaev and Rykov 1995; Tadj and Choudhury 2005). The state of capacitated resources, such as inventory, can be interpreted as the capacity (quantity) available to allocate to process executions. While execution mechanisms to change resource capacity or capability might vary by the type of resource, decisions to change the state of system resources focus on making sure resources are available to serve task requirements.

State-change applications in this section are organized by the two types of resource state: capability (section 7.2) and capacity (section 7.3), but the control functions are defined for resource states generally. The decision function maps the current state of a resource to the desired state (18). The actuator function changes the state of the resource to the newState (19):

$$\mathit{ChangeState}:\text{Resource.state}\mapsto \text{State}$$ (18)

$$\mathit{ChangeState}(\text{Resource, NewState})≔\text{Resource.state}\leftarrow \mathit{NewState}$$ (19)

7.1. Control Problem Formulation

A limited amount of literature explicitly models states and transitions of system resources. Usually resource states are not explicitly modeled, and state changes are only implied. For example, if task of type j (requiring process type j) is processed immediately after task of type i the same machine, then it is assumed that the machine changed setups in between processing epochs. The decision variable for state change denotes ‘which resource?’ and ‘to which state’ should it be changed (20).

$$x_j^R=1,\text{if resource}R\text{is changed to state}j$$ (20)

7.2. Changing Resource Capability

Resources might provide multiple services (capabilities), but only one at a time. For example, a machine could be capable of executing multiple types of process or producing several types of parts, but only one type at a time. Changing a resource’s capability (state) incurs costs such set-up time or re-positioning cost. This section draws parallels between machine setup and vehicle re-positioning as changes in resource state.

In make-to-stock production control problems, machine state is defined by the type of process it can execute in that state. Multi-class switching curve models support decisions to change production capability or set-up (state) of machines to accommodate specific part types (Johnson 1954; Ha 1997b; De Vericourt et al. 2000). In material handling and transportation systems, vehicle state is defined by its geographic location. Customer requests (tasks) to move loads (items) from one location to another can only be assigned to vehicles in a specified subset of states (locations). In dynamic fleet management, idle vehicles, empty shipping containers, and other auxiliary resources can be re-positioned to support tasks that cannot be served by available resources at their original locations (White 1972; Dejax and Crainic 1987; Godfrey and Powell 2002). Transshipment policies relocate inventory (resources) to make them available to fulfill customer orders (tasks) at different locations (states) (Paterson et al. 2011).

7.2.1. Anticipatory Moves and Pre-positioning

Tasks arriving at the system exhibit spatial and temporal uncertainty, but it takes time to change resource states to serve tasks. In anticipation of tasks requiring a particular capability, controllers decide ‘to what capability’ resource states should be changed, such as production capability or geographic location. These ‘change state’ decisions can be anticipatory (Potts and Kovalyov 2000) or proactive (Paterson et al. 2011). Idle resources might make anticipatory moves to respond better to the next service request (Lu and Gerchak 1998). For example, machines can make anticipatory transitions to a particular setup (Potts and Kovalyov 2000), ‘mobile’ resources can be pre-positioned at a desirable geographic location (Desrochers et al. 1990; Schuijbroek et al. 2017), and idle AS/R vehicles often return to an optimal dwell point (Rouwenhorst et al. 2000; Park 2001; Roodbergen and Vis 2009). A priori planning and pre-positioning key resources is critical in managing response efforts after emergency events; see, for example, ambulances in emergency care services (Hulshof et al. 2012), humanitarian logistics (Rawls and Turnquist 2010; Van Wassenhove and Pedraza Martinez 2012), and military logistics (Rawls and Turnquist 2010).

7.2.2. Tooling Selection in FMS

Tools contained in a flexible machine’s magazine determine which capabilities (process types) the machine is able to offer. In most systems, all tools needed must be acquired prior to processing a part (Hertz et al. 1998). Sharing tools among machines effectively increases magazine capacity and eliminates moving parts from machine to machine searching for a specific tool type (capability) (Kumar and Sridharan 2009). However, it introduces a trade-off between reducing down-time for particular set of capabilities (increasing the effective capacity) versus increasing the capability set (Hertz et al. 1998). Tool selection problems incorporate re-positioning decisions, too, since tools are shared and re-positioned between machine magazines, intermediate tool storage, and central tool storage (ElMaraghy 1985). A flexible machine and its tools can be modeled as a resource group (federation) capable of executing multiple processes.

7.2.3. Energy-Aware State Changes

In energy-aware scheduling models, the controller might shut down idle servers of non-bottleneck workstations (Bruzzone et al. 2012; Brundage et al. 2014; Zou et al. 2016). This approach extends server models with vacations, where idling single, non-bottleneck machines does not change system throughput, but reduces operation costs (Tadj and Choudhury 2005). Vacations can also be applied to maintenance models.

7.3. Changing Resource Capacity

The ‘change state’ decision can affect capacity of resources (compare to changing capabilities in section 7.2). This includes inventory replenishment and reordering, performing maintenance, and working overtime or outsourcing decisions. These decisions increase (or decrease) the capacity of target resources over some time period. The decision focuses on “how much to adjust a resource’s operational capacity?”

7.3.1. Capacity Renewal & Inventory Replenishment

Inventory replenishment decisions determine how much additional inventory (resource capacity) should be ordered, adding capacity to the system when delivered (Arrow et al. 1951). Warehouse inventory restocking decisions address how each SKU (resource) should be moved, redistributed, or replenished among multiple storage areas, such as moving from a reserve storage area to a forward pick area or offsite to onsite storage (Rouwenhorst et al. 2000; Gu et al. 2007; Roodbergen and Vis 2009; Wutthisirisart et al. 2015). Perishable inventory is an additional challenge to inventory replenishment strategies, especially when stock must be inspected to evaluate its condition (Pauls-Worm et al. 2016; Tai et al. 2018). Vehicle routing models with intermediate facilities allow vehicles to renew their capacity (Braekers et al. 2016; Ritzinger et al. 2016), which is especially important for electric vehicles including automated UAVs (Schneider et al. 2014; Grippa et al. 2016; Pelletier et al. 2016; Sassi and Oulamara 2017) Due to the lack of established infrastructure, disaster relief logistics face a modified problem for re-fueling transportation resources at a centralized operation base (Barbarosoğlu et al. 2002).

7.3.2. Maintenance (Capacity)

Maintenance control decisions trade off when to sacrifice capacity in the short-term to gain capacity in the long-term. Preventative maintenance can be run-based or time-based, and corrective maintenance is failure-based. Maintenance processes restore or improve operating capacity (state) of resources, and often maintenance actions trigger a renewal period for the machine’s capacity, returning it to a ‘good-as-new’ state (Cassady and Kutanoglu 2005). Machine availability can be optimized by selecting appropriate preventive maintenance rates or intervals that decrease the machine failure frequency or duration, respectively (Gharbi and Kenne 2000; Cassady and Kutanoglu 2005). Maintenance can also be performed opportunistically to minimize impact on production throughput (Gu et al. 2015; Zou et al. 2016). Maintenance tasks are then scheduled according to maintenance policies and executed by resources often dedicated to maintenance (Nikolopoulos et al. 2003; Cassady and Kutanoglu 2005). Maintenance-scheduling problems might incorporate resource assignment to complete tasks while maintenance is performed (Sriram and Haghani 2003; Sharma et al. 2011).

7.3.3. Overtime and Outsourcing

To deal with over-loaded production systems, controllers might seek additional production capacity by authorizing overtime, hiring temporary labor, or by outsourcing some tasks (Ebben et al. 2005; Herbots et al. 2007; Vermeulen et al. 2009; Geng et al. 2017). While regular capacity is the result of long-term strategic decisions, additional “non-regular” capacity can supplement regular capacity in the short-term, though typically this incurs significantly higher costs. For example, health care systems might adjust staffing levels by asking nurses to work overtime or getting help from qualified nurses of other departments (Dexter et al. 2005).

State-based models of resource behavior provide a unifying formulation for controlling resource capacity or capability. Often once the decision maker decides change a resource’s state, the system needs to generate an overhead task authorizing another system or auxiliary resource to execute the state change. These overhead tasks may be, for example, inventory orders, maintenance tasks, or set-up tasks. These tasks are executed by their respective systems using the same control functions discussed throughout this paper.

8. Joint Control Problems

Sections 3 through 7 each describe one ‘atomic’ control decision; functions that have only one effect on the system. These atomic functions can be combined to have multiple effects on the system, and analysis models can be formulated to make the decisions jointly. Many control problems can be derived by combining atomic control decisions. This section discusses scheduling and routing as joint control problems.

8.1. Scheduling

Assigning resources to each of a task’s process steps combined with sequencing tasks on each resource is considered scheduling (Lee and DiCesare 1994; Wysk and Smith 1995). Scheduling is the joint decision of assignment (section 5) and sequencing (section 4).

Many approaches to the scheduling problem decompose it into resource assignment and resource task sequencing (Bastos 1988; Brandimarte 1993). The separate problems then can be solved hierarchically, iteratively, etc. Dauzère-Pérès and Paulli (1997) use a digraph approach to integrate reassignment and resequencing methods by moving arcs around in the graph to jointly accomplish both control decisions simultaneously. However the authors state that “in all the approaches we are aware of, the assignment of operations to machines and the sequencing of operations on the machines are separated.” (Dauzère-Pérès and Paulli 1997). Shifting bottleneck heuristics exploit the separation of sequencing and machine assignment decisions (Adams et al. 1988). The following scheduling formulations (21, 22, 23) capture the resource assignment and task sequencing decisions in Bowman (1959), Wagner (1959), and Manne (1960), respectively.

$$y_{lt}^m=1,\text{if task}l\text{is processed by machine}m\text{during period}t$$ (21)

$$y_{lj}^m=1,\text{if task}l\text{is scheduled in the}{j}^{th}\text{position for processing on machine}m$$ (22)

$$y_{l{l}^{\prime }}^m=1,\text{if task}l\text{precedes task}{l}^{\prime }(\text{not necessarily immediately})\text{on machine}m$$ (23)

The joint inventory routing problem, like the scheduling problem, combines sequencing and assignment decisions for two kinds of resources: inventory stocks (consumable resources) and delivery vehicles (dis-crete state resources) (Federgruen and Zipkin 1984). The control problem sequences customers into service periods, assigns inventory stock or ‘capacity’, assigns customers to vehicles, and then sequences customers on each vehicle. Periodic VRP solution methods hierarchically organize methods for (periodic) pattern selection (tasks in periods), route assignment (assigning vehicle to set of tasks), and sequencing tasks (within a period and on a vehicle) (Hemmelmayr et al. 2009). Capacitated VRP exhibit joint sequencing and assignment decisions (Vidal et al. 2014).

8.2. Routing

When each process step can be performed by alternative machines, dynamic process planning combined with resource assignment is a routing problem (Singh and Mohanty 1991; Byrne and Chutima 1997; Bilge et al. 2008). In flexible manufacturing systems (FMS), process plan selection for a task is done in conjunction with assignment of operations and tools to each machine (Sarin and Chen 1987; Brandimarte 1999; Gamila and Motavalli 2003; Chan et al. 2006). FJSP with process plan flexibility (FJSP-PPF) is a composition of the following decision sub-problems (Özgüven et al. 2010): select a process plan for each task from a pre-determined set of process plans; assign a machine to each process step in the plans; and sequence the tasks assigned to each machine. The routing problem is formulated with separate variables for each decision (24, 25, 26) (Özgüven et al. 2010).

$$x_{l,j}^m=1,\text{if machine}m\text{is selected for process step}j\text{of task}l(O_{lj})$$ (24)

$$y_{lj,l^{\prime }{j}^{\prime }}^m=1,\text{if process step}j\text{of task}l(O_{lj})\text{precedes process step}{O}_{l^{\prime }{j}^{\prime }}\text{on machine}m$$ (25)

$$z_{l,k}=1,\text{if process plan}{\rho }_{l,k}\text{is selected for task}l$$ (26)

9. Summary of Operational Control Classification and Surveyed Literature

Previous sections surveyed the operational control literature and formalized the classification model for each control function. These functional definitions and supporting literature are summarized in this section. Table 1 summarizes the operational control functions that define the classification scheme. Each operational control function is defined by its decision function, actuator function, and decision variable. For more on these components, see section 2.2. Table 2 uses this classification to summarize the surveyed literature by function and domain.

Table 1.:

Overview of DELS Operational Control Functions.

‘Which tasks to serve?’ (Admission)
Decision Function	Admission : Task ↦ Bool
Actuator Function	Admit (Task) := System.taskSet ← System.taskSet ∪ Task
Decision Variable	xl = 1, if arriving task l ∈ $\widehat{\mathcal{L}}$ is accepted
‘When, or in what order, an admitted task is served?’ (Sequencing)
Decision Function	Index : Task ↦ $\mathbb{N}$
Actuator Function	Sequence(Index) := System.taskSet ← sort(System.taskSet, Index)
Decision Variable	xl,j = 1, if task l is served jth
‘Which resource is assigned to serve a task?’ (Assignment)
Decision Function	Assign : Task × Resource(s) ↦ Resource(s)
Actuator Function	Acquire(Task,Resource(s)) := Task:nextProcessStep.requiredInputResource ← Resource(s)
Decision Variable	$x_l^m$ = 1, if resource m ∈ $\mathcal{M}$ is assigned to execute the next process step of task l
‘Which process does the task required next? (Dynamic Process Planning)
Decision Function	DynamicProcessPlanning : ProcessPlan ↦ ProcessPlan′
Actuator Function	UpdateProcessPlan(Task, ProcessPlan′) := Task.processPlan ← ProcessPlan′
Decision Variable	xl,k = 1, if process plan ρl,k ∈ ${\mathcal{P}}_1$ is selected for task l
‘Which state should a resource be in? (Changing State)
Decision Function	ChangeState : Resource.state ↦ State
Actuator Function	ChangeState : Resource.NewState) := Resource.state ← NewState
Decision Variable	$x_j^R$ = 1, if resource R is changed to state j

Table 2.:

Overview of Surveyed Literature on DELS Operational Control.

Domain	Admission	Sequencing	Resource Assignment	Dynamic Process Planning	Resource State
Manufacturing	De et al. (1993); Kitaev and Rykov (1995); Duenyas (1995); Roundy et al. (2005) Herbots et al. (2007) Melchiors et al. (2018)	Hax and Meal (1975) Adolphson (1977); Graham et al. (1979); Blackstone et al. (1982) ; Adams et al. (1988); Valavanis (1990); Wein (1991); Fowler et al. (1992) De et al. (1993) ; Boysen et al. (2009); Chandra and Fisher (1994); Roundy et al. (2005); Chen (2010); Kim et al. (2015); van der Zee (2017)	Bastos (1988); Adams et al. (1988); Brandimarte (1993); Lee and DiCesare (1994) ; Wysk and Smith (1995); Dauzère-Pérès and Paulli (1997); Cassandras and Lafortune (2008); Hopp and Spearman (2011) Mati and Xie (2011) Kim et al. (2015)	Sarin and Chen (1987) Bastos (1988) Wein (1991); Lee and DiCesare (1994); Hutchinson and Pflughoeft (1994) ; Wysk and Smith (1995); Shen and Norrie (1999); Brandimarte (1999); Saygin and Kilic (1999) Gamila and Motavalli (2003); Özgüven et al. (2010); Doh et al. (2013); Bilge et al. (2015) Eguia et al. (2017); Sobeyko and Mönch (2017)	Johnson (1954); Kitaev and Rykov (1995); ElMaraghy (1985); Ha (1997b); Hertz et al. (1998); De Vericourt et al. (2000); Potts and Kovalyov (2000); Tadj and Choudhury (2005) Kumar and Sridharan (2009); Bruzzone et al. (2012) ; Brundage et al. (2014); Zou et al. (2016)
Warehouse	Zhang et al. (2016)	Gu et al. (2007); Roodbergen and Vis (2009); Meneghetti et al. (2015); Thomasson et al. (2018); Van Gils et al. (2018)	Daniels et al. (1998); Rouwenhorst et al. (2000); Gu et al. (2007); Roodbergen and Vis (2009); Bierwirth and Meisel (2010); Alonso-Ayuso et al. (2013); Wutthisirisart et al. (2015); Meneghetti et al. (2015); Yuan et al. (2018)	Petersen and Aase (2004); Gu et al. (2007); Chen et al. (2016); Van Gils et al. (2018)	Rouwenhorst et al. (2000); Park (2001); Roodbergen and Vis (2009); Wutthisirisart et al. (2015)
Transportation	Desrochers et al. (1990); Psaraftis et al. (2016); Ritzinger et al. (2016)	Federgruen and Zipkin (1984); Desaulniers et al. (2000); Dror and Trudeau (1990); Higginson and Bookbinder (1994); Godfrey and Powell (2002); Golden et al. (2008); Hemmelmayr et al. (2009); Toth and Vigo (2014) Klapp et al. (2016); Psaraftis et al. (2016); Grippa et al. (2016)	Golden et al. (1984); Salhi and Rand (1993); Hemmelmayr et al. (2009); Psaraftis et al. (2016); Grippa et al. (2016); Sassi and Oulamara (2017)	Christofides et al. (1981); Campbell et al. (1998); Lau and Woo (2008); Psaraftis et al. (2016); Grippa et al. (2016)	White (1972); Dejax and Crainic (1987); Desrochers et al. (1990) ;Godfrey and Powell (2002); Crainic et al. (1993); Schneider et al. (2014); Pelletier et al. (2016); Braekers et al. (2016); Grippa et al. (2016); Sassi and Oulamara (2017)
Inventory	Topkis (1968); Rabinowitz et al. (1995); Balakrishnan et al. (1996); Ha (1997a); Gallego and Van Ryzin (1997); Xie et al. (2016)	Federgruen and Zipkin (1984); Rabinowitz et al. (1995); Campbell et al. (1998); Cattani and Souza (2002); Lee et al. (2003); Khouja and Goyal (2008); Çetinkaya and Lee (2000); Deshpande et al. (2003); Ayanso et al. (2006); Caggiano et al. (2006); Xie et al. (2016); Alfieri et al. (2017)	Balakrishnan et al. (1996); Van Mieghem and Rudi (2002); Caggiano et al. (2006); Ayanso et al. (2006); Wutthisirisart et al. (2015); Elhafsi et al. (2015)		Arrow et al. (1951); Johnson (1954); Lee and Tang (1997); De Vericourt et al. (2000); Paterson et al. (2011); Pauls-Worm et al. (2016); Schuijbroek et al. (2017); Tai et al. (2018)
Health Care	Kusters and Groot (1996); Vissers et al. (2007); Hulshof et al. (2012); Ahmadi-Javid et al. (2017); Range et al. (2018)	Magerlein and Martin (1978); Dexter et al. (1999); Pham and Klinkert (2008); Hulshof et al. (2012); Ahmadi-Javid et al. (2017); Geng et al. (2017)	Magerlein and Martin (1978); Pham and Klinkert (2008); Punnakitikashem et al. (2008); Hulshof et al. (2012); Ahmadi-Javid et al. (2017); Range et al. (2018)	Hulshof et al. (2012)	Dexter et al. (2005); Hulshof et al. (2012); Geng et al. (2017)
Humanitarian		Haghani and Oh (1996); Barbarosoğlu et al. (2002); Golden et al. (2014); Özdamar and Ertem (2015)	Brown and Vassiliou (1993); Haghani and Oh (1996); Fiedrich et al. (2000); Özdamar et al. (2004); Balcik et al. (2008); Rawls and Turnquist (2012); Van Wassenhove and Pedraza Martinez (2012); Özdamar and Ertem (2015); Rettke et al. (2016); Hu et al. (2016); Song et al. (2018)	Barbarosoğlu et al. (2002); Özdamar et al. (2004); Vitoriano et al. (2011); Wang and Zlatanova (2016)	Barbarosoğlu et al. (2002); Rawls and Turnquist (2010); Van Wassenhove and Pedraza Martinez (2012); Özdamar and Ertem (2015)
Maintenance		Hoffman et al. (2018)	Caggiano et al. (2006); Nikolopoulos et al. (2003); Sriram and Haghani (2003)		Gharbi and Kenne (2000); Nikolopoulos et al. (2003); Cassady and Kutanoglu (2005); Sriram and Haghani (2003); Sharma et al. (2011); Gu et al. (2015); Zou et al. (2016); Ritzinger et al. (2016)
General	Hifi et al. (2004); Pekgün et al. (2008); Hartmann and Briskorn (2010); Öner-Közen and Minner (2018)	Lawler et al. (1993); Kuik et al. (1994); Buddhakulsomsiri and Kim (2006); Cheng et al. (2015)	Herroelen et al. (1998); Powell et al. (2001); Van Mieghem and Rudi (2002); Hartmann and Briskorn (2010)	Lenstra and Rinnooy Kan (1978)	Lu and Gerchak (1998); Ebben et al. (2005) Herbots et al. (2007); Vermeulen et al. (2009)

10. Conclusions

This paper surveys literature on operational control in discrete event logistics systems (DELS), classifying operational control problems using abstract functional definitions of the control decisions being made. It is proposed that operation control decision-making has only five possible concerns, described informally by the following questions: (1) ‘should a task be served?’ (admission); (2) if so, ‘when should the task be served?’ (sequencing); and, (3) ‘by which resource?’ (assignment); then, (4) ‘what process step does the task require next?’ (dynamic process planning); (5) as well as, ‘in which state does a resource need to be?’ (changing-state). Functional definitions of these control decisions have two related components: a decision function and an actuator function, specifying control behaviors of the controller and plant (system), respectively. The survey unifies the operational control literature for specialized DELS and provides evidence that these five decisions define a complete set of atomic operational control functions for DELS, either by themselves or in combination.

Standard definitions of operational control functions provide a theoretical foundation for DELS control modeling. The definitions link decision-support in controllers with decision execution in the plant. Standard DELS descriptions (models) enable libraries of interoperable control analysis methods and tools to be developed and integrated with decision-support software. These definitions also enable discovery or development of hardware components (actuators) capable of executing the corresponding actuator function. This enables application of DELS design methodologies to cyber-physical control components that can be deployed across heterogeneous DELS. Additional research is required to translate this theoretical foundation into a modeling and design methodology. Implementing (embodying) control functions into operational control system components (software and hardware) is the subject of a future paper.