The Phase Difference Between Neural Drives to Antagonist Muscles in Essential Tremor Is Associated with the Relative Strength of Supraspinal and Afferent Input

Abstract

The pathophysiology of essential tremor (ET), the most common movement disorder, is not fully understood. We investigated which factors determine the variability in the phase difference between neural drives to antagonist muscles, a long-standing observation yet unexplained. We used a computational model to simulate the effects of different levels of voluntary and tremulous synaptic input to antagonistic motoneuron pools on the tremor. We compared these simulations to data from 11 human ET patients. In both analyses, the neural drive to muscle was represented as the pooled spike trains of several motor units, which provides an accurate representation of the common synaptic input to motoneurons. The simulations showed that, for each voluntary input level, the phase difference between neural drives to antagonist muscles is determined by the relative strength of the supraspinal tremor input to the motoneuron pools. In addition, when the supraspinal tremor input to one muscle was weak or absent, Ia afferents provided significant common tremor input due to passive stretch. The simulations predicted that without a voluntary drive (rest tremor) the neural drives would be more likely in phase, while a concurrent voluntary input (postural tremor) would lead more frequently to an out-of-phase pattern. The experimental results matched these predictions, showing a significant change in phase difference between postural and rest tremor. They also indicated that the common tremor input is always shared by the antagonistic motoneuron pools, in agreement with the simulations. Our results highlight that the interplay between supraspinal input and spinal afferents is relevant for tremor generation.

Introduction

Essential tremor (ET) is the most common movement disorder in adults (Louis and Ferreira, 2010). It is characterized by a bilateral postural and, in many cases, also kinetic tremor of the hands, with frequency in the range of 4–12 Hz (Deuschl et al., 1998; Benito-León and Louis, 2006). Rest tremor with no other sign of parkinsonism is also present in 20–30% of ET patients (Cohen et al., 2003; Louis et al., 2011).

Tremor in ET is generated by the rhythmic activation of the affected muscles, which is ultimately caused by the projection of pathological oscillations, probably originating at cerebellothalamocortical pathways (Benito-León and Louis, 2006; Schnitzler et al., 2009; Helmich et al., 2013), to spinal motoneurons. The central mechanisms mediating ET are still controversial (Helmich et al., 2013; Louis et al., 2013), partly because of the lack of data on motoneuron behavior (the final common pathway; Heckman and Enoka, 2012) during tremor. For example, no study has directly investigated motor unit behavior across antagonist muscles in tremor, even though their strong mechanical and neural coupling (Hagbarth and Young, 1979; Jankowska, 1992) is likely to have great influence on tremor generation.

The phase difference between tremor bursts of antagonist muscles, as recorded with surface EMG, varies largely across ET patients (Deuschl et al., 1987; Raethjen et al., 2000; Milanov, 2001). This phenomenon, which likely reflects underlying pathophysiological differences, has not been systematically analyzed. To our knowledge, only Raethjen et al. (2000) has presented an analysis of coherence between rectified EMGs of the agonist–antagonist pair, to assess whether antagonist muscles receive the same synaptic input during postural tremor. Eighty percent of their muscle pairs had input from the same oscillatory source at the tremor frequency (Raethjen et al., 2000). Studies analyzing the phase difference between tremor bursts in ET patients report contradictory results. While Nisticò et al. (2011) report that all the analyzed muscle pairs exhibited in-phase (synchronized) activation during rest tremor, Milanov (2001) found both in-phase and out-of-phase patterns. The same was observed during postural tremor (Raethjen et al., 2000).

We investigated the determinants of the phase difference between tremorogenic neural drives to antagonist muscles. We hypothesized that their strong coupling has a large influence on the phase difference between their neural drives. Our analysis includes simulations with a model of an antagonist muscle pair, and motoneuron spike trains recorded in vivo during rest and postural tremor in 11 ET patients. Motoneuron activity was detected using a method thoroughly validated for essential and parkinsonian tremors (Holobar et al., 2012). In both cases, the neural drive to the muscles (i.e., the output of spinal motoneurons) was represented as the pooled motor unit discharges, rather than the surface EMG, to obtain the most accurate estimate of the common synaptic input to the motoneuron pools (Farina et al., 2014). We will show that the tremor in antagonist muscles originates from an oscillatory input always shared by the two motoneuron pools, with a phase difference determined by the relative strength of their supraspinal and spinal (Ia) inputs.

Materials and Methods

We first assessed, using the computational model, whether changes in the relative strength of the supraspinal tremor input to antagonist muscles could explain the previously observed variability across patients in the phase difference between tremorogenic neural drives. This analysis was performed both without and with a concurrent voluntary drive, to simulate rest and postural tremor. Besides characterizing the phase difference between neural drives, we assessed in which conditions there was a shared common synaptic input at the tremor frequency to the muscle pair. We then repeated these analyses for the experimental motor unit spike trains detected in vivo during postural and rest tremor. We interpreted the experimental results by comparing them with the simulations.

Simulations.

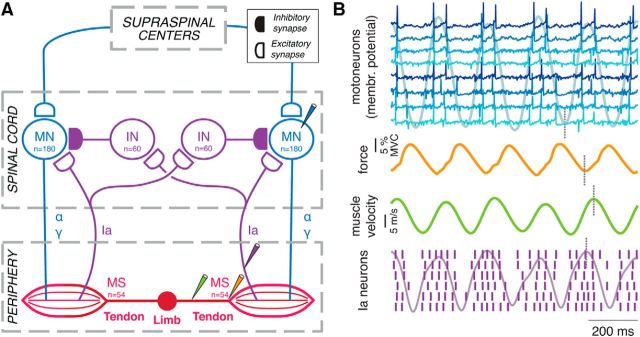
The model integrated a series of previously published models to characterize the interplay between the neural command, movement, and Ia afferent feedback in a pair of antagonist muscles. The model structure is depicted in Figure 1A. In brief, the output of two motoneuron pools determined the agonist–antagonist forces from which the dynamics of the muscle and tendon units were estimated. Ia afferent feedback was based on these mechanics. Motoneurons received supraspinal input, while afferent feedback was mediated by monosynaptic excitation (Jack et al., 1971; Finkel and Redman, 1983; Schieppati, 1987) and reciprocal disynaptic inhibition from Ia fibers (Jankowska and Roberts, 1972; Crone et al., 1987; Katz et al., 1991).

Figure 1.

Model overview and data flow. A, Submodels implemented within the model. The input to the model is the descending input arriving from supraspinal centers at each motoneuron population, while the output is the mechanical action of the limb (represented as the length of the musculotendon segments). The descending drive triggers α motoneuron activity that determines muscle force. Force determines the musculotendon mechanics, based on which activity of the muscle spindles is estimated and fed back to the motoneurons via Ia fibers, thereby closing an afferent loop. Interneurons receiving Ia input provide inhibitory input to the heteronymous motoneuron pool. Gamma motoneuron activity controls the muscle spindle responsiveness to muscle mechanics, while force is also determined by the muscle dynamics (force–length and force–velocity relations). B, Representative simulation example showing, from top to bottom, the membrane potentials of several motoneurons, superimposed to the low-pass-filtered (180-point Blackman–Harris window) CST of the whole pool; the resultant force exerted by that muscle; the muscle-contraction speed; and the discharges of several Ia neurons as a result of muscle contraction, superimposed to the low-pass-filtered (180-point Blackman–Harris window) CST of all the Ia neurons from that muscle. These variables are colored as the “probes” in A. The vertical marks (dotted gray lines) illustrate some of the delays in Table 1. MN, Motoneuron; IN, interneuron; MS, muscle spindle.

We simulated motor unit spike trains, muscle force, and limb movement when imposing sinusoidal current (representing descending tremor input) on the two motoneuron pools with the same phase but varying amplitudes. In all simulations, a subthreshold background excitation of 3.5 nA was imposed on both motoneuron pools (rheobase current of the smallest motoneuron was 4 nA). The central oscillations (frequency, 5 Hz; amplitude, 3 nA) were always projected to the motoneuron pool #1 with a gain of 1. The gain of the oscillatory input to motoneuron pool #2 was varied between 0 and 1, with 12 uniform increments. In this way, tremor was either imposed onto one pool only or onto both pools. In the latter case, the amplitude of the tremor input to pool #1 was greater or equal than to pool #2.

The background excitation to the motoneuron pools was varied (in three levels) to represent different conditions. At “rest,” only the subthreshold current (3.5 nA) was imposed on both motoneuron pools, whereas in the two “postural” conditions currents of 4.5 and 5.5 nA (inducing different levels of muscle activation) were imposed on pool #1; 3.5 nA was imposed on pool #2. Each condition was repeated three times to account for the many randomly assigned parameters in the model. These combinations of parameters (12 gain levels for the pool #2 × 3 subthreshold current levels × 3 repetitions per setting) yielded 108 simulations. Each simulation lasted 4 s, of which the last 3 s (where the simulations reached a steady state) were used for the analysis. In the following, each part of the model is detailed.

Spinal neuron population.

Neurons were simulated as Hodgkin–Huxley-type models (Cisi and Kohn, 2008). They consisted of two compartments (soma and dendrite) for motoneurons and one compartment (soma) for interneurons, with six conductances (leak conductances for the soma and dendrite, compartment-coupling conductances between the two compartments, and three voltage-dependent conductances, sodium Na, fast potassium Kf, and slow potassium Ks). The ranges of these parameters were adopted from Cisi and Kohn (2008), with exponential distributions across the motoneuron populations (Fuglevand et al., 1993).

One hundred and eighty motoneurons innervated each muscle. Efferent and afferent axonal lengths were set to 75 cm to reflect muscles acting on the wrist. Motoneuron axonal conduction velocities followed an exponential distribution, and were in the 60–100 m/s range (Barrett and Crill, 1971; Cullheim, 1978; Heckman and Binder, 1988). Sixty interneurons mediated reciprocal inhibition from Ia afferents, each of which projected to 20% randomly assigned motoneurons (Jankowska and Roberts, 1972).

We simulated supraspinal input to the motoneuron pools by injecting currents into the soma compartment of the motoneurons. Low-pass-filtered (<100 Hz; Negro and Farina, 2011b) white noise was imposed on this current, for which the SD was proportional to the mean value of the injected current, and adjusted so that the coefficient of variation for the motoneuron interspike intervals (ISIs) was between 10 and 30% (Clamann, 1969; Matthews, 1996; Moritz et al., 2005). Similarly, zero-mean white noise (SD, 0.15 nA; low-pass filtered, <100 Hz) was injected into the interneurons to represent the many types of excitatory and inhibitory synaptic inputs received by these neurons (Harrison and Jankowska, 1985). Its variability was adjusted so that action potentials only sporadically occurred [discharge rate, <2 pulses per second (pps)] without Ia activity (Jankowska, 1992).

Action potentials in afferent fibers or interneurons triggered an EPSC or IPSC that was injected into the soma compartment of the receiving neuron. EPSCs and IPSCs were modeled as exponential declines with time constants of 1 and 0.5 ms for inhibitory (Stuart and Redman, 1990) and excitatory currents (Finkel and Redman, 1983), respectively. The average EPSC and IPSC baseline amplitude was 1 and −2 nA, respectively (Stuart and Redman, 1990). Each synaptic connection was randomly assigned a synaptic strength, following a lognormal distribution (mean, 1; variance, 1; Kuno and Miyahara, 1969; Mendell and Henneman, 1971). The monosynaptic Ia EPSC amplitude was twofold stronger for high-threshold neurons compared with low-threshold neurons (Collins et al., 1984; Heckman and Binder, 1988). Synaptic strength of interneuron projections to the motoneurons was not dependent on neuron size (Powers and Binder, 1985; Heckman and Binder, 1991).

Proprioceptors.

A muscle spindle model simulated Ia afferent activity based on the gamma drive and the simulated muscle dynamics (Mileusnic et al., 2006). The number of muscle spindles in each of the two antagonist muscles was set to 54. Individual values of Ia axonal conduction velocity were randomly selected from a normal distribution (Hunt, 1954; Powers and Binder, 1985; Heckman and Binder, 1988; 100 ± 10 m/s). Each Ia afferent fiber projected monosynaptically to all motoneurons (Mendell and Henneman, 1971; Watt et al., 1976; Nelson and Mendell, 1978) and to 40% of the Ia inhibitory interneurons (Czarkowska et al., 1981; Jankowska et al., 1981). Gamma motoneuron discharge rates were based on the average discharge rate of randomly assigned α motoneurons. To maintain stable muscle spindle responsiveness when the muscle was shortened due to active contraction, the gamma discharge rate was obtained by scaling the α discharge rate by a factor of 6 (determined empirically by pilot simulations). Average gamma discharge rate has been reported to be several times higher than average α motoneuron discharge rates (Lund et al., 1979; Appenteng et al., 1980; Murphy, 2002).

Muscle force and limb dynamics.

Motor unit force was simulated based on the motoneuron discharge rate using a model of isometric force (Fuglevand et al., 1993), and scaled according to force–length and force–velocity relations (Zajac, 1989). The maximum voluntary contraction force (MVC) was set to 40 N, assuming a specific muscle tension of 22.5 N/cm² (Powell et al., 1984) and a physiological cross-sectional area of 1.8 cm² (Infantolino and Challis, 2010). Motor unit innervation numbers, determining the twitch-force amplitudes, were exponentially distributed with a 100-fold difference from smallest to largest motor unit, so the majority of motor units generated relatively low forces. Motor unit twitch contraction times were inversely related to twitch-force amplitude (Fuglevand et al., 1993). Limb dynamics were simulated based on a model of a pair of antagonist muscles (Oðuztöreli and Stein, 1982). Each muscle consisted of an active force-producing element with a parallel viscoelastic element and a parallel elastic element, representing the muscle fiber passive stiffness and viscosity respectively, and in series with an elastic element representing the tendon stiffness. The two muscles acted in opposing directions on a mass (50 g) representing a finger. Optimal muscle fiber length and tendon slack length were set to 30 mm (Infantolino and Challis, 2010).

Tendon stiffness increased steadily according to its length before reaching a plateau (6000 N/m) at strains above 3% (Morgan et al., 1978; Rack and Westbury, 1984; Proske and Morgan, 1987). Muscle passive tension was simulated as described in Magid and Law (1985). Muscle tissue viscosity was set to 20 N·s/m (Oðuztöreli and Stein, 1982).

Patients.

We collected data from 11 ET patients (four female, seven male; age: mean ± SD, 70.5 ± 4.3 years; range, 65–79 years) with a diagnosis of definite ET according to the criteria of the Tremor Investigation Group and the consensus of the Movement Disorder Society (Deuschl et al., 1998). All patients showed visible and persistent postural and kinetic tremor of the arms (unilateral or bilateral) and, in some cases (n = 5), also at rest. No patient had a history of neurological diseases other than ET, and none had features of parkinsonism (bradykinesia, rigidity) aside from isolated rest tremor. Average disease duration was 17.9 ± 9.5 years (mean ± SD; range, 6–32 years). Tremor severity ranged from mild to severe, with a mean score of 33.7 ± 12.2 (mean ± SD; range, 15–51) according to the Fahn–Tolosa–Marin scale (Fahn et al., 1993). Eight patients were taking antitremor drugs, which were continued during the recordings. Patients were selected for enrolment after examination by neurologists at Hospital Universitario 12 de Octubre, Madrid, Spain. They were informed beforehand and signed a written informed consent to participate. The ethical committee of Hospital Universitario 12 de Octubre approved the experimental protocol, granting its compliance with the Declaration of Helsinki.

Experimental procedures.

Bilateral hand tremor was recorded with surface EMG electrodes placed over both wrist flexor and extensor muscle groups. Surface EMG was detected using four 13 × 5 electrode grids with an interelectrode distance of 8 mm [Laboratory of Engineering of Neuromuscular System and Motor Rehabilitation (LISiN; Politecnico di Tornio; OT-Bioelettronica)]. Electrodes over the wrist extensors were centered laterally above the extensor digitorum communis and longitudinally above the muscle belly. Electrodes over the wrist flexors were centered laterally above the flexor carpi radialis and longitudinally above the muscle belly. A wrist bracelet soaked in water served as common reference. The signal was amplified (EMGUSB2, OT-Bioelettronica), bandpass filtered (10–750 Hz), and sampled at 2048 Hz by a 12 bit analog-to-digital converter. Before placing the electrodes, the skin was lightly abraded with abrasive paste (Meditec-Pharma) and cleansed afterward. The experiments were performed at Hospital Universitario 12 de Octubre, Madrid, Spain. The data were stored and analyzed off-line using Matlab (Mathworks) and R (R Foundation for Statistical Computing).

All recordings were performed while patients were seated in a comfortable armchair. Postural tremor was elicited by asking the patients to keep the hands outstretched with palms down, parallel to the ground, while the forearms were pronated and fully supported on an armrest. Rest tremor was recorded while both arms were completely relaxed and supported either on the armrests or on the patient's lap, depending on what he/she reported to be most comfortable. The recordings lasted between 40 s and 4 min. For the analysis, we selected the 30 s interval during which tremor had maximum amplitude, except for three rest trials where we analyzed 15–21 s of data (to maximize the number of active motor units).

EMG decomposition.

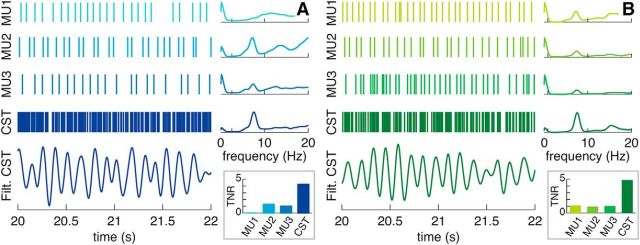
Motor unit spike trains were automatically identified from the multichannel surface EMG using the convolution kernel compensation algorithm (Holobar and Zazula, 2007), and then verified by an experienced operator (Fig. 2). The convolution kernel compensation algorithm has been extensively validated in >500 healthy subjects performing different types of contractions (Holobar et al., 2009, 2010) and, in the particular case of tremor, through the analysis of simulated (Holobar et al., 2012) and experimental signals from various types of patients (Holobar et al., 2012; Gallego et al., 2015). This validation proved that the algorithm is not influenced by high synchronization levels or by the occurrence of paired/tripled discharges with short ISI, which are typical of tremorogenic contractions (Dietz et al., 1974; Elek et al., 1991; Baker et al., 1992; Christakos et al., 2009; Holobar et al., 2012; Gallego et al., 2015).

Figure 2.

Representative example of neural drives to a pair of antagonist muscles in an ET patient. A, Data from the wrist extensors. B, Data from the wrist flexors. Each panel shows, from top to bottom, MU1–MU3, the spike trains of three of the motor units detected (of a total of 9 and 5 respectively), and their power spectral density; CST, the CST constructed by pooling the spike trains of all the detected motor units, and its power spectral density; Filt. CST, the filtered CST (3–10 Hz, zero-phase), showing a very clear oscillation at the tremor frequency. The inset represents the TNR for each motor unit and composite spike train (see Materials and Methods). Note how the spectral peak at the tremor frequency (TNR) increases its relative height when the motor unit spike trains are pooled into a CST. MU, Motor unit.

Decomposition accuracy was estimated for each of the detected motor units using the pulse-to-noise ratio (PNR; Holobar et al., 2014). For the analyses, we only considered the motor unit spike trains that were detected with high accuracy (PNR, ≥26 dB, after manual inspection), and which were present for ≥85% of the recording time. Note that although the surface EMG represents better, larger, and more superficial motor units (Farina et al., 2010), a random distribution of motor unit territories within a muscle would reduce this bias toward bigger units because of the effect of the distance from the electrodes (Fuglevand et al., 1992; Farina et al., 2008). Furthermore, even if the decomposition were biased toward the larger units, this would not influence the results, because the tremor synaptic inputs are common to the entire pool (Gallego et al., 2015). We included all muscles for which ≥2 motor units fulfilled these criteria, as well as seven muscles in which only one motor unit exhibited a clear spectral peak at the tremor frequency (thus reflecting the tremor synaptic input; see Results).

Data analysis and processing.

In all the analyses the neural drive to muscle was defined as the pooled discharges of all the detected motor units [cumulative spike train (CST); Negro and Farina, 2011a, 2011b, 2012; Dideriksen et al., 2012; Farina et al., 2013, 2014; Gallego et al., 2015; Fig. 2]. The CSTs were obtained by adding up all of the individual motor unit spike trains detected for the muscle under investigation.

Phase difference between neural drives.

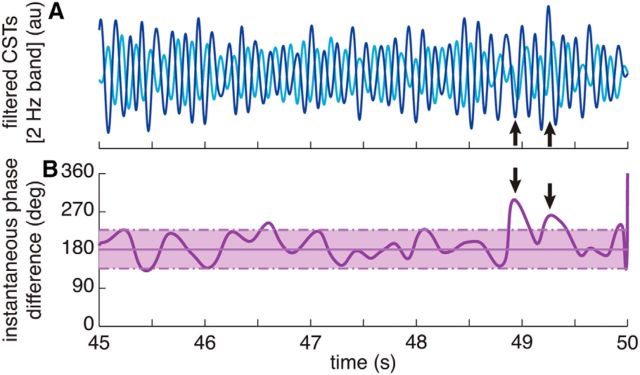
Because the neural drive to muscle and the tremor input are nonstationary (Timmer et al., 2000; de Lima et al., 2006), we characterized the instantaneous phase difference between the neural drives using the analytic signal approach (Fig. 3). This method has been successfully applied to the analysis of synchronization between cortical or corticomuscular oscillations (Gross et al., 2000; Schnitzler et al., 2000; Stam et al., 2007). The imaginary part of the analytic signal was computed using the Hilbert transform of the bandpass-filtered CST representing the neural drive to muscle (±1 Hz with respect to the tremor frequency in the coherence spectrum; Le Van Quyen et al., 2001). The choice of a narrow band is an intrinsic requisite for the analytic signal approach (Gross et al., 2000) that is inherently satisfied by the tremorogenic neural drive to muscle, because its frequency content is concentrated around the tremor frequency (Fig. 2). It was anticipated that when the phase difference between neural drives exhibited a clear relationship, the circular phase histograms (of the instantaneous phase difference) would deviate from a uniform distribution due to the significant association (Schnitzler et al., 2000) between oscillatory inputs (see Results; see Fig. 5D,H).

Figure 3.

Representative example of the instantaneous phase difference between tremorogenic neural drives to an antagonist muscle pair. A, Narrow band (±1 Hz with respect to the tremor frequency) filtered CSTs representing the neural drive to the wrist extensors (dark blue) and flexors (light blue). B, Instantaneous phase difference between the neural drives computed with the Hilbert transform (thick purple trace), with its mean ± SD (solid and dashed thin purple lines) calculated over the entire 30 s analysis window. The arrows indicate two brief fluctuations from the out-of-phase (180°) pattern otherwise characteristic of this trial, as reflected by the small SD over the mean. This figure illustrates the ability of the proposed method to detect fluctuations in the phase difference between tremorogenic neural drives. Data from the same trial as in Figure 2; Figure 5D shows the circular phase histogram for the entire trial.

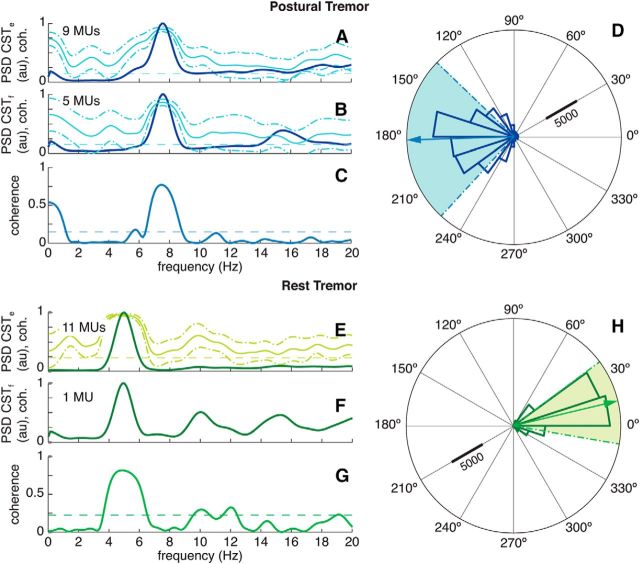
Figure 5.

Representative examples of shared common synaptic input across antagonist muscles and phase difference between their tremorogenic neural drives. A–D, An example of postural tremor for one of the patients. E–H, An example of rest tremor for another patient. A, B, Power spectral density (PSD) of the neural drive to the extensor (A) and flexor muscles (B; in dark color), and coherence between pooled motor unit spike trains, representing the properties of the common synaptic inputs to the respective motoneuron pools (mean ± SD; showed as light-colored lines; confidence limit displayed as dashed, light-colored lines). The number of motor units pooled in each CST is indicated in the respective panel. C, Coherence between CSTs, representing the spectral properties of the common synaptic input shared across motoneuron pools (solid line; confidence level displayed as a dashed line). D, Circular histogram of the instantaneous phase difference between the tremorogenic neural drives (CSTs) to both muscles (dark-colored), with their circular mean ± SD phase difference (light-colored arrow and dashed, light-colored lines, respectively). E–H are analogous to A–D.

The mean delay between tremorogenic neural drives was directly derived from the tremor frequency, f_tr, and the absolute value of the circular mean of the instantaneous phase difference, Ø_ND, as follows (Gross et al., 2000):

Note that, by using the circular mean, phase differences of >1 tremor cycle were truncated to 0–2π (by taking their modulo 2π).

Shared common synaptic input across motoneuron pools.

We analyzed whether motoneuron pools innervating antagonist muscles received the same common synaptic input at the tremor frequency, and whether the concurrent voluntary drive (De Luca and Erim, 1994; Negro and Farina, 2012; i.e., the common input with frequency, <2 Hz) was common across the motoneuron pools. We employed a new method that consisted of computing the coherence between the two CSTs that comprised all the motor units detected for each muscle, which represent their respective neural drives. This approach was inspired by studies using EMG– coherence to identify common inputs across motoneuron populations (Hurtado et al., 2000; Raethjen et al., 2000; Halliday et al., 2003; Farmer et al., 2007; Keenan et al., 2012).

The coherence, C_xy, was calculated as follows:

with X_xy being the cross-power spectrum of the two CSTs that represent the neural drive to each muscle, and X_xx and X_yy the power spectra of the CSTs that represent the neural drives to each antagonist muscle. Coherence functions were computed after the data were divided into nonoverlapping 1 s windows (Hann window; 0.125 Hz resolution) following the method described in Halliday et al., 1995. The existence of significant coherence peaks in the <2 Hz band and at the tremor frequency was interpreted as representing the shared synaptic input to motoneuron populations at their respective frequencies.

Before this analysis, we verified whether each motoneuron pool received a common synaptic input at the tremor frequency, as recently demonstrated in Gallego et al., 2015. To this end, we computed the mean coherence (same method as described above) between all combinations of pairs of pooled motor unit spike trains, each comprising half of the motor units detected for the muscle under investigation (Negro and Farina, 2012).

Motor unit discharge properties and population coding.

To characterize the transmission of tremor inputs by spinal motoneurons, we computed the ratio of the tremor peak in the power spectral density of the motor unit spike trains and the CSTs to their respective average power within the 0–50 Hz band, which we named tremor-to-noise ratio (TNR). Similarly, we defined the voluntary movement-to-noise ratio (VNR) as the ratio of the spectral peak at frequency <2 Hz (De Luca and Erim, 1994; Negro and Farina, 2012) to the average power within the 0–50 Hz band. We anticipated that both the TNR and the VNR would increase by pooling several motor unit spike trains into a CST, due to the population coding behavior (Averbeck et al., 2006) of spinal motoneurons (Negro and Farina, 2011a, 2012; Farina et al., 2013; Gallego et al., 2015).

The average motor unit discharge rate was computed after excluding discharges with ISI <10 ms or >3× the median ISI.

Statistics.

Throughout the manuscript, pairs of variables that were normally distributed were compared using the paired t test; we used the Mann–Whitney U test for those that were not. We tested for normality using the Lilliefors' test. Correlations between variables were assessed with Pearson's correlation test (all the examined samples conformed to normality). We compared the phase difference between rest and postural tremor with the Watson–Williams test, by assessing whether the pooled instantaneous phase difference (of all the antagonist pairs exhibiting tremor in both cases) was significantly different across conditions. To assess whether the relative delay between tremorogenic neural drives was significantly different between rest and postural tremor, we compared the mean delays (obtained as in Eq. 1) with the Mann–Whitney U test. For all the analyses, we accepted the respective hypotheses when p < 0.05. The confidence limits for the coherence spectra were obtained as described in (Rosenberg et al., 1989), and coherence values were considered significant if p < 0.01. Results are reported as mean ± SD, except for the circular variables, for which we provide their circular mean ± circular SD. Circular phase histograms of the instantaneous phase difference (calculated for each sample, at 2048 Hz) for every trial are represented with a resolution of 20° per bin.

Results

Simulations

For all the imposed relative amplitudes of supraspinal tremor input and strengths of voluntary drive, the model generated the typical oscillatory movement observed in tremor patients (Fig. 4A). Active force oscillations at the tremor frequency occurred even when the supraspinal tremor input was only imposed to one muscle (muscle #1; Fig. 4A, top), due to the Ia excitatory projections to the motoneuron pool #2 (Mendell and Henneman, 1971; Watt et al., 1976; Nelson and Mendell, 1978). The rhythmical, passive stretches of the relaxed muscle triggered afferent synaptic input high enough to generate tremor-like behavior. This indicates that tremor may originate from any combination of descending and afferent input, even from afferent (Ia) input alone.

Figure 4.

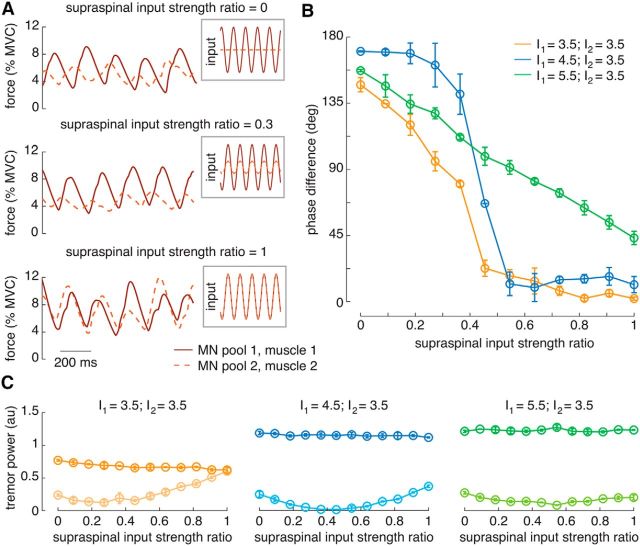
Simulations illustrating relevant properties of the neural drives to antagonist muscles as a function of the relative amplitude of the supraspinal tremor input. A, Examples of oscillatory input to the antagonistic motoneuron pools (insets) and resultant muscle force for three supraspinal input strength ratios during rest tremor (I₁ = 3.5 nA; I₂ = 3.5 nA). B, Mean phase difference between neural drives to the antagonist muscles as function of the relative amplitude of supraspinal tremor input, indicating a strong association between both variables for the three contraction levels simulated. C, Spectral power at the tremor frequency for the CST comprising all the motoneurons, as a function of the relative amplitude of supraspinal input. Each panel shows one of the voluntary drive levels; motoneuron pool #1 is represented in dark colors and motoneuron pool #2 in light colors. Data in B are represented as the circular mean (circles) ± SD (whiskers) of the three trials simulated for each of the 12 supraspinal input strength ratios; similarly, C represents the mean ± SD. All current amplitudes in nanoamperes. MN, Motoneuron.

The phase between neural drives depended on the primary source of oscillatory input. When the gain of the supraspinal tremor input to the motoneuron pool #2 was low, its net input was dominated by the afferent input induced by the passive stretch of the muscle. In these cases, the phase was determined by the conduction and mechanical delays of the system (see more details below). Specifically, the reflection of the active contraction of muscle #1 in the Ia feedback of muscle #2 arrived at its motoneuron pool ∼100 ms (∼50% of the tremor period) after the descending tremor burst to motoneuron pool #1, determining an out-of-phase pattern. When the gain of the supraspinal tremor input to the motoneuron pool #2 was high, implying that both motoneuron pools received approximately the same descending tremor input, the phase difference approached an in-phase pattern (Fig. 4A,B). A similarly strong supraspinal tremor input to the two muscles generated cocontraction and thus little limb movement, in turn generating low levels of afferent feedback. In this way, the phase difference could vary in the full 0–180°, depending on the relative amplitude of the supraspinal tremor input (Fig. 4B). These results suggest that the frequently observed in-phase muscle activation pattern during rest tremor (Milanov, 2001; Nisticò et al., 2011; see Experimental results) reflects a supraspinal tremor input to both antagonist muscles.

The phase difference was also influenced by the concurrent voluntary drive. When a voluntary input was also projected to motoneuron pool #1 to simulate postural tremor, the muscle activation pattern was more often out of phase than without voluntary input (Fig. 4B). Besides, as the descending voluntary input increased, the amount of supraspinal tremor input gains (Fig. 4B, values of the supraspinal input strength ratio) that caused the neural drives to be in phase decreased drastically. It should be then more likely to observe experimentally an out-of-phase behavior in postural than in rest tremor.

The different shapes of the phase difference to supraspinal tremor input ratio functions across levels of voluntary drive (Fig. 4B) are explained by the delays in the model (Table 1). When the voluntary input level to motoneuron pool #1 was 4.5 nA (first postural tremor condition), the total efferent–afferent delay was 198.7 ms, which matched almost perfectly the tremor period (200 ms). This means that when the gain of the descending tremor input to motoneuron pool #2 was small, the Ia excitatory input that drove the activity of motoneurons in pool #2 arrived almost perfectly out of phase with the descending tremor input [∼100 ms; the total efferent–afferent delay (198.7 ms) minus the delay between muscle-shortening to muscle-lengthening phases (99.3 ms); Table 1]. This way, the phase of the antagonist neural drive was driven by the afferent input (out of phase with the agonist) up until the point where the supraspinal tremor input was stronger (supraspinal input strength ratio, >0.4), where it changed abruptly to in-phase (Fig. 4B). On the contrary, the delay between the supraspinal and Ia input to motoneuron pool #2 did not equal half the tremor cycle for the other levels of voluntary input to motoneuron pool #1 (3.5 nA, 127.3 ms; 5.5 nA, 92.9 ms). For this reason, the neural drives were not completely out of phase at supraspinal input ratio 0, and the phase difference decreased more gradually when this ratio increased, since the more dominant input did not simply cancel the other out as when I₁ = 4.5 nA (Fig. 4B). These differences across the three conditions in the total efferent–afferent delay (Table 1) happened because of the systematic variations in the delays of some of the efferent–afferent loop components. For example, the tendency for the delay between muscle force and muscle-shortening velocity to decrease with increasing values of I₁ reflected that larger, and thus faster, motor units were recruited during the tremor bursts at higher levels of background excitation (average agonist muscle force was 6.3, 11.3, 18.1% MVC when I₁ = 3.5, 4.5, 5.5 nA, respectively). The increase in muscle-contraction speed led to higher muscle acceleration, which caused the peak Ia activity to occur earlier with respect to the movement (Table 1), because muscle spindle activation depends on muscle acceleration as well as velocity (Mileusnic et al., 2006).

Table 1.

Delays in the simulations for each of voluntary drive levels

	I1 = 3.5 nA	I1 = 4.5 nA	I1 = 5.5 nA
Motoneuron CST to force	82.1 ± 2.2 ms	86.0 ± 0.4 ms	84.4 ± 0.6 ms
Force to muscle-shortening velocity	48.1 ± 5.4 ms	37.8 ± 2.4 ms	26.7 ± 1.6 ms
Muscle shortening to muscle lengthening	131.7 ms	99.3 ms	100.2 ms
Muscle-lengthening velocity to Ia CST	−12.4 ± 4.0 ms	−31.9 ± 4.0 ms	−27.7 ± 1.4 ms
Ia conduction	7.5 ms	7.5 ms	7.5 ms
Average total efferent–afferent delay	257.0 ms	198.7 ms	191.1 ms

All the delays were computed using the cross-correlation function. Note that the muscle-shortening to muscle-lengthening time was not half a tremor cycle (100 ms) because the profile of the generated movement was not perfectly sinusoidal. The Ia CST was obtained by adding up the spikes of all the Ia neurons, similarly to the motoneuron CST.

The frequency of the tremor corresponded well to the imposed supraspinal oscillations for all conditions (4.98 ± 0.25 Hz). The power of the generated tremor in the motoneuron pool #2 was highest when it received strong supraspinal tremor input (values of supraspinal tremor ratio close to 1), indicating that the afferent tremor input never attained the same amplitude as that of the supraspinal tremor input (Fig. 4C). The delay between afferent and supraspinal inputs discussed above in some conditions led to their cancellation, which in turn made the amplitude curve U-shaped (Fig. 4C). When increasing the voluntary background input to motoneuron pool #1 to simulate postural tremor, the strength of its tremor output relative to that of the motoneuron pool #2 increased substantially, since the greater excitation allowed a larger number of motoneurons to be recruited by the oscillatory input. The power of the tremor when I₁ = 4.5 nA was almost as large as when I₁ = 5.5 nA because the total efferent–afferent delay matched almost perfectly the duration of a tremor cycle (198.7 vs 200 ms respectively), which caused Ia afferents to “amplify” the descending tremor input. The coherence between CSTs across antagonist muscles always presented a peak at the tremor frequency (0.95 ± 0.07), indicating that the tremor synaptic input was always shared by both motoneuron pools, independently of the relative amplitude of their supraspinal tremor input (or even in its absence, because of the common Ia projections).

In summary, the simulations allowed the following predictions, which were then tested experimentally: (1) the neural drives to antagonist muscles are more likely to be out of phase in postural than rest tremor; (2) antagonistic motoneuron pools share the same common tremor input during both postural and rest tremor.

Experimental results during postural tremor

Motor unit discharge properties and population coding

We identified accurately the spike trains of 289 motor units in the 40 muscle groups (of 11 patients) that exhibited postural tremor [average, 7.2 ± 4.7 motor units; range, 1 (for one muscle) to 16]. Their average discharge rate was 15.4 ± 6.9 pps (range, 4.82 ± 0.74 to 27.3 ± 22.1 pps). The large ISI variability, represented by the large SD of the discharge rate, corresponded to motor units that fired a lot of paired/tripled discharges.

Most of the detected motor unit spike trains (261 of 289) exhibited a spectral peak at the tremor frequency (6.18 ± 1.15 Hz; range, 4.50–8.88 Hz; Fig. 2), and also at frequencies <2 Hz (287 of 289), the latter reflecting the voluntary drive (De Luca and Erim, 1994; Negro and Farina, 2012; Fig. 2). Both spectral peaks were concurrently present in 259 of 289 motor unit spike trains. The TNR increased from 1.97 ± 1.68 (range, 0.12–8.92), when assessing individual motor units, to 5.38 ± 4.10 (range, 0.62–19.14), when evaluating CSTs comprising all the motor units detected for a muscle (Fig. 2). The VNR also increased, from 0.44 ± 0.47 (range, 0.02–2.86) to 0.89 ± 0.69 (range, 0.15–3.07), although it was significantly smaller (p < 0.001, Mann–Whitney U test). The increase in the strength of the tremor component demonstrates the population coding of tremor input by spinal motor units, analogously to that previously reported for voluntary contractions in healthy subjects (Negro and Farina, 2011a; Farina et al., 2014).

The coherence between pairs of CSTs (Fig. 5A,B) within a muscle showed that the motoneurons received a largely common synaptic input at the frequency of the tremor (coherence, 0.851 ± 0.122; frequency, 6.02 ± 1.22 Hz), together with a concurrent voluntary drive (coherence, 0.682 ± 0.122), in agreement with our previous results (Gallego et al., 2015).

Phase difference between tremorogenic neural drives

The phase difference between tremorogenic neural drives to antagonist muscles (Fig. 5D) was in most cases (13 of 20) close to out of phase, although it was relatively heterogeneous when pooling all limbs and patients together (average, 130.8 ± 48.3°; range, 22.7–178.6°; Fig. 6). Only in a few cases (4 of 20) the two neural drives were almost in phase (synchronized). The predominance of out-of-phase cases is in agreement with the simulations, and reflects a stronger supraspinal tremor input to one of the muscles, pointing to Ia fibers as primary sources of shared common synaptic input at the tremor frequency.

Figure 6.

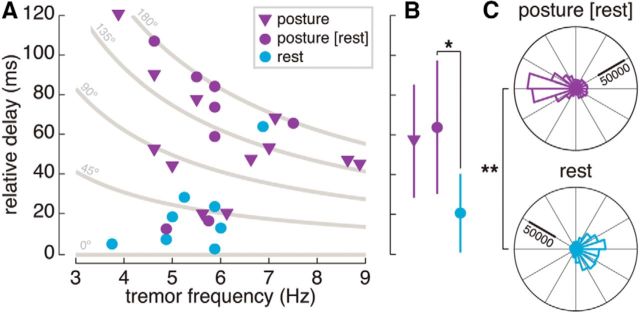
Relative delay between the tremorogenic neural drives to antagonist muscle pairs as function of the tremor frequency, for both postural and rest trials. Values were plotted after taking the absolute value of the mean phase difference. A, Relative delay for each antagonist muscle pair (markers). Relative delays during postural tremor are represented in purple, with muscle pairs that also exhibited rest tremor displayed as circles, and those that did not as triangles. The relative delay during rest tremor is displayed as light blue circles. The figure also displays the geometrical loci of several phase differences (gray traces), to highlight the relationship between relative delay, phase difference, and tremor frequency. B, Mean (markers) ± SD (whiskers) of the relative delay between the neural drives to the antagonist muscle pair. Trials are represented as in A. The asterisk denotes that the mean delay was significantly different across posture and rest (p = 0.021, Mann–Whitney U test). Note that the distributions of both subgroups of pairs of antagonist muscles during postural tremor are similar (p = 0.563, Mann–Whitney U test). C, Pooled instantaneous phase difference between tremorogenic neural drives to antagonist muscles at posture and rest, for all muscle pairs that exhibited tremor in both conditions. The double asterisk denotes that the instantaneous phase difference was significantly different across posture and rest (p < 0.001, Watson–Williams test).

The delay between neural drives also spanned a relatively wide range of values (average, 59.6 ± 29.9 ms; range, 12.9–120.1 ms; Fig. 6), and was not associated with the tremor frequency (p = 0.176, Pearson's correlation). This suggests that differences in tremor frequency did not account for the observed phase variability.

Shared synaptic inputs to antagonistic motoneuron pools

All pairs of antagonistic motoneuron pools (n = 20, from 11 patients) received a shared common tremor input, as revealed by the existence of a significant peak in the coherence spectra (coherence, 0.600 ± 0.169; range, 0.269–0.930; Fig. 5C). As expected, its frequency was similar to that of the neural drives to the muscles (CSTs; Fig. 5A,B). This observation was predicted by the simulations, and implies that in all cases the tremorogenic activity in the antagonist muscles originated from a common source, which could have been primarily supraspinal, primarily spinal, or a balanced combination of both, depending on the relative strength of supraspinal and afferent input (see Simulations; Fig. 4C).

In 13 of 20 muscle pairs, there was also a common input at a frequency <2 Hz (coherence, 0.374 ± 0.157; range, 0.155–0.649). This input reflects the voluntary drive that probably mediated the shared control of both muscles when holding the hands outstretched against gravity. The magnitude of the coherence representing this input was significantly smaller (p < 0.001, paired t test) than that of the common tremor synaptic input, and uncorrelated to it (p = 0.663, Pearson's correlation).

The amplitude of the coherence peak at the tremor frequency, which indicates to what extent the tremor input is shared across motoneuron populations, was not significantly correlated to the frequency of the tremor (p = 0.575, Pearson's correlation), or to the mean delay between tremorogenic neural drives (p = 0.860, Pearson's correlation).

Experimental results during rest tremor

Motor unit discharge properties and population coding

We identified accurately 67 motor units (average: 4.2 ± 5.1 motor units; range, 1–20) in the 16 antagonist muscle pairs that exhibited tremor at rest (n = 5 patients). Overall, the number of identified motor unit spike trains per muscle was smaller during rest than postural tremor (p = 0.047, paired t test), probably due to the lower muscle activation level. The average motor unit discharge rate was 15.0 ± 4.1 pps (range, 8.3 ± 5.8 to 26.9 ± 16.4 pps). The SD of the discharge rate was higher for those motor units that fired paired/tripled discharges most frequently, as in the case of postural trials.

Also similarly to postural tremor, most motor unit spike trains (61 of 67) presented a spectral peak at the tremor frequency, and at frequencies corresponding to the voluntary drive (66 of 67). Both were concurrently present in 60 of 67 motor units. The TNR of the individual motor unit spike trains (1.77 ± 1.39; range, 0.24–4.80) also increased substantially when they were pooled together into CSTs (3.70 ± 2.92; range, 0.98–11.1). This also happened to the VNR, although to a lesser extent (0.44 ± 0.50; range, 0.24–3.02, for the motor unit spike trains; 0.75 ± 0.43; range, 0.11–1.45, for the CSTs). Again, this shows that sampling from several motoneurons enhances the detection of neural inputs to the motoneuron pool.

All motoneuron pools investigated (n = 9, those for which we detected ≥2 motor units) received a common synaptic input at the tremor frequency (coherence, 0.852 ± 0.117; frequency, 5.08 ± 1.01 Hz), as occurred for postural tremor (Fig. 5E). We also detected a common voluntary input at frequency <2 Hz (coherence, 0.708 ± 0.112), indicating that there was a common voluntary drive, even if the limbs were at rest.

Phase difference between tremorogenic neural drives

The phase difference between tremorogenic neural drives to antagonist muscles varied across limbs and patients, averaging 34.84 ± 40.14° (range, 6.30–159.07°; Fig. 6). In agreement with the simulations, most of the antagonist muscle pairs (seven of eight) had neural drives that were close to in-phase (Fig. 5H), while the out-of-phase pattern that predominated during postural tremor was only observed in one muscle pair. This caused the overall delay (average, 20.6 ± 18.5 ms; range, 3.0–64.3 ms; Fig. 6) to be significantly smaller during rest than postural tremor when comparing the same muscle pairs (p = 0.021, Mann–Whitney U test; Fig. 6B). The phase difference was also significantly different between rest and posture (p < 0.001, Watson–Williams test). Therefore, the relative contribution of supraspinal and spinal tremor sources varied across conditions within the same patient.

Shared synaptic inputs to antagonistic motoneuron pools

The analysis of coherence between CSTs revealed that all pairs of antagonistic motoneuron pools (n = 9, from 5 patients) received the same common tremor synaptic input (coherence, 0.557 ± 0.199; range, 0.256–0.834), with a frequency (5.44 ± 0.94 Hz; range, 3.75–6.88 Hz) similar to that of the neural drives to the antagonistic muscles (Fig. 5G).

In four of the eight pairs of antagonistic motoneuron pools, we also detected a shared common voluntary drive (0.358 ± 0.252; range, 0.205–0.736). This indicates that in some cases the observed voluntary input to motoneurons was shared across antagonistic populations.

Discussion

The phase difference between tremorogenic neural drives to antagonist muscles in ET patients is different during rest and postural tremor. As predicted by the simulations, during postural tremor the neural drives are most frequently out of phase, while during rest tremor they are predominantly in phase. The simulations show that this phase difference is determined by the relative amplitude of the supraspinal tremor input to each motoneuron pool and the concurrent voluntary drive, which explains the observed change across conditions. Both simulation and experimental data also show that the two antagonistic muscles share the same tremor-related common synaptic input regardless the relative strength of supraspinal and afferent input to the motoneuron pools. Our findings highlight the relevance of the interaction between descending tremor input and Ia feedback in the generation of tremor in ET.

Motoneuron population coding of tremor inputs

We characterized the neural drive as the pooled discharges of several motor units (CST), which optimizes the detection of neural inputs to the motoneuron pool (Negro and Farina, 2011a; Farina et al., 2013, 2014). This occurs because the tremorogenic synaptic input is largely common to the pool during both posture and rest, as indicated by the large coherence between CSTs within a muscle at this frequency (Negro and Farina, 2012; Gallego et al., 2015). The concurrent voluntary drive was also common, as observed in healthy individuals (Negro and Farina, 2012; Farina et al., 2013).

Motoneurons “transmit” (common) synaptic inputs through their output discharge pattern (Heckman and Enoka, 2012; Farina et al., 2014). Because motor unit discharges become largely correlated (synchronized) when they receive a strong common projection (Sears and Stagg, 1976; Kirkwood and Sears, 1978), CSTs comprising relatively few motor units optimize the detection of neural inputs compared with individual units (Negro and Farina, 2011a, 2012; Gallego et al., 2015). For a tremor input, this happens independently of the occurrence of paired/tripled discharges (Fig. 5; Gallego et al., 2015). This “population code” was represented as an increase in the TNR of CSTs compared with individual motor unit discharges (Fig. 2; Results). A similar population coding behavior has been reported for populations of neurons within the motor (Baker et al., 2003), auditory (Ince et al., 2013), and visual (Paradiso, 1988) cortices, as they encode information by adding the response of several neural cells whose activity is also correlated (Averbeck et al., 2006). We provide the first demonstration of population coding of pathological neural input by spinal motoneurons.

Changes in the phase difference between tremorogenic neural drives to antagonist muscles, and influence of spinal circuits on the tremor

In patients, the neural drives to antagonist muscles were most often out of phase during postural tremor, and predominantly in phase during rest tremor, in agreement with the simulations. When comparing the same muscles across conditions, this difference was statistically significant (Fig. 6B,C). According to the model, this could be produced by a change in the relative contribution of supraspinal tremor sources, by the descending voluntary drive, or by a combination of both. The voluntary drive during posture would cause the observed phase change if the relative strength of descending tremor input to the pools were relatively similar across them and lied within a certain range of values (e.g., 0.3–0.7 in the simulations; Fig. 4B), because of a change in baseline recruitment. The activity within the cerebellothalamocortical pathways (Schnitzler et al., 2009; Helmich et al., 2013; where tremor in ET probably originates) that generates the voluntary drive could also increase the strength of the descending tremor input to the extensors (compared with the flexors), contributing to the observed phase change by making the supraspinal tremor strength ratios in Figure 4B tend to 0. This hypothesis builds on the observation that the neurons from the cerebellar recipient thalamic nucleus that are activated during voluntary movement are more likely coherent with the tremor than cells from several other thalamic nuclei (Hua and Lenz, 2005). Because of that, the affected motoneuron pool could receive increased descending tremor input from the motor cortex, e.g., because of the recurrent oscillations within thalamocortical pathways at the tremor frequency (Muthuraman et al., 2012), or from the cerebellum (Soteropoulos and Baker, 2008; Williams et al., 2010). According to the simulations, this increased common supraspinal tremor input (Gallego et al., 2015) to the extensors' motoneuron pool will cause the neural drives to be out of phase because (1) limb oscillations (tremor) will elicit activity in the monosynaptic Ia afferents to the antagonistic motoneuron pool (Mendell and Henneman, 1971; Watt et al., 1976; Nelson and Mendell, 1978) and (2) Ia disynaptic input to the heteronymous motoneuron pool (Czarkowska et al., 1981; Jankowska et al., 1981) will provide inhibitory input to the second muscle depending on the conduction delays and the tremor frequency (see below).

During physiological tremor, oscillations in spinal interneurons at the tremor frequency (∼10 Hz) are out of phase with the coherent tremor activity in several motor centers of the brain, which reduces or cancels out the descending tremor input at the motoneuron level, enabling improved motor control (Williams et al., 2010). Even though the frequency of physiological tremor is slightly higher than in ET, the question is raised as to what is the role of these circuits in the generation of tremor in ET. First, the phase inversion by spinal interneurons likely occurs because they respond differently than the brain motor centers to afferent input, since the response of spinal interneurons to pyramidal tract stimulation is noninverted (Koželj and Baker, 2014). Because tremor in ET is generated in the brain, descending input may bypass this “spinal filter” and arrive at the motoneuron pool. However, this “filter” could potentially contribute to dampen the afferent input related to the tremor. One possibility is that the “filter” is tuned to only attenuate oscillations at ∼10 Hz, in which case it could contribute to the well established observation that the higher-frequency tremor in ET (∼8 Hz) is milder than the lower-frequency tremor (Calzetti et al., 1987; Elble et al., 1994). However, any eventual effect cannot be easily dissociated from that of the low-pass filter characteristics of the muscle and limb mechanics (Milner-Brown et al., 1973; Prochazka et al., 1992; Baldissera et al., 1998). Second, as suggested by our simulations, Ia afferents may also effectively reduce some but not all combinations of descending tremor and voluntary drive amplitude. This implies that Ia feedback only attenuates tremor in ET in some specific conditions, and suggests that Ia afferents may be involved in the cancellation of physiological tremor (Williams et al., 2010, their Fig. 4D).

Common synaptic inputs to antagonist muscles

We proposed a new method for the detection of common synaptic projections to different muscles using pooled motor unit spike trains (CSTs) instead of the rectified EMG (Halliday et al., 1995; Farmer et al., 2007; Ward et al., 2013). By applying this method we directly observed, for the first time, that antagonistic motoneuron pools of ET patients always receive the same tremor synaptic input, both during postural and rest tremor. The only previous study that, to our knowledge, investigated this issue reported that ∼80% of antagonist muscle pairs exhibited coherent EMG activity during postural tremor (Raethjen et al., 2000). Our results, derived from the direct examination of population motor unit discharges, are more sensitive, and indicate that the shared tremor synaptic input to antagonist muscles is an invariable characteristic of tremor.

Both antagonist muscles also shared a common voluntary input while patients kept their hands outstretched (13 of 20 pairs). This common input appeared concurrently with the significantly stronger (compared with noise level) shared tremor projection. We believe the common voluntary input was not observed in all pairs because common projections to forearm muscles may only be relevant during more precise tasks, which likely require a stronger corticospinal drive (Hockensmith et al., 2005). Moreover, the shared tremor input may hinder the common projection of the voluntary drive due to the “decorrelation effect” that distorts the simultaneous projection of two common inputs by the pool (Negro and Farina, 2011b). Afferent feedback from muscle spindles may also contribute to this observation (De Luca et al., 2009).

There was also a shared common voluntary input to four of eight antagonist muscle pairs during rest tremor, and all 16 muscles exhibiting rest tremor received a common voluntary drive. It is likely that although patients were asked to be completely relaxed and their forearms were fully supported, there was a certain descending voluntary command, which could be (partially) an indirect consequence of limb oscillations because of the tremor.

Model limitations

The spinal circuits in the model included monosynaptic and disynaptic effects of the Ia afferent pathway, but not a number of pathways and motoneuron properties that can influence the correlation of the motor output. For example, varying degrees of Renshaw cell inhibition (Maltenfort et al., 1998; Williams and Baker, 2009) and active dendritic conductances (Taylor and Enoka, 2004) influence the spectrum of the motoneuron output. However, we believe that such factors would not change the conclusions reached from the simulations substantially due to the very high strength of the Ia pathway, best exemplified by its ∼30% contribution to the net motoneuron excitation in isometric conditions (Macefield et al., 1993). Besides, Ib inhibition is unlikely to affect the motoneuron input due to muscle spindle activation by the passive stretch, as Golgi tendon organs are only responsive to active force (Jami, 1992).

The observation that antagonist tremor activity mediated purely via afferent (Ia) feedback-generated out-of-phase muscle activity depended on the conduction and mechanical delays of the system. These, at the same time, were dependent on the model parameters, which we determined from various published studies, predominantly in humans, but in a few cases in animals. This provided a physiologically realistic, but somewhat generic, model. Therefore, the question arises as to whether the results would apply for the muscles most relevant for the generation of tremor in ET. More specifically, this implies an assessment of the sensitivity of the physiological delays in the efferent–afferent loop (Table 1), which determined the interaction between the afferent and supraspinal inputs, to uncertainty and cross-muscle variability in the model parameters. Because the conduction delays were relatively short (Ia conduction time, <8 ms), the validity of the results would not be compromised if the conduction velocities of the model were overestimated, as suggested by some studies (Munson and Sypert, 1979; Eisen et al., 1984). Similarly, the proximity of the muscle would not have a large impact on the results, which is further underlined by the fact that ET mainly affects distal muscles (Deuschl et al., 1998; Benito-León and Louis, 2006). The mechanical delays constituted the majority of the total delay, which made the results most sensitive to error/variability in these values. The muscle tetanic time-to-peak and half relaxation time may vary by ≤65 ms across muscles (Harridge et al., 1996), indicating potentially large changes in the delay between muscle activation and muscle movement, and thus in the activation of Ia afferents. Therefore, antagonist tremor activity due to spinal inputs may not always generate perfectly out-of-phase tremor across antagonist muscles, although data from humans and primates indicate that there are no substantial differences in the fiber-type composition between forearm and intrinsic hand muscles (McIntosh et al., 1985; Harridge et al., 1996; Enoka and Fuglevand, 2001).

We assumed that the antagonist muscle pair received the same supraspinal tremor with different synaptic projection strengths (amplitude). While the pathophysiology of ET is still controversial (Helmich et al., 2013), and little is known about the oscillator(s) causing it, our assumption provides a simple, plausible hypothesis, supported by the fact that the simulation results matched the experimental observations. In real conditions, the same effect would be achieved by two different muscles receiving the same input: the largest muscle or the one with the greater mechanical advantage would be more likely to entrain the limb movement and thus the afferent feedback.

Summary

Our simulations indicate that the phase difference between neural drives to an antagonist muscle pair in tremor depends on the relative strength of the supraspinal tremor inputs to the two muscles, as well as on the voluntary drive. They also anticipate that the neural drives to an antagonist muscle pair are most likely to be out of phase during postural tremor compared with rest tremor. This trend was fully verified by the experimental results in the patients. Besides, the experimental data revealed that antagonist muscles always share the same common synaptic input at the tremor frequency, as predicted by the simulations. Based on the computational model, we argue that these findings reflect the importance of the neural (via Ia afferents) coupling between antagonist muscles in the generation of tremor in ET.