Population Responses in V1 Encode Different Figures by Response Amplitude

Abstract

The visual system simultaneously segregates between several objects presented in a visual scene. The neural code for encoding different objects or figures is not well understood. To study this question, we trained two monkeys to discriminate whether two elongated bars are either separate, thus generating two different figures, or connected, thus generating a single figure. Using voltage-sensitive dyes, we imaged at high spatial and temporal resolution V1 population responses evoked by the two bars, while keeping their local attributes similar among the two conditions. In the separate condition, unlike the connected condition, the population response to one bar is enhanced, whereas the response to the other is simultaneously suppressed. The response to the background remained unchanged between the two conditions. This divergent pattern developed ∼200 ms poststimulus onset and could discriminate well between the separate and connected single trials. The stimulus separation saliency and behavioral report were highly correlated with the differential response to the bars. In addition, the proximity and/or the specific location of the connectors seemed to have only a weak effect on this late activity pattern, further supporting the involvement of top-down influences. Additional neural codes were less informative about the separate and connected conditions, with much less consistency and discriminability compared with a response amplitude code. We suggest that V1 is involved in the encoding of each figure by different neuronal response amplitude, which can mediate their segregation and perception.

Introduction

In a complex visual scene the visual system efficiently segregates numerous figures from the background and also distinguishes between figures, i.e., encodes each figure differently. This poses a conceptual computational problem (termed as the binding problem; von der Malsburg, 1981): how do features of the same figure bind together to form a coherent figure that is segregated from other features belonging to different figures? The neuronal mechanisms underlying the binding problem have been under debate (Singer and Gray, 1995; Lamme and Spekreijse, 1998; Roskies, 1999; Shadlen and Movshon, 1999; Roelfsema et al., 2004), and the neuronal encoding of multiple figures is not well understood. A simple and straight forward solution for the segregation of a figure from background has been proposed in which neurons encoding features of the same figure enhance their activity (Roelfsema et al., 2004; Roelfsema, 2006; binding-by-rate enhancement). This hypothesis has been supported by numerous studies showing that neurons encoding one figure (or a contour) enhance their activity compared with neurons encoding a background (Lamme, 1995; Zipser et al., 1996; Bauer and Heinze, 2002; Li et al., 2006; Roelfsema et al., 2007; Poort et al., 2012; Gilad et al., 2013). In addition, it was shown that attentional mechanisms can enhance neuronal activity to a target figure compared with a distractor figure (Roelfsema et al., 2007) implying that an amplitude code in V1 can differentiate between an attended figure and an unattended figure. However, what happens when several figures that are task-relevant are present? In this case, all neurons encoding any figure will enhance their activity thus assigning all figures with a similar label. Two possible solutions can be suggested to overcome this problem: (1) different figures are enhanced to a different level of activity or (2) a different neural code is used, e.g., a synchrony code in which neurons encoding features of the same figure synchronize their activity as opposed to neurons encoding features of different figures (von der Malsburg, 1981; Gray and Singer, 1989; Engel et al., 1991; Singer and Gray, 1995; Kreiter and Singer, 1996; but see Lamme and Spekreijse, 1998; Roelfsema et al., 2004; Palanca and DeAngelis, 2005; Gilad et al., 2012).

In a previous study, using a contour integration paradigm we found that population responses to a contour (figure) were enhanced, whereas population responses to the noisy background were simultaneously suppressed in V1 (Gilad et al., 2013), thus emphasizing the role of V1 in figure-ground segregation. Could this enhancement/suppression pattern be used also to segregate between two figures? Another possibility is that V1 is not involved in encoding multiple relevant figures. In this case V1 forwards similar labels for all figures (figure-ground information only) to higher areas and the different encoding for each figure (figure–figure information) is made only in higher areas without involving V1 (Marr, 1982; Biederman, 1987; Kosslyn, 1987; Felleman and Van Essen, 1991; Palmer and Rock, 1994; Malach et al., 1995; Kourtzi and Connor, 2011).

To investigate the neural code mediating the encoding of different figures we trained two monkeys to discriminate whether two elongated bars, embedded in a noisy background, are either separate or connected. Using voltage-sensitive dye imaging (VSDI) we find that a response amplitude code can distinguish between the two separate bars even at the single trial level. Thus, V1 may be involved in labeling each figure by a different amplitude level.

Materials and Methods

Behavioral tasks, visual stimuli, and eye position recordings

Separate versus connected discrimination task.

Two adult monkeys (Macaca fascicularis; males; Monkeys T and S; 13 and 11 kg, respectively) were trained to report whether two elongated bars were either separate or connected. The trial started when the animal fixated on a small (0.1°) fixation point displayed on a uniform gray background. After a random fixation interval (3000–4000 ms), a “separate” or “connected” stimulus appeared on the screen for 150–400 ms. The animal maintained fixation until the stimulus and fixation point were turned off. At this point, two small lateral targets appeared, one on each side of the screen, and the animal was required to indicate its visual perception by performing a rightward saccade for a separate report and leftward saccade for connected report. A trial was classified as correct only if the animal maintained fixation throughout the trial, responded with a saccade to the correct target, and fixated on the target for an additional 400 ms. The animal was rewarded with a drop of juice for each correct trial. In each recording session, the separate and connected stimuli appeared in 80% of the trials, whereas the remaining 20% trials were fixation-alone trials (no stimulus presentation, blank condition). These trials were used to remove the heartbeat artifact in the VSDI data (see VSDI analysis below) and the monkey was rewarded for maintaining fixation throughout the entire trial.

Discrimination performance is defined as the number of correct trials divided by the total number of trials (sum of separate and connected trials). The average discrimination performance (for 400 ms stimulus duration) was 97% (1% errors of the separate condition and 2% errors of the connected condition) for Monkey T and 82% (10% errors of the separate condition and 8% errors of the connected condition) for Monkey S. Discrimination performance for the short stimulus duration (150 ms) remained high (98%).

Visual stimuli.

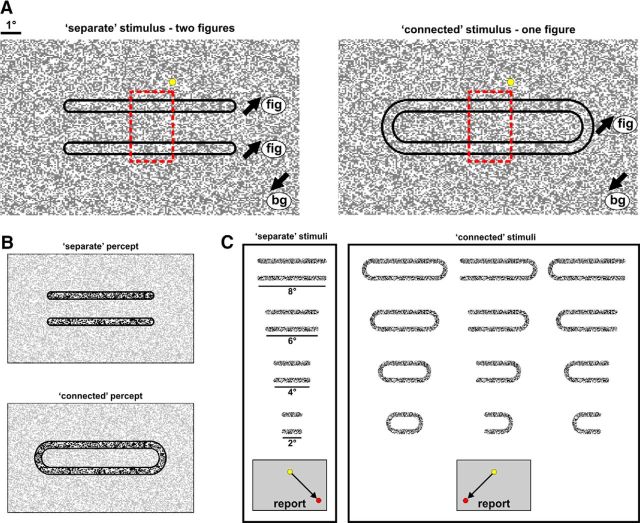
On each trial, the monkeys were presented with one of two types of stimuli: a separate or a connected movie (Fig. 1A), referred to as the separate or connected condition. In both movies the monkeys were presented with a pattern of random moving dots (black or white high contrast dots; each dot 0.057°; Roelfsema et al., 2007) during fixation. In the separate condition two separate and elongated subgroups of dots (Fig. 1A, left, outlined in black; length of each bar 2°–8°, width of each bar 0.5°, distance between bars 1°–1.5°) moved in one of the four diagonal directions (0.91°/s), whereas the remaining background dots moved in an opposite direction (Fig. 1A, left). Motion was present throughout stimulus presentation from stimulus onset (dots appearance) to offset (dots disappearance). This created the perception of two separate figures, i.e., two bars, embedded in the background (Fig. 1B, top). In the connected condition the two bars were connected by remote circular connectors with the same motion parameters of the bars themselves (Fig. 1A, right). This resulted in a perception of one figure, i.e., elongated annulus, embedded in the background (Fig. 1B, bottom).

Figure 1.

Behavioral paradigm and stimuli. A, The monkeys were presented with a pattern of random moving dots during fixation (yellow point denotes fixation point). Black arrows denote the motion direction. Left, Separate condition: two separate and elongated subgroups of dots moved in a common direction (fig) that was opposite to the motion direction of the background dots (bg). Right, Connected condition: the same two bars were connected by remote circular connectors with the same motion parameters. The dashed red rectangle, added only for illustration, approximately outlines the stimulus part that was retinotopically mapped onto the imaged V1 area. B, The outcome perception of the stimuli in A, highlighted with higher contrast. C, To generalize the task over separate and connected conditions, we used a set of different stimuli for each group (shown here without background for visualization purposes only). The monkeys were required to report whether the bars were connected (right box) or not (left box) regardless of their length, position, or connectivity type. The direction of saccadic report for each condition is depicted at the bottom.

Generalization of the separate versus connected discrimination task.

Theoretically to correctly discriminate between the two stimuli in Figure 1A, the monkey only needs to focus his attention and resources to just one edge while completely ignoring the rest of the stimulus. In this case, the monkey would be performing a simple pattern recognition task. To ensure that the monkeys will indeed discriminate between various separate and connected stimuli, we further generalized the visual paradigm (Fig. 1C). For example, we presented the monkeys with two bars connected only at one side. We also varied the length of the bars (2°, 4°, 6°, or 8°), and the retinotopic position. During training, the monkeys were presented with a mixture of different types of stimuli in random retinotopic locations. The monkeys were required to report whether the bars were separate (right saccadic report) or connected (left saccadic report) regardless of their size, position, or connectivity type. In addition, we minimized stimulus presentation to 150–200 ms during training. We note that the generalization of the visual paradigm comprised ∼75% of training time. This generalization ensured that the monkeys did not focus their attentional resources to one location, thus leading to pattern recognition, but rather distribute their attention across the whole stimulus, thus implying that the monkeys perceptually seek to segregate between the two bars.

Separation saliency task:

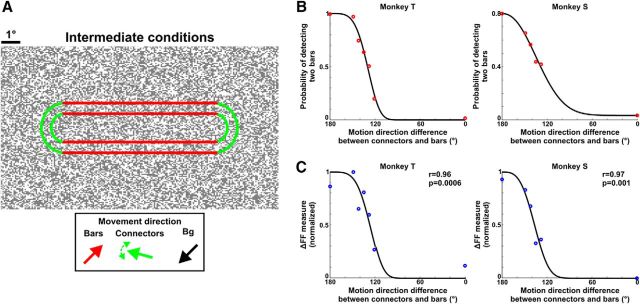
To study the effect of separation saliency on behavioral performance and population response in V1, the monkeys were tested on another task. In addition to the separate/connected stimuli, the monkeys were randomly presented with four to five stimuli in which the dots of the connectors moved in an intermediate direction between the dots of the bars and the background (121°, 128°, 135°, 142°, 149° relative to the bars' direction; see Fig. 6A). The motion direction of the bars and background remained unchanged. As the connectors' direction became less similar to the bars' direction and more similar to the background's direction, the saliency of the two separate bars, i.e., the separation saliency, increased. To ascertain that the monkeys report the separation saliency in these experiments we did the following: (1) in the separate/connected conditions (comprising 50% of the recording session), the monkey was rewarded only if it made a saccade to the correct target. This way we verified that the animal could easily discriminate the separate from the connected in these experiments (the discrimination performance of the separate/connected conditions remained high for both monkeys: 99% and 88% for Monkeys T and S, respectively). (2) For the intermediate conditions, the monkey was rewarded for either saccade to the right or left target. Therefore, the animal's decision was unbiased on the intermediate conditions, and these trials were classified as “separate detected” or “connected detected” only according to the direction of the report saccade (Gilad et al., 2013). A larger range of directions were used in additional training sessions. In general when the connectors' direction was smaller than 100° (relative to the bars' direction) the monkeys reported the connected condition almost exclusively. This is in line with the fact that a slight deviation from the background's direction (∼20°) is enough to elicit visible connectors, and thus leads to perceiving the connected condition (Wolfson and Landy, 1995).

Figure 6.

ΔFF measure is correlated with the separation saliency of the two bars and the monkeys' perceptual report. A, In another set of experiments we presented the monkeys with a set of stimuli in which we varied the motion direction of the dots in the connectors (outlined in green) relative to motion direction in the bars' (outlined in red; see Materials and Methods). As the connectors' direction became less similar to the bars' direction and more similar to the background's direction, the saliency of the two separate bars increased. B, The psychometric curve of Monkeys T (left) and S (right) displaying the probability of detecting two bars as a function of the connectors' direction (relative to the bars' direction; n = 5 and 4 recording sessions for Monkeys T and S, respectively). Points were fitted with a Weibull function (black curve). C, The neurometric curve for Monkeys T (left) and S (right) calculated for the ΔFF as a function of the motion direction difference between connectors and bars (same data as in B). Data were normalized between 0 and 1 for each recording session (Materials and Methods). Points are fitted with a Weibull function.

Eye position recording

Throughout the trial the animal maintained tight fixation and analysis was done on trials where fixation was maintained within ±1° (see Basic VSDI analysis). Eye position was monitored by an infrared eye tracker (Dr Bouis Device, Kalsruhe, Germany), sampled at 1 kHz and recorded at 250 Hz. In addition, if we detected a saccade or microsaccade the trial was truncated to remove the effects of these fixational eye movements (see Basic VSDI analysis).

Data acquisition

Two linked computers controlled the visual stimulation, data acquisition, and the monkey's behavior (CORTEX software package). The system was equipped with a PCI-DAS 1602/12 card to control the behavioral task and data acquisition. The protocol of data acquisition in VSDI was previously described in detail (Slovin et al., 2002). Single trials were saved on separate data files to enable single trial analysis.

Surgeries and VSDI imaging

The surgical procedure and voltage-sensitive dye staining have been reported in detail previously (Shoham et al., 1999; Shtoyerman et al., 2000; Arieli et al., 2002; Slovin et al., 2002). All materials and methods were performed according to the NIH guidelines, approved by the Animal Care and Use Guidelines Committee of Bar-Ilan University, and supervised by the Israeli authorities for animal experiments. Antibiotics and analgesics were applied before and after surgical procedures and adequate measurements were taken to minimize pain and discomfort. Briefly, craniotomy was performed under full anesthetization and aseptic conditions, and the dura mater was removed, exposing the visual cortex. To perform long-term VSDI, a transparent artificial dura was implanted over the cortical surface. The anterior border of the imaged area was typically 3–6 mm anterior to the Lunate sulcus. The center of the imaged V1 area laid 1°–3° below the horizontal meridian and 1°–2° from the vertical meridian. We imaged population response from part of V1 that covers eccentricities range of 0.5°–3.5°. We stained the cortex with RH-1691 or RH-1838 voltage-sensitive dyes (VSDs) supplied by Optical Imaging.

VSDI was performed using the Micam Ultima system based on a sensitive fast camera with up to 10 kHz sampling rate. We used a sampling rate of 10 ms/frame with a spatial resolution of 10,000 pixels where each pixel summed the activity from an area of 1702 μm². Each pixel sums the optical signal from the population activity of ∼500 neurons (0.17 × 0.17 × 0.4 × 40,000 cells/mm³). The exposed cortex was illuminated using an epi-illumination box with an appropriate excitation filter (peak transmission 630 nm, width at half-height 10 nm) and a dichroic mirror (DRLP 650), both from Omega Optical. A barrier postfilter above the dichroic mirror (RG 665, Schott) collected the fluorescence and rejected stray excitation light.

Data analysis

Data analysis was performed on 61 and 33 recording sessions (∼75 trials in each session) from two hemispheres in Monkeys T and S, respectively. This consisted of three types of datasets: retinotopic sessions (monkey was fixating only; n = 6 and 8 recording sessions from Monkeys T and S, respectively; and see below), separate versus connected discrimination task (stimulus duration = 400 ms; n = 24 and 13 recording sessions from Monkeys T and S, respectively; bar widths 4°, 6°, and 8° pooled together; additional 3 recording sessions for 2° bar width in Monkey T were analyzed separately; see Fig. 7), and separation saliency task (stimulus duration = 400 ms; n = 5 and 4 recording sessions from Monkeys T and S, respectively). MATLAB software was used for all statistical analyses and calculations (v2010b, MathWorks).

Figure 7.

ΔFF is also present in a close proximity to the connectors. A, A map of population response (right) obtained by presenting the two bars (2° length) with a gray background (left; dot depicts the fixation point). Color denotes ΔF/F. The top and bottom areas are approximately outlined in black. B, A map of population response (right) obtained by presenting the two connected bars with a gray background (left). In this case, the left connector is also imaged (outlined in white). C, The differential map for the example in A, B, but with a motion background (as in Fig. 3A). Despite the close proximity of the connector, the top ROI exhibits positive values whereas the bottom ROI exhibit slightly negative values. The connector ROI (white outline; Present only in the connected condition) shows negative ΔF/F values as expected. D, Histogram of the differential response of pixels shown in C for the top ROI (red) and the bottom ROI (blue). E, The ΔFF as a function of time (as in Fig. 4D) for the example in C (n = 56 trials). The dashed lines are mean ± 2STD for the ΔFF calculated on shuffled trials.

In an additional set of experiments, the monkeys performed separate versus connected discrimination task when stimulus duration was 150 ms (n = 12 recording sessions from Monkey T; used only for analysis presented in Fig. 8A,B) or when the background was replaced with a uniform gray (rather than motion of random dots; n = 7 and 8 recording sessions from Monkeys T and S, respectively). Finally in another set of experiments a monkey was presented with a stationary (rather than moving) pattern of random dots that did not induce any figure perception (n = 7 recording sessions from Monkey T; fixation alone).

Figure 8.

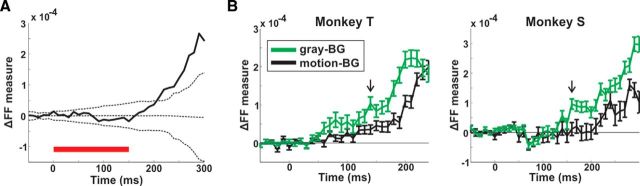
ΔFF dynamics on other stimulus conditions. A, Dynamics of ΔFF (as in Fig. 4D) induced by shorter stimulus presentation (150 ms; red bar at the bottom) in an example recording session (n = 124 trials). The dashed lines are mean ± 2STD for the ΔFF computed on trials with random label shuffling. B, ΔFF dynamics when presenting the bars on a gray background (gray-BG; green curve; no motion in the background) or background with motion (motion-BG; black curve). Monkey T is on the left and Monkey S is on the right. Error bars are SEM over trials (n = 190/167 and 187/124 trials in gray-BG and motion-BG respectively; Monkeys T/S). The arrow indicates the first time frame with a significant difference between conditions (140 and 160 ms in Monkeys T and S, respectively; Mann–Whitney U test; p < 0.05).

Basic VSDI analysis

The basic analysis of the VSDI signal was previously detailed (Slovin et al., 2002; Ayzenshtat et al., 2010). Briefly, this consisted of choosing pixels exceeding a fluorescence level ≥15% of maximal fluorescence (excluded pixels were mainly at the edge of the imaged area or over blood vessels), then removing background fluorescence by normalizing each pixel to its baseline fluorescence level (i.e., dividing by fluorescence of the few time frames before stimulus onset). Finally, to remove the heartbeat artifact, the average fixation-alone condition was subtracted from each stimulated trial (separate or connected). The latter subtraction is effective because all VSD data acquisition trials are triggered on the animal's heartbeat (Shoham et al., 1999; Slovin et al., 2002; measured using electrocardiogram signal). Fixation-alone trials were intermixed with stimulated trials. This basic analysis removes in unbiased manner, most of slow fluctuations originating from heartbeat artifact or dye bleaching (for review, see Grinvald et al., 1999). These steps are schematically illustrated and explained in Ayzenshtat et al., 2010 (their Fig. S12). VSDI maps were low-pass filtered with a 2D Gaussian filter (σ = 1.5 or 2.5 pixels) for visualization purposes only.

Although throughout the stimulus presentation the monkey was required to maintain tight fixation, it typically made a few (1–3) microsaccades or small fixational saccades throughout stimulus presentation. To remove the effects of saccadic eye movements on our analysis, we detected the time of onset of the first saccadic eye movement on each trial, by implementing an algorithm for microsaccades and saccades detection (Engbert and Mergenthaler, 2006; Meirovithz et al., 2012; Gilad et al., 2014) on the monkeys' eye position data. The algorithm could precisely detect saccadic eye movements >0.1°. Next, we truncated the VSDI signal of each trial 40 ms after the onset of the corresponding first saccadic eye movement. This analysis ensured that the VSDI signal was not affected by saccadic eye movements. As a result, the number of trials was reduced as a function of time, thus leaving only the first 250–350 ms for data analysis.

Retinotopic mapping of the two bars onto V1 and defining the ROIs

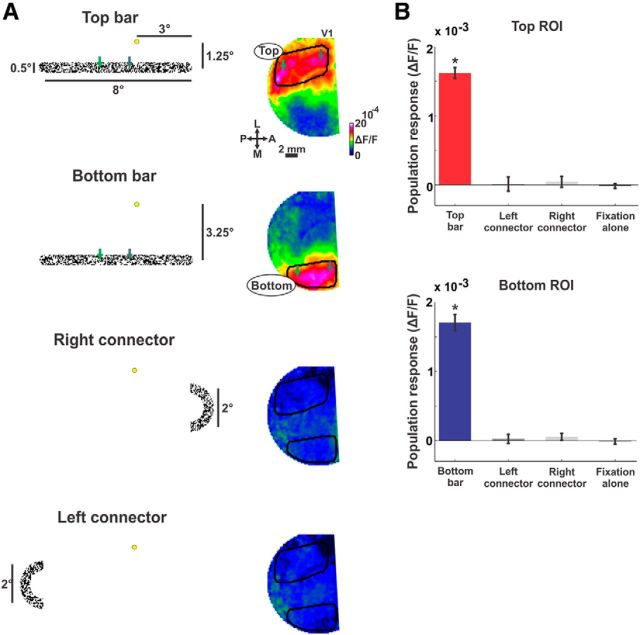
An important aspect that was taken into consideration when designing the visual paradigm was to enable simultaneous imaging of both bars but to exclude the direct effect of the connectors (both left and right) on neuronal populations in the imaging area (but see Fig. 7 for a different approach). For this purpose we performed additional retinotopic mapping sessions (at the beginning of each recording day) in which we presented each of the different relevant parts of the stimulus separately: top bar, bottom bar, left connector, or right connector (Fig. 2A, left column). Each stimulus part was presented against a uniform gray background, whereas motion in the stimulus part was similar to the figures in the behavioral task. During these experiments, the monkeys were required to maintain fixation. Each bar evoked a distinct activation patch (Fig. 2A). To define regions-of-interest (ROIs), we first outlined the activation patch evoked by each bar and all pixels inside this outline were further analyzed (Fig. 2A). Next, only pixels passing a threshold signal-to-noise ratio (SNR was defined as the response amplitude minus baseline amplitude divided by the STD in the baseline amplitude; threshold was SNR > 3; ∼92% of the pixels exceeded this threshold) and pixels below a threshold of intertrial STD (SD across trials; STD < 0.6 × 10⁻³) where included in the top, bottom, and background ROIs (background ROIs were defined as pixels between the top and bottom ROIs). These filtering operations mainly excluded pixels in the vicinity of large blood vessels or at the edge of the imaging area, where fluorescence level were lower. Thresholds were identical in both separate and connected conditions. The top, bottom, and background ROIs included 394 ± 147 (mean ± STD), 294 ± 137 and 558 ± 116 pixels in Monkey T, and 222 ± 71, 182 ± 71, and 185 ± 65 pixels in Monkey S (Monkey S had a smaller V1 available for imaging). The results were similar using equally sized ROIs and for variable SNR and intertrial STD thresholds. In addition the response in each ROI showed a very small and late modulation when the other bar was presented (e.g., the top ROI was influenced by the bottom bar presentation). This is expected as the VSD signal is sensitive to subthreshold activation that can propagate (Slovin et al., 2002; Petersen et al., 2003; Sato et al., 2012; Mohajerani et al., 2013; Muller et al., 2014) between the two adjacent ROIs, separated by only a few millimeters in the cortex.

Figure 2.

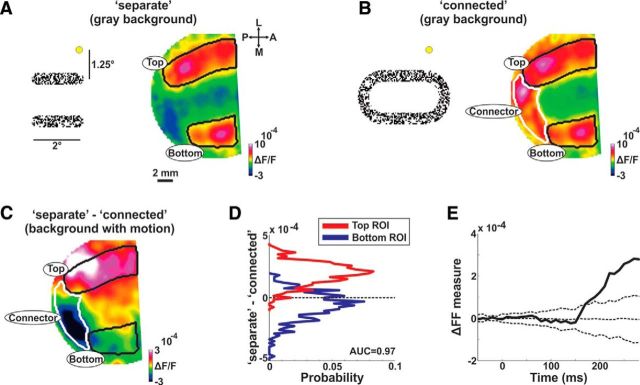
The imaged area in V1 is activated by both bars but not by the connectors. A, Maps of population response (right column) obtained by presenting each of the different parts of the stimulus (left column). From top to bottom (yellow dot depicts the fixation point): top bar, bottom bar, right connector, and left connector. Color denotes normalized fluorescence (ΔF/F). The areas activated by the top and bottom bars are approximately outlined in black on the relevant maps. The green arrows depict coordinates on the bars: in the visual field (left) and approximately on the imaged V1 area (right). B, Population response in the different ROIs (ROIs include pixels passing SNR threshold within the outlined areas in A; see Materials and Methods). Top, The mean population response (averaged between 150 and 300 ms after stimulus onset; also verified for earlier times: 80–150 ms), in the top ROI obtained by presenting the top bar (red), left connector (dark gray), right connector (light gray) or fixation alone (black; no stimulus presentation). Bottom, The average (as above) population response in the bottom ROI obtained by presenting the bottom bar (blue), left connector (dark gray), right connector (light gray), or fixation alone (black; no stimulus presentation). Error bars are SEM over recording sessions (n = 6 in Monkey T); *p < 0.05.

The classical receptive field (RF) size at the imaged eccentricities (0.5°–3.5°) is expected to be quite small 0.1°–0.6° (Angelucci et al., 2002) and the surrounding suppressive field is expected to be 2.5 times larger than the RF; i.e., ∼0.25°–1.5°, respectively (Sceniak et al., 1999; Cavanaugh et al., 2002). It is therefore unlikely the connectors (located typically 2.5°–3° from the edge of the imaged area and ∼4° from the center of the ROIs) affected directly the neuronal responses in the imaged top and down ROIs. In addition, we presented the connectors at varying distances corresponding to the different bars' lengths (2°, 4°, or 6°). Connectors in the 6° and 4° conditions did not affect the top and bottom ROIs, whereas the 2° elicited activation in both ROIs. Therefore, neuronal populations activated by both bottom and top bars are well defined and are not directly affected by the connectors (for the 2° condition, see Fig. 7). Thus, the local attributes, i.e., contrast luminance and motion direction, that evoked the different ROIs were highly similar between separate and connected stimuli differing only at relatively remote edges.

Finally, to investigate the relationship between response amplitude patterns and eccentricity we also defined iso-eccentric ROIs. To do this we used a 2D retinotopic model to predict which pixels in each ROI (i.e., top, bottom, and background ROIs) fall within a 2.5°–3.5° eccentricity limits (Schira et al., 2007; Ayzenshtat et al., 2012; Gilad et al., 2014).

Population response analysis and differential figure–figure measure

To investigate the population response (the amplitude of the VSD signal), we compared the population response [ROIs or maps; maps were low-pass filtered with a 2D Gaussian filter (σ = 1.5 or 2.5 pixels) for visualization purposes only] in the separate and connected conditions.

Normalization of the VSD signal in the analysis of Figure 3E.

Figure 3.

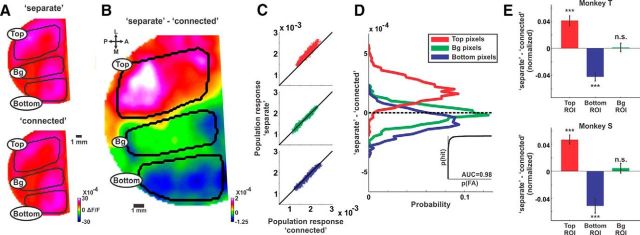
Separate response relative to connected response: population responses is enhanced for the top bar and suppressed for the bottom bar. A, The mean activation maps (averaged at 200–250 ms after stimulus onset) in the separate (top) and connected (bottom) conditions in one recording session (n = 124 and 128 trials in the separate and connected conditions respectively). The areas activated by the top and bottom bars as well as background (Bg) area are approximately outlined in black. B, The differential map (population response in the separate condition minus the population response in the connected condition) of the maps in A. C, Scatter plots of the population response in pixels, for B: top outlined area (red, top), background outlined area (green, middle), and the bottom outlined area (blue, bottom). Each dot depicts the population response (ΔF/F) in one pixel for the separate (y-axis) versus the population response in the connected (x-axis). D, Histogram of the differential response shown in B for the top (red), background (green), and bottom (red) outlined areas. The histogram shows the differential response of pixels, comprising each of the outlined areas. The ROC curve between top and bottom distributions is shown in the inset (AUC = 0.98). E, Grand average of the normalized differential response for each ROI averaged at the late phase (220–350 ms) shown for both monkeys (each trial was normalized to the mean activity in the 3 ROIs; see Materials and Methods). Error bars are SEM over recording sessions (n = 24 and 13 for Monkeys T and S, respectively); ***p < 0.001. n.s., Not significant.

The VSD signal of single trials can contain nonspecific slow spatio-temporal fluctuations (see for example Muller et al., 2014). This may lead to large variation across trials. To overcome this, we normalized the population response in each ROI to the mean response of the three ROIs (averaged at 220–350 ms; Eqs. 1–3; Fig. 3E). Previous studies have used a similar normalization where the median of the whole imaged area was subtracted/divided from each pixel (Chen-Bee and Frostig, 1996; Drew and Feldman, 2009). This was done separately for each separate or connected trial.

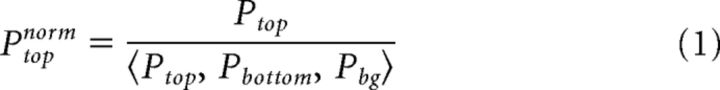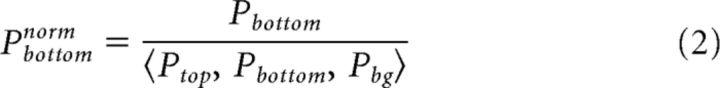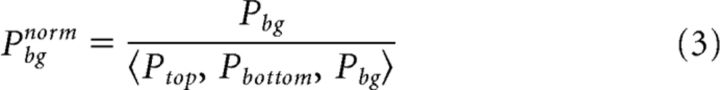Where P_top, P_bottom, and P_bg are the mean population responses (across pixels) in one trial (separate or connected) in the top, bottom, and background ROIs. norm is normalized (Fig. 3D). P_bg is the mean of these values. This normalization preserves differences in population responses between ROIs while reducing the variance across trials. In general, the responses in all ROIs covary across trials. We note that this normalization was performed only for the grand averages in Figure 3E. Figure 3A–D displays raw, non-normalized results. In addition, the differential figure–figure measure (Eqs. 4–6), and synchrony measure (Eqs. 8–10) below were calculated without this normalization.

Differential figure–figure measure.

The differential figure–figure measure (ΔFF; Fig. 4; Eqs. 4–6) reflects the difference between the top and bottom ROIs when the bars are separated compared with when the bars are connected. First, to remove any response difference due to uneven staining pattern, we subtracted the mean connected condition from the mean separate condition (Eqs. 4,5). This was done for each pixel (see differential response map in Fig. 3B) or each ROI (i.e., top or bottom; Fig. 4B). This step eliminates any response differences between ROIs, which are present in both separate and connected conditions due to uneven staining or common stimulus contribution, and therefore, only differences between conditions remain. Next, the ΔFF was defined as subtracting the bottom differential response (Δbottom) from the top differential response (Δtop; Eq. 6). Thus, the ΔFF reflects the difference between the top and bottom ROIs when the bars are separated compared with when the bars are connected. Positive ΔFF values reflect higher response in the top bar compared with the bottom bar and near-zero ΔFF values means no difference.

Where P^separate and P^connected are the mean (across trials and pixels) population response in the top or bottom ROIs for the separate and connected conditions, respectively.

Figure 4.

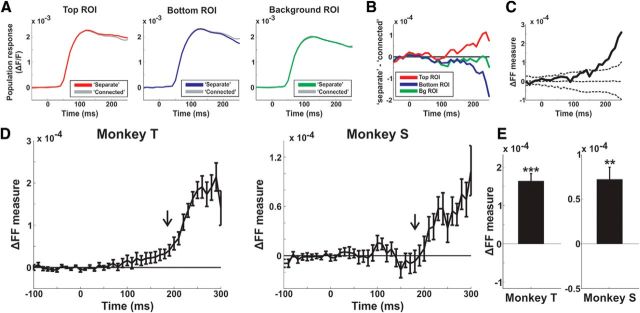
Dynamics of ΔFF. A, The population response in the top (red), bottom (blue), and background (green) ROIs for the separate and connected (gray) conditions in an example recording session. B, The difference (separate minus connected) of the responses in A for the top (red), bottom (blue), and background (green) ROIs. C, The ΔFF as a function of time in the example recording session from B (red curve minus blue curve in B). The dashed lines are mean ± 2STD for the ΔFF calculated on shuffled trials (see Materials and Methods). D, The grand average ΔFF as a function of time for each monkey (n = 24 and 13 for Monkeys T and S, respectively). Error bars are SEM over recording sessions. The black arrow indicates the median latency of the ΔFF measure. E, The grand average ΔFF, averaged at late times (220–350 ms) for each monkey. Error bars are as in D; **p < 0.01;***p < 0.001.

We defined the latency for the ΔFF measure as the time-to-peak of the second derivative. This was done for each recording session separately [on the mean measure smoothed with a Gaussian filter with a width (2σ) of 40 ms]. The second derivative could efficiently capture the beginning of the sharp increase of the ΔFF measure (Boudreau and Ferster, 2005; Meeks and Mennerick, 2007; Wang et al., 2014; Fig. 4E). We found similar results using different latency measures, for example time to 25, 33, or 50% of the maximum peak (Roelfsema et al., 2007). In all cases, latencies were relatively late (150–280 ms).

ΔFF measure for single trials.

Finally, to compare between separate and connected at the single trial level we also derived a ΔFF measure for single trials (separate or connected). First we subtracted the mean population response map in the connected condition from the population response map of each separate or connected trial (Fig. 5A–D, example trial maps; similar to the map in Fig. 3B but for single trials). Next, for each trial we subtracted the mean population response of the bottom ROI from the top ROI (ΔFF for each trial; similar to Eq. 6 but for a single trial, separate or connected). The first step (subtracting the mean connected condition from each trial) is just a linear shift performed equally for both distributions and thus does not affect the separation distance or separation accuracy between the two distributions. The ΔFF measure for single trials is very similar to the ΔFF measure (Eqs. 4–6) as it calculates the difference between the top and bottom ROIs compared with the mean connected condition. We note that filtering the VSD signal, e.g., high-pass (>2.5 Hz) or calculating the first derivative, did not improve the separation accuracy between single trials.

Figure 5.

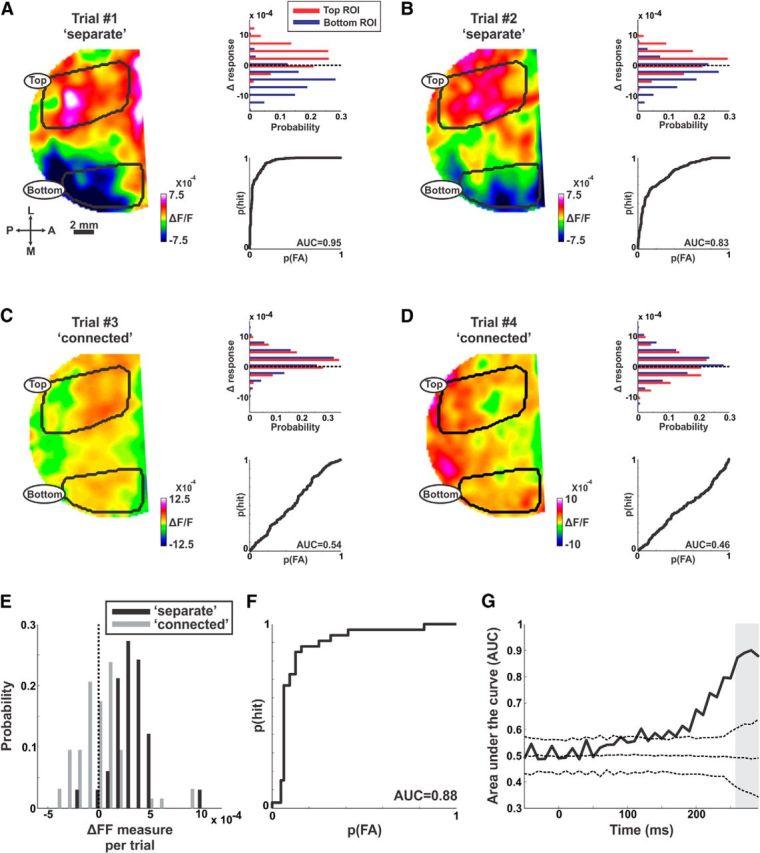
ΔFF measure is informative at the single trial level. An example from a typical recording session. A, B, Two example trials from the separate condition. Left, ΔResponse maps in the late phase (the mean population response in the connected condition was subtracted from each map). Top, Right, Distribution histograms of the Δresponse in the maps on the left. Each distribution shows Δresponse in pixels belonging the top ROI (red) and bottom ROI (blue). Bottom, Right, The ROC curves derived from the histograms in the top right panels. C, D, Same as in A, B, but for two example trials in the connected condition. E, Histograms of the ΔFF for single trials (averaged at 260–300 ms; gray bar in G; see Materials and Methods) in the separate (black; n = 124 trials) and connected (gray; n = 128 trials) conditions. F, The ROC curve (black) derived from the histogram in (E) between the ΔFF computed for separate and connected trials; AUC = 0.88. G, The AUC as a function of time. The ROC curve was calculated as in F but for each time frame after which the AUC was obtained. The dashed curves display the shuffled AUC (mean ± 2STD) derived from the shuffled data in which trials were given a random label.

Psychometric and neurometric curves as a function of separation saliency

To study the relation between the population response, the separation saliency and the perceptual report of the monkeys we performed another set of experiments. In these experiments we varied the motion direction of the dots in the connectors (Fig. 6A, outlined in green). As the connectors' direction became less similar to the bars' direction (Fig. 6A, outlined in red) and more similar to the background's direction, the saliency of the two separate bars increased. We then calculated the probability of reporting the separate condition (two separate bars) and computed the psychometric curve for the separate and connected conditions and for all the intermediate conditions. To study the effects of separation saliency on the population response, the neurometric curve was computed by calculating the ΔFF as a function of separation saliency (Eq. 7).

The neurometric curve values were normalized to maximal and minimal values in each recording session (to overcome the variable staining quality across recording sessions; Gilad et al., 2013). The neurometric curves were calculated at slightly earlier times (210–230 and 170–190 ms for Monkeys T and S, respectively; Fig. 6C) because in these recording sessions the monkeys had a slightly higher rate of fixational eye movements, thus reducing the amount of trials available for analysis (each trial was truncated after the first fixational saccade). There was a significantly positive correlation also when computing the neurometric curves at wider time window 170–350 ms (r = 0.93, p < 0.01 and 0.83, p < 0.05, for Monkeys T and S, respectively). We also report that the correlation between the non-normalized neurometric curve and the psychometric curve also reached significantly positive values (r = 0.78, p < 0.05, and 0.98, p < 0.001, for Monkeys T and S, respectively).

Synchrony and covariance analyses

In addition to the standard amplitude measures, we studied other neural codes for figure labeling. The visual paradigm in this study is an ideal platform to investigate the binding-by-synchrony hypothesis, because we measure two distinct neuronal populations (top and bottom ROIs) which encode the same visual features (locally), but in one case the features belong to two separate figures (separate) and in the other case the features belong to one coherent figure (connected). The binding-by-synchrony hypothesis proposes that the synchrony between the top and bottom ROIs should be lower in the separate condition compared with connected condition. To calculate synchrony we first subtracted the mean time course (across trials) from the time course of each pixel and trial (Eq. 8; Brody, 1999). This was done for the separate trials (subtracting the mean response in the separate condition) and for the connected trials (subtracting the mean response in the connected condition). This procedure removed most of the activity that is directly related to the stimulus onset.

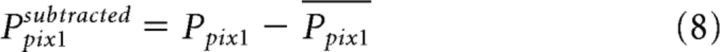Where P_pix1 is the population response in one trial (separate or connected) and one pixel and P_pix1 is the mean population response across trials (separate or connected) in one pixel.

Using a sliding rectangular window of 80 ms we calculated the mean correlation coefficient over time (termed as synchrony because we removed the stimulus contribution) between all the different pixel pairs between the top and bottom ROIs (Eq. 9):

where corr is the correlation coefficient function.

This was done for each trial (separate or connected) and each time window. We then averaged the results across trials obtaining the mean synchrony between the top and bottom ROIs as a function of time for the separate and connected conditions. Next, we calculated the Δ-synchrony by subtracting the mean synchrony in the connected condition from the mean synchrony in the separate condition (Eq. 10). This was done for each recording session.

It has been shown that when two neurons are stimulated by the same figure (curve) they tend to covary their activity (rate covariation; Eq. 11), i.e., at one trial both units displayed low activity and in another trial both units displayed high activity (Roelfsema et al., 2004). This measure is not a trial wise measure but can be calculated only across trials for each recording session. We calculated the correlation coefficient across trials between the population responses (averaged at 220–350 ms) in the top and bottom ROIs. This was done for each condition separately

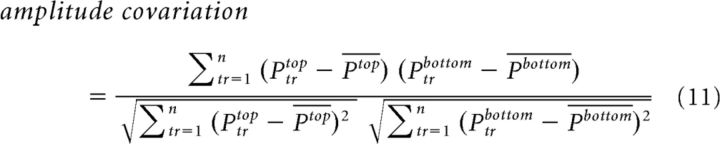Where P_tr^top and P_tr^bottom are the population responses in the top and bottom ROIs in one trial (tr = 1, …, n) and P^top and P^bottom are the mean population responses across trials in the top and bottom ROIs. Next, we calculated the Δcovariance by subtracting the amplitude covariation in the connected condition from the amplitude covariation in the separate condition (Eq. 12). This was done for each recording session.

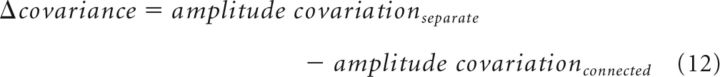Statistical analysis

Nonparametric statistical tests were used, signed rank test to compare a population's median to zero (Figs. 3E, 4E) or Mann–Whitney U test to compare between two medians from two populations (Fig. 5E). For a significance test of one measure (e.g., ΔFF or area under the curve; AUC) in one recording session, we created 1000 shuffled datasets with random trial labeling and calculated the same measure in each shuffled iteration. Next we compared our observed measure to the distribution of the shuffled measures and derived its p value (Figs. 4C, 5G, 7E, 8A). Exceeding mean ± 2 STD of the shuffled data were defined as a significant observation.

This statistical control was also performed for the Δsynchrony where each recording session was randomly labeled for each iteration.

Results

The main goal of this study was to examine whether and how V1 population responses can distinguish between separate objects and a connected object. We trained two monkeys to discriminate whether two elongated bars are separate (i.e., comprise two separate figures) or connected (i.e., comprise one figure; Fig. 1; see Materials and Methods). Following fixation, monkeys were presented with a pattern of random moving dots. In one condition, two separate groups of dots moved in a common direction that was opposite to the motion direction of the background dots (Fig. 1A, left). This generated the perception of two separate figures, i.e., two bars, embedded in the noisy background (separate; Fig. 1B, top). In the other condition, the two bars were connected by remote circular connectors with the same motion parameters (Fig. 1A, right). This resulted in a perception of one connected figure, i.e., elongated annulus, embedded in the noisy background (connected; Fig. 1B, bottom). Importantly, the local stimulus attributes of the bars were kept identical across the different stimuli conditions; only spatially remote, circular connectors, distinguished between separate and connected bars (see section below). After stimulus offset the monkeys were required to report whether the two bars are separate or connected (see Materials and Methods). To ensure that the monkeys could indeed discriminate between various separate and connected stimuli, we further generalized the visual paradigm (Fig. 1C). The monkeys were required to report whether the bars were separate (Fig. 1C, left box) or connected (Fig. 1C, right box) independently of the bars' lengths (varying between 2° and 8°), retinotopic position or connectivity type (1 or 2 connectors). For example, the connected condition included bars that were connected only at one edge (right or left) or both edges (Fig. 1C, right box). This generalization over connectivity type and bar's length affirmed that to solve the task the monkeys had to inspect the whole stimulus (rather than exploiting a single location on the stimulus which may result in pattern recognition). Using VSDI, we imaged at high spatial and temporal resolution the population responses in V1 that were activated by the bars. The dye signal measures the sum of membrane potential from all neuronal elements in the imaged area. Therefore, theVSD signal from each imaged pixel sums the membrane potential from neuronal populations (rather than single cells; Grinvald and Hildesheim, 2004). Data analysis was performed on a total of 61 and 33 recording sessions from two hemispheres of two monkeys, with a mean correct performance level of 82 and 97% (see Materials and Methods).

Retinotopic mapping of the two bars onto V1

An important aspect that was taken into consideration when designing the visual stimuli was to enable imaging of neuronal responses to both bars simultaneously while avoiding the direct effect of the connectors (both left and right) on neuronal populations in the imaged area. When presented separately, each of the bars clearly evoked a distinct activation patch in V1 (Fig. 2A, right column; maps were averaged 80–150 ms after stimulus onset). Pixels within the activation patch exceeding a signal-to-noise threshold were defined as the top ROI and the bottom ROI, respectively (see Materials and Methods). Importantly neither right nor left connectors activated the imaged area (Fig. 2A). Each ROI was significantly activated by the relevant bar (p < 0.05; signed rank test; n = 6 and 8 recording session for Monkeys T and S, respectively) but not by each connector (p > 0.05; signed rank test; n = 6 and 8 recording session for Monkeys T and S, respectively; Fig. 2B). Therefore the separate and connected stimuli differed only at relatively remote edges that had a minimal effect on the evoked activity of the bars (but see Fig. 7 for a different approach; see Materials and Methods). This enabled us to compare between neuronal populations that are activated by the same local stimulus features (contrast, luminance, and motion direction), differing only globally: by their connectedness at relatively remote locations (see additional controls below and Discussion).

One bar displays enhanced activity, whereas the second bar displays suppressed activity

The evoked VSD response by the separate or connected condition shows in both conditions increased population activity (i.e., increased fluorescence; Fig. 3A; example session) spread over the entire imaged area. To study the response difference between the two bars when they are separated or connected we computed the differential map, i.e., we subtracted the activation map in the connected condition from the activation map in the separate condition (Fig. 3B). The differential map averaged at late times (> 200 ms) clearly shows positive values in the top ROI, negative values in the bottom ROI and near-zero values in the background ROI (Fig. 3B; pixels between the top and bottom ROIs were defined as the background ROI; see Materials and Methods). This is further shown in Figure 3C as scatter plots of pixels in each ROI and their response values in the separate (y-axis) versus connected (x-axis) conditions. Figure 3D, further quantifies the effects revealed in the differential map (separate minus connected response Fig. 3B) showing positive, near zero, and negative histograms distribution of the pixels within each ROI. This means that when the two bars are separated, the population response at the top bar is enhanced whereas the population response at the bottom bar is suppressed (relative to the connected condition). We note that the top bar was closer to the fixation point and therefore more foveal (see Discussion). A receiver operating characteristic (ROC) analysis between the differential response distributions in the top and bottom pixels showed a high separation value (AUC = 0.98; Fig. 3D). Similar results were obtained for the grand average analysis across all sessions, where the normalized differential response was averaged at late times (220–350 ms). The normalized differential response (data normalized to mean response in three ROIs; Fig. 3E; see Materials and Methods; Eqs. 1–3) was significantly positive in the top ROI, significantly negative in the bottom ROI and not significant from zero in the background ROI for both monkeys (Fig. 3E; p < 0.001 for top and bottom ROIs; p > 0.05 for background ROI; signed rank test). In addition similar results were obtained when normalizing the differential response to the background ROI, i.e., for each trial dividing the population response in each ROI with the mean (across pixels) population response in the background ROI (p < 0.001 for top and bottom ROIs; signed rank test for each monkey separately). Using this normalization the top and bottom ROIs are independent of each other. Finally, similar results were obtained for non-normalized differential response pooled from both monkeys (p < 0.05 for top and bottom ROIs; p > 0.05 for background ROI; signed rank test).

This activity pattern was also present for iso-eccentric V1 locations (AUC = 0.94; for pixels falling within eccentricity range 2.5°–3.5°; see Material and Methods) further suggesting that the difference between the two bars in the separate condition (relative to the connected condition) does not result from eccentricity alone (see Discussion). In addition, the divergent pattern between top and bottom bars was not present at earlier times (60–100 or 100–180 ms; p > 0.05 for each ROI; signed rank test; Data not shown). Finally, in a different set of experiments, Monkey T was presented with a homogenous background, i.e., a stationary pattern of random dots which did not induce any figure perception (n = 7 recording sessions). As expected, the divergent response across ROIs was not present (p > 0.05 for each ROI; signed rank test; trials were randomly labeled separate or connected and ROIs were defined by a preceding retinotopic session; data not shown). Thus, it is evident that when the bars are separated one figure is enhanced, the other figure is suppressed, and the background remains relatively unchanged (relative to the connected condition).

The dynamics of the differential figure–figure measure

To quantify the activity pattern shown in the differential map of Figure 3B and to study the dynamics of this activation pattern, we defined a differential figure–figure measure (ΔFF; Fig. 4). The ΔFF measure (see below) quantifies the response difference between the top and bottom ROIs in the differential map (separate minus connected condition). Figure 4A displays the population response from an example session, in each ROI (top, bottom, and background) for the separate and connected condition (response not normalized). The population response in the top ROI (Fig. 4A, left) shows a slightly higher activation in the separate condition relative to the connected at late times (>150 ms). The population response in the bottom ROI (Fig. 4A, middle) shows a slightly lower activation in the separate condition relative to the connected. The population response in the background ROI shows similar activation in both conditions (Fig. 4A, right). To calculate the ΔFF measure we first subtracted the population response in the connected condition from the population response in the separate condition for the top ROI (Δtop, Eq. 4; Fig. 4B, red curve) and the bottom ROI (Δbottom, Eq. 5; Fig. 4B, blue curve). Next we subtracted the Δbottom (blue curve) from the Δtop (red curve), which resulted in the ΔFF measure as function of time (Fig. 4C; Eq. 6). Thus, the ΔFF reflects the response difference between the top and bottom ROIs, when the bars are separated compared with when the bars are connected. Positive ΔFF values mean higher response in the top bar compared with the bottom bar and near-zero ΔFF values means no difference. Figure 4C shows that ΔFF measure starts increasing ∼200 ms after stimulus onset, and becomes significantly positive when exceeding a chance level of mean ± 2STD of the ΔFF computed for the control condition: randomly shuffled labels of connected/separate trials. Similar results are shown for the grand average of ΔFF across all recording sessions in Figure 4D. The ΔFF starts to deviate from zero and becomes positive at late times. Next, we computed the latency of ΔFF in each recording session (see Materials and Methods). The median latency across recording sessions was 185 ± 15/180 ± 40 for the ΔFF measure (median ± MAD in Monkeys T/S; n = 24 and 13 recording sessions in Monkeys T and S, respectively).

Next we averaged the ΔFF at late times (220–350 ms) and we found this measure to be consistently positive in both monkeys (Fig. 4E; p < 0.01; signed rank test). ΔFF was significantly positive for all different connectivity types (one or two connectors; p < 0.05; Signed rank over trials for each type and monkey; n = 184 and 64 trials for one connector, Monkeys T and S, respectively; see Materials and Methods). ΔFF was significantly positive for different bar lengths (p < 0.05; signed rank test for trials; 8°: n = 569 and 535 trials, Monkeys T and S, respectively; 6°: n = 90 trials, Monkey T; 4°: n = 125 and 180 trials, Monkeys T and S, respectively; 2°: n = 75 trials, Monkey T; Fig. 7). As expected, ΔFF did not vary from zero when presenting just a stationary pattern of random dots that did not induce any figure perception (p > 0.05; Mann–Whitney U test; n = 152 trials in Monkey T). We conclude that the ΔFF, i.e., the population response difference between the top and bottom bars when the bars are separated compared with connected, developed at relatively late times and is comprised from a simultaneous increase in the top ROI and a decrease in the bottom ROI.

ΔFF measure can discriminate between separate and connected trials

Can the ΔFF measure be informative at the single trial level? Figure 5A–D depicts population response maps (left) averaged in the late phase, for two example separate trials and two example connected trials from one recording session. The mean population response map in the connected condition was subtracted from each trial (similar to Fig. 3B). Importantly, in the separate trials, the top ROI exhibits positive values, whereas the bottom ROI exhibits negative values (Fig. 5A,B). The negative value in the bottom ROI reflects a lower population response in the separate trial compared with the mean connected condition. The positive value in the top ROI reflects a higher population response in the separate trial compared with the mean connected condition. The histogram distribution of the response values in top (red) and bottom (blue) pixels along with the ROC analysis between the two distributions is shown on the right of each map. The connected trials did not show a difference between the ROIs (Fig. 5C,D). Therefore, amplitude differences between the top and bottom ROI can distinguish between separate and connected trials.

To discriminate between separate and connected trials we calculated a ΔFF measure for single trials (see Materials and Methods). The ΔFF measure for single trials is the mean population response in the top ROI (i.e., mean value of red histogram in Fig. 5A–D) minus the mean population response in the bottom ROI (i.e., mean value of blue histogram in Fig. 5A–D). In general, it is very similar to the ΔFF measure. The only difference between the measures is that the ΔFF for single trials is computed for each separate and connected trial separately (instead of the mean response). The ΔFF distribution across trials in one recording session shows a significant difference between separate and connected trials (Fig. 5E; p < 0.001; Mann–Whitney U test; see Materials and Methods). The AUC of the ROC curve between the ΔFF in separate and connected trials was high (Fig. 5F; AUC = 0.88). The AUC as a function of time (same data as in Fig. 5 E,F) started to increase ∼200 ms after stimulus, reaching high values at later times (Fig. 5G). An ROC analysis was performed on the ΔFF at the late phase for each recording session and the mean AUC was 0.81 ± 0.03 for Monkey T (mean ± SEM; n = 24 recording sessions; significantly different from 0.5, p < 0.001) and 0.71 ± 0.02 for Monkey S (mean ± SEM; n = 13 recording sessions; significantly different from 0.5, p < 0.001). In contrast to the late phase, the AUC in the early phase was much smaller and not significantly different from 0.5: 0.55 ± 0.02 (p = 0.12) and 0.52 ± 0.02 (p = 0.74) for Monkeys T and S, respectively. Our results indicate that the response difference between the top and bottom ROIs, only in the late phase, can be useful for making a behavioral decision at the single trial level.

The relation between separation saliency and population response

Next we wanted to study the relation between the population response, the saliency of separation, namely how well the two bars are separated, and the perceptual report of the monkeys. For this purpose the monkeys performed the task (i.e., report whether the two bars are separate or connected) when randomly presented with bars at various separation saliency levels. We varied the separation saliency by gradually changing the motion direction of the dots in the connectors (Fig. 6A). As the motion direction of the dots in the connectors' (depicted in green) became less similar to the motion direction of the dots in the bars (depicted in red) and thus more similar to the background's direction, the saliency of the two separate bars increased. For each of these intermediate conditions, we measured the behavioral report and neuronal responses (see Materials and Methods). The psychometric curve (the probability of detecting two separate bars as a function of relative motion direction between the bars and connectors) of both monkeys showed that when the motion direction of the connectors became similar to the bars' direction the probability of detecting two separate bars decreased (Fig. 6B).

The neurometric curve was then calculated by computing the ΔFF measure for each intermediate condition as well as separate and connected conditions (see Materials and Methods; same recording sessions as the psychometric curve). The neurometric curve showed a high similarity to the psychometric curve (Fig. 6C; r = 0.96 p < 0.001 and r = 0.97 p < 0.01, for Monkeys T and S, respectively). Because local stimuli properties were identical in the separate and connected conditions, the changes in the neurometric curve might be less related to the physical differences of the stimuli and more related to perceptual processing (see Discussion). These results further support the notion that the population response difference between the top and bottom ROIs in V1 can be useful for making a behavioral decision.

The relation between ΔFF and the location of the connectors and other stimulus parameters

In the vast majority of the stimuli the connectors themselves (present only in the connected condition and not in the separate condition) were positioned at a relatively remote location and did not directly affect the imaged area and the chosen ROIs (Fig. 2). However, what could be the direct effects of the connectors on the ΔFF measure? To address this we calculated the ΔFF measure when the connectors were positioned closer, well inside the imaging area. To precisely define the ROIs in this condition, we presented the monkeys with separate and connected bars (length of 2°) on a gray background (without motion) and outlined the top and bottom ROIs along with the left connector that fell within the imaged area (Fig. 7A,B). The retinotopic position of the imaged part of the bars and their ROIs, were similar to the stimuli in Figure 3A (where the connectors were remote). Figure 7C shows the differential map, separate minus connected condition (as in Fig. 3B; with a motion background). The differential map displayed positive values in the top ROI (Fig. 7C,D, red histogram) and slightly negative values in the bottom ROI (Fig. 7C,D, blue histogram; the connector ROI in the differential map shows negative response in the differential map, because it appears only in the connected condition). Interestingly this divergent activity was present also at sites adjacent to the connector. To quantify this we chose pixels in the top and bottom ROIs that were closest to the connectors (15% of the pixels closest to the connector out of each ROI). The separation value between the top and bottom pixel distribution remained high (AUC = 0.98 for 15% ROIs compared with AUC = 0.97 for all the pixels in the ROIs; Fig. 7D). The ΔFF as a function of time started to increase ∼160 ms, comparable to the a latency of 185 ms for bars of length 8° (Fig. 7E). In both cases, ΔFF latencies are late and suggest the involvement of top-down influences, since there is enough time for visual information to travel forward to higher areas and then travel back to lower areas (Zipser et al., 1996). One would expect that in the case where the connectors directly affect the response in the top and bottom ROIs they would affect the ΔFF early after stimulus onset, much before 160 ms (see Discussion). Finally, we calculated the response difference (connected minus separate) as a function of time in the connector ROI (Fig. 7B,C, white outline). In this case the connector was only present in the connected condition (can be considered as a figure), whereas in the separate condition the connector ROI was part of the background. Therefore this measure can be considered as a figure–ground measure (Roelfsema et al., 2007). We found that the latency of this figure-ground measure was 70 ms (in accordance with previous studies), which is 90 ms earlier then the latency of the ΔFF measure in the same recording session (Fig. 7E). This latency difference may further imply the dissociation between the figure-ground processing and the ΔFF measure.

To further dissociate the direct relation between the ΔFF measure and the connectors we calculated the ΔFF when the two bars where connected only on the right. In this condition, the two bars appeared in one hemifield and the connector was located in the opposite visual hemifield, and thus was mapped to the other, nonimaged hemisphere. In this case the connector did not directly activate the imaged hemisphere; nevertheless we found similar ΔFF dynamics that reached positive and significant values at relatively late times (250–310 ms; exceeding a chance level of mean ±2 STD of the ΔFF computed for trials with random label shuffling; n = 84 trials in Monkey T; see Discussion). This result suggests that ΔFF is not significantly affected by the proximity or presence of the connectors and therefore, it is more likely that top-down rather than only bottom-up influences are involved in ΔFF development. In addition, we found that when stimulus presentation was only 150 ms, the ΔFF increased with a similar temporal profile reaching positive and significant values, in the absence of the stimulus (Fig. 8A; exceeding a chance level of mean ± 2STD of the ΔFF computed for trials with randomly shuffled labels; n = 124 trials in Monkey T). The grand average across all recording sessions, shows a significantly positive ΔFF (ΔFF = 1.15 × 10⁻⁴ ± 0.21 × 10⁻⁴; mean ± SEM; n = 12 recording sessions from Monkey T; p < 0.01; signed rank test). This can further support the involvement of top-down influences rather than only bottom-up. Finally when the background was replaced with a uniform gray (rather than motion of random dots; thus the task is less difficult), ΔFF developed faster and reached higher values (Fig. 8B; ΔFF gray-BG was significantly higher than ΔFF motion-BG starting 140 and 160 ms after stimulus onset for Monkeys T and S, respectively; p < 0.05; Mann–Whitney U test; n = 190/167 trials gray-BG and 187/124 trials, motion-BG respectively; Monkeys T/S). This may suggest that the latency and amplitude of the ΔFF is modulated by contextual surround (uniform gray vs motion of random dots) and can be related to task difficulty.

Other neural codes

Can other neural codes be informative in labeling different figures? We investigated whether synchrony can distinguish between the two bars when they are separate or connected. The binding-by-synchrony hypothesis claims that neurons encoding separate figures will be less synchronized compared with when they are connected (Singer and Gray, 1995; Uhlhaas et al., 2009). Using a sliding window of 80 ms we calculated the Pearson correlation coefficient as a function of time of all pixel pairs between the top and bottom ROIs (see Materials and Methods). This was done for each trial separately after removing the direct stimulus contribution by subtracting the mean response from each pixel (see Materials and Methods). We find that synchrony in the separate condition was only slightly lower than synchrony in the connected condition. The Δsynchrony (separate minus connected) although very small, was still significantly negative over recording sessions in both monkeys (Δsynchrony = −0.01 ± 0.004 for Monkey T; Δsynchrony = −0.006 ± 0.002 p < 0.05 for Monkey S; mean ± SEM; exceeding a chance level of mean ± 2STD of the Δsynchrony computed for randomly shuffled sessions of connected/separate conditions) but only in a narrow time window (∼120–160 ms; each time point represent a ±40 ms window). In addition synchrony differences emerged slightly earlier than amplitude differences reaching significantly negative values at 140/120 ms (compared with a ΔFF latency of 185/170 ms, Monkeys T/S). Synchrony differences compared with amplitude differences were less consistent over recording sessions and could poorly discriminate between single trials (AUC = 0.53 ± 0.01 for Monkey T and AUC = 0.56 ± 0.01 for Monkey S; mean ± SEM; significantly different from 0.5, p < 0.01) and were only partially negatively correlated to separation saliency (r = −0.81 p < 0.05 for Monkey T and r = −0.58 p = 0.23 for Monkey S). We also calculated the amplitude covariance between the top and bottom ROIs across trials (Roelfsema et al., 2004) and found no significant difference between conditions (Δcovariance = −0.03 ± 0.03 p = 0.59 for Monkey T and Δcovariance = −0.01 ± 0.07 p = 0.95 for Monkey S; mean ± SEM; signed rank test; see Materials and Methods and Discussion). To conclude, a response amplitude difference code is better in discriminating between separate and connected bars, whereas other measures may hold additional information of lesser consistency and discriminability.

Discussion

We find that an amplitude modulation in V1 can efficiently encode, i.e., label, two figures that are task relevant. This is achieved by a divergent process of enhanced response to one figure and suppressed response to the other figure (the ΔFF measure). This activity pattern enabled single trial discrimination and was correlated with separation saliency. Our results extend previous studies focusing on single figure encoding (Lamme, 1995, 1999; Zipser et al., 1996) or two figures (target and distractor) in an attentional paradigm, where the animals had to attend one figure and ignore the second one (Roelfsema et al., 2007).

Can the divergent bar response reflect internal brain processing of figure labeling or does it emerge only from stimulus differences, i.e., the presence or nonpresence of the connectors? In other words, can the connectors directly affect the ΔFF measure? When presented alone, the remote connectors do not activate the top and bottom ROIs. However, the presence of the connectors could have a suppressive effect (Sceniak et al., 1999; Cavanaugh et al., 2002; e.g., surround suppression) on the bars which may influence the ΔFF measure. This option is less likely, because the suppression field size at the imaged area is predicted to be ∼0.25°–1.5° (Sceniak et al., 1999; Cavanaugh et al., 2002) whereas the connectors were typically 2.5°–3° away from the imaged area. In addition, short stimulus presentation evokes a similar divergent pattern mainly after stimulus offset, in the complete absence of the connectors. ΔFF shows a typical response also for a single-side connector that is mapped to the opposite hemisphere. However, what would one expect if the connectors were close enough to directly affect the top and bottom ROIs? Interestingly, the same divergent pattern appears (Fig. 7). Together, all these observations suggest that it is unlikely that ΔFF is affected directly by the connectors themselves.

The divergent bar response (ΔFF measure) can be mediated by V1 horizontal connections (Malach et al., 1993; Callaway, 1998), top-down feedback connections (Bullier et al., 2001; Li et al., 2006), or both. We find that the ΔFF starts to develop ∼200 ms complying with late top-down influences (Lamme, 1995; Zipser et al., 1996; Bullier et al., 2001; Li et al., 2006). If horizontal connections are involved, then one would expect that ΔFF latency will decrease for proximal connectors (Roelfsema, 2006). However, we find that ΔFF latency is rather late, even when the connectors are at close proximity (the latency slightly decreased from 185 to 160 ms for more proximal connectors). Thus, it is reasonable to assume that horizontal connections cannot solely explain the late divergent response development and that feedback influences are involved. In addition the simultaneous onset of the opposing responses (enhancement and suppression of each bar) suggest that a late feedback (excitation and inhibition), may play an important role in figure labeling (Isaacson and Scanziani, 2011; Haider et al., 2013). Finally, the divergent bar response, ΔFF measure, is correlated with the separation saliency of the two bars. Because the local parameters are kept identical for all stimuli types (differing only at remote locations), the ΔFF measure could also be linked to the monkeys' perception (rather than stimulus differences alone).

Could the divergent response pattern be used in a more complex scene where several figures appear? In this case, multiple levels of amplitude will be needed to successfully label all the different figures. An amplitude code clearly imposes that only a small number of different figures can be perceived simultaneously. An upper limit for the number of figures was reported in experiments where subjects were required to subitize (Kaufman and Lord, 1949), i.e., immediately judge the number of figures present in a visual scene. Only approximately four objects could be immediately perceived without effort implying that only four different levels of amplitude may be needed in the immediate stage whereas additional figures (from subitizing to counting) may recruit additional, more time consuming resources such as attention or eye movements (Mandler and Shebo, 1982; Trick and Pylyshyn, 1994; Bundesen, 1998; Schneider, 2013). Another possibility is that only two levels of amplitude are required, i.e., attended and unattended, in which case several attended objects may be perceived as one pattern (Yantis, 1992).

The ΔFF measure was found to be consistently positive, i.e., the population responses in the top bar were mostly higher than those of the bottom bar. Theoretically, encoding the two figures could also be established by a higher activation in the bottom bar compared with the top bar. Possible explanations for this can be: (1) the top-bar was always closer to the point of fixation and the response enhancement is prioritized based on the eccentricity of each bar. However, a positive ΔFF appeared at iso-eccentric locations for the two bars. Nevertheless, it could be that the mean eccentricity of each bar is important rather than local coordinates. Thus, more foveal figures (the top bar) are enhanced whereas more peripheral figures (the bottom bar) are correspondingly suppressed. To test this, a future study should exchange or vary the foveal and peripheral locations of the bottom and top bars. (2) Recording sessions were acquired after a long training period of several months. Thus, the monkeys could have developed a consistent strategy in separating the two bars by enhancing the top bar and suppressing the bottom bar. Finally, it is possible that the monkeys' strategy was to detect arcs (i.e., connectors) in the visual scene instead of discriminating between the separate and connected bars. Although we cannot completely rule this out, we feel that the tight fixation, along with high discrimination level over different connectivity types (left arc, right arc, or both), short stimulus duration, and spatial uncertainty makes it very hard for the animal to focus only on the arcs.

In addition to the late amplitude difference we find an earlier, very small synchrony difference. The synchrony between the top and bottom bars was lower when the bars were separate. This finding is in line with the binding-by-synchrony hypothesis (Singer and Gray, 1995). Nevertheless, when comparing between synchrony and amplitude codes, the latter is more consistent over recording sessions, could better discriminate at the single trial level, and is better correlated with the monkeys' perceptual report. However, it is possible that a synchrony code involves specific neuronal assemblies that are diluted in population response. It can be suggested that synchrony may initiate a labeling process possibly through horizontal connections. This process is made prominent only at later times via amplitude differences mediated possibly by feedback connections. Another explanation for the very weak synchrony differences is that the VSD signal emphasizes synaptic input and subthreshold activity and contains mainly low frequencies (Arieli et al., 1995; Gilad et al., 2012). Previous studies suggested that a synchrony code is linked more to the gamma band and spiking activity (Fries, 2009; Buzsáki and Wang, 2012; Jia et al., 2013), which are less emphasized in the VSD signal. Finally, amplitude covariation of the VSD signal across trials (this can correspond to spiking rate covariation) was not significantly different between conditions. Roelfsema et al. (2004) reported a lower rate covariation mainly in single units showing attentional modulation. Units without attentional modulation showed less or no rate covariation. Therefore, it is possible that in the population response, which sums both modulated and nonmodulated units, rate covariation differences are diluted.

To perform the behavioral task at high accuracy, the monkeys had to attend both figures. Although, the effects of attention in our task could not be differentiated from other processes, spatially based (Treue, 2001) and feature based attention (Treisman and Gelade, 1980; Maunsell and Treue, 2006) are less likely to affect the results: in both conditions the figures were presented in the same retinotopic positions and local stimulus features were identical between conditions. In object based attention neurons encoding an attended figure (target) enhance their activity compared with neurons encoding an unattended figure (distractor; Roelfsema et al., 1998). It is possible that in our study, the monkeys referred to the top bar as the target and the bottom bar as the distractor. Thus, when the bars are connected attention will spread over to the bottom bar resulting in a higher activation at the bottom bar for the connected condition compared with the separate condition. Although, this spread could explain some of the results, it is less probable, because the top bar (target) will need to be equally enhanced in both separate and connected conditions. Our results show that there is a higher activation for the top bar in the separate condition, relative to the connected condition. Finally our results extend previous studies by showing that a difference in neuronal responses between two figures can arise both from an enhancement of one figure and a suppression of the other figure (instead of the possibility for enhancing only one figure and keeping the other figure at baseline; Roelfsema et al., 2007).

To conclude, we find that a divergent amplitude code in V1 can discriminate between two figures. This pattern, which appears in single trials, is correlated with the monkeys' report. Therefore, an amplitude difference in V1 may mediate the labeling of different figures resulting in their segregation and perception.

Notes

Supplemental material for this article is available at http://neuroimag.ls.biu.ac.il/supp/SuppGilad_2015.pdf. This file contains three supplemental figures. This material has not been peer reviewed.