Longitudinal Changes in Adolescent Risk-Taking: A Comprehensive Study of Neural Responses to Rewards, Pubertal Development, and Risk-Taking Behavior

Abstract

Prior studies have highlighted adolescence as a period of increased risk-taking, which is postulated to result from an overactive reward system in the brain. Longitudinal studies are pivotal for testing these brain-behavior relations because individual slopes are more sensitive for detecting change. The aim of the current study was twofold: (1) to test patterns of age-related change (i.e., linear, quadratic, and cubic) in activity in the nucleus accumbens, a key reward region in the brain, in relation to change in puberty (self-report and testosterone levels), laboratory risk-taking and self-reported risk-taking tendency; and (2) to test whether individual differences in pubertal development and risk-taking behavior were contributors to longitudinal change in nucleus accumbens activity. We included 299 human participants at the first time point and 254 participants at the second time point, ranging between ages 8–27 years, time points were separated by a 2 year interval. Neural responses to rewards, pubertal development (self-report and testosterone levels), laboratory risk-taking (balloon analog risk task; BART), and self-reported risk-taking tendency (Behavior Inhibition System/Behavior Activation System questionnaire) were collected at both time points. The longitudinal analyses confirmed the quadratic age pattern for nucleus accumbens activity to rewards (peaking in adolescence), and the same quadratic pattern was found for laboratory risk-taking (BART). Nucleus accumbens activity change was further related to change in testosterone and self-reported reward-sensitivity (BAS Drive). Thus, this longitudinal analysis provides new insight in risk-taking and reward sensitivity in adolescence: (1) confirming an adolescent peak in nucleus accumbens activity, and (2) underlining a critical role for pubertal hormones and individual differences in risk-taking tendency.

Introduction

Adolescence is a natural time for explorative learning, risk-taking, and sensation seeking (Dahl, 2004; Steinberg, 2008). Cross-sectional studies have demonstrated that the nucleus accumbens (NAcc), an important region in the brain's reward circuitry (Delgado, 2007), shows peak activity in adolescence relative to childhood and adulthood when receiving rewards (Galvan et al., 2006; Braams et al., 2014), and this neural response correlates with self-report real-life risk-taking behavior (Galvan et al., 2007). These studies led to the hypothesis that NAcc activity may be an important contributor to adolescent risk-taking. However, the heightened NAcc response is not consistently found across studies (Bjork et al., 2004, 2010) and behavioral risk-taking measures do not always show the expected adolescent peak in risk-taking behavior (Defoe et al., 2015). In addition, few studies examined the relation between NAcc activity and risk-taking behavior directly (but see Galvan et al., 2007). Thus, despite the promising initial assumption that NAcc may be a biomarker for adolescent risk-taking, the relation between NAcc activity and risk-taking remains poorly understood.

One potential factor explaining the relation between NAcc activity and risk-taking behavior is the possible driving force of pubertal development, specifically testosterone levels (Nelson et al., 2005; Peper et al., 2013a; van Duijvenvoorde et al., 2014). A prior longitudinal study showed that changes in NAcc reactivity were related to changes in testosterone levels at the onset of puberty (Spielberg et al., 2014). A second factor, which may explain inconsistent results in prior studies, concerns individual differences in risk-taking tendency (Urošević et al., 2012; van Duijvenvoorde et al., 2014). Longitudinal studies are pivotal for testing these questions, because when there is high variability between individuals, individual slopes are more informative for detecting change. Moreover, longitudinal analyses give information about how individual differences in neural activity covary with risk-taking behavior over time (Crone and Elzinga, 2015).

The current study used a longitudinal design to test the relations between NAcc activity to rewards, pubertal development, and risk-taking behavior. All participants performed a gambling task in which they could win or lose money (Braams et al., 2014). In addition, participants completed the balloon analog risk task (BART), a well validated measure corresponding with real-life risk-taking behaviors, such as substance use (Lejuez et al., 2003) and the Behavior Inhibition System/Behavior Activation System (BIS/BAS) questionnaire to assess self-reported risk-taking tendency (Carver and White, 1994). Finally, all participants completed the Pubertal Development Scale (PDS; Petersen et al., 1988) and testosterone levels were collected from saliva (Peper et al., 2013a). For each variable, we tested, using nonlinear mixed models, linear [continuous rise (or fall) over development], quadratic (adolescent-specific U or inverted U shape), or cubic (adolescent emergent) developmental patterns (Ordaz et al., 2013; Somerville et al., 2013). Second, we tested whether changes in puberty and risk-taking behavior contributed to the presumed peak in NAcc activity in adolescence (Spielberg et al., 2014).

Materials and Methods

Participants

The current study was part of a large longitudinal study, referred to as Braintime, conducted at Leiden University, the Netherlands. On the first time point (T1) data were collected from 299 participants (Mean_age = 14.15 years; SD_age = 3.56; Range_age = 8.01–25.95 years; 143 males). Approximately 2 years later (Mean_{time-difference} = 1.99 years; SD_{time-difference} = 0.10; Range_{time-difference} = 1.66–2.47 years) all participants were invited for data collection for the second time point (T2). Thirteen participants indicated that they could not or did not want to participate again. Therefore, data were collected from 286 participants (Mean_age = 15.80 years; SD_age = 3.54; Range_age = 9.92–26.62 years; 135 males).

Of the 286 participants who took part at T2, 32 participants could not participate in the MRI session due to braces. For the group that was excluded from MRI participation, questionnaire measures and hormone samples were still collected. Sample sizes and reasons for exclusion for each measure (i.e., fMRI, PDS, testosterone, BART, and BIS/BAS questionnaire) are mentioned in the text and available data after exclusion for each measure on each time point are summarized in Table 1. All participants were right-handed, reported normal or corrected-to-normal vision, and an absence of neurological or psychiatric impairments. Results from the first measurements were previously published by Peper et al. (2013a), Braams et al. (2014), and Peters et al. (2014).

Table 1.

Analyzed data, after exclusion, for each measure on each time point

	Time point 1		Time point 2
	N (n males)	Age, mean (SD)	N (n males)	Age, mean (SD)
PDS	236 (117)	13.18 (3.65)	205 (98)	14.23 (3.54)
Testosterone	285 (138)	13.97 (3.66)	273 (13)	15.83 (3.54)
BART	294 (143)	13.97 (3.81)	250 (119)	16.07 (3.54)
BIS/BAS	277 (131)	14.01 (3.65)	286 (135)	15.81 (3.54)
fMRI	249 (102)	14.74 (3.65)	238 (116)	16.77 (3.54)

Estimated intelligence scores were obtained using two subscales of the Wechsler Adult Intelligence Scale (WAIS) for participants aged 17 and older or the Wechsler Intelligence Scale for Children (WISC) for participants aged 16 and younger. At T1 the subtests similarities and block design of the WISC/WAIS were administered, at T2 the subtests picture completion and vocabulary were administered. There was no correlation between estimated IQ scores and age on both time points (T1: n = 294, r = −0.041, p = 0.49; T2: n = 256, r = 0.045, p = 0.48). All participants provided written informed consent for the study (parental consent and participant assent for children and adolescents) at both time points. All procedures were approved by local institutional review boards. Participants received an endowment for participation in a larger study. Adult participants received 60 euro on each time point, participants aged 12–17 years received 30 euro and participants younger than 12 years received 20 euro on each time point. In addition to this endowment participants could win 4, 5, or 6 euros in the fMRI task (see fMRI task).

Procedure

Participants were prepared for the testing session in a quiet room. They were familiarized with the MRI scanner with a mock scanner and by listening to recordings of the scanner sounds. Next, participants received instructions for the fMRI task (Braams et al., 2014 provides a detailed report of instructions) and performed six practice trials of this task. After the scanning session, participants were seated alone behind a computer in a quiet room where they filled out the PDS and performed the BART. Participants filled out the BIS/BAS questionnaire and collected saliva for testosterone assessment at home before the testing session.

Experimental design and behavioral measures

fMRI task.

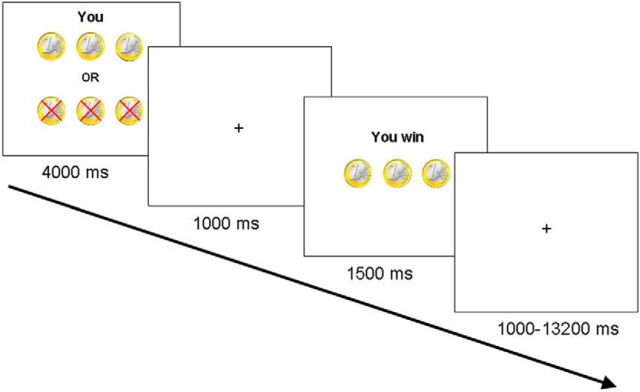
Participants played a heads or tails gambling game in which they could win or lose money (Braams et al., 2014a,b). On each trial participants guessed whether the computer would pick heads or tails and they won when the computer selected the chosen side of the coin. Each trial started with a trial onset screen (4000 ms) during which the participant indicated their choice to play for heads or tails. On the trial onset screen the participants also saw how much they could win or lose on that trial, explained in more detail below. The trial onset screen was followed by a fixation screen (1000 ms) and a feedback screen, which showed whether participants won or lost on that trial (1500 ms). Trials ended with a variable jitter (1000–13,200 ms; Fig. 1). Trial sequence and timing was optimized using OptSeq. Probabilities for winning were 50%. Three different distributions of coins were included; trials on which two coins could be won and five lost, trials on which three coins could be won or three lost and finally trials on which five coins could be won or two could be lost. These different distributions of coins were included to keep participants engaged in the task, but were not analyzed separately (Braams et al., 2014a,b). Participants were informed about the different distributions of coins and were familiarized with them during the practice task. Participants were explained that the coins won during the experiment translated to real money at the end of the experiment. Participants received 4, 5, or 6 euro's at the end of the task. Unbeknownst to the participants, the total earnings on the task did not relate to the amount won during the task but were chosen at random.

Figure 1.

Example of a trial. On trial onset, participants were presented with a screen for 4000 ms indicating how many coins could be won or lost. During this time, participants chose to play heads or tails by pressing the corresponding button. After a 1000 ms delay, trial outcome was presented for 1500 ms. Participants won when the computer randomly selected the same side of the coin as chosen by the participant (Braams et al., 2013).

Participants played 30 trials in the gambling game for themselves, 30 trials for their best friend, and 30 trials for another person. The goal of the current study was to specifically assess neural responses to rewards for self, therefore for the current study only trials on which the participants played for themselves were included (Braams et al., 2014a,b provides a description of the data of the first time point for the full task).

Pubertal development

PDS.

Pubertal development was assessed with the PDS (Petersen et al., 1988). The PDS is a self-report questionnaire, which contains questions about secondary sexual characteristics. In total, the PDS is comprised of five questions assessing growth spurt, body hair, changes in the skin, and for boys a question about change in voice and facial hair and for girls a question about breast development and menarche. Participants indicated on a four-point scale whether a physical characteristic: (1) had not yet started to develop, (2) was showing the first signs of development, (3) was showing clear development, or (4) had already finished developing. An average score was calculated and used for analyses (Collado-Rodriguez et al., 2014). Participants aged 17 and younger filled out the PDS. The PDS was administered to 265 participants on T1 and 217 on T2. Data from 29 participants on T1 and 12 participants on T2 were not usable for analyses due to computer problems. The final sample for the PDS in analyses was 236 on T1 and 205 at T2 (Table 1).

Testosterone.

Testosterone levels were assessed in morning saliva samples. Samples were collected by passive drool, directly after waking up, and before eating or brushing teeth. Females who had not yet reached menarche and males collected saliva on the day of fMRI testing. To control for menstrual fluctuations, postmenarcheal females and females who used contraceptives with a stopping period collected saliva on the seventh day of their menstrual cycle. At the seventh day of the menstrual cycle hormone levels are less influenced by fluctuations in the cycle (Mihm et al., 2011; Peper and Dahl, 2013). Females who used contraceptives without a stopping period, such as hormonal intrauterine devices, were excluded from testosterone assessment.

Testosterone levels for all saliva samples were assayed at the Department of Clinical Chemistry of the VU University Medical Centre. The lower limit of detection was 4 pmol/L. Salivary testosterone was determined by isotope dilution—online solid phase extraction liquid chromatography—tandem mass spectrometry (Peper et al., 2013a). Intra-assay coefficients of variation were 11% and 4% at 10 and 140 pmol/L, respectively, and interassay coefficients of variation were 8% and 5% at 31 and 195 pmol/L, respectively (de Water et al., 2013). Testosterone levels were not normally distributed; therefore, a log-transformed measure for testosterone levels was used in all analyses. Testosterone samples were collected from 292 participants on T1 and 274 participants on T2. Testosterone levels from 25 participants on T1 and three participants on T2 fell below the detection limit of 4 pmol/L. These participants were excluded from further analyses. Seven participants on T1 and one participant on T2 did not collect sufficient amount of saliva for detection. The final number of participants for whom testosterone data were available was 285 on T1 and 273 at T2 (Table 1).

BART.

To assess laboratory risk-taking behavior, we used the BART task (Lejuez et al., 2003; Peper et al., 2013a). Participants were seated in front of a computer screen, which displayed a small balloon, a pump, an indication of total amount earned, and an indication of how much was earned on the last balloon, as well as a cash-out button. Balloons could be inflated by mouse clicks and for each click participants earned €0.05, which was stored in a temporary money bank that was not shown on the screen. At any moment, participants could decide to stop inflating the balloon and collect the money earned on that trial by clicking the cash-out button. The money was then transferred to the permanent bank and the amount earned was displayed on the screen. If participants overinflated the balloon, the balloon popped and all money earned during that trial was lost.

The total task consisted of 30 trials with 10 orange, 10 yellow, and 10 blue balloons. Each color had a different average explosion point of 4, 16, or 64 pumps respectively. Participants were instructed to gain as much money as possible by pumping up balloons. They were explained that they could pump up balloons as far as they liked and they could stop at any time. They were also explained that each balloon would pop at some point and that this explosion could occur anywhere between the first pump and the moment when the balloon filled the full screen. Participants were not informed about the different probabilities of exploding. The total number of explosions was used as the dependent variable in analyses for the BART (Peper et al., 2013a).

The BART was administered during the laboratory visit. Therefore, only participants who participated in the MRI session performed the BART. In total 294 participants at T1 and 250 at T2 completed the BART. No participants were excluded from analyses (Table 1).

BIS/BAS questionnaire.

To measure self-reported risk-taking tendency participants completed the BIS/BAS questionnaire (Carver and White, 1994), which refers to the BIS and the BAS. The BIS/BAS questionnaire consists of 24 items and is comprised of four scales, one that measures punishment sensitivity (BIS) and three that measure individuals' risk-taking tendency (BAS Drive, BAS Fun Seeking, and BAS Reward Responsiveness). BAS Drive measures persistence in the pursuit of goals, BAS Fun Seeking measures a desire for rewards and the willingness to approach potential rewards, and BAS Reward Responsiveness measures responses to rewards or anticipation of rewards. Participants were asked to indicate on a four-point scale (1: strongly agree to 4: strongly disagree) how well a statement described them. Higher scores indicated greater punishment or risk-taking tendency. The final sample for BIS/BAS analyses was 277 on T1 and 286 at T2 (Table 1).

MRI data acquisition

Scanning was performed on a 3 tesla Philips scanner, with a standard whole-head coil. The functional scans were acquired using a T2*-weighted echo-planar imaging [TR = 2.2 s, TE = 30 ms, sequential acquisition, 38 slices of 2.75 mm, field-of-view (FOV) 220 mm, 80 × 80 matrix, in-plane resolution 2.75 mm]. The first two volumes were discarded to allow for equilibration of T1 saturation effects. After the functional runs, a high-resolution 3D T1-weighted anatomical image was collected (TR = 9.751 ms, TE = 4.59 ms, flip angle = 8°, 140 slices, 0.875 mm × 0.875 mm × 1.2 mm, and FOV = 224.000 × 168.000 × 177.333). Visual stimuli were displayed on a screen in the magnet bore. A mirror attached to the head coil allowed participants to view the screen. Foam inserts inside the coil were used to limit head movement. MRI data acquisition was similar at the two time points (Braams et al., 2014b).

fMRI preprocessing and statistical analyses

At T1 299 participants were included in the MRI session and at T2 254 participants. For fMRI analyses, 36 participants on T1 and 10 participants on T2 were excluded for moving >1 voxel. An additional 14 participants on T1, and six participants on T2, were excluded for not finishing the task, technical problems and/or artifacts during data collection. The final sample for fMRI analyses was therefore 249 participants on T1 and 238 participants on T2 (Table 1).

All data were analyzed with SPM8 (Wellcome Department of Cognitive Neurology, London). Images were corrected for slice timing acquisition and differences in rigid body motion. Structural and functional volumes were spatially normalized to T1 templates. Translational movement parameters never exceeded 1 voxel (<3 mm) in any direction for any participant or scan. The normalization algorithm used a 12-parameter affine transform together with a nonlinear transformation involving cosine basis functions and resampled the volumes to 3 mm³ voxels. Templates were based on the MNI305 stereotaxic space. Functional volumes were spatially smoothed with a 6 mm FWHM isotropic Gaussian kernel. Statistical analyses were performed on individual subjects data using the general linear model in SPM8. The fMRI time series were modeled as a series of zero duration events convolved with the hemodynamic response function (HRF). On trial onset, events were modeled separately for playing for self, friend, and other. On feedback onset winning and losing for self, friend, and antagonist were modeled. This resulted in three conditions at trial onset (self, friend, other) and six conditions at feedback onset (self win, self lose, friend win, friend lose, other win, other lose). Trials on which the participants failed to respond were modeled separately as covariate of no interest and were excluded from further analyses. The modeled events were used as regressors in a general linear model, along with a basic set of cosine functions that high-pass filtered the data and a covariate for session effects. The least-squares parameter estimates of height of the best-fitting canonical HRF for each condition were used in pairwise contrasts. The resulting contrast images, computed on a subject-by-subject basis, were submitted to random-effects group analyses. The contrast of interest was win > lose when playing for self, specified at the moment of feedback onset.

ROI analysis

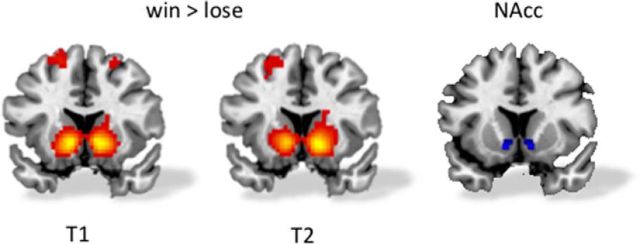
We used the MarsBaR toolbox (Brett et al., 2002; http://marsbar.sourceforge.net/) for SPM8 to perform region-of-interest (ROI) analyses to extract patterns of activation in an a priori defined NAcc cluster. Average β values, also known as parameter estimates, were used for ROI analyses. We used an anatomical mask of the left and right NAcc extracted from the Harvard–Oxford subcortical atlas, thresholded at 40%. In total, the mask for the left NAcc consists of 28 voxels and the mask for the right NAcc of 26 voxels. We specifically focused on the NAcc, since previous studies have highlighted this part of the ventral striatum as a key region in reward-based processing (Delgado, 2007; Braams et al., 2014b). Whole-brain analyses for the contrast win > lose yielded results in the bilateral ventral striatum, including the NAcc, on both time points (Fig. 2; Table 2).

Figure 2.

Win > lose when playing for self for T1 and T2 and the anatomical region of the nucleus accumbens used for analyses. All activation is familywise error corrected at voxel level. A threshold of 10 voxels was used as a cutoff for display purposes only. All slices MNI Y = 12.

Table 2.

Whole-brain table for neural activation for the contrast win > lose when playing for self on the first and second time points

Region	R/L	MNI			T (1488)	Voxels
		x	y	z
Time point 1
Caudate nucleus	L	−12	14	−5	12.64	831
	R	12	14	−5	12.64	831
Caudate nucleus	R	21	−16	25	5.82	43
Putamen	L	−24	−13	28	5.62	48
Anterior cingulate cortex	L	0	50	−2	7.72	171
Superior frontal gyrus	L	−18	17	58	6.52	127
	R	24	14	55	5.32	11
Middle cingulate cortex	R	3	−34	37	6.49	350
Paracentral lobule	L	−3	−28	58	5.67	36
Angular gyrus	R	48	−67	40	5.38	24
Angular gyrus	L	−48	−67	43	5.34	35
Inferior occipital gyrus	R	42	−79	−14	5.85	48
					T (1422)
Time point 2
Caudate nucleus	R	15	14	−5	13.07	680
	L	−12	14	−5	13.07	680
Superior frontal gyrus	L	−21	35	49	7.05	235
	R	21	32	52	5.43	29
	R	15	32	52	5.32	12
Superior medial gyrus	L	−3	56	4	7.39	380
Middle frontal gyrus	L	−39	53	1	5.31	45
Paracentral lobule	L	−3	−25	58	5.60	176
Postcentral gyrus	L	−27	−34	58	5.51	32
Precuneus	L	−6	−58	10	6.24	125
Angular gyrus	L	−48	−64	49	5.73	66
Cuneus	R	3	−82	25	5.07	20
Cerebellum	R	33	−85	−23	5.00	17

Reported clusters are familywise error corrected at the voxel level. Only clusters of ≥10 voxels are reported.

Mixed-model building procedure

Analyses were performed using a mixed models approach in R (R Core Team, 2014) and package nlme (Pinheiro et al., 2013). Mixed models (also known as hierarchical linear modeling, multilevel modeling, or random-effects modeling) allow for data hierarchies as observed in longitudinal datasets. Time points within a longitudinal dataset are nested within participants and a mixed-models approach recognizes this type of data dependency. Mixed models were used to determine general patterns, i.e., grand mean trajectories, of age-related change (linear, quadratic, or cubic) and within these general patterns, assess individual variation in intercepts (i.e., starting points) and slopes (i.e., pattern of change over time). These goals concur with: (1) the inclusion of fixed effects that account for a grand-mean trajectory thereby capturing the mean developmental pathway of the full sample, and (2) random effects that can test for individual variation in intercepts and slopes.

The first aim was to describe normative development of NAcc activity, self-reported puberty, testosterone levels, BART (laboratory risk-taking behavior) and BIS/BAS (self-reported risk-taking tendency) in relation to age. These normative developmental changes were investigated by testing which pattern of age-related change (linear, quadratic, or cubic) best explained the relationship between age and each of the measures (NAcc activity, PDS, testosterone, BART, and BIS/BAS). For all analyses we examined whether sex explained additional variance, based on prior studies which suggested that boys may be more sensitive to risk-taking than girls (Peper et al., 2013a).

To test developmental effects, all mixed-models followed a formal model-fitting procedure. That is, we started with a null model that included a fixed and a random intercept, to allow for individual differences in starting points and account for the repeated nature of the data. The null model with random intercept was compared against three additional models that tested the grand mean trajectory of age. These models were created by adding three polynomial terms (linear, quadratic, and cubic; mean-centered) for age to the null model. Linear effects of age indicate a monotonic change over age, quadratic effects of age indicate an adolescent-specific effect, in which adolescent responses differ from those of children and adults, and finally cubic effects of age indicate an adolescent emergent pattern in which responses are stable in childhood, then rise in adolescence and then stabilize in adulthood (Somerville et al., 2013). Akaike Information Criterion (AIC; Akaike, 1974) values as well as Bayesian Information Criterion (BIC; Schwarz, 1978) values were compared between the null model and each of the models with a polynomial term for age to test whether a null model, linear, quadratic or cubic model best explained the relationship between the dependent measure and age. AIC and BIC are standardized model-fit metrics that allows for comparison of models. Preferred models have lower AIC and BIC values. To formally compare whether models with lower AIC and BIC values were significantly better, we compared models differing one degree of freedom (i.e., null and linear, linear and quadratic, and quadratic and cubic) using a log likelihood ratio test. Note that the final model was only selected if the fixed age-term was also significant.

The next step in the model-building procedure was to determine whether there were significant individual differences in the effects of age by adding a random-slope of age to each of the best-fitting models. A random-slope of age allows the inclusion of different β-coefficients for each subject. A significant random-slope term would indicate significant individual differences for the effect of age. The significance of the random terms was determined via AIC and BIC evaluation for improvement in model fit, as well as a log likelihood ratio test. Level of significant used for the log likelihood ratio test was p < 0.05. Only if a random slope significantly improved model fit as indicated by a log likelihood ratio test, the random slope was included in the last step. For none of the models, except for one model described below, a random slope improved model fit indicating that the effect of age did not differ between participants. Only for the model describing the relationship between age and total explosions on the BART a random slope improved model fit. Therefore, a description of the random slope is included for this model and not for the other models.

In the last step, we added a fixed main effect of sex and an interaction between sex and age to the best-fitting model (i.e., with or without random slope of age). Sex was entered as a dummy variable with females coded as the reference group. Improvement of model fit was assessed with AIC and BIC values. Log likelihood ratio tests for the interaction with sex are not included because models with an interaction effect with sex differ more than one degree of freedom with models without an interaction with sex.

All models were fit with full information maximum likelihood estimates. A fitted mixed-model with only a mean-centered, linear term of age (referred to as Age Linear) reads in formal notation:

Level 1:

Level 2:

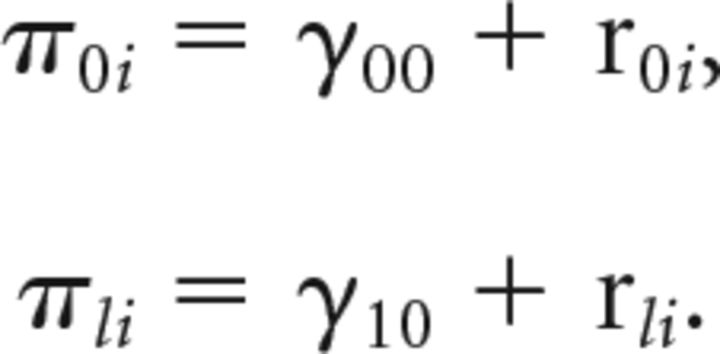In which Y_ti represents, for instance, testosterone level at the t′th time point for the i′th individual. Substitution of the second level model into the first level model gives the integrated model that was fitted to the data. As age is mean-centered, the fixed intercept γ₀₀ represents grand mean testosterone level at the mean age of the sample. γ₁₀ Represents the grand mean slope (main effect) of age (linear). The random intercept (r_0i) captures between-participant variance in the intercept (e.g., individual differences in the mean testosterone-level at the mean age of the sample), and individual differences in the slope(r_1i; i.e., the change in testosterone-level over age). Finally, the variance of e_ti denotes within-participant variance. We fitted separate models for each measure of interest (NAcc activity, PDS, testosterone, BART, BIS/BAS) and describe the best fitting model for each measure in the results section. The code used to fit a linear model in R reads as follows:

To fit a quadratic model the poly term is replaced by “poly(Age, 2)” and for a cubic term the poly term is replaced by “poly(Age, 3).” Including a random slope for age would be achieved by replacing “random = ∼1|Subject” by “random = ∼Age|Subject.” Main and interaction effects are included by adding +Sex for a main effect of Sex or ×Sex for an interaction effect, after the poly term.

The second aim was to test how puberty (PDS and testosterone) and risk-taking tendency (BART and BIS/BAS) explained variance in the presumed quadratic relation between NAcc activity and age. That is, we aimed to test a combined model of all measures, i.e., age, PDS, testosterone, BART score, and BIS/BAS, to account for NAcc neural activation. Our model-fitting procedure involved several steps. The first model was the best fitting-age model (linear, quadratic, or cubic term of age) for NAcc response determined in previous analysis. To test whether other measurements explained additional variance above age, we then added a linear, quadratic, and cubic term for each of the other measurements (PDS, testosterone, BART, BIS/BAS) separately. Improvement of model fit was assessed by evaluation of AIC values. If model fit improved, we tested which term (linear, quadratic, or cubic) explained most variance and higher terms were excluded. That is to say, if the linear term was significant, then the quadratic and cubic terms were omitted from the model. We then tested whether adding an additional measurement explained more variance until all measurements were added in a stepwise manner. This resulted in a model in which each included term explained unique variance in NAcc responses to rewards. We then tested whether significant differences in change over time existed for these measures by adding random slope terms for each measure. Again, model fit was assessed by evaluation of AIC and BIC values, and log likelihood ratio tests. Finally, the effect of sex was assessed by adding a fixed main effect of sex and an interaction term of sex. Evaluation of AIC and BIC values determined improved model fit. This model fitting procedure resulted in a most optimal model for explaining NAcc responses to rewards. Models were tested for neural responses to rewards in left, as well as right, NAcc.

Correlations within and between measures

Intraclass correlations (ICC) can be used to describe how strongly correlated units within the same group are, and in longitudinal samples to describe homogeneity of the data. To test whether homogeneity of the data were sufficient for mixed model procedures, ICC between the first and second time point were calculated for all measures (neural activity, PDS, testosterone, BART, and all subscales of the BIS/BAS). ICCs were modeled with a two-way mixed model with absolute agreement. ICC values were determined using IBM SPSS Statistics for Windows, v21. Average ICC values are reported in Table 3. All values are >0.10, which indicates sufficient nesting of observations within individuals, necessary for mixed model fitting procedures (Lee, 2000; Ordaz et al., 2013).

Table 3.

ICC for all variables between time points 1 and 2

Measure	ICC
PDS	0.762
Testosterone	0.842
BART	0.557
BIS	0.644
BAS Drive	0.577
BAS Fun seeking	0.430
BAS Reward Responsiveness	0.502
NAcc L	0.327
NAcc R	0.219

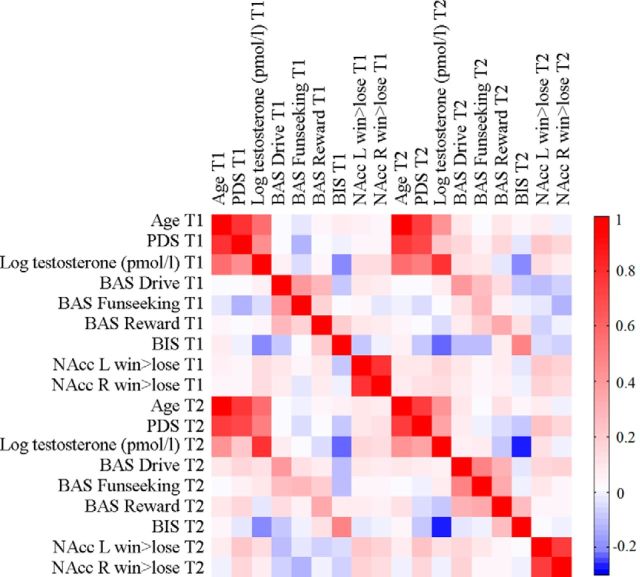
When measures are highly correlated this might result in erratic changes in coefficient estimates, therefore it is important to assess the relation between all the measures included in the current study. To assess correlations between measures (and between time points 1 and 2), Pearson's correlations were calculated. Correlations are reported in a colored correlation matrix in Figure 3. The correlation between age and PDS scores was high on both time points (T1: r = 0.78, p < 0.001; T2: r = 0.75, p < 0.001), as well as the correlation between left and right NAcc activity (T1: r = 0.81, p < 0.001; T2: r = 0.72, p < 0.001). Correlations between other measures were between r = −0.28 and r = 0.57.

Figure 3.

Correlation matrix of all variables on time points 1 and 2.

Results

Developmental effects

We tested, for each measure separately, whether age showed a linear, quadratic, or cubic relationship with NAcc activity, pubertal development (PDS, testosterone), and risk-taking tendency (BART, BIS/BAS). AIC and BIC values were used to guide which models were selected to characterize the relationship between age and each of the measures (see Mixed-model building procedure). A formal model comparison was done using a log likelihood ratio test. The AIC and BIC values for all null, linear, quadratic, and cubic models are listed in Table 4.

Table 4.

AIC and BIC values for null, linear, quadratic, and cubic models to describe the relationship with age and each of the measures reported in the table

Measure	Model
	Null		Linear		Quadratic		Cubic
	AIC	BIC	AIC	BIC	AIC	BIC	AIC	BIC
PDS	1033	1046	682	699	684	705	661	686
Testosterone	869	882	709	726	658	679	651	676
BART	2960	2973	2942	2959	2930	2952	2930	2956
BIS	2987	3000	2987	3004	2987	3009	2988	3014
BAS Drive	2426	2439	2427	2443	2428	2450	2428	2454
BAS Fun Seeking	2288	2301	2290	2307	2290	2312	2290	2316
BAS Reward	2278	2291	2279	2296	2280	2301	2280	2306
NAcc L	2249	2261	2250	2267	2239	2260	2241	2266
NAcc R	2279	2292	2281	2298	2271	2292	2273	2298

Preferred models are indicated in boldface type.

Relationship between NAcc activity and age

The relationship between NAcc activity (for both left and right NAcc) in response to rewards and age was best explained by a quadratic age-model. This model indicated that neural responses to rewards peak during adolescence (Fig. 4 shows raw data and predicted data from the model). Significant individual variability existed in the intercept, indicated by a random intercept. This shows that individuals vary significantly in the NAcc response. There was no main effect of sex or interaction between age (quadratic) and sex. See Table 5 for a full description of the model.

Figure 4.

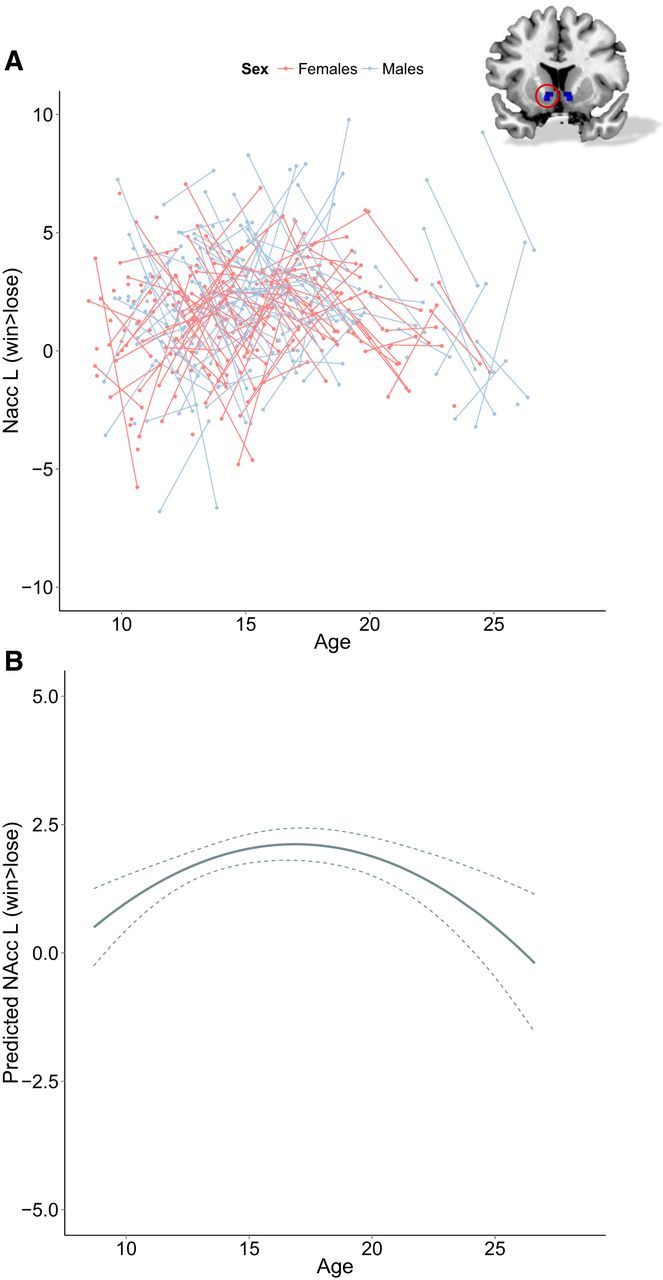
A, Longitudinal graphic representation of age at both time points and contrast values for win > lose for the left nucleus accumbens on both time points. Individual subjects are represented by individual lines. Subjects measured only once are represented by points. Right nucleus accumbens, not represented in a figure, shows similar effects. B, Predicted values for contrast values for win > lose for the left nucleus accumbens based on the optimal fitting model. Right nucleus accumbens, not represented in a figure, shows similar effects. Dotted lines represent 95% confidence interval.

Table 5.

Variances, beta's (β), p values, and 95% confidence intervals (CIs) for the best fitting models for age and NAcc activation (left and right), PDS, testosterone levels, BART, and all scales of the BIS/BAS questionnaire

	Variance	β	p	95% CI
				Lower	Upper
Nacc L
Random effect
Intercept	1.01			0.68	1.52
Fixed effects
Intercept		1.73	0.00	1.49	1.96
Age1		1.38	0.59	−3.67	6.43
Age2		−9.44	0.00	−14.42	−4.45
Nacc R
Random effect
Intercept	0.83			0.50	1.41
Fixed effects
Intercept		1.87	0.00	1.64	2.11
Age1		0.64	0.81	−4.48	5.76
Age2		−9.11	0.00	−14.18	−4.03
PDS
Random effect
Intercept	0.30			0.25	0.36
Fixed effects
Intercept		2.69	0.00	2.62	2.77
Age1		14.61	0.00	13.26	15.97
Age2		−1.52	0.02	−2.75	−0.29
Age3		−2.86	0.00	−3.98	−1.74
Sex		−0.37	0.00	−0.48	−0.27
Age1 × sex		−2.10	0.04	−4.13	−0.08
Age2 × sex		2.57	0.01	0.71	4.43
Age3 × sex		1.07	0.23	−0.68	2.82
Testosterone
Random effects
Intercept	0.18			0.15	0.22
Fixed effects
Intercept		1.27	0.00	1.23	1.31
Age1		3.36	0.00	2.26	4.45
Age2		−1.41	0.03	−2.65	−0.17
Age3		1.58	0.00	0.51	2.65
Sex		0.74	0.00	0.68	0.81
Age1 × sex		8.25	0.00	6.80	9.70
Age2 × sex		−5.32	0.00	−6.85	−3.79
Age3 × sex		−0.44	0.53	−1.81	0.93
BART
Random effects
Intercept	5.19			3.24	8.32
Age	0.33			0.20	0.54
Fixed effects
Intercept		11.26	0.00	10.90	11.62
Age1		17.57	0.00	8.44	26.69
Age2		−16.11	0.00	−24.94	−7.27
BIS
Random effect
Intercept	2.51			2.18	2.88
Fixed effect
Intercept		19.54	0.00	19.18	19.90
BAS Drive
Random effect
Intercept	1.39			1.18	1.62
Fixed effect
Intercept		10.78	0.00	10.57	10.99
BAS Fun Seeking
Random effect
Intercept	0.97			0.79	1.19
Fixed effect
Intercept		11.70	0.00	11.53	11.88
BAS Reward
Random effect
Intercept	1.08			0.90	1.30
Fixed effect
Intercept		17.16	0.00	16.98	17.33

Linear age terms are represented by Age¹, quadratic age terms by Age², and cubic age terms by Age³.

Relationship between PDS and age

The relationship between PDS score and age was best explained by a cubic age-model. This adolescent emergent effect indicates that PDS scores are stable in childhood, then rise steeply in adolescence, and then stabilize in adulthood (Fig. 5 shows the raw and predicted data from the model). For PDS, individual variability existed in the intercept. This indicates that individuals differ significantly in their PDS score.

Figure 5.

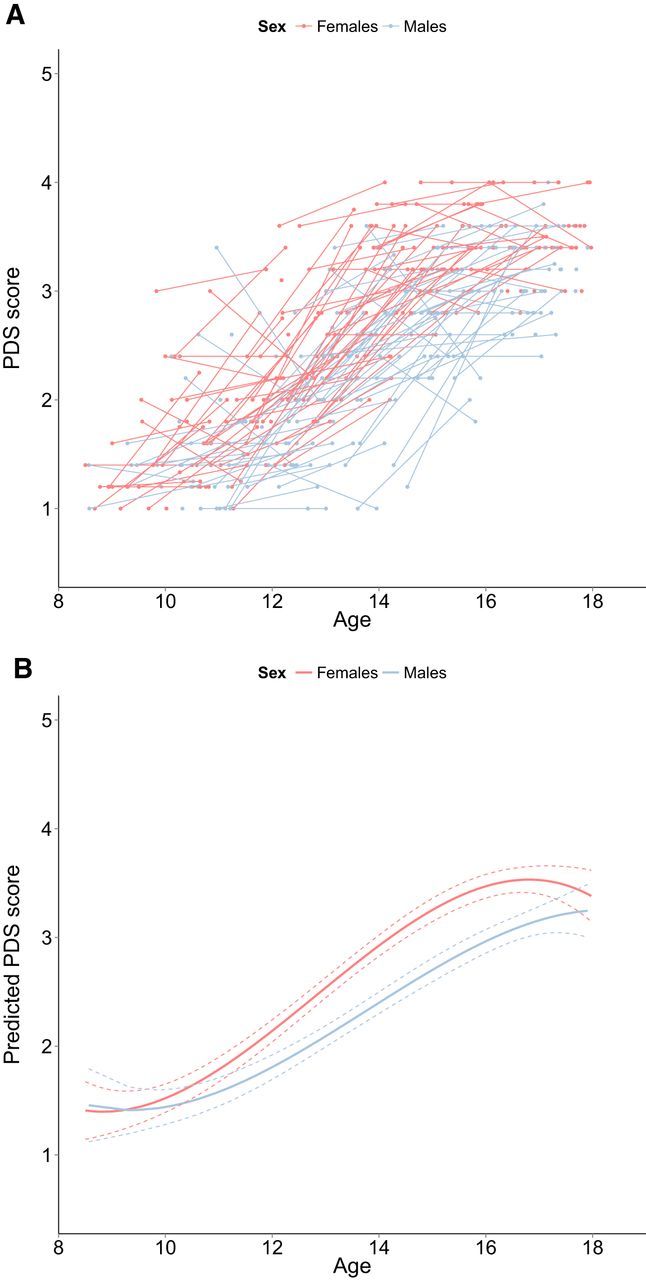
A, Longitudinal graphic representation of age at both time points and PDS scores on both time points. Individual subjects are represented by individual lines Subjects measured only once are represented by points. B, Predicted values for PDS scores based on the optimal fitting model. Dotted lines represent 95% confidence interval.

Adding a main effect and interaction of sex to the model resulted in lower AIC and BIC values, indicating improved model fit. The main effect of sex was significant, showing that girls had significantly higher PDS scores compared with boys. There was a significant interaction between age (linear) and sex, which indicates that girls showed a steeper increase in PDS scores compared with boys. In addition, the interaction between age (quadratic) and sex was significant. This interaction indicates that the quadratic fit is significantly different for boys and girls. The interaction of sex and age (cubic) was not significant, indicating that the cubic effect of age did not differ significantly between males and females (Table 5 shows a full description of the model).

Relationship between pubertal development (testosterone) and age

The relationship between testosterone and age was best explained by a cubic model. This adolescent emergent effect indicates that testosterone levels start low in childhood, then rise steeply in adolescence, and then stabilize in adulthood (Fig. 6 shows raw and predicted data from the model). For testosterone, individual variability existed in the intercept. This indicates that individuals differ significantly in their testosterone levels.

Figure 6.

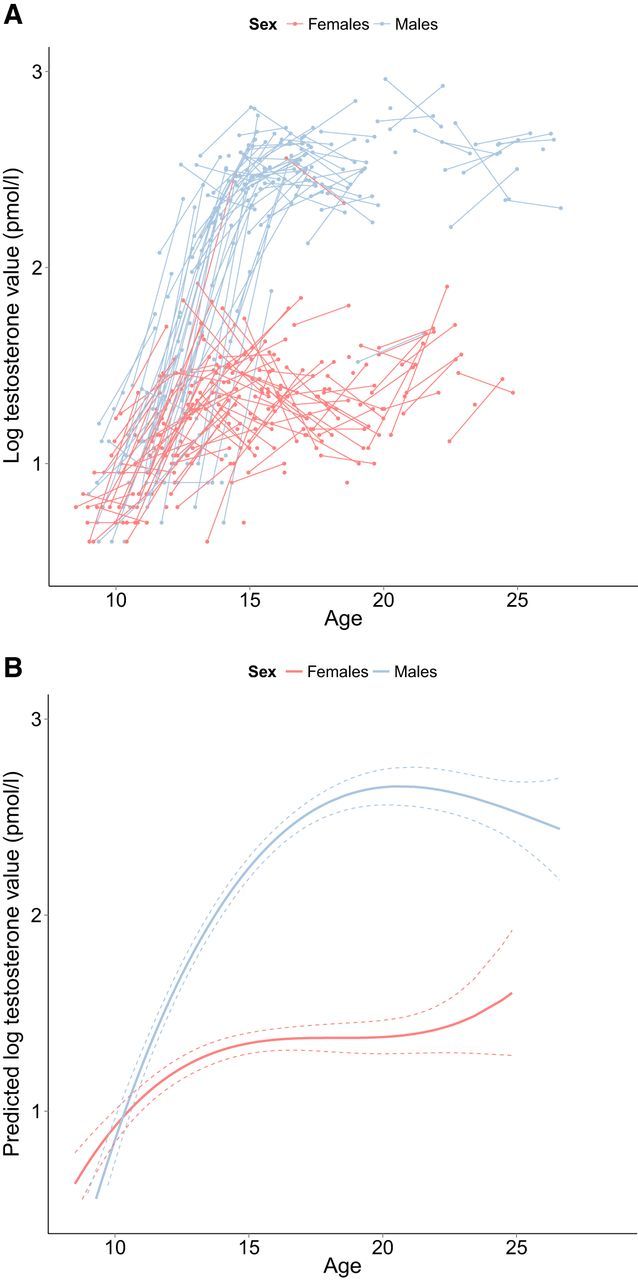
A, Longitudinal graphic representation of age at both time points and testosterone values on both time points. Individual subjects are represented by individual lines. Subjects measured only once are represented by points. B, Predicted values for testosterone values based on the optimal fitting model. Dotted lines represent 95% confidence interval.

Adding a main effect and an interaction with sex significantly improved the model fit. Significance test showed a main effect of sex, in which boys had higher testosterone values compared with girls. The interaction between sex and age (cubic) was not significant, indicating that the cubic effect of age did not differ significantly between males and females.

Relationship between risk-taking behavior (BART) and age

The relationship between BART and age was best explained by a quadratic age-model. This model indicates a peak in number of explosions on the BART during adolescence (Fig. 7 shows raw data and predicted data from the model). For total number of explosions, individual variability existed in the intercept and the random slope term. These findings indicate that individuals differ significantly in their number of explosions, and that variability existed in the change in number of explosions. Adding a main effect and interaction effect of sex did not significantly improve model fit (Table 5 shows a full description of the model).

Figure 7.

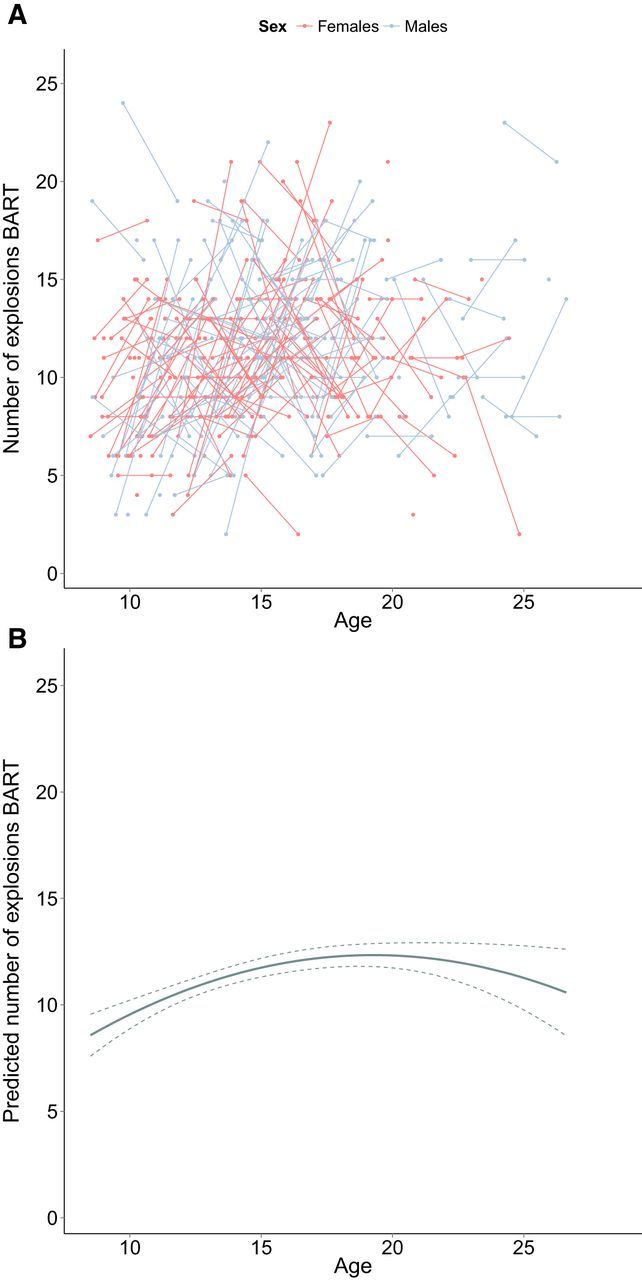
A, Longitudinal graphic representation of age at both time points and total number of explosions in the BART on both time points. Individual subjects are represented by individual lines. Subjects measured only once are represented by points. B, Predicted values for total numbers of explosions in the BART based on the optimal fitting model. Dotted lines represent 95% confidence interval.

Relationship between risk-taking behavior (BIS/BAS) and age

For all of the BIS/BAS scales the best model was the null model. This means that for none of the scales there was a significant effect of age (Table 5 shows a full description of the model).

Unique contributions

The analysis for unique contributions of testosterone, BART, and BIS/BAS to NAcc activity was performed twice; once for a model with age as the first predictor, and once for a model with PDS as the first predictor. The reason for performing these analyses twice is that age and PDS were highly correlated (T1: r = 0.78, p < 0.001; T2: r = 0.75, p < 0.001), therefore, adding them to the same model could result in erratic changes in coefficient estimates.

Relationship between NAcc responses, age, testosterone, BART, and BIS/BAS

The starting model was the model that best described the relationship between age and NAcc responses. This was for both left and right NAcc response a model with a quadratic age term, without a random slope term for age and no main or interaction effect of sex (left NAcc: AIC 1965, BIC 1985; right NAcc: AIC 2002, BIC 2023). We then added linear, quadratic, and cubic terms for testosterone, BART, and BIS/BAS. The model comparisons resulted in the following outcomes: (1) model fit did not improve by adding testosterone values (left NAcc: AIC 1967, BIC 1999; right NAcc: AIC 2008, BIC 2040). (2) Model fit did not improve when BART scores were added (left NAcc: AIC 1969, BIC 2002; right NAcc: AIC 2007, BIC 2040). (3) Model fit improved when adding BAS drive to the model (left NAcc: AIC 1964, BIC 1996; right NAcc: AIC 2000, BIC 2033). Only the linear term was significant and a model with only a linear term for BAS Drive was significantly better than the null model (left NAcc: AIC 1961, BIC 1985; right NAcc: AIC 1997, BIC 2022). (4) Stepwise inclusion of the other subscales, BAS Reward Responsiveness (left NAcc: AIC 1965, BIC 2001; right NAcc: AIC 2002, BIC 2039), BAS Fun Seeking (left NAcc: AIC 1967, BIC 2003; right NAcc: AIC 2003, BIC 2039), and BIS (left NAcc: AIC 1966, BIC 2002; right NAcc: AIC 2005, BIC 2036), did not result in improvement of model fit. (5) Finally, to test whether including sex improved the model fit, we added a main and interaction effect for sex. This resulted in a lower AIC value (left NAcc: AIC 1960, BIC 1993; right NAcc: AIC 2001, BIC 2034), but both the main and interaction effect of sex were not significant, therefore we excluded sex from the final model.

Together, the final model for both left and right NAcc comprised of a quadratic term for age and a linear term for BAS Drive. A description of the final model for both the left and right NAcc can be found in Table 6.

Table 6.

Variances, beta's, p values, and 95% confidence intervals (CI) for best fitting models for NAcc responses (left and right separately), and age and PDS

	Variance	β	95% CI		Upper
			p	Lower
Age models
Nacc L
Random effect
Intercept	0.94			0.60	1.46
Fixed effects
Intercept		1.69	0.00	1.45	1.93
Age1		1.16	0.64	−3.77	6.10
Age2		−9.22	0.00	−14.11	−4.34
BAS Drive		5.83	0.02	0.97	10.70
Nacc R
Random effect
Intercept	1.01
Fixed effects
Intercept		1.89	0.00	1.63	2.14
Age1		−0.57	0.83	−5.75	4.62
Age2		−8.65	0.00	−13.77	−3.52
BAS Drive		6.72	0.01	1.63	11.82
PDS models
Nacc L
Random effect
Intercept	0.75			0.31	1.81
Fixed effects
Intercept		1.77	0.00	1.50	2.04
PDS1		2.77	0.29	−2.37	7.91
Testosterone		6.39	0.02	1.21	11.57
BAS Drive		5.04	0.04	0.22	9.86
Nacc R
Random effect
Intercept	1.01			0.72	1.60
Fixed effects
Intercept		0.89	0.00	1.63	2.14
BAS Drive		7.43	0.01	2.29	12.58

Linear age terms are represented by Age¹ and quadratic age terms by Age².

Relationship between NAcc responses, PDS, testosterone, BART, and BIS/BAS

A separate analysis was performed for left and right NAcc relations with PDS. Again, for this model we tested whether model fit improved when including a linear, quadratic, and cubic term for PDS, followed by testosterone, BART, and BIS/BAS. The model fitting procedure for left NAcc resulted in the following outcomes: (1) adding PDS resulted in a significantly better model fit compared with the null model based on evaluation of AIC values (null model left NAcc: AIC 1979, BIC 1988; PDS model left NAcc: AIC 1473, BIC 1496). Only the linear term for PDS was significant. (2) Adding testosterone to the model improved model fit based on evaluation of AIC values and a log likelihood ratio test (left NAcc: AIC 1470, BIC 1496). The linear term for testosterone was significant. (3) Adding BART to the model did not improve model fit (left NAcc: AIC 1472, BIC 1501). (4) Including BAS Drive significantly improved model fit (left NAcc: AIC 1466, BIC 1496). Only the linear term for BAS Drive was significant. (5) A stepwise inclusion of the other BIS/BAS scales did not result in improvement of model fit (BIS left NAcc: AIC 1469, BIC 1502; BAS Fun Seeking left NAcc: AIC 1469, BIC 1503; BAS Reward Responsiveness left NAcc: AIC 1466, BIC 1500). (6) Finally, we assessed whether including a main and interaction effect of sex improved model fit. The main and interaction effects for sex were note significant for any of the measures (left NAcc: AIC 1470, BIC 1508).

Together, the final model for left NAcc comprised of a linear term for PDS, a linear term for testosterone and a linear term for BAS Drive. No random slope terms and no main effect or interaction effect for sex improved the model. For the right NAcc a model with only a linear term for BAS Drive without a random slope term or main, and interaction effect of sex was the most optimal model. A description of both models can be found in Table 6.

Discussion

This study describes longitudinal changes in neural activity in NAcc in response to rewards across childhood, adolescence, and early adulthood. We investigated exploratory relations with pubertal changes, as measured with testosterone and self-report, and risk-taking behavior, as measured with the laboratory BART task and self-reported risk-taking tendency. The first goal of this longitudinal study was to examine age related changes in NAcc activity to rewards, pubertal development (PDS and testosterone levels), and risk-taking behavior (laboratory risk-taking and self-reported risk-taking tendency) in a large sample with continuous age range between 8 and 27 years. The second goal was to investigate the relationship between neural responses to rewards and age, pubertal development, and risk-taking behavior. The discussion is organized to follow these objectives.

Relationship between age and pubertal development, testosterone, risk-taking, and reward sensitivity

The results of the longitudinal analyses confirmed the previously reported peak in NAcc activity in response to rewards (Ernst et al., 2005; Galvan et al., 2006; Van Leijenhorst et al., 2010; Braams et al., 2014b). Given the longitudinal assessment, these changes cannot be attributed to cohort-effects and are consistent with a prior longitudinal study showing structural quadratic change in NAcc volume (Urošević et al., 2012).

The same developmental change question was addressed for two complementary indices of pubertal development: self-reported puberty and testosterone levels. The results for self-reported pubertal changes concur with prior research on pubertal development showing that puberty starts earlier in girls than boys (Carskadon and Acebo, 1993; Sisk and Foster, 2004; Shirtcliff et al., 2009). That is, the data patterns show that girls and boys are comparable in pubertal development until approximately age 12, after which girls show faster pubertal development, as measured with the PDS compared with boys. At approximately age 17, PDS scores for girls and boys are again at the same level (Dorn and Biro, 2011). Testosterone levels followed a pattern with a sharp increase of testosterone levels for boys and a more modest increase for girls starting at approximately age 10. For girls testosterone levels stabilized approximately age 15, whereas for boys stability was observed approximately age 18, suggesting not only a steeper, but also a prolonged trajectory of testosterone change in boys than in girls. These results are consistent with a previous study in boys showing that testosterone levels are low until approximately age 10, and then start to rise (Khairullah et al., 2014).

Risk-taking behavior was assessed in two separate ways by using a well validated laboratory risk-taking task (Lejuez et al., 2002, 2003, 2007; the BART) and using a self-report risk-taking tendency questionnaire (BIS/BAS; Carver and White, 1994). Importantly, these two assessments followed different developmental trajectories. First, the laboratory risk-taking task used in this experiment, the BART, followed a quadratic pattern with a peak in mid-adolescence. This pattern resembles observations from two earlier studies examining risk-taking in the laboratory (Figner et al., 2009; Burnett et al., 2010), but also with trajectories of self-reported sensation-seeking (Steinberg et al., 2008; Shulman et al., 2015) and real-life risk-taking behavior (Eaton et al., 2012). In contrast, the self-assessment of risk-taking tendency did not change over age. This could be indicative of an individual difference measure that is not related to age. This is also in line with a longitudinal study assessing changes and stability in BIS/BAS in adolescents and young adults (Takahashi et al., 2007). A previous study investigating BIS/BAS development found a peak in risk-taking tendency across adolescence in a similar age range and with also two time points with a 2 year interval (Urošević et al., 2012). It is currently unclear what causes the differences in the current trajectory of risk-taking tendency and the results reported by Urošević et al. (2012). One possibility is that the current study used age as a continuous variable, whereas in the Urošević et al. (2012) study participants were divided into age groups. Future studies should investigate BIS/BAS development in more detail.

The correlation between BART performance and BIS/BAS scores was low with Pearson correlation coefficients ranging between r = −0.1 and r = 0.1, confirming that these two components of behavior capture different aspect of individual differences in risk-taking behavior. Similar results have been reported for impulsivity and sensation-seeking which also followed separable developmental trajectories (Steinberg et al., 2008). Possibly self-reported risk-taking is more indicative of reflected risk-taking tendency, which does not show an age-related change, whereas laboratory risk-taking is more indicative of sensation-seeking (Steinberg et al., 2008) or “hot” decision-making (Figner et al., 2009), which peaks in mid-adolescence.

Unique contributions of age, pubertal development, and risk-taking behavior to NAcc change

The next question was whether the trajectories of pubertal development and risk-taking could account for the peak in NAcc activity to rewards in mid-adolescence. This was tested in two separate models, the first assessed the unique contribution of testosterone and risk-taking behavior above age on NAcc activity in response to rewards. The second tested the unique contribution of testosterone and risk-taking behavior above self-reported puberty on Nacc activity in response to rewards.

The first model found that individual differences in self-reported risk-taking tendency, specifically BAS drive, accounted for variation in NAcc activity over time, showing that those individuals who showed a sharper increase in BAS drive scores over time also showed a sharper increase in NAcc activity, in addition to age-related change. These findings are similar to several other studies that examined relations with BAS scales and neural responses to images of food (Beaver et al., 2006) or monetary rewards (Costumero et al., 2013; van Duijvenvoorde et al., 2014). Thus, it is likely that individual differences in self-reported risk-taking tendency fluctuate with neural activity in NAcc.

Based on prior developmental models reporting increases in motivational value of rewards in adolescence (Nelson et al., 2005; Ernst et al., 2006; Somerville et al., 2010), we specifically addressed the question whether changes in testosterone and puberty accounted for changes in NAcc activity. Given that age and puberty were highly correlated, it was statistically challenging to dissociate these patterns; therefore, we tested for the relation between NAcc activity and puberty in a separate model in which age was not included. These analyses indicated that self-reported puberty was linearly related to NAcc activity. That is, we observed that increases in puberty were related to higher NAcc response to rewards. In contrast to the quadratic effects of age, we did not observe a peak in NAcc activation in mid-puberty. Puberty was assessed in participants of 17 years and younger. The peak in NAcc activity was found in mid-puberty, approximately age 15–17. Therefore, a linear relationship between NAcc activity and puberty was expected in participants 17 and younger. Testosterone was linearly related to NAcc activity as well, showing that those individuals with higher testosterone levels over time also showed higher NAcc activity to rewards. These findings are comparable to earlier longitudinal results by Spielberg et al. (2014) who reported in a small age range (11–13 years) that testosterone change predicted NAcc change to observation of emotional faces, to a cross-sectional study that found positive correlations between testosterone levels and NAcc activity when playing a gambling task (Op de Macks et al., 2011), and a study showing a relationship between risk-taking behavior on the BART and testosterone levels (Peper et al., 2013a). In addition, testosterone administration has been found to lead to increases in ventral striatum activity in a monetary anticipation task, suggesting a causal role of testosterone in reward responsiveness (Hermans et al., 2010).

Together, the current findings show that in this adolescent sample, individual differences in pubertal development account for significant variation in the trajectory of NAcc activation. These findings fit well with the Social Information Processing Model of adolescent development (Nelson et al., 2005) which describes risk-taking in terms of an overactive affective node, due to changes in hormone levels.

One limitation of the current study is that we did not parametrically manipulate rewards and losses, and therefore we were not able to distinguish between trajectories of NAcc activity to wins and losses. In addition, in the current study we focused particularly on the contrast winning versus losing. In this way, we were unable to distinguish whether our results are driven by response to rewards or punishment. It is possible that the peak in NAcc activity is driven by a decreased response to losses rather than an increase in response to wins. The results should therefore be interpreted as a relative difference. Future studies should focus on including a neutral baseline to distinguish the different trajectories of NAcc activation to wins and losses. Furthermore, future studies should test differences in neural responses to expected value, outcome and reward prediction errors (van Duijvenvoorde et al., 2015).

Conclusion

This study confirmed the hypothesis of a longitudinal peak in NAcc activity to rewards in mid-adolescence, but additionally showed that change in NAcc activity is associated with individual difference measures including a drive for rewards. Pubertal development was linearly related to NAcc activity suggesting a driving factor of puberty in the increased response to rewards (Crone and Dahl, 2012). An important direction for future research is to investigate which factors lead to stabilization of the response to rewards in early adulthood, which could potentially be related to reductions in NAcc volume with age (Urošević et al., 2012; Mills et al., 2014), top down control of prefrontal cortex over the NAcc (Peper et al., 2013b), or environmental factors. Understanding the longitudinal patterns of brain responses to motivational events is key for future understanding of deviant developmental trajectories, such as substance abuse or crime (Steinberg, 2008; Spear, 2013).