Opponent Identity Influences Value Learning in Simple Games

Abstract

Context plays a pivotal role in many decision-making scenarios, including social interactions wherein the identities and strategies of other decision makers often shape our behaviors. However, the neural mechanisms for tracking such contextual information are poorly understood. Here, we investigated how opponent identity affects human reinforcement learning during a simulated competitive game against two independent computerized opponents. We found that strategies of participants were affected preferentially by the outcomes of the previous interactions with the same opponent. In addition, reinforcement signals from the previous trial were less discriminable throughout the brain after the opponent changed, compared with when the same opponent was repeated. These opponent-selective reinforcement signals were particularly robust in right rostral anterior cingulate and right lingual regions, where opponent-selective reinforcement signals correlated with a behavioral measure of opponent-selective reinforcement learning. Therefore, when choices involve multiple contextual frames, such as different opponents in a game, decision making and its neural correlates are influenced by multithreaded histories of reinforcement. Overall, our findings are consistent with the availability of temporally overlapping, context-specific reinforcement signals.

SIGNIFICANCE STATEMENT In real-world decision making, context plays a strong role in determining the value of an action. Similar choices take on different values depending on setting. We examined the contextual dependence of reward-based learning and reinforcement signals using a simple two-choice matching-pennies game played by humans against two independent computer opponents that were randomly interleaved. We found that human subjects' strategies were highly dependent on opponent context in this game, a fact that was reflected in select brain regions' activity (rostral anterior cingulate and lingual cortex). These results indicate that human reinforcement histories are highly dependent on contextual factors, a fact that is reflected in neural correlates of reinforcement signals.

Introduction

Many decisions involve dynamically learning action and stimulus values from experience with reward and punishment. Real-world choice values are highly contextual: while one choice is highly valued in one contextual setting, it may have a low or even negative association elsewhere. Salient examples of the contextual nature of choice values come from social decision-making studies, in which high-level factors, such as reputation (Fehr and Gächter, 2002), perceived personality characteristics (King-Casas et al., 2005), and moral character (Delgado et al., 2005), greatly influence choices to trust, help, or punish others. Even basic stimulus-related value learned through reinforcement is contextual in that simple actions (e.g., approach and avoidance) take on different values in the presence of that stimulus, and the reinforcement history of a stimulus can transfer to novel choice pairings of that stimulus (Frank et al., 2004). By contrast, choice values can be influenced by social contexts much more dynamically in a multithreaded manner, such as when identical games are played against distinct opponents. How well humans can track context-specific values while those values are dynamically changing remains poorly understood, as do the supporting neural mechanisms.

Reward signals during simple games and other tasks are observed throughout the human (Vickery et al., 2011) and monkey (Barraclough et al., 2004; Seo and Lee, 2007; Lee et al., 2012; Donahue et al., 2013) brains, but how are such signals, resulting from interactions with different opponents, compartmentalized in the brain to selectively influence behavior? Consider the game of matching pennies. When games are repeated, human and monkey participants often play strategies that are well described by reinforcement learning algorithms, such that recently rewarded options are played with higher frequency (Mookherjee and Sopher, 1994, 1997; Erev and Roth, 1998). Suppose that two independent opponents are played in such a game. Recent choice–outcome associations against one player clearly would be irrelevant against an independent opponent. We face similar dilemmas constantly in both social and nonsocial tasks, wherein our choice set is identical or very similar to prior experience, but the physical or social context is different. In many cases, we might treat the multiple contexts as independent, and only learn from relevant choices and outcomes. Our memory of choices and outcomes should be “tagged” by context, such as opponent identity, when such conditions arise.

To examine the dynamic response of reward signals to context, we randomly interleaved plays of a matching-pennies game against two computerized opponents while participants were scanned with fMRI. We tested whether participants' choices depended on opponent context. In addition, we used a multivoxel pattern analysis (MVPA) to examine neural signals that discriminated wins from losses, and asked whether these reinforcement signals were more robust and discriminable on trials followed by the same opponent. In contrast to treating stimulus–reward associations themselves as contexts, here we isolated context by equalizing the overall probability of winning with respect to each choice in both contexts; choice values varied dynamically and independently for each opponent. We found that opponent identity modulated sustained neural reinforcement signals during decision making.

Materials and Methods

Participants.

Participants were 26 members of the Yale University and New Haven, Connecticut, community. Fifteen participants were male and ages ranged from 18 to 32 years (mean: 23.5 years). One participant did not complete the task due to equipment malfunction and was excluded from analysis.

Task.

Participants completed three stages of a matching-pennies game (Fig. 1A) against two randomly interleaved computerized opponents. The images of the opponents for all participants were two Caucasian males chosen for their distinctiveness (one opponent has facial hair, while the other does not) from the color FERET (Facial Recognition Technology) database (Phillips et al., 1998). Participants were informed that the faces represented two completely independent opponents, which were both controlled by a computer algorithm. They were informed that the algorithm would track their choices independently, and that each opponent's algorithm would not be “aware” of the other opponent's choices and outcomes. The participants were encouraged to treat the opponents independently to win the maximum reward. Monetary rewards were given according to the performance in the task. Participants were given a $15 endowment at the beginning of the experiment. Every win was rewarded with an additional $0.20, while every loss was penalized by the loss of the same amount. Misses (failing to respond within the allotted time) were heavily penalized (−$0.50) to strongly discourage missing responses. At the end of the experiment, the earned rewards were rounded up to the nearest dollar and added to the base compensation for the study. Participants were shown their current total at the end of every session of the task.

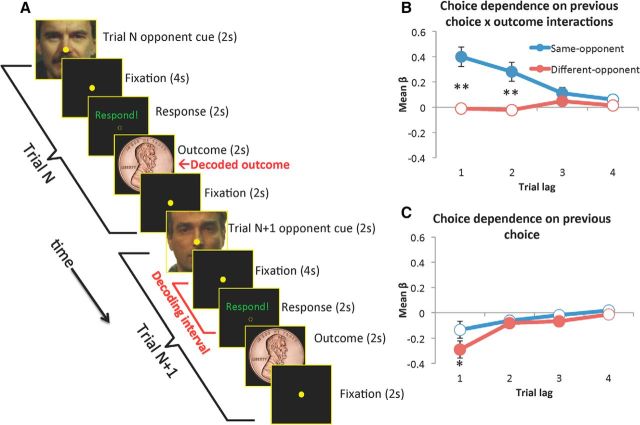
Figure 1.

Behavioral task and opponent-dependent reinforcement learning during matching-pennies game. A, Trial sequence (2 trials shown). B–C, Mean regression coefficients from a logistic regression on prior choice and choice × outcome interaction, split by whether the prior trial was played against the same or a different opponent. B displays mean coefficients for the interaction term. Positive values imply a win–stay, lose–switch strategy with respect to the given choice. Solid symbols indicate significant (p < 0.05) difference from zero, across participants. Asterisks indicate significant difference between same-opponent and different-opponent weights (**p < 0.001, *p < 0.05). Error bars represent SEs. C displays mean coefficients for the choice terms. Positive values imply staying; negative values switching.

A matching-pennies game was played in three stages that differed in speed and the exploitation by the computer opponents: (1) prescanning practice session (4 s/trial, exploitative, 3 × 100-trial blocks), (2) scanning practice session (12 s/trial, exploitative, 1 × 49-trial block), and (3) main scanning sessions (12 s/trial, nonexploitative, 6 × 49-trial blocks). Exploitative computer opponents attempted to detect and counter patterns in the participant's behavior (described below), whereas trials in the nonexploitative sessions produced predetermined orders of wins and losses. The reason for this change from prescanning to scanning blocks was to maximize the power of statistical analyses by equalizing the number of trials across different conditions as much as possible.

Prescanning practice sessions (fast, exploitative).

Before entering the scanner, participants completed three 100-trial practice blocks with fast timing against an algorithm that tracked and attempted to exploit serial dependencies in their behavior. Two participants only completed two 100-trial practice blocks due to late arrival at the imaging site. In each trial, participants were shown the face of one of two opponents, and were required to respond within 2 s with a key press indicating a choice of “heads” or “tails.” A circular, yellow fixation marker was superimposed on the face, and changed from empty to filled to indicate receipt of a response. Two seconds after the face cue onset, the outcome was shown in the form of the opponent's choice (a picture of the heads or tails side of a US penny). The outcome stayed up for 2 s and was replaced immediately with the next trial's opponent cue, which was either the same face seen in the prior trial, or the other opponent's face. Each session consisted of 50 trials against each opponent, randomly intermixed.

Scanning practice session (slow, exploitative).

After the participant was settled into the scanner, an additional practice session was completed while a structural scan was completed. This practice session served to acclimate participants to the slow-paced, fMRI version of the task, and preserved the “exploitative” nature of the opponent in the new timing scheme. Each trial began with an opponent cue superimposed with a filled yellow circular fixation marker (2 s), which was followed by 4 s of fixation, after which the fixation marker was emptied and the word “Respond!” was presented to indicate that a choice should be registered. The participant used a two-button response box to register a choice, after which the fixation marker was filled again to indicate that the response was received. Two seconds after the onset of the choice cue, the opponent's response was shown (heads or tails side of a penny) for 2 s. Finally, the fixation marker was shown alone for 2 s, followed by the opponent cue for the next trial. This session consisted of 49 trials, 24 against each opponent (randomly intermixed), plus an additional trial in the beginning against a randomly selected opponent. During this practice session, computer opponents' choices were again selected according to the algorithm described below.

Main scanning sessions (slow, nonexploitative).

During the main functional scanning sessions, trial timing was the same as in the scanning practice session. At the beginning of the scan, an additional five discarded acquisitions were obtained, resulting in a 10 s fixation period before onset of the first trial. The last trial in each session was followed by 12 s of fixation. Fixed trial timing without jitter was necessary due to our focus on decoding trial N outcomes during trial N + 1 brain activity, since jittering trials would have inconsistently shifted the outcome relative to the early activity of the subsequent trial.

The main difference between the scanning practice session and the main scanning sessions was the algorithm that controlled opponents' behaviors. Unbeknownst to participants until the end of the experiment, the exploitative algorithm (described below) was discontinued for the main sessions to balance, as much as possible, the number of wins and losses followed by same-opponent and different-opponent trials, as well as wins and losses in that subsequent trial. That is, we sought to equalize the number of win–same–win, win–same–loss, …, loss–different–loss trials (eight possible combinations of outcome in trial t, same/different opponent in trial t + 1, and outcome in trial t + 1). This was done to equate, as much as possible, the number of trials for different choice–outcome sequences for our MVPA analysis, as described below. As shown in the results, however, the disuse of the exploitative algorithms in the present study did not alter the major behavioral effects reported in our previous study (Vickery et al., 2011).

Computer opponent's algorithm.

The algorithm employed by the computer opponent during both practice sessions was based on the algorithm used in our previous experiments with the matching-pennies task (Barraclough et al., 2004; Vickery et al., 2011). Two instances of the same algorithm were applied independently for the two opponents. The algorithm maintained a history of all choices and outcomes (wins/losses) of the participant versus the opponent it represented. To make a choice in trial N, the participant's four most recent choices against the same opponent and their outcomes were identified. The algorithm examined patterns of length 1, 2, 3, and 4 choices that matched the pattern preceding trial N, and the participant's historical proportion of choosing either option following those patterns. It also examined similar patterns of choices and rewards in the last four trials. It subjected each of these eight proportions as well as the overall choice probability to a binomial test, and used the strongest bias (i.e., largest significant deviation from 0.5 probability of choosing heads) to make its own choice. For instance, if the strongest bias suggested the probability of the participant choosing heads was 0.7, then it would choose tails with a probability of 0.7 to counter the expected choice.

Behavioral analysis.

Choice behavior was analyzed using a logistic regression model, applied to individual participant's choice sequences. The dependent variable, choice on trial t, was coded as 0 (for tails) and 1 (for heads), and the probability of choosing heads was modeled as a function of each individual's last four choices (C) and the interaction of those choices with outcomes (O). As predictor variables, choices and outcomes were coded as 1 for heads, −1 for tails, 1 for win, and −1 for loss. The influence of choices and the interactions of choices with outcomes were modeled separately based on whether the prior trial was played against the same (C_S) or different (C_D) opponent:

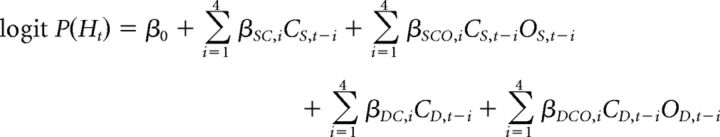In addition to this dual-opponent model, we also considered a single-opponent model, in which opponent identity played no role in determining choice based on trial history:

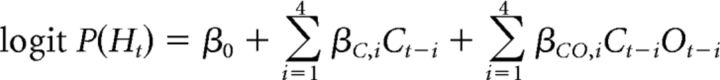We considered these models in the context of the full sequence of choices (including both scan and practice trials) and for scanning sessions alone. There was no major difference between scan and practice sessions that would influence our conclusions, so we present the results of a combined (practice and scanning) analysis.

To analyze the correlation between behavioral sensitivity to opponent and opponent-dependent decoding accuracy for neural data described below, we calculated an index of opponent dependency, I_OD, based on the results of the logistic regression analysis described above using the following equation: I_OD = |β_SCO,1| − |β_DCO,1|.

This score reflects the difference in the overall dependency on outcome × choice conjunction in the last trial for same and different opponents, regardless of the sign of that dependency, and captures how much the identity of the opponent alters the dependence of the current choice on the outcome in the previous trial. It also takes into account individual variation in how participants respond to previous wins and losses. For instance, a win–stay/lose–switch strategy and an equally strong win–switch/lose–stay strategy are treated equivalently by this measure. Therefore, it reflects an increase in the overall responsiveness to reward from the same opponent. If participants play win–stay/lose–switch in response to the same opponent, but play the opposite (win–switch/lose–stay) strategy in equal proportions when there is an opponent change, those tendencies cancel in the above measure.

fMRI sequence parameters.

fMRI data were acquired by a 3T Siemens Trio scanner and a 12-channel head coil. We acquired a high-resolution (1 mm³) T1-weighted MPRAGE structural image that was used for anatomical reconstruction, cortical and subcortical labeling, and participant coregistration. Functional scans were T2*-weighted gradient-echo EPI sequences, consisting of 34 slices with an oblique axial orientation and acquired with a resolution of 3.5 × 3.5 × 4.0 mm³ (sequence parameters: TR = 2000 ms; TE = 25 ms; flip angle, 90°; matrix, 64 × 64). Six functional scanning runs consisting of 305 volumes were acquired for each participant, with each run lasting 10 min, 10 s. The first five volumes were discarded before analysis.

Structural and functional preprocessing.

We applied Freesurfer's (http://surfer.nmr.mgh.harvard.edu/) automated routines for cortical labeling and subcortical parcellation based on the high-resolution structural image. Functional data for all analyses were motion corrected to the first volume of the first functional scan and slice-time corrected. For MVPA analyses, the data were not smoothed, but each voxel's activity within a run was corrected for drift using a detrending algorithm with second-order polynomial, and Z-normalized.

MVPA procedures.

In all analyses described in this paper, we decoded experimental variables for trial N based on the three volumes following the onset of opponent cue in trial N + 1. Our primarily analyses targeted the previous trial's outcome. MVPA was implemented using PyMVPA (v.2.3.1; Hanke et al., 2009), and a support vector machine (SVM) algorithm. In all cases, we used a linear kernel and penalty parameter (C) of 1. A linear SVM treats a pattern as a vector in a high-dimensional space, and tries to find a linear hyperplane that optimally separates the two trained categories, by maximizing the accuracy of the split in the training data as well as maximizing the margin between the hyperplane and the nearest samples (referred to as support vectors). The default value of the SVM parameter (C = 1) was chosen a priori and based on convention, due to a lack of power in our study to determine it independently, as it demonstrates good overall performance [we used the same default previously (Vickery et al., 2011)]. We approached classification in two different ways: first, using ROI-based analyses, and second, by a searchlight analysis. For the ROI analysis, 45 bilateral ROIs were determined based on the Automated Anatomical Labeling Atlas (Tzourio-Mazoyer et al., 2002), which was transformed to each subject's individual functional space. The ROIs covered most of the cortex and major subcortical gray-matter structures, excluding the cerebellum.

Events in our event-related design were determined jointly by the choices of both the participant and the computer opponent. To approximately conserve equal numbers of trials in each bin based on our trial-balancing criteria, we artificially fixed the number of wins and losses to be equal (except for the randomly selected outcome of the first trial of each scan) for each opponent. Nevertheless, event sequences were still not completely balanced due to the unpredictability of the participant's choices. To avoid confounds in the analysis, we balanced training and transfer sets by randomly removing trials for each subject to ensure that the results did not depend on a learned bias of the classifier. Such balancing was done independently within each of the two halves of the experiment as defined for the split-half cross-validation procedures. The factors that were balanced for the primary analysis were the outcome and computer's choices for trial N, as well as the opponent's identity (same or different as prior trial) in trial N + 1. Accordingly, eight classes were equalized: Win-Heads-Same, Win-Tails-Same, Lose-Heads-Same, Lose-Tails-Same, Win-Heads-Different, Win-Tails-Different, Lose-Heads-Different, Lose-Tails-Different (this also balanced participant choice). Thus, significant decoding of wins/losses could not be attributed to decoding of computer or participant choice.

Trials were divided into two halves for each experiment, and trial type was balanced independently for each half to prevent the acquisition or expression of bias in the classifier. Although trials were not temporally jittered in our experiment, the results from these decoding analyses are quite unlikely to result from any serial correlation in the hemodynamic response, since the behavioral events in successive trials were largely independent. Finally, in analyses not reported here, we did not observe differences in win/loss decoding between same-opponent and different-opponent trials before the opponent cue (all p's > 0.21), which would be expected if our results were driven by serial correlations.

Split-half cross-validation procedures were used to assess classifier performance within each ROI or searchlight. For our primary MVPA analysis, decoding of wins and losses was further split by opponent (same or different). Two independent classifiers were trained for same-opponent and different-opponent trials. For other MVPA analysis, including decoding same versus different opponent, only one classifier was employed. We evaluated statistical significance by adopting a permutation and bootstrapping scheme (Stelzer et al., 2013). First, we calculated the accuracy of the classifier within a given ROI or searchlight for each subject (averaging performance across the two split-half cross-validation runs). Then, we computed the accuracy of the classifier when labels were randomly permuted for each subject. Label permutations were conducted independently within each split-half section of the data, so as to preserve the balance of trial types within each half. To preserve spatial correlations within a particular permutation, the same permutation was applied to each ROI mask or searchlight within each sample. We computed 1000 permutations per subject for the ROI-based approach, and 100 permutations per subject for the searchlight-based approach. To compute group-level statistics, for each ROI and searchlight we computed 10⁵ bootstrap samples. To construct each bootstrap sample, one permuted accuracy map was randomly drawn per participant, and averaged (or, in the case of comparing same-opponent vs different-opponent classifiers, one permuted accuracy map per condition was drawn and differenced). Average performance (or average difference in performance) in each ROI/searchlight center was compared with the histogram of accuracies computed in this bootstrapping procedure to determine ROI or searchlight-wise significance. An additional stage of cluster-based significance testing was conducted for the searchlight analysis (see searchlight methods, below). For the ROI approach, significance values were corrected using false discovery rate (FDR) correction (Benjamini and Hochberg, 1995; q = 0.05 across ROIs).

We did not factor out the univariate response specific to wins and losses and/or opponent conditions before MVPA (e.g., by conducting a GLM and applying MVPA to residuals of that model). One reason for this was that our claims do not depend on our results being specific to MVPA. That is, MVPA, as employed here, can pick up both on overall activity differences between conditions, as well as subtler pattern differences that differentiate conditions. We do not make any claim about the specificity of decoding results to patterns per se rather than overall activity differences between conditions.

Searchlight procedures.

A searchlight analysis (Kriegeskorte et al., 2006) was conducted using procedures similar to the ROI-based approach but applied to spheres of voxels surrounding each voxel. For each voxel within the brain mask, a spherical volume surrounding it (but constrained to be within the brain mask) was formed. Searchlight radius was 2 voxels; thus, each searchlight volume encompassed 33 total voxels (the 3 × 3 × 3 cube plus the next voxel bordering the central voxel of each face) and had a maximum extent of 15 mm on the within-plane dimensions and 20 mm on the across-plane dimension. Decoding accuracy was determined within that volume for both the accurate labels and 100 randomly permuted condition labels, and assigned to the central voxel.

Group-level analysis was based on the bootstrap and conducted in a two-step procedure adopted from Stelzer et al. (2013). A total of 10⁵ bootstrap samples were calculated by independently sampling one map per subject of the 100 permuted accuracy maps, and then averaging accuracy. The original (nonpermuted) searchlight mean accuracy map was then compared with each of 10⁵ samples of the permuted accuracy maps and each searchlight location was assigned a significance level based on the noise histogram for that location. This map was thresholded at a significance level of p = 0.005 for cluster analysis. The same threshold procedure was applied to every bootstrap accuracy map to compute significance levels based on chance cluster size. For each bootstrap sample, the number and size of each cluster (defined by six-face connectivity) surviving the threshold procedure (p < 0.005) was computed, and the number of clusters of each size was computed. These were then aggregated across bootstrap samples to form a normalized histogram of cluster sizes obtained by chance. Cluster significance levels were based on cluster extent, determined by the following formula:

where H_cluster is the normalized cluster-size histogram and s^′ is the number of significant voxels in the cluster. These p values were then corrected by applying a step-up FDR procedure (Benjamini and Hochberg, 1995; q = 0.05). Clusters in the original group accuracy map and their significance were then computed according to their size to determine cluster significance.

Univariate (GLM) procedures.

For comparison, we conducted a univariate analysis, using FSL [Functional MRI of the Brain (FMRIB) Software Library, http://fsl.fmrib.ox.ac.uk/fsl/], although the design of our study was not optimized for such a procedure. For this analysis, fMRI data were subjected to additional preprocessing steps. In addition to slice-time correction and motion correction, a high-pass temporal filter (50 s cutoff) was applied, and data were smoothed with a 5 mm FWHM Gaussian kernel before analysis.

A first-level GLM was constructed for each run, modeling four conditions: wins and losses were independently modeled, split by whether the subsequent trial was against the same or different opponent (win→same, win→different, loss→same, loss→different). To roughly parallel MVPA procedures, the conditions were modeled using finite impulse response methods with separate 2 s stick regressor for each condition and time point. Eight such regressors were employed, covering a span of 16 s beginning with the volume collected during outcome display. At the first level, prewhitening was applied and the same temporal filtering applied to the data were also applied to the regressors. Simple contrasts were constructed for each time point and condition for aggregation at the subject level. Functional images were registered to the high-resolution structural image, which was in turn registered to a standard MNI image (2 × 2 × 2 mm resolution). Second-level, fixed-effects GLM analyses combined data across runs, separately for each subject, first converting each first-level contrast to standard space. The same 45 ROIs employed in MVPA were converted to each subject's standard space, and the time course of activity associated with each condition within each ROI was extracted from the subjects' second-level GLM estimates by averaging estimates within each ROI. Finally, within each subject, ROI, and condition bin, we averaged together the three estimates corresponding to the time points employed in MVPA analysis (activity corresponding to the 2–8 s interval following onset of the subsequent trial's opponent cue).

To estimate differences in activity between win and loss trials that varied depending on the subsequent trial's opponent, we subtracted the activity in loss trials from that in win trials and conducted a paired t test within each ROI [(win|same − loss|same) vs (win|diff − loss|diff)], a test that is equivalent to the 2 × 2 F test of the interaction between outcome and opponent conditions.

Results

Dependence of choice on opponent cues

We regressed choices on prior four choices and the prior four choice × outcome interactions, following previous work (Lee et al., 2004; Vickery et al., 2011). In the single-opponent model, the regressors were not separated for the same and different opponents. In the dual-opponent model, separate regressors were used for same and different opponents, depending on the match between the current trial and the prior trial. The dual-opponent model was nested within the no-opponent model, since constraining the regression coefficients to be equal for the two opponent conditions would result in the single-opponent model. By the likelihood ratio test, the dual-opponent model was preferred over the single-opponent model (χ² = 720.0, df = 200, p < 0.001). The dual-opponent model was also associated with a lower Akaike information criterion value (20,869) than the single-opponent model (21,187). Likelihood per trial was 0.537 and 0.561 for the single-opponent and dual-opponent models, respectively. These values are relatively close to the chance level of 0.5 because the performance of the participants was close to the optimal strategy for the matching-pennies task.

We examined the regression coefficients for the dual-opponent model to examine how prior choices and outcomes differently influenced behavior depending on opponent type and trial lag (Fig. 1B,C). We submitted the coefficients corresponding to the prior four trials' choice × outcome interactions (Fig. 1B) to a repeated-measures ANOVA, which revealed a significant interaction between opponent and lag (F_(3,78) = 10.8, p < 0.001) and significant main effects of opponent (F_(1,26) = 17.6, p < 0.001) and lag (F_(3,78) = 5.9, p = 0.001). The greatest differences between same-opponent and different-opponent coefficients were evident in the influence of the one-back and two-back choice × outcome interactions. According to post hoc contrasts, while the mean coefficients for different-opponent coefficients did not significantly differ from zero across participants, the same-opponent coefficients were strongly positive overall (both p < 0.001, one-sample t test vs 0) and significantly higher than the different-opponent coefficients (both p < 0.001, paired t tests). These results indicate that participants' choices were influenced by the outcomes of previous choices differently according to the identity of opponent encountered in multiple preceding trials.

Regression coefficients corresponding to prior choices also revealed switching behavior that was numerically enhanced by changing opponents. A repeated-measures ANOVA applied to the eight coefficients corresponding to four prior choices split by opponent (Fig. 1C) revealed a main effect of lag (F_(3,78) = 9.1, p < 0.001) and opponent identity (F_(1,26) = 5.7, p = 0.024), but the interaction only neared significance (F_(3,78) = 2.4, p = 0.073). Regression coefficients corresponding to the last three different-opponent choices were significantly below zero, although only the lag 1 influence was significantly more negative for different opponent than for same opponent (uncorrected p = 0.02).

Choices of participants were influenced by prior choice × outcome interactions against the same opponent, even those occurring >1 trial ago. To determine whether this dependence lasted across intervening trials against a different opponent, we conducted a separate logistic regression analysis. The modeled choices were restricted to those choices on which the immediate prior choice was played against the different opponent. The regressors were choice and choice × outcome interactions from the most recent trial played against the same opponent. The regression coefficient for the choice × outcome interaction was significantly >0 across participants (mean, 0.21; SD = 0.26, t₍₂₄₎ = 4.06, p < 0.001), implying that participants were playing win–stay, lose–switch with respect to temporally remote trials against the current opponent. Dependence on the choice term was not significantly different from zero across participants. Thus, players' actions were determined by the identity of the opponent encountered in multiple preceding trials, suggesting that information about previous choices and outcomes can be stored and retrieved subsequently according to the opponent identity in the current trial.

Effects of opponent identity on neural reinforcement signals

We first examined the persistence of BOLD reward signals from trial N during the period following the introduction of the opponent cue for trial N + 1. Focusing on same-opponent trials, SVM classifiers were trained and tested on the three-volume average following the next trial's opponent cue. This procedure was conducted for 45 bilateral ROIs. Despite potential noise introduced by the intervening opponent cue, wins versus losses were widely decoded throughout the brain, replicating our prior results (Vickery et al., 2011). Forty-two of 45 ROIs yielded significant win versus loss decoding results (FDR-corrected, q = 0.05, one-sided permutation/bootstrap test). The only regions without significant outcome decoding were the rectus, frontal midorbital, and Rolandic operculum regions.

Next, we examined how outcome signals varied according to opponent identity. Whereas 42 of 45 ROIs showed significant win versus loss decoding for same-opponent trials, only 30 of the 45 regions showed significant decoding for different-opponent trials (both tests independently FDR-corrected, q = 0.05, one-sided permutation/bootstrap test). This difference was significant (χ² = 10.0, p = 0.002, df = 1). Decoding accuracies for same-opponent and different-opponent trials were directly compared by submitting the results for 45 ROIs to an omnibus repeated-measures ANOVA, with two factors (ROI and opponent type). The dependent variable was performance of the classifier within each ROI and condition as measured by binomial Z-score. This test showed a significant main effect of opponent identity (F_(1,24) = 5.88, p = 0.023, partial η² = 0. 20), with better decoding performance in same-opponent (accuracy mean, 0.56) than in different-opponent (mean, 0.53) trials. There was also a main effect of ROI (F_(44,1056) = 2.23, p < 0.001, partial η² = 0.09), reflecting variability in overall decoding accuracy across ROIs. The interaction of ROI and opponent identity was not significant (F_(44,1056) = 1.04, p = 0.39).

We further tested the effect of opponent identity on decoding performance in individual ROIs. We computed a difference in the decoding accuracy for each ROI, and compared it to bootstrapped difference scores based on permuted condition labels, constructing a noise histogram for this difference score within each ROI and computing the significance value of each ROI on the basis of that histogram. Finally, we applied FDR correction (q = 0.05) to these significance values. Two individual ROIs showed an effect that survived FDR correction (q = 0.05): the anterior cingulate and lingual regions. Both regions showed better decoding performance for same-opponent than different-opponent trials. At an uncorrected (p < 0.05) threshold, an additional 11 regions showed the same pattern: superior parietal, inferior parietal, midcingulate, amygdala, fusiform, cuneus, superior occipital, calcarine, precuneus, angular gyrus, and putamen. No region approached even uncorrected significance levels in the opposite direction.

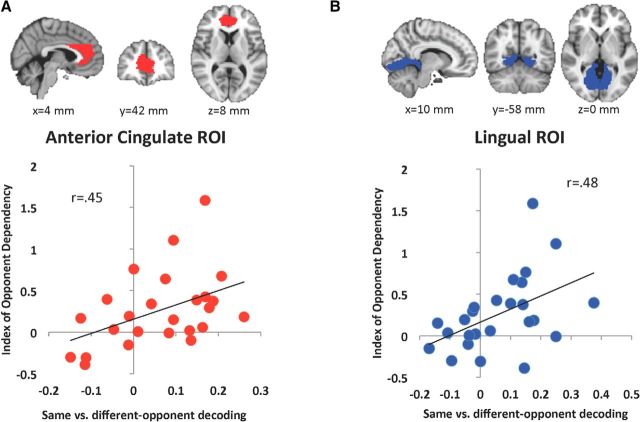
We next examined whether the individual variability in the magnitude of opponent-specific reinforcement signals was related to behavior. For each participant and ROI, we calculated a difference score for decoding accuracy in same-opponent versus different-opponent trials. We also calculated overall behavioral sensitivity to opponent identity (I_OD), which quantified how the reliance on the previous trial outcome depended on the opponent identity (see Materials and Methods). We correlated these two values across participants for the two ROIs that showed significant same > different win/loss decoding. Both correlations were significant (Fig. 2; ACC: r = 0.45, p = 0.024; lingual: r = 0.48, p = 0.016).

Figure 2.

A, B, Correlations between behavioral index of opponent dependency and same-opponent versus different-opponent win/loss decoding difference in ACC (A) and lingual (B) ROIs. ROIs are overlaid on the MNI standard brain.

Decoding of opponent switch, computer's choice, and congruency

Differential discriminability of reward signals for same-opponent and different-opponent trials could be due to other signal or noise differences related to opponent changes, regardless of reward encoding. To examine this possibility, we conducted two control analyses from the same interval and trials employed in the above analyses. First, we trained classifiers to distinguish same-opponent from different-opponent trials, collapsing across wins and losses. Second, we trained classifiers to distinguish the computer's choice (heads or tails, as indicated by the visual stimulus), and compared same-opponent with different-opponent trial outcomes.

Decoding of same versus different opponent trials was not significantly above chance in any ROI at an FDR-corrected q = 0.05 threshold. At an uncorrected threshold (p < 0.05), three regions were significantly above chance: superior frontal, the supplementary motor area, and precuneus. Notably, however, same versus different opponent decoding was not significantly above chance in either the anterior cingulate (mean, 0.508; uncorrected p = 0.29) or the lingual (mean, 0.507; uncorrected p = 0.31) ROIs that showed significant modulation of win/loss signals based on opponent identity.

Computer choice was also poorly decoded in every ROI, probably due to the more rapid decay of this information. No regions showed a significant ability to decode heads or tails in either same-opponent or different-opponent trials from this interval when corrected for multiple comparisons. Neither was the difference in decoding ability between same-opponent and different-opponent trials significant in any region. Focusing on visual regions, however, the strongest same-opponent classification accuracy arose within inferior occipital cortex (mean, 0.54; uncorrected p = 0.008). The same regions decoded heads versus tails above chance on different-opponent trials, as well (mean, 0.53; uncorrected p = 0.02). The difference was not significant (p = 0.41).

Both of these findings suggest that opponent-dependent reinforcement signals were not merely due to general effect of the opponent cue adding noise to decoding on different-opponent trials. There was no apparent effect of the opponent cue on decoding the recent visual stimulus representing the computer's choice. The status of the opponent cue (same vs different) was also very poorly decoded throughout the brain, including the two regions that showed significant modulation of outcome decoding by the changes in opponent identity.

An additional possible explanation for better reward decoding following same-opponent versus different-opponent cues is competition between representations of the most recent reward received with the reward expectancy from the opponent cue itself. For instance, when an opponent is repeated following a win, the expectancy of reward associated with the opponent is more consistent with the recent outcome, whereas if the opponent were changed, the most recent outcome would be unrelated to the recent history of outcomes associated with the next opponent. To examine this possibility, we focused on different-opponent trials, and split these trials into congruent and incongruent types, according to the immediate prior reward and the most recent experience with the next opponent. To balance this new congruency dimensions in the dataset, we excluded the identity of the prior opponent as a balancing factor, to obtain a sufficient number of trials necessary for MVPA analyses. We then trained and tested, as above, win versus loss decoding for congruent and incongruent different-opponent trials, independently. If the reduced decoding accuracy for different-opponent trials resulted from inconsistency in two different outcome signals, the decoding accuracy would be higher in congruent trials.

No region showed significantly better decoding of win/loss on congruent versus incongruent trials, when corrected for multiple comparisons. Critically, neither anterior cingulate nor the lingual region showed a trend in this direction (both uncorrected p > 0.1). However, eight other regions showed a trend in this direction according to uncorrected significance values (all p < 0.05, uncorrected). Additionally, 21 regions showed significant (FDR-corrected p < 0.05) win/loss decoding ability under congruent conditions, whereas no regions showed significant win/loss decoding ability under incongruent conditions. Thus, congruency between rewarding outcomes and prior reward associations with the opponent cue may play some role, but the evidence in favor of this is relatively weak in our dataset, especially within ROIs that showed maximal same-opponent versus different-opponent decoding differences.

An additional counter-explanation for the apparent opponent dependency of reward signals is that the expected value of a different-opponent cue may systematically differ from that of the same-opponent cue. In particular, the same-opponent cue may be expected to have a higher expected value following a win than a loss, whereas the different-opponent cue may show reduced or no difference between the immediately preceding win and loss. Thus, the classifier might incidentally decode the expected value of the subsequent cue. We conducted a series of behavioral analyses to test whether this confound was a viable explanation for opponent-dependent reinforcement signals.

First, we examined the conditional dependence of winning and losing based on opponent (the following statistics were calculated for scanning runs only, but all major patterns held true regardless of whether or not we included practice runs). The probability of winning any trial that shared the same opponent as the prior trial was the same as for trials that did not share the same opponent, 0.50, and did not differ significantly (t₍₂₄₎ = 1.10, p = 0.28). We further divided these trials based on whether the prior trial was a win or a loss. All four probabilities were equal to 0.50 when rounded to two significant digits, and when entered into an ANOVA we found that there were no significant main effects of either prior trial outcome (F_(1,24) = 0.38, p = 0.55) or opponent (F_(1,24) = 1.21, p = 0.28), and there was no significant interaction (F_(1,24) = 0.52, p = 0.48).

Second, we examined whether expected values might differ across these types of trials. Using our logistic regression models fitted to each individuals' data, we calculated P(heads) and P(tails) from the model for each trial, and took those values as a proxy for the expected value of each choice. Then, we calculated the expected value of each choice as a function of whether the prior trial was played against the same opponent or different opponent, and whether the prior trial was a win or a loss. We entered these values into a 2 × 2 ANOVA. If expected value of the opponent cue in the upcoming trial is incidentally decoded as the previous outcome, then we would expect to see an interaction of the cue's expected value based on opponent and reward. Only the main effect of opponent was significant (F_(1,24) = 6.35, p = 0.02), with participants choosing higher-value choices more frequently for trials following plays against the same opponent than those following plays against the different opponent, but showing no main effect of reward (F_(1,24) = 1.82, p = 0.19), nor a significant interaction (F_(1,24) = 2.48, p = 0.12). Thus, differences in expected value of the subsequent opponent cue were unlikely to account for higher decoding accuracy of wins and losses for same-opponent vs different-opponent trials.

Searchlight analysis

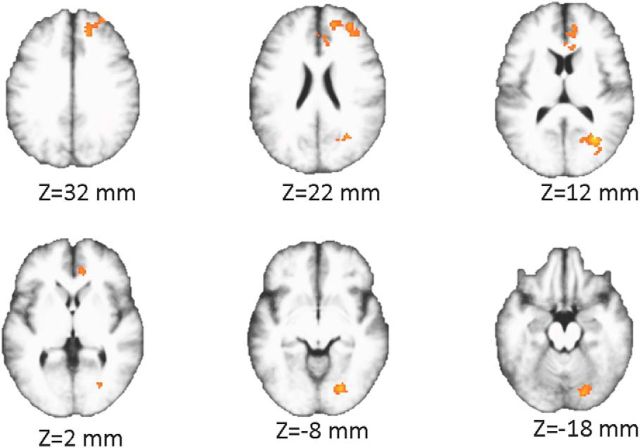
To supplement our ROI-based analysis, and to gain greater spatial specificity, we conducted two searchlight analyses of win/loss decoding in same-opponent and different-opponent trials. First, we conducted a whole-brain searchlight analysis with cluster correction. Using the permutation/bootstrap and cluster-correction method described in Materials and Methods (Stelzer et al., 2013), we derived cluster-corrected significance maps for both the same-opponent and different-opponent win/loss decoding. The result for the same-opponent classification analysis was a single massive cluster spanning 95,132 voxels (34% of all voxels within a brain mask) covering a diverse spectrum of brain regions in every lobe of the brain. The result for the different-opponent classification analysis was also one massive cluster, but one that extended across a reduced extent of 24,553 voxels (9% of brain-mask voxels).

We conducted a similar procedure for comparing same-opponent versus different-opponent win/loss decoding. First, we computed an average difference map for win/loss classification across same-opponent and different-opponent trials. Then, we masked this map by all regions in which either the same-opponent or different-opponent maps exceeded chance with a significance level of p ≤ 0.005. We applied the same procedure to all 10⁵ bootstrap samples to form a histogram of accuracy differences for each searchlight center, and thresholded all of these maps at p < 0.005. We then constructed a normalized cluster size histogram, FDR-corrected (q = 0.05) these p values, and computed the cluster-wise significance in the original accuracy difference map.

This procedure resulted in two significant clusters (Fig. 3). One cluster was located primarily in the right frontal lobe and extended across right rostral anterior cingulate and into the superior frontal cortex. The second cluster was located primarily in right lingual gyrus but also extended partially into cuneus, precuneus, and the inferior parietal lobe.

Figure 3.

Whole-brain searchlight results. Two clusters survived thresholding (p < 0.005) and cluster correction (q = 0.05). Right is shown as right in the figure.

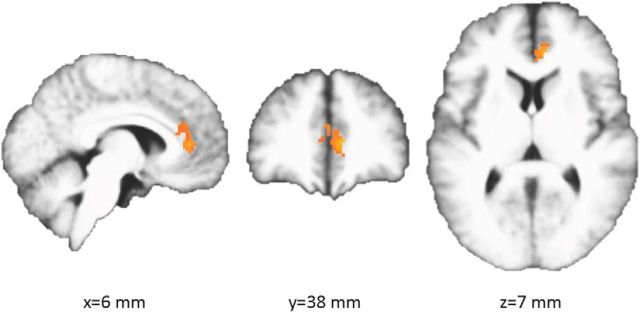
Second, to better understand the spatial specificity of the opponent specificity in the ACC ROI, we conducted a second follow-up analysis using a voxelwise FDR correction rather than a cluster correction, since a cluster-wise correction leaves ambiguity about the spatial locus of peak differences within significant clusters. For this test we constrained ourselves to the ACC ROI, because of the strict nature of voxelwise correction.

We calculated p values based on the bootstrapped noise distributions of same-opponent versus different-opponent difference in win/loss decoding accuracy for each searchlight centered in the ACC ROI. We then corrected for multiple comparisons using a voxelwise FDR correction. This revealed a set of 125 voxels passing this threshold, largely in right, rostral ACC (Fig. 4; peak MNI coordinates: X = 8, Y = 39, Z = 7), implying that the ROI-based results in ACC were primarily driven by this subset of voxels.

Figure 4.

Significant searchlight centers in ACC (q = 0.05, voxelwise small-volume correction), displayed on average of normalized subjects' brains.

Univariate ROI analysis

Results of a GLM analysis showed greater activity in response to wins than losses in a broad set of regions, averaged over the time points employed for MVPA analysis. A paired t test of the difference between wins and losses survived FDR correction in 28 of 45 regions, all of which showed greater mean activity in response to wins than losses. However, when the difference in activity for win and loss trials was contrasted between same-opponent and different-opponent trials, no region survived FDR correction. At an uncorrected threshold (p < 0.05), four regions showed significantly greater win than loss activity under same-opponent than different-opponent trials: medial frontal orbital, paracentral lobule, middle temporal pole, and superior temporal.

Discussion

Participants in the present study strongly relied on the history of reinforcement to make decisions in games, but only that portion of the history associated with the current opponent. These results demonstrate that humans can multiplex reinforcement histories threaded by contexts, such as opponent identities. Neural reinforcement signals were also modulated by context. In particular, accuracy of decoding outcomes from BOLD activity was significantly greater for right ACC and right lingual regions when the opponents stayed the same than when they switched. Moreover, across participants, the strength of opponent-specific modulation of reinforcement signals in these regions was correlated with the degree of behavioral dependence on opponent cues. These results support an important role for the right rostral ACC and right lingual regions in contextualizing the neural signals related to reinforcement.

Context-dependent modulation of reinforcement signals

Learning to choose based on probabilistic feedback might rely on the activity of a network of prefrontal, striatal, and perhaps parietal regions that encode reward values associated with actions (Daw and Doya, 2006; Kable and Glimcher, 2009; Lee et al., 2012). While widespread activity changes are detectable in response to wins and losses (Vickery et al., 2011), several brain regions exhibit signals that are tightly linked to specific aspects of reinforcement learning. For example, positive or negative outcomes can cause sustained neural activity in some regions, and such signals are related to future performance (Histed et al., 2009; Curtis and Lee, 2010). In addition, the dorsomedial prefrontal cortex might contribute to maintaining the balance between exploration and exploitation (Donahue et al., 2013) and switching away from a simple model-free reinforcement learning during competitive games (Seo et al., 2014).

All stimulus–reward or stimulus–response learning is, in a sense, contextual. The stimulus serves as the context, with different actions having different value depending upon the stimulus identity. It is also known that simple stimulus–reward learning results in generalization (Frank et al., 2004), thus stimulus–reward learning is not strictly confined to particular contexts. In contrast to prior work, this study examined dynamic learning of choice values, where those values varied only according to a simple contextual cue, and in which there was overall no advantage to either option. Further, the particulars of our design enabled us to focus upon the fate of sustained reinforcement signals following the presentation of contextual cues.

Recent work suggests that reinforcement signals are tailored to the specific demands of the learning environment. For instance, multiple value signals can be maintained in parallel for separate effectors (Gershman et al., 2009). Additionally, separable prediction error signals associated with multiple levels of a decision-making hierarchy have been observed (Daw et al., 2011; Diuk et al., 2013). Our study uniquely examines the effect of context on persisting reinforcement signals.

Consistent with the findings from these studies, we found reinforcement signals sustained in many brain areas for a period of time after each outcome, while opponent cues signaled the transition to a new state or maintenance of the prior state. If reinforcement signals are actively maintained in working memory to influence future choice, activity related to win versus loss outcomes might decay differently depending on the identity of the opponent cue. Indeed, reward-related signals attenuated faster when a different opponent was cued. The fact that this difference in the time course of reinforcement signals was related to the opponent specificity of behavioral adjustment suggests that persistent reward signals did not merely reflect passive decay of BOLD signals. Instead, more persistent activity observed in the same-opponent trials for some cortical areas might reflect the maintenance and amplification of reinforcement signals as they become incorporated into upcoming action selection. Although reinforcement signals were attenuated in these brain areas during different-opponent trials, our behavioral results also indicate that this information was not completely lost, since future choices were still dependent on the outcomes of the choices against the same opponent even after encountering another opponent. Future studies are needed to determine how information about the outcomes from previous interactions with the same opponent can be retrieved during the subsequent interaction with the same opponent.

Implication for cortical network for theory of mind

The essence of social decision making is the interdependence of choices made by multiple agents. Namely, the outcome of one's choice is determined jointly by the choices of multiple group members. Accordingly, knowledge and reasoning about other agents is an essential component of social decision making. The current findings are not necessarily constrained to the social domain; replacing faces in our study with nonsocial symbolic contextual cues might also lead to similar effects. Namely, the lack of a nonsocial condition in our experiment prevents us from inferring that our results genuinely depend on the social nature of our task. However, it is worth considering our findings in the context of prior findings of social decision making, given the strong role of agent context in that domain.

Even though our study did not manipulate the social nature of context, the current findings are consistent with prior evidence that the mPFC, including the ACC region reported in our study, supports a broad range of functions related to reasoning about other agents, and further suggests that the mPFC integrates signals related to agency with representations of actions and value (Behrens et al., 2009; Seo et al., 2014). When participants reason about the mental states of others, increased activation has consistently been observed in mPFC, posterior superior temporal sulcus, temporoparietal junction (TPJ), and posterior cingulate cortex (PCC; Gallagher and Frith, 2003; Amodio and Frith, 2006). Previous studies have suggested that a broad range of social reasoning tasks evoke activity in mPFC (Amodio and Frith, 2006), including person perception, while TPJ and PCC might show more specific responses to reasoning about the thoughts of others (Saxe and Powell, 2006). Activity in the regions related to theory of mind (ToM) has been further linked to the perceived agency of other decision makers and the complexity of reasoning about other agents during games. For instance, mPFC activity is greater during competitive (Gallagher et al., 2002; Boorman et al., 2013) and cooperative (McCabe et al., 2001; Hampton et al., 2008) games when partners are perceived to have agency than otherwise. Activity in the mPFC of monkeys also signals the disengagement from the use of a default model-free reinforcement learning algorithm during a simulated matching-pennies task (Seo et al., 2014). These results suggest that mPFC activity reflects explicit mentalizing during strategic reasoning.

In addition to its role in social cognition, mPFC activity is also often related to value-related computations (Daw et al., 2011). Further, mPFC carries value signals specifically related to belief-based value learning (Burke et al., 2010; Zhu et al., 2012), and associative learning of the reliability of social signals (Behrens et al., 2008). Connecting the reward-processing and social aspects of decision making, expected value signals in mPFC during a game are best explained by incorporating ToM constructs (Hampton et al., 2008; Watanabe et al., 2014). Further, a task that evokes mentalizing produces activity in mPFC that models an opponent's reward prediction errors (Suzuki et al., 2012). This suggests that ToM mechanisms may play some role in mPFC value representation. However, only one opponent was involved in this prior work, and thus opponent-dependent threading of reinforcement signals could not be observed. The current results link reinforcement signals in mPFC to representations of opponent identities. The mPFC, responsive to both value and agency, is a strong candidate as a region responsible for the integration of value representations with social reasoning.

This study also uncovered opponent-dependent reinforcement signals in lingual gyrus. Reward-related activity in this region was previously observed (Delgado et al., 2003; Elliott et al., 2003), but was dismissed as likely due to visual differences (Tricomi et al., 2004). Visual confounds cannot explain reward decoding in the present study since visual cues did not predict reward. Further investigation into the role of this region in decision making may be warranted.

In our study, TPJ and STS both carried reinforcement signals, but these were not contingent upon opponent identity. These regions might still be involved in reward-independent reasoning about other agents, a mechanism that may not have been evoked by our game task. This is supported by previous observations of signals in these areas related to whether opponents lie or tell the truth (Behrens et al., 2008), and by the correlation of STS activity with inferences about the influence of one's own actions on another player's actions (Hampton et al., 2008).

An important limitation of the current paper is that only a social task was employed. An avenue for further development is to investigate how context specificity in reinforcement signals may or may not differ between social and nonsocial tasks. An additional limitation is that the absence of jitter in this study prevented us from fully separating cue and outcome activity.

Overall, our results support evidence that mPFC plays an important role in representing context-specific reward signals during decision making. The mPFC may serve a vital role in integrating reinforcement signals with context signals to support value-based decision making.