Payoff Information Biases a Fast Guess Process in Perceptual Decision Making under Deadline Pressure: Evidence from Behavior, Evoked Potentials, and Quantitative Model Comparison

Abstract

We used electroencephalography (EEG) and behavior to examine the role of payoff bias in a difficult two-alternative perceptual decision under deadline pressure in humans. The findings suggest that a fast guess process, biased by payoff and triggered by stimulus onset, occurred on a subset of trials and raced with an evidence accumulation process informed by stimulus information. On each trial, the participant judged whether a rectangle was shifted to the right or left and responded by squeezing a right- or left-hand dynamometer. The payoff for each alternative (which could be biased or unbiased) was signaled 1.5 s before stimulus onset. The choice response was assigned to the first hand reaching a squeeze force criterion and reaction time was defined as time to criterion. Consistent with a fast guess account, fast responses were strongly biased toward the higher-paying alternative and the EEG exhibited an abrupt rise in the lateralized readiness potential (LRP) on a subset of biased payoff trials contralateral to the higher-paying alternative ∼150 ms after stimulus onset and 50 ms before stimulus information influenced the LRP. This rise was associated with poststimulus dynamometer activity favoring the higher-paying alternative and predicted choice and response time. Quantitative modeling supported the fast guess account over accounts of payoff effects supported in other studies. Our findings, taken with previous studies, support the idea that payoff and prior probability manipulations produce flexible adaptations to task structure and do not reflect a fixed policy for the integration of payoff and stimulus information.

SIGNIFICANCE STATEMENT Humans and other animals often face situations in which they must make choices based on uncertain sensory information together with information about expected outcomes (gains or losses) about each choice. We investigated how differences in payoffs between available alternatives affect neural activity, overt choice, and the timing of choice responses. In our experiment, in which participants were under strong time pressure, neural and behavioral findings together with model fitting suggested that our human participants often made a fast guess toward the higher reward rather than integrating stimulus and payoff information. Our findings, taken with findings from other studies, support the idea that payoff and prior probability manipulations produce flexible adaptations to task structure and do not reflect a fixed policy.

Introduction

Decision makers facing difficult perceptual decisions bias choices toward higher-paying alternatives (Diederich and Busemeyer, 2006; Diederich, 2008; Feng et al., 2009; Gao et al., 2011, Simen et al., 2009), sometimes approximating the optimal degree of bias. The neural mechanism underlying this effect has been explored with electrophysiology in monkeys (Leon and Shadlen, 1999; Platt and Glimcher, 1999; Rorie et al., 2010). These studies explore whether payoff information shifts the starting point of a putative evidence accumulation process (Laming, 1968; Gold and Shadlen, 2007) or increases the accumulation rate of evidence toward the higher-paying alternative. Most behavioral and electrophysiological experiments have thus far supported the starting point hypothesis (Simen et al., 2009; Rorie et al., 2010; Gao et al., 2011; Leite and Ratcliff, 2011; Mulder et al., 2012; Rao et al., 2012) or a variant in which payoff information is accumulated in a first stage and stimulus information is accumulated later (Diederich and Busemeyer, 2006; Diederich, 2008).

Here, we build on this previous work to investigate the neural basis of payoff effects on perceptual decisions in humans. We use electroencephalography (EEG) to further test the starting point hypothesis and to characterize the buildup of the effect on the starting point, if present. For this purpose, we investigated the time course of the payoff effect in the period before stimulus onset and in the poststimulus period. We focus on the lateralized readiness potential (LRP), an event-related brain potential thought to reflect a relative increase in neural activity contralateral to the responding hand (Kornhuber and Deecke, 1965; Vaughan et al., 1967) that may occur before overt responding (Miller et al., 1998; Scheibe et al., 2009). Although it is downstream from other decision areas, influences on the decision state may, in some conditions at least, flow continuously to the motor areas thought to generate the LRP (Gratton et al., 1988; but see Scheibe et al., 2009); payoff bias could also potentially affect motor preparation directly and unmediated by perceptual processes. We also record motor activity on dynamometers used as response sensors, allowing us to observe a tight association between LRP and motor activity that sometimes occurs in one or both hands before the participant's squeeze force reaches a criterion value.

Our results favor an alternative to the idea that payoff bias affects either the starting point or the rate of an evidence accumulation process. Response time, LRP, and dynamometer data instead support the idea that payoff bias affected a fast guess process that occurs on a subset of trials; a similar effect was previously found by Simen et al. (2009). A model based on this idea provides a better fit to our behavioral findings than the starting point and accumulation rate accounts. In the discussion, we suggest that the effects of payoff and stimulus probability may not be fixed characteristics of decision making; instead, they may reflect flexible adaptation to the constraints imposed by the task.

Materials and Methods

Design

Participants viewed a rectangular stimulus that was shifted 2 or 5 pixels either to the left or right of a central cross and were instructed to indicate the side of the shift before a deadline. Payoff information was presented on each trial before stimulus onset and was higher on the left, higher on the right, or equal on both sides. Payoff contingency varied randomly from trial to trial. In the biased payoff conditions, on half of the trials, the higher payoff was assigned to the side of the stimulus shift (congruent trials); on the other half, it was assigned to the direction opposite of the stimulus shift (incongruent trials). The payoff cue was uncorrelated with the direction of the stimulus and only indicated the amount of reward that could be obtained when the stimulus was in fact shifted in a given direction.

Participants

Twenty subjects participated in our experiment in exchange for payment; four participants dropped out of the study in the training phase due to various personal reasons and three participants were let go by the experimenter after not meeting the inclusion criteria for the EEG phase of the study (see “Training”). The remaining 13 subjects (3 females, 10 males; right-handed, mean age 22.46 years, range 19–30) participated in the EEG phase of the study after completing the training phase. All had normal or corrected-to-normal hearing and vision and satisfied inclusion criteria applied to their performance (see “Training”). Written informed consent, as approved by the Institutional Review Board of Stanford University, was obtained from all participants. The participants received a base pay ($5 initially for the training phase) per experimental session, plus the amount of money they earned during each session ($0.01 per point). Base pay was increased across the training phase of the study according to the participant's performance (see “Training”). For the EEG sessions, an additional $15 was added to the participant's base pay to compensate for the additional setup time. Each participant was involved in the experiment for 7–12 training sessions and 6 EEG sessions (25.5–33 h).

Stimuli and procedures

Visual stimuli were displayed on a Dell LCD monitor (1280 × 1024 resolution, 33.79 cm × 27.03 cm, 60 Hz) located 80 cm in front of the participant. Stimulus presentation and acquisition of behavioral responses were done using the Psychophysics Toolbox for MATLAB (Brainard, 1997). All stimuli were light gray on a darker gray background. Participants responded by squeezing one of two grip-strength sensors with their left or right hand (see “Overt response measurement”).

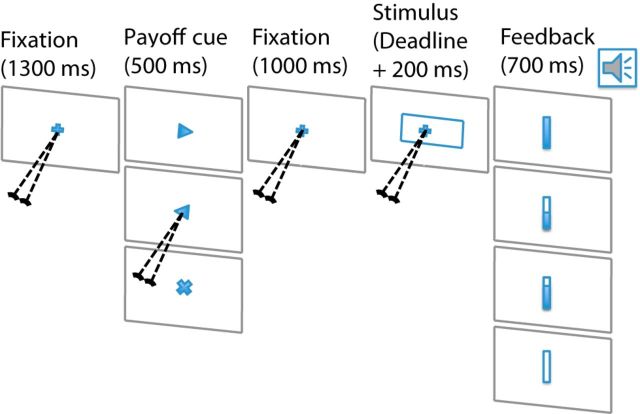
Each participant took part in seven to twelve behavioral training sessions and six EEG sessions. Each training session included six blocks of 120 trials (total of 720 trials/session) and each EEG session contained six blocks of 160 trials (total of 960 trials/session). Figure 1 illustrates the sequence of events in a typical trial (left to right). Trials began with the appearance of a fixation cross (0.19 × 0.19°²) for 1300 ms. Next, the pay-off cue appeared on the screen for 500 ms. For the biased payoff condition, this cue was a small arrow (0.30° horizontal) pointing either left or right, indicating which of the two responses, if correct, would lead to a 4-point reward as opposed to a two-point reward for the other alternative. For the neutral payoff condition, the payoff cue was a small × (0.23° horizontal), indicating equal payoff of 3 points for the two alternatives. Then, the fixation cross reappeared for 1000 ms and was followed by addition of the rectangular stimulus (300 × 100 pixels²; 5.67 × 1.89°²). The rectangular stimulus was shifted to the left or right of the screen center by 2 or 5 pixels (corresponding to 0.08 or 0.18 degrees of visual angle, respectively). Participants were asked to judge the direction of the horizontal shift and indicate their choice (left/right) by squeezing the left or right dynamometer.

Figure 1.

Perceptual decision task. On each trial, the participant viewed a rectangular stimulus and responded indicating the direction of horizontal shift (left or right) of its center relative to fixation. Each trial began with a fixation point, followed by a cue indicating whether the reward for a correct response would be biased (2/3 of trials, 4 points to 2, favoring either the right or the left response) or neutral (1/3 of trials; 3 points for both responses). After a second fixation period, the stimulus appeared, with the direction of shift determined randomly so that, on biased trials, it could be congruent or incongruent with the larger reward with equal probability. Participants were required to respond indicating their decision about the direction of shift before an individually determined deadline by squeezing the dynamometer held in the hand corresponding to their choice. Reaction time was measured as the elapsed time from stimulus onset to the time the participant's squeeze force met a criterion value. The difficulty of the task was determined by the amount of horizontal shift, either 2 or 5 pixels, of the rectangular stimulus. Difficulty, direction of shift, and payoff condition were all randomly assigned independently for each trial.

Participants were to respond within an assigned deadline (range: 375–475 ms depending on the participant's performance) after the onset of the rectangular stimulus. Responses were further monitored for an additional 200 ms after the deadline, at the end of which visual and auditory feedback was delivered. Feedback indicated whether the response occurred within the assigned deadline and, if so, whether it was correct. If participants responded correctly within their assigned deadline, they heard a cash register sound and earned either 2 or 4 points in the biased payoff condition or 3 points in the neutral payoff condition. Table 1 shows the payoff scheme for stimulus–response contingencies when the left alternative is the higher-paying one. Incorrect responses earned no points and were followed by an error auditory feedback. Responses that occurred too early (before stimulus onset) or too late also received no points and were followed by a different sound. The total time for feedback of any type was 700 ms.

Table 1.

Stimulus-response contingencies when the payoff cue points to the left

	Response
	Leftward	Rightward
Stimulus
Leftward	+$0.04	$0.00
Rightward	$0.00	+$0.02

Response measurement: continuous dynamometer activity and discrete choice and response time

To make a response, participants squeezed strain-gauge based isometric hand dynamometers (HD-BTA; Vernier Software and Technology) following established practice in LRP studies (Gratton et al., 1988). The dynamometer sensor amplified the force applied converting it into a voltage that was monitored by the Vernier LabPro interface and read in units of force (Newtons). This signal was digitized at 1 sample per ∼2.358 ms and provided a continuous measure of the force output of each hand. A MATLAB interface continuously read and recorded the force level and, when it reached an assigned criterion (see below), the occurrence of an overt “criterion” response was recorded and reaction time (RT) was assigned. The force measurement for each hand from the onset of the payoff cue until the criterion was reached was saved as a continuous measure of motor activity during each trial.

At the beginning of the first training session, the value of each participant's maximum squeeze force was measured separately for each hand. As in previous studies (Gratton et al., 1988), criterion values for each participant were set at 25% of the maximum force applied by that participant for that hand. Participants went through 20 practice trials in their first training session to ensure that they were comfortable with their assigned thresholds and an adjustment was made if necessary. In all subsequent sessions, this force criterion was used to determine the identity and RT of the overt choice response. The choice was assigned to the dynamometer in which the activity first reached this threshold and the RT was defined as the latency at which this criterion was crossed.

Training

All participants underwent a training phase comprised of 7–12 1.5-h-long behavioral sessions over several weeks before entering the EEG phase of the study. In the first training session, participants only received the neutral payoff condition to get better acquainted with the horizontal shift detection task under time pressure. The instructions explicitly encouraged participants to make fast responses: “Earn as many points as you can.” “Respond as fast as you can.” “Guessing is better than not responding at all.” “No points for late responses.”

In the second training session, participants were introduced to the unequal payoff condition and were encouraged to incorporate both stimulus and payoff information when making their decisions. We took several steps to ensure that participants would take payoff information into account because we found in pilot testing that participants did not always do so. Specifically, we observed that some participants were better at the task and met the initial deadline of 475 ms on almost all trials. These participants showed little or no sensitivity to the payoff information, making decisions based almost exclusively on the stimulus information alone; a similar tendency of some participants to disregard payoff information was also reported in earlier studies using a deadline (Diederich and Busemeyer, 2006; Diederich, 2008). Reliance on the payoff information may be of marginal utility to participants unless they are under fairly extreme time pressure because, with prolonged exposure to the stimulus, it may be possible to respond correctly on nearly all trials or at least on the half of trials involving a 5-pixel stimulus offset (easy trials). To enforce time pressure on all of our participants, we adjusted their deadlines starting in the third session of training by giving them a monetary incentive for performing quickly. According to the second session's performance, if a participant either met the initial deadline in >96% of the trials or met the initial deadline on >92% of the trials but did not exhibit any sign of payoff bias, we decreased the deadline by 25 ms and increased the base pay by $2 in the third session. From the fourth session onward, we used the same deadline update strategy as before except we paid $1 as incentive. We also explicitly instructed participants to make use of the payoff information when the manipulation was first introduced in the second session and at the start of each subsequent session by stating: “Preparing in advance to choose the higher-paying alternative then adjusting to take the stimulus into account if you have time is a strategy that may help you earn a high reward.” Once participants showed stable behavior (choice pattern across RT) over three consecutive sessions, they entered the EEG phase of the study. For each participant, the deadline was kept constant across the EEG phase of the study, ranging from 375 to 475 ms across participants. Participants who did not show stable behavior after >10 sessions were terminated from the study (n = 3).

EEG recording

The EEG phase of the study was composed of 6 2.5-h-long sessions. The EEG was recorded from 13 Ag/AgCl electrodes using an electrode cap with a standard 10/20 system layout (EasyCap). Scalp electrodes were F3, Fz, F4, C1, C3, Cz, C2, C4, P3, Pz, and P4. Electrodes were referenced to the Pz electrode online and were rereferenced to the average of the left and right mastoids offline. Bipolar vertical and horizontal electro-oculogram (EOG) activity was recorded by means of electrodes above and below the left eye and on the outer canthi of each eye. Electrode impedance was kept at <5 kΩ for the scalp electrodes and at <15 kΩ for the vertical and horizontal EOG electrodes.

EEG signals were acquired at 1000 Hz and band-pass filtered online from 0.01 to 100 Hz. Offline, the EEG was again low-pass filtered at 35 Hz. Recording, digitization, filtering, and rereferencing were performed with a Neuroscan Labs amplifier (SynAmps 1) and SCAN 4.3 acquisition software. Epoching of the continuous EEG data was done using EEGLAB software (Delorme and Makeig, 2004) and the rest of offline analyses were done using in-house MATLAB scripts.

Analysis of choice and RT data

Choice and RT data were examined separately for the following conditions: (1) congruent: the payoff cue pointed in the same direction as the stimulus shift; (2) incongruent: the payoff cue pointed in the opposite direction of the stimulus shift; and (3) neutral: equal payoffs were assigned to the two alternatives.

The accuracy curves of each participant were calculated by dividing the trials into 25 ms RT bins in the 200–550 ms time range. The probability of a correct response was calculated separately for the two stimulus difficulty levels for each payoff condition in each bin. The average accuracy per RT bin was then computed across the participants who had at least 10 trials per payoff condition in that bin. Figure 4 shows the resulting grand-average accuracy curves after removing time points in which the averages were computed from <5 participants. The number of participants that contributed to each RT bin in Figure 4 was {10, 12, 13, 13, 13, 12, 11}. The mean number of trials that contributed to each data point is shown in the bottom panel.

Figure 4.

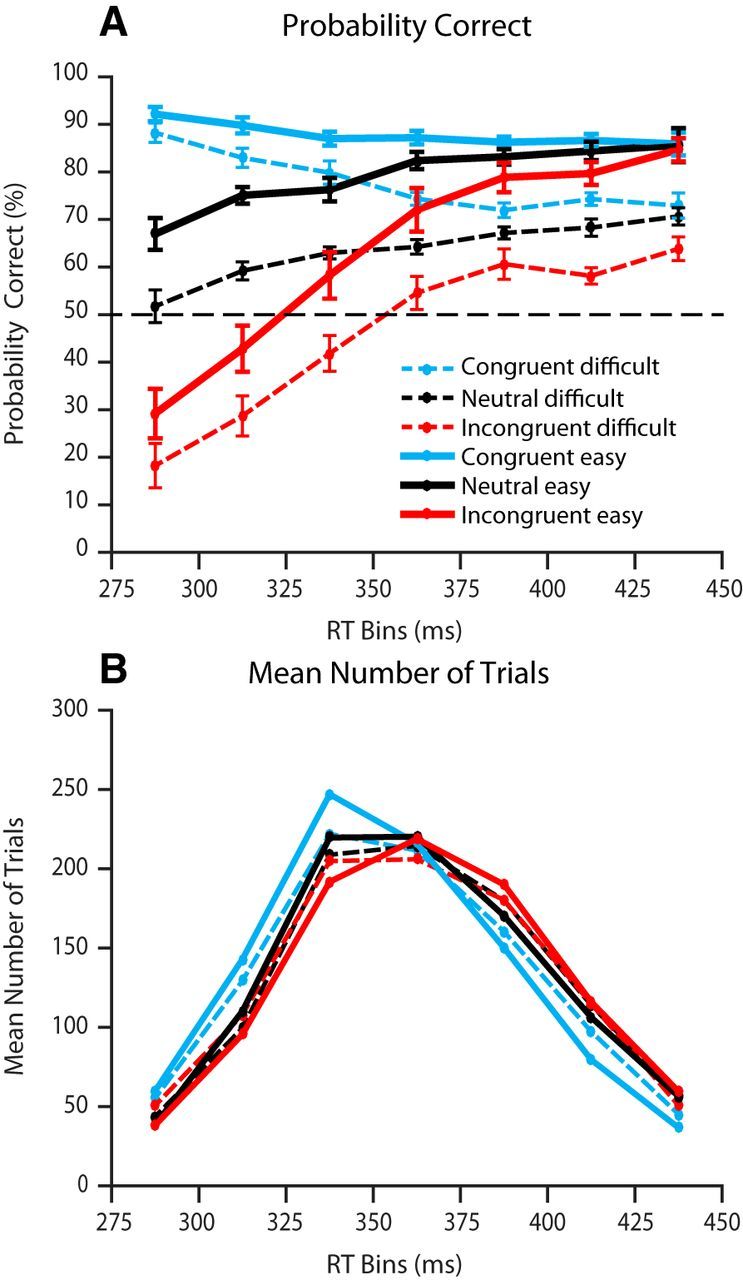
A, B, Probability correct (A) and mean number of trials (B) for each RT bin for neutral (black), congruent (blue), and incongruent (red) trials. Values on the x-axis correspond to the midpoint of each RT bin in milliseconds. Probability correct is higher for easy stimuli (5-pixel shift) compared with difficult stimuli (2-pixel shift). In the congruent and incongruent conditions, responses were more likely to be in the direction of the higher-paying alternative when participants made fast responses. This bias declined as RT increased. In the neutral condition (black), accuracy increased as RT increased. For the conditional accuracy, SEs are shown by the vertical bars.

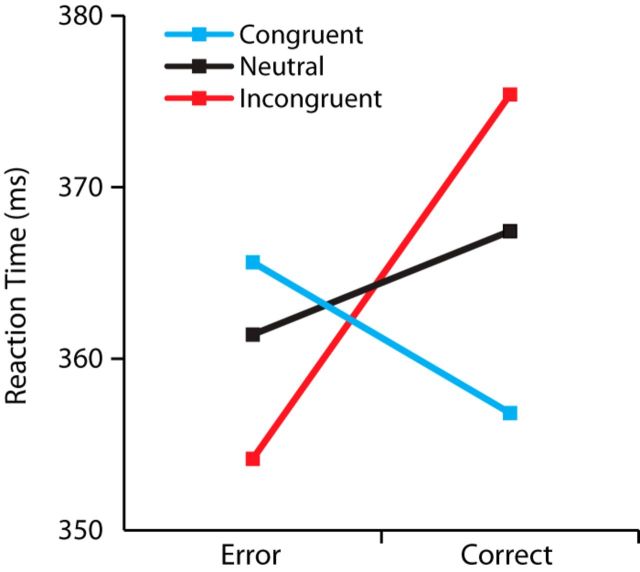
To test the effect of payoff condition on RT, we calculated the mean RT for correct and incorrect responses for the three payoff conditions (see Fig. 5). We analyzed the RT data by using a linear mixed-effects model. As fixed effects, we included categorical factors of payoff condition, response accuracy, and the interaction between payoff condition and response accuracy into the model. Payoff condition was coded as two contrast vectors: congruent versus neutral and incongruent versus neutral. Response accuracy was coded as correct versus incorrect. To account for between-subject RT variability, we used subjects as a random effect for both intercept and slope of the fixed effects excluding the interaction term. The model was analyzed using R (R Development Core Team, 2009) and the R packages lme4 (Bates et al., 2009) and languageR (Baayen, 2008). We considered an effect to be significant if its absolute t-statistic value was >2, as suggested by Baayen (2008).

Figure 5.

Mean response times of correct and incorrect responses across the three payoff conditions. Errors are faster than correct responses in the neutral condition and especially in the incongruent condition, but are slower than correct responses in the congruent condition.

Analysis of electrophysiological data

To investigate the effect of payoff information after payoff cue onset and around the time of the decision, epochs were created from the EEG data spanning from 400 ms before payoff cue presentation until 2000 ms after (i.e., 500 ms after stimulus onset). Furthermore, response-locked epochs were generated to examine the effect of payoff on motor response formation. These epochs started 600 ms before the overt response and lasted until 100 ms after. A baseline, computed as the average activity across the 400 ms before the onset of the payoff cue, was subtracted from all single trials before averaging for both stimulus-locked and response-locked epochs.

To detect artifacts in the stimulus-locked epochs, we focused on the activity of electrodes C3, C4, VEOG, and HEOG in the time window 600 ms before stimulus onset until 400 ms after. We first detected and removed trials with very large drifts and amplifier saturation. These trials were defined as trials in which the absolute value of the voltage at any of the four electrodes exceeded 180 μV. Eye blinks and eye movements were removed using the step detector technique (Luck, 2005), which uses a moving window of size 100 ms on the EOG channels. We removed trials in which the difference of average voltage in two adjacent 100 ms windows surpassed a threshold value of 50 μV. Furthermore, trials that contained drifts in C3, C4, VEOG or HEOG, defined as trials in which the difference between maximum and minimum voltage in an epoch exceeded 50 μV, were removed. These thresholds were determined by visually inspecting the EEG data. We also removed trials in which the subject made no response at all, even after the deadline. On average, 4.77% (3.12% SD across participants, range: 1.51–11.08%) of trials were discarded in the stimulus-locked epochs. For the response-locked epochs, the same artifact detection scheme was performed in the time window 600 ms before response to 100 ms after, which resulted in discarding, on average, 3.12% (2.01% SD across participants, range: 1.1–6.7%) of trials.

For each participant and for each payoff condition, LRP was calculated using the averaged waveforms recorded at centrolateral electrodes C3 and C4. To compute the LRP, first, the averaged signal recorded at the electrode ipsilateral to the responding hand was subtracted from the averaged signal at the electrode contralateral to the responding hand separately for right and left responses (C3-C4 for right responses, and C4-C3 for left responses). Then, the resulting difference signals were averaged across the two hands to eliminate non-movement-related lateralized activity (Coles, 1989).

We first focused on the influence of payoff cue on the LRP; that is, without regard to the influence of stimulus difficulty and participant's choice (see Fig. 6). We computed the stimulus-locked LRP for each participant per payoff condition, pooling across easy and hard stimulus difficulties as well as correct and incorrect responses, and then averaged the obtained LRP waveforms across participants. It should be noted that the hard and easy stimulus difficulty were approximately equally represented in the LRP data for each payoff condition even after artifact rejection (congruent hard: 11,815, congruent easy: 11,831, incongruent hard: 11,833, incongruent easy: 11,771, neutral hard: 11,783, neutral easy: 11,752). Within each payoff condition, the correct responses encompassed 81.97%, 59.78%, and 72.66% of the trial in the congruent, incongruent, and neutral conditions, respectively.

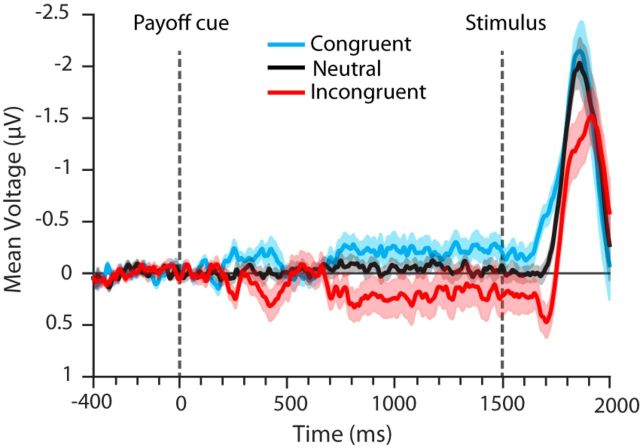
Figure 6.

Grand-average cue-locked LRP. The cue-locked LRP shows a transient shift in activity toward the higher-paying alternative in the congruent and incongruent conditions at around 250 ms after payoff cue onset, followed by another rise in activity toward the higher-paying alternative at ∼600 ms after payoff cue onset that is maintained until after stimulus onset. There is a transient rise in activity toward the higher-paying alternative at ∼150 ms after stimulus onset. The transparent shading around each line represents + 1 SE around the mean.

To investigate the manifestation of choice in LRP, in our second analysis (see Fig. 8), we computed each participant's average stimulus-locked LRP separately for the correct and incorrect trials within each stimulus difficulty level and then averaged across the two difficulty levels. The grand-average LRP activity was then obtained by averaging the LRPs across all 13 participants. In the congruent, incongruent, and neutral payoff conditions, the correct responses respectively encompassed 76.43%, 50.21%, and 64.82% of the trial in the difficult stimulus condition and 87.50%, 69.40%, and 80.53% of the trials in the easy stimulus condition.

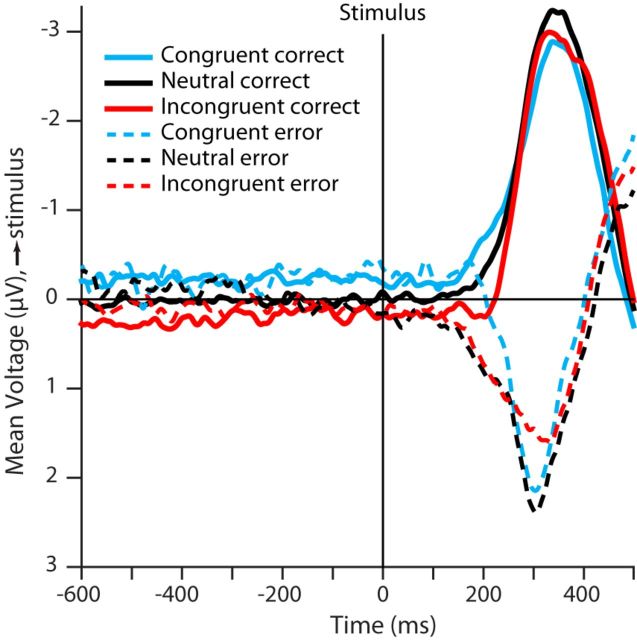
Figure 8.

Manifestation of choice in stimulus-locked LRP. In the congruent and incongruent conditions, the LRPs of correct (solid blue and red) and incorrect (dashed blue and red) responses show no significant difference until ∼150 ms after stimulus onset. This suggests that the prestimulus preparatory activity associated with payoff processing does not predict choice. However, the point of divergence between correct and incorrect responses coincides with the emergence of the first transient increase in payoff activity (Fig. 6) at ∼150 ms after stimulus onset.

LRP onset detection.

The criterion for LRP onset was set to 2.58 times the SD of the noise as estimated from the 200 ms before stimulus onset. The latency at which the LRP value first exceeded this criterion for 50 consecutive ms was defined as the onset latency. SEs of onset differences were estimated using the jackknife method, as described in Miller et al. (1998), and were used to calculate t-values for onset differences between experimental conditions. In brief, a jackknife subsample onset S_i was computed for each subject i (i = 1 … 13) by omitting subject i and calculating the LRP latency of the grand-average waveform computed from the remaining 12 subjects. This procedure was repeated for each subject, resulting in the subsample latencies S₁ … S₁₃. The jackknife-based SE was then estimated from these 13 subsample latencies and used for our statistical analysis instead of the usual SE measure computed from latency estimates of individual subjects.

Stimulus and payoff signals.

To investigate the temporal dynamics of payoff and stimulus processing separately, we extracted the payoff and stimulus signals from grand-averaged stimulus-locked LRPs of the two unbalanced payoff conditions (the LRPs that were created without respect to stimulus difficulty or accuracy). We assumed that LRP activity for the congruent and incongruent condition is composed of the summation of the activity related to payoff processing (payoff signal) and the activity related to stimulus processing (stimulus signal). In other words,

The stimulus signal was then obtained by averaging out the payoff signal from the LRP activity of congruent and incongruent conditions. Similarly, the payoff signal was obtained by averaging out the stimulus signal as follows:

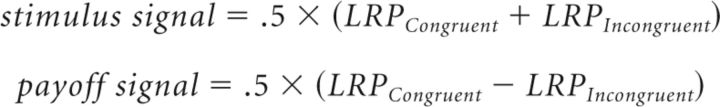We examined the difference in the onset latency of the stimulus effect and payoff effect signals using the jackknife method as described above.

Manifestation of choice in the LRP.

To determine the time at which the LRP became predictive of participant's choice, we used the following logistic regression model:

Where P_right is the observed probability of choosing the right-hand response and β_stim, β_payOffCue, and β_neural are fitted coefficients representing the effect of stimulus strength, payoff condition, and neural preparatory activity on this probability. β₀ represents the global bias that the participant has toward the rightward choice. S is the strength of the rectangular stimulus, in fractional units of the maximum shift used and signed according to the rightward shift. Therefore, S takes on the values {−1, −0.4, +0.4, +1}, where, for example, −0.4 refers to a leftward 2-pixels shift. R is the payoff cue condition that takes values {−1, 0, +1} referring to {higher payoff to left, neutral payoff, higher payoff to right}, respectively. Z is summed voltage differential between the left minus the right electrode (C₃ − C₄) over a defined time window, which measures the neural preparation toward a right-hand response. To study these effects over time, we chose a 100 ms window and moved it in steps of 50 ms starting 600 ms before stimulus presentation to 400 ms after.

Use of dynamometer data

Although not planned at the outset of the study, we found in the course of analysis that it was useful to consider the continuous activity recorded on dynamometers. Inspection of the dynamometer data revealed that, on a subset of trials, there was a low level of motor activity before stimulus onset on one or both hands and/or motor activity after stimulus onset in the hand that did not ultimately reach the criterion for assignment as the designated choice response. We used a threshold of 5 force units difference from baseline (average force over 20 sample points spanning 47 ms immediately after payoff cue onset) to designate whether motor activity occurred in the prestimulus epoch or during the poststimulus processing period.

Modeling evidence accumulation and the role of payoffs

Classical models of decision dynamics arising initially from the random walk or drift-diffusion models (Laming, 1968; Ratcliff, 1978; Busemeyer and Townsend, 1993) are often called one-dimensional models, in that they treat the underlying decision state as a single signed variable, favoring one alternative when positive and the other when negative. Many other models, however, can be called multidimensional models, in that they propose separate decision variables for each choice alternative (Vickers, 1970; Usher and McClelland, 2001; Mazurek et al., 2003; Roe et al., 2001). Behavioral data from studies similar to ours has been modeled previously using 1D models (Diederich and Busemeyer, 2006; Diederich, 2008; Simen et al., 2009). Although it is possible that such models could account for many features of our data, physiological evidence supports multidimensional models in that there is evidence that different populations of neurons accumulate evidence for each choice alternative (Shadlen and Newsome, 1996; Schall, 2001; Gold and Shadlen, 2007; Purcell et al., 2010; Shadlen and Kiani, 2013). Our findings reported below show that, on at least some trials, there was activity in both response hands, providing additional support for the use of separate decision variables for each alternative, each of which may produce measurable motor activity on some trials. Accordingly, we built our model in a multidimensional modeling framework.

As a framework within which to consider alternative accounts of the exact nature of the integration of payoff information in the decision process, we relied on the linear ballistic accumulator (LBA; Brown and Heathcote, 2008), a model that has had considerable recent success in the human behavioral decision-making literature (Ho et al., 2009; Forstmann et al., 2010). This model shares many features with other accumulator models of the decision-making process, particularly the physiologically grounded model of Mazurek et al. (2003) (also see Reddi and Carpenter, 2000; Reeves et al., 2005). The LBA attributes variability in choice and response time to trial-to-trial variation in the evidence accumulation rate and in the starting point of evidence accumulation rather than to variation in the moment-to-moment integration of evidence. In our view, all three sources of variability are likely to affect decision making, but including only the two sources included in the LBA may be sufficient to capture the key features of the behavioral data. When, as is often necessary, starting point and/or trial-to-trial evidence accumulation rate variability are included, the effect of within trial variability may be effectively masked (Gao et al., 2011). Furthermore, ignoring moment-to-moment variability makes it possible to write down the predicted choice proportions and response time distributions of the model in closed form, avoiding the need for extensive Monte Carlo simulations and facilitating parameter estimation and model comparison.

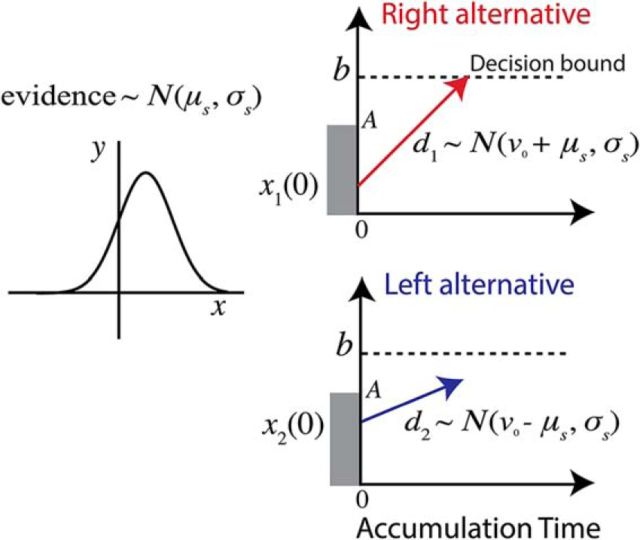
Figure 2 shows the base LBA model for a two-alternative decision task. The model posits a separate evidence accumulator for each choice alternative. On each trial, the activity in each accumulator starts at a random initial evidence value (the “starting point”) independently drawn from a uniform distribution between a minimum of 0 and a maximum value A. Activity of each accumulator increases linearly according to a drift rate (v_i) randomly drawn from separate Gaussian distributions for each accumulator with means E_[v1] and E_[v2], and equal SD, σ_s. Accumulation continues until one of the accumulators reaches the response threshold b, thereby determining both the choice outcome and the decision time T_d for the trial. The RT is equal to the decision time plus a constant T₀ representing nondecision time.

Figure 2.

LBA model. Two accumulators race from their independent randomly assigned starting points (between 0 and A) at rates d₁ and d₂ distributed as shown. The evidence variable μ_s is chosen randomly for each trial according to a distribution that favors the correct alternative. Choice is determined by the first accumulator to reach the bound and decision time is the time from the start of the race to the time the winning accumulator reaches the bound.

The mean drift rate for the two response accumulators, E_[v1] and E_[v2], are defined by two parameters: (1) v₀, the common drive for the two accumulators, a parameter that can be thought of as equivalent to the urgency signal in the model of Mazurek et al. (2003); and (2) μ_s, the stimulus-dependent drift rate (v₀ and μ_s are both constrained to be > 0). The mean of the drift rate distribution is set to v₀ + μ_s for the accumulator corresponding to the correct alternative and to v₀ − μ_s for the accumulator corresponding to the incorrect alternative. For simplicity, we combined the data across the 2 and 5 pixels of stimulus shift using a single value of the μ_s parameter to fit the combined results.

The LBA model is characterized by six parameters: (1) v₀, the base stimulus drift rate or the common drive to both accumulators; (2) μ_s, the mean stimulus-dependent drift rate; (3) σ_s, the SD of drift rate across trials; (4) A, the upper end of the starting point distribution such that the starting point for each alternative x_i(0) ∼ U[0, A]; (5) T₀, the non-decision time (see below); and (6) b, the decision boundary. To reduce the number of free parameters, we fixed b at 500 and estimated the five remaining free parameters based on a maximum-likelihood method.

The non-decision time T₀ consists of two parts: a sensory processing delay (T_s) and a motor execution delay (T_m). The total RT consists of the sum of these two times plus the decision time (T_d). The components of T₀ are not separately identifiable in the base model, but can play separate roles in models of payoff bias effects.

The cumulative distribution function (CDF) of each accumulator's time-to-bound can be computed analytically (for details, see Brown and Heathcote, 2008) as follows:

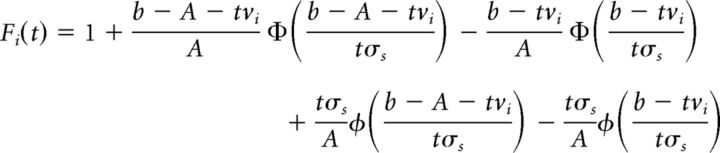Where the functions φ( · |μ, σ) and Φ( · |μ, σ) refer to the normal distribution's density and cumulative density functions, respectively.

The corresponding probability distribution function (PDF) of time-to-bound is given by the following:

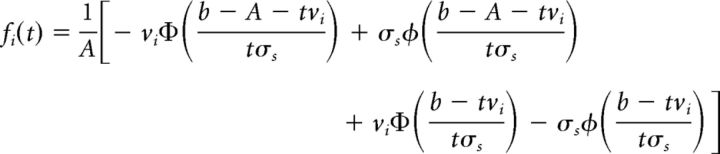Finally, the probability that accumulator i will be the first accumulator to reach threshold can be computed from the PDF and CDF for accumulator i, as well as the PDF and CDF of the other accumulator (indexed by subscript j) as follows:

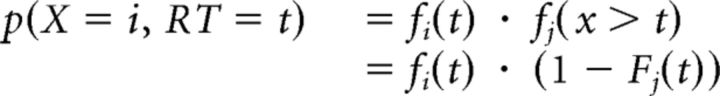Using the above model as a base, we compared three hypotheses about influences of payoff information on the decision process (Fig. 3): (1) the starting point shift hypothesis (Edwards, 1965; Link and Heath, 1975; Bogacz et al., 2006; Simen et al., 2009; Rorie et al., 2010; Gao et al., 2011; Leite and Ratcliff, 2011; Rao et al., 2012); (2) the drift rate change hypothesis (Ratcliff, 1981; Ashby, 1983; Hanks et al., 2011); and (3) our fast guess process hypothesis, similar to the “nonintegrative” responses described by Simen et al. (2009). We describe each model in detail below.

Figure 3.

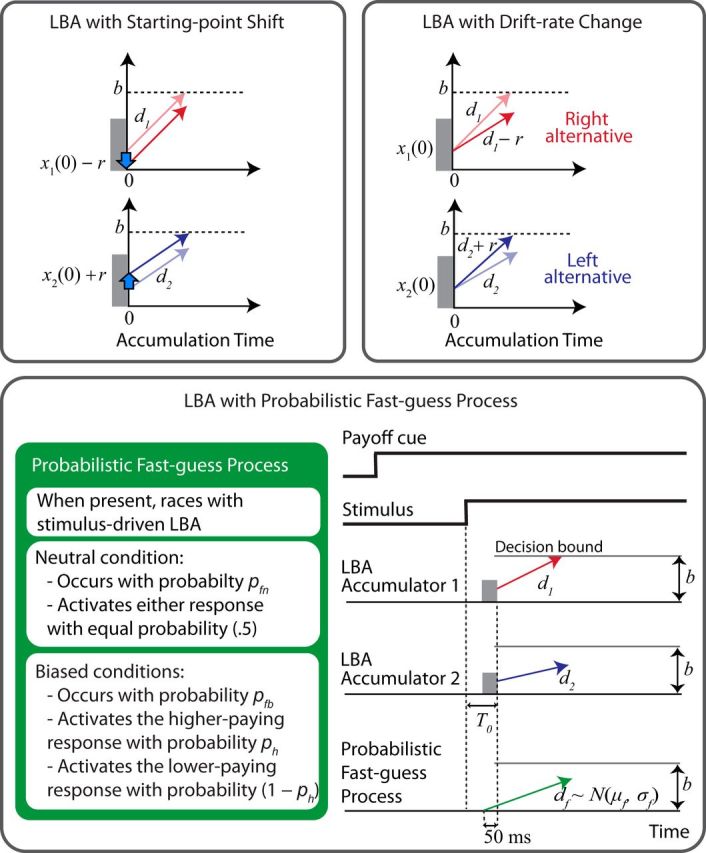
Models of payoff effects. A, Biased payoff shifts the starting point of the favored alternative up and the disfavored alternative down. B, Biased payoff increases the drift rate of the favored alternative and decreases the drift rate of the disfavored alternative. C, A fast guess process that occurs on a randomly determined subset of trials, triggered by stimulus onset, races with the two stimulus-driven accumulators. Biased payoff increases the probability that the fast guess will activate the response associated with the high reward.

LBA with starting point shift (LBAst).

According to the starting point shift hypothesis (Fig. 3, top left), payoff shifts the starting point of the higher-paying accumulator by an amount r toward the decision bound and shifts the starting point of the lower-paying accumulator away from the bound by the same amount. This shift in the starting point is equivalent to changing the decision bound b to b − r for the higher-paying accumulator and to b + r for the lower-paying accumulator, effectively making it easier for the higher-paying accumulator to win the race.

LBA with drift rate change (LBAdc).

According to the drift-change hypothesis, payoff increases the drift rate of the higher-paying accumulator by amount r and decreases the drift rate of the lower-paying accumulator by the same amount (Fig. 3, top right). This change in the drift rates of the accumulators leads to more high reward choices and lower response times for those choices. The drift rate change hypothesis can be interpreted as a time-dependent bias that results in a greater amount of bias for longer decision times; this can be advantageous if stimulus discriminability varies in a wide range from trial to trial because, in that case, long decision times occur more often with less discriminable stimuli, allowing bias to be greater when discriminability is lower, as it should be for optimizing payoffs across discriminability conditions (Hanks et al., 2011).

Fast guess LBA (FG-LBA).

The FG-LBA model (Fig. 3, bottom) relies on the idea that, on a subset of trials, a “guessed” response choice is selected before stimulus onset (Ollman, 1966; Yellott, 1967, 1971; Ratcliff, 1985; Simen et al., 2009). In our model, the “guess” may be affected by a range of factors, of which the participant may or may not be conscious, and can occur both when payoffs are unbiased (i.e., the neutral condition) as well as when they are biased. The model does not describe the guessing process itself, only specifying that, when it occurs, a guess response is prepared for triggering by detection of the onset of the shifted-rectangle stimulus. In cases in which payoffs are biased, the outcome of the guess process will tend to favor the higher-paying response alternative. That is, the probability that the higher-paying alternative will be selected on trials when a guess occurs (denoted p_h) will be >0.5. If a guessed response has been prepared on a given trial, detection of the onset of the stimulus then initiates activation of an additional accumulator associated with the guessed response. This accumulator triggers the guessed response if it reaches the decision bound before either of the two standard LBA evidence accumulators reaches its decision bound. From a physiological point of view, we would not rule out the possibility that there are two separate fast guess accumulators, one for a leftward response and one for a rightward response. If so, on trials when a guessed response has been prepared, only the accumulator associated with the guessed choice participates in the race to determine the trial outcome. In any case, there is only one set of parameters associated with the fast guess process. Therefore, the mathematical description of the model incorporates a total of three accumulators, as shown in Figure 3, and henceforth we speak of a single fast guess accumulator.

A feature of the model is that the fast guess accumulator is triggered by detection of the stimulus onset, whereas the standard LBA accumulators are driven by evidence that the stimulus is shifted to the left or right. In the Results section, we present evidence that, after stimulus onset, the payoff effect on LRP appears 50 ms before the stimulus effect. The same 50 ms offset was previously observed in experiments 2 and 3 of Simen et al. (2009). Based on these observations, we assume that the sensory processing delay, T_s, for the fast guess accumulator is 50 ms less than T_s for the stimulus-driven LBA accumulators. It should be noted that T_s and T_m (the motor processing delay) are not separately identifiable from the behavioral data and only their sum, T₀ is fitted to the data. Because T_m is assumed to be the same for all responses, the assumption that T_s is 50 ms faster for the fast guess accumulator than for the standard accumulators amounts to the assumption that T₀ is 50 ms shorter for fast guess responses than for other responses. In fitting the model, a single value of T₀ is adjusted for best fit, with 50 ms subtracted from this value in simulating the fast guess process.

We model the fast guess accumulator as a restricted LBA accumulator with starting point set to zero and the decision bound set to an arbitrary value (for comparability to the standard LBA accumulators, we set this bound to 500). Therefore, this accumulator corresponds to the accumulator used in the LATER model of speeded responding (linear approach to threshold with ergodic rate; Carpenter and Williams, 1995). The density of the finishing time t of this process is given by the recinormal distribution (Leach and Carpenter, 2001) as follows:

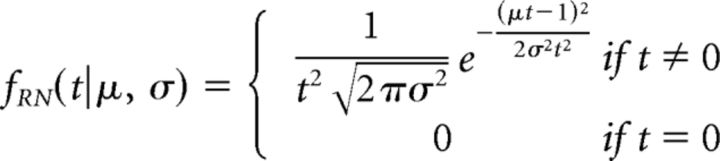Conceptually, the parameter μ represents the mean of the slope of the ballistic accumulation process and the parameter σ represents the SD of the slope from trial to trial.

We allow for the possibility that the probability of making a fast guess may be different for the neutral condition and the biased payoff condition and we represent these probabilities as p_fn and p_fb, respectively (we write p_fc in expressions that apply to both conditions n and b). On the trials when the fast guess process does occur, the fast guess wins when this process reaches its bound (called time to bound or T_b) before either of the stimulus-driven accumulators. This can be expressed as follows:

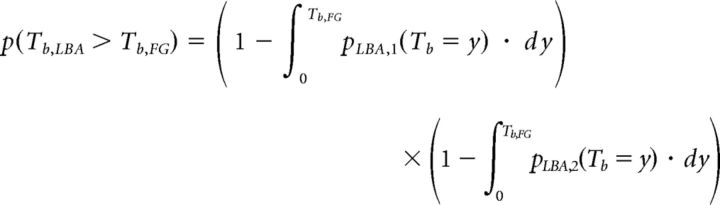On trials in which the bound is reached first by the fast guess process, the choice and time to bound T_b are determined independently of each other, so the joint distribution of choice and T_b is given by the following:

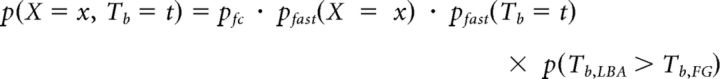Where p_fast(T_b = t) = f_RN(t, μ_f, σ_f) and

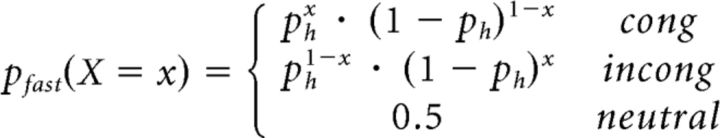Where p_h is the probability of choosing the higher-paying alternative, x = 1 represents a correct response, and x = 0 represents an incorrect response. The joint choice and T_b distribution of the stimulus-driven LBA process is given by the following:

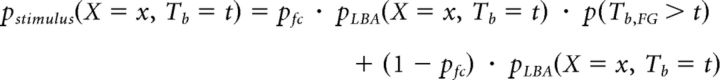Where

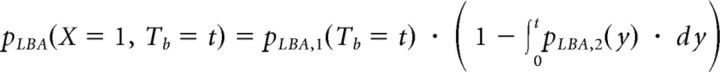and

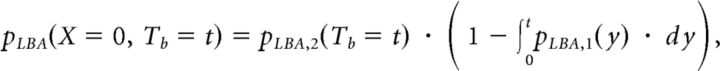capturing the race between the two accumulators in the LBA model.

This model adds five additional free parameters to the LBA model's five free parameters: (1) p_fb, the probability of engaging in a parallel fast guess process on any given trial in the biased payoff condition; (2) p_fn, the probability of engaging in a parallel fast guess process on any given trial in the neutral condition; (3) μ_f, the mean slope of the ballistic accumulator for the fast guess process; (4) σ_f, the SD of the slope of the ballistic accumulation for the fast guess process; and (5) p_h, the probability of choosing the higher-paying alternative in the fast guess process.

Model comparison

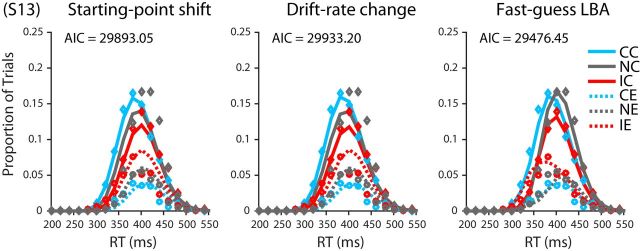
The parameters of the three variants of the LBA model were estimated using the method of maximum likelihood. The results from each participant were fit separately to find optimal parameter values. Consider one of the three models and the data from one of the 13 participants. The model (together with a set of specified parameter values) can be seen as predicting, for each condition of the experiment (neutral, congruent, or incongruent), the probability density for each alternative (correct or incorrect) at any time t. The joint distribution across both alternatives for a given condition is a proper probability density function in that the density sums to 1. For purposes of comparison of model and data, we discretized time into 20-ms-wide response time bins spanning RTs from 0 to 700 ms. Using one set of 20 ms time bins for correct responses and another set of bins for incorrect responses, we integrated the probabilities obtained from the model's PDF within a bin to obtain a predicted probability for each bin. These probabilities were then compared with the empirically observed distributions of responses falling within each bin using all of the RT data from all six sessions after the end of the practice phase of the experiment. For each of the three conditions (neutral, congruent, and incongruent), we tabulated the number of trials in each 20 ms RT bin, placing correct RTs in one set of bins and incorrect RTs in another set of bins. The result can be seen as a single 70-bin accuracy-by-RT histogram for the given condition to be fit by the model, forcing the model to account for the distributions of both correct and incorrect RTs and thus to account for the overall rates of correct and error responses, which correspond to the sums of the rates of responses over the 35 correct and error bins, respectively (see Fig. 15).

Figure 15.

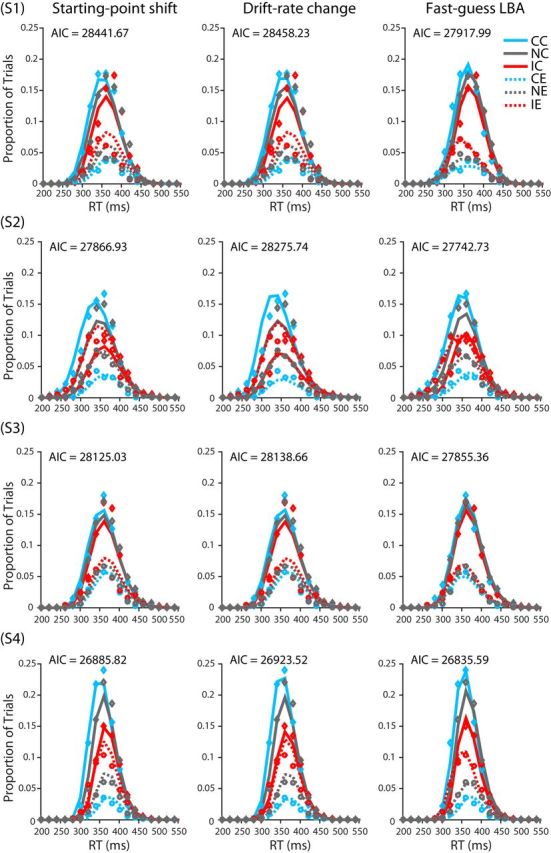
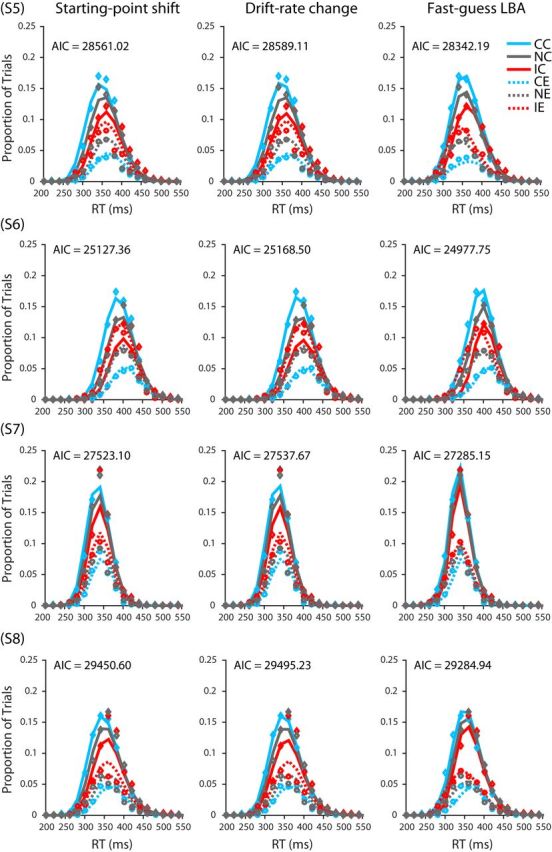
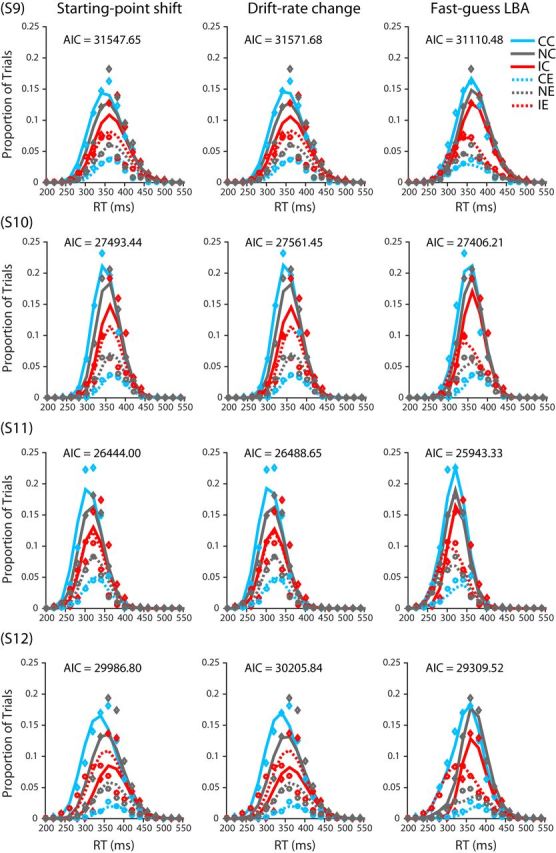
Data and model fits for each participant's RT histograms. Diamonds and circle points depict actual proportion of trials in each 20 ms bin for correct and incorrect responses, respectively. For a given condition, the sum of the proportions across correct and incorrect bins is equal to 1. Solid and dashed lines depict model-predicted proportions for correct and incorrect response trials respectively. CC, Congruent correct; IC, incongruent correct; NC, neutral correct; CE, congruent error; IE, incongruent error; NE, neutral error.

Accommodating outliers.

It has frequently been noted that participant's behavior is rarely pure and that, on occasion, relatively random responses may occur at any time during a trial. Including a provision for such random responses helps to ensure that differences in goodness of fit are not due to extreme and nonrobust differences between models in log likelihoods of very short or very long RTs (Ratcliff and Tuerlinckx, 2002). Accordingly, we incorporated a provision for a random guessing process in fitting all three models to the data. Specifically, we assumed that, on each trial, a random response could occur. Such responses were assumed to be equally likely to be correct or incorrect and could fall in each of the 70 histogram bins with equal probability. The overall probability of such occurrences was chosen so that the probability of a random response occurring in each bin was 0.00001 (this probability was added to the predicted probability in each bin and then the total probability of responses across all bins was renormalized to 1). The predicted probabilities discussed below incorporate this adjustment.

Log likelihood fit statistic.

Consider now the data from one participant for a given condition c (one of congruent, incongruent, or neutral). Denote the model's predicted probability of making a response in the j^th bin (where j runs over all 70 bins as previously discussed) by p_cj and the number of trials obtained from the histogram of responses that fall in the same j^th bin by N_cj. We can then express the likelihood function for responses across the histogram as follows:

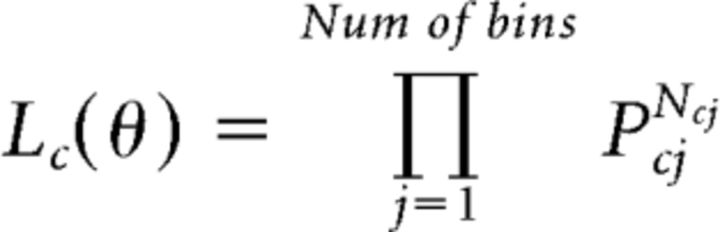Taking logs, the log likelihood (LL) for the given condition can be simply expressed as follows:

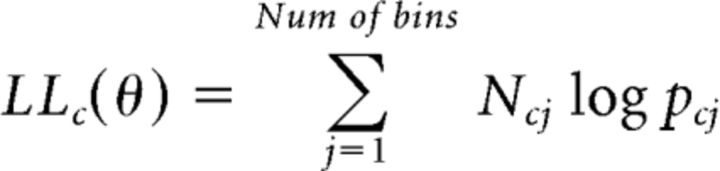This quantity is summed across the three distributions (for congruent, incongruent, and neutral trials) to obtain the total log likelihood (LL). We then find the estimates of the model's parameters, θ̂, that minimizes −LL(θ) for the data of the given participant. This function was optimized using the simplex algorithm (Nelder and Mead, 1965) implemented in MATLAB's fminsearchbnd() function. We repeated the optimization algorithm using 10 randomly assigned initial values and chose the resulting estimated parameters that corresponded to the best fit among the 10 repetitions.

To compare the goodness of fit among the models, we calculated the log likelihood, the Akaike information criterion (AIC), and the Bayesian information criterion (BIC) of each model for each participant separately. The AIC is defined as AIC = 2k − 2ln(L), where k is the number of free parameters in each model and L is the maximized value of the likelihood function of the model. The BIC is defined as BIC = kln(n) − 2ln(L), where n is the number of observations in our data.

To better assess the relative performance of the FG-LBA model compared with the LBAst and LBAdc models, we quantified the relative likelihood of each model for each subject by computing exp((AIC_min − AIC_i)/2). For all participants, the FG-LBA model had the minimum AIC among the three models. Therefore, we computed the likelihood of the LBAst and LBAdc relative to the FG-LBA model.

As a further check on the robustness of the fitting results against outlier effects, we calculated pseudo-log likelihoods and corresponding pseudo-AIC values for each model after removing singleton responses from the response histograms. That is, for any histogram bin containing an entry of only one response, we replaced that entry with 0. Individual participants exhibited 3–15 such singleton responses across the 210 histogram bins (70 for each condition).

Results

Our presentation of results consists of two parts. The first focuses on characterizing patterns in the empirical measurements of participants' behavioral and brain responses in our choice task and the second presents the results of a competitive model assessment in which we examine how well the effects of payoff bias in our behavioral choice and RT data can be explained by three alternative accounts. The first two of these accounts, in which bias affects the starting point of evidence accumulation or the drift rate, were our initial intended targets for comparison. The third account suggested itself after an examination of aspects of the behavioral and EEG data. According to this account, bias affects the distribution of fast, stimulus-onset-triggered guess responses that participants make on a subset of trials. We now turn to the patterns observed in the empirical measurements, highlighting those that motivated the development of the fast guess model.

Empirical observations

Benefit from unequal payoffs

We began by asking whether participants were able to increase their overall earnings when payoff information was biased. Because the average payoff for a correct response was the same for the neutral and biased conditions, participants would be expected to earn the same amount in the neutral and biased conditions if they simply ignored the payoff information. By taking the payoffs into account, they had the possibility of increasing their earnings, although some payoff-sensitive policies (e.g., always choosing the high reward alternative) might actually lead to reduced overall payoff. To ascertain whether participants indeed benefited from the use of payoff information, we compared earnings in the biased payoff condition with those in the neutral payoff condition. In the biased payoff condition, the subjects earned 0.06 cents/trial more on average than in the neutral condition (t₍₁₂₎ = 3.47, p = 0.002, one-tailed).

Basic choice and RT results

We next considered how payoff affected decision making, first by considering behavioral and then neural measures. We investigated the probability of correct responses as a function of RT in the neutral and biased payoff conditions (see Materials and Methods). Average probability correct for the three payoff conditions and two difficulty levels are shown in the top of Figure 4 and the average number of responses in each RT bin is shown in the bottom. Using a linear mixed-effects model, we regressed probability correct (PC) against stimulus difficulty, payoff condition, RT, and the interaction between payoff condition and RT. The model included a random effect of subject for the intercept. Across all payoff conditions, PC was higher for the easy stimuli (5 pixels shift, solid lines) than for the difficult stimuli (2 pixel shift, dashed lines, b = 0.82, SE = 0.02, p < 0.001). On average, probability correct increased with RT, suggesting that participants had accumulated more information about the stimulus as their RT increased (b = 5.72, SE = 0.25, p < 0.001). In the biased payoff conditions, participants were highly biased toward the higher-paying alternative in their fast responses and became less biased as they took more time to respond. In other words, there was a significant interaction between payoff condition and RT: relative to the neutral condition, the PC increased with RT in the incongruent condition (b = 8.80, SE = 0.31, p < 0.001) and decreased with RT in the congruent condition (b = −8.98, SE = 0.33, p < 0.001). This can be observed from higher-than-neutral PC in the congruent condition and lower-than-neutral PC in the incongruent condition for fast responses and their convergence toward the neutral condition's PC level as RT increased.

Not only did the unequal payoff cue bias participants' choices, but also it modulated their RTs. Figure 5 shows the average RT of correct and incorrect responses for the three payoff conditions. Using a linear mixed-effects model, we regressed RT against payoff condition, response accuracy, and the interaction between payoff condition and response accuracy (see Materials and Methods for details). The model included a random effect of subject for the intercept and for each of the fixed effects, but not for the interaction effect. The results of the model indicated a significant relationship between RTs and accuracy: overall, correct responses have a longer RT than incorrect responses (b = 0.006, SE = 0.001, t = 4.59). This pattern provided the first clue suggesting a possible fast guess process in the present experiment: errors are often slower than correct responses in RT experiments, particularly with stimuli that are difficult to categorize correctly (Ratcliff, 1978; Mazurek et al., 2003). However, if participants sometimes make fast guesses that are triggered, not by stimulus processing, but merely by detection of stimulus onset, then these guesses can generate many fast incorrect responses. A further, related finding was a significant interaction of payoff condition and probability correct on response times; the interaction was also observed comparing the neutral condition only with the congruent condition (b = −0.014, SE = 0.0005, t = −30.46) and comparing the neutral condition only with the incongruent condition (b = 0.015, SE = 0.0004, t = 35.41). Errors were fastest and correct responses slowest in the incongruent condition, whereas errors were slowest and correct responses fastest in the congruent condition. Such a pattern would be expected if fast guesses in the unequal payoff conditions tended to favor the high reward alternative; this would give rise to many fast correct responses in the congruent condition and many fast incorrect responses in the incongruent condition.

In summary, the RT data suggest a biased fast guess process as an alternative to the two accounts of the possible role of unbalanced payoffs that we were considering at the outset of this research. However, the findings may be consistent with other mechanisms. For example, if the starting point of a drift diffusion process was very strongly biased toward the higher-paying alternative, then this might produce many fast responses biased toward the high reward side as well (Ratcliff and Rouder, 1998; Usher and McClelland, 2001). Thus, although the pattern of findings does not unequivocally support a biased fast guess model, they do provide one motivation for exploring such an account.

Basic patterns in the LRP

We begin our consideration of the EEG results with the grand-average patterns observed in the LRP. These patterns reveal a bias toward the high reward response before the stimulus and then a bolus of activity toward the high reward side shortly after stimulus onset. Figure 6 shows the average LRP for the three payoff conditions averaged over participants, with averaging time locked to the onset of the payoff cue, which occurred 1500 ms before stimulus onset. Upward-going (negative) activity in this figure represents net activity contralateral to the stimulus and therefore also to the correct response. Therefore, in the congruent condition (blue), net activity toward the higher-paying alternative is represented by upward-going activity, whereas in the incongruent condition (red), it is represented by downward-going activity (away from the stimulus). Poststimulus activity eventually favors the correct response. In addition, both prestimulus and poststimulus effects of payoff information are evident in this figure. The prestimulus effect includes a transient lateralization toward the higher-paying alternative ∼200 ms after payoff cue onset, followed by a prestimulus baseline shift toward the higher-paying alternative starting ∼700 ms after payoff cue onset and maintained until ∼150 ms after stimulus onset. Although the average prestimulus LRP for the neutral condition was stable around zero, the LRP of the congruent and incongruent conditions were shifted upward and downward, respectively. The poststimulus effect is manifested as a rapid rise in activity (bolus-like activity) toward the higher-paying alternative ∼150 ms after stimulus presentation. This bolus is seen as an upward jump in the LRP for the congruent condition and as a downward jump in the direction opposite to that of the correct response for the incongruent condition.

Stimulus and payoff signals

To estimate the time course of the payoff signal and of the stimulus signal as manifested in the LRP, we treated the LRP as consisting of the simple addition of the two signals. Using this approach, we computed the payoff and stimulus signals from the grand-average LRPs of the biased payoff conditions, as described in the Materials and Methods. Figure 7A shows the time courses of these neurally derived payoff and stimulus signals. Upward-going (negative) voltages signify activity favoring a response toward the stimulus for the stimulus signal (purple) and toward the higher-paying alternative for the payoff signal (pink). The stimulus signal is approximately zero before stimulus presentation and begins increasing at ∼200 ms after stimulus onset. That is, stimulus processing starts affecting the LRP at ∼200 ms. The payoff signal (pink) also shows a time-dependent pattern. Initially, a transient shift in prestimulus activity toward the higher-paying alternative is observed ∼200 ms after the presentation of payoff cue, followed by another shift that is observed ∼700 ms after cue presentation and remains constant in the period preceding the stimulus and up to ∼150 ms after stimulus onset. At this time, a bolus of payoff activity appears. Two observations suggest that the payoff bolus signal (poststimulus transient shift in activity toward the higher-paying alternative) and the stimulus signal may reflect distinct processes associated with payoff and stimulus information: (1) the onset of the payoff bolus signal is earlier than the onset of the stimulus signal (t₍₁₂₎ = 5.1, p < 0.001, one-tailed); and (2) the computed stimulus signal closely matches the grand-average LRP for the neutral condition (comparison shown in Fig. 7B), which was not used in calculating the payoff and stimulus signals.

Figure 7.

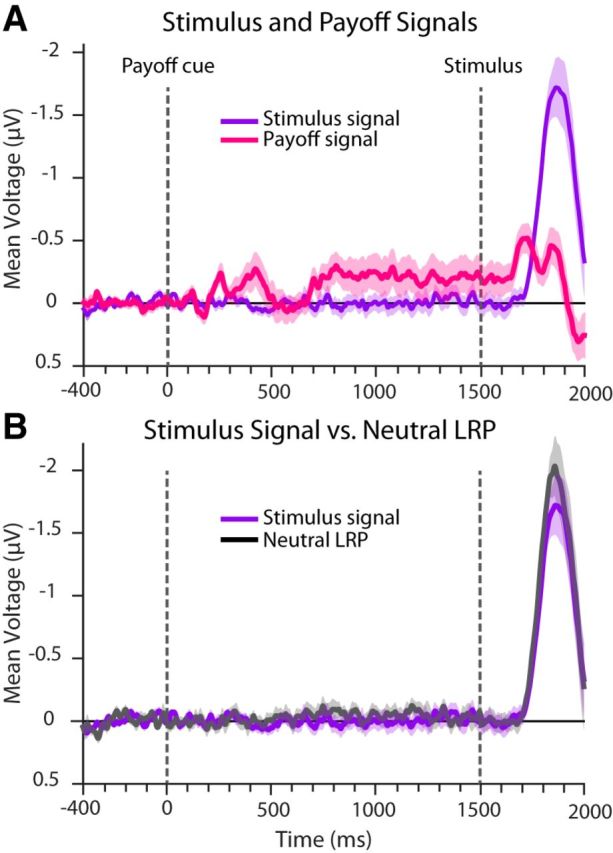
Payoff and stimulus signals were derived from a linear additive model and stimulus signal matched the neutral LRP closely. A, Payoff and stimulus signals. The stimulus signal shows that stimulus information is manifested in the LRP only starting 200 ms after stimulus onset. The payoff signal shows that the payoff information is manifested as a prestimulus shift in activity toward the higher-paying alternative followed by a transient increase of activity toward the higher-paying altenative at ∼150 ms and ∼300 ms after stimulus onset. B, Stimulus signal versus the neutral LRP. The stimulus signal derived from the additive linear model of the unbalanced payoff condition is depicted alongside the LRP of the neutral condition. The two signals, originating from separate trial sets, match closely. The transparent shading around each line represents ± 1 SE around the mean.

Manifestation of choice in stimulus-locked LRP

To investigate when LRP activity became predictive of participants' choices during a trial, we compared the grand-average stimulus-locked LRP between the correct and incorrect responses within each payoff condition (see Fig. 8; solid lines are correct responses and dashed lines are incorrect responses). In the neutral condition, the LRPs of correct and incorrect trials were not lateralized in any direction during the prestimulus period. The lateralization of incorrect neutral trials toward the incorrect response started immediately after stimulus onset and showed a sharp downward deflection about 150 ms after stimulus onset; for the correct neutral trials, lateralization toward the correct response did not become apparent until ∼200 ms after stimulus onset. This pattern is consistent with the possibility that, on a subset of trials, participants began activating a fast guess response upon detecting stimulus onset and before stimulus information influenced activation of the response. Such a guess would be equally likely to be correct or incorrect. Given that responses based on stimulus information would be likely to result in correct responses, a larger fraction of errors than correct responses will be fast guesses, explaining why the LRP evidence of such guess responses is more prominent in the LRP for errors than for correct responses.

In the biased payoff conditions, we initially expected that the baseline shift observed in the prestimulus payoff signal (see above, Fig. 7A) reflected a process that would participate in determining the choice outcome. However, the LRPs of the correct and incorrect responses in Figure 8 did not differ in their lateralization during the prestimulus period and even well into the stimulus presentation period. Therefore, it appears that the process generating the payoff signal during the prestimulus period played little or no role in determining participants' choices. LRPs of correct and incorrect trials started separating only at ∼150 ms after stimulus onset, suggesting that the poststimulus bolus-like component of the payoff signal (see Figs. 6, 7A) played an important role in participants' choice. For the incongruent condition, the poststimulus bolus-like LRP activity showed lateralization in the direction of higher payoff for both correct and incorrect trials (see Fig. 8, red lines), although it is clear that the bulk of the deflection in the average of correct and incorrect trials comes from the trials that ended in errors. A further interesting feature of the LRP curves on error trials is that they all show an upward going deflection toward the correct response near the end of the time window and after the strong downward going deflection. This reversal may arise from motor activity on the correct response side that occurs too late to count toward determining the scored outcome of the trial.

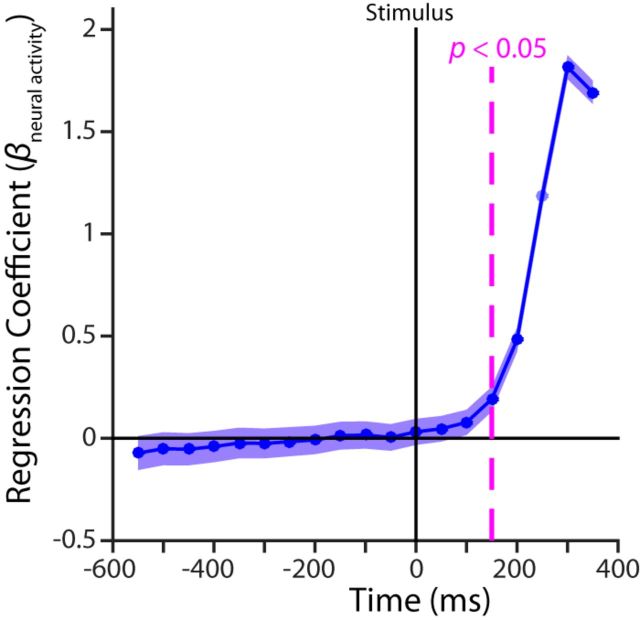
We next examined the time when the neural activity became predictive of the participant's choices using logistic regression (see Materials and Methods). We determined whether the trial-by-trial variation in our measure of neural activity (the difference between electrodes C3 and C4) changed the log odds of a rightward choice beyond the explanatory power of the stimulus and payoff information, combining the data across the congruent, incongruent, and neutral conditions. This regression was performed on a data window of 100 ms, which was repeated in steps of 50 ms over the whole stimulus-locked epoch. Fitting coefficients along with the associated SE are plotted at the midpoints of the 100 ms windows in Figure 9. We found that neural activity in the prestimulus epoch was not associated with the eventual choice response, confirming expectations from the results in Figure 8. Neural activity first became a significant predictor of participants' choices in the [100, 200] ms poststimulus time window (β_neural = 0.19, p = 0.001). Thus, the regression results further support the conclusion that the baseline shift observed in the prestimulus payoff signal does not affect the ultimate choice of participants, whereas the bolus-like poststimulus payoff signal does indeed affect the ultimate response choice.

Figure 9.

Coefficient of the neural activity predictor in the logistic regression on choice. Prediction is not reliable before window centered 150 ms after stimulus onset.

Prestimulus manual squeezes and relation to choice and RT

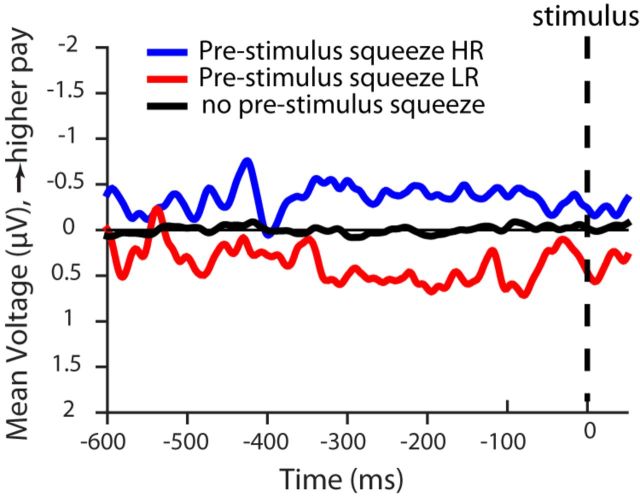
An important issue for understanding the LRP is the extent to which the neural activity it reflects is associated with motor activity. Specifically, it is useful to understand whether the shift in the prestimulus LRP baseline activity toward the higher-paying alternative reflects actual squeezing of the dynamometer by the hand associated with that alternative. We analyzed single-trial squeeze force data for the two hands over a window from 600 ms before stimulus onset to 50 ms after onset. The analysis revealed a partial squeeze, above prestimulus baseline but below criterion force level (see Materials and Methods), on one or both dynamometers before stimulus onset on some trials, both in the biased and neutral payoff conditions. For the two biased payoff conditions combined, Figure 10 shows the LRPs separately for trials in which prestimulus dynamometer activity was observed toward the high reward side only (18.3% of total trials), low reward side only (4.4% of total trials), or neither side (67.1% of total trials). The remaining 10.2% of trials showed dynamometer activity on both sides during this period. As expected, on trials with prestimulus dynamometer activity on one hand, the LRP favored the hand on which the dynamometer activity occurred. On trials with no prestimulus activity, there was also no prestimulus LRP. These findings are consistent with the possibility that, in our experiment at least, the LRP is a reflection, not of preparation to produce motor activity, but of motor activation itself. In the absence of motor activity, there is no LRP.

Figure 10.

Average stimulus-locked LRP in the biased payoff condition divided based on the presence of dynamometer activity in the prestimulus period. LRP shows a shift toward the higher or lower reward on trials with prestimulus dynamometer activity in the higher-reward hand (blue) or in the lower-reward hand (red), respectively. No net LRP shift was observed in the absence of prestimulus dynamometer activity (black).

Because of the dynamometer data provides a sensitive record of prestimulus squeeze events, we conducted a further analysis to determine whether this prestimulus motor activity was associated with subsequent choice or RT (see summary in Table 2). The probability of making a correct choice did not differ between trials with prestimulus motor activity favoring the high reward alternative (pre-high trials) and trials with no prestimulus dynamometer activity (no-pre trials) (t₍₁₂₎= 0.80, p = 0.44 for congruent trials, t₍₁₂₎ = −1.03, p = 0.33 for incongruent trials). Further, prestimulus motor activity favoring the high reward side had only a very slight, if any, relation to RT. In fact, for incongruent trials, there was no reliable difference in RT for correct or incorrect responses between pre-high and no-pre trials (t₍₁₂₎ = 0.26, p = 0.80 for correct responses; t₍₁₂₎ = −0.57 and p = 0.58 for incorrect responses). For congruent trials, there was no difference in RT for incorrect responses (t₍₁₂₎ = 0.004, p = 0.99). Correct responses in the congruent condition were on average 5.57 ms faster on pre-high trials than on no-pre trials (t₍₁₂₎ = −2.43, p < 0.05). This small consequence for RT in one of many contrasts should be considered marginal given the number of different comparisons considered; even if an effect is present, it would appear to be consistent with a generalized readiness effect: trials in the congruent condition with prestimulus dynamometer activity toward low reward (pre-low trials) also showed a numerically similar speedup compared with no-pre trials (see next paragraph). In summary, the overall lack of significance and the small numerical size of all of the contrasts considered indicates that prestimulus motor activity toward the high reward side had no detectable consequence for choice and only a very minor consequence for RT.

Table 2.

Behavioral measures contingent on prestimulus motor activity

Prestimulus motor activity	Probability correct			Mean RT for correct responses (ms)			Mean RT for incorrect responses (ms)
	High reward	Low reward	None	High reward	Low reward	None	High reward	Low reward	None
Congruent	0.83 (0.02)	0.76 (0.03)	0.82 (0.01)	352.98 (5.94)	353.93 (6.24)	358.55 (5.87)	368.48 (6.50)	359.59 (5.70)	368.47 (6.06)
Incongruent	0.57 (0.03)	0.58 (0.03)	0.59 (0.02)	377.32 (6.71)	368.48 (7.44)	378.16 (6.35)	352.58 (6.34)	353.49 (7.56)	354.09 (5.31)

Values shown are the mean value across participants (in parentheses, the SE).

A subtle but reliable relationship is present, however, between the trials with prestimulus motor activity favoring the low reward side (pre-low) and trials with no prestimulus (no-pre) motor activity. Compared with no-pre trials, pre-low activity was associated with: (1) fewer correct responses on congruent trials (mean difference = −0.06, t₍₁₂₎ = −2.83, p < 0.05); (2) faster errors (mean difference = −8.88 ms, t₍₁₂₎ = −2.41, p < 0.05) on congruent trials; and (3) faster correct responses (mean difference = −9.68 ms, t₍₁₂₎ = −3.06, p < 0.01) on incongruent trials. Correct responses were numerically faster on pre-low versus no-pre trials, though the difference was not statistically reliable (mean difference = −5.62 ms, t₍₁₂₎ = −1.63, p = 0.13). The RT difference between pre-low and no-pre errors on incongruent trials was not significant (mean difference = −0.59 ms, t₍₁₂₎ = −0.14, p = 0.89). The effect on response probability was fairly small and only appeared on congruent trials and none of the RT differences exceeded 10 ms. Nevertheless, the pattern indicates that, on at least some of the trials with prestimulus motor activity favoring the low reward side, this activity reflected a commitment toward the side opposite the alternative associated with a high reward and was associated with final choice and RT.

Overall, the findings suggest that prestimulus motor activity favoring the high reward side often occurs without signaling a strong precommitment, whereas pretrial activity favoring the low reward side sometimes does signal such a precommitment. Of course, we cannot rule out the possibility that some trials with prestimulus motor activity favoring the high reward side may also involve a strong precommitment. The effects of a few such trials mixed in with other, noncommitted trials would not necessarily show up in the comparison with the no-prestimulus motor activity trials.

LRPs on incongruent trials and their relation to manual responses

We next consider the relationship between the LRP on incongruent trials and manual responses. For this analysis, we separated trials into four subtypes based on the choice outcome (correct or incorrect) and the presence of non-negligible motor activity on just one or both of the dynamometers (unimanual or bimanual responses). The resulting LRPs are shown in Figure 11. Approximately 60% of incongruent trials were correct responses. Of these, about half (29% of total) were unimanual, whereas the remainder (31% of total) were bimanual. Importantly, the LRP for the unimanual correct responses showed no dip toward the incorrect side (solid black curve in figure), whereas the bimanual trials (dotted black curves) showed a slight dip toward the incorrect side followed by an abrupt rise toward the correct side. About 40% of the trials were errors and, of these, ∼2/3 (27.6% of total trials) were unimanual error responses. These responses (solid magenta curve) showed a very large LRP toward the incorrect side starting about 150 ms after stimulus onset. The remaining trials, constituting about 1/3 of errors (12.5% of total trials), came from bimanual error trials. Here, the LRP shows a very weak pattern with a relatively small and fairly late deflection toward to incorrect response side.

Figure 11.

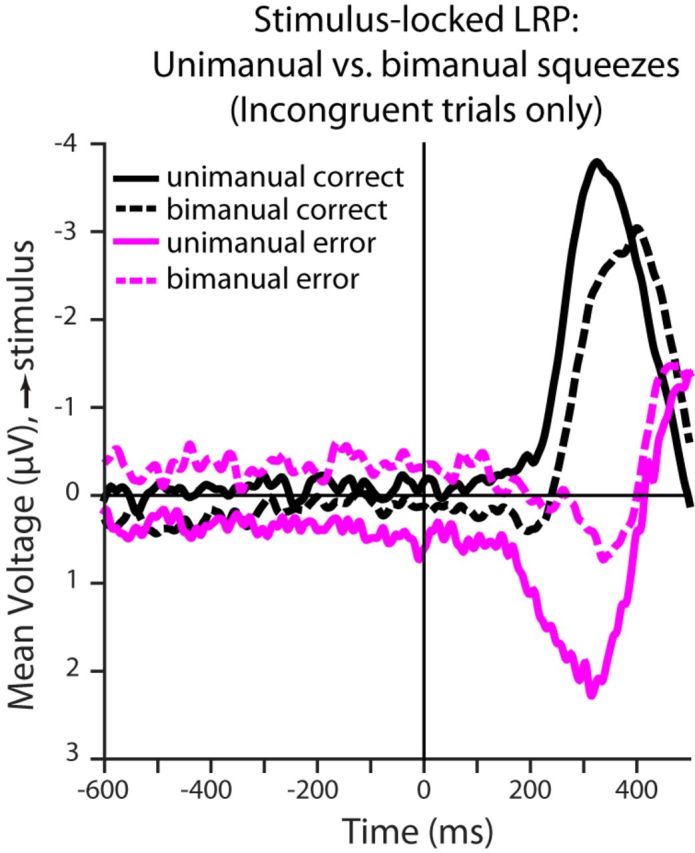
Average stimulus-locked LRPs for correct and error unimanual and bimanual responses in the incongruent condition. Unimanual responses (solid) are classified as trials in which a detectable squeeze was observed in only the sensor corresponding to the ultimate response; for “correct” responses, this corresponds to the lower-paying hand. Bimanual responses (dashed) correspond to trials in which a squeeze was detected in both of the sensors. Although a reversal in potential at ∼150 ms after stimulus presentation is observed in the LRP of bimanual correct responses for the incongruent condition, no such reversal is observed in the LRP of unimanual correct responses. The unimanual error responses show strong activity toward the higher-paying alternative before stimulus information is integrated in the decision process. The numbers of trials that contributed to each average are as follows: unimanual correct, 6844; bimanual correct, 7310; unimanual error, 6517; and bimanual error, 2933.

The LRP patterns shown in Figure 11 support several tentative inferences that motivated our consideration of a fast guess model of the effect of payoff bias on performance in our task. First, the absence of a downward going deflection of the unimanual correct responses is consistent with the idea that the bolus of activity toward the incorrect, high reward side arises from trials in which there was at least some degree of motor activity toward the incorrect response side. A consideration of the correct bimanual and incorrect unimanual LRP curves further supports the conclusion that a large part of the bolus of activity toward the incorrect, high reward side arises from trials that end up producing error responses because the downward trend in these two curves is far stronger for the unimanual errors than for the bimanual correct responses. The early onset of the downward deflection in the unimanual error curves is a key feature of the data supporting the conjecture that these errors may reflect a fast guess process triggered by stimulus onset and unaffected by the accumulation of evidence about the direction of shift of the stimulus. The subtle downward going deflection in the bimanual correct curve is consistent with the view that an early but weak, transitory, or slowly rising squeeze on the incorrect, high reward side, triggered by stimulus onset, was followed shortly thereafter with a strong stimulus-driven squeeze to the correct side that was the first or only response to reach threshold, making the outcome come out scored as correct. Finally, the late downward deflection of the curve for the bimanual error trials is consistent with the idea that these errors were predominantly driven by an slower, stimulus-driven process that happened to favor the incorrect response on this fraction of trials. Activity toward the correct response on these trials may be a mixture of weak, early signals and some late stimulus-driven activity toward the correct side that was too late to determine the outcome of the trial.

The idea that the incorrect unimanual responses in the incongruent condition largely arise from a fast guess process biased toward the high reward alternative predicts that the RTs for such responses will be relatively fast. The behavioral data confirm this prediction. Mean RT was 346 ms in the incorrect unimanual condition and this was faster than the mean RT in any of the other conditions (368 ms for correct unimanual responses; 372 ms for incorrect bimanual responses, and 385 for correct bimanual responses). All 13 participants had faster mean RTs for incorrect unimanual responses than any of the other response types (in all 13 cases, a t test comparing RTs for incorrect unimanual responses to responses of all other types showed the incorrect unimanual responses to be faster; t values ranged from ∼−10 to ∼−16, p ≪ 0.001 in all cases).

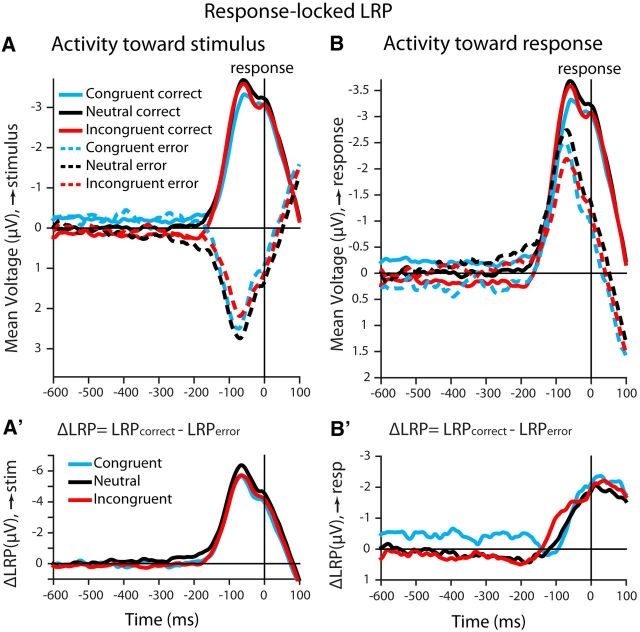
Manifestation of choice in response-locked LRP

The averaged response-locked LRPs of correct and incorrect trials in the three payoff conditions (Fig. 12A) revealed that there was no significant difference in lateralization of activity between correct and incorrect responses until very close to the response time. To better visualize this difference between lateralization of correct and incorrect responses, the differential activity between correct and incorrect was computed (Fig. 12A'). This differential activity was close to 0 up to 200 ms before response, suggesting that the information about choice was only reflected in the LRP close to the time that the response occurred. Furthermore, the observed difference in amplitude of the LRP waveform for correct and incorrect trials led us to reverse the LRP of the incorrect trials (Fig. 12B) to be able to better compare the amplitudes. A mixed-effects linear model of the maximum amplitude regressed on accuracy (correct vs incorrect) with random intercept and slope for subjects revealed that the LRP amplitude of correct trials was significantly larger than the LRP amplitude of incorrect trials (Fig. 12B′, b = 0.86, SE =.33, t = 2.63). One possible reason for this finding is that many error responses are followed by a later response on the correct side. Since the LRP reflects the difference in motor activity in the two hands, this later response may mask the later part of the motor activity produced by the error response itself.

Figure 12.

Manifestation of choice in response-locked LRP. A, The average response-locked LRP is shown for correct and incorrect trials for the three payoff conditions. The upward direction is defined to be activity toward the stimulus. A′, The difference between the response-locked LRP of correct and incorrect trials obtained from LRPs shown in A. The differential activity toward stimulus shows that there is no difference between the average lateralization of correct and incorrect trials in all payoff conditions up to ∼200 ms before response. B, Average response-locked LRP is shown for correct and incorrect trials in which the upward activity depicts lateralization toward the final response. B′, The differential activity between correct and incorrect trials as obtained from LRPs in B shows that correct trials on average have a higher LRP amplitude than LRPs of the incorrect trials. This was true across all three conditions.

Manifestation of RT in the LRP

Thus far, our analysis has concentrated on the ways in which the LRP is related to participants' choices. We next considered the relationship between LRP and participants' RT, focusing on correct trials only. For this analysis, we split the RTs into the fastest 40% and the slowest 40% for each participant across the three payoff conditions. For each participant, we computed the average stimulus-locked and response-locked LRPs for correct trials separately for each combination of RT speed (fast or slow) and each condition (congruent, neutral, or incongruent). We then averaged across participants separately for each of the six cases (Fig. 13). The stimulus-locked LRP waveforms (Fig. 13A) showed no difference in bias during the prestimulus period (defined as sum of LRP in the 200 ms time window before stimulus onset) in the fast trials compared with the slow trials in any of the payoff conditions (neutral: b = −8.09, SE = 18.87,−0.43; congruent: b = 9.15, SE = 19.03, t = 0.48; incongruent: b = −17.04, SE = 19.00, t = −0.90).

Figure 13.

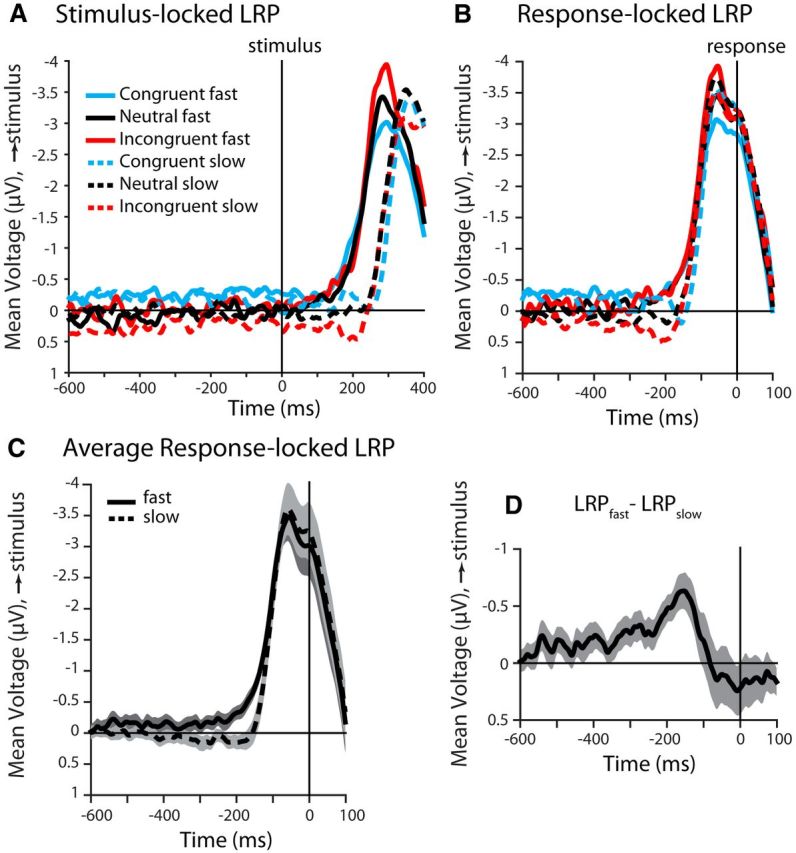
LRP of fast and slow correct trials. A, B, Stimulus-locked LRP (A) and response-locked LRP (B) for fast and slow correct trials. Solid lines show average LRP for fast trials and dashed lines show slow trials. C, Response-locked LRP of fast versus slow correct trials averaged across payoff conditions. D, Differential LRP waveform obtained from subtracting the slow LRP from the fast of C.

In the poststimulus period, fast trials in all payoff conditions were associated with a slowly rising activity immediately after stimulus presentation and before stimulus integration time (∼200 ms). For slow responses, this ramp-like activity before stimulus integration was absent. Furthermore, the LRPs of the slow trials, although shifted in time, demonstrated a sharper rise after onset than the LRP of fast trials. To determine whether this observed difference between fast and slow trial LRP waveforms was merely a result of smearing due to stimulus-locked averaging, we turn to response-locked LRP waveforms.

Response-locked LRPs (Fig. 13B) maintained the difference between fast and slow trials: the onsets of LRPs of fast trials (solid lines) were earlier with respect to response time than the onsets of LRPs of slow trials (dashed lines) across all payoff conditions. To better visualize this difference, the LRP waveforms of the three payoff conditions were averaged into a single waveform for each RT bin (Fig. 13C). The averaged LRPs of fast and slow responses showed a difference around the time of onset, with slow trials having a later onset, as well as a sharper rise, than the fast responses. The differential waveform (Fig. 13D) of fast versus slow responses, obtained by subtracting the response-locked LRP of slow trials from the corresponding LRP of fast trials, shows that this difference was indeed significant based on the 95% confidence interval around this difference score.

To delineate the source of the difference in response-locked LRPs of fast versus slow correct responses, we compared the response-locked manual squeeze behavior of the two RT groups using the dynamometer data. In all the trials considered, the response was scored correct—that is, the squeeze force on the correct dynamometer reached the criterion force level first. We calculated the average squeeze force to the dynamometers for the correct and incorrect hand and the difference between these averages for each payoff condition for each participant and then averaged across participants (Fig. 14). In slow trials, the average squeeze force activity (dashed line) showed muscle activity in the incorrect response dynamometer starting about 100 ms before the criterion is reached on the correct hand. This results in a “dip” in the force difference toward the incorrect response, suggesting that the slower RTs occurred on trials in which there was a subcritical squeeze on the incorrect hand before completion of activation on the correct hand.

Figure 14.

Average response-locked squeeze force of fast and slow correct responses, plotted separately for the correct channel (A) and the incorrect channel (B). C, Difference in squeeze force (correct minus incorrect). In A, neutral fast and slow and incongruent fast and slow curves are coincident. B shows activity in the incorrect channel that begins about 100 ms before the squeeze on the correct hand reaches criterion in slow trials in all three conditions (curves corresponding to congruent and neutral are coincident, for both fast and slow trials). In C, the difference in squeeze force activity on slow trials showed a “dip” toward the incorrect response ∼150 ms before response onset in all three conditions. On average, each participant contributed 730 trials to the congruent fast trials, 495 to congruent slow trials, 289 to incongruent fast trials, 580 to incongruent slow trials, 476 to neutral fast trials, and 580 to neutral slow trials.

A further finding from this analysis is that the rise in squeeze force on the correct hand does not differ between fast and slow trials. Such a finding is consistent with the view that the apparent steeper rise of the LRP on slow trials reflects, not a difference in activation of the correct response hand, but the presence of activity in the incorrect response hand on a subset of the slower trials that masks the early rise of LRP activity associated with the correct response hand.

Results of competitive model fitting

The results described above motivated the idea that payoff effects in our experiment were mediated by a fast guess process that tended to favor the high reward alternative. The high degree of payoff bias in relatively fast responses, coupled with the finding that a poststimulus LRP in the direction of the higher-paying alternative is only present in a subset of trials (those in which dynamometer activity in the incorrect hand is also present) suggested the possibility that the payoff bias seen both in behavior and in the LRP may be associated with a fast response in the direction of the higher-paying alternative on a subset of trials. Accordingly, we constructed a third model incorporating this idea into the competitive model fitting described in this section, along with models in which the effect of payoff is mediated by a shift in the starting point or the rate of accumulation of activation toward a response threshold. The fast guess, starting point, and drift rate models were all formulated within the framework of the LBA model, which captures several key elements of many other decision making models in a mathematically tractable formulation that facilitates model comparison (see Materials and Methods).

All of the models are thought to describe the buildup of activation to a bound corresponding to the squeeze-force threshold, encompassing buildup to the initiation of poststimulus motor activity as well as subsequent buildup of the motor activity to the squeeze-force threshold. It is interesting to consider the possibility that this entire buildup is transparently propagated through to motor activity detectable on the dynamometers. Although this is an intriguing possibility, we note that the models assume some buildup of stimulus-related activity in both accumulators on all trials, yet there are many trials in which there is no detectable motor activity on one of the two hands. This finding is consistent with the idea that, under the conditions of the present experiment, there is an intermediate bound in the evidence accumulation process that must be crossed before motor activity is propagated to the motor system and becomes detectable either in the LRP or in activation of the dynamometers. To keep the models analytically tractable, we have not incorporated this intermediate bound in any of the models.

The models that we had originally planned to compare are the LBA with starting point shift and the LBA with drift rate change. The additional model motivated by the findings reported above is the fast guess LBA model. As illustrated in Figure 3, all three models assume two LBAs for the accumulation of stimulus-driven activation toward the response threshold. As shown in Figure 3, the LBAst assumes that reward bias affects the starting points of the accumulators, whereas the LBAdc assumes that reward bias affects the drift rates of the two alternatives. The FG-LBA model introduces a third accumulator, corresponding to the proposed fast guess process, which is assumed to be triggered by detection of the onset of the stimulus on a subset of trials. This can occur in the neutral condition, but is more likely to occur when the payoff favors one of the two alternatives. In the latter case, the guess is usually, but not always, in the direction of the higher-paying alternative. These models were applied to the distributions of both correct and incorrect responses for the congruent, incongruent, and neutral conditions; each participant's data were fitted separately. For all participants, the FG-LBA shows the closest fit to the data when compared with the other two models (see Materials and Methods for full details of the models and the fitting process). Table 3 shows the mean estimates of the parameters of each model averaged across participants. The fits of the models to individual participant RT data are shown in Figure 15.

Table 3.

Mean parameter estimates for the three models

Parameters	LBAst	LBAdc	FG-LBA
B (fixed)	500	500	500
v0	1.25	1.14	1.55
μs	0.06	0.06	0.14
σs	0.15	0.14	0.22
A	92.19	87.36	62.67
T0	27.33	55.01	91.93
r	16.65	0.05	−
ppu	−	−	0.61
ppn	−	−	0.52
μf	−	−	1.5
σf	−	−	0.5
ph	−	−	0.83

To compare the performance of the three models, Table 4 provides the log likelihood, the AIC, and the BIC values averaged across participants. For all 13 participants, the FG-LBA had the best performance—highest log likelihood and lowest AIC and BIC values—compared with the LBAst and LBAdc models. Visual inspection of each of the 13 participants in Figure 15 reveals large and systematic deviations between predicted and observed patterns for both the LBAst and LBAdc models; the discrepancies are smaller for the FG-LBA model, consistent with the lower AIC and BIC values. Furthermore, the pattern of discrepancies makes clear where the disadvantage of the LBAst and the LBAdc lies: the error response distributions peak at shorter times than these models predict, whereas correct response distributions peak at longer times than these models predict. This pattern is easily seen in the fit to participant S1, for example. The error distributions (circles) have peaks at shorter times than is estimated by either the LBAst or LBAdc models (dashed curves), whereas the correct response distributions (diamonds) have peaks at longer times than estimated by either of these models (solid curves). In contrast, the fitted distributions for both correct and error responses from the FG- LBA model are much more closely aligned with the data histograms, capturing the faster occurrences of errors compared with correct responses. This pattern is characteristic of the advantage of the FG-LBA for all participants, although it is easier to see in the results of S1 than some other participants.

Table 4.

The FG-LBA model provides the best fit to the data as measured by log likelihood, AIC, and BIC

Model	df	Log likelihood	AIC	BIC
LBAst	6	−14123 (234)	28257 (469)	28297 (469)
LBAdc	6	−14161 (236)	28334 (471)	28374 (471)
FG-LBA	10	−13970 (223)	27961(446)	28027(446)

Average goodness-of-fit measures are shown for the three models. Values in parentheses are SE across13 participants for each measure.

To test whether the FG-LBA model was the best model for all participants, we used individual participant's AIC values and computed the relative likelihood of the FG-LBA model with respect to LBAst and LBAdc models (see Materials and Methods for more details). These single-subject AIC values, along with their relative likelihoods, are provided in Table 5. The results (Table 5, columns 5 and 6) can be interpreted as the relative probability that the ith model minimizes the information loss. The extremely low values observed for the relative likelihood of the LBAst and the LBAdc models compared with the FG-LBA model indicate that these models are several orders of magnitude less likely to minimize information loss compared with the FG-LBA model. It is unlikely that the reported results can be attributed to differential effects of outlier responses on fit statistics under the different models. We found that pseudo-AIC values computed after excluding RT bins containing only a single (potentially outlier) response (see Materials and Methods) were only ∼1% smaller than those computed as described above and the FG-LBA model still had the smallest AIC value for each participant by a margin comparable to that reported in Table 4. Overall, the model comparison results suggest that the starting point shift and drift rate change models do not adequately address our data, whereas the FG-LBA provides a far better fit.

Table 5.

AIC and relative likelihood values show the FG-LBA model fits best for each participant

Subject	AIC			Relative likelihood
	LBAst	LBAdc	FG-LBA	LBAst vs FG-LBA	LBAdc vs FG-LBA
S1	28442	28458	27918	1.64E-114	5.50E-118
S2	27867	28276	27743	1.19E-27	1.82E-116
S3	28125	28139	27855	2.35E-59	2.14E-62
S4	26886	26924	26836	1.39E-11	7.78E-20
S5	28561	28589	28342	2.78E-48	2.32E-54
S6	25127	25169	24978	4.42E-33	3.35E-42
S7	27523	27538	27285	2.08E-52	1.15E-55
S8	29451	29495	29285	8.99E-37	2.51E-46
S9	31548	31572	31110	7.75E-96	4.76E-101
S10	27493	27561	27406	1.28E-19	2.20E-34
S11	26444	26489	25943	1.62E-109	2.74E-119
S12	29987	30206	29310	9.80E-148	2.73E-195
S13	29893	29933	29476	2.82E-91	5.80E-100

Given the superior fit of the FG-LBA, it is worthwhile to consider the parameters of the model further. As expected, the probability of initiating a fast guess is higher in the biased payoff condition than in the neutral condition (p_fb = 0.61; p_fn = 0.52); in the biased condition, the guess is initiated in the direction of the higher-paying alternative most, but not all of the time (p_h = 0.83). The mean rate of the fast guess process (μ_f) is comparable to the value of the v₀ parameter, indicating that all three accumulators share a strong, stimulus independent drive toward the bound (mean μ_f and v₀ both ∼1.5). In comparison, the stimulus-dependent component is quite small (mean μ_s = 0.14). Therefore, it appears that the speed advantage of the fast guess process primarily depends on its being initiated 50 ms sooner than the stimulus-driven accumulation processes. It may be of some interest that the fast guess process has more variable drift rate than the stimulus-driven process (mean σ_f = 0.5; mean σ_s = 0.22). Given this variability, the fast guess process will sometimes lose to one of the stimulus-driven accumulators, so that the fast guess, when it occurs, does not always determine the response. This process may, however, often reach a level sufficient to generate a subcriterial squeeze, accounting for the relatively high frequency of trials with subcriterial dynamometer activity on the incorrect, high reward side in the incongruent condition. We estimated the average probability that the fast guess process wins when it occurs to be 0.56, based on the following reasoning. The probability of a fast guess determining the response in either biased conditions is equal to the probability that the fast guess process occurs, given by model parameter p_fb times the probability that it wins when it occurs (p_w). In the congruent condition, the fast guess is correct when it is in the direction of the high reward, given by model parameter p_h, whereas in the incongruent condition, the fast guess is correct when it is not in the direction of the high reward, which occurs with probability (1 − p_h). Therefore, the probability that a fast guess is correct in the congruent condition is equal to p_fbp_wp_h, whereas the probability that a fast guess is correct in the incongruent condition is equal to p_fbp_w(1 − p_h). Because the contribution of the stimulus-driven accumulators is the same for both conditions, it follows that the difference in probability correct between the congruent and incongruent conditions, (pc_c − pc_i) should equal the difference between the probabilities that the fast guesses are correct, pc_c − pc_i = p_fbp_w[p_h − (1 − p_h)]. For each participant, we determined the participant's values of pc_c and pc_i from the data and inserted these, along with the participant's fitted values of the parameters p_fb and p_h, into this expression and then solved for p_w. The mean of these values was 0.56 across participants, with individual values ranging from 0.34 to 0.67. Note that, in this model, the probability that the fast guess process wins is the same in the neutral condition as in the biased payoff conditions because the parameters that affect time to bound are not affected by payoffs in the model. Overall, then, the probability that the fast guess occurs and also wins is about 0.34 in the biased conditions (given by p_fbp_w) and about 0.29 in the neutral condition (given by p_fnp_w).

In spite of the relative success of the FG-LBA model, there is one aspect of the data that it does not perfectly capture. As Figure 4 illustrates, when correct and incorrect responses are considered together, the distribution of response times differs between the congruent and incongruent conditions, particularly for the easy five-pixel stimuli: there are relatively more responses in short RT bins in the congruent condition, and relatively more responses in long RT bins in the incongruent condition. However, the FG-LBA model predicts that these distributions should be the same. This is because, in the model, fast-guess responses are completely independent of stimulus information, and stimulus-driven responses are completely independent of the fast-guess process. In other words, there is a parallel race between the fast-guess and stimulus processes with no interaction between them. The fast guess should win out against the two stimulus processes just as often in both the congruent and incongruent conditions, affecting the overall distribution of RTs (again, disregarding response accuracy) equally in the two conditions. It might be possible for a version of the FG-LBA model to account for this discrepant aspect of the data by including an interaction between the fast-guess and stimulus-driven processes. For example, the stimulus-driven motor response might boost the fast-guess-driven motor response if the two are consistent or might dampen the fast-guess-motor response if the two are inconsistent. Further research is required to explore this possibility.

Comparison with findings of Simen et al. (2009)

A process very similar to the fast guess process in the FG-LBA model was observed in the studies of Simen et al. (2009), which found such effects with both a prior probability and a reward bias manipulation. These studies used a perceptual decision-making task with low-coherence random dot motion stimuli (we were unaware of these studies when we designed the study reported here). Comparison of our task and findings with those of Simen et al. (2009) reveals interesting similarities and differences. Experiment 2 in their study manipulated both prior probability and the duration of the response–stimulus interval (the time between the recording of a response to one stimulus and the presentation of the next one) and found that fast responses in which the latency distribution matched that of simple stimulus detection responses occurred on a subset of trials, with the size of the subset determined both by the degree of prior probability bias and the duration of the response-stimulus interval. Those investigators relied on an optimality analysis of the 1D drift diffusion model (Bogacz et al., 2006) to predict that the combination of a high bias and a short response–stimulus interval should lead to a starting point above the optimal evidence-integration-bound position, thereby supporting the strategy of choosing the more probable option upon detection of stimulus onset. Consistent with this, the fast responses that they observed were nearly always in the direction of the high probability option. Indeed, some participants appeared to adopt what was essentially a simple stimulus detection strategy in some conditions of their experiment, choosing the higher-probability option with a very short latency immediately after stimulus onset on every trial. A similar pattern was observed in the behavior of a subset of participants in their experiment 3, in which a bias was induced by a 3:1 reward ratio favoring one of the two responses. The remaining participants revealed only a slight reward bias captured as a small, suboptimal offset in the starting point of evidence accumulation in a fit of the DDM to their participant's data.

Our study differed from that of Simen et al. (2009) in a number of ways. First, we had two levels of stimulus difficulty rather than only one. Second, we used a stringent deadline to encourage fast responding, whereas they used a short response–stimulus interval. Third, we cued the payoff condition before each stimulus presentation and all payoff conditions were intermixed, whereas, in their studies, payoff was not explicitly cued, but was experienced over a block of trials with a homogeneous payoff. Nevertheless, both investigations found that the predominant effect of reward bias was to induce participants to rely on a fast guess process favoring the higher reward alternative. In both studies, a 50 ms lead time for fast guess responses relative to stimulus-driven responses was inferred from the data, suggesting that there is a 50 ms time cost associated with discriminative responding relative to triggering a predetermined response by the onset of a stimulus. Our findings differed from those of Simen et al. (2009), however, in two respects. First, we found fast guess responses even in the absence of a reward or probability bias in our neutral condition, whereas they found no such tendency in an equal probability condition. Second, we found that participants were not fully consistent in favoring the high reward alternative: they sometimes prepared a fast guess toward the low reward alternative. Below, we consider possible reasons for these differences.

Discussion

We investigated the effect of differential payoffs on perceptual decision making under time pressure using behavioral and LRP measures. As in other studies, payoff information affected choice and response time measures of behavior (Diederich and Busemeyer, 2006; Diederich, 2008; Simen et al., 2009; Rorie et al., 2010; Gao et al., 2011; Leite and Ratcliff, 2011; Mulder et al., 2012): participants chose the higher-paying alternative more frequently and did so with shorter response times, resulting in significantly higher earnings per trial in the unequal payoff condition compared with the neutral (equal payoff) condition.

Neurally, payoff asymmetry was represented in the LRP, which could be decomposed into stimulus- and payoff-related signals. The stimulus-related signal appeared ∼200 ms after stimulus onset. The payoff signal consisted of a shift in the LRP toward the higher-paying alternative before stimulus onset (static component) and an abrupt rise in activity (dynamic component) toward the higher-paying alternative ∼150 ms after stimulus onset and 50 ms before the stimulus-related signal. The prestimulus shift only occurred on the subset of trials with prestimulus motor activity and did not predict choice or response time when it favored the high reward alternative. Subtle choice and RT effects were observed, however, when prestimulus activity favored the low reward alternative. Other studies (Gratton et al., 1988; van Vugt et al., 2014) found early LRP effects that were more strongly associated with response outcomes. Our use of a stringent deadline and other methodological differences may be responsible for this difference between experiments.

The dynamic component of the LRP predicted both choice and response time. This component was also associated with motor activity toward the high reward side—activity that appears to reflect a fast guess response triggered by stimulus onset and usually directed toward the response associated with the higher reward.

Our work is different from most previous studies measuring the LRP in that we have related this measure to activity in the dynamometers used to record behavioral responses. Similar information may be measurable via the electromyogram (Gratton et al., 1988; Scheibe et al., 2009). As noted above, the static and dynamic payoff related LRP signals were only observed on trials where we also detected motor activity in the hand consistent with the direction of the LRP signal. Therefore, in our experiment, the LRP appears to be a motor activation signal, rather than a motor preparation signal. LRPs in other studies may reflect preparation below the level measurable in motor activity and it will be important for future work to assess this. A further point is that the complex shape of the LRP in some conditions can be traced to effects of motor responses on both hands within the same trial and/or to mixing of trials with different patterns of motor behavior. This raises the possibility that complex ERP patterns observed in other studies might similarly arise from the superposition of simpler components.

A model in which payoff bias affects an optional fast guess process fit our data better than alternatives in which payoff bias affects the starting point or the rate of activation toward the higher-paying choice. In our model, the fast guess is usually (but not always) the response with the higher payoff. A process with characteristics similar to our fast guess process was observed by Simen et al. (2009). Our findings corroborate that study's finding that a fast guess process can be initiated 50 ms faster than an activation process associated with stimulus-driven choice between alternatives.

Comparing findings across studies, it is apparent that payoff and stimulus probability manipulations affect processing in different ways depending on task details. For example, Rorie et al. (2010) found that a starting point shift accounted well for payoff bias effects in their task, which required monkeys to withhold responding until a go cue appeared, and Rao et al. (2012) found a similar effect of prior probability using a similar procedure. In contrast, Hanks et al. (2011) used a free-response RT task and found that prior probability predominantly affected drift rate. Each strategy is arguably optimal for the given task setting (Rorie et al., 2010; Hanks et al., 2011). Testing predictions from an optimality analysis presented in Bogacz et al. (2006), Simen et al. (2009) showed that a starting point shift can be optimal for moderate levels of bias in their task, but with extreme levels of bias, it becomes optimal simply to allow stimulus onset to trigger the favored response. Their study observed both starting-point- and fast-guess-like effects consistent with these considerations, although to a lesser extent than necessary to maximize payoff.

One major difference between our task and the above studies of payoff effects is the strong time pressure imposed on participants by the deadline. This may cause participants to rely on a fast guess process on some trials. In this respect, our task is similar to the deadlined decision-making tasks used by Diederich and Busemeyer (2006) and Diederich (2008). These studies explored models in which an early payoff-driven process may often lead to a response before stimulus evidence integration begins, similar to our fast guess process.

Scheibe et al. (2009) conducted an experiment that may have invoked a fast guess strategy as well. In their case, a first stimulus acted as a cue that provided information about the relative probability of the outcome of a subsequent decision. Scheibe et al. (2009) observed a delay in LRP onset when a precue valid 75% of the time proved invalid and used this to argue that there is inhibition between competing hands when there is a conflict between precue and stimulus. In our study, we were able to capture similar effects as consequences of a fast guess process favoring the cued alternative without invoking competitive inhibition. Further modeling work is required to determine whether their inhibition-based model or our fast guess model best describes both sets of data or whether different models are needed to account for performance in these two experiments.

The strategy that participants adopt in response to our task demands may also be affected by uncertainty about the stimulus difficulty, which, in our experiment, is randomly determined for each trial (for similar reasoning, see Hanks et al., 2011). In the case of the difficult stimuli (2 pixels shift), the right strategy may be to guess, whereas for the easy stimuli (5 pixels shift), the right strategy may be to allow the stimulus to determine the response. In a mixed difficulty setting such as our task, the FG-LBA could be seen as an attempt to benefit from both strategies. The race between the fast guess process and the stimulus-driven process sets up a situation in which the stimulus-driven process will be more likely to win the race when driven by a strong stimulus and more likely to lose it when driven by the weak stimulus.

In fitting the fast guess model to our data, we found that fast guesses were not always in the direction of the high reward. Therefore, even with a clear payoff bias, participants occasionally prepared a response favoring the lower-paying alternative. This strategy is clearly suboptimal and is reminiscent of the suboptimal “matching” (rather than “maximizing”) strategy of participants when the task is simply to guess which of two alternatives will appear on the next trial. Together with evidence that participants made fast guesses on some neutral trials in our experiment, the findings suggest that participants may attempt to guess the direction of the stimulus in the upcoming trial, with the payoff cue affecting the probability of a guess in one or the other direction. Such a strategy is superior to completely ignoring the payoff cue, but inferior to the strategy in which the fast guess responses are consistently made in the direction of the higher payoff. Guessing against the payoff bias and guessing in neutral conditions were not observed in the study of Simen et al. (2009), consistent with the idea that such strategies may arise as a response to a mixture of difficulty levels or to the strong deadline pressure in our experiment. Neither of these features was present in the Simen et al. (2009) experiments. However, there were other differences between the experiments. Different payoff conditions were intermixed and cued before each trial in our experiment, whereas they were fixed within a block in Simen et al. (2009), and this difference could have contributed to the differences in the pattern of results between the two studies.

In summary, our behavioral, neural, and muscle activation data support the idea that, under the conditions of our task, payoff information is incorporated in the decision-making process through a probabilistic fast guess process that races with stimulus-driven processes. This fast guess process is apparent in both the LRP data and in the dynamometer data. Our experiment shows that the use of the relatively high squeeze force criterion for the dynamometers allows elements of the decision-making process to be visible in motor behavior. Further experiments with these characteristics might be a fruitful way of allowing the use of muscle activation, as measured easily using dynamometers, to shed further light on the dynamics of decision making.

Notes

Supplemental material for this article is available at http://web.stanford.edu/group/pdplab/projects/NoorbaloochiEtAlPayoffBiases. The URL contains data used in our analyses, MATLAB code used to fit the Fast Guess LBA model, and a short description of all the files. This material has not been peer reviewed.