Posterior Parietal Cortex Encoding of Dynamic Hand Force Underlying Hand–Object Interaction

Abstract

Major achievements of primate evolution are skilled hand–object interaction and tool use, both in part dependent on parietal cortex expansion. We recorded spiking activity from macaque inferior parietal cortex during directional manipulation of an isometric tool, which required the application of hand forces to control a cursor's motion on a screen. In areas PFG/PF, the activity of ∼70% neurons was modulated by the hand force necessary to implement the desired target motion, reflecting an inverse model, rather than by the intended motion of the visual cursor (forward model). The population vector matched the direction and amplitude of the instantaneous force increments over time. When exposed to a new force condition, that obliged the monkey to change the force output to successfully bring the cursor to the final target, the activity of a consistent subpopulation of neurons changed in an orderly fashion and, at the end of a “Wash-out” session, retained memory of the new learned association, at the service of predictive control of force. Our findings suggest that areas PFG/PF represent a crucial node of the distributed control of hand force, by encoding instantaneous force variations and serving as a memory reservoir of hand dynamics required for object manipulation and tool use. This is coherent with previous studies in humans showing the following: (1) impaired adaptation to a new force field under TMS parietal perturbation; (2) defective control of direction of hand force after parietal lesion; and (3) fMRI activation of parietal cortex during object manipulation requiring control of fine hand forces.

SIGNIFICANCE STATEMENT Skilled object manipulation and tool use are major achievements of primate evolution, both largely dependent on posterior parietal cortex (PPC) expansion. Neurophysiological and fMRI studies in macaque and humans had documented a crucial role of PPC in encoding the hand kinematics underlying these functions, leaving to premotor and motor areas the role of specifying the underlying hand forces. We recorded spiking activity from macaque PPC during manipulation of an isometric tool and found that population activity is not only modulated by the dynamic hand force and its change over time, but also retains memory of the exerted force, as a reservoir to guide of future hand action. This suggests parallel parietal encoding of hand dynamics and kinematics during object manipulation.

Introduction

Major achievements of primate evolution are skilled hand action and tool use (Iriki and Taoka, 2012), consequences of the evolution of the corticospinal system (Lemon, 2008) and of parietal cortex (Orban et al., 2006; Padberg et al., 2007; Caspers et al., 2011; Mars et al., 2011). Inferior parietal lobule (IPL) (Taira et al., 1990; Sakata et al., 1995; Murata et al., 2000; Fogassi et al., 2005; Rozzi et al., 2006, 2008; Bonini et al., 2010; Sakaguchi et al., 2010) and ventral premotor (PMv) areas (Murata et al., 2000; Bonini et al., 2011) form a network that encodes object features and hand kinematics underlying hand–objects interaction in monkeys, as well as tool use in humans (Johnson-Frey et al., 2005; Peeters et al., 2009; Gallivan et al., 2013). The visual information about object properties is crucial to shape the hand geometry for grasping. However, in addition to kinematics, the specification of the direction, magnitude, and change over time of hand force is required because skilled hand actions depend on continuous and time-varying framing and updating of both kinematic and kinetic variables. Finally, memory of the dynamic force specified during manipulation is desirable for predictive hand action control.

It has been held since long time that parietal cortex is more concerned with movement kinematics than kinetics (Kalaska et al., 1989, 1990; Sergio et al., 2005; Hamel-Pâquet et al., 2006). However, force-related parietal cell activity has been analyzed during arm movement in superior parietal lobule (SPL) areas (2 and 5/PE) that lack visual input, never in IPL areas concerned with hand visuomotor control. Therefore, it remains to be determined where the specification of the dynamic force necessary for fine movements during hand interaction with objects occurs in parietal cortex. One can assume a strictly hierarchical scheme where higher-order parietal areas specify hand kinematics and downstream output-related frontal areas “add” kinetics to finely control force and its change over time. However, the reciprocal connectivity between IPL and PMv areas (Matelli et al., 1986; Rozzi et al., 2006) and the parallel nature of corticospinal projections from multiple frontal areas (Dum and Strick, 1991; Lemon, 2008) make this scheme problematic. Furthermore, there are several evidences in favor of a functional role of parietal cortex in a higher-order control of hand force. fMRI studies (Ehrsson et al., 2001) suggest that the anterior intraparietal cortex is more involved in the control of fine fingertip forces during object manipulation than during the application of larger forces, generally not necessary when manipulating delicate objects. In addition, while in humans TMS interference over IPL during force-field adaptation impairs learning the novel task dynamics (Della-Maggiore et al., 2004), parietal patients suffer from defective control of the direction of hand force (Ferrari-Toniolo et al., 2014). These studies in humans indicate that a force signal is available to parietal cortex. Based on anatomical and physiological results and on the putative correspondences between parietal areas across evolution, we predicted that in monkeys a force signals underlying grasping and object manipulation could be detected at single-cell level in IPL areas, such as PFG/PF (Gregoriou et al., 2006), which project to PMv. Therefore, the choice of the areas of recording was dictated by anatomical studies in monkeys, as well as by activation and lesion studies in humans, the latter from both reversible silencing of PPC in normal subjects and from parietal lesion in patients.

To address this issue, we have trained two macaque monkeys to exert forces in different directions on an isometric joystick, so as to move a visual cursor toward different targets on a visual display. We found that the population activity in IPL areas PF/PFG encoded the direction and amount of the “instantaneous” hand force changes. After the acquisition of a new visuomotor rule by the monkey, a significant number of force-related cells, dynamically changed their original neural representation of force, retaining memory of previous hand dynamics.

Materials and Methods

Animals and surgical procedures.

Two male rhesus monkeys (Macaca mulatta; Monkey 1 and Monkey 2; body weight 7.5 and 8.5 kg, respectively) were used. All surgical procedures were performed under aseptic conditions. The animals were preanesthetized with ketamine (10 mg/kg, i.m.) and anesthetized with a mix of oxygen/isoflurane (1%–3% to effect). A circular recording chamber (18 mm inner diameter) was mounted over the left inferior parietal lobule, to allow recording from inferior parietal areas PF/PFG (Gregoriou et al., 2006) (see Fig. 1C). At the end of the experiment, in a post-mortem examination, the dura was opened and reference pins were inserted at known chamber coordinates, so as to delimitate the recording region and facilitate recognition of the entry point of microelectrode penetrations and their reconstruction relative to key anatomic landmarks (see Fig. 1C), such as the central, the intraparietal, and the superior temporal sulcus.

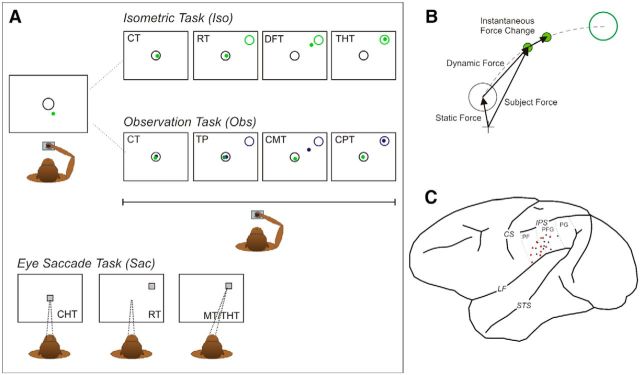
Figure 1.

Apparatus, tasks, and recording sites. A, The monkey controlled a cursor (green dot) on a screen, by applying a force pulse on an isometric joystick, so as to perform two types of intermingled trials of an Iso and Obs task. All trials began with the presentation of a circle on the center of the screen (A, leftmost panel), where the animal had to guide the cursor from its rest position (cross, B), by exerting a static force (B) for a variable CT. In the Iso trials, a peripheral green target was presented in one of eight positions, and within a given RT the monkey had to guide the cursor toward the new location, by exerting a dynamic force of appropriate magnitude and direction (DFT; THT). In the Obs trials, while keeping the cursor on the central target from the CT until the end of the trial, for the entire time in which the peripheral target (blue) was lighted, the animal observed the movement of a second cursor (blue dot), with movement kinematics determined in its own previous Iso trials (TP, CMT, CPT). In the Sac task, the monkey performed saccades to a visual target presented in one of eight locations. The animal used the right arm, contralateral to the recording chamber. B, Schematic representation of the different forces applied by the animal. C, Recording sites in areas PF/PFG of Monkey 1 (red) and Monkey 2 (black). CS, Central sulcus; IPS, intraparietal sulcus; LF, lateral fissure; STS, superior temporal sulcus.

Animal care, housing, and surgical procedures were in conformity with European (Directive 63-2010 EU) and Italian (DL 26-2014) laws on the use of nonhuman primates in scientific research.

Experimental apparatus, behavioral control, and tasks.

Animals were placed in a darkened, sound-attenuated chamber and seated on a primate chair, with their head fixed in front of a 40-inch monitor (100 Hz, 800 × 600 resolution, 32-bit color depth; monitor-eye distance 150 cm) and were instructed to control a visual cursor on the screen by applying a force pulse on an isometric joystick (ATI Industrial Automation), which measured the force applied with the hand in two dimensions, with a sampling frequency of 1000 Hz (see Fig. 1A). During the experiment, monkeys used the right arm, while their left arm was gently restrained.

Monkeys were initially trained in three different tasks (Iso, Obs, Sac, see below; see Fig. 1A). In addition, during some recording sessions, they were unexpectedly exposed to a fourth task (Re-Cal; see below) in which they were required to change the force output to adapt to a new force condition, without prior training. In each task, a minimum of 64 trials were collected because the animals performed at least eight replications for each movement directions. Successful trials were rewarded with water or fruit juice.

Isometric hand task (Iso).

In a classical center-out task, a central target [2 degrees of visual angle (DVA) in diameter] and a cursor (0.6 DVA in diameter) were first presented on the screen (see Fig. 1A), separated by a small offset distance. By exerting a force on the joystick, the animal was trained to move the cursor within the central target, and to keep it there by exerting a constant static force for a given control time (CT, 500–600 ms), at the end of which one of eight peripheral visual targets was presented (8 DVA eccentricity). After a reaction time (RT; upper limit 800 ms), by applying a dynamic force for a given time (dynamic force time, DFT, upper limit 2000 ms), the animal had to move the cursor from the center to the lighted target and maintain the cursor there for a variable target-holding time (THT, 50–100 ms). The reward was given if each trial was performed within the prespecified temporal limits. It is worth stressing that, to move and bring the visual cursor to the target, the animal applied a proper force amount in given directions, in the absence of joint movement. Typically a force pulse of 1N resulted in a cursor displacement of 2.5 DVA. Therefore, the animal had to increment its force exerted on the joystick of ∼3.2 N to bring the cursor from the center to the peripheral position (8 DVA eccentricity). The task was characterized by spatial compatibility because the cursor endpoint coincided with the position of the target, but the animal worked in a condition of spatial and temporal uncertainty, since he could not predict when and where the next target would have been presented. In this task, the animals were free to move their eyes without any particular constraint.

Observation task (Obs).

Intermingled with previous task, in 50% trials an Obs task was presented, with temporal structure similar to that of the Iso task (see Fig. 1A). During the CT (500–600 ms), the animal guided its cursor inside the central target; a peripheral target was then presented (TP), and after a variable time, that on average was equal to the RT of the Iso, another cursor started to move toward it. While holding its own cursor on the central target for the entire duration of the trial, the animal was required to look on the screen during the time characterized by the cursor's motion (CMT). From trial to trial, the cursor moved with variable velocity and acceleration, which on average were those of the cursor's movement resulting from the output force of the animal, as recorded in the Iso task. Indeed, the visual cursor kinematics in the Obs task was that determined by the hand output kinetics (applied force) of the monkey acting on the joystick in the Iso task. Similarly to the THT epoch of the Iso task, the moving cursor remained within the peripheral target for a variable time (CPT, 50–100 ms). The reward was given if the animal held its own cursor within the central target until the end of the CPT epoch. As in the Iso task, the animals were allowed to move their eyes freely. Iso and Obs trials were presented in a pseudo-random sequence, until in each task eight correct replicas were collected in any direction.

Recalibration task (Re-Cal).

To dissociate the direction from the amount of force exerted by the animal, a variation of the Iso task was used, by reducing to 1/2 the “gain” between the force exerted on the joystick and the cursor's displacement. Under this new condition, a force pulse of 1N determined a cursor displacement of 1.25 DVA. The animal had to recalibrate its hand force output, so as to compensate for the unexpected perturbation. After adaptation, the perturbation was removed during a “Wash-out” session, so as to allow the animal to return to its basic preperturbation performance (i.e., Iso task).

Saccade task (Sac).

To study the influence of eye-related signals on the neural activity recorded during the Iso, Re-Cal, and Obs, a saccadic eye movement task was used as control. The monkeys fixated a white central target for a variable center-holding time (CHT, 700–1000 ms). Then, one of eight peripheral targets was presented at 45° angular interval, on a circle of 8 DVA radius. To obtain a liquid reward, the monkey was required to make a saccade to the target and keep fixation there for a variable THT (300–400 ms). Upper limit for eye reaction time (eRT) and movement time (eMT) were both set at 800 ms.

In all task conditions, eye movements were sampled (at 220 Hz) through an infrared oculometer (Arrington Research) and stored together with joystick force signal and key events, which were sampled at 1 kHz.

The National Institutes of Health-funded software package REX was used to control stimuli presentation and to collect eye movement and hand force data.

Behavioral analysis.

The force applied by the animal (subject force) was measured through an isometric joystick. At the beginning of each trial, an offset was applied to the cursor's position (see Fig. 1B), requiring the subject to exert a force (static force) to bring it into the central target, and to keep it there during the CT. To move the cursor from the center to the peripheral target, the force had to be dynamically changed in amplitude and direction. Therefore, the vector describing the force exerted by the subject on the joystick can be decomposed in a static and a dynamic component, according to the relation: subject force = static force + dynamic force (see Fig. 1B).

The instantaneous force change during the cursor motion was defined at each time point as the difference vector between the force at a given 10 ms time bin t and the force at the previous time bin as follows:

where “force” can equally represent either the subject force or the dynamic force, being the static force component constant in time. Given that the cursor position on the screen was proportional to the applied force, the instantaneous force change was proportional to the displacement of the cursor between two consecutive time bins and, consequently, to its instantaneous velocity on the screen.

The force signal was low-pass filtered (FIR filter, cut frequency 30 Hz, order 100) and down-sampled to 100 Hz.

The RT was defined as the time elapsing from the presentation of peripheral target to the onset of the cursor's motion, whereas the DFT was defined as the time from the cursor's motion onset to its entry into the peripheral target, thus corresponding to the entire cursor's motion time. The cursor motion onset was determined as the first deviation of cursor velocity exceeding 3 SDs of the signal calculated around target onset (from 50 ms before to 50 ms after target onset time), for at least 90 ms.

Cursor trajectories.

To determine the degree of similarity of directional orientation of the cursor trajectories across different remapping conditions (Iso, Re-Cal, Wash-out), for each trial we calculated the polar coordinates (ρ, θ) of the moving cursor at the mid-time (t_M) of the DFT, which corresponds to the interval from the cursor's motion onset to its entry into the peripheral target. It is worth noticing that the angle θ of this “checkpoint” can be seen as a measure of the direction of the dynamic force at the time t_M. Then, for each of the 8 peripheral targets, we computed the differences between the angular means (<θ_Iso(i)>, <θ_Re-Cal(i)>, <θ_Wash-out(i)>, for i = 1, …, 8) of the three angular distributions ({θ_Iso(t_M)}, {θ_Re-Cal(t_M)}, {θ_Wash-out(t_M)}) obtained from all trials collected in the three task conditions. The significance of these differences was assessed through the Watson-Williams multisample test (Watson and Williams, 1956; Berens, 2009). This was performed for each target location to study the homogeneity of the three samples mean ({θ_Iso(t_M)}, {θ_Re-Cal(t_M)}, {θ_Wash-out(t_M)}). The test was performed both for the set of trials of a single session (as that shown in Fig. 4), as well as on the set of all trials pooled across different recording sessions.

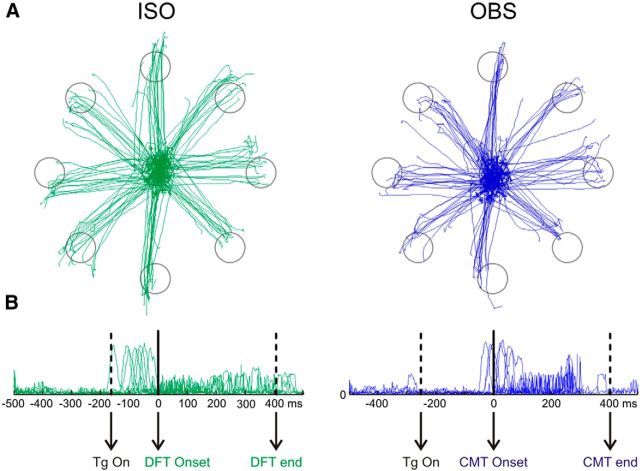
Figure 4.

Eye movement pattern in the Iso and Obs tasks from Monkey 2. A, Eye trajectories from the central position toward the eight peripheral targets (gray circles). B, Eye velocity profiles aligned to DFT onset (Iso, left), and to the cursor's motion onset (Obs, right). Conventions and symbols as in Figure 3C.

Electrophysiological recordings.

Neural activity from single cells was recorded extracellularly through a 5 channel multiple-electrode matrix (Thomas Recording) equipped with quartz-insulated platinum-tungsten fibers 80 μm diameter, 0.8–2.5 MΩ impedance. Electrodes were equidistantly disposed in a linear array with interelectrode distance of 0.3 mm and inserted through the intact dura into the cortical tissue, while grounding and reference were provided by the dura. The raw signal was amplified, digitalized, and optically transmitted to a digital signal-processing unit (RA16PA-RX5-2, Tucker-Davis Technologies) where it was stored together with the key events at 24 kHz. We also filtered in actual time the raw signal with a digital biquad filter (0.3–5 kHz), to obtain a threshold-triggered, window-discriminated single unit activity (SUA). SUA data were further discriminated offline.

Analysis of neural data

Single-unit activity.

To characterize the firing rate of a single unit in the different tasks and directions, the spike density function (SDF) during each trial was first calculated. The SDF, obtained by convolving the spike train data with a Gaussian kernel (30 ms width, 1 ms resolution), was then averaged over successive 10 ms time bins, thus obtaining the temporal evolution of the firing frequency with a sampling rate of 100 Hz. The mean firing frequency for the epochs of interest (RT, DFT) was calculated as the averaged SDF across replications during each epoch. A two-way ANOVA (Factor 1: epoch; Factor 2: direction) was used to assess significant modulation of cell activity within a particular epoch, relative to CT (p < 0.05 for any factor or for their interaction). A further two-way ANOVA (Factor 1: condition; Factor 2: direction) was used to test significant (p < 0.05, for Factor 1 or for the interaction) differences of cell activity across different tasks.

To evaluate the interdependency between the amount of applied force and single-cell activity, a correlation analysis was performed. In particular, for each cell, we measured the correlation of the firing rates differences computed between two remapping conditions (e.g., Iso vs Re-Cal) and the corresponding variation of force output. The data (activity or forces) recorded during DFT were first averaged at each time bin across replications, then for each direction and for each of the three different comparisons (Iso vs Re-Cal; Re-Cal vs Wash-out; Iso vs Wash-out), we computed the differences between data associated at each task condition. The 24 (3 comparisons × 8 directions) time series of these differences were then placed tip-to-tail to generate two single long signals, one for the activity and the other for the force variations, on which the correlation was then calculated. As force-related variables, we considered both the dynamic force and the force changes over time.

Population activity.

The population SDF was obtained by first standardizing each unit's SDF across all task conditions. The average activity and its standard error (SE) across all units was then computed for each bin, thus obtaining the temporal evolution of the standardized population SDF. To compare the population activity across two conditions (e.g., Iso vs Re-Cal), during epochs of interest, the average value of each unit's standardized SDF was computed. The resulting activities were then compared by means of a two-sample t test (p < 0.05).

Directional tuning of single cells.

The directional tuning of cell activity was computed through a nonlinear fitting procedure. A truncated cosine function was fitted into the experimental mean firing rates, calculated during the epochs of interest (e.g., RT, DFT, THT), using the least square method. The fitting model was described by the following directional tuning function as follows:

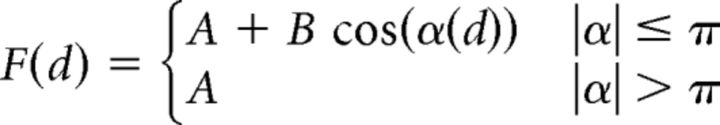where F is the firing rate (in Hz) as a function of the direction of movement (d) expressed in radians. The argument of the cosine function, α(d) = (d − PD) · π/TW, contains two fitting parameters: the preferred direction (PD) expressed in radians, and the tuning width (TW, radians). The other parameters resulting from the fitting procedure (A and B) are linked to the tuning gain (TG) and to the baseline firing rate (BF) by the relations: TG = 2B and BF = A − B.

The statistical significance of the directional tuning was assessed using a bootstrap procedure, to test whether the degree of directional bias of the tuning curve could have occurred by chance (Georgopoulos et al., 1988). The parameter used in this procedure was the tuning strength (TS), defined as the amplitude of the mean vector expressing the firing rate in polar coordinates (Crammond and Kalaska, 1996). This quantity represents the directional bias of the firing rate: TS = 1 identifies a cell that only discharges for movements in one direction, whereas TS = 0 represents a cell with uniform activity across all directions (Batschelet, 1981). A shuffling procedure randomly reassigned single-trial data to different target directions, and the TS was determined from the shuffled data. This step was repeated 1000 times, obtaining a bootstrapped distribution of TS, from which a 95% (one tailed) confidence limit was evaluated. A cell was labeled as directionally tuned in a specific epoch if the TS value calculated from the original unshuffled data was higher than the computed confidence limit (p < 0.05).

Population vector analysis.

To study the directional correspondence between the overall population activity and the behavioral output as a function of time, a population vector (PV) analysis was performed. The analysis was performed on the neural and behavioral data from 500 ms before to 500 ms after the cursor's motion onset.

The population vector $\overrightarrow{PV}$ for a given target direction d at a given time bin t, was calculated in standard fashion as follows:

where ${\overrightarrow{PD}}_i$ is the preferred direction of the i-th cell and w_dⁱ(t) is its weighted discharge rate during movements toward targets in direction d, at time t. The PDs were obtained from neural activity collected during DFT of Iso, Re-Cal, and Wash-out tasks.

The weight function for a given cell was defined as follows:

where FR_d(t) is the firing rate of that cell at time t for movements toward direction d, FR_avg(t) is its discharge rate averaged over all directions at each time bin (t), and R(t) = (max(FR_d(t)) − min(FR_d(t)))/2 represents the half-range of its activity across directions (Georgopoulos et al., 1988). By using this weight function, the contribution of each cell to the population vector is normalized, ranging from −1 to 1 for symmetrically distributed firing rates.

The population of cells used to compute the PV included only the units that showed a significant directional tuning (see above) during the DFT of the center-out task.

To assess how the population vector predicts the behavioral data, the time series of the ${\overrightarrow{PV}}_i$ was compared with that of the vectors (${\overrightarrow{FV}}_i$) representing time-varying force variables, such as dynamic force and instantaneous force change. The subject force (static force + dynamic force) was excluded from this analysis because the influence of the static component was constantly added along the entire duration of the trials (from the CT onset to the end of THT) and identical across tasks (Iso and Obs) and peripheral targets (1–8). Therefore, its contribution to neural activity, in our experimental setup, cannot be disentangled from that of the other forces. At each time point i, the angle between the ${\overrightarrow{PV}}_i$ and the ${\overrightarrow{FV}}_i$, associated to a given force was computed, and its average across all time bins was used as a measure of the distance between the two vector series. By shifting in time the $\overrightarrow{PV}$ relative to the $\overrightarrow{FV}$ (between −300 and 300 ms, in 10 ms steps), the time lag yielding the lowest distance was identified. This procedure was repeated for the two force parameters (dynamic force, instantaneous force change) to identify the one that was best represented by the $\overrightarrow{PV}$.

Decoded trajectories of cursor motion.

A neural representation of the applied force in time, and therefore of the resulting cursor trajectory, based on the information encoded by the population vector, was constructed following two different hypotheses. As a first hypothesis, the $\overrightarrow{PV}$ was assumed to encode the dynamic force, that is, the force to be exerted by the animal to bring the cursor from the center to the periphery (see Fig. 1B). Therefore, a representation of the applied force at each time bin was obtained by placing each instantaneous population vector ${\overrightarrow{PV}}_{\left(t\right)}$ at the center of the workspace. As a second hypothesis, the $\overrightarrow{PV}$ was assumed to encode the instantaneous force change (i.e., the infinitesimal increment of force applied at any given time). In this case, a representation of the predicted force exerted on the joystick was obtained by connecting tip-to-tail all the ${\overrightarrow{PV}}_{\left(t\right)}$, with t starting at the movement onset time (Georgopoulos et al., 1988). To quantify the similarity between the “actual” cursor trajectory resulting from animal force application and the “decoded” trajectory reconstructed from the PV analysis, a vector time series were first constructed from each of the trajectories to be compared, with elements representing the displacement between two consecutive points. The mean angular difference between these vector series was then computed as described above, and the resulting angle was used as a measure of the similarity between the decoded trajectories and the actual cursor's trajectories.

Results

In this section, neural data will be described in association to the animals' behavior as studied in a quantitative fashion during task performance.

Relationships between cell activity and hand force

We recorded the activity of 571 single cells in inferior parietal areas PF/PFG (Fig. 1C). The proportion of cells with activity significantly modulated and directionally tuned in the Iso, Obs, and Sac tasks is shown in Figure 2. Figure 3A₁ illustrates the activity of a typical neuron during isometric force production (Iso), visual observation (Obs), and saccadic eye movements (Sac) tasks, together with the behavioral variables recorded during spikes collection (Fig. 3A₂). In the Iso task, the firing rate of this neuron varied in a significant fashion (ANOVA, p < 0.05) during the RT and DFT, in both cases depending on the direction of the force output (p < 0.001). This cell was poorly modulated while the animal observed (Fig. 3A_1; Obs and Iso vs Obs) on the screen the cursor motion generated by its own force output. The cursor trajectories (not visible to the animal) are shown in Figure 3A₂. The difference in cell firing rate between the Iso and the Obs task emerged in a significant fashion (p < 0.001) during the DFT, although it was not present during the RT, as expected. It is worth stressing that, during the entire duration of the Obs trials, the animal held the cursor immobile on the center target, thus exerting only a static force of identical strength to the one applied in the Iso task during the CT and RT, as can be seen from the hand force and speed profiles (Fig. 3A₂). Therefore, during the time elapsing from peripheral target presentation to the onset of cursor motion (RT in Iso and TP in Obs), the Iso and Obs trials were behaviorally identical, at least in terms of force exerted by the animal on the joystick. In the Iso task, this cell's activity was described by a broad directional tuning function, with a significant preferred direction (PD) at 343° and 322°, during RT and DFT, respectively (Fig. 3B). No significant tuning was observed during the Obs and Sac task (Fig. 3A₁,B). The analysis of the population SDFs (Fig. 3C) showed that, in both monkeys, for the entire duration of DFT, the neural activity during the Iso task was significantly higher (p < 0.001) than during the Obs task. Interestingly, this difference was not significant (p = 0.17 for Monkey 1, p = 0.95 for Monkey 2) during the RT, when the animal exerted a similar static force under both task conditions, but emerged during the DFT, therefore during dynamic force production. This indicates that what is encoded at the population level are force modifications relative to the static force exerted during control time. The specific form (dynamic force or instantaneous force change) will be determined through the population vector analysis. At the population level, the comparison of Iso versus Obs task showed that the activity of approximately half of cells (51% in Monkey 1; 47% in Monkey 2) was significantly different during DFT. In a minority (7% in Monkey 1; 10% in Monkey 2) of cells, a significant difference between the firing rates in the two tasks was observed during the RT, with half of them differing also during the DFT.

Figure 2.

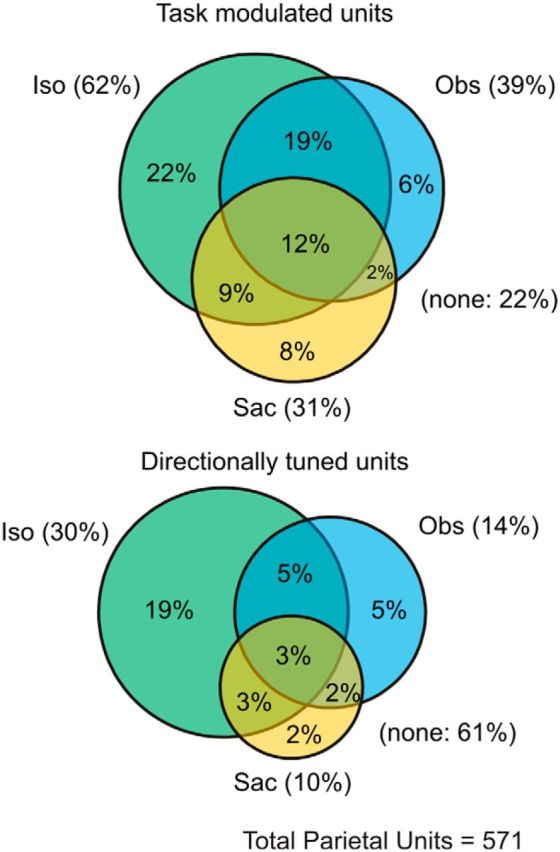
Percentages of cells modulated and directionally tuned. Venn diagrams showing the proportions of cells significantly modulated (ANOVA, p < 0.05) and directionally tuned (bootstrap, p < 0.05) in the different task conditions. Task acronyms as in Figure 1.

Figure 3.

Neural activity recorded from area PF/PFG during Iso and Obs task. A₁, Neural activity of a typical cell recorded during the Iso, Obs, and Sac task, displayed in the form of raster plots, with the SDFs superimposed in eight different directions. The comparison of the activity in the Iso and Obs task is shown (Iso vs Obs) with the relative SDFs. In the Iso and Obs tasks, activity is aligned to the onset of ramp force (0 ms; black vertical line). Gray vertical lines before and after the onset of DFT indicate target presentation and cursor's entry on the target, respectively. In the Sac task, neural activity is aligned to the onset of eye movement (0 ms; black vertical line). Red line indicates the end of the saccade. Gray lines before and after 0 ms indicate target presentation and end of the eye THT, respectively. A₂, Behavioral data collected during recording of cell activity shown in A₁: dynamic force pulses (thin curves), force velocity profile (thick curves) during the Iso and Obs tasks. For the Sac task, eye position (thin gray curve) and eye speed (thick black curve) are shown. Right, Cursor's motion trajectories toward the eight peripheral targets (gray circles) resulting from force application in the Iso task. B, Polar plot of mean firing rate (± SE) of cell shown in A₁, for different epochs of the Iso (green), Obs (blue), and Sac (yellow) task (CT, RT, DFT, THT of the Iso task; CT, TP, CMT, CPT of the Obs task; CT, eRMT, eTHT of the Sac task). For this cell, a significant tuning (PD, green arrow) is present only during the RT and DFT of the Iso task (CT, RT, DFT, THT epochs of the Iso task; TP, CMT, CPT epochs of the Obs task; eRMT, eTHT epochs of the Sac task). C, Mean standardized population SDF (± SE) relative to the Iso (green), Obs (blue), and Sac (yellow) tasks in both monkeys (N, number of units).

It is worth noticing that the difference in population activity between Iso and Obs tasks cannot be attributed to different eye movement strategies by the animals. Indeed, when animals made eye movements to the peripheral targets (Sac task), the population activity was not modulated in Monkey 1 (Fig. 3C), although it was weakly modulated in Monkey 2. However, in this case, the difference of population activity between Iso and Obs tasks cannot be considered as saccade-related because eye trajectories were very similar across these task conditions (Fig. 4A). This was true despite that the animals were free to select their own eye movement strategy, due to the absence of behavioral constraints. Furthermore, the reduction of population activity observed in the Obs task could potentially be due, not only to the lack of dynamic force application, but also to an overall absence of an intended action. Therefore, as it will be described below, to gain more information on the influence of force output on neural activity, we tested a subset of cells in a variation of the Iso task. In this new condition, the animals were unexpectedly required to exert a double amount of force on the joystick, to bring the cursor from the center to the peripheral target.

The neural basis of learning a new task dynamics

The activity of a group of 76 cells was studied in the Re-Cal task, during which the animal had to remap the force output on the cursor's motion by changing the hand force applied to the joystick. After adaptation, the cells were retested during a “Wash-out” session, in which the perturbation was removed, so as to allow the animal to return to the basic preperturbation performance typical of the Iso task (Figs. 5A₂, 6C).

Figure 5.

Neural activity recorded from area PF/PFG during Iso and Re-Cal task. A₁, Neural activity of a typical cell recorded during the Iso, Re-Cal task, and Wash-out task, displayed in the form of raster plots (dots), in eight directions. Gray shaded area represents the time elapsing form the onset to the end of cursor's motion on the screen. A₂, Behavioral data relative to recording session shown in A₁ and temporally aligned to cell activity. In each column, the 8 curves represent the mean dynamic force pulses during each task condition. A₁, A₂, Neural activity and force ramps are aligned to the onset of force application (0 ms). Vertical gray bars represent the mean time of peripheral target presentation. From the same recording session, cursor's trajectories (bottom) resulting from force application in each task conditions are plotted. B, Polar plots of mean firing rate (± SE) of the cell shown in A₁, computed during RT, DFT, and THT in the three task conditions: green represents Iso; red represents Re-Cal; blue represents Wash-out. In each plot, only significant PDs (arrows) are reported. C, Colored lines indicate for each peripheral location the mean angle of the checkpoint direction <θ(t_M)> in the three task conditions (colors as in B). Asterisks indicate movement directions for which the angles are significantly different (Watson-Williams test, p < 0.05) across task conditions, during this recording session. D, Examples of distributions of angular orientation of cursor trajectories across tasks. In each plot, the distributions of the “checkpoint” polar coordinates θ computed for each trajectory (after pooling data from different sessions) are represented for two typical peripheral target locations (45° and 225°). Each data point distribution associated to a given task (colors as in B) is plotted at arbitrary constant radial distances for graphical purposes. Mean values of θ angles for each distribution are represented by relative colored lines. For all task comparisons, the differences of mean angles are indicated. Statistical test (Watson-Williams test; p < 0.05) assesses significant differences of mean angles across the three task conditions. n.s., Not significant.

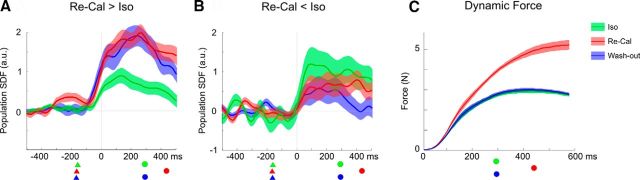
Figure 6.

Average instantaneous firing rates from cells that changed their activity after being exposed to a new task dynamic. A, Mean standardized population SDFs (continuous curves) and their SE (shaded area) from cells (N = 27) whose firing frequency was significantly (p < 0.05) enhanced in the Re-Cal task (red), relative to the Iso task (green). The population activity of these cells during the Wash-out (blue) remained higher (p < 0.001) than in the Iso task. B, Mean population SDFs from cells (N = 27) whose firing frequency was suppressed in the Re-Cal task (red), relative to the Iso task (green). The population activity of this subset of cells in the Wash-out (blue) task remained lower (p < 0.001) than it was during the Iso (green). A, B, The activity is aligned to onset of force application (0 ms). Triangles represent the mean time of target presentation. Circles represent the mean time of cursor's arrival on the peripheral target. C, Mean (± SE) amount of force exerted by the animal to bring the cursor from the center to the peripheral target in the three tasks, from the time of its application (0 ms). Conventions and symbols as in A and B.

As it can be seen in a typical cell shown in Figure 5A₁, B (associated animal's behavior reported in Fig. 5A₂), during the Re-Cal task, the cell firing rate changed significantly with respect to the Iso and did not return to the original level when retested in the Wash-out session. The first change resulted in a gain of the mean firing rate (pC < 0.01) during the Re-Cal, as well as in a variation of the directional tuning, both occurring in the DFT, with the emergence of a significant PD (354°) during this epoch (Fig. 5B, red arrow). The change of neural activity observed during DFT in the Wash-out produced a further change of both gain (firing rate 17 Hz vs 26 Hz; pC < 0.001) and directional properties (pCD = 0.01; Fig. 5B), with the cancellation of the significant PD observed in the Re-Cal condition. The pattern of activation observed across different tasks during DFT suggests that parietal cells, by retaining “memory” of the applied hand force, are more involved in dynamical remapping operations, therefore, in signaling force variations over time, rather than in strictly encoding the amount of hand force applied on the joystick. Interestingly, for this cell, no statistical differences across conditions were observed in the firing rate during static holding (THT) of the cursor on the target, despite the different forces (double in Re-Cal; Fig. 5A₂) required during the relative THT epochs. In this example cell during static holding, we only observed a loss of a significant directional tuning in the Re-Cal and Wash-out task, which was present (PD = 341°) instead when the cell was tested in the original Iso condition.

To test whether the emergence or cancellation of a significant PD across task conditions could be attributed to directional changes of force application, we analyzed the cursor trajectories across the three conditions. Potential changes were evaluated by measuring the mean directions of cursor's movement at the mid-time (t_M) of DFT (see Materials and Methods), separately in the three tasks. Significant differences among mean angular values were then tested through a Watson-William test. For the recording session shown in Figure 5, the angular differences between means, averaged across peripheral target locations, were 4°, 5°, and 4°, when comparing Iso versus Re-Cal, Re-Cal versus Wash-out, and Iso versus Wash-out. These differences were significant (Watson-Williams test, p < 0.05) for cursor movements only toward certain peripheral targets (Fig. 5C). Therefore, the changes in directional tuning can be in part attributed to small, but significant, variations of direction of force application, when different forces were applied to bring the cursor from the center to the periphery.

As in the example reported above, significant changes of cell activity during force-cursor remapping condition (Re-Cal) with respect to the Iso task were observed in 54 of 76 (71%) cells (two-way ANOVA; Factor 1: condition, pC < 0.05 and/or interaction factor: condition × direction, pCD < 0.05) during the DFT. The firing rate of 42 of 54 (77%) cells did not return to the original level when retested in the Wash-out session. A significant change during this session was also observed in the remaining 29% of cells, which did not show a change between Iso and Re-Cal. Approximately 30% of cells (Table 1, “Total” column) changed their tuning when tested in different conditions. These variations could consist of the emergence/cancellation of a significant PD or a significant shift of PDs. At the population level, the mean angular difference of PDs, measured during DFT, was 25° (±18° circular SD) after force increase (Iso vs Re-Cal), 26° (±25° circular SD) after force decrease (Re-Cal vs Wash-out), and 33° (±20° circular SD) when comparing the preperturbation and postperturbation activity (Iso vs Wash-out), which were characterized by an identical force output. All these differences were statistically significant (paired t test, p < 0.01) (see also Sergio and Kalaska, 2003). On the contrary, contrasting the angular differences of PDs computed during the static application of hand force (i.e., THT), we found no significant differences for the comparison Iso versus Re-Cal and Iso versus Wash-out, whereas a significant difference of 20° (±15° circular SD; p = 0.003) was observed comparing Re-Cal versus Wash-out. To further investigate whether the significant variations of tuning properties (PDs) observed during the epochs of DFT were dependent on potential directional changes of the cursor trajectories across the three task conditions, we compared the direction of the hand force output at a “checkpoint,” set at the instantaneous location of the cursor at the mid-time of the DFT. We found small (maximum 7°), but for some target locations significant, differences for cursor motion under different force conditions (Fig. 5D). However, because the PD mean differences reported above (25°, 26°, 33°) do not seem to mimic the differences in orientations of cursor motion of ∼5°, these findings suggest that single-cell activity in parietal cortex does not covary exclusively with the level and direction of hand force output.

Table 1.

Number of cells that changed their directional tuning when comparing different task conditions

	Shift	Emergence of PD	Disappearance of PD	Total
Iso versus Re-Cal	1	17	6	24/76 (32%)
Re-Cal versus Wash-out	2	7	12	21/76 (28%)
Iso versus Wash-out	1	13	17	21/76 (28%)

Among the cells (54 of 76; 71%) that were significantly modulated (see above) by the new visuomotor association, two main patterns of change (Fig. 6) were observed at the population level. The activity of the set of cells (27 of 54) that increased the firing rate in a significant fashion (t test, p < 0.05) in the Re-Cal task, during the subsequent Wash-out session (Fig. 6C) remained higher (t test, p < 0.001) than that observed in the Iso task (Fig. 6A). The other half of cells (27 of 54) with activity significantly (t test, p < 0.05) suppressed by the force change, when retested in the Wash-out condition displayed a firing rate that was lower than that of the Iso task (t test, p < 0.001; Fig. 6B). Thus, half of our sample signaled the change (consisting of a force increase from Iso to Re-Cal) of task dynamics by increasing the firing rate, whereas the other half by decreasing it, and in both cases cell firing frequency never returned to the original preperturbation activity when retested in the Wash-out condition. This suggests that force related cell modulation did not exclusively depend on the amount of force requested by the remapping processes.

To evaluate in a quantitative fashion the interdependency between the amount of applied force and the changes in neural activity, a correlation analysis was performed at single-cell level. We found that a vast majority of cells were significantly (p < 0.05) correlated with dynamic force (67 of 76; 88%) and with instantaneous force change (68 of 76; 89%). However, it is worth noticing that in both instances the correlation coefficients were on average rather low. By correlating the neural activity with dynamic force, approximately half of the cells were positively correlated with a mean r = 0.29, and the other half negatively correlated with a mean r = −0.25. Similar results were obtained when activity was correlated to the instantaneous force change (29 cells with r > 0, mean = 0.24; 39 cells with r < 0, mean = −0.23). These low values probably reflect the fact that after the perturbation the neural activity does not return to its original firing rate. Therefore, in area PFG/PF, force-related cells, far from being exclusively modulated by the amount of force output, are also critically influenced by the process of adapting, therefore learning, a new task dynamics, which depended on a new association rule (i.e., that between the force exerted and the cursor's motion on the screen).

Population coding of hand force output and cursor's kinematics

The fine neural representation of the behavioral output as a function of time was studied by comparing the temporal evolution of the instantaneous PV (computed at 10 ms time bins) with the evolution of two types of time-varying force vectors controlled in the Iso task, that is the dynamic force and the instantaneous force change (see Materials and Methods), as well as with the kinematics of the cursor, in the absence of any force change, during the Obs task. The results for one example direction (315°) are shown in Figure 7A₁. At first glance, the PV seems to predict, in a similar fashion, the dynamic force and its instantaneous force changes over time, as also suggested by the analysis of the mean angular difference between the PV and each of the two force vectors (dynamic force: 16° Monkey 1, 19° Monkey 2; instantaneous force changes: 18° Monkey 1, 18° Monkey 2). The similarity of these directional differences can be expected because the instantaneous force change vectors at each time share similar orientation with the dynamic force vector. Therefore, to disentangle the influence of these two aspects of force production on the population activity, we reconstructed the cursor's motion trajectory from the PV (i.e., the “decoded trajectory”), based on two different hypotheses: “dynamic force” encoding, and “instantaneous force change” encoding by the PV obtained from the activity of parietal cells. According to the first scenario, the cursor's trajectory should be well reconstructed by placing each instantaneous PV at the center of the workspace, with the relative tip representing the instantaneous position of the cursor, as schematically represented in the left of Figure 7A₁. On the other side, the “instantaneous force change” encoding hypothesis predicts that the cursor's trajectory would be reconstructed by connecting tip-to-tail (Fig. 7A₁, left) all the instantaneous PVs for each target direction. The results (Fig. 7A₂) show that the decoded trajectory of the cursor's motion resulting from force application was poorly reconstructed on the basis of the “dynamic force” hypothesis (mean angular difference between actual and decoded trajectory: 73° Monkey 1, 88° Monkey 2), although it was predicted with high fidelity following the “instantaneous force change” representation (mean angular difference between actual and decoded trajectory: 18° Monkey 1, 18° Monkey 2). The temporal evolution of the PV computed through the neural activity recorded during the Obs task did not predict the cursor motion associated to this task condition, reflecting the scarce influence of this parameter on cell activity, in the absence of any force production (Fig. 7A₁). What is illustrated in Figure 7A₁ for one selected direction generalizes to the force exerted in all movement directions, as shown in Figure 7B.

Figure 7.

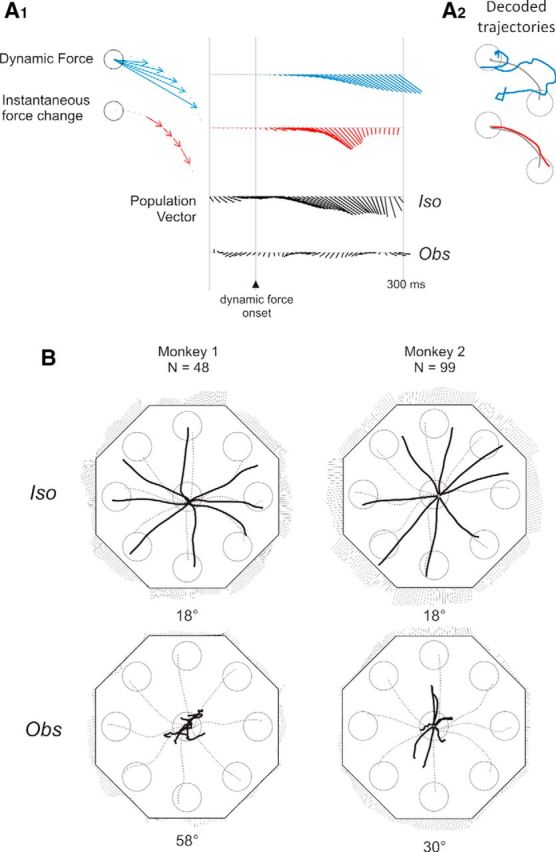
Population vectors and decoded trajectories of cursor motion. A₁, Time series of the dynamic force (blue), the instantaneous force change (red), and the neural PV (black) in the Iso and Obs tasks, of Monkey 1 in one particular direction (315°), aligned to the onset of dynamic force. Left, Schematic vectorial representation of different forces. A₂, The trajectories predicted by the PV on the basis of a “dynamic force” encoding hypothesis (blue curve) and of an “instantaneous force change” encoding hypothesis (red curve) are superimposed to the actual trajectory (gray curve). B, Decoded trajectory (black curve) of the cursor's motion toward the eight peripheral targets (circles), as predicted by the “instantaneous force change” encoding hypothesis, therefore obtained by connecting tip-to-tail all the PVs computed at each time bin from the activity recorded during the Iso and Obs tasks in Monkeys 1 and 2. Gray dotted lines indicate mean actual cursor's trajectories. For each force direction, the time series of the PV are shown next to each target, from 60 ms before to 310 ms after the DFT onset, with time increasing in a clockwise direction. The numbers under each plot indicate the mean angular difference between the decoded trajectories and the actual cursor's trajectories averaged over all directions.

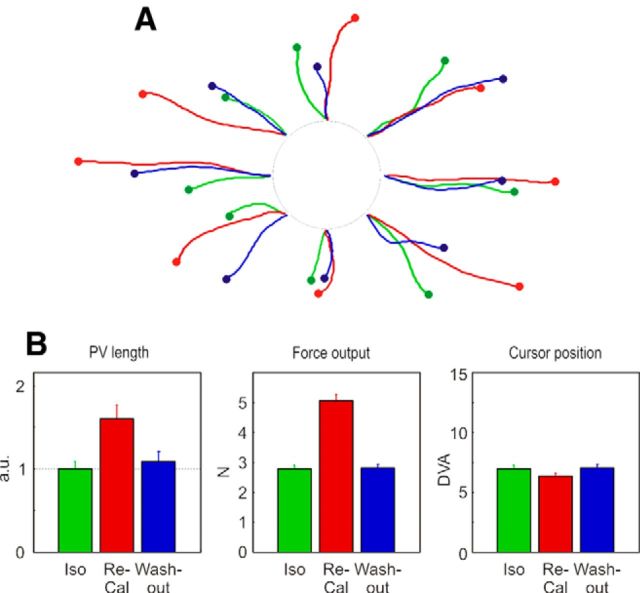
It is worth noticing that the lack of activation during the Obs task, with the consequent failure of the reconstruction of the cursor motion by the PV, can be due to the lack of force modulation in Obs condition, but also to the absence/suppression of an intended action to guide the cursor with the joystick. Therefore, to support the hypothesis that the neural activity in area PFG/PF is modulated by the force output, the PV analysis was repeated to compare the resulting decoded trajectories from activities recorded under different force applications (Iso, Re-Cal, Wash-out). It can be expected that the length of the PVs(t) in the Re-Cal condition, and consequently the length of the decoded trajectories, would be approximately twice as long as that associated to the Iso task. In Figure 8A, it can be seen that this was indeed the case. Furthermore, by plotting the values of decoded trajectory length, the magnitude of exerted force, and the cursor position at the end of DFT across conditions (Fig. 8B), we can conclude that PV better predicts the force variations, rather than the intended cursor position on the screen.

Figure 8.

Decoded trajectory and output force. A, Decoded trajectories in the eight directions of cursor motion obtained by using the PVs computed for different task conditions (green represents Iso; red represents Re-Cal: blue represents Wash-out), characterized by different amounts of force exerted by the animal, to bring the cursor from the center to the peripheral target. Trajectories are plotted from the DFT onset to the time the cursor enters the peripheral target (filled circles), by using only cells with significant tuning in each task. B, Average (± SE) values of decoded trajectory length (arbitrary units), force output (Newton), and cursor position (distance of the cursor from the central starting position, DVA) measured at the end of DFT.

Discussion

Any action requires the specification of movement kinematics and the appropriate time-varying muscle forces. We studied the relative influence on parietal activity of both dynamic force and instantaneous force change, as well as that of unexpected variations of the force to be applied to the joystick, through a task requiring the animal a remapping process between the force output and the visual cursor motion on the screen.

Single-cell analysis

Neural activity was tuned to the direction of isometric force output. Moreover, in 71% of cells studied, it changed when the animal changed force output, as to compensate for the novel force-cursor displacement relation, a condition where both the gain and the preferred direction of cells changed. After the monkey had adapted to the new dynamics and the perturbation was removed, at the end of the Wash-out period the firing rate of parietal cell did not return to the level observed in the preperturbation condition but signaled the remapping process by varying both the gain and the directional tuning of cells. Among those units signaling the change of visuomotor rule, half of them increased their activity, whereas the other half decreased it. In both cases, neural activity did not return to the original preperturbation rate when retested in the Wash-out condition. Therefore, these neurons encoded the variations in the remapping processes regardless of whether in the novel condition the animal exerted higher directional forces, as when attempting to face the unfamiliar task dynamics in the Re-Cal task, or lower forces, as when the animal decreases its force output to return to the original condition (Wash-out). This is reminiscent of what was observed in primary motor cortex (Li et al., 2001) when monkeys made arm movement under different force fields. Therefore, areas PF/PGF are probably involved in motor learning thanks to a population of dynamic force-related cells that can represent the underpinning of an internal model necessary to face changing relationships between force output and its consequences. This mechanism can be regarded as a reservoir for predictive visuomotor control of dynamic hand force.

Population vector analysis

The influence of the different types of forces on cell activity was clarified through the analysis of the temporal evolution of the PV, which was compared with the time-varying hand forces (Georgopoulos et al., 1992) acting on the joystick. We found that the time series of PV encodes the direction and amplitude of the instantaneous force changes exerted on the joystick, rather than the total amount of dynamic force, the latter expressing the force necessary to move the cursor from the center to the peripheral target (i.e., the subject force subtracted by the constant static force applied for the entire duration of the trial). This result is similar to what observed by earlier studies in motor cortex (Georgopoulos et al., 1992; Boline and Ashe, 2005) and suggests that common mechanisms and principles might underlie force encoding in the motor and visuomotor areas of the cerebral cortex. Through the PV, we then obtained the decoded trajectories of the cursor's motion that reproduced with great accuracy the actual ones.

In our study, the activity of ∼40% of neurons was influenced by the cursor's motion in the Observation task, in the absence of any dynamic force applied on the joystick. However, only a minority (14%) of them was directionally tuned. Therefore, the direction of the cursor's motion observed by the animal was poorly encoded, as also shown by the evolution in time of the PV obtained from the directionally tuned cells. For this subset of cells, the PV did not predict the observed cursor's trajectories as precisely as in the case of force exertion, suggesting that they played no significant role in shaping the population dynamics during force generation and development. In a similar fashion, saccade-related activity did not contribute to the population activity during the hand isometric task. Furthermore, the finding that the length of the PV matches the magnitude of the applied force on the joystick, as suggested by the comparison of three different force field conditions (Iso, Re-Cal, Wash-out), offers a further support to the evidence that parietal neurons are involved in force control.

In this study, we have documented, for the first time, that a dynamic directional force signal is encoded in areas PF/PFG neural activity, as an essential parameter within a lateral grasping processing stream where previous studies had highlighted important aspects of neural modulation mostly related to the kinematics of hand–object interaction (Taira et al., 1990; Sakata et al., 1995; Murata et al., 2000; Rozzi et al., 2008; Sakaguchi et al., 2010; Bonini et al., 2012) and action sequences (Bonini et al., 2011). Corticocortical connections (Rozzi et al., 2006) link area PFG to ventral premotor cortex (PMv). There is old evidence that cell activity in this area is modulated by force in a precision-grip task (Hepp-Raymond et al., 1994) and that its disruption by TMS (Davare et al., 2006) results not only in a disturbed hand shaping, but also in an impaired sequential recruitment of hand muscles during a grip-lift task. Therefore, a signal concerning hand force under visuomotor control seems to influence PMv, although its exact nature and source was not determined. A source of this signal can be parietal areas PF/PFG. This interpretation is supported by converging lines of evidences in humans. fMRI studies (Ehrsson et al., 2001) have shown that anterior intraparietal cortex is activated during the control of delicate object requiring small fingertip forces. Inactivation of a sector of the intraparietal sulcus (Della-Maggiore et al., 2004) impairs adaptation to a new force field. Finally, a case report of a patient with right parietal lesion tested in the same task of this study (Ferrari-Toniolo et al., 2014) revealed the presence of constant and variable endpoint errors while moving a cursor to visual targets. This study suggested that the defective control of the directional force output was consequence of a difficulty in remapping the information from hand force receptors to the visual target location signals. Interestingly, in this patient, the amount of force produced with both the right and left hand was similar and within normal limits.

Relations with previous cell studies on force encoding in parietal cortex

Previous studies on force encoding in parietal cortex have shown the existence of a modest relationships between cell activity and the force during reaching (Kalaska et al., 1990) and isometric hand action (Hamel-Pâquet et al., 2006), concluding that parietal cortex is more involved in the specification of movement kinematics than in movement kinetics. Nevertheless, a parietal population signal could be extracted that covaried systematically with the direction of desired isometric forces, although it was smaller than that described in the motor cortex (Hamel-Pâquet et al., 2006).

These studies were performed in SPL area 5 (PE), which is devoid of visual input and entertains reciprocal connection with motor cortex (Johnson et al., 1996). Within this reach-related stream, parietofrontal signaling, estimated in the order of ∼1.9 ms (Innocenti et al., 2014; Battaglia-Mayer et al., 2015), can allow combination of arm kinematics and dynamics without undue delays, even within a hierarchical scheme where force variables are added “downstream,” as a result of motor cortex operations. IPL areas PF/PFG operate under visual control and project to ventral premotor cortex (Rozzi et al., 2006), which in turn projects to motor cortex. This does not project back to PF/PFG. Therefore, a serial scheme where kinematic and kinetic variables are encoded by different parietal and frontal areas would not have a plausible anatomical substrate, and would imply conduction delays incompatible with the online, continuous, and time-varying specification of the hand force underlying grasping, hand–object interaction, and tool use, all dependent on visual control. Therefore, within a common cortical mechanism of force encoding, the detailed specification of the type of force and its combination with hand kinematics can be task and areal dependent.

In conclusion, the properties of neurons (Hyvärinen, 1981; Rozzi et al., 2008) and their selectivity for grip type and action goal (Bonini et al., 2012) suggest that areas PF/PFG play a higher-order role in visuomotor control of hand action. Coherent with this view, we have found that in this area the population coding of force is mainly related to its time-varying dynamic aspects, with a good representation of its direction and instantaneous change over time (see Smith et al., 1975; Georgopoulos et al., 1992; Boline and Ashe, 2005). Furthermore, neural activity retains memory of previous applied hand forces. All this provides not only parallel combination and processing of kinetics and kinematics necessary for fine hand–object manipulation and tool use, but also an internal model of dynamics necessary for future hand action.

However, the complex pattern of activity of sensory-motor neurons favors the view of a simultaneous encoding of many movement parameters by individual cells within the parieto-frontal system (Ashe and Georgopoulos, 1995; Battaglia-Mayer et al., 2001, 2005; Churchland and Shenoy, 2007). Therefore, it cannot be excluded that other movement variables are simultaneously represented in the activity of the cells studied, in addition to those controlled in our study.