Representation of Color Surfaces in V1: Edge Enhancement and Unfilled Holes

Abstract

The neuronal mechanism underlying the representation of color surfaces in primary visual cortex (V1) is not well understood. We tested on color surfaces the previously proposed hypothesis that visual perception of uniform surfaces is mediated by an isomorphic, filled-in representation in V1. We used voltage-sensitive-dye imaging in fixating macaque monkeys to measure V1 population responses to spatially uniform chromatic (red, green, or blue) and achromatic (black or white) squares of different sizes (0.5°–8°) presented for 300 ms. Responses to both color and luminance squares early after stimulus onset were similarly edge-enhanced: for squares 1° and larger, regions corresponding to edges were activated much more than those corresponding to the center. At later times after stimulus onset, responses to achromatic squares' centers increased, partially “filling-in” the V1 representation of the center. The rising phase of the center response was slower for larger squares. Surprisingly, the responses to color squares behaved differently. For color squares of all sizes, responses remained edge-enhanced throughout the stimulus. There was no filling-in of the center. Our results imply that uniform filled-in representations of surfaces in V1 are not required for the perception of uniform surfaces and that chromatic and achromatic squares are represented differently in V1.

SIGNIFICANCE STATEMENT We used voltage-sensitive dye imaging from V1 of behaving monkeys to test the hypothesis that visual perception of uniform surfaces is mediated by an isomorphic, filled-in representation. We found that the early population responses to chromatic and achromatic surfaces are edge enhanced, emphasizing the importance of edges in surface processing. Next, we show for color surfaces that responses remained edge-enhanced throughout the stimulus presentation whereas response to luminance surfaces showed a slow neuronal ‘filling-in’ of the center. Our results suggest that isomorphic representation is not a general code for uniform surfaces in V1.

Introduction

“… space and color are not distinct elements but, rather, are interdependent aspects of a unitary process of perceptual organization.” (Kanizsa, 1979).

The above quotation from Kanizsa's (1979) book guides our work on the neural basis of color perception. The brain needs to construct a color signal to recover the reflective properties of surfaces. Therefore, the neural mechanisms of color perception must make comparisons of the color signals from different locations in the visual image; they must take into account the spatial layout of the scene (Delahunt and Brainard, 2004; Shevell and Kingdom, 2008). It is not known yet in detail how the brain integrates form and color but many scientists who investigated the problem concluded that the primary visual cortex (V1) plays an important role (Johnson et al., 2001, 2008; Friedman et al., 2003; Wachtler et al., 2003; Hurlbert and Wolf, 2004).

Many investigators have reported the existence of color-responsive neurons in V1 of macaque monkeys (Thorell et al., 1984; Victor et al., 1994; Leventhal et al., 1995; Johnson et al., 2001; Friedman et al., 2003). Most of the color-sensitive neurons in V1 are double-opponent cells; they are orientation-tuned and respond best to intermediate spatial frequency gratings or to sharp edges in the visual image (∼30–40% of V1 cells). Double-opponent cells were shown to be sensitive to achromatic luminance patterns as well as to color patterns. Single-opponent cells comprise a smaller population (∼10–15% of V1 cells); they are color-specific (i.e., do not respond to luminance modulation) and respond best to large uniform surfaces of color (Thorell et al., 1984; Conway, 2001; Johnson et al., 2001; Friedman et al., 2003). The interaction between the single- and double-opponent populations and their different roles in the coding of color stimuli are still unknown.

Despite the large body of evidence regarding color sensitive cells in V1, the representation of color surfaces in the cortex has been studied much less. Friedman et al. (2003) investigated the neuronal responses to chromatic surfaces in V1 and V2 in awake macaque monkeys. They found that V1 and V2 neurons were mainly activated by the edges of color surfaces rather than the uniform center. Luminance-surface-coding in V1 is better understood. V1 responses to the edges of surfaces are higher than responses to the center (Friedman et al., 2003; Dai and Wang, 2012; Zurawel et al., 2014) resulting in a lower activation, a “hole,” located at center-related cortical regions. Several studies reported neuronal filling-in of the center's response in illusory and real surfaces (De Weerd et al., 1995; Lamme et al., 1999; Hung et al., 2001; Huang and Paradiso, 2008). This response pattern appearing at later time after stimulus onset, sometimes called an “isomorphic” representation, was suggested to encode the perceived lightness of real surfaces. However, the existence and perceptual importance of an isomorphic representation (image-like) are still under debate (von der Heydt et al., 2003; Sasaki and Watanabe, 2004; Cornelissen et al., 2006; Komatsu, 2006).

We asked: what is the representation in V1 cortical population responses of surfaces defined only by color? How does the color surface representation in V1 compare with its representation of an achromatic surface? And is there a uniform filled-in representation of the perceived visual image in V1? We studied color surface representations in monkey V1 with voltage-sensitive dye imaging (VSDI) that measured neuronal population activity in the upper layers of V1 (Slovin et al., 2002). VSDI enabled us to measure overall population responses without possible biases due to cell selection.

Materials and Methods

Visual stimulation and experimental setup.

Visual stimuli were presented on a 21 inch CRT Mitsubishi monitor at a refresh rate of 85 Hz. The monitor was located 100 cm from the monkey's eyes. Two linked personal computers managed visual stimulation, data acquisition, and controlled the monkey's behavior. We used a combination of imaging software (MicamUltima) and the NIMH-CORTEX software package. The behavior PC was equipped with a PCI-DAS 1602/12 card to control the behavioral task and data acquisition. The protocol of data acquisition in VSDI was described previously (Slovin et al., 2002). To remove the heartbeat artifact, we triggered the VSDI data acquisition on the animal's heartbeat signal (see information in VSD data analysis, and Slovin et al., 2002).

Behavioral task and visual stimuli.

Two adult male Macaca fascicularis (6 and 7 years old, 13 and 12 kg) were trained on a simple fixation task. Monkeys fixated before and during stimulus presentation. Prestimulus duration was varied randomly between 3 and 4 s, at the end of which, while monkeys maintained fixation, the stimulus was turned on for 300 ms. The monkeys were required to maintain tight fixation throughout the whole trial and were rewarded with a drop of juice for each correct trial. During the stimulus presentation fixation was within ±2° around the fixation point (See Eye movements below for further analysis on the eye position). Stimuli were centered at eccentricity 1.6°–3° below the horizontal meridian and 0.75°–2° from the vertical meridian. To generalize the results, the visual field positions of the stimuli varied across imaging sessions and across monkeys, covering most of the visual field area whose retinotopic projection fell within our imaging chamber. In each recording session, square surface stimuli appeared in 75–85% of the trials, whereas the remaining 15–25% trials were fixation-alone trials (no stimulus presentation, blank condition). These trials were used to remove the heartbeat artifact in the VSDI analysis (see VSDI data analysis below).

On each trial, the monkeys were presented with either a chromatic or an achromatic square surface displayed on a gray background [CIE-xy = (0.279, 0.28), luminance: 7.3, 15.5, or 32.3 cd/m²]. Chromatic squares were either red [CIE-xy = (0.616, 0.341)], green [CIE-xy = (0.288, 0.600)], or blue [CIE-xy = (0.149, 0.069); Table 1] and equal in luminance to the background. Achromatic squares were gray squares either darker (referred to as black) or brighter (referred to as white) than the background. The luminance contrast of the achromatic squares was adjusted to be similar to the L-M cone contrast of the chromatic squares (Weber contrast; Table 1). Cone excitations were calculated as the dot product of the cone absorption fundamentals (Smith and Pokorny, 1975) and the spectral energy distribution of the CRT gun primaries measured with a spectroradiometer (SpectroCAL MK II, Cambridge Research Systems). The energy distribution of each stimulus was then verified by a separate measurement using the spectroradiometer. The square surfaces differed in sizes between 0.5 × 0.5° and 8 × 8° (termed 0.5° and 8° throughout the paper). In another set of experiments we placed the square so that one of the edges' middle (either top or bottom edge) and the center of square were (on different trials) in the same location of the visual field.

Table 1.

CIE (1931) coordinates and contrasts for the different stimuli used

Color	CIE xyY	Background luminance (cd/m2)	Smith Pokorny L-M Weber contrast	Stockman Sharpe L-M Weber contrast	Luminance Weber contrast
Red	0.616, 0.341, 16	15.5	0.78	0.76	0.03
Black	0.279, 0.266, 3.3	15.5	0	0	−0.79
White	0.281, 0.283, 28.2	15.5	0	0	0.82
Green	0.288, 0.600, 15.5	15.5	−0.16	−0.145	0
Black	0.279, 0.280, 12.9	15.5	0	0	−0.17
Blue	0.149, 0.069, 7.7	7.3	0.61	0.66	0.04
Black	0.278, 0.264, 2.8	7.3	0	0	−0.62
Red	0.613, 0.341, 7.4	7.3	0.74	0.72	0.01
Green	0.288, 0.600, 7.2	7.3	−0.16	−0.18	0.01
Black	0.28, 0.276, 8.7	32.3	0	0	−0.73
White	0.28, 0.287, 56.3	32.3	0	0	0.74

The CIE (1931) xyY coordinates for stimuli used in the experiments. For each stimulus we calculated the L-M cone contrast (Weber contrast) compared to its background (the background changed for the different stimuli) using both Smith–Pokorny (Smith and Pokorny, 1975) and Stockman–Sharpe (Stockman and Sharpe, 2000) cone fundamentals.

Surgical procedures and voltage sensitive dye imaging.

The surgical, staining, and imaging procedures have been reported in detail previously (Slovin et al., 2002). All experimental procedures were approved by the Animal Care and Use Guidelines Committee of Bar-Ilan University, supervised by the Israeli authorities for animal experiments, and conformed to the NIH guidelines. Briefly, the monkeys were anesthetized, ventilated, and an intravenous catheter was inserted. A head holder and two cranial windows (25 mm, i.d.) were bilaterally placed over the primary visual cortices and cemented to the cranium with dental acrylic cement. After craniotomy, the dura mater was removed, exposing the visual cortex. A thin, transparent artificial dura of silicone was implanted over the visual cortex. Appropriate analgesics and antibiotics were given during surgery and postoperatively. The anterior border of the exposed area was 3–6 mm anterior to the Lunate sulcus. The size of the exposed imaged area covered ∼3–4° × 4–5° of the visual field, at the reported eccentricities. We used the Oxonol voltage sensitive dyes, RH-1691 or RH-1838 (Optical Imaging) to stain the cortical surface. The procedure for applying VSDs to macaque cortex is described in detail by Slovin et al. (2002). For imaging we used the MicamUltima system based on a sensitive, fast camera providing a resolution of 10⁴ pixels at up to a 10 kHz sampling rate. The actual pixel size was 170 × 170 μm², every pixel summing the neural activity mostly from the upper 400 μm of the cortex. This yielded an optical signal representing the population activity of ∼500 neurons/pixel (0.17 × 0.17 × 0.4 × 40,000 cells/mm³). Sampling rate was 100 Hz (10 ms/frame). The exposed cortex was illuminated by an epi-illumination stage with appropriate excitation filter (peak transmission 630 nm, width at half-height 10 nm) and a dichroic mirror (DRLP 650), both from Omega Optical. To collect the fluorescence and reject stray excitation light, a barrier postfilter was placed above the dichroic mirror (RG 665, Schott).

Retinotopic mapping of V1.

Retinotopic mapping of V1 and the V1/V2 border was obtained in a separate set of imaging sessions using VSD and optical imaging of intrinsic signals and has been described previously (Ayzenshtat et al., 2012). Briefly, during a simple fixation task, we presented to the monkeys small squares (0.1°–0.2°) or high contrast square contours (2°) at various eccentricities and imaged the evoked responses. Orientation maps were obtained by presenting full-field, square, moving gratings of horizontal and vertical orientations and then by computing differential maps. The orientation domains size and organization are different in V1 and V2 thus enabling us to detect the V1/V2 border.

Eye movements.

Eye position was monitored by a monocular infrared eye tracker (Dr Bouis, Karlsruhe, Germany), sampled at 1 kHz and recorded at 250 Hz. Only trials where the animals maintained tight fixation were analyzed. Although throughout the stimulus presentation the monkey was required to maintain tight fixation, it typically made a few (1–3) microsaccades or small fixational saccades throughout stimulus presentation. To remove the effects of saccadic eye movements on our analysis we detected the time of onset of the first saccadic eye movement on each trial, by implementing an algorithm for microsaccades and saccades detection (Engbert and Mergenthaler, 2006; Meirovithz et al., 2012) on the monkeys' eye position data. The algorithm could precisely detect saccadic eye movements larger than 0.1°. Next, we truncated the VSDI signal of each trial 40 ms after the onset of the corresponding first saccadic eye movement. This analysis assured that the VSDI signal was not affected by saccadic eye movements. As a result the number of trials was reduced as a function of time, thus leaving only the first 250–350 ms for data analysis. The distribution of the first saccade onset times were similar in sessions where achromatic and chromatic squares were presented. Therefore the truncation of the signal did not bias the results.

To verify that small drifts in the fixation position of the monkeys throughout the analysis period did not affect our results, in particular the edge versus center dynamics quantified using the depth modulation index (DMI; see Depth modulation index below, Eq. 1, and Figs. 4–6), we did the following analysis: in each trial we calculated the absolute difference value between the eye position at the early times (30–70 ms after response onset) and late times (130–170 ms) that were used to calculate the DMI values. This calculation of drift magnitude was done separately for the horizontal and vertical eye position axes. Next, we averaged the drift magnitude from all the trials in each session and obtained the mean horizontal and vertical drift magnitude per session. The mean value over all sessions was very small: 0.109° ± 0.005° and 0.094° ± 0.004° for the horizontal and vertical axes respectively (n = 142; 1°, 2° or 3° squares sessions). The mean drift magnitude value across the achromatic/chromatic sessions was highly similar for the horizontal eye position 0.101° ± 0.005°/0.119° ± 0.008° and for the vertical eye position 0.093° ± 0.005°/0.095° ± 0.005° (n = 77/65 achromatic and chromatic sessions). There was no significant difference between the chromatic and achromatic drift magnitude values (Mann–Whitney U test, p = 0.137 and 0.351 for the horizontal and vertical eye position, respectively). To verify that the variability in the fixation position across trials did not affect our results, the following analysis was done: we computed the mean eye position at stimulus onset, i.e., over the first 60 ms after stimulus onset in each trial and calculated the SD across trials for each session. The mean SDs over sessions was 0.587° ± 0.024° and 0.493° ± 0.026° for the horizontal and vertical axes, respectively (n = 166 sessions). The mean SD for achromatic/chromatic sessions was very similar: 0.552° ± 0.034°/0.628° ± 0.035° for the horizontal eye position and 0.463° ± 0.035°/0.529° ± 0.038° for the vertical eye position (n = 90/76 achromatic and chromatic sessions). Analysis of the DMI dynamics in single trials confirmed that our results were not due to different fixation position during stimulus onset in the different conditions.

Figure 4.

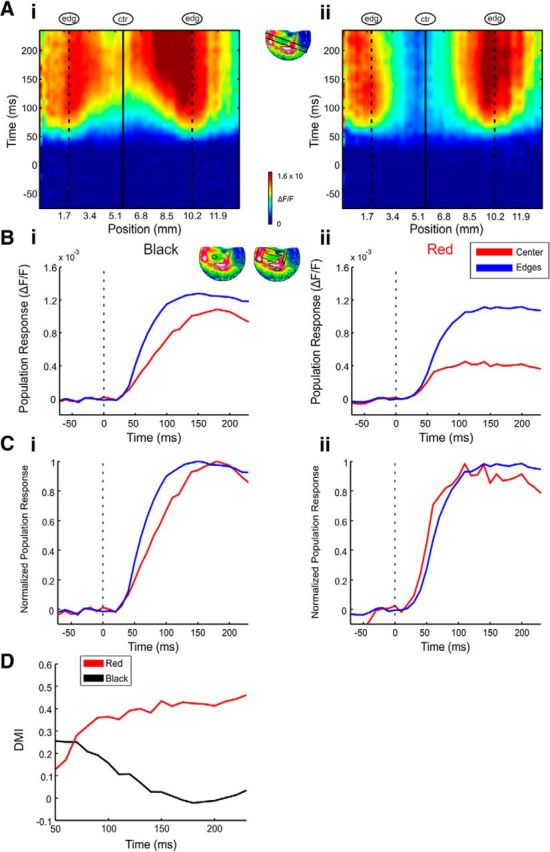
Center responses gradually increase for achromatic but not chromatic surfaces. A, Space–time maps of the spatial profile through the activation patch (inset, map) evoked by black (Ai) and red (Aii) 2° squares in an example recording session. The center position is marked by a continuous vertical line and the edges' positions are marked by vertical dashed lines. B, C, Average VSD response (B) and normalized (to peak response) VSD response (C) in two ROIs representing the center and edges of the black (Bi, Ci) and red (Bii, Cii) conditions. The center and edge ROIs are depicted in Bi (top right). Response was averaged over trials (n = 21 and 20 trials for the black and red squares, respectively, same session as A). Stimulus onset is marked by the dashed line. D, DMI calculated over time for the mean responses over trials of the black and red squares (same session as A).

Figure 5.

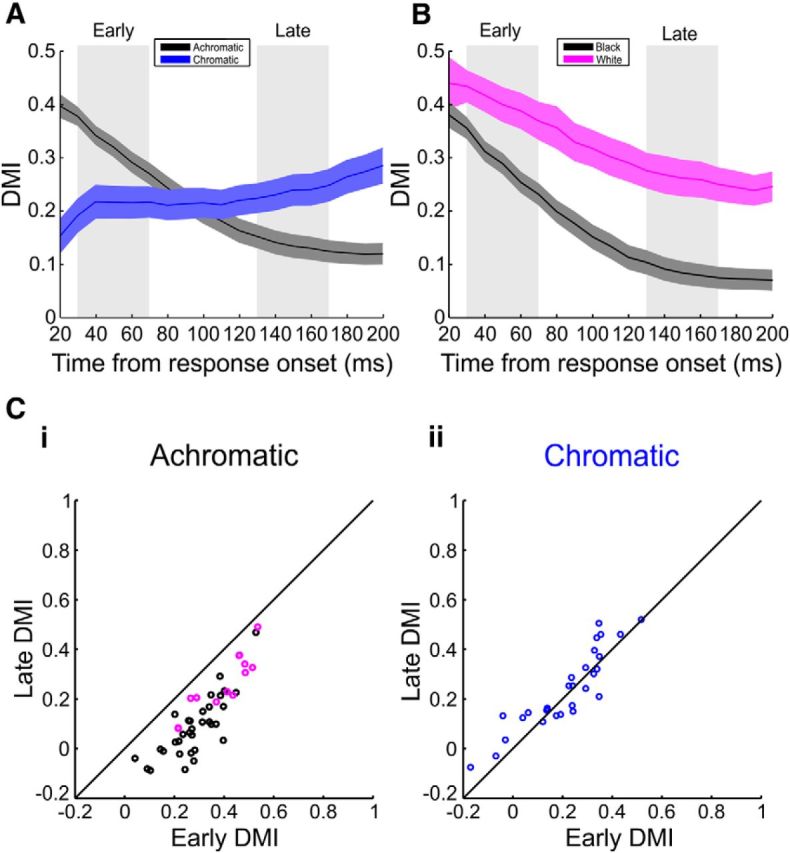
DMI indicates gradual increase of center responses compared with edge responses in achromatic but not chromatic surfaces. A, Grand average DMI over all imaging sessions from both monkeys for the achromatic (n = 46), and chromatic (n = 29) 2° squares. Each session was aligned to the time onset of edge responses to control for contrast differences (see Materials and Methods). Shaded areas represent ±1 SEM across sessions. B, Same as in A, but for black (n = 33, black line) and white (n = 13, magenta line) 2° squares, separately. C, A comparison of the DMI values for achromatic (Ci, black circles for black squares and magenta for white squares) and chromatic (Cii) squares in early times (A, left gray shade; 30–70 ms after edge response onset) and late times (A, right gray shade; 130–170 ms after edge response onset). Each dot represents an imaging session in which a 2° square was presented. The DMI in achromatic (Ci) squares decreased significantly with time (Wilcoxon signed rank test, p < 10⁻⁸), whereas the DMI in the chromatic squares (Cii) did not decrease.

Figure 6.

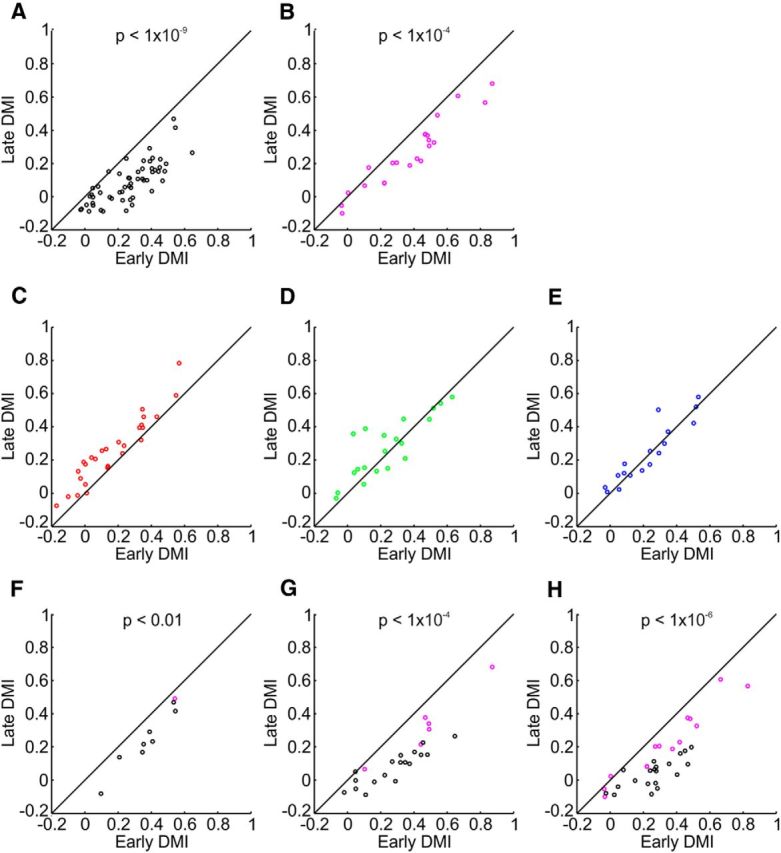
DMI indicates gradual increase of center responses compared with edge responses in achromatic but not chromatic surfaces; analysis of different colors. A–H, A comparison of the DMI values in early times (30–70 ms after edge response onset; Fig. 5A, left gray shade) and late times (130–170 ms after edge-response onset; Fig. 5A, right gray shade). Each dot represents an imaging session in which a 1°, 2°, or 3° square was presented. The DMI of the responses to black and white squares (A and B, respectively) decreased significantly with time (Wilcoxon signed rank test, p values stated in the figure), similar results were obtained for black and white squares with different luminance contrast (F, 17%; G, 62%; H, 79%; equivalent to the L-M cone contrast of the green, blue and red, respectively). There was no significant decrease for the red, green, and blue squares (C–E, respectively).

VSD data analysis.

VSDI data were obtained from a total of 192 sessions from two hemispheres in two monkeys: 166 sessions in which the chromatic and achromatic square stimuli paradigm was used (achromatic/chromatic: 69/50 sessions; 6/5, 14/18, 32/16, 10/5, 7/6 sessions for sizes: 0.5°, 1°, 2°, 3°, and 8° from Monkey T; achromatic/chromatic: 21/26 sessions; 4/8, 14/13, 3/5 sessions for sizes: 1°, 2°, and 3°, respectively, from Monkey H), 16 sessions in which the center and edge were positioned in the same location of the visual field in different trials (12/4 sessions in Monkeys T/H) and 10 retinotopic sessions (7/3 sessions in Monkeys T/H). Only trials with tight fixation were analyzed, resulting in typically ∼10–30 correct trials for each visual stimulus condition in a recording session. MATLAB software was used for statistical analyses and calculations. The basic VSDI analysis consisted of the following: (1) defining region-of-interest (ROI; only pixels with fluorescence level ≥15% of maximal fluorescence were analyzed), (2) normalizing to background fluorescence, (3) average blank subtraction (see schematic illustration of the basic VSDI analysis by Ayzenshtat et al., 2010, their supplemental Fig. S12), and (4) removal of pixels located on blood vessels. Blood-vessel-related pixels are marked as gray in all of the VSDI maps. For each recording session the VSDI signal was averaged over all the correct trials and the averaged signal was used for further analysis. VSDI maps shown in the paper were low-pass filtered with a 2D Gaussian filter (σ = 1 pixel) for visualization purposes only.

Averaging the time course over different colors and contrasts.

Contrast is well known to affect the latency of response (Albrecht, 1995; Meirovithz et al., 2010; Reynaud et al., 2012). Accordingly, VSD response latency varied over the various stimuli contrasts (cone contrast or luminance contrasts generated to match with the cone contrasts; Table 1). Therefore when averaging the VSD time courses from different color sessions we needed to control for this effect. This was done by aligning time courses on the time point of response onset before averaging (see Figs. 3, 5, 6, 7B). When averaging within session (see Figs. 1, 2, 4, 7A, 8), all conditions shared equal contrast and this practice was not necessary. The latency of response onset was calculated by fitting a linear regression line to the rising phase of activation and calculating its intersection with the baseline (Zurawel et al., 2014). Similar results were obtained when we computed the latency using a different approach: finding the point where the signal crossed 2 SDs of the baseline activity.

Figure 3.

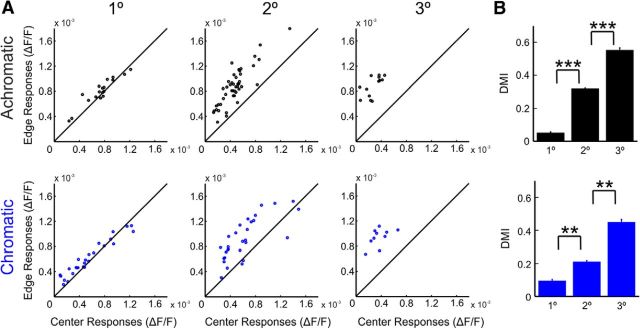
Edge-dominated responses to chromatic and achromatic surfaces early after response onset: grand analysis. A, Scatter plots comparing the edge and center responses for achromatic (top raw) and chromatic (bottom raw) squares. For each stimulus condition, the mean VSD signal over trials was aligned to response onset of the edges to control for contrast differences across colors and then averaged at early times after response onset (30–70 ms; see Materials and Methods). The comparison was done for different sizes (left, 1°; middle, 2°; right, 3°). Each dot represents a single imaging session. n = 18, 46, and 13 sessions for achromatic squares and n = 26, 29, and 10 sessions for chromatic squares of sizes 1°, 2°, and 3°, respectively. B, Mean DMI over sessions for squares of different sizes (n = 18, 46, and 13 sessions for achromatic squares and n = 26, 29, and 10 sessions for chromatic squares of sizes 1°, 2°, and 3°, respectively). Error bars represent SEM over sessions, Bonferroni corrected, Mann–Whitney U test, **p < 0.01, ***p < 0.001.

Figure 7.

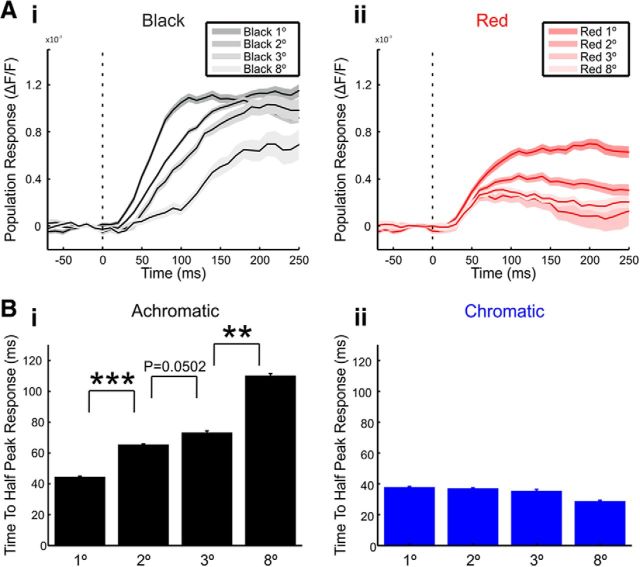
The center responses of achromatic squares increase slower with surface size. A, The mean center responses over trials in an example recording session evoked by black (Ai) and red (Aii) squares of different sizes. Shaded area represents ±1 SEM across trials (n = 21, 33, 13, and 9 trials for achromatic 1°, 2°, 3°, and 8° square sizes, respectively and n = 21, 32, 12, and 10 trials for chromatic 1°, 2°, 3°, and 8° square sizes, respectively). Stimulus onset is marked by the dashed line. B, The time to half-peak response in the center ROI averaged over all sessions. The time to half-peak response was calculated in achromatic (Bi, n = 18, 46, 13, and 7 sessions for 1°, 2°, 3°, and 8° square sizes, respectively) and chromatic (Bii, n = 26, 29, 10, and 6 sessions for 1°, 2°, 3°, and 8° square sizes, respectively) squares of different sizes. Error bars represents ±1 SEM across sessions. Bonferroni corrected, Mann–Whitney U test, **p < 0.01, ***p < 0.001.

Figure 1.

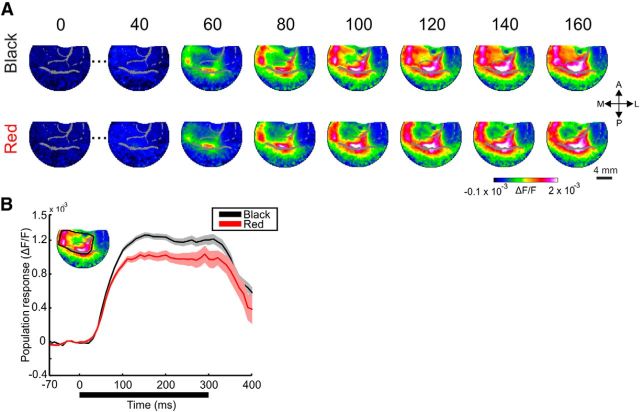
Spatiotemporal patterns of responses to black and red squares. A, A time sequence of VSD maps in V1, from an example session in which the monkey was presented with 2° black (top) or red (bottom) squares. Stimulus duration is 300 ms and times, in ms, are relative to stimulus onset. Each map is averaged across 20 ms. Pixels located on blood vessels are gray shaded (here and in all maps throughout the paper). B, Mean time course of the VSD signal. The signal was averaged over trials (n = 21 and 20 trials for the black and red squares, respectively) in a ROI including all the pixels in the activation patch (inset). Shaded areas represent ±1 SEM over trials. The thick black horizontal line represents stimulus duration.

Figure 2.

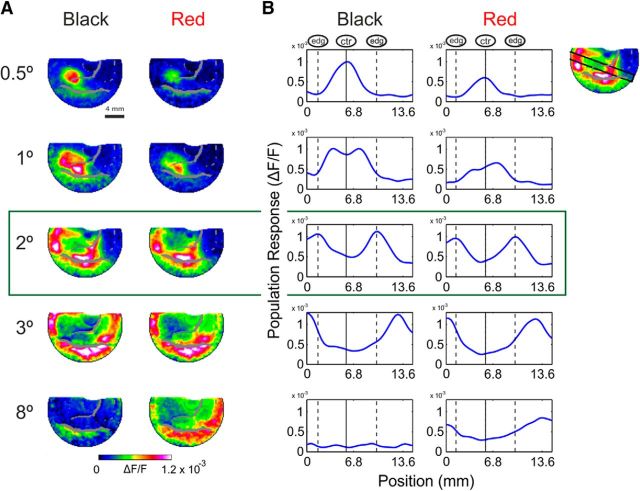
Spatial similarities between early responses to achromatic and chromatic surfaces of different sizes. A, The averaged early (60–100 ms after stimulus onset) VSD maps from an example session. Black (left column) and red (right column) square surfaces of different sizes (0.5°–8°) were presented while their center's position in the visual field was identical. B, Spatial profiles crossing through the edges and center of the activation patches, same example session as in A (an illustration of the spatial profile for the 2° square is shown in the top right corner; response was averaged over the profile width; see Materials and Methods). Spatial profiles for the black appear on the left and for the red on the right. The continuous vertical line marks the peak activation position in the 0.5° square response profile, which corresponds to the center of square in larger stimuli. The edge response position to a 2° square are marked by the vertical dashed lines.

Figure 8.

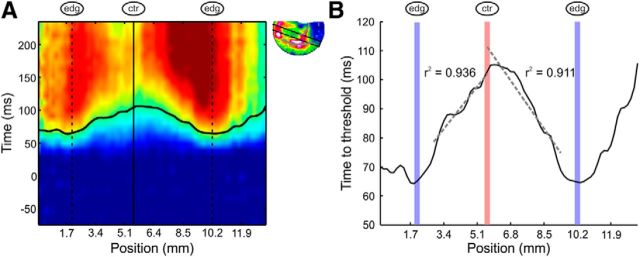
Achromatic square responses increase slower as a linear function of distance from the edges. A, Space–time map of the spatial profile through the activation patch evoked by a 2° black square (example recording session, same as Fig. 4Ai). The black curve indicates the time when each position along the spatial profile reached the predefined threshold amplitude. The edge locations are marked with dashed lines and the center location is marked with a continuous line. B, An enlargement of the curve from A: time to threshold response measured in a window of three pixels sliding over the spatial profile in a 2° black square. Linear regression lines were fitted for both sides of the center (avoiding the direct response of the edges; see Materials and Methods) and are marked in dashed lines. The edge locations are marked by vertical blue lines and the center location is marked by a vertical red line.

Analysis of spatial profiles and ROIs.

To analyze and compare responses at specific locations over the evoked response (center and edges), we set ROIs over specific cortical sites in the evoked pattern. The analysis was performed over the average response of all pixels within each ROI. In ∼50% of the imaging sessions the position of the center or edges of the squares were mapped using an independent retinotopic session, which preceded the chromatic and achromatic square sessions. In the mapping sessions, small high contrast 0.1 × 0.1° squares were presented in different positions in the visual field. The dots' positions corresponded to the position of the center or edges of the squares in the following sessions. Thus, the mapping ROIs were used to define the center and edge ROIs. For sessions that were not preceded with retinotopic mapping, the center ROI was selected at early times as the low activation region at the center of the evoked response. The mean size of the center ROIs was as follows: 109 ± 46 pixels (mean ± SD). The edge ROIs were selected as high activation regions at the border of the activation patch, during early response times. To avoid biased pixel selection, all the pixels falling at the edges were included in the edge ROI. Therefore bigger squares (2°–3°) had larger edge ROIs (1536 ± 394 pixels) than small squares (1°; 546 ± 99 pixels). The eccentricity of the stimulus also affected the size of the ROI because of cortical magnification factor and because in some eccentricities not all the edges of the square fitted the imaging chamber. To verify that our ROI choice was valid, we reanalyzed our data using circular ROIs with ∼60 pixels positioned in the center and edges of the squares. Our results were reproduced using these ROIs, and therefore the variability in ROI size did not affect our results. Additionally, we used a 2D analytical retinotopic model to map the stimulus onto the cortical surface (see Analytical retinotopic model below). We then could define the edge and center ROI based on this model and were able to reproduce our results in few example sessions using this other method of ROI selection. Importantly, regardless of the ROIs selection method, in each imaging day, identical ROIs were used for chromatic and achromatic squares of the same size displayed in the same visual field position.

To analyze and compare VSD maps evoked by chromatic and achromatic squares, we measured response profiles along spatial paths through the images (rectangular with a length of 39–103 pixels, ∼6.6–17.5 mm) spanning the entire activation patterns from side to side, in various orientations (see Figs. 2B, 4A, 8A). For each rectangular path we averaged VSD responses along the width (the narrow dimension of the rectangle, 10 pixels, ∼1.7 mm). The colocalization of the cortical spatial paths with the edges and center of the square in the visual field was validated using both independent retinotopic experiments as well as an analytical model (see Analytical retinotopic model below). For visualization purposes only, we smoothed the resulting 1-dimensional profiles by convolution with a Gaussian window (Fig. 2B; σ = 0.26 mm/1.5 pixels). All reported correlations for the spatial profiles were calculated without any smoothing.

Spatial correlations.

We calculated the Pearson correlation coefficients between the spatial profiles (see Analysis of spatial profiles and ROIs above) of responses to chromatic and black surfaces. The correlation was calculated for the average signal at early times after response onset (30–70 ms). Eight different spatial profiles were used. Four profiles passed along the four edges of the square. The other four were profiles through the middle of the edges and the center of the square at 0°, 45°, 90°, and 135° angles compared with the bottom edge. For sessions in which an edge or part of the edge was outside of the imaging chamber only part of the profile was used for the correlations. The correlations were calculated only for sessions in which a similar size black and colored square were presented in temporal proximity.

Depth modulation index.

We defined a DMI calculated as follows:

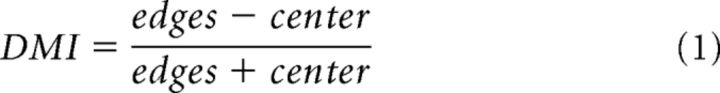Where edges and center are the mean response of pixels lying in the center and edge ROIs, respectively (see Analysis of spatial profiles and ROIs above). The index indicated the responses similarity to the edges and the center of the squares. Positive values of DMI (close to 1) indicate higher activation in the edges compared with the center, whereas zero indicates similar activation and negative values (close to −1) indicate higher center responses. DMI was calculated separately for each session.

Time to half-peak response calculation.

For each square we calculated the average time course over pixels in the center ROI. We then found the maximal amplitude of the signal and defined half of the peak amplitude as the “half-peak response” value. We found the time in which the amplitude crossed the half-peak response value and defined the time to half-peak response as the difference between this time and the response onset latency.

Measuring the time to threshold amplitude and propagation speed.

The spatial profiles for 1°, 2°, or 3° achromatic squares (see Analysis of spatial profiles and ROIs above) were smoothed using a sliding window (3 pixels, ∼0.5 mm). Next, for each point along the spatial profile we calculated the time to threshold amplitude. That is the time elapsed from response onset until the VSD signal reached a predefined threshold. The threshold was defined in the following way: for each point on the spatial profile, i.e., for each pixel, we found the peak VSD response over time. Out of these pixels response peaks, we selected the response peak with the lowest amplitude. The threshold was defined as 60% of that amplitude (other threshold values ranging from 10 to 90% were also used producing similar results; for similar analysis, see Jancke et al., 2004). This method enabled us to measure the time to threshold amplitude for each point along the spatial profile passing through the two edges and the center of the square (Fig. 8A, black curve). Next, for each edge (left or right) to center curve, we fitted a linear regression line (Fig. 8B). The linear regression line was then used to compute the propagation speed of the VSD response. This analysis was based on the assumption that the signal was propagating in space, thus reaching threshold amplitude at different times along the profile. Pixels located on the edges (Fig. 8; 5 pixels from each edge) were excluded from the regression analysis, since our aim was to evaluate the propagation of the signal originating from the edges rather than the signal at the edges themselves. Finally, we extracted the propagation speed from the slope of the linear regression lines using the following equation:

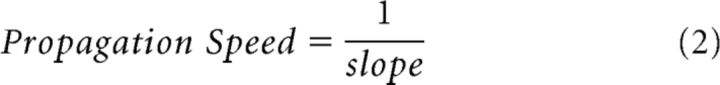where slope was calculated in units of seconds/meter. The propagation speed was calculated only for curves (right or left edge to center curves) in which the linear regression was a good fit (r ≥ 0.8). For each session the propagation speed was defined as the average between the propagation speeds calculated from the right and left to center curves (if existed). The grand average propagation speed was then calculated over all sessions. For some sessions (11 of 77) the fit of the linear regression line for both curves (right or left edge to center curves) did not pass our threshold (r = 0.8), these sessions were discarded from this analysis. The propagation speed analysis was performed in various spatial profiles (all profiles passing through the center, see Spatial correlations above) producing similar results.

Analytical retinotopic model.

To verify the choice of our ROIs and spatial profiles (see Analysis of spatial profiles and ROIs above) we implemented a retinotopic 2D analytical model that maps the visual field onto the cortical surface and used the monopole version (Schira et al., 2010) with a polar compression factor as previously described in (Ayzenshtat et al., 2012). The model's three free parameters (k, a, α) were determined for each imaged V1 hemisphere using a set of 7–11 control points obtained in an independent experiment (see Retinotopic mapping of V1 above; Ayzenshtat et al., 2012), and were a = 0.74, k = 2.95, and α = 1.54 for Monkey T, and a = 3.8, k = 1.2, and α = 0.59 for Monkey H. The model was implemented for few example sessions in which the results were reproduced.

Statistical tests.

Nonparametric statistical tests were used: the Mann–Whitney U test to compare between two medians from two populations (see Figs. 3B, 7B) or the signed-rank test to either compare a population's median to zero or compare the median of differences between paired samples to zero (see Figs. 3A, 5B, 6).

Results

To study the spatial patterns of population responses evoked by chromatic and achromatic surfaces, two monkeys were trained on a fixation task. During each fixation trial the monkey was presented with achromatic or chromatic squares (see Materials and Methods). Chromatic squares were red, green, or blue, equal in luminance to the surrounding gray background. The luminance of a black or white achromatic square was adjusted to generate a luminance contrast magnitude equivalent to the cone contrast magnitude of the chromatic squares (see Materials and Methods). Similar results were obtained for all the chromatic squares and therefore we used red as the example color throughout the paper. Using VSDI, we measured the evoked population responses in the striate cortex (V1) at high spatial and temporal resolution. The dye signal measures the sum of membrane potential changes of all neuronal elements (dendrites, axons, and somata) and therefore measures population responses rather than responses of single neurons (Slovin et al., 2002). Data were analyzed from two hemispheres of two adult monkeys (see Materials and Methods).

Early V1 population responses to uniform surfaces were edge enhanced

Figure 1A shows the spatiotemporal population response (fluorescence change, ΔF/F) evoked by 2° × 2° (termed 2° throughout the paper) squares from an example recording session. The response was evoked by the black (Fig. 1A, top) or red (Fig. 1A, bottom) square presented for 300 ms (green and blue squares were shown in additional sessions; data not shown). VSD response pattern to red and black stimuli were similar, mainly at early times (60–100 ms). Shortly after stimulus onset (∼60 ms) the maps had rectangle-like patterns in the V1 imaged area, as expected from the known retinotopic organization of V1. The early evoked response was activated mainly along the contour (edges) of the square while at the center of activation there was a hole resulting from a weaker VSD response (recently reported for 2° achromatic squares; Zurawel et al., 2014). The overall VSD response that was averaged over the entire activation patch (Fig. 1B, inset), was larger for the black response than for red, especially at times >100 ms (Fig. 1B). Both responses displayed similar onset latency. Similar results were observed for other colors (data not shown).

Figure 1 demonstrates the spatial response similarities for achromatic and chromatic squares mainly at early times (60–100 ms): the 2° squares evoked similar edge-dominated responses for both stimuli. However, it is not clear whether this chromatic-achromatic similarity appears only for 2° size squares. Therefore we investigated whether the red–black response-similarity extended over different square sizes. Figure 2A displays the results of an example recording session: population maps averaged over early times (60–100 ms after stimulus onset), evoked by red and black squares of different sizes. The squares' sizes varied between 0.5° and 8° and the centers of all squares were located at the same position in the visual field. The activation patches (Fig. 2A) evoked by the black and red squares were confined to similar retinotopic regions in V1. Figure 2B shows the responses along a spatial profile running through the edges and the center of the different squares (see Materials and Methods). The early averaged (60–100 ms) responses evoked by chromatic and achromatic surfaces displayed similar spatial patterns. The maps of the 2° squares and the spatial profiles, depicted in Figure 2A,B, middle row (green frame), showed high activation in regions corresponding to the edges of the square (edge position is marked with dashed lines in Fig. 2B) while regions corresponding to its center (center position is marked with a continuous line in Fig. 2B) had much weaker responses. This was evident also for the squares of 3° size (Fig. 2A,B, fourth row) and for the 1° size, but with a weaker modulation at the center (Fig. 2A,B, second row). The 0.5° squares maps and profiles (Fig. 2A,B, top row) displayed a Gaussian profile of activation peaking at the center of the square (Fig. 2B, continuous line). The peaks for the small 0.5° squares were positioned in the same location as the trough of responses to bigger squares. This result indicates that the weaker responses for the larger squares were indeed located at the cortical regions that receive visual input from the center of the square. For the 8° squares (Fig. 2A,B, bottom row), only the center of the square fitted the imaging chamber and therefore the most of V1 area in the chamber displayed weak responses (weaker for the black square than for the red square, see below). The cortical positions of the edge- and center-related regions were verified during independent retinotopic mapping sessions (see Materials and Methods).

To compare the cortical spatial profiles of red and black square responses we calculated the Pearson correlation coefficient (r) between the spatial profiles of responses to red and black squares (see Materials and Methods). The correlations between spatial profile of responses early after stimulus onset were high for squares of sizes 0.5°–3° (r = 0.99, 0.91, 0.95, 0.93 for sizes 0.5°, 1°, 2°, and 3°) but for the 8° square the correlation was lower (r = 0.44) mainly because the edges of the square appeared outside the imaging chamber. Similar results were obtained for the grand average analysis across all imaging sessions for different colors and square sizes. The correlation between spatial profiles of chromatic (red, green, and blue) and black squares was high (r = 0.8 ± 0.03, n = 66 correlations) indicating high similarity between the spatial patterns of responses to chromatic and achromatic squares. Other spatial profiles at different angles crossing through the edges and center of the squares were also used (see Materials and Methods) all showing high correlation coefficient values (mean Pearson correlation coefficient ranging from 0.82 to 0.9).

An interesting feature in the VSD spatial pattern evoked by the square stimuli was the edge dominance, e.g., the higher responses at regions corresponding to the edges of the square compared with the responses at regions corresponding to the center of the square. To quantify the edge-center differences we set two ROIs: one at the center of the activation patch and another at the edges (the selection of pixels for the ROIs was verified using independent retinotopic mapping sessions and a retinotopic computational model; see Materials and Methods). We compared the mean early (60–100 ms) responses at the center ROI (center responses) and the edge ROI (edge responses) across all recording sessions (Fig. 3A). This analysis was done for 1°, 2°, and 3° surfaces, where the square edges and center could be imaged simultaneously and map to different sites, in the exposed V1 area (the edges and the center of the 8° square could not fit the imaging chamber simultaneously, and therefore 8° data do not appear in Fig. 3; but see a different approach below). For 1°, 2°, and 3° surfaces, edge responses were significantly higher than the center responses (most data points are above the diagonal; each data point is an imaging session) for both chromatic and achromatic squares (Wilcoxon signed rank test, p < 0.05; n = 18, 46, and 13 sessions for achromatic squares and n = 26, 29, and 10 sessions for chromatic squares of sizes 1°, 2°, and 3° respectively). This result was consistent across the different squares of different colors (black, white, red, green, and blue, pooling over all sizes, Wilcoxon signed rank test, p < 0.001), implying that both achromatic and chromatic squares evoked edge-dominated responses early after stimulus onset.

To quantify the edge dominance effect further, we defined a DMI, calculated as the difference between the responses to edges and center divided by their sum (see Eq. 1). Positive values of DMI (close to 1) indicate higher activation in the edges compared with the center, while zero indicates similar activation; negative DMI values indicate higher center responses. The grand analysis in Figure 3B shows that for 1°, 2°, and 3° squares the DMI values in early times were all positive and significantly different from zero (Wilcoxon signed rank test, p < 0.05, n = 18, 46, and 13 sessions for achromatic squares and n = 26, 29, and 10 sessions for chromatic squares of sizes 1°, 2°, and 3° respectively). The value of the DMI increased significantly with the square size, meaning that there was more edge-dominance as square size increased (Fig. 3B; Bonferroni corrected, Mann–Whitney U test, p < 0.05).

Finally, the responses to the corners of the chromatic squares were significantly higher than the responses to the middle of the edges (Wilcoxon signed rank test, p < 10⁻⁵, n = 26; p < 10⁻⁵, n = 29; p < 0.01, n = 10 for 1°, 2°, and 3° squares, respectively). The higher corner responses were also evident for achromatic squares (Wilcoxon signed rank test, p < 10⁻³, n = 18; p < 10⁻⁸, n = 46; p < 10⁻³, n = 13 for 1°, 2°, and 3° squares, respectively). The ratio between corner and mid-edge responses was similar for all chromatic and achromatic stimuli (mean ratio ±1 SEM over edges: 1.35 ± 0.04 for achromatic 2° squares and 1.36 ± 0.05 for chromatic 2° squares; Zurawel et al., 2014).

Center responses gradually increased over time for achromatic but not chromatic surfaces

Next we investigated the temporal dynamics of edge and center responses. Figure 4A (same example session as Fig. 2, middle row) shows space–time maps for 2° black (Ai) and red (Aii) squares. The x-axis represents cortical distance along a spatial profile that slices through the image as illustrated in Figure 4A, inset. The cortical positions of the edge- and center-evoked activity are marked by dashed and continuous vertical lines respectively. The y-axis in Figure 4A is the time from stimulus onset. The space–time maps in Figure 4Ai,Aii shows that early after stimulus onset the responses were edge-dominant. However at later times for the black squares (Fig. 4Ai) the response at the center gradually increased and grew closer in amplitude to that of the responses to the edges. Moreover, Figure 4Ai suggests that the VSD response for the black square appeared to have propagated gradually from the edges to the center (see further analysis in Fig. 8). Figure 4Bi displays the time course of the center and edge responses of the VSD signal evoked by the black square. Figure 4Bi clearly shows that the center responses increased with time much more slowly than did the edge responses, arriving to peak at later times. The slower increase in the center responses to black squares were mostly due to the less steep rising phase of the center signal compared with edge signal rather than differences due to response onset latency. The normalized time course in Figure 4Ci (normalized to maximal response in each ROI) further confirms these observations.

Surprisingly, the dynamics of edge versus center responses to the equivalent red square were different from the black square's (Fig. 4Aii). Early responses were edge-dominant, but unlike the case of the black square, the responses to the red square remained edge-dominant at later times. The center-evoked activation displayed a fast increase reaching a stable low amplitude response (Fig. 4Bii,Cii; normalized response to peak in each ROI). Unlike the black center responses, the red center responses did not gradually increase at later times. The temporal profile of the red square mean center responses arrived to peak already ∼100 ms after stimulus onset (Fig. 4Bii,Cii) and therefore the V1 representation was not isomorphic to the image at any time.

Figure 4D displays the dynamics of the DMI aligned on stimulus onset, for the black and red 2° surfaces (same session as in Fig. 4A–C). The DMI of the black surface had a relatively high value (0.25) early after stimulus onset consistent with the early edge dominance. Later, due to the slow response increase at the center, the DMI declined to values close to zero. The DMI of the red surface however reached an early high value (∼0.35) in the first 100 ms and did not change much at later times (∼0.4), indicating edge-dominant activity throughout. We measured the DMI temporal dynamics for the different chromatic and achromatic surfaces in all of our recording sessions. The mean DMI dynamics over all of the 2° achromatic (n = 46 sessions) and chromatic (n = 29 sessions) squares is displayed in Figure 5A (to average over different colors and contrasts, the VSD signal in each session was aligned on response onset at the edges (rather than stimulus onset; Fig. 4D; see Materials and Methods). Similar to the example session, the mean DMI for achromatic squares displayed high early values gradually decreasing over time. The chromatic DMI dynamics indicated stable edge-dominance with almost no later change in the center dynamics. Figure 5B shows that the decrease in DMI appeared for both black and white squares, but to a smaller degree in white squares. Similar DMI dynamics were measured for the mean DMI over all the 1° and 3° squares.

For quantitative statistical comparisons, we compared the values of the DMI in early (30–70 ms after edge response onset) and late (130–170 ms after edge-responses onset) times (Fig. 5C). The early DMI in achromatic squares was significantly higher than the late DMI (Wilcoxon signed rank test, p < 10⁻⁸, n = 46 sessions). The DMI for chromatic squares did not decrease and even showed an increase (n = 29 sessions). The same results were achieved for 1° squares (p < 0.01, n = 18 and n = 26 sessions, for achromatic and chromatic squares, respectively), 3° squares (p < 10⁻¹³, n = 13 and n = 10 sessions, for achromatic and chromatic squares, respectively) and for each color and contrast separately (Fig. 6).

The DMI decrease for black squares only at late times could originate from either an increase in the center responses or a decrease in the edge responses. To examine this point, we compared the early and late responses at the center and edges, and found that for achromatic surfaces of sizes 1°–3° there was an increase in the center responses and no decrease in the edge responses (data not shown) indicating that the delayed DMI decrease is driven by center responses that increased relatively slowly with time after stimulus onset.

The observed VSD response differences (edge vs center) were reproducible across variable stimulus locations in the visual field and thus different cortical ROIs (see Materials and Methods). In addition, we wanted to investigate whether we could reproduce the results when the VSD responses of the edge and center were obtained from the same ROI. This approach enabled us to control for any unspecific VSD response changes across cortical locations (e.g., nonhomogeneous VSD staining; see Materials and Methods). To address this point further, a different set of experiments was performed. In these sessions the location of the square stimulus switched between two different positions in the visual field, on different trials. The square's center in one trial and the edges' middle (either top or bottom edges) in the next trial, were aligned to the same location in the visual field. Therefore we could measure the VSD response for the square's center and edge and compute the DMI using the same cortical ROI. Importantly in these experiments we were able to calculate the DMI for large squares (8°) that were too large to entirely fit into our imaging chamber. The calculated DMI exhibited similar temporal dynamics as in the original experiments for 2°, 3°, and 8° squares. The early DMI in achromatic squares was significantly higher than the late DMI (Wilcoxon signed rank test, p < 0.05, n = 8 sessions) indicating gradual enhancement of center responses in achromatic but not in chromatic surfaces (n = 8). This approach also supported the idea that the observed response differences between chromatic and achromatic squares were not related to any specific relation between a cortical ROI and the locations of achromatic/chromatic features in the visual image.

Achromatic center responses rise slower as square size increases

Next we asked whether the response dynamics at the center was influenced by distance from the edges. To do that we measured the population response in the center ROI of the surface for squares of different sizes (Fig. 7A, example session). Interestingly, the center responses of achromatic surfaces displayed size-dependent activity. In small achromatic squares the center reached its peak response already within 100 ms poststimulus onset. However, the time to peak became slower as square size increased. For the 8° square, time to peak was ∼200 ms. In contrast, the response at the chromatic squares center exhibited similar time to peak for all square sizes, i.e., it was invariant with size. To quantify the slower dynamics observed for the bigger black squares, we calculated the time to half-peak response (see Materials and Methods). The grand average over all recording sessions, revealed that the time to half-peak response increased significantly as the edges were more remote and square size increased for achromatic stimuli (Fig. 7Bi; Bonferroni corrected Mann–Whitney U test, n = 18, 46, 13, and 7 sessions for 1°, 2°, 3°, and 8° square sizes, respectively, p ≤ 0.05). The time to half-peak response for chromatic surfaces did not vary significantly with size of square (Fig. 7Bii; n = 26, 29, 10, and 6 sessions for 1°, 2°, 3°, and 8° square sizes respectively; no significant change, p > 0.87). These results suggest that there is a difference in the neural mechanism mediating late achromatic and chromatic center responses.

Figure 7A shows that the early response (<100 ms) to the center of the 8° black square is almost absent while there is substantial response to the 8° red square (Fig. 2A, bottom row). To quantify this we computed the sum of center responses over early times (0–100 ms). The sum of the early 8° black center responses was 0.35 × 10⁻³ ΔF/F while the red square displayed much higher values: 1.42 × 10⁻³ ΔF/F. The grand analysis showed similar results: the mean sum of the chromatic early 8° center responses was significantly higher than the achromatic (p < 0.05, Mann–Whitney U test, n = 7/6 achromatic/chromatic sessions; mean ± SEM: 0.36 × 10⁻³ ± 0.19 × 10⁻³/1.28 × 10⁻³ ± 0.31 × 10⁻³ ΔF/F). For the achromatic stimuli, the mean of sums was not significantly different from zero, whereas for the chromatic it was (Wilcoxon signed rank test, p = 0.11/p < 0.05; n = 6/7 achromatic/chromatic sessions). Additionally, the chromatic center responses were higher than the achromatic center responses in each time frame 30–120 ms after stimulus onset (significant difference 40–90 ms; p < 0.05, Mann–Whitney U test; 7/6 achromatic/chromatic sessions). These results were evident also for the 3° and 2° center responses but not for 1° (higher chromatic center responses 40–100 and 40–120 ms after stimulus onset, significant difference: 50 and 60–70 ms after stimulus onset for 3° and 2° center responses; p < 0.05, Mann–Whitney U test; 13/10 and 46/29 achromatic/chromatic 3° and 2° sessions).

Achromatic square responses increase slower as a function of distance from the edges

The response at the center of achromatic squares shows slower rising phase compared with the edge responses. We then asked: what are the dynamics of responses in intermediate regions between the edges and the center? Figure 4Ai suggests that the responses to the achromatic surfaces increase slower as a function of distance from the edges. To investigate and quantify this phenomenon further we measured the average response in a sliding 3-pixel size window over a spatial profile through the achromatic surface. Next we calculated how long it took the signal in each window to cross threshold response amplitude (see Materials and Methods). The time to a threshold amplitude in a spatial profile spanning through a 2° achromatic surface from an example session is depicted in Figure 8A,B. As expected the edges' responses were the fastest to reach the threshold. The time to threshold increases gradually when propagating from the edges to the center, reaching maximal value at the center. This gradual increase in the time to threshold seemed almost linear, to further study this we fitted a linear regression line to the time to threshold curve between the edges and center at each of the center sides (Fig. 8B, dashed lines). In 86% of the sessions in which an achromatic 1°, 2°, or 3° square was presented, the linear regression curve of center to edge was fitted with r² > 0.8 (n = 66 sessions; see Materials and Methods). The slope of the linear regression lines over sessions were significantly different from zero (Wilcoxon signed rank test, p < 10⁻¹¹) consistent with continuous propagation from the edges to the center. Finally we extracted the propagation speed from the slope of the linear regression line. The average speed was 0.088 ± 0.0045 m/s. This speed is in the range of the previously reported horizontal connections speed (Grinvald et al., 1994; Bringuier et al., 1999; Slovin et al., 2002). The derived velocities were reproducible across different square sizes and spatial profiles (see Materials and Methods).

Discussion

We measured population response in V1 of fixating monkeys presented with achromatic and chromatic squares. The evoked patterns showed similar early responses at the edges of both chromatic and achromatic squares, with noticeable corner-enhancement. At later times, the responses were surprisingly different; responses at the center of achromatic squares increased gradually, arriving closer to the response amplitude of the edges, whereas the responses at the center of chromatic squares were low and did not change much with time.

The role of edges in surface representation and perception

V1 is known to be highly sensitive to spatial luminance contrast (De Valois and De Valois, 1988; Friedman et al., 2003). Indeed, we found that early VSD responses to achromatic squares of different sizes (1°–3°) are strongest at the squares' edges (Zurawel et al., 2014). We also found that these edge-dominant responses are evident early after stimulus onset for chromatic squares, that is, square objects defined only by color difference with the background. The chromatic edge enhancement observed in the VSDI results is in accordance with previous electrophysiological studies showing that most color responsive neurons in V1 are more sensitive to color contrast (i.e., double-opponent cells) than to a uniform color field (Conway, 2001; Johnson et al., 2001; Friedman et al., 2003). Similar results were obtained using VEP measurements (Rabin et al., 1994). VSDI enabled us to measure the neuronal responses to the edges and center simultaneously without possible biases due to cell selection. Our results complement previous findings and show that V1 neuronal responses at the population level are edge-dominated.

The edges of surfaces have been shown to influence dramatically the perceived color and brightness of the surface. Phenomena like color and brightness induction (De Valois et al., 1986; Brown and MacLeod, 1997), Craik-O'Brien Cornsweet effect (Cornsweet, 1970; Wachtler and Wehrhahn, 1997) and more (Pinna et al., 2001) emphasize the importance of edges in determining perceived color and brightness. Our results support the psychophysical and perceptual findings on the important influence of edges in visual perception.

Is there a unified representation for surfaces in V1?

The existence of surface-responsive neurons in V1 has been reported in many studies (Johnson et al., 2001; Kinoshita and Komatsu, 2001; Friedman et al., 2003; von der Heydt et al., 2003; Roe et al., 2005; Dai and Wang, 2012). However, the representation of surfaces in V1 is under debate. Two main theories were suggested (for review, see Komatsu, 2006): the symbolic, or cognitive, theory states that early visual areas extract only contrast information at the surface border, and the color and shape of the surface are reconstructed in higher areas. The isomorphic theory assumes a pointwise representation of visual features, such as color or brightness in early visual areas. “Intermediate” theories have also been suggested (Komatsu, 2006). We found that the responses at the center of achromatic squares increased at late times, a result that might be partially consistent with a late isomorphic representation of surfaces (Figs. 5B, 6A; but the responses at the center of white squares of all sizes and 8° black squares were only mildly increased). However chromatic surface responses were edge-dominated throughout the neural response, inconsistent with the isomorphic theory. Consequently, we conclude that the neuronal population representation of surfaces in V1 does not appear to be exclusively isomorphic. Therefore an isomorphic representation in V1 is not required for uniform surface perception, and that the representations of chromatic and achromatic surfaces in V1 are not similar over time.

The literature regarding isomorphic representation in V1 is diverse. Some studies found no evidence for an isomorphic representation (Friedman et al., 2003; von der Heydt et al., 2003; Cornelissen et al., 2006), whereas others did (Komatsu et al., 2000; Sasaki and Watanabe, 2004; Meng et al., 2005; Huang and Paradiso, 2008). We found that different stimuli (specifically chromatic and achromatic squares) evoke different response patterns and therefore the apparently reported contradictions in the aforementioned studies might be reconcilable. VSDI is a population response that sums activity from all neuronal populations in the cortex. Therefore we cannot rule out the possibility that an isomorphic representation of chromatic surfaces exists in a specific cell population. For instance the small population of single-opponent cells, which are mainly sensitive to uniform color surfaces, may form an isomorphic representation. Another possibility is that an isomorphic representation exists only in deeper layers (Komatsu et al., 2000), whereas the VSD signal emphasizes the activity in upper layers.

Can the center responses to chromatic and achromatic stimuli reflect different spatial tuning of the stimuli?

Previous psychophysical studies showed that color contrast sensitivity is greater than monochromatic contrast sensitivity at low spatial frequencies (Mullen, 1985; Hass and Horwitz, 2013; lower than 0.5–2 cycles/°). Consistent with the psychophysical findings, we found that at early times after stimulus onset the responses to the center of squares ≥2° are higher for chromatic compared with achromatic squares (as evident in Fig. 7A,B), and this difference was most noticeable for the center of the 8° squares (Fig. 2A). Our results can be interpreted as a difference in achromatic and chromatic spatial tuning in V1 responses, but only at early times (<100 ms) after stimulus onset.

Different late center dynamics for achromatic and chromatic squares

The different dynamics of the center responses for achromatic and chromatic squares point into two questions: (1) What neuronal mechanism can underlie the achromatic late center responses and why is it different for chromatic squares? (2) Are there perceptual correlates to the late increase in the achromatic center responses? Below we address these questions.

Achromatic squares late increase of center responses may be explained by neuronal filling-in

The existence of neuronal filling-in in V1 surface representation was suggested by several studies (Sasaki and Watanabe, 2004; Roe et al., 2005; Huang and Paradiso, 2008). The underlying mechanism of neuronal filling-in involves early responses to the edges of the surface followed by propagation of activation from the edges to the center. We showed that the latency to peak response at the center of achromatic surfaces increased with distance from the edges and that the responses seemed to propagate linearly from the edges to the center. The mean propagation speed of the population response was well within the range of previously reported horizontal connections' speed (Grinvald et al., 1994; Bringuier et al., 1999; Slovin et al., 2002). Our findings therefore support a horizontal-connection-mediated neuronal filling-in mechanism for achromatic surfaces (Spillmann and De Weerd, 2003; Huang and Paradiso, 2008). Our results also suggest that there is no neuronal filling-in for chromatic surfaces (von der Heydt et al., 2003). The signal evoked by chromatic edges is likely to reflect mainly double-opponent cells' responses, whereas single-opponent cells are activated in the center. Consistent with our findings, von der Heydt et al. (2003) showed that color surface neurons (i.e., single-opponent neurons) did not change their firing patterns even when perceptual filling-in takes place. The lack of neuronal filling-in in chromatic surfaces may therefore imply low connectivity between double and single-opponent cells via horizontal connections in V1.

In addition to horizontal connections, other neuronal mechanisms could account for the slow increase in the center responses. Slower response properties of achromatic surface cells or inhibition may play a role in the slow responses to the center of achromatic surfaces. Solomon et al. (2004) showed that the center-surround fields of chromatic and achromatic sensitive cells are different; their findings may explain the different dynamics of achromatic and chromatic center responses. The different center-surround field can also affect the corner versus edge response ratio as suggested in Zurawel et al. (2014). However, we found similar corner to edge response ratio for both chromatic and achromatic surfaces.

Perceptual correlates of late center responses

Are there perceptual correlates of the late increase in the achromatic center responses? Our study did not include any behavioral report; therefore we cannot answer this question directly. However, we can predict that if there is a perceptual phenomenon that correlates to the increase in center responses in V1 it should exist for achromatic surfaces but not chromatic surfaces. Perceptual filling-in was suggested by some studies to correlate with a late increase of the center responses (De Valois et al., 1986; Paradiso and Nakayama, 1991; Sasaki and Watanabe, 2004; Huang and Paradiso, 2008). However perceptual filling-in exists also for chromatic surfaces as shown by several perceptual phenomena (color induction, Craik-O'Brien-Cornsweet effect, Chevreul effect, and more). It is possible that the magnitudes of the phenomena are different (Wachtler and Wehrhahn, 1997) or that the mechanisms underlying perceptual filling-in for chromatic and achromatic surfaces are different. Additional research in which the perceived color and luminance of a surface will be reported by the monkey is required to study this issue further.