Visual Learning Induces Changes in Resting-State fMRI Multivariate Pattern of Information

Abstract

When measured with functional magnetic resonance imaging (fMRI) in the resting state (R-fMRI), spontaneous activity is correlated between brain regions that are anatomically and functionally related. Learning and/or task performance can induce modulation of the resting synchronization between brain regions. Moreover, at the neuronal level spontaneous brain activity can replay patterns evoked by a previously presented stimulus. Here we test whether visual learning/task performance can induce a change in the patterns of coded information in R-fMRI signals consistent with a role of spontaneous activity in representing task-relevant information. Human subjects underwent R-fMRI before and after perceptual learning on a novel visual shape orientation discrimination task. Task-evoked fMRI patterns to trained versus novel stimuli were recorded after learning was completed, and before the second R-fMRI session. Using multivariate pattern analysis on task-evoked signals, we found patterns in several cortical regions, as follows: visual cortex, V3/V3A/V7; within the default mode network, precuneus, and inferior parietal lobule; and, within the dorsal attention network, intraparietal sulcus, which discriminated between trained and novel visual stimuli. The accuracy of classification was strongly correlated with behavioral performance. Next, we measured multivariate patterns in R-fMRI signals before and after learning. The frequency and similarity of resting states representing the task/visual stimuli states increased post-learning in the same cortical regions recruited by the task. These findings support a representational role of spontaneous brain activity.

Introduction

Fluctuations of spontaneous activity measured through the blood oxygenation level-dependent (BOLD) signal with functional magnetic resonance imaging (fMRI) have been shown to be coherent across multiple networks of brain regions (Biswal et al., 1995). Functional connectivity can be modulated by cognitive tasks (Fransson, 2006; Sun et al., 2007; Weisberg et al., 2007), sensory stimulation (Hampson et al., 2004), and learning (Waites et al., 2005; Albert et al., 2009; Lewis et al., 2009; Stevens et al., 2010; Tambini et al., 2010). Current theories hypothesize that functional connectivity, and its modulations, reflect changes in temporal synchronization and/or excitability between regions of the brain that are structurally connected (Raichle, 2010).

However, at the neuronal level, spontaneous activity can “replay” patterns evoked by a stimulus (Tsodyks et al., 1999; Kenet et al., 2003). And, during development, spontaneous activity patterns in visual cortex (VC) become tuned to the statistical properties of the visual environment (Berkes et al., 2011). These observations suggest that spontaneous activity may also play a “representational” role by encoding patterns of neuronal activity related to common and behaviorally relevant visual objects and stimuli (Harmelech and Malach, 2013).

In previous work, we found that visual perceptual learning modifies the resting functional connectivity between cortical regions recruited by the task (Lewis et al., 2009), suggesting that learning-dependent modulations of functional connectivity represent a system-level signature of the implicit memory related to the acquired skill (for example, see Albert et al., 2009; Tambini et al., 2010; Harmelech et al., 2013). Furthermore, individual differences in resting functional connectivity within visual cortex were found to be predictive of future performance, suggesting that spontaneous activity may represent a prior activity for stimulus-evoked neuronal activation (Baldassarre et al., 2012).

Here we examine whether changes in spontaneous activity after perceptual learning may reflect changes in the underlying stimulus/task representations. Specifically, we measured whether particular brain states recorded with fMRI during a highly trained visual discrimination task also emerged subsequently in spontaneous brain activity.

Multivariate pattern analysis (MVPA) has been used to analyze fMRI images (Haynes and Rees, 2006; Norman et al., 2006; Poldrack, 2008) and allowed discrimination between subtle variations of patterns elicited by different categories of visual stimuli (Haxby et al., 2001). Recently, it has been applied to detect specific activity patterns during the resting state (Schrouff et al., 2012; Tusche et al., 2014).

Using the data in Lewis et al. (2009), we trained a classifier to separate fMRI BOLD responses to learned versus novel visual stimulus arrays during a shape orientation discrimination task. Observers had previously become proficient in recognizing a specific stimulus orientation. We then determined whether classifier performance was related to subject performance to ensure its behavioral validity. Finally, we applied the same classifier to spontaneous activity measured before and after training to examine whether the frequency and similarity of patterns discriminating trained and untrained stimuli increased following perceptual learning. We predicted that if spontaneous brain activity partly represents underlying stimulus/task representations, then perceptual learning/task performance should induce a significant change in the patterns of activity representing the task stimuli.

Materials and Methods

Participants.

Eleven healthy, right-handed observers (N = 11; 6 females; age range, 20–30 years) with no psychiatric or neurological disorders, and normal or corrected-to-normal vision, participated in the study. They provided written informed consent approved by the Research Ethics Board of the University of Chieti.

Visual stimuli and experimental paradigm.

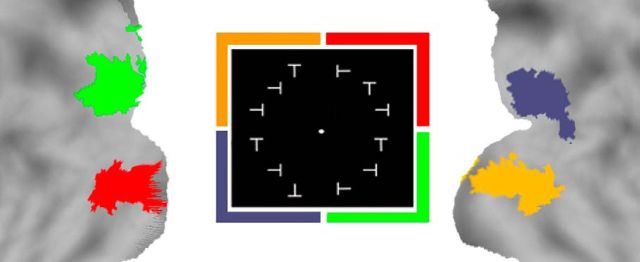
The stimulus array consisted of 12 “T” characters with four possible orientations (upright, inverted, and 90° rotated leftward or rightward) arranged in an annulus with a radius of 5° and displayed across the four visual quadrants. An inverted T was the trained target shape, while differently oriented Ts were the distractors. The target shape appeared only in the lower left quadrant of the screen in one of three random locations, while distractors appeared in the other quadrants (Fig. 1B). Observers were cued on each trial to the target shape; after a brief delay, they were asked to discriminate the presence/absence of the target shape without moving their eyes from a central fixation spot. The target appeared with a probability of 80%, while 20% were catch trials. The stimulus array was briefly presented (150 ms), and eye movements were recorded.

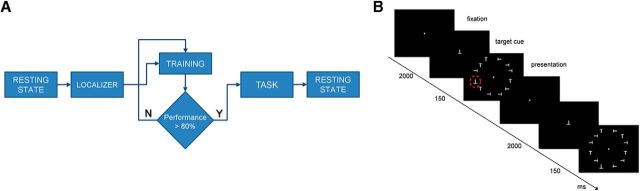
Figure 1.

Experiment sessions and paradigm. A, The sessions of the experiment: (1) first R-fMRI session before perceptual learning; (2) functional localizer task fMRI session (same day); (3) perceptual learning training on the shape orientation discrimination task (no imaging) until performance was >80% of correctly recognized target shapes on three consecutive blocks of trials (2–9 d on average); (4) T-fMRI session during shape orientation discrimination task; and (5) second R-fMRI session (same day). B, Experimental paradigm. Subjects fixated throughout the experiment. A cue indicating the target orientation was presented for 2 s. During perceptual learning, the target orientation was always an inverted T. During T-fMRI, the target orientation was the same as during perceptual learning during trained blocks of trial, and either a left- or right-tilted T during untrained blocks of trials. The stimulus array was briefly presented (150 ms) to minimize eye movements The target shape was always in the left lower quadrant, both for trained and untrained blocks of trials. N, No; Y, yes.

Experiment time line.

Before any exposure to the task, we acquired fMRI data during resting-state and visual localizer scans. During resting-state scans, subjects were instructed to fixate a small cross under low-level illumination. During visual localizer scans, the response to stimuli presented in each visual quadrant was mapped using six functional localizer runs. Each run consisted of 20 blocks: 16 stimulation blocks (4 for each quadrant) interlaced with 4 fixation blocks. The stimulus was a flashing array of 3 Ts (6.67 Hz for 13 s) presented in the relevant visual quadrant.

Following the first scanning session, subjects were trained on the shape orientation discrimination task described above. Each observer performed a daily training session involving, on average, 30 blocks (range, 10–45 blocks), with each block containing 145 discrimination trials (80% target, 20% catch trials). On average, participants took ∼5600 trials (average, 4 d; range, 2–9 d) to reach a criterion defined by ≥80% accuracy on 10 consecutive blocks. Importantly, the rate of hits was corrected for the rate of false alarms according to the following formula:

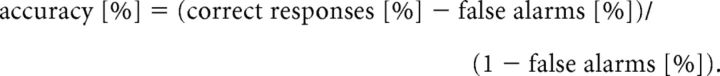Within a few days after the completion of training, a third fMRI session was run in which observers performed, alternating in a block design, the shape orientation discrimination task using respectively either “trained” or “novel” untrained targets. The only difference was that in different blocks observers were cued to discriminate either the trained target (inverted T, same as during training) or novel untrained targets (leftward or rightward rotated Ts). The shape orientation discrimination task was performed in blocks of trials (five blocks for trained and five blocks for untrained targets), alternating with visual fixation periods. Each block began with the presentation of the target shape at central fixation for 2.163 s, followed by six consecutive trials (12 s duration). Fixation blocks lasted randomly 6, 10, or 12 s with equal probability.

After the task fMRI data were acquired, we conducted six runs of resting state. The time line of the experiment is shown in Figure 1A.

fMRI data Acquisition.

fMRI data were collected using a 1.5 T Siemens Vision scanner. Functional images were acquired with a gradient echo sequence (TR = 2.163 s; TE = 50 ms; flip angle = 90°; slice thickness = 8 mm) in the axial plane (matrix = 64 × 64, 3.75 × 3.75 mm in-plane resolution). fMRI in the resting state (R-fMRI) runs (n = 6) included 128 frames (volumes) and lasted 4.6 min for a total scan time of 28 min. Task-evoked fMRI (T-fMRI) functional localizer runs (n = 6) included 117 frames and lasted 4.2 min for a total scan time of 25 min. Finally, T-fMRI task runs included 113 frames and lasted 4 min for a total scan time of 24 min.

fMRI preprocessing.

fMRI data were realigned within and across scanning runs to correct for head motion using an eight-parameter (rigid body plus in-plane stretch) cross-modal registration. Differences in the acquisition time of each slice within a frame were compensated for by sync interpolation. A whole-brain normalization factor was applied to each run to correct for changes in signal intensity between runs (mode of 1000). For each subject, an atlas transformation was computed on the basis of an average of the first frame of each functional run and MPRAGE structural images to the atlas representative target using a 12-parameter general affine transformation. All alignment transformations were performed in a single step. Functional data were interpolated to 3 mm cubic voxels in atlas space. The atlas representative MPRAGE target brain (711–2C) was produced by mutual coregistration (12-parameter affine transformations) of images obtained in 11 normal subjects. All preprocessing steps were performed using software developed in-house (fIDL tools from Washington University; www.nil.wustl.edu/labs/fidl).

Functional localizer images were analyzed using a general linear model with an assumed hemodynamic response function (Boynton hemodynamic model). Five regressors, one for each condition (fixation, upper left, upper right, lower left, and lower right quadrants), were used. Group effects were taken into account using voxelwise random-effects ANOVA, z-score maps were calculated for each condition, and statistical significance was assessed by means of a Montecarlo correction for multiple comparisons (p < 0.05). Voxels responding preferentially to a quadrant were selected by comparing, for each voxel, the β value in the quadrant z-score map with the average β value in the z-score maps of all other quadrants.

Pattern classification analysis.

Pattern classification analysis was performed using the Python package PyMVPA (Hanke et al., 2009) with the aim of classifying brain states according to their association with trained versus untrained stimulus; in the following sections, we describe the searchlight, the spatiotemporal, and the resting-state data analyses.

For each dataset, before pattern classification analyses, we performed a linear detrending for each voxel BOLD time series and a feature-wise z-score normalization to reduce the effect of voxelwise signal change (Pereira et al., 2009); moreover, this procedure helps the classifier to easily converge to solution (Pereira et al., 2009).

Searchlight analysis.

A searchlight analysis, first proposed by Kriegeskorte et al. (2006), was performed on the shape orientation discrimination task dataset. Using this technique, it is possible to map the information carried by each voxel neighborhood and thus its ability to well discriminate the stimuli. Here we adopted a variant of this method, as used by Connolly et al. (2012). The algorithm scrolls the entire fMRI image, and for each voxel builds a sphere of a given radius around it, and, using voxels within the sphere, it trains a classifier that discriminates between the trained and the untrained condition; the corresponding classification accuracy is then assigned to the central voxel of the sphere, thus producing a classification accuracy map.

The classification algorithm was a support vector machine with a Linear Kernel and C = 1, with a searchlight radius equal to 5 voxels (3 mm cubic), so that the sphere around each voxel contained 515 voxels. The dataset was split into two halves and used in a cross-validation model selection to cope with the high computational and timing costs of searchlight analysis. We obtained a map for each cross-validation fold; these were averaged to get a single information map.

Then, a group map was generated by assigning to each voxel its significance in a t test across subjects of classification accuracy versus chance level [thresholded at p < 0.01 with false discovery rate (FDR) correction].

ROI-based analysis and correlation with behavioral performance.

In view of the subsequent resting-state analysis, we sought to build a behaviorally significant classification scheme. This required assessing which voxels were task relevant from the searchlight and localizer analyses. We therefore calculated the correlation, across subjects, between classification accuracy and behavioral performance, in the following ROIs (shown in Figs. 2, 3): the right dorsal visual cortex; the whole localizer area; the right and left precuneus (PCu); the right and left intraparietal sulcus (IPS)/inferior parietal lobule (IPL); the right and left V3/V3a/V7; and the whole searchlight region.

Figure 2.

Localizer defined areas. Areas identified in the localizer session. Each quadrant is referenced by a color, and the same color is used in the brain map to represent the most activated voxels. ROIs were identified in each quadrant as showing the strongest visuotopic localizer responses compared with the average response to stimuli in the other quadrants (group-level, voxelwise, random-effects ANOVAs, multiple-comparison corrected over the entire brain with a p value of <0.05).

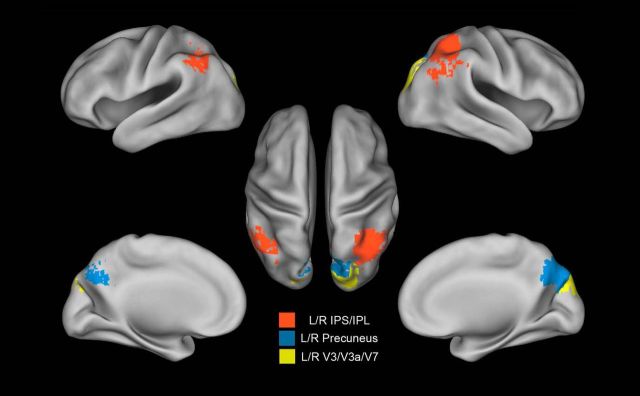
Figure 3.

Anatomical areas extracted from the searchlight map. ROI derived from the searchlight map: left (L) and right (R) precuneus in the medial parietal lobe (blue); lateral parietal left and right IPS/IPL within the lateral parietal lobe (red); and left and right dorsal visual V3/V3a/V7 (yellow).

First, we computed the classification accuracy for each ROI individually using the MVPA. Next, for each ROI, we calculated across subjects the Pearson correlation coefficient of the classification accuracy with the mean percentage of correct responses in stimulus recognition (averaged over trained and untrained blocks of trials). Since classification accuracies did not correlate with response accuracy using the ordinary spatial MVPA, we sought a different classification model that would be behaviorally significant for use in the resting-state analysis.

Spatiotemporal analysis.

A variant of the standard spatial analysis that did not consider single fMRI images as examples but considered the set of all voxel time courses in a single epoch was used (Mourão-Miranda et al., 2007). Data samples were built considering the time course in each task block for each voxel. The time course for each epoch in this case corresponded to the duration of each task block (seven frames or 14 s). Multiple epochs (5 blocks per scan × 6 scans) for a total of 30 data samples formed the dataset for each condition (trained, untrained; see Fig. 7, schematic). We used a support vector machine using a Linear Kernel and a regularization factor C = 1, using a leave-one-run-out cross-validation. No feature selection algorithm was used.

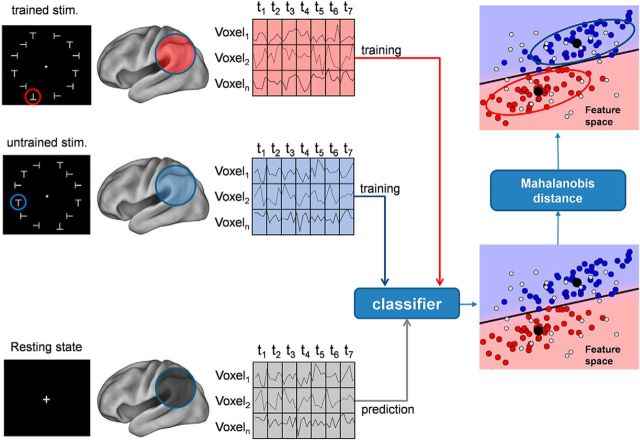
Figure 7.

Schematic of resting-state decoding. Schematic of the procedure to label brain states in the resting state using a spatiotemporal classifier model that classifies trained versus untrained stimuli in the discrimination task. We extracted voxels from a brain region (e.g., voxel 1 − voxel n). For each voxel, each data sample contains 7 frames of contiguous fMRI volumes (t₁–t₇). The classifier is first trained on the task data to recognize stimuli as belonging to the trained or untrained class, respectively (blue vs red dots in the scatter plot). This classifier is then used to label resting-state data (light gray dots) that have been subdivided into temporal epochs of the same duration using a sliding window approach (Fig. 8). After classification, a similarity criterion based on Mahalanobis distance is used to further select data samples. Samples with a distance smaller than a threshold value (blue and red ellipses) are considered similar to stimulus (trained/untrained) patterns. stim., Stimulation.

Resting-state data analysis.

In the resting state, brain states (or fMRI images) do not belong to any particular experimental condition. It is therefore necessary to train the classifier on the discrimination task data. Cross-decoding (Kriegeskorte, 2011) is a method that trains a classifier to learn a discriminant model on a primary task and then generalizes on a secondary task without further classifier training, as illustrated in Figure 7. It can provide insights into some brain mechanisms if the tasks share specific common effects in some brain regions. This analysis technique is also referred as transfer learning (Schwartz et al., 2012).

In our case, the primary task was the shape orientation discrimination task, while the secondary task was the resting state. The goal was to check whether spontaneous brain activity generates patterns similar to those elicited by the shape orientation discrimination task during visual perceptual learning. In other words, it checked whether some patterns occurring in the resting state were classified as belonging to the class of patterns associated with the trained or untrained target in the shape orientation discrimination task.

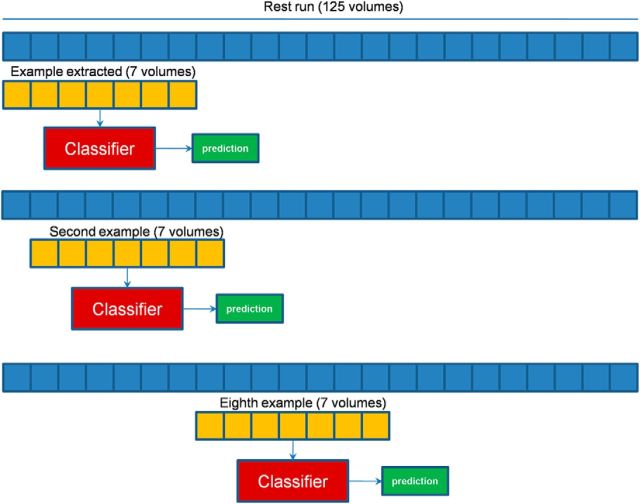
In the analysis of discrimination task data, we used voxel time courses that were 7 frames long, corresponding to a block of trials for either the trained or untrained task. Likewise, we divided the resting-state dataset epochs of the same duration. Since we did not have any a priori information as to when a particular pattern could occur during the spontaneous brain activity, we slid a window of the same duration of a block of trials (7 frames) during the entire time course of the resting state, advancing it by one time frame for each new example (see Fig. 8).

Figure 8.

Building of resting-state dataset examples for spatiotemporal classifier. The approach used to build the example from R-fMRI acquisition is shown: a window of 7 volumes is scrolled during the entire run time course; and the window is shifted by a volume to make further examples. Each example created was labeled using the classifier trained on task data, and further refinement is done using the similarity criterion based on Mahalanobis distance.

Similarity between labeled resting-state brain images and target brain images.

In a task experiment, each brain state belongs to one of a (usually small) number of experimental conditions, and the classification outcome can be checked against the actual labeling of brain states. In that case, the goal is to assess the discrimination ability of the model. This is not the case in resting-state data: On one hand, brain states do not belong to any particular experimental condition; on the other hand, we do not wish to assess a model, but rather to detect the presence of particular brain states (the model being already established from task data).

The fact that a given state was classified as belonging to a given class (e.g., trained stimulus) means that this state is closer to that class than to other classes, according to the model; but since we may expect, in the resting state, a large variability in brain states, it still may be very far from all classes. Therefore, we need a quantitative criterion to assess on statistical grounds whether the classified brain states from resting-state data are actually similar to those elicited in the task experiment. In statistical learning, the distance in data space is a measure of similarity between two patterns; indeed, many classification algorithms are based on a distance measure to discriminate classes (Hastie et al., 2009).

We can take advantage from outlier detection methods based on the Mahalanobis distance. These are very popular in a broad range of research areas (Peña and Prieto, 2001; Farber and Kadmon, 2003; Hodge and Austin, 2004; Suzuki et al., 2008). In neuroimaging studies, this technique has been explored by Fritsch et al. (2012) and Magnotti and Billor (2014), but the high dimensionality of neuroimaging data hampers the correct detection of outliers.

The expression for the Mahalanobis distance is as follows:

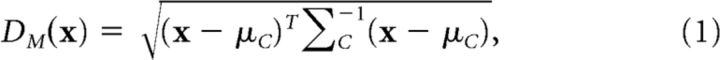where x is the brain image, and (μ_C, Σ_C) are the mean and covariance matrix of the class C.

It is well known that [D_M|μc,Σc(x)]² ∼ χ_n², where n is the dimension of x. We could set a confidence level of p = 0.01 and find the corresponding threshold distance D_M|μc,Σc*(x)², discriminating between images that are far from class C (although they are classified as belonging to C) and those that are close to class C. This was chosen as our similarity criterion; in the following sections, we define the similarity index, the p value associated with a given distance value.

The Mahalanobis distance depends on class mean and covariance (Eq. 1). To estimate these parameters for each class (trained, untrained), we used as observations the images that were correctly labeled in the task dataset. The covariance estimation using the empirical formula could turn out to be impossible because, due to the high dimensionality of the data, there is a high probability of linear dependency between observations, yielding a non-full-ranked matrix.

Several methods to robustly estimate a covariance matrix in high-dimensional problems have been developed (Huber, 2005); here we chose a shrunk estimation method published by Ledoit and Wolf (2004) and implemented in the scikit-learn package (Pedregosa et al., 2011).

Correction for multiple comparison.

All pattern classifications and analyses of pattern similarity are performed on six ROIs. A Bonferroni correction for multiple comparisons yielded a corrected p value threshold by dividing by the number of ROIs. All the reported p values are uncorrected, but for all of the main analyses we indicate which effects do, or do not, survive correction for multiple comparisons. As previously described, the searchlight map was corrected using false discovery rate correction.

Results

The strategy for analysis consisted of the following steps. First, we performed a searchlight analysis (Kriegeskorte et al., 2006) on the T-fMRI signal data obtained during the shape orientation discrimination task to identify which areas carried information about the trained stimulus and, hence, was putatively involved in perceptual learning. Second, we examined whether the accuracy for classifying trained versus novel stimuli in these areas was behaviorally meaningful by calculating the correlation with behavioral performance. Finally, to decode the spontaneous brain activity in the R-fMRI datasets, we trained a spatiotemporal classifier on the discrimination task dataset and then applied it without further training for classification of the resting-state dataset. We then applied to the classified data a similarity criterion based on the Mahalanobis distance to refine the classification results.

Searchlight analysis on task data

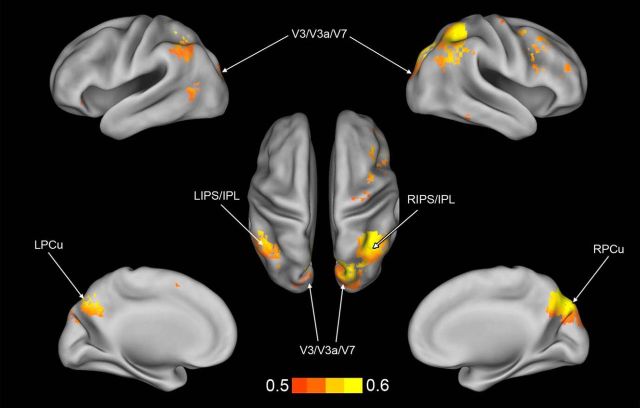
For each subject, a searchlight analysis was conducted on the spatial pattern of multivoxel activation during trained versus untrained blocks of trials (see Materials and Methods). To create a common information map, as shown in Figure 4, a group map was generated by assigning to each voxel its significance in a t test across subjects of classification accuracy versus chance level (thresholded at p < 0.01 with FDR correction). Common identified areas consisted of the following: cortex along the ventral, posterior, and anterior IPS belonging to the dorsal attention network (DAN); IPL and PCu belonging to the default mode network (DMN); a small portion of the temporal cortex along the right inferior temporal gyrus and a region in left lateral occipital (LO) cortex near middle temporal cortex (MT)/LO complex. The searchlight algorithm also found a bilateral dorsal visual region corresponding to V3/V3A/V7 based on the Caret atlas (Van Essen, 2005), but did not localize any predictive activity in early visual cortex (dorsal and ventral V1–V2) that were strongly activated by the passive presentation of the visual stimuli in the localizer session. The regions listed above therefore contain multivoxels patterns of activity that reliably distinguish between trained and untrained blocks of trials during the T-fMRI experiment on the shape orientation discrimination task.

Figure 4.

Searchlight information map. Map of the searchlight regions, thresholded at p = 0.01 (two-tailed t test, FDR corrected), showing significant discrimination. Color bar indicates the accuracy of classification. L, Left; R, right.

Classification on task data

We then sought to develop a classifier of the task data to be used for classification of the resting-state data. It should be noted that at this stage we performed a classification on voxels already selected by means of the searchlight algorithm and a thresholding criterion. The application of the searchlight procedure amounts to a feature selection in data space and is a potential source of bias on subsequent classification. Feature selection bias is different from sample selection bias and has been found in numerical simulations to be less severe in classification compared with regression (Singhi and Liu, 2006).

An important criterion for the classification scheme is that it is behaviorally meaningful. Not only should the classifier be able to discriminate between the trained and untrained stimulus conditions, but the classification results should also be consistent with the subject response scores. Therefore, for each ROI defined by the searchlight analysis we computed the Pearson correlation coefficient, across subjects, between classification accuracies and the mean percentage of correct responses on the shape orientation discrimination task (averaging over trained and untrained blocks of trials).

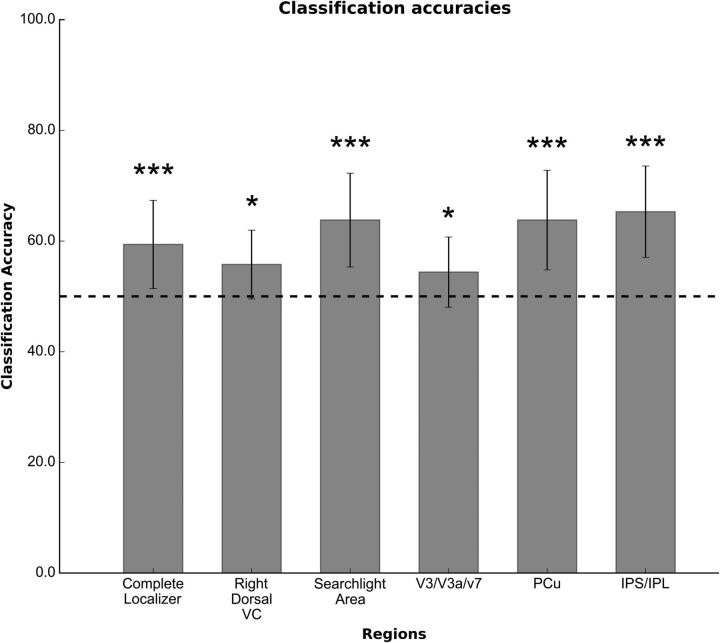
First, we performed MVPA using the standard multivoxel spatial pattern and obtained mean classification accuracies of ∼55% (whole localizer: 55%, p < 0.005; right dorsal VC: 53.5%, p < 0.05; whole searchlight area: 57.6%, p < 0.001). However, the accuracy of classification did not correlate with behavioral accuracy (whole localizer: r = 0.25, p = 0.46; right dorsal VC: r = 0.01, p = 0.97; whole searchlight area: r = 0.05, p = 0.89). Therefore, we chose a spatiotemporal classifier to take into account not only the spatial distribution of activity, but also the time course of the response over multiple trials.

Classification accuracy with the spatiotemporal model over the whole searchlight map was 63.79% with a p value of <0.005, derived from a two-tailed t test versus chance level (accuracy = 50%) to test for statistical significance (see also Table 1). We also found good classification accuracy by considering only voxels in IPS/IPL (65.30%; t₍₁₀₎ = 6.14; p < 0.005), precuneus (63.79%; t₍₁₀₎ = 5.07; p < 0.005), and V3/V3A/V7 (54.34%; t₍₁₀₎ = 2.29; p < 0.05). Significant classification accuracy was also obtained when averaging over the occipital visual regions identified by the localizer scans (59.39%; t₍₁₀₎ = 3.91; p < 0.005) and the visual region corresponding to the trained quadrant (right dorsal visual cortex: 55.76%; t₍₁₀₎ = 3.07, p < 0.05; Fig. 5); all the results survived after multiple-comparison correction with the exception of those from right dorsal visual cortex and V3/V3A/V7. It should be noted, however, that the Bonferroni correction in this case is exceedingly conservative because not all six ROIs are independent (actually, only four of six ROIs are independent).

Table 1.

Summary of spatiotemporal classification analysis

Subject	Complete localizer	Right dorsal VC	Searchlight region	V3/V3a/V7	Precuneus	IPS/IPL
Classification accuracies
1	60.00%	60.00%	71.67%	58.33%	66.67%	78.33%
2	58.33%	50.00%	51.67%	55.00%	50.00%	51.67%
3	68.33%	56.67%	73.33%	65.00%	75.00%	70.00%
4	46.67%	40.00%	61.67%	50.00%	60.00%	63.33%
5	63.33%	56.67%	76.67%	55.00%	71.67%	80.00%
6	70.00%	63.33%	58.33%	46.67%	70.00%	58.33%
7	58.33%	56.67%	63.33%	58.33%	68.33%	65.00%
8	55.00%	58.33%	50.00%	61.67%	51.67%	63.33%
9	46.67%	55.00%	61.67%	48.33%	53.33%	63.33%
10	68.33%	60.00%	68.33%	45.00%	61.67%	60.00%
11	58.33%	56.67%	65.00%	55.00%	73.33%	65.00%
Mean	59.39%	55.76%	63.79%	54.39%	63.79%	65.30%
SD	7.97%	6.21%	8.47%	6.34%	9.01%	8.26%
p	0.00291	0.0117	0.0003	0.0442	0.0004	0.0001
No. of voxels	359	1491	1729	94	679	895
Behavioral correlations
r	0.312	0.204	0.917	0.594	0.795	0.862
p	0.37438	0.56934	0.00006	0.06346	0.00404	0.00070

The table summarizes the classification accuracy for each subject and for each ROI, and the classification p value is calculated using a two-tailed t test between accuracies and chance level (50%). The bottom part of the table shows the Pearson's correlation coefficient calculated with classification accuracies versus behavioral performances, and the associated p value is calculated using the Student's t test.

Figure 5.

Classification accuracy on searchlight and visual localizer ROIs. The figure shows the classification accuracies of the spatiotemporal classifier, averaged across subjects, for each ROI. Dashed line indicates the chance level, while error bars represent the SD. *p < 0.05, not significant after multiple-comparison correction; ***p < 0.005, significant after multiple-comparison correction.

To examine the specificity of the ROI-based classification, we ran separate analyses in several control regions. We selected ROIs from the following three networks used in previous works (Lewis et al., 2009; Baldassarre et al., 2012; see Table 2): control network (Dosenbach et al., 2007); motor network (Astafiev et al., 2003, 2004); and auditory network (Belin et al., 2000). Each network was considered in the analysis as a single ROI. The areas composing the networks are summarized in Table 2. Each network was considered in the analysis as a single ROI. We found no significant spatiotemporal classification in any of the networks, as follows: control (55.30%; t₍₁₀₎ = 1.65; p = 0.127); auditory (50.61%; t₍₁₀₎ = 0.28; p = 0.779); and motor (51.36%; t₍₁₀₎ = 0.77; p = 0.458).

Table 2.

Control ROIs

Talairach coordinates (x, y, z)	Region	ROI/network	Voxels
+43, −09, +20	Right anterior temporal	Auditory	81
+44, −32, +16	Right posterior temporal		81
+58, −12, +2	Right temporal		81
+41, −26, +17	Right Heschl gyrus		282
+63 −27 + 14	Right superior temporal gyrus		54
−38, −34, +12	Left posterior temporal		81
−57, −02, +20	Left temporal		81
−57, −16, +1	Left anterior temporal		81
−45, −36, +2	Left Heschl gyrus		114
−62, −35, +7	Left superior temporal gyrus		117
+34, +17, +2	Right anterior insula	Control	81
−36, +13, +1	Left anterior insula		81
+4, +13, +39	Dorsal anterior cingulate cortex		81
−18, −51, −24	Left cerebellum	Motor	81
−32, −32, +52	Left central sulcus		81
−29, −17, +10	Left putamen		81
−39, −25, +18	Left SII		81
−1, −14, +51	Left supplementary motor area		81
−13, −25, +3	Left thalamus		81
+15, −50, −20	Right cerebellum		81
+32, −31, +55	Right central sulcus		81
+30, −16, +9	Right putamen		81
+36, −21, +20	Right SII		81
+4, −12, +49	Right supplementary motor area		81
+14, −25, +05	Right thalamus		81

The table is a list of areas used for control analyses. Values are expressed in x, y, z coordinates according to the Talairach and Tournoux (1988) atlas. Each network was considered as a single ROI in the analysis.

To examine the behavioral relevance of the regions identified by the spatiotemporal classifier, we correlated across subjects, and separately in each ROI, the classification accuracy with the mean accuracy of task performance (averaged over trained and untrained blocks of trials; Fig. 6); a strong positive correlation was obtained when considering the whole searchlight region (r = 0.92; p < 0.0001), as well as when considering only voxels in both lateral (IPS/IPL: r = 0.862; p < 0.001) and medial (precuneus: r = 0.795; p = 0.004) parietal cortex. No correlation was found when considering voxels in occipital visual regions defined by the localizer or in regions of networks that were not task relevant (control, motor, auditory networks).

Figure 6.

Correlation of classification accuracy versus behavioral performance. Scatter plots of classifier accuracies in various ROIs (y-axis) versus mean (over trained and untrained stimuli) behavioral accuracy (x-axis) across subjects (N = 10). Behavioral data from one observer were not recorded. The plots show very high correlation coefficients for the searchlight and the parietal regions, but a low correlation coefficient in the right dorsal VC.

Overall, the searchlight analysis indicates that activity in several regions in medial and lateral parietal cortex, as well as dorsal visual cortex (V3/V3A/V7), accurately classifies trained versus untrained blocks of trials/stimuli. This was confirmed by the classification of the spatiotemporal patterns in the ROI-based analysis. In visual cortex, above-chance classification with the spatiotemporal classification was also found across all localizer regions and in dorsal visual cortex region contralateral to the trained left inferior visual quadrant. Subjects whose patterns of activity in parietal cortex more strongly distinguish between trained and untrained blocks of trials also appear to be more accurate on the discrimination task.

It is important to underscore that the observed accuracy level may be inflated by a possible bias introduced by the feature selection operated by the searchlight algorithm. However, we also observed that the voxels showing robust accuracy of classification were also behaviorally relevant (i.e., correlated with performance).

Resting-state decoding

The next step was to examine whether multivariate states separating trained from untrained stimuli/blocks were present in the resting state, and whether they were modulated by learning and/or task performance. This analysis was performed on the ROIs independently selected from the task data.

The decoding of resting-state data, schematically illustrated in Figure 7, is complicated by two important factors. First, the absence of stimuli or task conditions prevents timing of the detection of specific spatiotemporal patterns. To solve this problem, we generated data samples by sliding on the data time series a window of the same width of the task data samples. Therefore, the data space used for classification of the resting data had the same spatiotemporal format as that used for the classification on the task data (Fig. 8).

Second, in the resting state, activity patterns can assume in principle a much larger number of possible configurations. In fact, due to the lack of an experimental task, a much greater variability in activity patterns is expected. When classifying these patterns according to the task data model, patterns are always classified as belonging to one of two states (trained or untrained) even when they are quite different from both. Although formally correct, this classification might not be meaningful for our purpose as we are looking for patterns that “replicate” (or are similar to) those observed during task performance. We therefore need an additional criterion after classification to exclude those patterns that are “too far” from the task patterns, while retaining those that are “close enough.” To solve this second problem, after decoding we further divided the resting-state data samples into those similar and nonsimilar to the task data samples (either trained or untrained respectively) by means of their Mahalanobis distance to the mean of the task data samples, separately for trained or untrained (see Materials and Methods). Furthermore, since by chance a percentage of patterns could be similar to those of interest, even before training, we compared both the frequency and similarity of the resting datasets to the task classifier before and after learning/task performance, and tested the variation in their occurrence and the degree of similarity for statistical significance. For the searchlight analysis, this test was performed for the selected regions and the visual localizer regions.

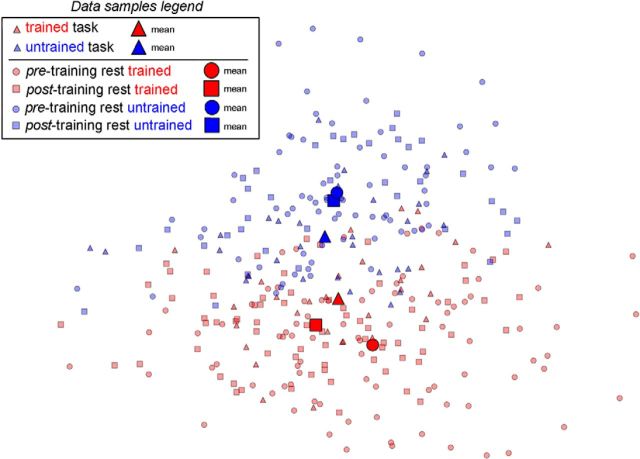
Figure 9 plots a 2D projection of data from a single subject (the best in terms of spatiotemporal classification accuracy) in the feature space corresponding to the whole searchlight region. We used a principal component analysis (PCA) to reduce the dimensionality of the entire dataset (resting state and task), and then we plotted the reduced dataset using the first two components, with the first one explaining ∼10% of variance, and the second one explaining ∼8% of variance. Van der Maaten et al. (2009) showed that a PCA is a suitable method to reduce dataset dimensionality in real-world application as fMRI. For comparison, we calculated in one subject the variance of the resting-state patterns that met the similarity criterion and found it was 25% of the total variance of the dataset. This shows that the PCs shown in the diagram represent a substantial fraction of the task states in the resting state. First, note that Figure 9 clearly shows the separation between task states as obtained from the classification into trained or untrained classes (red, blue triangles). Second, note that the resting data samples can be separated as well into a trained (red circles and squares) and an untrained (blue circles and squares) class, respectively, based on their Mahalanobis distance from the class means. The key finding is that the mean distance between task and rest data is smaller post-learning for both trained and untrained stimuli. In this specific subject, the similarity is stronger for trained than untrained stimuli.

Figure 9.

Subject's dataset projection on a 2D plane. Projection on a 2D plane of a subject spatiotemporal dataset (task and resting state). The feature space before projection corresponds to the whole searchlight region. A PCA was used to reduce the dataset dimensionality, then the transformed data are projected onto the plane defined by the two largest PCs. Triangles represent the task data samples belonging either to the trained (red) or to the untrained (blue) class. Squares represent the resting-state data samples after learning; and circles represent resting-state data samples before learning. The same color coding differentiates resting-state data samples between trained (red) and untrained (blue) as characterized by classification and by selection with the Mahalanobis distance similarity criterion. Larger markers represent the average across the data samples represented by the same shape and color. The means of the resting-state data samples (trained and untrained, respectively), after training, are closer to the means of the corresponding task data.

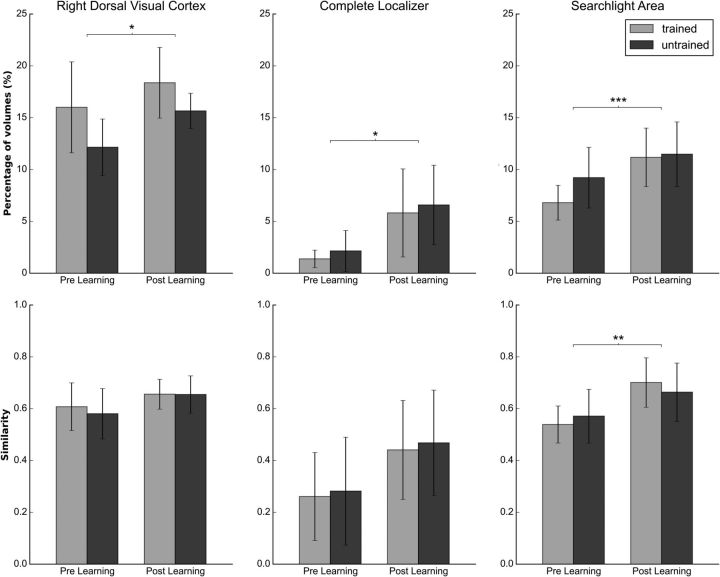
To statistically confirm this impression, we ran comparisons on the previously selected ROIs. Figure 10 compares, before and after training, the average (across subjects) number of patterns that meet the similarity condition (top row), as well as the average of the similarity in data space of the patterns that satisfy the similarity condition (bottom row). The latter quantity gives an indication of how similar the patterns of the two resting-state distributions are to the stimuli patterns and will be referred to as the similarity index. Both quantities were evaluated either using the trained task blocks/stimuli (gray bars) or untrained task blocks/stimuli (black bars) as the reference distribution.

Figure 10.

Comparison of resting-state data before and after training. The figure shows on the average number of brain states that meet the Mahalanobis criterion top row, the similarity index (see text) for each condition on the bottom row, and for each resting-state session in the following three areas: the right dorsal visual cortex, the overlap between the searchlight area and the complete localizer, and the complete searchlight area. Error bars represent the SD. *p < 0.05, **p < 0.01 are not significant after multiple-comparison correction, ***p < 0.005 significant after multiple-comparison correction.

A two-way ANOVA was run on each ROI separately using as the dependent variable the number of resting-state images with a pattern similar to the pattern elicited by the target, and as independent variables the target type (trained, untrained) and the resting-state run (pretraining, post-training).

Statistically significant differences in the frequency of task states post-learning were obtained in the right dorsal visual cortex, corresponding to the trained visual quadrant (F_(1,11) = 5.001; p = 0.047); in the whole localizer area, averaging across all visual occipital regions (F_(1,11) = 6.968; p = 0.023); and in the whole searchlight analysis-selected area (F_(1,11) = 10.931, p = 0.007; Fig. 10). After multiple-comparison correction, the searchlight area remained significant. In all significant regions, resting states were more similar to task states after learning compared with before learning. However, no consistent difference or interaction was detected for trained versus untrained blocks/stimuli. We found no significant effect on the frequency of task states in multiple control regions, as follows: control (F_(1,11) = 2.558; p = 0.138); motor (F_(1,11) = 0.763; p = 0.401); and auditory networks (F_(1,11) = 1.219; p = 0.293).

We also performed a two-way ANOVA on the normalized similarity index. Qualitatively, all regions show a higher similarity post-training (Fig. 7), with significantly different results in the whole searchlight analysis-selected area where the patterns generated during resting state after learning are more similar to the distributions of task/stimuli (trained/untrained) than before learning (F_(1,11) = 8.081; p = 0.016).

Similarity index differences with respect to resting-state run in the control network (F_(1,11) = 0.701; p = 0.42), motor network (F_(1,11) = 0.325; p = 0.58), and auditory network (F_(1,11) = 0.597; p = 0.45) were not statistically significant.

Overall, these findings indicate that the patterns of activity associated with the two different tasks/stimuli (trained and untrained) occurred in the resting state with a greater frequency and a higher similarity following perceptual learning. These patterns occur in cortical regions, visual cortex, and medial and lateral parietal regions that were recruited during perceptual training, the activity patterns of which correlate with performance on the shape orientation discrimination task.

Discussion

This study shows that task states measured during a shape orientation discrimination task are present in spontaneous activity measured at rest and are modified following several days of intense perceptual training.

Resting-state decoding using Mahalanobis distance

We used the Mahalanobis distance to estimate pattern frequency and similarity between the resting-state images acquired before and after training, and the patterns generated by the stimuli. The most novel result of this study was the demonstration that task states related to trained versus untrained visual stimuli were present at rest, and were modified by learning. Since the resting-state sessions were separated by ∼1 week of training, but the second session occurred following a set of task scans, we cannot separate between long-term or short-term visual learning.

Our results show an effect of visual learning on the spontaneous brain activity as a trace of the activity evoked by the trained stimuli. Not only did task-like states occur more frequently, but they also became more similar to the task pattern of activity after learning. However, we did not find significant differences post-learning in the frequency or similarity of resting states representing, respectively, trained and untrained tasks/stimuli. Our interpretation is that what is represented in the resting-state post-learning is the ensemble of processes and features that are recruited during the training on the shape orientation task. The task involves directing spatial attention to the left lower visual field to process stimuli in the periphery of the visual field. Since this task is typically performed in the fovea, this novel behavior requires extensive training that involves not only visual areas, but also attention/memory areas (Lewis et al., 2009). After training, subjects perform the fMRI experiments, alternating between blocks in which either the trained orientation (inverted T) or untrained orientations (e.g., left or right rotated T) are presented; thus, the task is very similar. The target shape is always presented in the left lower visual field, the position of the target shape in the left lower quadrant is randomized across three possible locations, and all distracter shapes in the other quadrants are identical. Therefore, in terms of early visual responses, most of the neural machinery to discriminate stimuli is the same. In contrast, we observe both in terms of task-evoked responses and classification accuracies stronger differences in higher-order visual areas and attention/memory-related areas. That is why we think it is entirely plausible that patterns of resting-state activity following the task would increase for both trained and untrained shapes. We cannot rule out possible differences in activation patterns across trained and untrained stimuli in early visual areas. Such differences would occur at spatial scales far below the resolution attainable with most MRI scanners.

The use of Mahalanobis distance to characterize the distribution of brain states in the resting-state dataset, and to select among them those that are similar to brain states in the training dataset is important. In fact, the difficulty in the classification of brain states belonging to the resting-state dataset lies in the fact that they have no label (no stimuli or variation of external conditions). A linear classifier may assign a specific brain state to a group, but a validity criterion is still needed. Here the property to be assessed was that the brain state should be a “replica” of a previously detected one. Mahalanobis distance in the data space applied a restriction on the classified brain states. It should be noted that without such a restrictive criterion, classification could have been meaningless due to the possibly large variability of rest states.

The presence of task states at rest and their modification after learning/task performance is consistent with the hypothesis that spontaneous brain activity patterns, and possibly their inter-regional correlation (but this was not measured in this study), do not reflect just the synchronization of excitability states in different areas, or the modulation of correlation between task-relevant regions (Engel et al., 2001; Varela et al., 2001; Lewis et al., 2009; Tambini et al., 2010; Harmelech and Malach, 2013), but also information states about stimulus/task representation, which relate in this case to the orientation discrimination task. While there have been reports in cat visual cortex for similarity of task and rest representations for orientation stimuli (Kenet et al., 2003), and in ferret visual cortex for increasing similarity in the course of development of spontaneous and stimulus-induced tuning functions of receptive field properties in visual cortex (Fiser et al., 2004; Berkes et al., 2011), to our knowledge this has not been shown in humans.

Interestingly, the regions of the brain in which task states were recovered in the resting state were both in visual cortex (whole localizer and trained visual quadrant), where stimuli were presumably analyzed, and in intermediate and higher-order visual areas (V3A-V7/IPS/IPL/PCu) thought to represent decision or memory variables. These regions significantly represented the difference between trained and untrained stimuli based on the searchlight analysis, and in some of these regions the classification was related to behavioral performance on the orientation discrimination task. The co-occurrence of modulation of spontaneous activity patterns, as well as the behavioral relevance of these patterns to the accuracy of the task may indicate a relationship between spontaneous activity and behavior that has been recently identified both on short (Sadaghiani and Kleinschmidt, 2013) and longer timescales (Palva et al., 2013).

Classification of task states

The searchlight analysis was used first to map voxels that carry discriminative information about the trained/untrained blocks and/or visual arrays. The map obtained after searchlight analysis is shown in Figure 2. We notice that the more informative areas were not contained in early visual cortex, as one might have expected. The voxels that carried most information were mostly localized in regions along the IPS that correspond to higher-order visual areas involved in spatial attention; that were also strongly recruited by the task, and in IPL/precuneus regions that belong to the default mode network; and that were strongly deactivated by the task (Lewis et al., 2009; Baldassarre et al., 2012). Significant discrimination was also found in dorsal visual occipital cortex corresponding to V3/V3A/V7, MT/LO complex, and several prefrontal regions.

The fact that the localizer visual occipital areas do not apparently discriminate between stimuli may be due to the geometrical nature of the stimuli that are always composed of a vertical and a horizontal bar. The difference between trained and untrained stimuli occurred only in the target shape presented in the left lower quadrant, which was separated by only a few degrees of visual angle from identical distractors in both sets of stimuli. It is therefore not surprising that such small differences in stimulus content did not selectively change the representation in visual cortex. Our result is consistent with the findings of Kahnt et al. (2011), who trained subjects to discriminate the orientation of a Gabor patch, and found no significant classification due to perceptual learning (based on multivariate analysis) in early visual cortex areas.

That higher-order visual attention and default areas were involved in representing trained versus untrained stimuli is also consistent with the findings of Shibata et al. (2012), who reported neural correlates of perceptual learning in dorsal visual cortex. The classification may represent either a decision variable representing relevant versus irrelevant information, or some attention state reflecting perhaps the relative saliency of trained versus untrained arrays over time. Interestingly, however, in the resting data, activity in visual cortex appeared to represent the task patterns to an extent similar to that in higher-order regions.

Correlation with performance

The classification of task states in parietal regions (IPS, IPL, PCu) of the DAN/DMN was significantly correlated with accuracy on the shape orientation discrimination task.

As previously reported, these parietal regions are strongly modulated by the task (Lewis et al., 2009). In fact, DAN regions (frontal eye field, IPS) show an attenuated level of activation post-learning, while DMN regions (IPL, PCu) show a weaker deactivation (negative BOLD response) post-learning. In addition, these regions show changes in functional connectivity with visual cortex. DAN regions, which at baseline show no correlation with visual occipital cortex, become more negatively correlated with the trained visual quadrant. In parallel, DMN regions that showed a negative correlation with untrained quadrants in visual cortex before learning lost their coupling after learning (Lewis et al., 2009). We interpreted these changes in functional connectivity to reflect adjustment in top-down control in the course of learning.

The significant correlation found in this study between classifier accuracy and behavioral performance, which was computed after many sessions of perceptual learning and after the mean level of activity in these regions had been significantly altered by training, indicates that the patterns of neural activity within these regions remain significantly task dependent even after learning. This is consistent with the role of these parietal regions in the representation of high-level (decision) variables in contrast to visual occipital areas more related to the analysis of low-level information about the stimuli (Shibata et al., 2011, 2014).

Conclusions

In this experiment, we show that multivoxel activity patterns related to task stimuli/tasks can be recovered in the resting state, and that their frequency and similarity can change after learning.

This demonstrates that spontaneous activity not only reflects random fluctuations of activity related to excitability, but underlies deterministic fluctuations of activity related to previously encoded information.