Integration of Multiple Spatial Frequency Channels in Disparity-Sensitive Neurons in the Primary Visual Cortex

Abstract

For our vivid perception of a 3-D world, the stereoscopic function begins in our brain by detecting slight shifts of image features between the two eyes, called binocular disparity. The primary visual cortex is the first stage of this processing, and neurons there are tuned to a limited range of spatial frequencies (SFs). However, our visual world is generally highly complex, composed of numerous features at a variety of scales, thereby having broadband SF spectra. This means that binocular information signaled by individual neurons is highly incomplete, and combining information across multiple SF bands must be essential for the visual system to function in a robust and reliable manner. In this study, we investigated whether the integration of information from multiple SF channels begins in the cat primary visual cortex. We measured disparity-selective responses in the joint left-right SF domain using sequences of dichoptically flashed grating stimuli consisting of various combinations of SFs and phases. The obtained interaction map in the joint SF domain reflects the degree of integration across different SF channels. Our data are consistent with the idea that disparity information is combined from multiple SF channels in a substantial fraction of complex cells. Furthermore, for the majority of these neurons, the optimal disparity is matched across the SF bands. These results suggest that a highly specific SF integration process for disparity detection starts in the primary visual cortex.

SIGNIFICANCE STATEMENT Our visual world is broadband, containing features with a wide range of object scales. On the other hand, single neurons in the primary visual cortex are narrow-band, being tuned narrowly for a specific scale. For robust visual perception, narrow-band information of single neurons must be integrated eventually at some stage. We have examined whether such an integration process begins in the primary visual cortex with respect to binocular processing. The results suggest that a subset of cells appear to combine binocular information across multiple scales. Furthermore, for the majority of these neurons, an optimal parameter of binocular tuning is matched across multiple scales, suggesting the presence of a highly specific neural integration mechanism.

Introduction

Our visual system possesses a remarkable function called stereopsis that allows perception of 3-D depths based on a pair of 2-D retinal images. As shown in a pair of stereo photographs in Figure 1A (Scharstein et al., 2014) and their cross-sections in Figure 1B, left and right images are generally similar but slightly shifted versions of each other due to the lateral placement of the eyes. Such small shifts between left and right retinal images are known as “binocular disparity,” and its accurate measurement is a central problem of stereopsis. Underlying neural mechanisms of stereopsis have been actively pursued with psychophysical (Helmholtz, 1910; Westheimer and McKee, 1980; Schor and Wood, 1983), physiological (Barlow et al., 1967; Poggio and Fischer, 1977; Ferster, 1981; Maunsell and Van Essen, 1983; Ohzawa et al., 1990; Uka et al., 2000; Cumming and DeAngelis, 2001; Tanabe et al., 2011), and computational (Marr and Poggio, 1979; Qian, 1994; Doi and Fujita, 2014; Li and Qian, 2015) approaches.

Figure 1.

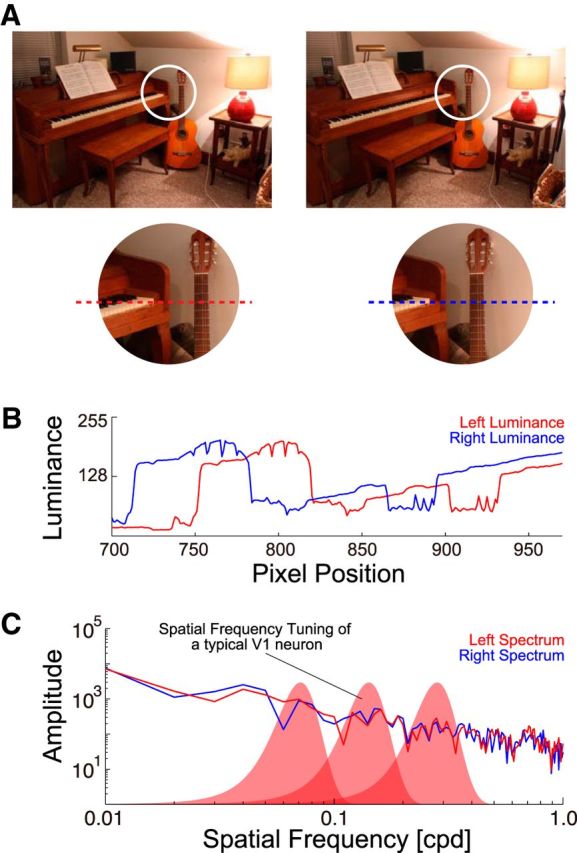
A, A pair of stereo photographs is shown (Source: Middlebury Stereo Datasets). Small parts of the left and right images within white circles are enlarged for close examination. B, Left and right luminance profiles for cross-sections of the images along the broken lines in A are plotted (red, left image; blue, right image). Cross-sections were taken after conversion to gray scale. C, Amplitude spectra of the profiles in B are shown. SF tunings of three typical A17 neurons are illustrated schematically with red filled curves. Multiple A17 neurons, tuned to different frequencies, are needed to represent the broad stimulus spectra. For reliable stereoscopic depth detection, integration of signals from multiple frequency bands may be required.

Generally, our external world is highly complex, with features at many scales existing simultaneously side-by-side or with overlap, sometimes with transparency, texture, shadows, and sharp edges of luminance. Clearly therefore, natural scenes are broadband, containing a broad range of spatial frequency (SF) components as shown in the spectral distributions in Figure 1C. Therefore, for a robust detection of binocular disparity, the brain must be able to use such broadband information. However, neurons in the first stage of binocular processing, area 17 (A17), are generally quite narrow-band (red filled curves), having a bandwidth of ∼1.3 octave on average (Movshon et al., 1978b). This means that integration of information from multiple SF channels must take place at some stage, if not in A17.

Where does such multifrequency integration begin in the visual pathway? Does it begin in A17, at least partially, or require a higher-order area? If such integrations take place in a given area, what are the fundamental rules that govern the combination of signals? Although a previous study reported a tendency for broadly tuned V4 neurons to show weak responses to anticorrelated (contrast inverted) stereograms (Kumano et al., 2008), no direct evidence of SF integration has been demonstrated to date.

In this study, we first examined whether the integration of multiple SF channels starts in neurons of A17 of the cat by measuring binocular interactions in the joint left-right SF domain. Our results indicated that a subset of complex cells appear to combine disparity information across multiple SF channels. Next, we examined the consistency of disparity preference across different SF bands. Most disparity-sensitive neurons that pool multiple SF channels showed a matched optimal disparity across channels, suggesting that the integration of different SF channels begins in A17 neurons and the integration process is quite precise.

Materials and Methods

Extracellular single-unit recordings were performed in A17 of 23 anesthetized and paralyzed adult cats (14 males and 9 females, 2.0–4.5 kg). Details about surgical procedure, animal maintenance, and single-unit recording were described previously (Sasaki and Ohzawa, 2007; Ninomiya et al., 2012). Only a brief account of the basic procedures and points different from the previous studies are provided here. All animal care and experimental procedures conformed to the guidelines established by the National Institutes of Health and were approved by the Osaka University Animal Care and Use Committee.

Animal preparation and maintenance.

After initial pre-anesthetic doses of hydroxyzine (Atarax, 2.5 mg) and atropine (0.05 mg), anesthesia was induced and maintained with isoflurane (2–3.5% in O₂) for the remainder of the surgical preparation. During surgery, lidocaine was injected subcutaneously or applied topically at all points of pressure and possible sources of pain. A body temperature was monitored and maintained near 38°C with a servo-controlled heating pad, and ECG electrodes were placed for monitoring heart rate. A tracheostomy was performed for the subsequent artificial respiration. After the animal was secured in a stereotaxic apparatus, anesthesia was switched to sodium thiopental (Ravonal, 1.0 mg · kg⁻¹ · h⁻¹) and paralysis was induced with an initial dose of gallamine triethiodide (Flaxedil, 10 mg · kg⁻¹ · h⁻¹). Artificial ventilation was performed with a gas mixture of 70% N₂O and 30% O₂. The respiration rate and stroke volume were adjusted to maintain the end-tidal CO₂ between 3.5 and 4.3% throughout the experiment. A craniotomy was then performed over the central representation of the visual field of A17 approximately at Horsley–Clarke coordinates P4 and L2. Pupils were dilated with 1% atropine sulfate, and nictitating membranes were retracted with 5% phenylephrine hydrochloride (Neosynesin). The corneas were protected using contact lenses of appropriate power with a 3–4 mm artificial pupil.

To record single unit activities, tungsten electrodes (A-M Systems) were lowered into a region of cortex exposed with craniotomy. Agar was applied around the electrodes to prevent drying, and melted wax was layered over the agar to seal as a chamber and reduce cortical pulsation. Electrical signals from the electrodes were amplified (×10,000) and bandpass filtered (300–5000 Hz). Spikes were sorted by their waveforms and time-stamped with 40 μs resolution (Ohzawa et al., 1997). When the electrodes were retracted, electrolytic lesions were made at intervals of 500–1200 μm for each electrode track.

At the end of an experiment, the animal was administered an overdose of pentobarbital sodium (Nembutal), perfused with buffered saline solution followed by 4% formalin in 0.1 m PBS, and cortical tissue was prepared for histological examination. Electrode tracks were reconstructed and cortical laminae were identified.

Visual stimulation.

Visual stimuli were generated by computer and displayed on a cathode ray tube display (a resolution of 1600 × 1024 pixels, refreshed at 76 Hz; GDM-FW900, Sony) using only the green channel to avoid color misconvergence across channels. In each experiment, the luminance nonlinearity of the display was measured using a photometer (Minolta CS-100) and linearized by gamma-corrected lookup tables. Fifty percent Michelson contrast was used for all grating stimuli used in this study. A haploscope was used to present stimuli to the left and right eye separately, and the visual fields of the monitor covered ∼23° × 30° for each eye at a viewing distance of 57 cm.

Once a single unit was isolated, its preferred orientation, SF, the center position, and the size of a receptive field (RF) were tested preliminarily under manual control. Subsequently, subspace mapping to measure tuning in the joint orientation and SF domain was performed for each eye with flashed gratings (Ringach et al., 1997; Nishimoto et al., 2005). After the optimal orientation, optimal SF and the range of SF were determined for each eye, the binocular measurement was conducted to obtain a binocular SF interaction profile in a 4-D domain (sf_L, sf_R, ph_L, ph_R), where “sf” and “ph” denote SF and phase, respectively, and the subscript indicates the eye. The stimuli were flashed gratings of various combinations of SFs and phases between the two eyes, oriented at the optimal orientation of the target cell (Ninomiya et al., 2012). Basically, 12 SFs and 8 phases per each eye were used, so the total number of stimuli presented in a single block was 9416, i.e., 9216 binocular (12 × 12 × 8 × 8), 192 monocular (2 eyes × 12 × 8), plus blank (8) conditions. The multiple blank conditions were used to increase the reliability of baseline response estimation. The blank stimuli had the same uniform luminance for both left and right display areas. All 9416 conditions were presented in one randomized block, and the block was repeated ∼8–20 times. The stimuli were updated at 38 Hz (every 2 video frames), and its size was adjusted to be slightly larger (∼1.5–3 times) than the size of the RF. The range of the SF was set to cover the cell's SF band sufficiently. After the binocular 4-D mapping was completed, tuning curves for orientation and SF were verified respectively using drifting grating stimuli. In some cases, the RFs of the cells were also measured using a standard reverse correlation procedure with dense white noise stimuli (Nishimoto et al., 2006; Sasaki and Ohzawa, 2007).

Data analysis.

Each cell was classified into simple or complex based on standard criteria (F1/F0 ratio; Skottun et al., 1991). The balance of responses between the two eyes was quantified using the binocularity index (Sasaki et al., 2010).

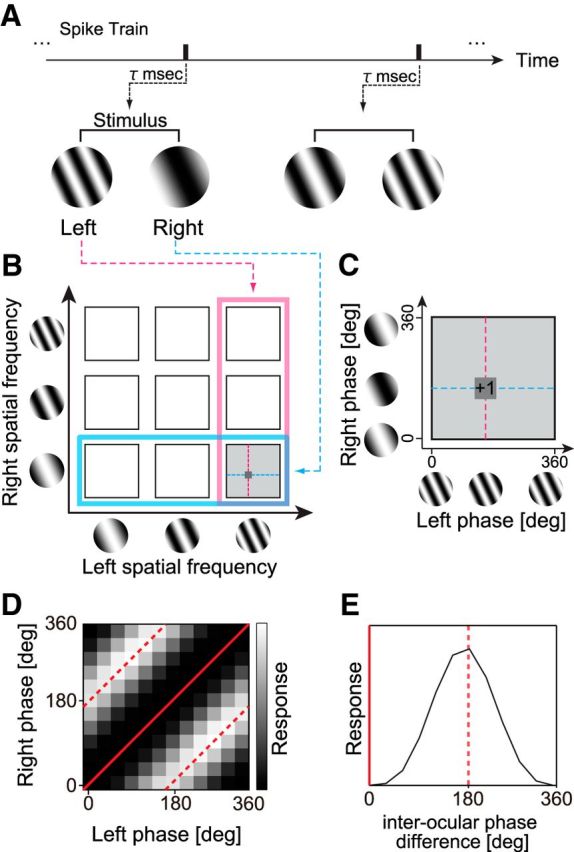
In this study, our goal is to elucidate possible contributions of multiple SF channels in a single neuron as illustrated in Figure 2, where neural responses to various left and right SF combinations are examined. However, the actual experiment requires that we also vary phases of the grating stimuli for each eye, because A17 neurons are highly sensitive to variations of stimulus phase monocularly (DeValois et al., 1978; Movshon et al., 1978a) for simple cells, and to variations of interocular phases binocularly (Freeman and Robson, 1982; Ohzawa and Freeman, 1986) for both simple and complex cells. This means that such an experiment must be done in the 4-D stimulus space (sf_L, sf_R, ph_L, ph_R). Such an experiment will completely specify the binocular disparity selectivity for all possible combinations of SFs and phases for the left and right eye stimuli.

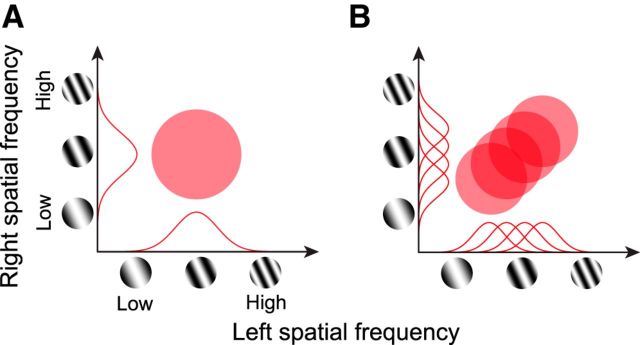
Figure 2.

Predictions of binocular responses are illustrated schematically for neurons with and without pooling in the SF domain. A, Neuron without pooling in the SF domain. A neuron having only a single SF channel would show a circular response profile in the joint left-right SF domain. Monocular SF tunings are indicated by red curves on horizontal and vertical axes for left and right eyes, respectively. B, Predicted binocular response profile for a neuron with pooling in the SF domain. In this scheme, multiple subunits as shown in A but with different optimal SFs are pooled. The profile lies on the diagonal, because A17 neurons are generally tuned to similar SFs through either eye.

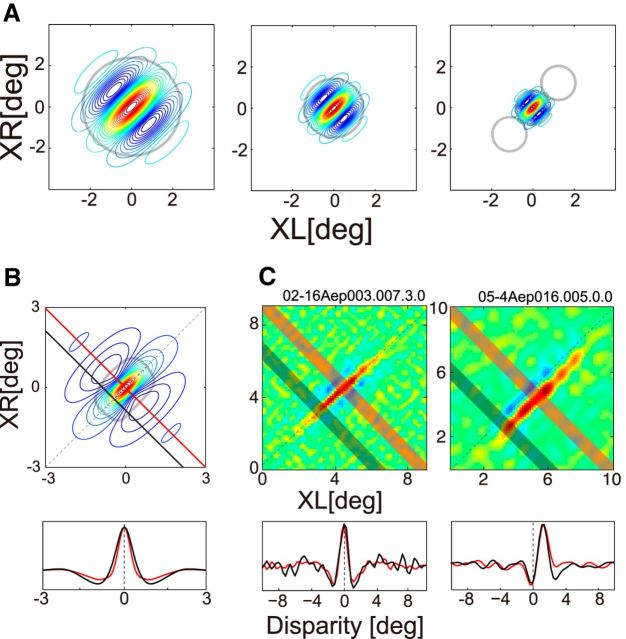
The 4-D dataset may be examined in various ways, but for our purposes, it is necessary to reduce the 4-D data into the 2-D form depicted in Figure 2. This process was conducted by following three steps as shown in Figure 3. First, for each combination of (sf_L, sf_R; Fig. 3B, square), we obtained a binocular phase combination selectivity. This created a map in the joint (ph_L, ph_R) domain (Fig. 3C), and for a disparity energy unit (Ohzawa et al., 1990) for example, it has a form depicted in Figure 3D. Second, we then computed an interocular phase-tuning curve (Fig. 3E) by integrating the map along constant interocular phase lines in Figure 3D (e.g., red straight and broken lines). The final step was to extract the strength of the tuning, which was given by the amplitude of a one-cycle sinusoid fitted to the interocular phase-tuning curve. The amplitude was obtained by Fourier analysis. Repeating these steps for all (sf_L, sf_R) combinations gave us a desired map as shown in Figure 2.

Figure 3.

Reverse correlation analysis was performed to obtain binocular phase selectivity maps for various SF pairs. A, Using spike data recorded while static sinewave grating stimuli were presented dichoptically in rapid flashes, a pair of spike-triggered stimuli was selected for an optimal correlation time delay. The spike-triggered SF and phase parameters in the left and right eyes were extracted for the selected grating pair. B, A spike was voted in a 4-D domain (sf_L, sf_R, ph_L, ph_R). For clarity of understanding the 4-D data, the procedure may be understood in the following steps. First, spike-triggered pair of SFs (sf_L, sf_R) was determined (left, pink; right, cyan). The selected pair is indicated by a gray square. C, Then, within the selected joint phase subdomain (ph_L, ph_R), the spike was voted into a particular phase combination for the triggered stimulus pair. Repeating this procedure for all recorded spikes, complete binocular phase selectivity maps were obtained for various SF pairs between the two eyes. D, The model response of a typical disparity energy unit is illustrated in the joint (ph_L, ph_R) subdomain, for the combination of optimal (sf_L, sf_R). The strength of response is shown with gray scale. Constant interocular phase-difference lines are indicated with red (solid line for 0° and broken line for 180°). E, One-dimensional tuning curve to interocular phase difference was derived from D by integrating it along constant disparity lines.

A complete dataset in the 4-D stimulus space (sf_L, sf_R, ph_L, ph_R) was constructed via a standard spike-triggered averaging (reverse correlation) as depicted in Figure 3A. Such a binocular interaction profile (binocular SF interaction map) was calculated for every recorded cell and evaluated. Specific analyses are described at the relevant places in Results.

Results

We recorded from a total of 74 cells in A17 of adult cats. Minimum set of measurements could be performed on 18 simple cells, 49 complex cells, and 7 unclassified type cells. For some specific types of measurements, the number of cells is reduced.

Prediction of binocular responses for neurons with and without pooling in the SF domain

As noted in Introduction, integration of information from multiple SF bands must happen at some stage along the visual pathway for robust estimation of binocular disparity. One of the first objectives of this study is to examine whether there are neurons that integrate or pool multiple SF channels in A17, and if present, to evaluate quantitatively the degree to which such a pooling takes place. This is achieved by measuring disparity selective responses for a variety of left-right combinations of different SFs as explained below. For a neuron consisting only of a single SF channel, predicted disparity selective response would be circular in the joint left-right SF domain as shown in Figure 2A. In addition, because most A17 neurons show nearly identical SF tuning for the two eyes, the circular binocular domain would be centered on the 1:1 diagonal.

On the other hand, for a neuron that integrates multiple of such single SF channels, each tuned to different SFs, the combined response would line up on the 1:1 diagonal as shown in Figure 2B. For such neurons, a response profile in binocular joint SF domain (hereafter, we call it “binocular SF interaction map”) would be an elongated region at 45°, rather than a circular profile. The degree of elongation, which may be quantified as an aspect ratio, would reflect the degree of pooling in the SF domain.

Selectivity to binocular phase combinations for various SF pairs between the two eyes

To quantify the response strength to be plotted in the binocular SF interaction map, we compute the amplitude of disparity tuning for each combination of left-right SFs (sf_L, sf_R). This is because we are interested in the mechanism by which disparity specific information is integrated, and not those that are due to monocular excitations. For a given combination of (sf_L, sf_R), we have a complete set of response data for all combination of different left and right phases (ph_L, ph_R). This gives us the phase-based disparity tuning for each (sf_L, sf_R), from which the amplitude of disparity tuning is computed easily. Therefore, once we obtain response data (spike counts) into bins defined in the 4-D parameter space (sf_L, sf_R, ph_L, ph_R), the binocular SF interaction map, as well as disparity tunings for all combinations of (sf_L, sf_R), can be computed.

The construction of the complete histograms in the original (sf_L, sf_R, ph_L, ph_R) space was performed via reverse correlation as illustrated in Figure 3. Responses of neurons were measured while sinewave grating pairs were presented dichoptically for various combinations of SFs and phases. Stimuli were delivered in rapid flashes at 38 stimuli/s. Because it is impossible to graphically present histograms in a 4-D space, we present our data in the format depicted in Figure 3B and C: as a matrix of left-right phase-tuning profiles (ph_L, ph_R). Here, (ph_L, ph_R) map is shown in Figure 3C and many of these are arranged into a matrix of (sf_L, sf_R) in Figure 3B. Each binocular phase-domain map generally take a map as shown in Figure 3D for a complex cell that is a disparity energy unit. Data were further reduced to obtain a disparity-tuning curve as a function of interocular phase difference (Fig. 3E). The amplitude of modulation in such a disparity-tuning curve is a good metric of the degree of binocular interaction for a given (sf_L, sf_R).

Figure 4A presents the data from a representative complex cell in the format described in Figure 3B and C. Each small map shows responses to binocular combinations of phases (ph_L, ph_R) for one SF pair (sf_L, sf_R), and such maps are arranged as a matrix of 13 × 13 binocular SF pairs. One of the maps marked with red border (sf_L: 0.48 cpd, sf_R: 0.57 cpd) is magnified in Figure 4B to show typical response property to phase combinations of the disparity selective complex cell. Clear response of band in 45° diagonals indicates that this cell has selectivity to a particular phase difference between the two eyes, in this case, ∼0°. Note that the interpretation of 0° phase difference requires care because the animal was in a paralyzed and anesthetized state without active fixation.

Figure 4.

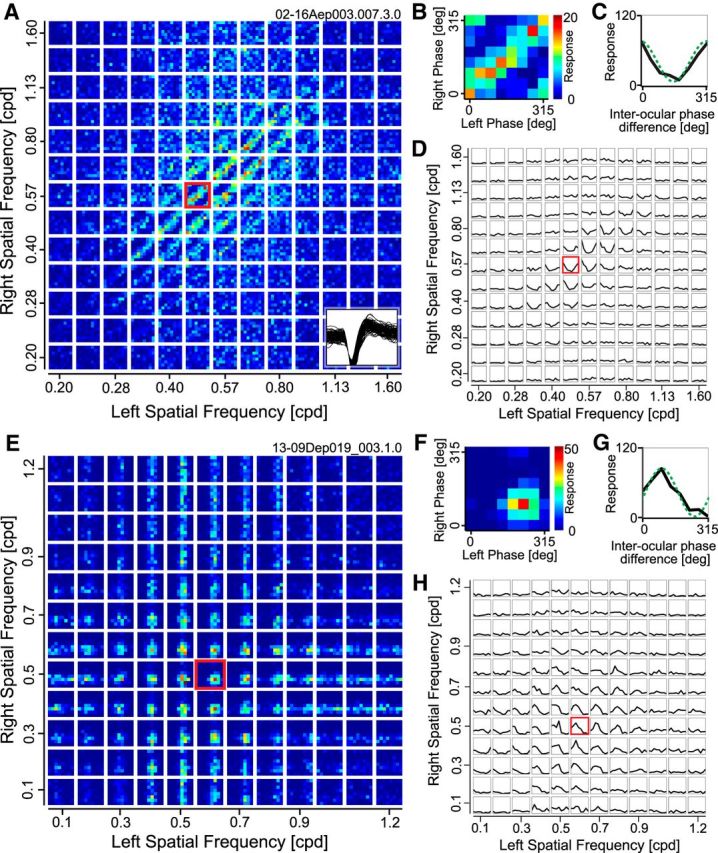
A–D, Responses are shown for a representative complex cell to stimuli containing various combinations of phases and SFs between the two eyes. A, The entire data are response strengths in a 4-D parameter space (sf_L, sf_R, ph_L, ph_R), and presented here as multiple cross sections (ph_L, ph_R) at each (sf_L, sf_R) for clarity. Each small domain is a binocular phase-selectivity map (ph_L, ph_R), illustrating responses to various combinations of left and right phases. These small maps are arranged as a 13 × 13 matrix of left and right SFs (sf_L, sf_R). Color scale shows the number of spikes collected for each pair of phases for the two eyes. One of the phase selectivity maps is marked with a red border and is magnified in B. Example spike waveforms of this cell are drawn superimposed at the bottom-right corner (100 spikes). B, Selectivity to binocular phase combination for the highlighted SF pair in A is shown. Strong responses are observed along a 45° diagonal where the interocular phase difference was constant. C, One-dimensional tuning curve to interocular phase difference was calculated from a binocular phase selectivity map shown in B by integrating responses to the same interocular phase difference between the two eyes. A sinusoid was fitted to the tuning curve to determine the modulation amplitude (green broken curve). D, Tuning curves to interocular phase difference are represented for all binocular combinations of SFs. The highlighted SF pair shown in C is indicated with a red border. The optimal SF and orientation for the dominant eye of this cell were 0.64 cpd and 19°, respectively. Values were similar for the nondominant eye (0.61 cpd, 8°). E–H, Responses are shown for a representative simple cell to stimuli containing various combinations of phases and SFs between the two eyes. E–H, The same format as A–D. Optimal SF and orientation for the dominant eye of this cell were 0.56 cpd and 9°, respectively. Values were similar for the nondominant eye (0.53 cpd, 30°).

To create a binocular SF interaction map for this neuron, we next evaluated the strength of disparity tuning for each (sf_L, sf_R) combination. This was done by integrating the response profile of Figure 4B along 45° paths (constant interocular phase difference lines) to obtain a 1-D tuning curve as a function of interocular phase difference (Fig. 4C). A degree of modulation of this tuning curve was extracted by fitting a sinusoid for the analysis described later (green broken curve). In Figure 4D, such tuning curves are shown for all (sf_L, sf_R) combinations as a matrix similar to Figure 4A in its arrangement. Notice that tuning curve has a strong modulation only for relatively matched SF pairs between the two eyes, and such modulation cannot be observed if difference of SF between the two eyes is large. The evidence of elongation is already clear visually in Figure 4A and C. However, one of the most likely candidates for artifacts is a contamination from multiple neurons each tuned to different SFs. To reduce this possibility, we have examined recorded spike waveforms for signs of multiple spike waveforms as shown Figure 4A, inset. Although such an examination of spike waveforms does not completely rule out the possibility of multispike contamination, it provides a reasonable safeguard for this artifact. Therefore, spike waveforms were examined carefully for all neurons identified to have substantial elongations.

Results from a representative simple cell are shown in Figure 4E–H. For this simple cell, response to (ph_L, ph_R) combinations shows a single peak centered at a particular phase pairs, rather than spreading along diagonal band (Fig. 4A,B). This result is obvious because a simple cell has a selectivity to the phase presented monocularly, and the intersection of the two monocular peaks becomes the peak in the joint domain.

Substantially elongated binocular SF interaction maps for a subset of complex cells

To visualize the degree of modulation clearly in Figure 4D and H, maps were created as density plots where each pixel represents the degree of modulation at each (sf_L, sf_R). Values were obtained as the amplitude of the first harmonic (F1) component of an interocular phase-tuning curve. Figure 5A presents such a plot derived from the complex cell data in Figure 4D. To evaluate the degree of elongation of the profile as we discussed in Figure 2, the map was fitted with a 2-D Gaussian function whose axes were constrained to the direction of 45° and 135° diagonals (Fig. 5B). The fitted function was always a Gaussian. In some cases, data were measured in logarithmically constant steps. In such cases, data and a contour of the fitted Gaussian were plotted in a logarithmic domain, resulting in the egg-shaped distortion. Elongation index in the SF domain (EIsf) was then computed as a ratio of a fitted σ along the 45° axis to that along the 135° axis. Clearly, with EIsf = 3.13, this complex cell exhibits a highly elongated shape along the 45° diagonal, suggesting that a substantial pooling occurs across different SF channels.

Figure 5.

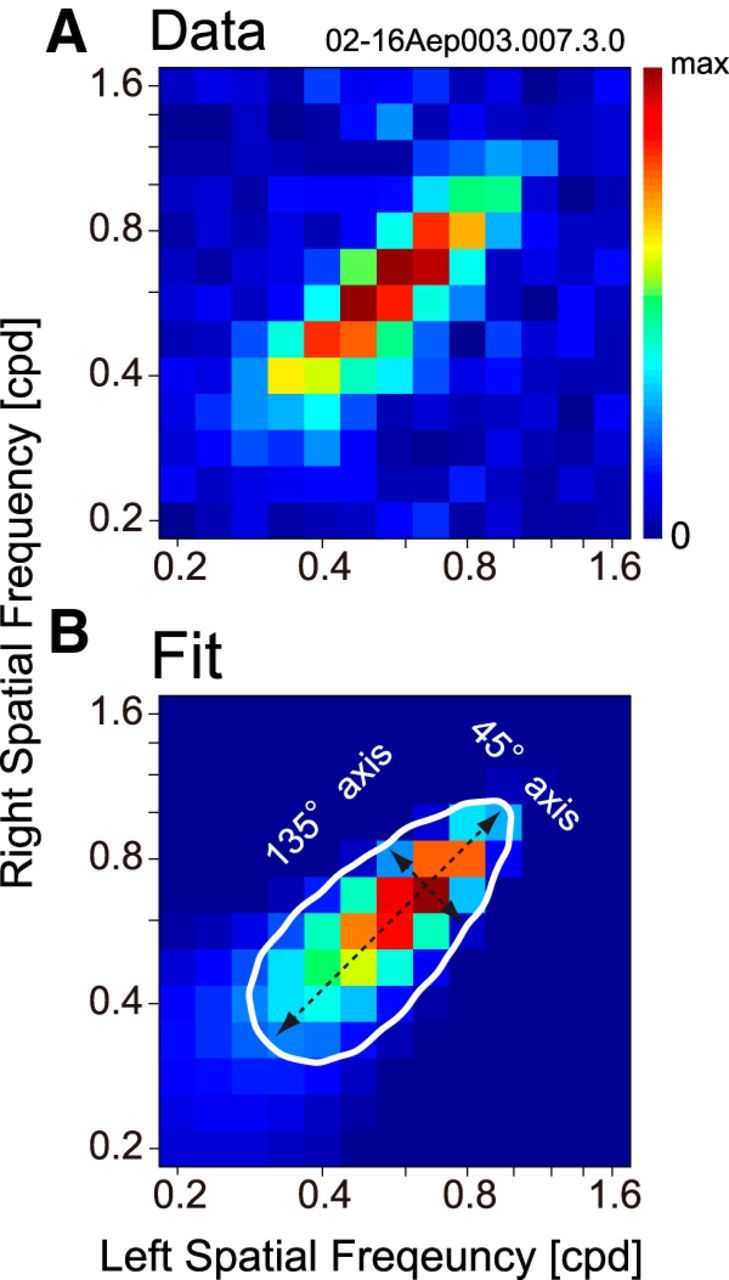
Binocular SF interaction maps were fitted for each neuron by a 2-D Gaussian function. A, A binocular SF interaction map was obtained by extracting the degree of modulation (i.e., amplitude of F1 component) in tuning curves to interocular phase difference for all binocular SF combinations (Fig. 4D). B, The 2-D Gaussian function that yielded the best fit to the data presented in A is shown. The axes of a Gaussian were constrained to the direction of 45° and 135° diagonals. The sigmas of the fitted Gaussian along the 45° and 135° axes were extracted to calculate the index, which indicates a degree of integration of SF channels. Specifically, elongation index in the SF domain (EIsf) was defined as a ratio of a σ along the 45° axis to that along the 135° axis. EIsf for this cell was 3.13.

Additional binocular SF interaction maps are shown in Figure 6 for six cells having various degree of EIsf. The maps are arranged in the descending order of EIsf (indicated by a number at the top-right corner of each map). For these six cells, various extent of elongation was observed from a small value of EIsf (1.10) to a large value (3.66). It suggests that there are multiple grades in integration of SF channels from one cell to another. Results for the previous simple cell (Fig. 4E–H) are shown in Figure 6F. This cell shows almost a circular shape of the binocular interaction map, showing the lack of pooling.

Figure 6.

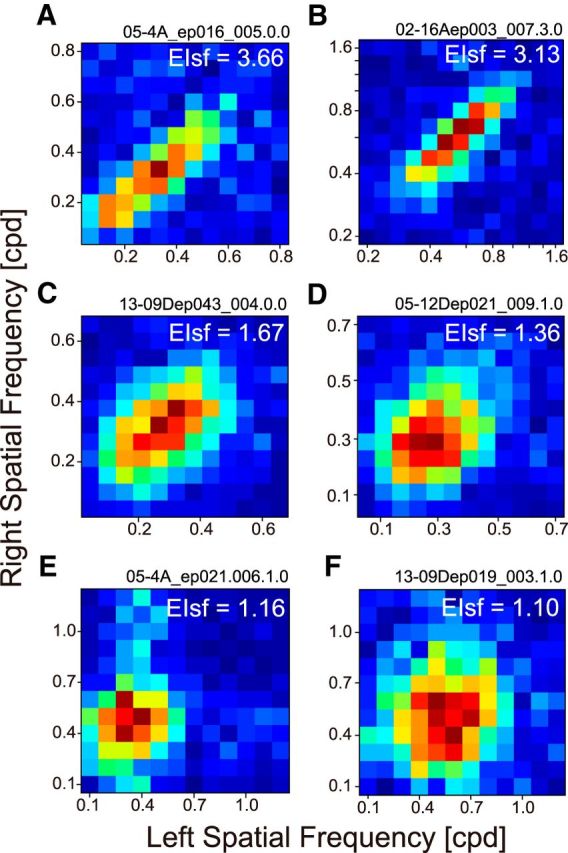
Binocular SF interaction maps showed various degrees of elongation across neurons. These maps are arranged in the descending order of EIsf. Value of EIsf is shown at the upper-right corner. A, Optimal SF was 0.36 cpd, and optimal orientation (OR) was 163° for the dominant eye. B, SF: 0.64 cpd, OR: 19°. C, SF: 0.30 OR: cpd, 96°. D, SF: 0.27 cpd, OR: 1°. E, SF: 0.38 cpd, OR: 103°. F, SF: 0.56 cpd, OR: 9°. Values were similar for the nondominant eye (data not shown). Cells for E and F were of simple type, whereas the remaining cells were complex.

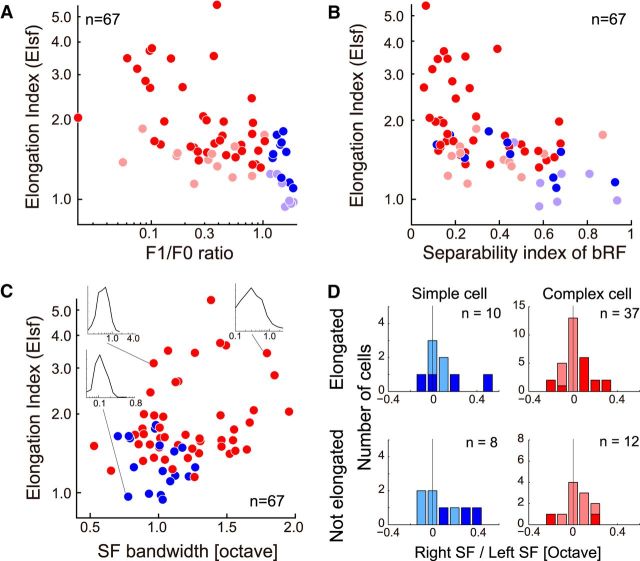
EIsf from all neurons in our sample are summarized in Figure 7A–C. To examine a possible relationship between the degree of pooling and the cell type (simple/complex), EIsf and F1/F0 ratio measured with drifting gratings for each neuron are plotted (Fig. 7A). Blue dots indicate simple cells while red dots represent complex cells. Statistical significance of elongation was tested for all the data and those that were significant are indicated in deeper color (EIsf > 1.0, bootstrap test, p < 0.01). A strong negative correlation between these two values was observed (r = −0.55, p < 0.001), suggesting that pooling of different SF channels is essentially absent for simple cells. Complex cells generally had large degree of elongation in comparison, but there were also some complex cells without elongation or small degree of elongation. For a verification of the baseline, we computed EIsf distribution for a standard binocular energy unit by simulation. Distribution of EIsf by model response was bell-shaped, where its mean and SD were 1.00 ± 0.03.

Figure 7.

Possible relationships are examined between the EIsf (elongation of binocular SF maps) and other response properties of cells. A, Relationship between F1/F0 ratio and EIsf is presented as a scatter plot for all the recorded cells (n = 67). Negative correlation was observed between these two values (r = −0.55, p < 0.001). Blue, Simple cells; red, complex cells. Deeper color indicates data with significant elongation (EIsf > 1.0, bootstrap test, p < 0.01). B, Relationship between separability of bRF and EIsf is presented as a scatter plot (n = 67). Detailed procedure of bRF calculation is explained in Figure 9. There was a significant negative correlation between these two values (r = −0.61, p < 0.01). C, Relationship between SF bandwidth and EIsf is plotted similarly (n = 67). Insets show SF tuning curves measured with drifting sinusoidal grating stimuli for three representative cells. D, Distributions of left and right optimal SF difference are summarized in the histograms. Horizontal axis shows optimal SF difference in an octave unit. Top row, Neurons with significant elongation in the SF domain (EIsf > 1.0), whereas the bottom row shows those without elongation. Color usage is the same as other panels (blue, simple cells; red, complex cells). Deeper color shows data with statistically significant SF difference obtained by a bootstrap test (p < 0.01).

Notice that even among simple cells, there were some with significant elongation. We wondered whether those cells might have complex-like mechanisms internally despite being classified as simple based on F1/F0 ratio. To examine this discrepancy in more detail, we also examined binocular RF (bRF) structure for each neuron. A separability index of a bRF is another metric that reflects the “simple-ness” based on binocular data, and appears to be a better metric as an indication of subunits (Sanada and Ohzawa, 2006). In contrast, F1/F0 ratio is usually defined monocularly. A separability index of a bRF being 1.0 indicates a totally separable map, whereas 0 indicates an inseparable map. An ideal simple cell with a linear Gabor-like RF for each eye will have the index of 1.0. The detailed procedure for obtaining a bRF of each cell is explained later. Figure 7B presents the relationship between the separability index of a bRF and EIsf, showing a significant negative correlation (r = −0.61, p < 0.01). For these results, simple cells with EIsf > 1.0 tended to show rather complex-like (inseparable) bRFs although they all had modulated responses to drifting grating stimuli. Such neurons may have intermediate property between simple and complex cells, as reported in the past studies (Sanada and Ohzawa, 2006; Sasaki et al., 2010).

Because expected consequence of pooling across SF channels is a widening of SF bandwidth, correlation between the SF bandwidth of a neuron and EIsf would be predicted. Therefore, we examined a relationship between the SF bandwidth measured with drifting grating stimuli and EIsf. There appears to be a correlation between these two values, although it was not significant (r = 0.23, p = 0.057; Fig. 7C).

The previous study that defined the separability index of bRF as noted above (Sanada and Ohzawa, 2006), primarily examined a difference of optimal SFs between the left and right eyes, possibly encoding 3-D slant. Is there any relationship between pooling in the SF domain and difference in the left and right optimal SF? Figure 7D shows distribution of left and right optimal SF difference for four groups of neurons. If a neuron pools multiple SF channels while being tuned to different left and right SF, the left-right SF ratio should remain constant for different SF channels. Consequently, the binocular SF interaction map of such a neuron may be elongated off the exact diagonal. Figure 7D, top row, represents cells with significant elongation in the SF domain (EIsf > 1.0), whereas the bottom histograms show data without elongation. Our data confirm the presence of cells with significant left-right optimal SF difference, indicated by deeper colors in the histograms. Among 50 neurons (10 simple, 37 complex, 3 unclassified) with significant elongation, 18 neurons showed significant SF difference between the two eyes. No particular tendency or relationship was found among the degree of elongation, cell type (simple/complex), and offset of a binocular SF map from the diagonal (data not shown).

Note that even if there is a difference in the optimal SFs between the two eyes, pooled SF channels should satisfy a specific relationship for maintaining the ability to signal consistent surface slant in depth (Sanada and Ohzawa, 2006). Specifically, because the slant is related directly to the ratio of optimal SFs, this ratio should be constant across pooled channels. This was examined as follows for 11 of such neurons with EIsf >1.5. We fitted binocular SF interaction maps of such neurons with an elongated 2-D Gaussian function, allowing its long axis to tilt from 45° diagonal. After fitting, two high and low left-right SF combinations along the fitted long axis were selected, which was separated by a distance of 0.8 σ from the fitted center. Left-right SF ratio was then calculated at each point and compared. Although the number of data are small (n = 11), there was a significant correlation of left-right SF ratios between low and high SF combinations, suggesting that these neurons might integrate signals while preserving consistency of surface slant information (Pearson's correlation coefficient, r = 0.77, p < 0.05).

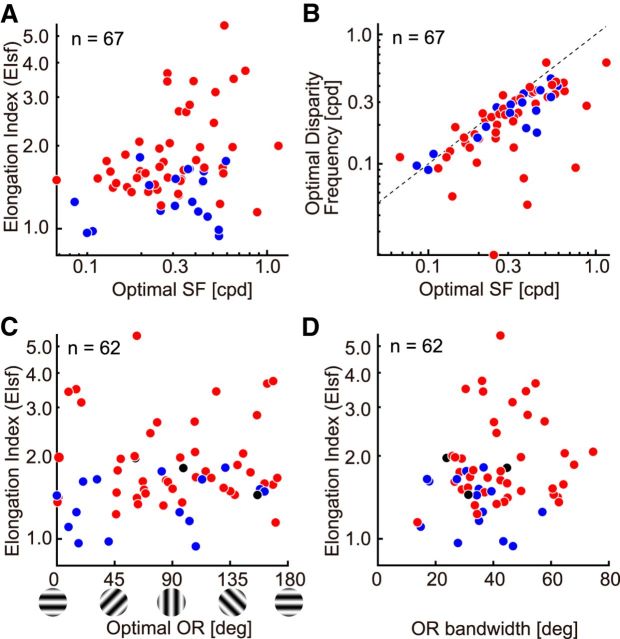
In Figure 8, the relationships among the other basic parameters are shown. Figure 8, A and B, represents the relation of optimal SF measured with monocular stimuli to EIsf and disparity frequency, respectively. There is a weak positive correlation between the optimal SF and elongation in the SF domain, suggesting that neurons tuned to higher SF may carry more reliable disparity signal than neurons tuned to lower SF (r = 0.24, p < 0.05). Furthermore, the scatter plot in Figure 8B shows a tendency also shown in previous studies (Ohzawa et al., 1997; Prince et al., 2002; Read and Cumming, 2003), where there is a strong correlation but the optimal SF generally is higher than optimal disparity frequency (r = 0.73, p < 0.001). Figure 8, C and D, shows the relationships of optimal orientation and its bandwidth to the EIsf. No special relationships were observed between the elongation in the SF domain and the optimal orientation or its bandwidth.

Figure 8.

Relationships among basic parameters are presented as scatter plots for all the recorded cells. Blue, Simple cells; red, complex cells; black, unclassified (for C and D). A, Relationship between optimal SF and EIsf is shown. Positive correlation was observed between these two values (r = 0.24, p < 0.05). B, Relationship between optimal SF and optimal disparity frequency is shown. Black broken line indicates 1:1 identity line. Positive correlation was observed between the two values (r = 0.73, p < 0.001). Most cells showed lower optimal disparity frequency than monocular optimal SF. C, Relationship between optimal orientation and EIsf is presented. Orientation here is defined that horizontal is 0°, and the value increases counterclockwise as illustrated at the bottom. D, Relationship between orientation bandwidth and EIsf is presented.

Reconstruction of bRFs and disparity tunings in the space domain

So far, we have shown that substantial pooling in the SF domain appears to occur in many A17 disparity-tuned neurons. Pooling, however, is a risky operation because it could potentially destroy a refined tuning of individual elements, if care is not used to preserve a tuning for a specific dimension, in this case, of binocular disparity. For example, when pooling multiple disparity detectors across (x, y) space, individual pooled detectors share the same preferred disparity (Sasaki et al., 2010). Does the same constraint apply for pooling across multiple SFs? In other words, for the pooling neuron to maintain or to improve disparity tuning, pooled elements should be tuned to the same disparity across different SF bands (Wagner and Frost, 1993, 1994). To address this question, the SF domain analysis is not appropriate, and we must return to the space domain where binocular disparity tuning may be obtained directly.

A disparity-tuning curve was calculated in two steps as follows. First, a reverse correlation analysis in the joint left-right space domain was performed to obtain a bRF using methods similar to previous studies (Anzai et al., 1999; Sasaki et al., 2010). Spike-triggered grating pairs were selected for an optimal correlation delay (Fig. 9A), and 1-D spike-triggered sinewaves were multiplied between the two eyes to produce binocular interaction terms (Fig. 9B). If contrasts are the same polarity between the two eyes (white-white or black-black), value of the interaction term becomes positive. On the other hand, when contrasts between the two eyes are opposite (white-black or black-white), the binocular interaction term becomes negative. By repeating the above calculation of binocular interaction terms for all spikes and summing them, a bRF was obtained in the joint left-right space domain (Fig. 9C). In this bRF map, binocular disparity is constant along the +45° diagonal, whereas it changes along −45° diagonal. Therefore, in the second step, a disparity-tuning curve is computed by integrating the map along the +45° diagonal.

Figure 9.

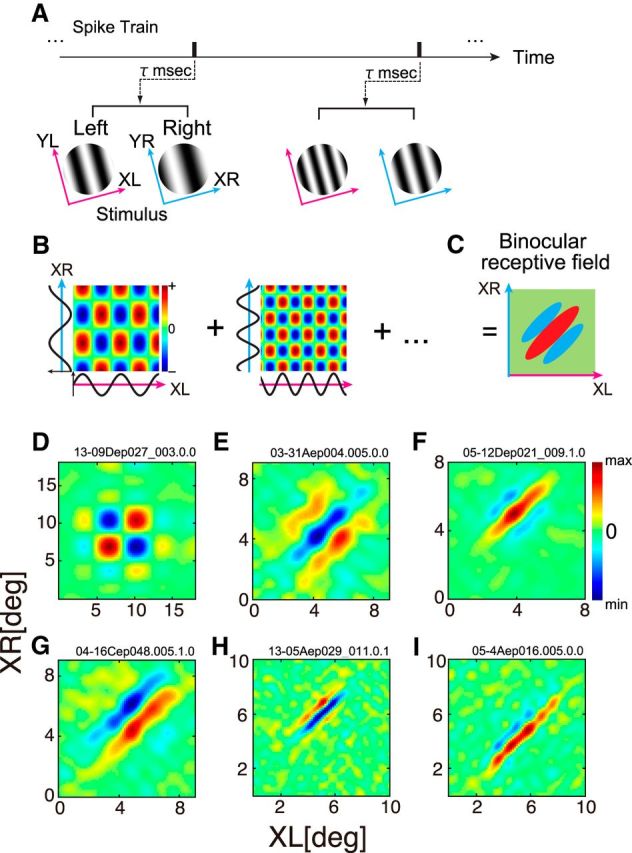
Although stimuli were defined in the SF and phase domain, it is possible to perform a reverse correlation analysis in the joint left-right space domain to obtain a bRF for a given neuron. A, Using a spike train recorded while binocular sinewave grating stimuli were presented, spike-triggered stimulus pairs were selected for an optimal correlation time delay. B, Binocular interaction terms were calculated from each pair of spike-triggered gratings as follows. The XL- and XR-axes are defined as the axis orthogonal to preferred orientation in the left and right eyes, respectively. These 1-D spike-triggered sinusoids in the XL- and XR-domains were multiplied to produce binocular interaction terms in the joint XL-XR domain. Positive values (red) mean that stimuli with the same contrast polarity were presented between the two eyes, whereas negative values (blue) mean those with the opposite polarity were presented between the two eyes. C, A bRF was obtained by summing these interaction terms for all spike-triggered stimulus pairs. Binocular disparity is constant along the +45° diagonal in the map, whereas disparity changes along −45° diagonal. D–I, Reconstructed bRFs are shown for several representative cells. The horizontal axis of each map indicates position in XL-axis, whereas the vertical axis indicates that in XR-axis. D, BRF of a simple cell. Optimal SF, optimal orientation and EIsf of this cell was 0.09 cpd, 176°, and 0.97, respectively. All the remaining cells were of complex type, and the parameters are indicated in the above order. E, Tuned inhibitory bRF (SF: 0.25 cpd, OR: 73°, EIsf: 1.62). F, Even-symmetric bRF (SF: 0.27cpd, OR: 1°, EIsf: 1.36). G, Odd-symmetric bRF (SF: 0.21 cpd, OR: 98°, EIsf: 1.81). H, I, BRFs of cells that had relatively large EIsf. Parameters for the cell in H (SF: 0.40 cpd, OR: 20°, EIsf: 3.42) and I (SF: 0.36 cpd, OR: 163°, EIsf: 3.66). The bRFs allow evaluation of pooling along x-axis (Sanada and Ohzawa, 2006) as EIx. Values of EIx were 1.04, 1.39, 1.80, 1.79, 3.39, and 4.31, for D–I, respectively.

Figure 9D–I shows results of the first step, i.e., bRFs for six example neurons because they are inherently much more informative than reduced 1-D disparity-tuning curves. In each map, red color indicates binocular response to the same contrast polarity for the two eyes, whereas blue represents that for the opposite contrast polarity. Horizontal and vertical axes define the position along the axis orthogonal to preferred orientation in the left and right eye, respectively.

Figure 9D shows a typical bRF for a simple cell. Because of the selectivity to monocular phase, the map shows a separable profile. On the other hand, bRFs for other five complex cells show inseparable shape oriented along the constant disparity line (Fig. 9E–I). The bRF in Figure 9E shows an inverted bRF profile, found relatively rarely, for which the strongest subregion is to a combination of opposite polarity contrasts across the eyes. If the central blue region is at zero disparity, it would be a tuned-inhibitory cell. Because our preparation was anesthetized and paralyzed, we do not have accurate information on retinal correspondence. Figure 9, F and G, shows even-symmetric and odd-symmetric bRFs, respectively. The maps in Figure 9, H and I, represent bRFs for the neuron that showed large degree of elongation in the SF domain with EIsf 3.42 and 3.66 for Figure 9H and I, respectively. Notice that, for these neurons, the reconstructed bRFs in the space domain (H and I) are also thin and highly elongated along +45° diagonal. This result suggests that some degree of pooling in the space domain may also occur in these neurons. Analysis on the relationship between pooling in the SF domain and the space domain is described later.

Are optimal disparities matched when pooling across different SF bands?

Having described the 2-D bRFs, we now return to the original question and examine binocular disparity-tuning curves. Are pooled elements tuned to the same common disparity across different SF sub-bands? For this purpose, we note that the bRF and disparity-tuning curve may be calculated for a subset of stimuli limited to a particular SF band. This is achieved by simply limiting the spike-triggered stimuli to within an arbitrary SF band during a reverse correlation analysis for constructing bRFs.

To compare disparity selectivity between mechanisms tuned to high and low SF, bRFs for two SF bands were obtained by using only upper half or lower half of the SF components. Figure 10 shows bRFs and disparity-tuning curves for a representative complex cell (the same cell shown in Figs. 4A–D and 6B). SF ranges used for each reconstruction are illustrated in the top row of Figure 10A–C in the form of binocular SF interaction maps. SF components outside the selected SF band are indicated by dark blue, and each bRFs are shown under the respective SF interaction map (Fig. 10A, all SF components were used; B, only lower half of SFs were used; C, only upper half of SFs were used).

Figure 10.

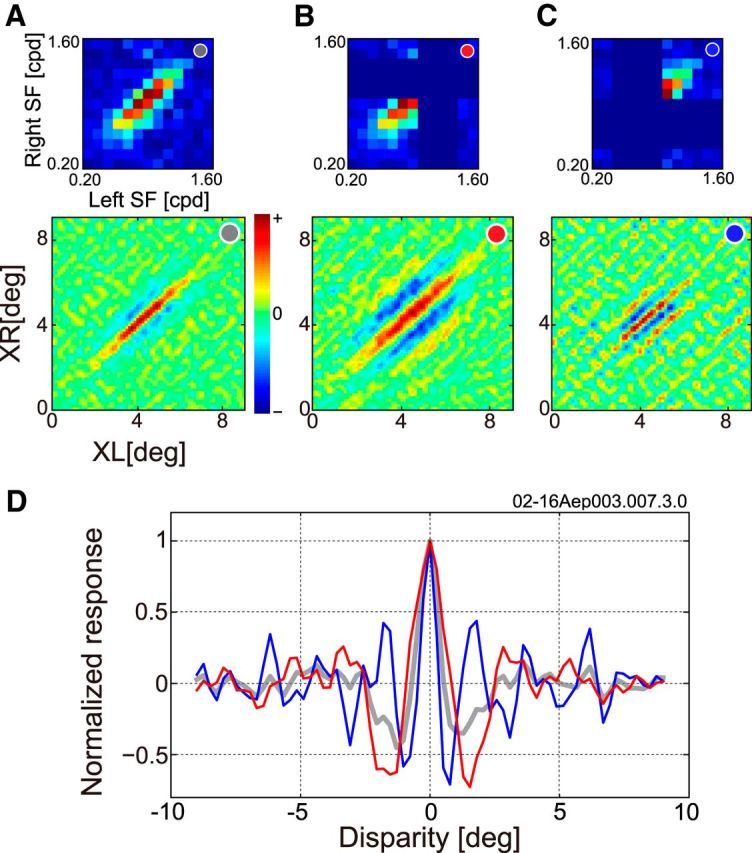
To allow visualization of properties of underlying pooled subunits, bRFs were reconstructed in different SF bands for a representative complex cell. In A–C, bRFs were reconstructed using limited SF bands. bSF interaction maps are presented in the top row to show SF components used to reconstruct bRFs. Reconstructed bRFs are shown in the bottom row. A, All SF components were used for reconstruction. B, Only the lower one-half of the SF components was used for reconstruction. C, Only the upper one-half of the SF components was used. Components that were not used for reconstruction are indicated by the darkest blue color. D, Disparity-tuning curves were obtained from the three bRFs. Color of the curves represents SF bands used for reconstruction (gray, all SF components; red, low SF components; blue, high SF components).

In Figure 10D, computed disparity-tuning curves of each bRFs are superimposed (gray: all SF components, red: low SF components, and blue: high SF components). Clearly, peaks of all the tuning curves are at the same disparity. The result suggests that this neuron pools input from multiple SF channels, but they are tuned to the same disparity. Such a pooling may allow more robust detection of disparity than the conventional disparity energy model is capable of, because responses to the false matches at side-lobes of a tuning curve may be reduced due to mutual cancellation of side lobes of tuning curves for different SF bands (Fig. 10D). However, notice that the care is needed for this analysis about interpretation of side-lobes, because based on an uncertainty principle, bandwidth limitation in the SF domain generates increased number of bounces in side-lobes in the space domain. The bandwidth-limited reconstructions of bRFs were performed using ∼1.5 octave bandwidth in Figure 10B and C (one-half of 3 octaves total). Although this is close to the average bandwidth of A17 neurons, at least part of side-lobes might have been due to the bandwidth limitation.

If a pooling in the SF domain of a disparity detector always occurs under the constraint of matched disparity for all SFs, neurons that pool multiple SF channels should show similar results to that shown in Figure 10. Therefore, we next examined whether this constraint is common in other neurons that showed large pooling in the SF domain. Neurons with EIsf 1.5 were examined with the same analysis as that for Figure 10, and the peak difference of disparity-tuning curves between low and high SF bands was evaluated. Figure 11A illustrates the calculation of “normalized peak difference,” which indicates the quantitative index of the difference. ΔPeak is the separation between the peaks of tunings between the different SF bands, and normalized peak difference is defined as the ΔPeak divided by the wavelength (1/SF) of disparity-tuning curve (all SF condition). Figure 11B shows the distribution of normalized peak difference and its relationship with the phase of original disparity-tuning curve for our sample of cells (n = 44). As the histogram at the top of Figure 11B shows, most cells had a relatively small peak difference of <0.1 between the low and high SF bands, indicating a good general match of encoded disparity across different SF sub-bands. Therefore, for the majority of disparity coding neurons, pooled subunits satisfy the rule of sharing the same preferred disparity. However, for a small fraction of the population, this was not the case. We wondered here whether the alignment of peak disparities might depend on the symmetry of disparity-tuning curves of pooled subunits. This is because the peak alignment is the same as centering alignment (of the envelopes) for even-symmetric disparity-tuning curves as illustrated in Figure 11A (blue and red curves). On the other hand, to peak-align odd-symmetric disparity-tuning curves across subunits, centers of disparity-tuning curves must be offset accordingly. In this case, it is conceivable that some neurons may pool across SF sub-bands with “zero-crossing” alignment presumably for different purposes. Results for an example neuron that shows such an alignment across different SF bands is indicated in Figure 11C. We do not have a definite conclusion on this, because there are only small numbers of neurons with a large normalized peak difference (>0.1). However, those all had nearly odd-symmetric disparity-tuning curves as indicated by the phase of disparity-tuning curves close to 90° or 270° (Fig. 11B).

Figure 11.

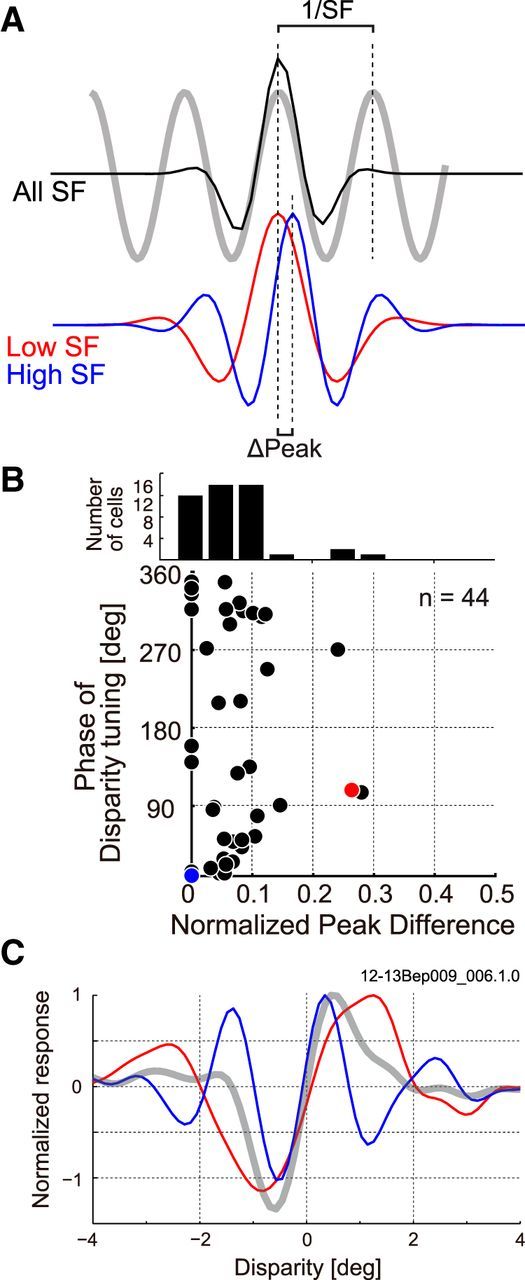
Are pooled SF sub-bands tuned to a common binocular disparity? A, Alignment of preferred disparities is evaluated between low and high SF sub-bands by normalized peak difference. ΔPeak is the separation between the peaks originally in the unit of degrees. Normalized peak difference is the ΔPeak expressed as a fraction of the wavelength (1/SF), where SF is determined from the tuning curve using all frequency components. B, Relationship between normalized peak difference and symmetry of disparity-tuning curve (phase of fitted Gabor function) is plotted for 44 cells, which showed EIsf larger than 1.5. The blue dot indicate a neuron shown in Figure 10. The histogram on the top shows distribution of normalized peak difference. C, An example cell that shows odd-symmetric tuning curve marked with red in B is indicated. Disparity-tuning curves obtained from three different bRFs in the same format as shown in Figure 10 are superimposed, suggesting zero-crossing alignment across different SF bands (gray, all SF components; red, low SF components; blue, high SF components).

Relationship between pooling in the SF domain and the space domain

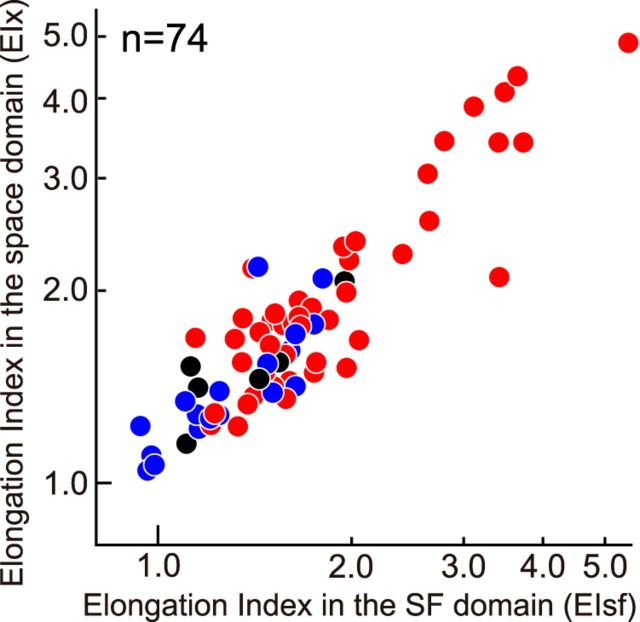
Recall that in some of the reconstructed bRFs, highly elongated shapes in the space domain were also observed (Fig. 9). As previous studies suggest, some degree of pooling in the space domain may occur for a portion of A17 disparity detectors (Sasaki et al., 2010). To investigate the relationship between the pooling in the SF domain and that in the space domain, we also computed the elongation index along the x-axis (EIx) to capture the degree of pooling in the joint left-right space domain. For EIx, aspect ratio of the Fourier spectrum of each bRF was calculated (Sanada et al., 2006). The relationship between EIsf and EIx is shown in Figure 12. There is a strong positive correlation between these two values (r = 0.82, p < 0.001). Superficially, the results suggest the possibility that pooling occur simultaneously to a closely similar degree in multiple domains, namely in the space domain, as well as in the SF domain, in A17 complex cells.

Figure 12.

Relationship is shown between EIsf and elongation index in the space domain along the x-axis (diagonal) in the bRF (EIx). Symbol colors blue, red, and black indicate simple, complex, and unclassified cells, respectively. A significant positive correlation was observed between the two values (r = 0.8, p < 0.001).

However, we now realize the possibility that the apparent diagonal elongation may arise purely from pooling in the SF domain alone. If pooling across multiple SF bands can reduce sidebands in disparity-tuning curves, it may essentially restrict the extent of bRF map along the −45° axis without necessarily extending bRF along the +45° axis (x-axis). To examine this possibility, we consider a disparity detector that pools only in the SF domain. Such a detector may be constructed by summing the output of multiple disparity energy units aligned at the center (Fig. 13). The bRF of the pooled unit is slightly elongated along the constant disparity (+45°) axis without any pooling in the space domain (Fig. 13B, gray elongated contour). Therefore, pooling purely in the SF domain itself may be responsible for a part of large EIx.

Figure 13.

A, Predicted response of three energy model units are shown in the format of bRFs. The three units are tuned to different SFs separated in steps of 1.7 (≈√3) times (therefore, the highest SF is 3 times larger than the lowest). Light gray circle indicates 10% contour of the envelope. For the unit tuned to the highest SF, additional two locations are shown diagonally in the bRF space to indicate a possibility of greater degree of spatial pooling at higher SF. B, A predicted response of a neuron that pools the three units shown in A is indicated. This is a model implementation of a neuron with pure SF pooling but without spatial pooling. The bRF is shown in the top, with the bRF envelope (25% of peak) depicted by a diagonally elongated light gray contour, calculated by Hilbert transform. Cross-sections of the bRF along the disparity axis (indicated as red and black lines) are compared in the bottom. Red curve shows a disparity-tuning curve obtained as the cross-section at the center, whereas black curve shows the cross-section near the edge of the bRF (50% of the maximum amplitude of its envelope where there is little contribution from the highest SF unit). Each curve was normalized to be 1.0 at the maximum. C, Data from two example neurons that had large EIx are shown. Top shows bRFs, whereas the bottom shows superimposed disparity-tuning curves at the center and at the edge (50% of the maximum amplitude of its envelope) of each bRF. Each tuning curve was calculated as an average of cross-sections within band-shaped regions (shown as light red and black bands in the bRF).

However, the predicted response of a neuron with pooling purely in the SF domain shows some distortion of the bRF not observed in the bRFs of actual neurons, as shown in Figure 13B. Because the bRF of a unit tuned to lower SF covers a larger space than that tuned to higher SF (Fig. 13A), the pooled bRF becomes sharpened only at the center, but remaining broad at the edges shown by superimposed tuning curves of cross-sections at the center and the edge in Figure 13B (bottom). On the other hand, actual neurons showed no such distortion of bRFs (Fig. 13C). Tuning curves at the center and the edge are almost identical for these neurons, although they show highly elongated shape of bRFs. Therefore, some degree of spatial pooling must occur for neurons shown in Figure 13C and others in our sample. A prediction from this analysis is that neurons with broadband SF tuning tend to have a corresponding degree of spatial pooling for maintaining consistent disparity tuning across all locations of bRFs. Unfortunately, we cannot precisely determine the degree of spatial pooling due to the complications noted above.

Discussion

In this study, we examined how the integration of information from different SF bands is achieved in disparity-sensitive binocular neurons in the striate cortex. A previous computational study proposed a model of combining outputs from multiple energy units at different scales for robust estimation of binocular disparity (Fleet et al., 1996). Physiologically, a previous study indicated that multiple excitatory and suppressive subunits contributed to generate disparity-selective responses in neurons of monkey V1 (Tanabe et al., 2011). However, no direct assessment has been conducted physiologically to evaluate the integration of multiple excitatory channels tuned to different SFs as illustrated in Figure 1. We obtained a binocular SF interaction map, which reflects the degree of integration by analyzing phase-based disparity tunings in the joint left-right SF domain. Based on our results, a subset of complex cells showed substantial elongation in the SF domain, suggesting that the initial part of this integration process starts in the primary visual cortex.

Relation to coarse-to-fine mechanism

Some of computational models of stereoscopic processing take a sequential approach, known as “coarse-to-fine” algorithms (Marr and Poggio, 1979; Quam, 1987; Chen and Qian, 2004; Li and Qian, 2015). In these algorithms, disparity information is hierarchically processed from coarse to fine scales, improving the accuracy of disparity detection as it proceeds. Do cortical neurons also implement a sequential refinement in integrating multiple SF bands? Although we cannot directly address this question, our analysis implies that neurons simply pool output of multiple subunits tuned to different SFs but with common preferred disparity. No explicit and nontrivial sequential interactions from coarse-to-fine (or from low SF to high SF) are assumed in this pooling scheme. Such a simple pooling mechanism appears sufficient to explain the results obtained.

However, there may be a sequential element of coarse-to-fine organization in the simple pooling process. It is well known that in monocular spectral-time receptive field analyses, the optimal SF increases from low to high as a function of response delay (Bredfeldt and Ringach, 2002; Mazer et al., 2002; Nishimoto et al., 2005). In other words, signals for high SFs arrive at the neuron with a longer temporal delay than low SF signals. The same phenomenon is also observed for binocular responses. Disparity-time response analyses reveal progressive shift of disparity frequency as a function of temporal delay (Menz and Freeman, 2003). Our own data also showed similar tendency in the time course of disparity tuning (data not shown). Specifically, our SF interaction map showed elongation in a single time delay (Fig. 5A), and at the same time, showed slight progressive shift of its optimal SF from low to high as the temporal delay was increased. Therefore, regardless of the implementation, the real visual system may also effectively achieve progressive computation and refinement of disparity information simply by summing signals from multiple subunits with various temporal delays.

Possible effects of suppressive elements

Although we have so far assumed that the elongated shape of a binocular SF interaction map is caused by SF pooling, possibility of other factors may not be negligible. Another possibility contributing to the elongated Gaussian shape of an interaction map is an effect of suppression (Tanabe et al., 2011). Instead of elongating a response region by adding subunits (Fig. 2), it is also possible that binocular response is inhibited at specific SF combinations where difference of SF is large between the two eyes. As a result, for example, both the upper-left and lower-right sides of the originally circular response region (Fig. 2A) may be scraped off, thereby making the map into an elongated profile along the 45° diagonal. Unfortunately, because our measurements contain too few blank stimuli to estimate the baseline response level accurately, it is difficult to evaluate suppressive responses for this purpose. However, although possible in principle, such a hypothetical scheme seems unlikely or at least inefficient, because units exerting suppression need to be constructed in the first place with inputs from highly unmatched SFs between the two eyes. Such neurons with a large difference in preferred SFs are not generally found (Sanada and Ohzawa, 2006).

Other schemes are also possible if one allows more complexity in the model. For example, inhibitory input from a neuron tuned to a slightly higher SF than the excitatory neuron may be present. If such an inhibitory neuron is turned off (assuming an appropriate disparity tuning) the result will be a disinhibition, which will result in net increase in excitation for the postsynaptic neuron. However, such schemes are indistinguishable from excitatory input as recorded from the postsynaptic neuron. Therefore, functionally, such schemes fall within the framework being considered. Unless there is a substantial functional difference, it is simpler and more natural to consider a detector that combines multiple excitatory subunits rather than one that use suppression.

Alignment of disparity-tuning curves for pooling across SF bands

Majority of neurons in our sample appeared to exhibit pooling of different SF bands with a common optimal disparity. As a previous computational study shows (Fleet et al., 1996), combining energy units under such a pooling rule would improve detection accuracy by increasing response probability at the true disparity and decreasing it at the false disparities. However, there are some neurons that showed a large difference in optimal disparity when pooling across SF bands (Fig. 11B). These neurons tended to have odd-symmetric disparity-tuning curves, and the results of multi-SF-band analysis show that disparity-tuning curves for high and low SFs are aligned approximately at zero-crossings rather than at peaks (Fig. 11C). Do such neurons play some functional roles?

In higher visual areas, especially those in the dorsal visual stream such as MT and MST, it is known that the number of disparity-selective neurons with odd-symmetric tuning curve substantially increases (Cumming and DeAngelis, 2001; DeAngelis and Uka, 2003). A possible role is suggested that output of these neurons provide a signal for oculomotor vergence control (Masson et al., 1997). Characteristics of signals required for fine vergence control may be different from those for depth perception. Specifically, it may be more important to achieve high sensitivity near 0 disparity for determining the direction and size of vergence: converge or diverge, rather than detecting a disparity. Neurons with odd-symmetric disparity can provide such a signal, although the same information may be obtained from peaks of multiple neurons. Such a vergence signal should also function for large disparity deviations. In other words, SF bands may be pooled such that the slope at zero-crossing is increased and the output maintained even at large disparities. This goal is achieved by pooling multiple SF components with zero-crossing alignment, as the famous Fourier series decomposition of a square wave indicates.

Effects of SF pooling on the shape of disparity-tuning curve

There are two known refinements in the shape of disparity-tuning curves in neurons beyond that of a disparity energy model. The refinement begins in A17 (Ohzawa, 1998; Haefner and Cumming, 2008; Tanabe et al., 2011) but become more pronounced in high-order areas, such as V4 and IT. One is the reduction of multiple side-lobes as illustrated in Figure 10, and noted by Fleet et al. (1996). The other is the reduction of responses to anti-correlated random-dot stereograms (aRDS; Janssen et al., 2003; Tanabe et al., 2004). These two factors are often discussed together but are distinct (Nieder and Wagner, 2001). In relation to the latter, a previous study shows that in monkey V4, disparity-sensitive neurons show a correlation between SF bandwidth and the degree of attenuation of response amplitude for aRDS compared with that for correlated RDS (cRDS; Kumano et al., 2008). They interpret this as a consequence of integrating multiple SF channels. However, pooling multiple disparity-selective units across SF bands by itself does not produce attenuation of response amplitude to aRDS. Responses to aRDS are merely inverted versions of disparity tuning for cRDS.

Interactions of pooling across multiple stimulus dimensions

In describing Figure 13, we examined an idea that elongations of bRFs may be produced solely by pooling multiple SF channels. This can indeed happen to a certain extent (Fig. 13B), but could not explain all of the features observed in actual bRFs, indicating that spatial pooling is also needed. In theory, other forms of interactions are conceivable across multiple stimulus dimensions. For example, pooling in the space domain might produce apparent elongations in the binocular SF interaction maps, the opposite of what we examined in Figure 13. Furthermore, given that neurons in the primary visual cortex are tuned sharply for orientation, pooling in the orientation dimension might also affect some of the properties we examined in the present study. Analyses of these complications will require a comprehensive and systematic examination, and are beyond the scope of this study.