Decoding a Wide Range of Hand Configurations from Macaque Motor, Premotor, and Parietal Cortices

Abstract

Despite recent advances in decoding cortical activity for motor control, the development of hand prosthetics remains a major challenge. To reduce the complexity of such applications, higher cortical areas that also represent motor plans rather than just the individual movements might be advantageous. We investigated the decoding of many grip types using spiking activity from the anterior intraparietal (AIP), ventral premotor (F5), and primary motor (M1) cortices. Two rhesus monkeys were trained to grasp 50 objects in a delayed task while hand kinematics and spiking activity from six implanted electrode arrays (total of 192 electrodes) were recorded. Offline, we determined 20 grip types from the kinematic data and decoded these hand configurations and the grasped objects with a simple Bayesian classifier. When decoding from AIP, F5, and M1 combined, the mean accuracy was 50% (using planning activity) and 62% (during motor execution) for predicting the 50 objects (chance level, 2%) and substantially larger when predicting the 20 grip types (planning, 74%; execution, 86%; chance level, 5%). When decoding from individual arrays, objects and grip types could be predicted well during movement planning from AIP (medial array) and F5 (lateral array), whereas M1 predictions were poor. In contrast, predictions during movement execution were best from M1, whereas F5 performed only slightly worse. These results demonstrate for the first time that a large number of grip types can be decoded from higher cortical areas during movement preparation and execution, which could be relevant for future neuroprosthetic devices that decode motor plans.

Introduction

Spinal cord injuries or motor diseases can lead to a disconnection of the spinal cord from the brain. Such paralyzed patients have reported that hand and arm functions are very important for them to recover (Anderson, 2004, Snoek et al., 2004). For these patients, myoelectric prosthetics are not applicable, because they depend on activated nerves in limbs or chest (Kuiken et al., 2009). In comparison, cortical neural interfaces can directly access brain activity and translate it into assistive control signals (Hatsopoulos and Donoghue, 2009, Scherberger, 2009). A better understanding of the cortical motor system together with improved decoding algorithms led to the development of brain interfaces for the control of computer cursors (Taylor et al., 2002; Ganguly and Carmena, 2009; Kim et al., 2011; Gilja et al., 2012) and robotic grippers (Hochberg et al., 2012; Collinger et al., 2013) that allow tetraplegic patients to regain physical interaction with their environment.

Despite these impressive advances, the neural guidance of hand prosthetics remains a major challenge. Although reaching in space involves three degrees of freedom (DOFs), this number increases to at least 23 DOFs when all joint angles of an anthropomorphic hand are considered. Controlling so many DOFs exclusively under visual feedback explains the difficulty of the neuroprosthetic substitution of hand function (Vargas-Irwin et al., 2010).

Alternatively, movement intentions can be decoded from higher-order planning signals of premotor and parietal cortices (Musallam et al., 2004; Townsend et al., 2011). Decoding higher-order motor plans (i.e., grip types) instead of many individual DOFs could help reduce the dimensionality problem for such decoding applications (Andersen et al., 2010). The ventral premotor cortex (specifically area F5) and the anterior intraparietal cortex (AIP) that show strong bidirectional anatomical connections (Luppino et al., 1999, Borra et al., 2008) are particularly well suited for this kind of task. Functionally, they are responsible for translating visual signals into hand-grasping instructions. Neurons in both areas were identified to reflect visual information about the object being grasped (Murata et al., 1997, 2000) and the performed grip type (Baumann et al., 2009; Fluet et al., 2010). Compared with the primary motor cortex (M1), information in these areas is already accessible well before movement execution and has been used to decode vastly different grip types, such as power and precision grips (Carpaneto et al., 2011; Townsend et al., 2011). However, the question remains open whether detailed hand shapes could be differentiated from these areas as well.

In this study, we demonstrate for the first time that fine differences in hand configurations can be decoded accurately from the cortical areas AIP and F5 during motor planning and execution. Furthermore, we compared the decoding capabilities of AIP and F5 with that of M1 and found major differences between them. Finally, the grip types selected from 27 DOFs of the primate hand and arm could be translated to an anthropomorphic arm and hand of 16 DOFs, hence demonstrating the possibility of converting high-level neural motor commands into neuroprosthetic robotic grips.

Materials and Methods

Basic procedures

Two purpose-bred macaque monkeys (Macaca mulatta) participated in this study (animal Z, female, 7.0 kg; animal M, male, 10.5 kg). They were first trained in a delayed grasping task to grasp a wide range of different objects while wearing a kinematic data glove (Fig. 1), then a head holder was implanted on the skull, and electrode arrays were permanently inserted in the cortical areas AIP, F5, and M1. In subsequent recording sessions, neural activity and hand kinematics were simultaneously recorded while animals performed the grasping task. All analysis was performed offline. Animal care and all experimental procedures were conducted in accordance with German and European law and were in agreement with the Guidelines for the Care and Use of Mammals in Neuroscience and Behavioral Research (National Research Council, 2003).

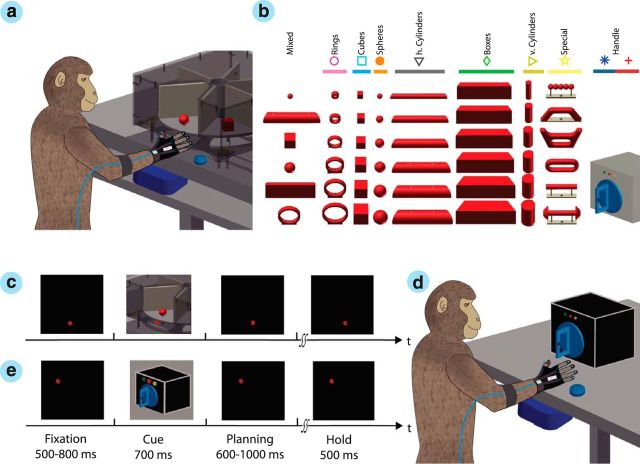
Figure 1.

Experimental task. a, Two macaque monkeys were trained to grasp a wide range of objects presented on a personal computer-controlled turntable. b, In total, the animal grasped 48 objects mounted on eight exchangeable turntables. c, On each turntable, objects were presented in a pseudorandom order and were grasped within a delayed task consisting of eye-fixation, cue, planning, movement, and hold epochs. The monkeys performed the task in darkness, except during the cue epoch, when the objects were illuminated. d, Within each recording session, monkeys also grasped a handle with two additional grips. e, In this task, two supplementary LEDs instructed the animal to perform either a precision (yellow LED) or a power (green LED) grip.

Experimental setup

For behavioral training and experiments, the monkey sat in a customized primate chair with its head fixed. Graspable objects (handle or objects on a turntable) were presented in front of the animal at a distance of 25 cm at chest level (Fig. 1a). The setup design allowed a fast exchange of turntables in <1 min, and individual objects could be lifted vertically by 30 mm. Custom-made software was used to control the turntable position and the pseudorandom sequence of object presentation. Object lifting and turntable position was monitored with a photoelectric barrier.

To obtain a high variation of grip types, we designed objects of different shapes and sizes (Fig. 1b), including rings (outer diameter, 10, 20, 30, 40, 50, and 60 mm), cubes (length, 15, 20, 25, 30, 35, and 40 mm), spheres (diameter, 15, 20, 25, 30, 35, and 40 mm), cylinders (length, 140 mm; diameter, 15, 20, 25, 30, 35, and 40 mm), and bars (length, 140 mm; height, 50 mm; depth, 15, 20, 25, 30, 35, and 40 mm). Furthermore, a mixed turntable was used, holding mid-sized objects of various shapes for fast exchange (sphere, 15 mm; horizontal cylinder, 30 mm; cube, 30 mm; bar, 10 mm; ring, 50 mm), and a special turntable was used that contained objects of abstract forms (Fig. 1b). All objects had a uniform weight of 120 g (independent of size and shape).

In addition, power and precision grips were performed on a graspable handle (Baumann et al., 2009; Fluet et al., 2010). On the handle, two touch sensors were placed in small, clearly visible recessions to detect the contact of the animal's thumb and index finger during precision grips, whereas power grips were detected by an infrared light barrier at the inside of the handle and a pulling force sensor.

Behavioral paradigm

Monkeys were trained in a delayed grasp and hold paradigm (Fig. 1c). While in complete darkness, an animal could initiate a trial by pressing a home button near its chest. Then, it had to fixate a red LED light while maintaining its hand on the home button. After fixating this red LED for a variable time (fixation epoch, 500–800 ms; mean, 650 ms) a spotlight was switched on that illuminated the graspable object for 700 ms (cue epoch). When the spotlight was switched off, the animal had to withhold movement execution until the fixation LED blinked (planning epoch, 600–1000 ms; mean, 800 ms), which indicated the animal to grasp and lift the object (movement epoch) and hold it for 500 ms (hold epoch) to receive a liquid reward (small amount of juice). A following trial could be initiated shortly afterward (intertrial interval, 1000 ms). Error trials were immediately aborted without providing reward. In case of the graspable handle (Fig. 1d), an additional yellow LED (or green LED) was turned on during the cue epoch to instruct the animal to perform a precision grip (or power grip), as shown in Figure 1e.

Objects were mounted on eight turntables in groups of six (Fig. 1b, columns). During each block of trials, the objects of one turntable were presented in pseudorandom order until all objects were grasped successfully at least 10 times. Then, the turntable was exchanged and another block of trials started until all objects were tested. Finally, power and precision grip trials were performed with the graspable handle (10 trials pseudorandomly interleaved). To maintain a high motivation, animals were restricted from water access up to 24 h before training or testing.

Eye movements were monitored with an infrared camera (ISCAN) through a half-mirror. All behavioral and task-relevant parameters, i.e., eye position, button presses, and stimulus presentations, were controlled using custom-written behavioral control software that was implemented in LabVIEW Realtime (National Instruments).

Surgical procedures and imaging

Before surgery, we performed a 3D anatomical MRI scan of the animal's skull and brain to locate anatomical landmarks (Townsend et al., 2011). For this, the animal was sedated (e.g., 10 mg/kg ketamine and 0.5 mg/kg xylazine, i.m.) and placed in the scanner (GE Healthcare Signa HD or Siemens TrioTim; 1.5 Tesla) in a prone position, and T1-weighted images were acquired (iso-voxel size, 0.7 mm³).

Then in an initial procedure, a head post (titanium cylinder; diameter, 18 mm) was implanted on top of the skull (approximate stereotaxic position: midline, 40 mm anterior, 20° forward tilted) and secured with bone cement (Refobacin Plus; BioMed) and orthopedic bone screws (Synthes). After recovery from this procedure and subsequent training with head fixation, each animal was implanted in a second procedure with six floating microelectrode arrays (FMAs; MicroProbes for Life Science). Specifically, two FMAs were inserted in each area AIP, F5, and M1 (Fig. 2). FMAs consisted of 32 non-moveable monopolar platinum–iridium electrodes (impedance, 300–600 kΩ at 1 kHz), as well as two ground and two reference electrodes per array (impedance, <10 kΩ). Electrode length ranged from 1.5 to 7.1 mm and were configured as in the study by Townsend et al. (2011).

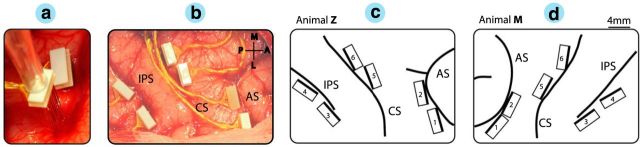
Figure 2.

Electrode array implantation. a, b, Animals were implanted with multiple FMAs in areas AIP, F5, and M1. Each array consisted of 32 individual electrodes of variable length (1.5–7.1 mm) (a) and were placed in the bank of the sulcus (b). In animal Z (b, c) and animal M (d), two arrays were implanted in each area: at the lateral end of the intraparietal sulcus (IPS) in AIP, in the posterior bank of the arcuate sulcus (AS) in area F5, and in the anterior bank of the central sulcus (CS) in the hand area of M1. c, d, Schematics of FMA placements also show the FMA numbering for animal Z (right hemisphere) and animal M (left hemisphere), respectively. The dark edge of each FMA indicates the row of longest electrodes (maximum of 7.1 mm). Annotations as in b. In this study, individual arrays are labeled as F5lat (#1), F5med (#2), AIPlat (#3), AIPmed (#4), M1lat (#5), and M1med (#6). Scale: the long edge of FMA is 4 mm. A, anterior; L, lateral; M, medial; P, posterior.

Electrode array locations are depicted in Figure 2, c and d. In both animals, the lateral array in AIP (AIPlat) was located at the end of the intraparietal sulcus at the level of area PF, whereas the medial array (AIPmed) was placed more posteriorly and medially at the level of area PFG (Borra et al., 2008). In area F5, the lateral array (F5lat) was positioned approximately in area F5a (Belmalih et al., 2009; Borra et al., 2010), whereas the medial array (F5med) was located in F5p in animal Z and at the border of F5a and F5p in animal M. Finally, both arrays in M1 (M1lat and M1med) were positioned in the hand area of M1 (anterior bank of the central sulcus at the level of the spur of the arcuate sulcus and medial to it; Rathelot and Strick, 2009).

All surgical procedures were performed under aseptical conditions and general anesthesia (e.g., induction with 10 mg/kg ketamine, i.m., and 0.05 mg/kg atropine, s.c., followed by intubation, 1–2% isoflurane, and analgesia with 0.01 mg/kg buprenorphene, s.c.). Heart and respiration rate, electrocardiogram, oxygen saturation, and body temperature were monitored continuously. Systemic antibiotics and analgesics were administered for several days after each surgery. To prevent brain swelling while the dura was open, the animal was mildly hyperventilated (end-tidal CO₂ <30 mmHg), and mannitol was kept at hand. Animals were allowed to recover for at least 2 weeks before behavioral training or recording experiments recommenced.

Hand kinematics

To record the kinematics of the monkey's hand and arm, we have developed an instrumented glove for small primates, as described previously (Schaffelhofer and Scherberger, 2012). This kinematic tracking device is based on an electromagnetic tracking system (WAVE; Northern Digital) and consists of seven sensor coils that are placed on all fingertips, the back of the hand, and at the lower forearm just proximal to the wrist (Fig. 1a). For calibration purposes, an additional sensor was also temporally placed on top of each metacarpal phalangeal joint (MCP). Using this instrumented glove, the dynamic 3D position of the distal interphalangeal joint (DIP), the proximal interphalangeal joint (PIP), and the MCP position of all fingers were determined, as was the 3D position and orientation of the hand. Furthermore, the wrist sensor provided the orientation of the forearm and hence the 3D position of the elbow. Because the monkey was head fixed, the shoulder position could be assumed constant. This provided a full kinematic description of the arm and hand (including 18 joints and 27 DOFs) with a temporal resolution of 100 Hz. Data acquisition, processing, and visualization were realized in a custom-made Graphical User Interface in MATLAB (MathWorks).

Electromagnetic sensors could be tracked even when visually occluded, because they did not depend on line of sight to a camera. However, they can be influenced by the presence of inductive metals (Raab et al., 1979). Therefore, ferromagnetic materials had to be mostly avoided in the setup, including the turntable, all graspable objects, and the primate chair.

Neural recordings

From the implanted electrode arrays, we recorded spiking activity (single units and multiunits) simultaneously from a total of 192 electrodes in AIP, F5, and M1 (Fig. 2). Neural activity was sampled at a rate of 24 kHz with a resolution of 16 bit and stored to disk together with behavioral data and hand and arm kinematics using a RZ2 Biosignal Processor (Tucker Davis Technologies).

Data analysis

Hand kinematics.

The trajectories of all 18 joints of the moving hand and arm as well as of the fingertips were used to drive a 3D musculoskeletal model (see Fig. 6a) that was scaled to match the primate-specific anatomy (Holzbaur et al., 2005; Schaffelhofer et al., 2014). The model was implemented in OpenSim (Delp et al., 2007) and allowed extracting all hand and arm joint angle positions, which included the following: (1) flexion/extension (MCP, PIP, DIP) and adduction/abduction (MCP) of all fingers; (2) wrist flexion/extension, adduction/abduction, and pronation/supination; (3) elbow flexion; and (4) shoulder elevation, rotation, and adduction/abduction (in total, 27 DOFs).

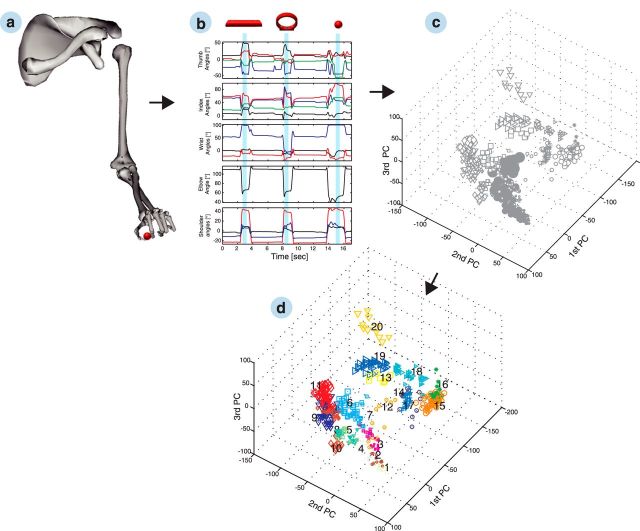
Figure 6.

Grip-type clustering. a, Recorded joint positions of the upper limb were used to drive a 3D musculoskeletal model. Applying the kinematics to the primate-specific model allowed extracting joint angles of the hand and arm (27 DOFs). A selection of features is shown in b. Presented are from top to bottom: thumb and index angles (carpometacarpal adduction/abduction in black, carpometacarpal flexion/extension in red, proximal interphalangeal flexion/extension in blue, and distal interphalangeal flexion/extension in green), wrist angles (deviation in black, flexion/extension in red, and pronation/supination in blue), elbow angle (flexion in black), and shoulder angles (adduction/abduction in black, elevation in red, and rotation in blue). The hold epoch (used for classification) is highlighted in blue for grasping a horizontal bar, ring, and small ball. Subplot c illustrates the joint angles of the hold epoch as principal component (PC) transforms. Each symbol reflects an individual and correctly performed trial within the space of the first three principal components. Different symbols represent different object shapes, whereas their size reflects the object size. Applying hierarchical clustering to the multidimensional kinematic data allowed us to recluster the trials based on the applied grip type (d). The 20 most different hand configurations of the example session are numbered consecutively, and trials from the same grip-type class share the same color.

Spike sorting.

All spike sorting relevant for analysis was performed offline. First, we applied WaveClus (Quiroga et al., 2004) for automatic sorting and then used the OfflineSorter (Plexon) for subsequent manual resorting. This procedure provided an objective and automatized classification of neurons and an additional evaluation of cluster quality with respect to signal stability (e.g., drift) and interspike interval histograms.

Single-unit and population activity.

Firing rate histograms were created to present tuning attributes of example neurons from AIP, F5, and M1 (Fig. 3a,d,g). For this, the spike rates were visualized by replacing each spike with a Gaussian kernel function (σ = 50 ms) that were then averaged across all spikes and trials (Baumann et al., 2009).

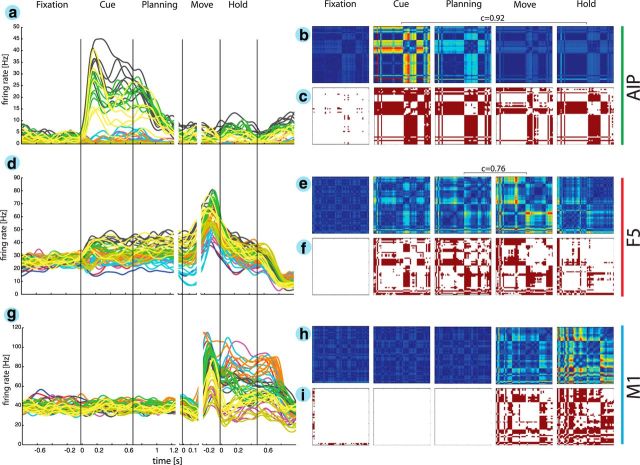
Figure 3.

Neural coding of grasping actions. a, d, g, Firing rate histograms are shown for three simultaneously recorded example neurons from areas AIP, F5, and M1, respectively. Each line represents the average firing rate for a specific grasping condition (i.e., 50 objects) versus time. The color code matches the object shape as in Figure 1b. b, e, h, Cross-modulation depth plots reflect the relative difference in firing rate between all pairs of grasping conditions (50 × 50 pairs) for all five epochs. Firing rates were normalized relative to the maximum MD found across all epochs. Pixels toward red represent pairs with maximum MD, whereas pixels toward blue represent pairs without difference in firing rate. c, f, i, Furthermore, a multicomparison analysis revealed significant differences (in red) between condition pairs. The order of columns/rows for cross-modulation depth- and multicomparison plots is the same as in Figure 5a. a–c, The AIP neuron showed the highest MD during the cue epoch and an additional bump during the hold epoch. d–f, The example F5 neuron demonstrated a high MD in the planning epoch and an additional increase during motor execution. g–i, The M1 motor neuron showed no significant coding during motor preparation (i.e., cue and planning) but became highly active during motor execution (i.e., movement and hold). Horizontal brackets indicate significant correlation coefficient c of MD maps between epochs.

Furthermore, we computed the cross-modulation depth of individual neurons (Fig. 3b,e,h). The modulation depth (MD) between two conditions (e.g., x and y) was defined as the absolute difference of the averaged firing rate (across all n trials) of the neural activity f between condition x and y:

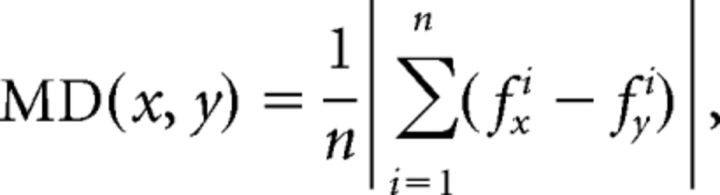The MD between all condition pairs was computed, and the resulting matrix was plotted as a color map for individual task epochs. To obtain information about the significance of the MD of individual condition pairs, we performed a multicomparison test across all task conditions (ANOVA and post hoc Tukey–Kramer criterion, p < 0.01; MATLAB functions anova1 and multcompare; Fig. 3c,f,i). Furthermore, we defined the coefficient of separability (CS) for each neuron and task epoch as the fraction of significant condition pairs with respect to all pairs.

Finally, the large number of conditions allowed comparing the encoding properties of individual neurons between different task epochs. For this, we computed the Pearson's correlation coefficient between the MD maps.

For visualizing the population activity during the task, we computed for each neuron a sliding ANOVA (p = 0.01; time steps, 20 ms) across the six conditions of the mixed turntable. The fraction of significantly modulated neurons at each time step was then calculated separately for each area and recording array (Fig. 4).

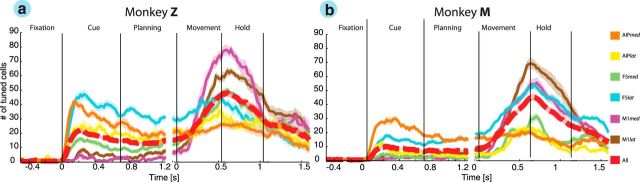
Figure 4.

Population activity. Individual curves describe the percentage of tuned units versus time separately for monkey Z (a) and monkey M (b) for recording arrays AIPmed, AIPlat, F5med, F5lat, M1med, and M1lat. The color code for each array is consistent throughout text.

Decoding.

For decoding, our goal was to predict the presented object or the intended grip type from the recorded neuronal activity as accurate as possible. For this, the decoding classes (or categories) were defined as the presented objects (50 classes) or the grips used for grasping these objects (20 classes; see below, Grip-type classification). For each decoding procedure, only simultaneously recorded spiking activity from single units and multiunits were included. This way, real-time decoding could be simulated as closely as possible. The mean firing rate of all single units and multiunits were computed for the specific task epochs and used as the input parameters for the classifier.

We used a naive Bayesian classifier for decoding that has been shown to reach close to optimal performance within a large family of classifiers for this kind of data (Scherberger et al., 2005; Subasi et al., 2010; Townsend et al., 2011). (Naively) assuming statistical independence between the firing rates f_i of a set of neurons (i = 1,…, n), the likelihood function L(c) can be computed as L(c) = ${\displaystyle {\prod }_{i=1}^{N}p\left(c|f_i\right)}$, where p(c|f_i) denotes the probability of observing condition c for a given firing rate f_i of neuron i. Using the following Bayes equation,

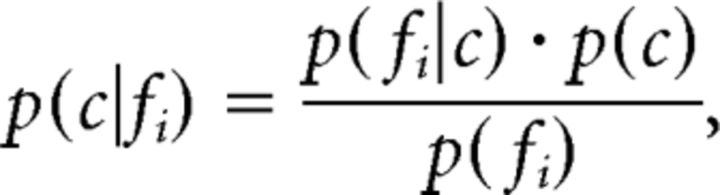this probability can be expressed with p(f_i|c), which denotes the probability of observing the firing rate f_i, given condition c. Furthermore, the uniformly distributed term p(c) and the term p(f_i), which is independent of c, can be summed as k_i, which reduces the equation to p(c|f_i) = k_i × p(f_i|c). Because the factor k_i is constant across all conditions, the likelihood function can be further reduced to

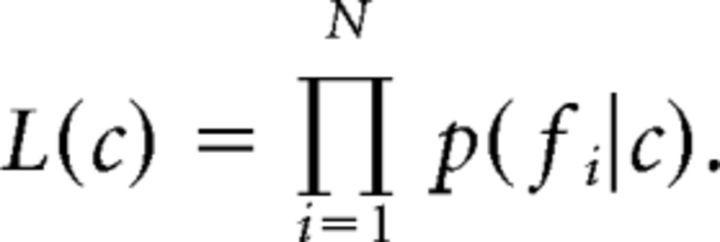The condition showing the highest likelihood for the observed firing rates was then selected as the decoded condition:

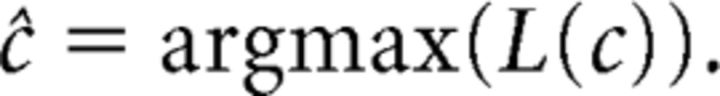To train the decoder, the probability distributions p(f_i|c), which were estimated from the mean firing rates observed in the training data under the assumption of a Poisson distribution, had to be determined for each condition. For testing decoding performance, we applied a leave-one-out cross-validation, which ensured that datasets used for training were not used for testing.

Neuron-drop analysis.

To measure the decoding accuracy as a function of neurons used for decoding, we performed a neuron-dropping analysis. This simple algorithm started by training the decoder with a randomly selected neuron. Then, the number of cells included for decoding was increased in steps of 1 until all available neurons were included. At each step u, the random selection of u cells used for decoding was repeated 100 times. The neuron-drop analysis was applied separately for each microelectrode array and allowed a direct and objective comparison between cortical areas and subareas. Paired t tests (p < 0.01) were applied for statistical comparison between areas and task epochs.

Grip-type classification.

Electrophysiological studies in the macaque hand areas AIP and F5 revealed not only motor discharges but also responses to the visual representation of objects, and it was assumed that such visual cells code attributes of objects, such as shape, size, and/or orientation (Murata et al., 1997, 2000). To demonstrate that hand configurations (i.e., hand shape) can be decoded independently from such object information, we classified the performed trials based on the grips applied to the many objects. This regrouping of trials according to grip type allowed an object-independent decoding and furthermore could help reduce redundancies among different objects, e.g., for objects of different shape that were grasped by the same grip.

For the classification of grip types, we recorded finger, hand, and arm kinematics in each recording session simultaneously with cortical recordings. The hold epoch revealed the highest variation of grip type under the most stable kinematic conditions. Therefore, we selected the hold epoch to extract joint angles for grip-type classification.

To find the similarities or differences in the classification of grip types across performed trials and kinematic dimensions (i.e., >500 trials and 27 DOFs), we computed the Euclidean distance between each pair of trials (MATLAB function pdist). Based on this distance measure, a hierarchical cluster tree was created that described the proximity of trials to each other (MATLAB function linkage, criterion “ward”). As a final step, we were searching for natural groupings within the dataset (number of clusters). Because of the large number of trials and objects used, the kinematic space represented a natural and nondiscrete distribution of hand configurations. As a result, the dataset did not reveal an optimal number of clusters that showed a maximum separation (silhouette test). Therefore, we set the number of clusters heuristically to a value of 20, hence demonstrating a good compromise between quantity of grip types and quality of kinematic separability (see Fig. 6d). Furthermore, the constant number of clusters across multiple recordings allowed a more objective comparison between the decoding results of sessions and animals.

Offline robotic control

To illustrate the possible translation of the primate arm and hand model with its 27 DOFs in a lower-dimensional robot arm and hand (here 16 DOFs), we used a 7 DOFs robot arm (WAM Arm; Barrett Technology) and a five-fingered robotic hand (SCHUNK). To translate the primate model on the robot arm and hand, we solved the inverse kinematic problem for the arm and used linear transforms for the fingers. Although the robot arm had equal DOFs as the primate arm, its rotation axes (3 DOFs for shoulder, 3 DOFs for wrist, and 1 DOF for elbow) differed from the primate model. We solved this inverse kinematic problem (Paul, 1982) by matching the robot posture to the primate upper arm orientation with respect to the shoulder and to the primate hand orientation with respect to the forearm.

The five-fingered robotic hand had 9 actuated DOFs: (1) thumb abduction; (2) combined carpometacarpal joint, MCP, and DIP flexion of thumb; (3) index MCP flexion; (4) combined PIP and DIP flexion of the index finger; (5) middle MCP flexion; (6) combined PIP and DIP flexion of the middle finger; (7) combined MCP, PIP, and DIP flexion of the ring finger; (8) combined MCP, PIP, and DIP flexion of the little finger; and (9) combined spread of digits. Each actuated DOF of the robot hand was linearly coupled to the corresponding DOF of the primate hand, such that the movement range of the primate DOF was mapped linearly on the robotic movement range.

Results

The data in this study present in total 20 recording sessions from two macaque monkeys (10 recordings per monkey). Both animals were implanted with six 32-channel FMAs in the hand-grasping areas AIP, F5, and M1 (two FMAs per area; 192 channels in total). This facilitated simultaneous recording from 355 ± 20 and 202 ± 7 (mean ± SD) single units and multiunits in monkeys M and Z, respectively. All implanted arrays were functional and allowed recording of stable neuronal populations. Across areas, the acquired single units and multiunits were distributed as follows: 25.2% for AIP, 32.3% for F5, and 42.5% for M1 in animal M; and 29.2% for AIP, 37.3% for F5, and 33.5% for M1 in animal Z.

Simultaneous to the neural recordings, we tracked finger, hand, and arm movements across all recording sessions using an instrumented glove (Schaffelhofer and Scherberger, 2012) and fit a musculoskeletal model of the primate hand and arm that consisted of 27 DOFs at 18 joints (Schaffelhofer et al., 2014). From these movement kinematics, we then classified and decoded a wide range of hand configurations that the animal applied to grasp the 50 heterogeneous objects of our task.

Neuron tuning properties

Neurons recorded in this study presented attributes consistent with previous studies of area AIP (Murata et al., 2000; Baumann et al., 2009), F5 (Rizzolatti et al., 1988; Raos et al., 2006; Fluet et al., 2010), and the hand area of M1 (Schieber, 1991; Schieber and Hibbard, 1993; Vargas-Irwin et al., 2010).

In AIP, neurons showed a strong response and tuning during the cue epoch of the task, when the objects were illuminated. These attributes are illustrated by the example neuron in Figure 3a. It demonstrated a rapid increase in firing rate after cue presentation and a high selectivity for grasping conditions (i.e., for specific objects). Visually presenting the horizontal cylinders and the bar objects resulted in the highest response. These object groups shared similar visual attributes (i.e., being long and horizontal) but also required similar kinds of grips (enclosure of big objects with flexed digits and wide aperture between the index finger and thumb). Figure 3b visualizes the relative differences in firing rate (i.e., the MD) between all pairs of conditions (i.e., objects) in the considered task epochs (see Materials and Methods). For this neuron, MD was maximal (34.4 Hz) in the cue epoch. Neural tuning was consistent throughout the task, as indicated by the high correlation coefficient between the MD matrix of the cue and hold epochs (c = 0.92). Furthermore, we performed a multicomparison analysis within each task epoch to identify those task condition (object) pairs for which the neural firing rate was significantly different (Tukey–Kramer criterion, p < 0.01; see Materials and Methods). Pairs of conditions with significant differences are shown in red in Figure 3c. Overall, 57.5 and 51.83% of all condition pairs had significantly different firing rates in the cue and planning epochs, respectively (CS; see Materials and Methods), thus demonstrating a high object selectivity of this AIP neuron.

Figure 3d illustrates an example neuron of F5. It was activated during cue presentation (CS, 33.95%), reached its maximum selectivity (Fig. 3f) in the planning epoch (CS, 42.9%), and was followed by a strong response in the movement epoch (CS, 42.2%). Maximum MD was observed during movement execution (39.8 Hz; Fig. 3f). Furthermore, not only was the CS similar during motor preparation and execution but so was neural tuning, as demonstrated by the high correlation between the MD maps of the planning and movement epochs (c = 0.76).

Not surprisingly, M1 neurons demonstrated the strongest response during movement execution (Fig. 3g). None of the condition pairs were significantly tuned before or during the preparation epoch (Fig. 3h). However, in the movement and hold epochs, when the monkey grasped and held the objects, 38.2 and 54.8% of the condition pairs were significantly different (CS; Fig. 3i). The illustrated M1 neuron showed a maximum MD of 72.3 Hz during the hold epoch (Fig. 3h).

All example neurons showed a high selectivity during motor execution, especially neurons recorded from M1 and F5. They demonstrated a surprisingly high differentiation between a wide range of grip-type conditions. In AIP and F5, these attributes were also represented during the motor preparation epochs (cue and planning). The multicomparison analysis and the correlation of MD matrices between planning and motor epochs highlight that these neurons represent movement well before execution, which makes them potentially suitable for the decoding of intended hand configurations, i.e., well before movement execution.

Individual neurons could demonstrate tuning already in the fixation epoch. This effect is explained by the blockwise task design required for presenting the large number of conditions (i.e., grips on handle and individual turntables). In Figure 3g, the example neuron showed an increased firing rate when the handle was mounted in front of the animal; therefore, the presented cell could differentiate between the handle and the turntable task (Fig. 3i). However, none of the neurons showed significant tuning in the fixation epoch within the group of the handle or the turntables, which demonstrates the nonpredictability of individual conditions within each block of trials.

The attributes of single units could be confirmed at the population level (Fig. 4). Similar to the example cell in AIP, the population of AIP units showed a strong response to the presentation of objects. However, we found important differences between AIPlat and AIPmed. Whereas AIPmed showed its strongest response in the cue epoch with a fraction of 42% (monkey Z) and 30% of significantly tuned units (monkey M), the population from AIPlat had a peak activation during motor execution with a fraction of 36% (animal Z) and 23% of tuned units (animal M, sliding window ANOVA; p < 0.01). These consistent results from both animals suggest a more visual role of AIPmed, whereas AIPlat might be rather motor related (Fig. 4).

Similar to AIP, we also found substantial differences between the medial and lateral arrays of F5. In both animals, F5lat showed a higher fraction of tuned units during the planning epoch than the F5med population. However, in contrast to AIPmed that showed its strongest contribution during the cue epoch, F5lat demonstrated an additional increase of tuned units during movement execution. Although F5med had a weaker planning activity than F5lat, its contribution to our task was essential, as indicated by the fraction of 51% (animal Z) and 32% of tuned cells (animal M) during movement execution.

In M1, the main population response occurred during the movement epoch with a fraction of 78% of tuned units in M1med of monkey Z and of 69% in M1lat of monkey M, whereas only a small fraction of units represented planning activity. Also, M1 motor responses showed their peak activity aligned to the beginning of the hold epoch, which further supports the important role of M1 for hand-movement generation. Together, the F5 and AIP populations both showed strong planning activity at the single-unit level, which underscores the potential significance of these areas for decoding applications.

Object-based decoding

Previous studies have investigated higher cortical regions, such as area AIP and/or F5, to decode grip types before movement execution (Subasi et al., 2010; Carpaneto et al., 2011, 2012; Townsend et al., 2011). However, these studies focused exclusively on large differences in hand configurations, such as precision and power grips, applied to handles of different orientations (up to 10 conditions) or when grasping objects of highly different shape. In contrast, here we investigated the possibility of decoding fine differences of grips performed on a large number of objects. In total, the monkeys grasped ∼50 objects that caused a high variability of hand shapes. Note that small differences in object size, while sharing the same object shape, elicited fractional difference in hand shape (see below, Grip type-based decoding). Similar to previous studies (Baumann et al., 2009; Fluet et al., 2010; Townsend et al., 2011; Lehmann and Scherberger, 2013), we focused on the planning and hold epochs that were performed in darkness. This way, visual responses were avoided, whereas preparatory and motor signals became disambiguated.

Decoding results of one example session are presented in Figure 5. Using maximum likelihood decoding with cross-validation (see Materials and Methods), we found a high correlation between the real conditions and the decoded conditions in both the planning and hold epochs, as illustrated in the confusion matrices (Fig. 5a). Error trials did not spread across all conditions but were most likely attributed to neighboring condition classes (e.g., cylinders of 30 mm in diameter could be confused with cylinders of 35 mm diameter). Objects were arranged in the matrix according to their similarity (shape and size). These effects were further visualized in Figure 5b, in which success and error rates were plotted on a logarithmic scale against distance from the confusion matrix diagonal. For the recording session displayed in Figure 5a, 53.0 and 62.4% of all trials were assigned correctly during the planning and hold epochs, respectively. However, the majority of error trials (58 and 64% for planning and hold, respectively) were assigned to a class that was neighboring the correct (true) class. To evaluate the total error distribution, we additionally averaged the confusion matrices across all sessions from both animals. In this population, the majority of trials were correctly decoded with 51.3 and 60.7% during the planning and hold epochs, respectively, similar to the presented example session (Fig. 5a). Again, most of the errors were assigned to an adjacent class. Of all errors, 59% (planning) and 62% (hold) were classified incorrectly to a neighboring class. Therefore, allowing the assignment to such an adjacent class would boost the decoding performance to 80.2 and 85.2% (planning and hold, respectively), whereas chance level would increase only to 6% (3 of 50 conditions). These “relaxed” accuracies are highlighted for the example session in Figure 5b (green bars).

Figure 5.

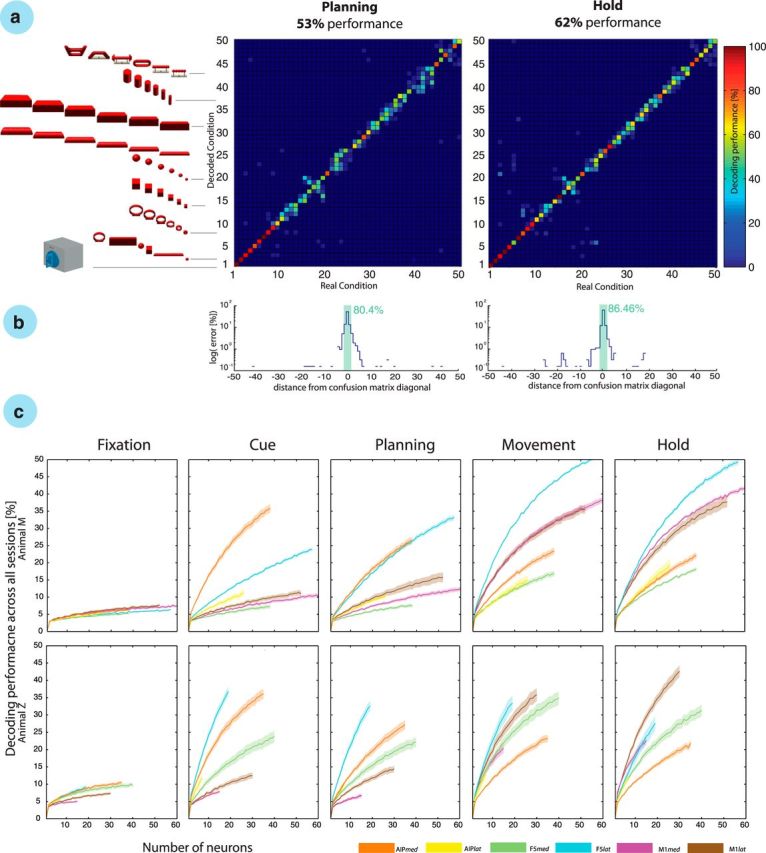
Object-based decoding. a, The confusion matrix shows the decoding results from the planning and hold epochs of a single recording session. Each decoding condition is illustrated by the 3D object grasped by the monkey. From 1 to 50: 1–2, precision and power grip on handle; 3–8, mixed turntable; 9–14, rings; 15–20, cubes; 21–26, balls; 27–32, horizontal cylinders; 33–38, bars; 39–44, vertical cylinders; and 45–50, abstract forms. b, Error distribution in the confusion matrix as a function of distance to the matrix diagonal; note the logarithmic scale for the planning and motor epochs. Green bar sums the percentage of trials with correct and distance-1 errors. c, Neuron-drop analysis for all task epochs and both animals across all recording sessions. Decoding performance is plotted versus the number of randomly selected neurons for each of the implanted microelectrode arrays for each epoch and animal. Solid lines show the mean decoding performance for specific arrays, whereas shades indicate SEM across 10 sessions in each animal. Lines stop at the minimal number of recorded neurons across all sessions.

Across the entire dataset of 10 decoding sessions per animal, the 50 object conditions could be decoded from the planning epoch with an accuracy of 48.7 ± 3.6 and 51.9 ± 3.4% (mean ± SD) in animals M and Z, respectively. This performance was 23.9× and 26× above chance (2%). During motor execution (i.e., from the hold epoch), the average decoding accuracy was even larger: 62.9 ± 3.6 and 61.4 ± 4.1% (monkeys M and Z, respectively), corresponding to 31.5× and 30.7× above chance (2%). This means that decoding accuracy in the hold epoch was on average 14.2 and 9.5 percentage points higher than in the planning epoch (animals M and Z, respectively). This improvement was significant (p < 0.001, two-way ANOVA) in both animals.

Furthermore, we explored the functional differences of the various cortical areas and recording sites separately in each electrode array: (1) F5lat; (2) F5med; (3) AIPlat; (4) AIPmed; (5) M1lat; and (6) M1med (array numbering as in Fig. 2). To make the analysis fair, we applied a neuron-drop procedure that evaluated the decoding performance as a function of the number of randomly selected neurons included in the analysis (Fig. 5c). This analysis allowed the following key observations: in the motor preparation epochs (i.e., cue and planning epochs), AIPmed and F5lat achieved the best decoding results in both animals, which was reflected in the steepest performance increase as a function of number of neurons included for decoding. Therefore, the information content on these arrays was significantly higher than on the supplemental arrays (AIPlat and F5med; t test, p < 0.01). Please note that no statistical comparison was possible for the array AIPlat in animal Z because of the small number of neurons detected. However, mean values were still smaller than in AIPmed, as shown in Figure 5c (animal Z, cue). In animal M, the decoding performance of F5med was even lower than in the M1 arrays. This was surprising because the recording quality on this array was quite high.

Additional interesting observations were made for the M1 arrays. First, both arrays achieved performances above chance already during the planning epoch, indicating the presence of preparatory activity in M1. However, in both animals, the more lateral array (M1lat) provided significantly better decoding accuracies during motor preparation than its medial counterpart (M1med). However, surprisingly, we found that the F5lat array performed better than both M1 arrays not only during motor planning but also during motor execution (movement epoch). In the hold epoch M1lat, M1med, and F5lat achieved best accuracies, but with different order in both animals.

When comparing the decoding performances across task epochs, we observed a strong role of AIPmed in motor preparation (cue and planning epochs), whereas decoding performance decreased strongly during motor execution (movement and holding epochs). In contrast, M1 showed a continuous increase in decoding performance over time, with best performance during the hold epoch, as expected.

Together, higher motor cortical areas in premotor and parietal cortices could be used to decode a wide range of grasping actions in 50 different object conditions. Decoding results from these areas were almost as high during motor preparation as during motor execution. Conversely, decoding from M1 was strongest during grasp execution. Furthermore, we found strong differences between the subareas of F5 and AIP. Recording sides F5lat and AIPmed demonstrated most informative planning signals consistently in both animals. In particular, F5lat was best suited for decoding during both motor preparation and execution. Therefore, this area might be a good target for a hybrid brain–computer interface that is capable of exploiting both grasp planning and movement execution.

Grip-type decoding

One major goal of this study was to decode motor signals rather than visual object attributes. For this reason, we focused on the planning and hold epochs of the task that were performed in darkness. Furthermore and importantly, we also decoded the grip types applied to the objects based on the kinematic measures from the instrumented glove. This way, trials were assigned to specific grip types rather than individual objects.

For the classification of grip types, we recorded the 3D trajectories of 18 joint locations of the hand and arm with an electromagnetic tracking glove (Fig. 1a; Schaffelhofer and Scherberger, 2012) in parallel to the neural data. This technology allowed us to record the movements continuously, even when fingers were hidden behind an object or obstacle. Furthermore, we used the recorded marker trajectories to drive a primate-specific musculoskeletal model (Fig. 6a; Schaffelhofer et al., 2014). The model allowed extracting 27 DOFs of the primate's upper extremity (Fig. 6b) that were subsequently used to classify the applied grips. For this analysis, we focused on the hold epoch, because it showed the highest variability of hand shapes under the most stable conditions. Figure 6c presents the hand configurations of the hold epoch as principal component transforms with each of the correctly performed trials represented as a single marker in principal component analysis (PCA) space (marker symbols as in Fig. 1b, with marker size reflecting object size).

Using hierarchical cluster analysis, we then identified the 20 most different grip types from the multidimensional hand configuration dataset (27 DOFs) of holding the 50 objects 10 times (see Materials and Methods). The resulting separable grip-type clusters are differentiated by color in Figure 6d and demonstrate highly variable hand configurations.

Furthermore, the hand configuration that each cluster represents is shown in Figure 7a. Apparently, the high quality of the hand-tracking data allowed differentiating quite small grip differences. For example, grip types 1 and 2 were very similar in shape. However, they showed a minor but relevant difference: grip type 1 was applied to the small balls, which were the smallest objects of the set, whereas grip type 2 was applied to the small rings and required a slightly larger thumb–index aperture. Grips 3–6 represented whole-hand grips of different apertures, requiring one (i.e., grip 3) to four (i.e., grip 6) digits. Grasping the large balls (i.e., grip 7) additionally required support from the little finger and a strong spread to enclose these large round objects. Grips 8–11 were applied to the long horizontal objects including bars and horizontal cylinders that needed variable apertures, not only of the digits 2–5 but also of the thumb. For example, grip 8 was applied to a cylinder of smallest diameter, whereas grip 11 was applied to the thickest bar. Also, there was a high similarity between the classes 9 and 10. Both required similar apertures of thumb and index, but the proximal and distal phalanges had to be more flexed for enclosing a cylinder (i.e., grip 10) than for the bars that required more extended fingers. A special hand configuration was applied to the average-sized rings. In this case, the monkey was using a hook grip with the index finger to lift the object (i.e., grip 12). Grips 13–20 required a variable amount of wrist rotation (Fig. 6d, 1st PC). Minimal wrist rotation was applied when grasping the large cubes (i.e., grip 13), whereas the wrist was rotated to almost 180° when the big cylinders were lifted from below (i.e., grip 20). Furthermore, grips 16 and 17 reflected precision and power grips applied to the handle. The index finger and thumb were used to perform the precision grip (grip 17), whereas all digits were used to enclose and pull the handle (grip 16). Finally, classes 18 and 19 reflect the grips performed onto the vertical cylinders, which were similar to grips 8 and 10 for the horizontal cylinders, but with the wrist supinated by ∼90°.

Figure 7.

Grip-type decoding. a, Hand configurations 1–20 and confusion matrices expressing decoding performance during the planning and hold epochs, respectively, of one recording session. Grip types were decoded using simultaneously recorded neurons from areas AIP, F5, and M1. Hand configurations and grip-type numbers as in Figure 6. b, c, Grip-type decoding performances are summarized across all recording sessions for each implanted microelectrode array during the planning and hold epochs (mean ± SD). Note that array-specific decoding results were limited to a maximum of 30 neurons to allow a fair comparison of arrays. Color code as in Figure 5c.

Categorizing the trials based on the performed grips instead of the presented objects not only improved the separation between visual and motor features but also reduced redundancies within objects. For example, different objects that required the same or similar grips could be merged into the same cluster. Training the decoder on these hand–configuration classes readily allowed decoding these 20 grip types highly accurately. Figure 7a shows an example session in which hand configurations were decoded with an accuracy of 86 and 92% from the planning and hold epochs, respectively.

The independence of grip types from visual features was apparent particularly in two specific grip-type classes: grip types 10 and 20 were applied to the same object, the big cylinder. The monkey decided to grasp this object in some instances from above with the hand pronated or in some trials from below with the hand in supination. Another example is the pair of grips 16 and 17. Again, these grips were applied to the same object (the handle), but these grip types could be predicted with high accuracy already during the planning epoch (motor preparation). Both examples demonstrated that the decoder can differentiate these grips, although they were performed on the same objects, thereby demonstrating object-independent decoding. However, a complete independent classification of objects and grips is not possible in general, because the shape of the hand is highly linked to the shape of the object being grasped (Fig. 6d). Therefore, individual grip-type classes often reflected particular objects.

Similar to object decoding, the results of grip-type decoding across all recording session (Fig. 7b) demonstrated that decoding accuracy was highest when data from all cortical areas were considered, during both the planning (73 ± 6.2 and 74.7 ± 3.5% for animals Z and M, respectively) and hold (82.15 ± 5.0 and 89.2 ± 1.7% for animals Z and M, respectively) epochs. Again, AIPmed and F5lat contributed most during the planning epoch, whereas M1lat and M1med predicted in both animals the grip types best during movement execution. However, across all electrode arrays, F5lat achieved the highest performance when considering both planning and execution epoch.

These results demonstrate that higher cortical areas can indeed be used to decode complex hand configurations already during motor planning and with only slightly lower decoding performance than in the motor execution phase. This is impressive because grip types were classified during the hold epoch and should therefore reflect the decoded hand configurations best. Nevertheless, the contribution of AIP and F5 during motor preparation led to a decoding performance that was on average only 8.6 and 14.5 percentage points smaller than during the hold epoch (animals Z and M, respectively).

Spike sorting affects decoding performance

For future real-time applications, the instantaneous processing of action potentials in large populations, i.e., spike sorting, might be difficult. The classification of action potentials to individual neurons can cause extensive computations, such as principal component transformation or template-matching algorithms across a large number of channels. Previous studies have demonstrated minimal loss of decoding performance when advanced spike-sorting methods were replaced by simple thresholding techniques (Gilja et al., 2011) or when spikes recorded from the same channel were merged to a single multiunit (Gilja et al., 2012; Hochberg et al., 2012; Collinger et al., 2013). These procedures limit the number of available units to the number of electrodes and mostly avoid the computational cost of spike sorting.

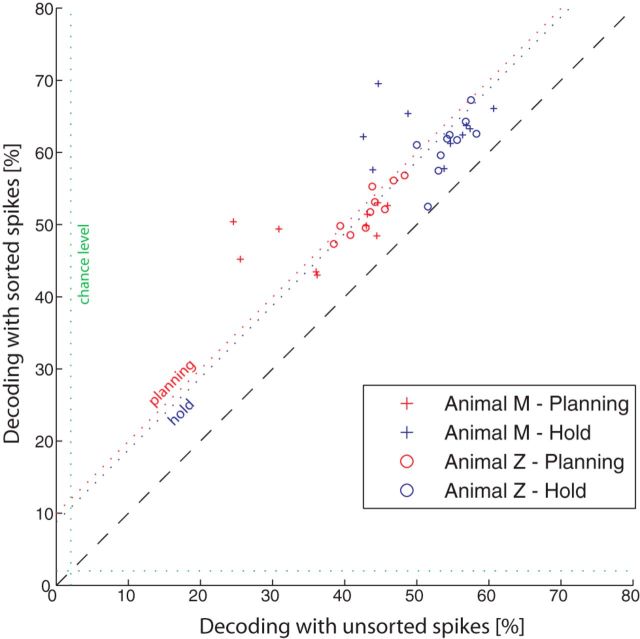
When comparing both methods in our decoding analysis, we found, as expected, better decoding accuracies when applying spike sorting instead of simple thresholds (Fig. 8): decoding accuracy increased on average by 9.9 and 8.8 percentage points during the planning and hold epochs, respectively, across all sessions and animals. Although these differences were significant (ANOVA, p < 0.01), the clusters were still located close to the unity line in the scatter plot, suggesting that simple thresholding could be used to decode a wide range of conditions with a negative effect of decoding accuracy of <10 percentage points.

Figure 8.

Spike sorting affects decoding accuracy. Scatter plot comparing the decoding performance using sorted (y-axis) and unsorted (x-axis) spiking activity. Symbols indicate decoding results during the planning (red) and hold (blue) epochs for both animals.

Offline robotic control

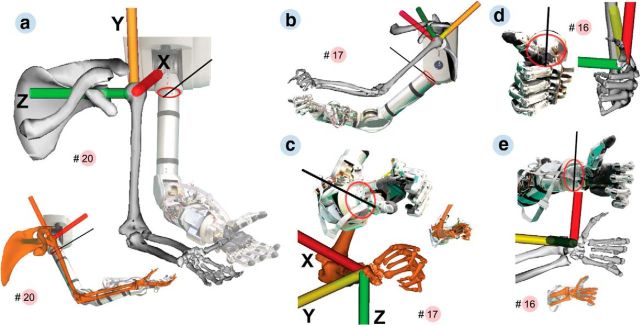
Finally, for future robotic applications, we also tested the translation of the decoded hand configurations into postures of an anthropomorphic arm and hand (Fig. 9). Because of noncongruent architectures and common under-actuation of currently available robotic hands (one motor actuates several DOFs), such transformations are often nontrivial. Using a simple transformation method (see Materials and Methods), we could demonstrate the translation of the 20 grip-type classes (defined by 27 DOFs) in a 16 DOFs robotic arm and hand (Barrett Technology arm, 7 DOFs; SCHUNK hand, 9 DOFs; Fig. 9). Two problems were encountered in translating the grip. One was that the thumb abduction of the robot rotated about a different axis than the primate thumb (Fig. 9a, inset, b). Our approach was to visually match the ranges in which both thumbs coincided in orientation and restricting the robot movement to this range. The second problem concerned the execution of the ring and little fingers, because both robotic fingers were actuated by only 1 DOF. This was solved by averaging the little and ring finger joint angles of the primate model (Fig. 9c–e). Together, although this robotic illustration was performed offline and rather qualitatively, it nevertheless demonstrates the feasibility of the primate hand model for future neuroprosthetic applications.

Figure 9.

Execution of arm pose and grip type by a low-dimensional prosthetic device. Execution was compared with the primate skeletal model. To infer the frame of reference of the device from photographs, an oval (red) was drawn matching the circumference of its upper arm or wrist. The direction of the robot axis was estimated with a secant (black) cutting the oval in two equal parts and touching a physical marker painted on the robot. The model was manually aligned to set the x-axis of the skeletal model (red) parallel to the secant and the y-axis of the skeletal model (yellow) parallel to the upper or lower arm of the robot. a, Reproduction of grip 20 (see Fig. 7) by the prosthetic device. The device can enact the hand and arm pose as rendered by the skeletal model. Inset, Medial view. b, c, Arm and hand during grip 17. Digits 2–5 represent the grip well except at the distal phalanges that have no separate control on the robot. Inset, Superposition of both grips. d, e, Frontal and lateral views of grip 16 (as in Fig. 7). The grip is well represented except for the distal phalange angles.

Discussion

The extensive experimental task design has let us record kinematics of the primate hand together with neural activity of the cortical areas AIP, F5, and M1 that are known to be involved in hand-movement generation. From the planning and execution signals of these areas, we demonstrated accurate decoding of a wide range of hand configurations that animals used to grasp 50 different objects.

Object-based decoding

As a first approach, we evaluated the decoding capabilities of AIP, F5, and M1 on the full set of 50 objects. This number of conditions was larger than in previous studies (Vargas-Irwin et al., 2010; Carpaneto et al., 2011, 2012; Aggarwal et al., 2013) and caused a high variability of hand shapes, ranging from precision to power grips, as well as many different grasp apertures (Fig. 6d). Grasp-planning areas AIP and F5 were capable of resolving the many grip-type conditions even during movement preparation. Decoding performances during the planning phase were only moderately lower (<15%) than in the movement epoch. Selective responses at the population level (Fig. 4) and distinct modulations of individual neurons (Fig. 3) are able to explain the planning quality of the AIP and F5 population.

Although the decoding performance was on average ∼30 times larger than chance (execution epoch), the actual correlation between real and decoded conditions was even higher. Most of the decoding errors were made to adjacent objects of similar shape and size (Fig. 5). This closeness of grip conditions was intended: in contrast to previous studies that classified a few vastly different grip types (Townsend et al., 2011; Carpaneto et al., 2012), we have introduced object similarities to evaluate the nature of the neural signals at the various recording sites.

Training the Bayesian classifier separately with neuronal ensembles from each individual electrode array revealed significant differences across the recorded populations. In both animals, the arrays F5lat and AIPmed carried significantly more information about the upcoming grip than their complementary array in the same area (F5med and AIPlat). Interestingly, we also found differences in terms of planning activity between the two M1 arrays. M1lat, located at the level of the principle sulcus, achieved higher decoding performances during grasp planning than M1med. However, these effects were marginal compared with the activity during movement execution, when the majority of neurons at both sites (M1lat and M1med) showed strong selective responses (Fig. 4), in line with the known direct cortico-motoneuronal connections of M1 to the distal limb musculature (Rathelot and Strick, 2009). These results highlight clearly the importance of M1 for hand-movement control and its suitability for potential neuroprosthetic applications with larger number of objects.

Grip type-based decoding

Areas AIP and F5 are part of the frontoparietal network that is highly relevant for transforming visual attributes of objects into motor commands for grasping (Jeannerod et al., 1995; Luppino et al., 1999; Rizzolatti and Luppino, 2001; Brochier and Umiltà, 2007). In both areas, preparatory neuronal activities have been reported that reflected context-specific object information, as well as 2D and 3D object features (Murata et al., 2000; Raos et al., 2006; Baumann et al., 2009; Fluet et al., 2010; Theys et al., 2012a; Theys et al., 2012b; Romero et al., 2014). In agreement with these findings, neurons from AIP and F5 responded selectively to the presentation of various objects (Fig. 4).

To demonstrate the capability to decode motor plans rather than visual attributes, we evaluated the preparation activity during the planning epoch when animals were in complete darkness. Furthermore, we classified neural activity based on the applied grip type rather than the observed object. For this, we tracked finger, hand, and arm movements with an instrumented glove equipped with electromagnetic sensors (Schaffelhofer and Scherberger, 2012). From the 3D marker trajectories, we then extracted the joint angles in 27 DOFs and classified them into 20 grip-type classes. This classification method not only created classes based on the applied grip but also reduced redundancies among conditions, because some objects were grasped with the same grip. We have selected a relatively high number of grip types to test the limits of the decoder and signals. However, a lower number of hand configurations would be sufficient in daily life and could potentially increase the decoding performance (Bullock et al., 2013).

The rather good performance for these grip-type conditions demonstrated clearly, to our knowledge for the first time, that a large number of hand configurations can be decoded precisely from both motor planning and motor execution signals: whereas AIPmed and F5lat contributed strongest during movement preparation, M1 showed the best performance during object grasping.

Because animals were allowed to grasp the objects intuitively, some objects, such as the horizontal cylinders, were sometimes grasped with alternative grips (e.g., with pronated vs supinated hand). Although the object attributes were identical in such cases, we were able to classify the correct grip, therefore demonstrating the decoding of a motor plan rather than objects.

However, a strict separation between visual and motor attributes is generally not possible. This conclusion is supported by the PCA that demonstrated a clear link between object shape and the applied grip type (Fig. 6d). This statement is relevant for decoding applications and for our general understanding of grasp coding in AIP and F5. Clearly, the simple neuronal responses and decoding analysis presented here cannot reveal the real nature of the neural signals in terms of their object or motor representations. Because either visual object features or the intended motor plan could generate the observed object selectivity, additional investigations of the neural state space are necessary to address these questions.

Implications for neuroprosthetics

Previous work has presented striking examples of neural interfaces for the control of arm prosthetics. However, most of these studies did not consider dexterous control of an anthropomorphic hand. Instead, they implemented 1D controls for simple grippers that essentially could be opened and closed (Velliste et al., 2008). Whereas hand orientation was not or was only manually controlled in the past (Hochberg et al., 2012), a recent study achieved an additional neural control of the wrist (Collinger et al., 2013). Although some offline studies demonstrated a continuous reconstruction of finger and hand movements (Vargas-Irwin et al., 2010; Bansal et al., 2012; Aggarwal et al., 2013), none of them demonstrated the capability for closed-loop applications, because they were decoded in parallel to the actual movement. Therefore, the neural control of the many DOFs of the hand under visual guidance remains the major challenge. Accessing higher cortical areas that reflect motor intentions rather than individual joint angle control might help reduce the dimensionality problem for real-time applications (Carpaneto et al., 2011; Townsend et al., 2011). Here, we demonstrated the decoding of a wide range of complex hand configurations from motor preparatory activity, ranging from precision grips to power grips.

Furthermore, as a test for prospective real-time applications, we illustrated the possibility of translating hand postures to anthropomorphic 16 DOFs hand and arm. Inverse kinematics and a linear translation of hand configurations allowed executing a total of 20 grip types on the robotic device. This offline test demonstrated the possibility of physically executing complex hand configurations as decoded from neuronal planning and execution signals.

Although decoding motor intensions significantly reduced the decoding complexity of the primate hand, it is important to note that such an open-loop approach could not work as a stand-alone application. For real-time applications, the instant processing of neural activity for aperture control and error correction would be required. One possibility would be a hybrid neural interface that accesses both planning and motor execution signals for grasping. Such an approach could consist of three major steps: (1) detecting the planning state before movement onset (Aggarwal et al., 2013); (2) decoding the intended grip type from preparatory activity; and (3) closing the aperture of the decoded hand configuration with continuous decoders (e.g., Kalman filter) in closed-loop applications under visual guidance (Collinger et al., 2013). In our study, the ventral premotor cortex showed similar or even better performance during movement execution than M1. The redundancy between both interconnected areas (Dum and Strick, 2005) was already reported in previous decoding studies (Aggarwal et al., 2013). However, driving a hybrid neural interface with access to planning and motor activity could benefit from both areas and lead to a significant increase in decoding performance and usability. Therefore, motor execution signals may not necessarily have to originate from the motor cortex. As shown in Figure 5c, the lateral part of F5 demonstrated the best performance across planning and motor epochs and hence might be well suited for this kind of applications.