Synaptic Consolidation: From Synapses to Behavioral Modeling

Abstract

Synaptic plasticity, a key process for memory formation, manifests itself across different time scales ranging from a few seconds for plasticity induction up to hours or even years for consolidation and memory retention. We developed a three-layered model of synaptic consolidation that accounts for data across a large range of experimental conditions. Consolidation occurs in the model through the interaction of the synaptic efficacy with a scaffolding variable by a read-write process mediated by a tagging-related variable. Plasticity-inducing stimuli modify the efficacy, but the state of tag and scaffold can only change if a write protection mechanism is overcome. Our model makes a link from depotentiation protocols in vitro to behavioral results regarding the influence of novelty on inhibitory avoidance memory in rats.

Introduction

A continuous stream of sensory events bombards us, but we only retain a small subset in memory. This selectivity avoids memory overload, preventing overwriting previously formed memories (Nadal et al., 1986; Carpenter and Grossberg, 1987; Amit and Fusi, 1994).

Several brain areas contribute to memory storage (Dudai, 1989), including the hippocampus (Tulving and Markowitsch, 1998; Quiroga et al., 2005). Memory formation in the hippocampus, as well as in other areas, rests upon changes in synaptic connections (Bliss and Collingridge, 1993; Rogan et al., 1997; Martin et al., 2000; Whitlock et al., 2006). From this perspective, sensory events imprint traces at the level of synapses, reflecting potential memories. These synaptic memory traces occur through changes in the synaptic weight, or as modulations of synapse shape and chemical composition (Redondo and Morris, 2011). Selectivity of memory implies that some synaptic traces decay whereas others persist.

Experimentally, various stimulation protocols induce synaptic memory traces, including high-frequency stimulation of presynaptic pathways (Bliss and Lomo, 1973), stimulation of presynaptic pathways in combination with postsynaptic depolarization (Artola et al., 1990; Ngezahayo et al., 2000), eliciting tightly timed presynaptic and postsynaptic spikes (Markram et al., 1997; Bi and Poo, 2001), or combinations thereof (Sjöström et al., 2001). All of the above protocols involve “Hebbian” coactivation of the presynaptic and postsynaptic neuron (Hebb, 1949) triggering long-term potentiation (LTP) or long-term depression (LTD) of synapses as a “visible” manifestation of synaptic traces.

Synaptic strength changes induced by Hebbian protocols deteriorate over a few hours (early LTP or e-LTP) unless they are consolidated (Dudai and Morris, 2000; Nader et al., 2000). The concept of synaptic tagging and capture (STC) (Frey and Morris, 1997) suggests that the initial trace of synaptic plasticity sets a tag at the synapse, serving as a marker for potential consolidation of the changes in synaptic efficacy. Consolidation then requires the capture of plasticity-related products (PRPs; Redondo and Morris, 2011), which include proteins (Frey and Morris, 1997; Govindarajan et al., 2006) and mRNA synthesis (Nguyen et al., 1994).

Importantly, only tagged synapses can be consolidated (Frey and Morris, 1997). Conceptually, the synaptic tag represents both the eligibility of specific synapses for consolidation and the functional unit that captures PRPs to transform e-LTP into late LTP (l-LTP; Krug et al., 1984; Reymann and Frey, 2007). Subsequent experiments have suggested that tags do not correspond to single molecules but rather to a complex state of the synapse (Lisman et al., 2002; Lee et al., 2009; Okamoto et al., 2009; Ramachandran and Frey, 2009; Redondo et al., 2010; Redondo and Morris, 2011).

Here, we not only translate the above conceptual theory into a compact computational model, but extend it by a write-protection mechanism critical to describing a wealth of in vitro data including experiments on cross-tagging (Frey and Morris, 1997; Sajikumar and Frey, 2004b), tag-resetting and depotentiation (Bashir and Collingridge, 1994; Sajikumar and Frey, 2004a), metaplasticity (Abraham, 2008), and the influence of novelty on behavior (Moncada and Viola, 2007).

Materials and Methods

Similar to previous plasticity models (Rochester et al., 1956; Bienenstock et al., 1982; Gerstner et al., 1996; Song et al., 2000; Fusi, 2002; Pfister and Gerstner, 2006; Morrison et al., 2008), coactivation of presynaptic and postsynaptic neurons induces synaptic memory traces. A central ingredient of our computational model is that synaptic traces are described with three different variables that evolve on different effective timescales. Consolidation requires the transmission of information from a “fast” synaptic trace to a “slow” one (Fusi et al., 2005) through a “write” process. However, in contrast to earlier models of consolidation (Fusi et al., 2005; Clopath et al., 2008; Barrett et al., 2009), the state of the slow synaptic trace is normally protected against overwriting and cannot change unless a “write-now” signal is given (Crow, 1968; Carpenter and Grossberg, 1987; Izhikevich, 2007; Frémaux et al., 2010; Frégnac et al., 2010; Pawlak et al., 2010). The write-now signal in our new model has two stages. The first stage is linked to the formation of tags and is required for the transition from initiation of LTP to e-LTP; the second stage is linked to the production of PRPs for the transition from e-LTP to l-LTP. In this section, we describe the synapse model in detail and finish with a few remarks on network simulation, neuron model, and numerical procedures.

Synaptic variables and write protection.

A model synapse connects a presynaptic neuron (index j) to a postsynaptic neuron (index i). Synapse-specific variables have a double index ij, whereas variables that are shared among synapses onto the same postsynaptic neuron only an index i. In the case of spatial effects in dendrites of compartmental neuron models, the index i would denote one local compartment with shared PRPs. Spatial compartmentalization is beyond the scope of the present study (O'Donnell and Sejnowski, 2014).

The state of a synapse is characterized by three synapse-specific variables: first, the weight variable w_ij, which is linked to the experimentally measurable synaptic conductance Δg_ij by a linear transform Δg_ij = w₋ + (w_ij + 1)(w₊ − w₋)/2 with parameters w₋ and w₊; second, the tagging-related variable T_ij, which cannot be measured directly in experiments; and finally the scaffold variable z_ij. All three variables follow the same bistable dynamics: τ_xẋ = f (x) = $-\frac{dU}{dx}$ with U(x) = $\frac{x^4}{4}-\frac{x^2}{2}$ corresponding to the double well potential of Figure 1A. These dynamics have two stable fixed points, x = +1 and x = −1, corresponding to the high and low states, respectively. If the weight variable takes the value w_ij = −1 or +1, then the measured weight is Δg_ij = w₋ or w₊. We set the value of the high weight to be w₊ = k_ww₋ (Table 1).

Figure 1.

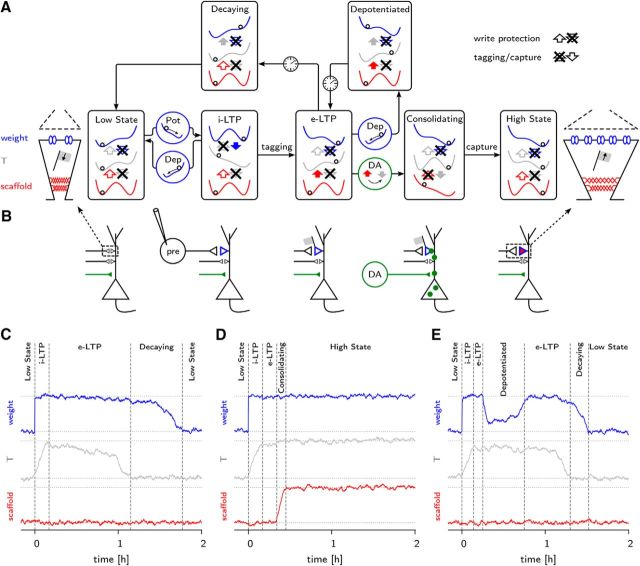
States and transitions of the synapse model. Potentiating protocols applied to the model have different outcomes. A, Schematic view of the different synaptic states. On the left is a sketch of the low state of a synapse. It consists of three elements, a weak weight (blue) and two hidden variables, the tagging-related variable T (gray), currently in its lower state, and a small scaffold (red). The diagram focuses on potentiation from the low to the high state. The synapse's internal variables are represented by three double well potentials (blue, gray and red curves). These variables are coupled to each other (shown by large arrows), which alters their stability properties. A variable in its low state is represented by a ball on the left side of a panel and a variable in its high state by a ball on the right side. The directions of the couplings depend on the synapse state and on its recent history. In the low state, all three variables are in the lower potential well and the couplings are upstream, from the scaffold to the tagging variable T and from T to the weight. A potentiating plastic event carries the weight to its strong state (w = +1) without affecting the two other layers. It also reverses the coupling from the weight to T. The synapse exhibits then initial LTP. After LTP induction, within ∼10 min, a tag is set (T = +1) due to the influence of the first layer on the second (filled blue arrow). The coupling between the first two layers then comes back to its resting direction from bottom to top. If an appropriate neuromodulation (e.g., dopamine) is delivered to the postsynaptic neuron, production of PRP is triggered, allowing for stabilization of recent plastic changes. It reverses the direction of the coupling between T and the scaffold for ∼2 h, enabling the last layer to follow its neighbor to the large state (z = +1). This changes the long-term stability of the synapse. In the absence of external input, a tagged synapse decays back to its resting state within a few hours. The timescale of the decay is determined by the time needed for noise to push T out of the metastable potential well. When a depotentiating protocol is applied to a tagged synapse, the weight is reset to its weak state. Both the first and second layer are then in a metastable situation. Because the potential barrier for the weight is lower than for T, the weight will bounce back up, setting the synapse back into the e-LTP state. It allows either for capture of PRPs if there was any dopamine release or for decay to the synapse's low state. This stands in contrast to the case in which depotentiation occurs before a tag had time to be set. In this situation, the synapse is directly set back to the low state. On the right of the diagram is a sketch of the high state of a synapse. In contrast to the sketch on the left, the weight is strong, T is up, and the scaffold is large. B, Sketch of a postsynaptic neuron and of its incoming synapses. The upper synapse's state corresponds to the one in A directly above. A synapse can be in the low state (small black triangle), in the i-LTP state (large blue triangle), in the e-LTP state (blue triangle and gray flag), or in the high state (blue triangle filled in red). Consolidation occurs through the presence of PRPs (green circles). C, Typical behavior of a synapse during an e-LTP-inducing protocol. We show the time course of the three layers of a synapse (blue, gray, and red lines) and the synaptic state to which it corresponds. D, As in C, but with a stronger stimulus-inducing l-LTP. Note that consolidation occurs because of the presence of PRPs. E, As in C, with a resetting stimulus 15 min after the start of potentiation.

Table 1.

Model parameters

Neuron model
Membrane		Threshold		Connections
V exc	0 mV	τthr	5 ms	τampa	5 ms	τadapt	250 ms
Vrest	−70 mV	ϑrest	−50 mV	τgaba	10 ms		100 msb
V inh	−80 mV	ϑspike	100 mV	τnmda	100 ms	gspike	10
τm	20 ms (10 msa)			β	0.5		1b

Synaptic model
Synaptic state				Plasticity induction		PRPs
τw	200 s (20 sa)	awT/Tz	3.5	A−	2 × 10−4	kup	1 s−1
τT	200 s	aTw	1.3	A+	5 × 10−4	kdown	1/7200 −1
τz	200 s	azT	0.95	τx	16.8 ms
kw	3 (5a)	τγ	600 s	τy	33.7 ms
σ	10−4	ϑγ	0.37	τtriplet	40 ms

Behavioral simulations contexts
Input → spatial				Spatial → fear
Afamiliar−	1.5 · 10−4	Afamiliar+	10−4	Afamiliar−	10−6	Afamiliar+	10−6
Anew−	5 · 10−3	Anew+	10−4	Anew−	10−6	Anew+	10−6
AIA−	1.5 · 10−4	AIA+	3 · 10−2	AIA−	10−6	AIA+	10−4

Behavioral simulations neural network
Group size		Connection weight		Input firing rate
Ninput	3 × (500 ± 5)	w−input→spatial	0.2	Δgexc→inh	0.1	νinputon	10 Hz
Nspatialexc	1000	w−spatial→fear	0.1	Δginh→exc	0.4		8 Hza
Nspatialinh	250			Δgfear→action	1	νinputoff	0.1 Hz
Nfear	100			Δginput→action	0.5		1 Hza
Naction	100			Δgext→*	0.5	νextspatial	100 Hz
						νextfear	20 Hz
							150 Hzb

Neuron Model: ^afor inhibitory neurons (Figure 5). ^bused in behavioral simulations. Synaptic model: ^aused in behavioral simulations (k_w = 5 only for the spatial → fear connection). Behavioral simulations neural network: ^afiring rates during OF exploration. ^brate during IA training.

Importantly, the above three variables are coupled via time-dependent gating variables which implement the write protection mechanism. The gate between the weight and the tagging-related variable is given by the synapse-specific variable G_ij and the gate from tag to scaffold is given by the neuron-specific variable p_i. The full system reads as follows:

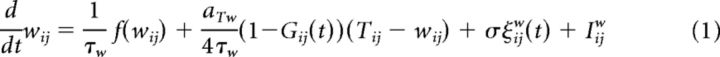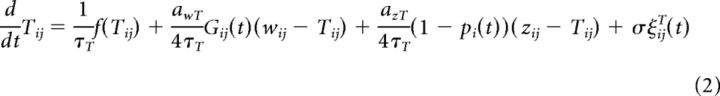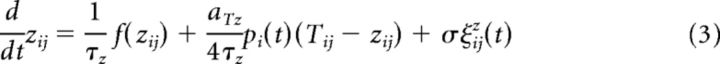where the terms ξ_ij(t) are independent Gaussian white noise processes with the properties 〈ξ_ij(t)〉=0 and 〈ξ_ij(t)ξ_ij(t′)〉 = δ(t − t′).

Note that write protection of the tagging-related variable corresponds to G_ij = 0; that is, the weight variable is unable to influence the tagging-related variable (whereas the tagging-related variable can influence the weight). The write protection is completely removed if G_ij = 1. Similarly, the scaffold is “write protected” if p_i = 0 and write protection is removed for p_i = 1.

Plasticity-inducing protocols (to be discussed in the next subsection) act on the dynamics in two different ways. First, plasticity can directly drive the weight evolution as an input I_ij^w to Equation 1. Second, plasticity also drives the gating dynamics via a plasticity-inducing stimulus I_ij^γ. The subtle difference between I_ij^w and I_ij^γ is discussed further below. To evaluate the momentary state of the gating variable G_ij(t), we calculate a low-pass filter of the plasticity-inducing stimulus I_ij^γ as follows:

and switch the value of the gating variable G_ij if γ_ij passes a threshold ϑ_γ:

where H(x) is the Heaviside step function with H(x) = 1 if x > 0 and 0 else. In other words, a strong plasticity inducing protocol or a weak one that is maintained on a timescale τ_γ can drive the gating variable above threshold. As a result, the write protection is removed and the momentary weight value w_ij can influence the tagging-related variable T_ij.

The coupling variable p_i between the tagging-related variable and the scaffold represents the availability or concentration of PRP in the postsynaptic neuron i. To increase the PRP concentration and remove the second write protection, an external reward or novelty signal, likely to be related to dopamine (DA), is required. In our model, the action of dopamine is described by the following equation:

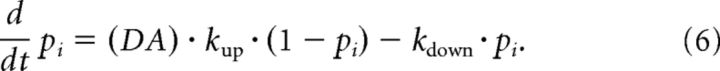The dopamine variable (DA) has no index because we assume that the same dopamine signal is received by many neurons in parallel. The presence of dopamine corresponds to a value (DA) = 1. Dopamine is necessary to trigger synthesis of PRPs. In our model, we take the rate k_up as a constant, but in a more detailed model, k_up could also depend on the availability of additional molecules necessary for PRP synthesis. We emphasize that the concentration of PRP is, in our model, uniform across the whole neuron so that p_i has a single subscript, that of the postsynaptic neuron, but extensions to spatial compartments are possible. For all values of the different parameters, see Table 1.

Plasticity induction.

In this section, we describe the input terms I_ij^W and I_ij^γ acting on the weight and on the gating variable responsible for the tagging process. They are both based on the same standard Hebbian learning rule but differ in the details. We use the triplet spike-timing-dependent plasticity (STDP) rule (Pfister and Gerstner, 2006) with the original set of parameters extracted from hippocampal slices. The spike train of a neuron j is defined as S_j(t) = ${\displaystyle {\sum }_k\delta \left(t-t_j^k\right)}$, with t_j^k being its k^th spike time and δ the Dirac δ-function.

In the triplet rule, LTP induction is as follows:

is driven at the moment of postsynaptic spikes S_i(t) and proportional to the two ‘traces’ x_j⁺(t) and y₁^triplet (t) left by earlier presynaptic or postsynaptic spikes. Therefore, an optimal drive occurs for a spike triplet in a rapid sequence of post-pre-post (hence the name triplet rule). ε is a small positive number. LTD induction is as follows:

LTD induction is independent from LTP induction and occurs in the model at the moment of presynaptic spikes S_j(t) and proportional to a trace y_i⁻(t) left by earlier postsynaptic spikes. Therefore, LTD is optimally stimulated by a pair “post-pre,” just like in standard STDP. The traces are given by the following:

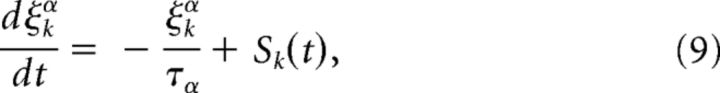where ξ^α ∈ {x⁺, y^triplet, y⁻} (see Table 1 for the time constants).

In the original paper, parameters of the triplet rule have been optimized for weight induction (Pfister and Gerstner, 2006). Because weight induction and tagging are two independent processes (as corroborated by the tag-resetting protocols; Sajikumar and Frey, 2004a) and are represented by two different variables, w_ij and G_ij, in our model, there is no fundamental reason to assume that the triplet rule would act completely symmetrically on both variables. Moreover, the original paper did not consider the scaffold state. We assume that LTD induction is enhanced, if the momentary weight variable w_ij is larger than the scaffold variable z_ij and LTP induction is enhanced if the momentary weight variable w_ij is smaller than the scaffold variable z_ij. Therefore, we write for the drive of weight induction as follows:

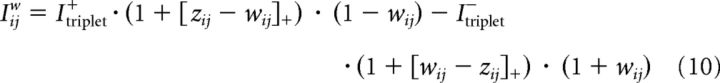where [x]₊ = xH(x) denotes linear rectification. Note that we multiplied the potentiation and depression terms by factors (1± w_ij) to ensure that STDP does not push the weight beyond the boundaries of the bistable dynamics. We emphasize that if the initial state coincides with one of the stable states of the synapse (w_ij = T_ij = z_ij), as is probably the case in standard LTP and STDP experiments, then our model of induction of LTP and LTD is identical to that of Pfister and Gerstner (2006). Differences only arise in sequences of potentiation and depotentiation protocols spread out over several minutes.

In the model, the write protection of the tagging-related variable for LTP induced tags can only be removed if the momentary weight w_ij is larger than the scaffold value z_ij, whereas that for LTD can only be removed if the momentary weight w_ij is smaller than the scaffold value z_ij. Therefore we set:

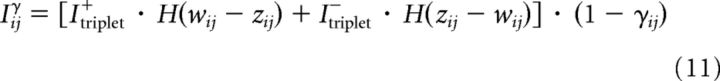Where, again, the term 1 − γ_ij is to ensure that the variable stays between 0 and 1.

Simulation of slice experiments.

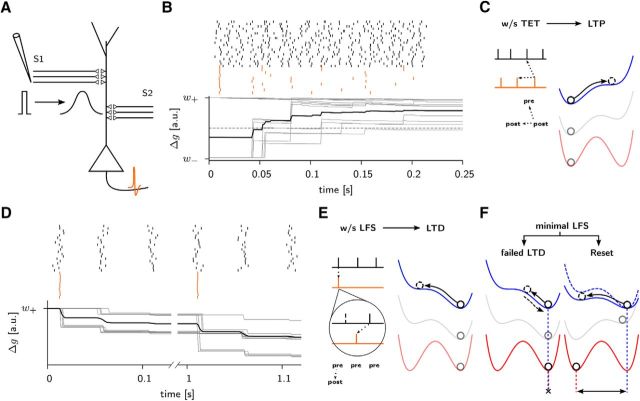
Inputs consisted of two groups of 2000 Poisson neurons, each projecting onto 10 leaky integrate-and-fire (LIF) neurons with a connection probability of 10% (Fig. 2A). To simulate a stimulation pulse occurring at time t₀, we drew for each presynaptic neuron a spike time t_j from a Gaussian distribution with mean t₀ and a SD of 3 ms (Fig. 2D). Because triplets of spikes are needed for potentiation, only tetanic stimuli lead to potentiation (Fig. 2B,C), whereas low-frequency protocols lead to depression (Fig. 2D–F) or depotentiation (Fig. 2F).

Figure 2.

Stimulation protocols. A, Two groups (S1 and S2) of 2000 input units project onto 10 AIF neurons (only one is shown) with a connection probability of 10%. An extracellular stimulation pulse is modeled by a Gaussian packet of action potentials with a SD of 3 ms, with 1 spike per axonal projection. For three or fewer consecutive packets separated by 50 ms (as in a sLFS protocol, see D), a postsynaptic neuron generates a single spike, whereas several spikes are emitted if stimulation occurs at 100 Hz (as in a wTET, see B). B, Detailed view of a wTET protocol. Spike arrivals at 20 synapses (black bars) are shown together with spikes of all 10 postsynaptic units (red bars). The effect on individual weights can be seen in the bottom (gray lines). Note that potentiation happens only after the second postsynaptic spike of a neuron. Only those synapses crossing the long-term stability barrier (dashed horizontal line) will undergo a long-lasting change. The mean weight is shown in black. C, Tetanic stimulation protocols. A wTET (21 pulses at 100 Hz) or a sTET (3 × 100 pulses at 100 Hz) is strong enough to overcome neuronal adaptation so that the postsynaptic neuron fires several spikes (red bars, schematic). Because potentiation needs at least two postsynaptic spikes (post-pre-post triplet), a high postsynaptic firing rate gives rise to LTP (Pfister and Gerstner, 2006; Clopath et al., 2010), indicated as a shift to the metastable state on the right. D, With a sLFS protocol (3 pulses at 20 Hz repeated every second), the postsynaptic neuron fires only once per second (top, interrupted time axis). Synapses initially in the high state (gray traces) become weaker on average (black). Note that the first and second volley of spike arrivals, ∼50 ms after the postsynaptic spike, lead to synaptic depression. E, Low-frequency stimulation protocols. During a sLFS, we have one postsynaptic spike (red bar, schematic) for three presynaptic spikes (black) at the same synapse arising from three subsequent stimulation volleys, which gives rise to a strong post-before-pre LTD. During a wLFS (900 pulses at 1 Hz, top), the postsynaptic neuron fires once per volley, but because spikes arrive approximately in the middle of the packet (compare first stimulus in D), approximately half the synapses perceive a post-before-pre pattern leading to LTD, whereas the other half perceives an isolated pre-before-post causing no effect. The accumulation of the 900 pulses makes the LTD stimulus strong enough to have a long-lasting effect. In the case of an sLFS, the larger fraction of post-before-pre spikes gives rise to a larger effect. F, Resetting effect. A reset protocol (250 at 1 Hz) is not enough to produce any LTD on a synapse in the high state (left) because the number of pulses is not enough to push the weight variable over the potential barrier. For a synapse in the e-LTP state (right) the barrier for depression is lower because the meta-stable position of the tag is somewhat shifted to the left. This enables softer protocols to have a clear depotentiation effect.

For slow onset LTP, the stimulations followed the timing of the protocol of Navakkode et al. (2007) and were given 1, 3, 5, 11, 15, 21, 25, and 30 min after start of DA delivery and then every 15 min up to 3 h after the start of DA delivery. In the simulations of the model, each stimulation was mimicked by randomly selecting 5% of synapses and setting their tagging-related variable to “up” T_ij = 1. Dopamine was given (i.e., its value was set to DA = 1) during 60 s before the first stimulation (cf. Eq. 6).

Simulation of behavioral data.

For information on the different parameters used in our neural network implementing behavioral experiments, see Table 1. The basic structure of the network consisted of a population of input neurons connected to a spatial node and to action neurons, whereas fear is represented by a group of amygdala-like neurons in the pathway from the spatial node to action neurons.

Population of input neurons.

The population of input neurons consisted of three groups of 500 ± 5 spiking neurons, representing patterns of activity in the home cage, the experimental setup (training cage) during inhibitory avoidance (IA) training, and the open field environment, respectively. On average, 50 neurons were shared by any two patterns. Only one pattern was active at a given time. An active neuron is represented by a Poisson spike train of firing rate v_input^on = 10 Hz (8 Hz in the case of the open field exploration), and an inactive neuron by a rate v_input^off = 0.1 Hz (1 Hz for the open field). The values for open fields are different because we assume that it is a novel stimulus for which the network does not yet have strongly tuned neurons.

Population for spatial representation (spatial node).

We simulated a population of 1000 excitatory adaptive LIF neurons and 250 inhibitory LIF neurons. Each excitatory neuron received 25 inputs from presynaptic neurons in the inhibitory population, as well as 135 ± 10 inputs from the input population. Connections from the input to the excitatory population included our new synapse model; others were nonplastic (see Table 1 for the connection weights). Each inhibitory neuron received exactly 100 inputs from presynaptic neurons in the excitatory population. Every neuron (excitatory or inhibitory) received also independent noise in the form of a Poisson spike train with rate v_ext^spatial = 100 Hz.

Population for fear encoding.

The population consisted of 100 inhibitory LIF neurons. Each neuron received 100 inputs from the excitatory population of the spatial node. These connections were plastic and described by our new synapse model. Each neuron received also independent noise in the form of a Poisson spike train with rate v_ext^fear = 20 Hz. This external input became stronger in the case of a fearful event, with a firing rate of 150 Hz.

Population of action neurons.

We simulated 10 groups of 100 adaptive LIF neurons each. Every neuron received 10 inputs from the fear population as well as 50 ± 1 inputs from the pattern coding for the experimental setup (training cage). All connections were nonplastic.

For each group m, we calculated the time-averaged population activity ν_m on-line via the following:

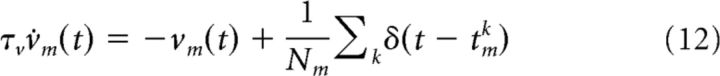where N_m is the size of group m and t_m^k is the time of the k^th spike among all neurons in group m. We chose a timescale of τ_ν = 100 ms.

The jump time in the model was defined by the time when, for the majority of the action groups, the rate ν_m had reached at least once a threshold ϑ_jump. We set an upper bound of 100 s on the jump time.

Neuron model.

In our simulations, we used LIF neurons (parameters in Table 1) with conductance-based synapses (Gerstner et al., 2014). The evolution of the membrane potential of neuron i is given by the following:

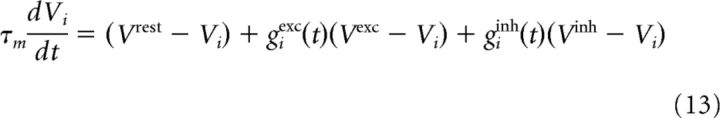where g_i^exc and V^exc are the excitatory conductance and reversal potential (and analogously for inhibition). A spike is emitted when the potential reaches the threshold ϑ_i. After a spike, V_i is reset to V^rest and ϑ_i is set to ϑ^spike to implement refractoriness. The threshold then relaxes back to its rest value according to the following:

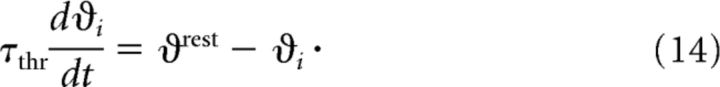The excitatory conductance g_i^exc has an AMPA and an NMDA component and is defined as g_i^exc = βg_i^ampa + (1 − β)g_i^nmda where β is the relative contribution of AMPA. The time course of conductances is given by a first-order low-pass filter as follows:

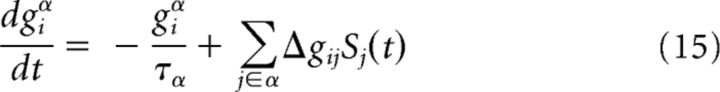for the contribution of the AMPA receptor channel g_i^ampa = g_i^α, where Δg_ij is the plastic synaptic weight of the connection from neuron j to i; and by a second-order low-pass filter as follows:

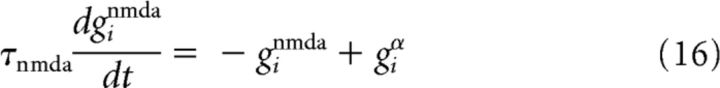for the contribution of the NMDA channel. The voltage dependence of NMDA is neglected for the sake of computational efficiency.

For nonadaptive leaky integrate-and-fire neurons, the inhibitory conductance is g_i^inh=g_i^gaba = 0 in the slice experiments; in the behavioral experiments, it is described by g_i^inh=g_i^gaba where g_i^gaba follows the dynamics of Equation 15 with a fixed weight Δg_ij = Δg and S_j the spike trains arriving at the inhibitory synapse. For adaptive integrate-and-fire neurons, we add a spike-triggered self-inhibition g_i^inh = g_i^gaba + g_i^adapt where the adaptation conductance is increased by an amount g^spike at each spike of neuron i, and else relaxes exponentially to zero as follows:

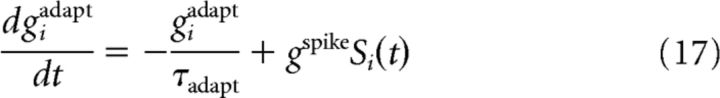For parameter values, see Table 1.

Numerical simulations.

Numerical simulations were performed with a time step of 0.1 ms. For differential equations that could be solved analytically, we used the exact solution. For all the others, a forward Euler method with the same time step was used. An exception to this were the three internal synaptic variables w_ij, T_ij, and z_ij for which we used a time step of Δt = 100 ms. This updating time was chosen so that $\left|\frac{dx}{dt}\right|\Delta t^{-3}$ for all x ∈ {w_ij, T_ij, z_ij}.

The code was written in C++ using Open MPI and the Boost libraries and compiled with the GNU C compiler. Simulations were run on a Linux workstation equipped with Intel Core i7 CPUs. The bottleneck for simulation time was the total number of plastic synapses, first because their number grows as ∼N² (with N the number of neurons) and second because of their large amount of internal variables. For simulating our behavioral network, the speed-up factor was ∼2, meaning that it took approximately half a day to simulate 24 h of biological time.

In all behavioral paradigms where the interval between IA training and the final testing was 1 d, we stopped the simulations after 8 h biological time. We justify this choice by the fact that no significant weight change compared with the level of noise could be measured after this time in a preliminary longer test run.

Choice of model and parameter tuning.

Our model of synaptic plasticity has a total of five variables: three variables (related to synaptic weight, tag, and scaffold) to describe the state of the synapses and two variables that control the read-write process between these. The choice of the variables was based on the following considerations.

In the classic model of synaptic tagging and capture (Frey and Morris, 1997), there was no fundamental distinction between e-LTP and tagging. More recent experiments, however, showed that tagging and e-LTP are dissociable (Ramachandran and Frey, 2009; Redondo et al., 2010; Redondo and Morris, 2011). Similarly, an early model of synaptic tagging and capture (Clopath et al., 2008) identified tagging with e-LTP and therefore had only two state variables (see also Fusi, 2002; Brader et al., 2007). The increase in the number of state variables to three is necessary to account for the separation of tagging and e-LTP and to explain the tag-resetting experiments involving a sequence of potentiation and depotentiation events (see Fig. 4D).

Figure 4.

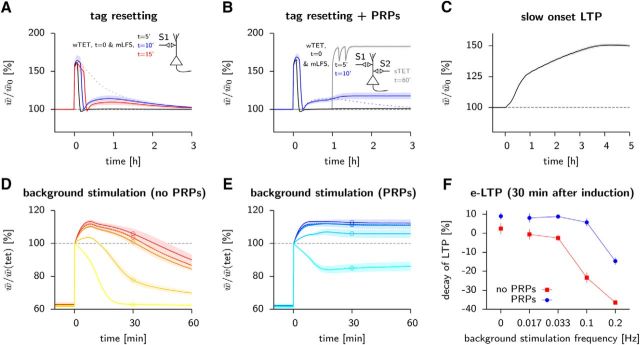
Nonstandard synaptic tagging and capture. A, Tag resetting: if a depressing stimulus is applied shortly after a wTET on the same pathway, the synaptic weights are reset to their weak state (w = −1). If the reset happens 5 min after potentiation no tag had time to be set (T = −1) and the mean weight lies on the 100% line (black line). When the time difference is longer than 10 minutes, a rebound can be observed (blue and red lines) due to the synaptic tags dragging along the corresponding weights back to the strong state (T = +1, w → + 1). B, As in A, except PRPs are made available via an sTET on a second pathway (S2) 1 h after the wTET on the first pathway (S1). When the time difference between potentiation and depotentiation is ∼10 min, synapses can experience consolidation (blue line). C, Slow onset LTP. If, every few minutes, a weak stimulus is applied in the presence of dopamine (see Materials and Methods), synaptic weights slowly increase over hours. D, The decay of e-LTP is activity dependent. After an LTP induction protocol (100 pulses at 100 Hz), we randomly stimulated model neurons to fire at some background frequency ranging from 0 Hz (red) to 0.2 Hz (yellow), in the absence of PRP. E, As in D, but in the presence of PRP for the same frequency range (from blue to cyan). F, Amount of decay 30 min after tetanization without (red symbols corresponding to the circles in D; vertical bars are SD over 10 repetitions) or with PRPs available (blue symbols, corresponding to the circles in E). Increasing the frequency accelerates the decay when no consolidation is present due to the resetting effect as the frequency approaches 1 Hz. Up to ≈0.1 Hz, PRPs are able to rescue early changes. Past this limit, the weights are reset before tags are set.

The dynamic write protection mechanism requires the two additional variables mentioned above. In the classic cascade model (Fusi et al., 2005), a dynamic write protection is absent because transitions between discrete states occur at constant rates. In the state-based model (Barrett et al., 2009), write protection is not a part of the dynamics, but indirectly implemented by explicit stimulus-dependent conditions.

Our final model of synaptic plasticity has 17 parameters (Table 1). The five parameters of the triplet model of plasticity induction in Equations 7–9 were adopted from (Pfister and Gerstner, 2006), except A⁻ and A⁺, which were retuned (Table 1). The remaining 12 parameters of e-LTP, tagging, and scaffold were hand-tuned to the slice data, guided by theoretical consideration, and kept fixed for all figures. The round values given in Table 1 for these parameters indicate that no fine-tuning was necessary, suggesting that the model behavior is robust against changes in the parameters.

For the neuron model (Gerstner et al., 2014), a plausible set of standard parameters with “round” values were chosen before starting any plasticity modeling and kept fixed throughout the modeling process. The network connectivity for behavioral data was set up by hand using plausible numbers.

Relation to other models of synaptic consolidation.

In the cascade (Fusi et al., 2005) or the state-based (Barrett et al., 2009) models, a single discrete variable, which can be in one of N different states, characterizes each synapse. In our model, multiple variables describe the state of a synapse, which grants a variety of transitions and provides the flexibility necessary to implement plastic and metaplastic phenomena. Although only two states in our model (weak-down-small and strong-up-large) exhibit long-term stability (in contrast with, for example, a tristable system; Pi and Lisman, 2008), the model also has six metastable states (e.g., strong-up-small). Metastability arises because of the write protection mechanism that prevents changes to be transmitted into long-term memory.

In electrophysiological experiments in which only the weight variable is measured, there is typically no control of the initial state of the synapse. When a simplified learning rule is extracted from such plasticity experiments, metastable “hidden” states lead to an interpretation of “metaplasticity” (Abraham and Bear, 1996) or a “sliding threshold” (Bienenstock et al., 1982). Plasticity models depending on internal parameters and PRP availability have been called “neo-Hebbian” (Lisman et al., 2011).

Results

Synaptic plasticity is a widespread phenomenon in the brain, but details vary across brain areas, species, neuron and synapse type and age. Although basic conceptual aspects of plasticity are probably conserved across several variants and are therefore describable by the same modeling framework, quantitative fits of the model to experimental data need to be limited to one synapse type. For model fitting, we mainly focus on glutamatergic excitatory synapses onto hippocampal CA1 neurons.

The Results section is organized in three parts. First, we introduce the model of synaptic consolidation and highlight a few essential results based on simulations and analysis of the model. Second, we show that the consolidation model can account for previously unexplained experimental observations after a sequence of potentiation and depotentiation stimuli. Finally, we use the model in a simulation of “behavioral tagging” experiments so as to predict macroscopic effects from microscopic synaptic dynamics.

Basic model features

Plasticity manifests itself experimentally across many different timescales (Kelleher et al., 2004; Reymann and Frey, 2007) that correspond to three different variables in our model of synaptic consolidation. First, minimal LTP stimulation protocols indicate that changes in the amplitude of the postsynaptic current (PSC) or postsynaptic potential (PSP) are visible already a few seconds after the induction protocol (Petersen et al., 1998; O'Connor et al., 2005). In our model, observations on the rapid timescale of synaptic plasticity correspond to changes of the synaptic weight w_ij between the presynaptic neuron j and the postsynaptic neuron i. The synaptic weight, which is “visible” in electrophysiological experiments, can be related to the number and phosphorylation state of AMPA receptors (Lisman and Spruston, 2005), as well as the release probability of presynaptic vesicles (Tsodyks et al., 1998). After plasticity induction, the synapse is in the state of initial LTP (i-LTP), likely to be related to associative short-term plasticity (Erickson et al., 2010).

Second, tags are set on a timescale of a few minutes and spontaneously decay after 1 or 2 h (Frey and Morris, 1997; Reymann and Frey, 2007). Tags correspond to complex synaptic states (Redondo and Morris, 2011) which are not directly visible in electrophysiological experiments but must be inferred indirectly by pharmacological (Lisman et al., 2002; Sajikumar and Frey, 2004a; Ramachandran and Frey, 2009; Redondo et al., 2010) or spine imaging experiments (Lee et al., 2009; Okamoto et al., 2009). In our model, the internal state of the synapse from neuron j onto neuron i corresponds to the tagging-related variable T_ij.

Third, the synapses can switch to a consolidated state of I-LTP on the timescale of <1 h and remain in this state for many hours (Frey and Morris, 1997). In our model, the consolidated state of a synapse from neuron j to neuron i is described by a variable z_ij, which may be interpreted as the state of the synapse scaffold (Redondo et al., 2010).

Long-term stability of the scaffold variable z_ij in the presence of molecular turnover requires multistability (Crick, 1984; Lisman, 1985). In the model, we assume generic bistable dynamics of z_ij, which can be visualized as a ball moving downward in a double-well potential (Fig. 1A). A classic example of bistability in biochemistry is an autocatalytic process such as autophosphorylation (Lisman, 1985), but many other processes with self-feedback also show the same generic form of bistability. Because we interpret the z_ij variable as the scaffold variable, our model effectively assumes bistability of the scaffold. Described by a standard bistable equation (see Materials and Methods), the continuous variable z_ij can switch between a stable low value z_ij = −1 (“small” scaffold) and an equally stable high value z_ij = +1 (“large” scaffold).

Because the notion of “tagging” is binary (i.e., a tag is either set or not), the tagging-related variable T_ij is described with an equation analogous to that of z_ij with two stable states at T_ij = +1 (up) and T_ij = −1 (down). The tagging-related variable can be up either because of a recent LTP-inducing event or because the synapse has been in the stable, “large-scaffold” state for a long time. We say that a tag is set if the tagging-related variable is in a different state than the scaffold variable. For example, a configuration T_ij ≈ + 1, whereas z_ij ≈ − 1 implies that a tag for LTP has been set; whereas T_ij ≈ − 1 and z_ij ≈ + 1 implies tagging for LTD. A transition from T_ij ≈ − 1 to T_ij ≈ + 1 can occur either because a tag for LTP has been set or because a tag for LTD has decayed. In the following, we sometimes refer to the tagging-related variable T_ij simply as the “tag” even though the tag is formally the difference between the tagging-related and the scaffold variable.

Finally, minimal stimulation protocols suggest that induction of plasticity leads to switch-like events (Petersen et al., 1998; O'Connor et al., 2005). We therefore assume that the maximal synaptic conductance Δg_ij that characterizes the amplitude of the excitatory PSC can switch from “weak” Δg_ij = w₋ to the “strong” Δ g_ij = w₊. We refer to Δg_ij also as the “weight” of the synapse. In the model, Δg_ij is linearly related to the weight variable w_ij (see Materials and Methods). In summary, the three variables, w_ij, T_ij, and z_ij, that together characterize the momentary state of a synapse, all have similar bistable dynamics except for a difference in response time: after induction of LTP by a strong protocol (see Materials and Methods), the weight switches after a few seconds, the tagging-related variable after a few minutes, and the scaffold after half an hour (Fig. 1D).

In the absence of external stimulation, the synapse will converge to one of two stable states. In the globally stable low state, the synaptic weight is weak, the tagging-related variable is down, and the scaffold is small (Fig. 1A, left), whereas in the globally stable high state, all three variables are at their other stable point, strong, up, and large, respectively (Fig. 1A, right).

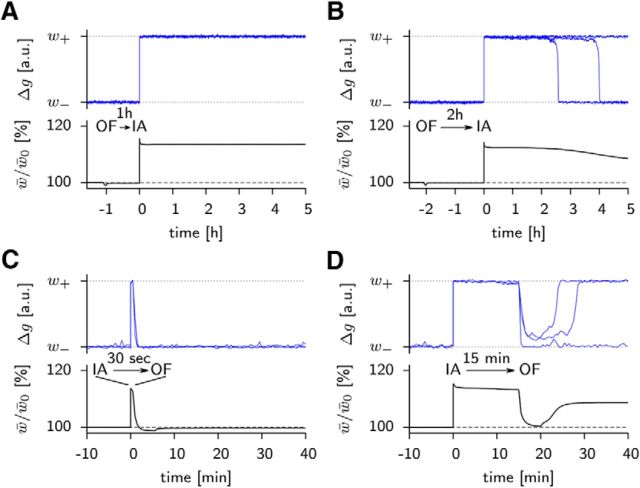
Stimulation of ∼2000 synapses by a weak LTP induction protocol (see legend of Fig. 1C and Materials and Methods) transiently shifts the mean value of the weight to strong, followed by a transient increase in the mean value of the tagging-related variable (Fig. 1C). However, after the tagging-related variable has decayed back to its resting value, the weight will also, over a time of 2–3 h, return back to rest (Fig. 1C and see Fig. 4A).

These simulation results are a consequence of the coupling between the three variables. The tagging-related variable is bidirectionally coupled to the weight and the scaffold so that the total number of vertical coupling arrows between variables is four. However, in the absence of stimulation, the (relatively) slow variables are write protected so that they cannot be influenced by a faster one (write protection indicated by crossed downward arrows in Fig. 1A). Therefore, in the absence of stimulation, the present value of the slowest variable (i.e., the state of the scaffold) influences the dynamics of the tagging-related variable, which in turn influences the dynamics of the weight (upward arrows in Fig. 1A), leading to the asymmetric slightly tilted bistability curves in Figure 1A favoring the weak weight if the scaffold is small and the strong weight value if the scaffold is large.

The effect of an LTP induction protocol on the synapse model is twofold (Fig. 1B). First, a potentiation protocol tilts the bistable weight dynamics toward larger values, so that the strong weight becomes the only stable state of the system. The state of i-LTP corresponds to a strong weight, whereas the tagging-related variable and scaffold remain down and small, respectively. Second, if the potentiation protocol is strong or sustained (see Materials and Methods), the write protection from weight to tag is removed so that the tagging-related variable is now influenced by the weight. Therefore, a few minutes later, the tagging-related variable increases to the up value and the synapse exhibits e-LTP. However, because the value of the tagging-related variable is only metastable, it will eventually decay back to the down state, followed by a decay of the weight.

Tag setting thus leads to e-LTP, but requires that a first write protection is removed. Consolidation of a synapse to the high state of l-LTP is possible only if a second layer of write protection is overcome so as to allow the tagging-related variable to influence the scaffold variable. In our model, the second write protection can be removed only if PRPs are available (see Materials and Methods). PRPs in turn require the presence of a neuromodulator such as dopamine. Indeed, strong LTP induction protocols in slices costimulate dopaminergic fibers (Reymann and Frey, 2007; Lisman et al., 2011). Therefore, under the assumption that dopamine is present after a strong LTP induction protocol, weights are consolidated (Fig. 1D).

Simulated tagging and cross-tagging experiments

Simulations of the model can reproduce a wide variety of experimental results in vitro, accumulated by different laboratories (Figs. 3, 4). Because most classical LTP and consolidation protocols in slices use extracellular stimulation of fiber bundles, we mimic experiments by stimulating one or two groups of ∼2000 model synapses converging onto 10 different postsynaptic neurons (see Materials and Methods). In each group, two-thirds of the synapses are initially in the low state and one-third in the high state. A single extracellular pulse corresponds in the model to the near-synchronous arrival of spikes at all 2000 synapses with a temporal jitter of 3 ms. The postsynaptic neuron is an adaptive LIF model (Gerstner et al., 2014) and LTP induction is described by a standard model of STDP (Pfister and Gerstner, 2006). For details, see Materials and Methods.

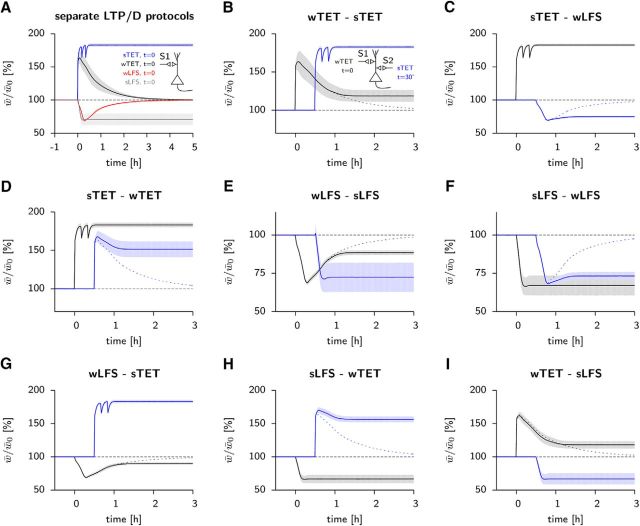
Figure 3.

The model accounts for classic tagging and cross-tagging experiments. One (A) or two (B–I) groups of 2000 Poisson neurons project onto 10 postsynaptic AIF neurons with 10% connection probability. A, Four standard stimuli used in hippocampal slice tagging experiments simulated separately: a wTET consisting of 21 pulses at 100 Hz (black), a sTET, 3 blocks of 100 pulses at 100 Hz separated by 10 min (blue), a wLFS, 900 pulses at 1 Hz (red) and an sLFS, 900 blocks of 3 pulses at 20 Hz separated by 1 s (gray). Only the two strong stimuli involve delivery of dopamine, necessary for stabilization of the changes. The weak stimuli decay to baseline within a few hours. The evolution of the mean scaled synaptic weight w̄/w̄₀ is shown (lines) together with its SD over 10 repetitions (shaded area). B, e-LTP is rescued by a strong stimulus. Thirty minutes after a wTET has been applied on a first pathway (S1, black), another set of synapses onto the same neurons (S2, blue) experience a sTET, making PRPs available to all synapses. The dashed line represents a weakly tetanized pathway in a different neuron for comparison. C, Cross tagging between potentiation and depression. A sTET in one pathway (S1, black) can provide the PRPs necessary for the stabilization of synapses after a wLFS applied on another pathway (S2, blue). The time course of a wLFS alone is shown for comparison (dashed line). D–I, Other combinations of weak and strong stimuli in synaptic tagging and capture. Synapses on the first pathway (S1) are shown in black, those on the second pathway (S2) in blue. Dotted lines show the outcome of the weak protocol on a separate slice without interaction. wTET/sTET, Weak/strong tetanic stimulation; wLFS/sLFS, weak/strong low-frequency stimulation.

First, we find that a weak tetanic stimulation (21 pulses at 100 Hz) leads to e-LTP but not to l-LTP, whereas a strong tetanic stimulation (3 × 100 pulses at 100 Hz) leads to consolidated synapses (L-LTP, Fig. 3A) consistent with experiments (Frey and Morris, 1997). Similarly, a weak low-frequency stimulus (900 pulses at 1 Hz) leads to e-LTD but not l-LTD, whereas a strong low-frequency stimulus (3 pulses at 20 Hz, 900 times, every second) causes l-LTD (Fig. 3A), consistent with experiments (Sajikumar and Frey, 2004b).

Note that, in our model, PRPs are shared among synapses onto the same neuron, whereas weight, tagging, and scaffold variables are synapse specific. Indeed, the model accounts for the fact that e-LTP induced by weak tetanic stimulation can be transformed into l-LTP (Fig. 3B) if a second group of synapses receives, within 1 h, a strong tetanic stimulation (Frey and Morris, 1997). Synapses along additional control pathways that are not stimulated are not affected by the strong tetanic stimulation, indicating synapse-specificity of l-LTP (data not shown).

Interestingly, a strong tetanic stimulation that leads to l-LTP in a first group of synapses can also transform e-LTD after a weak depression inducing stimulus into l-LTD (Fig. 3C), consistent with the experimental observation of cross-tagging between potentiation and depression (Sajikumar and Frey, 2004b). Other combinations of weak or strong depressing or potentiating stimuli are also reproduced by the model (Fig. 3D–I).

Simulated tag-resetting experiments

Although previous models of consolidation (Clopath et al., 2008; Barrett et al., 2009; Smolen et al., 2012) were able to account for the above results, experiments on tag resetting (Sajikumar and Frey, 2004a) remained unexplained. The so-called tag-resetting paradigm consists of a sequence of potentiation and depotentiation events. The most intriguing scenario is that of an LTP-inducing stimulus followed 10 min later by a depotentiating stimulus. In this case, the measured synaptic strength goes down after the depotentiation event, but comes back up again within the next half hour (Sajikumar and Frey, 2004a); our model is able to account for this behavior (Fig. 4A).

Analysis of the model dynamics shows that, during depotentiation, the synaptic weight is reset while the tagging-related variable persists in the up-state (when the resetting stimulus occurs after 10 min) or has not yet been upregulated (when the resetting stimulus occurs after 5 min; Fig. 1E). The reason is that, during the 10 min of waiting time between the potentiating and depotentiating stimulus, the tagging-related variable has had enough time to go from the down to the up state, so that the synapse is in the metastable state of e-LTP (Fig. 1E). The subsequent depotentiating event (Fig. 1A, top) is able to shift the fast weight variable to the weak state, whereas the tagging-related variable remains in the up state (Fig. 1E). Because the depotentiating stimulus is not strong enough to remove the write protection, the tagging-related variable remains write protected in the up state. Therefore, the new weight cannot influence the tagging-related variable, but the tagging-related variable in the up state can influence the weight and pull it back up to the strong value. It is only over the next hour that background noise will make the tagging-related variable and later the weight decay back to their down and weak values, respectively. Therefore, the data of Sajikumar and Frey (2004a) are explained in our theory by the dissociation of early weight changes and tagging into two separate variables, whereas an earlier model that identified e-LTP with tagging (Clopath et al., 2008) is unable to account for this set of experiments.

The back-and-forth between weak and strong weights does not occur if the depotentiation stimulus is given within 5 min and is less pronounced if given 15 min after potentiation (Fig. 4A), consistent with experiments (Sajikumar and Frey, 2004a). Moreover, if PRPs are available after a strong tetanic stimulation of a second group of neurons, then synapses in a first group that underwent a sequence of potentiation and depotentiation events separated by 10 min can be consolidated in the high state, both in the model (Fig. 4B) and in experiments (Sajikumar and Frey, 2004a).

A sequence of potentiation and depotentiation events in slice experiments can be interpreted as an approximation to ongoing stimulus-induced activity that a synapse is expected to experience in vivo. We checked the model (data not shown) under different potentiation-depotentiation protocols (Table 2), including 100 Hz high-frequency stimulation, theta burst stimulation consisting of a sequence of short bursts given at 5 Hz, and 250 Hz tetanic stimulation for potentiation, and, for depression, 2 Hz low-frequency stimulation and 5 Hz theta pulse stimulations (Bashir and Collingridge, 1994; Martin, 1998; Stäubli and Chun, 1996). Because the slice preparations are different across experiments coming from different laboratories, we modified three parameters of the model (the learning constants A⁺ and A⁻ and the noise level) to describe these data; all other parameters were kept at their previous values.

Table 2.

Previous study reproducibility

Mechanism	Protocol	Study	Z	CZ	BB
Early/late LTP & e-LTP → l-LTP	TET	Frey and Morris, 1997	✓	✓	✓
Early/late LTD & e-LTD → l-LTD	LFS	Sajikumar and Frey, 2003	✓	✓	✓
Cross tagging	TET, LFS	Sajikumar and Frey, 2004b	✓	✓	✓
e-LTP/tag-setting dissociation	Pharmacology (actin)	Ramachandran and Frey, 2009	✓	X	✓
	Pharmacology (CaMKII)	Redondo et al., 2010
Depotentiation	TET, LFS	Sajikumar and Frey, 2004a	✓	X	X
	TET, LFS (2Hz)	Bashir and Collingridge, 1994	✓a
	TBS, TPS	Stäubli and Chun, 1996	✓a
	TET (250Hz), LFS (5Hz)	Martin, 1998	✓a
Measurement frequency influence on e-LTP	TET	Fonseca et al., 2006	✓	X	X
Slow-onset LTP	Pharmacology	Navakkode et al., 2007	✓	X	X

Selected articles on important aspects of STC theory. A check sign means that a particular model can account for the data of the study of the same line, whereas an X means that it cannot. Z, Ziegler, the new model presented in this article; CZ, Clopath and Ziegler, the model from Clopath et al. (2008); BB, Barrett and Billings, the model from Barrett et al. (2009)). TBS, Theta burst stimulation; TPS, theta pulse stimulation.

^aSmall modifications on A⁺, A⁻, g^spike, and σ were sometimes necessary.

We wondered whether the resetting of the early phase of LTP is functionally useful. In a noisy environment, the presence of a reset mechanism implies that evidence needs to be accumulated before imprinting plasticity (Brader et al., 2007; Elliott and Lagogiannis, 2012). Ideally, a synapse should remain unchanged when driven by noise. Let us consider a discrete synapse experiencing a noisy but meaningless signal with rate λ₊ = 0.1/s of potentiation and λ₋ = 0.9 s for depotentiation. The synapses might be upregulated by the first potentiating stimulus and immediately afterward reset by a depotentiating one. The net result is no change. The probability of staying in (or returning to) the initial low state approaches rapidly a stationary value of 9/10.

We contrast this result with a hypothetical model in which early LTP cannot be reset. In this case, the first potentiation event would trigger the tag immediately even if a depotentiation event follows thereafter. In this case, the probability of staying in the initial low state decays exponentially with λ₊T. Therefore, the probability that a synapse stays unaffected by noise (i.e., not tagged) is bigger for the model with reset than for the one without.

Recording frequency and slow-onset LTP

In experiments, synaptic weights are usually recorded at most once per minute, corresponding to a frequency of 0.0167 Hz. However, going to higher recording frequencies accelerates the decay of LTP when no PRPs are available (Fonseca et al., 2006). In our model of consolidation, we found that the mean synaptic weight measured 30 min after induction was up to 40% lower when recorded at 0.2 Hz than when recorded at one pulse per minute or not at all (Fig. 4D,F), but was affected much less by the recording frequency in the presence of PRP (Fig. 4E,F). Therefore, paradoxically, the early phase of plasticity does, at high levels of synaptic activity, depend on the availability of PRP. The reason is that PRPs remove the write protection from the tagging-related variable to the scaffold so that the scaffold variable can switch to the new stable state before background stimulation leads to a depotentiation of the synapse.

Slow onset LTP is observed experimentally when dopamine receptors D1/D5 agonists are applied to a hippocampal slice (Navakkode et al., 2007). The slow rise in synaptic weight requires that a presynaptic stimulus, even a weak one, is applied regularly. Slow onset LTP has been shown to rely on the presence of PRPs and also to depend on NMDA receptors, which are known to mediate the tagging process. We modeled this phenomenon by turning the dopamine signal on for 60 s so as to trigger formation of PRP, followed by randomly setting 5% of the tags to their up-state T_ij → +1 at each weak synaptic stimulation to mimic the contribution of NMDA receptors toward tag formation. During the 3 h of weak stimulation repeated every few minutes (see Materials and Methods, above), we observed a slow increase of the mean weight that finally settled at around 150% (Fig. 4C). We emphasize that the sequence of very weak stimuli would not be sufficient by itself to cause LTP. However, because of the presence of PRP after the initial dopamine stimulus, the write protection from the tagging-related variable to scaffold was removed. Therefore, in our model, the tagging-related variable could stay for a sufficiently long time in the up state (T_ij = +1) to pull the weights upward, eventually leading the synapse to its globally stable high state. Our consolidation model with three coupled variables can therefore simulate classic experiments in which weight changes induced by an LTP protocol lead to tagging and consolidation, as well as those in which tagging precedes the visible weight changes.

Behavioral tagging

Experimental work (Frey et al., 1990; Sajikumar and Frey, 2004b; Lisman and Grace, 2005) has linked the production of PRP and the maintenance of memory to the presence of neuromodulators such as dopamine. A phasic increase in dopamine in turn can be caused by behavioral and environmental cues such as novelty, reward prediction error, aversive events,or attention (Ljunberg et al., 1992; Hollerman and Schultz, 1998; Redgrave and Gurney, 2006; Schultz, 2007; Bethus et al., 2010; Lisman et al., 2011). We therefore wondered whether our synaptic model of consolidation could potentially explain behavioral experiments that suggested an important role of novelty for memory retention (Moncada and Viola, 2007; Ballarini et al., 2009; Wang et al., 2010; de Carvalho Myskiw et al., 2013).

In the “behavioral tagging” experiment of Moncada and Viola (2007), a weak electric foot shock in an IA task did not lead to a significant change in the behavior of rats 24 h later, unless rats were exposed to a novel open field (OF) environment within 1 h before or after the electric foot shock. Because exploration of an OF for at least 5 min is known to trigger dopamine release in the rat hippocampus (Li et al., 2003), it has been hypothesized earlier that these behavioral results could potentially be related to the transformation of tagged synapses from early LTP to late LTP through protein synthesis triggering events (Moncada and Viola, 2007).

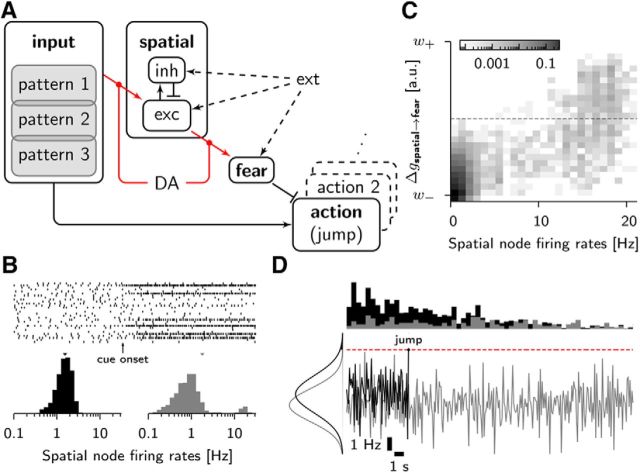
To test this hypothesis in the model, we designed a network consisting of several populations of model neurons (Fig. 5A). A central role is played by a population of excitatory and inhibitory neurons (hippocampal cells or spatial module) representing different spatial contexts (Treves and Rolls, 1992). This spatial context module is driven by a population of input neurons which signal different stimuli representing the known home cage, the training cage containing an elevated platform for IA training, or the novel environment for OF exploration. When an unknown pattern (e.g., training cage or open field) is presented for the first time, the excitatory neurons of the spatial population fire irregularly at ∼1 Hz and with a log-normal firing rate distribution (Fig. 5B; cf. Hromádka et al., 2008). Connections from the input neurons to excitatory neurons in the spatial context pool can undergo plasticity, described by our model of synaptic consolidation. After training, we find that each of the three input patterns is represented by a set of highly active hippocampal neurons that form a memory engram (Ramirez et al., 2013) of the spatial context, similar to a k-winner-take-all system in artificial neural networks (Kohonen, 1982; Maass, 2000) or to sets of place cells in biology (O'Keefe and Nadal, 1971).

Figure 5.

Behavioral simulation paradigm. A, Network architecture. The input consists of three patterns of ∼500 Poisson neurons each with a 10% overlap and projects to the spatial population and to the action units. The spatial cluster is composed of 1000 excitatory AIF neurons and 250 inhibitory LIF neurons that project to the fear population consisting of 100 LIF neurons that inhibit the 10 × 100 AIF action neurons. Background Poisson input (ext) is given to the spatial cluster and to the fear neurons via one-to-one connections (dashed arrows). Plastic connections (or neuromodulation thereof) are shown in red. B, Rate distribution in the spatial module in the absence (black) and during presentation of a spatial cue (gray). The spike raster shows that a few neurons are highly active after stimulus onset. C, Two-dimensional histogram of the momentary synaptic weights from spatial to fear neurons immediately after IA training. The horizontal axis represents the firing rate of neurons in the spatial module while the simulated rat is in the training cage. The gray value indicates the fraction of synapses with a given presynaptic firing rate (horizontal) and a given weight (vertical axis). Only the highly active spatial neurons have strong links to the fear neurons (top-right corner). Other connections remain weak because the weights stay below the barrier (dashed horizontal line) and therefore eventually decay back to the low state. D, Jump mechanism. The simulations are stopped and the jump time is recorded when the firing rate (averaged over 0.1 s) in the majority of the population encoding the action jump hits a threshold (dashed red line). We show two example traces in a naive scenario (black) and in a situation where fear is present (gray). On the left firing rate distributions show the inhibitory effect of encoded fear. Top, Histograms of jump times in the naive case (black) and in a case where fear is present (gray).

The excitatory population of the spatial module projects to the fear population (which represents amygdala neurons; Davis, 1992), again, using plastic synapses described by our model. In nonfearful situations, the fear neurons have a firing rate that is too low to cause any change in the weights of their incoming synapses. In the case of a fearful event, a strong external input increases neuronal activity so that synapses from the currently active spatial neurons to the fear population undergo long-term potentiation, whereas synapses from less active presynaptic neurons to the fear neurons show a limited, transient increase in strength (Fig. 5C).

Finally, fear neurons are connected by inhibitory model synapses to action neurons representing the action “jump down.” Excitatory input from the input pattern coding for the training cage onto the action neurons normally produces the urge to jump down, unless strong inhibitory input from the fear population suppresses the action (“freezing”). In the model, the jump occurs when the population activity of the pool of action neurons reaches a preset threshold (Fig. 5D; see Materials and Methods for details).

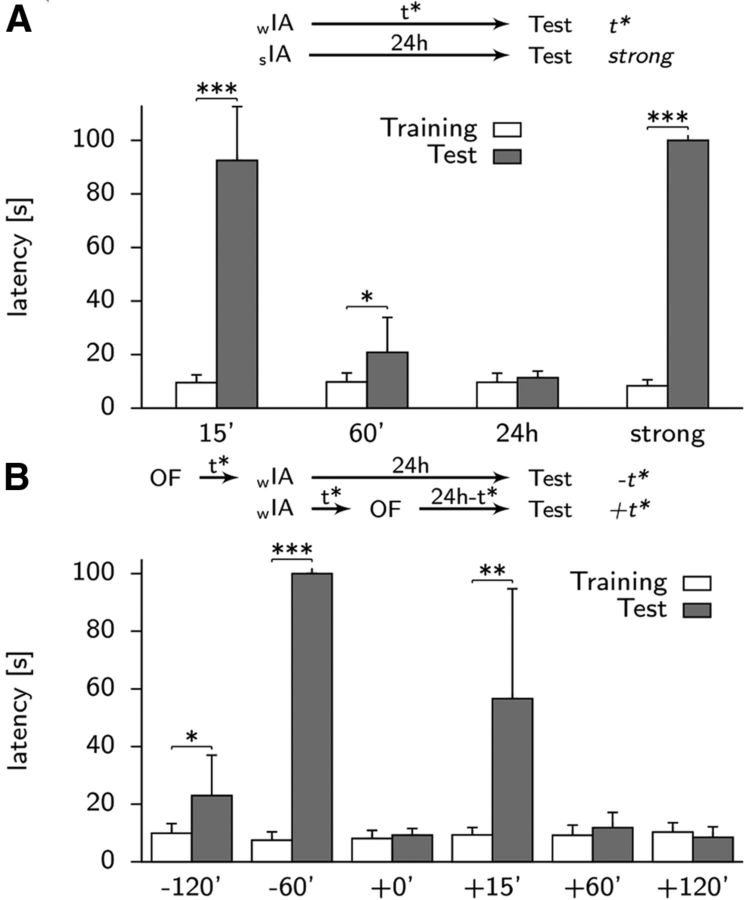
Fear memory was formed in a single trial in the training cage in all four groups of 10 simulated animals each. During training, our simulated rats remained inactive for ∼10 s before the activity threshold for the action jump down was reached. Test sessions after different waiting times (Fig. 6A) indicated that, 15 min after fear encoding, the latency increased to ∼90 s (Group 1), whereas after 60 min (Group 2), latencies were ∼20 s and thus still significantly higher than before training. However, 24 h after the fearful event (Group 3), all memory was lost, indicating that model synapses did not consolidate. A stronger foot shock during training (Group 4), implemented in our model as a phasic dopamine signal, increases the waiting time, measured after 24 h, to ∼100 s (Fig. 6A). In this situation, PRPs triggered by dopamine, can remove the write protection from the tagging-related variable to the scaffold so that synapses from the input to the place representation as well as from the spatial module to the fear neurons are consolidated.

Figure 6.

Behavioral simulations results. A, Latencies during inhibitory avoidance training (white boxes) and at different times t* after training (gray boxes, for t* = 15 min, 60 min, 24 h) in the case of a weak foot shock (paired t tests, n = 10; t* = 15, p < 0.001; t* = 60, p = 0.049). A stronger stimulation involving dopamine delivery (strong) is able to rescue the memory trace (p < 0.001), which otherwise has disappeared after t* = 24 h. Error bars show SD. B, Long-term memory can also be rescued by novelty. If an OF setup was applied to the network either before (−t) or after (+t) the fear encoding in a specific time window, the dopamine delivery associated to it could trigger the necessary protein synthesis to consolidate the synaptic connections (paired t tests, n = 10; t = −120, p = 0.028; t = −60, p < 0.001; t = +15, p = 0.004). The hole at t = +0 is due to a reset of previously formed connections during the OF stimulation. Because it happens within the 10 min window when tags were not set yet, the memory trace is totally erased.

In a second set of simulations, we inserted 5 min of exposure to a novel OF environment either before or after a training session with a weak foot shock. At the end of the exploration period, a dopamine signal (Lisman et al., 2011) triggered by the novel experience was turned on in the model. Six groups of 10 simulated rats were tested 24 h after IA training. In trials in which the OF exploration preceded the IA training, the mean latency of the action jump down was ∼20 s (23 ± 14 s, mean and SD across 10 simulated animals) when the OF exposure was 2 h (Group 1) before, whereas it was 100 ± 2 s when the OF exposure was 1 h (Group 2) before IA training (Fig. 6B). In our model, this outcome was determined by the PRP concentration that remained at the time of exposure to the training cage. The closer the novelty exploration to IA training, the higher the protein concentration and thus the stronger the consolidation of any encoded change in synaptic efficacy (Fig. 7A,B). In experiments, the half-life of PRPs has been measured to be ∼1–2 h (Korz and Frey, 2004).

Figure 7.

Synaptic traces during behavioral protocol. A, OF exploration preceding inhibitory avoidance training (OF → IA) by 1 h. Top, Weight traces of three individual synapses (blue lines) from input neurons active in the training cage to neurons in the spatial population. Bottom, Mean weight over all synapses originating from input neurons that are highly active in the training cage. B, As in A but with a delay of 2 h between OF and training. C, OF exploration following inhibitory avoidance training after 30 s. Top, Individual synaptic weight traces. Bottom, Mean synaptic weight. Note the rapid increase and immediate reset of weights. D, As in C but with a time difference of 15 min. During OF exposure, synapses are depotentiated. Whereas one of the sample synaptic weight traces (blue) remains at the low value after the OF stimulation, two others recover to their high values. The result for the mean weight (black line, 113% at t = 15 minutes and 109% at t = 40 minutes) indicates that ∼70% of those synapses that were tagged before OF exposure returned to their high efficacy values thereafter.

In trials in which the OF exploration followed the IA training, memory retention is maximal for a delay of +15 min (Group 4) with latencies of ∼60 s (57 ± 38 s mean and SD across 10 simulated animals; Fig. 6B), in agreement with experimental results. In the model, memory retention after 24 h is weak (not significantly different from the first trial) if the interval between OF and avoidance training is +60 min or more (Groups 5 and 6).

Interestingly, the increase in latency to jump is negligible (Fig. 6B) if the delay is +0 min (Group 3), indicating an interference of the two spatial environments, in agreement with experiments (Moncada and Viola, 2007).

In the model, a 5 minute exploration of the OF is described by an input population where many neurons fire at ∼1 Hz, whereas a few neurons fire at a higher rate (see Materials and Methods). During the creation of a neural representation of the OF in the spatial module, neurons in the module are active and receive at the same time low presynaptic activity from the input neurons. The coactivation of presynaptic and postsynaptic neurons (with low presynaptic activity) leads to depotentiation of synapses that were previously potentiated during the training cage exposure (Fig. 7C). Because depotentiation within <5 min implies that initial LTP cannot be transformed to e-LTP (Fig. 4A), the spatial context of the training cage is not remembered, observable in the behavioral experiment as “interference” between the two environments.

Our model of synaptic traces thus links behavioral results (Moncada and Viola, 2007) to the electrophysiology of synapses during depotentiation protocols (Sajikumar and Frey, 2004a).

Based on the above link between synapse electrophysiology and behavior, we hypothesized that delayed OF exposure would correspond in our model to a delayed depotentiation event on previously potentiated synapses. As discussed earlier in Figure 1E, a delayed depotentiation event gives the synaptic dynamics enough time to overcome write protection of the tagging-related variable so that e-LTP is formed. In analogy to Figure 1E, we therefore expect that, during an experiment in which IA is followed by OF 15 min later, some synapses switch from weak to strong (induced by potentiation during IA training), then to weak (induced by depotentiation during OF exposure), and finally back to strong values because the tagging-related variable in the up state pulls the weights back up (Fig. 7D). In the behavioral experiment, the spatial context of the training cage is encoded during IA training in the synapses from the input neurons to the spatial module neurons.

Indeed, we find that, during IA training, synapses that connect highly active input neurons to active spatial module neurons switch to the high state (see three sample traces in Fig. 7D). These synapses are subsequently tagged and tags have not yet decayed back when, after a delay of 15 min, the OF stimulus starts. While the OF stimulus rapidly resets the weights to low values (see the three sample traces in Fig. 7D at t = 15 min), the previously tagged synapses can take advantage of the PRP triggered by the dopamine wave caused by the OF environment. Therefore the tagging-related variable in the up state can be further stabilized by changes in the scaffold, leading to a final switch to the stable high state of ∼70% of the previously tagged synapses (Fig. 7D, black trace). Therefore, the spatial context of the IA training stored in the synapses onto neurons in the spatial module is consolidated and remembered over a long time.

We expect that more detailed behavioral memory models that include theta cycles and memory replay during sharp-wave ripples (Lubenov and Siapas, 2008) would change the quantitative latency results, but not the qualitative structure of the above argument.

Predictions of behavioral tagging model

Our simulations provide an explicit link between cellular and behavioral consolidation mechanisms (Bekinschtein et al., 2007; Moncada and Viola, 2007; Wang et al., 2010) and make two specific predictions.

Novel stimuli can rescue long-term memory when given either before or after fear memory encoding, but not if the novel stimulus directly follows the IA training (see the “hole” at + 0 min in Fig. 6B). First, our model predicts that this hole is caused by depotentiation of synapses. In particular, the model predicts that the hole is asymmetric in time: whereas a novel stimulus immediately after a “to-be-learned” event can reset the learning, a novel stimulus that preceded the learning event cannot. This prediction may look surprising in view of the existing literature (cf. Ballarini et al., 2009 vs Moncada and Viola, 2007).

Second, for a delay of the novel open field of 15 min, our model predicts that single synapses make multiple transitions (e.g., weak-strong-weak-strong; Fig. 7D). The sequence of transitions could be visible as a sequence of several abrupt changes in presynaptic release probability, postsynaptic density of AMPA receptors, intraspine actin networks, or spine volume. Similar changes of single synapses would also be expected in vitro under a suitable potentiation-depotentiation protocol. The sequence of back-forth transitions may be considered as a very characteristic, and strong, prediction of the model.

Discussion

Our synapse model accounts for slice and behavioral data using three variables: the synaptic weight, the tagging-related variable and the scaffold. The coupling between these quantities is controlled by a write-protection mechanism, which is described by two further variables. Here, we discuss the biological and functional interpretation and potential generalizations and predictions of the model.

Biological interpretation

A model with five variables likely represents the simplest formulation of a phenomenological model. A reduction in the number of variables would explain significantly fewer experiments (Materials and Methods). The variables represent “reporters” indicating important changes in the molecular configuration of the synapse and should not be viewed as single molecules.

Although the synaptic weight can be measured experimentally, the tagging-related and scaffold-related variables are hidden, requiring indirect deduction. The initial weight change in the model after LTP induction can connect to an increase in the amount, and phosphorylation state, of AMPA receptors (AMPARs) in the postsynaptic density of the postsynaptic membrane (Lisman et al., 2002; Redondo and Morris, 2011). In addition, presynaptic factors can also change synaptic efficacy (Tsodyks et al., 1998; Redondo and Morris, 2011).

Ca²⁺ influx in the postsynaptic density through NMDA receptors induces the early weight changes and tag setting in hippocampal synapses (Navakkode et al., 2007), but our model explicitly describes neither NMDA nor Ca²⁺ (Smolen et al., 2012). The tag corresponds to a complex synaptic state including several molecules and signaling cascades (Redondo and Morris, 2011). In hippocampal synapses, calcineurin participates in setting tags for LTD (Zhou et al., 2004). Fluorescence imaging of spines suggests a transient role for CaMKII during tag setting for LTP (Lee et al., 2009). Tag-related processes include transformations in intraspine actin networks (Lee et al., 2009; Okamoto et al., 2009; Redondo and Morris, 2011). Our phenomenological model summarizes the signal processing chain during tagging by one single tagging-related variable. Tag setting for LTP (LTD) corresponds to the state transition “tag down → tag up” (“tag up → tag down”) while the scaffold variable remains small (large). If the changes are consolidated, the tagging-related variable remains in its new state while the scaffold switches to large.

The scaffold variable also does not correspond to a single molecule, because at least two mechanisms contribute to sustained changes in synaptic efficacy (Cingolani and Goda, 2008): first, the creation of new slots for inserting AMPARs in the membrane and, second, a structural reconfiguration of the whole postsynaptic density. Furthermore, the list of proteins linked to maintenance of LTP remains incomplete, but likely includes GluR1, Homer1a, PKMζ, and ARC (Miyashita et al., 2008).

Write protection and neuromodulators

The three variables (weight, tag, and scaffold) are coupled to each other. In the absence of stimulation, the scaffold influences the tagging-related variable and the latter the weight, whereas influences in the opposite direction are impossible due to write protection. The write protection from weight to the tagging-related variable is removed only when the stimulus is sufficiently strong or sustained so that, after low-pass filtering, a threshold is attained. This integrate-and-threshold mechanism secures that ongoing small weight fluctuations cannot lead to long-term changes (Brader et al., 2007; Elliott and Lagogiannis, 2012).

Although the removal of this first write protection is synapse specific, the removal of the write protection from the tagging-related variable to the scaffold is not. However, because the tagging-related variable in our model is synapse specific, only those synapses that have previously been marked by a tag can be consolidated (Frey and Morris, 1997). The synthesis of PRPs, which is necessary for the removal of the second write protection, requires the presence of dopamine or other neuromodulators. Dopamine is broadly diffused across several brain areas (Foote and Morrison, 1987; Gasbarri et al., 1994) and would therefore be likely to be available in many cells at about the same time. However, whereas dopamine is necessary to trigger synthesis of PRPs in hippocampal neurons, it is not sufficient if other conditions are not met.

Complications of such a simple picture arise because of multiple neuromodulators and spatial compartmentalization. First, different neuromodulators may target different dendritic compartments of a given neuron (Reymann and Frey, 2007) and different neurons. Second, synthesized PRPs are not uniformly spread out across the dendrite, but remain localized in different dendritic compartments (Kelleher et al., 2004; Govindarajan et al., 2006; Redondo and Morris, 2011). Extensions of our synapse model toward multicompartment neurons with locally shared PRPs (Govindarajan et al., 2006; O'Donnell and Sejnowski, 2014) are possible and would allow for competition between synapses for proteins (Fonseca et al., 2006).

Because dopamine (or other neuromodulators) is necessary for consolidation of weight changes, models of synaptic tagging and capture formally resemble the reward signal of reinforcement learning and R-STDP (Sutton and Barto, 1998; Izhikevich, 2007). In these theories, learning rules make use of an eligibility trace that represents potential changes, only transformed into effective synaptic alterations upon arrival of an external reward signal (Crow, 1968; Izhikevich, 2007; Frémaux et al., 2010; Frégnac et al., 2010; Pawlak et al., 2010).

Three important differences are worthy of discussion. First, whereas eligibility traces in reinforcement learning are invisible, in our model, the synaptic changes after LTP induction are visible as real weight changes a few seconds or minutes after induction, even if they are not consolidated later on. Second, the relevant timescale of eligibility traces in reinforcement learning is one or a few seconds, whereas the lifetime of tags is on the order of an hour. Third, whereas in reinforcement learning, dopamine is related to the reward (Schultz et al., 1997; Sutton and Barto, 1998; Schultz, 2007), in our model, the neuromodulator could also represent novelty, surprise, or “interestingness” of a stimulus (Redgrave and Gurney, 2006; Bethus et al., 2010; Lisman et al., 2011), similar to classic (Carpenter and Grossberg, 1987) or modern (Schmidhuber, 2006; Brea et al., 2013; Rezende and Gerstner, 2014) learning theories.

Conceptual predictions

First, our model exhibits a two-step write protection mechanism that is very different from the classic STC model. Under a hypothetical drug that prevents tag-setting while allowing the induction of LTP in a behavioral experiment, our model would predict that, if injected before encoding, the drug would leave short-term memory unchanged, but would disrupt consolidation into long-term memory. The result would thus be similar to that with protein synthesis inhibitors (that disrupt the transition from tagged to consolidated state), but the signaling chain would be interrupted earlier (from LTP induction to tagging). Similarly, a weak LTP-inducing stimulus that is not strong enough to overcome the write protection to the tag could be sufficient to set tags in the presence of ryanodine, known to facilitate the tag transition (Sajikumar et al., 2009).

Second, imagine a hypothetical experiment in which a stable and large synapse is pharmacologically manipulated by a direct change of the scaffold to the small state while keeping the weight and tagging-related variables in the strong and up state, respectively. After the manipulation, the configuration of the synapse is then identical to an initially weak synapse that underwent a strong LTP protocol. Therefore, we predict that, in the absence of dopamine or PRPs, the synapse would decay on the timescale of 1 h, whereas in the presence of dopamine or PRPs, it would reconsolidate to the stable strong state—even if no potentiating or depotentiating stimulus is applied.

Third, in our model, the notion of tag has undergone a fundamental shift. In the classic conceptual model of STC (Frey and Morris, 1997), as well as in early mathematical models (Clopath et al., 2008), the tag is assumed to be some transiently activated chemical compound. In our model, however, the tag is the difference between two synaptic variables, one tagging related and the other scaffold related. Our model predicts that the tagging-related variable exhibits transient state changes only in synapses that are not consolidated after an LTP- or LTD-inducing protocol. This reinterpretation may change the spectrum of candidates for tagging-related compounds (Lisman et al., 2011; Redondo and Morris, 2011).

Finally, although parameters of our model have been optimized for hippocampus, we believe that the same model should also be applicable to other brain areas, albeit with different parameters. For example, we predict that, in brain areas where induction of weight changes and removal of the first write protection occur on the same timescale and with the same stimulation threshold, tag-resetting experiments with subsequent recovery of the weight will not be possible.

Extensions and conclusions

Our model of synaptic plasticity accounts for a large variety of STC experiments and makes a link from synapses to behavior. Functionally, the model combines several aspects contributing to memory lifetime, in particular write protection (Crow, 1968), multiple timescales (Fusi et al., 2005), and bistability of essential components (Crick, 1984; Lisman, 1985). Extensions of the model should aim at inclusion of spatial compartmentalization of PRP (Kelleher et al., 2004; Fonseca et al., 2006; Govindarajan et al., 2006; O'Donnell and Sejnowski, 2014), explicit modeling of neuromodulator signals in terms of novelty and surprise (Schmidhuber, 2006; Rezende and Gerstner, 2014), as well as tests of the model in a broader set of behavioral paradigms (Wang et al., 2010; Ramirez et al., 2013; Li et al., 2014). Our model focused on consolidation at the synaptic level, whereas other mechanisms at the system level, such as theta rhythms, replay, and slow-wave sleep, also affect memory maintenance (Lubenov and Siapas, 2008; Rossato et al., 2009). Nonetheless, we have been able to show that the STC data are sufficient to capture the essence of behavioral phenomena observed in an IA task (Moncada and Viola, 2007).