Monitoring of Vacuolar-Type H⁺ ATPase-Mediated Proton Influx into Synaptic Vesicles

Abstract

During synaptic vesicle (SV) recycling, the vacuolar-type H⁺ ATPase creates a proton electrochemical gradient (ΔμH⁺) that drives neurotransmitter loading into SVs. Given the low estimates of free luminal protons, it has been envisioned that the influx of a limited number of protons suffices to establish ΔμH⁺. Consistent with this, the time constant of SV re-acidification was reported to be <5 s, much faster than glutamate loading (τ of ∼15 s) and thus unlikely to be rate limiting for neurotransmitter loading. However, such estimates have relied on pHluorin-based probes that lack sensitivity in the lower luminal pH range. Here, we reexamined re-acidification kinetics using the mOrange2-based probe that should report the SV pH more accurately. In recordings from cultured mouse hippocampal neurons, we found that re-acidification took substantially longer (τ of ∼15 s) than estimated previously. In addition, we found that the SV lumen exhibited a large buffering capacity (∼57 mm/pH), corresponding to an accumulation of ∼1200 protons during re-acidification. Together, our results uncover hitherto unrecognized robust proton influx and storage in SVs that can restrict the rate of neurotransmitter refilling.

Introduction

Maintenance of synaptic transmission requires the retrieval and reuse of neurotransmitter-laden synaptic vesicles (SVs; Harata et al., 2001; Sudhof, 2004). After endocytosis, newly regenerated SVs are energized by the activity of the vacuolar-type H⁺ ATPase (V-ATPase), a process that powers the refilling of neurotransmitters into SVs through their respective vesicular transporters (Edwards, 2007). Because complete blockade or partial disturbance of the proton electrochemical gradient (ΔμH⁺) can lead to alterations in quantal release, as well as short-term plasticity during a sustained stimulation (Zhou et al., 2000; Ertunc et al., 2007), the generation of ΔμH⁺ is crucial to ensure the fidelity of synaptic transmission. However, to date, a quantitative description of proton influx into SVs at living synapses has not been provided. Nonetheless, because of the low estimates of free protons in the SV lumen, it has been envisioned that ΔμH⁺ can be made and dissipated with the flux of a limited number of protons (Blakely and Edwards, 2012).

In support of this notion, SV re-acidification has been reported previously to occur with a relatively fast time constant (τ of ∼3–5 s; Atluri and Ryan, 2006; Balaji and Ryan, 2007; Granseth and Lagnado, 2008; Kwon and Chapman, 2011). The aforementioned studies used the same indicator of vesicular pH (pH_v); the pH-sensitive fluorescent protein pHluorin fused to one of the major SV proteins (Miesenböck et al., 1998). SV re-acidification was approximated from the decay of pHluorin fluorescence, from either single vesicle events or newly endocytosed re-acidifying SVs after repetitive stimulation. These estimates of re-acidification kinetics were substantially faster than those of glutamate loading (τ of ∼15 s; Hori and Takahashi, 2012) and vesicle reuse (∼30 s; Ryan et al., 1993), indicating that, under physiological conditions, the generation of ΔμH⁺ may not be a rate-limiting step for the refilling and reuse of SVs.

Despite the fact that the pHluorin-based probes have been used frequently to monitor the re-acidification process during SV recycling, we were concerned that previous measurements suffered from the limited response range of pHluorin to the luminal pH. Given that the resting pH_v of SVs is ∼5.7 (Miesenböck et al., 1998), it is reasonable to assume that the pKa of pHluorin (∼7.1; Sankaranarayanan et al., 2000) is too high to precisely monitor the late, acidic phase of re-acidification, which would thus lead to an underestimation of re-acidification kinetics. Therefore, in this study, we re-investigated re-acidification kinetics by using the mOrange2 probe (Shaner et al., 2008), whose pKa is optimal for measuring the luminal pH of SVs. In addition, the previous pHluorin-based studies have focused exclusively on vesicular free [H⁺] and did not consider the amount of total proton influx in SVs that would have affected the electrical component of ΔμH⁺. Therefore, we measured the luminal buffering capacity (BC) of SVs to estimate the net proton influx during re-acidification.

Materials and Methods

Molecular biology.

To express synaptophysin–mOrange2 (syp–mOr) and synaptophysin–pHluorin (sypHy) in a neuron-specific manner, we used lentivirus-based vectors in combination with the Tet-Off system (Hioki et al., 2009). Two vectors were used: (1) a “regulator” vector expressing an advanced tetracycline transactivator under the control of human synapsin1 promoter; and (2) a “response” vector that expressed sypHy or syp–mOr under the control of a modified tetracycline-response element (TRE) composite promoter. SypHy incorporated into a pEGFP–C1 vector (a kind gift from Dr. L. Lagnado, London, UK) and mOrange2 positioned within a pTEC16 vector (Addgene) were amplified by PCR and inserted independently into the plenti6pPW vector that included a TRE promoter (a kind gift from Dr. Y. Fukazawa, Nagoya, Japan).

Neuronal cultures.

Primary hippocampal cultures were prepared from 0- to 1-d-old wild-type ICR or C57BL/6 mice of either sex as described previously (Kumamaru et al., 2014). Results from both lines were identical and thus pooled. Briefly, hippocampal cells dissociated after incubation in 20 μg/ml papain (Worthington) were plated onto 27-mm-diameter glass-bottom dishes (FPI), coated with 1 mg/ml poly-d-lysine (Sigma) at a density of 25,000–30,000 cells/cm², and kept in a 5% CO₂ humidified incubator. At 3 d in vitro (DIV), 40 μm fluorodeoxyuridine (Sigma) and 100 μm uridine (Sigma) were added to inhibit the growth of glial cells. One-third of the culture medium was replaced with fresh medium every 3–4 d. At 6–7 DIV, cultures were infected with a pair of lentiviruses. Infected cultures were then imaged at 13–16 DIV. Animals were purchased from Shimizu Laboratory Supplies and treated according to our institutional guidelines for the care and use of animals.

Lentivirus production.

The lentiviruses used to express sypHy and syp–mOr in cultured neurons were produced in human embryonic kidney (HEK) 293T cells, using a protocol modified from a previous report (Naldini et al., 1996). Briefly, HEK 293T cells were transfected with the lentiviral backbone and helper plasmids using a calcium phosphate transfection method (Chen and Okayama, 1987). Ten to 16 h after transfection, culture medium was replaced with fresh DMEM supplemented with 10 μm forskolin (Calbiochem). Supernatants were collected at 24 and 48 h after transfection and centrifuged at 3000 rpm for 5 min. Viral particles were concentrated ∼100 times using PEG-it Virus Precipitation Solution (System Biosciences) according to the instructions of the manufacturer.

Fluorescence imaging.

Cells cultured on a 27-mm-diameter glass-bottom dish were placed in a custom-made imaging chamber on a movable stage (Scientifica) and perfused continuously with standard extracellular solution containing the following (in mm): 140 NaCl, 2.4 KCl, 10 HEPES, 10 glucose, 2 CaCl₂, 1 MgCl₂, 0.02 CNQX, and 0.025 d-APV, pH 7.4. Solutions used during image acquisition were applied directly onto the area of interest with a combination of a fast flow exchange microperfusion device (Warner Instruments) and a bulb controller (BioResearch Center), both of which were controlled by Clampex 10 (Axon Instruments). For acid quench of surface probes, MES-buffered (pKa 6.1, 10 mm) solution at pH 5.5 was applied. Acidic buffer treatment frequently induced a fluorescence transient in the cultured cells, probably attributable to an increase in neuronal firing. To prevent this, Ca²⁺-free solutions were used over the entire image acquisition except during electrical stimulation, at which point a standard extracellular solution was applied. When CaCl₂ was removed from the extracellular solution, MgCl₂ was increased to 3 mm to keep the divalent ion concentration constant. Field electrical stimulation was delivered via a theta glass pipette (20–40 μm tip diameter) filled with the extracellular solution and positioned ∼1 mm away from the target boutons. A mixture of ionophores composed of 20 μm carbonyl cyanide p-trifluoromethoxyphenylhydrazone (FCCP), 10 μm valinomycin, 10 μm nigericin, and 0.02% Triton X-100 in K⁺-rich calibration solution (see below) at pH 7.4 was puff applied onto target boutons using a pulse pressure device (WPI). The puffer pipette had a tip diameter of 3–5 μm and was generally positioned ∼1 mm in the horizontal plane and 500–700 μm above from the target boutons.

Fluorescence live imaging was performed at room temperature (∼24°C) on an inverted microscope (Olympus) equipped with a 60× (1.35 numerical aperture) oil-immersion objective and 75 W xenon lamp. Images (600 × 900 pixels) were acquired with a scientific cMOS camera (Andor) in a streaming mode at five frames per second under the control of MetaMorph software (Molecular Devices). sypHy was imaged with 470/22 nm excitation and 514/30 nm emission filters. syp–mOr was imaged with 556/20 nm excitation and 600/50 nm emission filters.

Spectral measurement of syp–mOr fluorescence was performed in various Cl⁻ concentrations using a fluorometer (Hitachi). Briefly, syp–mOr was expressed in HEK 293T cells using Ca²⁺-phosphate transfection and extracted by incubating the collected cell pellet in solutions with various Cl⁻ concentrations and 0.1% Triton X-100 for 15 min. The same amount of cell pellet was used for each sample to obtain similar protein content among samples. To prepare solutions with different Cl⁻ concentration, the following two solutions were mixed: (1) 140 mm NaCl and 10 mm HEPES, pH7.4; and (2) 140 mm Na-gluconate and 10 mm HEPES, pH7.4. After solubilization, the lysates were centrifuged at 12,000 rpm for 10 min at 4°C, and supernatants were used for spectral measurements. The excitation wavelength was fixed at 545 nm, and the emission was scanned from 550 to 630 nm.

Estimation of the pKa and Hill coefficient of pH probes.

Measurements of sypHy and syp–mOr fluorescence were performed in cultured neurons under conditions of defined pH. Neurons were treated with a mixture of ionophores composed of 20 μm FCCP, 10 μm valinomycin, 10 μm nigericin, 2 μm bafilomycin A₁, and 0.02% Triton X-100 in standard extracellular solution to equilibrate the pH_v to extracellular pH. Neurons were then exposed to K⁺-rich calibration solutions that were clamped at a given pH. The calibration solution contained the following (in mm): 122.4 KCl, 20 NaCl, 10 HEPES or MES, 10 glucose, 2 CaCl₂, and 1 MgCl₂. MES buffer was used for solutions with pH set to below 6.2, and HEPES buffer was used for solutions with pH set above 6.8. The fluorescent intensities at each pH were normalized to that at pH 8.6 (Fig. 1A) and fitted with the following equation:

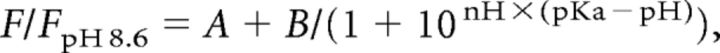where pKa is the pH at which 50% of the probe molecules are protonated, and nH is the Hill coefficient, which is proportional to slope of the fitting curve at pKa. Parameters A and B are signal offset and gain, respectively. pKa and nH values (as well as A and B) were obtained by the least squares method using Microsoft Excel software.

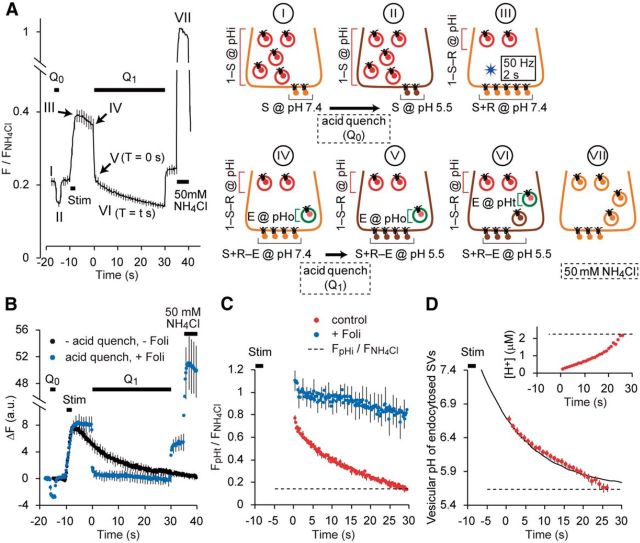
Figure 1.

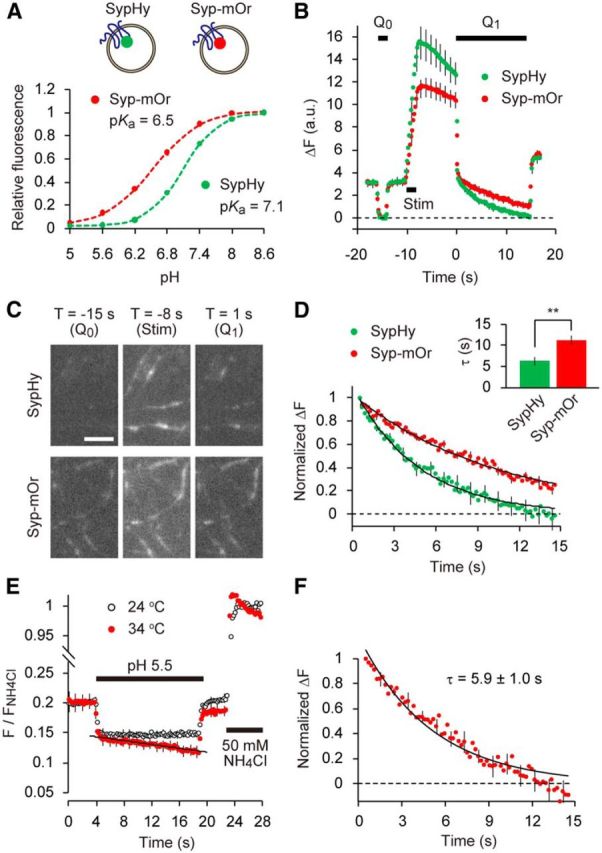
SV re-acidification monitored by mOrange2. A, Titrations of sypHy (green) and syp–mOr (red) expressed in cultured hippocampal neurons. pHluorin and mOrange2 were positioned at the luminal part of synaptophysin. Fluorescence intensities at each pH were normalized to those at pH 8.6 and were expressed as a function of pH. Both data were well fitted by a single-site titration model (see Materials and Methods). The pKa and nH were determined as 6.54 ± 0.05 and 0.99 ± 0.02 for syp–mOr and 7.09 ± 0.02 and 1.35 ± 0.02 for sypHy (n = 6 experiments with 38 boutons for sypHy and n = 5 experiments with 64 boutons for syp–mOr). B, Comparison of fluorescence between sypHy and syp–mOr during the acid-quench experiment. Acidic solution (pH 5.5) was applied before (Q₀) and after (Q₁) field electrical stimulation (50 Hz, 2 s). The decay in fluorescence during poststimulus acid quench (Q₁) represented re-acidification of the endocytosed SVs retrieved within an 8 s interval (n = 14 experiments with 280 boutons for sypHy and n = 14 experiments with 214 boutons for syp–mOr). C, Fluorescence images of presynaptic boutons expressing sypHy (top) and syp–mOr (bottom), during Q₀, 50 Hz stimulus and at the onset of Q₁. T indicates a time point on the horizontal axis of the plot shown in B. Scale bar, 5 μm. D, The fluorescence from sypHy and syp–mOr during poststimulus acid quench (Q₁) shown in B was normalized to the fluorescence during Q₀. Inset, The time constant obtained from a single-exponential fit to the syp–mOr fluorescence was significantly larger than that to sypHy fluorescence (**p < 0.01, Student's t test). E, Temperature-dependent effect of acid exposure on syp–mOr fluorescence. Fluorescence was monitored at either 24°C (room temperature; black open circles) or 34°C (physiological temperature; red filled circles) and normalized to the fluorescence obtained by 50 mm NH₄Cl application (n = 7 experiments with 104 boutons for 24°C and n = 7 experiments with 140 boutons for 34°C). The fluorescence apparently declined at 34°C, which was linearly fitted with a slope of −0.0016 ± 0.0004 s⁻¹. This artificial decline of baseline fluorescence also potentially contributed to the fluorescence decay during poststimulus acid quench when measured at 34°C. F, Normalized fluorescence decay during re-acidification measured at 34°C (n = 10 experiments with 154 boutons). To obtain this, acid-quench experiments were performed similar to B and combined with 50 mm NH₄Cl application. F/F_NH4Cl during acid treatment was corrected by subtracting the re-acidification-independent decline seen in E. Dashed line indicates the fluorescence during Q₀. Error bars indicate SEM.

Estimation of pH_v.

Resting pH_v was estimated in the manner that is conceptually similar to a previous study by Mitchell and Ryan (2004), albeit with some differences in the calculations. We further developed this method to estimate the pH_v of endocytosed re-acidifying SVs from syp–mOr fluorescence during poststimulus acid quench. The total fluorescence of syp–mOr in a given terminal is thought to be the sum of the fluorescence derived from different probe fractions, including those on the cell surface, those within resting SVs, and those within already-endocytosed “re-acidifying” SVs. As illustrated in Figure 2A, we modeled the contribution of individual probe fractions to the total fluorescence during the measurement and derived values of pH_v arising from endocytosed re-acidifying SVs. Detailed procedures are described in Results (Fig. 2).

Figure 2.

Estimate of pH_v from syp–mOr fluorescence. A, Average trace of syp–mOr fluorescence during acid-quench experiments with 30 s Q₁ (n = 27 experiments with 263 boutons) and a schematic illustration of the experiment. We divided the time course of fluorescence measurement into seven steps, indicated by I–VII (trace), and modeled the contributions of individual probe fractions to the total fluorescence at each step (images depicting the presynaptic terminal). The three different probe fractions consisted of the surface, resting, and endocytosed “re-acidifying” SVs, which were indicated by gray, red, and green lines, respectively. From step I to step VI, each fraction was described by a combination of the initial surface fraction (S), released fraction (R) and the endocytosed fraction retrieved by the onset of poststimulus quench (E). The endocytosed fraction retrieved during acid quench (brown SV in step VI) was indistinguishable from the quenched surface fraction and was thus not considered in the analysis. The resting pH_v was indicated as pHi. The pH_v of endocytosed SVs at the onset of (T = 0 s) and during (T = t s) the poststimulus quench are shown as pHo and pHt, respectively. Fluorescence during the application of 50 mm NH₄Cl (step VII) was used for signal normalization. B, Average changes in syp–mOr fluorescence (n = 10 experiments with 72 boutons) in control (black) and in the presence of 120 nm folimycin (blue) measured sequentially in the same boutons. Acid quenching (Q₀, Q₁) was performed only in the presence of folimycin (Foli). The peak amplitude of ΔF was not significantly changed in the presence of folimycin (p = 0.84, Student's t test), indicating that substantial endocytosis did not occur during electrical stimulation (50 Hz, 2 s). C, Normalized fluorescence of the endocytosed re-acidifying fraction calculated according to the above model. Results in the absence (red) and presence (blue) of folimycin were obtained from the acid-quench experiment shown in A and B, respectively. The dashed line refers to normalized fluorescence from resting SVs, calculated from the trace shown in A. D, Average pH_v of endocytosed fraction. Normalized fluorescence from C (red trace) was segmented into bins with a width of 1 s and converted to pH. The binning process was performed to reduce uncertainty in the pH calculation, especially at low signal level. However, in a few cases, fluorescence values in the last few seconds could not be converted to pH and were thus excluded. A single-exponential fitting yielded a time constant for re-acidification of 14.9 ± 1.7 s. The dashed line indicates the resting pH_v, which corresponded to 5.64 ± 0.03. Inset, [H⁺]_v in the lumen of endocytosed SVs calculated from the average plot of the pH_v. Dashed line indicates [H⁺] in the resting state. Error bars indicate SEM.

Calculation of the BC.

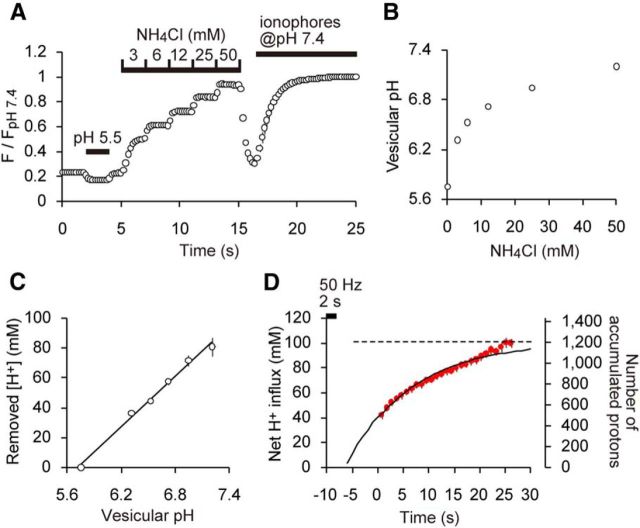
The BC of SV lumen was estimated using an ammonium pulse method described previously (Gekle and Silbernagl, 1995; Barriere et al., 2009) with some modifications. syp–mOr fluorescence was measured during the application of various concentrations of NH₄Cl. Because ammonia is a membrane-permeable weak base, the treatment induced a rapid increase in pH_v. BC was defined as the amount of acid or base required to shift the pH by one unit and was calculated as thus:

where Δ[NH₄⁺]_v is the change in ammonium ion concentration inside the SV lumen and ΔpH_v is the change in pH_v.

pH_v was calculated for each individual NH₄Cl application using the same method for estimating the resting pH_v (see Results), except that the fluorescence was normalized to that measured during the application of the ionophore mixture rather than 50 mm NH₄Cl treatment, the former of which faithfully clamped pH_v at 7.4. [NH₄⁺]_v was equivalent to the amount of protons removed from SVs and calculated as follows:

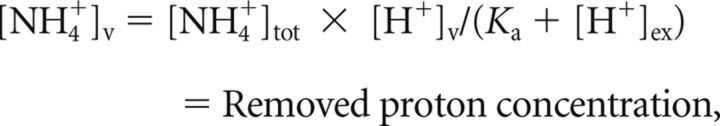where [NH₄⁺]_tot represents the applied NH₄Cl concentration, [H⁺]_v is the vesicular proton concentration, [H⁺]_ex is the extracellular proton concentration, and K_a is the dissociation constant of NH₄⁺. Removed proton concentrations were plotted against resulting pH_vs in Figure 5C and demonstrated a linear relationship. BC was estimated as the slope of the linear fit.

Figure 5.

Luminal BC of SVs. A, Average trace of syp–mOr fluorescence in response to stepwise NH₄⁺ treatments (n = 14 experiments with 215 boutons). For pH calibration, a solution of pH 5.5 was applied for 2 s before the NH₄⁺ applications, and a solution of pH 7.4 containing a mixture of ionophores was applied at the end of imaging. Fluorescence was normalized to the value at pH 7.4. B, Resulting pH_v as a function of NH₄⁺ concentration. C, Relationship between quenched [H⁺] and resulting pH_v. The slope of a linear fit revealed that the BC of SVs was 57.4 ± 4.8 mm/pH regardless of luminal pH. D, Estimated H⁺ influx during acid quench. Net H⁺ influx (in millimolar at the left axis) and the number of accumulated protons (right axis) were calculated based on Figure 2D and the measured BC.

Image analysis.

Acquired images were analyzed using MetaMorph software. Active synapses were identified by changes in live measurements of sypHy or syp–mOr fluorescence. Changes in fluorescence were quantified by subtracting an average of five consecutive images taken during an initial baseline period from the average of five consecutive images taken just after the electrical stimulation. Circular region of interests (ROIs; 2.26 μm diameter and 4 μm² area) were positioned manually at the center of the highlighted fluorescence puncta. Another five ROIs of the same size were positioned at regions in which no cell structures were visible, and their average fluorescence was subtracted as a background signal. For acid-quench experiments (five frames per second acquisition rate in a streaming mode for 65 s), photobleaching may have affected the small signal change during surface quenching. Thus, before each experiment, the extent of photobleaching was quantified at each bouton using the same image acquisition protocol, without any experimental manipulation. The averaged decay in F/F₀ was fitted with a double exponential, which was used to correct the signal from the subsequent recording. For BC measurements, we selected puncta that showed stable signals during treatment with the ionophore mixture. This was necessary to ensure precise estimation of the pH_v. Data of <20 boutons from a single experiment were averaged and counted as n = 1. Data were collected from at least five different dishes.

Results

Re-acidification of SVs monitored by syp–mOr probe

For greater accuracy in pH_v measurements, we chose mOrange2 (pKa of ∼6.5) as a pH probe and fused it to the second luminal loop of synaptophysin (syp–mOr). Both syp–mOr and sypHy (a super ecliptic-pHluorin fused to synaptophysin at the same position; Granseth et al., 2006) were expressed in cultured hippocampal neurons and exhibited a punctate distribution that mostly overlapped with antibody labeling of the presynaptic marker synaptotagmin I (data not shown). By performing pH titration of syp–mOr in neurons treated with a mixture of ionophores, we confirmed that syp–mOr retained the intrinsic pKa of mOrange2 (∼6.5; Fig. 1A). Our initial trials to resolve syp–mOr fluorescence changes that resulted from single action potentials failed because of the substantial background fluorescence from resting SVs, as well as a relatively small fluorescence jump (ΔF) elicited by a pH shift from rest to 7.4. Therefore, we used the “acid-quenching” method developed by Atluri and Ryan (2006). After repetitive electrical stimulation and an interval of several seconds, the surface pool of syp–mOr was quenched rapidly by treatment with an acidic solution (pH 5.5; Q₁; Fig. 1B). Thus, only fluorescence from SVs endocytosed by the onset of acidic treatment was followed. Fluorescence arising exclusively from the resting SVs before the stimulation was estimated by a brief application of acidic solution before the repetitive stimulation (Q₀). These values defined the baseline fluorescence for fitting traces during the second acid application (Q₁; see also below). Eight seconds after electrical stimulation (100 pulses at 50 Hz), we found that both sypHy and syp–mOr fluorescence declined markedly during the Q₁ phase (Fig. 1B,C). In Figure 1D, we compared the fluorescence of sypHy and syp–mOr during Q₁. Values were normalized by taking the fluorescence at the beginning of Q₁ as 1.0 and the average fluorescence during Q₀ as 0.0. The decay of sypHy fluorescence during the 15 s poststimulus acid quench was described by a single-exponential function with an apparent time constant of 6.3 ± 0.9 s, which was in close agreement with previous reports (Atluri and Ryan, 2006; Granseth and Lagnado, 2008; Kwon and Chapman, 2011). In contrast, the fluorescence decay of syp–mOr was substantially slower than that of sypHy and was fitted by an exponential function with a τ of 11.3 ± 1.1 s (Fig. 1D), suggesting that post-endocytic re-acidification takes longer than reported previously with pHluorin-based probes. It should be emphasized that, at the end of the 15 s acid quench, syp–mOr fluorescence did not return to the resting fluorescence level, whereas sypHy fluorescence almost did (Fig. 1D, dashed line).

To characterize the temperature dependency of re-acidification, we repeated the acid-quench experiment at a more physiological temperature (34°C; Fig. 1E,F). We soon realized that the application of acidic solution itself produced a gradual decline of the baseline, which was negligible at 24°C (Fig. 1E). To control for this experimental artifact, we subtracted the decline in the baseline from the signals obtained during the second acid application. Using this procedure, the decay time constant of syp–mOr fluorescence was 5.9 ± 1.0 s at 34°C, much faster than the time constant measured at room temperature (Fig. 1F). Correspondingly, the Q₁₀ of the syp–mOr fluorescence decay was calculated as 1.9. This value was substantially smaller than that determined previously with pHluorin (>5), again probably attributable to the inaccuracy of pHluorin-based probes when they are positioned within the relatively acidic lumen of the SV (Granseth and Lagnado, 2008). It is important to mention that, in a similar hippocampal neuron culture preparation, Watanabe et al. (2013, 2014) proposed recently that ultrafast endocytosis, which is completed within ∼100 ms after stimulation, is the predominant form of endocytosis at physiological temperatures. However, in our acid-quenching experiments at 34°C, we observed a large decrease in the syp–mOr signal in response to acid application, even 8 s after stimulation (data not shown). This implies that a large fraction of syp–mOr still remained on the cell surface and that the majority of vesicular proteins (e.g., synaptophysin in this case) were not retrieved by the proposed ultrafast endocytosis mechanism under our experimental conditions in which multiple SVs were exocytosed. It remains unclear whether ultrafast endocytosis occurs predominantly in response to modest stimulations such as a single action potential.

Conversion of syp–mOr fluorescence to pH_v

The analysis described above demonstrates that the pKa of the pH probe clearly affects the decay of fluorescence during re-acidification and that syp–mOr was the more appropriate choice in probe. However, as evident in the titration curve shown in Figure 1A, even syp–mOr fluorescence did not exhibit a linear correlation with SV pH over the full range. Therefore, conversion of the probe fluorescence to pH_v is required for greater precision when describing re-acidification kinetics. In principle, the total fluorescence in the acid-quenching experiment (Fig. 1) could have conceivably originated from three different probe fractions: (1) cell surface; (2) immobile resting SVs; and (3) endocytosed re-acidifying SVs. Our goal was to isolate fluorescence arising from the endocytosed re-acidifying fraction from the total fluorescence and convert it to pH. To this end, we modeled the contribution of individual probe fractions to the total fluorescence at seven steps (I to VII) as illustrated in Figure 2A. The trace in Figure 2A shows normalized fluorescence of syp–mOr measured during the acid-quench experiment at room temperature, in which Q₁ was elongated to 30 s to monitor the later phase of re-acidification that eluded detection with 15 s of Q₁ (Fig. 1). In this model, we defined the initial surface fraction, the fraction exocytosed by electrical stimulation, and the endocytosed fraction retrieved by the onset of Q₁ as S, R, and E, respectively. In addition, the resting pH_v was set as pHi (shown in red), and pHs of the endocytosed fraction at the onset of Q₁ (shown in green in steps IV and V) and during Q₁ (shown in green in step VI) were set as pHo and pHt, respectively. Because the fluorescence of an individual probe fraction at a given pH (pH X) could be expressed by the product of the probe fraction and the fluorescence of all probe molecules at pH X (F_{pH X}), total syp–mOr fluorescence at each step (F_I–F_VI) could be described as follows:

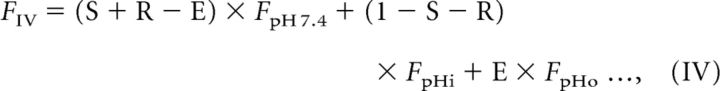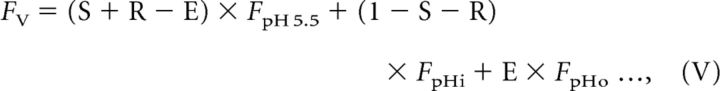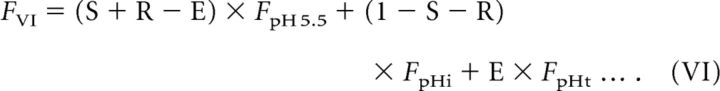Here, we made an assumption that endocytosis during electrical stimulation (50 Hz, 2 s) was negligible so that we could simplify the equations. Indeed, in the presence of the V-ATPase inhibitor folimycin (120 nm), the peak intensity of syp–mOr fluorescence after stimulation did not differ from that in the absence of folimycin (Fig. 2B), indicating that limited endocytosis occurred during stimulation. It should be mentioned that this assumption could not be applied to recordings performed at physiological temperatures, because at some synapses vesicle recycling (including endocytosis) is accelerated several-fold when temperature is increased (Kushmerick et al., 2006; Granseth and Lagnado, 2008).

To obtain the parameters defined above, we divided both sides of Equations I–VI by the fluorescence during the application of 50 mm NH₄Cl (F_NH4Cl) and solved them to obtain the following parameters:

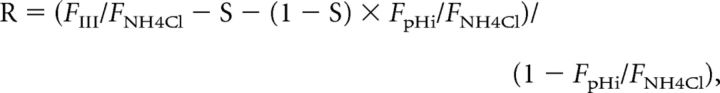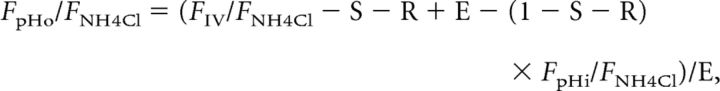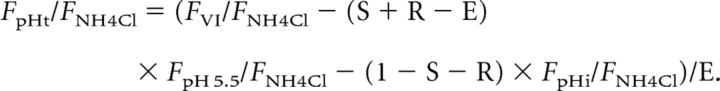It has been reported that 50 mm NH₄Cl effectively equilibrates the lumen of SVs with the extracellular pH (Fernandez-Alfonso and Ryan, 2008). However, we determined independently the pH_v during application of 50 mm NH₄Cl as 7.20 ± 0.03 (see Fig. 5B). Accordingly, F_{pH 5.5}/F_NH4Cl could be given by the Henderson–Hasselbalch equation as follows:

where the pKa of syp–mOr was 6.5. The nH for syp–mOr was omitted, because it was ∼1.0 (Fig. 1A). The initial surface, released, and endocytosed fractions during the 8 s interval were then determined as 0.07 ± 0.01, 0.20 ± 0.01, and 0.12 ± 0.01, respectively. Normalized fluorescence arising from resting SVs (F_pHi/F_NH4Cl) and the endocytosed fraction (F_pHo/F_NH4Cl, F_pHt/F_NH4Cl) are shown in Figure 2C. To test the validity of our model, we also applied it to the result in the presence of folimycin (Fig. 2B, blue plot) and found that the normalized value was sustained at ∼1, albeit with a slight decrease (Fig. 2C, blue plot). Because folimycin should trap SVs in an alkaline state (pH of ∼7.4), we reasoned that our model was appropriate for estimating pH_v. We then calculated the pH_vs—pHi, pHo, and pHt—as follows:

The pH_v of endocytosed SVs at the onset of Q₁ was determined as 6.67 ± 0.05 and gradually approached the resting pH of 5.64 ± 0.03. It should be noted that the last few seconds were not included in these data because, in a few cases, the normalized fluorescence calculated in Figure 2C became negative and, therefore, could not be applied to the Henderson–Hasselbalch equation. This was presumably because the signal-to-noise ratio (SNR) was strongly reduced when the pH_v was close to the resting pH. Another possible explanation for the negative normalized fluorescence was that the prolonged acid treatment (30 s) may have acidified the cytoplasm, thereby decreasing the pH_v beyond its resting state. Indeed, the calculated pHs from our model tended to be more scattered during the later phases. Nevertheless, the pH_v was fitted by a single-exponential function with a time constant of ∼14.9 ± 1.7 s (Fig. 2D). When pH_v was then converted to [H⁺]_v, it became evident that [H⁺] did not obey the first-order kinetics but increased relatively slowly before accelerating as the SV lumen became more acidic (Fig. 2D, inset). Although a pHo of ∼6.7 suggested that substantial re-acidification had occurred during the 8 s interval, because of the logarithmic scale, this represented only a small increase in [H⁺]_v (<10% of the resting [H⁺]).

Theoretical comparison of syp–mOr and sypHy for monitoring re-acidification

With the rationale that the pKa of syp–mOr (∼6.5) would provide more accurate measurements of SV pH, we report that SV re-acidification proceeds markedly slower (τ = ∼15 s) than estimated previously using pHluorin-based probes. However, the lower pKa of syp–mOr would also produce a relatively high level of background fluorescence. Arising from both the resting SVs and the surface probes during acid quench, this high background may have distorted our measurements of re-acidification kinetics. Thus, we next estimated the influence of syp–mOr background fluorescence (F₀) on the sensitivity of our re-acidification measurements using an analytical framework established by Sankaranarayanan et al. (2000). The sensitivity of fluorescence measurement is, in general, represented by the SNR, which is determined by the size of the signal of interest (ΔF) relative to the baseline signal fluctuation. Assuming that the baseline signal fluctuation arises solely from photon-counting statistics of the probe fluorescence, the SNR can be described as ΔF/$\sqrt{F_0}$. In our model, the signal of interest during acid quench (ΔF_(Q1)) corresponds to E × F_pHt (Fig. 2A) and is expressed as thus:

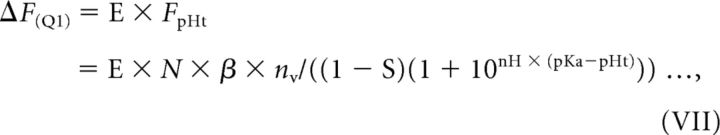where N is the total number of resting SVs, β is the fluorescence of a single probe molecule, and n_v is the number of probes per vesicle. The background signal during Q₁ (F_0(Q1)) is given by subtracting E × F_pHt from F_VI and derives from Equation VI:

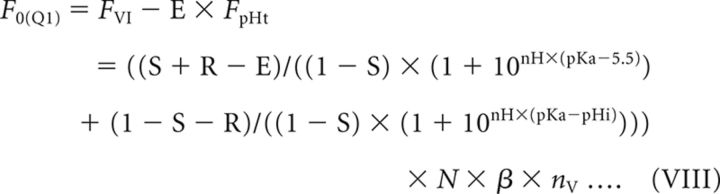Therefore, the SNR for re-acidification measurements corresponds to ΔF_(Q1)/$\sqrt{F_{0\left(Q1\right)}}$, and can be calculated using Equations VII and VIII.

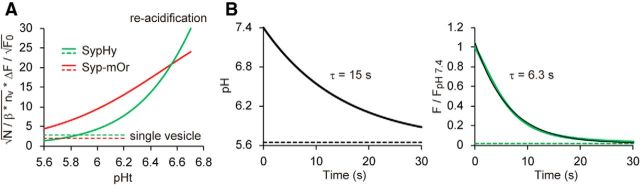
In Figure 3A, we calculated $\sqrt{N/\beta \times n_{\text{v}}}\times \Delta F_{Q1}/\sqrt{F_{0\left(Q1\right)}}$ for both sypHy and syp–mOr as an index of the SNR. Most of the parameters were determined from our own experiments (S = 0.07, R = 0.20, E = 0.12, and pHi = 5.64), whereas the vesicle number N was set to 100, as estimated previously from cultured hippocampal boutons (Ikeda and Bekkers, 2009). The index of the SNR was then plotted as a function of pHt (Fig. 3A). For comparison, we also calculated the SNR for the exocytosis of single vesicles. This was performed by dividing the fluorescence increase derived from a single vesicle exocytosis (ΔF_(1SV)) by the square root of the background fluorescence at rest (F_0(rest)). The values of $\sqrt{N/\beta \times n_{\text{v}}}\times \Delta F_{\left(1\text{SV}\right)}/\sqrt{F_{0\left(\text{rest}\right)}}$ for both sypHy and syp–mOr were calculated according to Sankaranarayanan et al. (2000) and shown as dashed lines in Figure 3A. This analysis indicated that the SNR for re-acidification measurements with syp–mOr was substantially greater than that for sypHy below pHt of ∼6.5 and was higher than that for single vesicle measurements with sypHy even when the pHt was near resting values. Thus, it is unlikely that re-acidification kinetics measured with syp–mOr were biased critically by a relatively high background fluorescence. It should be noted that the SNR of pHluorin on a pH shift from 5.6 to 7.4 is much higher than that of mOrange2 and, thus, more ideal for monitoring vesicle recycling. In comparison, pHluorin is less suitable for quantitative measurements of re-acidification compared with syp–mOr (Granseth et al., 2006).

Figure 3.

Theoretical evaluation of the mOrange probe for re-acidification measurement. A, The sensitivity of the re-acidification measurement was compared for the sypHy (green) and syp–mOr (red) probes. An index of the SNR was plotted as a function of pHt, the pH_v of endocytosed re-acidifying SVs. Equations VII and VIII and the values used to calculate this parameter are described in Results. The dashed lines indicate values of the same index calculated for the exocytosis of single vesicles. B, Theoretical trace of sypHy fluorescence during SV re-acidification. The left shows an exponential decay of pH with τ of 15 s, as measured from the syp–mOr fluorescence imaging. Resting pH_v of 5.64 (Fig. 2) was used as a baseline (dashed line). Time course of normalized fluorescence of sypHy was calculated according to the Henderson–Hasselbalch equation and was shown in the right (black trace). Single-exponential fitting of the trace yielded a τ of 6.3 s (green trace). Note that this value was almost identical to that of decay kinetics of sypHy fluorescence measured in our experimental condition (Fig. 1D).

To further test whether the pKa of pHluorin was responsible for the underestimation of the time constant (Fig. 1D; Atluri and Ryan, 2006; Granseth and Lagnado, 2008; Kwon and Chapman, 2011), we simulated changes in sypHy fluorescence from the pH change determined by syp–mOr imaging (Fig. 3B). Supposing a decrease in pH_v from 7.4 to 5.6 could be described by a single-exponential decay with τ of 15 s (Fig. 3B, left), sypHy fluorescence at each pH point could be calculated based simply on the titration curve defined by the pKa and nH of sypHy (Fig. 1A). When the resulting trace of sypHy fluorescence decay (Fig. 3, right) was fitted with a single-exponential function, a τ of ∼6.3 s was obtained, which matched perfectly our measurements in Figure 1D. These results suggest strongly that the different decay kinetics of the fluorescence obtained with sypHy and syp–mOr probes could be almost exclusively attributed to the difference in their pH sensitivity. In addition, we confirmed that syp–mOr was insensitive to changes in Cl⁻ concentration, which may have occurred during SV re-acidification (data not shown; Stobrawa et al., 2001; Schenck et al., 2009).

Re-acidification kinetics of different SV populations

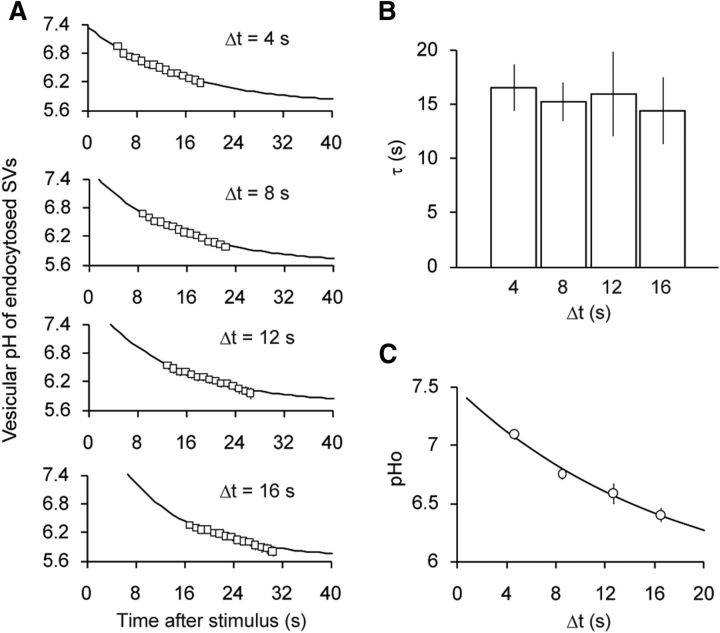
So far, we have monitored the re-acidification kinetics of SVs that were endocytosed within an 8 s period after stimulation. However, the timing of endocytosis may have influenced our estimates of re-acidification kinetics. This possibility was investigated previously using pHluorin-tagged synaptobrevin2 (SpH; Atluri and Ryan, 2006) but could not be elucidated fully because of the poor sensitivity of the probe at the lower end of SV luminal pH. Here we tested the influence of endocytosis timing by varying the interval between stimulation and acid quench, Δt, from 4, 8, 12, to 16 s and monitored syp–mOr fluorescence. Given that the estimate of pH_v became imprecise after prolonged acid application (Fig. 2D), we restricted the acid quench to 15 s. syp–mOr fluorescence was converted to pH_v (pHt) using the model described in Figure 2 and plotted as a function of time by taking the end of stimulus as t = 0 s (Fig. 4A). All traces were well fitted by a single-exponential function with a τ of ∼15 s regardless of Δt (Fig. 4A,B). As was expected, we found that the average starting point of SV re-acidification, predicted from the intersection of pH 7.4 and the extrapolated single-exponential fit, was right shifted as Δt increased (Fig. 4A). Moreover, when the average pH at the onset of acid treatment (pHo) was plotted against Δt, the decay of pHo was well approximated by a single-exponential decay with a τ of 17.8 s (Fig. 4C), which, as expected for similar re-acidification kinetics regardless of the timing of endocytosis, resembled closely the individual data (Fig. 4B).

Figure 4.

Re-acidification kinetics of different SV populations. A, Luminal pH of SVs endocytosed during varying stimulus-to-quench intervals (Δt). After stimulus, a 15 s acid quench was applied after Δt of 4 s (n = 9 experiments with 112 boutons), 8 s (n = 9 experiments with 129 boutons), 12 s (n = 10 experiments with 145 boutons), and 16 s (n = 10 experiments with 131 boutons). pHs of the endocytosed vesicle fraction were calculated as described in Figure 2. B, Comparison of the re-acidification kinetics measured with different Δt. The time constants were ∼15 s regardless of Δt (p = 0.96, ANOVA). C, pH_vs of endocytosed fraction at the onset of poststimulus acid quench (pHo) plotted against Δt. A single-exponential fitting yielded a time constant of 17.8 s. Error bars indicate SEM.

BC of SV lumen

The increase in luminal [H⁺] appeared to accelerate under more acidic conditions (Fig. 2D). This somewhat counterintuitive observation raised two possibilities: (1) either the V-ATPase activity accelerated as the lumen became more acidic; or (2) luminal buffers became less effective under more acidic conditions. To decipher the underlying mechanism, we measured the BC of the SV lumen. BC is defined by the concentration of acid or base that produces a shift of one pH unit. To quantify the BC over the pH range of interest, we applied defined concentrations of ammonium ions (NH₄⁺; Gekle and Silbernagl, 1995; Barriere et al., 2009). When NH₃ diffuses into SVs, it is converted to NH₄⁺, thus alkalizing the lumen. We found that this alkalization caused a swift and step-like increase in syp–mOr fluorescence (Fig. 5A). Fluorescence intensities at each step were converted to pH (Fig. 5B; see Materials and Methods) and plotted against [H⁺] quenched by NH₃ (Fig. 5C). The resulting relationship was well fitted by a linear function (Fig. 5C), and the BC was calculated to be 57.4 ± 4.8 mm/pH from the slope in Figure 5C regardless of pH. The constant BC indicated that the same H⁺ supply would result in a larger pH change at lower pH than at a higher pH, explaining the odd kinetics of [H⁺] increase shown in the inset of Figure 2D. Multiplying the difference in pH from 7.4 (7.4 − pHt) in Figure 2D by the BC provided an estimate of net proton influx into an individual SV (Fig. 5D). In contrast to the increase in [H⁺]_v, net proton influx could be described by first-order kinetics (τ of ∼15 s), as with the change in pH_v. Given that the pH of SVs dropped ∼1.7 pH units during re-acidification, we calculated that the net proton influx was ∼100 mm, which corresponded to ∼1200 protons in an SV with 40 nm in diameter.

Discussion

We have revealed hitherto unrecognized re-acidification kinetics of SVs by using a mOrange2-based probe as a pH indicator. Compared with the pHluorin-based probes, the mOrange2 more accurately covered the pH range encountered in the lumen of SVs. As evident in the titration curves in Figure 1A, pHluorin lacked adequate sensitivity below pH of ∼6. Although a difference between pH 6.0 and pH 5.7 (the resting pH) seems trivial, it corresponds to the difference in [H⁺] equivalent to that between pH 7.4 and pH 6.0, accounting for the latter half of the [H⁺] increase. Furthermore, it became evident that the approximation of re-acidification kinetics by the decay of probe fluorescence should not be valid for quantitative analysis unless a linearity of the probe in the range of pH of interest is verified rigorously. In the present study, we thus introduced a simple model to calculate the pH of re-acidifying SVs in the acid-quenching measurements and showed that re-acidification as a decay of pH_v occurred with a time constant of ∼15 s, threefold to fourfold slower than values reported previously from the fluorescence decay of pHluorin-based probes (Atluri and Ryan, 2006; Granseth and Lagnado, 2008; Kwon and Chapman, 2011). Much faster re-acidification kinetics (τ of ∼0.5 s) have also been reported by monitoring the decay of SpH fluorescence after single action potentials (Gandhi and Stevens, 2003). However, the interpretation of this ultrafast decay was complicated by the fact that exocytosed SpH exchanged with the large surface pool, resulting in probe diffusion out of the synapse (Fernández-Alfonso et al., 2006; Granseth et al., 2006; Wienisch and Klingauf, 2006). We also noted that detection of the SpH fluorescence of single vesicle events suffered from a very low SNR, in which the insufficient response range of pHluorin would additionally lead to severe misinterpretation, casting additional doubt on such rapid re-acidification kinetics. Nevertheless, because our current measurements of the re-acidification kinetics relied solely on the measurements of multiple SVs after repetitive stimulations, we cannot rule out a possibility that re-acidification of SVs after a single action potential exhibits considerably faster kinetics. Future development of a pH probe with a high SNR and an appropriate pKa will certainly help to determine re-acidification kinetics after single action potentials and to estimate how diverse the re-acidification of individual SVs can be. In addition to the precise monitoring of re-acidification kinetics, we quantified the BC of the SV lumen and estimated the dynamics of proton influx during re-acidification, whose kinetics were simply a mirror image of re-acidification because of the constant BC.

Recently, the kinetics of glutamate refilling into SVs at the calyx of Held synapse was reported to occur with a time constant of ∼15 s (Hori and Takahashi, 2012), which closely resembled the re-acidification kinetics and rate of proton influx shown here. Biochemical studies have suggested that glutamate uptake into SVs is driven predominantly by the electrical component of ΔμH⁺, which presumably correlates to the rate of proton flux rather than ΔpH (Maycox et al., 1988; Bellocchio et al., 2000; for an alternative view proposing a contribution of ΔpH, see Tabb et al., 1992). Therefore, our results suggest that the rate of glutamate loading could be critically limited by the rate of proton influx into SVs. Thus, it is implied that the kinetics of proton influx, or re-acidification, will have a greater effect on short-term plasticity than believed previously, although whether, and to what extent, vesicles are reused rapidly before complete refilling of neurotransmitter has been debated intensely (He and Wu, 2007; Rizzoli and Jahn, 2007; Wu et al., 2007). Interestingly, the number of protons accumulated into SVs (∼1200 in total) corresponds well with the estimated number of glutamate molecules in SVs (Riveros et al., 1986; Burger et al., 1989). Although the mechanism of glutamate loading, for example, coupling of protons to glutamate transport, has been enigmatic (Edwards, 2007; Jahn, 2010), our findings raise the possibility that protons and glutamate molecules are almost simultaneously transported in SVs in the physiological condition. The majority of neurons investigated in this study use glutamate as a neurotransmitter, and thus the proton dynamics in SVs described here should be interpreted for only SVs that accumulate glutamate. Because dependence of neurotransmitter filling on ΔpH is known to be diverse (Edwards, 2007), it is possible that proton dynamics in SVs for other neurotransmitters may show different properties.

To the best of our knowledge, the present study provides the first quantitative description of proton storage in SVs at living synapses. Budzinski et al. (2011) recently reported the luminal BC of isolated SVs to be much higher than our value (∼139 mm/pH). In their study, pHluorin was introduced transgenically into the SV lumen and used to monitor pH_v. Given the relative inaccuracy of pHluorin to report changes in pH below 6, it is likely that they overestimated the apparent BC (note that an underestimation of pH changes in response to NH₄⁺ application would also artificially enhance estimates of the BC). Compared with other intracellular organelles (Gekle and Silbernagl, 1995; Chandy et al., 2001; Sonawane and Verkman, 2003; Barriere et al., 2009), SVs possess a relatively large BC, which might be conferred by the high density of integral membrane proteins that cover the majority of the luminal surface (Takamori et al., 2006). The extracellular solution taken up during SV recycling can contribute to the luminal BC. In our experimental conditions, the 10 mm HEPES present in both the culture medium and bath solution would theoretically exhibit a peak BC of ∼5.8 mm/pH at pH 7.5. This maximum value corresponds to only ∼10% of the luminal BC we report and thus does not represent a major source of our estimates of SV BC. Similarly, given that the effective pKa of the carboxyl group of glutamate is ∼4.1, the amount of loaded neurotransmitter is also unlikely to have strongly affected our estimates of BC. The large luminal BC of SVs measured in this study allows for the storage of ∼1200 protons per vesicle and argues against the notion that re-acidification of SVs is a rapid process that requires a limited number of protons to move across the SV membrane (Blakely and Edwards, 2012). Moreover, our results may have important physiological implications concerning the role of protons as a neurotransmitter. The “buffered” protons inside SVs will be liberated during exocytosis to the synaptic cleft. Alterations in the synaptic cleft pH have been implicated in the regulation of synaptic transmission by modulating the properties of synaptic molecules, including voltage-dependent Ca²⁺ channels and ionotropic receptors for glutamate, GABA, and acid-sensing channels (Traynelis and Cull-Candy, 1991; DeVries, 2001; Hosoi et al., 2005; Dietrich and Morad, 2010; Wemmie et al., 2013). Although it no doubt depends heavily on extracellular buffers, the huge capacity of SVs for protons would support a significant contribution of protons as a neurotransmitter that mediates and/or regulates synaptic transmission (Palmer et al., 2003; Du et al., 2014).

Our results may also shed new light on ATP economics at presynaptic terminals. Given the proposed coupling H⁺/ATP ratio of the V-ATPase to be ∼2 (Johnson et al., 1982), re-acidification of a single vesicle would consume ∼600 ATP molecules. This value is considerably less than the 10⁶ free ATP molecules present within a typical hippocampal synaptic bouton at rest (Rangaraju et al., 2014). Even after high-frequency stimulation, the activity of V-ATPase is unlikely to dramatically deplete ATP levels. For example, after 300 action potentials, cytoplasmic ATP concentrations are likely to be reduced by approximately half (∼1 mm). If we assume that ∼100 vesicles are recycled in this stimulation train, only 60,000 ATP molecules will be consumed during their re-acidification. This value represents <6% of total free ATP molecules, collectively indicating that ATP consumptions by the V-ATPase do not severely interfere with other ATP-demanding processes, such as SNARE complex disassembly and vesicle trafficking (Ly and Verstreken, 2006; Harris et al., 2012). Presynaptic terminals are equipped with a sufficient supply of energy to support the neurotransmitter loading process that is so essential for the fidelity of signal transfer in the brain.