Stimulus Statistics Shape Oscillations in Nonlinear Recurrent Neural Networks

Abstract

Rhythmic activity plays a central role in neural computations and brain functions ranging from homeostasis to attention, as well as in neurological and neuropsychiatric disorders. Despite this pervasiveness, little is known about the mechanisms whereby the frequency and power of oscillatory activity are modulated, and how they reflect the inputs received by neurons. Numerous studies have reported input-dependent fluctuations in peak frequency and power (as well as couplings across these features). However, it remains unresolved what mediates these spectral shifts among neural populations. Extending previous findings regarding stochastic nonlinear systems and experimental observations, we provide analytical insights regarding oscillatory responses of neural populations to stimulation from either endogenous or exogenous origins. Using a deceptively simple yet sparse and randomly connected network of neurons, we show how spiking inputs can reliably modulate the peak frequency and power expressed by synchronous neural populations without any changes in circuitry. Our results reveal that a generic, non-nonlinear and input-induced mechanism can robustly mediate these spectral fluctuations, and thus provide a framework in which inputs to the neurons bidirectionally regulate both the frequency and power expressed by synchronous populations. Theoretical and computational analysis of the ensuing spectral fluctuations was found to reflect the underlying dynamics of the input stimuli driving the neurons. Our results provide insights regarding a generic mechanism supporting spectral transitions observed across cortical networks and spanning multiple frequency bands.

Introduction

Oscillations are an information-rich mechanism of neural signaling (Engel et al., 2001; Varela et al., 2001; van Atteveldt et al., 2014). Rhythmic neural activity involves intermittent synchronous patterns between distant yet simultaneously activated regions (Wang, 2010) and have been suggested to shape communication timing between neural populations (Fries, 2005) and to be centrally involved in the binding of sensory representations (Engel and Singer, 2001; Engel et al., 2001). However, cortical networks exhibiting synchronous dynamics cannot be considered in isolation; neural populations are continually subjected to myriad (stochastic) influences. Afferent fluctuating stimuli impact the dynamics of neural networks both by recruiting individual neurons, and also by shaping collective synchronous activity of neuronal populations.

The nonstationarity of power spectra in the brain has been robustly observed across neurophysiologic measures both intracranially (Schroeder and Lakatos, 2009; Whittingstall and Logothetis, 2009; Ray and Maunsell, 2010; Musall et al., 2014) and noninvasively at the scalp surface (Van Zaen et al., 2010, 2013; Thut et al., 2012). The nature and features of the input shape the peak frequency and power of ongoing cyclic activity among neurons in a nontrivial and time-dependent way, operating on multiple frequency bands (Cohen, 2014). Fluctuating coherently with stimulation dynamics, the frequency of ongoing neural oscillations typically increases alongside input intensity (Whittington et al., 1995; Ermentrout and Kopell, 1998). Yet, the mechanisms responsible for this phenomenon are currently poorly understood.

Changes in the peak frequency displayed by synchronous neural ensembles are typically ascribed to alterations in circuit features, such as network structure or synaptic timescales. However, the occurrence of such changes over timescales as short as 100 ms suggests that other input-dependent mechanisms may underlie rapid fluctuations in power spectra, rather than neuromodulatory and/or plastic changes in circuitry. Mechanisms involved in the generation and shaping of gamma-type activity have been well characterized (Whittington et al., 1995; Wang and Buzsáki, 1996; Ray and Maunsell, 2010) and are considered a signature of highly local synaptic processing (Jadi and Sejnowski, 2014). However, these mechanisms are likely distinct from those supporting modulations of slower oscillations (Lakatos et al., 2008; Schroeder and Lakatos, 2009; Burgess, 2012). Alpha activity is believed to rely on larger scale processes (Hindriks et al., 2014) supported by delayed network interactions (Cabral et al., 2014) operating over longer timescales (Haegens et al., 2014). Here, we specifically investigate how such delay-induced alpha activity is modulated by changes in stimulation dynamics and demonstrate how peak frequency and power reflect the activation state of the neurons on a larger spatial scale. To do this, we investigated mathematically the spectral response of a simple, yet nonlinear neural population model subjected to stochastic spike-like inputs. Using mean-field analysis, our results reveal a dependence of the system's effective nonlinearity on stimulus statistics. Specifically, they were shaped by changes in inputs while all other parameters were kept constant, such that alpha-type oscillatory activity was fully regulated by the dynamics of the stimulus. Time-dependent fluctuations in peak frequency and power can therefore result from a fully generic property of synchronous nonlinear networks, while echoing the dynamics and statistics of underlying inputs.

Materials and Methods

Model description

To analyze the spectral response of synchronous networks to inputs, we deliberately chose a simple, yet nonlinear, sparse and random system to enforce the generality of the results. Using this model, described in detail below, we developed a mean-field representation of the dynamics to determine the effect of stimulus statistics on the activity pattern of the modeled neurons. We then performed a thorough stochastic stability analysis while the system remained close to oscillatory instabilities. Throughout, we studied the effect of changes in input statistics, and no other parameter was varied.

In what follows, we deliberately consider a simplified network of synchronous neural units subjected to delayed and nonlinear reciprocal interactions and stimulated by another, upstream population via independent trains of modeled action potentials. The associated representation of our model is aimed to provide a description of brain dynamics at the mesoscopic (centimeter) scale (Freeman, 1975; Wright and Liley, 1995; Jirsa and Haken, 1997), in which slower rhythmic activity modulates faster, more local oscillations (Osipova et al., 2008). A schematic illustration is shown in Figure 1. The quantity u_i(t) with i = 1,…,N represents the mean somatic membrane activity of the ith subunit in the network, and obeys the nonautonomous set of dimensionless evolution equations:

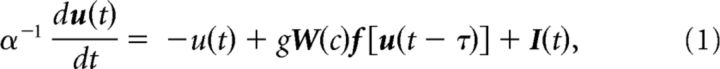where α = 50 ms defines the mean synaptic rate of the neuronal population, I(t) is a vector of stochastic inputs of dimension N, and the vector f of dimension N denotes the nonlinear response functions of the neurons. The synaptic efficacies of the neurons are identical and given by g = g_oN⁻¹, where again N is the number of units in the network. Without constraining generality the nonlinear response function displays the sigmoid-like shape f [u]_j = f_o[1 + exp(−βu_j)]⁻¹, where β = 100 is the steepness, or gain, of the neural responses. The quantity f_o, here set to 100 Hz, is the maximum firing rate of the neurons. For simplicity, network interactions are conditioned by a unique and constant propagation delay τ = 30 ms, which approximates well the distribution of interaction latencies in sparse and random networks (Roxin et al., 2005). This approximation is, however, not mandatory, and τ can be thought to represent the maximal (i.e., longest) interaction latency. Units in the network are also subjected to independent time-varying stimuli. Spiking activity of individual units in the network follows a nonhomogeneous Poisson process, i.e., X_i(t)→Poisson(f(u_i(t))).

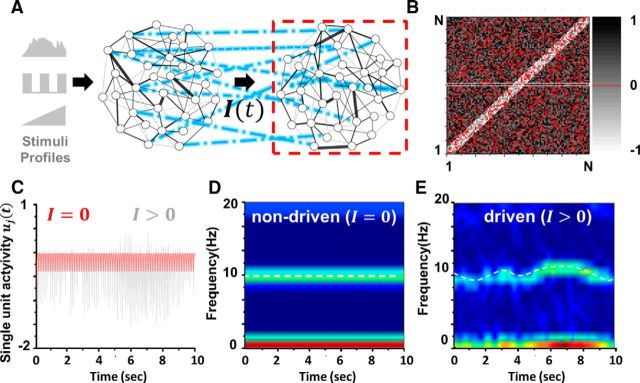
Figure 1.

Driven nonlinear network model. A, This illustration shows a sparse and randomly connected network dynamically driven by another upstream population, itself responding to changes in input. The stimulation profile I(t), which consists of stochastic trains of action potentials, impacts the mean activity of the driven network consisting of N recurrently connected units. B, The matrix W(c) defines the connectivity of the driven network (dashed box). Connection probability is c = 0.8, and matrix elements w_ij = 0 are encoded in red, but otherwise displayed in gray shading. Interactions are locally (r < 5) excitatory but distally inhibitory (r > 5): for proximal units i and j such that |i − j| < r indicates that the connections are positive, and negative otherwise. These positive- and negative-valued connection strengths are uniformly sampled from the interval [0, 1] or [−1, 0], respectively. C, Even in the absence of stimulation (I = 0, red trace) spontaneous synchronous activity emerges in the network as the result of the chosen network connectivity. The activity of a single unit in the network is displayed. Whenever an input drives the network (I > 0, gray trace), the dynamics becomes perturbed. D, Power spectrum of the nondriven state in which no input drives the network (I = 0). Stable oscillations in the alpha band (10 Hz) are expressed by the network. E, When spiking inputs stimulate the neurons (I > 0), frequency and power of ongoing rhythms fluctuate in time; the power spectrum is thus not stationary. The model is detailed in the Material and Methods section. Parameters are N = 100, α = 50 Hz, τ = 30 ms, β = 100/mV, g_o = 0.1 mVs, f_o = 100 Hz, r = 4, and w̄(c) = −0.35. Unless otherwise noted, these parameters remain fixed throughout the study.

The network's synaptic connectivity matrix W(c) is depicted in Figure 1B. Its structure is assumed to be sparse and random with connection probability c = 0.8. Random synaptic weights, sampled from a density ρ_W(W), are assumed to be locally excitatory and distally inhibitory: synaptic weights [W]_ij = w_ij for which |i − j| < r, given some radius r, are made positive valued (within the interval [0,1]), while all others are negative (within the interval [−1, 0]). Synaptic weights are uniformly distributed over their respective intervals, i.e., ρ_W(w_ij) = 1. In addition, an amount (1 − c)N⁻¹ of synaptic weights is randomly picked and set to zero to represent sparseness. The connectivity scheme used here is in line with previous work outlining the importance of inhibitory processes in the generation of oscillatory cortical activity patterns at the mesoscopic scale (Wilson and Cowan, 1972; Amari, 1977), most notably with respect to alpha synchrony (Lopes da Silva et al., 1976; Mazaheri and Jensen, 2008, 2010; Lorincz et al., 2009) and slow-wave activity (Melzer et al., 2012).

Given our aim to assess oscillatory synchrony in the network, we were careful not to choose connectivity structures that would lead to localized states of persistent activity or propagating activity waves that are known to exist in systems such as Equation 1 (Roxin et al., 2005). We instead focus our attention on regimes for which the activity remains homogeneous (i.e., spatially uniform), which is ensured by the present connectivity scheme. We note that Equation 1 corresponds to a discretized neural field equation, for which the connectivity kernels would have been corrected for sparseness and randomness. In the absence of stimulation, i.e., I = 0, and for strong and wide enough inhibition (i.e., g is large enough while r is taken to be sufficiently small), the network in Equation 1 engages spontaneously in a stable alpha activity, oscillating with a frequency of ∼10 Hz, despite the random and sparse nature of the connections. The frequency of the oscillations is primarily determined by the mean delay τ, in a way we will detail below. Oscillatory dynamics of the network is shown in Figure 1C.

Mean-field dynamics

The use of mean-field representations is a well established approach used to characterize the dynamics of large neural ensembles and is thus well suited to assess the impact of stimulation at scales that are relevant to population-level recordings in which spectral fluctuations might be observed, such as EEG (Deco et al., 2008). In the following, we develop a representation of driven network dynamics from the perspective of an ensemble average < u(t) > = ū(t) seen as a scalar readout measure of network collective activity when the population is large. Previous theoretical studies have shown that the ensemble average ū(t) is a reasonable model for the EEG (Robinson et al., 2001; Nunez and Srinivasan, 2006). The mean-field formulation further holds on presumed adiabatic dynamics, in which the system evolves in a mean-driven regime where the external fluctuations have smaller amplitudes compared with the autonomous dynamics of the system (i.e., the oscillations). The input timescale is also considered to be small compared with the synaptic rate α and interaction delay τ. The stochastic stimuli are also assumed to be sufficiently small and further to exhibit stationary statistics. Given that these conditions hold, the activity of individual units in Equation 1 can be expressed as small deviations v of dimension N from the ensemble average ū, i.e.,

where we introduce the unit vector 1. Since |v_j| ≪ |ū|, we assume that the small deviations are subjected to the mean-corrected stimulus and obey the Langevin equation:

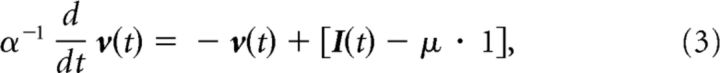where μ = < I > stands for the ensemble average of the stimulus. Replacing Equation 2 into Equation 1 yields the following:

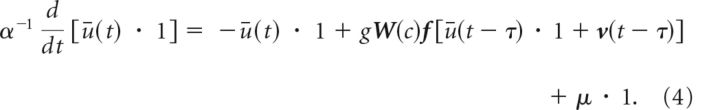Here, μ = < I > is the ensemble average of the stimulus. Deviations [v]_j = v_j obeying the dynamics in Equation 3 above are identically distributed with probability density ρ_v(v) with zero mean and moments denoted < vⁿ >.

Taking the ensemble average of Equation 4 yields a mean-field description of the dynamics of ū(t) when N goes to infinity. Given that g ∼ O(N − 1), we may use the independence and ergodicity of the local perturbations v to obtain an expression of the corrected nonlinear neural response function (Shiino, 1987):

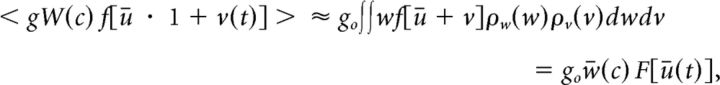which can further be written as follows:

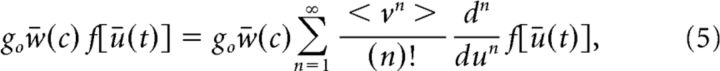with the probability densities ρ_v(v) and ρ_w(w) and where < vⁿ > = ${\displaystyle \int v^n{\rho }_v\left(v\right)dv}$. The term w̄(c) represents the mean effective connectivity and F is the stimulus-corrected response function of the neurons.

The above rather technical derivations provide a clear message: the shape of the nonlinear response function of the neurons is altered by the inputs. As seen in Equation 5, the system response function now fully depends on the input statistics, and exhibits stimulus-dependent corrections to all nonlinear orders via the moments < vⁿ >. Consequently, the external input alters the system's effective topology and dynamics.

Stimulus-corrected response function.

In the network, inputs to the neurons take the form of stochastic trains of actions potentials. We thus defined neural inputs as independent Poisson shot-noise signals of rate λ and amplitude S,

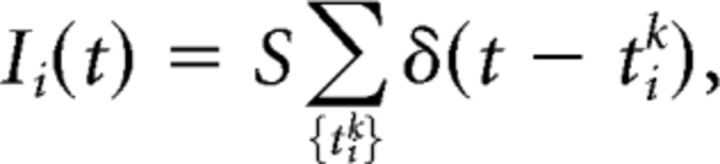where the pulses δ(.) are Dirac delta functions with random arrival times t_i^k obeying a Poisson distribution. We assume that I_i(t) displays stationary statistics, i.e., both amplitude S and rate λ are constant in time. We also assume that the fixed rate λ is large enough such that ρ_v(v) displays a stationary Gaussian profile. In contrast to other stochastic signals, such as Gaussian white noise, for instance, the mean and variance are not independent. It suffices to characterize the influence of the mean μ=< I > = Sλ on the dynamics, for which the variance of the linear process in Equation 3 becomes σ_v² = $\frac{1}{2}$S² λ = $\frac{1}{2}$Sμ (Gardiner, 2009). Using these expressions and inserting Equation 5 into Equation 4, the input-corrected mean-field dynamics simply reads

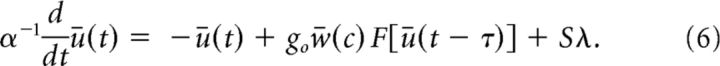For high values of the gain β, the response function f behaves like a step function centered at zero, i.e., f(u) ≈ H(u) where H is the Heaviside step function such that H(u) = 1 for u ≥ 0 and zero otherwise. In such conditions, the corrected response function F in Equation 6 above simplifies to the following (to second-order):

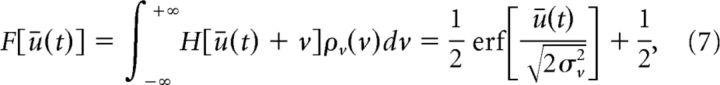where erf [·] is the error function and σ_v² = < v² > = $\frac{1}{2}$S² λ = $\frac{1}{2}$Sμ is the variance of the linear zero-mean process in Equation 3 with Poisson inputs. Once more, comparing Equation 6 and Equation 1 elucidates the influence exerted by the inputs on the recurrent architecture of the system. Figure 2B shows the nonlinear gain, which is proportional to the system's response to external inputs. In sum, increasing the input variance renders the response function more flat and the stimulus response smaller.

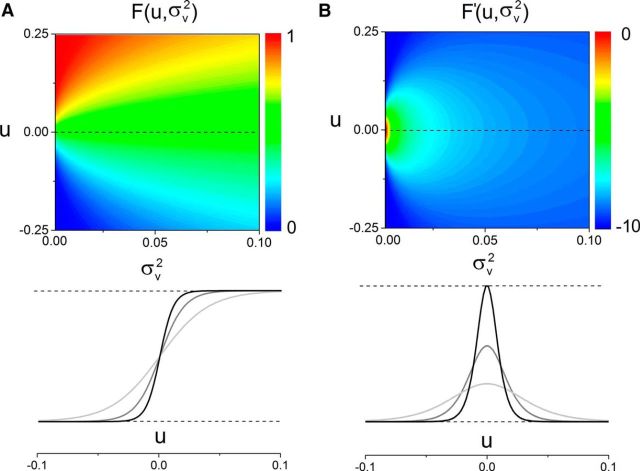
Figure 2.

Network response function is shaped by stimuli. According to Equation 7, the variance σ_v² modulates the nonlinear structure of the system, and reshapes the effective neural response function of the neurons. A, Upon stimulation, network dynamics is linearized: F(u) becomes more linear than its nondriven counterpart f(u). As σ_v² increases, the response function becomes smoother. The sigmoidal shape is preserved but the sharpness is decreased. One might note that the effective impact on the system is equivalent to a smooth variance-dependent decrease in the activation gain β. B, The nonlinear gain F′ is also greatly affected by the variance-induced corrections. Displaying an inverted Gaussian profile centered at u = 0, increases in the variance σ_v² decreases both the absolute magnitude and sharpness of the susceptibility curve: the susceptibility diffuses. The heat map encodes for amplitudes, properly scaled to the left of A and B. Bottom, Examples of the successive linearization and diffusion effects as the stimulus intensity increases (from black to gray).

Network stability

Based on the derived mean-field dynamics, the steady-state activity in Equation 6 is given by the following:

The equilibrium ū_o results from the interplay between the mean excitatory force delivered by the input, and the feedback it triggers in the network. As seen in Fig. 3A, the equilibrium activity changes nonmonotonically as the Poisson stimulus intensity is increased. The stimulation train inhibits the network for moderate intensities, and then excites it as the intensity increases revealing how the input regulates mean network activity. Stimuli also alter the stability network dynamics. To see this, a linearization of Equation 6 about the equilibrium state given in Equation 8 yields the following:

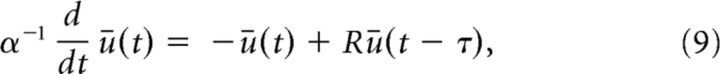with the characteristic equation

for the nonlinear susceptibility R[ū_o, σ_v²] = g_ow̄ F′[ū_o], where F′[ū_o] is the nonlinear gain shown in Figure 2B. The variable λ = a + iω is the complex eigenvalue, where ω defines the frequency of the oscillations and a is the damping rate. Figure 3B shows that the susceptibility varies significantly whenever the input fluctuates and its amplitude |R| first increases and then decreases as the stimulus intensity increases. This peculiar nonlinear mapping of the network response is determinant, as it indicates that the stimulus influences bidirectionally the efficacy of network interactions: changes in intensity can both increase or decrease the susceptibility.

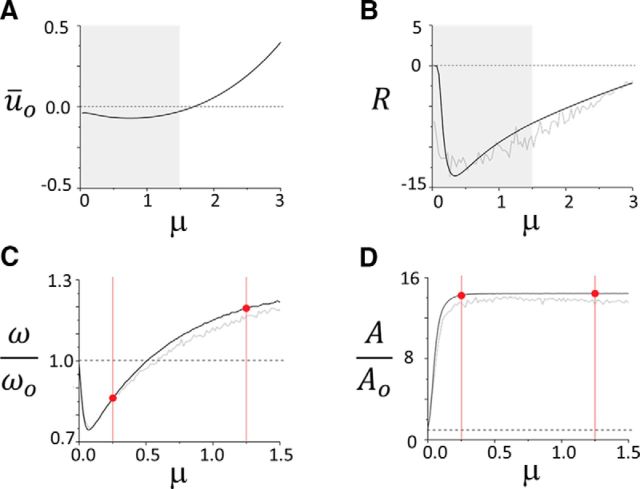
Figure 3.

Impact of stimulus intensity on network equilibrium and oscillations. A, Stimuli shift the position of the steady state of the network, around which oscillatory activity evolves. As the intensity μ = Sλ of the inputs increases, the equilibrium is displaced. The excitation delivered by the stimulus causes a smooth amplification of mean equilibrium activity, whose rise is tempered by the inhibitory feedback, especially when μ is small. Smooth shift from subthreshold to suprathreshold regimes can be observed. The value of the equilibrium is given by Equation 8. B, As the equilibrium is displaced, the stimulus also changes the way the response function maps the dynamics. The magnitude of the susceptibility R[ū_o, σ_v²] is first amplified by μ, which implies that the network enters a regime of high nonlinearity and high variance. As μ increases even more, the susceptibility slowly decays back to its original value. The gray line portrays the susceptibility computed numerically based on the full model, shown along the theoretical susceptibility derived from the mean-field equation (black line). The highlighted regions in gray specify the range of values of μ on which we focus our attention in the remainder of the analysis. C, Normalized peak frequency (defined as the ratio of the driven (ω) over the nondriven, or baseline (ω_o ≈ 10 Hz) oscillation frequency) as a function of the stimulus mean μ. As predicted by the stability analysis in Equation 11 and according to the profile of R plotted in B, the network frequency is bidirectionally modulated by the input. A drop, followed by an increase, characterizes the modulation performed by the pulse-train stimuli on ongoing synchronous activity. The mean-field formulation (bold black line) captures the frequency shift of the original system (gray line). D, The amplitude of the oscillations increases with μ, but in a purely monotonic fashion. Saturation is observed as the sigmoidal nonlinearity f reaches plateaued value. Once again, the mean-field dynamics reproduces well the response of the network. To vary μ, the stimulus intensity S was varied, while its frequency was maintained at λ = 30.

This influence of stimuli on susceptibility also provides a mechanism underlying input-induced suppression of oscillatory activity, in which incoming inputs fully destabilize ongoing network oscillations, such as during event-related desynchronization observed in EEG. Indeed, using Equation 10, one can also determine the stimulus amplitude and/or rate at which stability of synchronous network states is lost. This occurs whenever the following equation

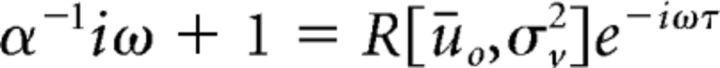is satisfied for a particular set of stimulation parameters. A specific example of this can be seen in Figure 4B, where the stimulus causes a complete suppression of ongoing cyclic activity. Stimuli statistics in this simulation were chosen purposely such that they exceeded the stability threshold of endogenous network oscillations.

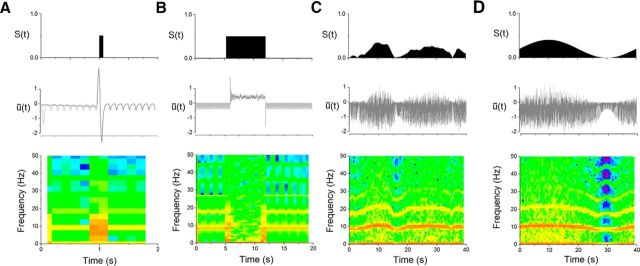
Figure 4.

Dynamic spectral responses in the model network. Responses of the network mean activity to time-dependent inputs with various envelopes. Inputs are stochastic, and constituted of Poisson pulse trains of time-varying intensity S(t). The time evolution of the input amplitude S(t) is plotted (top), along the oscillatory response of the network mean activity (middle) and the associated single-trial behavior in the time-frequency domain (bottom). Coherent oscillatory activity emerges spontaneously in the network, at a baseline (nondriven) frequency of ω_o ≈ 10 Hz, and is perturbed by afferent stimuli. A, Network response to a brief high amplitude burst of spikes. Amplified power at the baseline frequency can be observed at stimulus onset and for 50 ms duration. After stimulation, the amplitudes of oscillations return to their prestimulus values. The trial-averaged response is plotted in dark gray, where the stimulus was chosen to drive the system at random phases of ongoing oscillations. A single-trial response is also plotted in light gray. B, Response of the network to a prolonged pulse of 600 ms duration, where oscillations are destabilized and the network effectively desynchronized. The power of ongoing oscillatory activity is fully suppressed during stimulus onset, and the network synchronizes again once the input vanishes. C, As the mean input amplitude is decreased but varied continuously in time, synchronous oscillations can be seen to be accelerated and/or slowed down around the baseline frequency. Note how both the amplitude and frequency of the oscillations increase (decrease, respectively) when stimuli amplitude is high (low, respectively). D, When the intensity S(t) is set to follow a sine wave, the nonlinear frequency mapping follows, especially for higher harmonics of the network frequency. The trend follows the nonmonotonic mean-field prediction in Figure 3, C and D. While the amplitude of the Poisson spike-train stimuli was varied within the interval [0.0, 0.5], the rate was kept constant to λ = 50. In A and B, the input amplitude was set to a fixed value of 0.5, and was varying in C and D. Other parameters are identical as in Figure 1.

Driven oscillations.

Having established a mean-field representation of Equation 1 and exposed input-induced corrections to the system's nonlinear response function and stability equation, we now needed to expose the mapping between oscillation frequency, amplitude, and input statistics. Transition to synchrony in the network occurs in Equation 6 whenever Equation 10 above is satisfied for a = 0 and ω ≠ 0, in which case the system undergoes a so-called supercritical Andronov–Hopf bifurcation, transitioning from steady activity about ū(t) = 0 to global cyclic activity, or the other way around. The implicit dependence of the susceptibility R on input statistics, as seen in Figure 3B, implies that extrinsic fluctuations impact the oscillatory properties of the network. In more detail, an oscillatory instability (Andronov–Hopf bifurcation) emerges in the mean-field system for eigenvalues λ = i ω_c and

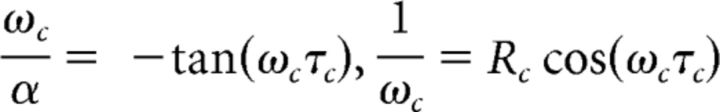for critical values R_c and delay τ_c.

Aware of the effect of the inputs on the susceptibility R, perturbation analysis around the oscillatory bifurcation allows us to observe the influence of input statistics on the resulting peak frequency. Assuming that the system's baseline frequency is close to the critical frequency of the bifurcation, i.e., ω_o ≈ ω_c, effects of the stimuli can be seen as perturbations around the baseline, i.e., nondriven state. The peak frequency reads as follows:

with γ = (2 ατ + 1/(ω_c² τ² − (1 + ατ)²)), ΔR = (R − R_c)/R_c. Equation 11 provides the desired mapping between input parameters and peak frequency and relates observed oscillatory activity with underlying stimulation dynamics. Fig. 4, C and D, displays the normalized frequency $\frac{\omega }{{\omega }_o}$ and the normalized amplitude of the oscillations subjected to μ, respectively. The normalized frequency follows the trend of the susceptibility R, cf. Fig. 3B, whereas the amplitude saturates for large input stimuli.

In summary, the synergistic interaction between input dynamics and network nonlinear structure (which takes place via changes in the neural response function and in the susceptibility R) generically shapes the peak frequency by distorting the stability equation and provoking the observed change in oscillation frequency. Fluctuations in input mean and variance are echoed on-line by concomitant changes in susceptibility, causing the network peak frequency and amplitude to waver. The effect is also bidirectional: as plotted in Figure 3C, the spike trains delivered to the networks first slow down ongoing cyclic activity, and the normalized frequency displays a value smaller than 1. The trend changes, however, as μ = Sλ increases and the peak frequency of the network starts to increase: stimuli now accelerate the dynamics. Together, these analyses show how spectral features can be modulated by stimuli without any change in circuitry.

Results

To understand the contribution of input statistics on time-dependent fluctuations in power and peak frequency, we investigated the influence of irregular spiking inputs on the ongoing cyclic activity of a neural population using a combination of dynamical systems analysis and numerical simulations. Inputs to the network take the form of trains of spikes with time-variable amplitudes and rate, representing signals sent to the network by other neuronal populations located upstream, relaying changes in physical stimuli or alterations in cognitive state (Fig. 1A). As seen in Figure 4A, brief and strong stimuli generate stereotyped, transient responses predominantly in the alpha band. Ongoing oscillations remain stable after the stimulus and express identical peak frequency and power. However, when such pulses are prolonged as pictured in Figure 4B, suppression of activity can be observed. Yet, after stimulus offset, spectral features of the system are recovered. These more transient responses are to be contrasted with those generated by weaker, dynamically varying stimuli in which spectral modulation caused by inputs can be observed (Fig. 4C,D). Indeed, as seen in Figure 4C, changes in the stimulation intensity generate epochs of acceleration and deceleration, i.e., ongoing oscillations respond either by increasing or decreasing their frequency as the stimulus varies. Throughout, the amplitude of network oscillations fluctuates along with input intensity. This becomes even more transparent in Figure 4D, where the stimulus amplitude follows a sine wave. There, one can clearly observe the nonlinear mapping of stimulus response in the spectral domain. Yet, aside from the stimuli, no parameter was varied and this effect is purely input driven.

To understand the mechanism responsible for this effect, we developed and investigated a mean-field representation of the dynamics (see Materials and Methods), focusing on stimulation signals with stationary statistics, i.e., with nonfluctuating amplitude and rate. The stochastic analysis revealed that inputs support a gain control mechanism in which susceptibility is enhanced with respect to baseline in a nonmonotonic fashion. Based on our mathematical framework, it was possible to show that the nonlinearity of the network response, going from decelerated to accelerated synchrony, follows the stochastic dependence of the susceptibility: the frequency is proportional to |R| (cf. Fig. 3C; Eq. 11). The amplitude (and thus power) of network oscillations was also found to be tightly linked to the stimulus intensity, yet in a monotonic fashion. Figure 5 exposes the effect of the external stochastic input on the system's oscillation frequency in more detail. Increasing the amplitude of stimulation trains at weak intensities slows down ongoing activity by reducing the network oscillatory frequency (ω) with respect to the nondriven state, oscillating at baseline frequency (ω_o). The opposite occurs at larger intensities when the network peak frequency is shifted to higher values with respect to the nondriven state while increasing the stimulus intensity: the effect is thus bidirectional.

Figure 5.

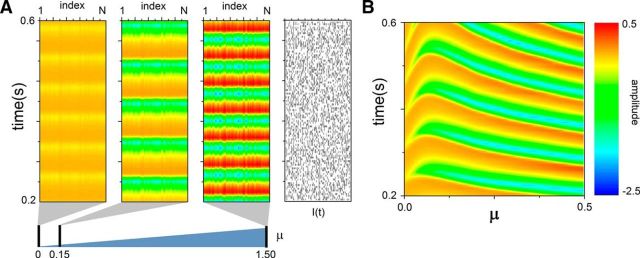
Bidirectional modulation of synchronous oscillations. The Poisson stimuli driving the network influence synchronous activity by modulating the oscillation frequency of the network in a nonmonotonic way. Full network activity is depicted for various stimulation intensities, and compared with the nonstimulated case. A, For μ = 0.15, the oscillation frequency is decreased throughout the network. A 10-fold increase in stimulus intensity (μ = 1.5) accelerates network oscillations, which are now faster than the nondriven case. Amplitudes, in contrast, monotonically increase with stimulus strength. B, Sample local activity (at unit i =N/2) as the stimulus intensity μ is smoothly changed from 0 to 0.5. One can appreciate the nonmonotonic aspect of the transitions. In each simulation, the initial conditions of the network are identical. The color encodes for the amplitudes.

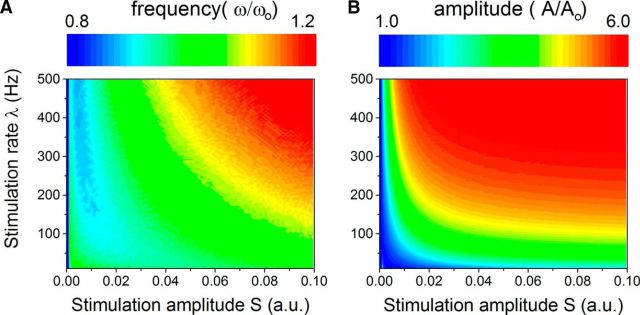
The analysis further exposed a nonlinear mapping between the stimulus intensity μ = Sλ, and the network oscillation frequency and its amplitude, pictured in Figure 6. The magnitude of the frequency modulation is substantial: it allows fluctuations of about 20% around ω_o induced by stimulus amplitude fluctuations of one order of magnitude. Strong input-induced decelerations were notably found to occur in a specific region of parameter space only, where stimulation rate is very high (100–500 Hz) but displayed amplitude is weak. We note that throughout, model parameters were kept constant and only the input was allowed to vary, showing the stimulus-driven nature of the effect.

Figure 6.

Network peak frequency and amplitude with respect to stimuli statistics. A, Normalized peak frequency, defined as the ratio of the network oscillation frequency with and without inputs (ω/ω_o) as a function of the input rate λ and amplitude S. If the input has a low amplitude but a high frequency, deceleration of network oscillations can be observed. In contrast, strong stimulation accelerates network synchronous oscillations. The modulation ranges from 0.8 to 1.2 for the range of parameters explored here (which means that the response frequency can vary here from 8 to 12 Hz solely due to the action of inputs), implying that frequency shifts spanning 20% of the baseline frequency can be observed. B, Normalized amplitude of network oscillations (A/A_o) as a function of input parameters. Here, the effect is monotonic: input intensity and/or rate amplify network oscillation amplitude (i.e., power). Together, these results show that fluctuating, dynamic inputs, with time-varying rates and amplitudes as shown here, should be viewed as trajectories in the (S, λ) plane, and where frequency and power expressed by the systems fluctuates concomitantly. Note that for all points for which S = 0 or λ = 0, the normalized frequency and amplitude are equal to 1.

Discussion

Oscillatory activity is a key component of brain dynamics and has been the focus of an increasing number of neuroscientific investigations. For example, neuronal oscillations have been considered a possible mechanism through which internal states exercise top-down influences on stimulus processing to impact perception (Engel et al., 2001; Varela et al., 2001). In particular, the synchronization of oscillatory components seems to be relevant for many cognitive processes (Fell and Axmacher, 2011) and may operate across multiple scales of brain circuitry (Singer and Gray, 1995; Engel and Singer, 2001). In light of such, it is critical to understand how these oscillations are shaped by the inputs they receive and how this impacts information processing and communication across systems (Buzsáki and Wang, 2012). Time-dependent transitions in oscillatory activity are reliably observed across a wide range of frequencies in neurophysiologic measures (Lakatos et al., 2008; Schroeder and Lakatos, 2009; Ray and Maunsell, 2010; Thut et al., 2012; Van Zaen et al., 2013) and across a variety of computational models (Cohen, 2014). In particular, fluctuations in gamma peak frequency have been well characterized (Whittington et al., 1995; Wang and Buzsáki, 1996; Jadi and Sejnowski, 2014) while lower frequencies, which likely rely on different cellular mechanisms and operate over longer timescales, were also found to be significantly volatile (Haegens et al., 2014).

The robustness of these observations, along the short timescales on which they occur, suggest that peak frequency and power fluctuations may rely on a generic input-response feature of recurrent neural networks. The frequency and power/amplitude of coherent synchronous oscillations is commonly thought to reflect the underlying structural properties of neural networks and the features of its neural constituents. A direct consequence of this view is that the power spectrum of brain signals is oftentimes erroneously assumed to be time stationary. Our results add to a growing body of evidence showing that this is not the case, even in simplistic networks, and further add that the jittering of frequency and power must be regarded as a dynamic signature of fluctuating activation patterns. Using a fully nonlinear and stochastic approach, our analyses suggest that the spectral fluctuations observed in recurrent neural networks are caused by a synergetic interaction between inputs and the system's nonlinearity; an interaction that shapes the system's response function and resulting oscillatory behavior. While our study has primarily focused on the impact of afferent spiking inputs (by looking at Poisson shot noise), our conclusions would apply to a broader range of stochastic signals (e.g., Gaussian white noise) as well as those emanating from other, nonafferent sources. The range of frequencies expressed by our network, here located in the alpha band, can also be modified by adjusting the system's parameters, such that our findings would apply to other frequencies as well. We further add that despite the fact that our analysis was focused on input-induced spectral modulation, our model was nonetheless capable of expressing responses similar to those commonly observed with electroencephalography, such as event-related potentials (Fig. 4A) and event-related desynchronization (Fig. 4B).

Delay-induced synchrony is a candidate mechanism for the generation of oscillatory resting-state activity in the brain (Deco et al., 2011; Nakagawa et al., 2014), which is clearly distinct from the more local mechanism believed to be responsible for gamma activity. Operating at larger spatial scales for which synaptic conduction time lags become substantial (Cabral et al., 2014), our analysis shows that delay-induced synchrony can sustain the experimentally observed spectral variability of the alpha peak frequency, and thus that the power spectrum of neuroelectric signals can be seen as nonstationary across a wide range of frequency bands. As such, our work adds to a growing body of experimental and theoretical studies reporting complex, nonlinear interactions between endogenous oscillatory activity across multiple frequency bands and external stimulation patterns that build on and substantially extend various mechanisms such as resonance (Spiegler et al., 2011; Thut et al., 2012), plasticity (Fründ et al., 2009), or input-induced changes in the neurons' response functions (Doiron et al., 2001).

Cohen (2014) has recently put forward the concept of “frequency sliding” to describe dynamic changes in the peak frequency of modeled and empirical neural responses. The present complementary results go a step further by detailing a generic mechanism potentially responsible for these fluctuations and their reliability, providing a framework in which the spectral features of cortical networks can be directly linked to input statistics in a rigorous quantitative manner. In this vein are recent advances in adaptive frequency tracking, which have likewise provided empirical support to the proposition that stimuli can produce robust changes in the frequency of the responses of neural activity across a wide range of frequencies (cf. Van Zaen et al., 2013, their Fig. 8), which in turn vary as a function of whether or not stimuli induced the perception of an illusory contour. The directionality (increase/decrease) likewise varied as across frequency bands, which suggests that inputs might recruit differentially distinct recurrent structures. Such results provide additional empirical demonstration of the general principles revealed by the present computational model. Collectively, these show that network parameters alone cannot provide a full account for the observed pattern of neural responses; stimulus statistics and features are of equal relevance.

Response profiles of the modeled network followed a pattern consistent with divisive normalization (Carandini and Heeger, 2012), which is expected given the inclusion of diffuse, spatially wide inhibition in our model. Importantly, our results also suggest that mechanisms of divisive normalization are directly linked to those mechanisms engendering bidirectional frequency modulation. Such a link has also rightfully been outlined in both computational (Jadi and Sejnowski, 2014) and empirical (van Atteveldt et al., 2014) studies. Accordingly, our results show that normalization can be enhanced or suppressed, on-line, according to stimulus statistics and dynamics. This is also in accordance with the recent propositions of Cohen (2014) that frequency sliding may constitute a type of gain control mechanism wherein slower frequencies promote a lower threshold for firing while faster frequencies do the opposite.

We note that the present findings are distinct from resonance and entrainment phenomena in which rhythmic inputs either amplify (Ali et al., 2013) or override ongoing oscillatory activity effectively replacing the peak of the power spectrum (Thut et al., 2012). These mechanisms rely on the input itself having a rhythmic structure. Instead, our findings show how an unstructured stochastic input can bidirectionally modulate the power spectrum of ongoing oscillatory activity. Thus, in an era where neurostimulation becomes increasingly popular to support a wide variety of clinical interventions (Paulus, 2011; Baertschi, 2014; Cabrera et al., 2014; Gevensleben et al., 2014; Glannon, 2014; Schlaepfer and Bewernick, 2014), our results promote, in contrast, the idea that persistent yet weak stimulation of cortical networks can significantly amplify the power displayed at specific frequencies most likely engaged in the processing of sensory information, a mechanism that could constitute an alternative and/or complementary strategy to noninvasively tune ongoing cyclic brain dynamics.

Conclusion

We show that the peak frequency and power displayed by neural populations evolving in coherent synchrony are context-dependent and nonstationary quantities that fluctuate according to the statistics of the inputs. This effect is due to a synergetic interaction between the system's intrinsic nonlinearity and input variability. As such, oscillatory properties of recurrently connected neural populations cannot be regarded as static, and the peak frequency must be seen as echoing the dynamics of the drive received by the neurons. The existence of these frequency transitions further suggests that classical neural spectral bands (e.g., theta, delta, alpha, beta, gamma, etc.) are mutually bound, where power can naturally transit from one band to another due to the action of exogenous and endogenous drive. New developments in adaptive frequency tracking are allowing for more accurate quantification of oscillatory activity and its dynamic modulation (Uldry et al., 2009; Van Zaen et al., 2010, 2013). Notably, spectral dynamics could be used alongside other methods to probe ongoing activity of cortical networks and trace event-related activation patterns in real time. Furthermore, our findings provide an important insight for future developments in quantitative analyses and simulations of oscillatory dynamics, including modeling of their alteration and breakdown to emulate disease states.