Augmin accumulation on long-lived microtubules drives amplification and kinetochore-directed growth

Vertebrate cells assemble mitotic spindles through multiple pathways. It is shown that Augmin-dependent, noncentrosomal nucleation generates the vast majority of microtubules in metaphase spindles. This results in a strong directional bias of microtubule growth toward individual kinetochores.

Abstract

Dividing cells reorganize their microtubule cytoskeleton into a bipolar spindle, which moves one set of sister chromatids to each nascent daughter cell. Early spindle assembly models postulated that spindle pole–derived microtubules search the cytoplasmic space until they randomly encounter a kinetochore to form a stable attachment. More recent work uncovered several additional, centrosome-independent microtubule generation pathways, but the contributions of each pathway to spindle assembly have remained unclear. Here, we combined live microscopy and mathematical modeling to show that most microtubules nucleate at noncentrosomal regions in dividing human cells. Using a live-cell probe that selectively labels aged microtubule lattices, we demonstrate that the distribution of growing microtubule plus ends can be almost entirely explained by Augmin-dependent amplification of long-lived microtubule lattices. By ultrafast 3D lattice light-sheet microscopy, we observed that this mechanism results in a strong directional bias of microtubule growth toward individual kinetochores. Our systematic quantification of spindle dynamics reveals highly coordinated microtubule growth during kinetochore fiber assembly.

Introduction

In dividing cells, the spindle apparatus congresses chromosomes to the cell equator and subsequently moves sister chromatids to the poles so that each daughter cell inherits a complete copy of the genome. Spindles start forming upon mitotic entry, when the interphase microtubule (MT) network converts into an antiparallel, bipolar array (Heald and Khodjakov, 2015; Petry, 2016; Prosser and Pelletier, 2017). Vertebrate spindles attach a “fiber” of ∼20–40 MTs to a confined region on each replicated sister chromatid, termed the kinetochore (KT; Rieder, 1981; McDonald et al., 1992; McEwen et al., 1997; Walczak et al., 2010; DeLuca and Musacchio, 2012; Nixon et al., 2015). Each pair of sister kinetochore fibers (k-fibers) binds to opposing spindle poles, enabling faithful chromosome segregation (Cimini et al., 2001; Tanaka, 2010).

Early spindle assembly models postulated that each MT in a k-fiber nucleates at one of the centrosomes to individually grow and capture KTs upon random encounter (Kirschner and Mitchison, 1986). Although stochastic capture events were observed in live cells (Hayden et al., 1990; Rieder and Alexander, 1990), mathematical modeling and computational simulations suggested that the probability of centrosomal MTs contacting all KTs within the typical duration of mitosis is extremely low (Wollman et al., 2005). Indeed, many MTs are now known to nucleate at pole-distal regions of the spindle, which is expected to increase the probability of KT capture. MTs can nucleate in cytoplasmic regions surrounding chromosomes (Gruss et al., 2001; Sampath et al., 2004; Maresca et al., 2009; Petry and Vale, 2015; Scrofani et al., 2015; Meunier and Vernos, 2016), directly at KTs (Khodjakov et al., 2003; Sikirzhytski et al., 2018), or on the outer walls of existing MTs via the Augmin complex (Goshima et al., 2007, 2008; Lawo et al., 2009; Petry et al., 2011, 2013; Kamasaki et al., 2013).

The relative contributions of these alternative MT generation pathways to spindle assembly appear to vary across species and cell types (Meunier and Vernos, 2016). Centrosomal nucleation is thought to be the main source of spindle MTs in most animal cells (Prosser and Pelletier, 2017). Indeed, a comprehensive study in Drosophila melanogaster embryonic cells confirmed this is the default dominant pathway, despite the fact that all act synergistically to ensure robust assembly of a bipolar spindle in a variety of perturbation conditions (Hayward et al., 2014). In mammalian cells, all of these pathways coexist (Gruss et al., 2002; Kalab et al., 2006; Tulu et al., 2006; Kamasaki et al., 2013). Yet, the contribution of each pathway to spindle assembly remains unclear. Importantly, the extent to which multiple processes are integrated in unperturbed mitosis is unknown.

Acentrosomal MT nucleation is best characterized in cytoplasmic extracts of Xenopus laevis eggs, where it has long been thought to play a pivotal role in spindle assembly (Carazo-Salas et al., 1999; Kalab et al., 1999). Quantitative studies of the spatial distribution of MT plus ends in this system demonstrate that acentrosomal nucleation makes an outstanding contribution to the assembly of the X. laevis meiotic spindle, allowing it to span radial distances of 50–300 µm (Petry et al., 2011; Brugués et al., 2012; Ishihara et al., 2014; Decker et al., 2018). The distribution of MT plus ends in somatic cells from mammals (PtK-1 cells; Tirnauer et al., 2002) and Drosophila (Mahoney et al., 2006) appear to be inconsistent with a model of predominantly centrosomal nucleation. These observations call into question the early models of spindle assembly, which proposed the centrosome as the dominant source of MTs, and highlight the need for a formal quantification across multiple systems.

Here, we used live-cell microscopy and mathematical modeling to study spindle assembly in human somatic cells. We found that MT plus ends arriving at metaphase chromosomes almost entirely originate from noncentrosomal regions via Augmin-mediated amplification of MT lattices. This pathway establishes a strong directional MT growth bias toward individual KTs, which promotes rapid formation of bioriented k-fibers. Our systematic quantification provides an integrated view on assembly and steady-state maintenance of vertebrate spindles.

Results

A large fraction of the MTs that reach metaphase chromosomes do not originate from spindle poles

Current models for MT nucleation pathways predict the generation of plus ends in distinct regions of the mitotic spindle. Whereas the Augmin- and chromosome-dependent pathways can be expected to generate MTs across the entire spindle body (Kamasaki et al., 2013; Oh et al., 2016), centrosomal nucleation produces radial MT arrays. Considering the spherical geometry of these arrays, the density of MT plus ends growing from centrosomes should decrease rapidly with increasing distance from spindle poles. To determine the relative contribution of centrosomal and noncentrosomal MTs to spindle assembly in human cells, we quantified MT plus end density at increasing distances from spindle poles.

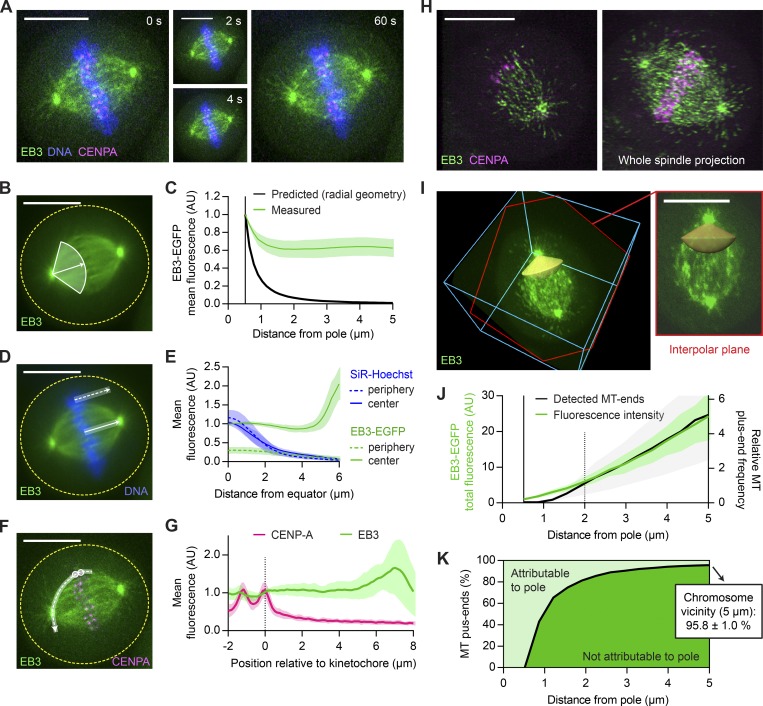
We acquired confocal time-lapse videos of HeLa cells (Fig. 1 A and Video 1) and hTERT-RPE1 cells (Fig. S1 A and Video 2) stably expressing EGFP-tagged EB3 (EB3-EGFP), which labels growing MT plus ends (Stepanova et al., 2003; Dragestein et al., 2008), and CENP-A-mCherry, a marker for KTs. Further, we stained chromosomes with the live-cell DNA marker SiR-Hoechst (Lukinavičius et al., 2015). In metaphase cells, the intensity of EB3-EGFP fluorescence and overall morphology of the spindle remained practically constant throughout 1-min videos (Videos 1 and 2). We therefore assumed photobleaching to be negligible and the MT plus end distribution to be in a steady state. We projected all time frames to generate a smooth map of the average MT plus end density (Figs. 1 B and S1 A) and quantified EB3-EGFP mean fluorescence in sectors extending from the spindle pole to the spindle center to determine MT plus end densities. Considering a 3D spherical geometry of MTs growing radially from centrosomes, the density of MT plus ends is expected to decrease by the inverse of the squared distance from spindle poles. If all MTs radiating from the centrosome rim grow to a length of 5 µm, the density of plus ends measured at that distance should thus fall to 1% (Fig. 1 C, black). The EB3-EGFP fluorescence measured in interpolar spindle regions, however, decreased <40% near the spindle pole and then remained roughly constant (Fig. 1 C, green). For distances between 1 and 5 µm from the pole, the mean fluorescence stabilized at 63.1 ± 9.9% (mean ± SD) in HeLa cells (Fig. 1 C) and 69.6 ± 9.3% in hTERT-RPE1 cells (Fig. S1 B). This indicates that only a small fraction of MT plus ends arriving at the metaphase plate can be part of the radial MT network originating from centrosomes.

Figure 1.

The majority of MT plus ends that reach metaphase chromosomes do not originate from spindle poles. (A–G) Live-cell confocal microscopy of HeLa cells expressing EB3-EGFP (green) and mCherry-CENPA (magenta), stained with SiR-Hoechst (blue). (A) Metaphase cell imaged for 1 min at 2 s/frame (see Video 1). (B and C) Quantification of MT plus end distribution from the spindle poles (see Materials and methods for details). (B) All time frames were registered to correct for spindle rotation (see Video 3) and projected to obtain mean-intensity images. EB3-EGFP fluorescence was measured in interpolar spindle regions, along a series of circumferential lines of increasing radius centered on the spindle poles. The quantification region extends from the pole to the spindle center (full white line; arrow indicates direction of the pole–pole axis). (C) Mean EB3-EGFP fluorescence measured as in B (n = 25 cells; individual measurements normalized to the centrosome rim). The black line indicates predicted signal dilution by radial geometry. (D and E) Quantification of EB3-EGFP and SiR-Hoechst fluorescence across the chromosome–cytoplasm boundary. (D) Mean intensities were profiled along lines placed either inside the spindle (full white line) or in its immediate periphery (dotted white line); results are plotted in E (n = 25 cells). (F) Quantification of fluorescence of EB3-EGFP and mCherry-CENPA along curved lines connecting pairs of sister KTs (dashed white line) to one of the spindle poles in maximum-intensity projections of three sequential video frames. (G) Mean intensity profiles, aligned to the midpoint between sister KTs (n = 42 profiles in 7 cells). (H–K) HeLa cells imaged during metaphase by 3D lattice light-sheet microscopy (n = 11). (H) Maximum-intensity projections of 5 (left) and 60 (right) consecutive slices of a deconvolved z-stack. (I) EB3-EGFP fluorescence was measured in nondeconvolved stacks inside conical ROIs defined around the interpolar axis (yellow). Shown is the same cell as in H; bounding box is 23 × 24 × 11 µm. The slice highlighted in red follows the plane defined by the spindle poles and a random KT. (J) Distribution of MT plus ends in interpolar spindle regions, estimated from the EB3-EGFP fluorescence measured as in I (green) or from the EB3-EGFP particles detected as in Fig. S1 F (black). Fluorescence intensities were normalized to the centrosome rim; the count profiles shown in Fig. S1 G were normalized to 2 µm from the spindle poles. (K) Fractions of MT plus ends attributable (light green) and not attributable (dark green) to nucleation at the spindle poles as a function of distance from the pole. Computed from the fluorescence measurements shown in J as detailed in Materials and methods. Lines and shaded areas denote mean ± SD, respectively. Scale bars, 10 µm. Yellow dotted lines indicate cell boundaries. AU, arbitrary units.

Given the dynamic instability of MT plus ends (Mitchison and Kirschner, 1984), not all MTs nucleated at centrosomes are expected to reach metaphase chromosomes, further decreasing the fraction of interpolar MT plus ends that can be attributed to centrosomal origin. A model taking both dynamic instability and spherical geometry into account predicts that 98.8 ± 0.2% (mean ± SD) of the MT plus ends observed at 5 µm from the pole must originate from noncentrosomal regions (Fig. S1 C; see Materials and methods for details). A high abundance of acentrosomal MT nucleation was previously shown to drive the formation of huge MT asters in egg extracts of X. laevis (Brugués et al., 2012; Ishihara et al., 2014; Decker et al., 2018). Our data show that also in the much smaller metaphase spindles of human somatic cells most MTs are acentrosomal, which fully compensates for the dispersion imposed by the geometry of spherical MT arrays.

To determine the predominant sites of noncentrosomal MT generation, we investigated whether MT plus ends might be locally enriched around the metaphase plate. We measured EB3-EGFP fluorescence across the chromatin–cytoplasm boundary (Fig. 1 D). Line profiles placed perpendicular to the metaphase plate showed only marginal enrichment in the direct vicinity of chromosomes, irrespective of their position inside or in the periphery of the main spindle (Figs. 1 E and S1 D). Analysis of EB3-EGFP fluorescence along curved line profiles connecting KTs with spindle poles also showed no substantial local increase when approaching KTs (Fig. 1, F and G; and Fig. S1 E). Hence, MT plus ends are not locally enriched around chromosomes or KTs.

We next investigated the distribution of EB3-EGFP in a 3D volume. The photosensitivity of mitotic cells limits the analysis of MT plus ends in 3D by conventional confocal microscopy. Lattice light-sheet microscopy offers high spatial resolution and ultra-fast image acquisition rates at minimal phototoxicity (Chen et al., 2014). Moreover, it uses scanned Bessel beams to illuminate extremely thin sample sections. This provided high-resolution 3D images of entire metaphase cells (Fig. 1 H). We analyzed MT plus end distributions by automatically detecting both spindle poles in each video frame using in-house–developed software (see Materials and methods for details). We then quantified the EB3-EGFP fluorescence intensity in interpolar regions of the spindle, inside two pole-focused conical regions of interest (ROIs; Fig. 1 I). The total fluorescence increased steadily with increasing distance from the pole (Fig. 1 J, green), such that 95.8 ± 1.0% (mean ± SD) of the signal sampled at a 5-µm distance could not be attributed to centrosomal origin (Fig. 1 K). This result agrees with our previous estimates (Fig. S1 C), indicating that the contribution of out-of-focus fluorescence was small and confocal images can in principle be used to characterize the distribution of EB3-EGFP in the spindle.

To determine whether the measured fluorescence intensity profiles accurately reflect the distribution of MT plus ends, we next aimed to detect individual EB3-EGFP–labeled particles in the spindle (Fig. S1, F and G). At pole-proximal regions, the density of MT plus ends was too high for reliable particle detection. However, in pole-distal regions, where density was low enough for reliable particle detection, the observed distribution closely matched that of the total fluorescence measurements (Fig. 1 J, black). This indicates that the contribution of background fluorescence to these measurements is negligible; thus, a quantification of fluorescence intensity can in principle be used to estimate the distribution of MT plus ends in the metaphase spindle. Overall, these data indicate that centrosomes generate only a very minor fraction of the MTs whose plus ends arrive at the spindle equator.

Most MT plus ends in metaphase spindles are generated in an Augmin-dependent manner

Given the continuous increase in MT plus end number from spindle poles to the equator (Fig. 1 J), we hypothesized that they might be predominantly generated by a MT lattice–dependent mechanism. Two such mechanisms have been described: MT severing by Katanin (McNally and Vale, 1993; McNally et al., 2006; Roll-Mecak and McNally, 2010) and Augmin-mediated nucleation on the lattices of preexisting MTs. Transfection of siRNAs targeting Katanin (Dong et al., 2017) did not affect the distribution of EB3-EGFP fluorescence (Fig. S2). We hence considered Augmin-mediated nucleation as a major source of MT plus ends, as previously proposed (Goshima et al., 2007, 2008; Zhu et al., 2008; Lawo et al., 2009; Uehara et al., 2009; Kamasaki et al., 2013; Petry et al., 2013).

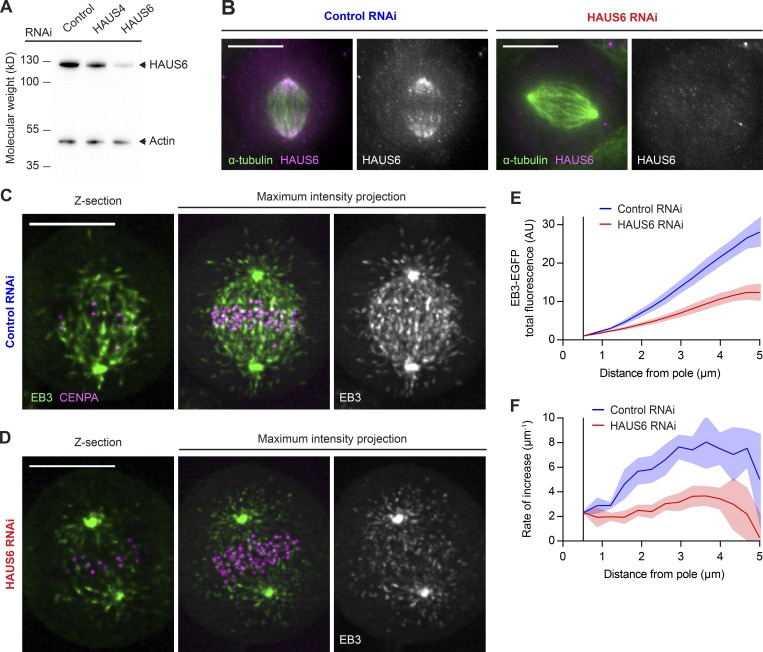
To quantify the contribution of the Augmin complex to MT plus end generation, we depleted its HAUS6 subunit by RNAi (Fig. 2, A and B). As observed before (Zhu et al., 2008), Augmin depletion caused chromosome attachment errors in metaphase cells (Fig. S3). To study MT plus end distributions, we recorded 3D lattice light-sheet microscopy videos of HAUS6 RNAi cells expressing EB3-EGFP (Fig. 2, C and D). HAUS6 depletion noticeably reduced the amount of MT plus ends in interpolar regions of the spindle compared with control RNAi cells (Fig. 2 E), consistent with observations in fixed cells (Zhu et al., 2008). Depletion of HAUS6 reduced the accumulation of MT plus ends from the pole by twofold. Importantly, the accumulation rate is substantially reduced along the entire length of the spindle (Fig. 2 F), indicating a widespread defect in MT plus end generation within the spindle body. We observed a similar reduction in MT plus end density in HAUS6-depleted hTERT-RPE1 cells (Fig. S4, A and B).

Figure 2.

Most MT plus ends in metaphase spindles are generated in an Augmin-dependent manner. (A) HAUS6 protein levels analyzed by Western blotting in HeLa cells transfected with control, HAUS4-targeting, or HAUS6-targeting siRNAs. (B) HAUS6 and α-tubulin visualized by immunofluorescence in metaphase spindles of HeLa cells transfected with control or HAUS6-targeting siRNAs. (C and D) 3D lattice light-sheet microscopy of HeLa cells expressing EB3-EGFP (green) and mCherry-CENPA (magenta), transfected with either nontargeting control siRNAs (C) or siRNAs targeting HAUS6 (D). 2.5-min videos of metaphase cells were acquired at 1 s/frame. Deconvolved images are shown. (E) EB3-EGFP fluorescence intensities measured in interpolar regions of the spindle as in Fig. 1 I for control and HAUS6 RNAi cells (n = 7 and 11 cells, respectively, collected in two independent experiments). (F) First derivative of EB3-EGFP fluorescence profiles shown in E, indicating rate of increase for MT plus end numbers. Lines and shaded areas denote mean ± SD, respectively. Scale bars, 10 µm. AU, arbitrary units.

To test whether the reduced MT plus end density was a specific effect of Augmin depletion, we examined cells transfected with siRNAs targeting HAUS4, another subunit of this complex. Metaphase spindles of HAUS4- or HAUS6-depleted cells showed similarly reduced MT plus end density compared with those of control RNAi cells (Fig. S4, C and D). Along KT-to-pole trajectories (as in Fig. 1 F and G), MT plus end density was reduced overall but showed no peak in the vicinity of KTs (Fig. S4 E). Thus, we could find no evidence of HAUS6-independent MT generation at KTs. To corroborate that the observed spindle perturbations were caused by on-target depletion of Augmin, we transfected cells with a plasmid encoding an siRNA-resistant mutant of HAUS6 and monitored its expression by visualization of EGFP fluorescence (Fig. S4 F; see Materials and methods for details). These cells maintained normal spindles after transfection of HAUS6-targeting siRNAs, whereas control cells expressing only EGFP showed the expected decrease in MT plus end density (Fig. S4 G). Hence, addback of the siRNA-resistant HAUS6 could completely suppress the RNAi phenotype. Together, our results indicate that Augmin-dependent nucleation is the main source of MT plus ends in interpolar regions of the metaphase spindle.

Augmin is thought to amplify a preexisting MT network by generating new MTs on the lattice of others (Goshima et al., 2008; Petry et al., 2013). To investigate how the steady-state MT plus end distribution in metaphase spindles relates to the distribution of template MTs, we mapped MT lattice densities in metaphase HeLa cells stably expressing EGFP-α-tubulin (Fig. S5, A and B). We formulated a mathematical model that adds to the centrosome-derived plus ends those expected to arise from amplification of the mapped MT network. The molecular factors driving MT amplification were set to distribute evenly across all template lattices to promote local plus end generation at a constant rate, such that the instantaneous frequency of pole-distal plus end generation is a linear function of the EGFP-labeled MT template distribution (Fig. S5 C; see Materials and methods). This model predicted a sharp increase in MT plus end numbers along the spindle axis, partly explaining the distribution measured in EB3-EGFP–expressing HeLa cells (Fig. S5 D). However, the fit was not perfect, predicting a relative excess of MT plus ends in pole-distal regions. Thus, although most MT plus ends in the metaphase spindle are Augmin dependent, their steady-state radial distribution does not fit well to a uniform amplification of all MT lattices.

The discrepancy between predicted and measured data indicates that the distribution of acentrosomal MT generation events within the spindle does not exactly match that of EGFP-α-tubulin. We hence considered the possibility that Augmin might distribute nonuniformly across the metaphase MT network. To test this, we examined the distribution of Augmin in fixed metaphase spindles by costaining them with antibodies targeting HAUS6 and α-tubulin. We found that HAUS6 is enriched in pole-proximal spindle regions relative to α-tubulin (Fig. S5, E and F). This could explain why our model of uniform MT lattice amplification predicted a slight excess of plus ends in pole-distal regions of the spindle.

SiR-tubulin is a marker for aged MT lattices

Augmin’s enrichment in spindle regions close to the poles might be explained by the kinetics by which Augmin interacts with MTs. If Augmin gradually accumulates on MT lattices, then it would reach highest levels on those stretches of MTs that have lived longest. Because of the net-poleward movement of spindle MTs, aged lattice stretches can be expected to accumulate near spindle poles. Prior work showed that cold-induced depolymerization of unstable MTs in metaphase spindles only slightly reduces HAUS6 abundance in interpolar regions (Zhu et al., 2008), consistent with an enrichment of Augmin on stable MTs. Thus, we considered that measuring the distribution of aged MT lattices might enable more accurate predictions of plus end distributions. As cold treatment perturbs the spindle geometry, we aimed to establish a live-cell marker for long-lived parts of MT lattices.

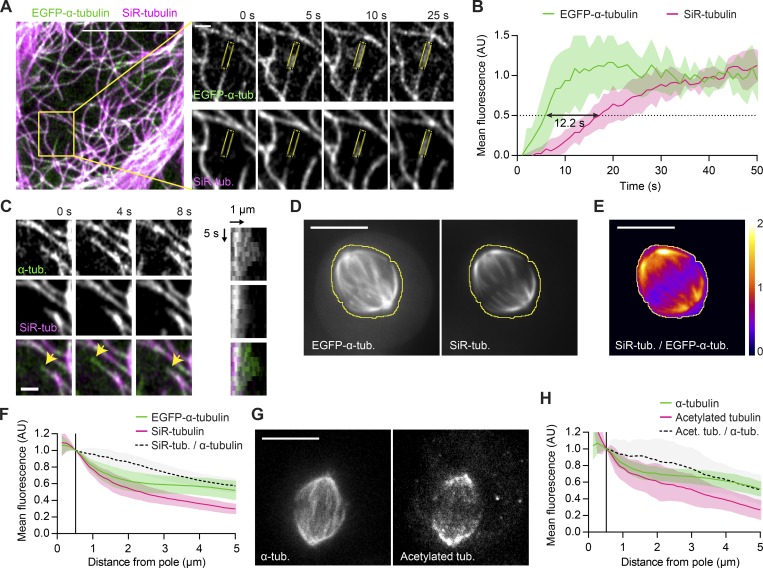
In vitro, the fluorescent Taxol derivative Flutax-1 binds to MTs with relatively slow kinetics (Díaz et al., 2000). We thus hypothesized that the nontoxic, plasma membrane–permeant variant of Flutax-1, SiR-tubulin (Lukinavičius et al., 2014), might also bind to the lattice of MTs with a detectable delay and hence label MTs in an age-dependent manner. To test this, we incubated live HeLa cells expressing EGFP-α-tubulin in the presence of SiR-tubulin and recorded confocal time-lapse videos of the bottom surface of interphase cells to resolve individual MTs as they polymerize (Fig. 3 A and Video 4). This showed that SiR-tubulin indeed labeled MT lattices with a delay of 12.2 ± 1.5 s (mean ± SEM) relative to their polymerization, as visualized by EGFP-α-tubulin (Fig. 3 B). Because of this delay, SiR-tubulin did not label those stretches of MT lattice that persisted for <12 s before their disassembly owing to dynamic instability (Fig. 3 C). Hence, SiR-tubulin enables selective visualization of long-lived MT lattices.

Figure 3.

SiR-tubulin is a live-cell marker for long-lived MT stretches. (A) Live interphase HeLa cell expressing EGFP-α-tubulin incubated with 100 nM SiR-tubulin imaged at 1 s/frame (see Video 4). Insets show a typical MT growth event (scale bar, 1 µm); mean fluorescence intensities were quantified in ROIs as illustrated (yellow). (B) Quantification of mean fluorescence in growing MTs as illustrated in A (n = 13 MTs in 9 cells; individual profiles normalized to the mean values measured at t >30 s). Black arrow indicates lag time between the 50% fluorescence value of EGFP-α-tubulin and SiR-tubulin, respectively. (C) Selected example of a growing MT undergoing a catastrophe event (arrowheads point to EGFP-labeled growing tip). A kymogram is shown on the right. (D–F) A live EGFP-α-tubulin–expressing HeLa cell incubated with 50 nM SiR-tubulin. The yellow line denotes the spindle boundary. (E) Ratiometric image of SiR-tubulin/EGFP-α-tubulin, calculated based on temporal projections of 30-s videos for the cell shown in D. (F) Mean fluorescence intensities in interpolar regions quantified as in Fig. 1 (B and C; n = 35 cells). (G and H) Acetylated tubulin and α-tubulin visualized by immunofluorescence in metaphase spindles of HeLa cells (n = 26 cells imaged in two independent experiments). (H) Mean fluorescence intensities quantified in interpolar regions as in Fig. 1 (B and C). Lines and shaded areas denote mean ± SD, respectively. Scale bars represent 10 µm unless otherwise indicated. AU, arbitrary units.

To map the distribution of SiR-tubulin-stained MTs in metaphase spindles, we recorded 1-min time-lapse videos of cells expressing EGFP-α-tubulin, as a reference marker for total MTs (Fig. 3 D). We found that central spindle regions contained substantially lower ratios of SiR-tubulin to EGFP-α-tubulin fluorescence, compared with pole-proximal regions (Fig. 3 E). The average fraction of stained lattices decreased steadily with increasing distance from the spindle poles such that at 5 µm, it is only 57 ± 8.3% of the fraction measured at the centrosome rim (Fig. 3 F). Thus, long-lived stretches of MTs accumulate in pole-proximal spindle regions.

To corroborate this observation, we visualized aged MT lattices with an alternative probe. Acetylation is a posttranslational modification of α-tubulin thought to accumulate on MT lattices in an age-dependent manner (Szyk et al., 2014; Janke and Montagnac, 2017). We imaged metaphase spindles in fixed cells costained with an antibody targeting acetylated tubulin and another that recognizes α-tubulin irrespective of acetylation (Fig. 3 G). We found that pole-proximal spindle regions were substantially enriched in acetylated tubulin, whose relative distribution closely resembled that of SiR-tubulin (Fig. 3 H, compare with Fig. 3 F). This validates SiR-tubulin as a marker for aged MT lattices and demonstrates that long-lived parts of MTs enrich in spindle regions close to the poles.

MT plus end distribution in metaphase spindles fits a uniform amplification of long-lived MT lattices

We hypothesized that amplification of long-lived parts of MTs might provide a more accurate prediction of plus end distributions than our initial model of uniform amplification of all EGFP-α-tubulin–stained lattices. To test this, we used our model to predict steady-state MT plus end distributions using the measured SiR-tubulin fluorescence profiles as a template (Fig. S5 G). These simulations yielded plus end distributions that fit the measured data more accurately, with the standard error of the estimate decreasing by 43%. This is consistent with a model where Augmin accumulates on long-lived stretches of MTs to generate MT plus ends of the metaphase spindle.

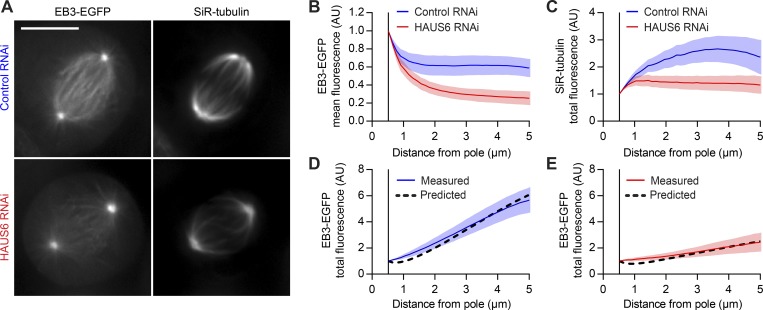
Next, we tested whether this model can also explain the altered MT plus end distributions in cells with reduced Augmin levels (Fig. S4, C and D). To visualize long-lived stretches of MTs, we treated control and HAUS6 RNAi cells with SiR-tubulin (Fig. 4 A). EB3-EGFP imaging verified that SiR-tubulin labeling did not affect the distribution of MT plus ends (Fig. 4, A and B). HAUS6 depletion led to a reduction in the integrated mass of SiR-tubulin–stained MTs at distances from the pole >2 µm (Fig. 4 C), showing that Augmin depletion affects the distribution of aged MT lattices in the spindle. Thus, for each condition, we calculated MT plus end distributions using the measured SiR-tubulin distributions as templates. The model predicted the observed MT plus end distribution in control cells (Fig. 4 D), as well as in HAUS6-depleted cells, but only when we accounted for the reduction in the available pool of amplification factors (Figs. 4 E and S5 H). Thus, our model can explain the spatial distribution of MT plus ends observed in control metaphase spindles and predict the consequences of depleting Augmin. Furthermore, the prediction for MT plus end distribution in HAUS6 RNAi cells was less accurate when the SiR-tubulin distribution of control cells was used as template (Fig. S5 H, blue dotted line), despite adjusting for the reduced size of the Augmin pool. Therefore, the model is sensitive to changes in the spatial distribution of template MTs.

Figure 4.

Augmin-mediated MT amplification explains most of the plus end distribution in the metaphase spindle. (A) EB3-EGFP–expressing HeLa cells transfected with either nontargeting (control) or HAUS6-targeting siRNAs were incubated with 100 nM SiR-tubulin; average-intensity projections of registered videos. (B and C) EB3-EGFP (B) and SiR-tubulin (C) fluorescence, quantified as in Fig. 1 (B and C; n = 32 and 35 cells for control and HAUS6 RNAi cells, respectively). SiR-tubulin fluorescence in interpolar spindle regions (C) served as amplification template in a mathematical simulation of MT plus end density (see Fig. S5 C and Materials and methods for details). (D and E) Comparison between the predicted distributions of MT plus ends (black dashed line) and the measured EB3-EGFP total fluorescence for control (D) and HAUS6 RNAi (E) cells. Lines and shaded areas denote mean ± SD, respectively. Scale bars represent 1 µm unless otherwise indicated. AU, arbitrary units.

We next aimed to test whether Augmin-mediated MT amplification might explain the distribution of growing plus ends in a dynamic steady state. To represent the equilibrium dynamics of metaphase spindles, we extended our model by introducing a bulk poleward MT flux of 0.57 µm/min, as estimated by others in mammalian spindles (Lecland and Lüders, 2014). We ran computational simulations where, as in our initial mathematical formulation, Augmin was set to distribute evenly across all available MT lattices. Bound Augmin was set to generate additional MTs at a fixed rate before dissociating from lattices (see Materials and methods for details). In vitro reconstitution of Augmin binding to MTs revealed two interaction modes with different residence times: <1 s and 3–13 s (Hsia et al., 2014). Simulations with a 13-s residence time of Augmin yielded a good fit to MT plus end distributions, whereas shorter Augmin residence times yielded lower fitting accuracies (Fig. S5, I and J). Overall, our quantitative imaging and simulations support a model in which Augmin accumulates to higher levels on long-lived stretches of MT lattices to generate the majority of plus ends in dynamic metaphase spindles.

MT growth direction is highly biased toward individual KTs

Unlike centrosomes, which generate point-symmetric radial arrays of MTs, Augmin generates MTs that grow at shallow angles relative to the parental MT (Kamasaki et al., 2013; Petry et al., 2013). Since many parental MTs in the mitotic spindle are bound to KTs, this directional bias could promote efficient formation of k-fibers. Indeed, Augmin depletion has been shown to impair k-fiber assembly (Goshima et al., 2008; Zhu et al., 2008; Bucciarelli et al., 2009; Lawo et al., 2009; Uehara et al., 2009). However, MT branch points are relatively scarce in electron tomograms of mitotic cells (Kamasaki et al., 2013). In vitro, Augmin-mediated branching can generate bundles of parallel MTs, but the presence of TPX2, a spindle-associated factor that enriches on k-fibers (Bird and Hyman, 2008), stimulates the formation of splayed MT arrays instead (Petry et al., 2013). Thus, whether Augmin-mediated branching generates MTs with focused growth toward individual KTs has remained unclear.

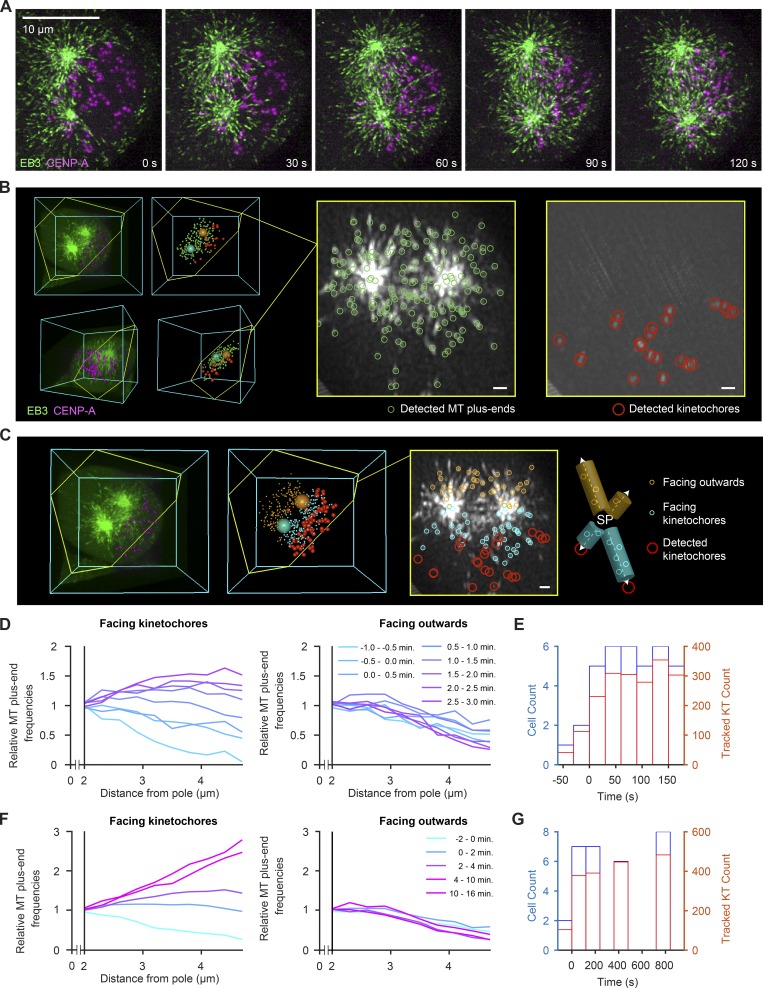
To test whether MT growth is biased toward KTs during k-fiber assembly, we visualized individual growing MT plus ends and KTs in early prometaphase spindles imaged by lattice light-sheet microscopy (Fig. 5 A and Videos 5 and 6). Using the poles as fiduciaries, we constructed ROIs for each time point of the video to determine whether and when MTs begin to grow preferentially toward the ensemble of chromosomes. We specified two regions around each spindle pole, either facing the ensemble of KTs or facing outward to the cell cortex (Fig. 5, B and C), and profiled the number of MT plus ends in each region as a function of distance from the pole (Fig. 5, D–G). Immediately after nuclear envelope disassembly, neither region showed an increase in the number of MT plus ends with distance from spindle pole. However, as early as 0.5 min after nuclear envelope disassembly, the number of MT plus ends increased significantly at pole-distal regions facing KTs, but not in regions facing outward (Fig. 5 D). The number of MT plus ends growing toward the KT ensemble continued to increase throughout mitosis, such that within 10 min after nuclear envelope disassembly, their spatial distribution within the spindle was indistinguishable from that observed in steady-state metaphase spindles (Fig. 5 F). Thus, MT growth increases in spindle regions facing toward the ensemble of chromosomes during early stages of spindle assembly.

Figure 5.

Noncentrosomal MTs increase in spindle regions facing toward KT already during early prometaphase. (A–C) HeLa cell expressing EB3-EGFP (green) and mCherry-CENPA (magenta), imaged during prometaphase by 3D lattice light-sheet microscopy. (A) Maximum-intensity projections of deconvolved video frames (t = 0 s, nuclear envelope disassembly). (B) Automated 3D detection of MT plus ends and KTs in EB3-EGFP and CENP-A images, respectively. The slice highlighted in yellow follows the plane defined by the spindle poles and a randomly chosen KT. The thickness of the projection is 600 nm. (C) Distribution of plus ends mapped to regions “facing KTs” and “facing outward.” MT plus ends facing KTs are mapped in 500-nm-wide cylinders around individual pole–KT axes, whereas MT plus ends facing outward are mapped to “mirror” cylinders facing the opposite direction. (D) Quantification of detected MT plus ends at increasing distances from the nearest spindle pole throughout early prometaphase (t < 5 min, n > 268 video frames analyzed per minute). Counts in individual cells are normalized to the value at 2 µm distance (lines denote mean; n = 9 cells). (E) Histograms of cell and KT counts for data shown in D. (F) Quantification of MT plus ends from early prometaphase to metaphase. Counts in individual cells are normalized to the value at 2 µm distance from the pole (lines denote mean, n = 22 cells). (G) Histograms of cell and KT counts for data shown in F. Scale bars, 10 µm.

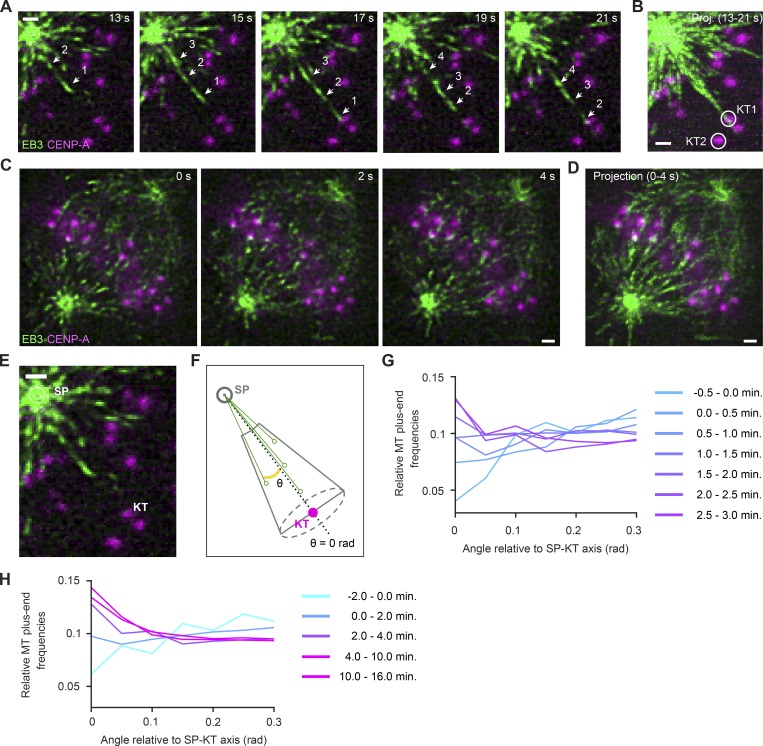
It has been proposed that molecular gradients generated around chromatin stabilize MTs growing toward chromosomes during early spindle assembly (Athale et al., 2008). This could at least partially explain the higher MT plus end densities measured in Fig. 5 but is not expected to cause a bias toward individual KTs relative to adjacent regions. To elucidate the MT growth direction relative to individual KTs, we first inspected z-sections in which isolated KTs were in focus with a spindle pole. In early prometaphase cells, we observed several instances in which many MT plus ends grew along the respective pole–KT axis at much higher densities than in adjacent regions (Fig. 6, A and B). This was more prominent in metaphase cells, in which many MT plus ends grew along trajectories leading to KTs (Fig. 6, C and D). These observations support a model where a MT bound to a KT promotes directional growth of additional MTs along its lattice.

Figure 6.

MT growth direction is highly biased toward KTs. (A–E) Lattice light-sheet microscopy of EB3-EGFP and mCherry-CENPA–expressing HeLa cells. Scale bars, 1 µm. (A and B) KT-directed MT growth in an early prometaphase cell; detail of video shown in Fig. 5 A (t = 0 s, nuclear envelope disassembly). (A) Each frame is a maximum-intensity projection of five z-sections, the center section being the focal place of the KT highlighted in B (KT1, circle). A series of MT plus ends are shown growing toward the KT (arrows). (B) Maximum-intensity projection of video shown in A. (C) KT-directed MT growth in a metaphase cell imaged at one stack of 50 z-sections/s. Each frame shows a single z-section. (D) Temporal projection of a 4-s interval, as shown in C. (E and F) Illustration of assay for automated quantification of MT growth direction relative to pole–KT axes. (E) Spindle poles and KTs were automatically detected as in Fig. 4 to calculate conical ROIs centered on pole–KT axes. MT plus ends at a distance <2 µm to the pole were not considered, as they were not reliably resolved as individual objects. (F) MT plus ends were mapped in conical ROIs, and for each, the angle of an axis connecting to the spindle pole was calculated relative to the pole–KT axis. Solid green circles on black arrows illustrate radial positions of MT plus ends. (G and H) Radial distributions of MT plus ends relative to spindle pole–KT axes. Each curve represents data from all detected KTs (sampled as described in Fig. 5, E and G) and MT plus ends for the indicated time interval relative to nuclear envelope disassembly (0 min). SP, spindle pole.

To quantify the directional bias in MT growth, we established a computational procedure to map the distribution of MT plus ends relative to individual KTs. Based on the automatically detected positions of spindle poles and KTs, we defined cone-shaped 3D ROIs connecting spindle poles with each individual KT, beginning at a minimal distance of 2 µm from the spindle pole (example illustrated in Fig. 6, E and F). We then measured the angle between the pole–KT axis and each pole–MT plus end axis to profile MT plus end densities according to different angles relative to the pole–KT axis (Fig. 6 F). To analyze the full videos, we tracked the pole and respective KT over time and integrated MT plus end positions of all KTs and all time points. Before and immediately after nuclear envelope disassembly, MTs did not preferentially grow toward KTs (Fig. 6 G, −0.5 to 1.5 min). Thereafter, however, MT plus end density increased substantially along directions pointing toward KTs (Fig. 6, G and H). Hence, the cytoplasmic space is not equally explored by growing MTs but highly biased toward KTs as the spindle matures.

Discussion

Our analysis of MT plus end distribution reveals the relative contributions of centrosomal and acentrosomal MT generation to mitotic spindle assembly in human cells. Although centrosome nucleation generates most MTs during the initial moments of spindle assembly, the fraction of MTs generated within the main spindle body increases rapidly after nuclear envelope disassembly. By metaphase, ∼90% of the MTs arriving at chromosomes are generated in pole-distal regions, which compensates for the dilution of MT density in the radial arrays generated by centrosomes. This compensation was previously shown to enable the assembly of very large MT asters in X. laevis egg extracts (Ishihara et al., 2014, 2016). Our work shows that noncentrosomal MT nucleation is the predominant source of spindle MTs also in human somatic cells. Importantly, our analysis of HAUS6-depleted cells shows that the Augmin complex is responsible for this activity.

Mathematical modeling of Augmin-mediated amplification of preexisting MTs yield MT plus end distributions that closely resemble those observed in interpolar regions of the metaphase spindle. The observed distributions are best explained by a model that considers Augmin’s uneven distribution across the spindle network, which we characterize by quantitative imaging. This uneven distribution, skewed toward spindle poles, approximates that of aged MT lattices, which we found to be selectively labeled by the live-cell dye SiR-tubulin. This might be due to a rate-limiting association time of Augmin with MT lattices, resulting in a gradual accumulation on those lattice stretches that have lived longest, i.e., the minus end–proximal segments in pole-proximal spindle regions. In vitro experiments with purified components indeed showed that a fraction of Augmin associates with MTs for ∼3–13 s (Hsia et al., 2014). This behavior might explain why, also in vitro, <3% of branching points are found near the plus end of the parent MT (Petry et al., 2013). The increasing abundance of noncentrosomal MTs during progression from prometaphase to metaphase could therefore reflect the increasing number of long-lived, KT-bound MTs.

If the majority of spindle MTs are nucleated away from centrosomes, then the establishment of robust pole–KT attachments requires that their minus ends move efficiently toward the poles. Indeed, prior work showed that the minus ends of acentrosomal MTs are transported poleward by motor proteins (Lecland and Lüders, 2014). This transport slows down in pole-proximal regions, resulting in a local accumulation of MT minus ends, an observation consistent with our finding that aged MT lattices are enriched in these regions. It is known that the formation of the large X. laevis spindle relies on the sorting of MTs nucleated away from the poles (Yang et al., 2007, 2008; Needleman et al., 2010; Brugués et al., 2012; Decker et al., 2018). This study highlights the importance of further characterizing motor activity in human somatic spindles. Our mathematical model explains how amplification of a steady-state MT template network gives rise to the distribution of growing MT plus ends during metaphase; future efforts must be aimed at understanding how the stabilization and motor-dependent reorganization of nascent MTs gives rise to the evolving template network.

Lattice light-sheet microscopy revealed a directional bias of MT growth toward individual KTs. This might be explained by the shallow angle of Augmin-nucleated MTs relative to the parental MT (Kamasaki et al., 2013; Petry et al., 2013). However, KT-directed MT growth also often occurred along curved trajectories, particularly in metaphase spindles, suggesting that the respective plus ends remain associated with MTs that have already attached to KTs. This might be mediated by interactions between MT lattices, as observed in mature k-fibers (Petry et al., 2013; Nixon et al., 2015), or by plus end–associated factors forming compliant connections with neighboring MT lattices (Molodtsov et al., 2016).

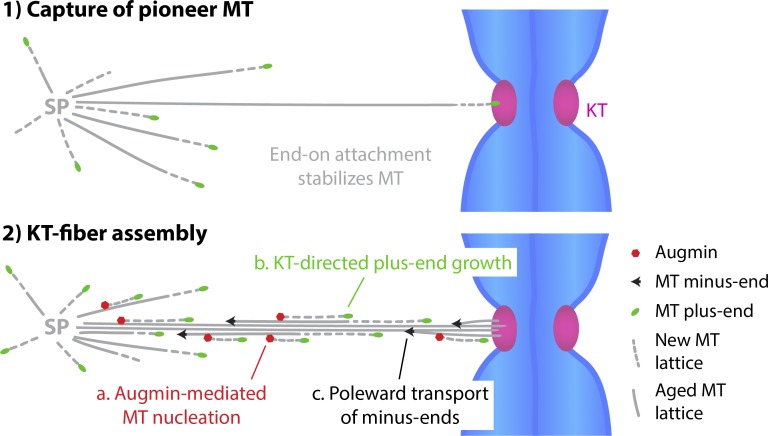
Overall, our study shows that k-fibers assemble by coordinated growth of multiple MTs rather than by a sequence of independent stochastic search-and-capture events. Our data support the existence of a positive feedback mechanism whereby the capture of pioneer MTs during early prometaphase generates a long-lived template for Augmin-driven amplification (Fig. 7). Having the vast majority of spindle MTs nucleated on and guided along previously captured MTs imposes a strong directional bias which, coupled to poleward transport of minus ends, is conducive to efficient bundle formation. As metaphase spindles continue to turn over their MTs, KT-directed MT growth might further contribute to the maintenance of KT–MT interactions and the resolution of incorrect merotelic attachments. Our quantitative assays provide a resource to further study this and the mechanisms underlying KT-directed MT guidance.

Figure 7.

Model for k-fiber assembly. Once “pioneer” MTs generated at the spindle poles (SPs) attach to KTs, they become templates for Augmin-mediated amplification. Augmin accumulates on long-lived MT lattices and generates an increasing fraction of spindle MTs (a). This leads to a measurable KT-directed bias in MT plus end growth (b). Together with stabilization and poleward transport of MTs (c), this amounts to a strong positive feedback loop conducive to rapid k-fiber assembly.

Materials and methods

Cell lines and cell culture

HeLa cell lines stably expressing fluorescent reporter proteins were derived from a HeLa Kyoto line obtained from S. Narumiya (Kyoto University, Kyoto, Japan) and validated by a multiplex human cell line authentication test. The EB3-EGFP/mCherry-CENPA and EGFP-α-tubulin/H2B-mCherry lines were previously reported (Dick and Gerlich, 2013; Cuylen et al., 2016) and generated as described in Schmitz and Gerlich (2009). Briefly, reporter constructs were subcloned into IRESpuro2b or IRESneo3 vectors that allow expression of resistance genes and tagged proteins from a single transcript. The resulting plasmids were transfected into the parental cell lines using X-tremeGENE9 DNA transfection Reagent (Sigma-Aldrich) according to the manufacturer’s instructions. The EB3-tagRFP line was generated by transfecting a plasmid derived from a EB3-EGFP construct reported previously (Stepanova et al., 2003): the EGFP sequence was replaced with tagRFP (FP142; Evrogen) by restriction enzyme cloning. For selection of reporter construct expression, cells were cultured in medium containing 500 µg/ml G418 (11811-031; Thermo Fisher Scientific) and 0.5 µg/ml puromycin (540411; Merck).

The RPE1 cell line stably expressing EB3-EGFP and mCherry-CENPA was generated from a parental hTERT-RPE1 line obtained from ATCC using a lentiviral vector system pseudotyped with murine ecotropic envelope that is rodent-restricted (RIEP receptor system), as previously described (Samwer et al., 2017). Briefly, the hTERT-RPE1 cells were first engineered to express RIEP on the cell surface and then infected with virus carrying lentiviral transfer plasmids encoding each of the reporter constructs. The virus were packaged in HEK293T cells transfected using25K linear polyethylenimine (23966-1; Polysciences, Inc.). 48 h after infection, hTERT-RPE1 cells were thoroughly washed with PBS and cultured in DMEM containing 10 µg/ml blasticidin (15205; Sigma-Aldrich) for selection of viral integration. Another 48 h later, the washing step was repeated and cells were FACS sorted for the respective fluorescent marker.

HeLa and RPE1 cells were cultured in DMEM (produced in-house at Institute of Molecular Biotechnology of the Austrian Academy of Sciences) supplemented with 10% (vol/vol) FBS (Thermo Fisher Scientific), 1% (vol/vol) penicillin–streptomycin (Sigma-Aldrich), and GlutaMAX (Thermo Fisher Scientific) at 37°C with 5% CO₂ in a humidified incubator. All cell lines used in this study are listed in Table S1 and have been regularly tested negatively for mycoplasma contamination.

Plasmids

We aimed to use minimally tagged HAUS6 variants. To monitor expression levels via EGFP, we designed plasmids containing the P2A sequence (2A peptide from porcine teschovirus-1 polyprotein; Szymczak et al., 2004). The ribosome fails to insert a peptide bond at the two last amino acids of the P2A sequence, yielding two separate polypeptides from a single mRNA. To generate EGFP-P2A-HAUS6, a HAUS6 cDNA clone was obtained from the PlasmID Repository (pCR-BluntII-TOPO_HAUS6; see Table S1 for details) and amplified by PCR with the following primers: 5′-AAG​AGA​ATC​CTG​GAC​CGA​CCG​GTA​TGA​GCT​CGG​CCT​CG-3′ (forward) and 5′-CTG​GAT​CGG​AAT​TCG​GAT​CCT​CAT​CTT​GTC​AAG​TCA​GAC​G-3′ (reverse). Alternatively, to generate the EGFP-P2A control construct, amplification with the forward primer 5′-AAG​AGA​ATC​CTG​GAC​CGA​CCG​GTA​TGA​GCT​CGG​CCT​CGG​TCA​CC-3′ was used to introduce a stop codon two amino acids downstream of the start methionine of HAUS6. The amplified sequences were inserted via Gibson Assembly (New England Biolabs) into a previously described EGFP-P2A-BAF_IRES_Blast construct (Samwer et al., 2017), replacing the BAF gene. To generate an siRNA-resistant HAUS6 variant, we introduced five mismatches in the siRNA target region without changing the amino-acid sequence (see Fig. S4 F for sequence details). The mutated gene region was produced by gene synthesis (gBlocks; Integrated DNA Technologies) and swapped into the EGFP-P2A-HAUS6 plasmid described above by Gibson assembly. All plasmids were verified by DNA sequencing and will be distributed via the Addgene repository (http://www.addgene.org). For the RNAi phenotype complementation experiments, the EGFP-P2A-HAUS6* and EGFP-P2A–encoding plasmids were delivered to EB3-tagRFP–expressing cells 24 h after siRNA transfection (see below). In each reaction, 200 ng plasmid was transfected using X-tremeGENE9 DNA transfection Reagent (Roche) according to the manufacturer’s instructions.

siRNA transfection

siRNAs (see Table S1) were delivered at a final concentration of 20 nM using Lipofectamine RNAiMAX (Thermo Fisher Scientific). 6.8 pmol siRNA was dissolved in 20 µl OptiMEM; 2 µl RNAiMAX was diluted in 20 µl OptiMEM. Both solutions were combined, mixed by pipetting, and incubated for 20–30 min. Cells were harvested by trypsinization, resuspended in fresh DMEM medium, and seeded onto LabTek II chambered coverglass (Thermo Fisher Scientific). 2 × 10⁴ HeLa cells or 3 × 10⁴ RPE1 cells were seeded per well in 300 µl DMEM medium. 40 µl of the above transfection mix was added dropwise to the cells directly after seeding. Cells were analyzed 48 h later by confocal live-cell microscopy (or lysed for quantification of protein levels). Alternatively, cells were harvested by trypsinization 24 h after siRNA transfection and then seeded onto precleaned 5-mm coverslips for analysis by lattice light-sheet microscopy 24 h later.

Immunoblotting

Where quantification of protein levels by immunoblotting was preformed, samples were prepared in parallel as those meant for live-cell imaging. All steps were done at RT. HeLa cells treated as above were lysed in 1× SDS loading buffer 48 h after siRNA transfection. Samples were separated by Novex NuPAGE SDS-PAGE system (Thermo Fisher Scientific) using 4–12% BisTris 1.5-mm gels in MES running buffer, according to the manufacturer’s instructions. Proteins were transferred to a nitrocellulose membrane (Protran BA 83; Sigma-Aldrich) by semidry blotting in a Trans-Blot SD Cell (Bio-Rad). Membranes were blocked in 5% (wt/vol) milk powder + 0.02% NP-40 in TBS (blocking solution) for 30 min, then incubated for 1.5 h with the primary antibodies diluted in blocking solution at the concentrations indicated in Table S1. Membranes were washed three times in blocking solution (sequentially for 5, 10, and 10 min), then incubated for 1.5 h with species-specific secondary antibodies coupled to HRP at the concentrations indicated in Table S1. Membranes were washed three times in blocking solution for 5 min and then three more times in 0.02% NP-40 in TBS (sequentially for 5, 10, and 10 min). Finally, membranes were rinsed once with ddH₂O and incubated for 5 min in ECL Plus Western Blotting Substrate (Thermo Fisher Scientific). Chemiluminescence was documented on a ChemiDoc MP (Bio-Rad) system. All immunoblots were recorded with no saturated pixels.

Immunofluorescence

HeLa Kyoto WT cells were cultured as described above. All subsequent steps were done at RT, unless otherwise stated. See Table S1 for antibody dilutions used. Cells were fixed for 6 min in −20°C methanol and then washed three times with PBS supplemented with Tween 80 (PBST), each for 5 min. Samples were blocked with 10% fetal calf serum in PBST (blocking solution) for 30 min and then incubated with the primary antibody in blocking solution for 14 h, at 4°C. Samples were washed two times with PBST, each for 10 min, and then incubated with the respective secondary antibody in blocking solution for 3 h. Samples were washed for 10 min in PBS (repeated three times) and then imaged on a spinning-disk confocal microscope (UltraView VoX; PerkinElmer) controlled by Volocity software, with a 100×/1.45 NA oil objective. Two 3D volumes were sequentially acquired by illuminating with 488-nm and 561-nm lasers.

Confocal live-cell microscopy

Cells were imaged on LabTek II chambered coverglass (Thermo Fisher Scientific) in DMEM containing 10% (vol/vol) FBS and 1% (vol/vol) penicillin–streptomycin, but without phenol red and riboflavin to reduce autofluorescence (Samwer et al., 2017). Where indicated, the imaging medium additionally contained 50 nM SiR-Hoechst or 50–100 nM SiR-tubulin (as specified in the respective figure legends), and cells were preincubated in it for >2 h. Cells were maintained at 37°C in a humidified atmosphere of 5% CO₂, provided by incubation chambers (European Molecular Biology Laboratory) installed on every microscope used.

To study the spatial distributions of EB3-EGFP–labeled MT plus ends, α-tubulin–labeled MTs, and SiR-tubulin–stained MTs, fast time-lapse imaging was performed on a spinning-disk confocal microscope (UltraView VoX) controlled by Volocity software with a 100x/1.45 NA oil objective. Images were recorded with a Hamamatsu EMCCD 9100–13 camera. Single z-sections were acquired at 1–2 s/frame for a total of 30 s to 1 min (as indicated in the respective figure legends).

To investigate the timing of SiR-tubulin binding to growing MT lattices, cells stably expressing EGFP-α-tubulin were imaged on a Zeiss LSM880 AxioObserver scanning confocal microscope equipped with an Airyscan detector and controlled by ZEN 2011 software, with a Plan-Apochromat 63×/1.4 NA oil objective (Zeiss). Single z-sections were acquired at 1 s/frame, for a total of 2 min, in superresolution mode.

To quantify Mad2 levels at KTs, cells were imaged on a Zeiss LSM780 AxioObserver scanning confocal microscope controlled by ZEN 2011 software, with a Plan-Apochromat 63×/1.4 NA oil objective. Cells were found in prophase, based on the morphology of SiR-Hoechst stained chromosomes, and their progression through mitosis monitored. Two 3D volumes (7 z-sections, 3 µm total thickness) of EGFP-Mad2 and mCherry-CENPA were acquired 15 min after nuclear envelope disassembly by sequentially illuminating each scanned line with 488-nm and 561-nm lasers.

Lattice light-sheet microscopy

Cells were grown on precleaned 5-mm coverslips and maintained in DMEM containing 10% (vol/vol) FBS and 1% (vol/vol) penicillin–streptomycin, but without phenol red, at 37°C. Lattice light sheet microscopy was performed on the instrument described previously (Chen et al., 2014). Briefly, the coverslips were mounted on the microscope in CO₂-independent L15 medium containing 10% FBS, without phenol red, and maintained at 37°C for the duration of the experiment.

In experiments where unperturbed cells were imaged (Figs. 1, 5, and 6), we first identified prophase cells based on increased EB3-EGFP density around asters; the exclusion of soluble EB3-EGFP from nuclear areas indicated that the nuclear envelope was still intact. Using widefield time-lapse microscopy, we monitored mitotic progression for every cell. We recorded the onset of prometaphase, defined by the influx of cytoplasmic EB3-EGFP into the nucleus due to nuclear envelope disassembly. We then switched to fast 3D lattice light-sheet imaging, performed using a 15-µm-long square excitation lattice pattern of outer NA equal to 0.50 and inner NA equal to 0.42. For each cell, 3D two color volumes of EB3-EGFP and mCherry-CENPA were acquired by sequentially illuminating each plane with 488-nm and 560-nm lasers. 75–150 time points were acquired at a volumetric imaging rate of 1 Hz. After imaging, 44 of 45 cells subsequently entered anaphase, indicating minimal phototoxicity.

For analysis of HAUS6-depleted spindles (Fig. 2), we identified metaphase cells based on spindle morphology and KT congression to the equatorial plane. 3D lattice light-sheet imaging was performed using an excitation pattern of outer NA equal to 0.55 and inner NA equal to 0.44. For each cell, 3D two color volumes of EB3-EGFP and mCherry-CENPA were acquired by sequentially illuminating each plane with 488-nm and 589-nm lasers. 150 time points were acquired at a volumetric imaging rate of 1 Hz.

All images were recorded with an Orca Flash 4.0 v2 sCMOS camera (C11440-22C; Hamamatsu). Images were acquired in sample-scan imaging mode with a lateral translation of 0.4 µm and subsequently deskewed in postprocessing, as described in detail previously (Chen et al., 2014). Final voxel dimensions for all lattice light-sheet image datasets were 104 nm × 104 nm × 210–217 nm. The microscope was controlled by custom-made software.

Processing and analysis of confocal microscopy images

Spindle registration

Wherever confocal time-lapse videos were recorded for analysis of the average spatial distribution of fluorescent markers in the metaphase spindle, the video frames were first registered using the MultiStackReg Fiji plugin (Thévenaz et al., 1998) to correct for translation and rotation of the spindle (rigid body transformation). See Video 3 for an example. Registration of EB3-EGFP videos was first performed on filtered images (Gaussian blur: σ = 5 pixels) to make sure individual plus ends did not impact the transformation. If EB3-EGFP videos were collected, then registration was performed on them and the transformation matrices obtained subsequently applied to unfiltered images of all channels. Where EB3 was not imaged (Fig. 3, D–F; and Fig. S5 A), registration was based on the EGFP-α-tubulin instead.

Fluorescence intensity profiles from the spindle pole

To study the spatial distribution of fluorescent markers in spindles imaged by live-cell microscopy, we quantified the respective fluorescence intensities in average temporal projections of the registered time-lapse videos. Only cells that had both poles in the same focal plane were imaged. To study the distribution of acetylated tubulin and HAUS6 in immunofluorescence images, we quantified fluorescence intensities in the central plane of suitably oriented spindles, with both poles in focus.

We analyzed the distribution of fluorescence intensity in a polar coordinate system centered on one of the spindle poles (d = 0). The reference axis is a manually drawn line extending toward the second pole. The fluorescence intensity was measured along a series of circumferential line profiles (radius increment of 1 pixel = 130 nm) placed between the first spindle pole and the cell equator. The mean and total intensities measured within the inner one-third (interpolar) section of the profiles were normalized to the cytoplasm of individual cells and then to the mean value measured at d = 520 nm (or 4 pixels), taken as the rim of the centrosome.

Fraction of MT plus ends not attributable to the pole

The number of MT plus ends in imaged spindles could not be directly measured by detection of individual EB3-EGFP spots, as detection accuracy was limited by spot density and unreliable in pole-proximal regions of the metaphase spindle. Therefore, we inferred the relative number of MT plus ends from the mean EB3-EGFP fluorescence intensity I, measured as a function of distance from the pole (d), as described above. The measured curves should reflect the distribution of plus end density D along the spindle axis:

$$\frac{D\left(d\right)}{D\left(rim\right)}\approx \frac{I\left(d\right)}{I\left(rim\right)}.$$

The spherical geometry of centrosomal MT growth predicts that MT plus end density decreases by the inverse of the squared distance from the origin (d = rim). Thus, the relative number of plus ends N is given by

$$N\left(d\right)\approx N\left(rim\right)\times \frac{I\left(d\right)}{I\left(rim\right)}\times \frac{d^2}{ri{m}^2}.$$

The probability that a dynamically instable MT nucleated at the centrosome grows to a certain length depends on the catastrophe and growth rescue rates, which are in turn thought to be length dependent (Foethke et al., 2009; Wordeman and Stumpff, 2009). If this were the case, then the number of MT plus ends growing from centrosomes is expected to decrease exponentially as a function of distance from the pole. If the number of growing MT plus ends at the centrosome rim is N(rim), then the number expected at any given distance d is

$$N_{predicted}\left(d\right)=N\left(rim\right)\times e^{-\left(d-rim\right)/\lambda }.$$

The characteristic MT length λ is itself a function of the parameters describing the dynamic instability behavior, namely, the frequencies of catastrophe (f_cat) and rescue (f_res) over time:

$$\lambda =\frac{v_{growth}\times v_{shrink}}{f_{cat}{v}_{shrink}-f_{res}{v}_{growth}},$$

where v_growth and v_shrink are the growth and shrinkage rates of dynamic MTs (Verde et al., 1992). The decay constant k that governs the distribution of plus end number is 1/λ. We calculated a decay constant k of 0.08 µm⁻¹ based on catastrophe and rescue frequencies measured in the outer spindle regions of LLCPK-1α cells (Rusan et al., 2001). At any given distance d, the fraction of plus ends that cannot be explained by this model of dynamic instability is thus:

$$\frac{N\left(d\right)-N_{predicted}\left(d\right)}{N\left(d\right)}=1-\frac{ri{m}^2.I\left(rim\right)}{d^2.I\left(d\right)}\times e^{-0.08\times }{}^{\left(d-rim\right)}.$$

EB3-EGFP and SiR-Hoechst intensities from the metaphase plate

The fluorescence intensities were measured in average temporal projections of registered time-lapse videos and normalized to the cytoplasm of individual cells. Mean intensity profiles were taken along a 10-pixel-thick line connecting the center of the spindle (i.e., the midpoint of the interpolar axis) to one of the poles. Measurements were then taken along a line of the same length and thickness, also parallel to the interpolar axis, displaced sideways to the spindle periphery. Both profiles were normalized to the mean of the first five values measured inside the spindle body.

EB3-EGFP intensity along pole–KT trajectories

To minimize distortions caused by KT motion, we quantified EB3-EGFP fluorescence in projections of 6-s intervals of our registered videos. Maximum-intensity projections were generated for three sequential frames using the Running ZProjector Fiji plugin. In selected frames of the projections, 5-pixel-wide segmented lines were drawn, connecting selected KT pairs to one of the spindle poles (Fig. 1 F). To avoid measurement artifacts resulting from the periodic KT oscillations, CENPA loci that showed little motion blur were selected; the drawn lines were typically curved, following the natural curvature of k-fibers. The fluorescence intensities measured along the lines were normalized to the cytoplasm of individual cells in all three imaged channels. All profiles were aligned to the midpoint between the two sister KTs, identified as local maxima in the mCherry-CENPA profile. Fluorescence intensities were normalized to the average values measured in a 5-pixel-wide window around the last local maxima, i.e., the KT closest to the spindle pole.

Models of MT amplification

At any given distance from the spindle pole (d), the total number of MT plus ends attributable to centrosomal activity is predicted to be $N\left(rim\right)\times e^{-k\left(d-rim\right)}$, where rim is the estimated radius of the centrosome. Due to the spherical geometry of centrosomal MT arrays, a decreasing fraction of these plus ends is visible in the thin optical planes we analyze:

$$N_c\left(d\right)=\frac{rim}{d}\times N\left(rim\right)\times e^{-k\left(d-rim\right)}.$$

Our models add to this array of centrosome-generated plus ends those expected to result from MT branching, i.e., de novo generation on the lattices of preexisting MTs, N_b:

$$N_{predicted}\left(d\right)=N_c\left(d\right)+N_b\left(d\right).$$

While the component N_c(d) is solely a function of the number of MT plus ends generated at the spindle poles (and directly inferred from the mean EB3-EGFP fluorescence measured at d = rim), N_b(d) will depend on the frequency of MT plus end generation across the entire spindle. It has been proposed that the activity of MT nucleation factors can be spatially modulated by chromatin-generated molecular gradients. Notably, the RanGTP effector TPX2 has been shown to stimulate Augmin-mediated MT branching in vitro (Petry et al., 2013). By interacting with preexisting MTs, Ran-activated factors like TPX2 can reach high concentrations in the main body of human mitotic spindles (Oh et al., 2016). However, it remains unclear whether TPX2 activity varies significantly within the spindle body and how acentrosomal MT nucleation rates may vary as a result. The concentration gradients of both RanGTP and TPX2 appear rather diffuse, reaching all the way from chromosomes to the spindle poles (Kalab et al., 2006; Oh et al., 2016). In summary, there is currently no evidence of a differential in acentrosomal nucleation activity along the axis of human mitotic spindles. Hence, for simplicity, we assumed in our model that the MT branching frequency Bra is not spatially modulated, not depending on distance from the pole but only on the local abundance of branching factors.

In our static model of MT amplification (Fig. 4 and respective supplemental panels), we estimate steady-state template distributions by quantifying either EGFP-α-tubulin or SiR-tubulin fluorescence in metaphase cells. We then assume that the branching factors continuously redistribute across template MTs to drive local generation of MT plus ends. The local branching activity Bra(d) is then a linear function of the template distribution Template(d), depending only on the total amount of branching factors available (Aug):

$$Bra\left(d\right)=Template\left(d\right)\times \frac{Aug}{{{\displaystyle \Sigma }}_{d\in \left[0,D\right]}^{d}Template\left(d\right)}.$$

It is crucial to consider not only Bra(d), the plus ends generated at d in any given instant of time, but also the plus ends that were generated in preceding instants (at all distances from the pole a, a ∈ [rim, d]) and grew to reach d in the intervening time. Since Augmin is known to nucleate MTs at shallow angles, with the same polarity as the parent lattices (Kamasaki et al., 2013; Petry et al., 2013), we assumed that plus ends generated by branching share the directionality of the template network, their angle to the centrosome remaining constant. Further, we assumed that their growth is governed by the same dynamic instability parameters as centrosomal MTs. The probability that a MT generated by branching at d = a reaches any given distance from pole is thus $p\left(d\right)=e^{-k\times \left(d-a\right)}$, where k is the decay constant that depends on catastrophe and rescue rates. The total number or plus ends generated by branching is given by

$$N_b\left(d\right)=\underset{a\in ]rim,d]}{\overset{a}{\Sigma }}Bra\left(a\right)\times e^{-k\times (d-a)}.$$

The two components combine to generate a total number of plus ends given by

$$N_{predicted}\left(d\right)=\frac{rim}{d}\times N\left(rim\right)\times e^{-k(d-rim)}+\underset{a\in ]rim,d]}{\overset{a}{\Sigma }}Bra\left(a\right) \times e^{-k(d-a)}.$$

Since we do not know how the measured fluorescence units relate to MT number, both Template(d) and Bra(d) are unitless. Consequently, the amount of branching factors Aug is also an abstract quantity and the one free parameter in the model. In every simulation, we predicted plus end distributions for a range of Aug values (0–5 in 0.1 increments) and chose the one that minimized the mean standard error of the estimate (MSE; see Fig. S5 D for an example):

$$MSE=\sqrt{\frac{{{\displaystyle \Sigma }}_{d\in \left[rim,D\right]}^d{\left[N\left(d\right)-N_{predicted}\left(d\right)\right]}^2}{D-rim}}.$$

A Kolmogorov–Smirnov test (nonparametric, not assuming normality) was used to compare the best-fitting predicted distribution with the total EB3-EGFP fluorescence measured in cells. The resulting statistics are given in the respective figure legends.

To test whether this model could explain MT plus end distributions in a dynamic steady-state spindle (Fig. S5, I and J), we ran computational simulations that further considered the net poleward flux of spindle MTs, as well as a dynamic binding and unbinding of Augmin to preexisting lattices.

We define each MT by the distance of its minus and plus ends to the spindle pole (d_m and d_p, respectively). Thus, MTs are here considered to move in one-dimensional space. For simplicity, all MTs are set to move poleward at a constant rate v_f = 0.57 µm/min. MT minus ends that reach the pole (d_m = 0) start depolymerizing at the same rate. Growing MT plus ends move at a speed of (v_p − v_f), where v_p is the polymerization rate; shrinking MT plus ends move at (−v_s − v_f), where v_s is the depolymerization rate. v_p and v_s were set to values measured in spindles of LLCPK-1α cells (Rusan et al., 2001): 12.76 and 14.14 µm/min, respectively. Catastrophe and rescue rates were set to 0.058 and 0.045 s⁻¹, as determined in the same study. MT plus ends are not allowed to grow past the spindle equator (estimated in our cells at d_p = 6 µm).

As in the static model described above, an Augmin pool of limited size is set to distribute across all available MT lattices. We assume unbound Augmin can bind to any MT, anywhere along the MT lattice (d_p − d_m), at a fixed rate k_b. Bound Augmin generates additional MTs at a fixed rate k_bra before dissociating from lattices at a rate of k_u. The distribution of bound Augmin, Aug_b, is thus, at any given time t,

$$Au{g}_b\left(d,t\right)=\left(1-k_u\right)\times Au{g}_b\left(d+ v_f,t-1\right)+k_b\frac{Aug-{{\displaystyle \sum }}_{d\in \left[rim,D\right]}^{d}Au{g}_b\left(d,t-1\right)}{{{\displaystyle \sum }}_{d\in \left[rim,D\right]}^{d}Lat\left(d,t\right)},$$

where Lat(d, t) is the distribution of MT lattices. In this extended model, the local branching activity Bra is a linear function of Aug_b rather than any directly measured template distribution: Bra(d,t) = k_braAug_b(d,t). In every simulation, we predicted plus end distributions for a range of Aug and k_bra values. Because we are interested in steady-state solutions, we chose the one that minimized the mean standard error of the estimate averaged across the last half of the iterations (3.5 min).

Both our models were implemented in custom written MATLAB code (available upon request). Described data fitting and statistical testing were also done in MATLAB.

Quantification of SiR-tubulin binding to MT lattices in interphase cells

Instances where an EGFP-α-tubulin–labeled lattice grew into a region of low MT density were identified by visual inspection. Mean EGFP-α-tubulin and SiR-tubulin fluorescence intensities were then measured in rectangular ROIs placed in front of the growth event (each 350 nm in width and 1.4–1.6 µm in length, as depicted in Fig. 3 A) in each of the subsequent 60 frames. The background fluorescence values measured at t = 0 s (when the lattice has not yet grown into the ROI) was subtracted from each of the two channels, respectively. The profiles were finally normalized to the mean value measured at t > 30 s.

Quantification of Mad2-EGFP intensities on individual KTs

Mean Mad2-EGFP fluorescence intensities were measured in individual optical sections, inside circular ROIs (≈420 nm radius) manually placed on CENPA-positive KTs. For each cell, the median EGFP intensity across all KTs was normalized to the median fluorescence measured in the cytoplasm. All measurements were then normalized to the mean of all control cells. Differences observed were tested for statistical significance not assuming a normal distribution, with a Kolmogorov–Smirnov test, in Prism 7 software.

Analysis of lattice light-sheet microscopy data

The analyses of lattice light-sheet microscopy data were performed with the U-track 3D framework (Roudot et al., 2017) developed in MATLAB (MathWorks). Of a dataset of 65 cells imaged by lattice-light sheet microscopy, 39 contained the entire spindle volume and had sufficiently homogeneous signal-to-background ratio for automated MT plus end detection. These were considered for further analysis. Each video represented 1- to 2-min intervals and together covered mitotic stages from 2 min before nuclear envelope disassembly until 16 min after nuclear envelope disassembly. The automatic analysis pipeline consists of three steps: (1) definition of dynamic ROI (dROI) inside the spindle, (2) MT plus end detection or intensity sampling, and (3) measurement mapping in dROI to interrogate MT plus end statistics and integration across nonsynchronous videos.

dROI definition

The high concentration of MT plus ends at the spindle pole results in a bright signal that moves with the whole spindle. As such, these large clusters are excellent fiducials to build a dROI for the spindle and associated frame of reference.

The spindle poles are detected in a statistical framework that first establishes a set of candidate objects using the size of detected clusters in the 3D volume. A scale map is estimated using 3D Laplacian of Gaussian filtering at multiple scales (Lindeberg, 1998). The scales range from twice the size of a diffraction limited spot (see MT plus end detection) to 2 µm, using steps of 100 nm. The candidate locations are the local maximum across all filtered scales. Those candidate locations are then tracked over time using a Brownian motion prior with a maximal interframe displacement of 1 µm and allowing temporary disappearance of up to one frame (Jaqaman et al., 2008). Each resulting track is then scored according to the product of its lifetime and median intensity. The two best candidates are selected as the spindle poles.

KTs are also tracked over time in order to interrogate MT plus end location statistics between the spindle poles and moving KTs. Each KT’s location is estimated using a 3D implementation of an algorithm described previously (Aguet et al., 2013). Sharp transitions in KT motion between pre- and post-MT capture make trajectory estimation difficult with conventional methods. To solve this problem, we applied a recent algorithm for tracking erratic motion via piecewise-stationary motion modeling to each KT trajectory (Roudot et al., 2017). The combination of pole and KT trajectories enables the creation of multiple dROIs and associated frame of reference for quality control in 3D data and statistical analysis.

MT plus end detection

MT plus ends are detected using the centroid of the region masked with an adaptive thresholding algorithm described previously (Aguet et al., 2013). This algorithm requires a single parameter, an estimate of the scale of the diffraction-limited objects. To estimate the scale of a diffraction limited MT plus end, the scale of each object is approximated using the fitting of a 3D Gaussian function and the set of resulting scales is fitted with a Gaussian mixture model. The mode of the resulting distribution is kept as the estimated scale. Quality control was performed by automatic rendering of dROI and detection overlay in MATLAB. All MT plus ends were counted, regardless of their growth direction.

3D measurements of fluorescence intensity in lattice light-sheet microscopy videos

Intensity measurements inside the spindle are performed through random sampling inside the 3D ROI with a constant density of 100 loci/µm³.

Quantification of MT plus end densities facing KTs and outward

The definition of ROIs “facing KT” and “facing outward” to study MT plus end density at different distances from spindle poles was performed using a collection of cylindrical ROIs between the spindle poles and each KT with a radius of 500 nm. Each KT is associated to only one pole (the closest pole at the end of the trajectory), resulting in two sets of dROIs $R1\left(t\right)=\left\{R_1^1\left(t\right),\dots ,R_1^n\left(t\right)\right\}$ and $R2\left(t\right)=\left\{R_2^1\left(t\right),\dots ,R_2^n\left(t\right)\right\}$. Outward-facing areas are defined through point reflection of each dROI using the spindle pole as a center. Let us denote P the set of labeled plus end and x^* the coordinate of plus end in the frame of reference associated to its closest dROI $R_p^{*}$. The histogram of distance from spindle pole of detected MT plus end is defined as

$$C\left(d,t\right)={{\displaystyle \sum }}^{\text{}}\left|\left\{x\in P{{\displaystyle \cup }}^{\hspace{0.17em}}{R}_1\left(t\right){{\displaystyle \cup }}^{\hspace{0.17em}}{R}_2\left(t\right)\backslash \left|x^{*}-d\right|\right\}<ϵ \right|,$$

where |.| denotes the set cardinality, d is the polar distance ranging from 2 to 6 µm, and ϵ is a binning parameter set to 150 nm. To make measurement comparable and interpretable, relative frequencies counts rather than probability distributions are shown:

$$N\text{'}\left(d,t\right)=\frac{C\left(d,t\right)}{C\left(2,t\right)}.$$

Integrating count statistics of multiple ROI also has to take into account the different length of each ROI. To do so, each relative count according to the number of dROI sampling the respective distance was taken into account:

$$N\left(d,t\right)=N\text{'}\left(d,t\right)\times \frac{\left|\left\{R\left(t\right)\in R_1\left(t\right){{\displaystyle \cup }}^{\hspace{0.17em}}{R}_2\left(t\right)\right\}\right|}{\left|\left\{R\left(t\right)\in R_1\left(t\right){{\displaystyle \cup }}^{\hspace{0.17em}}{R}_2\left(t\right)\backslash l\left[R\left(t\right)\right]<d\right\}\right|},$$

where l[.] denotes the length of the dROI. Quality control for this normalization process was performed on multiple videos presenting stationary metaphase. The same process was performed symmetrically for outward-facing dROIs.

Quantification of MT growth direction relative to the pole–KT axis

To determine the density of MTs growing along the pole–KT axis relative to adjacent regions, KTs were analyzed individually as illustrated in Fig. 6, using conical dROIs with an angle of 0.5 radian. Let us denote ${\theta }_p^i$, the elevation of a MT plus end detected in the dROI $R_p^i$. The angle histogram is then defined as

$$A\left(\theta ,t\right)={\displaystyle \sum }_{p\in \{1,2\}}{\displaystyle \sum }_{i\in \left\{1,\mathrm{...},n\right\}}{A}_p^i\left(\theta ,t\right),$$

with

$$A_p^i(\theta ,t)=\left|\{x \in P {\cup }^{\text{}}{R}_p^i\left(t\right)\backslash |{\theta }_p^i-\theta |<ϵ \}\right|.$$

θ ranges from 0 to 0.5 radian and ε is a binning parameter set to 0.025 radian. As MT plus ends can be counted multiple times and the changes in dROI shape over time must be taken into account considering the volume of a 3D cone, let us denote angular histograms normalized as

$$A_p^i\text{'}\left(\theta ,t\right)=\frac{A_p^i\left(\theta ,t\right)}{\pi l{\left[R_p^i\left(t\right)\right]}^3\times \left[\tan {\left(\theta +\raisebox{1ex}{$ϵ$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}^2-\tan {\left(\theta -\raisebox{1ex}{$ϵ$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}^2\right]}.$$

This normalization enables to integrate thousands of dROI across space, time, and acquisitions. The probability distributions, A(θ,t), were then computed for different time intervals relative to nuclear envelope disassembly as shown in Fig. 6.

Data visualization

Data were plotted using GraphPad Prism 7 software. 3D renderings shown in Figs. 1 I, 5 (B and C), and S1 F were generated using Amira (Thermo Fisher Scientific) for visualization purposes only. In Fig. 5 D, the EB3-EGFP signal was deconvolved (Richardson–Lucy deconvolution with a scale of 1.5 and 10 iterations).

Online supplemental material

Fig. S1 shows validation experiments related to Fig. 1, including the quantification of MT plus end distributions in metaphase spindles of hTERT-RPE1 cells and the raw MT plus end counts in HeLa cells imaged by 3D lattice light-sheet microscopy. Fig. S2 shows that Katanin depletion does not impact MT plus end distributions. Fig. S3 shows the quantification of Mad2 levels on KTs of Augmin-depleted cells. Fig. S4 contains validation experiments related to Fig. 2, showing that MT plus end densities are also severely reduced in HAUS6-depleted hTERP-RPE1 cells and HAUS4-depleted HeLa cells; Fig. S4 (F and G) also shows that the Augmin-depletion phenotype can be suppressed by expressing siRNA-resistant HAUS6. Fig. S5 shows the mathematical modeling of plus end generation by amplification of the EGFP-α-tubulin–labeled MT network (A–D). Fig. S5 also shows the distribution of immunostained HAUS6 in metaphase spindles (E and F), and Fig. S5 (G–J) contains additional results for our modeling of age-dependent MT amplification (related to Figs. 3 and 4). Table S1 lists all the key resources and reagents used in this study. Videos 1 and 2 show growing MT plus ends in live HeLa and hTERT-RPE1 cells (respectively). Video 3 shows another example, meant to illustrate the effect of movie registration. Video 4 shows MTs growing in the presence of SiR-tubulin. Videos 5 and 6 show MT plus ends and KTs in a prometaphase cell imaged by 3D lattice light-sheet microscopy.