Predicting Local Inversions Using Rectangle Clustering and Representative Rectangle Prediction

Abstract

As a specific type of structural variation, inversions are enjoying particular traction as a result of their established role in evolution. Using third-generation sequencing technology to predict inversions is growing in interest, but many such methods focus on improving sensitivity, giving rise to either too many false positives or very long running times. In this paper, we propose a new framework for inversion detection based on a combination of two novel theoretical models: Rectangle Clustering and Representative Rectangle Prediction. This combination can automatically filter out false positive inversion predictions while retaining correct ones, leading to a method that has both high sensitivity and high positive prediction values (PPV). Further, this new framework can run very fast on available data. Our software can be freely obtained at https://github.com/UTbioinf/RigInv.

I. Introduction

STRUCTURAL variations (SVs) are important in evolutionary biology and speciation, amplifying genetic diversity in mammals [1] and attributing to heritable genetic diseases [2], [3] and cancers [4], [5]. SVs include insertions, deletions, inversions, translocations, and copy number variants (CNVs). Among them, inversions are balanced structural variations that have been playing a vital role in chromosomal evolution. It has been clearly shown that they can affect phenotypes and be adaptive in many species [6]–[8]. Many polymorphic inversions have also been discovered in human genomes [9], [10], some of which have been linked to diseases. For example, the iduronate 2-sulphatase (IDS) gene when interrupted by some inversions can lead to Hunter syndrome [11]. For these reasons, it is important to predict and catalog inversions.

Early SV detection methods largely rely on experimental data such as array comparative genome hybridization (array-CGH, e.g., [12]). These approaches, however, hardly locate exact breakpoints and are incapable of discovering balanced structural variations such as inversions. To overcome these issues, sequencing data have been leveraged, and all the sequence-based SV detection methods utilize one or more of the following approaches: i) Detecting aberrant alignments of paired reads [13]–[15]; ii) analyzing inferred read depths to unveil copy number variants (CNV) (e.g., [16]–[18]); iii) using inferred split reads and/or poorly aligned reads to pinpoint novel breakpoints [19], [20]; iv) reconstructing potential breakpoints by local-assembly for better prediction (e.g., [21],[22]). Some implementations even combine two or more of these four methods [23]–[26].

Even though newer sequencing platforms have been effective in predicting smaller SVs, shorter reads face challenges with repeat-rich regions. Third-generation sequencing platforms, such as PacBio and Oxford Nanopore, are generating much longer reads that are advantageous in de novo assembly [27], [28] and in SV prediction [29]–[36]. For example, PBHoney [34] uses two algorithms to predict SVs including PBHoney-Spots that considers long-read discordance, and PBHoney-Tails that considers interrupted mapping. Sniffles [30] performs extensive coverage analysis at high-mismatch regions and uses split-read alignments. NextSV [33] is basically a combination of PBHoney and Sniffles, and uses ANNOVAR [37] to better predict SVs. Special types of SVs have also been considered. For example, CORGi [31] focuses on complex SVs with more than 2 breakpoints. NpInv [32] is designed for detecting non-allelic homologous recombination inversions. Finally, InvDet [35] was designed for large inversions whose left and right neighbors may be unclear.

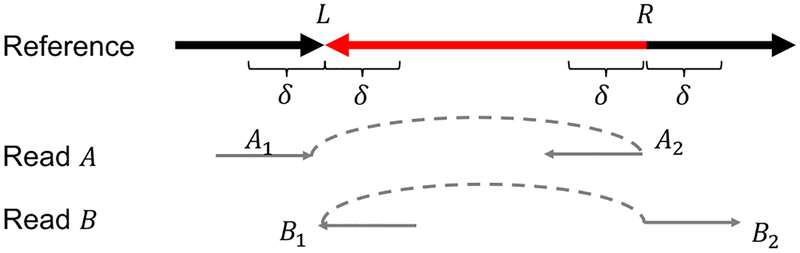
In this paper, we focus on predicting large local inversions (≥ 1000bp) using PacBio long reads. We define a local inversion as an inverted interval such that its neighboring regions around the two breakpoints do not have substantial changes (see Fig. 1 for an example). More specifically, for an inverted interval (L, R) in the reference sequence and an integer δ > 0, if the intervals (L−δ, L), (L, L+δ), (R−δ, R), and (R, R + δ) are only subject to indels and variations, we call (L, R) a “local” inversion.

Fig. 1.

Definition of local inversions. The red segment (L, R) in the reference is a local inversion if it is reverse complemented (as in the figure), and the four indicator segments of length δ are only subject to small variations/indels. Two reads A and B must be split and aligned (in pair) in different orientations to the reference in the manner exactly as shown here, where the dashed lines indicate the ordering of the split reads. These split alignments covering the four δ segments guarantee that the four δ segments do not change substantially.

The contributions of this work are threefold.

• We propose a new Rectangle Clustering framework to group predicted interval pairs (i.e., rectangles) that are “close” to one another. Extant methods mostly focus on clustering intervals that cover the same breakpoints. These approaches may perform well if the goal is to predict a deletion but they may ignore the relationships between pairs of breakpoints. Our Rectangle Clustering model and algorithm, however, are able to acknowledge these relationships and generate more robust clusters.

• We propose a novel Representative Rectangle Prediction problem that, for each rectangle cluster, predicts a small interval pair (i.e., a small rectangle) that contains the pair of breakpoints of a local inversion with high confidence. Although designed for our framework, we expect this formulation may also improve other split read-based SV prediction methods.

• The combination of the Rectangle Clustering and Representative Rectangle Prediction schemes predicts relatively unique inversions. Other methods often report two or more predictions that may form two cliques of intervals around the two (predicted) breakpoints. We overcome these issues with our new framework RigInv.

The rest of this paper is organized as follows. Section II presents the detailed algorithms of our local inversion prediction framework, including those for the new Rectangle Clustering problem and the novel Representative Rectangle Prediction problem. Section III shows some experimental results on synthetic E. coli K12 and An. gambiae PEST, and an empirical conjecture on the real An. gambiae PEST. Section IV concludes our work.

II. Methods

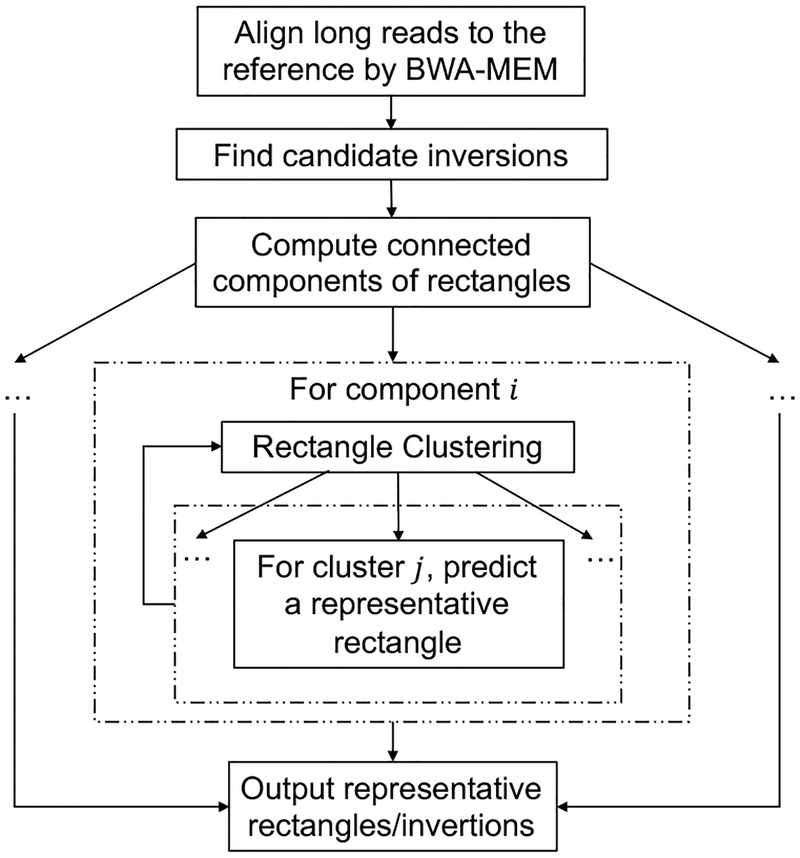
Our framework (see Fig. 2) takes as input read alignments, and generates an initial result file in which each line contains a predicted inversion. We represent each inversion (both the candidate inversions and final predictions) as a rectangle, and the pair of end points of each inversion (i.e., the breakpoints) as a single point in 2-D space. Next, based on the current candidate inversions, we predict small and nearly non-overlapping inversions using a heuristic Rectangle Clustering algorithm and a novel Representative Rectangle Prediction algorithm.

Fig. 2.

An overview of our local inversion detection framework. The step of partitioning connected components of rectangles decomposes a large input into smaller-scale inputs. This allows the successive steps of higher time complexity to be parallelized.

A. Candidate inversion detection

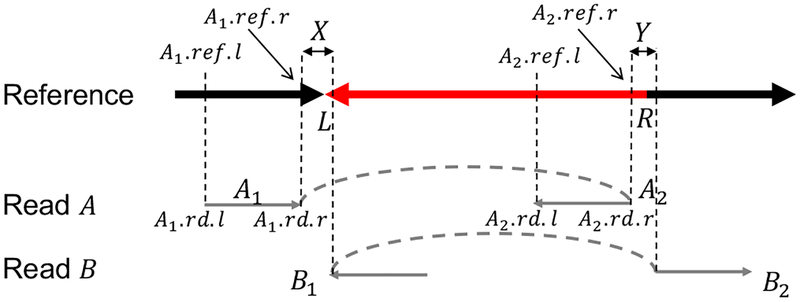
As shown in Fig. 3, to locate intervals X and Y covering the two breakpoints of an inversion (L, R), we need two types of indicator alignment segments; the L type indicator alignment is obtained by splitting a single read A into two disjoint alignments (usually by tools such as BLASR [38] and BWA-MEM [39]) A₁ and A₂ such that A₁ is followed by A₂, A₁ is aligned to the left neighbor of the inversion (L, R), and A₂ is aligned to the very right end of (L, R) but in the opposite orientation w.r.t. A₁. Similarly, the R type indicator alignment is obtained by splitting a single read B into two parts B₁ and B₂ such that B₁ is followed by B₂, B₁ is aligned to the very left end of (L, R), and B₂ is aligned to the right neighbor of (L, R) but in the opposite orientation w.r.t. B₁.

Fig. 3.

Intervals X and Y covering the two breakpoints of an inversion. In practice, it is more reasonable to predict an interval X (resp., Y) covering the left (resp., right) breakpoint L (resp., R). In this example, X = (A₁.ref.r, B₁.ref.l) and Y = (A₂.ref.r, B₂.ref.l). This representation of candidate inversions complies with the definition of a local inversion but leads to a quadratic number of candidate inversions. This issue can be resolved by considering an L (resp., R) type candidate inversion for each L (resp., R) type indicator alignment. As in this figure, since the distance of A₁ and A₂ in read A is d = A₂.rd.r − A₁.rd.r (assuming the coordinates are w.r.t. the orientation of A₁), the left and right candidate intervals covering L and R are X_A = (A₁.ref.r, A₁.ref.r + d) and Y_A = (A₂.ref.r, A₂.ref.r + d), respectively. The L type candidate inversion/rectangle w.r.t. read A and the reference sequence is therefore denoted by (X_A, Y_A, L). The R type candidate inversion/rectangle w.r.t. read B and the reference sequence can be represented similarly.

To simplify the notation, we also say that A₁, A₂, B₁, and B₂ are intervals inferred from the indicator alignments. For each indicator alignment C, we denote the corresponding interval in a reference sequence as (C.ref.l, C.ref.r), where C.ref.l (resp., C.ref.r) is the left (resp., right) end point of the alignment. Similarly, we denote the aligned region in the read as (C.rd.l, C.rd.r), where C.rd.l and C.rd.r are the coordinates calculated according to the orientation of the read in the input. Then the interval covering the left (resp., right) breakpoint of the inversion is X = (A₁.ref.r, B₁.ref.l) (resp., Y = (A₂.ref.r, B₂.ref.l)).

We can find all possible pairs of intervals covering the breakpoints of inversions based simply on this definition. Note, however, that if there are two other indicator alignment segments $A_1^{\prime }$, $A_2^{\prime }$ and $B_1^{\prime }$, $B_2^{\prime }$ aligned to similar locations of A₁, A₂ and B₁, B₂, then we will have to consider four pairs of indicator alignments: A v.s. B, A v.s. B′, A′ v.s. B, and A′ v.s. B′. In general, there will be a quadratic number of pairs of the given indicator alignment segments, leading to a steep increase in memory and running time in the successive predictions.

To mitigate this issue, we detect specific intervals X and Y using indicator alignments of A and B separately, but also using the inferred distance between the split reads. We also annotate whether the prediction is anchored by the left neighbor or the right neighbor. More specifically, for alignments A₁ and A₂, we determine:

1. X_A = (A₁.ref.r, A₁.ref.r + |A₂.rd.r − A₁.rd.r|),

2. Y_A = (A₂.ref.r, A₂.ref.r + |A₂.rd.r − A₁.rd.r|), and

3. this indicator alignment is an L type alignment.

Such a detection is called an L type candidate inversion and denoted by (X_A, Y_A, L). For alignments B₁ and B₂, we can obtain an R type candidate inversion (X_B, Y_B, R) such that

1. X_B = (B₁.ref.l − |B₁.rd.l − B₂.rd.l|, B₁.ref.l),

2. Y_B = (B₂.ref.l − |B₁.rd.l − B₂.rd.l|, B₂.ref.l), and

3. this indicator alignment is an R type alignment.

In light of these definitions, there are only a linear number of candidate inversions.

Even so, if we extract all the possible candidate inversions based on unfiltered input alignments, unclassified repeats and other complex features will still induce false positives. Therefore, in the remainder of this paper, we describe new algorithms and methods that best predict a single pair of relatively small inversion intervals with higher accuracy.

B. Connected components of rectangles

For each inversion, its pair of breakpoints can be viewed as a point c in 2-D space. For each candidate inversion (X, Y, L) or (X, Y, R), we can view (X, Y) as a rectangle in 2-D space. For simplicity of notation, we reuse (X, Y, L) and (X, Y, R) to represent candidate rectangles. For a “regular” rectangle without a third component (e.g., final predictions by our framework), we simply use (X, Y). It then follows that each point contained in a candidate rectangle is possibly a desired breakpoint c. Because the input data (here, long read alignments) span larger intervals and have a high rate of sequencing errors, we assume that a large portion of these rectangles contain a common single point c. Thus, our ultimate goal is to find the smallest possible rectangle with consensus.

To help deal with the high time complexity of the successive steps in our processing, we partition the set of candidate rectangles into smaller groups based on their connected components in 2D. The connected components of the candidate rectangles are defined by viewing each candidate rectangle as a vertex in an undirected graph; if two candidate rectangles overlap, then we add an edge between the two corresponding vertices in the graph. Next, we find all connected components in this graph since they can be processed independently (and in parallel). Computing connected components of rectangles in 2-D has been well studied and can be done in O(n log n) time using complex data structures, where n is the number of rectangles [40]–[42]. Here, to avoid implementing complicated data structures, we consider a simple O(n²) time algorithm combined with some heuristics, because the number of candidate rectangles may not be large in each resulted connected component, and, in most cases, we speculate that their configuration will not be complex.

We first partition the rectangles by considering only their connectivity along the x-axis. In this case, there are n intervals in the plane and the x-connected components of these intervals can be found easily in O(n log n) time. Next, for each resulted group of the above partition, we consider only their y-axis connectivity, which can be partitioned similarly. Finally, a trivial quadratic-time algorithm is applied to partition each group of rectangles thus resulted into connected components of rectangles. In practice, this heuristic approach can substantially reduce the amount of running time.

C. Rectangle clustering

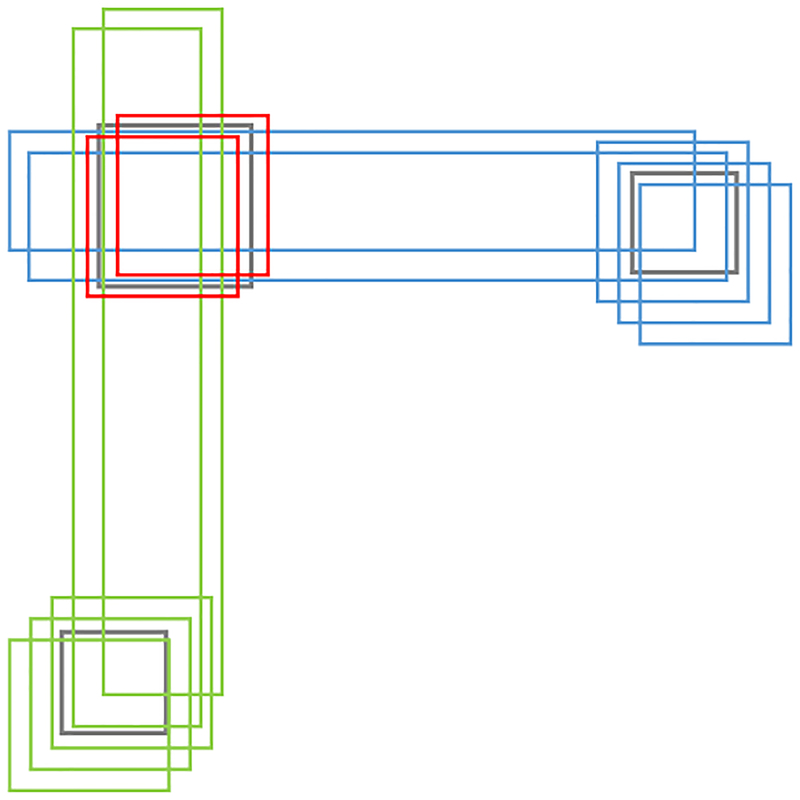
Next, we want to cluster candidate rectangles that are “close” to one another since they are likely to represent (contain) a single structural variant. To illustrate our idea, suppose the given rectangles are as shown in Fig. 4 with three clusters: red, blue, and green. In this example, it is not obvious how to assign each rectangle uniquely to one of the three clusters. To resolve this issue, we apply a soft-clustering such that some candidate rectangles can be assigned to multiple clusters. We define the soft-clustering problem as follows.

Fig. 4.

Soft clustering of three clusters of rectangles. In this example, the two long blue rectangles can be assigned to both the blue and red clusters; the two long green rectangles can be assigned to both the green and red clusters.

Definition 1:

Let Rects = {r₁, r₂, …, r_n} be a set of n (candidate) rectangles. Let F be a prediction function whose input is a subset of Rects and output is either a rectangle or “None”. The objective is to assign the n rectangles to k (k is determined by the algorithm) clusters such that the predictions (by F) for each cluster are disjoint. Each rectangle can be assigned to 0 or more clusters. Further, the assignment should be maximal, i.e., for the set N of (candidate) rectangles that are not assigned, the following two conditions should hold:

1. For ∀N′ ⊆ N, f(N′) always returns “None”, and

2. For ∀N′ ⊆ N and any cluster C_i (i = 1, …, k), the output of f(N′ ∪ C_i) is either “None” or a rectangle that must intersect with the other predicted rectangles.

In short, we want to ignore any (candidate) rectangles ended up in the set N while best determining the optimal number of clusters (inversions). This behavior is similar to the well-known DBSCAN clustering algorithm [43] except that our formulation is heavily dependent on the definition of f, which makes our version of the problem more difficult. To overcome this difficulty, we propose a simple probabilistic model as the prediction function f. We will show that a combination of this probabilistic model and our soft-clustering algorithm defined above improves the overall results.

The basic idea of our approach is to first partition the 2D plane into a grid using horizontal and vertical lines passing through the boundary edges of the n rectangles. We then count, for each cell of the grid, the number of rectangles that cover that cell. We say that a grid cell is a local maximal if the coverage numbers of its adjacent left, right, top, and bottom cells are not larger than that of the cell. Then for each local maximal cell, we invoke f to predict a representative rectangle for all the rectangles covering that cell. Because the representative rectangles thus predicted could still be very close to one another in distance, we repeat this process iteratively until there are no new predictions. Specifically, in successive iterations, we partition the grid and count the coverage for each grid cell using only the representative rectangles, but when we compute new representative rectangles, we use the union of the original rectangles. The detailed pseudocode of the algorithm is given in Algorithm 1.

D. Representative rectangle prediction

The function f, which is the second input item to Algorithm 1, takes as input an array of candidate rectangles of both types L and R (where L and R are the third component of candidate rectangles as defined in Section II-A), and outputs a representative rectangle. Here, we design a specific prediction function f. The first step of f is to decide whether there are enough candidate rectangles of both types. Let n_L and n_R be the numbers of type L and type R rectangles in the input, respectively. If min {n_L, n_R} ≤ c₁ or min {n_L, n_R} / max {n_L, n_R} ≤ c₂, where c₁ and c₂ are user-defined parameters, then f returns “None”. Otherwise, it proceeds to the next step for the Representative Rectangle Prediction (RRP) problem, which will be discussed in detail below.

There are two trivial ways to define and solve the RRP problem. First, we simply take the intersection of all the rectangles. The downside for this approach is that there are likely errors in the candidate predictions and resulted clusters. Even if the intersection of these rectangles is not empty, predicting a rectangle in this way will fail to capture true breakpoints (or the point c defined in the first paragraph of Section II-B). Second, we can take the minimum rectangle covering all the rectangles as our prediction. The downside here is that the predicted rectangle may be too large; even though the prediction may capture the target point with an extremely high probability, very large intervals make it difficult to validate the predictions, pinpoint biologically important features, and perform further analysis. In addition, when we plug this approach into Algorithm 1, after the first iteration, the set of candidate rectangles covering a local maximal cell will be increasingly scattered. In such a case, this approach would predict terribly large rectangles and may yield as bad as a single cluster, resulting in low PPV and maybe low sensitivity. As a result, it is imperative to predict a rectangle that is both small and still contains relevant breakpoints with a high probability. Also, the approach should be able to return “None” when the candidate rectangles do not form a cluster. With this in mind, we define the Representative Rectangle Prediction (RRP) problem, as follows.

Definition 2:

Let c be an unknown point on the plane. Let S be a set of n i.i.d. rectangles sampled from some probability distribution such that, with probability p, each rectangle of S contains the point c. For a value δ ∈ (0, 1), the objective is to find a rectangle r′ that contains the point c with probability at least 1 − δ, such that the area of r′ is as small as possible.

Before delving into the corresponding algorithm, let us briefly justify the underlying rationale for this RRP formulation. The basic idea behind Definition 2 is that we want to use a common parameter p to predict a representative rectangle for each of the clusters. The point c, however, will be different for every cluster. This implies that each instance of the RRP problem corresponds to a different probability space. On the other hand, if we define a random variable for each probability space appropriately, it is possible that these random variables will follow the same distribution. Suppose we define the random variable for each cluster as the following indicator function:

$$1_c(r)=\{\begin{array}{ll}1\hfill & \text{ if the rectangle }r\text{ contains }c\hfill \\ 0\hfill & \text{ otherwise }\hfill \end{array}$$

Then the probability P(1_c = 1) is basically the “proportion” of the rectangles in S containing c. In practice, we can assume, for all the clusters coming from the same dataset, that P(1_c = 1) shares a common lower bound p that is large enough, since otherwise the dataset itself will not contain sufficient information for inversion prediction. It follows that Definition 2 is merely a simplified version such that all the instances follow the same distribution.

We now propose a simple algorithm that guarantees only that the representative rectangle found contains c with probability at least (1 − δ). Let S.l be the set of left boundary edges of S. Denote S.l_i as the i-th smallest value in S.l. Likewise, we define S.r, S.b, and S.t as the sets of right, bottom, and top boundary edges of S, respectively, and denote S.r_i, S.b_i, and S.t_i, similarly. If we know in advance that the number of rectangles not containing c is k, then we claim that the rectangle (S.l_n−k, S.r_k+1, S.b_n−k, S.t_k+1) is either the smallest possible rectangle that is guaranteed to contain c, or not a rectangle (say, S.l_n−k > S.r_k+1), in which case the prediction should be “None”. As a result, we only need to compute the largest k such that the probability of at most k rectangles in S not containing c is at least (1 − δ).

Let X be a random variable following a binomial distribution B(n, p). Then the goal is to find the largest k such that P[X ≥ n − k] ≥ 1 − δ. Formally,

$$\text{max}\left\{k:\sum _{i=n-k}^n\left({}_i^n\right)p^i{(1-p)}^{n-i}\ge 1-\delta \right\},$$

which is equivalent to

$$\text{min}\left\{k:\sum _{i=0}^k\left({}_i^n\right)p^{n-i}{(1-p)}^i\ge 1-\delta \right\}.$$

We do not use any tail inequalities because there are plenty of packages [44], [45] providing functions for efficient calculation of ${\sum }_{i=0}^k\left({}_i^n\right)p^{n-i}{(1-p)}^i$ with high precision. Therefore, we can apply binary search to determine k by calling such a function a logarithmic number of times.

Note that in practice, we do not know the value p and it is difficult to estimate a lower bound for p given raw alignment data. We simply empirically guess the lower bound of p based on existing predictions.

III. Experiments & Results

We compare our approach (denoted by RigInv) with InvDet [35] and Sniffles [30], two long-read only methods, and four short-read only tools: Lumpy [23], Hydra [15], Delly [26], and Pindel-C [24]. We evaluate our results on synthetic E. coli data and An. gambiae data, and derive an empirical conjecture based on the experiments on real An. gambiae data.

A. Results on synthetic E. coli

Here we introduce random inversions, translocations, indels, and mismatches into the complete reference genome of E. coli K12 and attempt to predict them using real PacBio long reads (accession NC 000913) and Illumina Miseq paired-end reads that correspond to the alternative (real) karyotype [46]. Note that long reads are used by InvDet, Sniffles, and our new method (i.e., RigInv), while Illumina data are used by the other methods.

We generate different synthetic reference genomes to observe the accuracy of these tools as the variants get larger. We prepare four sets of simulations with the lengths of inversions uniformly randomly falling in the ranges of (500, 1000), (1000, 5000), (5000, 10000), and (10000, 50000), respectively. The first three simulations contain 50 inversions and the last one contains 30. To guarantee the credibility of these experiments, we also introduce 20 relocations with each relocated interval uniformly randomly selected from the range (500, 50000), and 0.01% of insertions, deletions, and variations each.

We calculate the sensitivity (denoted by S), PPV, and F₁ score for each experiment, where:

$$\begin{gathered} \text{S}=\frac{TP}{TP+FN}=\frac{TP}{\text{ number of true inversions }}, \\ PPV=\frac{TP}{TP+FP}=\frac{TP}{\text{ number of predicted inversions }}, \\ {F}_1=2\cdot \frac{\text{S}\cdot \text{PPV}}{\text{S}+\text{PPV}}. \end{gathered}$$

Note that the predictions of Sniffles, Lumpy, Hydra, Delly, and Pindel-C are not “clean” since there may be repetitive predictions for a single inversion. To account for this issue, we use two alternative approaches to calculate the three metrics and report the metrics by choosing for each tool the approach yielding the better trade-off metrics throughout the experiments. The first alternative is that we consider only distinct true predictions when we calculate sensitivity but retain repetitive predictions when calculating PPV. For the second alternative, if two predictions (X₁, Y₁) and (X₂, Y₂) overlap, i.e., X₁ overlaps with X₂, and Y₁ overlaps with Y₂, then the two predictions are merged into a single prediction (X, Y), where:

$$\{\begin{array}{l}X=\left(\text{min}\left\{X_1[1],X_2[1]\right\},\text{max}\left\{X_1[2],X_2[2]\right\}\right)\hfill \\ Y=\left(\text{min}\left\{Y_1[1],Y_2[1]\right\},\text{max}\left\{Y_1[2],Y_2[2]\right\}\right)\hfill \end{array}$$

This guarantees that the predictions of all these tools are “clean” and the T P s in both sensitivity and PPV are identical.

The calculated metrics are presented in Table I. Since our framework is designed for large local inversions (≥1000bp), it is not surprising that RigInv achieves the best trade-off between sensitivity and PPV for larger variants. The F₁ score is a widely used metric as a trade-off between sensitivity and PPV, and, again, RigInv has the highest score when compared to the alternatives. Although the sensitivity of RigInv in this experiment is high, our ensuing experiments show that the sensitivity can be improved further. This is in part a result of our stronger requirements that both L and R type indicator alignments should appear to support a potential inversion, which is not strictly observed by other tools like Sniffles. Note that InvDet is designed to detect “global” large inversions and as such should have lower sensitivity and PPV. Sniffles has the highest sensitivity but lower PPV for large inversions, which may be impacted by the simulated translocations in the synthetic reference genomes based on the results in the next section. When using Illumina data, Lumpy achieves the best trade-off between sensitivity and PPV, with almost the highest F₁ score. Even so, RigInv outperforms Lumpy in all the metrics used. Although Delly and Hydra always have the highest sensitivity, their PPVs decrease when inversions get larger. Pindel-C always has extremely low PPV, maybe because it was designed to predict very short inversions.

TABLE I.

Simulation results for E. coli K12.

INV len range	500 ~ 1000				1000 ~ 5000				5000 ~ 10000				10000 ~ 50000
metrics	S	PPV	F1	time	S	PPV	F1	time	S	PPV	F1	time	S	PPV	F1	time
RigInv (ours)	0.8	0.976	0.879	32s	1.0	0.98	0.99	47s	0.98	1.0	0.99	41s	1.0	0.968	0.984	42s
InvDet	0.2	1.0	0.182	9s	0.66	0.943	0.777	8s	0.8	0.87	0.834	7s	0.833	0.862	0.847	8s
Sniffles	1.0	0.883	0.938	1h45m	1.0	0.944	0.971	2h13m	1.0	0.746	0.854	2h13m	1.0	0.588	0.74	2h5m
Lumpy	0.94	0.94	0.94	18m43s	0.92	0.92	0.92	19m19s	0.9	0.957	0.928	18m56s	0.967	0.935	0.951	17m23s
Delly(PRECISE)	0.86	0.93	0.893	1h1m	0.92	0.948	0.934	54m9s	0.88	0.868	0.874	57m48s	0.933	0.672	0.781	43m15s
Delly	1.0	0.862	0.926	1h1m	1.0	0.865	0.928	54m9s	1.0	0.818	0.9	57m48s	1.0	0.656	0.792	43m15s
Hydra	1.0	0.933	0.966	1h18m	1.0	0.933	0.966	1h6m	1.0	0.858	0.924	1h13m	1.0	0.674	0.805	1h4m
Pindel-C	0.7	0.009	0.018	1d10h	0.76	0.01	0.02	1d9h	0.88	0.015	0.029	1d10h	0.9	0.011	0.021	1d8h

Apropos to the running time, InvDet runs the fastest, followed by RigInv. Indeed, RigInv spends most of its running time (about 40s) in parsing the SAM file and partitioning the input dataset for easier parallelization in successive steps. Lumpy also runs very fast, but when compared with InvDet and RigInv, it is much slower.

B. Results on synthetic An. gambiae

Before applying our tool to the An. gambiae data with established inversions, we first experiment with synthetic An. gambiae data to assess alignment quality/power and to assess the needed parameters and overall potential of each method.

We first use the An. gambiae PEST [47] reference sequence and generate 50X of PacBio long reads by PBSIM [48] and 50X of Illumina Miseq short PE reads by ART [49]. We then introduce simulated inversions and assess the ability of RigInv and the other tools to detect these simulated inversions. We introduce up to 10 inversions in each chromosome of An. gambiae PEST using exactly the same approach we did for E. coli K12, where each inversion has a length between 1Mbp and 10Mbp. We also introduce 0.01% of insertions, deletions, and variations apiece. For simplicity, we do not introduce translocations for these assessments. At the end, we simulate three An. gambiae PEST-based test sequences with 38, 37, and 35 inversions, respectively.

Table II shows the results of these three experiments. Although Sniffles achieves the best results in terms of sensitivity and the trade-off between sensitivity and PPV, it takes over five days of user and system time. RigInv and Lumpy always have the best PPV, but RigInv has higher sensitivity than Lumpy, and a higher F₁ score than all the other tools aside from Sniffles. We note, however, that RigInv runs the fastest (over 2500X faster than Sniffles), which could help in faster analysis (e.g., high priority cancer typing) and allow researchers to experiment with different parameter settings.

TABLE II.

Simulation results for An. gambiae PEST.

Dataset	dataset 1				dataset 2				dataset 3
metrics	S	PPV	F1	time	S	PPV	F1	time	S	PPV	F1	time
RigInv (ours)	0.842	1.0	0.914	3m12s	0.811	1.0	0.896	3m7s	0.771	1.0	0.871	2m57s
Sniffles	0.947	0.973	0.96	5d16h	0.973	1.0	0.986	5d12h	0.971	0.971	0.971	5d4h
Lumpy	0.605	1.0	0.764	13m50s	0.514	1.0	0.679	14m	0.514	1.0	0.679	14m15s
Delly(PRECISE)	0.789	0.875	0.83	4m56s	0.811	0.939	0.87	4m5s	0.8	0.979	0.88	4m11s
Delly	0.789	0.79	0.79	4m56s	0.811	0.836	0.823	4m5s	0.8	0.885	0.84	4m11s
Hydra	0	0	-	9m59s	0	0	-	9m5s	0	0	-	7m42s
Pindel-C	0.316	0.002	0.003	1d12h	0.297	0.002	0.003	1d11h	0.257	0.001	0.002	1d6h

Some tools are not listed since they took more than days to generate predictions.

As expected, sensitivity is universally low for the chromosome UNKN in An. gambiae PEST, which is a random assortment of all sequences not assigned to specific chromosomes. Only Sniffles can detect the introduced inversions in this hodgepodge chromosome composed of repeat rich regions. For example, it is known that UNKN contains repetitive X and some Y chromosome sequences that are difficult to assemble [50]. We therefore conjecture that this made-up chromosome abounds with inverted repeats, resulting in aligners such as BWA-MEM to extensively align input reads in these regions.

C. Results on real An. gambiae

Our long interest in computational methods for malaria mosquito genome analysis prompted us to predict actual inversions relative to the An. gambiae PEST genome. There are four known inversions on the 2R arm [51] and one on the 2L arm [52]. Because these inversions are detected using a microscope and specific isolated cells, the wet-lab approach for locating inversions is very time consuming. Moreover, the exact genome-based locations of mosquito inversion breakpoints are not known, which makes more efficient tests such as PCR-based assays not feasible. As a result, it is imperative to devise computational approaches to better predict inversion breakpoints to facilitate mosquito variation research.

Since chromosome X has no known inversions in An. gambiae, this negative control provides a general but more accurate estimate of PPV of the available methods. Significantly, only RigInv fully passes this test. Lumpy predicts 1, indicating that its predictions are also quite accurate. Sniffles predicts 5. Delly(PRECISE) predicts 26 and Delly predicts 1333. InvDet, Hydra, and Pindel-C did not finish after running days on our computational machine cluster. The conclusions of the PPVs on RigInv, Lumpy, Sniffles, and Delly(PRECISE)/Delly are consistent with the conclusions derived from our synthetic An. gambiae data.

Next, with prior cytogenetic knowledge of the 2L and 2R arms providing general locations of the known inversions, we examine the predictions of all the tools relative to these known large-scale variants. Although we loosely define a correct prediction as being within 3Mbp of the known inversion breakpoints, none of the available tools including RigInv can predict any of the five known inversions. This indicates that there are features of these important mosquito inversions that have long been overlooked. We intend to further improve RigInv based on this cytogenetic data and other emerging data such as chromosome contact (HiC) data to better predict these ecologically important inversions.

Finally, we note that RigInv and Sniffles both recently predicted two new inversions in An. gambiae on 3R. This indicates that these two inversions are more likely to be real and will be validated by our biological collaborators using in situ chromosome hybridization (FISH).

IV. Conclusions

The importance of SV detection in disease etiology and other biological applications has prompted us to develop a new framework for inversion detection. Based on a combination of two novel theoretical models, Rectangle Clustering and Representative Rectangle Prediction, our new framework outperforms all the known short read methods in terms of PPV and the trade-off between sensitivity and PPV even with uncorrected PacBio reads. Our new framework also has higher PPV and competitive F₁ score relative to Sniffles according to our simulation experiments. Further, we showed that known inversions in important mosquito species are not yet detectable with current methods. In the future, we aim to identify their characteristics and further improve our framework to predict these new types of inversion signatures.