Bayesian hierarchical EMAX model for dose-response in early phase efficacy clinical trials

Abstract

A primary goal of a phase II dose-ranging trial is to identify a correct dose before moving forward to a phase III confirmatory trial. A correct dose is one that is actually better than control. A popular model in phase II is an independent model that puts no structure on the dose-response relationship. Unfortunately, the independent model does not efficiently use information from related doses. One very successful alternate model improves power using a pre-specified dose-response structure. Past research indicates that EMAX models are broadly successful and therefore attractive for designing dose-response trials. However, there may be instances of slight risk of non-monotone trends that need to be addressed when planning a clinical trial design. We propose to add hierarchical parameters to the EMAX model. The added layer allows information about the treatment effect in one dose to be ‘borrowed’ when estimating the treatment effect in another dose. This is referred to as the hierarchical EMAX model. Our paper compares three different models (independent, EMAX, and hierarchical EMAX) and two different design strategies. The first design considered is Bayesian with a fixed trial design, it has a fixed schedule for randomization. The second design is Bayesian but adaptive, it uses response adaptive randomization. In this article, a randomized trial of severe traumatic brain injury patients is provided as a motivating example.

1. Introduction

Phase II dose-ranging studies can have multiple learning objectives. While this can be phrased as “understanding the dose-response curve,” we typically are interested in identifying the best therapeutic dose and understanding whether that best dose provides a therapeutic benefit worthy of conducting confirmatory phase III trials. Statistical identification of a dose and whether it is effective enough to move forward depends on the modeling assumptions about the dose-response relationship. As early phase trials tend to be smaller in size, dose-response modeling can improve the strength of these decisions. In this paper we present a strong yet flexible dose-response model that can have general use in many dose-ranging trials. We demonstrate its use in a dose-ranging trial of hyperbaric oxygen for the treatment of severe traumatic brain injury (TBI).

An important initial step in the design of a phase II trial having quantitative doses is to identify the functional form that will be used in the primary analysis. One of the most popular dose-response models is the pairwise independent model, whereby individual doses are considered independent and for analysis purposes are individually compared to each other and to control. This pairwise independent model has no structure between doses. From the Bayesian framework when using a flat prior, this independent model has similar properties to several Fisher’s exact tests for categorical data.¹ This lack of structure between the doses can have inefficiencies when there is smoothness to the dose-response curve. This can result in lower power for identification of the correct dose, as well as wider intervals relative to alternative model strategies. The risk of assuming a relationship is the misspecification of the model, potentially leading to poor inferences.

Alternatively, with the addition of assumptions regarding the dose response relationship into the modeling framework (i.e. response improves with increasing dose up to some threshold) there can be improved precision in the estimation of the efficacy at each dose, leading to better dose selection and better go/no-go decision. There are many options for the functional form of models that one can choose for inferences, including, but not limited to, EMAX, logistic, double logistic, exponential, normal dynamic linear, and quadratic.² While all of these models have their particular benefits and drawbacks depending on the true functional form, the EMAX model with “Hill” parameter close to 1.0¹ has been shown to provide good empirical fit for designing and analyzing dose-response data across a wide range of pharmaceutical studies³. The impressive empirical success of the parametric EMAX model makes it quite attractive for dose-ranging trials and can provide improved power and precision when appropriate. Bretz et al.² provide an approach that is a hybrid of a multiple comparisons (through statistical testing) and modeling techniques. This “blend” of modeling approaches is called multiple comparison procedure or by using a modeling approach (MCPMod)⁴ and demonstrated strong in proof of activity probabilities, including the EMAX model. Thus, parametric EMAX models should be considered in the design of future dose-response studies, especially when there is strong belief in a monotonic dose-response relationship.

Unlike the situations where the EMAX model has been successful, there may be dose response examples where non-monotonic or non-EMAX relationships may be plausible. Such examples include the situation where a higher dose may cause decreased tolerability or practical implementation issues (e.g. more intense intervention mitigates increased side effects and decreases response) causing decreased efficacy or a plateau effect. This risk of non-monotonic dose-response potential motivated the need for more flexible, yet powerful, models. An alternative strategy is proposed which includes a single dose-response model that reacts to possible non-monotonic relationships yet preserves the efficiencies in power and precision of the EMAX model. One approach that preserves functional model efficiencies but is fairly robust to non-monotonicity utilizes the EMAX model with the addition of random effect parameters for each dose that represent variations from the EMAX curve per dose. Each of the random effects per dose are modeled hierarchically. Essentially, the random effect deviations for each dose are added to the EMAX curve. Because this off-curve effect for dose is modeled hierarchically with a mean of zero⁵ their estimates shrink towards zero, and the amount of shrinkage depends dynamically on how well the EMAX model captures the overall trend in the empirical dose-response data. For example, if the EMAX model fit the data perfectly the random effect parameters will have strong shrinkage towards zero and the dose response-curve will be an EMAX. However, if there is deviation from the EMAX model then the off-curve effects will shrink less towards zero, creating a more flexible fit of the dose-response. Use of the hierarchical EMAX model provides a robust means to have some of the efficiencies in power and precision of the EMAX model, while also allowing increased flexibility to the model to address deviations if necessary.

The focus of this article is to present and discuss the hierarchical EMAX model and its use for an ongoing early phase dose selection study. The motivating example is a randomized trial of severe traumatic brain injury patients with the goal of selecting among seven possible active doses compared to control to achieve favorable functional outcomes. Three different models and two different design strategies are compared. The three models compared are: 1) pairwise independent, 2) EMAX, and 3) hierarchical EMAX. Each of these models are compared across two different designs:1) fixed randomization and 2) response adaptive randomization (RAR). Results of a simulation study can be discussed more generally, where the same general approach also applies to other randomized dose-ranging trials.

2. Methods

2.1. Motivating Trial

The motivating trial is the Hyperbaric Oxygen Brain Injury Treatment (HOBIT) trial (NCT02407028⁶). This is a phase II Bayesian adaptive clinical trial for selecting the optimal dose regimen of hyperbaric oxygen treatment, defined as the regimen (hyperbaric oxygen at different pressure levels with or without normobaric hyperoxia) which produces the greatest improvement in the rate of good neurological outcome versus standard of care for subjects with severe traumatic brain injury (TBI). A second goal of this phase II trial is to determine if there is any hyperbaric treatment that has at least a 50% probability of demonstrating improvement in the rate of good neurological outcome versus a control (i.e. standard care) in a subsequent phase III confirmatory trial, assumed to be 500 in the control and 500 in the arm treated with the selected optimal dose regimen of hyperbaric oxygen.

HOBIT is designed as a multicenter, prospective, randomized, adaptive phase II clinical trial. The primary outcome is a sliding dichotomized severity⁷ adjusted GOS-E at 6 months (26 weeks). The trial will explore seven different active treatment arms for relative efficacy in comparison of the control arm. Subjects may be randomized to hyperbaric oxygen at one of four possible atmospheric pressures (1.0, 1.5, 2.0 and 2.5 atmospheres absolute (ATA)) with or without additional 100% normobaric oxygen (NBH).

2.1.1. Dose

The original study design⁶ uses a Bayesian adaptive design with response adaptive randomization, early stopping for success or futility, and longitudinal modeling to handle the missing data for subjects with incomplete data at the time of an interim analysis. The primary outcome uses a pairwise independent model (described later) as the primary analysis. Following NIH peer review suggestion, it was decided to improve efficiency with a more structured dose-response model. Two possible definitions of dose were considered – one in which the two factors of treatment – 4 levels of atmospheric pressure, and added use of NBH – were modeled separately, and secondarily where the dose was defined as a singular monotonic dose as a function of the total oxygen toxicity acquired during treatment. We chose the latter because of its strong power and precision. Table 1 defines the eight treatment arms considered in the trial. Dose strength as defined in Table 1 is the daily oxygen toxicity units per 100 (OTU/100). See Appendix A for specific calculations of OTU dose strength.

Table 1.

Dosing each of the arms in the traumatic brain injury (TBI) trial.

Dose index d	Arm Name	OTUs vd * 100	Dose strength vd
d=1	Control (1.0 ATA)	N/A*	N/A*
d=2	1.5 ATA	260	v2=2.60
d=3	2 ATA	417	v3=4.17
d=4	NBH (100% FiO2 at 1.0 ATA)	540	v4=5.40
d=5	2.5 ATA	592	v5=5.92
d=6	1.5 ATA+NBH	620	v6=6.20
d=7	2 ATA+NBH	776	v7=7.76
d=8	2.5 ATA+NBH	952	v8=9.52

^*NOTE: In the control arm, subjects will be at 1.0 ATA, however the percent of FiO2 will not be regulated. Thus, it is theoretically possible that these subjects are accumulating OTUs. For the purposes of this study they will consider the “dose” to be zero and this arm will be modeled separately. The FiO2 will be recorded throughout the study. Patients will receive at least 21% O2 outside of the chamber, but the level of oxygen supplementation may be higher though not typically exceeding 50%.

2.2. Models

The probability an individual subject has a favorable outcome, P_d, is modeled for each dose, where dose is indexed d ∈ {1, …, 8}. We use v_d ∈ {2.6, 4.17, 5.4, 5.92, 6.2, 7.76, 9.52} as the effective dose strength, for example v₂ = 4.17, for the dose indexed d=2. The probability of a favorable outcome across doses is modeled with three different dose-response models for all inferences in the trial. Assume all of the nd subjects randomized to dose index d have a summed binomial outcome Yd:

$$Y_d~Binomial\left(n_d,P_d\right).$$

The log-odds of the probability of favorable outcomes, ${\theta }_d=log\left(\frac{P_d}{1-P_d}\right)$, are modeled. In addition, for all models the single control arm (indexed d=1) is modeled separately from the active doses and has a prior distribution of θ₁ ~ N(−.41, .75²). This vague prior on the P₁ scale has a median of 0.40 and 95% equal-tailed interval of .09–.83.

In the following sections, the three different dose-response models for the active doses are described.

2.2.1. Independent model

The pairwise independent model has no structure in the active dose portion of the model. Specifically, we model the active doses with independent prior distributions:

$${\theta }_d~N\left(-0.41,1^2\right).d\in \{2,\dots ,8\}.$$

2.2.2. EMAX model

The specification of the EMAX model is:

$${\theta }_d={\varphi }_1+\frac{{\varphi }_2{v}_d}{v_d+{\varphi }_3},d\in \{2,\dots ,8\}$$

where νd is the effective dose strength. The EMAX parameters are ϕ1, ϕ2, and ϕ3:

• ϕ1 is a constant offset, and the logistic response when the effective dose strength is 0. The prior distribution is ϕ₁ ~ N(−0.41,1²).

• ϕ2 is a scalar coefficient of the fraction of the response due to the effective dose strength. It is the theoretical maximum effect above the constant offset that can be achieved. The prior distribution is ϕ₂ ~ N(−0,5²).

• ϕ3 is a positive scalar representing the effective dose strength that achieves 50% of the theoretical maximal effect. The prior distribution is ϕ₃ ~ N⁺(3,10²). The notation N⁺ represents a positively truncated normal distribution.

As dose tends to infinity the theoretical maximum efficacy on the logit scale $\underset{v_d\to \infty }{\text{lim}}({\varphi }_1+\frac{{\varphi }_2{v}_d}{v_d+{\varphi }_3})={\varphi }_1+{\varphi }_2$, thus is called the EMAX. For an effective dose-strength of v_d=ϕ₃ the log-odds is ${\varphi }_1+\frac{{\varphi }_2}{2}$.

2.2.3. Hierarchical EMAX model

The Hierarchical EMAX model builds on the EMAX using the following structure:

$${\theta }_d={\varphi }_1+\frac{{\varphi }_2{v}_d}{v_d+{\varphi }_3}+{\psi }_d,d\in \{2,\dots ,8\}.$$

Where ν_d is the effective dose strength and the individual dose effects are modeled as:

$${\psi }_d~N\left(0,{\varphi }_4^2\right),d\in \{2,\dots ,8\}.$$

The hyperparameters are constrained such that ∑ψ_d = 0. The prior distribution is ${\psi }_d~N\left(0,{\varphi }_4^2\right)$ where the hyper prior ${\varphi }_4^2~Inverse-Gamma(0.1,0.001)$. All other priors are the same as defined in the EMAX model.

The model has a mean curve that is the EMAX model, but with an additional additive term per dose, ψ_d, for an off-curve effect that allows for a more flexible model. The additive ψ_d terms are considered hierarchical because a priori they share a common normal distribution having a hyperprior. The beauty of the random effect modeling is that when the EMAX provides a good fit to the data the random effect parameters, ψ_d, are shrunk toward 0, hence gaining the power of the EMAX structure. When there are significant deviations from the EMAX model, the hyperparameter ${\varphi }_4^2$ will be larger and there is less shrinkage towards the EMAX model, allowing the individual dose effects to create a custom fit. At the extremes, ${\varphi }_4^2=0$ the EMAX model, and when ${\varphi }_4^2\to \infty$ the model is the model is the pairwise independent model. The hierarchical EMAX model will be like the EMAX model, unless the data deviates from the EMAX relationship, then it will respond accordingly. This feature suggests that its power lies between the independent and EMAX models but is more robust to model misspecifications.

It’s worth a bit more discussion as to how the prior distribution for the hyper prior ${\varphi }_4^2~Inverse-Gamma(0.1,0.001)$ was derived. One rational is to specify ${\varphi }_4^2~Inverse-Gamma\left(\frac{{\mathrm{\Lambda }}_n}{2},\frac{{\mathrm{\Lambda }}_{\mu }^2{\mathrm{\Lambda }}_n}{2}\right)$, where Λ_μ is the hierarchical prior central value and Λ_n is the hierarchical prior weight. One must select these parameters carefully to avoid over or under fitting of the model.⁹ A very sound strategy is to specify Λ_μ as a reasonable value of the upper limit in the difference in responses on the logit scale. In our application to the HOBIT trial design we found Λ_μ = .1 to be reasonable. For the prior weight we find that in general Λ_n = .1. The is a very good start, however, after some tweaking through simulations we ultimately went with Λ_n = .2 choices for the specification of these parameters will depend on outcome type and expectation of the dose-response for the particular application.

2.3. Bayesian Quantities of Interest

In order to draw conclusions from the above model, the posterior probability for each of the doses is converted to quantities of interest related to the main questions: the probability that each dose is the maximal effective dose, the probability each dose is superior to the control, and the predictive probability a dose would win a phase III trial compared to control. The Bayesian quantities rely on calculating the joint posterior distribution of the probability of a favorable outcome for each dose. These joint posteriors are calculated using standard Markov chain Monte Carlo (MCMC) algorithms. The quantities of interest are as follows.

2.3.1. Posterior Probability of Treatment Difference

For each active dose, d=2,…,8 the posterior probability that the dose is superior to control, P(P_d – P₁ >0) is calculated. The estimate of this quantity is the proportion of MCMC samples in which P_d > P₁.

2.3.2. Maximum Effective Dose

The maximum effective dose (D_Max) is the dose with the greatest probability of a favorable outcome. The posterior probability each dose is the maximally effective dose, Pr(D_Max), is calculated as the frequency of the MCMC samples in which each dose is the maximum.

2.3.3. Posterior Predictive Probability of Future Trial Success

We assume a future phase III trial would be a fixed design, equally randomized 1000 subjects between control and one active dose, with a final analysis a test of superiority. Thereby, for each active dose, the predictive probability of success in a future hypothetical trial is calculated as Pr(Phase III Success; n = 500,α = 0.025,δ = 0). For each dose this is calculated by averaging the power function over the posterior distribution for each dose and the control probabilities of favorable outcomes. This is different from the power for such a trial, in that the power calculations typically assume a fixed treatment effect, whereas the predictive probability of success averages over the posterior distribution of the treatment effect. Thus, knowledge of the treatment effect and the uncertainty in that knowledge are formally incorporated.

2.4. Final Evaluation Criteria

At the final analysis, the trial is considered successful if all of the following criteria are satisfied:

$$\begin{gathered} \text{Pr}\left(P_d>P_1\right)>\beta \text{for}d=\text{greatest}\text{Pr}\left(D_{Mar}\right),\text{and} \\ \text{Pr}\left(\text{Phase III Success};n=500,\alpha =0.025,\delta =0\right)>0.5\text{ for }d=\text{greatest}\text{Pr}\left(D_{Max}\right). \end{gathered}$$

Note, for fixed β the type I error rate changes depending on the model choice for the final analysis. Thus so that all models have the same type I error rate β will vary by the choice of model used. To provide 10% type I error rates across models, β is set to 0.975, 0.92, and 0.922for independent, EMAX, and hierarchical EMAX models respectively.

3. Results

3.1. Illustrative Examples

In this section, three single simulated trials are used as examples to illustrate the differences between independent, EMAX, and hierarchical EMAX models. These example datasets were created for illustrative purposes and then fitted using the Windows Bayesian inference Using Gibbs Sampling (WinBUGS)⁸ code in the appendix. In these examples, the total sample size is 200 with 39 allocated to control and the rest equally allocated to the seven active doses.

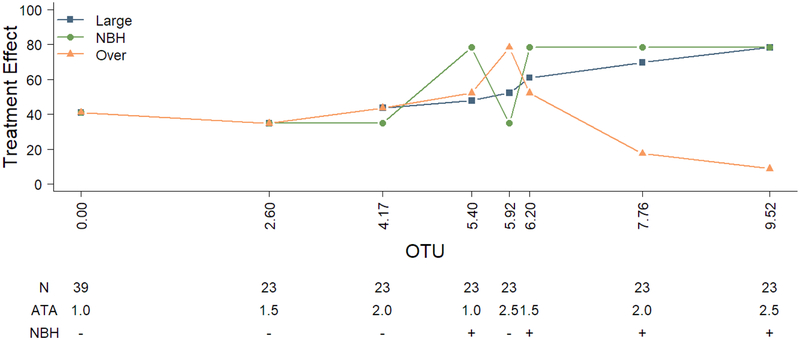
Figure 1 and Table 2 depict the three single simulated datasets whereby it is assumed that there is a large monotonic dose effect, an effect for the NBH dose only, and an over dose effect. The large monotonic effect is a scenario in which favorable response increases with dose in the active arms in a large monotone fashion. The second example is a scenario in which higher responses in the active doses take place in a monotonic fashion but only in those doses that involve NBH. The third example is a scenario in which toxicity is involved and results in an upside down U-shape distribution. Here toxicity prevails in doses with higher oxygen toxicity units and thus causes a high number of poor responses at higher doses.

Figure 1.

Illustrative data for the exploration of posterior distributions for assumed responses.

Table 2.

Illustrative data for the exploration of posterior distributions for assumed responses.

	Dose	d=1	d=2	d=3	d=4	d=5	d=6	d=7	d=8
	Strength	Control	2.60	4.17	5.40	5.92	6.20	7.76	9.52
	n	39	23	23	23	23	23	23	23
Large Monotone
Response	y	16	8	10	11	12	14	16	18
%Response	100*y/n	41.0%	34.8%	43.5%	47.8%	52.2%	60.9%	69.6%	78.3%
NBH Only
Response	Y	16	8	8	18	8	18	18	18
%Response	100*y/n	41.0%	34.8%	34.8%	78.3%	34.8%	78.3%	78.3%	78.3%
Over-Dose
Response	Y	16	8	10	12	18	12	4	2
%Response	100*y/n	41.0%	34.8%	43.5%	52.2%	78.3%	52.2%	17.4%	8.7%

3.1.1. Example 1: Large Monotone Effect

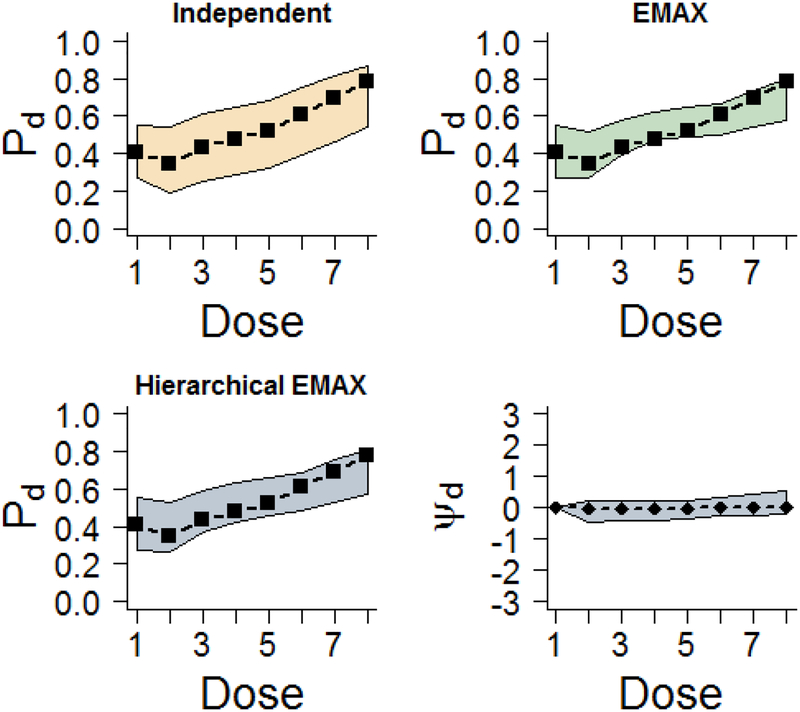
Figure 2 provides the median of the posterior distribution and 95% credible intervals with the observed rates for the three models. For a non-Bayesian this is analogous to a point estimate and 95% confidence interval. The independent model has wider credible intervals than the EMAX and the hierarchical EMAX models. The latter two models are very similar in location and width, demonstrating better precision than the independent model. The monotonic increase of the response and intervals, as well as the observed rates, are covered by all models. The reason that the latter two models appear so similar to one another is because the EMAX portion in both models follows the monotone pattern and the off-curve effect at each dose is essentially zero as illustrated by its posterior median. With respect to the Bayesian quantities of interest across dose as shown in Table 3, the posterior probability of treatment difference and posterior predictive probability of future trial success are all very similar across EMAX and hierarchical EMAX and doses, but different for the independent model as it spreads P(DMax) across the three highest doses. For all three models d =greatest Pr(D_Max)=8, which has an effective dose strength of ν₈ =9.52, and at that dose all of the models have Bayesian quantities that lead to trial success, specifically Pr(P_d > P₁)> 0.975, 0.92, and 0.922 for independent, EMAX, and hierarchical EMAX models respectively, and Pr(Phase III Success; n = 500,α = 0.025,δ = 0) > 0.5 for d =8. In summary for the large monotonic effect, the EMAX and hierarchical EMAX model provide similar conclusions and both are preferable over the independent model.

Figure 2.

Results for fitting models in the large effect example. The ‘▭’ in the first three frames represent the observed rate and the shaded regions are the 2.5%-tile and 97.5%-tile from models (e.g. 95% intervals) for P_d for all models. The last frame shows the 50%-tile (point estimate) and 2.5%-tile and 97.5%-tile for ψ_d in the hierarchical EMAX model.

Table 3.

Bayesian quantity results from fitting the large monotonic effect example.

Large Effect		d=1	d=2	d=3	d=4	d=5	d=6	d=7	d=8
		Control	2.60	4.17	5.40	5.92	6.20	7.76	9.52
P(DMax)	Independent	0.00	0.00	0.00	0.01	0.02	0.07	0.24	0.66
	EMAX	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00
	Hierarchical EMAX	0.00	0.00	0.00	0.00	0.01	0.01	0.08	0.89
Pr(Pd > P1)	Independent	0.00	0.32	0.57	0.69	0.79	0.92	0.98	1.00
	EMAX	0.00	0.43	0.81	0.95	0.98	0.98	1.00	1.00
	Hierarchical EMAX	0.00	0.43	0.79	0.93	0.96	0.98	0.99	1.00
Pr (Phase III Success)	Independent	0.02	0.17	0.37	0.49	0.61	0.81	0.93	0.98
	EMAX	0.03	0.22	0.57	0.82	0.88	0.90	0.97	0.99
	Hierarchical EMAX	0.03	0.23	0.55	0.78	0.85	0.89	0.97	0.99

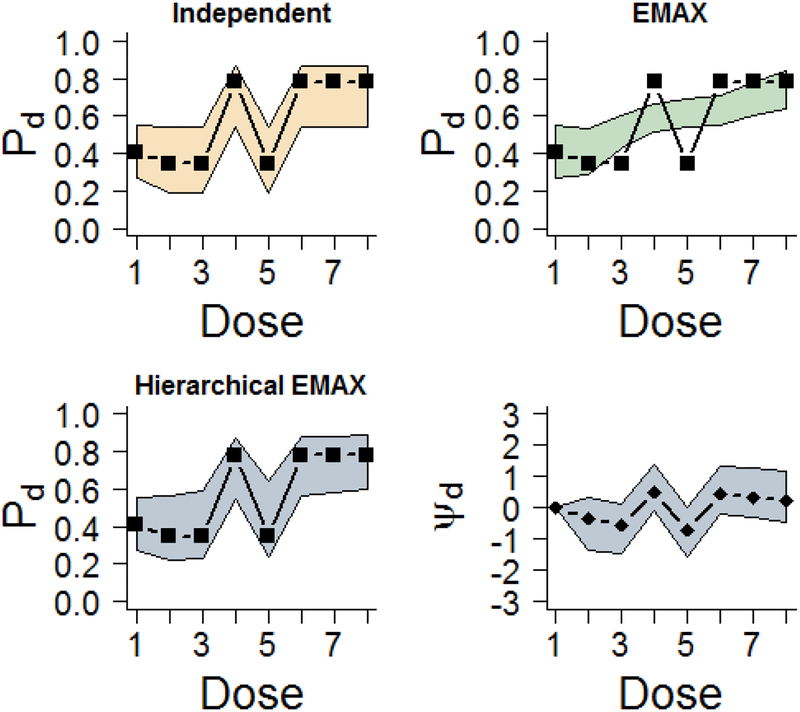
3.1.2. Example 2: NBH Effect

As with the previous example, Figure 3 illustrates the median of the posterior distribution and 95% credible intervals with the observed rates for the independent, EMAX, and hierarchical EMAX models. In this case, the independent model covers all of the point estimates but has wide intervals. The nonlinear response is not well represented by the EMAX model. It under estimates two of the early doses that use NBH and overestimates some of the other doses that do not have NBH. However, the added flexibility of the hierarchical EMAX model follows the patterns quite well, covering all of the observed rates. As shown in the fourth panel of Figure 3, the hierarchical model has better coverage because the off-curve effect is larger than zero at each if the four NBH doses. The Bayesian quantities of interest across doses shown in Tables 4 also provide information about the utility of these three models. The maximum effective dose is essentially zero for all the doses except the highest for the EMAX, whereas the hierarchical EMAX model spreads the probability across more of the doses with NBH. In addition, the posterior probability of future trial success has a notable divergence in agreement at dose 5.92 across the two parametric models. However, when going to three digits, just like in the previous example, all three models d =greatest Pr(D_Max)=8, which has an effective dose strength of ν₈ =9.52, and at that dose all of the models have Bayesian quantities that lead to trial success, specifically Pr(P_d > P₁)> 0.975, 0.92, and 0.922 for independent, EMAX, and hierarchical EMAX models respectively, and Pr(Phase III Success; n = 500,α = 0.025,δ = 0) > 0.5 for d=8. In this situation, the hierarchical EMAX model provides more flexibility and thus investigators would have increased insight into the best dose to carry forward into the future trial.

Figure 3.

Results for fitting models in the NBH only effect example. The ‘▭’ in the first three frames represent the observed rate and the shaded regions are the 2.5%-tile and 97.5%-tile from models (e.g. 95% intervals) for P_d for all models. The last frame shows the 50%-tile (point estimate) and 2.5%-tile and 97.5%-tile for ψ_d in the hierarchical EMAX model.

Table 4.

Bayesian quantity results from fitting the NBH only example.

NBH Only		d=1	d=2	d=3	d=4	d=5	d=6	d=7	d=8
		Control	2.60	4.17	5.40	5.92	6.20	7.76	9.52
P(DMax)	Independent	0.00	0.00	0.00	0.25	0.00	0.25	0.25	0.25
	EMAX	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00
	Hierarchical EMAX	0.00	0.00	0.00	0.16	0.00	0.18	0.25	0.40
Pr(Pd > P1)	Independent	0.00	0.32	0.32	1.00	0.32	1.00	1.00	1.00
	EMAX	0.00	0.49	0.90	0.99	0.99	1.00	1.00	1.00
	Hierarchical EMAX	0.00	0.43	0.54	1.00	0.61	1.00	1.00	1.00
Pr(Phase III Success)	Independent	0.02	0.18	0.17	0.98	0.17	0.98	0.98	0.98
	EMAX	0.03	0.27	0.71	0.92	0.96	0.97	0.99	1.00
	Hierarchical EMAX	0.03	0.24	0.35	0.98	0.44	0.99	0.99	0.99

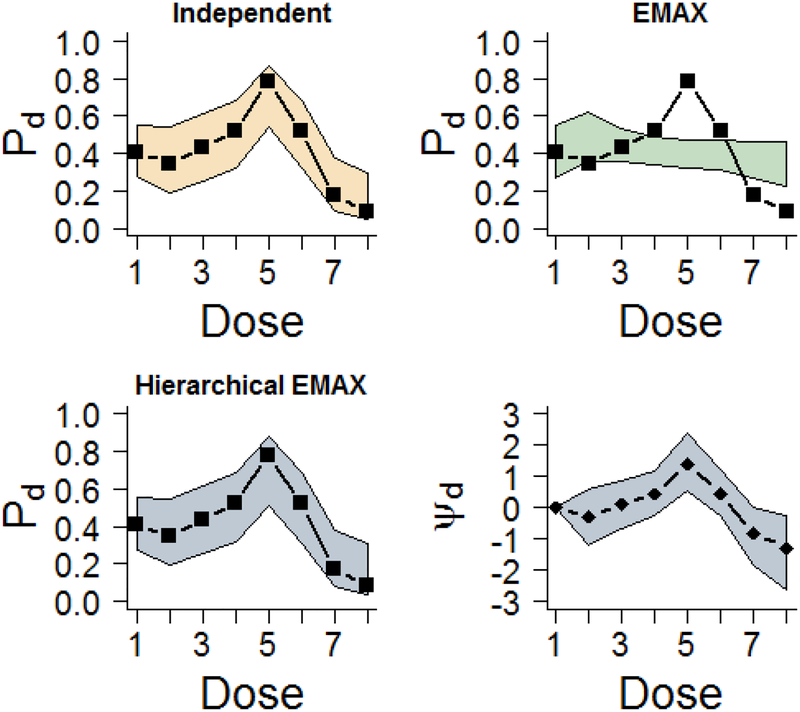
3.1.3. Example 3: Over Dose

Figure 4 provides the median of the posterior distribution and 95% credible intervals with the observed rates for the independent, EMAX, and hierarchical EMAX models for the over dose example. Again the independent covers the observed rates but with wide intervals. Further, the nonlinear response is not well modeled at all by the EMAX model. It severely under estimates one of the middle doses before the dose becomes harmful. However, as in the NBH example the flexibility of the hierarchical EMAX model follows the patterns quite well, covering all of the observed rates. The reason that the hierarchical EMAX model does a better job of coverage is because as shown in the fourth panel of Figure 4 the off-curve effect is bumped up at the middle dose and then goes down during the more harmful later doses. Table 5 presents the Bayesian quantities of interest across doses. In this scenario, the maximum effective dose is too small for detection by the EMAX model, whereas the hierarchical EMAX model correctly identifies the middle dose as the best. In addition, the posterior probabilities correctly reflect what is expected given this scenario of toxicity. The hierarchical EMAX model choses the middle dose as having over twice the probability of being better than control relative to the EMAX model. Lastly, the probability of future trial success has a notable difference in this dose across the two models. Turning to the independent model, in terms of the results in Figure 4 and Table 5, it has very similar results to the hierarchical EMAX, suggesting that both may behave similarly in this over dose effect shape. In this example the three models resulted in different trial conclusions. For both the independent as well as the hierarchical EMAX models d =greatest Pr(D_Max)=5, which has an effective dose strength of ν₅ =5.92. The EMAX model has a lower dose with d =greatest Pr(D_Max)=2, which has an effective dose strength of ν₂ =2.60. However, only the independent and the hierarchical EMAX achieve trial success because Pr(P_d > P₁)> 0.975 and 0.922, respectively and Pr(Phase III Success; n = 500,α = 0.025,δ = 0) > 0.5 for d=5. The EMAX does not achieve trial success as both Pr(P_d > P₁)<0.92 and Pr(Phase III Success; n = 500,α = 0.025,δ = 0) <0.5 for d=2. We will further explore this result in the next section using several simulated datasets. In the situation of toxicity, the hierarchical EMAX model would provide investigators with a clear dose winner that reflects the nonlinear trend in the observed rates.

Figure 4.

Results for fitting models in the over dose effect example. The ‘▭’ in the first three frames represent the observed rate and the shaded regions are the 2.5%-tile and 97.5%-tile from models (e.g. 95% intervals) for P_d for all models. The last frame shows the 50%-tile (point estimate) and 2.5%-tile and 97.5%-tile for ψ_d in the hierarchical EMAX model.

Table 5.

Bayesian quantity results from fitting the over dose example.

Over dose		d=1	d=2	d=3	d=4	d=5	d=6	d=7	d=8
		Control	2.60	4.17	5.40	5.92	6.20	7.76	9.52
P(DMax)	Independent	0.00	0.00	0.01	0.04	0.92	0.04	0.00	0.00
	EMAX	0.00	0.93	0.00	0.00	0.00	0.00	0.00	0.07
	Hierarchical EMAX	0.00	0.00	0.01	0.04	0.91	0.04	0.00	0.00
Pr(Pd > P1)	Independent	0.00	0.32	0.57	0.79	1.00	0.79	0.04	0.01
	EMAX	0.00	0.79	0.65	0.52	0.46	0.43	0.31	0.23
	Hierarchical EMAX	0.00	0.34	0.57	0.77	0.99	0.77	0.04	0.01
Pr(Phase III Success)	Independent	0.03	0.17	0.37	0.61	0.98	0.61	0.01	0.00
	EMAX	0.03	0.58	0.38	0.25	0.21	0.20	0.13	0.09
	Hierarchical EMAX	0.03	0.19	0.37	0.59	0.97	0.59	0.01	0.00

3.2. Simulation Study

The previous section provided an illustration of the properties of the three different models using a single simulated dataset. A more thorough investigation of the relative properties of these models (independent, EMAX, and hierarchical EMAX), and the trial operating characteristics such as fitted response, proportion dose was identified as having the largest P(D_Max), average sample size, and proportion of time we select the correct dose (e.g. power) are evaluated through repeated simulations using different assumptions of the dose-response curves (“large monotone”, “NBH only”, and “over-dose”).

The trial operating characteristics were calculated using commercial software Fixed and Adaptive Clinical Trial Simulator 6.2 (FACTS) (Berry Consultants, Austin, TX). In each scenario, 10,000 simulated trials are used. We considered two designs both having n=200.

First, a fixed allocation ratio of 1:4 control to active doses, spread evenly across active doses. As reported in the examples, to provide 10% type I error rates across models, β is set to 0.975, 0.92, and 0.922 for independent, EMAX, and hierarchical EMAX models respectively.

Second, a response adaptive randomization (RAR) allocation⁹ is used with the same allocation ratio of 1:4 control to active dose, but after the first 53 randomized the allocation among active doses changes. Instead of being spread evenly across active doses, the allocation among active doses was proportional to:

$$\sqrt{\frac{Var\left({\theta }_d\right)\text{Pr}\left(d=D_{MAX}\right)}{\left(n_d+1\right)}.}$$

This RAR is updated after every 21 subjects are enrolled. For the RAR design, to provide 10% type I error rates across models, β was slightly modified to 0.970, 0.925, and 0.925 for independent, EMAX, and hierarchical EMAX models respectively.

The true response rates assumed for each scenario are shown in Table 6. In choosing effect sizes to evaluate the models, the “large” response (Table 6) is expected to favor the EMAX since it is monotone; however, for “NBH” and “over-dose” there is a nonlinear effect caused by NBH or an over dose of oxygen. Thus these dose response effects are expected to favor the hierarchical EMAX or independent models.

Table 6.

Favorable response rates assumptions used for simulations. Shaded regions are doses expected to be better than control (e.g. correct arm).

	d=1	d=2	d=3	d=4	d=5	d=6	d=7	d=8
Effect	Control	2.60	4.17	5.40	5.92	6.20	7.76	9.52
Large	0.40	0.59	0.60	0.61	0.62	0.63	0.64	0.65
NBH	0.40	0.40	0.40	0.70	0.40	0.70	0.70	0.70
Over Dose	0.40	0.40	0.50	0.55	0.70	0.40	0.35	0.30

3.2.1. Fitted Response and P(D_Max) Selection Across Simulations

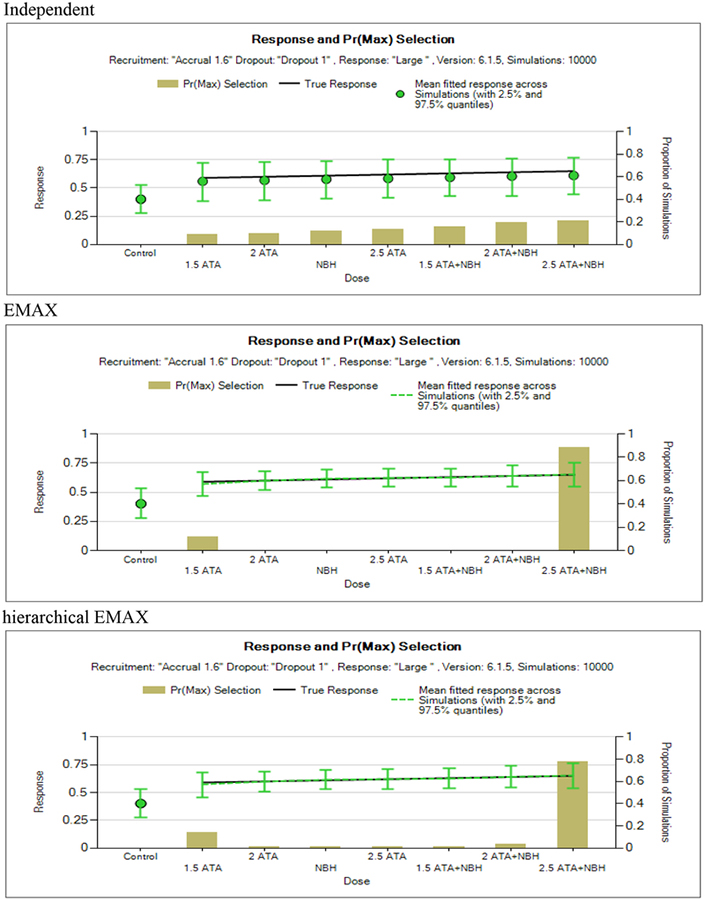
In order to evaluate how well each model fits the proposed dose response effect, Figures 5, 6, and 7 show the estimated means with 2.5% and 97.5% quantities for the probabilities of response and the proportion of simulations a dose was identified as having the largest P(D_Max) for the fixed design (there are similar plots for the adaptive design but for brevity not shown). These are presented so that we can understand how well the models fit the data and how these models result in a dose as being selected as maximum response relative to control and a candidate to move forward to phase III. Recall the dose with maximum response relative to control has to also achieve the success criteria presented in section 2.4. Previously it was shown that the amount of deviation from a monotone model in the Bayesian hierarchical EMAX model is determined by the data, i.e. the greater the deviation, the greater the spread in the drift-parameters. Thus the hierarchical EMAX model more readily responds to deviations than the EMAX. The large effect scenario (Figure 5) shows similarities between the hierarchical EMAX and EMAX. The point estimates and the 95% quantiles are almost identical. The independent model has similar point estimates but the 95% quantiles are much wider. In addition, compared to the independent model, the EMAX and hierarchical EMAX models have a higher frequency of correctly identifying the highest dose as having the having the largest P(D_Max).

Figure 5.

Large monotone effect.

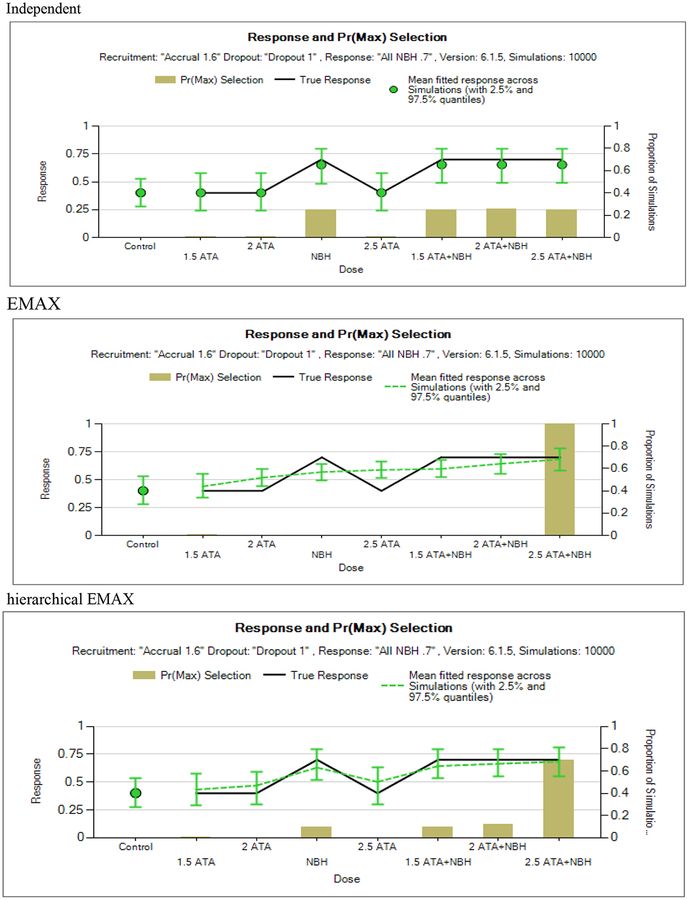
Figure 6.

NBH only.

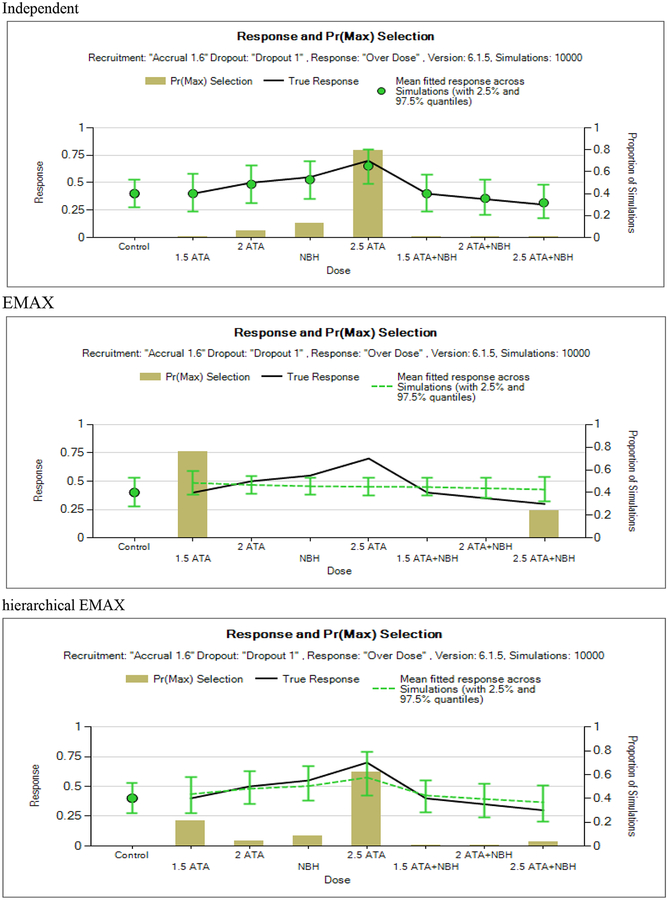
Figure 7.

Over dose.

The NBH only scenario (Figure 6) shows deviations between the hierarchical EMAX and the EMAX models in that the hierarchical EMAX reacts to the non-linear spikes in the responses as the point estimates and quantiles cover the true response probabilities whereas the EMAX model misses four doses. Like the hierarchical EMAX model, the independent model has close point estimates and intervals that cover the truth for all doses but the intervals are wider than the hierarchical model. However, as identified by the P(D_Max), the independent model has a slightly higher chance of selecting NBH than the hierarchical EMAX, conversely hierarchical EMAX leans more towards the highest dose than the independent model does.

The over dose scenario (Figure 7) also shows deviations between the hierarchical EMAX and the EMAX models in that the hierarchical reacts to the non-linear spikes in the responses as the point estimates and quantiles cover the true response probabilities whereas the EMAX model severely misses two doses. The point estimates and interval widths are similar in this scenario between hierarchical EMAX and independent models. In fact, it looks like the independent model does pretty well in this case. The hierarchical EMAX does much better at quantifying the maximum probability at the middle highest response rate than the EMAX. The independent model does the best in choosing the best dose.

3.2.2. Probability a Correct or Incorrect Arm is Selected: Fixed Trial

In evaluating the doses, the interest is the probability of selecting a treatment dose that actually is better than control (e.g. a correct arm). For these simulations, the “correct” dose, defined as concluding efficacy where P_d > P₁, is dependent on the effect assumed, and is shown in Table 6 as a shaded region. The proportion of correct decisions, as well as the probability of selecting an incorrect arm, for each model across the scenarios are provided in Table 7. The EMAX model is close to or has the highest probability of choosing a correct dose, in all scenarios, except for the ‘over dose’, where it is fails miserably having 0 correct decisions. But it also has unacceptable probability of incorrect doses. The hierarchical EMAX has a much higher probability of selecting a correct dose than the independent model in all scenarios except over dose case. The independent model is the only one that performs reasonably well in the over dose scenario. Although the probability of choosing the correct dose in the other scenarios is not as high as the other models, it does still perform very well.

Table 7.

Operating characteristics of the models for fixed design (n=200). All designs are calibrated to have a Type I error rate of 10%.

Fixed Effect	Independent P(Correct)	P(Incorrect)	Emax P(Correct)	P(Incorrect)	Hierarchical EMAX P(Correct)	P(Incorrect)
Large	0.808	0.000	0.939	0.000	0.936	0.000
NBH Only	0.899	0.003	0.950	0.012	0.960	0.004
Over Dose	0.635	0.008	1 0.000	0.317 1	0.450	0.091

3.2.3. Probability a Correct or Incorrect Arm is Selected: RAR Trial

Table 8 also shows the probability of choosing a correct arm and the probability of choosing an incorrect arm for each model across the scenarios. The EMAX model has the highest probability of choosing a correct arm in the first two scenarios, but as with the fixed design it does not provide acceptable probabilities for correct selection for the over dose scenario. The hierarchical EMAX more likely to pick a correct arm than independent model in all scenarios except over dose case. The hierarchical EMAX model has a lower probability of choosing an incorrect dose than the EMAX does. The independent model, while slightly worse for the large and NBH only dose response effects, offers significantly greater protection in the case where the over-dose scenario is the true treatment effect.

Table 8.

Operating characteristics of the models for adaptive design with longitudinal modeling (n_max=200). All designs are calibrated to have a Type I error rate of 10.

Adaptive Effect	Independent P(Correct)	P(Incorrect)	Emax P(Correct)	P(Incorrect)	Hierarchical EMAX P(Correct)	P(Incorrect)
Large	0.847	0.000	0.944	0.000	0.933	0.000
NBH Only	0.945	0.001	0.979	0.002	0.972	0.004
Over Dose	0.769	0.004	0.000	0.087	0.554	0.064

4. Discussion

The HOBIT trial, as in many dose response phase II trials, has a clinical goal for identifying the treatment dose that produces best outcomes for sick patients, in this case severe TBI. It is strongly believed that higher doses of oxygen will improve outcomes in a monotonically increasing fashion. However, these high doses have not been explicitly tested in the clinical setting, so it is important for statisticians and clinicians to think about how models will react to possible deviations from monotonicity. That is why we investigated the up and down scenarios provided by the NBH and the over dose. It allowed us to see if our model choice is robust to risky deviations in dose response structures. Not surprisingly there was not a clear winner across the scenarios. In thinking about the results, on the one hand obtaining a good fit across all parameters puts us in a better place if we don’t want to select the highest dose, poweris important but maybe not if the models differ by a few percentages, and the same with sample size-there is a tradeoff between risk to the patient, duration/cost of trial, but there may need to be additional information for estimating safety and for secondary data analysis plans.

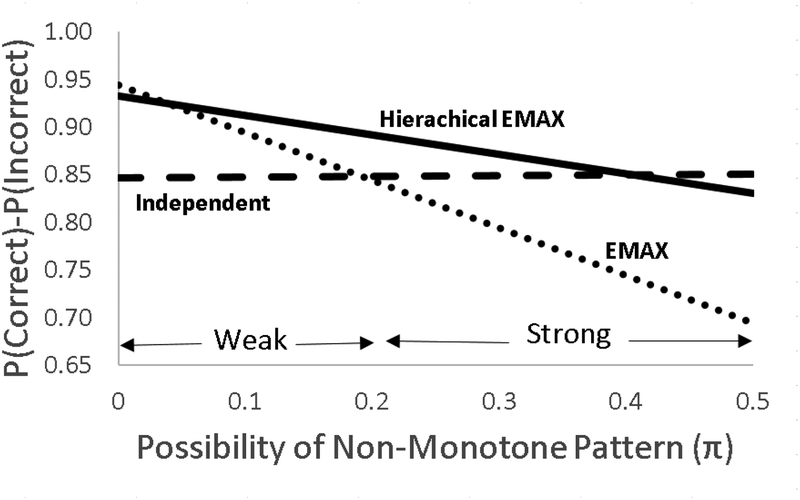
Because of the strong opinion of monotone structure, in this case (and many) of dose-response phase II trials a very good starting point is to use the EMAX approach. However, deciding whether to add the hierarchical and how to borrow across groups depends on how much you think the true dose-response curve is likely to deviate from the EMAX. For example, is there a strong or weak possibility of an over dose or other mechanisms that may cause non-monotone patterns? If there is no possibility of non-monotone patterns one should go with the EMAX. It is the clear winner. If there is a weak possibility of non-monotone patterns one should go with the hierarchical EMAX. In this case the amount of shrinkage or lack of reaction to irregularities is determined by an inverse gamma hyperprior on the variance term for the off-curve effect. The parameters in this model can be decided based on careful scenario construction and simulation can be used to investigate the balance between power and robustness. Finally, if there are strong possibilities of non-monotone patterns, one should go with the independent model. These decisions can be made by investigating scenarios and simulation results can be reviewed and discussed among investigators, DSMB, and other stakeholders such as the sponsor. These groups should investigate power, probability of getting the correct (or incorrect) dose and the best dose, the sample size, and the time in which it takes to finish the trial. A possible way to discuss this is by presenting plots such as the one in Figure 8 that shows the tradeoff off of identifying correct or incorrect doses as a function of possibility of non-monotone patterns.

Figure 8.

Presented is the probability of identifying correct dose minus the probability of identifying incorrect dose as a function of possibility of a non-monotone scenario. The possibility of non-monotone pattern produces a combination of the effects Large, NBH Only, and Over Dose. Let π be the probability of a non-monotone pattern (this probability is split between the two non-monotone patterns NBH Only and Over Dose), then the difference in probability correct (Pc) and probability of incorrect (PI), where I=Pc-PI, for each model is calculated as a function of the probability of the effects, therefore this operating characteristic becomes πI_Large + (π/2)I_NBH + (π/2)I_{over Dose}. Notice that no model is best across all possibilities of non-monotone patterns however hierarchical EMAX model works very well across a broad range.

Some non-Bayesians may have more experience or comfort with traditional model averaging techniques¹⁰ than fitting Bayesian models. The strategy in this paper essentially combines models in the modeling stage. Model averaging combines models in the outcomes stage. We prefer the modeling strategy described in this paper. But for a trialist or statistician who may be more comfortable in the model averaging literature, one may follow the techniques described in the frequentist literature to combine independent doses model with EMAX to achieve a similar goal.

The mention of model averaging motivates thoughts of possible future extensions to the Hierarchical EMAX model. For example, it might be a benefit to allow a correlation between consecutive doses ‘residuals’, the ψ_d’s may want to consider a broad dose range with. Further, seven doses are a lot, though more sponsors many doses (for example in phase II oncology therapeutic trials and other cancer related studies, such as smoking cessation and/or weight loss studies), especially when using modeling rather than an independent doses model. The questions then become: (1) Does this work as well with fewer doses? At what point does the EMAX assumption come to dominate? Or does added flexibility of the hierarchical component contribute differently with more vs. less doses? Tackling these issues are our next steps in this line of research.

In conclusion, with the ability to have adequate power and other trial operating characteristics, the hierarchical EMAX model is an important alternative in the phase II dose-response setting. Further, as a general pre-trial or trial start-up activity in the case of phase II dose selection trials, we have found that, often, insufficient attention is devoted to the potential vulnerabilities of the trial with respect to modeling choice. This article provides a general framework for how other studies may approach evaluating alternative modeling choices to further safeguard the trial without appreciable loss of power or significant modification of the underlying protocol.

6. Appendix A: Dose calculations

The oxygen toxicity exposure per dive is calculated as the number of minutes breathing 100% oxygen. For each dive, subjects are compressed/decompressed at a rate of 2 feet per minute, where a 10 m dive reduces the atmospheres by approximately 1 unit. That is, the compression or decompression time for a 1.5 ATA dive is 8.25 minutes respectively, 16.5 minutes for a 2.0 ATA dive, and 25 minutes for a 2.5 ATA dive. That is:

$$P{O}_2=100\%O_2\times ATA$$ (1)

$$Compression[\text{min}]=\left(P{O}_{2_f}-P{O}_{2_s}\right)\times \frac{10m}{1ATM}\times \frac{3.281f}{1m}\times \frac{1min}{2f}$$ (2)

To calculate the OTU for the decompression/compression:

$$OTU=\frac{\frac{3}{11}time(mins)}{P{O}_{2f}-P{O}_{2_i}}\times \left[{\left(\frac{P{O}_{2_f}-0.5}{0.5}\right)}^{\frac{11}{6}}-{\left(\frac{P{O}_{2_i}-0.5}{0.5}\right)}^{\frac{11}{6}}\right]$$ (3)

Once compressed, subjects will be treated at the specified pressure for 60 minutes, with NBH treatment defined as 100% O2 for 3 hours following decompression. The NBH without HBO2 treatment will be 100% O2 for 4.5 hours at 1.0 ATA. To calculate the OTU at constant depth:

$$OTU=time(mins)\times {\left(\frac{0.5}{P{O}_2-0.5}\right)}^{\frac{-5}{6}}$$ (4)

Thus, the total OTU dose per dive is:

Dose	ATA	Compress/Decompress Time	OTUs (x 2)†	Constant Pressure Time	OTUs ‡	NBH Time	OTUs ‡	Total OTU per dive
1.5 ATA	1.5	8.25	11.5	60	106.9	0	0	130.0
2 ATA	2	16.5	29.2	60	149.9	0	0	208.3
NBH (100% FiO2 at 1.0 ATA)	1	0	0.0	0	0.0	270	270	270.0
2.5 ATA	2.5	25	53.2	60	190.5	0	0	296.8*
1.5 ATA+NBH	1.5	8.25	11.5	60	106.9	180	180	310.0
2 ATA+NBH	2	16.5	29.2	60	149.9	180	180	388.3*
2.5 ATA+NBH	2.5	25	53.2	60	190.5	180	180	476.8*

^†Using the decompression/compression formula;

^‡Using the constant depth formula

^*Due to differences in rounding, the effective OTU dose for arms 2.5 ATA, 2 ATA+NBH and 2. ATA + NBH are calculated as 52, 776, and 952 (see Table 2).

7. Appendix B: WinBUGS code

###Control Separately

#### hierarchical EMAX

model

{

####Difference from Control

y[1]~dbin(P[1],n[1])

logit(P[1])<-theta[1]

theta[1]~dnorm(−.41,invV)

invV<−1/pow(.75,2)

####Difference from Control

thetadiff[1]<- -1000000

Pdiff[1]<- -1000000

for (d in 2:8)

{

###Active Dose Model

y[d]~dbin(P[d],n[d])

logit(P[d])<-theta[d]

theta[d]<-a[1]+a[2]*nu[d]/(nu[d]+a[3])+psi[d] ## replace “+psi[d]” with “#+psi[d]” to make Emax

##Repace with theta[d]~dnorm(−.41,1) for independent

####Difference from Control

thetadiff[d]<-theta[d]-theta[1]

Pdiff[d]<-P[d]-P[1]

}

a[1]~dnorm(−.41,1)

a[2]~dnorm(0,.04)

a[3]~dnorm(3,.01)I(0,) ####This is right

psi[1]<−0 ### Probably not necessary

psi_adj[1]<−0

for (d in 2:8)

{

psi_adj[d]~dnorm(0,inva24_adj)

psi[d]<-psi_adj[d]-mean(psi_adj[2:8])

}

inva24_adj<−6/7*inva24

inva24~dgamma(.1,.001)

a[4]<-sqrt(1/inva24)

####Probability max relative to control

max(max(max(max(max(max(thetadiff[2],thetadiff[3]),thetadiff[4]),thetadiff[5]),thetadiff[6]),thetadiff[7]),thetadiff[8])

diffMAX[2]<-thetadiff[2]-

max(max(max(max(max(max(thetadiff[1],thetadiff[3]),thetadiff[4]),thetadiff[5]),thetadiff[6]),thetadiff[7]),thetadiff[8])

diffMAX[3]<-thetadiff[3]-

max(max(max(max(max(max(thetadiff[1],thetadiff[2]),thetadiff[4]),thetadiff[5]),thetadiff[6]),thetadiff[7]),thetadiff[8])

diffMAX[4]<-thetadiff[4]-

max(max(max(max(max(max(thetadiff[1],thetadiff[2]),thetadiff[3]),thetadiff[5]),thetadiff[6]),thetadiff[7]),thetadiff[8])

diffMAX[5]<-thetadiff[5]-

max(max(max(max(max(max(thetadiff[1],thetadiff[2]),thetadiff[3]),thetadiff[4]),thetadiff[6]),thetadiff[7]),thetadiff[8])

diffMAX[6]<-thetadiff[6]-

max(max(max(max(max(max(thetadiff[1],thetadiff[2]),thetadiff[3]),thetadiff[4]),thetadiff[5]),thetadiff[7]),thetadiff[8])

diffMAX[7]<-thetadiff[7]-

max(max(max(max(max(max(thetadiff[1],thetadiff[2]),thetadiff[3]),thetadiff[4]),thetadiff[5]),thetadiff[6]),thetadiff[8])

diffMAX[8]<-thetadiff[8]-

max(max(max(max(max(max(thetadiff[1],thetadiff[2]),thetadiff[3]),thetadiff[4]),thetadiff[5]),thetadiff[6]),thetadiff[7])

for (d in 1:8)

{

pMAX[d]<-step(diffMAX[d])

pPBO[d]<-step(thetadiff[d])

pPBOf[d]<-step(Pdiff[d]-.1)

}

####Allocation Weights Done in Excel

#####Now do phase IIII success prediction

ntx<−500

nc<−500

yc~dbin(P[1],nc)

Phatc<-yc/nc

for (d in 1:8)

{

ytx[d]~dbin(P[d],ntx)

Phattx[d]<-ytx[d]/ntx

V[d]<-Phatc*(1-Phatc)/nc+Phattx[d]*(1-Phattx[d])/ntx

Z[d]<-(Phatc-Phattx[d])/sqrt(V[d])

pvalue[d]<-phi(Z[d])

PphaseIIIS[d]<−1-step(pvalue[d]-.025)

}

}

list(inva24=1)

#######For paper (n=200); 20% control, equal elsewhere

###Large effect

list(

n=c(39, 23, 23, 23, 23, 23, 23, 23),y=c(16, 8, 10, 11,12,14,16,18),

nu=c(0, 2.6, 4.17, 5.4, 5.92, 6.2, 7.76, 9.52))

###NBH only:

list(n=c(39, 23, 23, 23, 23, 23, 23, 23),y=c(16,8,8,18,8,18,18,18),

nu=c(0, 2.6, 4.17, 5.4, 5.92, 6.2, 7.76, 9.52))

###Over dose

list(

n=c(39, 23, 23, 23, 23, 23, 23, 23),y=c(16, 8, 10, 12, 18,12,4,2),

nu=c(0, 2.6, 4.17, 5.4, 5.92, 6.2, 7.76, 9.52))