Multi-Site Harmonization of Diffusion MRI Data via Method of Moments

Abstract

Diffusion MRI is a powerful tool for non-invasive probing of brain tissue microstructure. Recent multi-center efforts in acquisition and analysis of diffusion MRI data significantly increase sample sizes and hence improve sensitivity and reliability in detecting subtle changes associated with development, aging, and diseases. However, discrepancies resulting from different scanner vendors, acquisition protocols, and image reconstruction algorithms can cause data incompatibility across imaging centers. In this paper, we introduce a model-free method that is based on the method of moments (MoM) for direct harmonization of diffusion MRI data to reduce site-specific variations. Our method directly harmonizes diffusion-attenuated signal without the need to fit any diffusion model. Moreover, our method allows the explicit definition of well-behaved mapping functions with properties such as invertibility, smoothness, and injectivity. We show that our method is effective in lowering variations of diffusion scalars of traveling human phantoms scanned at different sites from 1%–3% to less than 0.9% for fractional anisotropy (FA) and mean diffusivity (MD), and from 1%–2.5% to 0.3%–1.2% for generalized fractional anisotropy (GFA). We also demonstrate its ability in preserving individual differences and in increasing across-site consistency in tractography and white matter connectivity.

I. Introduction

CONGLOMERATION of data collected at multiple imaging sites allows analyses to be done with greater statistical power [1, 2, 3, 4]. Data pooling also provides opportunities for meta analyses, reproducible research, and avoiding the file drawer problem. However, imaging sites might differ in terms of scanner types, imaging protocols (e.g., field of view, coil channels, gradient directions, etc.), reconstruction algorithms, magnetic field strengths [5, 6], resulting in data incompatibility.

In [7], diffusion MRI data of eight healthy subjects collected using three different sequences, each of them having a different gradient table, were used to study the variation of diffusion scalars across acquisition sequences. The authors reported inter-sequence variability, in terms of coefficient of variation (CoV), from 5.45% to 7.34% in fractional anisotropy (FA) and from 1.72% to 5.56% in mean diffusivity (MD). Magnotta and colleagues [8] investigated the site effect on diffusion scalars by scanning five healthy subjects at eight different imaging centers. The inter-site CoV was reported to be from 1% to 3% across all regions and diffusion scalars while the intrasite CoV was less than 1%. Additionally, a recent study by Mirzaalian and colleagues [9] showed significant FA and MD differences among 116 age-matched healthy control subjects with diffusion MRI data acquired at 7 different sites. These non-linear variations across sites reduce statistical power [5].

A simple solution to correct for inter-site variability is to account for it using a covariate in a statistical model. For example, one can use a covariate to represent sites and remove the site effect in FA or MD [10]. This approach, although extensible to include factors such as imaging protocols and scanner vendors, is only feasible for simple measurements such as FA and MD and becomes impractical for sophisticated entities like tractograms.

An alternative approach is to model diffusion scalars at each site as site-specific global shifting and scaling from values common to all sites, determined by curve fitting using LOESS (LOcally Estimated Scatterplot Smoothing) or LOWESS (LOcally WEighted Scatterplot Smoothing) [11, 12]. Although the method accounts for nonlinearity, its reliance on curve fitting limits its utility when the sample size is small.

In [13, 14], using RAVEL (Removal of Artificial Voxel Effect by Linear regression), the authors addressed the inter-site variation problem by using a control region containing cerebrospinal fluid (CSF) to estimate the latent factors causing the variation, which is assumed to be generalizable to all voxels. Their method is based on the observation that the FA value in the CSF should be zero, hence, any fluctuation in the CSF FA corresponds to site-specific effects. However, this method cannot account for site effects that are spatially varying, such as those caused by magnet inhomogeneity.

A more sophisticated approach presented in [15] reduces site variance by considering it as a surrogate variable that is not related to any biological covariates of interest and eliminating it using Surrogate Variable Analysis (SVA) [16]. While this approach can be performed voxel-wise, its reliance on defining a set of biological covariates of interest limits its applications. Taking a step forward, Fortin and colleagues adapted COMBAT — a model developed for studying gene expression, to directly harmonize diffusion scalars with comprehensive consideration of imaging sites, number of scans per site, and the location and scale of measurements [12]. Despite shown to be effective, the COMBAT model is restricted to diffusion scalars derived from the diffusion-weighted (DW) images.

Recently, Mirzaalian et al. [6] proposed using rotational invariant spherical harmonic (RISH) features to harmonize multi-center datasets. Using a registration framework, the authors showed that their method can lower inter-site variation and preserve individual differences by matching the RISH features of multiple target image groups with a reference image group. While effective, the reliance of the method on spherical harmonic (SH) fitting implies that (i) a sufficient number of DW images are required for reasonable SH fitting, (ii) the data will be smoothed due to the truncation of higher-order SH terms, and (iii) the numbers of gradient directions of the target and reference datasets should be roughly the same so that the same number of SH terms can be fitted.

To tackle these issues, we present in this paper a harmonization approach, which is based on the method of moments (MoM), for direct data harmonization without the need to fit any diffusion models, including SHs. Our method does not rely on the matching of SH coefficients and can be applied to datasets collected with different numbers of gradient directions.

Moreover, our method allows the explicit definition of well-behaved mapping functions with properties such as invertibility, smoothness, and injectivity. We will show that our method is effective in lowering inter-site variation of diffusion scalars using traveling phantom data of subjects scanned at different sites. We will also demonstrate its ability in preserving individual differences and in increasing across-site consistency in tractography and white matter connectivity.

II. Methods

A. Signal Harmonization via the Method of Moments (MoM)

In diffusion MRI, the diffusion-attenuated MR signal S_b (g) is acquired with diffusion-sensitizing gradient direction g and diffusion weighting b. For a fixed b-value, the n-th raw spherical moment is defined as the integral of the signal, raised to the power of n:

$$M_n[S_b]=E[S_b^n]={\int }_{{\mathbb{S}}^2}{S}_b^n(g)\mathit{dg}.$$ (1)

We harmonize a target signal T using a reference signal R via a mapping function f_θ(⋅) with parameter set θ. The parameters are determined by matching moments {M_n[R_b]} with moments {M_n[f_θ(T_b)]}. In this work, we match the first moment M₁ and second central moment C₂ of each b-shell:

$$\begin{gathered} M_1[R_b]=M_1[f_{\theta }(T_b)], \\ {C}_2[R_b]=M_2[R_b-M_1[R_b]]=M_2[f_{\theta }(T_b)-M_1[f_{\theta }(T_b)]] \\ =C_2[f_{\theta }(T_b)]. \end{gathered}$$ (2)

The first moment corresponds to the spherical mean and the second central moment corresponds to the spherical variance, which measures the signal deviation from the spherical mean. Matching the spherical mean can be seen as matching the per-axon microstructural characteristics [17, 18]. Matching the second central moment can be seen as matching the orientation dispersion [19]. Note that the mapping function is applied isotropically to all gradient directions and is hence rotational invariant. This ensures that the mapping will not introduce artificial orientations.

To ensure that the mapping is well-behaved, we require f_θ(⋅) to be smooth (no abrupt changes), one-to-one (topology preserving), strictly increasing (contrast preserving), and invertible (data recoverable). A simple and convenient option satisfying these properties is the linear mapping function:

$$f_{\theta =\{\alpha ,\beta \}}(S)=\alpha S+\beta ,$$ (3)

where we restrict α > 0 to ensure that the signal is not inverted, i.e., high (or low) signal remains high (or low). From (2), the mapping parameters for the b-shell can be calculated as:

$${\alpha }_b=\sqrt{\frac{C_2[R_b]}{C_2[T_b]}},$$ (4)

$${\beta }_b=M_1[R_b]-{\alpha }_b{M}_1[T_b].$$ (5)

Exact moment matching as described above can be problematic in regions with isotropic diffusion, such as the ventricles, where the spherical variance is dominated by noise. In this case, we will actually harmonize noise and not signal. A possible solution is to remove noise before calculating the moments for harmonization. However, this could result in zero or very small spherical variance, causing the estimation of α in (4) to be unstable. To address this problem, we solve for the parameters by minimizing the following cost function:

$$J({\alpha }_b,{\beta }_b)={\Vert \left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \zeta \hfill \end{array}\right)\left(\begin{array}{c}\hfill M_1[R_b]-M_1[f_{{\alpha }_b,{\beta }_b}(T_b)]\hfill \\ \hfill C_2[R_b]-C_2[f_{{\alpha }_b,{\beta }_b}(T_b)]\hfill \end{array}\right)\Vert }_2^2+\psi ({\alpha }_b,{\beta }_b),\zeta =\frac{M_1[R_b]}{C_2[R_b]},$$ (6)

where ζ is a scaling factor for preventing the solution from being driven only by the first moment. The penalization function ψ(α, β), defined as:

$$\psi (\alpha ,\beta )=\gamma \left\{\left[1-e^{-\frac{{(\alpha -1)}^2}{2}}\right]+\left[1-e^{-\frac{{\beta }^2}{2}}\right]\right\},$$ (7)

encourages α and β to stay at 1 and 0, respectively. γ is a tuning parameter with γ = 0 corresponding to no penalization (i.e., exact matching) and γ → ∞ to no harmonization (i.e., identity mapping). We determine the optimal γ via grid search. The mapping parameters are determined by minimizing the cost function (6) by solving an unconstrained multivariable optimization problem using a quasi-Newton algorithm [20]. Compared with (2), this relaxes moment matching and yields parameter estimates that are more stable and robust to noise. Note that our framework is flexible in allowing higher-order moments and more complex mapping functions to be considered for harmonization. We found that the choice of using moments up to the second order and the linear mapping function to be sufficient for our datasets.

B. Construction of Reference

It is common for imaging studies to collect, at each imaging center, images from multiple subjects with the same imaging protocol. It is not always clear how the reference for harmonization should be constructed. An inappropriately selected reference for harmonization might bias outcome, especially in the presence of outliers. Moreover, harmonization should ideally not bias toward a single subject since the goal is to reduce site differences, not between subject variations. The reference should therefore be constructed at the population level.

A population reference can be constructed by spatially warping the moment images of the individual subjects to a common space and then computing the average moment image. However, this approach is sensitive to outliers, which can result from anomalies associated with brain disorders. For greater robustness to outliers, we compute the median moment image instead. The median is a robust statistic with a maximal breakdown point of 0.5. The mean, on the other hand, has a breakdown point of 0. This implies that the population can have up to 50% outliers before the median is affected. Therefore, when normal control and patient cohorts are simultaneously harmonized, the median can tolerate disease prevalence of up to 50%.

C. Implementation Issues

1). Signal Scaling:

Since the signal scale can differ across sites, scanners, and subjects, we divide the DW images by the non-DW b0 image. If needed, after harmonization, the signal in the original scale can be recovered by multiplying the harmonized DW images with the b0 image.

2). Noise Removal:

To reduce the effects of noise on the estimation of the mapping parameters, we first denoised the DW images via coefficient thresholding of tight graph framelets [21]. The mapping parameters were determined based on the moments computed from the denoised DW images. The corresponding mapping functions were applied to the denoised DW images. The residuals, obtained by subtracting the denoised DW images from the original ones, were added to the mapped DW images to retain the original noise distribution.

3). Block-Based Parameter Estimation:

Structural misalignments between diffusion data of among subjects can occur due to registration errors and also natural inter-subject anatomical variations. To alleviate the effects of misalignments on harmonization, the estimation of the mapping parameters at each voxel is based the average moments of a 3 × 3 × 3 voxel neighborhood (i.e., radius = 1 voxel).

D. Method Summary

Harmonization of data at target site(s) with respect to data at reference site(s) is carried out via the following steps:

• 1)Compute the spherical moments of each dataset in its native space.
• 2)Spatially warp all moment images to a common space defined by the target data.
• 3)Construct the reference and target population moment images in the common space.
• 4)Obtain mapping parameters by matching the population moments.
• 5)Warp mapping parameters to subject native spaces.
• 6)Apply mapping functions voxel-wise to the target data. This procedure is illustrated in Fig. 1. Signal scaling and noise removal are done prior to Step 1 and block-based estimation is done in Step 4.

Fig. 1. Harmonization Pipeline.

Harmonization of datasets at the target site. Reference and target moments, and mapping parameters are computed in a common space defined by the target data.

III. Experiments

A. Evaluation Strategy

We evaluated the effectiveness of our method by considering the following: (i) Inter-site variations of FA, MD, and GFA; (ii) Deviation of the FA, MD, and GFA from their expected values with harmonization; (iii) Angular and spatial smoothing associated with SH harmonization; (iv) Harmonization of datasets collected with different acquisition parameters; (v) Preservation of individual differences after harmonization; and (vi) The effects of harmonization on tractography and connectivity. Both synthetic and in-vivo data were used in evaluation. We will also discuss potential pitfalls and solutions.

B. Synthetic Data

To demonstrate the ability of our method in preserving individual differences (e.g., due to pathology) after harmonization, we use Phantomas [22] to synthesize two datasets based on the geometric model used in the ISBI 2013 HARDI challenge¹:

• 1)The reference set, which consists of 20 control datasets, each created using the 30-direction gradients used by the Siemens scanners described below for the in-vivo data. Signals were generated from both one- and two-tensor models with each tensor having FA=0.7 and MD=0.25 × 10⁻³ mm²/s. This represents a group of normal subjects at the reference site.
• 2)The target set, which consists of 19 control datasets representing normal subjects, created with the 32-direction gradients used by the Philips scanners described below for the in-vivo data, with FA=0.7, MD=0.25 × 10⁻³ mm²/s. 1 additional ‘pathological’ dataset was included in the target set, created using the same 32 directions but with FA=0.65 and MD=0.27 × 10⁻³mm²/s. The ratio of 1 abnormal out of 20 normal data was to simulate the pathological prevalence of 5%.

The process for generating the synthetic data is summarized in Fig. 2. Harmonization was carried out at the population level as described in Section II-B.

Fig. 2. Data Generation.

Generation of the synthetic dataset for evaluation of the preservation of individual differences after harmonization. Control dataset is generated with FA=0.7, MD=0.25 × 10⁻³ mm²/s, ‘pathological’ dataset with FA=0.65, MD=0.27 × 10⁻³ mm²/s.

Differences in FA (ΔFA = 0.05) and MD (ΔMD = 0.02 × 10⁻³ mm²/s) between the healthy and unhealthy subjects before harmonization were compared with those after harmonization to investigate the preservation of individual differences. Rician noise of different levels was added with 100 repetitions to test for robustness.

C. In-Vivo Data

To demonstrate the efficacy of our method, we employed the “DWI Traveling Human Phantom Study” dataset obtained from OpenfMRI². The dataset consists of diffusion MRI data of 5 healthy control subjects scanned at 8 different imaging centers with two protocols per center, both with b = 1000 s/mm²:

• Vendor-provided gradient directions – 30 directions for Siemens scanners (denoted ‘30-dir’) and 32 directions for Philips scanners (denoted ‘32-dir’), and

• Customized 71 gradient directions for both types of scanners (denoted ‘71-dir’).

A detailed description of the dataset is provided in [8]. Eddy currents and motion correction were performed prior to harmonization [23]. The deformation field for each dataset to the target space was determined using spatial registration with FA and non-DW (b0) images [24].

This traveling phantom dataset allows us to evaluate the effects of harmonization without being confounded by intersubject differences. However, traveling human phantoms data are not common and in practical scenarios different subjects are typically scanned at different sites. We emulated this situation by dividing the five subjects into four reference subjects and one target subject. The subjects in the reference and target sets were hence different.

The reference and target moments were computed based on the DW images of the reference subjects and the target subject for the eight sites. To avoid numerical errors, the moments were computed in the subject native spaces. Then, the moments of the reference subjects were warped to the target space to construct the reference moments at the population level. Warping the moment images instead of the DW images avoid the need for signal reorientation, which is common in registration algorithms for diffusion MRI [25]. As described in Section II-B, the reference moments were determined as the medians of the moments of reference subjects. In total, there were eight different pairs of target moment images (first and second moments) for the target subject, corresponding to the eight sites. We warped the moments images of the four reference subjects to the target spaces at the eight sites and compute the median moment images to form eight sets of reference moment images. Exhaustive cross-validation evaluation was performed by permuting the reference subjects and the reference site. For five subjects at eight sites, our experimental setting led to forty permutations. Harmonization across acquisition settings (i.e., different numbers of gradient directions) was also evaluated.

D. Evaluation Criteria

1). Harmonized vs. Unharmonized:

We computed the FA, MD, and GFA intra-subject inter-site coefficients of variation (CoVs) across eight sites before and after harmonization. The CoV was computed as the ratio (in percent) of the inter-site standard deviation to the mean of a measurement. Before harmonization, the CoV was non-zero due to inter-site differences, as reported in [8]. Harmonization was performed within or between 30/32-and 71-direction sets. Harmonization is expected to lower the CoV.

2). Direct Signal Harmonization vs. Spherical Harmonic Harmonization:

We evaluated the advantages of direct signal harmonization over SH-based harmonization in terms of bias resulting from data smoothing. SH-based harmonization was done according to [6] with matching using a 3 × 3 × 3 voxel neighborhood to account for misalignment. Inter-site variation can be artificially reduced by smoothing out noise and details. This will however result in the deviation of the signal and the derived diffusion scalars from their expected values, e.g., FA reduction. A metric that takes into account variation and bias is the root-mean-square deviation (RMSD):

$$\text{RMSD}=\sqrt{E[{(\widehat{y}-E[\widehat{y}])}^2]+{(E[\widehat{y}]-y)}^2},$$ (8)

where $\widehat{y}$ represents the harmonized FA/MD/GFA values of the target subject at the different sites and y is the true FA/MD/GFA value. The term $E[{(\widehat{y}-E[\widehat{y}])}^2]$ is the variance, i.e., σ², measuring inter-site variations, whereas ${(E[\widehat{y}]-y)}^2$ is the squared bias, quantifying deviation from the expected value. Since for the in vivo dataset we do not have the ground truth FA/MD/GFA, we estimated the expected value y as the median of the unharmonized FA/MD/GFA values across all sites.

3). Tractography and Connectivity:

We investigated the effects of harmonization on tractography and connectivity. For each target dataset before and after harmonization, we estimated the fiber response functions and fiber orientation distribution functions (FODFs) using spherical deconvolution [26]. Then tractograms were generated with second-order integration over fiber orientation distributions (iFOD2) algorithm [27]. Spherical-decovolution informed filtering of tractograms (SIFT) was applied to match the tractograms with the FODFs and filter out any tracts that do not match the structural constrains obtained from high-resolution T1-weighted images (i.e., tracts that go into CSF) [28]. Connectivity matrix was obtained as the normalized fiber-count matrix connecting the 84 regions of interest (ROIs) parcellated from the T1-weighted images [29, 30, 31]. The ROIs and their abbreviations are summarized in Table I. With eight sites, this results in sixteen connectivity matrices (before and after harmonization). Cross validation was performed by permuting the reference site and the target subject. The 30/32-direction dataset was used in this evaluation as they cover the whole brain.

TABLE I.

Regions based on Desikan-Killiany cortical atlas and Freesurfer parcellation.

Region	Abbrev.	Region	Abbrev.
Left Banks Superior Temporal Sulcus	L.BSTS	Right Banks Superior Temporal Sulcus	R.BSTS
Left Caudal Anterior-cingulate Cortex	L.CACG	Right Caudal Anterior-cingulate Cortex	R.CACG
Left Caudal Middle Frontal Gyrus	L.CMFG	Right Caudal Middle Frontal Gyrus	R.CMFG
Left Cuneus Cortex	L.CU	Right Cuneus Cortex	R.CU
Left Entorhinal Cortex	L.EC	Right Entorhinal Cortex	R.EC
Left Fusiform Gyrus	L.FG	Right Fusiform Gyrus	R.FG
Left Inferior Parietal Cortex	L.IPG	Right Inferior Parietal Cortex	R.IPG
Left Inferior Temporal Gyrus	L.ITG	Right Inferior Temporal Gyrus	R.ITG
Left Isthmuscingulate Cortex	L.ICG	Right Isthmuscingulate Cortex	R.ICG
Left Lateral Occipital Cortex	L.LOG	Right Lateral Occipital Cortex	R.LOG
Left Lateral Orbital Frontal Cortex	L.LOFG	Right Lateral Orbital Frontal Cortex	R.LOFG
Left Lingual Gyrus	L.LG	Right Lingual Gyrus	R.LG
Left Medial Orbital Frontal Cortex	L.MOFG	Right Medial Orbital Frontal Cortex	R.MOFG
Left Middle Temporal Gyrus	L.MTG	Right Middle Temporal Gyrus	R.MTG
Left Parahippocampal Gyrus	L.PHIG	Right Parahippocampal Gyrus	R.PHIG
Left Paracentral Lobule	L.PaCG	Right Paracentral Lobule	R.PaCG
Left Pars Opercularis	L.POP	Right Pars Opercularis	R.POP
Left Pars Orbitalis	L.POR	Right Pars Orbitalis	R.POR
Left Pars Triangularis	L.PTR	Right Pars Triangularis	R.PTR
Left Pericalcarine Cortex	L.PCAL	Right Pericalcarine Cortex	R.PCAL
Left Postcentral Gyrus	L.PoCG	Right Postcentral Gyrus	R.PoCG
Left Posterior-cingulate Cortex	L.PCG	Right Postcentral Gyrus	R.PCG
Left Precentral Gyrus	L.PrCG	Right Precentral Gyrus	R.PrCG
Left Precuneus Cortex	L.PCU	Right Precuneus Cortex	R.PCU
Left Rostral Anterior Cingulate Cortex	L.RACG	Right Rostral Anterior Cingulate Cortex	R.RACG
Left Rostral Middle Frontal Gyrus	L.RMFG	Right Rostral Middle Frontal Gyrus	R.RMFG
Left Superior Frontal Gyrus	L.SFG	Right Superior Frontal Gyrus	R.SFG
Left Superior Parietal Cortex	L.SPG	Right Superior Parietal Cortex	R.SPG
Left Superior Temporal Gyrus	L.STG	Right Superior Temporal Gyrus	R.STG
Left Supramarginal Gyrus	L.SMG	Right Supramarginal Gyrus	R.SMG
Left Temporal Pole	L.TP	Right Temporal Pole	R.TP
Left Frontal Pole	L.FP	Right Frontal Pole	R.FP
Left Transverse Temporal Cortex	L.TTG	Right Transverse Temporal Cortex	R.TTG
Left Insula	L.IN	Right Insula	R.IN
Left Cerebellum Cortex	L.CER	Right Cerebellum Cortex	R.CER
Left Thalamus Proper	L.TH	Right Thalamus Proper	R.TH
Left Caudate	L.CA	Right Caudate	R.CA
Left Putamen	L.PU	Right Putamen	R.PU
Left Pallidum	L.PA	Right Pallidum	R.PA
Left Hippocampus	L.HI	Right Hippocampus	R.HI
Left Amygdala	L.AM	Right Amygdala	R.AM
Left Accumbens Area	L.AC	Right Accumbens Area	R.AC

To quantify how site-specific noise affects connectivity, we computed several network measures across sites before and after harmonization, including global efficiency, local efficiency, and betweenness centrality [32]. Global efficiency is the average of the inversed shortest path lengths of the network. Local efficiency is the global efficiency of the immediate neighbors of a node. Betweenness centrality is the fraction of all shortest paths in the network that are connected to a node. Ideally, there should be minimal variation of these measures across sites for the same target subject.

IV. Results

A. Synthetic Data

1). Individual Differences:

Fig. 3 presents the differences in FA and MD between the simulated healthy and unhealthy subjects before and after harmonization. The differences are computed between the values given by the patient subject and the median values of the healthy subjects. Although the difference deviates from the ground truth (ΔFA = 0.05, ΔMD = 0.02 × 10⁻³ mm²/s) when the signal-to-noise ratio (SNR) varies, the deviation is not statistically significant (smallest p = 0.428). This demonstrates that our method preserves individual differences so that they remain detectable after harmonization.

Fig. 3. Preservation of Individual Differences.

Differences of FA and MD (×10⁻³) between normal and pathological simulated data before (red) and after (green) harmonization at various levels of noise. The dashed line marks the true differences between normal and pathological data. The lines and error bars show the means and variances computed based on 100 repetitions.

B. In-Vivo Data

1). Mapping Parameters:

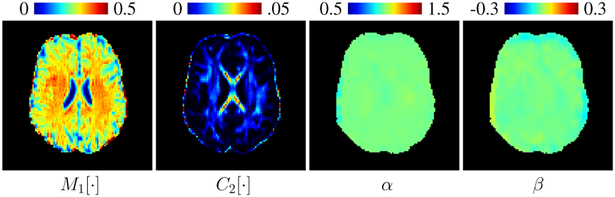
It can be observed from Fig. 4 that the mapping parameters α and β are not tissue-specific and do not vary significantly across space, unlike the first and second moments. This allows us to harmonize the data voxel-wise without being dependent on parcellated regions, unlike [9].

Fig. 4. Moment Images and Mapping Parameters.

Note that although the first moment (M₁ [⋅]) and second moment (C₂ [⋅]) are tissue-specific, the mapping parameters α and β do not vary significantly across space.

2). Regularization Parameter:

Fig. 5 shows the relationship between γ and RMSD. The value γ = 0.1 is reasonably optimal. A smaller value results in more exact matching. A larger value results in less harmonization with greater tendency in retaining the original signal values.

Fig. 5. Regularization.

Relationship between regularization parameter γ and the inter-site root-mean-square deviation (RMSD) of FA and MD (×10⁻³) after harmonization.

3). Smoothing Effects:

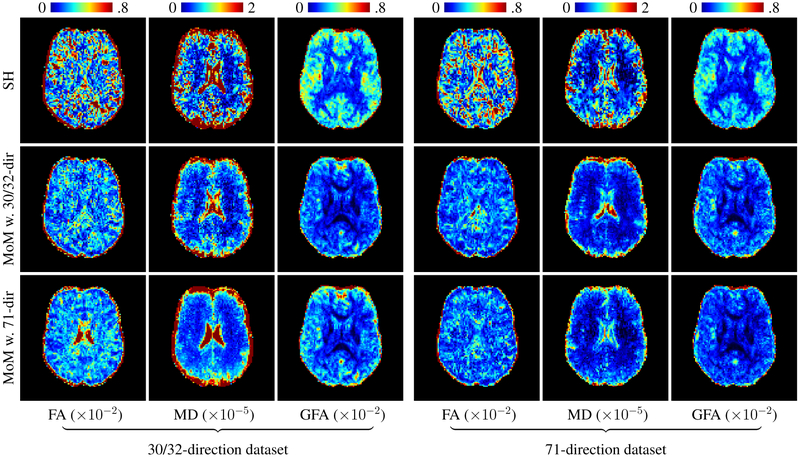
Our method allows for direct harmonization of the diffusion signal, unlike SH-based methods. For reasonable SH fitting, the number of DW images needs to equal or exceed the number of coefficients. That is, 15 for up to 4-th order, 28 for up to 6-th order, and 45 for up to 8-th order. For example, SHs up to only the 6-th order can be fitted to the 30/32-direction dataset. Therefore, the higher-order terms are truncated, resulting in angular smoothing of the data. Note also that the difference between the number of DW images and the number of SH coefficients can be potentially large, since the number of SH coefficients increases in steps of (2n + 1) with order n. Moreover, since the target SH coefficients are required to match the reference SH coefficients, which are group averaged, spatial smoothing is introduced. An example of the smoothing effects on the 30/32-direction dataset is shown in Fig. 6. It can be observed that our method for direct signal harmonization preserves spatial details comparable to the unharmonized data, whereas the SH-based method causes smoothing.

Fig. 6. Smoothing Effects.

Diffusion-weighted images before harmonization and after SH and MoM harmonization.

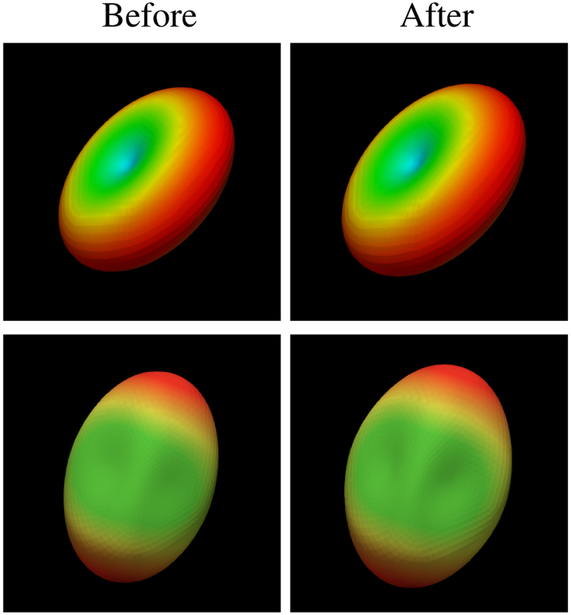
4). Preservation of Signal Scale and Shape:

Fig. 7 shows the diffusion signal profile before and after harmonization. Osur method preserve the general shape and directional information of the signal profile.

Fig. 7. Diffusion Signal Profile.

The diffusion signal profile before (left) and after (right) harmonization with MoM. The shape and directional information of the signal profile are preserved after harmonization.

5). Inter-Site Coefficient of Variation:

Fig. 8 shows the inter-site CoVs for FA, MD, and GFA. The variation in the 30/32-direction dataset, with gradients provided by the vendors, is higher than the 71-direction dataset, with consistent gradients across sites. One can clearly observes that after harmonization using MoM the standard deviations of all FA, MD, and GFA decreases, regardless of whether the 30/32-or 71-direction dataset was used as reference. Note that unlike [6, 9] the MoM method does not require the reference and target datasets to have the same number of gradient directions. Table II shows the results for white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF). Notice that using the 71-direction dataset to form the reference produces better results on both the 30/32-and 71-direction datasets.

Fig. 8. FA, MD, and GFA inter-site coefficient of variation.

Comparison between the unharmonized data and the harmonized 30/32-direction (left) and the 71-direction (right) data. In the middle and bottom rows, the 30/32-direction and 71-direction datasets were used respectively as the reference. The coefficient of variation is shown in percentage.

TABLE II.

Inter-site coefficients of variation (%) of FA, MD, and GFA before and after harmonization with different references.

		30/32-dir dataset			71-dir dataset
		Unharmonized	MoM with 30/32-dir dataset	MoM with 71-dir dataset	Unharmonized	MoM with 30/32-dir dataset	MoM with 71-dir dataset
	CSF	2.852	0.808	0.813	2.104	0.768	0.723
FA	GM	1.642	0.809	0.852	1.546	0.466	0.458
	WM	1.412	0.802	0.888	1.053	0.521	0.496
	CSF	2.605	0.592	0.302	1.931	0.209	0.182
MD	GM	1.322	0.303	0.379	1.118	0.187	0.132
	WM	1.023	0.233	0.221	1.101	0.113	0.104
	CSF	2.537	1.482	1.474	1.952	1.383	1.182
GFA	GM	2.652	1.492	1.488	2.105	1.402	1.214
	WM	1.312	0.819	0.803	1.032	0.612	0.416

6). Inter-Site Root-Mean-Square Deviation:

To compare our method with the SH-based method, the RMSD was used to measure both the variance of diffusion scalars and their deviation from the expected value. Fig. 9 and Table III support our expectation that overall, the SH method, while effective in reducing variation, biases the diffusion scalars. In contrast, our method does not rely on model fitting and reduces both variance and bias. This is further confirmed in Table IV, where our method yields smaller bias in FA, MD, and GFA when the 71-dir dataset is harmonized with the reference constructed from the same dataset. The SH method, however, produces large bias, which is notable for the 30/32-dir dataset due the smoothing effect resulting from SH truncation.

Fig. 9. FA, MD, and GFA Root-Mean-Square Deviation.

Comparison between harmonization using the SH method (top row) and the MoM method with reference to the 30/32-direction dataset (middle row) and from the 71-directions dataset (bottom row). The harmonization results of the 30/32-direction and 71-direction datasets are shown respectively on the left and right. Note that for the SH method, harmonization can only be performed when the number of gradient directions matches between the reference and the target.

TABLE III.

Inter-site root-mean-square deviation (RMSD) of FA (×10⁻²), MD (×10⁻⁵), and GFA (×10⁻²) after harmonization using the Spherical Harmonic (SH) method and the Method of Moments (MoM) with different references.

		30/32-dir dataset			71-dir dataset
		SH	MoM with 30/32-dir dataset	MoM with 71-dir dataset	SH	MoM with 30/32-dir dataset	MoM with 71-dir dataset
	CSF	1.011	0.732	0.739	0.337	0.293	0.258
FA	GM	0.657	0.455	0.466	0.360	0.301	0.253
	WM	0.624	0.456	0.459	0.329	0.300	0.259
	CSF	3.883	2.650	2.863	1.137	1.104	1.023
MD	GM	2.882	1.648	1.760	0.669	0.619	0.606
	WM	1.676	0.958	1.058	0.533	0.503	0.427
	CSF	1.227	0.422	0.497	1.013	0.483	0.322
GFA	GM	1.041	0.355	0.362	0.823	0.418	0.311
	WM	0.352	0.301	0.309	0.335	0.282	0.219

TABLE IV.

Bias from expected FA (×10⁻²), MD (×10⁻⁵), and GFA (×10⁻²) values after harmonization using the Spherical Harmonic (SH) method and the Method of Moments (MoM) with different references.

		30/32-dir dataset			71-dir dataset
		SH	MoM with 30/32-dir dataset	MoM with 71-dir dataset	SH	MoM with 30/32-dir dataset	MoM with 71-dir dataset
	CSF	0.892	0.182	0.420	0.371	0.133	0.003
FA	GM	0.427	0.211	0.233	0.235	0.190	0.100
	WM	0.458	0.189	0.201	0.268	0.150	0.071
	CSF	2.338	0.192	0.001	0.957	0.181	0.001
MD	GM	2.503	0.201	0.012	0.235	0.099	0.001
	WM	1.976	0.103	0.023	0.222	0.101	0.002
	CSF	0.722	0.178	0.201	0.431	0.266	0.002
GFA	GM	0.746	0.146	0.197	0.476	0.091	0.011
	WM	0.682	0.101	0.121	0.333	0.112	0.057

7). Tractography and Connectivity:

Fig. 10 shows the variation of tractograms of the same subject across eight sites before harmonization. In particular, the tractograms are visually different at site 4 and site 8. This discrepancy might be due to the fact that data at site 2, 4, and 8 were acquired with 32 gradient directions using Philips scanners, whereas the others were acquired with 30 gradient directions using Siemens scanners. After harmonization, the tractograms are more consistent, confirming the effectiveness of our method in harmonizing the data for applications such as tractography.

Fig. 10. Tractograms.

Comparison of tractograms before and after harmonization. Tractograms are more consistent between sites after harmonization.

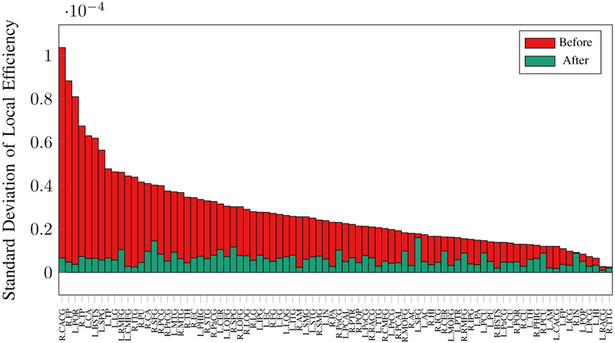
We further investigated the variation in connectivity metrics. Fig. 11 shows that harmonization significantly reduces the variation in global efficiency while maintaining a comparable median. Figs. 12 and 13 show that the variation of local efficiency and betweenness centrality is significantly lowered for all nodes, indicating greater network consistency.

Fig. 11. Global Efficiency.

Network global efficiency across 8 sites before and after harmonization.

Fig. 12. Local Efficiency.

Standard deviation of local efficiency of 84 network nodes across 8 sites before and after harmonization. Values are sorted based on those before harmonization.

Fig. 13. Betweenness Centrality.

Standard deviation of betweenness centrality of 84 network nodes across 8 sites before and after harmonization. Values are sorted based on those before harmonization.

V. Discussions and Conclusions

Our experiments confirm that inter-site variations affect diffusion scalars, tractography, and connectivity. Inter-site harmonization significantly reduces these variations and make the data more comparable across sites.

A. Higher-Order Moments and Non-Linear Mapping Functions

Our results show that harmonization using the first and second order moments with the linear mapping function is adequate to significantly reduce inter-site variation. The dataset we used was reported to have 1% to 3% inter-site variation in terms of CoV across all regions for FA and MD [8]. Although subtle, we have shown that the variation in this dataset also affects tractography and structural networks. Harmonization using our method reduces the CoVs of FA and MD to less than 0.9%. The CoV of connectivity measures is reduced from 17% to 9%. The CoV of GFA is also reduced from 1%-2.5% to 0.3% to 1.2%.

It is interesting to understand how scaling (via α) and shifting (via β) in the linear mapping function f(S) = αS + β affect harmonization. Parameter estimation for the scaling function f(S) = αS and shifting function f(S) = S + β can be estimated by considering only the first moment, i.e., the spherical mean. In Fig. 14 we show that scaling or shifting accounts only part of the inter-site variation. Using both scaling and shifting, and hence the first and second moments, further reduces inter-site variation.

Fig. 14. Mapping Functions.

Inter-site coefficients of variation of diffusion scalars (FA, MD, and GFA) associated with different mapping functions.

Our framework is general and allows harmonization using higher-order moments and non-linear mapping functions, provided that they satisfy basic mathematical properties, such as smooth (no abrupt changes), one-to-one (topology preserving), strictly increasing (contrast preserving), and invertible (data recoverability).

Higher-order moments can be included in the cost function:

$$J({\theta }_b)={\Vert W\left(\begin{array}{c}\hfill M_1[R_b]-M_1[f_{{\theta }_b}(T_b)]\hfill \\ \hfill M_2[R_b]-M_2[f_{{\theta }_b}(T_b)]\hfill \\ \hfill \dots \hfill \\ \hfill M_n[R_b]-M_n[f_{{\theta }_b}(T_b)]\hfill \end{array}\right)\Vert }_2^2+\psi ({\theta }_b),$$ (9)

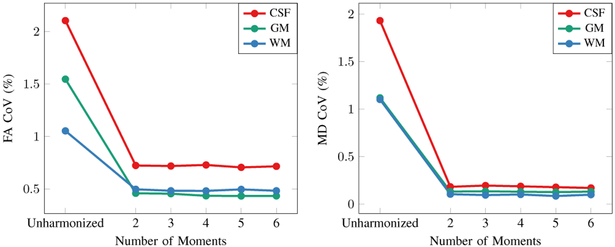
where M_n[⋅] is the n-th order moment (raw moment for the first order and central moments for higher orders) and W = diag[w₁, w₂,..., w_n] is the weighting matrix with w_n = M₁[R_b]/M_n[R_b]. We tested this with the linear mapping function (3) by using varying the number of moments. Figure 15 indicates that the improvement given by more than two moments is not significant and that our method is robust to noise in the higher-order moments.

Fig. 15. Number of Moments.

Relationship between the number of moments and the CoVs (%) of FA and MD.

B. Preservation of Individual Differences

It is important to ensure that individual differences are preserved after harmonization so that pathologies remain detectable. The ability of our method in preserving individual differences, as demonstrated in Section IV-A1, is due to penalized parameter estimation and outlier rejection in constructing population-based moment images for harmonization. Penalization prevents the estimation of parameters α and β to be solely driven by the differences in the moments. In pathological cases, parameters deviating too far from α = 1 and β = 0 due to moment differences are penalized. Outlier rejection using median, as described in Section II-B, allows population-based moment images to be constructed for harmonization without being affected by pathological samples with a prevalence of up to 50%.

C. Individual and Population Harmonization

The datasets of a population of subjects can be harmonized individually or jointly:

• Individual harmonization: Harmonization of the dataset of a target individual can be based on a reference constructed from either a subject or a population of subjects. The former is useful for intra-subject harmonization, e.g., repeated scans of a single subject at the same site. This can reduce data variation caused, for example, by signal drift [33, 34]. The latter is useful for intra-site intersubject harmonization to reduce variation associated with changes in MR signal due to varying imaging conditions [5, 35, 36].

• Population harmonization: Joint harmonization of the datasets of a population of subjects is useful for inter-site variation and preservation of pathological differences.

To investigate the effectiveness of the proposed method in these different scenarios, we performed the evaluation in Section III-C by varying the ratio between the number of target subjects to the number of reference subjects, i.e., 1:4, 2:3, 3:2, and 4:1. Fig. 16 shows slight variations in inter-site variation of diffusion scalars when the ratio is varied. However, the differences are not statistically significant (smallest p = 0.312). This implies that our method is robust to the target-reference ratio and is effective for individual harmonization of single targets and population harmonization of multiple targets.

Fig. 16. Target-Reference Ratio.

Inter-site standard deviation of FA and MD (×10⁻³) after harmonization with varying target-reference subject ratios.

D. Advantages and Limitations

Our method lowers inter-site variation without introducing significant bias. The ability to directly harmonize the DW images affords the flexibility in post-harmonization analysis based on microstructure and tractograms. Our method is simple to implement, fast, and hence practical. Moreover, unlike SH-based methods, our method does not require the number of gradient directions to be similar among datasets.

Recently, methods based on deep learning have been developed for data harmonization [37, 38, 39]. While effective, deep learning approaches require training data, i.e., subjects scanned at multiple sites and with different scanners or protocols. However, such data are not available in most studies. In contrast, our method does not require training data. The traveling phantom data were used only for evaluation purposes.

Our method currently does not consider the possibility that the data from multiple sites might differ in terms of spatial resolution and diffusion weightings (i.e., b-values). In this case, the DW images of the reference site can be resampled to match the data of the target site in terms of spatial resolution and b-values. Harmonization can then be performed by matching the moments of the target data with the moments of the resampled reference data.

E. Concluding Remarks

We have presented a harmonization method that can be applied directly to diffusion-weighted images and demonstrated its efficacy in lowering inter-site variation in terms of diffusion scalars, tractography, and connectivity. Future work will be directed to investigating the effects of using higher-order moments with non-linear mapping functions.