Abstract
We test the effect of the introduction of Medicare Part D on physician prescribing behavior by using data on physician visits from the National Ambulatory Medical Care Survey (NAMCS) 2002–2004 and 2006–2009 for patients aged 60–69. We use a combined DD-RD specification that is an improvement over either the difference-in-difference (DD) or regression discontinuity (RD) designs. Comparing the discrete jump in outcomes at age 65 before and after 2006, we find a 35% increase in the number of prescription drugs prescribed or continued per visit and a 55% increase in the number of generic drugs prescribed or continued, providing evidence of physician response to changes in patient out-of-pocket costs.
Keywords: Medicare, Part D, prescription drug, expenditure of health care, prescribing pattern
1. Introduction
In the past 50 years, resources devoted to health care have outpaced resources devoted to many other sectors of the U.S. economy.1 The expansion of the third-party payment system, which results in higher medical care utilization and may stimulate the development and adoption of advanced treatment choices, has often been cited as an important driving force behind rising health expenditures (Weisbrod 1991). Because of asymmetric information between physicians and patients, physicians serve not only as providers of health care services to patients, but also as advisors to patients, thus taking on a crucial role in the interplay between health insurance, health care utilization, and treatment choices (Arrow 1963). Indeed, physician agency is considered to be a possible explanation for rising health expenditures associated with insurance coverage (Feldstein 1970).2 Thus, understanding the impact of health insurance on physicians’ treatment decisions has become critical for identifying the sources of health expenditure growth and for evaluating a host of health policies that aim to improve the efficiency and efficacy of health care delivery.
The relationship between a patient’s insurance status and a physician’s treatment decision can be analyzed using a standard principal-agent framework (Arrow 1963) in which both principals (patients) and agents (physicians) maximize their expected utility. As agents, physicians typically are assumed to maximize the combination of income and non-financial factors, such as utility stemming from adherence to standards of practice and ethics, as well as concern for patient welfare (Chalkley & Malcomson 1998; Ellis & McGuire 1986). When insurance coverage becomes available, physicians may recommend more procedures and services if they take patients’ out-of-pocket costs into consideration (at least partial agency). Although some literature has shown that physicians consider and incorporate patients’ health insurance status into their clinical decision making (Wynia et al. 2003; Meyers et al. 2006), other work (Federman 2004) does not find evidence of this. In fact, there exists little empirical work quantifying the effect of a patient’s health insurance status on physicians’ treatment decisions. We therefore attempt to contribute to the literature by examining the impact of the adoption of Medicare Part D on physicians’ prescribing behavior.
The introduction of Medicare Part D provides a good opportunity for studying the impact of a patient’s health insurance status on physicians’ clinical decisions. First, the primary goal of Medicare Part D, adopted in January 2006, is to provide drug coverage for Medicare beneficiaries.3 It does not come with supply-side reforms, such as a change in the payment system or pay-for-performance, that might restrict or encourage a change in physicians’ treatment patterns. So, our estimates should not be confounded by supply-side incentives. Second, unlike in some Asian countries (Iizuka 2007; Liu et al. 2009), U.S. physicians only prescribe; they do not dispense drugs. So, although there is evidence that physicians alter practice patterns in response to financial incentives (Gruber & Owings 1996; Yip 1998), since U.S. physicians are not compensated (either by an insurance reimbursement system or by pharmaceutical manufacturers) on the number or type of drugs they prescribe, there are no obvious pecuniary incentives attributable to Part D for physicians to change prescribing patterns. Finally, there are typically a number of pharmaceutical options for each therapeutic condition. The discrete nature of pharmaceutical treatments makes it easier to measure this aspect of physician treatment compared to others, and makes it possible to measure it beyond a binary decision.
This paper makes several contributions to the literature. First, unlike previous studies that examine the effect of insurance on the use of health care services (Card et al. 2009; Anderson et al. 2014), which is a combined decision of physician and patient, we specifically study only physicians’ treatment decisions. Using the National Ambulatory Medical Care Surveys (NAMCS), a unique nationally-representative survey of health care use during physician office visits, we study whether physicians changed the quantity and type of drugs they prescribe after the adoption of Part D.
Second, the institutional and contextual features of Part D and pharmaceutical decisions allow us to delve more deeply into examining how physicians act as “agents”. Ideally, if physicians act as “perfect agents” (Pauly 1980), they should make prescribing decisions considering out-of-pocket costs to the patient, taking into account the cost-sharing features or formulary of benefit design (e.g.. patients’ costs are lower if generic drugs are prescribed) of the patient’s health insurance plan. We estimate how physicians change prescribing patterns for those aged 65 and over before and after the adoption of Part D, compared to changes for those under age 65. In a separate dataset which contains information on the utilization of prescription drugs, we also estimate relative changes in the pattern of use of prescription drugs for those aged 65 and over before and after 2006. Similar magnitudes of the two estimates could indicate that observed changes in patients’ use of prescription drugs due to changes in cost-sharing may come more from physician behavior than from patient behavior.
Third, we analyze whether physicians might be “double agents”: agents not only for patients but also for pharmaceutical companies. Studies show that physicians may change their prescribing patterns in response to marketing efforts of pharmaceutical companies (Lurie et al. 1990; Engelberg et al. 2013; Sacks 2013). In the context of Part D implementation, pharmaceutical companies may increase their promotional activities (e.g. detailing, free samples). While historically it has been hard for pharmaceutical companies to compensate physicians directly for prescribing a particular drug (Stern & Trajtenberg 1998), physicians’ prescribing decisions may be affected by advertising levels for prescription drugs. However, since advertising efforts intensified only marginally after the adoption of Part D, we argue that our empirical strategy described below can difference out the impact from advertising levels simply by comparing the sample before and after 2006.4 We also perform several additional tests of whether physicians appear to act particularly in the interest of pharmaceutical companies, in terms of prescribing newer drugs or more brand-name drugs.
Fourth, we employ a combined difference-in-differences (DD) and regression discontinuity (RD) estimation strategy (DD-RD hereafter), an improvement over either DD or RD alone.5 The main idea of the DD-RD specification is to compare the outcome discontinuity at age 65 before the adoption of Part D to the outcome discontinuity at age 65 after its adoption. Using restricted NAMCS data allowed us to identify the exact age (in days) of a patient at the time of a physician office visit. The DD-RD specification relaxes the stringent assumptions underlying the DD and RD methods. Compared to DD, DD-RD allows treatment and control groups to have different trends in outcomes by including controls for the running variable, patients’ age at the time of visit, as a flexible polynomial function and interacting with the treatment variable (year 2006 or later). Additionally, we can estimate the effect of Part D by comparing the effect of turning 65 before and after 2006, since the confounding effect of Medicare eligibility for most individuals at at age 65 that would plague RD estimation can be differenced out, assuming that the effect of overall Medicare eligibility on the use of medical care is the same before and after 2006. We perform an extensive list of robustness checks in order to ensure that all assumptions of the DD-RD specification are met in our sample. In addition, we use supplementary datasets to examine the impact of Part D on patients’ utilization of and expenditure on prescription drugs.
Fifth, this paper contributes to a growing literature that evaluates the various effects of Part D, an important national health program accounting for a substantial fraction of health care spending.6 Most existing studies focus on the effect of Part D on the use and out-of-pocket cost of prescription drugs (Lichtenberg & Sun 2007; Yin et al. 2008; Briesacher et al. 2011; Ketcham & Simon 2008; Engelhardt & Gruber 2011; Liu et al. 2011; Kaestner & Khan 2012), the utilization of non-drug health care services (Engelhardt & Gruber 2011; Liu et al. 2011; Kaestner & Khan 2012; Zhang et al. 2009; Kaestner et al. 2014), drug prices (Duggan & Morton 2010; Duggan & Morton 2011), and pharmaceutical companies’ R&D spending (Blume-Kohout & Sood 2013). The effect of Part D on physician prescribing behaviors has received almost no attention in previous work despite the fact that is a potential mechanism behind any changes in prescription drug consumption or the use of other health care services. For this reason, the extent to which physicians tailor their prescribing to insurance coverage after Part D is a fundamental, policy-relevant question that merits thorough examination.
Finally, this paper adds to a broader literature on physician incentives. A number of empirical studies have shown that physicians respond to a change in financial incentives by changing their practice of medicine, including their treatment choice (Gruber & Owings 1996), hospital referral patterns (Ho & Pakes 2013), or provision of elective procedures and adoption of technology (Clemens & Gottlieb 2014). In the context of prescription drugs, previous studies also show that physicians respond to markups of drugs in countries where prescribing and dispensing drugs are not separate functions (Iizuka 2012; Iizuka 2007; Liu et al. 2009; Lu 2014; Nguyen 2011). However, relatively few empirical studies have documented the response of physicians to non-pecuniary incentives, in part because of the difficulty in observing changes in non-pecuniary incentives.7 The Part D setting introduces an arguably exogenous change that enables us to study the effect of non-financial incentives on physicians’ behavior.
2. Background on Medicare Part D
Prior to the passage of the Medicare Prescription Drug, Improvement, and Modernization Act of 2003 (MMA 2003), Medicare had only two fee-for-service components, Part A and Part B, and one managed care component, Part C. Parts A and B are plans for inpatient and outpatient care and related medical services, with no comprehensive prescription drug coverage. Prior to Part D, some Medicare beneficiaries obtained drug coverage through employer-sponsored plans, Medicare HMO plans, Medigap plans, Medicaid plans, and state Pharmacy Assistance programs, though some sources of coverage had restrictive terms or high copayments. And in 2003, about 27% of seniors aged 65 and above lacked any source of insurance coverage for prescription drugs. Because of the lack of drug coverage, many beneficiaries were paying for prescription drugs out-of-pocket, and out-of-pocket costs for prescription drugs were increasing faster than for other types of health care services. Medicare beneficiaries paid $644 out-of-pocket for prescription drugs in 2000 on average, rising to $996 in 2003 (The Henry J. Kaiser Family Foundation 2003).
In order to ensure access to prescription drugs and to limit the financial burden associated with prescription drug costs, Medicare Part D was created as part of the MMA 2003, and went into effect on January 1, 2006. Under Part D, eligible persons can participate voluntarily by enrolling in one of two types of private insurance plans in their area of residence: a Prescription Drug Plan (PDP) that covers only prescription drugs, or a Medicare Advantage-Prescription Drug Plan (MA-PD) that covers both medical services and prescription drugs.8
The adoption of Part D affected Medicare beneficiaries in several ways. First, it resulted in sharp changes in prescription drug coverage for those aged 65 and over after compared to before 2006. Although it is voluntary for Medicare beneficiaries to enroll in a Part D plan, about 53% of Medicare beneficiaries were enrolled in Part D plans in 2006. Seniors had an incentive to enroll if they had no plan prior to Part D or if they had a plan whose coverage was not as good as the coverage offered under Part D. ( Beneficiaries could keep their previousplan as long as the coverage for prescription drugs was at least as comprehensive compared to a standard plan under Part D, in which case the previous plan is considered creditable.) Only dual-eligible beneficiaries -- those Medicare beneficiaries who are also Medicaid recipients -- are automatically enrolled in Part D plans. After the initial enrollment period, the enrollment numbers continued to grow, reaching around 60% in 2010 (The Henry J. Kaiser Family Foundation 2010). The percentage of Medicare beneficiaries without any drug coverage decreased from 19% in 2002 to 10% in June 2006. To avoid the problem of adverse selection, Medicare beneficiaries were charged a financial penalty if they joined the program after May 15, 2006 unless they were able to demonstrate that they had access to creditable coverage elsewhere. This rule ensured that transition into drug coverage plans for seniors happened quickly in 2006.
Part D substantially decreased the out-of-pocket (OOP) costs of prescription drugs for patients aged 65 and older relative to patients under age 65 after 2006 compared to before 2006 (Lichtenberg & Sun 2007; Yin et al. 2008; Briesacher et al. 2011; Ketcham & Simon 2008; Engelhardt & Gruber 2011; Liu et al. 2011; Kaestner & Khan 2012). Medicare subsidizes the cost of plan coverage for all types of beneficiaries through various types of plan subsidies, including direct subsidies, individual reinsurance, risk sharing payments, and low-income subsidies. These subsidies target costs of prescription drugs at various stages of plan coverage, or for specific beneficiaries. For example, direct subsidies reimburse plans for the cost during the initial coverage period; individual reinsurance reimburses plans for the cost during periods of catastrophic coverage; and risk-sharing payments finance unexpectedly high costs to help with plans’ potential losses.9 The low income subsidy helps with premium and prescription drug costs for those who are eligible for Medicaid or those with income under 150% of the federal poverty line.10 As a result, Medicare subsidizes about 75 percent of the cost of standard drug coverage on average.
Last but not least, plans often set their own formulary, which is a tiered structure with different levels of cost sharing across therapeutically similar drugs. Since generic drugs are bioequivalent to, but much less expensive than, their brand name counterparts, private insurers administering Part D plans adopt various formulary and benefit designs to steer enrollees toward less-expensive generic alternatives.11 Plans often place generics on a tier of formulary with the lowest copayment, preferred brand-name drugs are on a tier with a higher copayment, and non-preferred brand name drugs are on a tier with the highest copayment.12 Through design of plan formularies, Part D plans thus encourages the use of generic drugs, in order to help control costs in the plan and to provide a competitive enough premium to attract potential consumers.
3. Physician Model
In this section, we develop a model of physician treatment decisions during patient visits, in a fashion similar to the work in Acemoglu & Finkelstein (2008). Our model allows us to study whether the expansion of drug coverage is theoretically likely to result in a change in physician prescribing behavior of the provision of other health care services.
A. Set Up of the Model
We model the physician-patient relationship as a single period interaction. The patient visits the doctor’s office, and the doctor uses diagnostic skills and information from various sources about patients’ insurance coverage, as well as about drugs from pharmaceutical companies, to make treatment decisions. Then the doctor writes a prescription.
Assume the physician cares about patients’ utility. The physician’s utility function during this one-time interaction can be written as:
| (1) |
where represents the number of drug treatments for patient , is the effort level physicians make to treat the patient, and Ti is the quantity of other medical care services performed in the physician’s office for patient .13 is a production function, producing health from inputs of prescription drugs, other medical care services, and physician effort. We assume that is increasing in all three inputs and is twice continuously differentiable for positive levels of input. Health enters positively into patients’ utility functions and each unit of health is worth . The list price of each unit of prescription drugs and other medical care services are Pd and Pt, respectively. Although the generosity of coverage is different, patients only need to pay a fraction of the list price for both prescription drugs and other medical care services. The fraction for prescription drugs is kd and for other services is kt.
In Eq. (1), physicians’ effort level is typically not observable to patients. If physicians are perfect agents, they will not only attend to their patients’ health needs but also tailor treatment plans to a patient’s financial circumstances. To achieve these goals, physicians will need to acquire the necessary knowledge or information about relevant insurance policies, formularies, and drug pharmacology. The optimal level of physician effort occurs when the marginal benefit of A is equal to zero. Nevertheless, when effort levels are hard to observe, physicians may instead choose to act as perfect agents along a dimension that is observable to patients. We will discuss physician effort levels in more detail in Section 3.C.
B. Physician Choice About Drug Prescribing and Other Treatment Decisions
The adoption of Part D lowers the OOP cost of prescription drugs for Medicare patients. Specifically, the out-of-pocket cost fraction of prescription drugs, kd, decreases. Thus, we can analyze the effect of the adoption of Part D policy as comparative statics of kd. Given the objective function Eq. (1), we have the following propositions (proofs are shown in Appendix B):
PROPOSITION 1: Let and be the optimal choices for patient at the copay kd. Then .
PROPOSITION 2: Assuming to be homogeneous of degree in and , we can get , in which exhibits constant returns to scale. Let the local elasticity of substitution between drug and non-drug treatment be . Thus we have if and only if .
Proposition 1 implies that when the copay for drug treatment decreases for a certain patient, physicians increase the quantity of prescription drugs prescribed, that is, . However, the quantity of other health care provided could increase, decrease, or stay the same, depending on the relative size of “decreasing returns” to scale () and the elasticity of substitution between prescription drugs and other services () (Proposition 2). For example, if , i.e., the two types of treatments are complementary in the health production function, then the quantity of other services will increase as the copayment for prescription drugs decreases. If and , then there is enough substitutability between the two services and the quantity of other services will decrease.
C. Physician Prescription of Generic Drugs
To analyze the effect of Part D on physicians’ prescription of generic drugs, we separate prescribed drugs in Eq. (1) into two categories – generic and branded drugs-- assuming physicians prescribe units of generic drugs and units of branded drugs. The OOP cost fraction of the price patients need to pay for generic drugs is and for branded drugs is . To simplify exposition without the loss of generality, we leave T out of the equation. Then the objective function can be written as
| (2) |
PROPOSITION 3: Assuming to be homothetic in and , then the move from less generous prescription drug coverage to more generous drug coverage may affect the generic-branded drug ratio. Using and to indicate the number of prescribed generic and branded drugs after the adoption of Part D, we have
Proposition 3 implies that when the relative generosity of insurance coverage for generic and branded drugs changes, the ratio of generic drugs and branded name drugs in physicians’ prescriptions will change as well. Specifically, when Part D increases the generosity of coverage for generic drugs more than for branded drugs-- that is, the OOP cost fraction for generic drugs decreases more than that for branded drugs, , the result will be that the prescription of generic drugs increases more than that of branded drugs, i.e.., . (Otherwise, if the copayment was higher for generic than branded drugs, then the prescription of generic drugs would increase less than that for branded drugs .)
D. The Impact of Part D on Physician (Non-Observable) Effort
Previously, we assumed that physicians’ efforts to acquire the necessary knowledge to make a treatment decision incurred no cost. We relax this assumption here denoting the cost as , where is convex and monotonic. Together with equation (1), the optimal prescription decision and the optimal effort level (denoted as ) will be characterized by the first order conditions: and .
Suppose physicians do not act as perfect agents and maximize their own utility, , where is patients’ utility, denoted by equation (1). We assume , indicating that physicians are not purely altruistic. Thus, to make a treatment decision, physicians maximize the objective function: . The optimal drug prescription D will be characterized by the same first-order condition as equation (1).14 The optimal effort level (denoted as ) will be characterized by . The optimal effort level is lower than , because the marginal benefit is smaller. That is, when physicians do not act as perfect agents, effort is less and physicians may not respond to Part D by changing prescription behavior to better tailor toward patients’ changed OOP costs.
4. Data
Our main analyses use the National Ambulatory Medical Care Surveys (NAMCS) 2002–2004 and 2006–200915 to estimate the impact of Medicare Part D on physicians’ prescribing patterns. The NAMCS is conducted by the National Center for Health Statistics. It collects data on a nationally-representative sample of visits to non-federally employed office-based physicians in the U.S., excluding radiologists, anesthesiologists, and pathologists. To select physicians for interview, NAMCS uses a multistage probability sample design; this design is described elsewhere (Bryant & Shimizu 1988). Each physician in the sample is randomly assigned to a one-week reporting period, and information on a systematic random sample of about 30 visits is then collected. Physicians and patients may be selected multiple times, but there is no identification number to link either patients or physicians longitudinally. Each physician is asked to record information on up to eight drugs (six drugs in 2002) that were ordered, supplied, administered, or continued during the single visit. Prescription drugs, over-the-counter drugs, immunizations, allergy shots, anesthetics, chemotherapy, and dietary supplements are included.16
We first examine prescribing patterns as measured by the number of drugs prescribed or continued during a NAMCS visit. NAMCS has 27,973 visit records for patients aged 60–69 years old for the sample period 2002–2004 and 2006–2009. We limit the sample to 26,474 visits (9,737 for 2002–2004 and 16,737 for 2006–2009), excluding 1,509 (5.39%) visits for patients who have missing information on any variable used in the analyses.17 We also consider prescribing patterns as measured by the number of drugs prescribed that have a generic equivalent. We do this by combining information on drugs prescribed in the NAMCS with information from the Food and Drug Administration (FDA) Orange Book database containing generic status, as well as date of drug approval.18 Our definition of generic status therefore consists of a measure of whether or not a generic version of the relevant active ingredient exists.19 We also use prescription-level data to test whether any increase in prescribing occurs particularly for new drugs likely to be the most heavily marketed by pharmaceutical companies. For drugs with different manufacturers, strengths, or packages, we merge the earliest date of FDA approval for the active ingredient contained in the drug and application type onto the NAMCS data.20 We use the earliest date of approval for the active ingredient since we have no information about drug formulation in the NAMCS. Although some formulation changes may bring about significant improvements in drug delivery, others may be small changes such as a change from pill to liquid form. Since previous research finds a strong overall correlation between initial drug approval (of an active ingredient) and pharmaceutical investment and advertising (CBO 2009, Vakratsas and Ambler 1999, Roth 1996), we therefore use the earliest date of approval. We use the drug name for merging since there are no other variables available that identify drugs in both the NAMCS data and the FDA data. We exclude over-the counter (OTC) drugs from our analyses using drug information from the NAMCS. After excluding both OTC and injectable drugs, the merge rate between the NAMCS and FDA data is 95%. (Most of the non-merged drugs were approved prior to 1982 since the FDA orange book only contains approval dates for drugs approved since 1982.) (The NAMCS data contain no information on dosage.) Thus, we examine the effect of the introduction of Medicare Part D on the overall number of drugs prescribed or continued, the number prescribed or continued that have generic equivalents, and the age of drugs prescribed or continued. For this last variable, our prescription-level sample has 54,132 observations for patients aged 60–69.
The NAMCS data also include information on patients’ demographic characteristics, such as gender, race, and diagnosis categories defined by ICD-9 codes, and on physician characteristics including metropolitan statistical area (MSA) status, whether theirs is a solo practice or not, their adoption of electronic medical records, specialty categories, and state of practice. We control for these variables as covariates in our specification. Sample statistics for our control variables are listed in Table A2.
Although our main dataset is the NAMCS, we also use the 2002–2004 and 2006–2009 Medical Expenditure Panel Survey (MEPS), a nationally-representative survey of respondents drawn from the National Health Interview Survey, to examine the impact of Part D on patients’ utilization of and expenditure on prescription drugs. Although patients are required to have a physician’s prescription before a drug can be dispensed, they typically can decide whether or not to fill the prescription. To some extent, patients’ compliance may reflect the extent to which their interests are aligned with physicians’ objective functions (equation 1). Thus, if patients increase drug utilization after Part D by nearly as much as prescriptions increase, this may suggest that physician responses are aligned with patients’ preferences (as far as they can detect).
MEPS is a two-year panel with information on the number of prescriptions filled, total expenditure for prescription drugs, and expenditure for drugs from different sources, such as self-pay (OOP costs), Medicare, Medicaid, or private sources. For independent variables, we control for patients’ gender, race/ethnicity, poverty category, census region, MSA status, education level, marital status, and prior health conditions.21 Sample statistics are reported in Table A3. After excluding observations with any missing information on the variables we use, we are left with 276,774 observations for the group of respondents aged 60–69.
5. Empirical Strategy
We propose an empirical approach that combines DD and RD (we call this specification DD-RD hereafter) in order to identify the average treatment effect of Medicare Part D, implemented on January 1, 2006, for individuals aged 65 and over.
The difference-in-difference (DD) approach is a commonly-used strategy to identify treatment effects. In the context of this paper, we use it to estimate the effect of a certain policy by exploiting relative changes in prescription drug utilization by patients aged 65 and older (i.e., those aged 65–69, the treatment group) who visited physicians’ offices before and after January 1, 2006, compared to those of patients under age 65 (i.e., those aged 60–64, the control group) who visited physicians’ offices before and after January 1, 2006.
One weakness of the DD approach is that it assumes that trends in prescribing patterns are the same for both the treatment and control groups prior to policy implementation, so that the DD estimator identifies only the effect of Part D. However, trends in prescribing patterns are likely to differ by patient age, which makes them differ for treatment and control groups.22 In some past literature, the DD approach took this difference into account by limiting the sample to a narrow age range, but this does not fully address the issue or verify the validity of the basic assumptions of the DD model. The validity of the assumption of equal prescription trends for treatment and control groups prior to policy implementation is even more questionable due to the possibility of anticipatory effects, as we will discuss in Section 6.C,
A second empirical approach, more popular in recent policy analyses, is the regression discontinuity (RD) design. Here, the main idea is to compare the change in outcomes for patients who are just before and just after age 65, using only data from after policy adoption (Card et al. 2009). For the RD design, the key assumption is that assignment to either side of the discontinuity threshold is as good as random (Lee & Lemieux 2010). Unfortunately, as mentioned earlier, there is a confounding policy discontinuity at the age 65 cutoff. Most individuals become eligible for Part D and for inpatient and outpatient coverage at age 65 because they also become eligible for Medicare Parts A and B. If we adopted the RD specification to analyze the effect of Part D, then it would violate the RD assumption that potential outcomes are continuous in the absence of treatment. Thus it would be difficult to disentangle the impact of Part D policy from the impact of Medicare eligibility more generally, due to the confounding effect of Medicare eligibility that occurs for most individuals at age 65.
When we combine the two strategies and use the DD-RD specification, we essentially estimate the discontinuities in outcomes beginning in 2006 for those aged 65 to 69 as compared to those aged 60 to 64. The estimation equation is as follows:
| (5) |
where Outcomeij is the outcome (number of drugs prescribed or continued, number of drugs with a generic equivalent prescribed or continued, number of drugs without a generic equivalent prescribed or continued, etc.) for patient i seen by physician j; 1(age>=65)i is an indicator for whether patient i is aged 65 or older, and the variable 1(year>=2006)i indicates whether the visit takes place on or after January 1, 2006. The specification includes control variables for patient characteristics, Xi (gender, race, year the visit took place, seasonal fixed effect, Charlson index23, and dummies for the major diagnostic category associated with the visit24), physician practice characteristics, Yj (specialty of the physician25, whether the physician is in a solo practice or uses electronic medical records, whether the practice is within a metropolitan statistical area, and percentage of revenue from Medicare patients), and state fixed effects Statej, which control for any time-invariant characteristics of physician practice patterns in different states. We estimate the equation using ordinary least squares (OLS).26 All analyses use sample weights, and standard errors account for the complex design of the NAMCS survey using Stata software version 12 (Stata-Corp, College Station, Texas).
In order to best model physician prescribing patterns by patients’ age, we take advantage of the exact dates of birth in the NAMCS data. Accordingly, Agei is the number of days between the patient’s age at visit and his/her 65th birthday. We include g(Agei),which is a flexible polynomial function of Agei fully interacted with age 65 and year 2006 dummies. By including g(Agei), we allow prescribing patterns to take different forms on either side of the age 65 cutoff, before and after year 2006. Our basic specification uses a cubic form for age in the analysis of NAMCS data.27 Daysi is the number of days between the visit date and December 31, 2001, the beginning of our sample period. By using exact dates of visits in the NAMCS data and including g(Daysi), a flexible polynomial function of Daysi and their interaction terms with the year 2006 dummy, we can also more precisely model trends in physician prescribing patterns over time, while still allowing for the discrete change at the time of adoption of the policy.
The identification strategy we present here requires less stringent assumptions than the RD or the DD specifications. We do not require that the treatment and control groups experience the same trend in outcomes in the absence of policy adoption, nor do we require that all other patients and practice characteristics be continuous across the age 65 threshold. The only two assumptions required by this specification are:
The confounding discontinuities must be time-invariant. This is equivalent to the RD condition about continuity of potential outcomes; and
The treatment effect and the confounding effect are additive. This is equivalent to the additivity conditions in the DD specification (Grembi et al. 2011).
Under the identifying assumption that other determinants of prescribing patterns are continuous at the age 65 cutoff (defined by whether patients are at least at their 65th birthday when they visit the physician), both before and after year 2006, the coefficient of the interaction of the age 65 dummy and the year 2006 dummy (β3 in Equation (5)) will be an unbiased DD-RD estimate of the effect of Part D on outcomes.
The DD-RD design enables us to identify the treatment effect while addressing the internal validity issue that was discussed for the DD specification. The intuition is that the confounding policy, which is Medicare program eligibility for most individuals at age 65, is time-invariant in the sample period. We can estimate this discontinuity prior to the adoption of Part D, and subtract that effect from the estimated discontinuity after the adoption of Part D. As long as the discontinuity resulting from the confounding policy is constant, we can address the confounding issue using the DD-RD specification.
In addition to visit-level regressions, we perform prescription-level regressions to see whether the age of the active ingredient contained in drugs prescribed or continued by physicians changed beginning in 2006. The dependent variable is AgeDrugijk (age of the active ingredient contained in the drug, measured in months between time of visit to the physicians’ office and date of FDA approval). We include all controls from Equation (5); we also add fixed effects for primary drug class categories.28
We test the validity of assumptions for the DD-RD specification and the robustness of results in a number of ways. First, we check the density of the running variable Agei around the age 65 cutoff, both before and after year 2006, in order to test whether the eligibility criteria is manipulated around the threshold (McCrary 2008). Second, we estimate specifications using different age bandwidths and different orders of polynomial functions of age, both with and without covariates. Third, we implement the DD-RD specification with covariates as outcomes in order to validate the basic assumption of the DD-RD specification: that all underlying characteristics are smooth around the age 65 threshold in the absence of the treatment. Fourth, we implement a placebo DD-RD estimation at an arbitrary cutoff defined as age 64 and above.
6. The Impact of Part D on Physicians’ Prescribing Patterns
A. Graphical Evidence
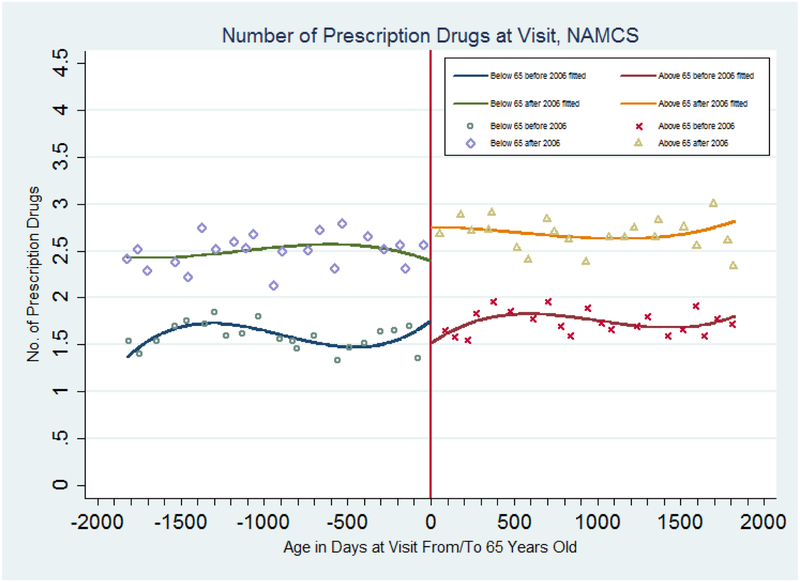
We first present graphical evidence of the impact of Part D on physician prescribing behavior, using NAMCS data. Figure 1 plots the mean for the number of prescription drugs prescribed or continued by physicians by age per quarter, as well as the fitted age profiles from regressions that include cubic terms in age (in days from/to 65th birthday), and full interactions with age 65 and year 2006 dummies. There is a small but noticeable decrease in the number of drugs prescribed or continued when patients turn 65 for the 2002–2004 sample. (A statistical test of the difference in the jumps at age 65 for the 2006–2009 relative to the 2002–2004 samples in Figure 1 is contained in the top panel of Table 1 (first column, model without covariates) and discussed below.) After the adoption of Part D, the average number of drugs prescribed or continued per patient increases from 2.4 prescriptions for patients under 65 to around 2.7 prescriptions when patients turn 65.
Figure 1: Number of Drugs Prescribed of Continued During a Physician Visit, NAMCS 2002–2004 and 2006–2009.
Note: Samples are based on data from the National Ambulatory Medical Care Survey (2002–2004 and 2005–2009). The estimated discontinuities (and standard errors) at age 65 and the fitted lines are from a regression with a cubic polynomial in age fully interacted with a dummy for age greater than or equal to 65 and a dummy for year in or after 2006. Points represent means for people in each age cell (measured in quarters).
Table 1:
Regression Results for Prescribing Patterns, NAMCS 2002–2004 and 2006–2009
| Number of Drugs Prescribed or Continued During Physician Visits | Number with Generic Equivalents | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| DD-RD | Before 2006 | After 2006 | DD-RD | DD-RD | DD-RD | Before 2006 | After 2006 | DD-RD | DD-RD | ||
| Panel A: sample without 2005 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | |
| Age 65 * Year 2006 | 0.606* | −0.286 | 0.292* | 0.563** | 0.621** | 0.260* | 0.025 | 0.265*** | 0.256** | 0.318** | |
| (0.310) | (0.226) | (0.155) | (0.267) | (0.310) | (0.137) | (0.099) | (0.086) | (0.127) | (0.155) | ||
| Covariates | No | Yes | Yes | Yes | Yes | No | Yes | Yes | Yes | Yes | |
| Order of Polynomial | 3 | 3 | 3 | 3 | 4 | 3 | 3 | 3 | 3 | 4 | |
| R-squared | 0.041 | 0.187 | 0.189 | 0.204 | 0.204 | 0.054 | 0.123 | 0.136 | 0.161 | 0.161 | |
| Observations | 26,474 | 9,737 | 16,737 | 26,474 | 26,474 | 26,474 | 9,737 | 16,737 | 26,474 | 26,474 | |
| Panel B: sample with 2005 | |||||||||||
| Age 65 * Year 2006 | 0.770*** | −0.397** | 0.292* | 0.715*** | 0.628** | 0.465*** | −0.134 | 0.265*** | 0.425*** | 0.423*** | |
| (0.285) | (0.188) | (0.155) | (0.253) | (0.274) | (0.139) | (0.097) | (0.086) | (0.130) | (0.162) | ||
| Covariates | No | Yes | Yes | Yes | Yes | No | Yes | Yes | Yes | Yes | |
| Order of Polynomial | 3 | 3 | 3 | 3 | 4 | 3 | 3 | 3 | 3 | 4 | |
| R-squared | 0.035 | 0.190 | 0.189 | 0.203 | 0.204 | 0.050 | 0.124 | 0.136 | 0.158 | 0.158 | |
| Observations | 29,775 | 13,038 | 16,737 | 29,775 | 29,775 | 29,775 | 13,038 | 16,737 | 29,775 | 29,775 | |
Control variables for all regressions include a dummy for year 2006 or later, age 65 or over, a polynomial control of age in days and full interaction with the age 65 dummy and year2006 dummy.
Additionally, specifications with covariates include patient sex, race, Charlson index dummies, disease category by primary diagnosis codes, visit quarter, physician specialty type, whether it is a solo practice or not, electronic medical records utilization (yes or no), metropolitan statistical area (MSA) status and dummy for revenue from Medicare patients above median of the sample.
***Significant at the 1% level (two-tail test); ** Significant at the 5% level (two-tail test); * Significant at the 10% level (two-tail test).
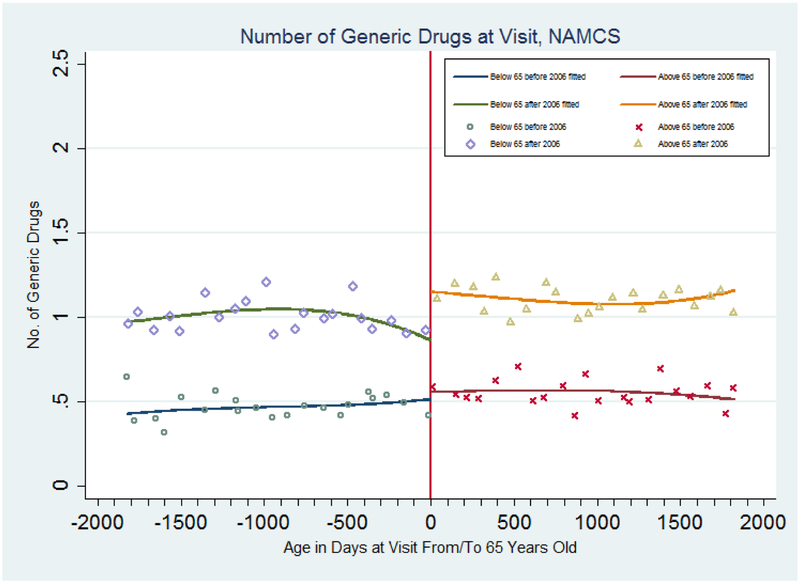
Figure 2 shows the mean for the number of drugs with a generic equivalent that physicians prescribe or continue per quarter by patient age and the fitted age profiles from regressions with a cubic function of age for each side of the age 65 and the year 2006 cutoffs. There is no discernible jump in the outcome from below age 65 to above age 65 before policy adoption. The average number of drugs with a generic equivalent prescribed or continued during patient visits does increase from 0.9 prescriptions to more than 1.2 prescriptions, or roughly a 0.3 prescription increase, after policy adoption. (A statistical test of the difference in the jumps at age 65 for the 2006–2009 relative to the 2002–2004 samples in Figure 2 is contained in the top panel of Table 1 (sixth column, model without covariates) and discussed below.)
Figure 2: Number of Drugs with A Generic Equivalent Prescribed or Continued During a Physician Visit, NAMCS 2002–2004 and 2006–2009.
Note: Samples are based on data from the National Ambulatory Medical Care Survey (2002–2004 and 2005–2009). The estimated discontinuities (and standard errors) at age 65 and the fitted lines are from a regression with a cubic polynomial in age fully interacted with a dummy for age greater than or equal to 65 and a dummy for year in or after 2006. Points represent means for people in each age cell (measured in quarters).
B. Regression Results
In the top panel of Table 1, we summarize the regression estimates of the change in the number of all prescription drugs and drugs with a generic equivalent prescribed or continued.29 The first column is the DD-RD specification without any covariates, allowing for a cubic functions of age on either side of the 65 and year 2006 cutoffs. The coefficient on the interaction term between the age 65 dummy and the year 2006 dummy is positive and significant. This indicates that there is a 0.61 prescription increase for patients aged 65 and above relative to patients under age 65 after adoption of the Part D policy.
Next we separate the 2002–2004 and the 2006–2009 samples and run a conventional RD regression with each. The results are shown in the second and third columns of the top panel. For the regression using the sample after 2006, the coefficient of interest is positive and significant, implying that there is a 0.3 prescription increase for patients aged 65 and above. This increase is similar in magnitude to that of the discontinuity from Figure 1. For the 2002–2004 sample, the RD coefficient is negative with a magnitude of 0.29 prescriptions. This implies that before the adoption of the Part D policy, the number of drugs prescribed or continued at physician visits decreased discontinuously at age 65. That negative coefficient may reflect the fact that patients aged 65 and above were likely to lose their prescription drug coverage from employer-sponsored insurance or other public/private coverage at age 65. Subtracting the estimated effect for the sample before 2006 from the effect for the sample after 2006, we find a 0.6 prescription change for the group of patients aged 65 and above relative to patients under age 65 after the adoption of Part D.
In the fourth column, the estimated DD-RD coefficient is slightly lower after controlling for covariates than the estimate without controls, but is still significant with a 0.56 prescription increase. This supports the assumption that there are no other changes occurring at age 65 in 2006 that are confounding our analysis. It also confirms our observation from Figure 1, that physicians increase their prescriptions (either new or continued) to patients aged 65 and above by 35 percent on average (calculated as 0.5625 divided by 1.5995, the mean for the number of drugs prescribed or continued for non- patients aged 65 and above before 2006 from Table A1) after the adoption of Part D, compared to drugs prescribed or continued for patients under age 65. The coefficient on the interaction term is still significant if we change the order of the polynomial function of age to a quartic function in column (5). Consistent results across different specifications imply that the estimated effect is robust to various functional forms for age, i.e., that the significance of estimates of the impact of Part D is not an artifact of how we specify the age control function.
Columns (6) - (10) summarize results for the number of generic drugs prescribed. In the top panel, the estimated result for the regression with a cubic function of age is positive and significant, indicating an increase of 0.26 prescriptions on average. This is similar to the magnitude of the increase shown in Figure 2. We find similar results with regressions using the 2006–2009 sample, using the DD-RD specification with controls and with higher order polynomial functions of age. This indicates that after the adoption of Part D, physicians are likely to increase the number of drugs with a generic equivalent prescribed or continued during visits among patients aged 65 and above relative to patients under age 65 by 55 percent (calculated as 0.2556 divided by 0.4676, the mean of number of drugs with a generic equivalent prescribed or continued during visits for patients under age 65 before 2006).
C. Anticipatory Effect
The bottom panel of Table 1 presents regression results for a sample that includes patients visiting physician offices in 2005. We find that the magnitudes of effects using the DD-RD specification, with or without covariates, are all greater than those in the top panel. After stratifying the sample according to the year 2006 cutoff and running separate regressions on the sample before and after 2006, we find that the estimated effect for the sample before 2006 is negative and significant for the number of drugs prescribed or continued. Comparing results in the second column of the bottom panel to those in the top panel, it is apparent that the difference comes from the decrease in the number of drugs prescribed or continued for patients aged 65 and above in 2005. It appears that those patients and their physicians anticipated the upcoming Part D policy and postponed or reduced the number of drugs prescribed or continued until the time that Part D coverage took effect. After we include the 2005 sample in the regression, we estimate that Part D results in physicians increasing the number of drugs with a generic equivalent prescribed or continued for patients aged 65 and above by 45 percent, a more than 28 percent greater effect than comes from our previous DD-RD estimation. This effect is similar in size to the anticipatory effect found in Alpert (2012). There is also evidence that this anticipatory effect exists for the number of drugs with a generic equivalent prescribed or continued.
D. Validity of Specifications and Robustness Checks
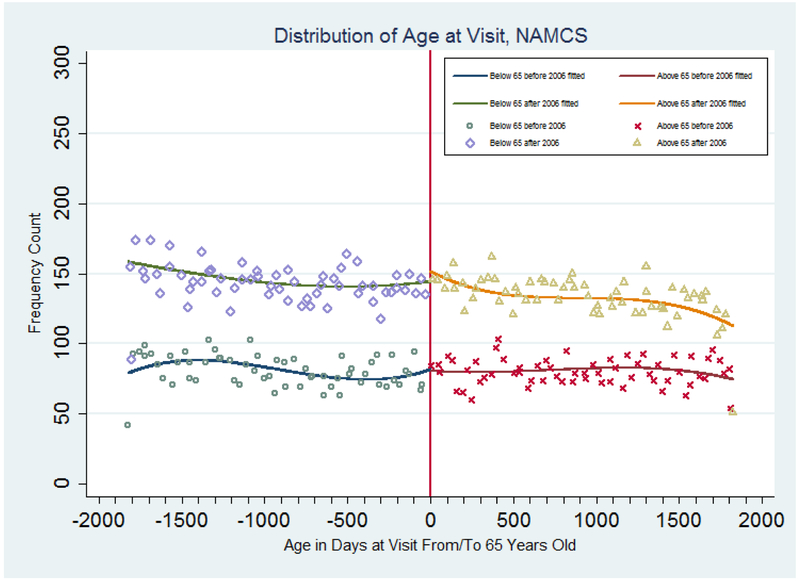
This subsection describes our test of the assumptions of the DD-RD specification, and the sensitivity analyses we performed in order to check the robustness of our main results. First, we graphically examined the evidence for sample selection bias in our specification. With the RD design, sample selection bias is a major threat to identification, because the estimated effect may reflect the change in the composition of the sample, not the effect of the policy adoption itself. In our context, if the sample before and after the age 65 cut-off was different before and after 2006, then our estimates of the DD-RD specification would be biased. In order to validate the null hypothesis of continuity of the age profile at the age 65 cutoff for the 2002–2004 and the 2006–2009 samples, Figure 3 shows scatter plots and fitted cubic age polynomial regression results. If patients were less likely to go to their physicians’ office just before they became eligible for Part D coverage and were more likely to go after they became eligible then our estimates would suffer from selection bias. Figure 3 instead supports our assumption and shows no sign of such bias. There is not much difference in visit density at the age 65 cutoff between the 2002–2004 and the 2006–2009 sample. As a matter of fact, patients have little incentive to change their frequency of visits to their physicians’ office, because patients aged 65 and above are usually eligible for Medicare coverage of physician visits, while patients under age 65 are infrequently eligible for Medicare coverage of physician visits.
Figure 3: Distribution of Patient Age at Physician Visits, NAMCS 2002–2004 and 2006–2009.
Note: Samples are based on data from the National Ambulatory Medical Care Survey (2002–2004 and 2005–2009). The estimated discontinuities (and standard errors) at age 65 and the fitted lines are from a regression with a cubic polynomial in age fully interacted with a dummy for age greater than or equal to 65 and a dummy for year in or after 2006. Points represent means for people in each age cell (measured in quarters).
Second, we check whether covariates are distributed smoothly across the age 65 cutoffs for both samples before and after 2006 to further look for selection bias. We estimate a DD-RD specified model with the covariates as outcome variables. Our results are summarized in Table 2. All but one variable show no differential jump at the age 65 cutoffs between the two time periods. The coefficient for the race indicator-- that is, the non-white dummy -- is only significant at 10%, and excluding this variable does not affect our basic results in the main analyses.30 These results further validate our assumptions for the DD-RD specification and reduce the possibility of omitted variable bias.
Table 2:
Robustness Checks, DD-RD Estimates for Covariates, NAMCS 2002–2004 and 2006–2009
| Female | Nonwhite | Charlson Index=1 | Charlson Index=2 | MSA Status | Solo Practice | EMR | |
|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| Age 65 * Year 2006 | 0.049 | −0.073* | 0.042 | 0.005 | 0.037 | −0.051 | 0.078 |
| (0.073) | (0.042) | (0.034) | (0.035) | (0.045) | (0.065) | (0.066) | |
| Order of Polynomial | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| R-squared | 0.002 | 0.002 | 0.003 | 0.001 | 0.004 | 0.005 | 0.075 |
| Observations | 26,474 | 26,474 | 26,474 | 26,474 | 26,474 | 26,474 | 26,474 |
Control variables include a dummy for year 2006 or later, age 65 or over, a polynomial control for age in days and full interaction with the age 65 dummy and year2006 dummy. EMR indicates electronic medical record use.
In results not included here, we also test whether there is any confounding other physician and patient characteristics, including physician specialty, patient major disease categories, and seasonal dummies.
***Significant at the 1% level (two-tail test); ** Significant at the 5% level (two-tail test); * Significant at the 10% level (two-tail test).
Next, we test the robustness of our main results by estimating the DD-RD model using different bandwidths, with and without covariates. The results are summarized in Table 3. We control for different polynomial functions of age in the samples with different bandwidths. In the first column, we control for age linearly with a bandwidth of one year on each side of the age 65 cutoff. In the second and third columns, we use quadratic and cubic age functions, with a bandwidth of two years on each side. The fourth column shows the results with a cubic age function and a bandwidth of three years. The fifth and sixth columns show the results with quartic age functions and bandwidths of five and six years on each side of the age 65 cutoff, respectively. All of the regression coefficients for the number of drugs prescribed or continued and the number of drugs with a generic equivalent prescribed or continued, with or without covariates, are significantly positive, with magnitudes similar to those shown in Table 1. We conclude that adoption of Part D leads to an increase in the number of drugs prescribed or continued during physician visits for patients beginning at age 65, especially drugs with a generic equivalent.
Table 3:
Robustness Checks, DD-RD Estimates for Different Bandwidths and Specifications, NAMCS 2002–2004 and 2006–2009
| Age 63–66 | Age 62–67 | Age 61–68 | Age 59–70 | Age 58–71 | ||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Number of Drugs Prescribed or Continued During Physician Visits | ||||||
| Panel A: without controls | ||||||
| Age 65 * Year 2006 | 0.500* | 0.508* | 0.694* | 0.683** | 0.840** | 0.594* |
| (0.269) | (0.293) | (0.390) | (0.325) | (0.358) | (0.317) | |
| R-squared | 0.045 | 0.041 | 0.042 | 0.042 | 0.041 | 0.042 |
| Panel B: with controls | ||||||
| Age 65 * Year 2006 | 0.460* | 0.512** | 0.583* | 0.664** | 0.784** | 0.587** |
| (0.235) | (0.257) | (0.336) | (0.284) | (0.309) | (0.277) | |
| R-squared | 0.216 | 0.210 | 0.211 | 0.207 | 0.201 | 0.198 |
| Order of Polynomial | 1 | 2 | 3 | 3 | 4 | 4 |
| Number of Drugs with Generic Equivalents Prescribed or Continued | ||||||
| Panel A: without controls | ||||||
| Age 65 * Year 2006 | 0.251** | 0.252* | 0.340* | 0.350** | 0.327** | 0.261* |
| (0.125) | (0.133) | (0.182) | (0.150) | (0.159) | (0.136) | |
| R-squared | 0.053 | 0.052 | 0.053 | 0.055 | 0.055 | 0.058 |
| Panel B: with controls | ||||||
| Age 65 * Year 2006 | 0.241** | 0.254** | 0.295* | 0.345** | 0.313** | 0.266** |
| (0.112) | (0.125) | (0.174) | (0.140) | (0.148) | (0.129) | |
| R-squared | 0.165 | 0.163 | 0.164 | 0.164 | 0.158 | 0.158 |
| Order of Polynomial | 1 | 2 | 3 | 3 | 4 | 4 |
| Observation | 10,538 | 15,772 | 15,772 | 21,072 | 31,898 | 37,400 |
We include in all regressions a dummy for year 2006 or later, age 65 or over, a polynomial control for age in days and full interaction with the age 65 dummy and year2006 dummy. Additionally, in panel B for both outcomes, we adjust for patient sex, race, Charlson index dummies, disease category by primary diagnosis codes, visit quarter, physician specialty type, whether it is a solo practice or not, electronic medical records utilization, metropolitan statistical area (MSA) status and dummy for revenue from Medicare patients above median.
***Significant at the 1% level (two-tail test); ** Significant at the 5% level (two-tail test); * Significant at the 10% level (two-tail test).
Finally, we conduct an extensive set of placebo tests for the main analysis sample (age 60–69), and for samples with varying bandwidths, ensure sure that our results represent a causal relationship rather than spurious correlation between Part D and outcomes. We set age 64 as the cutoff and estimate the DD-RD specification, with and without covariates, on all samples. Our results are summarized in Table 4. The results are statistically significant for only three out of 32 specifications, and only at the 10 percent levels. Thus the placebo test suggests that our results are not due to spurious correlation.
Table 4:
Robustness Checks, DD-RD Estimates for Number of Drugs Prescribed or Continued During Physician Visits With Placebo Cut-off, NAMCS 2002–2004 and 2006–2009
| Age 63–66 | Age 62–67 | Age 61–68 | Age 60–69 | Age 59–70 | Age 58–71 | |||
|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| Number of Drugs Prescribed or Continued | ||||||||
| Age 64 * Year 2006 | −0.141 | −0.418 | −0.310 | −0.541 | −0.302 | −0.719* | −0.341 | −0.550 |
| (0.301) | (0.344) | (0.406) | (0.363) | (0.332) | (0.393) | (0.373) | (0.349) | |
| R-squared | 0.043 | 0.041 | 0.042 | 0.041 | 0.040 | 0.041 | 0.041 | 0.042 |
| Age 64 * Year 2006 | −0.233 | −0.440 | −0.407 | −0.536 | −0.423 | −0.665* | −0.450 | −0.609* |
| (0.272) | (0.321) | (0.382) | (0.346) | (0.314) | (0.376) | (0.358) | (0.329) | |
| R-squared | 0.216 | 0.210 | 0.210 | 0.207 | 0.204 | 0.204 | 0.201 | 0.198 |
| Order of Polynomial | 1 | 2 | 3 | 3 | 3 | 4 | 4 | 4 |
| Number of Drugs with a Generic Equivalent Prescribed or Continued | ||||||||
| Age 64 * Year 2006 | −0.064 | −0.163 | −0.054 | −0.150 | −0.159 | −0.170 | −0.156 | −0.209 |
| (0.146) | (0.167) | (0.213) | (0.189) | (0.157) | (0.203) | (0.181) | (0.168) | |
| R-squared | 0.052 | 0.052 | 0.053 | 0.055 | 0.054 | 0.054 | 0.055 | 0.058 |
| Age 64 * Year 2006 | −0.084 | −0.149 | −0.082 | −0.133 | −0.187 | −0.130 | −0.166 | −0.220 |
| (0.139) | (0.162) | (0.206) | (0.183) | (0.154) | (0.202) | (0.178) | (0.164) | |
| R-squared | 0.164 | 0.163 | 0.164 | 0.164 | 0.161 | 0.161 | 0.158 | 0.158 |
| Order of Polynomial | 1 | 2 | 3 | 3 | 3 | 4 | 4 | 4 |
| Observation | 10,538 | 15,772 | 15,772 | 21,072 | 26,474 | 26,474 | 31,898 | 37,400 |
Control variables for regressions include a dummy for year 2006 or later, age 65 or over, a polynomial control for age in days and full interaction with the age 65 dummy and year2006 dummy, patient sex, race, Charlson index dummies, disease category by primary diagnosis codes, visit quarter, physician specialty type, whether it is a solo practice or not, electronic medical records utilization, metropolitan statistical area (MSA) status and dummy for revenue from Medicare patients above median.
***Significant at the 1% level (two-tail test); ** Significant at the 5% level (two-tail test); * Significant at the 10% level (two-tail test).
7. Is the Change in Prescriptions in the Best Interest of Patients?
Our basic results suggest that physicians do take patients’ cots into consideration and do respond to non-pecuniary incentives by increasing the number of drugs prescribed or continued during physician visits. In this section, we describe a series of supplementary analyses we conduct in order to evaluate other changes in physician practice patterns in physician offices and possible mechanisms for the documented increase in the number of drugs prescribed or continued.
A. Other Practice Pattern Changes
What effect does Part D have on practice patterns in office settings, other than prescription drug prescribing? We use the DD-RD specification again with cubic and quartic functions of age. Results are summarized in Table 5; those with a cubic polynomial of age are in the top panel, and those with a quartic polynomial of age are in the bottom panel.
Table 5:
Regression Results for Other Practice Patterns, NAMCS 2002–2004 and 2006–2009
| Number of Tests | Time Spent | Age of Active Ingredients | Number of Branded Drugs | |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Age 65 * Year 2006 | −0.052 | 2.892 | 4.861 | 0.307 |
| (0.123) | (1.788) | (9.654) | (0.226) | |
| Order of Polynomial | 3 | 3 | 3 | 3 |
| R-squared | 0.322 | 0.070 | N/A | 0.135 |
| Observations | 26,474 | 26,474 | 54,132 | 26,474 |
| Age 65 * Year 2006 | 0.006 | 4.332 | −9.639 | 0.302 |
| (0.150) | (2.748) | (11.519) | (0.272) | |
| Order of Polynomial | 4 | 4 | 4 | 4 |
| R-squared | 0.322 | 0.071 | N/A | 0.136 |
| Observations | 26,474 | 26,474 | 54,132 | 26,474 |
Control variables for regressions include a dummy for year 2006 or later, age 65 or over, a polynomial control for age in days and full interaction with the age 65 dummy and year2006 dummy, patient sex, race, Charlson index dummies, disease category by primary diagnosis codes, visit quarter, physician specialty type, whether it is a solo practice or not, electronic medical records utilization, metropolitan statistical area (MSA) status and dummy for revenue from Medicare patients above median.
The R-squared statistics is not available for regressions with the dependent variable consisting of the age of active ingredients because these are censored regressions; the date of approval for drugs in the Orange Book database is only available after 1982.
***Significant at the 1% level (two-tail test); ** Significant at the 5% level (two-tail test); * Significant at the 10% level (two-tail test).
First, we examine the effect of Part D on the number of tests 31conducted in the physicians’ office (column 1) and patients’ time spent with their doctor (column 2). These outcomes may be complementary measures of treatment intensity during a doctor’s visit. We find no significant effects of Part D on these two outcomes with either cubic or quartic polynomials in age as controls. This indicates that physicians do not change treatment patterns for their patients 65 and above in these other ways when their patients are more likely to have drug coverage. These results imply that laboratory tests or patients’ time spent with their doctor are neither complements nor substitutes for drug treatments (Proposition 2).
B. Perfect Agent for Patients or Pharmaceutical Companies?
So far, we have used the increase in drugs prescribed or continued during physician visits as evidence that physicians act as patients’ agents. However, if Medicare Part D increases pharmaceutical advertising (Lakdawalla et al. 2013), then it is possible that the increase in drugs prescribed or continued comes from the fact that physicians are acting in the interest of pharmaceutical companies. We cannot directly test the mechanism that drives physicians’ behaviors; nevertheless, we provide several pieces of evidence suggesting that physicians change their behavior more to do with the change in costs for patients than with the behavior of pharmaceutical companies.
First, we link NAMCS and US FDA Orange Book data to analyze the effect of Part D on the age of active ingredients of drugs prescribed or continued during physician visits. We find no significant results for this outcome, with either cubic or quartic polynomials in age as controls (column 3, Table 5). This suggests that physicians did not prescribe (or continue) newer (or older) drugs after the implementation of Part D. Nor do we find a significant impact of Part D on the number of brand-name drugs (i.e., drugs without a generic equivalent) prescribed or continued during physician visits (column 4, Table 5). If physicians act more in the interests of pharmaceutical companies than patients, then we would likely expect an increase in the number of new drugs or brand-name drugs prescribed or continued during physician visits. However, our results do not support that hypothesis.
Second, we use the 2002–2004 and 2006–2009 MEPS to examine the impact of Part D on patients’ utilization of and expenditure on prescription drugs, again using the DD-RD design. Although we don’t have specific date of birth and date of interview in the MEPS data, we are still able to control for a polynomial function of age in years at the time of interview. Results are reported in Table 6. These results are consistent for all outcomes, controlling for either a linear or quadratic function of age. The number of prescription drugs increases by a statistically significant 8.3 to 11.8 prescriptions per year on average. This means that patients increase their use of prescription drugs by 39–55 percent when they turn age 65 after the adoption of Part D as compared to before its adoption. Total expenditures on prescription drugs per individual per year and expenditures on prescription drugs from Medicare sources also increase at the age 65 cutoff after 2006, although the coefficients for the former outcome are not precisely estimated. OOP cost and the sign and magnitude of estimated effects are consistent with those in previous literature.32 However, our effects on these outcomes are not significant.33 Also, we find that Part D is associated with decreases in expenditures on prescription drugs from Medicaid and private sources. Overall, our results suggest that patients did increase drug utilization after Part D.
Table 6:
Regression Results for Utilization of and Expenditure on Prescription Drugs, MEPS 2002–2004 and 2006–2009
| Number of Rx Drugs | Exp for Rx Drugs | OOP cost per prescription | Rx Expense from Medicare Sources | Rx Expense from Medicaid Sources | Rx Expense from Private Sources | |
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Age 65 * Year 2006 | 8.289* | 727.553 | −0.835 | 986.473*** | −66.023 | −438.286 |
| (4.700) | (500.927) | (6.005) | (289.892) | (79.854) | (284.976) | |
| Order of Polynomial | 1 | 1 | 1 | 1 | 1 | 1 |
| R-squared | 0.281 | 0.153 | 0.025 | 0.115 | 0.087 | 0.077 |
| Observations | 16,931 | 16,931 | 16,931 | 16,931 | 16,931 | 16,931 |
| Age 65 * Year 2006 | 11.879** | 893.210 | −3.491 | 874.434*** | −70.948 | −274.355 |
| (5.200) | (556.599) | (6.741) | (311.782) | (109.848) | (320.956) | |
| Order of Polynomial | 2 | 2 | 2 | 2 | 2 | 2 |
| R-squared | 0.281 | 0.153 | 0.026 | 0.115 | 0.087 | 0.078 |
| Observations | 16,931 | 16,931 | 16,931 | 16,931 | 16,931 | 16,931 |
Control variables for regressions include a dummy for year 2006 or later, age 65 or over, a polynomial control for age in days and full interaction with the age 65 dummy and year2006 dummy, patient sex, race, poverty categories, census region dummies, education level categorical dummies, marital status dummies, prior medical conditions and metropolitan statistical area (MSA) status.
***Significant at the 1% level (two-tail test); ** Significant at the 5% level (two-tail test); * Significant at the 10% level (two-tail test).
Together, these results suggest that the introduction of Part D increased the number of drugs prescribed by physicians due to changes in patient OOP costs, and not most or mostly for drugs that are likely to be most profitable for pharmaceutical companies.
8. Conclusion and Discussion
In this paper, we examine the impact of insurance expansion on a specific physician behavior, prescribing drugs to patients. To exploit the considerable change in coverage of prescription drugs that resulted from the adoption of Medicare Part D, we compare physicians’ prescribing patterns for those who were eligible for Part D after 2006 to those who were not. Our results are consistent with physician consideration of patients’ interests since we find that they increased the number of drugs prescribed or continued during physician visits. Specifically, for each patient’s visit to a physician’s office, we estimate a 35% increase in the number of drugs prescribed or continued and a 55% increase in the number of drugs with a generic equivalent prescribed or continued following the implementation of Medicare Part D. We use a DD-RD specification to identify the effect of Part D on physician prescribing behavior, a robust identification strategy with the identifying assumption that other determinants of prescribing patterns are continuous at the age 65 cutoff before and after 2006, i.e., that other determinants of prescribing patterns do not change precisely at age 65 and precisely in 2006 for reasons other than the introduction of Medicare Part D. We also perform an extensive list of robustness checks to assure that all assumptions of the DD-RD specification are met in our sample. Together those results suggest that physicians take patients’ costs into consideration by increasing the number of drugs with a generic equivalent prescribed of continued during physician visits.
We also study whether physicians anticipated the upcoming drug coverage provided by Part D and thus deferred drug prescription until the time of its adoption, a possibility suggested by past literature. Specifically, we compare the estimated effect of Part D on prescription decisions for the sample period with and without the year 2005. Results with, compared to without, 2005 data suggest that ignoring the deferment of some prescriptions in 2005 would result in a more than 30% overestimation of the Part D effect. This is consistent with the magnitude of the estimated anticipatory effect in Alpert (2012), and provides additional evidence that physicians consider patients’ cost when prescribing drugs.
To address the issue that physicians may be affected by marketing efforts from pharmaceutical companies, we perform several additional analyses. First, we link the NAMCS and US FDA Orange Book data in order to analyze the effect of Part D on the age of active ingredients in drugs prescribed or continued during physician visits and whether drugs prescribed or continued have a generic equivalent. If physicians act primarily in the interest of pharmaceutical companies, then they might change their practice patterns based on new development of molecules and the advertising level for branded drugs. However, we find that physicians are no more likely to prescribe (or continue) newer drugs after Part D compared to before, nor are they more likely to increase prescriptions for brand-name drugs. We also use the MEPS to examine the impact of Part D on patients’ utilization of and expenditure on prescription drugs. Although physicians have the authority to prescribe drugs, they do not have the authority to force patients to comply. Patients’ compliance reflects their own interests or preferences; they decide whether to comply or not. If patients increase their drug utilization after Part D by nearly as much as the increase in the number of prescriptions, it suggests that physicians’ responses to it are broadly aligned with their patients’ interests as far as they can detect. Indeed, we find that utilization of prescription drugs per person per year rose by 39% after Part D, which is close to what we observe in the NAMCS data.34
However, there are caveats to our findings. We estimated the average effect of the adoption of Part D. Because around two-thirds of Medicare beneficiaries had access to drug coverage before 2006, the marginal effect of Part D on those who did not have prescription drug coverage before 2006 could be greater than what we estimated in this paper. Additionally, there may be spillover effects, as physicians may change their prescribing patterns for patients with insurance sources other than Medicare. Finally, although we find an increase in the number of drugs prescribed or continued during physician visits for those aged 65–69 after 2006 relative to a control group of patients aged 60–64, we do not distinguish whether the increase is in new prescriptions written or in increased continuation or renewal of prescriptions. These points may suggest possible directions for future research.
Acknowledgments
I thank Mary E. Deily and participants at the 2012 Eastern Economic Association Annual Meeting, 2012 American Society of Health Economists Conference, and seminars at Harvard University, University of Pennsylvania, the Johns Hopkins University and the National Center for Health Statistics, CDC. The findings and conclusions in this article are those of the authors and do not necessarily represent the views of the Centers for Disease Control and Prevention.
Appendix A: Description of the data-merging procedure
The FDA drug approval database was retrieved from: http://www.fda.gov/Drugs/InformationOnDrugs/ucm129689.htm (August, 2011).
Three zipped ASCII files were downloaded from the website. The one under the name products.txt was the one containing information about ingredient, dosage form, trader name, approval date and type (whether a prescription drug or not). We transferred the data into Stata format using StatTransfer. We cleaned the data to calculate the approval date for each drug, counting drugs with different manufacturers or strengths or packages as the same drug.
The NAMCS data has variables called MED1-MED8 (up to MED6 if before 2003). These variables are coded using a different coding system beginning in 2006, but with the SAS program (DRUGCHAR_MULTUM_`year’.sas) provided available from NCHS, one can update the coding for variables from NAMCS 2002–2005 so that they are coded as are the variables for 2006 and forward. We then identify the drug trade name using appendix B (drug entry codes and names in numeric order) from the FDA site. We imported data into Stata and merged this list with NAMCS data.
This resulted in the drug trade names appearing in both the FDA and NAMCS datasets, so we could then merge the FDA approval date with the NAMCS data using the first word of the drug name. (Most of the drugs can be identified with the first word in its name). The merge rate for drugs prescribed in the NAMCS drug sample was 95% with this method.35
Appendix B: Proofs for Propositions in Section 2
The utility function for an individual patient can be written as:
| (A1) |
The partial derivatives are , and the second derivatives are , and .
We will also assume is homothetic or homogeneous in and . And the health production function satisfies the Inada conditions. That is
| (A2) |
and
| (A3) |
PROPOSITION 1: Let and be the optimal choices for patient at the copay . Then
PROPOSITION 2: assume is homogeneous of degree in and , we get , in which exhibits constant returns to scale. Let the local elasticity of substitution between drug and non-drug treatment be . Thus we have
Proof: The first order conditions of this maximization problem are:
and
for prescription drug and other medical care services.
The first order conditions are necessary and sufficient for the maximization of patients’ utility function. Taking the total differential of the two first order conditions with respect to , and , we have:
Appling Cramer’s rule, we get . The second order condition for maximization of the patient’s utility function ensures that while the concavity of ensures that . Thus .
We also get after applying Cramer’s rule. Thus, will be positive if , and it will negative it .
Assuming is homogenous of degree in and () we have
The definition for the local elasticity of substitution indicates . Because exhibits constant returns to scale, we derive
The above two equations imply that if and only if and if and only if . Thus we can derive equation (13).
PROPOSITION 3: Assume is homothetic in and , then the move from less generous prescription drug coverage to more generous drug coverage may affect the generic-branded drug ratio. Using and to indicate the number of prescribed generic and branded drugs after the adoption of Part D, we have
| (A4) |
if and only if
| (A5) |
Proof: The first order conditions for this maximization problem are:
| (A6) |
and
| (A7) |
for generic and branded prescription drugs.
Taking the ratio of (A6) to (A7) we have:
| (A8) |
Applying the same procedure to derive the equation for the number of prescription drugs after the adoption of Part D, we have:
| (A9) |
Further taking the ratio of (A9) to (A8), we obtain
| (A10) |
When is homothetic in and , the left side of equation (A10) is a decreasing function of . Then we can establish the relationship between equation (A4) and equation (A5).
Appendix Tables
Table A1:
Summary of Utilization and Expenditure, NAMCS 2002–2004 and 2006–2009
| Before 2006 | After 2006 | |||
|---|---|---|---|---|
| Below 65 | Above 65 | Below 65 | Above 65 | |
| Number of Rx Drugs | 1.600 | 1.742 | 2.498 | 2.689 |
| (0.049) | (0.060) | (0.067) | (0.073) | |
| Number of Generic Drugs | 0.468 | 0.555 | 1.007 | 1.106 |
| (0.025) | (0.028) | (0.034) | (0.034) | |
| Any Rx Drugs | 0.596 | 0.620 | 0.737 | 0.744 |
| (0.012) | (0.014) | (0.010) | (0.010) | |
| Number of Brand Name Drugs | 1.132 | 1.187 | 1.491 | 1.583 |
| (0.038) | (0.044) | (0.047) | (0.051) | |
| Number of OTC Drugs | 0.317 | 0.352 | 0.425 | 0.420 |
| (0.017) | (0.019) | (0.017) | (0.017) | |
| Number of Drugs | 1.988 | 2.158 | 3.014 | 3.212 |
| (0.060) | (0.071) | (0.078) | (0.084) | |
| Number of Diagnostic Tests | 0.973 | 0.991 | 1.095 | 1.076 |
| (0.026) | (0.034) | (0.020) | (0.022) | |
| Time Spent with MD | 19.085 | 18.201 | 20.464 | 20.314 |
| (0.394) | (0.347) | (0.285) | (0.587) | |
| Age of Active Ingredient | 163.2512 | 164.3038 | 209.0620 | 205.9645 |
| (1.646) | (1.614) | (1.377) | (1.171) | |
| Sample size | 4,857 | 4,880 | 8,589 | 8,148 |
The outcome “Age of Active Ingredient” is measured in months. The sample size is different from other outcomes because we use a prescription level sample. The sample size is 6,657, 7,317, 20,090 and 20,068, respectively, for samples under age 65 and before 2006, at least age 65 and before 2006, under age 65 and after 2006 as well as above age 65 and after 2006.
All means and standard deviations are weighted statistics.
Standard deviations are in parentheses.
Table A2:
Summary Statistics for Independent Variables, NAMCS 2002–2004 and 2006–2009
| Mean | Std. Dev. | |
|---|---|---|
| Patient Characteristics | ||
| 1(Age=65) | 0.498 | (0.005) |
| Age | 64.411 | (0.027) |
| Female | 0.561 | (0.005) |
| Nonwhite | 0.137 | (0.008) |
| Charlson Index=1 | 0.068 | (0.003) |
| Charlson Index=2 | 0.056 | (0.003) |
| Infectious and Parasitic Diseases | 0.054 | (0.003) |
| Neoplasms | 0.098 | (0.004) |
| Endocrine, Nutritional and Metabolic Diseases, and Immunity Disorders | 0.008 | (0.001) |
| Diseases of The Blood and Blood-Forming Organs | 0.030 | (0.002) |
| Mental Disorders | 0.097 | (0.003) |
| Diseases of The Nervous System and Sense Organs | 0.146 | (0.004) |
| Diseases of The Circulatory System | 0.079 | (0.004) |
| Diseases of The Respiratory System | 0.041 | (0.002) |
| Diseases of The Digestive System | 0.047 | (0.002) |
| Diseases of The Genitourinary System | 0.043 | (0.002) |
| Diseases of The Skin and Subcutaneous Tissue | 0.107 | (0.004) |
| Diseases of The Musculoskeletal System and Connective Tissue | 0.002 | (0.000) |
| Congenital Anomalies | 0.068 | (0.002) |
| Symptoms, Signs, and Ill-Defined Conditions | 0.131 | (0.005) |
| Visit Quarter==2 | 0.280 | (0.010) |
| Visit Quarter==3 | 0.242 | (0.009) |
| Visit Quarter==4 | 0.237 | (0.008) |
| Physician Practice Characteristics | ||
| Metropolitan Statistical Area (MSA) | 0.857 | (0.032) |
| Solo Practice | 0.341 | (0.013) |
| Electronic Medical Record | 0.331 | (0.014) |
| Internal Medicine | 0.216 | (0.009) |
| Pediatrics | 0.005 | (0.001) |
| General Surgery | 0.027 | (0.002) |
| Obstetrics & Gynecology | 0.028 | (0.002) |
| Orthopedic Surgery | 0.065 | (0.005) |
| Cardiovascular Diseases | 0.054 | (0.003) |
| Dermatology | 0.039 | (0.003) |
| Urology | 0.036 | (0.002) |
| Psychiatry | 0.020 | (0.001) |
| Neurology | 0.014 | (0.001) |
| Ophthalmology | 0.089 | (0.004) |
| Otolaryngology | 0.018 | (0.001) |
| Other specialties | 0.161 | (0.008) |
| Oncologists | 0.008 | (0.001) |
| Mid-level provider | 0.002 | (0.000) |
| Dummy (above median of prmcare=1)* | 0.688 | (0.011) |
| Sample Size | 26,474 |
“prmcare” stands for percent of revenue from Medicare patients. Missing values are imputed using predicted values from a tobit regression as a function of year dummies, physician specialty dummies, interactions between specialty dummies and the percent of population age 65 years or older, interactions between specialty dummies and the percent of patients age 65 or older, whether the physician use electronic medical records. The cutoff value for visit level analyses 0.25 and for drug level analyses is 0.30.
All means and standard deviations are weighted statistics.
Standard deviations are in parentheses.
Table A3:
Summary Statistics for Independent Variables, MEPS 2002–2004 and 2006–2009
| Mean | Std. Dev. | |
|---|---|---|
| Female | 0.525 | (0.004) |
| Black | 0.095 | (0.004) |
| Other Race | 0.055 | (0.004) |
| Hispanic | 0.072 | (0.004) |
| Poverty Category: Near Poor (100% To Less Than 125%) | 0.041 | (0.002) |
| Poverty Category: Low Income (125% To Less Than 200%) | 0.120 | (0.004) |
| Poverty Category: Middle Income (200% To Less Than 400%) | 0.273 | (0.006) |
| Poverty Category: High Income (Greater Than Or Equal To 400%) | 0.480 | (0.007) |
| Census Region: Midwest | 0.220 | (0.009) |
| Census Region: South | 0.379 | (0.010) |
| Census Region: West | 0.207 | (0.008) |
| Metropolitan Statistical Area (MSA) | 0.791 | (0.011) |
| Education Level: High School | 0.493 | (0.007) |
| Education Level: Bachelor Degree | 0.155 | (0.005) |
| Education Level: Post Degree | 0.120 | (0.005) |
| Education Level: Other Degree | 0.070 | (0.004) |
| Marital Status: Widowed | 0.104 | (0.004) |
| Marital Status: Divorced | 0.161 | (0.004) |
| Marital Status: Separated | 0.017 | (0.001) |
| Marital Status: Never Married | 0.046 | (0.002) |
| Prior Condition: Asthma | 0.096 | (0.003) |
| Prior Condition: High Blood Pressure | 0.542 | (0.006) |
| Prior Condition: Angina | 0.053 | (0.002) |
| Prior Condition: Heart Attack | 0.072 | (0.003) |
| Prior Condition: Joint Pain | 0.519 | (0.006) |
| Prior Condition: Stroke | 0.056 | (0.003) |
| Prior Condition: Emphysema | 0.044 | (0.002) |
| Prior Condition: Arthritis | 0.444 | (0.006) |
| Prior Condition: Other Heart Conditions | 0.136 | (0.004) |
| Observations | 276,774 |
All means and standard deviations are weighted statistics.
Standard deviations are in parentheses.
Footnotes
National health expenditure as a share of GDP grew from about 5% in 1960 to about 17% in 2012. (Source: http://www.cms.gov/Research-Statistics-Data-and-Systems/Statistics-Trends-and-Reports/NationalHealthExpendData/NationalHealthAccountsHistorical.html)
Physician agency” is a collective term referring to the issues related to physicians’ market power, behaviors and incentives (McGuire 2000)
Part D has since become the primary source of drug coverage for Medicare beneficiaries, covering more than half of all beneficiaries (57%) in 2006. It decreased the percentage of Medicare beneficiaries with no source of prescription drug coverage from 27% in 2003 to 10% in 2007 (The Henry J. Kaiser Family Foundation 2003; The Henry J. Kaiser Family Foundation 2006; The Henry J. Kaiser Family Foundation 2007), and lowered the fraction of prescription drug costs that many Medicare beneficiaries had to pay out-of-pocket at the point of service.
Prior work found that advertising of drugs increased only slightly after the introduction of Part D, mostly among drug classes with less competition (defined by the number of advertised drugs within the drug class prior to Part D implementation) or among dominant drugs (defined by higher market share of advertising before the implementation of Part D). (Lakdawalla et al. 2013).
We are aware of two working papers that also use similar empirical strategies: Chay, Kim, and Swamina (2010) and Grembi et al. (2011).
Part D has shifted prescription drug costs from Medicaid or other private payers to Medicare, and has contributed to a net increase in federal spending. The Medicare share of total national spending on prescription drugs increased from 2% in 2005 to 22% in 2006, and the net federal cost of the Part D program is estimated to be $982 billion for nine years between 2007 and 2016 (The Henry J. Kaiser Family Foundation 2007).
Some past studies are closely related to the topic we study and have examined whether physicians respond to changes in patients’ cost by adjusting their prescription patterns when there is no financial incentive for them to change behavior. Lundin (2000) found that physicians were less likely to prescribe trade-name versions of drugs to patients who have to pay a large sum out-of-pocket. There is also evidence that physicians increase prescription of a certain drug due to patent expiration (Carrera et al. 2013) or when the cost was covered by a third party (Dalen et al. 2010).
Beneficiaries enrolled in traditional Medicare (non-managed care) plan usually obtain drug coverage through a PDP; those enrolled in a managed care plan through a MA organization generally have to obtain drug coverage from MA-PD plans. In 2006, about 16.5 million people enrolled in stand-alone PDPs, 6 million people enrolled in MA-PD plans, and 6.8 million people had other forms of creditable coverage from employer or unions (The Henry J. Kaiser Family Foundation 2006).
Direct subsidy is a monthly prospective payment paid by CMS, which mainly reimburses the plan for the cost of initial coverage. Individual reinsurance is provided for a certain percentage of drug spending above enrollees’ catastrophic coverage. Medicare finances some unexpectedly high costs, or achieves unexpectedly high profits in order to limit plans’ potential losses or gains, which are called risk-sharing payments.
Low-income subsidies mean that those who are also eligible for Medicaid or under 135% of the federal poverty line pay no premium and have no deductible, and those whose income is between 135% and 150% of the federal poverty line pay a reduced premium and annual deductible. Both groups have a lower copayment for covered drugs as a result.
According to the Congressional Budget Office, generic drugs save consumers an estimated $8 to $10 billion a year at retail pharmacies.
Part D plan formularies are subject to some regulation. For example, they are required to cover all drugs in a protected drug class and at least two drugs in each therapeutic class.
In NAMCS, information is also collected on whether some other tests are ordered or provided during a physician visit including blood pressure check, X-ray, EKG/ECG, Pap test, urinalysis, PSA test, and CBC (complete blood count).
The first order condition for D is , where will cancel out.
We exclude the year 2005 from the main analysis because of the possible existence of anticipatory effects, which we will explain in detail in Section 6.C.
Information on whether drugs associated with a NAMCS visit were “new” or “continued” was collected beginning in 2005, when approximately 70 percent of drugs were categorized as continued.
We impute one variable, percent of revenue from Medicare patients, for 6.29 percent of the sample. Missing values are imputed using predicted values from a tobit regression as a function of year dummies, physician specialty dummies, interactions between specialty dummies and the percent of population age 65 years or older, interactions between specialty dummies and the percent of patients age 65 or older, whether the physician use electronic medical records. The cutoff value for visit level analyses 0.25 and for drug level analyses is 0.30.
The FDA orange book database contains information on the date of FDA approval and application type by drug name for drugs approved since January 1, 1982. Application type can be NDA or ANDA, which indicate whether it is a brand-name drug or generic drug, respectively (available from http://www.fda.gov/Drugs/InformationOnDrugs/ucm129689.htm).
For drugs with a generic equivalent, physicians in the NAMCS sometimes write down the generic name and sometimes a brand name for the drug. This may not measure physician intent, since subsequent substitution to the generic may be made at the pharmacy, a possibility that physicians seem likely to be aware of.
See Appendix A for a description of the process of merging FDA data with the NAMCS data.
Prior health condition indicates whether the individual has certain types of chronic conditions including asthma, high blood pressure, angina, heart attack, joint pain, stroke, emphysema, arthritis or other heart disease.
We calculate the number of prescription and generic drugs prescribed or continued by physicians by age group and perform a Wald test to examine whether there is a statistically significant difference between means of outcomes between pair-wise ages and p-values from results to reject the null hypothesis that means are equal.
The Charlson index is a numerical score indicating the severity of patient comorbidities. Each condition is associated with a particular score and the scores for each of three possible diagnoses associated with a NAMCS visit are totaled to calculate the index. The Charlson comorbidity index has been shown to predict subsequent mortality (Charlson et al., 1987).
Major disease category include infectious and parasitic diseases, neoplasms, endocrine, nutritional and metabolic diseases, and immunity disorders, mental disorders, congenital anomalies, as well as diseases of the blood and blood-forming organs, nervous system and sense organs, circulatory system, respiratory system, digestive system, genitourinary system, skin and subcutaneous tissue, musculoskeletal system and connective tissue. Also symptoms, signs, and ill-defined conditions.
Internal Medicine, Pediatrics, General Surgery, Obstetrics & Gynecology, Orthopedic Surgery, Cardiovascular Diseases, Dermatology, Urology, Psychiatry, Neurology, Ophthalmology, Otolaryngology, or other specialties relative to General/Family Practice.
We also estimate the model using Generalized Least Square (GLM) regressions. The results are similar to results we present from OLS regressions.
We decide the order of polynomial for the function of age using two methods. We compare the goodness-of-fit among specifications with different order of polynomial function according to Lee and Lemieux (2009). We also adopt a Wald test to examine the joint significance of additional polynomial terms. The results for both tests are available upon request.
One issue with the data is that the FDA orange book database assigns the value of “Prior to Jan 1, 1982” to drugs approved before 1982. For this reason, we use censored normal regression for the prescription-level analysis with the outcome of age of drugs prescribed, allowing the censoring value to vary from observation to observation.
We also performed GLM regression with a log link and Gaussian distribution, as determined by the Park test. The significance of results from OLS regression still holds and the calculated marginal effects are similar to what we have from OLS regressions.
In results not included in Table 2, we tested whether there was any confounding issue for all other physician and patient characteristics, including physician specialties, patients’ major disease categories and seasonal dummies. None of the coefficients from this set of regressions were significant except for one major disease category: (diseases of the digestive system). Again, excluding these covariates does not affect our main results.
We compute the number of tests by counting how many test among those recorded in NAMCS data the patients took. The list of test recorded in NAMCS is blood pressure check, X-ray, EKG/ECG, Pap test, urinalysis, PSA test, and CBC (complete blood count).
Lichtenberg & Sun (2007) found that in 2006, Medicare Part D reduced OOP daily cost of therapy by 18.4 percent and increased number of days of therapy by about 12.8 percent compared to that for users under the age of 65. Yin et al. (2008) find a 5.9% increase in monthly average drug utilization and a 13.1% decrease in monthly OOP cost after the penalty free period (i.e., after June 2006) using those aged 60–63 as the reference group. Ketcham & Simon (2008) estimate that days’ supply and number of individual prescriptions filled increase by 8.1% and 4.8% respectively, and OOP costs fall by 17.2% for the always eligible group (over 66 as of 2007) as compared to those who are always ineligible for Medicare (58–64 as of 2007). Engelhardt & Gruber (2011) find that Part D has a relatively small impact on OOP spending, and Liu et al. (2011) find that Part D is associated with a $179.86 reduction in OOP cost and an increase of 2.05 prescriptions per patient year. Kaestner & Khan (2012) found that getting drug coverage is associated with an approximately 70% increase in the use of prescription drugs for the general population of those aged65 to 85 years old, and a 60% increase in the use of prescription drugs for those with chronic conditions. Briesacher et al. (2011) simulated post-Part D outcomes using time-series regressions with a first-order autoregressive correlation structure and pre-Part D data, and compared those with observed results. They concluded that average prescription fills per person increased significantly by 1.8 fills in 2006 and 3.4 fills in 2007, compared to a 0.9 fill increase per year before Part D. They also found that average OOP drug costs decreased significantly in both 2006 and 2007, by $143 and $148 per year respectively.
The insignificance of our results for some outcomes in the MEPS could result partly from insufficient information in the public use version of the MEPS data to precisely estimate age profiles and time trends of outcomes.
The measure for the utilization of prescription drugs is aggregated to the patient-year level, which is different from the patient-visit level data that are available in NAMCS data for the utilization of prescription drugs. The difference between the estimate from NAMCS and MEPS may be due in part to the fact that different drugs require different day supply amounts and rates of refill.
We also tried to merge the FDA data with the NAMCS analytic sample using the whole string in the drug name field. The merge rate was about 80%.
Reference:
- Acemoglu D & Finkelstein A, 2008. Input and Technology Choices in Regulated Industries: Evidence from the Health Care Sector. Journal of Political Economy, 116(5), pp.837–880. [Google Scholar]
- Alexander GC, Casalino LP & Meltzer DO, 2003. Patient-physician communication about out-of-pocket costs. JAMA : the journal of the American Medical Association, 290(7), pp.953–8. [DOI] [PubMed] [Google Scholar]
- Alpert A, 2012. The Anticipatory Effects of Medicare Part D on Drug Utilization. SSRN Electronic Journal. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson ML, Dobkin C & Gross T, 2014. The Effect of Health Insurance on Emergency Department Visits: Evidence from an Age-Based Eligibility Threshold. Review of Economics and Statistics, 96(1), pp.189–195. [Google Scholar]
- Arrow KJ, 1963. Uncertainty and the Welfare Economics of Medical Care. The American Economic Review, 53(5), pp.941–973. [Google Scholar]
- Blume-Kohout ME & Sood N, 2013. Market Size and Innovation: Effects of Medicare Part D on Pharmaceutical Research and Development. Journal of public economics, 97, pp.327–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briesacher BA et al. , 2011. Medicare Part D and Changes in Prescription Drug Use and Cost Burden: National Estimates for the Medicare Population, 2000 to 2007. Medical care, 49(9), pp.834–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryant EE & Shimizu I, 1988. Sample Design, Sampling Variance, and Estimation Procedure for the National Abulatory Medical Care Survey. Vital and Health Statistics. Series 2, Data Evaluation and Methods Research, 108, pp.1–39. [PubMed] [Google Scholar]
- Card D, Dobkin C & Maestas N, 2009. Does Medicare Save Lives? The quarterly journal of economics, 124(2), pp.597–636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrera M, Goldman D & Joyce G, 2013. Heterogeneity in Cost-Sharing and Cost-Sensitivity, and the Role of the Prescribing Physician. [Google Scholar]
- Chalkley M & Malcomson JM, 1998. Contracting for health services when patient demand does not reflect quality. Journal of Health Economics, 17(1), pp.1–19. [DOI] [PubMed] [Google Scholar]
- Charlson ME, Pompei P, Ales KL & MacKenzie CR, 1987. A New Method of Classifying Prognostic Comorbidity in Longitudinal Studies: Development and Validation. Journal of Chronic Diseases, 40(5):373–83. [DOI] [PubMed] [Google Scholar]
- Chay KY, Kim D & Swamina S, 2010. Medicare, Hospital Utilization and Mortality: Evidence from the Program’s Origins., Available at: http://www.chicagofed.org/digital_assets/others/events/2010/health_care_conference/paper_chay.pdf [Accessed August 21, 2014]. [Google Scholar]
- Clemens J & Gottlieb JD, 2014. Do Physicians’ Financial Incentives Affect Medical Treatment and Patient Health? †. American Economic Review, 104(4), pp.1320–1349. Available at: http://www.aeaweb.org/articles.php?doi=10.1257/aer.104.4.1320 [Accessed August 7, 2014]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Congressional Budget Office (CBO). 2009. Promotional Spending for Prescription Drugs. Available from http://www.cbo.gov/sites/default/files/12-02-drugpromo_brief.pdf, Accessed October 29, 2014. [Google Scholar]
- Dalen DM, Sorisio E & Strom S, 2010. Choosing Among Competing Blockbusters: Does the Identity of the Third-Party Payer Matter for Prescribing Doctors? [Google Scholar]
- Duggan M & Morton FS, 2010. The Effect of Medicare Part D on Pharmaceutical Prices and Utilization. American Economic Review, 100(1), pp.590–607. [DOI] [PubMed] [Google Scholar]
- Duggan MG & Morton FS, 2011. The Medium-Term Impact of Medicare Part D on Pharmaceutical Prices. American Economic Review, 101(3), pp.387–392. [DOI] [PubMed] [Google Scholar]
- Ellis RP & McGuire TG, 1986. Provider behavior under prospective reimbursement. Journal of Health Economics, 5(2), pp.129–151. [DOI] [PubMed] [Google Scholar]
- Engelberg J, Parsons CA & Tefft N, 2013. First, Do No Harmml: Financial Conflicts in Medicine. SSRN Electronic Journal. Available at: http://papers.ssrn.com/abstract=2297094 [Accessed August 6, 2014]. [Google Scholar]
- Engelhardt GV & Gruber J, 2011. Medicare Part D and the Financial Protection of the Elderly. American Economic Journal: Economic Policy, 3(4), pp.77–102. [Google Scholar]
- Federman AD, 2004. Don’t ask, don’t tell: the status of doctor-patient communication about health care costs. Archives of internal medicine, 164(16), pp.1723–4. Available at: http://www.ncbi.nlm.nih.gov/pubmed/15364663 [Accessed September 15, 2014]. [DOI] [PubMed] [Google Scholar]
- Grembi V, Nannicini T & Troiano U, 2011. Do Fiscal Rules Matter? A Difference-in-Discontinuities Design. SSRN Electronic Journal. Available at: http://papers.ssrn.com/abstract=1852523 [Accessed August 24, 2014]. [Google Scholar]
- Gruber J & Owings M, 1996. Physician financial incentives and cesarean section delivery. The Rand journal of economics, 27(1), pp.99–123. [PubMed] [Google Scholar]
- Ho K & Pakes A, 2013. Hospital Choices, Hospital Prices and Financial Incentives to Physicians. [DOI] [PubMed] [Google Scholar]
- Iizuka T, 2007. Experts’ agency problems: evidence from the prescription drug market in Japan. The Rand journal of economics, 38(3), pp.844–62. [DOI] [PubMed] [Google Scholar]
- Iizuka T, 2012. Physician Agency and Adoption of Generic Pharmaceuticals. American Economic Review, 102(6), pp.2826–2858. [DOI] [PubMed] [Google Scholar]
- Kaestner R & Khan N, 2012. Medicare Part D and Its Effect on the Use of Prescription Drugs and Use of Other Health Care Services of the Elderly. Journal of Policy Analysis and Management, 31(2), pp.253–279. [Google Scholar]
- Kaestner R, Long C & Alexander GC, 2014. Effects of Prescription Drug Insurance on Hospitalization and Mortality: Evidence from Medicare Part D. Available at: http://www.nber.org/papers/w19948 [Accessed September 15, 2014]. [Google Scholar]
- Ketcham JD & Simon KI, 2008. Medicare Part D’s Effects on Elderly Patients’ Drug Costs and Utilization. The American journal of managed care, 14(11 Suppl), pp.SP14–22. [PubMed] [Google Scholar]
- Lakdawalla D, Sood N & Gu Q, 2013. Pharmaceutical advertising and Medicare Part D. Journal of health economics, 32(6), pp.1356–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee DS & Lemieux T, 2010. Regression Discontinuity Designs in Economics. Journal of Economic Literature, 48(2), pp.281–355. [Google Scholar]
- Lichtenberg FR & Sun SX, 2007. The Impact of Medicare Part D on Prescription Drug Use By the Elderly. Health affairs (Project Hope), 26(6), pp.1735–44. [DOI] [PubMed] [Google Scholar]
- Liu FX et al. , 2011. The Impact of Medicare Part D on Out-Of-Pocket Costs for Prescription Drugs, Medication Utilization, Health Resource Utilization, and Preference-Based Health Utility. Health services research, 46(4), pp.1104–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y-M, Yang Y-HK & Hsieh C-R, 2009. Financial incentives and physicians’ prescription decisions on the choice between brand-name and generic drugs: evidence from Taiwan. Journal of health economics, 28(2), pp.341–9. [DOI] [PubMed] [Google Scholar]
- Lu F, 2014. Insurance coverage and agency problems in doctor prescriptions: Evidence from a field experiment in China. Journal of Development Economics, 106, pp.156–167. [Google Scholar]
- Lundin D, 2000. Moral Hazard in Physician Prescription Behavior. Journal of Health Economics, 19(5), pp.639–662. [DOI] [PubMed] [Google Scholar]
- Lurie N et al. , 1990. Pharmaceutical Representatives in Academic Medical Centers: Interaction with Faculty and Housestaff. Journal of general internal medicine, 5(3), pp.240–3. [DOI] [PubMed] [Google Scholar]
- McCrary J, 2008. Manipulation of the Running Variable in the Regression Discontinuity Design: A Density Test. Journal of Econometrics, 142(2), pp.698–714. [Google Scholar]
- McGuire TG, 2000. Chapter 9 Physician agency. Handbook of Health Economics, 1, pp.461–536. [Google Scholar]
- Meyers DS et al. , 2006. Primary care physicians’ perceptions of the effect of insurance status on clinical decision making. Annals of family medicine, 4(5), pp.399–402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen H, 2011. The principal-agent problems in health care: evidence from prescribing patterns of private providers in Vietnam. Health policy and planning, 26 Suppl 1(suppl_1), pp.i53–62. [DOI] [PubMed] [Google Scholar]
- Pauly M, 1980. Doctors and Their Workshops: Economic Models of Physician Behavior, National Bureau of Economic Research, Inc. [Google Scholar]
- Roth Martin S. 1006. Patterns in Direct-to-Consumer Prescription Durg Print Advertising and Their Public Policy Implications. Journal of Public Policy and Marketing 15(1): 63–75. [Google Scholar]
- Sacks DW, 2013. Physician Agency , Compliance , and Patient Welfare : Evidence from Anti-Cholesterol Drugs, Available at: https://bepp.wharton.upenn.edu/bepp/assets/File/AE-F13-Sacks.pdf. [Google Scholar]
- Stern S & Trajtenberg M, 1998. Empirical Implications of Physician Authority in Pharmaceutical Decisionmaking, Available at: http://www.nber.org/papers/w6851 [Accessed August 24, 2014]. [Google Scholar]
- The Henry J. Kaiser Family Foundation, 2003. The Medicare Prescription Drug Benefit Fact Sheet,
- The Henry J. Kaiser Family Foundation, 2010. The Medicare Prescription Drug Benefit Fact Sheet,
- The Henry J. Kaiser Family Foundation, 2006. The Medicare Prescription Drug Benefit Fact Sheet,
- The Henry J. Kaiser Family Foundation, 2007. The Medicare Prescription Drug Benefit Fact Sheet,
- The Henry J. Kaiser Family Foundation. 2007. Medicare Spending and Financing Fact Sheet.
- Vakratsas Demetrios and Ambler Tim. 1999. How Advertising Works: What Do We Really Know? Journal of Marketing 63(1): 26–43. [Google Scholar]
- Weisbrod BA, 1991. The Health Care Quadrilemma: An Essay on Technological Change, Insurance, Quality of Care, and Cost Containment. [Google Scholar]
- Wynia MK et al. , 2003. Do physicians not offer useful services because of coverage restrictions? Health affairs (Project Hope), 22(4), pp.190–7. [DOI] [PubMed] [Google Scholar]
- Yin W et al. , 2008. The Effect of the Medicare Part D Prescription Benefit on Drug Utilization and Expenditures. Annals of internal medicine, 148(3), pp.169–77. [DOI] [PubMed] [Google Scholar]
- Yip WC, 1998. Physician response to Medicare fee reductions: changes in the volume of coronary artery bypass graft (CABG) surgeries in the Medicare and private sectors. Journal of health economics, 17(6), pp.675–99. [DOI] [PubMed] [Google Scholar]
- Zhang Y et al. , 2009. The Effect of Medicare Part D on Drug and Medical Spending. The New England journal of medicine, 361(1), pp.52–61. [DOI] [PMC free article] [PubMed] [Google Scholar]