Thermal performance across levels of biological organization

Abstract

Thermal performance curves are widely used to describe how ambient temperature impacts different attributes of ectothermic organisms, from protein function to life-history traits, and to predict the potential effects of global warming on ecological systems. Nonetheless, from an analytical standpoint, they remain primarily heuristic and few attempts have been made to develop a formal framework to characterize these curves and disentangle which factors contribute to their variation. Here we employ a nonlinear regression approach to assess if they vary systematically in shape depending on the performance proxy of choice. We compare curves at contrasting levels of organization, namely photosynthetic rates in plants (n = 43), running speeds in lizards (n = 51) and intrinsic rates of population increase in insects (n = 47), and show with discriminant analyses that differences lie in a single dimension accounting for 99.1% of the variation, resulting in 75.8% of classification accuracy. Differences revolve primarily around the thermal range for elevated performance (greater than or equal to 50% of maximum performance), which is broader for photosynthetic rates (median of 26.4°C), intermediate for running speeds (19.5°C) and narrower for intrinsic rates of increase (12.5°C). We contend, confounding taxonomic factors aside, that these differences reflect contrasting levels of biological organization, and hypothesize that the thermal range for elevated performance should decrease at higher organization levels. In this scenario, instantaneous or short-term measures of performance may grossly overestimate the thermal safety margins for population growth and reproduction. Taken together, our analyses suggest that descriptors of the curve are highly correlated and respond in tandem, potentially resulting in systematic variation in shape across organization levels. Future studies should take into consideration this potential bias, address if it constitutes a general pattern and, if so, explain why and how it emerges.

This article is part of the theme issue ‘Physiological diversity, biodiversity patterns and global climate change: testing key hypotheses involving temperature and oxygen’.

1. Introduction

Global climate change poses one of the greatest threats to biodiversity, with climate forecasts predicting an increase in global average temperatures ranging from 1.7 to 4.9°C [1]. Theoretical and empirical approaches indicate that global warming will impact the mean temperatures of local environments, as well as the magnitude of geographical, diel and seasonal variation [1–3]. Furthermore, the expected increase in frequency of extreme environmental conditions is likely to have an even greater impact on biodiversity than the increase in average temperatures [4–7]. For these reasons, temperature effects on energy turnover rates and limits to survival and reproduction have been the focus of a large body of research [8–11], and the repercussions of predicted changes in thermal conditions are being assessed with mechanistic niche models that combine physiological knowledge with climate projections [12,13]. This can be achieved either by using theoretical approaches and biophysical ecology or by employing the information provided by thermal performance curves, which describe the relationship between body temperature and performance in ectotherms, and have been recurrently employed to determine how different species will respond to ongoing climate change [8,9,12,14].

Thermal performance curves provide a compelling heuristic tool to describe and predict temperature effects on biological systems across different levels of organization [15–17]. Their overall shape presumably reflects the combined effects of thermodynamics on biochemical rates of reaction and on protein function and stability [18], physico-chemical constraints with potentially widespread ecological and evolutionary repercussions given how often the unimodal and asymmetric classic thermal performance curve is reported in empirical studies at higher levels of biological organization. Much attention has been given to understanding how thermal performance curves or different proxies, such as critical thermal limits, vary through space and time [10,11,19,20], employing on multiple occasions short-term performance measures that have been adopted for logistic reasons and whose association with Darwinian fitness is often unclear [12]. Although these studies remain highly informative, and in spite of the enormous variation in thermal sensitivity observed across taxonomic groups and biological systems [17,21], to what extent these curves may be contingent on the indices of performance employed and whether there is systematic variation across curves remain virtually unexplored. As pointed out by Schulte et al. [18], for instance, it is not entirely clear why thermal performance curves of aerobic metabolism at the organismal level should exhibit the same attributes or behaviour as the underlying biochemical components, as evidenced in some organisms that exhibit bimodal curves [22]; hence it remains to be seen whether descriptors of thermal performance curves are invariant across different levels of biological integration or complexity.

Here we study whether thermal performance curves vary systematically with the level of organization in question. Global change biologists have traditionally focused on traits at specific levels of organization as indicators of the responses to human-induced perturbations [8–11,20]. However, an explanation of the mechanisms underlying global environmental problems is becoming increasingly important, not only for our understanding of cause–effect relationships, but also for predicting the optimal range of habitats and stressor thresholds for different organisms in natural and managed ecosystems. As a preliminary step in this direction, we first propose an intuitive mathematical framework to describe thermal performance curves employing parameters that are biologically realistic from a thermodynamic perspective (figure 1). Subsequently, we apply this framework to demonstrate with empirical data that some aspects of the performance curves seem to vary systematically across different levels of biological organization. And finally, we discuss how this finding might impact predictions on the impact of climate change on the vulnerability of organisms based on the study of thermal performance curves.

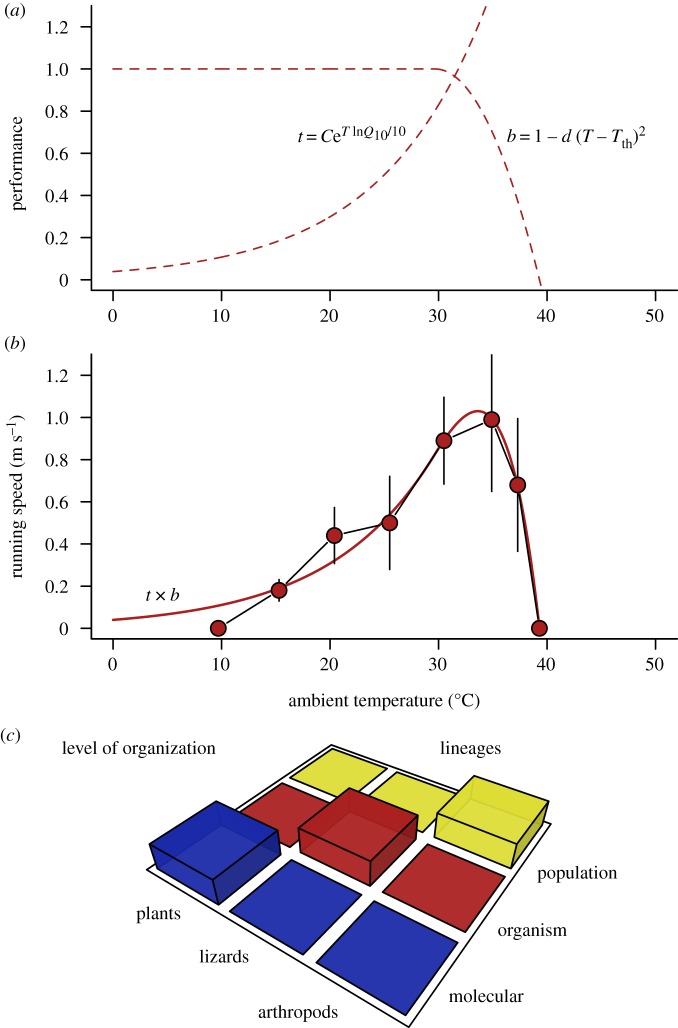
Figure 1.

Studying thermal performance across levels of biological organization. (a) Graphical representation of our model (equation (2.3)), which combines temperature effects on chemical reaction rates (function t for ‘thermodynamics’) and protein stability (b for ‘biochemistry’). (b) The thermal performance curve obtained after fitting t × b for running speeds measured in Ctenotus regius [23]. (c) Taxa and level of biological organization studied here, illustrating the generality of the proposed approach and the effects of taxonomic identity and organization level that are confounded in our analysis (but see figure 4).

2. Material and methods

(a). Datasets

We compiled thermal performance data on three different variables from the literature: photosynthetic rates in higher plants, sprint speeds in lizards and intrinsic rates of population increase estimated in insects. These variables were selected because they provide illustrative examples at contrasting levels of biological organization and thermal effects that have been documented extensively in a relatively large number of studies. Raw temperature and performance estimates for a given set of species and/or acclimation treatments were extracted from tables or original plots (in which case the data were retrieved with GraphClick 3.0; http://www.arizona-software.ch/graphclick/). A total of 89 datasets comprising measurements of photosynthetic rates, 64 for sprint speeds and 78 for intrinsic rates across different temperatures were obtained from the literature. Convergence of the nonlinear model and adequate parameter estimation of the thermal performance curve (see below) were the sole criteria of inclusion in analyses. Thus, all curves whose parameters could not be quantified owing to the limitations of the data (e.g. a small number of measurements or a reduced temperature range) or because the proposed model did not converge were excluded. The resulting dataset discussed hereafter comprises 43 thermal performance curves for photosynthetic rates, 51 for sprint speeds and 47 for the intrinsic rates of increase (total n = 141 curves). The raw data and the original references are provided in the electronic supplementary material (appendix A).

(b). Statistical analyses

Our performance function describes the antagonistic effects of temperature on chemical reaction rates and protein denaturation. Whereas reaction rates increase nearly exponentially with temperature, resulting in a positive effect on performance on the one hand, denaturation should result in a loss of function and negatively impact performance at higher temperatures on the other hand (figure 1). In this context, the thermodynamic component t of the model can be defined as:

$$t=C{\mathrm{e}}^{T\ln Q_{10}/10},$$ 2.1

where T corresponds to ambient or body temperature (°C), Q₁₀ defines the fold change in performance as a consequence of increasing the temperature by 10°C, and C is a constant describing shifts in the vertical axis that are independent of temperature (for instance, if one is studying the rate of degradation of a substrate by a particular enzyme, C will be proportional to enzyme concentration).

The effects of temperature on biochemical denaturation can be expressed as a proportion of functional molecules/total molecules. Assuming that these effects are triggered at a given temperature, one can calculate the biochemical component b as:

$$b=\{\begin{array}{ccc}1& \mathrm{if}& T<T_{\mathrm{th}}\\ (1-d{(T-T_{\mathrm{th}})}^2)& \mathrm{if}& T>T_{\mathrm{th}}\end{array},$$ 2.2

where d is a constant controlling the rate of decay from threshold temperature T_th upwards (the curvature of the decaying function is assumed to exhibit a quadratic form). Total performance pf is then obtained by multiplying t × b, resulting in the full model:

$$\mathrm{pf}=\{\begin{array}{ccc}(C{\mathrm{e}}^{T\ln Q_{10}/10})& \mathrm{if}& T<T_{\mathrm{th}}\\ (C{\mathrm{e}}^{T\ln Q_{10}/10})\times (1-d{(T-T_{\mathrm{th}})}^2)& \mathrm{if}& T>T_{\mathrm{th}}\end{array}.$$ 2.3

Consequently, thermodynamics is primarily responsible for changes in performance in colder temperatures, while denaturation gains importance as temperature rises above T_th and eventually causes a collapse in performance as b approaches 0 (figure 1).

We fitted the thermal performance curve to the empirical data and estimated the four parameters Q₁₀, C, T_th and d, with nonlinear least-squares fitting. Nonlinear estimation is particularly advantageous because it can accommodate empirical estimates of performance = 0 (i.e. the lower and upper critical thermal limits), which is not mathematically possible when log-transforming trait values to estimate parameters with a linear model [24,25]. Additionally, maximal performance, the optimal temperature T_opt in which performance is maximized and the temperature range in which performance remains above 50% of its maximum (T_breadth) [26] were obtained from the fitted nonlinear model. All analyses were performed with R (https://cran.r-project.org), employing an ad hoc script available in the electronic supplementary material (appendix B).

Subsequently, parameter estimates describing the thermal performance curves were compared between the three datasets employing a regular ANOVA, followed by a linear discriminant analysis to determine how the interaction between these parameters give rise to performance curves with different shapes. Even though several variables were right-skewed (Q₁₀ and T_breadth), we report comparisons with the untransformed data for simplicity because results remained qualitatively identical after improving normality (the only exception was d, which exhibited a lognormal distribution and was log-transformed prior to analyses). Because we are primarily concerned about the generality of the model and its potential applications to study thermal performance curves across different traits, we estimated parameter C but did not include it in analyses for two reasons: C cannot be compared between two different measures of performance because it is expressed in the same units as the response variable (whereas Q₁₀ is dimensionless, T_th is expressed in °C and d in °C⁻², see equation (2.3)), and it describes primarily changes on the vertical axis and has no impact on the overall shape of the thermal performance curve (electronic supplementary material, figure S1). Thus, while parameter C can be biologically informative and should be taken into consideration to understand how a single measure of performance (e.g. photosynthetic rates, running speeds or intrinsic rates of increase) might vary across lineages or treatments, here we focus primarily on variation in parameters Q₁₀, T_th and d, which affect the overall shape of the curve. Nonetheless, parameters obtained for all curves are listed in the electronic supplementary material (appendix C).

3. Results

(a). Parameter estimates and the shape of thermal performance curves

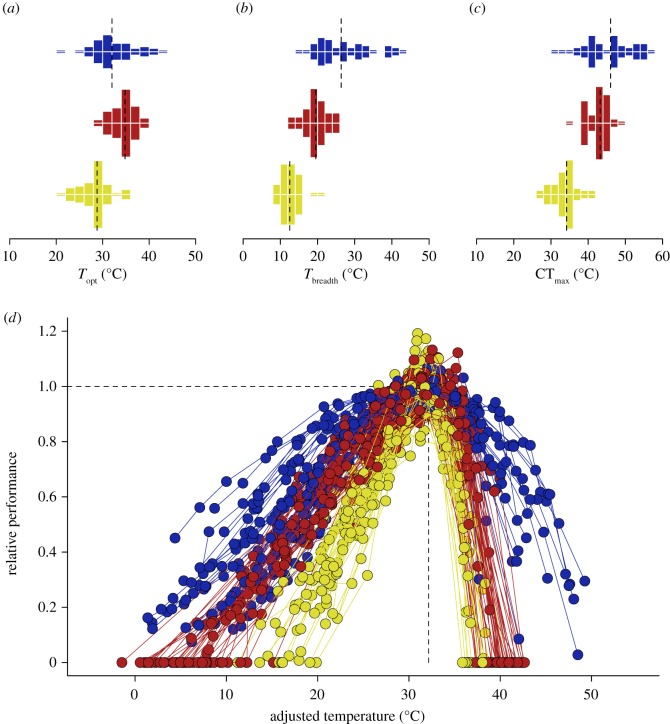
The nonlinear regression analysis converged for a total of 141 performance curves, which contained a range of 5–26 empirical measurements per curve. Overall fit was good based on visual inspection and R² = 0.957 ± 0.044 (±s.d.) from predicted versus observed linear regressions, indicating that the thermal performance function developed here (equation (2.3)) provides an adequate description of the relationship between performance measures and T for multiple curves obtained across different traits (figure 2). Overall, analyses indicate that Q₁₀ and d differ significantly between traits whereas T_th does not (table 1). Interestingly, a linear discriminant analysis including these three parameters suggests that 99.1% of the variation in shape across curves falls in a single linear dimension (electronic supplementary material, figure S2), which resulted in 75.8% curves correctly classified. In accordance with results from univariate ANOVAs, Q₁₀ and log-transformed d exhibited the highest standardized coefficients in the discriminant function (Q₁₀ = 0.75, T_th = 0.09 and d = 1.48); hence these are the parameters that best separate the curves across traits.

Figure 2.

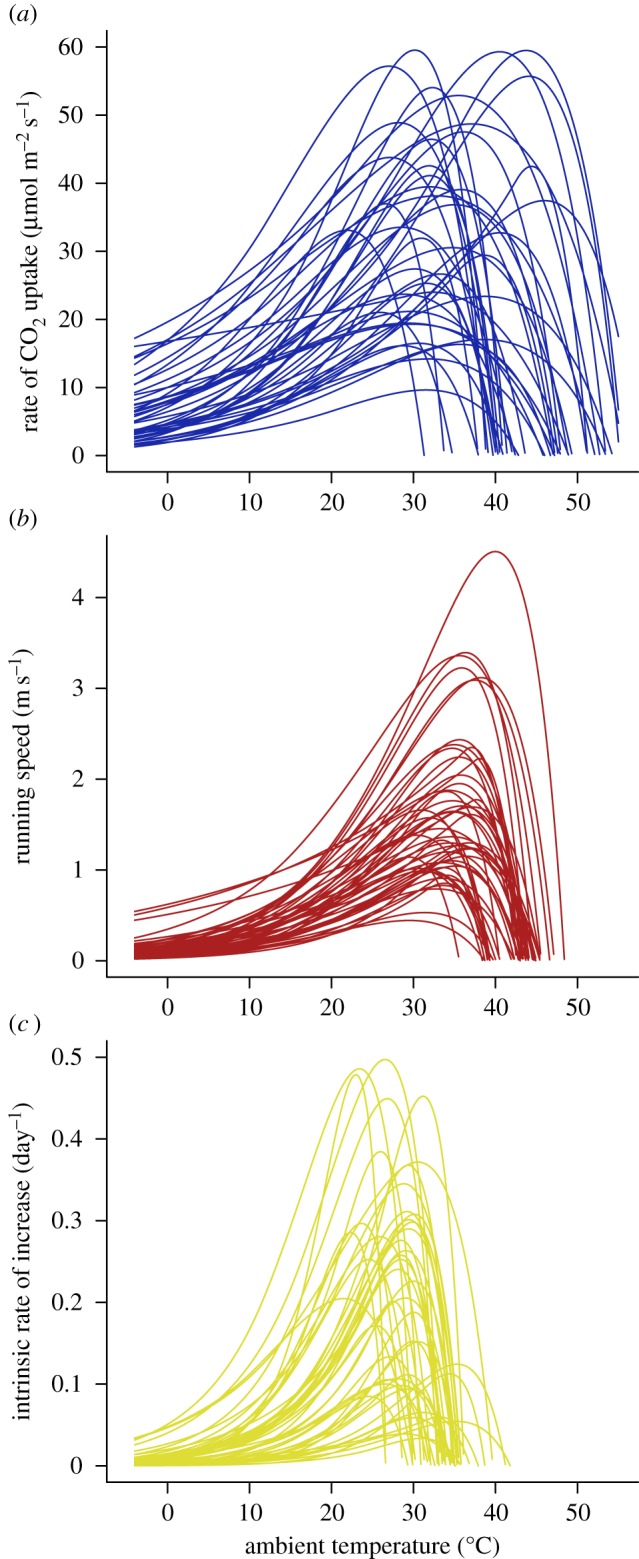
Thermal performance curves fitted to empirical data for (a) photosynthetic rates in plants (n = 43), (b) running performance in lizards (n = 51) and (c) fitness in insects (n = 47).

Table 1.

Parameter estimates of the thermal performance curves fitted for different traits and results from a regular ANOVA comparing them. Median and 95% confidence intervals are reported.

	rate of CO2 uptake	running speed	intrinsic rate of increase
Ca	5.77 (2.00, 17.02)	0.129 (0.035, 0.568)	0.008 (0.001, 0.048)
Q10	1.813 (1.331, 2.767)	2.356 (1.416, 3.675)	3.789 (2.326, 8.417)	F2,138 = 63.1	p < 2.2 × 10−16
Tth (°C)	16.21 (6.98, 35.33)	17.45 (3.47, 36.88)	20.96 (10.72, 26.41)	F2,138 = 2.14	p = 0.121
d (°C−2)b	0.0013 (0.0005, 0.0069)	0.0016 (0.0007, 0.0268)	0.0051 (0.0018, 0.0262)	F2,138 = 33.9	p = 1.1 × 10−12
Topt (°C)	32.0 (25.93, 44.38)	34.8 (29.70, 38.17)	28.8 (22.40, 35.08)	F2,138 = 36.5	p = 1.8 × 10−13
Tbreadth (°C)	26.37 (16.98, 43.05)	19.54 (13.51, 24.64)	12.54 (9.15, 18.47)	F2,138 = 109.2	p < 2.2 × 10−16
CTmax (°C)	46.02 (33.81, 55.71)	43.26 (38.48, 47.04)	34.20 (26.98, 41.00)	F2,138 = 87.3	p < 2.2 × 10−16

^aComparing C is not meaningful because its units vary with the measured traits (figure 2).

^bANOVA on log-transformed values to improve normality.

The observed variation in parameter estimates translates into striking differences in the overall shape of the thermal performance curves across traits (figure 3). Succinctly, all descriptors of the temperature performance curve were statistically different according to univariate ANOVAs (table 1). While observed differences in the temperature optimum T_opt across traits do not seem to reflect their level of organization, the temperature range in which performance remains elevated (i.e. above 50% of maximum performance) was higher for photosynthetic rates, intermediate for running speeds and lower for intrinsic rates of increase. Importantly, differences in T_breadth are quite large, with median estimates for one trait generally falling outside the 95% confidence intervals estimated for the other traits (figure 3b). To illustrate the differences in T_breadth across traits, and presumably across levels of biological organization, we set the maximum performance of the fitted curves to 1, centred the curves to the mean T_opt = 32.15°C observed across the entire dataset and mapped the original measurements onto this normalized temperature axis (figure 3d). This can be readily accomplished without affecting the overall shape of the curve because, analytically, T_opt can be quantified by calculating $\mathrm{\partial }\mathrm{pf}/\mathrm{\partial }T=0$ (equation (2.3)), which leads to:

$$T_{\mathrm{opt}}=T_{\mathrm{th}}-{\displaystyle \frac{10}{\ln Q_{10}}+\sqrt{{\displaystyle \frac{1}{d}+{\left({\displaystyle \frac{10}{\ln Q_{10}}}\right)}^2}}.}$$ 3.1

That is, manipulating T_th effectively shifts the thermal performance curve along the temperature axis without affecting its general shape, and after curves are centred on a common T_opt the differences in T_breadth between traits become quite evident (figure 3d).

Figure 3.

Thermal performance curves differ in shape across different levels of organization, as shown for (a) the optimal temperature where performance is maximal, (b) the temperature range where performance remains above 50% of its estimated maximum and (c) the upper critical temperature where performance drops to zero. Dashed lines show the distribution medians. (d) Differences in the temperature range across curves are evident when the raw data are expressed as relative performance and centred on the same optimal temperature. Colours as in figures 1 and 2.

Importantly, the remainder of this equation is also informative because ΔT = T_opt − T_th, or the temperature difference between where the denaturation curve starts dropping and where this effect fully compensates the rise in performance due to thermodynamics (figure 1), depends solely on Q₁₀ and d. This is why the interaction between Q₁₀ and d ultimately determines the shape of the curve, and more specifically its thermal range, and why these two parameters were the most important variables obtained in the linear discriminant analysis above (electronic supplementary material, figure S2). While this finding is interesting on its own merit, its repercussions are far from trivial as it indicates that the relationship between T_opt and the upper critical thermal limit CT_max is expected to vary. Accordingly, the thermal window estimated as CT_max − T_opt differs significantly between traits (F_2,138 = 107.6, p < 2.2 × 10⁻¹⁶), corresponding to 12.1 ± 3.4°C for photosynthetic rates, 8.0 ± 1.4°C for running speeds and 5.5 ± 1.1°C for intrinsic rates of increase (figure 3d).

These analyses conclusively show that the overall shape of the thermal performance curve differs between traits, even though results include the confounding effects of taxonomic identity (figure 1c). To determine if patterns hold in analyses involving comparable taxa, we compared results for running performance against the few curves described for enzymatic activities that we are aware of in lizards (n = 4, electronic supplementary material, figure S3) [27], and CT_max estimates at the population level in insects against values obtained individually with ramping experiments (n = 215, data from supplementary material, table S1 in [11]). Results remain qualitatively identical (figure 4). In lizards, thermal breadth and CT_max estimated for enzymatic activity are significantly higher than estimates for running performance (Welch's unequal variances t-test, t = 3.89, d.f. = 3.5, one-tailed p = 0.011 and t = 3.18, d.f. = 3.5, two-tailed p = 0.020, respectively). The same is true for CT_max in insects, whose average of 42.7 ± 4.6°C obtained in ramping assays is 8.8°C higher than estimates obtained at the population level (t = 15.17, d.f. = 101.9, one-tailed p < 1.1 × 10⁻¹⁶). By contrast, estimates of CT_max at the organismal level are virtually indistinguishable between lizards and insects (figure 4b,c, t = 0.14, d.f. = 146.9, one-tailed p = 0.443), highlighting that different taxa may not necessarily exhibit different thermal performance curves at comparable levels of organization. Interestingly, the same result holds for comparisons at the ‘molecular’ level (sensu figure 1), i.e. if we compare T_breadth (t = 1.08, d.f. = 7.67, one-tailed p = 0.16) and CT_max (t = 1.01, d.f. = 7.11, one-tailed p = 0.17) obtained for enzymatic activities in lizards versus photosynthetic rates in plants. Thus, at least in this restricted set of comparisons, differences across curves seem to emerge from variation in the levels of biological organization instead of taxonomic identity, supporting our contention that thermal performance curves may vary systematically with biological complexity.

Figure 4.

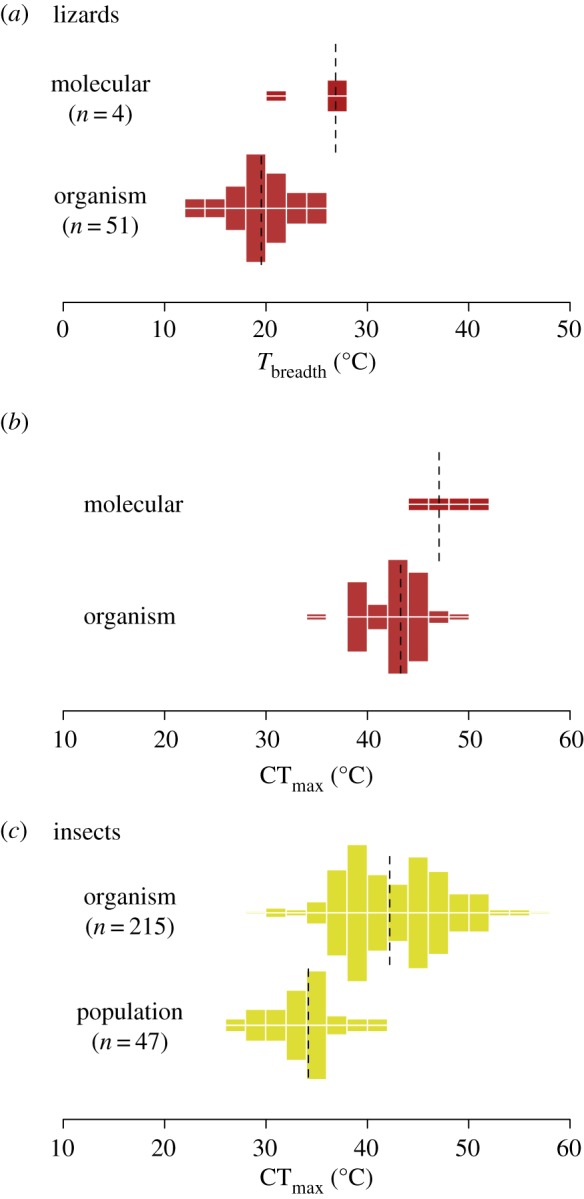
Descriptors of the thermal performance curve differ across organization levels within taxonomic groups, as shown here for (a,b) lizards (see also electronic supplementary material, figure S3) and (c) insects. Dashed lines show the distribution median. Thermal breadth and heat tolerance significantly decrease with increasing biological complexity (one-tailed p ≤ 0.02 in all pairwise comparisons), which mirrors the results obtained for the full dataset. This supports our contention that, confounding taxonomic issues aside (see figure 1 and main text), thermal performance curves vary consistently in shape across different levels of organization. Note that thermal breadth could not be calculated for insects because their upper critical temperature is estimated employing protocols that do not require the characterization of the entire thermal performance curve.

(b). Thermal safety margins

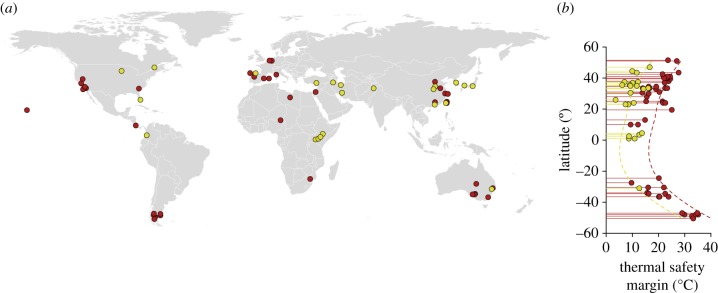
Descriptors of the thermal performance curve, such as critical thermal limits or optimal temperatures, are being increasingly employed for predictive purposes. In this context, differences in specific estimates such as CT_max across traits may be substantial, as shown for the insect dataset, and may have important effects on estimations of resilience to climate change such as temperature safety margins [9,12,28–30]. To illustrate this point, we estimated the thermal safety margin for running performance and intrinsic rates of increase as CT_max – T_max, where T_max corresponds to the average temperature of the warmest month encountered by the studied populations [31], and analysed how it varies with latitude. As expected, the thermal safety margins for intrinsic rates of increase are considerably lower than those inferred from locomotor performance (figure 5), in the order of 9.1°C according to a linear regression of thermal safety margin estimates on absolute latitude (latitude effect, F_1,72 = 61.8, P = 2.8 × 10⁻¹¹ and trait effect, F_1,72 = 55.7, P = 1.5 × 10⁻¹⁰). Importantly, the contrasting estimates of thermal safety margins obtained with this approach are comparable to the 8.8°C difference observed between CT_max estimated in insects at the organismal versus population level (figure 4), suggesting that this result does not stem from taxonomic differences and indeed reflects the effects associated with distinct levels of biological organization.

Figure 5.

Predicted vulnerability and resilience to ongoing global warming can change considerably depending on the organization level used to characterize the thermal performance curve. (a) Collection sites for the lizards (red) and insects (yellow) included in the dataset. (b) Thermal safety margins, estimated as the difference between CT_max and the average temperature of the warmest month, differ by roughly 9.1°C between curves obtained for running speeds and intrinsic rates of increase. (Online version in colour.)

4. Discussion

(a). Standard functions to study thermal performance curves

Which mathematical model is best suited to characterize performance curves remains a crucial and yet unanswered question in thermal biology [32,33]. Here we provide a general framework to analyse, describe and ultimately compare thermal performance curves. The proposed mathematical model is biologically realistic and contains few parameters (k = 4) that are relatively straightforward to interpret and whose contribution to the overall shape of the thermal performance curve can be readily understood (electronic supplementary material, figure S1). By contrast, previous studies have either focused on the region of exponential increase in performance [8,17,21,34,35], or worked with ad hoc models that are primarily phenomenological [32,33] or contain statistical parameters with limited biological significance [9,32], or more realistic models that can be prohibitively complex owing to the high number of parameters involved (k = 6) [36,37]. And while we have employed Q₁₀ as an estimator of thermal sensitivity to thermodynamic effects, which is generally more intuitive to interpret than activation energy, the Boltzmann–Arrhenius model can also be implemented with this approach and activation energy calculated as E_a = − T²RlnQ₁₀/10, where R is the gas constant and T is expressed in kelvin. While this equality emphasizes that Q₁₀ is not entirely constant across different T [38], models employing equation (2.1) and its Boltzmann–Arrhenius counterpart exhibit virtually identical behaviours and indicate that assuming a constant Q₁₀ constitutes a good approximation (E. L. Rezende 2018, personal observation).

Importantly, in the proposed model, the relationship between classical descriptors of the thermal performance curve, such as the critical thermal limits CT_min and CT_max, the thermal breadth, T_opt and maximum performance, and parameters C, Q₁₀, T_th and d is relatively intuitive. Whereas C and T_th describe displacements of the curve in the vertical and horizontal directions, everything else being equal, variation in Q₁₀ and d falls in a single dimension that describes thermal breadth (electronic supplementary material, figure S2), with low values giving rise to broad curves and high values narrow ones. The overall scenario is more complex, however, because both the descriptors and the parameters of the curve are highly integrated and expected to respond in tandem (electronic supplementary material, figure S1). For instance, one might intuitively expect selection for increased cold tolerance (i.e. a lower CT_min) to favour a lower Q₁₀ or a lower T_th, but these responses will lead to a major drop in performance, respectively, across the whole thermal range or at higher temperatures. Accordingly, a close inspection shows that all parameters contribute to maximum performance, which increases with C, Q₁₀ and T_th and decreases with d (electronic supplementary material, figure S1). While this indicates, on the one hand, that organisms could maximize their performance in multiple ways even under this simple model, this result might also suggest that thermal performance curves are highly constrained and that their descriptors may not be able to respond in an independent fashion to different selective pressures. This should not be surprising because a crucial determinant of performance is thermodynamics [8,15,17,21,34,35], which is expected to affect the shape of performance curve in one way or the other regardless of the formal functions employed to describe it.

In this context, we argue that adopting a set of standard thermal performance curves, with biologically realistic parameters and a mathematical behaviour that is well understood, can be highly beneficial to the field for multiple reasons. First, it opens the way to quantify and compare different thermal performance curves employing common mechanistic parameters, such as Q₁₀ and T_th, and heuristic descriptors, such as T_opt and CT_max, to investigate broad generalities in thermal biology and bridge the gap across research areas. Here, for instance, we were able not only to study the putative effects of biological complexity in thermal breadth combining a set of different variables measured in different units and contrasting conditions (figure 2), but also to estimate CT_max for photosynthetic rates despite the scarcity of empirical estimates reported for this physiological variable (figure 3). Second, it provides an a priori set of rules that describe how multiple descriptors of the thermal performance curve might respond in tandem, effectively constraining the range of possible responses and opening up a way to disentangle presumably adaptive responses from putative correlated ones. The interrelationship between descriptors of the curve is expected to vary according to different evolutionary scenarios—e.g. the warmer-is-better hypothesis proposes that T_opt and maximum performance are positively correlated due to thermodynamic constraints [39–41], whereas the allocation hypothesis suggests a generalist-specialist trade-off and a negative association between maximum performance and thermal breadth [42–44]—hence a more holistic understanding of what is actually theoretically possible is not only desirable but also highly necessary. Third, parameter estimation with standard approaches might shed light on previously unnoticed general rules. For instance, while it is generally acknowledged that the sensitivity of physiological systems to temperature change ranges between Q₁₀ = 2 and 3 [38,45], our analyses might indicate that intrinsic rates of increase and other descriptors of fitness exhibit a higher thermal sensitivity with Q₁₀ ≥ 3 (electronic supplementary material, figure S2). Accordingly, previous studies have reported E_a in the order of 0.65 eV for physiological processes and respiration rates [17,46], which corresponds to a Q₁₀ approximately equal to 2.3 at 25°C (see above), and in the order of 0.98 eV or Q₁₀ approximately equal to 3.8 for population measures [17,19,39,41,47]. While one could argue that these results might reflect a bias towards smaller organisms whose population dynamics are highly sensitive to temperature, these alternative hypotheses might eventually be answered precisely by adopting standardized analytical functions to study and describe thermal performance curves. Fourth, by understanding what the general rules are we may also study how exceptions emerge, such as the bimodal metabolic curve reported in intertidal snails, which presumably reflects the overlap of curves with different optima since these animals are active at cold temperatures underwater and must also cope with high air temperatures during periods of inactivity at low tide [22]. In this context, the adoption of a common framework should also open the way to understanding how multiple processes, many of them dependent on T and encompassing different levels of organization, interact to give rise to patterns of thermal dependence that scale up with biological complexity.

(b). Temperature range and biological complexity

The thermal performance curves describing the effects of temperature on photosynthetic rates, running speeds and intrinsic rates of increase vary substantially in shape (figures 2 and 3), with the pronounced reduction in the thermal range in which performance is elevated being the most relevant pattern unravelled by our analysis (figure 3d). To put these results in the appropriate context, T_breadth extreme values were 8.7 and 44.4°C, which constitutes a massive difference given that they estimate the temperature range in which the system is functional at 50% of its maximum capacity at the least. We argue that the levels of organization involved and ultimately complexity are the main drivers of this pattern even though, admittedly, observed effects are confounded with taxonomic identity (figure 1c) and possibly, to a lesser degree, with geographical origin (see below).

While the information remains highly fragmented because measurements at different levels of organization often involve different lineages for practical reasons—i.e. measuring how locomotor performance varies with temperature in a lizard is fairly straightforward, whereas the same sort of study estimating intrinsic rates of increase is logistically very difficult—multiple lines of evidence support our general interpretation. For instance, comparisons, where we can actually disentangle these effects, indicate that curves differ between levels of biological organization but not necessarily between taxa (figure 4). In addition, Dell et al. [17, p. 10 593] reported in their exhaustive review that ‘level of organization is also a strong predictor of mean rise activation energies, with internal and individual having a much lower mean E_a than population’, though once again their analyses pool different variables measured across different organisms. On the decreasing side of the curve, Somero [48] reports 50% loss of protein structure at temperatures between 45 and 68°C in vertebrate species that encounter maximum temperatures in the range of −2°C and 47°C, showing that upper limits in protein structure far exceed comparable estimates at the organismal or population level. And last but not least, different ecological patterns, such as seasonal reproduction or migration, reflect to a large degree the common observation that individuals can frequently tolerate thermal conditions that, in the long term, would be detrimental at the population level and ultimately be unsustainable.

Importantly, while additional work is certainly necessary to shed light on how thermal sensitivity may vary across different biological systems, the fragmented evidence compiled here indicates that differences across levels of biological organization may be substantial (e.g. 8.8°C between CT_max estimated at the organismal versus population level in insects; figure 4). Future studies may address empirically how thermal dependence varies within taxa across multiple biological levels, which is realistic at least for some study models. Biochemical reaction rates, whole-organism performance and intrinsic rates of population increase can all be measured in some species of insects (e.g. aphids, Drosophila), for instance, and experimental designs comparing cold- versus warm-adapted populations and/or species would open the way to studying how performance curves might differ across levels of organization as a result of thermal adaptation.

(c). Repercussions

Here we develop a theoretical framework to study thermal performance curves and show that the range of temperatures in which performance remains elevated becomes constrained as biological complexity increases (figure 3). In hindsight, this result is not entirely surprising, comparative physiologists have long recognized that the thermal range for growth and reproduction is narrower than the range required for short-term survival [49,50], and here we were able to study this phenomenon employing thermal performance curves. More importantly, however, indices such as critical thermal limits or optimal temperatures are being increasingly employed for predictive purposes to assess how vulnerability to climate warming varies across lineages or geographical locations [9–12,20,28,29], rendering it imperative to assess whether the bias we observe in our dataset constitutes a general phenomenon. In this context, differences in specific estimates such as CT_max across traits may be substantial, as shown for the insect dataset (above), and may have important effects on estimations of resilience to climate change such as temperature safety margins and on niche distribution models [13]. If the general pattern reported here holds across traits, lineages and/or geographical locations, then both the breadth of the performance curve as well as thermal safety margins may have been grossly overestimated in previous analyses employing organismal performance as a proxy for fitness. It is also unclear whether qualitative patterns, such as the presence of latitudinal variation in some descriptors of the curve (of absence thereof), actually hold across levels of biological organization, which is particularly important given that CT_max at the organismal level is seemingly independent of latitude in many ectothermic lineages ([10,11], but see [49]).

Ultimately, our analyses provide a reminder that the adequacy of the overall framework of thermal performance curves as a predictive tool relies on the validity of its underlying assumptions, a crucial one being that the index of performance under study is correlated with fitness [12]. Certainly, thermal performance curves differ in shape even across different life-history measures of fitness (i.e. the net reproductive rate and the intrinsic rate of increase employed here), and their correlation with different life-history components such as development rates or life-time fecundity can vary substantially, albeit being generally positive and often high [51]. In spite of these uncertainties, multiple adaptive patterns and broad geographical trends have been reported and, therefore, the main question remains how to dampen the overall uncertainty in parameter estimation of the curve to enhance predictive power. The use of instantaneous performance measures remains imperative in a multitude of (if not most) organisms for practical reasons [12,14], and therefore future studies must find a balance between what is logistically feasible and what is biologically informative. Given the increasing amount of information available both on different proxies of thermal tolerance and on climate forecasts, as a rule-of-thumb we would strive for future analyses to consider the temporal dimension of both the thermal stress [52] and the response [53,54] when forecasting biological responses to future climate scenarios. While short-term fluctuations may affect instantaneous performance and/or survival [53–55], in the long term, cumulative effects of sub-lethal temperatures on energy balance [8], fecundity or developmental rates [51,54] may scale up and ultimately impair fitness and population resilience. Because thermal performance curves estimated at different levels of organization implicitly involve a temporal dimension (i.e. an organism exposed to extreme temperatures may die within minutes or hours, whereas generation times underlying population dynamics may vary from days to years), employing thermal descriptors that somehow acknowledge this dimension, such as average daily maxima when working with knockdown or lethal temperatures or monthly means for fitness estimations in short-lived organisms, might provide more reliable forecasts of resilience or vulnerability to ongoing climate change.

From a mechanistic perspective, our results require further examination. Given the general effects of temperature in biological systems, ranging from biochemical reactions to life-history attributes, an integrative theory of thermal adaptation must somehow address how temperature effects scale up with biological organization. Our analysis could indicate that, at a fundamental level, the temperature range in which performance can be maximized decreases with biological complexity. In this scenario, ‘thermal adaptation’ might constitute an emergent property that varies systematically across organization levels, and if this happens to be the case, one must wonder exactly how does this happen and how to employ this knowledge with the ultimate purpose of predicting, in the near future, the potential responses of natural populations to ongoing global warming. In this context, while we agree with the recent proposition that ‘we need to better understand the relationship between instantaneous performance and long-term fitness, for example, via longitudinal studies in nature, or via molecular or physiological markers of performance characteristics of wild-caught animals' [14, p. 1382], we would also emphasize that much has to be gained from more theoretical attempts to unravel how responses to temperature and thermal performance curves emerge with complexity from the bottom up [44,56].

Data accessibility

Data and scripts are available in the electronic supplementary material.

Authors' contributions

E.L.R. and F.B. designed the study. E.L.R. compiled the data and performed the analyses. Both authors worked on the original draft.

Competing interests

We declare we have no competing interests.

Funding

This work was funded by FONDECYT grants no. 1170017 to E.L.R. and no. 1190007 to F.B., and by CONICYT PIA/BASAL FB0002 line 3 to F.B.