Genome-wide association study and genomic predictions for exterior traits in Yorkshire pigs

Abstract

The objectives of this study were to identify informative genomic regions that affect the exterior traits of purebred Korean Yorkshire pigs and to investigate and compare the accuracy of genomic prediction for response variables. Phenotypic data on body height (BH), body length (BL), and total teat number (TTN) from 2,432 Yorkshire pigs were used to obtain breeding values including as response variable the estimated breeding value (EBV) and 2 types of deregressed EBVs—one including the parent average (DEBVincPA) and the other excluding it (DEBVexcPA). A final genotype panel comprising 46,199 SNP markers was retained for analysis after quality control for common SNPs. The BayesB and BayesC methods—with various π and weighted response variables (EBV, DEBVincPA, or DEBVexcPA)—were used to estimate SNP effects, through the genome-wide association study. The significance of genomic windows (1 Mb) was obtained at 1.0% additive genetic variance and was subsequently used to identify informative genomic regions. Furthermore, SNPs with a high model frequency (≥0.90) were considered informative. The accuracy of genomic prediction was estimated using a 5-fold cross-validation with the K-means clustering method. Genomic accuracy was measured as the genomic correlation between the molecular breeding value and the individual weighted response variables (EBV, DEBVincPA, or DEBVexcPA). The number of identified informative windows (1 Mb) for BH, BL, and TTN was 4, 3, and 4, respectively. The number of significant SNPs for BH, BL, and TTN was 6, 4, and 5, respectively. Diversity π did not influence the accuracy of genomic prediction. The BayesB method showed slightly higher genomic accuracy for exterior traits than BayesC method in this study. In addition, the genomic accuracy using DEBVincPA as response variable was higher than that using other response variables. Therefore, the genomic accuracy using BayesB (π = 0.90) with DEBVinPA as a response variable was the most effective in this study. The genomic accuracy values for BH, BL, and TTN were calculated to be 0.52, 0.60, and 0.51, respectively.

Introduction

External appearance traits such as body length (BL) and body height (BH) are major criteria in the pig breeding industry. Several studies have reported positive genetic correlations between body conformation-related traits and body growth, sow reproductive efficiency, and longevity (Hoge and Bates, 2011; Nikkilä et al., 2013; Le et al., 2016). Teat number, another important exterior trait, has also been frequently reported for causing involuntary culling occurrences in the selection criteria for sow breeding goals. In the modern pig industry, dam lines have been selected for the genetic improvement of reproductive traits such as litter size. Accordingly, maternal ability, indicated by teat number, has become a more important trait in nursery sows as litter sizes increase.

At present, the availability of commercial dense platforms of SNP markers from companies such as Illumina, Neogen-GeneSeek, and Affymetrix have offered new opportunities that may lead to greater genetic improvements compared with using only pedigree and phenotypic records in the livestock industry. A number of quantitative trait loci (QTLs) affecting external appearance traits in pigs have been reported (Pig QTLdb, https://www.animalgenome.org/cgi-bin/QTLdb/SS/index; Hu et al., 2016). However, only a few research groups have attempted a genome-wide association study (GWAS) approach to investigate QTLs for body conformation- and teat number-related traits (Fan et al., 2011; Fernández et al., 2012; Wang et al., 2014; Yang et al., 2016; Le et al., 2017), rather than candidate gene associations using a linkage mapping approach. To date, 2 major QTL regions affecting body conformation-related traits such as BH and BL have been identified, located on SSC17 at 17 Mb (a candidate region for the BMP2 gene) and SSC1 at 270 Mb (a candidate region for the PAPPA gene). A region significantly affecting teat number-related traits, around the VRTN gene, was also identified using GWAS (Arakawa et al., 2015; Yang et al., 2016).

To maximize the response to selection in pig breeding, independent culling for poor external appearance traits should be minimized through genetic improvements. In addition, improving the accuracy of selection for external appearance traits using genomic information from dense SNP markers, also commonly referred to as genomic selection, would provide a great benefit to the pig breeding industry. To date, it has not been studied to have focused on assessing the accuracy of genomic prediction for body conformation- and teat number-related traits in Korean Yorkshire pigs. Therefore, the objectives of the current study were 1) to identify putative QTL regions affecting the external appearance of pigs and 2) to investigate and compare the accuracy of genomic prediction methods for response variables using dense SNP markers in purebred Korean Yorkshire pigs.

MATERIALS AND METHODS

Genotype and Phenotype Editing

A total of 3,195 Yorkshire pigs from 3 great grand parents (GGP) farms in Korea were genotyped using Illumina PorcineSNP60 version 2 (Illumina, San Diego, CA) comprising 61,565 SNP markers. Of the 3,195 Yorkshire pigs, 600 genotyped animals (from 2 GGP farms) were only recorded for the total teat number (TTN) phenotype, whereas rest of the genotyped animals (from one GGP farm) were recorded for BH, BL, and TTN at 90 ± 5.0 kg. The SNP markers were quality-controlled using the following 3 exclusion criteria: 1) SNPs not mapped to the porcine reference genome build Sscrofa10.2 (http://www.ensembl.org/Sus_scrofa/Info/Index), 2) SNPs on sex chromosomes, and 3) SNPs with a poor call rate (<0.95). This led to a total of 46,199 available SNP markers for analysis. Duplicated animals (n = 60), which occurred because of regenotyping for acceptable call rates, and animals with lower call rates (n = 30) were removed after comparing the animals’ call rates; animals with <0.95 call rates (n = 33) were also removed. Parentage tests were performed using the SEEKPARENTF90 software (Aguilar et al., 2014) with known parent–offspring in the pedigree file based on genotyped animals. A conflict threshold of 10% was used to detect paternity errors and to correct the pedigree file. Consequently, 274 genotyped animals were removed to correct the pedigree file. Furthermore, genotype identifications that could not be matched to corresponding animals (n = 426) in the phenotypic and pedigree files were removed. After applying such restrictions, 2,432 genotyped animals remained for GWAS and genomic prediction. Imputation for missing SNP genotypes (0.24%) was performed using FImpute version 2.2 (Sargolzaei et al., 2014).

Estimated Breeding Values and Deregression of Estimated Breeding Values for Response Variables

The program ASReml version 4.1 (Gilmour et al., 2015) was used to estimate the variance components and genetic parameters (Table 1), which were required as prior information for genomic prediction modeling, estimated breeding values (EBVs), and the corresponding reliability of the genotyped animals and their sires and dams for the 3 exterior traits BH, BL, and TTN. Phenotypes were adjusted for contemporary groups; farm of origin, birth-year and season, and sex were used as fixed effects. The effect of a common litter environment was also considered in our animal model for those parameters and EBV. We used the methodology provided by Garrick et al. (2009) to define the 2 kinds of deregression of EBVs (DEBVs): 1) a combination of deregression (dividing by the reliability of EBV) and adjusting for ancestral information (parents’ average values), such that the values included only their own and their descendants’ information (hereafter referred as “DEBVexcPA”), and 2) in contrast to Garrick et al. (2009), the EBV parent average (PA) was added back to DEBV (hereafter referred to as “DEBVincPA”) to account for breed and family differences in subsequent analyses. Both DEBVexcPA and DEBVincPA were obtained using the following defined mixed model equation:

Table 1.

Variance components and heritability estimates for growth and reproductive traits in Yorkshire pigs

Trait1	Additive genetic variance	Phenotypic variance	Heritability
BH	2.169	6.994	0.310
BL	7.237	21.061	0.344
TTN	0.370	0.899	0.412

¹BH = body height; BL = body length; TTN = total teat number.

$${\displaystyle \begin{array}{l}{\displaystyle {\left[\begin{array}{ll}{Z^{\prime }}_{PA}{Z}_{PA}+4\lambda & {\displaystyle -2\lambda }\\ -2\lambda & {\displaystyle {Z^{\prime }}_i{Z}_i+2\lambda }\end{array}\right]}^{-1}\left[\begin{array}{l}{y}_{PA}^{\ast }\\ y_i^{\ast }\end{array}\right]=\left[\begin{array}{l}{{\displaystyle \widehat{g}}}_{PA}\\ {{\displaystyle \widehat{g}}}_i\end{array}\right]}\end{array}}$$

where ${\widehat{g}}_{PA}$ is the PA for the EBV,${\widehat{g}}_i$ is the individual EBV, and λ is calculated as $(1-h^2)/h^2$. The diagonal elements on the left-hand side matrix were solved by ${Z^{\prime }}_{PA}{Z}_{PA}=\lambda (0.5\alpha -4)+0.5\lambda \sqrt{({\alpha }^2+16/\delta )}$and ${Z^{\prime }}_i{Z}_i=\delta {Z^{\prime }}_{PA}{Z}_{PA}+2\lambda (2\delta -1)$ using a direct approach, where $\alpha =1.0/(0.5-r_{PA}^2)$, $\delta =(0.5-r_{PA}^2)/(1.0-r_i^2),$ and $r_{PA}^2=\frac{r_{sire}^2+r_{dam}^2}{4}$. Through above mixed model equation, deregressed information and the corresponding reliability values—ignoring the PA—were obtained as $y_i^{\ast }/(\lambda +{Z^{\prime }}_i{Z}_i)$, and $1.0-\lambda /(\lambda +{Z^{\prime }}_i{Z}_i)$. The DEBV was calculated by dividing by EBV reliability, $\frac{y_i^{\ast }/(\lambda +{Z^{\prime }}_i{Z}_i)}{1.0-\lambda /(\lambda +{Z^{\prime }}_i{Z}_i)}$. More details on these approaches for DEBV are described by Garrick et al. (2009). The response variable was weighted to account for the heterogeneous variance of DEBV due to the differences in EBV reliabilities among genotyped animals. The weighting factor ($w_i$) for each animal i was calculated following Garrick et al. (2009):

$${\displaystyle \begin{array}{l}{\displaystyle w_i=\frac{(1-h^2)}{\{c+[(1-r_i^2)/r_i^2]\}{h}^2}}\end{array}}$$

where $r_i^2$ is the reliability of deregressed EBV, h² is the heritability of the trait, and c is the proportion of genetic variation not explained by markers. In this study, c was assumed to be 0.40, as previously suggested (Saatchi et al., 2012). Finally, after removing animals with a reliability of <0.10, a total of 1,857 registered Yorkshire pigs were used for further analysis.

Statistical Methods

We considered 3 models from the Bayesian alphabet family—BayesB (Hayes and Goddard, 2001), BayesC (Kizilkaya et al., 2010), and BayesCπ (Habier et al., 2011)—as representative of the most widely used methods for genomic prediction in livestock industry; these methods depend on the real distribution of SNP marker effects relative to other genomic prediction methods, such as GBLUP and RR_BLUP. The BayesB and BayesC methods, with estimated π (BayesCπ) and various fixed π values and weighting factors, were used to estimate SNP marker effects using GenSel4R software (Garrick and Fernando, 2013) for GWAS and genomic prediction models. The BayesB and BayesC methods use mixture models assuming that a fraction (π) of SNP markers have zero effects. The BayesB method assumes locus-specific variances with respect to SNP variances, whereas BayesC and BayesCπ consider common variances across loci (Habier et al., 2011). In addition, π is treated as an unknown with a uniform (0,1) prior in the BayesCπ model. Finally, π can be drawn from a beta distribution and the staring value for π was set to 0.5 in GenSel4R software (Garrick and Fernando, 2013). For each trait, the following model was fitted to estimate SNP marker effects for these 3 Bayesian methods:

$${\displaystyle \begin{array}{l}{\displaystyle y_i=1\mu +{\displaystyle \underset{j=1}{{\displaystyle \sum ^k}}}{Z}_{ij}{u}_j{\delta }_j+e_i}\end{array}}$$

where y_i is the response variables (DEBVexcPA, DEBVincPA, and EBV) for each animal i for each trait; μ is the population mean; k is the number of SNP markers; Z_ij represents allelic state at locus j (AA = −10, AB = 0, and BB = 10) in individual i; u_j is the random substitution effect for marker j, which follows a mixture distribution for this random substitution effect according to indicator variable $({\delta }_j)$, a random 0/1 variable indicating the absence or presence of marker j in the model, with u_j assumed to be normally distributed N(0,${\sigma }_u^2$) when ${\delta }_j=1$, and otherwise u_j assumed 0; and $e_i$ is a random residual effect assumed normally distributed N(0,${\sigma }_e^2$).

The posterior distributions of the parameters and effects were obtained using Gibbs sampling for a total number of 110,000 Markov chain Monte Carlo (MCMC) iterations, where the first 10,000 samples were discarded as the burning period. Finally, a total of 10,000 samples were collected after the burning period by saving every tenth sample to avoid autocorrelation (thinning). These samples were used for the estimation of the posterior means of SNP marker effects and variances. All procedures for GWAS and genomic predictions were implemented using GenSel4R software (Garrick and Fernando, 2013).

Identification of Significant Window Regions and SNP Markers

A value of 1.0% for additive genetic variance, which was estimated as a fraction of the total genetic variance explained by all SNPs, was used for the significance level of the putative informative 1-Mb window region. A total of 2,451 of 1-Mb windows located on autosomes were involved in the analyses. The theoretical proportion to the genetic variance of a trait was assumed approximately 0.041% (100%/2,451), but the stringent cutoff of 1% which indicates more than 25 times higher proportion was considered in subsequent analyses. Furthermore, SNPs with a high model frequency (≥0.90; i.e., the putative SNP was included in the model for over 90% of MCMC iterations), defined as the proportion of fitted models to estimate SNP marker effects, were also used to determine SNPs with significant associations.

The Accuracy of Genomic Prediction

Cross-validation

A 5-fold cross-validation strategy was used to estimate the accuracy of genomic predictions. For each exterior trait of interest in this study, genotyped animals were split into 5 groups using K-means clustering to reduce the relationships between training and testing populations, following the procedures outlined by Saatchi et al. (2011). A total of 3,969 pedigree data values relating to 1,857 genotyped Yorkshire pigs were used for K-means clustering. The number of individuals within each fold, within and between fold averages of a_max and a_ij, and their SD are given in Table 2, which also shows that the data were successfully partitioned by K-means clustering, whereby the relatedness was maximized within each partitioned group and minimized between each partitioned group.

Table 2.

Comparison of the relationships among animals within and across clusters with 5-fold cross validations using the K-means clustering method

No. of clusters	No. of animals	inBreC1	a max_within 2	a max_between 3	a ij_within 4	a ij_between 5
1	456	0.043	0.54 (0.08)	0.44 (0.12)	0.14 (0.02)	0.07 (0.01)
2	337	0.037	0.52 (0.08)	0.44 (0.13)	0.13 (0.02)	0.07 (0.01)
3	410	0.042	0.53 (0.08)	0.44 (0.12)	0.13 (0.02)	0.07 (0.01)
4	269	0.048	0.56 (0.06)	0.19 (0.12)	0.13 (0.02)	0.01 (0.00)
5	385	0.026	0.50 (0.09)	0.44 (0.12)	0.08 (0.02)	0.06 (0.01)

¹inBreC = inbreeding coefficients within clusters.

² a _{max_within} = the average a_max value (the maximum value of relationships for each individual) within clusters.

³ a _{max_between} = the average a_max value between clusters (training and testing).

⁴ a _{ij_within} = the average a_ij values (relationships) within clusters.

⁵ a _{ij_between} = the average a_ij value between clusters (training and testing).

Estimation of the accuracy of genomic prediction

We used a bivariate animal model with the molecular breeding value (MBV; sum of all SNP marker effects) of the genotyped animal from each validation set, weighted response variables (EBV, DEBVexcPA, and DEBVincPA), and pedigree information related to genotyped animals for genetic correlations in the evaluation using ASReml version 4.1 (Gilmour et al., 2015). MBV and weighted response variables were used as dependent variables. The model with MBV used a fixed effect for the intercept, a random additive genetic effect, and a residual with variance fixed at 0.0001% of unweighted phenotypic variance of the response variable. The model for each response variable used a fixed effect for the intercept, a random additive genetic effect, and a weighted random residual of $Var(e)=W{\sigma }_e^2$, where W is the r-inverse weighting according to the reliability of genotyped animals and similarity to that used in the training set for the estimation of SNP effects. The additive genetic and unweighted residual variances were fixed with 0.4 and 0.6, respectively, based on the deregressed unweighted phenotypic variance of the response variable. In addition, we provided the accuracy (accessed by simple Pearson’s correlation) and bias (accessed by regression) using single-step genomic BLUP approach with same cross-validation method in Supplementary Table S1.

RESULTS AND DISCUSSION

GWAS of 3 Exterior Traits

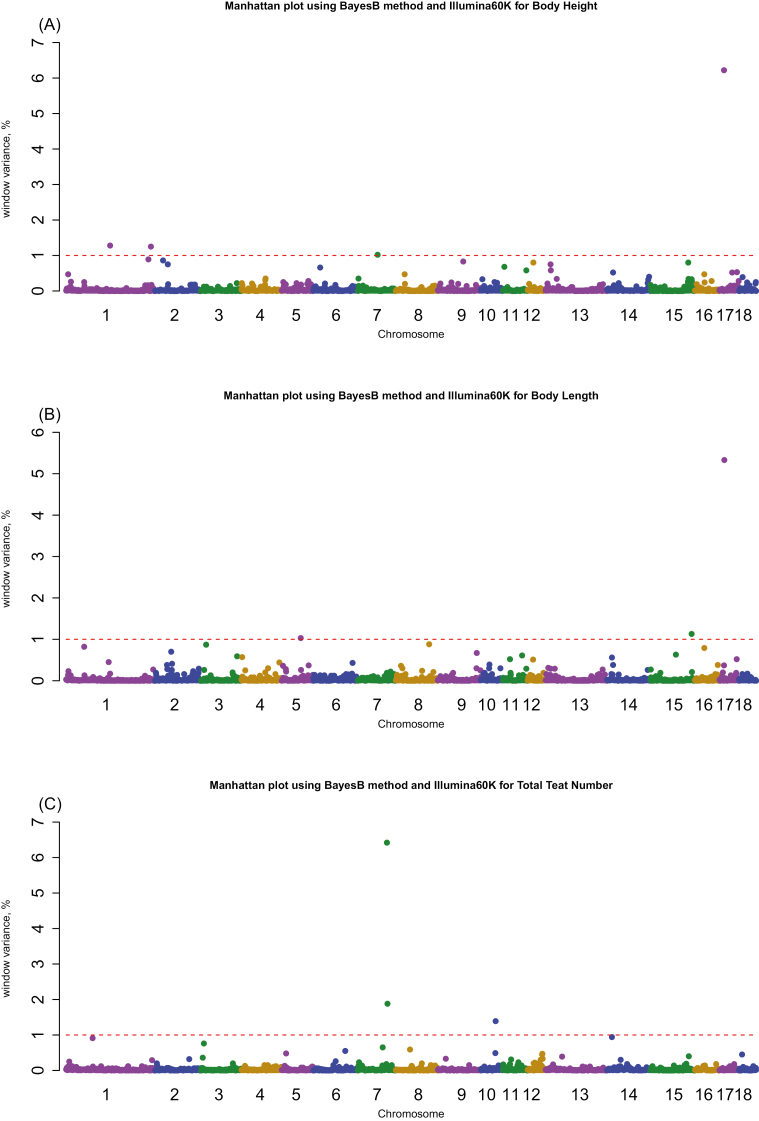
GWAS was performed using the BayesB method with a high π value (0.99) to allow only regions with the strongest associations to be identified, as well as the DEBVincPA response variable for 3 exterior traits in Yorkshire pigs; these characteristics were chosen because the informative window region and significant SNP markers were similarly distributed across all 3 response variables, Bayesian methods, and various π values. The results of these associations are shown in Table 3 and Fig. 1. We performed a GWAS analysis using a commercially developed Porcine SNP genotyping platform (PorcineSNP60 BeadChip) to identify the most informative window regions and the most frequent model-selected SNPs within these regions. Table 3 shows the results of our analysis of the 3 exterior traits, including chromosomal and window location (Mb), the percentage variance of 1-Mb genome windows for the informative window regions or for the most significant windows, SNP name, physical genome position (bp), model frequency, gene frequency, and the additive effect of significant SNPs within these regions in Yorkshire pigs. Manhattan plots based on the percentage of explained additive genetic variance in each 1-Mb window region for 3 exterior traits in Yorkshire pigs are shown in Fig. 1. A total of 2,451 of 1-Mb genome windows were found in the porcine genome, with an average of 19 SNP markers per window. The most significant SNP marker (ALGA0075964), based on the model frequency of the SNP markers, was associated with BH and BL and was located on SSC14 at 21.70 Mb, between 2 novel candidate genes (NEK1 and SH3RF1). For TTN, the ASGA0035563 marker on SSC7 (105.28 Mb) was the most significant region. The highest percentage of additive genetic variance (6.22%) for BH was identified on SSC17, between the 16.46- and 16.99-Mb regions, and contained 15 SNPs. Similarly, a region on the same chromosome containing 10 SNPs (SSC17; 17.10 to 17.92 Mb) accounted for the highest percentage of additive genetic variance (5.33%) for BL. The BMP2 gene on SSC17, a member of the bone morphogenetic protein family regulating early myogenesis, also resides within these regions. Fan et al. (2011) also reported that this gene was associated with body conformation (BL and body depth) and loin muscle area traits, consistent with our results. We identified 3 regions affecting TTN on SSC7 and SSC10; 2 regions on the former were about 2 Mb apart from each other. On SSC7, 2 significant SNP markers (DIAS0000795 at 103.59 Mb; ASGA0035500 at 103.57 Mb) accounted for the highest percentage of additive genetic variance (6.42%) based on the model frequency of SNP markers. Both markers were also found to be situated close to 2 candidate genes known as NPC2 and DLST. Previous studies (Mikawa et al., 2011; Fan et al., 2013) have identified a QTL from the VRTN gene, located at 103.40 Mb on SSC 7, using Sscrofa10.2. In addition, SSC7 (105.16 to 105.98 Mb) harbored a significant SNP marker at 105.28 Mb (ASGA0035563), with the highest model frequency accounting for 1.88% of additive genetic variance. Other QTL windows were also identified on SSC10 at 52.00 Mb for TTN, accounting for 1.88% of additive genetic variance for TTN. However, the detection of multiple markers for body conformation in adjacent regions could be due to their high linkage disequilibrium within the same QTL. To account for this, future studies will require a fine-mapping study using a high-density genotyping array from Affymetrix (Axiom porcine 660K), or sequencing data, to pinpoint the causal variants in these identified QTL regions, especially for those containing the BMP2 and VRTN genes, which are associated with the 2 body composition and TTN traits.

Table 3.

Informative 1-Mb genome windows and informative SNPs within windows associated with BH, BL, and TTN in Yorkshire pigs from genome-wide association study using markers from Illumina PorcineSNP60

Trait1	SSC_Mb2	%GV3	Informative SNPs	Position (Mb)	Effect	Model freq.4	Gene freq.	Region annotation	Candidate gene annotation
BH	17_16	6.22	ALGA0093437	16.77	1.210	0.996	0.124	Intergenic	CHGB (dist = 897485)	BMP2 (dist = 285054)
	1_156	1.28	INRA0004431	156.99	−0.117	0.249	0.163	Intergenic	SELENOS (dist = 924259)	UBE3A (dist = 793234)
			ALGA0006162	156.15	−0.107	0.240	0.168	Intergenic	SELENOS (dist = 86276)	UBE3A (dist = 1631217)
			H3GA0002868	156.89	−0.109	0.237	0.163	Intergenic	SELENOS (dist = 820957)	UBE3A (dist = 896536)
	1_301	1.25	H3GA0004927	301.11	0.357	0.927	0.342	Intergenic	MIR9793 (dist = 71100)	LMX1B (dist = 42143)
	7_70	1.02	MARC0112179	70.69	−0.295	0.808	0.719	Intergenic	SNX6 (dist = 694738)	NONE
BL	17_17	5.33	MARC0070553	17.48	1.890	0.938	0.130	Intergenic	BMP2 (dist = 66669)	HAO1 (dist = 1335045)
	15_146	1.13	H3GA0045481	146.93	−0.268	0.428	0.286	Intergenic	DIS3L2 (dist = 73972)	EIF4E2 (dist = 32189)
			H3GA0053491	146.13	−0.180	0.311	0.424	Intergenic	NMUR1 (dist = 128051)	NPPC (dist = 218413)
	5_67	1.03	ALGA0032447	67.82	0.460	0.767	0.607	Intergenic	KCNA5 (dist = 160778)	AKAP3 (dist = 187257)
TTN	7_103	6.42	DIAS0000795	103.59	−0.126	0.531	0.613	Intergenic	NPC2 (dist = 12395)	DLST (dist = 340321)
			ASGA0035500	103.57	0.104	0.438	0.387	Intronic	NPC2
	7_105	1.88	ASGA0035563	105.28	−0.137	0.607	0.090	Intergenic	TGFB3 (dist = 81987)	GPATCH2L (dist = 90032)
			MARC0027367	105.31	−0.038	0.311	0.598	Intergenic	TGFB3 (dist = 115876)	GPATCH2L (dist = 56143)
	10_52	1.39	M1GA0025060	52.8	−0.044	0.358	0.304	Intergenic	HSPA14 (dist = 1136282)	PRPF18 (dist = 1978)

¹BH = body height; BL = body length; TTN = total teat number.

²SSC_Mb = sus scrofa chromosome_magabase-pair.

³%GV = percentage of additive genetic variance explained by SNP markers within each 1-Mb window region

⁴Model freq. = proportion of Markov chain Monte Carlo iterations that included the corresponding SNP marker.

Figure 1.

Manhattan plots of the results of Bayesian GWAS (BayesB with π = 0.99) on 18 porcine autosomes for 3 exterior traits. The y-axis represents the percentage variance within each 1-Mb genomic region, and the x-axis represents the chromosomal location of each window. The red dotted horizontal lines indicate the threshold of the 1-Mb window variance, which was set at >1.0% to identify associations within traits: (A) body height, (B) body length, and (C) total teat number.

Comparison of Genomic Accuracy

In this study, the comparison of genomic accuracy was performed using various levels of π (0.50, 0.80, 0.90, and 0.99), estimated pi (π_e), and 2 Bayesian methods (BayesB and BayesC). The π_e value was derived from the BayesCπ method, and the differences due to the levels of π were assessed according to the response variables and traits. Using EBV as a response variable, the estimated value of π_e for BH, BL, and TTL were 0.997, 0.995, and 0.999, respectively. Using DEBVexpPA and DEBVincPA, distinct variable measures of π_e were derived for BH (0.986; 0.981), BL (0.982; 0.976), and TTL (0.999; 0.998), respectively (Table 4). The genomic accuracy ranges for different response variables using the BayesB method also differed slightly for the investigated traits. The genomic accuracy ranges for BH at different π and π_e values were between 0.390 and 0.415 (EBV), between 0.396 and 0.411 (DEBVexcPA), and between 0.507 and 0.516 (DEBVincPA). Using the BayesC method, the obtained accuracy ranges for BH based on EBV, DEBVexcPA, and DEBVincPA from 0.382 to 0.408, 0.350 to 0.370, and 0.473 to 0.486, respectively. The genomic accuracy for BL using BayesB ranges from 0.416 to 0.451 for EBV, 0.503 to 0.543 for DEBVexcPA, and 0.568 to 0.613 for DEBVincPA, whereas the BayesC-based ranges were 0.408 to 0.424, 0.390 to 0.467, and 0.499 to 0.539, respectively. The obtained BayesB-based ranges for TTN also varied among response variables; we obtained values of 0.399 to 0.416 (EBV), 0.370 to 0.399 (DEBVexcPA), and 0.485 to 0.507 (DEBVincPA). For the same trait, the BayesC estimates for genomic accuracy using EBV, DEBVexcPA, and DEBVincPA were found to be 0.395 to 0.423, 0.323 to 0.396, and 0.444 to 0.491, respectively. Of the 3 exterior traits, the genomic accuracy ranges for BL were higher than those for BH or TTN (Table 5). The differences in genomic accuracies among different π values were not significant for the studied traits. However, the BayesC method is generally more sensitive to the actual distribution of the marker effects than the other Bayesian methods (Fernando and Garrick, 2013). Thus, it is likely that there would be a significant difference in the accuracy using BayesC according to levels of π. However, we did not find such differences in this study. In this study, the genomic accuracy for exterior traits using the BayesB method was slightly higher than the accuracy using BayesC. The differences between the accuracies among traits were generally within the ranges of their SE, except with those of the BL trait using π values of 0.50, 0.80, and 0.90. The heterogeneous marker variance values assumed in BayesB were often more effective than the homogeneous marker variance values assumed in BayesC. According to Fernando and Garrick (2013), the performance of BayesB is generally better than that of BayesC if an approximated value of π is used. In addition, diversity factors would influence the accuracy of genomic prediction. The response variables in this study, deemed the most influential factor in terms of their derived outcomes, were dependent on the structure and characteristics of the data. Previous studies reported that using EBV as a response variable was more suitable due to the limited applicability of the information (Guo et al., 2010; Gao et al., 2013). In contrast, in this study, the use of EBV as a response variable showed a lower accuracy than DEBVs for all studied traits. One possible explanation for this low performance could be the double counting of pedigree information (Ostersen et al., 2011; Song et al., 2018). Another possible explanation could be the low reliability of EBV, which caused a double shrinkage of the genomic values (Ostersen et al., 2011). In general, the use of EBV, as opposed to DEBV, is considered to be preferable when the EBV reliability of all genotyped animals is somewhat similar. However, the reliability of the genotyped animals was highly variable in this study. An advantage of excluding PA was that double counting was avoided, as this would have shrunk the individual EBV toward the PA (Garrick et al., 2009). On the other hand, the inclusion of PA after deregression had the added advantage of accounting for differences in PA among genotyped animals, such as between-family differences (Lee et al., 2015). For the studied exterior traits, DEBV, as the response variable, showed higher genomic accuracies when PA was included. Model performance was less strongly affected by double counting because it targeted both offspring and parents with genotype information, and our study included genotypic information from sires only. The farm breeding scheme also facilitated the genotyped animals in this study to be less connected from families. Therefore, we believe that the DEBVincPA was the most advantageous for the genomic selection of exterior traits in Korean Yorkshire pigs. This study is the first to attempt to predict the genomic accuracy of exterior traits and could be a useful resource for future studies. However, due to the scarcity of other investigations to support these findings, further studies are required with larger animal samples to confirm these outcomes in Korean Yorkshire pigs.

Table 4.

Estimated pi (π_e) values using the BayesCπ method based on various response variables

Trait1	EBV2	DEBVexcPA3	DEBVincPA4
BH	0.997	0.986	0.981
BL	0.995	0.982	0.976
TTL	0.999	0.999	0.998

¹BH = body height; BL = body length; TTN = total teat number.

²EBV = estimated breeding value.

³DEBVexcPA = deregressed EBV excluding parent average.

⁴DEBVincPA = deregressed EBV including parent average.

Table 5.

Accuracy and standard errors of genomic prediction according to 2 Bayesian methods, various response variables, and various π values

		BayesB						BayesC
Traits1	Response variable2	π = 0.50	π = 0.80	π = 0.90	π = 0.99	πe3	Response variable	π = 0.50	π = 0.80	π = 0.90	π = 0.99	πe3
BH	EBV	0.39 (± 0.034)	0.40 (± 0.034)	0.40 (± 0.034)	0.42 (± 0.033)	0.40 (± 0.033)	EBV	0.38 (± 0.034)	0.39 (± 0.034)	0.39 (± 0.034)	0.41 (± 0.033)	0.40 (± 0.033)
	DEBVexcPA	0.40 (± 0.045)	0.40 (± 0.045)	0.41 (± 0.045)	0.40 (± 0.045)	0.40 (± 0.045)	DEBVexcPA	0.35 (± 0.046)	0.35 (± 0.460)	0.36 (± 0.046)	0.37 (± 0.045)	0.37 (± 0.045)
	DEBVincPA	0.51 (± 0.042)	0.52 (± 0.042)	0.52 (± 0.042)	0.51 (± 0.042)	0.51 (± 0.042)	DEBVincPA	0.47 (± 0.043)	0.48 (± 0.043)	0.48 (± 0.043)	0.48 (± 0.043)	0.49 (± 0.043)
BL	EBV	0.44 (± 0.034)	0.45 (± 0.034)	0.45 (± 0.034)	0.43 (± 0.034)	0.42 (± 0.035)	EBV	0.42 (± 0.035)	0.42 (± 0.035)	0.42 (± 0.034)	0.42 (± 0.035)	0.41 (± 0.035)
	DEBVexcPA	0.54 (± 0.046)	0.54 (± 0.046)	0.53 (± 0.046)	0.50 (± 0.047)	0.51 (± 0.047)	DEBVexcPA	0.39 (± 0.050)	0.40 (± 0.050)	0.41 (± 0.049)	0.47 (± 0.048)	0.46 (± 0.048)
	DEBVincPA	0.61 (± 0.042)	0.60 (± 0.042)	0.60 (± 0.042)	0.57 (± 0.044)	0.59 (± 0.043)	DEBVincPA	0.50 (± 0.045)	0.50 (± 0.045)	0.51 (± 0.045)	0.54 (± 0.044)	0.54 (± 0.044)
TTN	EBV	0.40 (± 0.036)	0.41 (± 0.036)	0.42 (± 0.035)	0.42 (± 0.035)	0.40 (± 0.035)	EBV	0.40 (± 0.036)	0.41 (± 0.035)	0.41 (± 0.035)	0.42 (± 0.035)	0.40 (± 0.035)
	DEBVexcPA	0.37 (± 0.042)	0.38 (± 0.042)	0.39 (± 0.042)	0.40 (± 0.042)	0.39 (± 0.042)	DEBVexcPA	0.32 (± 0.043)	0.33 (± 0.043)	0.34 (± 0.043)	0.40 (± 0.042)	0.39 (± 0.042)
	DEBVincPA	0.50 (± 0.039	0.51 (± 0.039)	0.51 (± 0.039)	0.50 (± 0.039)	0.49 (± 0.039)	DEBVincPA	0.44 (± 0.040)	0.45 (± 0.040)	0.46 (± 0.040)	0.49 (± 0.039)	0.48 (± 0.039)

¹BH = body height; BL = body length; TTN = total teat number.

²EBV = estimated breeding value; DEBVexcPA = deregressed EBV excluding parent average; DEBVincPA = deregressed EBV including parent average.

³Estimated π-values derived from BayesCπ method.

CONCLUSION

In this study, we identified candidate genes affecting exterior traits in Korean Yorkshire pigs and then evaluated and compared the accuracy of the genomic predictions using various levels of π, response variables, and 2 Bayesian methods (BayesB and BayesC). A total of 11 informative window regions for exterior traits were identified. Diversity π showed no influence on the accuracy of genomic prediction. The BayesB method displayed a slightly higher genomic accuracy for exterior traits than the BayesC method in this study. In addition, the genomic accuracy when using DEBVincPA as a response variable was higher than when other response variables were used. The genomic accuracy values using BayesB (with π = 0.90) based on DEBVincPA for BH, BL, and TTN were 0.52, 0.60, and 0.51, respectively. Therefore, we suggest that a fine-mapping study is necessary to pinpoint the causal variants within these informative genomic regions to improve the genomic accuracy for exterior traits. Furthermore, this genomic selection model for exterior traits could be a useful tool for future genomic evaluations in purebred Korean Yorkshire pigs.