Microorganisms are a major component of Earth’s biosphere, and their activity significantly affects the biogeochemical cycling of bioavailable elements. To correctly determine the flux of carbon and energy in the environment, reliable estimates of microbial abundances and cellular carbon content are necessary. However, accurate assessments of cellular carbon content and dry weight are not trivial to obtain. Here we report direct measurements of cell dry and carbon mass of environmentally relevant prokaryotic microorganisms using a microfluidic mass sensor. We show a significant nonlinear relationship between carbon mass and cell volume and discuss this relationship in the light of currently used cellular mass models.
KEYWORDS: bacterioplankton, carbon content, microbial biomass, microorganisms, subsurface
ABSTRACT
Microbial biomass is a key parameter needed for the quantification of microbial turnover rates and their contribution to the biogeochemical element cycles. However, estimates of microbial biomass rely on empirically derived mass-to-volume relationships, and large discrepancies exist between the available empirical conversion factors. Here we report a significant nonlinear relationship between carbon mass and cell volume (; ) based on direct cell mass, volume, and elemental composition measurements of 12 prokaryotic species with average volumes between 0.011 and 0.705 μm3. The carbon mass density of our measured cells ranged from 250 to 1,800 fg of C μm−3 for the measured cell volumes. Compared to other currently used models, our relationship yielded up to 300% higher carbon mass values. A compilation of our and previously published data showed that cells with larger volumes (>0.5 μm3) display a constant (carbon) mass-to-volume ratio, whereas cells with volumes below 0.5 μm3 exhibit a nonlinear increase in (carbon) mass density with decreasing volume. Small microorganisms dominate marine and freshwater bacterioplankton as well as soils and marine and terrestrial subsurface. The application of our experimentally determined conversion factors will help to quantify the true contribution of these microorganisms to ecosystem functions and global microbial biomass.
IMPORTANCE Microorganisms are a major component of Earth’s biosphere, and their activity significantly affects the biogeochemical cycling of bioavailable elements. To correctly determine the flux of carbon and energy in the environment, reliable estimates of microbial abundances and cellular carbon content are necessary. However, accurate assessments of cellular carbon content and dry weight are not trivial to obtain. Here we report direct measurements of cell dry and carbon mass of environmentally relevant prokaryotic microorganisms using a microfluidic mass sensor. We show a significant nonlinear relationship between carbon mass and cell volume and discuss this relationship in the light of currently used cellular mass models.
INTRODUCTION
Global biomass estimates suggest that microorganisms are the second-largest biomass component on Earth. Specifically, prokaryotic microorganisms, such as bacteria and archaea, together constitute 14% of the global biomass (1). In marine environments alone, microorganisms (mainly bacteria and protists) might account for ca. 70% of the total marine biomass (1) and play a key role in the cycling of biogeochemically active elements (2–4). In eutrophic aquatic systems the bacterial biomass (particulate carbon) tends to constitute up to around 30% of total microbial biomass (5, 6). This can increase under oligotrophic conditions when bacteria can dominate over the phytoplankton carbon and constitute the major fraction of particulate organic carbon (up to 60% [7–9]). However, microbial biomass estimates are associated with large uncertainties. In order to calculate the total biomass of a microbial population, cell abundances are converted to biomass using a defined conversion factor (e.g., carbon content per cell). Since direct mass measurements of single cells are difficult, cell mass is often extrapolated from empirically derived mass-to-volume relationships (10–12).
The relationship between cell carbon mass and volume has been determined for a wide range of organisms (13–15). The most basic relationship assumes that the cell volume-to-biomass ratio remains the same for cells of different sizes (e.g., 560 fg of C/μm3 [16], 380 fg of C/μm3 [17], 175 fg of C/μm3 [18], 30 to 162 fg of C/μm3 [19], and 86 fg of C/cell [20]). However, the majority of current models seem to agree that the conversion factor depends on bacterial volume. Some models consider a linear relationship between volume and carbon content, albeit only for a defined narrow cell size range (e.g., 20 fg of C/cell for volumes of 0.036 to 0.073 μm3 [17] and 12.4 and 30.2 fg of C/cell for oceanic and coastal bacterial assemblages with cell sizes of ≤0.8 μm3, respectively [21]). More commonly, the ratio is thought to be dependent on cell size with the shape of a power function (12, 14, 19, 22–24). For example, the allometric relationship reported by Verity and colleagues ( [14]) has been used to determine the biomass of environmentally relevant prokaryotic and picoeukaryotic microorganisms (25, 26). Interestingly, despite its power function, the relationship reported by Verity et al. is not much different from a linear relationship because its scaling factor (0.86) is close to unity. In contrast, Simon and Azam (24) proposed a significant nonlinear relationship between cellular carbon mass and volume with the much lower scaling factor of 0.59 (or 0.72, as reported in reference 27). A compilation of published models showed a relatively weak relationship between cell volume and carbon content (; [28]).
The wide range of the reported relationships between cellular biomass and volume reflects the fact that cellular biomass was largely derived indirectly using different methods on a variety of pro- and eukaryotic organisms (for an overview, see, e.g., references 28 and 29). In this study, we directly determined the mass of single cells of 12 cultivated bacteria and archaea covering a range of volumes typically encountered in aquatic environments. Cell volume and elemental composition were determined in parallel. Together, these measurements were used to determine the relationship between microbial cell volume and carbon, nitrogen, oxygen, sulfur, and phosphorus mass.
RESULTS AND DISCUSSION
Cell dry mass-to-volume relationships.
Cell volume distributions were determined for pure cultures of 12 bacterial and archaeal species of different sizes and shapes (Nitrosopumilus NAOA6, Formosa Hel3_A1_48, Lentimonas CC151, Muricauda MAR_2010_75, Maribacter Hel1_7, Cellulophaga Hel_I_12, Lacinutrix Hel_I_90, Methyloceanibacter methanicus LMG 29429, Methyloceanibacter caenitepidi LMG 28723, Methyloceanibacter stevinii LMG 29431, Nitrotoga fabula KNB, and Kuenenia stuttgartiensis). Environmental representatives related to these species are known to play key roles in the biogeochemical cycling of carbon and nitrogen (for examples, see references 30, to ,32). For proper volumetric measurements, cultures were critical point dried (CPD) directly after fixation and immobilization. To additionally preserve cell morphology, cells were not subjected to vacuum filtration but pipetted onto a poly-l-lysine (PLL)-coated silicon wafer. Volumes of individual cells were calculated from their length and width determined with scanning electron microscopy (SEM) (Fig. 1).
FIG 1.
Representative scanning electron micrographs of the 12 investigated bacterial and archaeal species. All microorganisms were fixed, immobilized on silicon wafers, and critical point dried prior to imaging. The micrographs are ordered according to the cell median volume as follows: Nitrosopumilus NAOA6, Formosa Hel3_A1_48, Lentimonas CC151, Muricauda MAR_2010_75, Maribacter Hel1_7, Cellulophaga Hel1_12, Lacinutrix Hel1_90, Methyloceanibacter methanicus LMG 29429, Methyloceanibacter caenitepidi LMG 28723, Nitrotoga fabula KNB, Kuenenia stuttgartiensis, and Methyloceanibacter stevinii LMG 29431. Scale bars represent 2 μm.
Literature evidence suggests that sample preparation for SEM imaging (chemical fixation, filtration, and staining) tends to alter cell size and shape, resulting in misestimation of cell volume compared to that of living cells (16, 19, 33). Thus, to prove the validity of using SEM for volume determination and/or to establish a correction factor for fixed versus live cell volume calculation, we measured aliquots of the same microbial culture (Formosa Hel3_A1_48) as both fixed, CPD-treated cells with SEM and living cells with atomic force microscopy (AFM). AFM is a scanning-probe microscopic technique that gives highly accurate measurements of not only cell length and width but also height, with a very high spatial resolution. Application of AFM to live and suspended cells is challenging because cells tend to be easily displaced during measurements. Thus, the method is comparably tedious and low throughput, compared to, e.g., SEM. Using our test culture we could not detect significant differences in cell volumes between these two measurements (see Fig. S5a in the supplemental material). We thus proceeded to determine cell volumes from SEM images obtained from fixed and CPD-treated cells.
SEM images revealed that the 12 investigated species represented four distinct cell shape types: (i) rod shaped (Muricauda MAR_2010_75, Cellulophaga Hel1_12, Lacinutrix Hel1_90, Methyloceanibacter methanicus LMG 29429, and Methyloceanibacter caenitepidi LMG 28723), (ii) coccoid (Formosa Hel3_A1_48, Lentimonas CC151, and Kuenenia stuttgartiensis), (iii) prolate spheroid shaped (Nitrosopumilus NAOA6, Maribacter Hel1_7), and (iv) C shaped (Nitrotoga fabula KNB and Methyloceanibacter stevinii LMG 29431). The volume of individual cells from the 12 analyzed species ranged from 0.004 μm3 to 1.357 μm3, revealing an almost 500-fold difference in volumes between analyzed cells (Fig. S1). The median volumes of the 12 bacterial and archaeal species varied ca. 65-fold, with Nitrosopumilus NAOA6 having the smallest (0.011 μm3/cell) and Methyloceanibacter stevinii LMG 29431 the largest (0.705 μm3/cell) median volumes of the investigated species. Interestingly, the variability in the measured volumes of the investigated microbial species was rather large and ranged between 5 and 30% (see Table S1).
Next, buoyant masses of single cells were determined using a suspended microchannel resonator (SMR) device. From these data, dry masses of single cells were calculated as described in reference 34. As with volume measurements, at first comparison measurements were made between living and fixed cells of the same microbial culture (Muricauda MAR_2010_75). No significant differences could be found between the masses of fixed and living cells for this species (Fig. S5b). We thus proceeded to use fixed cells for the SMR measurements, as this way the same sample batches could be used for both SMR and SEM. The samples contained single suspended cells, as confirmed by SEM imaging.
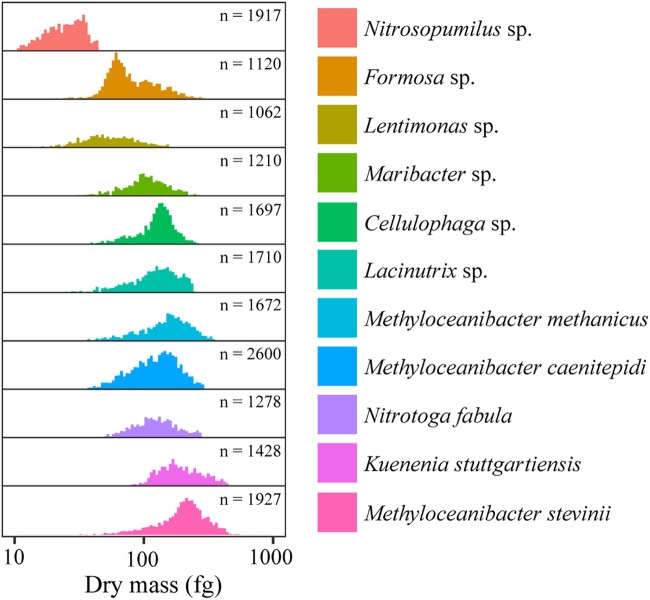
The SMR revealed large differences in the mass of the different species, with Nitrosopumilus NAOA6 being the lightest of the investigated species (24.6 fg/cell) and Methyloceanibacter stevinii LMG 29431 the heaviest (266.5 fg/cell). Median dry masses of these two microbial strains varied ca. 10-fold, thus less than their median volumes. Correspondingly, the median dry masses of the other 10 investigated species exhibited smaller differences. Cellular dry mass distributions of individual species followed a Gaussian-like distribution (Fig. 2) similar to previous observations on other bacterial species (35–38).
FIG 2.
Cellular dry mass distributions of the 12 investigated bacterial and archaeal species as determined with a suspended microchannel resonator (SMR). The microorganisms are ordered according to their increasing median cell volumes. Numbers of measured individual cells (n) that were used for the dry mass calculation are indicated. Note that the x axis represents a log scale of dry masses expressed in femtograms (1 fg = 10−15 g).
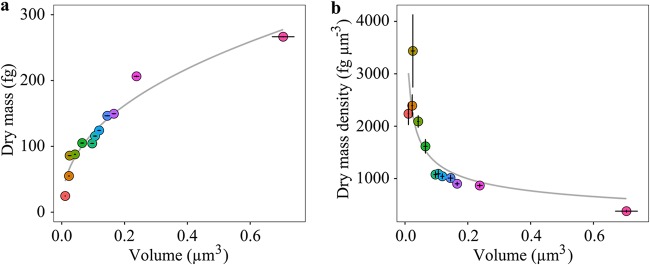
The median volumes and dry masses of all analyzed species were used to determine the relationship of cell volume to dry mass (Fig. 3a). We found a significant (chi-square analysis of variance [ANOVA], P < 0.005) nonlinear relationship between cell volume and dry mass. This relationship can be represented by the following equation:
| (1) |
where V refers to cell volume in cubic micrometers and mdry stands for dry mass in femtograms. The equation shows that the value of the scaling factor (0.43; equation 1) is less than 1, meaning that the ratio of dry mass to volume is not constant. The effects of using nonlinear relationship over linear are more pronounced on smaller cells than on larger cells. For example, small cells with a volume of about 0.01 μm3 end up with a ca. 14-fold-higher mass than in a linear relationship where a scaling factor equals unity (equation 1; ). Larger cells with a volume about 0.1 μm3 are less affected by this effect but still exhibit a ca. 4-fold-higher mass than in a linear relationship.
FIG 3.
Cellular dry mass scaling to cellular volume for the 12 investigated bacterial and archaeal species. (a) A significant (chi-square ANOVA, P < 0.005) nonlinear relationship exists between cellular volume and dry mass of the investigated species (). (b) A significant (chi-square ANOVA, P < 0.05) nonlinear relationship also exists between cellular volume and dry mass per unit cell volume (i.e., dry mass density; ). The gray lines represent best fits for the respective data, described by the equations for panel a and for panel b, where , , and V are dry mass in femtograms, dry mass density in femtograms per cubic micrometer, and volume in cubic micrometers, respectively. Error bars indicate SEs. Color coding of the individual data points corresponds to the color coding of the investigated species outlined for Fig. 2.
A nonlinear relationship between cell volume and dry mass of bacterial cells has been reported previously (12, 23). However, for small cells, these models consistently yield lower dry masses than our relationship. For example, our relationship yields dry masses of 44 and 120 fg for cells with volumes of 0.01 and 0.1 μm3, respectively (equation 1). This is 50 to 80% higher than the values obtained with the model presented in reference 23, in which the same cells have dry weights of 8 and 60 fg, respectively. This implies that currently used relationships for dry mass estimation of bacterial cells underestimate the mass of microbial cells, with greater bias for small cells (∼0.01 to 0.1 μm3).
Dry mass expressed per unit cell volume (i.e., dry mass density, , in femtograms per cubic micrometer) correlated significantly (chi-square ANOVA, P < 0.05) with cell volume (Fig. 3b). This relationship could be expressed as follows:
| (2) |
The nonlinear form of this relationship is consistent with the nonlinear relationship between dry mass and cell volume. The negative scaling factor (equation 2) indicated that smaller cells tend to have considerably higher dry mass content per cell volume than larger cells. This relationship deviates from the previously reported relationship, i.e., (12), and the relationship derived from the dry mass equation reported in reference 23, .
Elemental composition and cell volume relationships.
The C, N, O, P, and S masses of individual cells (in femtograms per cell) were determined by combining their dry cellular masses (in femtograms per cell, as reported above) and their relative elemental content (expressed as percent; measured with energy-dispersive X-ray spectroscopy [EDS]).
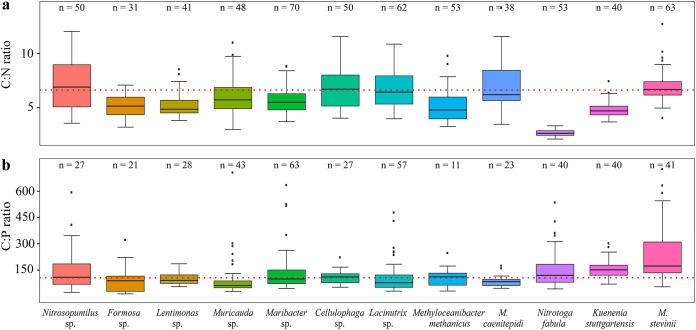
The measured median relative carbon content constituted 55.8% ± 1.3% (median ± standard error [SE]) of cell dry mass for all analyzed microbial species, with Formosa Hel3_A1_48 possessing the smallest relative carbon content of the investigated species (45.1%) and Methyloceanibacter caenitepidi LMG 28723 and Methyloceanibacter stevinii LMG 29431 the largest (61.4%). The median N, O, P, and S contents of these strains were 11.4% ± 1.2%, 15.7% ± 1.3%, 1.8% ± 0.1%, and 1.6% ± 0.2%, respectively. Interestingly, the median C/N/P molar ratio for all 12 microbial species was 105:18:1 and thus very similar to the Redfield ratio (39) of 106:16:1 (Fig. 4a and b), which has been determined for phytoplankton algae.
FIG 4.
Distribution of cellular ratios of carbon to nitrogen (C:N) (a) and carbon to phosphorus (C:P) (b) for 12 bacterial and archaeal species measured using EDS. The ratios are presented in forms of boxes indicating the 25th and 75th percentiles; error bars represent 10th and 90th percentiles, and the lines indicate median molar ratios. The number (n) of measured individual cells is specified above each box. Redfield ratios of 106:16 (C:N) and 16:1 (C:P) are represented by the red dotted lines.
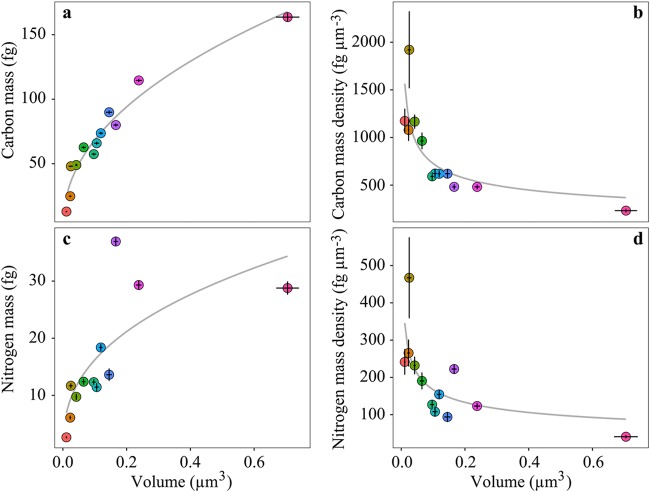
The calculated median cellular carbon mass for the investigated prokaryotic microorganisms ranged from 12.9 fg of C for Nitrosopumilus NAOA6 to 163.6 fg of C for Methyloceanibacter stevinii LMG 29431 (Fig. 5a). Median cellular N, O, P, and S masses ranged between 2.7 and 36.9 fg of N, 4.4 and 40.1 fg of O, 0.4 and 40.1 fg of P, and 0.6 and 3.1 fg of S (Fig. 5c and Fig. S2a, S3a, and S4a). Both cellular carbon and nitrogen masses showed significant (chi-square ANOVA, P < 0.005 and P < 0.05, respectively) nonlinear relationships with cell volume (Fig. 5a and c) that were best described by the following equations:
| (3) |
| (4) |
where V refers to cell volume expressed in cubic micrometers and mcarbon and mnitrogen in femtograms. The scaling factor of the relationship between cellular carbon mass and cell volume (0.46 [equation 3]) was lower than unity (Fig. 5a). As with the dry mass-volume relationship, this implies that smaller cells have a higher carbon mass/volume ratio than larger cells. This is also reflected by increasing carbon and nitrogen mass densities (i.e., masses of C and N per unit cell volume) with decreasing cell volume ( and , respectively [Fig. 5b and d]). These observations are in line with previous studies suggesting that small microbial cells contain less water and are richer in carbon and nitrogen (24). This phenomenon was attributed to the fact that smaller microorganisms need to sustain a minimum amount of necessary proteins/enzymes, lipids, and DNA despite a greatly reduced cell volume.
FIG 5.
Cellular carbon and nitrogen mass scaling to volume. (a) A significant (chi-square ANOVA, P < 0.005) nonlinear relationship exists between cellular volume and carbon mass (). (b) A significant (chi-square ANOVA, P < 0.05) nonlinear relationship also exists between cellular volume and carbon mass density (carbon mass per unit cell volume, ). Significant (chi-square ANOVA, P < 0.05) nonlinear relationships also exist between between cellular volume and nitrogen mass () (c) and cellular volume and nitrogen mass density (nitrogen mass per unit cell volume, ) (d). Gray lines represent best fits, described by the equations for panel a, for panel b, for panel c, and for panel d, where and are carbon and nitrogen masses in femtograms, and are carbon and nitrogen mass densities in femtograms per cubic micrometer, and V is cell volume in cubic micrometers. Error bars indicate SEs. Color coding of the individual data points corresponds to the color coding of the investigated species outlined for Fig. 2.
Our observed relationship between cell volume and carbon mass (Fig. 5a) differs from most published relationships (for examples, see references 14 and 19) and is most similar to the weak relationship observed for a compilation of published data (; [28]).
We also found nonlinear relationships (Fig. S2a, S3a, and S4a) between cellular volume and O, P, and S masses, which were best described by the following:
| (5) |
| (6) |
| (7) |
It should be noted that the calculated R2 values for O, P, and, S mass-volume relationships were lower than for C and N. Nonetheless, the scaling factors for O, P, and S mass-volume relationships (equations 1, 2, and 3) were smaller than unity, implying that smaller cells have more O, P, and S per cell volume than larger cells. This was also reflected by increasing O, P, and S mass densities with decreasing cell volume (Fig. S2b, S3b, and S4b), represented by significant (chi-square ANOVA, P < 0.05, P < 0.005, and P < 0.05, respectively) nonlinear relationships between the volumes and the densities (, , and ).
Implications for microbial biomass estimates.
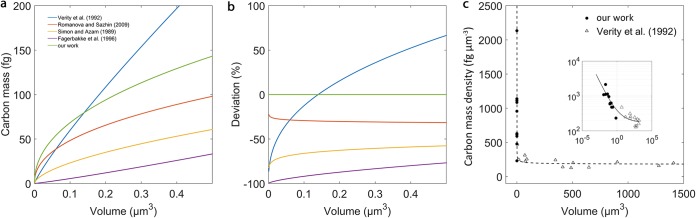
Our results show that, with one exception, all published single-cell carbon biomass-to-volume relationships significantly underestimate the carbon mass of small (<0.5-μm3) microbial cells (Fig. 6a and b). An exception is the model of Verity et al. (14), which underestimated the carbon mass only for cells <0.15 μm3 (by as much as 70%) and overestimated the mass of cells >0.15 μm3 by 65% (Fig. 6a and b). This could be due to true inherent differences between large (>1-μm3) picoeukaryotic algal cells, which were mainly used to establish the equation of Verity et al., and smaller prokaryotic cells used to derive our equation. It thus appears that whereas the equation of Verity et al. is suitable for estimating biomass of larger cells, it might not correctly predict the allometric mass relationship for small cells.
FIG 6.
Calculated cellular carbon mass as determined from our work and other currently used relationships. (a) The modeled relationships are as follows: (our work; green), (reference 14; blue), (recalculated from Table 5 in reference 24; yellow), (reference 19; purple), and (reference 28; red). (b) Deviation of carbon mass estimates between our and other currently used models. (c) Compilation of our data and those reported in Fig. 4 in reference 14 expressing a carbon mass density-to-volume relationship. The black dashed line represents best fit for all data points. The inset shows the same carbon mass density-to-volume relationship as a log-log plot.
A compilation of our data and the data published in reference 14 showed that cells with larger volumes (>0.5 μm3) display a constant (carbon) mass-to-volume ratio, whereas cells with volumes below 0.5 μm3 exhibit a nonlinear increase in (carbon) mass density with decreasing volume (Fig. 6c). Estimates of microbial biomass that assume a more or less constant cellular mass/volume ratio (for examples, see references 17 and 40) will thus severely underestimate the biomass contributions of smaller cells (Fig. 6b). It should be noted that also the published nonlinear relationships (for example, see reference 24) generally underestimate the mass of smaller cells (Fig. 6b).
At this point we call for caution when transferring the established mass-to-volume relationships to living cells. The presented relationships were established from properties of fixed and dried cells, and any systematic changes in cell volume or mass during cell preparation would lead to an over- or underestimation of the mass of living cells. In our two investigated species we could not detect any significant changes in volume or mass between living and fixed cells. However, there is literature evidence that suggests that cells tend to shrink during common sample preparation procedures (19, 41). Thus, it should be kept in mind that living cells might in fact have larger volumes than their fixed counterparts and the established relationships could overestimate their “in situ” dry mass/cell element density.
Cell-specific carbon content estimates are crucial for, e.g., correct estimates of the biomass and generation times of microorganisms in the seafloor. These, in turn, are fundamental for determining the role of the microbial deep biosphere in the global carbon cycling. It has been proposed that microbial adaptation to life in these low-energy environments includes cell volume reduction and shrinkage. Current estimates of average cell size in the marine subsurface range between 0.005 μm3 (42) and 0.21 μm3 (43), but a value in between these end members is often used (0.04 μm3 [44], 0.05 μm3 [42], or 0.06 μm3 [45]). In any case, microbial cells in the deep biosphere are predominantly very small (<0.05 μm3). The currently used conversion factors range between 14 fg cell−1 and 65 fg cell−1 (1, 42–45). Based on our relationship, and assuming that volumes of living cells are not significantly larger than those of measured fixed cells, the cellular carbon mass will be in the range of 17 fg for cells with average volumes of 0.005 μm3, whereas it will reach ca. 50 fg cell−1 for average cell volumes of 0.05 μm3 and 94 fg cell−1 for cell volumes of 0.2 μm3. We estimate, based on the cell counts (2.9 × 1029 cells) and average cell size (0.042 μm3) reported in reference 44, that the microbial biomass in the deep biosphere could represent 13.3 Pg of C, which is 220% higher than estimated originally (4.1 Pg of C [44]) and 33% higher than the most recent assessment (10 Pg of C [1]).
Notably, also the most abundant microbial taxa in freshwater and marine water columns, such as Prochlorococcus, Pelagibacter (SAR11), Actinobacteria, and marine group I (MGI) Thaumarchaea, are largely represented by cells substantially smaller than 0.5 μm3 (=coccoid cell with a diameter of 1 μm). Our results show that the (carbon) mass of these small cells tends to be underestimated by the commonly used models, and it is thus likely that the overall biomass of marine and freshwater bacterioplankton is larger than currently believed. Additionally, application of the correct estimates of cellular carbon and nitrogen contents will allow for a more precise quantification of the microbial C and N turnover rates and their contribution to the biogeochemical element cycles.
MATERIALS AND METHODS
Cultivation.
Twelve bacterial and archaeal cultures were grown as described below, and subsamples from these 12 cultures were used for all subsequent measurements.
The ammonia-oxidizing archaeon Nitrosopumilus NAOA6 was grown in a modified synthetic crenarchaeota medium (30) with 200 nM P for 10 months (>12 transfers). Cells were harvested in stationary phase and then fixed with formaldehyde (1.5% final concentration) at room temperature for 1 h. Fixed cells were resuspended in 50% ethanol––50% 1× phosphate-buffered saline (PBS) solution and stored at −20°C.
Nitrotoga fabula KNB was grown in nitrate oxidizer medium (46) and fixed in stationary phase with paraformaldehyde (PFA; 4% final concentration) at room temperature for 0.5 h, then washed two times in 1× PBS, resuspended in 60% ethanol–40% 1× PBS solution, and stored at −20°C.
Formosa Hel3_A1_48 was grown in HaHa100V medium (47) for 2 weeks at room temperature under continuous shaking. Stationary-phase cells were fixed using PFA (2% final concentration) at room temperature for 1 h.
Lentimonas CC151 was grown in a minimal medium containing 20 mM morpholinepropanesulfonic acid (MOPS; pH 8.0) as a buffer, sea salts (35 g/liter), EDTA (1.3 mM), ammonium chloride (10 mM), mannose (2 g/liter), 1 mM phosphate, iron sulfate, mixed vitamins, sodium molybdate, and trace metal solution (48) for ∼24 h at 37°C under continuous shaking. Cells were harvested at early exponential phase.
Muricauda MAR_2010_75, Maribacter Hel1_7, Cellulophaga Hel1_12, and Lacinutrix Hel1_90 were grown in 2216 marine broth (Difco, BD, NJ) for ∼40 h at room temperature under continuous shaking (49). All cultures were fixed in early stationary phase and stored.
Methyloceanibacter methanicus LMG 29429, Methyloceanibacter caenitepidi LMG 28723, and Methyloceanibacter stevinii LMG 29431 were grown in NaCl-dANMS media (50) supplemented with methanol (1% [vol/vol]) for ∼4 days at 28°C under continuous shaking. All cultures were harvested in either late exponential or early stationary phase.
The anammox bacterium Kuenenia stuttgartiensis was grown as described in reference 51. Harvested cells were fixed with PFA (2% final concentration) at room temperature, resuspended in 50% 1× PBS–50% ethanol solution, and stored at −20°C.
Volumetric measurements with SEM.
(i) Critical point drying. Microbial cultures were critical point dried (CPD) to preserve cell morphology for volumetric measurements using scanning electron microscopy (SEM). The CPD procedure was conducted on PFA-fixed samples that were stored at −20°C in an ethanol-PBS solution. Aliquots (1 ml) of fixed cells were washed twice by centrifugation for 5 min at 3,000 × g and subsequently resuspended in 1 ml of Milli-Q. Prior to immobilizing the cells onto a silicon wafer, the surface of the wafer was coated with 20 μl of poly-l-lysine solution (PLL; 1 mg/ml; Sigma-Aldrich, Germany) for 15 min. Washed cells (30 μl) were immobilized onto the PLL-coated silicon wafer for 0.5 h and then transferred into 30% ethanol. All samples with immobilized cells underwent series of water replacing steps in 30%, 50%, 70%, 80%, and 99% ethanol with a 5-min residence time for each concentration of ethanol. After the dehydration of the cells, the silicon wafer was transferred into a critical point dryer (Leica EM CPD300; Leica, Wetzlar, Germany). The ethanol inside the cells was exchanged with liquid carbon dioxide in slow gas in/out mode during 14 process cycles. The liquid CO2 was then evaporated at its critical point. Each sample was critical point dried separately to prevent cross contamination due to poor immobilization.
(ii) Scanning electron microscopy. After the CPD treatment, silicon wafers with immobilized cells were mounted on electrically conductive adhesive tags (Leit-Tab, Plano GmbH, Wetzlar, Germany) and loaded into a field emission SEM Quanta 250 FEG (FEI, Eindhoven, The Netherlands). The SEM images were obtained at an acceleration voltage of 2 keV under high-vacuum conditions. Images were captured at a magnification of ×30,000 using an Everhart-Thornley secondary electron detector (ETD). Each image represents an integrated and drift corrected array of 128 images captured with a dwell time of 100 ns. The sizes of single cells were determined from SEM images using the software FEI xT Microscope Control (FEI GmbH, Frankfurt, Germany). Visual inspection confirmed that cells retained their three-dimensional structure and did not show any signs of flattening due to the dehydration step of CPD, which would have biased the length/width measurements (42).
(iii) Cell volume calculation. The scanning electron micrographs of bacterial and archaeal species were analyzed using the software FEI xT Miscoscope Control (FEI GmbH, Frankfurt, Germany). For each strain more than 50 individual cells were analyzed. The general method of the cell volume calculation was based on the geometric assignment of shape- and size-defining parameters of the cells, such as the length and the radius. Cell volumes were calculated according to the following formulas, with the assumption that cell width equals cell height.
For rod-shaped and C-shaped cells the volume was calculated using the equation
where r is radius of a cell and , where L is the length of the cell.
For prolate spheroid-shaped cells, the volume was calculated using the equation
where a is the length of the minor axis and b is the length of the major axis of the cell.
For coccoid cells, the volume was calculated using the equation
where r is the radius of the cell.
Elemental analysis with EDS.
Analysis of the elemental composition was conducted on PFA-fixed samples that were stored at –20°C in ethanol-PBS solution prior to the measurements. Aliquots (1 ml) of fixed cells were washed twice by centrifugation for 5 min at 3,000 × g, with subsequent resuspension in 1 ml of Milli-Q. Thirty microliters of the washed cell suspension was then air dried for 2 h on a clean silicon wafer. After the dehydration of the cells, the silicon wafers were mounted on electrically conductive adhesive tags (Leit-Tab; Plano GmbH, Wetzlar, Germany). The elemental composition of the cells was determined via energy-dispersive X-ray spectroscopy (EDS) at an acceleration voltage of 10 keV under high-vacuum conditions. Micrographs were captured with the double detector system Quantax (Bruker Nano GmbH, Berlin, Germany), equipped with two detectors (XFlash 6/30) with energy resolutions of <123 eV at Mnkα and 48 eV at Ckα, allowing a better quantification of light elements. The performance of the EDS was regularly monitored by the use of calibrated standards. The EDS mapping measurements of each microbial species were used for elemental cellular content calculation with Quantax 400 (Bruker Nano GmbH) software. The primary energy loss that occurs due to potential sample charging during the measurements was compensated for by the continuous adjustment of the energy for each recorded X-ray spectrum. Next, the subtraction of continuum X rays (Bremsstrahlung) from each measured spectrum as a background was performed using a physical model with the calculation of the background based on the identified elements in the spectrum. The applied method yields an accurate form of the background considering both calculations of the absorption edges and the efficiency of the detector. Peak deconvolution was then performed to extract the peaks of measured spectra using the FIT model. For the deconvolution, the background corrected peak intensities were assigned to the identified elements in the spectrum, and a theoretical spectrum was calculated. This theoretical spectrum was compared with the measured spectrum based on the least-squares model analysis. Since our samples have topography, the standardless P/B-ZAF method was used for quantification, allowing for measurement of light (e.g., carbon) to heavy elements (e.g., calcium) in samples that are characterized by rough surfaces. Elements with energy below 1 keV were quantified with the phi-rho method.
Dry mass measurements with suspended microchannel resonator.
(i) Suspended microchannel resonator. Mass measurements were conducted using a home-built suspended microchannel resonator (SMR) device at the Max Planck Institute for Biophysical Chemistry, Göttingen, Germany (52). Torsional SMR with two microfluidic channels having a cross section of 3 by 8 by 100 μm (channel height by width by length) each, embedded in the structure oscillating at ∼2 MHz in a vacuum, was used for the cell mass measurements. Electrostatic excitation was used to drive the SMR into the mechanical resonance. The SMR had a readout noise level ∼0.15 Hz at a 1-kHz sampling rate and mass responsivity of ∼27 mHz/fg (1 fg = 10−15 g) calculated in a calibration process using polystyrene particles of 1.54 ± 0.04 μm (catalog no. 64040; Polysciences, Eppelheim, Germany).
(ii) Cell measurements. For mass measurements of the cells, PFA-fixed cells were resuspended in water-based solution (1× PBS in H2O) and deuterium oxide-based solution (1× PBS in D2O). The sample was introduced into one of the two bypass channels, and the remaining bypass channel was filled with a wash solution (H2O for the sample embedded in water-based solution and D2O for the sample in deuterium oxide-based solution). By varying the externally applied pressures, cells were pushed through the SMR for ∼60 s and then the flow was reversed for ∼30 s to rinse the channel with wash solution. This procedure was performed several times. Control of the SMR conditions, such as pressure, sampling rate, looping parameters, and the record of the time-frequency arrays, was conducted using LabVIEW interface. Measured time-frequency arrays were utilized for dry mass and dry density calculations.
(iii) Dry mass calculation. Dry mass of the sample was calculated using paired buoyant mass measurements in water-based and deuterium oxide-based solutions (34). Median buoyant masses of a strain, and in H2O- and D2O-based solutions, respectively, were calculated using the predefined mass responsivity constant. The median buoyant masses of cells were used to calculate cell dry density, (the density of the cell dry material), and cellular dry mass, , using the following equations (36):
where and are the densities of the H2O- and D2O-based solutions.
We used median buoyant masses of a strain to calculate the median dry density and dry mass. To assess the uncertainty of the strain dry mass, the process of the dry mass calculation was bootstrapped 1,000 times. Dry mass distributions were calculated using strain dry density, , as follows:
where is a single-cell buoyant mass measured in H2O-based solution.
Supplementary Material
ACKNOWLEDGMENTS
We thank Jens Harder, Tanja Fischer, Katharina Kitzinger, Andreas Sichert, and Bram Vekeman for providing bacterial and archaeal cultures, and we thank Daniela Tienken and Swantje Lilienthal for assistance in the laboratory. Mike Jetten and Boran Kartal are thanked for providing the Kuenenia stuttgartiensis culture.
This work was funded by the Max Planck Society. Martin Könneke was financially supported by the DFG Heisenberg Program (KO 3651/3-1). Travis Meador was supported by DFG Eigenestelle grant ME 4594/2-1. Soeren Ahmerkamp was supported by the DFG-Research Center/Cluster of Excellence (The Ocean in the Earth System) at the University of Bremen.
We declare no competing financial interests.
Footnotes
Supplemental material for this article may be found at https://doi.org/10.1128/AEM.00493-19.
REFERENCES
- 1.Bar-On YM, Phillips R, Milo R. 2018. The biomass distribution on Earth. Proc Natl Acad Sci U S A 115:6506–6511. doi: 10.1073/pnas.1711842115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Arrigo KR. 2005. Marine microorganisms and global nutrient cycles. Nature 437:343–348. [DOI] [PubMed] [Google Scholar]
- 3.Cotner JB, Biddanda BA. 2002. Small players, large role: microbial influence on biogeochemical processes in pelagic aquatic ecosystems. Ecosystems 5:105–121. doi: 10.1007/s10021-001-0059-3. [DOI] [Google Scholar]
- 4.Offre P, Spang A, Schleper C. 2013. Archaea in biogeochemical cycles. Annu Rev Microbiol 67:437–457. doi: 10.1146/annurev-micro-092412-155614. [DOI] [PubMed] [Google Scholar]
- 5.Fuhrman JA, Ammerman JW, Azam F. 1980. Bacterioplankton in the coastal euphotic zone—distribution, activity and possible relationships with phytoplankton. Mar Biol 60:201–207. doi: 10.1007/BF00389163. [DOI] [Google Scholar]
- 6.Holligan PM, Harris RP, Newell RC, Harbour DS, Head RN, Linley EAS, Lucas MI, Tranter PRG, Weekley CM. 1984. Vertical distribution and partitioning of organic carbon in mixed, frontal and stratified waters of the English Channel. Mar Ecol Prog Ser 14:111–127. doi: 10.3354/meps014111. [DOI] [Google Scholar]
- 7.Cho BC, Azam F. 1988. Major role of bacteria in biogeochemical fluxes in the Oceans interior. Nature 332:441–443. doi: 10.1038/332441a0. [DOI] [Google Scholar]
- 8.Cho BC, Azam F. 1990. Biogeochemical significance of bacterial biomass in the Oceans euphotic zone. Mar Ecol Prog Ser 63:253–259. doi: 10.3354/meps063253. [DOI] [Google Scholar]
- 9.Simon M, Cho BC, Azam F. 1992. Significance of bacterial biomass in lakes and the ocean—comparison to phytoplankton biomass and biogeochemical implications. Mar Ecol Prog Ser 86:103–110. doi: 10.3354/meps086103. [DOI] [Google Scholar]
- 10.Bakken LR, Olsen RA. 1983. Buoyant densities and dry-matter contents of microorganisms: conversion of a measured biovolume into biomass. Appl Environ Microbiol 45:1188–1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mullin MM, Sloan PR, Eppley RW. 1966. Relationship between carbon content, cell volume, and area in phytoplankton. Limnol Oceanogr 11:307–311. doi: 10.4319/lo.1966.11.2.0307. [DOI] [Google Scholar]
- 12.Norland S, Heldal M, Tumyr O. 1987. On the relation between dry matter and volume of bacteria. Microb Ecol 13:95–101. doi: 10.1007/BF02011246. [DOI] [PubMed] [Google Scholar]
- 13.Bratbak G, Dundas I. 1984. Bacterial dry matter content and biomass estimates. Appl Environ Microbiol 48:755–757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Verity PG, Robertson CY, Tronzo CR, Andrews MG, Nelson JR, Sieracki ME. 1992. Relationships between cell volume and the carbon and nitrogen content of marine photosynthetic nanoplankton. Limnol Oceanogr 37:1434–1446. doi: 10.4319/lo.1992.37.7.1434. [DOI] [Google Scholar]
- 15.Vrede K, Heldal M, Norland S, Bratbak G. 2002. Elemental composition (C, N, P) and cell volume of exponentially growing and nutrient-limited bacterioplankton. Appl Environ Microbiol 68:2965–2971. doi: 10.1128/AEM.68.6.2965-2971.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bratbak G. 1985. Bacterial biovolume and biomass estimations. Appl Environ Microbiol 49:1488–1493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lee S, Fuhrman JA. 1987. Relationships between biovolume and biomass of naturally derived marine bacterioplankton. Appl Environ Microbiol 53:1298–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pelegri SP, Dolan J, Rassoulzadegan F. 1999. Use of high temperature catalytic oxidation (HTCO) to measure carbon content of microorganisms. Aquat Microb Ecol 16:273–280. doi: 10.3354/ame016273. [DOI] [Google Scholar]
- 19.Fagerbakke KM, Heldal M, Norland S. 1996. Content of carbon, nitrogen, oxygen, sulfur and phosphorus in native aquatic and cultured bacteria. Aquat Microb Ecol 10:15–27. doi: 10.3354/ame010015. [DOI] [Google Scholar]
- 20.Whitman WB, Coleman DC, Wiebe WJ. 1998. Prokaryotes: the unseen majority. Proc Natl Acad Sci U S A 95:6578–6583. doi: 10.1073/pnas.95.12.6578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fukuda R, Ogawa H, Nagata T, Koike I. 1998. Direct determination of carbon and nitrogen contents of natural bacterial assemblages in marine environments. Appl Environ Microbiol 64:3352–3358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gundersen K, Heldal M, Norland S, Purdie DA, Knap AH. 2002. Elemental C, N, and P cell content of individual bacteria collected at the Bermuda Atlantic Time-Series Study (BATS) site. Limnol Oceanogr 47:1525–1530. doi: 10.4319/lo.2002.47.5.1525. [DOI] [Google Scholar]
- 23.Loferer-Krössbacher M, Klima J, Psenner R. 1998. Determination of bacterial cell dry mass by transmission electron microscopy and densitometric image analysis. Appl Environ Microbiol 64:688–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Simon M, Azam F. 1989. Protein content and protein synthesis rates of planktonic marine bacteria. Mar Ecol Prog Ser 51:201–213. doi: 10.3354/meps051201. [DOI] [Google Scholar]
- 25.Krupke A, Mohr W, Laroche J, Fuchs BM, Amann RI, Kuypers MM. 2015. The effect of nutrients on carbon and nitrogen fixation by the UCYN-A–haptophyte symbiosis. ISME J 9:1635–1647. doi: 10.1038/ismej.2014.253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Martínez-Pérez C, Mohr W, Löscher CR, Dekaezemacker J, Littmann S, Yilmaz P, Lehnen N, Fuchs BM, Lavik G, Schmitz RA, LaRoche J, Kuypers MMM. 2016. The small unicellular diazotrophic symbiont, UCYN-A, is a key player in the marine nitrogen cycle. Nat Microbiol 1:16163. doi: 10.1038/nmicrobiol.2016.163. [DOI] [PubMed] [Google Scholar]
- 27.Norland S. 1993. The relationship beween biomass and volume of bacteria In Kemp PF, Sherr BF, Sherr EB, Cole JJ (ed), Handbook of methods in aquatic microbial ecology. CRC Press, Boca Raton, FL. [Google Scholar]
- 28.Romanova ND, Sazhin AF. 2010. Relationships between the cell volume and the carbon content of bacteria. Oceanology 50:522–530. doi: 10.1134/S0001437010040089. [DOI] [Google Scholar]
- 29.Posch T, Loferer-Krößbacher M, Gao G, Alfreider A, Pernthaler J, Psenner R. 2001. Precision of bacterioplankton biomass determination: a comparison of two fluorescent dyes, and of allometric and linear volume-to-carbon conversion factors. Aquat Microb Ecol 25:55–63. doi: 10.3354/ame025055. [DOI] [Google Scholar]
- 30.Könneke M, Bernhard AE, Torre RD, Walker CB, Waterbury JB, Stahl DA. 2005. Isolation of an autotrophic ammonia-oxidizing marine archaeon. Nature 437:543–546. doi: 10.1038/nature03911. [DOI] [PubMed] [Google Scholar]
- 31.Kuypers MMM, Sliekers AO, Lavik G, Schmid M, Jørgensen BB, Kuenen JG, Sinninghe Damsté JS, Strous M, Jetten MSM. 2003. Anaerobic ammonium oxidation by anammox bacteria in the Black Sea. Nature 422:608–611. doi: 10.1038/nature01472. [DOI] [PubMed] [Google Scholar]
- 32.Teeling H, Fuchs BM, Bennke CM, Krüger K, Chafee M, Kappelmann L, Reintjes G, Waldmann J, Quast C, Glöckner FO, Lucas J, Wichels A, Gerdts G, Wiltshire KH, Amann RI. 2016. Recurring patterns in bacterioplankton dynamics during coastal spring algae blooms. eLife 5:e11888. doi: 10.7554/eLife.11888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bowden WB. 1977. Comparison of two direct-count techniques for enumerating aquatic bacteria. Appl Environ Microbiol 33:1229–1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Feijo Delgado F, Cermak N, Hecht VC, Son S, Li Y, Knudsen SM, Olcum S, Higgins JM, Chen J, Grover WH, Manalis SR. 2013. Intracellular water exchange for measuring the dry mass, water mass and changes in chemical composition of living cells. PLoS One 8:e67590. doi: 10.1371/journal.pone.0067590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bryan AK, Hecht VC, Shen W, Payer K, Grover WH, Manalis SR. 2014. Measuring single cell mass, volume, and density with dual suspended microchannel resonators. Lab Chip 14:569–576. doi: 10.1039/c3lc51022k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cermak N, Becker JW, Knudsen SM, Chisholm SW, Manalis SR, Polz MF. 2017. Direct single-cell biomass estimates for marine bacteria via Archimedes’ principle. ISME J 11:825–828. doi: 10.1038/ismej.2016.161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Grover WH, Bryan AK, Diez-Silva M, Suresh S, Higgins JM, Manalis SR. 2011. Measuring single-cell density. Proc Natl Acad Sci U S A 108:10992–10996. doi: 10.1073/pnas.1104651108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lewis CL, Craig CC, Senecal AG. 2014. Mass and density measurements of live and dead gram-negative and gram-positive bacterial populations. Appl Environ Microbiol 80:3622–3631. doi: 10.1128/AEM.00117-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Redfield AC. 1958. The biological control of chemical factors in the environment. Am Sci 46:205–221. [PubMed] [Google Scholar]
- 40.Bertilsson S, Berglund O, Karl DM, Chisholm SW. 2003. Elemental composition of marine Prochlorococcus and Synechococcus: Implications for the ecological stoichiometry of the sea. Limnol Oceanogr 48:1721–1731. doi: 10.4319/lo.2003.48.5.1721. [DOI] [Google Scholar]
- 41.Malfatti F, Samo TJ, Azam F. 2010. High-resolution imaging of pelagic bacteria by atomic force microscopy and implications for carbon cycling. ISME J 4:427–439. doi: 10.1038/ismej.2009.116. [DOI] [PubMed] [Google Scholar]
- 42.Braun S, Morono Y, Littmann S, Kuypers M, Aslan H, Spivack AJ, Braun S. 2016. Size and carbon content of sub-seafloor microbial cells at Landsort Deep, Baltic Sea. Front Microbiol 7:1375. doi: 10.3389/fmicb.2016.01375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Parkes RJ, Cragg BA, Bale SJ, Getliff JM, Goodman K, Rochelle PA, Fry JC, Weightman AJ, Harvey SM. 1994. Deep bacterial biosphere in Pacific Ocean sediments. Nature 371:410–413. doi: 10.1038/371410a0. [DOI] [Google Scholar]
- 44.Kallmeyer J, Pockalny R, Adhikari RR, Smith DC, D’Hondt S. 2012. Global distribution of microbial abundance and biomass in subseafloor sediment. Proc Natl Acad Sci U S A 109:16213–16216. doi: 10.1073/pnas.1203849109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lipp JS, Morono Y, Inagaki F, Hinrichs KU. 2008. Significant contribution of Archaea to extant biomass in marine subsurface sediments. Nature 454:991–994. doi: 10.1038/nature07174. [DOI] [PubMed] [Google Scholar]
- 46.Kitzinger K, Koch H, Lücker S, Sedlacek CJ, Herbold C, Schwarz J, Daebeler A, Mueller AJ, Lukumbuzya M, Romano S, Leisch N, Karst SM, Kirkegaard R, Albertsen M, Nielsen PH, Wagner M, Daims H. 2018. Characterization of the first “Candidatus Nitrotoga” isolate reveals metabolic versatility and separate evolution of widespread nitrite-oxidizing bacteria. mBio 9:e01186-18. doi: 10.1128/mBio.01186-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hahnke RL, Bennke CM, Fuchs BM, Mann AJ, Rhiel E, Teeling H, Amann R, Harder J. 2015. Dilution cultivation of marine heterotrophic bacteria abundant after a spring phytoplankton bloom in the North Sea. Environ Microbiol 17:3515–3526. doi: 10.1111/1462-2920.12479. [DOI] [PubMed] [Google Scholar]
- 48.Tibbles B, Rawlings D. 1994. Characterization of nitrogen-fixing bacteria from a temperate saltmarsh lagoon, including isolates that produce ethane from acetylene. Microb Ecol 27:65–80. doi: 10.1007/BF00170115. [DOI] [PubMed] [Google Scholar]
- 49.Hahnke RL, Harder J. 2013. Phylogenetic diversity of Flavobacteria isolated from the North Sea on solid media. Syst Appl Microbiol 36:497–504. doi: 10.1016/j.syapm.2013.06.006. [DOI] [PubMed] [Google Scholar]
- 50.Holmes AJ, Costello A, Lidstrom ME, Murrell JC. 1995. Evidence that particulate methane monooxygenase and ammonia monooxygenase may be evolutionarily related. FEMS Microbiol Lett 132:203–208. doi: 10.1111/j.1574-6968.1995.tb07834.x. [DOI] [PubMed] [Google Scholar]
- 51.Kartal B, Geerts W, Jetten MSM. 2011. Cultivation, detection, and ecophysiology of anaerobic ammonium-oxidizing bacteria. Methods Enzymol 486:89–108. doi: 10.1016/B978-0-12-381294-0.00004-3. [DOI] [PubMed] [Google Scholar]
- 52.Burg TP, Godin M, Knudsen SM, Shen W, Carlson G, Foster JS, Babcock K, Manalis SR. 2007. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature 446:1066–1069. doi: 10.1038/nature05741. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.