Mechanism of Sulfate Activation Catalyzed by ATP Sulfurylase - Magnesium Inhibits the Activity

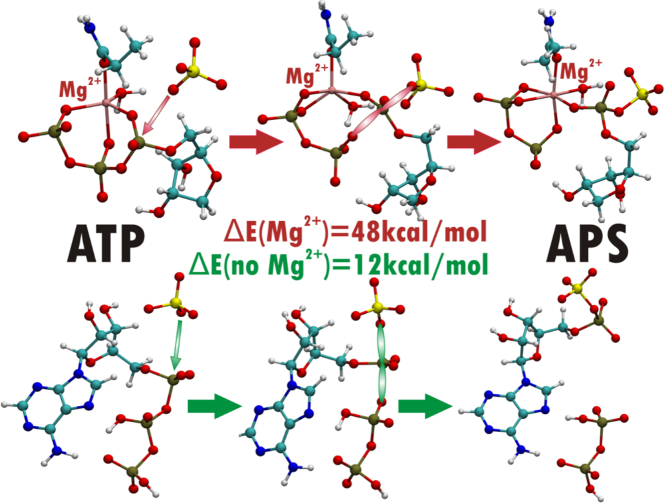
Abstract

ATPS Sulfurylase (ATPS) is the first of three enzymes in the sulfate reduction pathway - one of the oldest metabolic pathways on Earth, utilized by Sulfate Reducing Bacteria (SRB). Due to the low redox potential of the sulfate ion, its reduction requires activation via formation of adenosine 5′-phosphosulfate (APS), which is catalyzed by ATPS. Dispersion-corrected hybrid density functional theory (DFT/B3LYP-D3) was used to test three reaction mechanisms proposed for conversion of ATP to APS: two-step SN-1 reaction running through AMP anhydride intermediate, two-step reaction involving cyclic AMP intermediate and direct SN-2 conversion of ATP to APS molecule. The study employed five different cluster models of the ATPS active site: one containing magnesium cation and four without it, constructed based on the crystal structure (PDB code: 1G8H) solved for ATPS from Saccharomyces cerevisiae in complex with APS and pyrophosphate (PPi), where Mg²⁺ was not detected. The model with magnesium ion was constructed based on the representative structure obtained from trajectory analysis of the molecular dynamics simulations (MD) performed for the hexameric ATPS-APS-Mg²⁺-PPi complex. The results obtained for all considered models suggest that ATPS-AMP anhydride intermediate is a highly energetic and unstable complex, while formation of cyclic AMP molecule requires formation of unfavorable hypervalent geometry at the transition state. Among all tested mechanism, the energetically most feasible mechanism of the ATPS reaction is SN-2 one-step conversion of ATP to APS occurring via a pentavalent transition state. Interestingly, such a reaction is inhibited by the presence of Mg²⁺ in the ATPS active site. Magnesium cation forces unfavorable geometry of reactants for SN-2 mechanism and formation of pentavalent transition state. Such a reaction requires rearrangement of Mg²⁺ ligands, which raises the barrier from 11-14 kcal/mol for the models without Mg²⁺ to 48 kcal/mol for model with magnesium ion included.

Graphical Abstract

1. Introduction

Sulfate Reducing Bacteria (SRB) are involved in the dissimilatory reduction of sulfate (SO₄²⁻) to sulfide (S²⁻), which constitutes one of the oldest enzymatic pathway on Earth and begun more than three billions years ago [1]. Among SRB, there are bacteria and archea that under anaerobic conditions are able to use sulfate as a terminal electron acceptor in their metabolism [1]. The process of sulfate reduction occurs via sulfite (SO₃²⁻) intermediate and is used as an energy conservation since its connection to oxidative phosphorylation reactions [1]. SRB play an important role in the biogeochemical sulfur cycle, biodegradation of aromatic pollutants and as regulators of important processes in soils, such as turnover of organic matter or mercury methylation [1,2]. Three cytoplasmic enzymes are involved in the pathway of dissimilatory reduction of sulfate to anionic sulfide: ATP Sulfurylase (ATPS), adenosine 5′-phosphosulfate (APS) Reductase (APSR) and dissimilatory sulfite Reductase (dSIR) [1,3]. ATPS catalyzes activation of sulfate anion to adenosine 5′-phosphosulfate (APS), by formation of SO₄²⁻-AMP bond, which is connected with release of the pyrophosphate [4,5]. Such an activation of SO₄²⁻ is required since due to its low redox potential, it cannot be directly reduced by organic acids or molecular hydrogen [1,6,7]. Sulfide released via this metabolic pathway may influence the corrosion of metallic constructions in SRB habitats, e.g. soil and ground water. [1,5,8].

In the assimilatory pathway performed in eukaryotes, some bacteria and algae, the APS product of ATPS reaction is a substrate for APS kinase, which phosphorylates it at 3′-position, producing 3′-phosphoadenosine 5′-phosphosulfate (PAPS) [[9], [10], [11], [12], [13], [14], [15]]. PAPS acts as a sulfuryl donor for many sulfur containing compounds. It might also be reduced to sulfide, required in biosynthesis of cysteine, which in turn may be a sulfur donor for methionine [9,12,13,15]. In metazoa, oomycetes, fungi and some algae ATPS and APS kinase are gathered in one protein named PAPS synthetase [1,12,16]. Interestingly, in microalgae a large variety of ATPS isoforms was found [11,12]. In red lineage of algae, ATP Sulfurylases exist in parallel as bifunctional isoforms combined with APS kinase (coccolithophorids, diatoms) or with APS reductase (dinoflagellates) and as a monofunctional enzyme [11,12]. Therefore, it is hypothesized that bifunctional enzyme is involved in sulfonation, while monofunctional ATPS operates sulfate reduction pathway [11,12]. In cyanobacteria and green lineage of algae, lack of bifunctional isoform indicates that monofunctional enzyme is involved in both sulfonation and sulfate reduction metabolic pathways [11,12]. Based on the variety of ATPS isoforms in see and freshwater algae, it is suggested, that life in different sulfate availability could affect the evolution of ATPS enzyme [10,12].

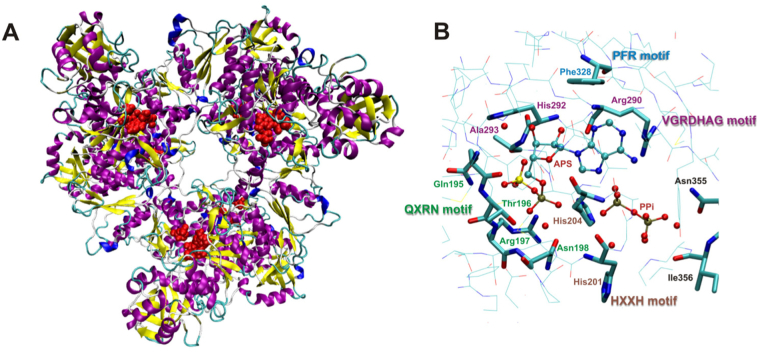
The present work is devoted to the mechanism of the reaction catalyzed by the first enzyme of the SRB pathway, i.e. ATP Sulfurylase (ATPS). ATPS is an enzyme ubiquitous in Nature, catalyzing the reversible reaction of sulfate activation with the employment of ATP, which leads to APS and pyrophosphate anion products. ATPS from SRB, yeast and plants are characterized as monomers or homo-oligomeric structures [1,[17], [18], [19]]. There are crystal structures available for ATPS in complex with intermediates of the native catalytic reaction as well as with its inhibitors. The crystals with the following PDB codes: 4MAF, 1I2D, 1G8H, 1G8G, 1V47, 1JEE [9,[20], [21], [22], [23]] were solved for the enzyme-APS complex, whereas 1G8F, 1JHD are structures for enzyme-sulfate complexes [22,24]. The structures of ATPS-APS complex are available for the following organisms: soybean (PDB code: 4MAF), Penicillium chrysogenum (PDB code: 1I2D), Saccharomyces cerevisiae (PDB codes: 1G8H, 1G8G, 1JEE) and Thermus thermophillus (PDB code: 1V47). However, there is only one structure available with both reaction products of ATPS - APS and pyrophosphate (PPi) molecules: 1G8H [22]. The quaternary structure of ATPS from Saccharomyces cerevisiae (PDB code: 1G8H), similarly to the one from Penicillium chrysogenum (PDB code: 1I2D), was determined as a homohexameric assembly arranged as two trimeric rings stacked with a twist of 60^∘ (D3 symmetric arrangement [21,22], Fig. 1).

Fig. 1.

A. Hexamer structure of ATPS-APS-Mg²⁺-pyrophosphate complex obtained after 20 ns of Molecular Dynamics (MD) simulations; B. Four conserved motifs observed in the known ATPS sequences presented in the 1G8H crystal structure;

In the active site of ATP Sulfurylase, four conserved motifs are observed in the available ATPS sequences and crystal structures: QXRN (Gln195-Thr196-Arg197-Asn198), HXXH (His201-Arg202-Ala203-His204), VGRDHAG (Val288-Gly289-Arg290-Asp291-His292-Ala293-Gly294) and PFR (Pro327-Phe328-Arg329) motifs presented in Fig. 1 [1,21,22].

Based on the crystal structures solved for the ATP Sulfurylase from Saccharomyces cerevisiae and Penicillium chrysogenum, the role of the mentioned conserved motifs were described in the works published by Ullrich et al. and MacRae et al. [21,22]. The QXRN module is hypothesized to be involved in anchoring of the phosphosulfate group of adenosine 5′-phosphosulfate - the product of the ATPS enzymatic reaction. The side chain of Thr196, which is not strictly conserved in all sequenced ATPS, has been observed to form a hydrogen bond with one of phosphate oxygen. In the structure of ATPS-APS-PPi complex from Saccharomyces cerevisiae, Gln195 is within hydrogen bond distance with the sulfate group of APS, the side chains of Thr196 and Asn198 are involved in hydrogen bonds with the phosphate non-bridging oxygen atoms [22]. Very similar interactions between QXRN motif and phosphosulfate moiety of APS are observed in the ATPS-APS crystal structure from Penicillium chrysogenum [21]. According to the solved crystal structure of ATPS-APS-PPi complex (PDB code:1G8H), His204 from the HXXH motif is within hydrogen bonding distance with pyrophosphate non-bridging oxygen and is positioned between pyrophosphate anion and phosphate group of APS [22]. In many nucleotidylyl transferases two histidines of HXXH module coordinate α and β phosphate groups of nucleotide, but in the ATPS-APS complex His201 from the HRAH motif is within the distance of 5.7 Å from α phosphorus [22]. Therefore, presumably His201-X-X-His204 motif does not assists in the cleavage of the α-β phosphodiester bond, but might be involved in the stabilization of the ATP conformation and anchoring of the pyrophosphate in the active site. Such an observation has been done by Leatherbarrow et al. and Perona et al. for related aminoacyl-tRNA Synthetases [22,25,26]. The structure of ATPS-ATP complex modeled by Ullrich et al. with SYBYL (Tripos Inc.,St Louis, MO) suggested that in the active site the ATP molecule adopts horseshoe conformation, where β phosphate of ATP interacts with His204, while the His201 is hydrogen bonded to ATP γ phosphate. It is worth to mention, that ATP binding enzymes commonly bind ATP in complex with Mg²⁺ coordinating to the β and γ phosphates [27], while in the mentioned crystal structure of the ATPS-APS-PPi (PDB code: 1G8H) and derived from it ATPS-ATP modeled complex, magnesium ion has not been observed [22]. The site directed mutagenesis studies preformed with the murine and human bifunctional ATP Sulfurylase/APS Kinase revealed that replacement of one of histidines or arginine from the HRAH motif by alanine inhibits sulfurylase activity, while all mutants retain their kinase activity [[28], [29], [30]]. The sequence VGRDHAG seems to be a part of a common adenyl binding motif, called “PP loop”, observed in enzymes catalyzing cleavage of the bond between α and β phosphates in ATP molecule [28,31]. The highly conserved VGRDHAG motif, known as GRD-loop, is responsible for substrate binding. Site directed mutagenesis studies with ATPS and related citydyl-transferases from different organisms showed that alanine mutants of any of the residue from the VGRDHAG sequence revealed reduced or no activity of the considered enzymes [22,29,32,33]. This observation indicates that the VGRDHAG module is presumably responsible for sulfurylase activity as well as for binding of the nucleotide substrate [22].

Crystallographic studies performed for ATPS from Saccharomyces cerevisiae and Penicillium chrysogenum revealed, that ATP binding leads to the significant displacement within the hexameric ATPS structure [21,22]. It was found that the ATPS is an allosteric enzyme which may adopt at least two conformations: R state with higher affinity for the substrates and T state preferring allosteric inhibitors [21]. The important role in the transition between R and T is presumably played by the PFR motif, since in the absence of the substrate, the phenyl ring of the Phe328 occupies the adenyl binding site [22]. The ATP binding causes displacement of Phe328 side chain and ATPS adopts its R state [22,23]. These three conserved motifs make the unique architecture of the ATPS active site and that results in a different mode of substrate binding than in the related citydylyltransferases [22,34]. The fold of the domain II containing an active site region may suggest that ATPS belongs to the superfamily of α/β phosphodiesterases, but the architecture of the protomer and independent topologies present in one protein chain may also suggest that ATPS could be a representative of a new α/β proteins class.

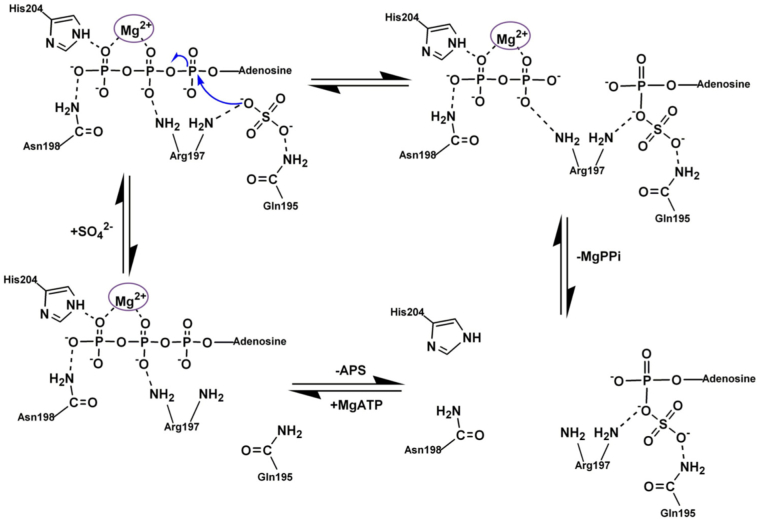
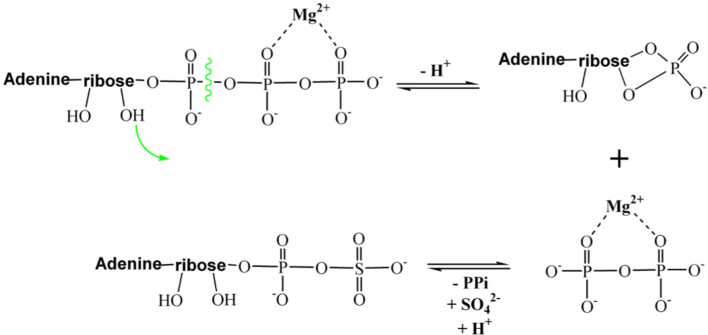
There are two main hypotheses how the reaction catalyzed by ATPS occurs. The first one is suggested based on the isotope trapping, mass spectroscopy and kinetic studies performed for the ATPS from the Escherichia coli K12 [35]. The ATPS from Escherichia coli is a tetramer composed of two heterodimers encoding by cysD and cysN genes [35], involved in the sulfate activation part of the assimilatory metabolic pathways [[35], [36], [37], [38]]. Based on the isotope trapping experiment, it was concluded that the ATPS reaction in Escherichia coli is a GTP-dependent two-step process. Firstly, the enzyme-AMP anhydride intermediate and pyrophosphate is formed, then after dissociation of pyrophosphate, the sulfate anion (SO₄²⁻) comes to the active site and APS is formed as is presented in Fig. 2 [35]. However, it is worth to mention that production of AMP intermediate was GTP-dependent and was inhibited by the addition of the sulfate [35]. Therefore, the one-step SN-2 reaction of directed conversion of ATP and sulfate molecules to APS and pyrophosphate can not be excluded. The horseshoe conformation of ATP molecule, modeled with SYBYL based on the ATPS-APS-PPi crystal structure from Saccharomyces cerevisiae, makes the in-line nucleophilic attack of the sulfate molecule very likely [22]. Such a one-step SN-2 reaction mechanism is presented in Fig. 3.

Fig. 2.

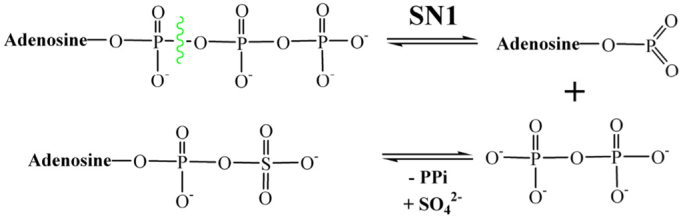
The two-step SN-1 reaction mechanism proposed for ATPS running through AMP anhydride intermediate.

Fig. 3.

The one-step SN-2 reaction mechanism proposed for ATPS based on the modeled ATPS-ATP-sulfate structure [22].

The structural data collected by Ullrich et al. stays in agreement with stereochemical studies by Zhang et al. devoted to ATPS whose results suggest a mechanism of SN-2 substitution with stereochemical inversion at the phosphorus α of ATP, which leads directly to APS molecule [22,39]. It is hypothesized that ATPS active site residues stabilize pentavalent transition state of the SN-2 reaction between ATP and sulfate [22]. Such a suggestion is in disagreement with reaction mechanism proposed for other nucleotidyl transferases, where an HXXH module is considered to contribute, as a proton donor, in the hydrolysis of a bond between α and β phosphate groups of ATP and in the dissociation process [22].

The isotope exchange experiments and theoretical studies performed on the B3LYP/6-31G(d,p) level showed that the hydrolysis of the APS molecule occurs presumably by cleavage of the P—O bond, which is confirmed by the absence of oxygen exchange between APS and water [40]. This observation precludes the ATPS mechanism involving formation of AMP intermediate and sulfate-water oxygen exchange [40].

In the presented work molecular dynamics (MD) simulations have been used to model the structure of ATPS in complex with APS, Mg²⁺ and pyrophosphate anion. However, the QM calculations revealed that the presence of the magnesium ion in the active site enforces such a conformation of APS and PPi that is unfavorable for the most likely SN-2 one-step ATPS mechanism. Therefore, the present work is mainly devoted to the results obtained for ATPS QM models constructed based on the crystal structure solved for ATPS-APS-pyrophosphate complex without presence of Mg²⁺.

2. Models and Methods

2.1. QM Models

The present study is focused on the enzyme-products (E-P) ATPS complexes and modeling of the backward reaction, since such a crystal structure is available in Protein Data Bank. Moreover, MD simulations performed for the hexameric enzyme-substrate (E-S) complex containing six ATP, six SO₄²⁻ molecules and six magnesium ions provided very diverse geometries of active site in each of six ATPS subunits.

Five cluster models of the active site were considered. Model MG for the E-P complex containing magnesium ion was constructed based on the results obtained from Molecular Dynamics (MD) simulations performed for the hexameric ATPS-APS-Mg²⁺-PPi complex. The stable conformation of the active site binding APS, PPi and Mg²⁺ was chosen based on the clustering analysis of MD trajectory, described in the Supplementary Data. The other four models for ATPS-APS-PPi (E-P) complexes deprived of magnesium ion were constructed based on the crystal structure labeled as 1G8H in the Protein Data Bank [22].

2.1.1. ATPS-APS-Mg²⁺-Pyrophosphate Model

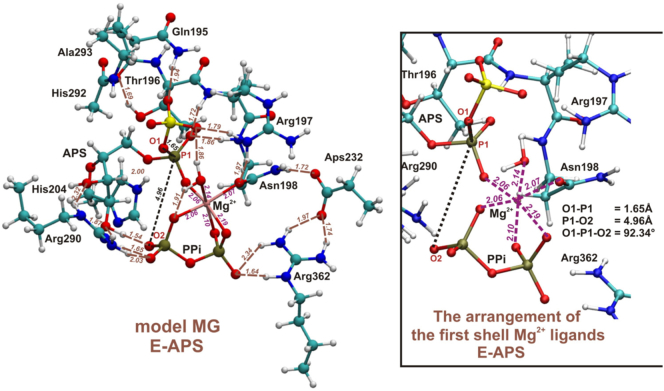
Model MG, constructed based on the most stable conformation obtained from MD trajectory analysis (Fig. 5), besides Mg²⁺, pyrophosphate ion and APS with adenine moiety replaced by the hydrogen atom, includes the following nine protein residues: Gln195, Thr196, Arg197, Asn198 (QXRN motif) with Gln195 N amino and Asn198 C carbonyl atoms of protein backbone replaced by hydrogen atoms, His204 (HXXH motif) truncated on the Cα-Cβ bond, Arg290 (VGRDHAG motif), Asp232 and Arg362 with carbonyl and amino groups of protein backbone replaced by hydrogen atoms and Ala293 with backbone fragment of His292 (VGRDHAG motif) (CO backbone moiety of Ala293 replaced by hydrogen atom). In order to maintain the rigidity of the protein backbone, constraints were imposed on all carbon atoms from protein backbone and hydrogens replacing backbone moieties.

Fig. 5.

The optimized model MG, constructed based on the results of MD simulations performed for hexamer structure of ATPS-APS-Mg²⁺-PPi complex. In magenta coordination bonds between Mg²⁺ and its ligands, in brown hydrogen bonds, while in black distances and the angle important for ATPS reaction.

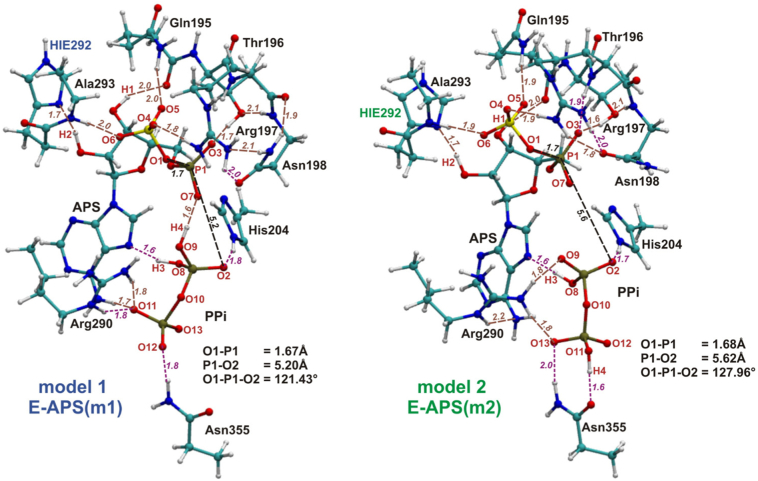
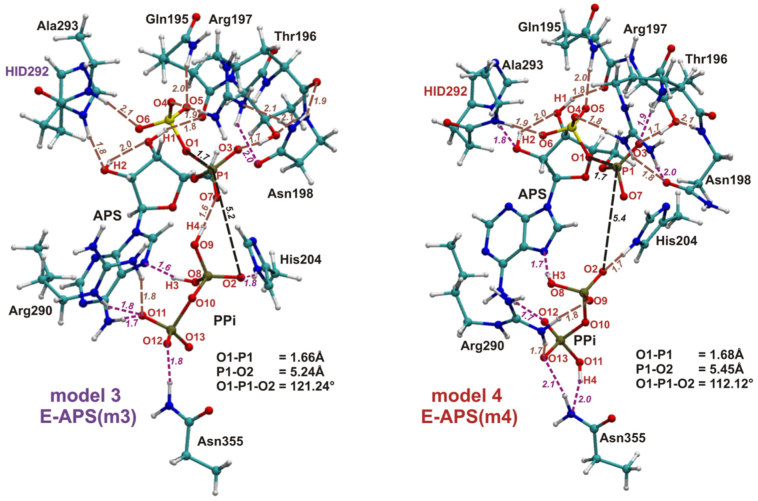
2.1.2. ATPS-APS-Pyrophosphate Model

Four QM cluster models of active site with no magnesium ion were constructed based on the crystal structure solved for the ATPS-APS-pyrophosphate complex from Saccharomyces cerevisiae (PDB code:1G8H, Fig. 1B). This is the only structure available for ATPS with both products, but Mg²⁺ was not observed within the active site [22]. All four models presented in Fig. 7, Fig. 8, labeled as model 1–4 consist of APS, pyrophosphate and the following nine protein residues: Gln195, Thr196, Arg197, Asn198 (QXRN motif) with N backbone atom of Gln195 and carbonyl backbone group of Asn198 replaced by hydrogen atoms, His204 (HXXH motif) truncated to 5-methylimidazole, Arg290 (VGRDHAG motif) and Asn355 with NH and CO backbone moieties replaced by hydrogens, and His292-Ala293 protein fragment (VGRDHAG motif), where His292 amino and Ala293 carbonyl groups of protein backbone are replaced by hydrogen atoms. During geometry optimization procedure constraints were imposed on all of the atoms replacing or constituting protein backbone atoms. Four mentioned models differ only in the manner of protonation of pyrophosphate anion and His292. The protonation mode of protein residues and molecules covered by the models was assigned based on the results from the Propka 3.1 program and visual inspection [41,42]. For the model without Mg²⁺ Propka 3.1 suggested double protonation of pyrophosphate (in model with Mg²⁺ bound according to Propka.3.1, pyrophosphate should not be protonated - charge −4) and neutral charge of His292. Therefore, for pyrophosphate two possible protonation states were considered, compare models 1 and 3 (pyrophosphate protonation labeled as v1) with models 2 and 4 (pyrophosphate v2) in Figs. 7 and 8. In case of His292, two possible protonation states seem equally probable, it is within the hydrogen bonding distance with a hydroxyl group of APS ribose moiety, i.e. His292-Nδ (His292 protonated on its Nε atom - HIE 292) may form hydrogen bond with H atom from a hydroxyl group of APS ribose, as well as His292-N δH (His292 protonated on its Nδ atom - HID292) may interact with hydroxyl oxygen, thus both options were tested (compare models 1 and 2 (HIE292) in Fig. 7 with 3 and 4 (HID292) in Fig. 8).

Fig. 7.

The optimized model 1 and 2, constructed based on the 1G8H crystal structure of ATPS-APS-PPi complex. In black - distances and the angle important for the reaction of direct conversion of ATP and SO₄²⁻ to APS and PPi, in brown - hydrogen bonds maintained during reaction, while in magenta - H-bonds which are not observed in all stationary points obtained for SN-2 type ATP-APS conversion.

Fig. 8.

The optimized model 3 and 4, constructed based on the 1G8H crystal structure of ATPS-APS-PPi complex. In black - distances and the angle important for the reaction of direct conversion of ATP and SO₄²⁻ to APS and PPi, in brown - hydrogen bonds maintained during reaction, while in magenta - H-bonds which are not observed in all stationary points obtained for SN-2 type ATP-APS conversion.

Summarizing, model 1 includes pyrophosphate v1 and His292 with protonated Nε (HIE292), model 2 - pyrophosphate v2 and HIE292, model 3 - pyrophosphate v1 and His292 with protonated Nδ (HID292), model 4 - pyrophosphate v2 and His292 with protonated Nδ (HID292).

2.2. MD Methods

MD simulations were performed for the ATPS-APS-Mg²⁺-pyrophosphate complex in order to model the structure with bound magnesium ion, and check its coordination mode in the enzyme active site. The starting structure of ATPS hexamer was build with the help of the PISA server, based on the 1G8H crystal structure solved for ATPS dimer, as it was suggested by Ullrich et al. [22]. Lacking Met1 residue in each subunit was modeled with Modeller program [43,44]. Protonation states of residues of hexamer were evaluated using Propka 3.1 program and visual inspection [41,42]. Parameters for all protein residues were applied from the AMBER FF03 force field, using AMBER 12 package [45,46]. Parameters missing in the AMBER force field were derived from QM calculations. In APS molecule, only phosphosulfate moiety was parametrized completely, while for adenine and ribose groups all parameters besides partial charges were taken from parameters available in the AMBER force field for ATP molecule. In the parametrization procedure whole APS molecule was fully optimized using DFT-D3/B3LYP/6-311++G(d,p). Partial charges were assigned for whole APS molecule using RESP procedure method, while the bonding parameters for bonds and angles were assigned only for phosphosulfate moiety based on vibrational analysis calculated for optimized APS model. All parameters including partial charges (RESP) and parameters characterizing bonds and angles for pyrophosphate molecule were assigned based on the QM calculations performed for pyrophosphate using the same DFT-D3/B3LYP/6-311++G(d,p) method. The water molecule forming hydrogen bonds with two oxygen atoms bound to different phosphorus atoms of pyrophosphate in the 1G8H crystal structure was replaced by magnesium ion (see Fig. 1B). The constructed hexameric complex was solvated with the TIP3P water. Since the total charge of the system was -114, it was compensated by addition of 114 Na⁺ ions.

The cluster analysis of the last nanosecond of MD trajectory obtained during 20 ns of simulations was performed to obtained a representative geometry of ATPS-APS-Mg²⁺-pyrophosphate complex. The details are described in the Supplementary Data.

2.3. QM Methods

Quantum mechanical (QM) calculations were performed with the Gaussian 09 program [47]. The constraints in each model were imposed on carbon atoms of protein backbone, as well as all hydrogen atoms replacing the groups from protein backbone. All stationary points were optimized using DFT method combining B3LYP (hybrid exchange-correlation) functional with Grimme's dispersion interaction (D3) [47,48]) and double-ζ basis set def2-SVP [49]. The D3 correction was computed with the Becke-Johnson damping [50]. The available crystal structures revealed that the ATPS active site is filled with many water molecules, which can not be included explicitly in the QM cluster model, thus all geometry optimizations were performed with addition of the macroscopic continuum PCM model simulating water surrounding. For all stationary point structures the energy is a combination of the single point B3LYP-D3/def2-TZVP/PCM(water) energy and zero point energy obtained from vibrational analysis.

3. Results and Discussion

The present work started with modeling of the ATPS structure in complex with APS and pyrophosphate-Mg²⁺. Since in the crystal structure, Mg²⁺ - a common companion of the ATP dependent reactions, is not observed, such a structure was modeled using MD simulations. After the clustering analysis of the MD trajectory, the QM model, which is a representation of E-P complex structure, have been selected. This model labeled as model MG was applied in study of the backward ATPS reaction. Since the arrangements of ATP/APS-pyrophosphate molecules in the active site forced by the presence of magnesium ion proved to be far from being optimal for the reaction mechanisms investigated, we also considered models deprived of Mg²⁺ constructed based on the 1G8H crystal structure. The description of the obtained stationary points for each model starts from the ATPS-products (ATPS-APS-(Mg²⁺)-PPi) complex. The energy profiles obtained for each model as well as energy barriers are described for the forward reaction.

Three reaction mechanisms were tested. The first one presented in Fig. 3, suggested by Ullrich et al., is one-step SN-2 mechanism leading directly from ATP and sulfate to APS and pyrophosphate ion via a pentavalent transition state [22]. The second one is two-step reactions proposed by Liu et al., where ATP is cleaved to enzyme-AMP anhydride-pyrophosphate intermediate, which after dissociation of the pyrophosphate anion reacts further with sulfate, giving the APS product [35]. The third mechanism presented in Fig. 4 is a two-step mechanism running through the cyclic AMP intermediate (Fig. 4).

Fig. 4.

The two-step reaction mechanism running through cyclic AMP intermediate.

3.1. ATPS-APS-Mg²⁺-Pyrophosphate Model

In the Fig. 5, the optimized geometry of the ATPS in complex with APS, magnesium ion and pyrophosphate is presented. This model, constructed based on the trajectory analysis of MD simulations, was employed in the studies of the three above mentioned mechanisms (see Fig. 2, Fig. 3, Fig. 4 and 4). However, only the mechanism of direct conversion of ATP to APS is presented, since for the other two pathways regardless of the model used, the same conclusions were reached. Both of these two-step reactions running either through AMP anhydride or cyclic AMP intermediate were proven to be unlikely, independently of the presence of Mg²⁺, thus the results of the studies devoted to these mechanisms are discussed and summarized in the section focusing on models without magnesium ion.

The reaction pathway, which we present in this subsection is the one-step reaction leading directly from ATPS-ATP-SO₄²⁻ to ATPS-APS-PPi complex. This is an SN-2 reaction, which may involve a reasonable barrier only when the appropriate geometry of the transition state may be achieved, i.e. the angle between three atoms directly involved in the SN-2 reaction is close to 180_°.

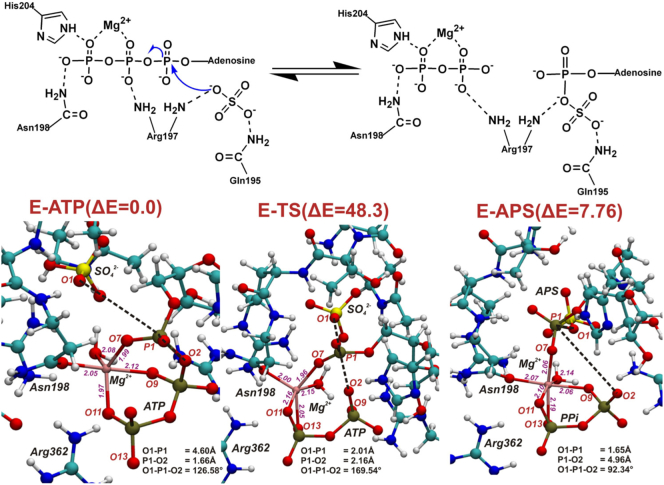
Already, in the optimized model MG (E-P complex) we may observed that magnesium ion present in the active site affects the geometry of the ATPS-APS-Mg²⁺-pyrophosphate complex, causing O1-P1-O2 angle to be equal 92^∘ (Fig. 5). Therefore, reaching the transition state optimal for SN-2 reaction requires reorganization of magnesium ligands. The structure of optimized model MG significantly differs from the ATPS-APS-PPi complex crystallized and solved by Ullrich et al., where the O1-P1-O2 angle equals 131.6^∘, and based on which SN-2 one-step mechanism was suggested [22]. The arrangements of Mg²⁺ ligands in the optimized structures of stationary points of the considered SN-2 mechanism is presented in Fig. 6. As it might be observed the E-S (ATPS-Mg²⁺-ATP-SO₄²⁻) complex reveals trigonal bipyramidal geometry of Mg²⁺ first shell, where magnesium ion is coordinated by five ligands, while in the E-P (ATPS-Mg²⁺-PPi-APS) complex, Mg²⁺ is coordinated by six ligands arranged in the tetragonal bipyramid. In the transition state structure magnesium ion is bound by five ligands forming the geometry of the distorted trigonal bipyramid. Therefore, exploring the Potential Energy Surface (PES) along the direction of the reaction coordinate, from the ATPS-Mg²⁺-ATP-SO₄²⁻ through E-TS1 to ATPS-Mg²⁺-PPi-APS, it was found that the arrangement of Mg²⁺ ligands changes from trigonal bipyramid through distorted trigonal bipyramid to tetragonal bipyramid, respectively (Fig. 6). In the transition state structure the Mg²⁺-O9 coordination bond is cleaved, while Mg²⁺-O13 one is formed in comparison to the E-S geometry. This process is required to obtain proper E-TS1 geometry for proposed SN-2 reaction with O1-P1-O2 angle of 169.54^∘ (Fig. 6). Such rearrangement of magnesium ligands is related to the very high energy barrier of 48.3 kcal/mol, which was confirmed by the single point calculations performed for the obtained stationary points structures truncated to the reactants (ATP/APS, SO₄²⁻/PPi), Mg²⁺ and its ligands: H₂O and Asn198. When the protein residues forming hydrogen bonds to reactants are removed, the barrier is 46.5 kcal/mol, supporting the explanation given above that the high barrier arises due to unfavorable coordination of the Mg²⁺ ion. This shows that the presence of magnesium ion inhibits the proposed ATPS mechanism of direct conversion of ATP to APS via pentavalent transition state [22,39].

Fig. 6.

SN-2 reaction of direct conversion of ATP to APS studied with model MG. The arrangement of Mg²⁺ first shell ligands in optimized geometries of ATPS-Mg²⁺-ATP-SO₄²⁻, ATPS-TS and ATPS-Mg²⁺-PPi-APS complexes. In red their final energies in kcal/mol with respect to the ATPS-Mg²⁺-ATP-SO₄²⁻ complex.

Therefore, the further part of the studies on this mechanism was devoted to the ATPS models deprived of magnesium ion in the active site.

3.2. ATPS-APS-Pyrophosphate Models

Four QM models constructed based on the 1G8H crystal structure [22] were employed (see Table 1). The models differ in the manner of protonation of His292 and PPi (see Figs. 7 and 8). The most important distances are gathered in Table S 4. In the optimized models of ATPS-APS-PPi complex the O1-P1-O2 angle remains in a range between 112.12^∘ and 127.96^∘ (Figs. 7 and 8), which is in much better agreement with the corresponding angle from the crystal structure (111.48^∘-131.56^∘ depending on which pyrophosphate atom is labeled as O2) than the structure obtained for model MG (92.34^∘). Differences in the structures of the E-APS-PPi complex caused by replacing HIE292 by HID292 might be observed comparing model 1 with 3, where pyrophosphate protonation mode is denoted as v1 and model 2 with 4 containing pyrophosphate protonated according to the v2 manner (Figs. 7 and 8).

Table 1.

The summary of the modeling of SN-2 one-step reaction leading directly from ATPS-ATP-SO₄²⁻ to ATPS-APS-PPi complex performed with models 1, 2, 3 and 4. In columns relative energy with respect to the most stable ATPS-ATP-SO₄²⁻ structure obtained for model 4, the critical O1-P1-O2 angle and number of hydrogen bonds characterized by the distance shorter than 2.80 Å for each stationary point optimized with each of considered models.

Summary-direct conversion of ATP and S042−to APS and pyrophosphate molecules-models without Mg2+
Stationary point	model	ΔE [kcal/mol]	01-P1–02 angle [°]	Number of H-bonds in model (<2.80 Å)
E-ATP	1	5.27	164.87	25
	2	1.55	171.96	27
	3	8.60	165.07	24
	4	0.00	172.31	29
E-TS1	1	16.31	171.70	25
	2	15.11	171.88	25
	3	19.65	171.76	25
	4	11.85	171.64	26
E-APS	1	−18.20	121.43	28
	2	−19.14	127.96	29
	3	−15.00	121.24	29
	4	−15.79	112.12	29

In models 1 and 3 with two protons positioned on two oxygen atoms bound to the same pyrophosphate phosphorus, different protonation of His292 only affects the hydrogen bond system formed directly by His292, the remaining hydrogen bonds form the same arrangement in both structures. In model 1 containing HIE292, the hydrogen bond is formed between imidazole Nδ atom and H2 hydroxyl hydrogen from ribose moiety of APS (distance of 1.69 Å), while in model 3 HID292 proton bound to Nδ atom creates hydrogen bonding interaction with hydroxyl oxygen of APS ribose (1.77 Å). In model 3, the additional internal hydrogen bond in APS might be observed, between H2 hydroxyl atom and oxygen from the second hydroxyl group of APS ribose (1.96 Å - Fig. 8). Bigger structural diversity, caused by change of the His292 protonation mode, are observed between model 2 and 4 with v2 pyrophosphate protonation manner. Besides the hydrogen bonds formed by HIE292 Nδ and H2 atoms in model 2 (distance of 1.70 Å), HID292 and hydroxyl APS oxygen (1.86 Å) together with internal interaction between H2 and second hydroxyl group of APS ribose in model 4 (2.02 Å), observed also in models 1 and 3, some additional differences are noticed. In model 2, H4 atom from pyrophosphate molecule forms hydrogen bond with side chain carbonyl group of Asn355 (1.61 Å), while in model 4, H4 is involved in interaction with nitrogen atom of Asn355 side chain (distance of 2.04 Å). In model 4 there is also hydrogen bond between O12 pyrophosphate oxygen and amino group of APS adenine moiety (distance of 1.71 Å), which is not observed in model 3.

Much stronger influence on the structures of ATPS-APS-PPi complex has different protonation mode of pyrophosphate. To observe the difference in ATPS-APS-PPi complex between models containing v1 and v2 pyrophosphate, models 1 and 3 should be compared with models 2 and 4. In models 1 and 3, characterized by v1 protonation manner of pyrophosphate, there are following seven unique hydrogen bonds, which are not observed in models 2 and 4 (Figs. 7 and 8): H-bond between H4 pyrophosphate proton and O7 phosphate oxygen from APS (distance of 1.60 Å in both 1 and 3 models), O11 pyrophosphate oxygen - amino moiety of APS adenine (1.67 Å in model 1 and 1.65 Å in model 3), two hydrogen bonds between O11 pyrophosphate oxygen and guanidine group of Arg290 (1.76/1.78 and 1.75/1.78 Å in models 1 and 2, respectively), H-bond between O12 pyrophosphate oxygen and amino side chain moiety of Asn355 (1.77 Å in both models), and two hydrogen bonds formed by amino side chain of Asn198 with carbonyl group of protein backbone and with guanidine moiety of Arg197 (1.92 and 2.12 Å in both 1 and 3 models). In models 2 and 4 there are five such a hydrogen bonds which are not observed in the models 1 and 3: hydrogen bond between O3 phosphate oxygen of APS and protein backbone amino group of Arg197 (distance of 1.87 and 1.88 Å in model 2 and 4, respectively), O9 pyrophosphate oxygen - guanidine group of Arg290 interaction (1.77 and 1.80 Å in model 2 and 4, respectively), H-bond between O13 pyrophosphate oxygen and guanidine side chain of Arg290 (1.76 and 1.74 Å in model 2 and 4, respectively), H-bonding interaction between O13 pyrophosphate oxygen and amino side chain group of Asn355 (1.98 and 2.09 Å in model 2 and 4, respectively) and H-bond formed by side chain carbonyl moiety of Asn198 and guanidine group of Arg290 (1.84 Å in both 2 and 4 models).

Comparing models 1 and 3 with models 2 and 4, guanidine group of Arg290 interacts with v1 pyrophosphate by two hydrogen bonds accepted by its O11 oxygen in models 1 and 3, while in models 2 and 4 with v2 pyrophosphate by two H-bonds with O9 and O13 oxygen atoms (Figs. 7 and 8).

Among the considered models without magnesium ion, ATPS-APS-PPi complex obtained for model 2, with v2 protonation mode of pyrophosphate and HIE292, is the most stable. This species optimized for model 1 (v1 pyrophosphate and HIE292) is by 0.9 kcal/mol less stable, while ATPS-APS-PPi structures obtained for models 3 and 4, containing HID292, lie by 4.1 (model 3) and 3.3 kcal/mol (model 4) higher in energy than their equivalent for model 2. This observation may lead to the conclusion that the manner of His292 protonation affects the stability of the E-P complex.

3.2.1. SN-1 Two-Step Reaction Mechanism Involving AMP Anhydride Intermediate

The reaction mechanism, proposed by Liu et al. [35] and presented in Fig. 2, was investigated applying model 1 and 2, as well as the model MG. For all considered models the backward reaction was modeled, starting from the ATPS-APS-PPi. The study on this two-step mechanism begun with the scan of O1-P1 distance (Fig. 9) in order to obtain an ATPS model in complex with AMP anhydride, SO₄²⁻ and PPi molecules. As it might be noticed in the graph presented in Fig. 9, the elongation of O1-P1 bond is correlated with increasing energy of the considered system, which for the distance of 3.10 Å reaches 50 kcal/mol with respect to the corresponding E-P complexes. Further elongation of P1-O1 distance leads back to the formation of APS molecule, but with another oxygen atom of sulfate bound to P1. Model 3 and 4 differ from model 1 and 2 in only the protonation mode of His292, which does not directly interact with phosphate and sulfate moiety, thus the similar results are expected. All of the trials to obtain stable geometry of the ATPS in complex with AMP anhydride failed, which leads to the conclusion that AMP-anhydride is short living species, that is not stabilized by the environment provided by the ATPS active site.

Fig. 9.

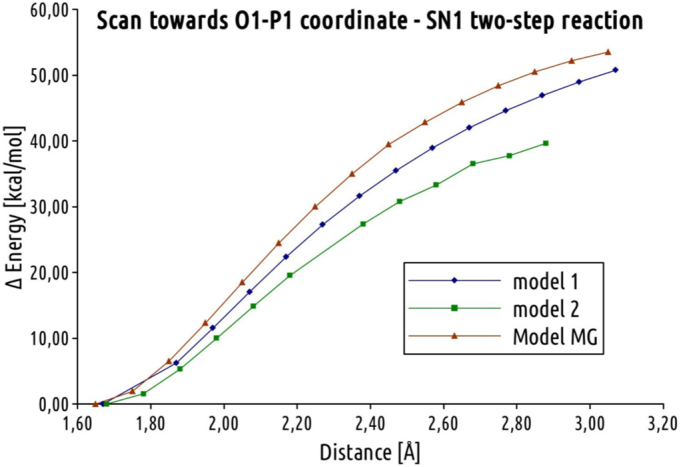
The scan of O1-P1 distance performed for model 1, 2 and model MG in order to obtain ATPS-AMP anhydride-PP1-SO₄²⁻ complex.

3.2.2. Two-step Reaction Mechanism Involving Cyclic AMP Intermediate

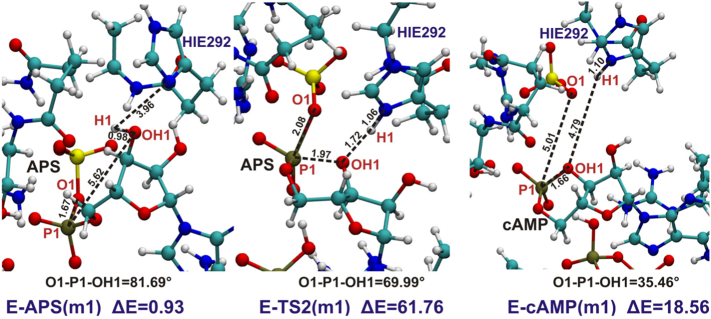
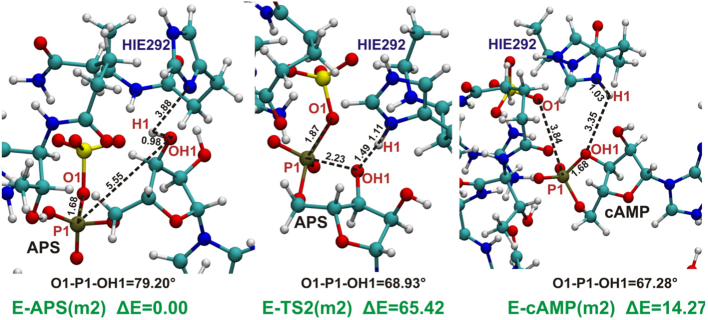
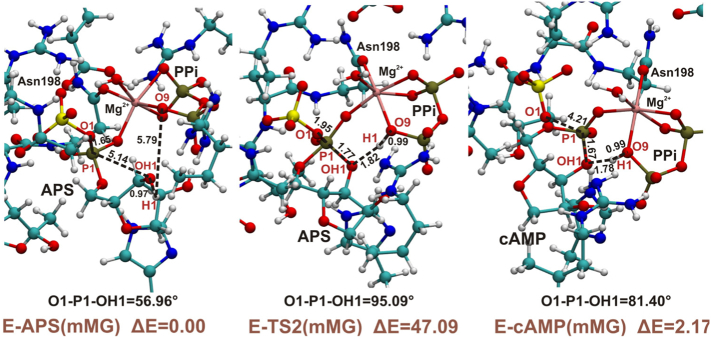
The mechanism presented in Fig. 4, running through cyclic AMP (cAMP) intermediate, was investigated for model MG, model 1 and 2. These two models lacking Mg²⁺ have been selected, since both of them contain HIE292 and thus Nδ of His292 may serve as an acceptor of proton H1 released from hydroxyl group of APS ribose moiety. For all three models this mechanism was studied in the backward direction running from ATPS-APS-PPi product to the ATPS-cAMP-SO₄²⁻-PPi intermediate complex (Fig. 10, Fig. 11, Fig. 12 and 12). This process is associated with formation of the bond between OH1 hydroxyl ribose oxygen and P1 phosphorus atom coupled with cleavage of the O1-P1 bond and releasing of H1 proton and sulfate ion. Simultaneous O1-P1 bond cleavage and formation of the OH1-P1 bond might be classified as a typical SN-2 reaction, thus to obtain reasonable barrier, in transition state the O1-P1-OH1 angle should not deviate too much from 180_°.

Fig. 10.

The optimized stationary points of model 1 obtained for the reaction of formation of cyclic AMP. In black distances and angle critical for such process. Relative energy in kcal/mol with respect to the most stable ATPS-APS complex obtained for model 2 is denoted as “ΔE”.

Fig. 11.

The optimized stationary points of model 2 obtained for the reaction of formation of cyclic AMP. In black distances and angle critical for such process. Relative energy in kcal/mol with respect to the most stable ATPS-APS complex obtained for model 2 is denoted as “ΔE”.

Fig. 12.

The optimized stationary points of model MG obtained for the reaction of formation of cyclic AMP. In black distances and angle critical for such process. Relative energy in kcal/mol with respect to the ATPS-APS complex is denoted as “ΔE”.

Fig. 10, Fig. 11 and 12 present fragments of studied models with denoted distances and angles critical for the reaction. In the optimized structure of ATPS-APS-PPi complex the O1-P1-OH1 angle equals 57.0^∘, 81.7^∘ and 79.2^∘, in models MG, 1 and 2, respectively. In the crystal structure (PDB code: 1G8H), the O1-P1-OH1 angle equals 80.15^∘, revealing much better agreement with the corresponding angle in models 1 and 2 than in model MG. However, in all studied models the angle between the atoms directly involved in the SN-2 reaction of cleavage of O1-P1 and formation of P1-OH1 bond remains rather far from the most favorable straight angle. The conformation of APS, similar in each model, causes formation of highly energetic hypervalent structure in the ATPS-TS2 transition state complex. In the ATPS-TS2 optimized geometries (Fig. 10, Fig. 11 and 12) the critical O1-P1-OH1 angle equals 69.99^∘, 68.93^∘ and 95.09^∘ in model 1, 2 and model MG, respectively. Therefore, the first step of backward mechanism (from APS to cAMP), as well as second step of forward reaction (from cAMP to APS) are characterized by high energy barrier in all studied models remaining in the range: 47–65 kcal/mol and 43–51 kcal/mol for backward and forward reaction, respectively (Fig. 10, Fig. 11 and 12). In case of model 1 and 2, H1 proton released from hydroxyl group of APS is transferred to Nδ atom of HIE292 (Fig. 10, Fig. 11 and 12), while in model MG the best acceptor of H1 hydroxyl proton is O9 pyrophosphate oxygen (Fig. 12).

The geometry of model MG reveals some difference with respect to models 1 and 2. The presence of magnesium ion causes changes in APS and PPi conformations in active site and thus the pattern of hydrogen bonds formed with protein pockets differs from that observed in crystal structure solved without Mg²⁺.

The cyclic AMP in contrast to the AMP anhydride is a far more stable intermediate characterized by energy 17.7 kcal/mol for model 1, 5.7 kcal/mol for model 2 and 2.2 kcal/mol for model MG higher than the ATPS-APS-PPi complex in the corresponding model.

A general conclusions, that can be drawn based on the results described in this subsection, is that shape of the ATPS active site forces the arrangement of phosphosulfate and ribose moieties of APS unfavorable for the mechanism proceeding through cyclic AMP.

3.2.3. SN-2 Mechanism of Direct Conversion of ATP to APS Molecule

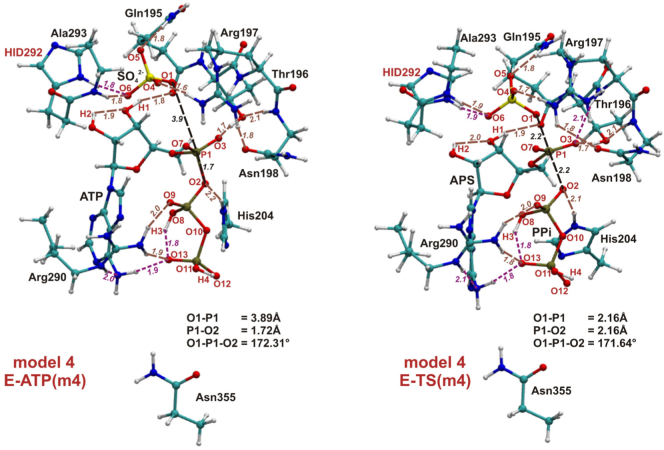
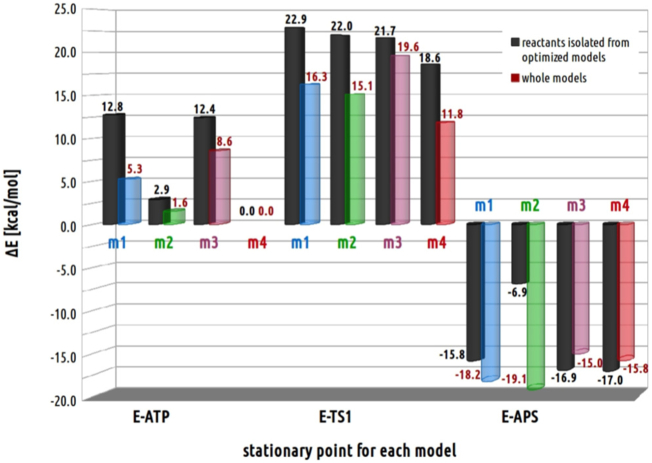
The SN-2 one-step reaction of ATP and sulfate anion leading to APS and PPi was modeled for all four models constructed based on the crystal structure solved for ATPS in complex with products. Therefore, this process was investigated in the backward direction, started with the known ATPS-APS-PPi structure. Fig. 13 present the optimized E-S structures (ATPS-ATP-SO₄²⁻ complexes labeled as E-ATP) as well as transition states (E-TS1) obtained for model 4 (the optimized geometries of E-ATP and E-TS1 obtained for models 1, 2 and 3 are presented in Supplementary Data in Fig. S 6, 7 and 8). The energy profiles obtained for models 1 (m1), 2 (m2), 3 (m3) and 4 (m4) are presented in Fig. 14, where each of the stationary point is characterized by relative energy calculated with respect to the most stable E-S complex obtained for model 4 and denoted as E-ATP(m4).

Fig. 13.

The optimized geometries of ATPS-ATP-SO₄²⁻ and ATPS-TS1 complexes found with model 4. In black - distances and the angle important for the reaction of direct conversion of ATP and SO₄²⁻ to APS and PPi, in brown - hydrogen bonds maintained during reaction, while in magenta - H-bonds which are not observed in all stationary points obtained for SN-2 type ATP-APS conversion.

Fig. 14.

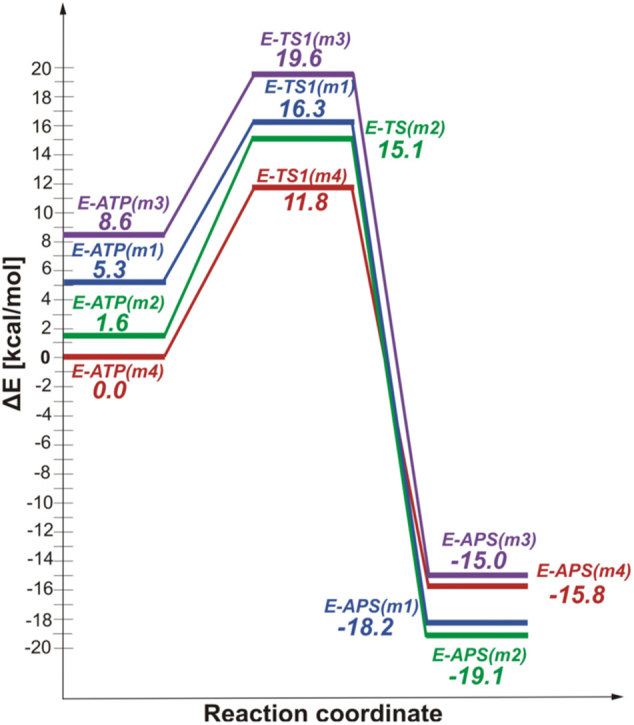
The energy profiles of direct conversion of ATP to APS according to SN-2 mechanism with pentavalent TS1 obtained for models 1 (m1), 2 (m2), 3 (m3) and 4 (m4).

Models of the optimized ATPS-ATP-SO₄²⁻ active site complex reveal much more suitable arrangement of the reactants (ATP and SO₄²⁻) for subsequent SN-2 reaction than was observed in the corresponding structure for the model including magnesium ion (model MG in Fig. 6). In E-S complex, the O1-P1-O2 angle equals 165.0^∘, 172.0^∘, 165.1^∘ and 172.3^∘ in model 1, 2, 3 and 4, respectively, in comparison to 126.6^∘ in model MG.

Three hydrogen bonds observed in all four models of ATPS-APS-PPi complex, i.e. adenine ring - H3 proton of pyrophosphate, guanidine group of Arg197 - side chain carbonyl moiety of Asn198 and between O2 phosphate oxygen and imidazole ring of His204, are not observed in ATPS-ATP-SO₄²⁻ complex in any of considered models. All interactions between pyrophosphate molecule and Asn355 observed in ATPS-APS-PPi complex are absent in all optimized versions of the ATPS-ATP-SO₄²⁻ complex, since in the E-S stationary point PPi moiety constitutes an integral part of ATP and thus it adopts different position in the active site than in the E-P complex. Such relocation of pyrophosphate group results also in the cleavage of the H-bond formed by O11 and O12 pyrophosphate oxygen atoms with Arg290 group, present in E-P complexes of models 1 and 3 (Fig. 7, Fig. 8), as well as O2 pyrophosphate oxygen - His204 H-bond observed in all ATPS-APS-PPi complexes and absent in ATPS-ATP-SO₄²⁻ structures.

Among four models of the active site without Mg²⁺, the most stable ATPS-ATP-SO₄²⁻ complex was obtained for model 4, thus relative energies of stationary points optimized for all models and presented in profiles in Fig. 14 were calculated with respect to its energy. The E-S complex obtained using model 4 is only by 1.6 kcal/mol more stable than model 2, characterized by the same v2 protonation mode of pyrophosphate moiety of ATP, while in comparison to models 1 and 3, containing v1 pyrophosphate, it lies lower in the energy by 5.3 and 8.6 kcal/mol, respectively. A similar relationship might be noticed between relative energies of E-TS1 complex. Transition state optimized for models 2 and 4, including v2 pyrophosphate, are more stable than their counterparts obtained for models 1 and 3 with v1 pyrophosphate. The relative energy of transition state obtained using model 4 is more stable by 3.3 kcal/mol than the corresponding structure obtained for model 2 and by 4.5 and 7.8 kcal/mol in comparison to models 1 and 3, respectively. However, different dependence between the manner of pyrophosphate protonation and relative energy in the energy diagram has been observed for E-P (ATPS-APS-PPi) structures. From Fig. 14 it can be noticed that the most stable E-P complex was optimized with models 1 and 2, containing HIE292 (ΔE equals −18.2 and −19.1 kcal/mol, respectively). In comparison, the ATPS-APS-PPi complex obtained for models 3 and 4 (including HID292) are by 4.1 and 3.3 kcal/mol, respectively, less stable than their counterpart obtained for model 2. Such an observation leads to the conclusion that His292 and its protonation state plays an important role in stabilization of APS molecule in the ATPS active site.

It is worth to mention that the energy of stationary points optimized with each of the model is not only the consequence of the stabilizing interactions provided by protein residues, but there is also contribution from the internal energy of reactants. This internal energy contribution was checked by single point calculations performed for small models constructed based on obtained stationary point geometries, but truncated to reactants only (ATP/APS and SO₄²⁻/PPi). As it might be noticed from Fig. 15, model 4, provide the most stable geometry of reactants in ATPS active site. The arrangements of reactants cut from E-S complex optimized with models 1, 2 and 3 are by 12.8, 2.9 and 12.4 kcal/mol, respectively, less stable than their counterpart from model 4. The similar observation applies to reactants conformations derived from E-TS1 structures, where model 4 truncated only to ATP and sulfate molecules reveals the lowest relative energy (18.6 kcal/mol) with respect to the corresponding structures constructed based on models 1 (22.9 kcal/mol), 2 (22.0 kcal/mol) and 3 (21.7 kcal/mol). Comparing the relative energies of E-S and E-TS1 structures optimized with four models and corresponding energies of model fragments truncated only to reactants, it might be concluded that in all models the protein surrounding stabilize ATPS-ATP-SO₄²⁻ and ATPS-TS1 stationary points (Fig. 15). Slightly different conclusion might be drawn from analysis of structures obtained for E-P complex. Comparing the geometries of products (APS and PPi), the most stable reactant arrangement is derived from model 4. The conformations of APS and PPi molecules cut from models 1, 2 and 3 are characterized by 1.2, 10.1 and 0.1 kcal/mol less stable energy with respect to model 4. However, the inclusion of protein surrounding changes the models stability, which is a consequence of destabilizing impact of interactions provided by protein residues in models 3 and 4. Moreover, since the models 3 and 4 differ from 1 and 2 only by protonation manner of His292, this observation confirms previous hypothesis that His292 play an important role in binding of APS molecule.

Fig. 15.

The energy histograms presenting relative energies of full and truncated models of stationary points optimized for direct conversion of ATP to APS according to SN-2 mechanism with pentavalent TS1. Relative energies were computed with respect to the ATPS-ATP-SO₄²⁻ complex optimized with model 4.

Since the enzymatic reaction catalyzed by ATPS is reversible, the energy barriers of forward and backward reaction should be kept in mind when selecting the most likely mechanism and active site model. Comparing barriers of forward reaction and transition state relative energy obtained for all models deprived of magnesium ion, model 4 is most preferred with reaction cost of 11.8 kcal/mol. For models 1, 2 and 3 the relative energy connected with TS1 structure is by 4.5, 3.3 and 7.8 kcal/mol higher than for model 4. Considering energy barriers for backward reaction, the best results was obtained also for model 4, with the lowest barrier of 27.6 kcal/mol, comparing to the reverse mechanism cost of 34.5, 34.2 and 34.6 kcal/mol, calculated the reverse reaction with models 1, 2 and 3, respectively (Fig. 14).

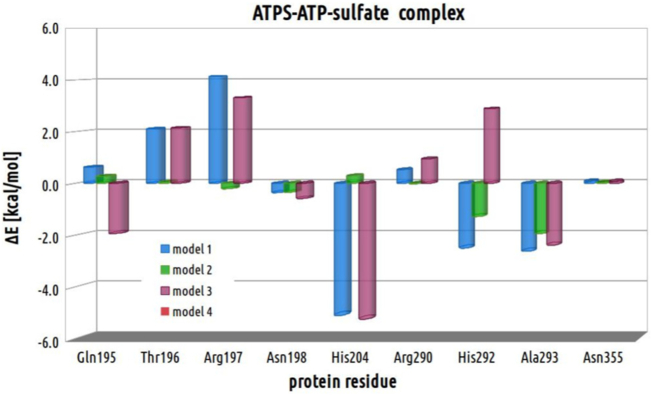
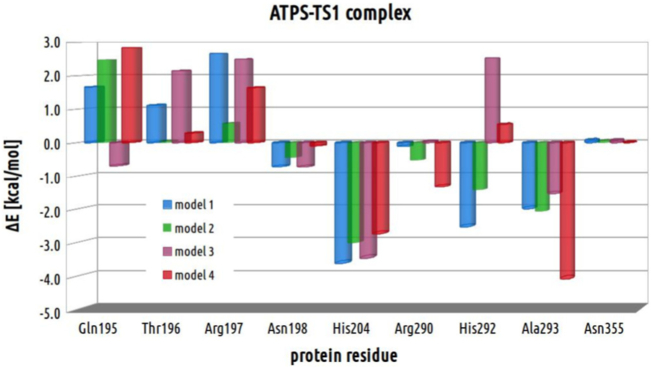
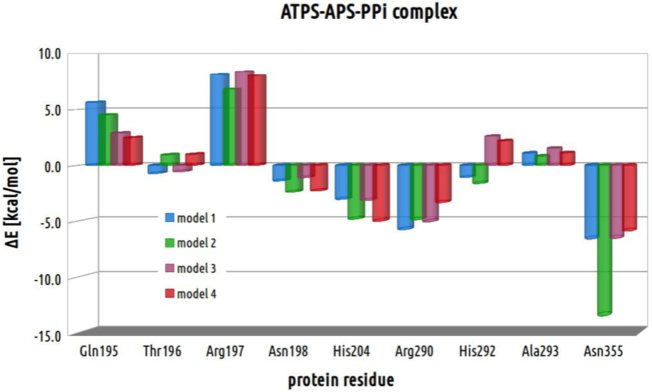
In order to evaluate the impact on reaction energetics of each residue, the models deprived of each of the residue were constructed based on the geometries of optimized stationary points and used in single point calculations. The relative energy of each of the truncated model was calculated with respect to the corresponding geometry derived from model 4. The resulting energy histogram for each of the protein residue within each of the stationary point structure is presented in Fig. 16, Fig. 17, Fig. 18 and 18.

Fig. 16.

The energy histograms presenting the impact of each protein residue, included in four considered models non-binding Mg²⁺, on the E-S complex. Relative energies was computed with respect to the ATPS-ATP-SO₄²⁻ complex optimized with model 4.

Fig. 17.

The energy histograms presenting the impact of each protein residue, included in four considered models non-binding Mg²⁺, on the E-TS1 complex. Relative energies was computed with respect to the ATPS-ATP-SO₄²⁻ complex optimized with model 4.

Fig. 18.

The energy histograms presenting the impact of each protein residue, included in four considered models non-binding Mg²⁺, on the E-P complex. Relative energies was computed with respect to the ATPS-ATP-SO₄²⁻ complex optimized with model 4.

Analyzing stabilizing effect of each protein residue following the reaction coordinate for direct conversion of ATP to APS, it might be concluded that the biggest stabilizing effect provided by Gln195 in E-S complex is observed in model 3 (−1.9 kcal/mol with respect to corresponding structure obtained for model 4). In models 1 and 2 Gln195 acts slightly destabilizing on ATPS-ATP-SO₄²⁻ complex in comparison to model 4 (by 0.6 and 0.3 kcal/mol, respectively), which is a consequence of weaker H-bonding interaction between hydroxyl moiety of ATP ribose and Gln195 amino side chain group in E-S structures obtained with models 1 and 2 (including HIE292) than in 3 and 4 (with HID292). In ATPS-TS1 and ATPS-APS-PPi complexes Gln195 residue reveals less stabilizing effect than in corresponding E-S, providing destabilization of E-TS1/E-P complexes with respect to their E-S counterparts by 1.0/5.0, 2.2/4.2, 1.2/4.8 and 2.8/2.5 kcal/mol for models 1, 2, 3 and 4, respectively. This observation is reflected by weaker interaction between Gln195 and sulfate observed in E-P than in E-S complexes.

Thr196 provides less stabilizing interactions by about 2 kcal/mol in E-S complex obtained with model 1 and 3 (v1 pyrophosphate) in comparison to models 2 and 4 (v2 pyrophosphate), which is associated with weaker H-bonds provided by Thr196 side chain to ATP phosphate oxygen in ATPS-ATP-SO₄²⁻ complexes for models 1 and 3 than the rest stationary points obtained for all models. Therefore, in comparison to corresponding ATPS-ATP-SO₄²⁻ complexes, the ATPS-TS1/ATPS-APS-PPi structures reflects stabilizing effect of Thr196 in models 1 and 3 (−1.0/−2.8 and −0.01/−2.7 kcal/mol, respectively) and negligible or slightly destabilizing in models 2 and 4 (0.0/0.9 and 0.3/1.0 kcal/mol, respectively).

For Arg197, similarly to Thr196, in E-S structures we may observe destabilizing effect in models 1 and 3 (4.1 and 3.3 kcal/mol, respectively) in comparison to models 2 (−0.2 kcal/mol) and 4 (0.0 kcal/mol). Arg197 provides many interactions to sulfate ion, α phosphate group of ATP and Asn198 residue in all considered models. However, such a difference in Arg197 contribution between E-S complexes including v1 and v2 pyrophosphate might be a consequence of presence significantly stronger hydrogen bond between Arg197 and O7 oxygen from α phosphate ATP group in models 2 (1.85 Å) and 4 (1.86 Å) in comparison to 1 (2.00 Å) and 3 (2.08 Å). In E-TS1 structures this bond is much weaker for models 2 and 4, while in E-TS1 obtained for models 1, 3 and E-P of all models it is cleaved. The existence of this strong H-bonding interaction in E-S complex of models 2 and 4 influences on the energetic contribution of Arg197 in E-TS1 and E-P complexes with respect to their E-S counterparts. In ATPS-TS1 structures obtained for models 1 and 3, Arg197 provides stabilizing contribution with respect to corresponding E-S by 1.5 and 0.8 kcal/mol, respectively, while it slightly destabilizes transition state optimized with models 2 and 4 (0.8 and 1.6 kcal/mol, respectively, in comparison to E-S counterparts). All ATPS-APS-PPi structures revealed destabilizing contribution of Arg197 with respect to corresponding E-S complexes, which might be a results of weakening the interaction between Arg197 and O4 sulfate oxygen in E-P with respect to E-S and E-TS1 complexes in all models.

Asn198 residue impact in ATPS-ATP-SO₄²⁻ and ATPS-TS1 complexes reveals rather negligible difference comparing structures obtained for all four models. The Asn198 stabilizing contribution is observed in E-P structures (−1.0, −2.0, −0.5 and −2.3 kcal/mol with respect to corresponding E-S structure). In contrast to E-S and E-TS1 complexes of all models, the ATPS-APS-PPi geometries include additional H-bond between carbonyl moiety of Asn198 side chain and guanidine group of Arg197.

As it might be noticed in Fig. 16, Fig. 17 and 18, the biggest role in studied mechanism might be played by His204, which in E-S complex provides bigger stabilizing effects for models 1 (−5.1 kcal/mol) and 3 (−5.2 kcal/mol) in comparison to models 2 (0.3 kcal/mol) and 4 (0.0 kcal/mol). This is a consequence of hydrogen bond provided by His204 to O8 ATP phosphate oxygen observed only in ATPS-ATP-SO₄²⁻ complex obtained for models 1 and 3 (Supplementary Data). In E-S structures of all models, hydrogen bond between O2 phosphate oxygen directly involved in studied reaction and His204 is very weak (distance of 2.39 and 2.25 Å in models 2 and 4, respectively) or does not exist (3.24 and 3.17 Å in models 1 and 3, respectively) in E-S complex, while in E-TS1 it becomes stronger (2.16, 2.11, 2.15 and 2.11 Å in models 1, 2, 3 and 4, respectively) to finally create strong H-bonding interaction in E-P complex (1.76, 1.70, 1.76 and 1.67 Å in models 1, 2, 3 and 4, respectively). All these interactions are reflected by His204 energetic contribution to E-TS1 and E-P complexes with respect to the corresponding E-S structures. The large stabilizing effect is provided by His204 to ATPS-TS1 and ATPS-APS-PPi stationary points optimized with models 2 (−3.3 and −5.1 kcal/mol, respectively, in comparison to E-S) and 4 (−2.7 and −5.0 kcal/mol, respectively in comparison to E-S). In models 1 and 3, His204 reveals less stabilizing impact on E-TS1 (1.5 and 1.8 kcal/mol, respectively) and E-P (2.1 kcal/mol in both models) with respect to their E-S counterparts. Such a result is a consequence of cleavage of O8-His204 bond (present in E-S) to form interaction between phosphate O2 oxygen in E-TS1 and E-P.

Within structures of E-S, Arg290 provides slightly bigger stabilizing impact in models 2 (−0.02 kcal/mol) and 4 (0.0 kcal/mol) than in models 1 (0.5 kcal/mol) and 3 (1.0 kcal/mol). Considering Arg290 energetic contribution to ATPS-TS1, in all models small stabilizing effect might be observed with respect to corresponding E-S complex (−0.6, −0.5, −0.9 and −1.3 kcal/mol for models 1, 2, 3 and 4, respectively). The bigger stabilizing impact of Arg290, might be observed comparing E-P structures (−5.2, −4.9, −6.0 and −3.3 kcal/mol for models 1, 2, 3 and 4, respectively), where Arg290 strongly interacts with pyrophosphate (Fig. 7, Fig. 8).

The impact of His292 residue depends on its protonation manner. HIE292 included in models 1 and 2 provides larger stabilizing effect in E-S (−2.5 and −1.3 kcal/mol, respectively), E-TS1 (−2.5 and −1.4 kcal/mol, respectively) and E-P (−1.1 and −1.6 kcal/mol, respectively) complexes in comparison to the corresponding structures optimized with models 3 (2.9, 2.5 and 2.6 kcal/mol in E-S, E-TS1 and E-P complexes, respectively) and 4 (0.0, 0.5, 2.2 kcal/mol in E-S, E-TS1 and E-P complexes, respectively), containing HID292 (Fig. 16, Fig. 17, Fig. 18).

The interactions derived from Ala293 in models 1 (−2.6 kcal/mol), 2 (−1.9 kcal/mol) and 3 (−2.4 kcal/mol) stronger stabilize ATPS-ATP-SO₄²⁻ complex than in model 4 (0.0 kcal/mol), while among the ATPS-TS1 structures the strongest stabilization is observed in model 4 (−4.1 kcal/mol with respect to −1.9, −2.1 and −1.5 kcal/mol in models 1, 2 and 3, respectively), which presumably has a significant impact on the most favorable barrier obtained for model 4 (Fig. 14). Comparing the ATPS-APS-PPi structures, similar effect provided by Ala293 is observed in all models (1.1, 0.8, 1.5 and 1.1 kcal/mol in models 1, 2, 3 and 4, respectively).

Asn355 residue provides large stabilizing impact only in ATPS-APS-PPi structures optimized with all models (−6.6, −13.4, −6.5 and −5.9 kcal/mol for models 1, 2, 3 and 4, respectively), which is a consequence of hydrogen bonding interactions formed between Asn355 and pyrophosphate.

The performed analysis suggests that the lowest relative energy of ATPS-APS-PPi complex obtained for model 2 (Fig. 14) might be a result of the largest impact provided by Asn355. Moreover, Fig. 16, Fig. 17, Fig. 18 show that the biggest impact on energy barrier is derived from His204 and Ala293. Ala293 interacts with sulfate oxygen by its NH protein backbone fragment, while His204 provided hydrogen bond to O2 oxygen bridging α and β phosphorus atoms. Therefore, considering site direct mutagenesis studies the best aim to efficiently inhibit ATPS reaction is His204. This observation is in agreement with experimental data obtained by Deyrap et al., Park et al. and Venkatachalm et al. for the murine and human bifunctional ATP Sulfurylase/APS Kinase. The mutagenesis studies revealed that replacement of arginine or one of histidines from HXXH motif (His201-His204 in 1G8H PDB structure) by alanine inhibits sulfurylase activity [[28], [29], [30]].

4. Conclusions

Five models were applied to study the activation of sulfate to adenosine 5′-phosphosulfate (APS) catalyzed by ATP Sulfurylase. One model was constructed based on the results of MD simulations performed for the ATPS complex with substrates (ATP and SO₄²⁻) and magnesium ion and four were constructed based on the crystal structure deprived of the Mg²⁺ (Table 1). All models were used to test three reaction mechanisms, i.e. two-step SN-1 reaction running from ATPS-ATP-SO₄²⁻ through ATPS-AMP-anhydride-PPi-SO₄²⁻ intermediate to ATPS-APS-PPi complex [35], two-step mechanism proceeding through cyclic AMP intermediate and one-step direct conversion of ATP and sulfate to APS and pyrophosphate molecules occurring according to SN-2 mechanism [22,39]. The results show that in all considered models AMP-anhydride intermediate is a very unstable and highly energetic species, which is not favored by the protein environment provided by the ATPS active site (Fig. 9). The two-step reaction via cyclic AMP was also excluded since the arrangements of ATP and APS-PPi molecules in all active site cluster models lead to the highly energetic (about 40–43 kcal/mol) transition state characterized by hypervalent structure Fig. 10, Fig. 11 and 12. Therefore, most of the work devoted to the reaction catalyzed by ATPS was focused on SN-2 mechanism of direct conversion of ATPS-ATP-SO₄²⁻ to ATPS-APS-PPi complex via pentavalent transition state presented in Fig. 3. The studies performed for model MG showed that the presence of the magnesium ion forces such a geometry of reactants, that is unfavorable for SN-2 mechanism since the angle between atoms directly involved in the reaction (O1-P1-O2) is 126^∘, i.e. far from 180^∘, which is ideal for SN-2 (Fig. 6). Moreover, reaching the transition state for such reaction requires rearrangement of the Mg²⁺ ligands. Moving along the reaction coordinate, the first shell ligands of Mg²⁺ change its geometry from trigonal bipyramid (Mg²⁺ coordinated by O7, O9 and O11 ATP phosphate oxygen atoms, Asn198 and water molecule) in E-S, via distorted trigonal bipyramid (Mg²⁺ coordinated by O7, O11, O13 phosphate oxygen atoms, Asn198 and water molecule) in E-TS1 to tetragonal bipyramid (Mg²⁺ coordinated by O7, O9, O11, O13 phosphate oxygen atoms, Asn198 and water molecule) in E-P complex (Fig. 6). Such a rearrangement around magnesium ion is presumably responsible for the high energy barrier of 48.3 kcal/mol obtained for this process. Since the studies performed for model of active site binding Mg²⁺ revealed that magnesium ion might rather inhibit than catalyze ATPS reaction, the work was extended to four models deprived of Mg²⁺, constructed based on the crystal structure solved for ATPS complex with APS and PPi, where the magnesium was not observed in the active site (PDB code: 1G8H, [22]). A comparison of the ATPS-APS-PPi models with Mg²⁺ (model MG) and without Mg²⁺ (models 1, 2, 3 and 4), shows that in the latter the O1-P1-O2 angle (112–128^∘) is in much better agreement with the corresponding angle in the crystal structure (111–131^∘) than in the model MG (92.34^∘). The four models of the active site without magnesium ion differ only in the manner of binding of two protons (H3 and H4) to pyrophosphate moiety and one proton to His292 residue, thus their final energy might by compared. The relative energy presented in the energy diagram in Fig. 14 was computed respect to the most stable ATPS-ATP-SO₄²⁻ structure obtained with model 4. Energy barriers obtained for forward reaction for all models deprived of Mg²⁺ are comparable and equal 11.0, 13.5, 11.0 and 11.8 kcal/mol for models 1, 2, 3 and 4, respectively. However, when stationary points are compared between models we may conclude that the most stable E-S and E-TS1 complexes were obtained with model 4 (Fig. 14). Due to the reversibility of ATPS reaction the barriers of backward reaction should also be taken into account. The APS-ATP backward conversion is characterized by energy barriers of 34.5, 34.2, 34.6 and 27.6 kcal/mol for models 1, 2, 3 and 4 respectively, thus model 4 performs best also in this case. Summarizing, the ATPS active site model 4 provides the most favorable conditions to perform direct conversion of ATP and SO₄²⁻ to APS and PPi molecules proceeding according to SN-2 mechanism with the barrier of 11.8 kcal/mol. The analysis of impact of each residue included in active site models showed that the most important interactions stabilizing transition state structure are provided by protein backbone fragment of Ala293 and side chain of His204, which is in agreement with site directed mutagenesis studies performed for bifunctional ATP Sulfurylase/APS Kinase enzymes. The experimental studies revealed that replacement of arginine or one of the histidines from the His201-XX-His204 conserved motif by alanine inhibits ATP Sulfurylase activity [[28], [29], [30]].

Appendix A. Supplementary Data

Supplementary material

: Details about modeling of the structure of ATP Sulfurylase (ATPS) hexamer in complex with adenosine 5′ phosphosulfate (APS) molecule, pyrophosphate and Mg²⁺; The geometries of ATPS-Mg²⁺-ATP-SO₄²⁻ and ATPS-TS1 stationary points optimized for the SN-2 direct conversion of ATP to APS with model MG; Detailed description of the hydrogen bonding interactions observed in four ATPS active site models deprived of magnesium ion; Cartesian coordinates and energies for optimized stationary points of considered ATPS mechanisms and models.