Abstract
Aims
Recurrent hospitalizations are a major part of the disease burden in heart failure (HF), but conventional analyses consider only the first event. We compared the effect of sacubitril/valsartan vs. enalapril on recurrent events, incorporating all HF hospitalizations and cardiovascular (CV) deaths in PARADIGM‐HF, using a variety of statistical approaches advocated for this type of analysis.
Methods and results
In PARADIGM‐HF, a total of 8399 patients were randomized and followed for a median of 27 months. We applied various recurrent event analyses, including a negative binomial model, the Wei, Lin and Weissfeld (WLW), and Lin, Wei, Ying and Yang (LWYY) methods, and a joint frailty model, all adjusted for treatment and region. Among a total of 3181 primary endpoint events (including 1251 CV deaths) during the trial, only 2031 (63.8%) were first events (836 CV deaths). Among a total of 1195 patients with at least one HF hospitalization, 410 (34%) had at least one further HF hospitalization. Sacubitril/valsartan compared with enalapril reduced the risk of recurrent HF hospitalization using the negative binomial model [rate ratio (RR) 0.77, 95% confidence interval (CI) 0.67–0.89], the WLW method [hazard ratio (HR) 0.79, 95% CI 0.71–0.89], the LWYY method (RR 0.78, 95% CI 0.68–0.90), and the joint frailty model (HR 0.75, 95% CI 0.66–0.86) (all P < 0.001). The effect of sacubitril/valsartan vs. enalapril on recurrent HF hospitalizations/CV death was similar.
Conclusions
In PARADIGM‐HF, approximately one third of patients with a primary endpoint (time‐to‐first) experienced a further event. Compared with enalapril, sacubitril/valsartan reduced both first and recurrent events. The treatment effect size was similar, regardless of the statistical approach applied.
Keywords: Heart failure, Hospitalization, Recurrent events, Neprilysin inhibitor
Introduction
Recently, it has been suggested that analysis of recurrent non‐fatal, along with fatal, events might be a better means of evaluating the true burden of heart failure (HF) as a disease and the effect of treatment, than the conventional time‐to‐first event analysis.1, 2, 3, 4, 5, 6, 7 Although most life‐saving therapies also reduce the risk of admission to hospital with worsening HF, hospitalization remains a common problem, readmission is frequent and the total number of admissions during a patient's life accounts for the greatest proportion of the overall cost of the illness. Assessing the effect of treatment on the time‐to‐first admission does not, therefore, reflect its impact on the full burden of disease, especially as it is possible that the efficacy of treatment may decline over time or patients with repeat admissions might represent a subset of those resistant to therapy. Consequently, we have examined the effect of sacubitril/valsartan (previously described as LCZ696), an angiotensin receptor neprilysin inhibitor (ARNI), compared with enalapril, on repeat as well as first hospitalizations and the totality of events [i.e. HF admissions and cardiovascular (CV) deaths], a pre‐specified exploratory analysis, in the Prospective comparison of ARNI with ACEI to Determine Impact on Global Mortality and morbidity in Heart Failure trial (PARADIGM‐HF).8, 9 In addition to this clinical question there is also a question about the choice of statistical method to evaluate the effect of treatment on recurrent events.2, 3, 4, 5, 6, 7 Analysis of recurrent hospitalizations in an unbiased way is difficult because of the competing risk of death and potentially different follow‐up times in the different treatment groups if one therapy is more effective than the other in reducing mortality. At present, there is no single method that has gained universal acceptance and for that reason we have compared a number of different analytical approaches that have been applied to this problem. We used these various methods to compare the effect of sacubitril/valsartan to enalapril on recurrent events in PARADIGM‐HF.
Methods
Study design and patients
The PARADIGM‐HF trial (http://clinicaltrials.gov ID number: NCT01035255) has been described in detail previously and the results published.8, 9, 10 Patients had New York Heart Association (NYHA) class II–IV symptoms, an ejection fraction ≤40% (changed to ≤35% by amendment), and a plasma B‐type natriuretic peptide (BNP) ≥150 pg/mL [or N‐terminal pro‐BNP (NT‐proBNP) ≥600 pg/mL]. Patients who had been hospitalized for HF within 12 months were eligible with a lower natriuretic peptide concentration (BNP ≥100 pg/mL or NT‐proBNP ≥400 pg/mL). Patients were required to be taking an angiotensin‐converting enzyme (ACE) inhibitor or angiotensin receptor blocker (ARB) in a dose equivalent to enalapril 10 mg daily for at least 4 weeks before screening, along with a stable dose of a beta‐blocker (unless contraindicated or not tolerated) and a mineralocorticoid receptor antagonist (if indicated). The exclusion criteria included history of intolerance to ACE inhibitors or ARBs, symptomatic hypotension (or a systolic blood pressure < 100 mmHg at screening/<95 mmHg at randomization), an estimated glomerular filtration rate (eGFR) <30 mL/min/1.73 m2, a serum potassium concentration > 5.2 mmol/L at screening (>5.4 mmol/L at randomization), and a history of angioedema. After a run‐in period [during which patients had to tolerate enalapril 10 mg twice daily for 2 weeks (single‐blind) and then sacubitril/valsartan (single‐blind) for an additional 4 to 6 weeks, initially at 49/51 mg twice daily and then 97/103 mg twice daily], patients were randomized to either enalapril 10 mg twice daily or sacubitril/valsartan 97/103 mg twice daily.
PARADIGM‐HF was conducted in accordance with the Declaration of Helsinki. The Ethics Committee of each of the 1043 participating institutions in 47 countries approved the protocol, and all patients gave written informed consent.
Outcomes
The primary outcome of PARADIGM‐HF was a composite of death from CV causes or a first hospitalization for HF. HF hospitalizations were adjudicated by a clinical events committee according to standardized definitions. All deaths were also classified by the committee.
Statistical analyses
Recurrent events are commonly analysed using count data methods (e.g. negative binomial regressions), and using time to event data methods [e.g. Wei, Lin and Weissfeld (WLW),11 and Lin, Wei, Ying and Yang (LWYY)12 models], all of which are extensions of Cox proportional hazards regression. More recently the joint frailty model has been used to examine recurrent events with a competing terminal event.4, 5 The methods used in the current analyses were pre‐specified in the trial statistical analysis plan.13 We calculated the HF hospitalization rate by treatment group by dividing the total number of HF hospitalizations by the total number of follow‐up years in each group. The cumulative rates of HF hospitalizations over time by treatment group were plotted as cumulative incidence curves using the non‐parametric Ghosh and Lin method, accounting for the competing risk of death.14 The effect of sacubitril/valsartan compared to enalapril on all HF hospitalizations and on the composite of all HF hospitalizations and CV death was analysed using the LWYY, WLW, negative binomial and joint frailty methods. For the WLW method, we estimated time to the i‐th HF hospitalization and time to the i‐th HF hospitalization including CV death as an event for i = 1 to 6.
The effect of sacubitril/valsartan compared to enalapril was modelled adjusting for the randomization stratification variable of region. All analyses were repeated with adjustment for differences in baseline characteristics including age, sex, heart rate, eGFR, left ventricular ejection fraction, body mass index, NYHA class, duration of HF, history of HF hospitalization, hypertension, diabetes, atrial fibrillation, myocardial infarction, stroke, and log NT‐proBNP.
A two‐sided P‐value of <0.05 was considered significant. The analyses were undertaken using R version 3.2.3, SAS version 9.4 (SAS Institute Inc., Cary, NC, USA), and Stata version 14 (Stata Corp., College Station, TX, USA).
Results
In the enalapril group (n = 4212), 658 patients (15.6%) had at least one hospitalization for HF; the respective number in the sacubitril/valsartan group (n = 4187) was 537 (12.8%) (Table 1). In the enalapril group, 418 patients had one admission for HF, 143 had two admissions, and 97 had ≥3 admissions during the trial (Table 1). The corresponding numbers in the sacubitril/valsartan group were 367, 110, and 60. The total number of admissions for HF was 1079 in the enalapril group and 851 in the sacubitril/valsartan group.
Table 1.
Number of patients with endpoint event and number of endpoint events per patient
| HF hospitalization | Composite of CV death and HF hospitalization | |||
|---|---|---|---|---|
| Sacubitril/valsartan | Enalapril | Sacubitril/valsartan | Enalapril | |
| Patients, n | 4187 | 4212 | 4187 | 4212 |
| Events per patient | ||||
| 0 | 3650 (87.2%) | 3554 (84.4%) | 3273 (78.2%) | 3095 (73.5%) |
| 1 | 367 (8.8%) | 418 (9.9%) | 629 (15.0%) | 751 (17.8%) |
| 2 | 110 (2.6%) | 143 (3.4%) | 186 (4.4%) | 204 (4.8%) |
| 3 | 33 (0.8%) | 53 (1.3%) | 59 (1.4%) | 96 (2.3%) |
| 4 | 9 (0.2%) | 22 (0.5%) | 17 (0.4%) | 34 (0.8%) |
| 5 | 5 (0.1%) | 16 (0.4%) | 7 (0.2%) | 17 (0.4%) |
| 6 | 3 (0.1%) | 2 (0%) | 5 (0.1%) | 11 (0.3%) |
| 7 | 6 (0.1%) | 1 (0%) | 4 (0.1%) | 1 (0%) |
| 8 | 1 (0%) | 0 (0%) | 4 (0.1%) | 0 (0%) |
| 9 | 2 (0%) | 2 (0%) | 0 (0%) | 0 (0%) |
| 10 | 0 (0%) | 0 (0%) | 2 (0%) | 2 (0%) |
| 11 | 0 (0%) | 1 (0%) | 0 (0%) | 1 (0%) |
| 18 | 1 (0%) | 0 (0%) | 1 (0%) | 0 (0%) |
| At least one event | 537 (12.8%) | 658 (15.6%) | 914 (21.8%) | 1117 (26.5%) |
| At least two events | 170 (4.1%) | 240 (5.7%) | 285 (6.8%) | 366 (8.7%) |
| Total events | 851 | 1079 | 1409 | 1772 |
| Total follow‐up years | 9308 | 9235 | 9308 | 9235 |
| Total CV deaths | 558 (13.3%) | 693 (16.5%) | ||
| Total all‐cause deaths | 711 (17.0%) | 835 (19.8%) | ||
CV, cardiovascular; HF, heart failure.
Baseline characteristics of hospitalized patients
The characteristics of patients who were not hospitalized during follow‐up, those who were admitted once and those admitted two or more times are shown in Table 2. Patients who were admitted were older, more likely to be male and from North America, to have more severe HF as assessed by length of diagnosis, health status (NYHA class and KCCQ score), renal function, natriuretic peptide levels, co‐morbidity and diuretic and digoxin use. Patients admitted for worsening HF during follow‐up were more likely to have been admitted previously (before enrolment in the trial). Of those not admitted during follow‐up, 61% had a history of HF hospitalization; of those admitted once, 72% had a prior admission and of those admitted twice or more, 81% had a previous admission. Compared with patients admitted once, those admitted more than once were more often male (87% vs. 78%, P < 0.001), more often had diabetes (51% vs. 43%, P = 0.006) and renal disease (30% vs. 23%, P = 0.007), while differences in the prevalence of chronic obstructive pulmonary disease was not significant (21% vs. 17%, P < 0.001). All these findings were similar when comparing baseline characteristics according to number of HF hospitalizations/CV death during follow‐up, except that chronic obstructive pulmonary disease was significantly more frequent among patients admitted more than once compared with those admitted once (20% vs. 14%, P = 0.001) (supplementary material online, Table S1).
Table 2.
Baseline characteristics by number of hospitalizations during follow‐up
| 0 hospitalization (n = 7204) | 1 hospitalization (n = 785) | ≥2 hospitalizations (n = 410) | P‐value* | |
|---|---|---|---|---|
| Age at screening (years) | 63.7 ± 11.4 | 64.4 ± 11.5 | 65.0 ± 11.5 | 0.022 |
| Female sex | 1609 (22.3%) | 171 (21.8%) | 52 (12.7%) | <0.001 |
| Region | <0.001 | |||
| North America | 460 (6.4%) | 85 (10.8%) | 57 (13.9%) | |
| Latin America | 1285 (17.8%) | 107 (13.6%) | 41 (10.0%) | |
| Western Europe | 1751 (24.3%) | 204 (26.0%) | 96 (23.4%) | |
| Central Europe | 2413 (33.5%) | 272 (34.6%) | 141 (34.4%) | |
| Asia/Pacific and other | 1295 (18.0%) | 117 (14.9%) | 75 (18.3%) | |
| Race | <0.001 | |||
| White | 4725 (65.6%) | 541 (68.9%) | 278 (67.8%) | |
| Black | 343 (4.8%) | 54 (6.9%) | 31 (7.6%) | |
| Asia | 1311 (18.2%) | 121 (15.4%) | 77 (18.8%) | |
| Other | 825 (11.5%) | 69 (8.8%) | 24 (5.9%) | |
| Systolic blood pressure (mmHg) | 121.5 ± 15.2 | 120.4 ± 15.9 | 121.1 ± 16.2 | 0.131 |
| Heart rate (beats per minute) | 72.1 ± 11.9 | 73.8 ± 12.9 | 74.3 ± 12.3 | <0.001 |
| eGFR (mL/min/1.73 m2) | 68.3 ± 20.1 | 64.2 ± 18.9 | 63.2 ± 22.1 | <0.001 |
| Serum creatinine (µmol/L) | 98.2 ± 25.8 | 104.4 ± 28.4 | 108.9 ± 28.9 | <0.001 |
| Ischaemic HF aetiology | 4311 (59.8%) | 466 (59.4%) | 259 (63.2%) | 0.383 |
| Ejection fraction (%) | 29.6 ± 6.2 | 28.6 ± 6.5 | 28.6 ± 6.7 | <0.001 |
| Body mass index (kg/m2) | 28.1 ± 5.5 | 28.7 ± 5.7 | 28.8 ± 6.2 | <0.001 |
| Current smoking | 1030 (14.3%) | 118 (15.0%) | 60 (14.6%) | 0.847 |
| NYHA class | <0.001 | |||
| I | 355 (4.9%) | 24 (3.1%) | 10 (2.4%) | |
| II | 5121 (71.2%) | 524 (66.8%) | 274 (67.0%) | |
| III | 1671 (23.2%) | 226 (28.8%) | 121 (29.6%) | |
| IV | 45 (0.6%) | 11 (1.4%) | 4 (1.0%) | |
| Duration of HF | <0.001 | |||
| ≤1 year | 2298 (31.9%) | 159 (20.3%) | 66 (16.1%) | |
| 1–5 years | 2740 (38.0%) | 325 (41.4%) | 167 (40.7%) | |
| >5 years | 2166 (30.1%) | 301 (38.3%) | 177 (43.2%) | |
| A history of | ||||
| Hypertension | 5052 (70.1%) | 577 (73.5%) | 311 (75.9%) | 0.009 |
| Diabetes | 2364 (32.8%) | 334 (42.5%) | 209 (51.0%) | <0.001 |
| Myocardial infarction | 3069 (42.6%) | 370 (47.1%) | 195 (47.6%) | 0.010 |
| Valvular heart disease | 463 (6.4%) | 78 (9.9%) | 63 (15.4%) | <0.001 |
| Atrial fibrillation | 2561 (35.5%) | 336 (42.8%) | 194 (47.3%) | <0.001 |
| HF hospitalization | 4378 (60.8%) | 565 (72.0%) | 331 (80.7%) | <0.001 |
| Stroke | 597 (8.3%) | 79 (10.1%) | 49 (12.0%) | 0.012 |
| COPD | 864 (12.0%) | 132 (16.8%) | 84 (20.5%) | <0.001 |
| Cancer | 341 (4.7%) | 46 (5.9%) | 26 (6.3%) | 0.150 |
| Renal disease | 1148 (15.9%) | 181 (23.1%) | 124 (30.2%) | <0.001 |
| Use of | ||||
| Beta‐blocker | 6718 (93.3%) | 722 (92.0%) | 371 (90.5%) | 0.051 |
| MRA | 3989 (55.4%) | 451 (57.5%) | 231 (56.3%) | 0.513 |
| Diuretic | 5679 (78.8%) | 691 (88.0%) | 368 (89.8%) | <0.001 |
| Digoxin | 2130 (29.6%) | 259 (33.0%) | 150 (36.6%) | 0.002 |
| Any ICD (including CRT‐D) | 985 (13.7%) | 166 (21.1%) | 92 (22.4%) | <0.001 |
| CRT | 449 (6.2%) | 77 (9.8%) | 48 (11.7%) | <0.001 |
| BNP (pg/mL) | 256 [251–262] | 362 [339–387] | 400 [363–439] | <0.001 |
| NT‐proBNP (pg/mL) | 1651 [1615–1687] | 2383 [2220–2557] | 2674 [2424–2948] | <0.001 |
| KCCQ clinical summary score | 76.7 ± 19.0 | 72.1 ± 20.9 | 69.4 ± 20.1 | <0.001 |
BNP, B‐type natriuretic peptide; COPD, chronic obstructive pulmonary disease; CRT, cardiac resynchronization therapy; CRT‐D, cardiac resynchronization therapy‐defibrillation; eGFR, estimated glomerular filtration rate; HF, heart failure; ICD, implantable cardioverter‐defibrillator; KCCQ, Kansas City Cardiomyopathy Questionnaire; MRA, mineralocorticoid receptor antagonist; NT‐proBNP, N‐terminal pro‐B‐type natriuretic peptide; NYHA, New York Heart Association.
P‐value is for comparison between 1 hospitalization and ≥2 hospitalizations.
Effect of sacubitril/valsartan compared with enalapril
Table 1 shows the proportion of patients with one or one or more hospitalizations for HF. Figures 1, 2, 3 show the effect of sacubitril/valsartan, compared with enalapril, on recurrent events.
Figure 1.
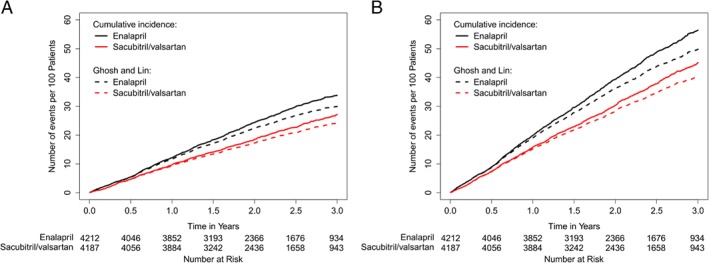
Cumulative rate of heart failure hospitalizations (A) and the primary composite endpoint (B).
Figure 2.
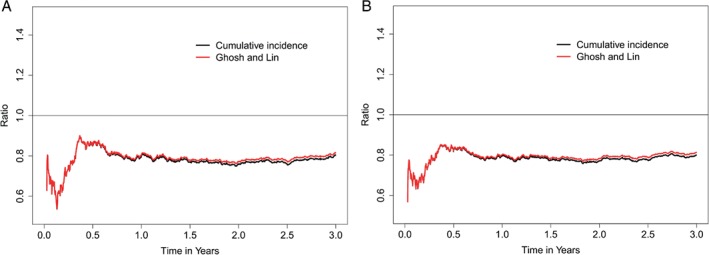
Ratio (sacubitril/valsartan vs. enalapril) for the conditional rate of cumulative heart failure hospitalizations (A) and the primary composite endpoint (B).
Figure 3.
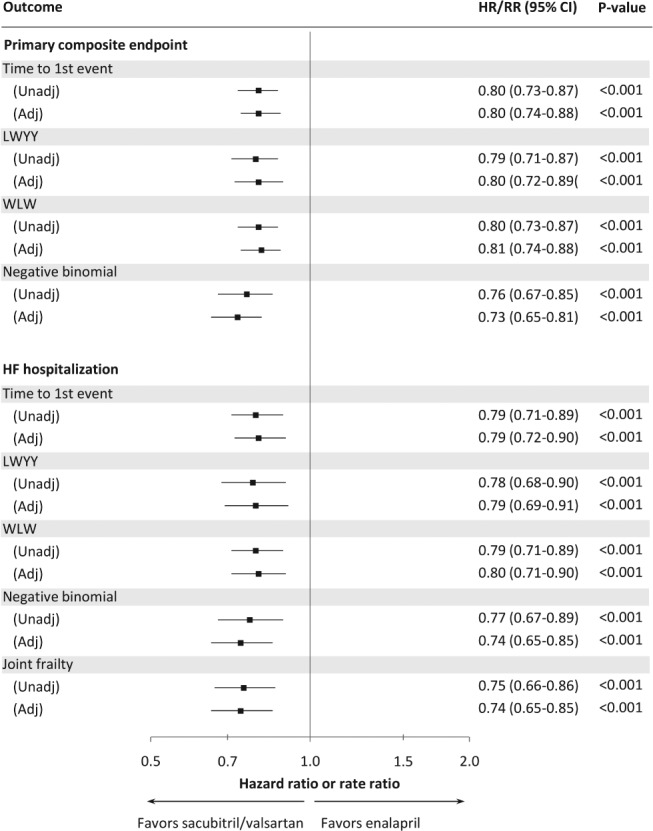
Treatment effect of sacubitril/valsartan compared with enalapril according to different methods in unadjusted and adjusted analyses. Adj, adjusted; CI, confidence interval; HF, heart failure; HR, hazard ratio; LWYY, Lin, Wei, Ying and Yang method; RR, rate ratio; Unadj, unadjusted; WLW, Wei, Lin and Weissfeld method. HR and RR have a similar interpretation: HR represents the common ratio (sacubitril/valsartan over enalapril) of the instantaneous risk at any time while RR represents the common ratio of the expected change in the cumulative rate of events over time.
There was a reduction in the proportion of patients with one or one or more HF hospitalizations. These reductions were not offset by an increase in risk of other CV admissions or non‐CV hospitalizations, despite the longer survival time in the sacubitril/valsartan group (data not shown).
Both the cumulative incidence method (Nelson‐Aalen estimator, where death is considered as independent censoring) and the Ghosh and Lin method (where death is handled as informative censoring, i.e. incorporated as a competing risk recognizing zero hospitalizations after death) demonstrated that the number of HF hospitalizations was lower in the sacubitril/valsartan compared to the enalapril group (Figure 1). This effect was evident early in the trial and was consistent after the initial 6 months as more events accumulated (Figure 2).
Several recurrent event analyses were used to examine the effect of sacubitril/valsartan on recurrent HF hospitalizations (Figure 3). Compared to the estimate using a traditional time‐to‐first event analysis [hazard ratio (HR) 0.79, 95% confidence interval (CI) 0.71–0.89, P < 0.001], sacubitril/valsartan reduced the number of HF hospitalizations to a very similar degree regardless of the methods used. The LWYY proportional rates model gave a rate ratio (RR) of 0.78 (95% CI 0.68–0.90, P < 0.001). The WLW model gave an overall HR of 0.79 (95% CI 0.71–0.89, P < 0.001). The HRs for the first and subsequent hospitalizations were similar (Table 3). The unadjusted RR from the negative binomial model for all HF hospitalizations was very similar to the other models (0.77, 95% CI 0.67–0.89, P < 0.001). When CV death was added to the negative binomial model as a composite endpoint, the reduction in HF hospitalizations and CV death with sacubitril/valsartan was essentially unchanged. The joint frailty model also gave a similar estimate of the effect of sacubitril/valsartan on recurrent HF hospitalizations when CV death was accounted for (RR 0.75, 95% CI 0.66–0.86, P < 0.001). Adjusting the above models for the differences in baseline characteristics according to number of HF hospitalizations made little difference to the estimates (Figure 3). Excluding patients with an extreme number of hospitalizations (11 or 18 HF hospitalizations) yielded similar results (data not shown).
Table 3.
Hazard ratios (sacubitril/valsartan vs. enalapril) from the Wei, Lin and Weissfeld model for the first and subsequent hospitalizations for heart failure
| Unadjusted HR (95% CI) | P‐value | |
|---|---|---|
| Hospitalization for HF | ||
| Time to 1st | 0.80 (0.71–0.89) | <0.001 |
| Time to 2nd | 0.69 (0.57–0.84) | <0.001 |
| Time to 3rd | 0.61 (0.44–0.84) | 0.002 |
| Time to 4th | 0.60 (0.37–0.98) | 0.04 |
| Time to 5th | 0.81 (0.43–1.51) | 0.50 |
| Time to 6th | 2.14 (0.81–5.65) | 0.12 |
| Average | 0.79 (0.71–0.89) | <0.001 |
| Hospitalization for HF, including CV death as an eventa | ||
| Time to 1st | 0.80 (0.73–0.87) | <0.001 |
| Time to 2nd | 0.79 (0.71–0.88) | <0.001 |
| Time to 3rd | 0.78 (0.70–0.87) | <0.001 |
| Time to 4th | 0.79 (0.71–0.88) | <0.001 |
| Time to 5th | 0.80 (0.72–0.89) | <0.001 |
| Time to 6th | 0.81 (0.72–0.90) | <0.001 |
| Average | 0.80 (0.73–0.87) | <0.001 |
CI, confidence interval; CV, cardiovascular; HF, heart failure; HR, hazard ratio.
If a patient experienced CV death prior to event no. 6, then CV death was also included for this patient's subsequent event numbers up to event no. 6.
Discussion
The analysis of PARADIGM‐HF shows that even in individuals with predominantly mild symptoms, 658 of 4212 patients (16%) in the enalapril group were admitted at least once with worsening HF in a relatively short period (median follow‐up 27 months), despite excellent pharmacologic therapy. Of these 658 patients, 240 (36%) were readmitted more than once and experienced a total of 661 admissions. Although important from a personal and societal perspective, the repeat (i.e. second or subsequent) hospitalizations (n = 421) experienced by these patients are not counted in a conventional time‐to‐first event analysis, despite accounting for 39% of all admissions for HF in the enalapril group.
Therefore, there is increasing recognition that assessment of the full burden of HF necessitates consideration of repeat events.2, 3, 4, 5, 6, 7 Similarly, to be truly effective, the benefit of treatment must be maintained after an initial hospitalization. In other fields (e.g. cancer and infection), the effectiveness of treatment may be less on recurrent events. Theoretically, pathophysiological processes such as re‐activation of the renin–angiotensin–aldosterone system or treatment tachyphylaxis could reduce the effect of sacubitril/valsartan or enalapril on second and subsequent events. The difficulty, however, is choosing the statistical method to evaluate the effect of treatment on repeat events. The analysis of recurrent hospitalizations is challenging because of the competing risk of death and different follow‐up times in the different treatment groups. Hospitalization and death are clearly related in that death leads to loss of sicker individuals more likely to be hospitalized (and, conversely, hospitalization is associated with a higher subsequent risk of death). Longer survival and follow‐up time means a longer time at risk of admission and a difference in hospitalization rate could reflect an effect of treatment on death alone. This is particular true for the non‐parametric method of Ghosh and Lin, which adjusts estimates of cumulative recurrent hospitalization rates over time for differences in death rate and the follow‐up time observed in the study by explicitly accounting for the fact that patients who have died will subsequently have zero hospitalizations.14
The negative binomial model, on the other hand, can be considered as a method that implicitly employs model‐based estimation of missing count data for patients with incomplete follow‐up by assuming that the counts for HF hospitalizations that would have been collected if a patient had not died (or had not been lost to follow‐up or censored) were missing at random. It is assumed that rates follow a Poisson distribution for each subject, and that rates are constant and proportional, conditional on a subject‐specific frailty. The resulting effect estimate can be interpreted as a marginal RR or ratio of expected number of endpoint events, assuming a latent process continuing after death. An advantage of the negative binomial regression is that it is easy to use, that correlation of events in the same individual is naturally accounted for through the inclusion of a random effect term, and that the resulting effect size estimates are easy to interpret. However, it has the disadvantage in that it assumes a constant event rate and cannot examine potential time‐varying effects.
The WLW model uses a total‐time approach considering times from randomization to the first, second and subsequent events. HRs from a Cox proportional hazards model for each ordered event (e.g. hospitalization) are combined to give an ‘average effect’, although, in this case, the individual HRs do provide evidence of a sustained effect of treatment beyond the first hospitalization. For the analysis of the composite primary endpoint, the weight of CV death in the combined statistic is greater than that of the i‐th HF hospitalization (i = 1, ..., 6). In this example, if a patient dies from a CV reason without a prior HF hospitalization, then CV death will be counted six times before weighting in the combined statistic (i.e. the estimated treatment effect size can be considered as weighted towards CV death). While preserving randomization, the WLW approach has been criticized because it assumes that a patient is at risk for a second event before having experienced a first event.15
The LWYY model is based on a gap‐time approach considering the time since a previous event (or the inter‐event times), and is essentially a modified Andersen and Gill model,16 with a robust variance estimator (sandwich estimator) to account for the dependency of within‐subject events. In the LWYY model, the two rate functions for having an event over any given time period in each treatment group are assumed, conditional on being at risk and not having died from CV reasons, to be proportional to each other. Loss to follow‐up and death due to non‐CV reasons are considered as independent censorings. This approach accounts for the fact that counting process is not defined after death and has the disadvantage of potentially diluting estimates of the treatment effect if the drug reduces both HF hospitalization and death.
The joint frailty model estimates a RR for HF hospitalization, whilst incorporating the competing risk of CV death, and a HR for CV death that allows for HF hospitalizations. This approach is appealing in that it allows a distinct treatment effect to be estimated for each of the individual outcomes while taking account of the association between the two through a common ‘frailty term’. Here, ‘frailty’ refers to a subject‐specific random term that accounts for the fact that some patients are at higher risk (larger frailty) than others (smaller frailty) of experiencing HF hospitalization and CV death. Compared with the WLW and Ghosh and Lin method, use of a joint frailty model has been found to give more unbiased estimates of treatment effect in the presence of dependent censoring (correlation between HF hospitalization and CV death).17 However, this approach is limited in two aspects. First, the resulting RR is not a marginal estimate but is conditional on having the same frailty. Second, it assumes that the individual‐specific frailties affect each outcome in the same way and that the model correctly captures this relationship.
While CV deaths were handled as competing risks (informative censoring) in the joint frailty model, deaths due to non‐CV reasons were handled as non‐informative censoring. Non‐CV deaths were also handled as non‐informative censoring in the LWYY, the WLW, and the negative binomial methods. In PARADIGM‐HF, the majority of deaths were due to CV causes (81%) and the rate of non‐CV causes was almost equal in the two treatment groups [enalapril, n = 142 (3.4%) vs. sacubitril/valsartan, n = 153 (3.7%)]. Thus, there was no indication that the competing risk of non‐CV deaths biased the estimated treatment effects.
All analytical methods used to evaluate the effect of study drug on total events (first and subsequent) gave consistent estimates of the treatment effect, similar to the time‐to‐first event although, in some cases, with slightly wider 95% CIs. The joint frailty model showed a greater reduction in the rate of recurrent HF hospitalizations (i.e. larger treatment effect), presumably due to accounting for the correlation with CV death, for which a hazard reduction of 20% was observed in the sacubitril/valsartan group in PARADIGM‐HF. Relative to the LWYY approach, for which a slight dilution of treatment effect was expected due to the positive effect of sacubitril/valsartan on CV death, the negative binomial model showed slightly more reduction in the rate of both HF hospitalization and the composite endpoint of CV death and recurrent HF hospitalization.
Analyses of recurrent events have an advantage over the traditional time‐to‐first‐event approach in capturing treatment effects on the total disease burden, and it may increase statistical power. The European Medicines Agency guidance for trials on therapies for chronic HF acknowledges recurrent HF hospitalizations as a potentially acceptable primary endpoint, while highlighting the importance of adjudication of events and a clear methodological strategy.18 The United States Food and Drug Administration has also accepted the use of recurrent events as a primary outcome,19, 20, 21 but none of the regulatory bodies have recommended a single or specific statistical approach.
We are not able to recommend any statistical method over another based on the present study, but find it reassuring that each method gave overall similar estimates of the treatment effect. Until a consensus on the analysis of recurrent events has been established, the method or methods used will depend on trial‐specific regulatory guidance. We are aware of at least one new trial in HF which has analysis of recurrent events as its primary endpoint.21
In summary, although each of the statistical methods described has strengths and weaknesses, in PARADIGM‐HF, where the investigational treatment reduced both CV death and HF hospitalization individually, each analytical approach gave a similar estimate of the effect of sacubitril/valsartan on total (i.e. first and recurrent) events. Sacubitril/valsartan was superior to enalapril not just in reducing first events but also total events, with a similar treatment effect size on all events as seen on first events. Consequently, the absolute treatment benefit was considerably larger when total events were considered (54 vs. 29 fewer hospitalizations per 1000 patients treated over a median of 27 months).
Funding
This work was supported by the Danish Heart Foundation (grant number 16‐R107‐A6786‐22960) to U.M.M. PARADIGM‐HF was funded by Novartis.
Conflict of interest: except for U.M.M. and L.S., all authors or their institutions have received payments from Novartis for their involvement in PARADIGM‐HF. J.G., M.P.L, and G.M. are employees of Novartis. U.M.M. has received honoraria for lectures from MSD and Novo Nordisk outside the submitted work.
Supporting information
Table S1. Baseline characteristics by number of hospitalizations/cardiovascular death during follow‐up.
References
- 1. Neaton JD, Gray G, Zuckerman BD, Konstam MA. Key issues in end point selection for heart failure trials: composite end points. J Card Fail 2005;11:567–575. [DOI] [PubMed] [Google Scholar]
- 2. Anker SD, McMurray JJ. Time to move on from ‘time‐to‐first’: should all events be included in the analysis of clinical trials? Eur Heart J 2012;33:2764–2765. [DOI] [PubMed] [Google Scholar]
- 3. Rogers JK, McMurray JJ, Pocock SJ, Zannad F, Krum H, van Veldhuisen DJ, Swedberg K, Shi H, Vincent J, Pitt B. Eplerenone in patients with systolic heart failure and mild symptoms: analysis of repeat hospitalizations. Circulation 2012;126:2317–2323. [DOI] [PubMed] [Google Scholar]
- 4. Rogers JK, Pocock SJ, McMurray JJ, Granger CB, Michelson EL, Ostergren J, Pfeffer MA, Solomon SD, Swedberg K, Yusuf S. Analysing recurrent hospitalizations in heart failure: a review of statistical methodology, with application to CHARM‐Preserved. Eur J Heart Fail 2014;16:33–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Rogers JK, Jhund PS, Perez AC, Bohm M, Cleland JG, Gullestad L, Kjekshus J, van Veldhuisen DJ, Wikstrand J, Wedel H, McMurray JJ, Pocock SJ. Effect of rosuvastatin on repeat heart failure hospitalizations: the CORONA Trial (Controlled Rosuvastatin Multinational Trial in Heart Failure). JACC Heart Fail 2014;2:289–297. [DOI] [PubMed] [Google Scholar]
- 6. Borer JS, Bohm M, Ford I, Komajda M, Tavazzi L, Sendon JL, Alings M, Lopez‐de‐Sa E, Swedberg K; SHIFT Investigators . Effect of ivabradine on recurrent hospitalization for worsening heart failure in patients with chronic systolic heart failure: the SHIFT Study. Eur Heart J 2012;33:2813–2820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Anker SD, Schroeder S, Atar D, Bax JJ, Ceconi C, Cowie MR, Crisp A, Dominjon F, Ford I, Ghofrani HA, Gropper S, Hindricks G, Hlatky MA, Holcomb R, Honarpour N, Jukema JW, Kim AM, Kunz M, Lefkowitz M, Le Floch C, Landmesser U, McDonagh TA, McMurray JJ, Merkely B, Packer M, Prasad K, Revkin J, Rosano GM, Somaratne R, Stough WG, Voors AA, Ruschitzka F. Traditional and new composite endpoints in heart failure clinical trials: facilitating comprehensive efficacy assessments and improving trial efficiency. Eur J Heart Fail 2016;18:482–489. [DOI] [PubMed] [Google Scholar]
- 8. McMurray JJ, Packer M, Desai AS, Gong J, Lefkowitz MP, Rizkala AR, Rouleau J, Shi VC, Solomon SD, Swedberg K, Zile MR; PARADIGM‐HF Committees and Investigators . Dual angiotensin receptor and neprilysin inhibition as an alternative to angiotensin‐converting enzyme inhibition in patients with chronic systolic heart failure: rationale for and design of the Prospective comparison of ARNI with ACEI to Determine Impact on Global Mortality and morbidity in Heart Failure trial (PARADIGM‐HF). Eur J Heart Fail 2013;15:1062–1073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. McMurray JJ, Packer M, Desai AS, Gong J, Lefkowitz MP, Rizkala AR, Rouleau JL, Shi VC, Solomon SD, Swedberg K, Zile MR; PARADIGM‐HF Investigators and Committees . Angiotensin‐neprilysin inhibition versus enalapril in heart failure. N Engl J Med 2014;371:993–1004. [DOI] [PubMed] [Google Scholar]
- 10. Packer M, McMurray JJ, Desai AS, Gong J, Lefkowitz MP, Rizkala AR, Rouleau JL, Shi VC, Solomon SD, Swedberg K, Zile M, Andersen K, Arango JL, Arnold JM, Belohlavek J, Bohm M, Boytsov S, Burgess LJ, Cabrera W, Calvo C, Chen CH, Dukat A, Duarte YC, Erglis A, Fu M, Gomez E, Gonzalez‐Medina A, Hagege AA, Huang J, Katova T, Kiatchoosakun S, Kim KS, Kozan O, Llamas EB, Martinez F, Merkely B, Mendoza I, Mosterd A, Negrusz‐Kawecka M, Peuhkurinen K, Ramires FJ, Refsgaard J, Rosenthal A, Senni M, Sibulo AS Jr, Silva‐Cardoso J, Squire IB, Starling RC, Teerlink JR, Vanhaecke J, Vinereanu D, Wong RC; PARADIGM‐HF Investigators and Coordinators . Angiotensin receptor neprilysin inhibition compared with enalapril on the risk of clinical progression in surviving patients with heart failure. Circulation 2015;131:54–61. [DOI] [PubMed] [Google Scholar]
- 11. Wei LJ, Lin DY, Weissfeld L. Regression analysis of multivariate incomplete failure time data by modeling marginal distributions. J Am Stat Assoc 1989;84:1065–1073. [Google Scholar]
- 12. Lin DY, Wei LJ, Yang I, Ying Z. Semiparametric regression for the mean and rate functions of recurrent events. J R Stat Soc Series B Stat Methodol 2000;62:711–730. [Google Scholar]
- 13. PARADIGM study protocol and statistical analysis plan . http://www.nejm.org/doi/suppl/10.1056/NEJMoa1409077/suppl_file/nejmoa1409077_protocol.pdf (27 December 2017).
- 14. Ghosh D, Lin DY. Nonparametric analysis of recurrent events and death. Biometrics 2000;56:554–562. [DOI] [PubMed] [Google Scholar]
- 15. Metcalfe C, Thompson SG. Wei, Lin and Weissfeld's marginal analysis of multivariate failure time data: should it be applied to a recurrent events outcome? Stat Methods Med Res 2007;16:103–122. [DOI] [PubMed] [Google Scholar]
- 16. Andersen PK, Gill RD. Cox's regression model for counting processes: a large sample study. Annals of Statistics 1982;10:1100–1120. [Google Scholar]
- 17. Rogers JK, Yaroshinsky A, Pocock SJ, Stokar D, Pogoda J. Analysis of recurrent events with an associated informative dropout time: application of the joint frailty model. Stat Med 2016;35:2195–2205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Guideline on clinical investigation of medicinal products for the treatment of chronic heart failure. http://www.ema.europa.eu/ema/pages/includes/document/open_document.jsp?webContentId=WC500235089 (27 December 2017).
- 19. Abraham WT, Stevenson LW, Bourge RC, Lindenfeld JA, Bauman JG, Adamson PB. Sustained efficacy of pulmonary artery pressure to guide adjustment of chronic heart failure therapy: complete follow‐up results from the CHAMPION randomised trial. Lancet 2016;387:453–461. [DOI] [PubMed] [Google Scholar]
- 20. Greenberg B, Butler J, Felker GM, Ponikowski P, Voors AA, Desai AS, Barnard D, Bouchard A, Jaski B, Lyon AR, Pogoda JM, Rudy JJ, Zsebo KM. Calcium upregulation by percutaneous administration of gene therapy in patients with cardiac disease (CUPID 2): a randomised, multinational, double‐blind, placebo‐controlled, phase 2b trial. Lancet 2016;387:1178–1186. [DOI] [PubMed] [Google Scholar]
- 21. Solomon SD, Rizkala AR, Gong J, Wang W, Anand IS, Ge J, Lam CS, Maggioni AP, Martinez F, Packer M, Pfeffer MA, Pieske B, Redfield MM, Rouleau JL, Van Veldhuisen DJ, Zannad F, Zile MR, Desai AS, Shi VC, Lefkowitz MP, McMurray JJ. Angiotensin receptor neprilysin inhibition in heart failure with preserved ejection fraction: rationale and design of the PARAGON‐HF Trial. JACC Heart Fail 2017;5:471–482. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1. Baseline characteristics by number of hospitalizations/cardiovascular death during follow‐up.


