Improved patient-specific calibration for agent-based cancer modeling

Macklin et al., (2012) recently introduced a mechanistic agent-based cell model, with application to ductal carcinoma in situ (DCIS)—a precursor to invasive breast cancer. The work included the first patient-specific calibration method to use pathology data from a single time point, as might be expected in a pre-surgical biopsy. The key measurements included the proliferative index (PI: the percentage of cycling cells), the apoptotic index (AI: the percentage of cells apoptosing), the mean viable rim thickness 〈T〉, the mean duct radius 〈R_duct〉, the mean nuclear radius 〈R_N〉, mean cell density 〈ρ〉, and the cell confluence f (fraction of the viable rim occupied by cell mass).

The authors demonstrated the calibration for an individual patient with solid-type DCIS with comedonecrosis, and used the calibrated model to predict the patient’s DCIS growth rate and pathology-mammography size correlations. While the model predictions were quantitatively consistent with literature reports for similar cases, the calibration over-predicted the patient’s proliferative index (PI), underpredicted the cell density, and overpredicted the patient’s viable rim size. The authors attributed the discrepancy in PI to neglecting the post-mitotic G₁ phase in the calibration method (daughter cells stain positive for Ki-67 after mitosis as they continue to cycle and grow, then exit to G₀), while they concluded that approximating the viable rim as 100% confluent likely caused the discrepancies in the cell density and viable rim size.

We now present and demonstrate an improved calibration method that addresses these shortcomings. We find that the new calibration substantially improves the model match to the patient’s PI, AI, 〈ρ〉, and 〈T〉 measurements; this should make possible better quantitative model predictions of individual patients’ tumor growth. In the interests of brevity, we only present the changes in the calibration. A MATLAB script is provided at MathCancer.org to help automate the calibration.

Population dynamics:

Let PI₁ be the pre-mitotic cycling cells (S, G₂, M, and possibly parts of G₁, with duration τ₁), and let PI₂ be the cells in the post-mitotic G₁ phase (with duration τ_{2 =} τ_G1). Let AI be as before, with duration τ_A. Note that PI₁ + PI₂ = PI and τ₁ + τ₂ = τ_P. PI₁, PI₂, and AI satisfy

$${\stackrel{.}{\text{PI}}}_1=\langle {\alpha }_{\text{P}}\rangle \left(1-\text{AI}-\text{PI}\right)-\frac{1}{{\tau }_1}\left({\text{PI}}_1+{\text{PI}}_1^2\right)+\frac{1}{{\tau }_{\text{A}}}{\text{PI}}_1\cdot \text{AI,}$$ (1)

$${\stackrel{.}{\text{PI}}}_2=\frac{2}{{\tau }_1}{\text{PI}}_1-\frac{1}{{\tau }_2}{\text{PI}}_2+\frac{1}{{\tau }_{\text{A}}}{\text{PI}}_1\cdot \text{AI},$$ (2)

$${\stackrel{.}{\text{AI}}}_2={\alpha }_{\text{A}}\left(1-\text{AI}-\text{PI}\right)-\frac{1}{{\tau }_1}{\text{PI}}_1\cdot \text{AI}-\frac{1}{{\tau }_{\text{A}}}\left(\text{AI}-{\text{AI}}^2\right).$$ (3)

As in Macklin et al., (2012), we assume a steady-state population dynamic and set ṖI₁, ṖI_2, and ȦI equal to zero. Assuming we have measurements for AI, PI, τ_A, τ₁, and τ₂, we must solve for PI₁ (or PI₂), 〈α_P〉, and α_A. Eq. (2) can be explicitly rewritten to solve for PI₁ by substituting PI₂ = PI − PI₁. Hence

$${\text{PI}}_1=\frac{{\tau }_1}{{\tau }_1+2{\tau }_2+\text{AI}\frac{{\tau }_1{\tau }_2}{{\tau }_{\text{A}}}}\text{PI}.$$ (4)

Using this, we can solve for 〈α_P〉, and α_A:

$$\langle {\alpha }_{\text{P}}\rangle =\frac{\frac{1}{{\tau }_1}\text{PI}{}_1\left(1+{\text{PI}}_1\right)-\frac{1}{{\tau }_{\text{A}}}{\text{PI}}_1\cdot \text{AI}}{1-\text{AI}-\text{PI}},$$ (5)

$${\alpha }_{\text{A}}=\frac{\frac{1}{{\tau }_{\text{A}}}\left(\text{AI}-{\text{AI}}^2\right)+\frac{1}{{\tau }_1}\text{AI}\cdot {\text{PI}}_1}{1-\text{AI}-\text{PI}}.$$ (6)

The remainder is as in Macklin et al. (2012).

Cell geometry:

We do not have quantitative measurements of the patient’s confluence, but we estimate f ~ 0.90. We continue to set 〈R_N〉 = 5.295 μm. If 〈A〉 is the mean cell cross-sectional area and 〈R〉 is the mean cell radius,

$$f=\langle \rho \rangle \langle A\rangle \approx \langle \rho \rangle \pi {\langle R\rangle }^2.$$ (7)

Next, we relate 〈R〉 to the quiescent cell radius $\overline{R}$ via the AI, PI₁ and PI₂ fractions from above:

$$\langle V\rangle =\frac{4}{3}\pi {\langle R\rangle }^3={\text{PI}}_1\langle V_1\rangle +{\text{PI}}_2\langle V_2\rangle +\text{AI}\langle V_{\text{A}}\rangle +\left(1-\text{AI}-\text{PI}\right)\langle V_{\text{Q}}\rangle ,$$ (8)

Where 〈V_x〉 is the mean cell volume in the x phenotypic state $\left(\chi \in \left\{{\mathcal{P}}_1,{\mathcal{P}}_2,\mathcal{A},\mathcal{Q}\right\}\right).$ For the model in Macklin et al. (2012),

$$\begin{array}{l}\langle V_1\rangle =\frac{4}{3}\pi {\overline{R}}^3,\langle V_2\rangle =\pi {\overline{R}}^3,\\ \langle V_A\rangle =\frac{4}{3}\pi {\overline{R}}^3\text{\hspace{1em} and \hspace{1em}}\langle V_{\text{Q}}\rangle =\frac{4}{3}\pi {\overline{R}}^3.\end{array}$$ (9)

Using these, we directly solve for $\overline{R}$ and $\overline{V},$ the equivalent radius and cell volume in the quiescent state $\mathcal{Q}.$ More detailed cell volume models (e.g., as in Mumenthaler et al., in preparation) require adjusting these per-state mean volumes.

Oxygen:

We modify the oxygen equation such that oxygen is uptaken at rate λ in the confluent fraction of the viable rim, and at rate λ_b in the non-confluent portion of the rim. This gives a mean uptake rate of λ_viable = fλ+(1−f)λ_b in the viable rim, and λ_core = λ_b in the necrotic core. Define the length scales

$$L_{\text{V}}=\sqrt{D/{\lambda }_{\text{ viable }}}=L_0/\sqrt{f+\left(1-f\right){\lambda }_{\text{b}}/\lambda }$$ (10)

and

$$L_{\text{N}}=\sqrt{D/{\lambda }_{\text{ core }}}=L_0/\sqrt{{\lambda }_{\text{b}}/\lambda },$$ (11)

in the viable rim and necrotic core, respectively, where L₀(100 μm) is the viable oxygen diffusion length scale. Define the mean necrotic core radius 〈R_NC〉 = 〈R_duct−T〉. After adjusting the oxygen equations from Macklin et al., (2012) to use these uptake rates, solving analytically, and evaluating at the duct boundary, we find the updated oxygen boundary value σ_B via:

$$\frac{{\sigma }_{\text{B}}}{{\sigma }_{\text{H}}}=\cosh \left[\frac{\langle T\rangle }{L_{\text{V}}}\right]+\frac{L_{\text{V}}}{L_{\text{N}}}\tanh \left[\frac{R_{\text{NC}}}{L_{\text{N}}}\right]\sinh \left[\frac{\langle T\rangle }{L_{\text{V}}}\right].$$ (12)

The mean oxygen in the viable rim is obtained via

$$\frac{\langle \sigma \rangle }{{\sigma }_{\text{H}}}=\frac{L_{\text{V}}}{\langle T\rangle }\left[\sinh \left[\frac{\langle T\rangle }{L_{\text{V}}}\right]+\frac{L_{\text{V}}}{L_{\text{N}}}\tanh \left[\frac{R_{\text{NC}}}{L_{\text{N}}}\right]\left(\cosh \left[\frac{\langle T\rangle }{L_{\text{V}}}\right]-1\right)\right].$$ (13)

Cell–cell mechanics:

For the general case where f ≠ 1, we determine the mean cell–cell spacing s in the confluent region by

$$s=\sqrt{\left(2f\right)/\left(\sqrt{3}\langle \rho \rangle \right)}.$$ (14)

The mechanics calibration continues as in Macklin et al. (2012) with this altered mean cell–cell spacing in the confluent region.

Updated parameter values:

Using this updated calibration for the patient data presented in Macklin et al. (2012), the new patient-specific parameters are given in Table 1.

Table 1.

Updated patient-specific parameters for Patient 100019 for the DCIS model.

Parameter	Physical meaning	Value
$\overline{R}$	Quiescent cell radius	9.536 μm
RN	Cell nuclear radius	5.295 μm
σB	Oxygen value on the BM	0.257280
〈σ〉	Mean oxygen level in viable rim	0.218997
〈αP〉	Mean $\mathcal{Q}\to \mathcal{P}$ transition rate	0.00826266 h−1
${\overline{\alpha }}_{\text{P}}^{-1}$	Mean waiting time prior to $\mathcal{Q}\to \mathcal{P}$ transition when σ = 1	172.43 min
αA	$\mathcal{Q}\to \mathcal{A}$ transition rate	0.00123827 h−1
s	Cell spacing	17.985 μm
Ccca	Cell-cell adhesive force coefficient	0.0489414 cccr
Ccba	Cell-BM adhesive force coefficient	10 Ccca

Comparison against the original calibration:

We simulated 45 days of growth using the updated parameter values above. As in Macklin et al. (2012), we post-processed the original and new simulations in 1-h increments to calculate the simulated PI, AI, cell density, and viable rim thickness. Further post-processing details and open source C++ code can be found in Macklin et al., (2012) and at 〈http://MathCancer.org/JTB_DCIS_2012/〉.

For each simulation, we calculated the mean and standard deviation of these statistics from T₁₅₀ to 45 days. (T₁₅₀ is the first time the “cropped” portion of the viable rim has at least 150 cells. This helps us to more directly compare the simulations while (1) eliminating early transient dynamics and (2) including at least 15 days of simulated data as in Macklin et al., 2012.) For the original simulation in Macklin et al. (2012), T₁₅₀ = 21.04 days; for the new parameter values, T₁₅₀ 29.29 days.

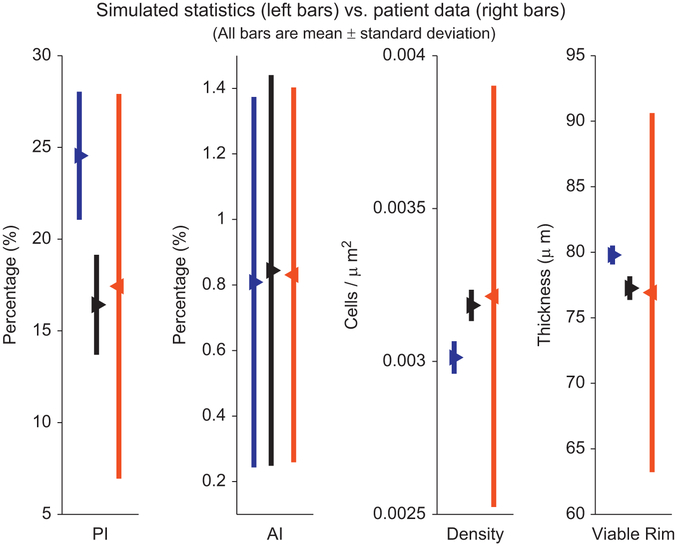
In Fig. 1, we plot the means (triangles) of PI, AI, density, and viable rim size for the patient (right red bars), original parameter values (left blue bars), and new parameter values (middle black bars). The bars represent ± one standard deviation of each quantity, to give a sense of the variability of each measurement. Our new calibration (middle black bars) is much more successful than our old calibration (left blue bars) at matching the patient’s mean PI, density, and viable rim size. See Table 2.

Fig. 1. Comparison of calibration methods:

We compare the simulated (left bars) and patient (right bars) PI (column one), AI (column two), cell density (column three), and viable rim thickness (column four) for our original calibration method (left blue bars) and the improved calibration (middle black bars), from T₁₅₀ to 45 days in our simulations. While the original calibration (left blue bars) was consistent with the patient data (right red bars), the new calibration (middle black bars) gives simulated means that match the patient data much more closely. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this article.)

Table 2. Verification of the patient-specific calibration:

Comparison of the patient (second column) and computed (third and fourth columns) mean and standard deviation for the proliferative index, apoptotic index, cell density, and viable rim thickness. All computed quantities are within the range of patient variation; the new calibration (third column) is substantially better than the original (fourth column).

Quantity	Patient data	New calibration	Old calibration
PI (%)	17.43±9.25	16.42 ±2.72	24.55 ±3.49
Corrected AI (%)	0.831±0.572	0.844 ±0.596	0.809 ±0.565
Cell density (cells/μm2)	3.213e−3±5.95e−4	3.183e−3±5.09e−5	3.013e−3±5.30e−5
Viable rim thickness (μm)	76.92±12.51	77.26±0.90	79.79±0.72

All measurements given as mean ± standard deviation.

Final thoughts:

As suggested in Macklin et al. (2012), agent-based model calibration to individual patients can be substantially improved by accounting for (1) post-mitotic Ki-67 positive cells in the G₁ phase, and (2) the viable rim cell confluence. In our tests, the new calibration better matches the patient’s PI, density, and viable rim size. In continuing work, we are applying this new calibration to a larger number of patients for a case-by-case validation of personalized predictions of cancer progression.