Warnings and Caveats in Brain Controllability

Abstract

A recent article by Gu et al. (Nat. Commun. 6, 2015) proposed to characterize brain networks, quantified using anatomical diffusion imaging, in terms of their “controllability”, drawing on concepts and methods of control theory. They reported that brain activity is controllable from a single node, and that the topology of brain networks provides an explanation for the types of control roles that different regions play in the brain. In this work, we first briefly review the framework of control theory applied to complex networks. We then show contrasting results on brain controllability through the analysis of five different datasets and numerical simulations. We find that brain networks are not controllable (in a statistical significant way) by one single region. Additionally, we show that random null models, with no biological resemblance to brain network architecture, produce the same type of relationship observed by Gu et al. between the average/modal controllability and weighted degree. Finally, we find that resting state networks defined with fMRI cannot be attributed specific control roles. In summary, our study highlights some warning and caveats in the brain controllability framework.

1. Introduction

There is large consensus within the neuroscience community on the usefulness of network theory in contributing to describe the complex, self-organizing structure of the human brain (Bullmore and Sporns, 2009; Sporns, 2014). In the last two years, an increasing number of studies have applied the tools of control theory on brain networks (Kenett et al., 2018; John Dominic Medaglia et al., 2017a, 2017b; Tang et al., 2017; Wu-Yan et al., 2017) to quantify how anatomical network structure, defined by human connectome data (i.e., white matter pathways derived from diffusion tensor or diffusion spectrum imaging), constrain or facilitate changes in brain state trajectories. Indeed, the analysis of controllability has the potential to unveil how specific nodes, and/or sets of nodes, control the dynamics of the entire network (Medaglia et al., 2017b) and thus might provide insights on whether and how manipulating the local activity of specific nodes would fully or partially affect network functions and the activity of the other brain regions (see section 2.1 and below for in-depth discussion).

The idea of applying network control theory to neuroscience is thus based on the hypothesis that we can describe the dynamics of neuronal activity at brain resting state via a set of differential equations (Abdelnour et al., 2014; Galán, 2008; Messé et al., 2015; Saggio et al., 2016) linearized around the resting state, which is itself a first strong assumption (see section 2.3). In this context, most of the studies on brain controllability have investigated if a single brain region can control the whole-brain dynamics via external stimulation, and attempted to identify the brain regions that possess a prominent control role.

Controllability of brain networks is important not only on theoretical grounds, but potentially also for clinical studies (Muldoon et al., 2016). Indeed, modern brain stimulation (NIBS) techniques, including deep brain stimulation (DBS), vagal stimulation (VS), transcranial magnetic (TMS) and electrical stimulation (TES) have the potential to enhance normal cognitive functions, and restore functions impaired by the effects of brain injuries or diseases either directly or by potentiating rehabilitation or drug therapies (Dayan et al., 2013; Figee et al., 2013). The potential of these methods would be tremendously increased if supported by computational models of the brain controllability that define target sites according to a rigorous mechanistic framework.

Recently, Gu and collaborators (Gu et al., 2015) proposed to quantify the ability of a single brain region (i.e., network node) to control the brain dynamics by measuring the average and modal controllability (see section 2.2 for the mathematical definition). For example, they found that regions characterized by high average controllability have high node strength and this would facilitate the brain to easily reach many of its cognitive states. In contrast, high modal controllability, characterized by low node strength, would promote the transition to difficult-to-reach states. Furthermore, Gu et al. found that brain activity is controllable from a single node, and the topology of brain networks provides an explanation for the types of control roles that different regions play in the brain.

Here we present new results based on the analysis of four human anatomical brain connectivity datasets, data on C. Elegans connectomes and numerical simulations, highlighting some warning and caveats in the use of brain controllability. In particular we show that there is no statistical evidence that brain networks are controllable from one single region and that biophysically irrelevant null models produce identical quantitative results as in prior work, highlighting the crucial role of proper experimental control and hypothesis-testing. We end with a discussion of how the brain controllability framework should be theoretically developed to fulfill the aim of modeling the effect of the external perturbation on brain functions.

2. Material and Methods

2.1. Controllability Framework

In a broader context, controllability defines whether or not a dynamical system can be controlled through one or more external inputs. In mathematical terms, consider a system composed by n entities (e.g., brain regions) each described at time t by a state variable x_i(t) (e.g., its activity). Assume that dynamics is described by the discrete time equation x(t + 1) = Ax(t), where x(t) = {x₁(t),x₂(t),…,x_n(t)} is the column vector collecting all the states, A is a matrix depending on the network anatomical connectivity and incorporating the effective interactions in the (linear) dynamics between the states. We will specify it for the case of brain networks in section 2.3.

Controllability is a property of dynamical system with inputs, namely of systems of the form

$$x\left(t+1\right)=Ax\left(t\right)+Bu\left(t\right),$$ (1)

where u(t) = {u₁(t),u₂(t),…,u_p(t)} is a column vector collecting the p external inputs and B is a n × p matrix, called input matrix, whose entry B_ij is one if the input u_j(t) affects the state x_i(t), otherwise it is zero. Systems of this form are said to be controllable if any desired final state x^f = x(t → ∞) is achievable through a suitable choice u(t) It can be proved that a system is controllable if the so-called n × np Kalman controllability matrix C = [B AB A²B … Aⁿ⁻¹B] has full rank (Chen, 1995; Kalman, 1963). There exists an equivalent condition for controllability. If all eigenvalues of A lie in the unit circle¹, namely the system Eq. (1) is stable, then it can be proved that the equation W − AWA′ = BB′² has a unique solution W that is $W={\sum }_{m=0}^{\infty }{A}^{m}B{B}^{\prime }{(A^{\prime })}^m$ that is called the discrete controllability Gramian. It has been shown that the system is controllable if and only if W is positive definite or equivalently if the minimum eigenvalue of W is strictly larger than zero (Chen, 1995).

In order to avoid confusion, we need to distinguish between “controllability” as originally defined by Kalman (Chen, 1995; Gu et al., 2015) and “structural controllability” (Dion et al., 2003; Lin, 1974; Shields and Pearson, 1976). Indeed, while controllability is a property depending on the system matrices A,B and hence also on the weights of the network, structural controllability depends only on the system (topological) structure or graph, which is given by fixing all nonzero entries of the systems matrices A and B. Therefore, the system structure can be defined by the binary matrices (i.e. graphs) $\overline{A}$ and $\overline{B}$ and a realization of the structure is any weighted matrix (i.e. network) pair A, B in which we allow the entries to be nonzero only where the entries of $\overline{A},\overline{B}$ are nonzero. A system structure is structurally controllable if there exists any realization A, B which yields a Kalman controllable system (Lin, 1974; Tu, 2015).

In many cases, the weights of the matrix A are not known, or they are known only approximately, or it is known only which weights are zero, i.e., only the graph associated with A is available from data. For this reason the notion of structural controllability has been promoted as the right tool in these cases since it depends only on the topological properties of the network (Lin, 1974; Shields and Pearson, 1976; Reinschke, 1988; Dion et al., 2003; Liu et al., 2011; Godsil, 2012). In particular, Liu et al. (Liu et al., 2011) developed analytical tools to assess the minimum number of driver nodes N_D able to structurally control the system. They mapped the problem into a matching problem (i.e., finding independent edge set in a direct graph (Liu et al., 2011)) showing that: (i) if there is a perfect matching in the network, then N_D is equal to one; (ii) otherwise, N_D coincides with the number of unmatched nodes with respect to any maximum matchings (see Liu et al., 2011 for more details).

Nevertheless, we think that, at the current stage, these results are of limited interest to understand the controllability of human brain anatomical networks for two main reasons. First, the networks derived from diffusion imaging techniques are symmetric, and thus the above theorems cannot be used. Second, even if a network is structurally controllable, it may happen that the energy of the input needed to control the system is so huge that the system is not controllable in practice.

In order to have a way to actually understand how controllable is our system, we can define the “energy” needed to control a network. Since there are many inputs u(t) driving the system from the initial state x₀ = 0 to the desired final state x_f, then one can try to find the input with minimum energy. It is known that this minimum energy depends on the controllability Gramian W and, in the worst case, coincides with the inverse of its minimum eigenvalue, i.e. ${ϵ}_{min}={\lambda }_{min}^{-1}\left(W\right)$. Notice that, if ϵ_min is very high, then the system is very difficult to control (Pasqualetti et al., 2014). In fact, the energy to control the entire network with one node increases exponentially with the number of nodes in the graph (Kim et al., 2017).

2.2. Controllability of the Brain Network

Gu and collaborators (Gu et al., 2015) focused their study on the Kalman controllability of the brain network. In particular, referring to a previous theoretical work (Pasqualetti et al., 2014), they considered the average controllability and the modal controllability of a network. The first is defined as the average input energy from a set of control nodes and over all possible target states (Marx et al., 2004; Shaker and Tahavori, 2013). From this definition, it follows (Pasqualetti et al., 2014) that it can be calculated as the trace of the inverse of the Gramian matrix, i.e. (W_k⁻¹), where W_k is the Gramian calculated from the node k. However, in practice and in our case of interest (brain networks), the Gramian may result very close to be singular (i.e., very ill-conditioned). Therefore, Gu and collaborators proposed to use the trace of the Gramian as a reliable measure of the network average controllability. In this way it is also natural to define the average controllability of the k-th node of the network by d_k = Tr(W_k). Finally, they assumed that regions with high average controllability are, on average, most influential in the control of network dynamics over all different target states. Note that, as defined by Eq. (1), controllability is a property of a system with respect to external inputs u. When assessing the control role of a given region (or node) we are always considering the effectiveness of the external input u_k applied on the brain region k, in coordinating other brain regions activity state. This is not the same as saying that the internal, spontaneous activity of region k (which crucially depends on its dynamics) can easily control other regions (in the absence of the external input u_k). In other words, one cannot embed a region as a state variable in a dynamical system, while also treating it as an external input. While there may be situations in which this is true, it is not true in general.

On the other hand, the modal controllability is calculated from the eigenvalues and eigenvectors of the matrix A, i.e., it is given by ${\varphi }_i={\sum }_{j=1}^n(1-{{\lambda }_j\left(A\right)}^2){\nu }_{ij}^2$ where v_ij is {i,j}-th entry of eigenvector matrix and (λ₁,⋯,λ_n) are the corresponding eigenvalues of A. The modal controllability is interpreted as the ability of a node to control the dynamics of the network toward “difficult to reach” states, i.e. states with high energy with respect to the other states. Nevertheless, we highlight that this is more an interpretation than a quantitative result, as the definition of modal controllability involves all the eigenvalues and eigenvectors of the linearized system dynamics given by the matrix A. We cannot offer an alternative interpretation of this quantity, as it is far from evident how it is related to the Gramian controllability matrix.

2.3. Whole Brain Modelling Framework

As explained above, in order to apply Control Theory to the brain network, we need to specify the equations describing the dynamics of the system activity. In our case the system is the brain, and thus we need a model that is able to capture, at least qualitatively, the neural activity of the brain regions during resting state. Following Gu et. al. (see Supplementary Material of their work, section 1), we employed a simplified linear discrete-time neural dynamics model. This model is a noise-free variation of the Galán model (Galán, 2008) and can be derived from the linearization of a general Wilson-Cowan system (for strengths and weakness of this model see (Galán, 2008; Honey et al., 2009; Muldoon et al., 2016)). We then discretized the linearized dynamics and obtained the explicit form of the linearized dynamics given by the matrix A:

$$A=\left(1-\alpha \mathrm{\Delta }t\right)I+cM\mathrm{\Delta }t$$ (2)

where α is the inverse of the relaxation time (i.e., the characteristic time needed to return to a quiescent state after a burst of activity), Δt is the time step that we use to update the brain state in time, I is the n × n identity matrix, M is the matrix describing the anatomical connectivity of the brain and c is a normalization constant. As we will explain in the following subsection, we characterized the anatomical connectivity matrix M in different ways, from computer-generated random networks, with no or little biological realism, to real brain networks based on diffusion tensor or diffusion spectrum imaging (DTI/DSI) data from different studies (Brown et al., 2012, 2011; Hagmann et al., 2008). We compared our results with those reported by Gu and collaborators who however did not use Eq. (2) in their controllability framework but directly derived the matrix A from DTI and diffusion spectrum imaging (DSI) data. Although we do not agree on this procedure that neglects the differences between the linearized system dynamics given by the matrix A and the brain connectivity structure given by the matrix M, we note that, for the case of the Wilson-Cowan modeling framework, in practice there is no relevant difference between the two approaches on the final results. However, some critical issues should be highlighted at this point:

1. Depending on the model, the relation between the linearized matrix A and the structural (i.e., anatomical) connectivity M will be different. From a methodological point of view, it is worth noting that Gu et al. did not derive the matrix A from any model, but they used directly the anatomical structural connectivity. If one uses the DTI (weighted) graph as the (linear) dynamical model A (as in Gu et al. work), then the analysis of the dynamical model reduces to the analysis of the graph, thus assessing dynamics features (and, consequently control properties) from strictly static data.

2. The networks A for the different datasets are always unstable. Adopting the Gu et al. approach implies the necessity to perform a normalization (i.e., A_norm = A/(1 + λ_max(A)), where λ_max(A) is the maximum absolute value of the eigenvalues of the matrix A) to ensure that the controllability metrics in question are well-defined. Therefore, the edge weights of the networks (i.e. the intrinsic linear dynamics of each brain region) are set on the basis of mathematical convenience, without a proper analysis on the limitations or biological meaning of this procedure.

3. The premise that the brain can be linearized about a dominant fixed point is a strong assumption. In fact, at local circuit levels it is generally accepted that neurons can embody quite different dynamical regimes (e.g., synchronization, oscillations, etc.) depending on the overall network state, which cannot be accounted for by linear generative models. Thus, any conclusions made through this framework only hold locally in what is likely a very limited region of the actual traversed state space of neural activity.

We finally note that Gu and collaborators did not perform any comparison with random null models. The use of a null model, as we will now show, is crucial to formally assess the specific role of the brain topology in determining the observed results, and it is a standard approach in network science (Grilli et al., 2017; Molloy and Reed, 1995; Newman, 2010).

2.4. Brain Networks: Data, Synthetic Random Networks and Random Null Models

Human Brain Data

We first applied the controllability framework to four empirical datasets of anatomical (DTI or DSI) brain networks. All datasets are open access and were obtained from the Human Connectome Project (“USC Multimodal Connectivity Database,” n.d.), i) the APOE-4 dataset (Brown et al., 2011) (N = 30 APOE-4 non-carrier and N = 25 APOE-4 carrier individuals; gray matter parcellation into n = 110 large scale regions); ii) the Rockland dataset (Brown et al., 2012) (N = 195 healthy subjects, n = 188 large scale regions); iii) the Hagmann dataset (Hagmann et al., 2008) (average matrix corresponding to N = 5 healthy subjects, n = 66 cortical regions) and iv) the Autism dataset (Brown et al., 2012) (N = 94 healthy subjects, n = 264 large scale regions). For more specific details on the data acquisition and preprocessing we refer to the original studies.

C. Elegans data

As previously noted, for directed graphs the minimum set of driver nodes making the system structural controllable can be computed. Therefore, we employed the framework of structural controllability (see section 2.1) to investigate the minimum number of driver nodes to control the directed connectome of C. Elegans. It is interesting to compare the results on the number of minimum control nodes using different methods (Kalman vs. structural) on different datasets (human vs. C. Elegans). We considered the neuronal connectivity of the N2U (a hermaphrodite adult) and the JSH (a L4 male) worms. Both data were taken from the Worm Atlas (WormAtlas, n.d). Network connectivity encompasses chemical synapses and gap junctions. Because the edge weights do not affect the analysis of structural controllability, we just considered the corresponding directed binary networks by assigning 1 if there existed a connection between neurons i and j, i.e. M_ij = 1, and zero otherwise. Following the methodology proposed by Liu et al., 2011, we applied the analysis directly on the C. Elegans connectome M. The N2U network included a giant connected component composed by 190 neurons and 2815 edges as well as 12 isolated nodes; while L4 network contained a single giant connected component composed by 202 neurons and 3007 edges.

Synthetic Random Networks

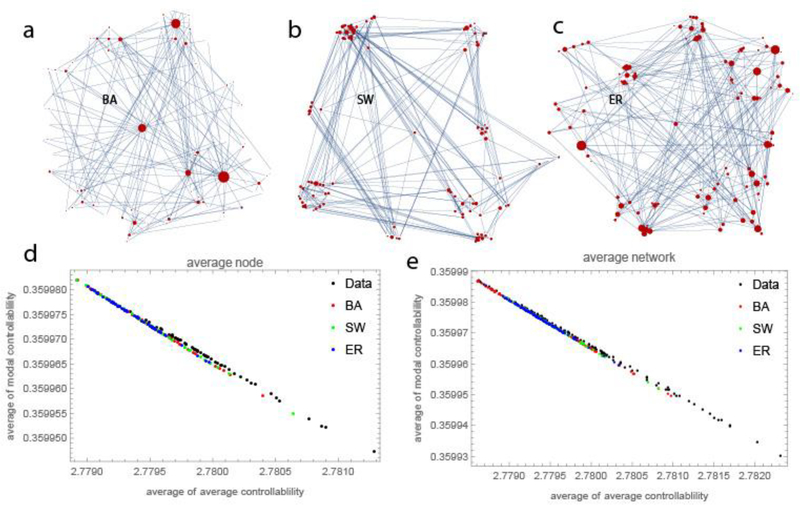
We generated three types of synthetic brain anatomical random networks, namely, the Barabasi-Albert (BA) scale-free, Small-World (SW) and Erdős–Rényi (ER) networks (Newman, 2010). We used the same node number, connectivity and edge weight distribution of the averaged DTI matrix of the APOE-4 brain dataset. The synthetic random networks were generated using standard routines available in the Mathematica software. We applied the controllability framework to synthetic random networks to assess the number of the minimum subset of control nodes (Table 1) for a fixed amount of energy, and the controllability profile of the average and modal controllability (Figure 1).

Table 1:

The minimum number of nodes (and fraction with respect the size of the network) that are needed to control the system spending a minimum energy not greater than ϵ_min = 10¹⁰. We here show results for the APOE-4 data and the corresponding Barabasi-Albert network (BA), Small-World network (SW) and Erdős–Rényi network (ER) (of same size, connectivity and edge weight distribution) following the procedure described in the main text. For a given sequence, “High” is the rank from the largest to the smallest, while “Low” is the rank from the smallest to the largest.

	Data		BA		SW		ER
Centrality measure	Low	High	Low	High	Low	High	Low	High
Degree centrality	51/0.46	49/0.45	44.64/0.41	42/0.38	45/0.41	43.5/0.40	44.64/0.41	42/0.38
Betweenness centrality	52/0.47	46/0.42	45/0.41	42.52/0.38	46/0.42	42.5/0.39	45/0.41	42.52/0.39
Eigenvector centrality	50/0.45	51/0.46	45.76/0.42	42.16/0.38	46/0.42	44/0.4	45.76/0.42	42.16/0.38
Page-rank centrality	51/0.46	47/0.42	44.84/0.41	42.36/0.39	47.5/0.43	43/0.39	44.84/0.41	42.36/0.39
Random sequence	46/0.41	47/0.42	44.08/0.40	43.48/0.40	45.5/0.41	43.81/0.40	44.08/0.40	43.48/0.40

Figure 1:

This figure shows that empirical data and different network models have inherently similar controllability profiles. Panels a, b and c show an example of the different synthetic random networks used in this study: Barabasi-Albert network (BA); Small-World network (SW) and Erdős–Rényi network (ER). The number of nodes and edges in these networks are approximately the same of those in the brain networks of APOE-4 dataset. Similarly, the weights are drawn from the empirical distribution estimated from the dataset. Panels d, e show that brain networks cannot be uniquely distinguished in this 2-dimensional controllability space (modal vs. average controllability), although their structure differs from classic random network models. For each type of network model, the number of the generated realization is the same as the instances (number of individuals) of the corresponding empirical brain networks in the dataset. In panel d, we report the average values computed over all networks and each point represents a node. In panel e, we report the average values computed over all nodes and each point represents a network.

Random Null Models

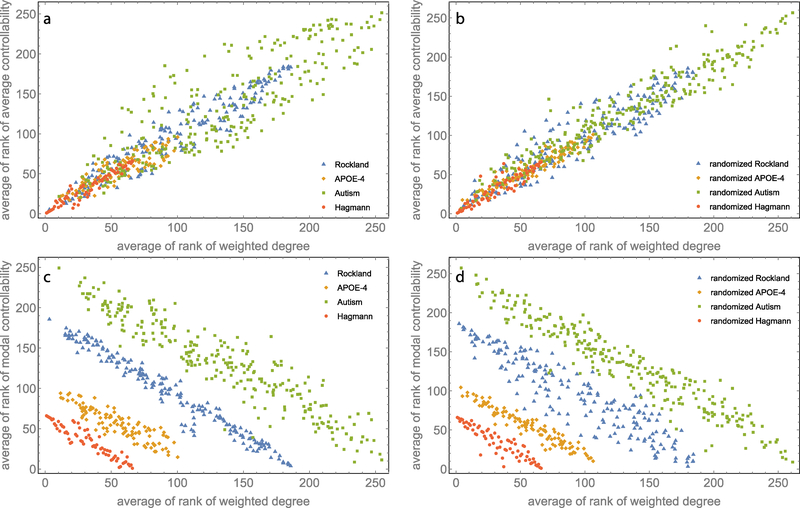
We also generated random null models of the brain network data by randomizing the network structure of the DTI matrices M with the exception of some topological properties (Newman, 2010). In this way one can understand which and how much the specific properties of network explain the observed results. This approach is widespread in the study of ecological and biological networks (Maslov and Sneppen, 2002; Suweis et al., 2013). If some properties of the complex system are observed (for example stability to perturbations), is there something characteristic in the way species interact that lead to the observed phenomena? To answer this question, we need to compare the results observed for real data, with those generated by networks that have, for example, the same size and connectivity, but different high order network structure (e.g., degree distribution, cluster coefficient, etc.). We designed two different random null models to understand the specific role of the brain network topology on the results of controllability analyses. In the first one we randomly rewired all links of a real brain network, keeping only the symmetry and the diagonal entries of the original matrix. The resulting null model has the same number of nodes, connectivity, diagonal, and edge weight list of the original data, but all the other properties are free to vary over permutations. We applied the controllability framework to random rewired networks in order to investigate the relations between weighted degrees and average/modal controllability (Figure 2). In the second null model, beyond the constraint of null model 1, we also kept the in-degree and out-degree of each node. This is also called configuration model/network and it conserves also the average degree sequences of the original networks (Maslov and Sneppen, 2002; Molloy and Reed, 1995; Suweis et al., 2015). Other high order topological properties (clustering coefficient, motifs, etc.) are instead different. We use the configuration network to assess the role of the topological properties of the resting state networks (RSNs) in the modes of controllability (Figure 3).

Figure 2:

Comparing controllability measures between empirical data and randomized data. Scatter plot of the average of the ranks for weighted degrees versus average of the ranks of the average controllability for (a) the empirical data and (b) their randomized counterpart. Scatter plot of the average of ranks for weighted degrees versus the average of ranks of the modal controllability for (c) empirical data and (d) their randomized counterpart.

Figure 3:

Comparison between real brain networks (Hagmann dataset) and the corresponding configuration null model (see Section 2.4 for details) in terms of how average controllability would assign control roles to different resting state networks (RSNs). The similarity suggests that the control role of the RSNs mainly depends on their overall degree centrality rather than other higher degree topological properties.

2.5. Centrality measures

We investigated in both real and synthetic random networks the role of node centrality with respect to its impact on average network controllability (see Result section). In network science, centrality addresses the question of which are the most important nodes in a network, from different perspectives. Degree centrality considers that node’s importance as depending on the number of connections to other nodes and it refers to the number of links for a given node to other nodes (Newman, 2010). Betweenness centrality considers that node’s importance as depenings on the number of the shortest paths that pass through the node v and is given by ${\sum }_{s\ne v\ne t}{n}_{st}\left(v\right)/n_{st}$ where n_st is the total number of shortest paths from node s to node t and n_st(v) is the number of those paths that pass through the node (Newman, 2010). Eigenvector centrality considers that node’s importance as depending on the connections to other nodes that are themselves important and it is given by the vector c which solves the equation $c=\frac{1}{\lambda }{A}^{T}c$, where A is the adjacency matrix and λ is the corresponding largest eigenvalue (Newman, 2010). Page-rank centrality considers that node’s importance as depending on the number and quality of edges to a node and it given by the vector x which solves the equation x = αAD⁻¹x + β1, where 1 is the vector (1, 1, 1, …), D is the diagonal matrix with elements ${\mathrm{D}}_{ii}=\max (k_i^{out},1)$ and $k_i^{out}$ is the out-degree of node i (Newman, 2010). For random networks, all these centralities measures are correlated one to another.

3. Results

3.1. Brain controllability with finite energy and role of node centralities

We first applied the controllability framework to the four empirical open access datasets of large-scale anatomical brain connectivity. Following the original work of Galán (Galán, 2008), we fixed α = 1.0,Δt = 0.2. The input matrix B_K identifies the set of control points K in the brain, where K = {k₁,⋯,k_p} and $B_K=\left[e_{k_1},···,e_{k_p}\right]$, where e_i denotes the i-th canonical vector of dimension n. We found that, when K contains only one node/region, all the minimum eigenvalues of the controllability Gramian associated with the brain networks we analyzed were negative: ${\lambda }_{min}\left(W_K\right)=-2.137\cdot {10}^{-14}\pm 4.821\cdot {10}^{-14}$ (Rockland dataset), ${\lambda }_{min}\left(W_K\right)=-8.555\cdot {10}^{-17}\pm 2.298\cdot {10}^{-17}$ (APOE-4), ${\lambda }_{min}\left(W_K\right)=-7.68\cdot {10}^{-16}\pm 2.990\cdot {10}^{-15}$ (Autism dataset) and ${\lambda }_{min}\left(W_K\right)=-7.650\cdot {10}^{-17}\pm 3.352\cdot {10}^{-17}$ (Hagmann dataset). Nevertheless, all the λ_min(W_K) are statistically compatible with zero and thus the associated controllability Gramian cannot be inverted. These results show that it is not possible to infer one node controllability of the brain numerically.

Next, we studied the role of nodes’ topological properties in controlling the brain network, but in a more practical way by fixing an upper bound on the minimum level of energy allowed to control the system. We arbitrarily set this threshold to ϵ_min = 10¹⁰ and we then search for the minimum number of nodes that are needed to control the system spending a minimum energy not greater than ϵ_min. If we remove the upper bound (ϵ_min → ∞), we find that we cannot assess the theoretical controllability of the brain, i.e., a threshold is necessary if we want to numerically study the brain controllability in a meaningful way. The results presented in Table 1 have been obtained using the averaged DTI matrix for each group of individuals (M_av). In the Hagmann dataset, the average fraction of nodes to control the system with energy not greater than ϵ_min is 0.3. For the other two datasets, the precise computation of the minimum fraction of nodes to control the system with ϵ ≤ ϵ_min becomes computationally unfeasible (too large network sizes).

Following Gu and collaborators’ claim on the importance of nodes centrality (Gu et al., 2015), we first ranked all networks nodes according to five distinct centrality measures (see Methods section) following both the ascending and descending order. Then we generated a list of nodes in random order, irrespective of the nodes properties. For each of these two nodes sequences (“low” and “high”), we determined the minimum subset of nodes needed to control the brain network with an energy ϵ_min = λ⁻¹(W_K). We have repeated this analysis for the APOE-4 datasets as well as for synthetic brain networks generated with a desired network topology. Table 1 presents the results for the number of the minimum subset of control nodes with respect to the five different centralities measures for the APOE-4 data (Brown et al., 2011) (n = 110 nodes), synthetic random Barabasi-Albert network (BA), Small-World network (SW) and Erdős–Rényi network (ER) (Newman, 2010). All synthetic random networks have the same node number, connectivity and edge weight distribution of the APOE-4 dataset to allow a proper comparison.

No matter which centrality measure is adopted and how we generated the node sequences, the size of the minimum subset was similar in all cases (and as expected larger than one). This result suggests that the topological characteristic of the single brain region may play a specific role in the one node theoretical controllability (Kim et al., 2017), but in practice when fixing the energy all regions (nodes) seem to play an equivalent role in the average and modal controllability of the network. We highlight that this is not true in general for any networks, but in the case of not-so-sparse and undirected symmetric matrices, as in the case of human brain DTI/DSI networks. Pruning or introducing a direction in the network edges will have thus a remarkable impact on the role of topology and hence on the network controllability (Kim et al., 2017), as we will also show with the analysis of the C. Elegans connectome.

3.2. Relation between nodes weighted degree and the corresponding average/modal controllability

The next step was to investigate whether the linear relationship between weighted degrees and the average/modal controllability observed for human brain networks (see Figure 2 in Gu et al., 2015) is due to the specific brain network topology, or if it also holds for random networks.

First, we examined the relationship between average controllability and modal controllability of each node in synthetic random networks of different types (see section 2.4 and Figure 1 a-c) and compared it with results for the APOE-4 dataset. Not surprisingly, we found that for APOE-4 data, average and modal controllability are linearly and negatively correlated. Indeed, this is expected if both controllability measures correlate with the network weighted degree. Nevertheless, the same linear relationship also holds for all the synthetic random networks (see Figure 1 d). However, the range in controllability covered by the brain network data seems to be somehow larger with respect to the corresponding random synthetic networks. At the same time, the range in values of both average and modal controllability is extremely limited, a feature not evident in the work of Gu et al. (Gu et al., 2015) as they showed only rank-rank plots.

Second, following the procedure adopted by Gu et. al. (Gu et al., 2015) (Fig. 2 b and d in their main text), we computed the average of the rank plots between one node average/modal controllability and weighted degree of our four brain dataset (see Figure 2; for details on average rank plots see Gu et al.’s methods section). As Fig. 2a and 2c show, for all the analyzed real data we found the same relation between controllability and network centrality reported by Gu et al. We then randomized the anatomical connectivity data and calculated average/modal controllability as a function of nodes’ properties in the random networks. Surprisingly, as shown in Fig. 2b and 2d, we still found exactly the same relationship as before. We stress that the relationships in average controllability and modal controllability between real and randomized networks are not an artifact of the rank-rank plots. In fact, controllability measures between real and randomized networks are not distinguishable also by examining unranked magnitudes (although the values ranges are very limited, similarly to what shown in Figure 1).

Indeed, as also shown by Gu et al., the relation between average node controllability and node centrality can be inferred analytically in the limit of “small” values of the entries of A (i.e., a_ij ≪ 1, that is always satisfied for the normalization condition). This was noted in the Supplementary Information of Gu et al. (p.5), where they show that the d_j – average controllability of the node j – is simply the j-th diagonal element of the matrix ${(\mathbb{I}-{\mathrm{A}}^2)}^{-1}\approx \mathbb{I}+{\mathrm{A}}^2$, where $\mathbb{I}$ is the identity matrix, resulting in ${\mathrm{d}}_{\mathrm{j}}=1+{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{a}}_{\mathrm{i}\mathrm{j}}^2$, while the degree centrality is ${\mathrm{k}}_{\mathrm{j}}={\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{a}}_{\mathrm{i}\mathrm{j}},$ thus proving that “a positive correlation between node degree and average controllability is mathematically expected”. But this is true for any network satisfying a_ij ≪ 1, also the random ones.

We performed a linear fit y=mx +q for both data and random networks and we found that the angular coefficients (m) describing the relation shown in our Figure 2 between node controllability and degree centrality are compatible within 3 standard deviations in all dateset (see Table 2). In other words, there is no significant difference between the observed linear relations in the data and in the corresponding randomized dataset.

Table 2.

For each element of the table, we show the results of the linear fit describing the relation between node controllability and degree. Upper row: empirical brain data; lower row: the corresponding randomized networks. Each cell includes an angular coefficient, its standard error and the goodness of fit (R²).

	Rockland	APOE-4	Autism	Hagmann
Average controllability	m=0.93 ±0.021 R2=0.91 m=0.90±0.024 R2=0.88	m=0.76±0.038 R2=0.79 m=0.83±0.023 R2=0.92	m=0.88±0.031 R2=0.75 m=0.86±0.016 R2=0.92	m=0.96±0.036 R2=0.92 m=0.92±0.05 R2=0.84
Modal controllability	m=−0.97±0.014 R2=0.96 m=−0.88±0.028 R2=0.84	m=−0.76±0.038 R2=0.79 m=−0.83±0.023 R2=0.92	m=−0.84±0.019 R2=0.88 m=−0.84±0.016 R2=0.91	m=−0.94±0.043 R2=0.88 m=−0.91±0.053 R2=0.82

3.3. Role of the topological properties of the RSNs in the modes of controllability

Finally, we tested if different RSNs can be characterized in terms of different modes of controllability. RSNs were defined for the Hagmann dataset according to published RSNs templates (Sizemore et al., 2016). Following Gu et al.’s procedure, we considered the twenty nodes with highest average controllability, and then calculated a vector c_data, where its j-th component gives the percentage of the nodes that belongs to the j-th RSN. We highlight that the method proposed by Gu and collaborators to construct the vector c depends on how one defines the controllability hubs. In fact, the choice to consider hubs the twenty nodes (thirty in their case) with the highest average controllability are arbitrary. The problem is that the results of relation between RSNs networks and their controllability roles are dependent on this choice. We tested different rankings of highest average node’s controllability, and we obtained different results. This is a caveat that must be taken in account when drawing conclusions from these results. The data used here, and the corresponding RSN templates, are based on 66 regions and thus we have considered a different number of nodes with highest average controllability with respect to Gu et al. (who used a parcellation with 234 regions).

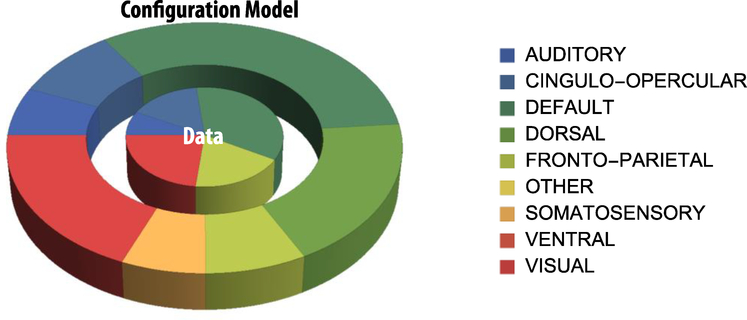
We repeated the Gu et al. analysis using the configuration null model (section 2.4), obtaining c_rand from random networks that retained the degree distribution of the original dataset, but had lost all other higher degree topological properties. We found that both real and randomized networks displayed very similar results on the modes of controllability of the different RSNs (see Table 3 and Figure 3), as also attested by a significant Pearson correlation ρ = 0.762. In other words, we found that RSNs cannot be attributed to specific control roles based on the present controllability framework.

Table 3.

Each element of the table includes the node number, and the normalized percentage in a given cognitive system. Additionally, the correlation between the real data and the averaged randomized network (keeping fixed the degree sequences) is r=0.762. In this analysis we have considered the first 20 nodes with the highest average controllability as this number maximizes the correlation between the results of the configuration model with respect to the corresponding Hagmann dataset.

	AUDITORY	CINGULO-OPERCULAR	DEFAULT	DORSAL	FRONTO-PARIETAL	OTHER	SOMATOSENSORY	VENTRAL	VISUAL
DATA	1/0.078	4/0.155	6/0.349	0/0	4/0.186	0/0	0/0	0/0	5/0.233
RANDOM	1/0.064	3/0.096	7/0.338	1/ 0.193	2/0.077	1/0.039	0/0	0/0	5/0.193

3.4. Controllability of the C. Elegans Connectome

We finally investigated the controllability of the anatomical brain networks of C. Elegans data recently presented in Yan et al., 2017. In that case, the authors aimed at understanding the neural path involved in the control of a given activations or tasks, using target control analysis (Gao et al. 2014).

Using the same data, we can also properly calculate the minimum number of nodes N_D to control the brain of C. Elegans (see Section 2.4) using rigorous analytical results based on maximum matching (see Section 2.1 and Liu et al., 2011). For the two individuals analyzed in this work we found that N_D is around 20 nodes (N_D = 18 and N_D = 21 to control the N2U and L4 individuals, respectively). Therefore, even for simple organisms like the C. Elegans we found that N_D is much greater than 1. Unfortunately, the current structural controllability framework does not allow one to infer the associated energy needed to control the system using the N_D driver nodes.

4. Discussion and Conclusions

The idea to apply network controllability to brain resting state activity is a remarkable contribution to neuroscience, opening up many fascinating avenues. The seminal work of Gu and collaborators (Gu et al., 2015) has been an inspiration for many subsequent studies in the attempt to better understand and master brain network controllability. But in science, progress goes in hand with understanding limits and inaccuracies of previous theories. Our work aims to help the progress in understanding how network control theory can be applied in neuroscience by highlighting some warnings and caveats in the current theoretical framework.

In order to study single node controllability (in Kalman sense), Gu and collaborators (Gu et al., 2015) calculated the controllability Gramian from each node of a network derived from average anatomical connectivity (DTI/DSI) data (as we have done in section 2.1). Their first finding was that the brain network can be theoretically controllable by a single region/node, i.e., the smallest (in absolute value) of the eigenvalues of the controllability Gramian λ_min(W_K) from each brain region taken as a control node was greater than zero. However, in agreement with our results, they found that the energy needed to control the system is so large (i.e., ${ϵ}_{min}={\lambda }_{min}^{-1}\left(W_K\right)={10}^{-23}$) that in practice the system is not controllable. Indeed, as the same authors recognized in a subsequent paper (Menara et al., 2017), in order to assess the controllability of the brain network from one region in a proper way, it is not necessary to compute λ_min(W_K) (which may also be not statistically different from zero, as in our cases and in Gu et al. (Gu et al., 2015)), but one has to prove that existence of a Hamiltonian path from each control region. That is, one has to prove that the brain network is Hamiltonian-connected (Menara et al., 2017). This is a NP hard problem (Alspach, 2012), so it may not be trivial to infer that the brain network is controllable from one single region.

A second important result of Gu et al. (Gu et al., 2015) is that average controllability was strongly correlated with the weighted degree, whereas modal controllability was strongly anti-correlated with the weighted degree. From these results they concluded that single brain regions have different control roles due to their different centrality in the brain network, suggesting a relation between the specific brain network topological structure and the control role of the different brain regions.

Finally, Gu et al. also evaluated the control contribution of different brain sub-networks associated with known cognitive process (i.e., resting state networks (RSNs)), and found that different RSNs have different control roles. In particular they suggested that 30% of average control hubs laid in the default mode system, while 32% of modal control hubs laid in the front-parietal cingulo-opercular cognitive control systems, supporting the hypothesis that the average and modal controllability deal with different control role. However, the present study shows that the same results hold for random computer-generated networks without biological realism. Indeed, we also found that the relationships between average/modal controllability and weighted degree also hold for randomized data, which implies that this method cannot be used to attribute specific control roles to different RSNs. In other words, the results of the controllability analysis do not reveal a specific or optimized network organization in the brain, but are simply a consequence on the definition of average and modal controllability, which in their definitions encapsulate also a correlation with the node degree (positive and negative, respectively). The positive correlation between average controllability and weighted degree can be explained analytically.

Though theoretically intriguing, our understanding of the relationship between controllability and anatomical brain network remains elusive. In particular, using high precision data on C. Elegans connectomes (Yan et al., 2017), we have shown that even small connectomes cannot be controlled from a single node. This is highly probably true for the human brain, although current numerical analysis cannot confirm this result. Indeed, directionality of the anatomical brain connectivity is an important information to perform rigorous analysis for structural controllability. Nevertheless, as we have shown in this work, developing reliable methods for estimating directed resting state effective connectivity (Gilson et al., 2016; Jobst et al., 2017; Saggio et al., 2016), which yields to accurate directed graphs is only but one aspect of the resolution of the underlying model formulation problem. Moving to a controllability framework beyond linear models, where the dynamical complexity is effectively captured, is also a fundamental gap in the current literature. Another future step of crucial importance is to move from one node to multiple nodes controllability analysis of the brain network. Indeed, as we have shown, results obtained with one-node controllability Gramian have no or very limited practical (e.g., clinical) applicability. In fact, many experimental results suggest that Network-Based Statistic (NBS) techniques are unlikely to change brain states from one node. It is hard to modify fMRI connectivity using Transcranial Magnetic Stimulation (TMS), as long as only a single region is stimulated (Capotosto et al., 2014; Fox et al., 2014). On the other hand, concurrent stimulation of several locations on the scalp may be feasible in the near future (possibly synchronized with electrical activity in a given frequency band) (Baker et al., 2017; Vosskuhl et al., 2016) and developing a theoretical framework to understand the multi-node controllability of brain network is an primary and timely objective for future studies.

Controllability is not a monolithic concept, nor is the notion of a brain network (which can be defined at multiple spatial and temporal scales). Attempting to understand the controllability of the brain in some all-encompassing sense is ill-defined. In this work we have highlighted many critical issues that must be tackled in its specificity if we want to move from a purely theoretical approach to experimental applications to real brains. We believe that the potential of theoretical tools based on control theory are of inestimable value for neuroscience and that further development of this framework might bridge the gap between theoretical brain controllability and possible application in translational neuroscience.